α-Synchronization of a Class of Unbounded Delayed Inertial Cohen–Grossberg Neural Networks with Delayed Impulses

Abstract

As an essential dynamic behavior, the synchronization of inertial Cohen–Grossberg neural networks (ICGNNs) has received considerable attention due to its successful applications in neural cryptography, public channel cryptography, security communications, and image encryption. In this article, the $\alpha$-synchronization of a class of non-autonomous unbounded delayed inertial Cohen–Gossberg neural networks with delayed impulses is investigated. Firstly, several non-autonomous impulsive differential inequalities are established, where unbounded delays, delayed impulses, and time-variable coefficients are incorporated. Subsequently, based on the proposed impulsive differential inequalities and Lyapunov function approach, the feedback controllers are designed, and some criteria for $\alpha$-synchronization are provided. Finally, the validity of the presented theoretical findings is demonstrated by two specific examples. It is shown that delayed impulses can be viewed as perturbations or stabilizing sources for non-autonomous ICGNNs.

1. Introduction

Cohen–Grossberg neural networks (CGNNs) were initially proposed by Cohen and Grossberg in 1983 [1] and could be viewed as one generalization of cellular neural networks (NNs), Hopfield NNs, bidirectional associative memory NNs, and other NNs. Consequently, the mathematical model of CGNNs is challenging, since they are more general and complex. Meanwhile, CGNNs have important application potential in different fields, including signal processing, pattern recognition, tasks of classification, associative memory, and combinatorial optimization [2,3,4]. Due to the existence of interesting phenomena in their dynamical behaviors, many scholars have made significant efforts in the stability analysis of CGNNs, and a series of achievements [2,3,4,5,6] have been reported. On the other hand, when the inertia term is introduced to NNs, some more complex properties have appeared, including instability, quasi-periodic motion, spontaneous oscillation, and chaotic response [7,8]. Recently, the asymptotic characteristics of inertial NNs (INNs) have also been researched extensively [9,10,11,12,13,14].

In many real scenarios, the occurrence of time delays is unavoidable, which may deteriorate system performance and lead to instability. Generally, time delays comprise bounded time delays and unbounded delays. Recently, a great deal of work on the stability analysis and control issues of NNs with various delays has been carried out. Particularly, for inertial CGNNs (ICGNNs) with bounded delays, exponential stability [15,16] has been investigated using the homeomorphism theorem and inequality technique. Furthermore, the issue of the global exponential stabilization [17] of ICGNNs has been handled in light of the non-reduced-order approach via feedback and adaptive control schemes. For ICGNNs with proportional delays, as one kind of special unbounded delay, fixed-time stabilization [18] and asymptotic stabilization [19] have been discussed based on fixed-time stability theory and a direct analysis strategy, respectively. For general unbounded delayed NNs (UDNNs), many approaches have been developed. For instance, in [20], the concept of global $\mu$-stability was proposed, and several mild conditions for the stability of UDNNs were presented. In [21], global robust $\mu$-stability in the mean square of uncertain stochastic UDNNs was examined using the LMI technique and stochastic theory. In [22], the master–slave asymptotic synchronization of UDNNs was investigated based on adaptive control strategies. Meanwhile, $\mu$-stability and multiple $\psi$—stability were further generalized to complex-valued UDNNs [23], fractional-order UDNNs [24], and positive UDNNs [25]. For stochastic delayed nonlinear systems, stabilization was discussed using event-triggered feedback control in [26]. Furthermore, the stability of switching stochastic nonlinar systems with state-dependent delay has been analyzed by employing multiple Lyapunov–Krasovskii functionals and stochastic analysis techniques [27].

In addition, impulses can characterize some cases in which system states undergo abrupt changes at certain moments, and delayed impulses also have an important impact on the dynamic properties. Usually, delayed impulses can be categorized into time-varying delayed impulses (TDIs) and distributed delayed impulses (DDIs). In [28], combining impulsive control theory and the ADT method, the stability of nonlinear impulsive systems with TDIs was analyzed, and the proposed results were also applied to cellular NNs. In [29], by the vector Lyapunov function method and stochastic theory, input-to-state stability was discussed. In [30], by utilizing average-delay impulsive control, the synchronization of chaotic NNs with TDIs was explored. Furthermore, with the help of the Halanay-like delayed differential inequality [31] and Razumikhin method [32], the stability and synchronization issues of nonlinear systems with DDIs were tackled. Meanwhile, in [33], the Ulam stability of one solution to fractional a differential equation with a non-instantaneous integral impulse was considered.

Synchronization, as a significant collective dynamic behavior, has greatly attracted scholars’ attention because of its potential applications in various fields involving chemical reactions, secure communications, circuit systems, ecology systems, and NNs. Currently, many results concerning the synchronization of inertial CGNNs (ICGNNs) have emerged. For instance, in [34], by designing appropriate feedback controllers, the issue of the exponential synchronization of IGGNNs was studied. In [35,36], based on adaptive feedback control, several criteria for the asymptotic synchronization of ICGNNs with time delays were acquired. Furthermore, in virtue of finite-time and fixed-time stability theories, the finite-time and fixed-time synchronization [37,38] of ICGNNs with time delays has been examined. It can be observed that all the abovementioned findings [34,35,36,37,38] only concern bounded delays, and unbounded delays (UDs) and impulsive effects (IEs) are ignored for ICGNNs. On the other hand, in [39,40], the $\mu$-stability of non-autonomous systems with UDs and IEs was analyzed, but the impulsive part did not contain time delays. In [41,42,43,44], the $\mu$-synchronization of network systems with UDs and delayed impulses was discussed, and the coefficients were constant rather than time-varying. Actually, the impulses in the results [39,40,41,42,43] can be viewed as perturbances, while the relevant findings regarding stabilizing impulses for non-autonomous systems were not addressed.

Inspired by the aforementioned discussions, this article aims to investigate the $\alpha$-synchronization of a class of unbounded delayed ICGNNs with delayed impulses (DIs). The innovation points are summarized below: (1) Compared with the findings in [39,40,41,42,43,44], some novel impulsive delay differential inequalities are established, which include time-varying coefficients, unbounded delays, and delayed impulses simultaneously. In particular, Lemma 1 reveals that the impulses can be viewed as external perturbances, while Lemma 2 indicates that the impulses can be regarded as one significant stabilizing factor. (2) Since unbounded delays and delayed impulses are introduced to the ICGNNs, the considered model becomes more complex. Meanwhile, by utilizing the constructed impulsive delay differential inequalities, feedback controllers are designed and some criteria for the $\alpha$-synchronization of ICGNNs with UDs and DIs are derived. (3) By choosing various $\alpha$-type functions, the concept of $\alpha$-synchronization is explained. Furthermore, different types of synchronization, such as exponential synchronization and power synchronization, can be discussed based on various unbounded delays.

The framework of the article is arranged as follows. In Section 2, preliminaries and model formulations are described. In Section 3, some vital impulsive delay differential inequalities are established. Moreover, by utilizing inequalities, two criteria for the $\alpha$-synchronization of ICGNNs with UDs and DIs are put forward. In Section 4, two examples and numerical simulations are demonstrated to illustrate the validity of the findings presented in this paper. Finally, the concluding remarks and directions for future work are presented.

Notation 1. 

Let $\mathbb{R}$, ${\mathbb{R}}^{+}$, and ${\mathbb{R}}^n$ denote the sets of real numbers, non-negative real numbers, and $n$—dimensional Euclidean spaces, respectively. ${∥z∥}_q={\left({\sum }_{i=1}^n{\left|z_i\right|}^q\right)}^{\frac{1}{q}},q\ge 1$ denotes the $q$—norm of vector z. For any subset $\mathbb{L}\subseteq \mathbb{R}$, any vector subspace $\mathbb{F}\subseteq {\mathbb{R}}^n$, $C(\mathbb{L},\mathbb{F})$ = $\{z:\mathbb{L}\to \mathbb{F}\subseteq \mathbb{R}\}$ denotes the set where every function is continuous. $PC(\mathbb{L},\mathbb{F})$ = $\{z:\mathbb{L}\to \mathbb{F}\subseteq \mathbb{R}\}$ represents the set where every function is continuous everywhere except at certain moments, and $z\left(t^{+}\right)$ and $z\left(t^{-}\right)$ exist. $D^{+}V={\displaystyle \underset{\epsilon \to 0}{lim\; sup}}\frac{V(t+\epsilon )-V\left(t\right)}{\epsilon }$ stands for the upper right Dini derivative.

2. Preliminaries

In this paper, the ICGNNs with UDs are considered as follows:

$$\begin{array}{cc}\hfill \frac{d^2{\mathcal{X}}_i\left(t\right)}{d{t}^2}=& -{\lambda }_i\left(t\right)\frac{d{\mathcal{X}}_i\left(t\right)}{dt}-{\beta }_i\left({\mathcal{X}}_i\left(t\right)\right)[h_i\left({\mathcal{X}}_i\left(t\right)\right)-{\displaystyle \sum _{j=1}^n}{d}_{ij}\left(t\right){\mathfrak{f}}_j\left({\mathcal{X}}_j\left(t\right)\right)\hfill \\ \hfill & -{\displaystyle \sum _{j=1}^n}{b}_{ij}\left(t\right){\mathfrak{g}}_j\left({\mathcal{X}}_j\left(t-\delta \left(t\right)\right)\right)]+I_i\left(t\right),\hfill \end{array}$$

(1)

for $i=1,2,\cdots ,n$, where $\frac{d^2{\mathcal{X}}_i\left(t\right)}{d{t}^2}$ is called an inertial term of system (1); ${\mathcal{X}}_i\left(t\right)$ represents the state variable of the i-th neuron, ${\lambda }_i\left(t\right)\in C({\mathbb{R}}_{+},\mathbb{R})$; $d_{ij}\left(t\right)\in C({\mathbb{R}}_{+},\mathbb{R})$; $b_{ij}\left(t\right)\in C({\mathbb{R}}_{+},\mathbb{R})$; ${\beta }_i(.)$ denotes an amplification function; $h_i(.)$ expresses the behaved function; ${\mathfrak{f}}_j(.)$ and ${\mathfrak{g}}_j(.)$ are the activation functions of the j-th neuron; $\delta \left(t\right)$ is the time delay; and $I_i\left(t\right)$ are the external inputs. The initial values are ${\mathcal{X}}_i\left(s\right)={\phi }_i\left(s\right),\frac{d{\mathcal{X}}_i\left(s\right)}{ds}={\psi }_i\left(s\right),s\in (-\infty ,t_0]$, in which ${\psi }_i\left(s\right)$ and ${\phi }_i\left(s\right)$ are bounded continuous functions.

Let ${\zeta }_i$ denote one chosen positive constant scalar. By adopting the variable transformation

$${\mathcal{Y}}_i\left(t\right)=\frac{d{\mathcal{X}}_i\left(t\right)}{dt}+{\zeta }_i{\mathcal{X}}_i\left(t\right),i=1,2,\cdots ,n,$$

(2)

system (1) is rewritten in the following form:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\frac{d{\mathcal{X}}_i\left(t\right)}{dt}=-{\zeta }_i{\mathcal{X}}_i\left(t\right)+{\mathcal{Y}}_i\left(t\right),\hfill \\ \frac{d{\mathcal{Y}}_i\left(t\right)}{dt}=L_i\left(t\right){\mathcal{X}}_i\left(t\right)-P_i\left(t\right){\mathcal{Y}}_i\left(t\right)-{\beta }_i\left({\mathcal{X}}_i\left(t\right)\right)[h_i\left({\mathcal{X}}_i\left(t\right)\right)-{\displaystyle {\sum }_{j=1}^n}{d}_{ij}\left(t\right){\mathfrak{f}}_j\left({\mathcal{X}}_j\left(t\right)\right)\hfill \\ -{\displaystyle {\sum }_{j=1}^n}{b}_{ij}\left(t\right){\mathfrak{g}}_j\left({\mathcal{X}}_j\left(t-\delta \left(t\right)\right)\right)]+I_i\left(t\right),\hfill \end{array}\right.\end{array}$$

(3)

where $L_i\left(t\right)={\zeta }_i({\lambda }_i\left(t\right)-{\zeta }_i)$, $P_i\left(t\right)={\lambda }_i\left(t\right)-{\zeta }_i$, and the initial conditions of system (1) can be denoted by ${\mathcal{X}}_i\left(s\right)={\phi }_i\left(s\right),\frac{d{\mathcal{X}}_i\left(s\right)}{ds}={\psi }_i\left(s\right),{\mathcal{Y}}_i\left(s\right)={\psi }_i\left(s\right)+{\zeta }_i{\phi }_i\left(s\right),s\in (-\infty ,t_0]$. Taking into account the impulsive effects, system (3) takes the following form:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\frac{d{\mathcal{X}}_i\left(t\right)}{dt}=-{\zeta }_i{\mathcal{X}}_i\left(t\right)+{\mathcal{Y}}_i\left(t\right),\hfill \\ \frac{d{\mathcal{Y}}_i\left(t\right)}{dt}=L_i\left(t\right){\mathcal{X}}_i\left(t\right)-P_i\left(t\right){\mathcal{Y}}_i\left(t\right)-{\beta }_i\left({\mathcal{X}}_i\left(t\right)\right)[h_i\left({\mathcal{X}}_i\left(t\right)\right)-{\displaystyle {\sum }_{j=1}^n}{d}_{ij}\left(t\right){\mathfrak{f}}_j\left({\mathcal{X}}_j\left(t\right)\right)\hfill \\ -{\displaystyle {\sum }_{j=1}^n}{b}_{ij}\left(t\right){\mathfrak{g}}_j\left({\mathcal{X}}_j\left(t-\delta \left(t\right)\right)\right)]+I_i\left(t\right),\hfill \\ {\mathcal{X}}_i\left(t_k\right)={\varphi }_k^1{\mathcal{X}}_i(t_k^{-}-{\sigma }_k),\hfill \\ {\mathcal{Y}}_i\left(t_k\right)={\varphi }_k^2{\mathcal{Y}}_i(t_k^{-}-{\sigma }_k),\hfill \end{array}\right.\end{array}$$

(4)

where the impulse moment $t_k$ satisfies $0<t_1<t_2<\cdots <t_k\to \infty$ as $k\to \infty$. Without a loss of generalization, suppose that ${\mathcal{X}}_i\left(t_k^{+}\right)={lim}_{ϵ\to 0^{+}}{\mathcal{X}}_i(t_k+ϵ)$, ${\mathcal{X}}_i\left(t_k^{-}\right)={lim}_{ϵ\to 0^{-}}{\mathcal{X}}_i(t_k+ϵ)$, and the constants ${\varphi }_k^1$, ${\varphi }_k^2$ represent the strength of impulses. System (4) can be viewed as the drive system; accordingly, its response system is described by

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\frac{d{\overline{\mathcal{X}}}_i\left(t\right)}{dt}=-{\zeta }_i{\overline{\mathcal{X}}}_i\left(t\right)+{\overline{\mathcal{Y}}}_i\left(t\right),\hfill \\ \frac{d{\overline{\mathcal{Y}}}_i\left(t\right)}{dt}=L_i\left(t\right){\overline{\mathcal{X}}}_i\left(t\right)-P_i\left(t\right){\overline{\mathcal{Y}}}_i\left(t\right)-{\beta }_i\left({\overline{\mathcal{X}}}_i\left(t\right)\right)[h_i\left({\overline{\mathcal{X}}}_i\left(t\right)\right)-{\displaystyle {\sum }_{j=1}^n}{d}_{ij}\left(t\right){\mathfrak{f}}_j\left({\overline{\mathcal{X}}}_j\left(t\right)\right)\hfill \\ -{\displaystyle {\sum }_{j=1}^n}{b}_{ij}\left(t\right){\mathfrak{g}}_j\left({\overline{\mathcal{X}}}_j\left(t-\delta \left(t\right)\right)\right)]+I_i\left(t\right)+u_i\left(t\right),\hfill \\ {\overline{\mathcal{X}}}_i\left(t_k\right)={\varphi }_k^1{\overline{\mathcal{X}}}_i(t_k^{-}-{\sigma }_k),\hfill \\ {\overline{\mathcal{Y}}}_i\left(t_k\right)={\varphi }_k^2{\overline{\mathcal{Y}}}_i(t_k^{-}-{\sigma }_k),\hfill \end{array}\right.\end{array}$$

(5)

where $u_i\left(t\right)=K_i\left(t\right)({\overline{\mathcal{Y}}}_i\left(t\right)-{\mathcal{Y}}_i\left(t\right))$ denotes the controller.

For the purpose of simplicity, letting $e_i\left(t\right)={\overline{\mathcal{X}}}_i\left(t\right)-{\mathcal{X}}_i\left(t\right)$, $v_i\left(t\right)={\overline{\mathcal{Y}}}_i\left(t\right)-{\mathcal{Y}}_i\left(t\right)$, and $z\left(t\right)={(e^T\left(t\right),v^T\left(t\right))}^T={[e_1,e_2,\cdots ,e_n,v_1,v_2,\cdots ,v_n]}^T={[z_1,z_2,\cdots ,z_{2n}]}^T$, the error system can be formulated as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\frac{d{e}_i\left(t\right)}{dt}=-{\zeta }_i{e}_i\left(t\right)+v_i\left(t\right),\hfill \\ \frac{d{v}_i\left(t\right)}{dt}=L_i\left(t\right)e_i\left(t\right)-P_i\left(t\right)v_i\left(t\right)+{\beta }_i\left(x_i\left(t\right)\right)[{\displaystyle {\sum }_{j=1}^n}{d}_{ij}\left(t\right)({\mathfrak{f}}_j\left(x_j\left(t\right)\right)-{\mathfrak{f}}_j\left({\overline{x}}_j\left(t\right)\right))\hfill \\ +{\displaystyle {\sum }_{j=1}^n}{b}_{ij}\left(t\right)({\mathfrak{g}}_j\left(x_j\left(t-\delta \left(t\right)\right)\right)-{\mathfrak{g}}_j\left({\overline{x}}_j\left(t-\delta \left(t\right)\right)\right))]\hfill \\ +({\beta }_i\left(x_i\left(t\right)\right)-{\beta }_i\left({\overline{x}}_i\left(t\right)\right))\left[{\displaystyle {\sum }_{j=1}^n}{d}_{ij}\left(t\right){\mathfrak{f}}_j\left({\overline{x}}_j\left(t\right)\right)+{\displaystyle {\sum }_{j=1}^n}{b}_{ij}\left(t\right){\mathfrak{g}}_j\left({\overline{x}}_j\left(t-\delta \left(t\right)\right)\right)\right]\hfill \\ -[{\beta }_i\left(x_i\left(t\right)\right)h_i(x_i\left(t\right)-{\beta }_i\left({\overline{x}}_i\left(t\right)\right)h_i\left({\overline{x}}_i\left(t\right)\right]+K_i\left(t\right)v_i\left(t\right),\hfill \\ e_i\left(t_k\right)={\varphi }_k^1{e}_i(t_k^{-}-{\sigma }_k),\hfill \\ v_i\left(t_k\right)={\varphi }_k^2{v}_i(t_k^{-}-{\sigma }_k).\hfill \end{array}\right.\end{array}$$

(6)

Subsequently, the following assumptions are imposed on the considered system, and the necessary definitions are given, which are essential to derive our theoretical results.

Assumption 1. 

For each $i=1,2,\cdots ,n$, the amplification functions ${\beta }_i(.)$ are differentiable and satisfy $|{\beta }_i^{\prime }(.)|<{\mathsf{\Lambda }}_i$, ${\underline{\beta }}_i<{\beta }_i(.)<{\overline{\beta }}_i$.

Assumption 2. 

Let $H_i\left(x\right)={\beta }_i\left(x\right)h_i\left(x\right)$. Meanwhile, suppose that the behaved functions $h_i(.)$ are differentiable, and there is one parameter $C>0$ satisfying

$$|L_i\left(t\right)-H_i^{\prime }\left(x\right)|⩽C.$$

(7)

Assumption 3. 

For each $j=1,2,\cdots ,n$, there exist constants $l_{\mathfrak{f}}>0$, $l_{\mathfrak{g}}>0$, $F_j>0$, $G_j>0$ satisfying

$$\begin{array}{cc}\hfill & |{\mathfrak{f}}_j\left({\xi }_1\right)-{\mathfrak{f}}_j\left({\xi }_2\right)|⩽l_{\mathfrak{f}}|{\xi }_1-{\xi }_2|,|{\mathfrak{f}}_j\left(\xi \right)|<F_j,\hfill \\ \hfill & |{\mathfrak{g}}_j\left({\xi }_1\right)-{\mathfrak{g}}_j\left({\xi }_2\right)|⩽l_{\mathfrak{g}}|{\xi }_1-{\xi }_2|,|{\mathfrak{g}}_j\left(\xi \right)|<G_j.\hfill \end{array}$$

(8)

for $\forall {\xi }_1,{\xi }_2,\xi \in \mathbb{R}$.

Definition 1. 

If function $a\left(t\right)$ satisfies the following properties:

(i) Function $a\left(t\right)$ is continuous;

(ii) When $t>t_0,a\left(t\right)⩾0$, while when $t⩽t_0$, $a\left(t\right)=0$, and $a\left(t\right)\to +\infty ,t\to +\infty$, then we call $a\left(t\right)\in \mathbb{K}$.

Definition 2. 

Response system (5) is said to be globally α-synchronized with drive system (4); equivalently, error system (6) is globally α-stable if there exists a function $\alpha \left(t\right)\in \mathbb{K}$ and one positive constant M such that

$${||z\left(t\right)||}_q={∥Y\left(t\right)-X\left(t\right)∥}_q⩽Mexp\{-\alpha \left(t\right)\},t⩾t_0,$$

(9)

where $X\left(t\right)={(\mathcal{X}\left(t\right),\mathcal{Y}\left(t\right))}^T$, $Y\left(t\right)={(\overline{\mathcal{X}}\left(t\right),\overline{\mathcal{Y}}\left(t\right))}^T$.

3. Main Results

In this section, some impulsive delay differential inequalities are established, and sufficient conditions for power stability and exponential stability are derived. Furthermore, by designing feedback controllers and employing the obtained inequalities, two criteria for the $\alpha$-synchronization of ICGNNs with UDs and DIs are put forward.

Consider the following delay impulsive differential inequality:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{D}^{+}Q\left(t\right)⩽-\lambda \left(t\right)Q\left(t\right)+{\gamma }_1\left(t\right)Q\left(t-{\delta }_1\left(t\right)\right)+{\gamma }_2\left(t\right)Q\left(t-{\delta }_2\left(t\right)\right)+\cdots \hfill \\ +{\gamma }_n\left(t\right)Q\left(t-{\delta }_n\left(t\right)\right),t\ne t_k,\hfill \\ Q\left(t\right)={\mu }_{k}Q\left(t^{-}-{\sigma }_k\right),t=t_k,k\in Z_{+},\hfill \end{array}\right.\end{array}$$

(10)

where $G\left(t\right)\in PC\left(R,R_{+}\right)$, $\lambda \left(t\right)$, ${\gamma }_i\left(t\right)\in C\left(R_{+},R_{+}\right)$, ${\mu }_k\in R_{+}$, time delays $0⩽{\delta }_i\left(t\right)⩽+\infty$, $0⩽{\sigma }_k<+\infty$, ($i=1,2,\cdots ,n$, $k=1,2,\cdots$), ${\sigma }_0=0$, $t_0<t_1<t_2<\cdots <t_k<\cdots$, and $k\in Z_{+}$, and let ${\overline{t}}_0={\displaystyle \underset{1⩽i⩽n,k\in Z_{+},t\in \left[t_0,\infty \right)}{min}}\left\{t-{\delta }_i\left(t\right),-{\sigma }_k\right\}$.

Lemma 1. 

Suppose that there exists a function $\alpha \left(t\right)\in \mathbb{K}$ satisfying

$$-\lambda \left(t\right)+{\displaystyle \sum _{i=1}^n}{\gamma }_i\left(t\right)exp\left\{\alpha \left(t\right)-\alpha \left(t-{\delta }_i\left(t\right)\right)\right\}+D^{+}\alpha \left(t\right)<0,t⩾t_0;$$

(11)

then,

$$Q\left(t\right)⩽{\mathsf{\Phi }}_{k}exp\left\{-\alpha \left(t\right)\right\},t\in \left[t_0,t_k\right),$$

(12)

in which ${\mathsf{\Phi }}_k={\prod }_{i=0}^{k-1}\left(1\vee exp\left\{\alpha \left(t_i\right)-\alpha \left(t_i-{\sigma }_i\right)\right\}{\mu }_i\right)\tilde{Q}\left(t_0\right),{\mu }_0=1,\tilde{Q}\left(t_0\right)={\displaystyle \underset{s\in \left[{\overline{t}}_0,t_0\right]}{sup}}Q\left(s\right)$.

Proof. 

When $\tilde{Q}\left(t_0\right)=0$, obviously, one can determine that $Q\left(t\right)=0$, which implies that the conclusion (12) is valid. In general, suppose that $\tilde{Q}\left(t_0\right)\ne 0$. The following is verified:

$$exp\left\{\alpha \left(t\right)\right\}Q\left(t\right)⩽{\mathsf{\Phi }}_k,t\in \left[t_0,t_k\right).$$

(13)

Take the auxiliary function $\mathcal{G}\left(t\right)=exp\left\{\alpha \left(t\right)\right\}Q\left(t\right)$. First of all, it is claimed that

$$\mathcal{G}\left(t\right)⩽{\mathsf{\Phi }}_1,t\in \left[t_0,t_1\right).$$

(14)

When $t=t_0$, it can easily be derived that $\mathcal{G}\left(t_0\right)=exp\left\{\lambda \left(t_0\right)\right\}Q\left(t_0\right)⩽\tilde{Q}\left(t_0\right)={\mathsf{\Phi }}_1$. Assume that inequality (14) is not satisfied; then, there exists $t^{*}\in \left[t_0,t_1\right)$ such that $\mathcal{G}\left(t^{*}\right)={\mathsf{\Phi }}_1$, $\mathcal{G}\left(t\right)⩽{\mathsf{\Phi }}_1$, $t\in \left[t_0,t^{*}\right)$, and $D^{+}\mathcal{G}\left(t^{*}\right)⩾0$. Since $\mathcal{G}(t^{*}-{\delta }_i\left(t^{*}\right))\le \mathcal{G}\left(t^{*}\right)$, together with condition (2), it can be determined that

$$\begin{array}{cc}\hfill & D^{+}{\mathcal{G}\left(t\right)|}_{t=t^{*}}=D^{+}exp\left\{\alpha \left(t\right)\right\}{{|}_{t=t^{*}}Q\left(t^{*}\right)+exp\left\{\alpha \left(t^{*}\right)\right\}{D}^{+}Q\left(t\right)|}_{t=t^{*}}\hfill \\ \hfill & ⩽{\left.D^{+}\alpha \left(t\right)\right|}_{t=t^{*}}\mathcal{G}\left(t^{*}\right)+exp\left\{\alpha \left(t^{*}\right)\right\}\left[-\beta \left(t^{*}\right)Q\left(t^{*}\right)+{\displaystyle \sum _{i=1}^n}{\gamma }_i\left(t^{*}\right)Q\left(t^{*}-{\delta }_i\left(t^{*}\right)\right)\right]\hfill \\ \hfill & ⩽{\left.D^{+}\alpha \left(t\right)\right|}_{t=t^{*}}\mathcal{G}\left(t^{*}\right)-\lambda \left(t^{*}\right)\mathcal{G}\left(t^{*}\right)+{\displaystyle \sum _{i=1}^n}{\gamma }_i\left(t^{*}\right)exp\left\{\alpha \left(t^{*}\right)-\alpha \left(t^{*}-{\delta }_i\left(t^{*}\right)\right)\right\}\mathcal{G}\left(t^{*}-{\delta }_i\left(t^{*}\right)\right)\hfill \\ \hfill & ⩽\left[{\left.-\lambda \left(t^{*}\right)+{\displaystyle \sum _{i=1}^n}{\gamma }_i\left(t^{*}\right)exp\left\{\alpha \left(t^{*}\right)-\alpha \left(t^{*}-{\delta }_i\left(t^{*}\right)\right)\right\}+D^{+}\alpha \left(t\right)\right|}_{t=t^{*}}\right]\mathcal{G}\left(t^{*}\right)\hfill \\ \hfill & <0,\hfill \end{array}$$

which leads to a contradiction with $D^{+}\mathcal{G}\left(t^{*}\right)⩾0$. Therefore, inequality (14) holds.

Now let us suppose that when $k=N$, we have $\mathcal{G}\left(t\right)⩽{\mathsf{\Phi }}_N,t\in \left[t_0,t_N\right)$. Subsequently, it will be verified that when $k=N+1$, the following assertion holds:

$$\mathcal{G}\left(t\right)⩽{\mathsf{\Phi }}_{N+1},t\in \left[t_0,t_{N+1}\right).$$

(15)

Noting that $\mathcal{G}\left(t\right)\le {\mathsf{\Phi }}_N,t\in \left[t_0,t_N\right)$ and ${\mathsf{\Phi }}_N⩽{\mathsf{\Phi }}_{N+1}$, it can be deduced that $\mathcal{G}\left(t\right)⩽{\mathsf{\Phi }}_{N+1},$$t\in \left[t_0,t_N\right)$, which means that it only needs to be claimed that

$$\mathcal{G}\left(t\right)⩽{\mathsf{\Phi }}_{N+1},t\in \left[t_N,t_{N+1}\right).$$

(16)

When $t=t_N$, one can calculate that

$$\begin{array}{cc}\hfill \mathcal{G}\left(t_N\right)& =exp\left\{\alpha \left(t_N\right)\right\}Q\left(t_N\right)\hfill \\ \hfill & ⩽exp\left\{\alpha \left(t_N\right)\right\}{\mu }_{N}Q\left(t_N^{-}-{\sigma }_N\right)\hfill \\ \hfill & ⩽exp\left\{\alpha \left(t_N\right)-\alpha \left(t_N^{-}-{\sigma }_N\right)\right\}{\mu }_N\mathcal{G}\left(t_N^{-}-{\sigma }_N\right)\hfill \\ \hfill & ⩽exp\left\{\alpha \left(t_N\right)-\alpha \left(t_N^{-}-{\sigma }_N\right)\right\}{\mu }_N{\mathsf{\Phi }}_N\hfill \\ \hfill & ⩽{\mathsf{\Phi }}_{N+1}.\hfill \end{array}$$

If Equation (16) does not hold, there exists $t^{**}$$\in \left[t_N,t_{N+1}\right)$ satisfying $\mathcal{G}$$\left(t^{**}\right)$$={\mathsf{\Phi }}_{N+1}$, $\mathcal{G}\left(t\right)⩽{\mathsf{\Phi }}_{N+1}$, $t\in [t_N,$$t^{**})$, and $D^{+}{\mathcal{G}\left(t\right)|}_{t=t^{**}}⩾0$. Furthermore, it can be determined that

$$\begin{array}{cc}\hfill & D^{+}{\mathcal{G}\left(t\right)|}_{t=t^{**}}=D^{+}exp\left\{\alpha \left(t\right)\right\}{{|}_{t=t^{**}}Q\left(t^{**}\right)+exp\left\{\alpha \left(t^{**}\right)\right\}{D}^{+}Q\left(t\right)|}_{t=t^{**}}\hfill \\ \hfill & ⩽\left[{\left.D^{+}\alpha \left(t\right)\right|}_{t=t^{**}}-\lambda \left(t^{**}\right)+{\displaystyle \sum _{i=1}^n}{\nu }_i\left(t^{**}\right)exp\left\{\alpha \left(t^{**}\right)-\alpha \left(t^{**}-{\delta }_i\left(t^{**}\right)\right)\right\}\mathcal{G}\left(t^{**}\right)<0,\right.\hfill \end{array}$$

which yields a contradiction. Therefore, it follows that

$$\mathcal{G}\left(t\right)=Q\left(t\right)exp\left\{\alpha \left(t\right)\right\}⩽{\mathsf{\Phi }}_{N+1},t\in \left[t_0,t_{N+1}\right).$$

(17)

Then, $Q\left(t\right)exp\left\{\alpha \left(t\right)\right\}\le {\mathsf{\Phi }}_k$, $t\in \left[t_0,t_k\right)$, which indicates that $Q\left(t\right)⩽{\mathsf{\Phi }}_{k}exp\left\{-\alpha \left(t\right)\right\}$, $t\in \left[t_0,t_k\right)$. □

Particularly, when $\alpha \left(t\right)=ln{(1+t)}^{{\eta }_0},{\eta }_0>0$, ${\delta }_i\left(t\right)=(1-p_i)t$, $0<p_i<1$, according to Lemma 1, the corollary below can be acquired immediately.

Corollary 1. 

For the delay impulsive differential system (10), assume that the following conditions hold:

$$\begin{array}{cc}\hfill & {\displaystyle \prod _{i=0}^{k-1}}\left(1\vee {\left(\frac{1+t_i}{1+t_i-{\sigma }_i}\right)}^{{\eta }_0}{\mu }_i\right)=M<\infty ,1+t_i-{\sigma }_i>0,\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & -\beta \left(t\right)+{\displaystyle \sum _{i=1}^n}{\gamma }_i\left(t\right)p_i^{-{\eta }_0}+\frac{{\eta }_0}{1+t}<0;\hfill \end{array}$$

(19)

then,

$$\begin{array}{c}\hfill Q\left(t\right)⩽M\tilde{Q}\left(t_0\right)\frac{1}{{(1+t)}^{{\eta }_0}},t\in [t_0,t_k).\end{array}$$

(20)

Remark 1. 

It can be seen that from Corollary 1 that the addressed system with unbounded proportional delays has polynomial stability if conditions (18) and (19) hold. Meanwhile, when both the intensity of impulses and the bound of impulsive delays are sufficiently small, the delay impulses can be viewed as perturbations. By utilizing Corollary 1, the polynomial synchronization of one class of ICGNNs with proportional delays can be dealt with.

Furthermore, when $\alpha \left(t\right)={\eta }_0(t-t_0),{\eta }_0>0$, ${\delta }_i\left(t\right)=(1-p_i)t$, $i=1,2,\cdots ,n$, accordingly, by means of Lemma 1, the assertion below is acquired.

Corollary 2. 

For the delay impulsive differential system (10), assume that the following conditions hold:

$$\begin{array}{c}\hfill -\lambda \left(t\right)+{\displaystyle \sum _{i=1}^n}{\gamma }_i\left(t\right)e^{{\eta }_0(1-p_i)t}+{\eta }_0<0;\end{array}$$

(21)

then,

$$\begin{array}{c}\hfill Q\left(t\right)⩽{\displaystyle \prod _{i=0}^{k-1}}(1\vee e^{{\eta }_0{\sigma }_i}{\mu }_i)\tilde{Q}\left(t_0\right)e^{-{\eta }_0(t-t_0)},t\in [t_{k-1},t_k).\end{array}$$

(22)

In particular, if $1\le e^{{\eta }_0{\sigma }_{k-1}}{\mu }_{k-1}\le e^{\omega (t_k-t_{k-1})}$, then

$$\begin{array}{c}\hfill Q\left(t\right)⩽\tilde{Q}\left(t_0\right)e^{-({\eta }_0-\omega )(t-t_0)}.\end{array}$$

(23)

Lemma 2. 

Assume that there exists a function $\lambda \left(t\right)\in \mathbb{K}$ and a positive constant $\rho >0$ such that

$$-\lambda \left(t\right)+{\displaystyle \sum _{i=1}^n}\rho {\gamma }_i\left(t\right)exp\left\{\alpha \left(t\right)-\alpha \left(t-{\delta }_i\left(t\right)\right)\right\}+D^{+}\alpha \left(t\right)<-\frac{ln{\theta }_{k-1}}{t_k-t_{k-1}},t\in \left[t_{k-1},t_k\right);$$

(24)

then,

$$Q\left(t\right)⩽\rho \tilde{Q}\left(t_0\right)exp\left\{-\alpha \left(t\right)\right\},$$

(25)

where ${\theta }_k=exp\left\{\alpha \left(t_k\right)-\alpha \left(t_k-{\sigma }_k\right)\right\}{\mu }_k$, $0<{\theta }_k<1$, $k\in Z_{+}$, ${\mu }_0=1$, $\tilde{Q}\left(t_0\right)={\displaystyle \underset{s\in \left[{\overline{t}}_0,t_0\right]}{sup}}Q\left(s\right)$, $\rho ={\displaystyle \underset{k\in Z_{+}}{sup}}\left\{\frac{1}{{\theta }_k}\right\}>1$.

Proof. 

Let $\mathcal{G}\left(t\right)=exp\left\{\alpha \left(t\right)\right\}Q\left(t\right)$. When $t\in \left[t_0,t_1\right)$, similar to Lemma 1, it is not difficult to verify $\mathcal{G}\left(t\right)⩽\tilde{Q}\left(t_0\right)⩽\rho \tilde{Q}\left(t_0\right)$. Subsequently, it will be proved that

$$\mathcal{G}\left(t\right)⩽\rho \tilde{Q}\left(t_0\right),t\in \left[t_1,t_2\right).$$

(26)

When $t=t_1$, noting that $0<{\theta }_1<1$, it follows that

$$\begin{array}{cc}\hfill \mathcal{G}\left(t_1\right)& =exp\left\{\alpha \left(t_1\right)\right\}Q\left(t_1\right)\hfill \\ \hfill & ⩽exp\left\{\alpha \left(t_1\right)\right\}{\mu }_{1}Q\left(t_1^{-}-{\sigma }_1\right)\hfill \\ \hfill & ⩽exp\left\{\alpha \left(t_1\right)-\alpha \left(t_1^{-}-{\sigma }_1\right)\right\}{\mu }_1\mathcal{G}\left(t_1^{-}-{\sigma }_1\right)\hfill \\ \hfill & ⩽{\theta }_1\mathcal{G}\left(t_1^{-}-{\sigma }_1\right)\hfill \\ \hfill & ⩽{\theta }_1\tilde{Q}\left(t_0\right)⩽\tilde{Q}\left(t_0\right).\hfill \end{array}$$

If Equation (26) is not satisfied, then there exists $t_1^{*}=inf\left\{t\in \left[t_1,t_2\right),\mathcal{G}\left(t\right)>\rho \tilde{Q}\left(t_0\right)\right\}$ such that $\mathcal{G}\left(t^{*}\right)=\rho \tilde{Q}\left(t_0\right)$. On the other hand, since $\mathcal{G}\left(t\right)$ is continuous, there also exists $t_1^{**}=sup\left\{t\in \left[t_1,t_1^{*}\right),\mathcal{G}\left(t\right)\le \tilde{Q}\left(t_0\right)\right\}$ such that $\mathcal{G}\left(t^{**}\right)=\tilde{Q}\left(t_0\right)$. Therefore, when $t\in \left[t_1^{*},t_1^{**}\right)$, we have $\tilde{Q}\left(t_0\right)=\mathcal{G}\left(t^{**}\right)⩽\mathcal{G}\left(t\right)⩽\mathcal{G}\left(t^{*}\right)=\rho \tilde{Q}\left(t_0\right)$ and $\mathcal{G}\left(t-{\delta }_i\left(t\right)\right)⩽\rho \tilde{Q}\left(t_0\right)⩽\rho \mathcal{G}\left(t\right)$. According to condition (24), when $t\in \left[t_1^{**},t_1^{*}\right)$, through computation it can be determined that

$$\begin{array}{cc}\hfill & D^{+}\mathcal{G}\left(t\right)=exp\left\{\alpha \left(t\right)\right\}{D}^{+}\alpha \left(t\right)Q\left(t\right)+exp\left\{\alpha \left(t\right)\right\}{D}^{+}Q\left(t\right)\hfill \\ \hfill & ⩽D^{+}\alpha \left(t\right)\mathcal{G}\left(t\right)-\lambda \left(t\right)\mathcal{G}\left(t\right)+{\displaystyle \sum _{i=1}^n}{\gamma }_i\left(t\right)exp\left\{\alpha \left(t\right)-\alpha \left(t-{\delta }_i\left(t\right)\right)\right\}\mathcal{G}\left(t-{\delta }_i\left(t\right)\right)\hfill \\ \hfill & ⩽\left[-\lambda \left(t\right)+\rho {\displaystyle \sum _{i=1}^n}{\gamma }_i\left(t\right)exp\left\{\alpha \left(t\right)-\alpha \left(t-{\delta }_i\left(t\right)\right)\right\}\right.+D^{+}\alpha \left(t\right)]\mathcal{G}\left(t\right)\hfill \\ \hfill & <-\frac{ln{\theta }_1}{t_2-t_1}\mathcal{G}\left(t\right),\hfill \end{array}$$

which means that $\frac{D^{+}\mathcal{G}\left(t\right)}{\mathcal{G}\left(t\right)}<-\frac{ln{\theta }_1}{t_2-t_1}$. Integrating both sides of the above inequality from $t_1^{**}$ to $t_1^{*}$, one finds that

$${\int }_{t_1^{**}}^{t_1^{*}}\frac{D^{+}\mathcal{G}\left(s\right)}{\mathcal{G}\left(s\right)}<{\int }_{t_1^{**}}^{t_1^{*}}-\frac{ln{\theta }_1}{t_2-t_1}ds.$$

Moreover, it can be computed that

$$ln\mathcal{G}\left(t_1^{*}\right)-ln\mathcal{G}\left(t_1^{**}\right)=ln\rho \tilde{Q}\left(t_0\right)-ln\tilde{Q}\left(t_0\right)=ln\rho <-\frac{ln{\theta }_1}{t_2-t_1}\left(t_1^{*}-t_1^{**}\right)⩽ln\frac{1}{{\theta }_1}⩽ln\rho ,$$

which yields a contradiction. Hence, it can be determined that $\mathcal{G}\left(t\right)⩽\rho \tilde{Q}\left(t_0\right),t\in \left[t_1,t_2\right)$.

Now let us suppose that when $t\in \left[t_{k-1},t_k\right)$, $k=1,2,\cdots ,N$, $\mathcal{G}\left(t\right)⩽\rho \tilde{Q}\left(t_0\right)$. Next, it is claimed that for $k=N+1$,

$$\mathcal{G}\left(t\right)⩽\rho \tilde{Q}\left(t_0\right),t\in \left[t_N,t_{N+1}\right).$$

(27)

When $t=t_N$, it can be found that $\mathcal{G}\left(t_N\right)⩽{\theta }_N\mathcal{G}\left(t_N^{-}-{\sigma }_N\right)⩽{\theta }_N\rho \tilde{Q}\left(t_0\right)⩽\tilde{Q}\left(t_0\right)$. If Equation (27) does not hold, then there must be $t_N^{*}=inf\left\{t\in \left[t_N,t_{N+1}\right),\mathcal{G}\left(t\right)>\rho \tilde{Q}\left(t_0\right)\right\}$ such that $\mathcal{G}\left(t_N^{*}\right)=\rho \tilde{Q}\left(t_0\right)$. Meanwhile, there also exists $t_N^{**}=sup\left\{t\in \left[t_N,t_N^{*}\right),\mathcal{G}\left(t\right)⩽\tilde{Q}\left(t_0\right)\right\}$ such that $\mathcal{G}\left(t_N^{**}\right)=\tilde{Q}\left(t_0\right)$. Accordingly, it can be inferred that $\mathcal{G}\left(t-{\delta }_i\left(t\right)\right)⩽\rho \tilde{Q}\left(t_0\right)⩽\rho \mathcal{G}\left(t\right)$, $t\in \left[t_N^{**},t_N^{*}\right)$. By repeating the previous proof procedure, we can also determine that $\frac{D^{+}\mathcal{G}\left(t\right)}{\mathcal{G}\left(t\right)}⩽\frac{-ln{\theta }_N}{t_{N+1}-t_N}$. Integrating both sides of the above inequality, one has

$${\int }_{t_N^{**}}^{t_N^{*}}\frac{D^{+}\mathcal{G}\left(s\right)}{\mathcal{G}\left(s\right)}<{\int }_{t_N^{**}}^{t_N^{*}}\frac{-ln{\theta }_N}{t_{N+1}-t_N}ds.$$

Moreover, it can be computed that $ln\rho <\frac{-ln{\theta }_N}{t_{N+1}-t_N}\left(t_N^{*}-t_N^{**}\right)⩽ln\frac{1}{{\theta }_N}⩽ln\rho$, which means that a contradiction arises and Equation (27) holds. It is equivalent to

$$\mathcal{G}\left(t\right)⩽\rho \tilde{Q}\left(t_0\right),t\in \left[t_0,t_k\right),$$

which means that $Q\left(t\right)⩽\rho \tilde{Q}\left(t_0\right)exp\left\{-\alpha \left(t\right)\right\}$, $t\in \left[t_0,t_k\right)$. □

Remark 2. 

It is worth pointing out that impulses can be used to stabilize the considered system as stabilizing sources in Lemma 2. Meanwhile, when the impulsive interval, intensity of impulses, and upper bound of impulsive delay are smaller, impulses can play a more important role in stabilizing the systems. Consequently, compared with Lemma 1, the conditions of Lemma 2 are easily verified by designing appropriate impulses. Moreover, according to Lemma 2, the synchronization issue of one class of ICGNNs with general unbounded delays can be tackled.

By choosing function $\alpha \left(t\right)=ln{(1+t)}^{{\eta }_0},{\eta }_0>0$, ${\delta }_i\left(t\right)=(1-p_i)t$, $0<p_i<1$, $i=1,2,\cdots ,n$, $\lambda \left(t\right)=\overline{\lambda },{\gamma }_i\left(t\right)={\overline{\gamma }}_i$, ${\sigma }_k=\frac{t_k}{2}$, according to Lemma 2, the following assertion can be acquired immediately.

Corollary 3. 

For the delay impulsive differential system (10), assume that the following conditions hold:

$$\begin{array}{c}\hfill -\overline{\lambda }+{\displaystyle \sum _{i=1}^n}\rho {\overline{\gamma }}_i{p}_i^{-{\eta }_0}+{\eta }_0<-\frac{ln{\theta }_{k-1}}{t_k-t_{k-1}},t\in \left[t_{k-1},t_k\right),\end{array}$$

(28)

where ${\theta }_k=2^{{\eta }_0}{\mu }_k$; then,

$$G\left(t\right)⩽\rho \tilde{G}\frac{1}{{(1+t)}^{{\eta }_0}}.$$

(29)

Remark 3. 

In [39,40], the μ-stability of non-autonomous systems with UDs and IEs were analyzed, but the impulsive part did not contain time delays, and our paper takes into account this case. In [41,42,43,44], the μ-synchronization of network systems with UDs and constant coefficients was discussed, but the time-varying coefficients are dealt with here. Actually, the impulses in the results [39,40,41,42,43] can be viewed as perturbances. In our paper, Lemma 1 reveals that the impulses can be viewed as external perturbances, while Lemma 2 indicates that the impulses can be regarded as one significant stabilizing factor. On the other hand, in [45], by utilizing the Razumikhin method, several improved stability criteria for stochastic systems with bounded time delays and impulsive effects were acquired. In contrast to the work in [45], the unbounded delays and delayed impulses were incorporated, and some delay impulsive differential inequalities were proposed.

Theorem 1. 

Let Assumptions 1–3 hold. If there exists a function $\alpha \left(t\right)\in \mathbb{K}$ satisfying

$${\mathsf{\Theta }}_1\left(t\right)+{\mathsf{\Theta }}_2\left(t\right)exp(\alpha \left(t\right)-\alpha (t-\delta \left(t\right))+D^{+}\alpha \left(t\right)<0,t⩾t_o,$$

(30)

then response system (5) is globally α-synchronized with drive system (4), i.e.,

$${∥z\left(t\right)∥}_1⩽{\displaystyle {\displaystyle \prod _{i=0}^{k-1}}}\left(1\vee exp\left(\alpha \left(t_i\right)-\alpha (t_i-{\sigma }_i)\right){\mu }_i\right){\displaystyle \underset{s\in [\overline{t_0},t_0]}{sup}}{∥z\left(s\right)∥}_{1}exp(-\alpha \left(t\right)),t⩾t_0,$$

(31)

where ${∥z\left(t\right)∥}_1={\sum }_{i=1}^n\left[|e_i\left(t\right)|+|v_i\left(t\right)|\right]$, ${\mathsf{\Theta }}_1\left(t\right)=max\{{\displaystyle \underset{1\le i\le n}{max}}\{-{\zeta }_i+{\sum }_{j=1}^n|d_{ji}\left(t\right)|l_{\mathfrak{f}}{\overline{\beta }}_j$

$+{\mathsf{\Lambda }}_i({\sum }_{j=1}^n|d_{ij}\left(t\right)|F_j+{\sum }_{j=1}^n|b_{ij}\left(t\right)|G_j)+C\},$${\displaystyle \underset{1\le i\le n}{max}}\{1-P_i\left(t\right)+K_i\left(t\right)\}\}$, ${\mu }_0={\varphi }_0^1={\varphi }_0^2=1$,

${\mathsf{\Theta }}_2\left(t\right)={\displaystyle \underset{1\le i\le n}{max}}{\sum }_{j=1}^n\left|b_{ji}\left(t\right)\right|l_{\mathfrak{g}}{\overline{\beta }}_j$, and ${\mu }_k=max\left\{|{\varphi }_k^1|,|{\varphi }_k^2|\right\},k=0,1,2,\cdots$.

Proof. 

Choose the appropriate Lyapunov function,

$$U\left(t\right)={\displaystyle \sum _{i=1}^n}\left[|e_i\left(t\right)|+|v_i\left(t\right)|\right].$$

(32)

Noting that functions ${\alpha }_i\left(x\right)$ and $h_i\left(x\right)$ are differentiable, by utilizing the differential mean value theorem, it follows that

$$\begin{array}{cc}\hfill & {\beta }_i\left(x_i\left(t\right)\right)-{\beta }_i\left({\overline{x}}_i\left(t\right)\right)={\beta }_i^{\prime }\left({\varsigma }_i\right)e_i\left(t\right),\hfill \\ \hfill & {\beta }_i\left(x_i\left(t\right)\right)h_i(x_i\left(t\right)-{\beta }_i\left({\overline{x}}_i\left(t\right)\right)h_i({\overline{x}}_i\left(t\right)=H_i\left(x_i\left(t\right)\right)-H_i\left({\overline{x}}_i\left(t\right)\right)=H_i^{\prime }\left({\overline{\varsigma }}_i\right)e_i\left(t\right),\hfill \end{array}$$

(33)

where both ${\varsigma }_i$ and ${\overline{\varsigma }}_i$ are between $x_i\left(t\right)$ and ${\overline{x}}_i\left(t\right)$. For $t\ne t_k$, in virtue of assumption $H_3$ and Equation (33), the derivative of $U\left(t\right)$ along the trajectories of model (6) yields that

$$\begin{array}{c}{D}^{+}U\left(t\right)={\sum }_{i=1}^n[D^{+}\left|e_i\left(t\right)\right|+D^{+}\left|v_i\left(t\right)\right|]\hfill \\ ⩽{\sum }_{i=1}^n[-{\zeta }_i\left|e_i\left(t\right)\right|+\left|v_i\left(t\right)\right|+\left|L_i\left(t\right)-H_i^{\prime }\left({\overline{\varsigma }}_i\right)\right|\left|e_i\left(t\right)\right|-P_i\left(t\right)\left|v_i\left(t\right)\right|\hfill \\ +{\overline{\alpha }}_i{\sum }_{j=1}^n\left|d_{ij}\left(t\right)\right|l_{\mathfrak{f}}\left|e_j\left(t\right)\right|+{\overline{\alpha }}_i{\displaystyle {\sum }_{j=1}^n}\left|b_{ij}\left(t\right)\right|l_{\mathfrak{g}}\left|e_j(t-\delta \left(t\right))\right|\hfill \\ +{\mathsf{\Lambda }}_i({\displaystyle {\sum }_{j=1}^n}|d_{ij}\left(t\right)|F_j+{\displaystyle {\sum }_{j=1}^n}|b_{ij}\left(t\right)|G_j)|e_i\left(t\right)|+K_i{v}_i\left(t\right)]\hfill \\ ⩽{\displaystyle {\sum }_{i=1}^n}{\displaystyle {max}_{1\le i\le n}}\left(-{\zeta }_i+{\displaystyle {\sum }_{j=1}^n}\left|d_{ji}\left(t\right)\right|l_{\mathfrak{f}}{\overline{\alpha }}_j+{\mathsf{\Lambda }}_i({\displaystyle {\sum }_{j=1}^n}|d_{ij}|F_j+{\displaystyle {\sum }_{j=1}^n}|b_{ij}|G_j)+C\right)\left|e_i\left(t\right)\right|\hfill \\ +{\displaystyle {\sum }_{i=1}^n}{\displaystyle {max}_{1\le i\le n}}\{1-P_i\left(t\right)+K_i\left(t\right)\}\left|v_i\left(t\right)\right|+{\displaystyle {\sum }_{i=1}^n}{\displaystyle {max}_{1\le i\le n}}({\displaystyle {\sum }_{j=1}^n}\left|b_{ji}\left(t\right)\right|l_{\mathfrak{g}}{\overline{\alpha }}_j)\left|e_i(t-\delta \left(t\right))\right|\hfill \\ ⩽{\mathsf{\Theta }}_1\left(t\right)U\left(t\right)+{\mathsf{\Theta }}_2\left(t\right)U(t-\delta \left(t\right)).\hfill \end{array}$$

(34)

Subsequently, when $t=t_k$, it can easily be determined that

$$\begin{array}{cc}\hfill U\left(t_k\right)& ={\displaystyle \sum _{i=1}^n}[\left|e_i\left(t_k^{+}\right)\right|+\left|v_i\left(t_k^{+}\right)\right|]\hfill \\ \hfill & ={\displaystyle \sum _{i=1}^n}[|{\varphi }_k^1|\left|e_i(t_k^{-}-{\sigma }_k)\right|+|{\varphi }_k^2|\left|v_i(t_k^{-}-{\sigma }_k)\right|]\hfill \\ \hfill & ⩽{\mu }_{k}U(t_k^{-}-{\sigma }_k).\hfill \end{array}$$

(35)

Cobining (34) and (35) and employing Lemma 1, it can be derived that

$$U\left(t\right)⩽{\displaystyle {\displaystyle \prod _{i=0}^{k-1}}}\left(1\vee exp\left(\alpha \left(t_i\right)-\alpha (t_i-{\sigma }_i)\right){\mu }_i\right){\displaystyle \underset{s\in [{\overline{t}}_0,t_0]}{sup}}U\left(s\right)exp(-\alpha \left(t\right)),t⩾t_0,$$

(36)

which implies that

$${∥z\left(t\right)∥}_1⩽{\displaystyle \prod _{i=0}^{k-1}}\left(1\vee exp\left(\alpha \left(t_i\right)-\alpha (t_i-{\sigma }_i)\right){\mu }_i\right){\displaystyle \underset{s\in [\overline{t_0},t_0]}{sup}}{∥z\left(s\right)∥}_{1}exp(-\alpha \left(t\right)),t⩾t_0.$$

(37)

□

Remark 4. 

In Theorem 1, by designing appropriate feedback control, the synchronization of ICGNNs with unbounded delays and delayed impulses between the drive system and response system is realized, and some sufficient conditions are derived. In contrast to the results in [39,40,41,42,43], α-synchronization is considered, which includes exponential synchronization and power synchronization based on various unbounded delays. Meanwhile, delayed impulses can be seen as disturbances. A numerical simulation example is provided to verify the above theoretical result in Section 4.

Theorem 2. 

Suppose that Assumptions 1–3 hold. If there exists a function $\alpha \left(t\right)\in \mathbb{K}$ such that

$${\overline{\mathsf{\Theta }}}_1\left(t\right)+{\overline{\mathsf{\Theta }}}_2\left(t\right)exp(\alpha \left(t\right)-\alpha (t-\delta \left(t\right))+D^{+}\alpha \left(t\right)<0,$$

(38)

then response system (5) is globally α-synchronized with drive system (4), i.e.,

$${∥z\left(t\right)∥}_q⩽{\displaystyle \prod _{i=0}^{k-1}}{\left(1\vee exp\left(\alpha \left(t_i\right)-\alpha (t_i-{\sigma }_i)\right){\overline{\mu }}_i\right)}^{\frac{1}{q}}{\displaystyle \underset{s\in [\overline{t_0},t_0]}{sup}}{∥z\left(s\right)∥}_{q}exp[-\frac{\alpha \left(t\right)}{q}],t⩾t_0,$$

(39)

where ${∥z\left(t\right)∥}_q={\left({\sum }_{i=1}^n\left[|e_i{\left(t\right)|}^q+{|v_i\left(t\right)|}^q\right]\right)}^{\frac{1}{q}}$, ${\overline{\mathsf{\Theta }}}_1\left(t\right)=max\left\{{\displaystyle \underset{1\le i\le n}{max}}\left(-q{\zeta }_i+q-1+{\mathfrak{A}}_1\right),{\displaystyle \underset{1\le i\le n}{max}}\left(1-q{P}_i\left(t\right)+q{K}_i\left(t\right)+(q-1){\mathfrak{A}}_2\right)\right\}$, ${\overline{\mathsf{\Theta }}}_2\left(t\right)={\sum }_{i=1}^n{\displaystyle \underset{1\le i\le n}{max}}\left|b_{ji}\left(t\right)\right|l_{\mathfrak{g}}{\overline{\beta }}_j$, ${\overline{\mu }}_k=max\left\{|{\varphi }_k^1{|}^q,\right.\left.|{\varphi }_k^2{|}^q\right\}$, and ${\overline{\mu }}_0={\varphi }_0^1={\varphi }_0^2=1$, ${\mathfrak{A}}_1={\sum }_{j=1}^n\left|d_{ji}\left(t\right)\right|l_{\mathfrak{f}}{\overline{\beta }}_j+{\mathsf{\Lambda }}_i({\sum }_{j=1}^n|d_{ij}\left(t\right)|F_j+{\sum }_{j=1}^n|b_{ij}\left(t\right)|G_j)+C$, ${\mathfrak{A}}_2={\sum }_{j=1}^n\left|d_{ij}\left(t\right)\right|l_{\mathfrak{f}}{\overline{\beta }}_i+{\sum }_{j=1}^n\left|b_{ij}\left(t\right)\right|l_{\mathfrak{g}}{\overline{\beta }}_i+{\mathsf{\Lambda }}_i({\sum }_{j=1}^n|d_{ij}\left(t\right)|F_j+{\sum }_{j=1}^n|b_{ij}\left(t\right)|G_j)+C$, $q\ge 2$.

Proof. 

Consider the Lyapunov function as follows:

$$U\left(t\right)={\displaystyle \sum _{i=1}^n}\left[|e_i{\left(t\right)|}^q+{|v_i\left(t\right)|}^q\right],q⩾2.$$

(40)

For $t\ne t_k$, the derivative of $U\left(t\right)$ along the trajectories of model (6) yields that

$$\begin{array}{cc}{D}^{+}U\left(t\right)\hfill & ={\displaystyle {\sum }_{i=1}^n}[D^{+}{\left|e_i\left(t\right)\right|}^q+D^{+}{\left|v_i\left(t\right)\right|}^q]\hfill \\ \hfill & ⩽{\displaystyle {\sum }_{i=1}^n}[-p{\zeta }_i{\left|e_i\left(t\right)\right|}^q+q|e_i{\left(t\right)|}^{q-1}\left|v_i\left(t\right)\right|+q|v_i\left(t\right){|}^{q-1}(\left|L_i\left(t\right)-H_i^{\prime }\left({\overline{\varsigma }}_i\right)\right|\left|e_i\left(t\right)\right|\hfill \\ \hfill & -P_i\left(t\right)\left|v_i\left(t\right)\right|+{\overline{\beta }}_i{\displaystyle {\sum }_{j=1}^n}\left|d_{ij}\left(t\right)\right|l_{\mathfrak{f}}\left|e_j\left(t\right)\right|+{\overline{\beta }}_i{\displaystyle {\sum }_{j=1}^n}\left|b_{ij}\left(t\right)\right|l_{\mathfrak{g}}\left|e_j(t-\delta \left(t\right))\right|\hfill \\ \hfill & +{\mathsf{\Lambda }}_i({\displaystyle {\sum }_{j=1}^n}|d_{ij}\left(t\right)|F_j+{\displaystyle {\sum }_{j=1}^n}|b_{ij}\left(t\right)|G_j)|e_i\left(t\right)|+K_i\left(t\right)v_i\left(t\right)].\hfill \end{array}$$

Obviously, it is not difficult to see that there are the following inequalities:

$$\begin{array}{c}q{\left|e_i\left(t\right)\right|}^{q-1}\left|v_i\left(t\right)\right|⩽(q-1){\left|e_i\left(t\right)\right|}^q+{|v_i\left(t\right)|}^q,\hfill \\ q{\left|v_i\left(t\right)\right|}^{q-1}\left|e_j\left(t\right)\right|⩽(q-1){\left|v_i\left(t\right)\right|}^q+{|e_j\left(t\right)|}^q,\hfill \\ q{\left|v_i\left(t\right)\right|}^{q-1}\left|e_j(t-\delta \left(t\right)\right|⩽(q-1){\left|v_i\left(t\right)\right|}^q+|e_j{(t-\delta \left(t\right)|}^q.\hfill \end{array}$$

(41)

According to the above inequalities (41), it follows that

$$\begin{array}{cc}{D}^{+}U\left(t\right)\hfill & ⩽{\displaystyle {\sum }_{i=1}^n}{\displaystyle {max}_{1\le i\le n}}\left(-q{\zeta }_i+q-1+{\mathfrak{A}}_1\right){\left|u_i\left(t\right)\right|}^q\hfill \\ \hfill & +{\displaystyle {\sum }_{i=1}^n}{\displaystyle {max}_{1\le i\le n}}\left(1-q{P}_i\left(t\right))+q{K}_i\left(t\right)+(q-1){\mathfrak{A}}_2\right){\left|v_i\left(t\right)\right|}^q\hfill \\ \hfill & +{\displaystyle {\sum }_{i=1}^n}{\displaystyle {max}_{1\le i\le n}}{\displaystyle {\sum }_{j=1}^n}\left|b_{ji}\left(t\right)\right|l_{\mathfrak{g}}{\overline{\beta }}_j{\left|u_j(t-\delta \left(t\right))\right|}^q\hfill \\ \hfill & ⩽{\overline{\mathsf{\Theta }}}_1\left(t\right)U\left(t\right)+{\overline{\mathsf{\Theta }}}_2\left(t\right)U(t-\delta \left(t\right)).\hfill \end{array}$$

(42)

where ${\mathfrak{A}}_1={\sum }_{j=1}^n\left|d_{ji}\left(t\right)\right|l_{\mathfrak{f}}{\overline{\beta }}_j+{\mathsf{\Lambda }}_i({\sum }_{j=1}^n|d_{ij}\left(t\right)|F_j+{\sum }_{j=1}^n|b_{ij}\left(t\right)|G_j)+C$, ${\mathfrak{A}}_2={\sum }_{j=1}^n\left|d_{ij}\left(t\right)\right|$$l_{\mathfrak{f}}{\overline{\beta }}_i+{\sum }_{j=1}^n\left|b_{ij}\left(t\right)\right|l_{\mathfrak{g}}{\overline{\beta }}_i+{\mathsf{\Lambda }}_i({\sum }_{j=1}^n|d_{ij}\left(t\right)|F_j+{\sum }_{j=1}^n|b_{ij}\left(t\right)|G_j)+C$.

Moreover, when $t=t_k$, one finds that

$$\begin{array}{cc}\hfill U\left(t_k\right)& ={\displaystyle \sum _{i=1}^n}\left[{\left|u_i\left(t_k\right)\right|}^q+{\left|v_i\left(t_k\right)\right|}^q\right]\hfill \\ \hfill & ={\displaystyle \sum _{i=1}^n}\left[|{\varphi }_k^1{|}^q{\left|u_i(t_k^{-}-{\sigma }_k)\right|}^q+{|{\varphi }_k^2|}^q{\left|v_i(t_k^{-}-{\sigma }_k)\right|}^q\right]\hfill \\ \hfill & ⩽{\overline{\mu }}_{k}U(t_k^{-}-{\sigma }_k),\hfill \end{array}$$

(43)

where ${\overline{\mu }}_k=max\{|{\varphi }_k^1{|}^q,|{\varphi }_k^2{|}^q\}$. Analogously to Theorem 1, combining Equation (42) and Equation (43) and employing Lemma 1, it can be determined that

$$U\left(t\right)⩽{\displaystyle \prod _{i=0}^{k-1}}{\left(1\vee exp\left(\alpha \left(t_i\right)-\alpha (t_i-{\sigma }_i)\right){\overline{\mu }}_i\right)}^{\frac{1}{q}}{\displaystyle \underset{s\in [\overline{t_0},t_0]}{sup}}U\left(s\right)exp\{-\frac{\alpha \left(t\right)}{q}\},t⩾t_0,$$

(44)

which means that

$${∥z\left(t\right)∥}_q⩽{\displaystyle \prod _{i=0}^{k-1}}{\left(1\vee exp\left(\alpha \left(t_i\right)-\alpha (t_i-{\sigma }_i)\right){\overline{\mu }}_i\right)}^{\frac{1}{q}}{\displaystyle \underset{s\in [\overline{t_0},t_0]}{sup}}{∥z\left(s\right)∥}_{q}exp\{-\frac{\alpha \left(t\right)}{q}\},t⩾t_0.$$

(45)

□

Theorem 3. 

Assume that there exists a function $\alpha \left(t\right)\in \mathbb{K}$ and a positive scalar $\rho >0$ such that

$${\mathsf{\Theta }}_1\left(t\right)+{\mathsf{\Theta }}_2\left(t\right)\rho exp\left\{\alpha \left(t\right)-\alpha \left(t-\delta \left(t\right)\right)\right\}+D^{+}\alpha \left(t\right)<-\frac{ln{\theta }_{k-1}}{t_k-t_{k-1}},t\in \left[t_{k-1},t_k\right);$$

(46)

then, response system (5) is globally α-synchronized with drive system (4), i.e.,

$${∥z\left(t\right)∥}_1⩽\rho {\displaystyle \underset{s\in \left[{\overline{t}}_0,t_0\right]}{sup}}{∥z_i\left(s\right)∥}_{1}exp\left\{-\alpha \left(t\right)\right\},$$

(47)

where ${∥z\left(t\right)∥}_1={\sum }_{i=1}^n\left[|e_i\left(t\right)|+|v_i\left(t\right)|\right]$, ${\mathsf{\Theta }}_1\left(t\right)=max\{{\displaystyle \underset{1\le i\le n}{max}}\{-{\zeta }_i+{\sum }_{j=1}^n|d_{ji}\left(t\right)|l_{\mathfrak{f}}{\overline{\beta }}_j$

$+{\mathsf{\Lambda }}_i({\sum }_{j=1}^n|d_{ij}\left(t\right)|F_j+{\sum }_{j=1}^n|b_{ij}\left(t\right)|G_j)+C\},$${\displaystyle \underset{1\le i\le n}{max}}\{1-P_i\left(t\right)+K_i\left(t\right)\}\}$, ${\mu }_0={\varphi }_0^1={\varphi }_0^2=1$,

${\mathsf{\Theta }}_2\left(t\right)={\displaystyle \underset{1\le i\le n}{max}}{\sum }_{j=1}^n\left|b_{ji}\left(t\right)\right|l_{\mathfrak{g}}{\overline{\beta }}_j$, and ${\mu }_k=max\left\{|{\varphi }_k^1|,|{\varphi }_k^2|\right\},k=0,1,2,\cdots$, $\rho ={\displaystyle \underset{k\in Z_{+}}{sup}}\left\{\frac{1}{{\theta }_k}\right\}>1$, ${\theta }_k=exp\left\{\alpha \left(t_k\right)-\alpha \left(t_k-{\sigma }_k\right)\right\}{\mu }_k$, $0<{\theta }_k<1$, $k\in Z_{+}$.

Proof. 

Take the same Lyapunov function $U\left(t\right)={\sum }_{i=1}^n\left[|e_i\left(t\right)|+|v_i\left(t\right)|\right]$. By adopting a similar procedure to the proof of Theorem 1, it can be derived that

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill D^{+}U\left(t\right)& ⩽{\mathsf{\Theta }}_1\left(t\right)U\left(t\right)+{\mathsf{\Theta }}_2\left(t\right)U(t-\delta \left(t\right)),\hfill \\ \hfill U\left(t_k\right)& ⩽{\mu }_{k}U(t_k^{-}-{\sigma }_k).\hfill \end{array}\right.\end{array}$$

(48)

Based on Equation (48) and Lemma 2, it can be concluded that

$$U\left(t\right)⩽\rho {\displaystyle \underset{s\in \left[{\overline{t}}_0,t_0\right]}{sup}}{U}_i\left(s\right)exp\left\{-\alpha \left(t\right)\right\},$$

(49)

which implies that

$${∥z\left(t\right)∥}_1⩽\rho {\displaystyle \underset{s\in \left[{\overline{t}}_0,t_0\right]}{sup}}{∥z_i\left(s\right)∥}_{1}exp\left\{-\alpha \left(t\right)\right\}.$$

(50)

□

Theorem 4. 

Assume that there exists a function $\alpha \left(t\right)\in \mathbb{K}$ and a positive constant $\rho >0$ satisfying

$${\overline{\mathsf{\Theta }}}_1\left(t\right)+{\overline{\mathsf{\Theta }}}_2\left(t\right)\rho exp\left\{\alpha \left(t\right)-\alpha \left(t-\delta \left(t\right)\right)\right\}+D^{+}\alpha \left(t\right)<-\frac{ln{\theta }_{k-1}}{t_k-t_{k-1}},t\in \left[t_{k-1},t_k\right);$$

(51)

then, response system (5) is globally α-synchronized with drive system (4), i.e.,

$${∥z\left(t\right)∥}_q⩽{\rho }^{\frac{1}{q}}{\displaystyle \underset{s\in \left[{\overline{t}}_0,t_0\right]}{sup}}{∥z_i\left(s\right)∥}_{q}exp\left\{-\frac{\alpha \left(t\right)}{q}\right\},$$

(52)

where ${∥z\left(t\right)∥}_q={\left({\sum }_{i=1}^n\left[|e_i{\left(t\right)|}^q+{|v_i\left(t\right)|}^q\right]\right)}^{\frac{1}{q}}$, ${\overline{\mathsf{\Theta }}}_1\left(t\right)=max\left\{{\displaystyle \underset{1\le i\le n}{max}}\left(-q{\xi }_i+q-1+{\mathfrak{A}}_1\right),{\displaystyle \underset{1\le i\le n}{max}}\left(1-q{P}_i\left(t\right))+q{K}_i\left(t\right)+(q-1){\mathfrak{A}}_2\right)\right\}$, ${\overline{\mathsf{\Theta }}}_2\left(t\right)={\sum }_{i=1}^n{\displaystyle \underset{1\le i\le n}{max}}\left|b_{ji}\left(t\right)\right|l_{\mathfrak{g}}{\overline{\beta }}_j$, ${\overline{\mu }}_k=max\left\{|{\varphi }_k^1{|}^q,\right.\left.|{\varphi }_k^2{|}^q\right\}$, and ${\overline{\mu }}_0={\varphi }_0^1={\varphi }_0^2=1,q\ge 2$, ${\theta }_k=exp\left\{\alpha \left(t_k\right)-\alpha \left(t_k-{\sigma }_k\right)\right\}{\overline{\mu }}_k$, $0<{\theta }_k<1$, $k\in Z_{+}$, ${\mathfrak{A}}_1={\sum }_{j=1}^n\left|d_{ji}\left(t\right)\right|l_{\mathfrak{f}}{\overline{\beta }}_j+{\mathsf{\Lambda }}_i({\sum }_{j=1}^n|d_{ij}\left(t\right)|F_j+{\sum }_{j=1}^n|b_{ij}\left(t\right)|G_j)+C$, ${\mathfrak{A}}_2={\sum }_{j=1}^n\left|d_{ij}\left(t\right)\right|l_{\mathfrak{f}}{\overline{\beta }}_i+{\sum }_{j=1}^n\left|b_{ij}\left(t\right)\right|l_{\mathfrak{g}}{\overline{\beta }}_i+{\mathsf{\Lambda }}_i({\sum }_{j=1}^n|d_{ij}\left(t\right)|F_j+{\sum }_{j=1}^n|b_{ij}\left(t\right)|G_j)+C$, ${\theta }_k=exp\left\{\lambda \left(t_k\right)-\lambda \left(t_k-{\sigma }_k\right)\right\}{\overline{\mu }}_k$, $0<{\theta }_k<1$, $k\in Z_{+}$, $\rho ={\displaystyle \underset{k\in Z_{+}}{sup}}\left\{\frac{1}{{\theta }_k}\right\}>1$.

Proof. 

Similarly to Theorem 2, we take the same Lyapunov function

$$U\left(t\right)={\displaystyle \sum _{i=1}^n}\left[|e_i{\left(t\right)|}^q+{|v_i\left(t\right)|}^q\right].$$

(53)

By adopting a similar proof procedure to that for Theorem 2, it can be derived that

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill D^{+}U\left(t\right)& ⩽{\mathsf{\Theta }}_1\left(t\right)U\left(t\right)+{\mathsf{\Theta }}_2\left(t\right)U(t-\delta \left(t\right)),\hfill \\ \hfill U\left(t_k\right)& ⩽{\overline{\mu }}_{k}U(t_k^{-}-{\sigma }_k).\hfill \end{array}\right.\end{array}$$

(54)

Based on Equation (54) and Lemma 2, it can be concluded that

$$U\left(t\right)⩽{\rho }^{\frac{1}{q}}{\displaystyle \underset{s\in \left[{\overline{t}}_0,t_0\right]}{sup}}{U}_i\left(s\right)exp\left\{-\frac{\alpha \left(t\right)}{q}\right\},$$

(55)

which implies that

$${∥z\left(t\right)∥}_q⩽{\rho }^{\frac{1}{q}}{\displaystyle \underset{s\in \left[{\overline{t}}_0,t_0\right]}{sup}}{∥z_i\left(s\right)∥}_{q}exp\left\{-\frac{\alpha \left(t\right)}{q}\right\}.$$

(56)

□

Remark 5. 

It can be seen that various synchronizations of ICGNNs with time delays have been investigated, including exponential synchronization [34], asymptotic synchronization based on adaptive control [35,36], finite-time synchronization [37], and fixed-time synchronization [38]. The above results require that the delays are bounded and impulsive effects neglected. In our article, we analyze the α-synchronization of non-autonomous ICGNNs with UDs and DIs. Additionally, compared with the results in [40], more general NNs and the effects of delayed impulses are further considered.

Remark 6. 

It is noted that all the findings in our paper consider the case of unbounded delays. Actually, these findings can also be applied in the case of bounded delays, which can be proved by a similar procedure. Specifically, in Theorem 1 and Theorem 3, if we let ${\alpha }_0=\epsilon t$ and $0\le {\delta }_i\left(t\right)\le \overline{\delta }$, then conditions (30) and (46) are reduced to ${\mathsf{\Theta }}_1\left(t\right)+{\mathsf{\Theta }}_2\left(t\right)exp\left(\epsilon \overline{\delta }\right)+\epsilon <0$ and ${\mathsf{\Theta }}_1\left(t\right)+{\mathsf{\Theta }}_2\left(t\right)exp\left(\epsilon \overline{\delta }\right)+\epsilon <-\frac{ln{\theta }_k}{t_k-t_{k-1}}$, respectively. Correspondingly, the exponential synchronization of ICGNNs can be realized.

Remark 7. 

As is well known, impulses are ubiquitous in many practical applications, including circuit systems, ecological systems, and control engineering. Specifically, the practical exponential stability [46] of impulsive stochastic food chain systems and the synchronization [47] of epidemic systems with delayed impulses have been analyzed. Moreover, the theories of stability and synchronization for various practial systems can be further developed.

4. Simulation Examples

In this section, two examples and simulations are provided to verify the validity of the obtained theoretical findings.

Example 1. 

Let us consider the following ICGNNs with unbounded time delays and delayed impulses:

$$\begin{array}{cc}\hfill \frac{d^2{\mathcal{X}}_i\left(t\right)}{d{t}^2}=& -{\lambda }_i\left(t\right)\frac{d{\mathcal{X}}_i\left(t\right)}{dt}-{\beta }_i\left({\mathcal{X}}_i\left(t\right)\right)[h_i\left({\mathcal{X}}_i\left(t\right)\right)-{\displaystyle \sum _{j=1}^n}{d}_{ij}\left(t\right){\mathfrak{f}}_j\left({\mathcal{X}}_j\left(t\right)\right)\hfill \\ \hfill & -{\displaystyle \sum _{j=1}^n}{b}_{ij}\left(t\right){\mathfrak{g}}_j\left({\mathcal{X}}_j\left(t-\delta \left(t\right)\right)\right)]+I_i\left(t\right),i=1,2,\hfill \end{array}$$

(57)

where ${\lambda }_i\left(t\right)=\frac{1}{4(1+t)}+4.5$, ${\beta }_i\left({\mathcal{X}}_i\left(t\right)\right)=2+\frac{1}{4(1+{\mathcal{X}}_i^2)}$, $h_i\left({\mathcal{X}}_i\left(t\right)\right)={\mathcal{X}}_i$, ${\mathfrak{f}}_j\left({\mathcal{X}}_j\left(t\right)\right)={\mathfrak{g}}_j\left({\mathcal{X}}_j\left(t\right)\right)=\frac{1}{16}sin\left({\mathcal{X}}_j\left(t\right)\right)$, $K_i\left(t\right)=-5$, $I_i\left(t\right)=\frac{1}{4}$, ${\sigma }_k=\frac{1}{4}$, ${\varphi }_k^1=\frac{1}{3}$, ${\varphi }_k^2=\frac{1}{2}$, $H_i\left({\mathcal{X}}_i\left(t\right)\right)={\beta }_i\left({\mathcal{X}}_i\left(t\right)\right)h_i\left({\mathcal{X}}_i\left(t\right)\right)=2{\mathcal{X}}_i+\frac{{\mathcal{X}}_i}{4(1+{\mathcal{X}}_i^2)}$, and

$$\begin{array}{c}\hfill {\left(d_{ij}\left(t\right)\right)}_{n\times n}=\left(\begin{array}{cc}\frac{1}{1+t}& -\frac{2}{3(1+t)}\\ -\frac{1}{1+t}& \frac{2}{1+t}\end{array}\right),{\left(b_{ij}\left(t\right)\right)}_{n\times n}=\left(\begin{array}{cc}-\frac{1}{1+t}& \frac{1}{4(1+t)}\\ \frac{1}{2(1+t)}& \frac{3}{1+t}\end{array}\right).\end{array}$$

Through calculations, it can be verified that $2⩽{\beta }_i\left({\mathcal{X}}_i\left(t\right)\right)⩽\frac{9}{4}$, $|{\beta }_i^{\prime }\left({\mathcal{X}}_i\left(t\right)\right)|⩽\frac{1}{4}$, $\frac{7}{4}\le H_i^{\prime }\left({\mathcal{X}}_i\left(t\right)\right)\le \frac{9}{4}$, $|L_i\left(t\right)-H^{\prime }\left(\mathcal{X}\right)|⩽\frac{1}{1+t}+\frac{1}{4}$,

$$\begin{array}{c}\hfill |{\mathfrak{f}}_j\left({\xi }_1\right)-{\mathfrak{f}}_j\left({\xi }_2\right)|⩽\frac{1}{16}|{\xi }_1-{\xi }_2|,|{\mathfrak{f}}_j\left({\mathcal{X}}_i\left(t\right)\right)|⩽\frac{1}{16},\\ \hfill |{\mathfrak{g}}_j\left({\xi }_1\right)-{\mathfrak{g}}_j\left({\xi }_2\right)|⩽\frac{1}{16}|{\xi }_1-{\xi }_2|,|{\mathfrak{g}}_j\left({\mathcal{X}}_i\left(t\right)\right)|⩽\frac{1}{16}.\end{array}$$

Moreover, taking ${\zeta }_i=4$, $l_{\mathfrak{f}}=l_{\mathfrak{g}}=\frac{1}{16}$, $F_j=G_j=\frac{1}{16}$, ${\overline{\beta }}_i=\frac{9}{4}$, ${\mathsf{\Lambda }}_i=\frac{1}{4}$, $C=\frac{5}{4}$, $\alpha \left(t\right)=ln(1+t)$, $\delta \left(t\right)=\frac{1}{5}t$, ${\mu }_k=\frac{1}{2}$, $t⩾t_0$, one can determine that

$$\begin{array}{c}\hfill {\mathsf{\Theta }}_1\left(t\right)+{\mathsf{\Theta }}_2\left(t\right)exp(\alpha \left(t\right)-\alpha (t-\delta \left(t\right))+D^{+}\alpha \left(t\right)=-\frac{11}{4}+\frac{6483}{3072(1+t)}<0,\end{array}$$

(58)

where ${\mathsf{\Theta }}_1\left(t\right)=max\{{\displaystyle \underset{1\le i\le n}{max}}(-{\zeta }_i+{\sum }_{j=1}^n|d_{ji}\left(t\right)|l_{\mathfrak{f}}{\overline{\beta }}_j+{\mathsf{\Lambda }}_i({\sum }_{j=1}^n|d_{ij}|F_j+{\sum }_{j=1}^n|b_{ij}|G_j)+C)\}$, ${\displaystyle \underset{1\le i\le n}{max}}\{1-P_i\left(t\right)+K_i\left(t\right)\}\}=max\left\{-\frac{11}{4}+\frac{207}{384(1+t)},-\frac{1}{1+t}-4.5\right\}=-\frac{11}{4}+\frac{207}{384(1+t)}<0$, ${\mathsf{\Theta }}_2\left(t\right)={\displaystyle \underset{1\le i\le n}{max}}{\sum }_{j=1}^n\left|b_{ji}\left(t\right)\right|l_{\mathfrak{g}}{\overline{\beta }}_j=\frac{117}{256(1+t)}$.

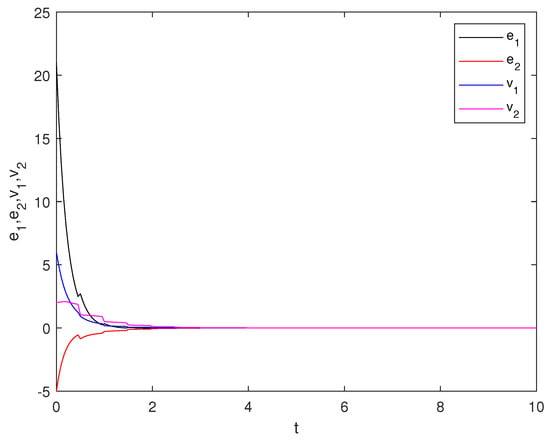
Hence, all the conditions of Theorem 1 are satisfied, and we can infer that the response system is globally polynomially synchronized with drive system (57). Furthermore, Figure 1 shows the evolution of synchronization errors $e_1\left(t\right)$, $e_2\left(t\right)$, $v_1\left(t\right)$, and $v_2\left(t\right)$ with initial values $e_1\left(0\right)=21$, $e_2\left(0\right)=-5$, $v_1\left(0\right)=6$, and $v_2\left(0\right)=2$. We can observe that the error trajectories converge to a zero vector under feedback control in Figure 1.

Figure 1. The evolution of synchronization errors $e_1\left(t\right)$, $e_2\left(t\right)$, $v_1\left(t\right)$, and $v_2\left(t\right)$ with initial values $e_1\left(0\right)=21$, $e_2\left(0\right)$=−5, $v_1\left(0\right)=6$, and $v_2\left(0\right)=2$ in Example 1.

Example 2. 

Reconsider system (57) with the corresponding parameters and functions: ${\lambda }_i\left(t\right)=\frac{11}{4}$, ${\beta }_i\left({\mathcal{X}}_i\left(t\right)\right)=1.5+\frac{1}{2(1+{\mathcal{X}}_i^2)}$, $h_i\left({\mathcal{X}}_i\left(t\right)\right)={\mathcal{X}}_i$, $H_i\left({\mathcal{X}}_i\left(t\right)\right)={\beta }_i\left({\mathcal{X}}_i\left(t\right)\right)h_i\left({\mathcal{X}}_i\left(t\right)\right)=1.5{\mathcal{X}}_i+\frac{{\mathcal{X}}_i}{2(1+{\mathcal{X}}_i^2)}$, ${\mathfrak{f}}_j\left({\mathcal{X}}_j\left(t\right)\right)=\frac{1}{12}sin({\mathcal{X}}_j\left(t\right)$, ${\mathfrak{g}}_j\left({\mathcal{X}}_j\left(t\right)\right)=\frac{1}{9}sin({\mathcal{X}}_j\left(t\right)$, $K_i\left(t\right)=0.5$, $I_i\left(t\right)=\frac{1}{2}$, $t_k=\frac{k}{2},$$k=0,1,2,\cdots$, ${\sigma }_k=\frac{1}{6}$, ${\varphi }_k^1=\frac{1}{7}$, ${\varphi }_k^2=\frac{1}{6}$, and

$$\begin{array}{c}\hfill \left(d_{ij}\left(t\right)\right)=\left(\begin{array}{cc}\frac{2}{1+t}& -\frac{1}{1+t}\\ \frac{4}{5(1+t)}& \frac{2}{3(1+t)}\end{array}\right),{\left(b_{ij}\left(t\right)\right)}_{n\times n}=\left(\begin{array}{cc}-\frac{1+\sqrt{t}}{2(1+t)}& \frac{1+\sqrt{t}}{1+t}\\ \frac{1+\sqrt{t}}{3(1+t)}& -\frac{1+\sqrt{t}}{2(1+t)}\end{array}\right).\end{array}$$

It can be verified that $1.5⩽{\beta }_i\left({\mathcal{X}}_i\left(t\right)\right)⩽2$, $|{\beta }_i^{\prime }\left({\mathcal{X}}_i\left(t\right)\right)|⩽0.5$, $1\le H_i^{\prime }\left({\mathcal{X}}_i\left(t\right)\right)\le 2$, $t_k-t_{k-1}=\frac{1}{2}$, ${\mu }_k=\frac{1}{6}$, ${\theta }_k=exp\left\{\alpha \left(t_k\right)-\alpha \left(t_k-{\sigma }_k\right)\right\}{\mu }_k=\frac{1}{5}$,

$$\begin{array}{c}\hfill |{\mathfrak{f}}_j\left({\xi }_1\right)-{\mathfrak{f}}_j\left({\xi }_2\right)|⩽\frac{1}{12}|A{\xi }_1-{\xi }_2|,|{\mathfrak{f}}_j\left({\mathcal{X}}_i\left(t\right)\right)|⩽\frac{1}{12},\\ \hfill |{\mathfrak{g}}_j\left({\xi }_1\right)-{\mathfrak{g}}_j\left({\xi }_2\right)|⩽\frac{1}{9}|{\xi }_1-{\xi }_2|,|{\mathfrak{g}}_j\left({\mathcal{X}}_i\left(t\right)\right)|⩽\frac{1}{9}.\end{array}$$

Set ${\zeta }_i=2$, $l_{\mathfrak{f}}=\frac{1}{12}$, $l_{\mathfrak{g}}=\frac{1}{9}$$F_j=\frac{1}{12}$, $G_j=\frac{1}{9}$, ${\overline{\beta }}_i=2$, ${\mathsf{\Lambda }}_i=0.5$, $C=0.5$, $\alpha \left(t\right)=ln(1+t)$, $\delta \left(t\right)=t-\sqrt{t}$, $\rho =5$. Through calculation, one can derive that

$$\begin{array}{c}{\mathsf{\Theta }}_1\left(t\right)+\rho {\mathsf{\Theta }}_2\left(t\right)exp(\alpha \left(t\right)-\alpha (t-\delta \left(t\right))+D^{+}\alpha \left(t\right)-\frac{ln{\theta }_{k-1}}{t_k-t_{k-1}}\hfill \\ ⩽-1.5+\frac{191+20(1+\sqrt{t})}{120(1+t)}+\frac{5}{3}-2ln5\hfill \\ <0,\hfill \end{array}$$

(59)

which also means that

$${\mathsf{\Theta }}_1\left(t\right)+\rho {\mathsf{\Theta }}_2\left(t\right)exp(\alpha \left(t\right)-\alpha (t-\delta \left(t\right))+D^{+}\alpha \left(t\right)⩽\frac{ln{\theta }_{k-1}}{t_k-t_{k-1}},$$

(60)

where ${\mathsf{\Theta }}_1\left(t\right)=max\{{\displaystyle \underset{1\le i\le n}{max}}(-{\xi }_i+{\sum }_{j=1}^n|d_{ji}\left(t\right)|l_{\mathfrak{f}}{\overline{\beta }}_j+{\mathsf{\Lambda }}_i({\sum }_{j=1}^n|d_{ij}|F_j+{\sum }_{j=1}^n|b_{ij}|G_j)+C)\}$,

${\displaystyle \underset{1\le i\le n}{max}}\{1-P_i\left(t\right)+K_i\left(t\right)\}\}=max\left\{-1.5+\frac{71+20(1+\sqrt{t})}{120(1+t)},-\frac{1}{2(1+t)}-2\right\}=-1.5+\frac{71+20(1+\sqrt{t})}{120(1+t)}<0$, ${\mathsf{\Theta }}_2\left(t\right)={\displaystyle \underset{1\le i\le n}{max}}{\sum }_{j=1}^n\left|b_{ji}\left(t\right)\right|l_{\mathfrak{g}}{\overline{\beta }}_j=\frac{1+\sqrt{t}}{3(1+t)}$.

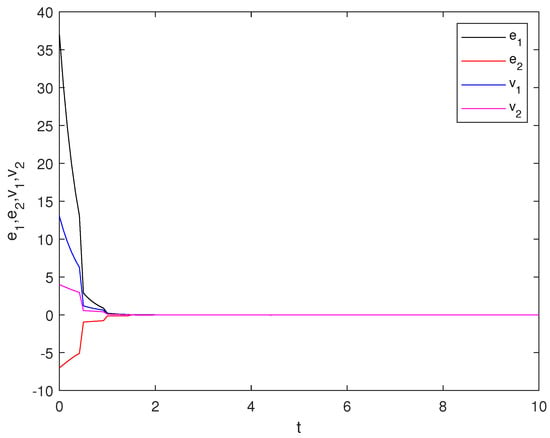
Therefore, all the conditions of Theorem 2 are satisfied, and we can further infer that global polynomially synchronization is achieved between the drive system and the response system. Furthermore, Figure 2 shows the evolution of synchronization errors $e_1\left(t\right)$, $e_2\left(t\right)$, $v_1\left(t\right)$, and $v_2\left(t\right)$ with initial values $e_1\left(0\right)=37$, $e_2\left(0\right)=-7$, $v_1\left(0\right)=13$, and $v_2\left(0\right)=4$. Obviously, it can be found that the error trajectories converge to a zero vector under feedback control in Figure 2.

Figure 2. The evolution of synchronization errors $e_1\left(t\right)$, $e_2\left(t\right)$, $v_1\left(t\right)$, and $v_2\left(t\right)$ with initial values $e_1\left(0\right)=37$, $e_2\left(0\right)=$ −7, $v_1\left(0\right)=13$, and $v_2\left(0\right)=4$ in Example 2.

Remark 8. 

It can be observed that the polynomial synchronization of ICGNNs is achieved in the above examples by selecting $\alpha \left(t\right)=ln(1+t)$. Specifically, in Example 1, impulses can be viewed as perturbations, while impulses can be considered as stabilizing sources in Example 2. Moreover, since the delayed impulses, unbounded delays, and time-variable coefficients are taken into account, the findings in [34,35,36,37,38] cannot be applied to the above circumstances, but our theoretical results can cope with their validity efficiently.

5. Conclusions

This paper aimed to deal with the issue of the $\alpha$-synchronization of a class of non-autonomous unbounded delayed inertial Cohen–Gossberg neural networks with delayed impulses. Some novel criteria for the $\alpha$-synchronization of ICGNNs were established. Concretely, two non-autonomous impulsive differential inequalities were proposed, where unbounded delays, delayed impulses, and time-variable coefficients were incorporated. Furthermore, based on the proposed impulsive differential inequalities and Lyapunov function approach, feedback controllers were designed, and several sufficient conditions were given which guaranteed the realization of synchronization. Furthermore, from the perspective of $\alpha$-stability, different types of synchronization, such as exponential synchronization and power synchronization, could be analyzed based on various unbounded delays. This also revealed that delayed impulses can be viewed as perturbations or stabilizing sources. In the future, the stability and synchronization of discrete network systems and other practical systems with unbounded delays and delayed impulses will be further explored.