Residual Strength Modeling and Reliability Analysis of Wind Turbine Gear under Different Random Loadings
Abstract
:1. Introduction
2. Residual Strength Model of Multistage Loading Based on the Fatigue Damage Accumulation Theory
2.1. Nonlinear Fatigue Damage Accumulation Model
2.2. Boundary Conditions of the Residual Strength Model
2.3. Residual Strength Model under Multistage Loading
2.4. Verification of Residual Strength Model
2.4.1. One-Level Loading
2.4.2. Two-Level Loading
3. Modeling of Residual Strength of Wind Turbine Gears
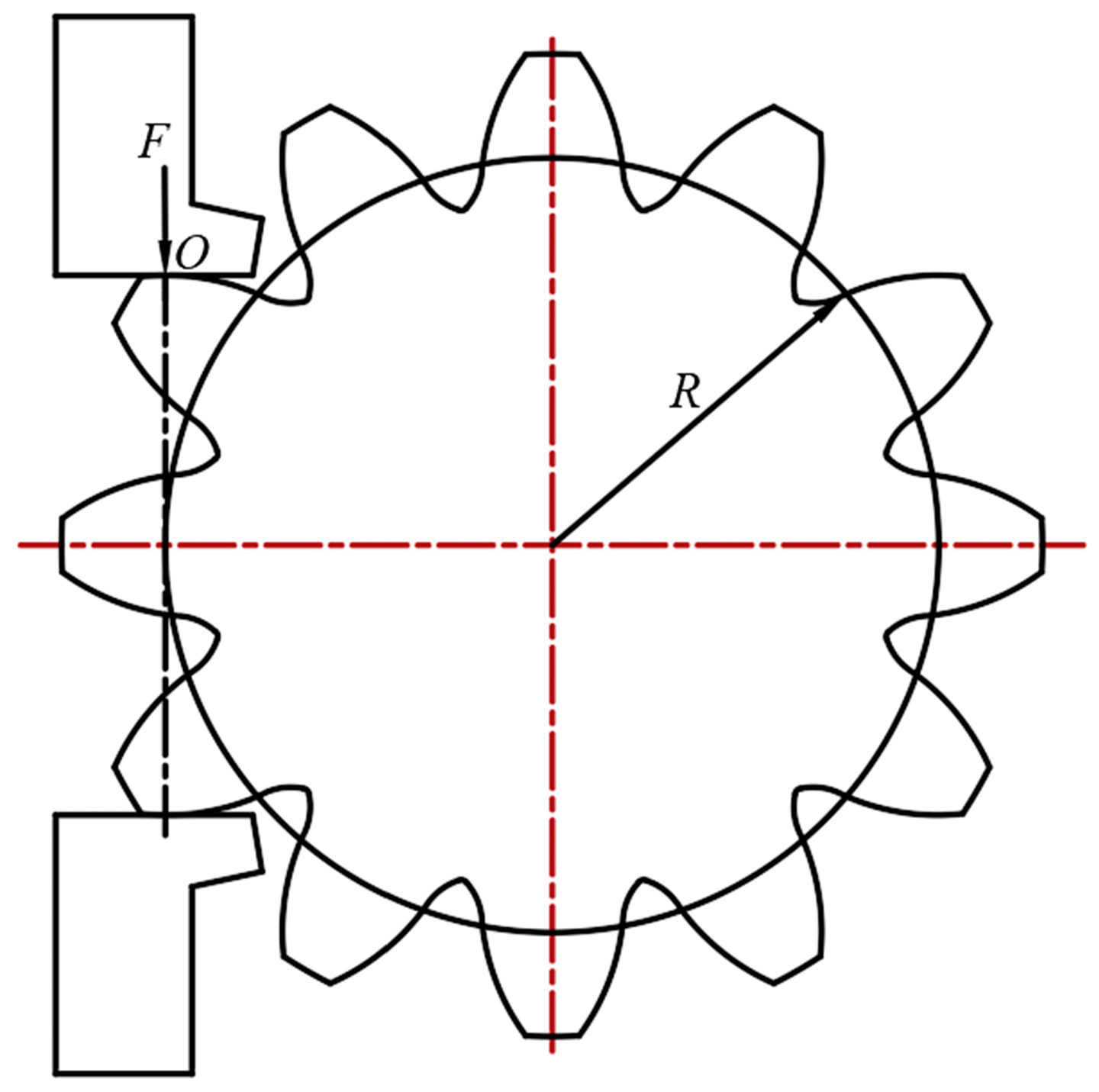
3.1. Fatigue Failure Mode Analysis of Gears and Fatigue Life Curve Fitting
- (1)
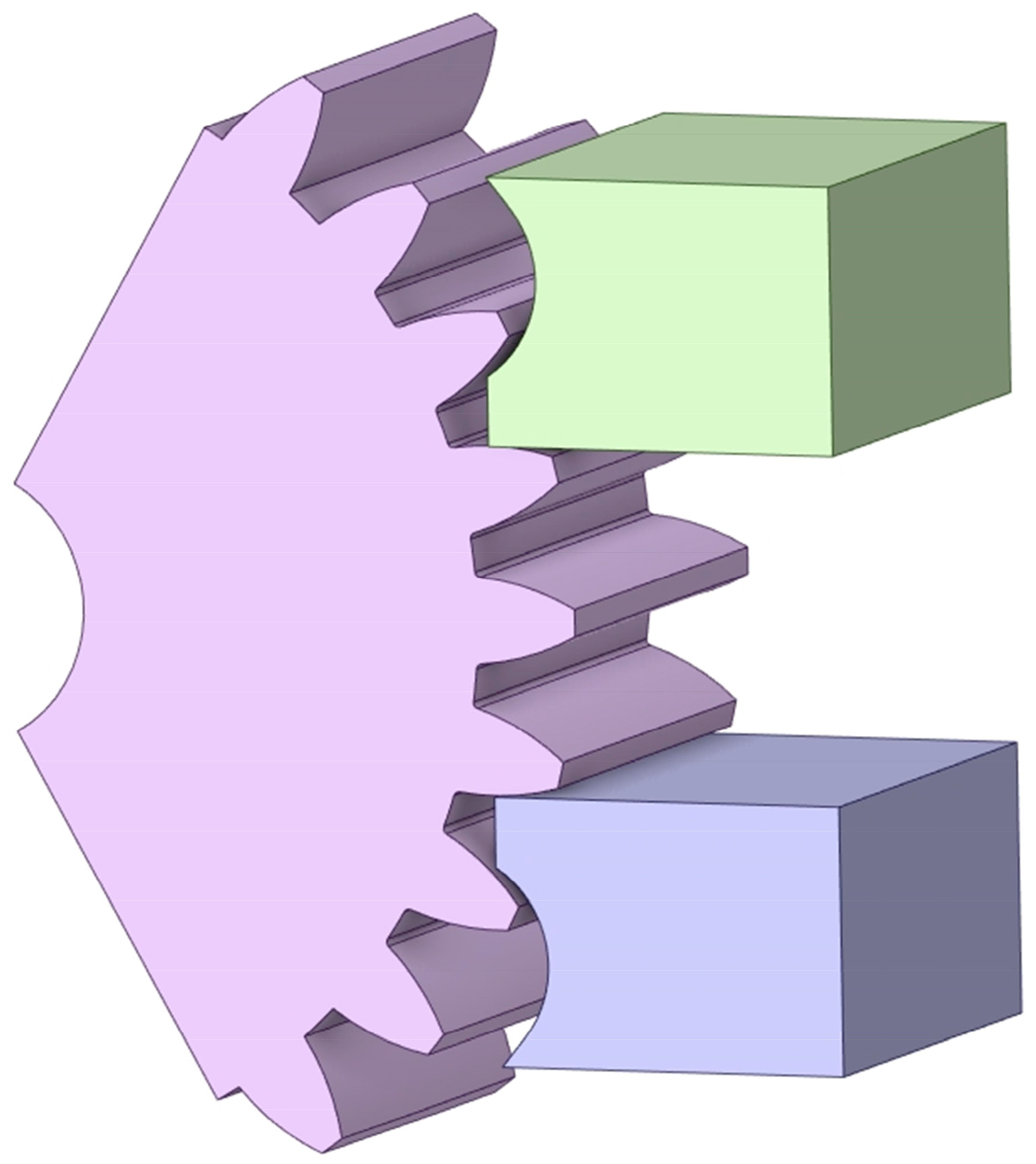
- Establish a three-dimensional model as shown in Figure 7.
- (2)
- Set the material parameters. The elastic modulus of the material 20CrMnTi is 207 GPa, Poisson’s ratio is 0.25, the hardness is 40 HB, and the tensile strength is 2747 MPa. Considering the influence of the deformation of the contact head on the simulation results, it is set as a rigid body.
- (3)
- Mesh generation. Firstly, the whole mesh is divided by a multi-zone. Then, the contact surface between the gear and the upper and lower support heads is densified locally, and the mesh of the tooth root part is refined.
- (4)
- Set the contact type. In the part of the contact between the support head and the tooth surface, the contact is not separated.
- (5)
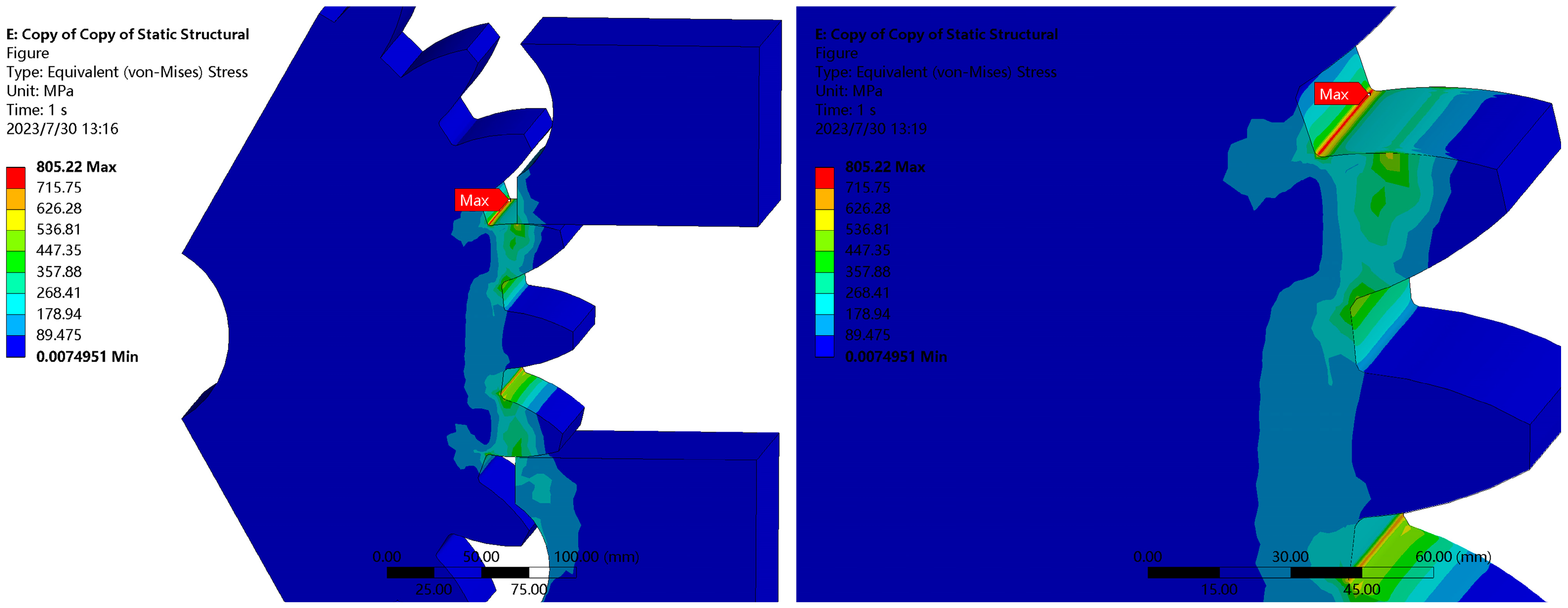
- Set loads and boundary conditions. The upper support head only retains the movement of the z-axis. Fully fixed constraints are applied to the lower support head. The inner hole of the gear only retains the rotational freedom of the y-axis. A vertical downward load is applied to the upper end of the upper support head. Five groups of loads are set up, which are 200 KN, 400 KN, and 600 KN, respectively. In this study, the simulation results of 400 KN are employed to illustrate the results.
3.2. Bending Stress Distribution of Gear under Four-Season Loads
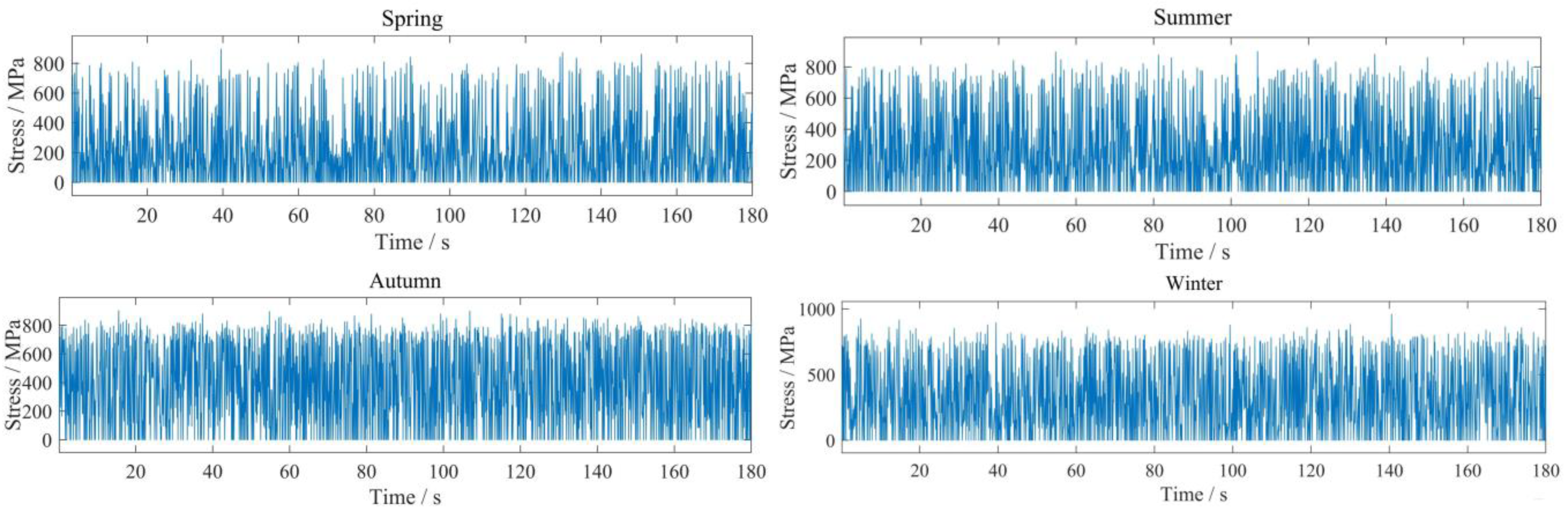
3.2.1. The Bending Stress of Gear Is Calculated by Wind Speed
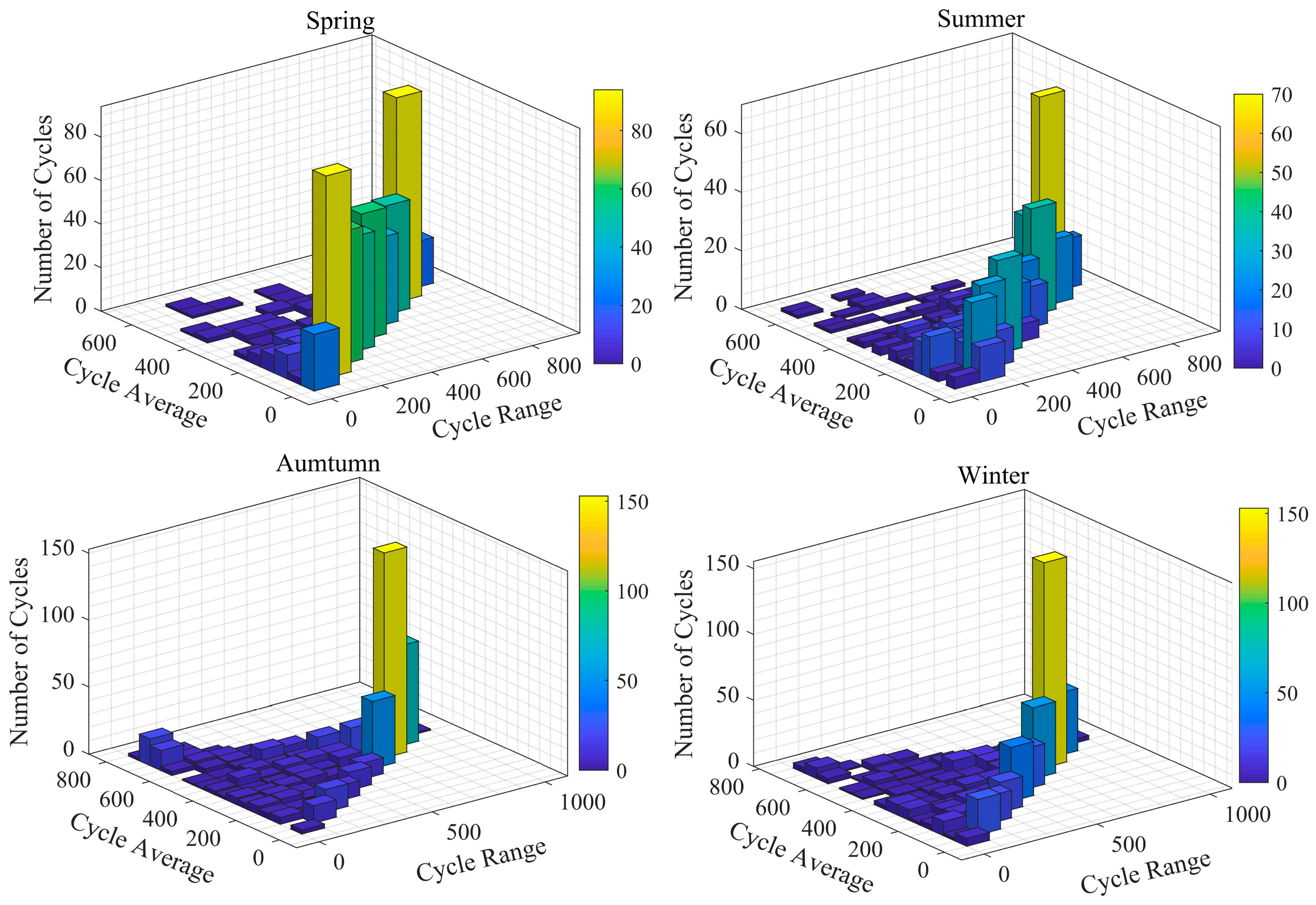
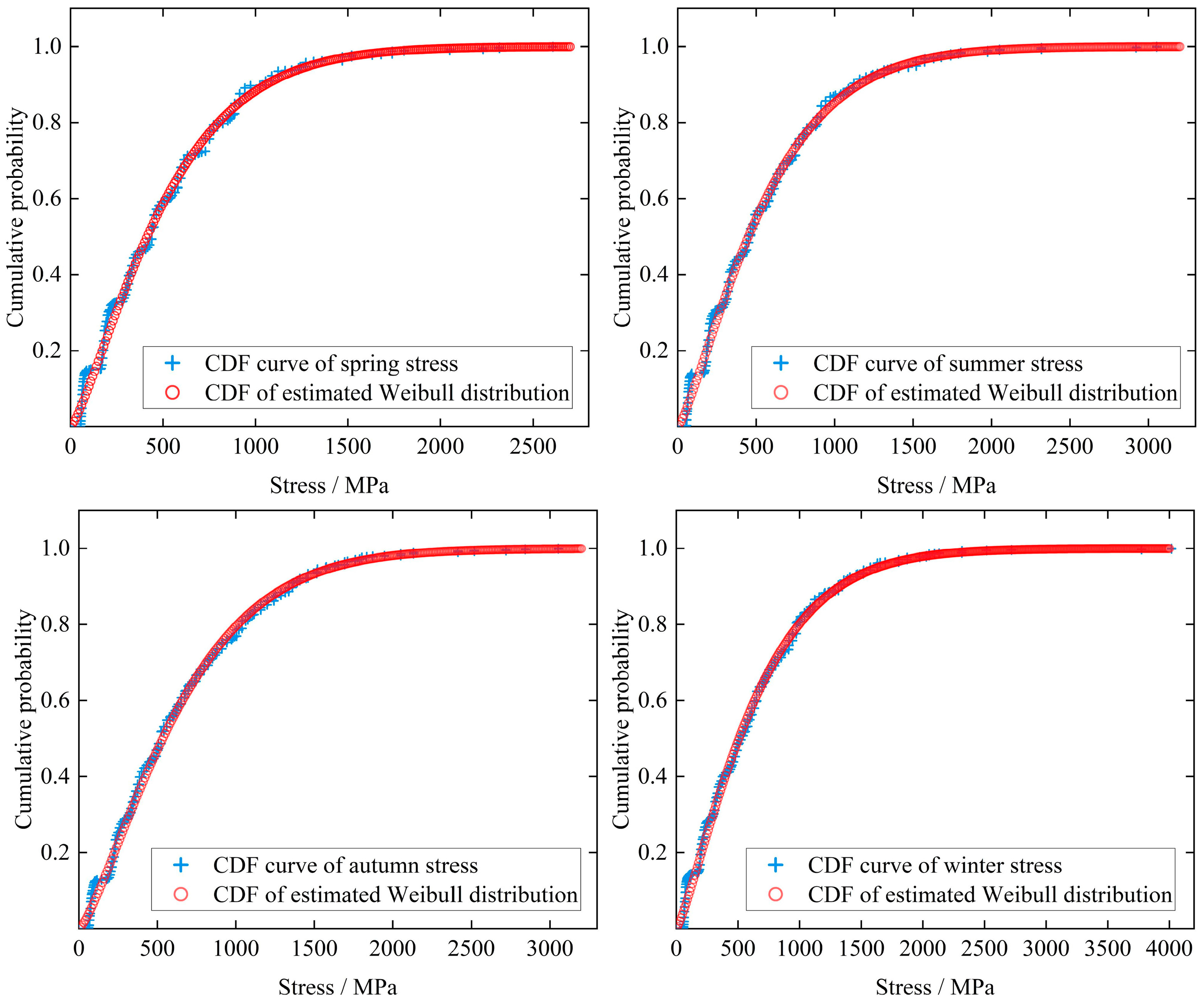
3.2.2. Random Stress Is Treated as Symmetrical Cyclic Stress
4. Analysis of the Residual Strength and Dynamic Reliability of Gear
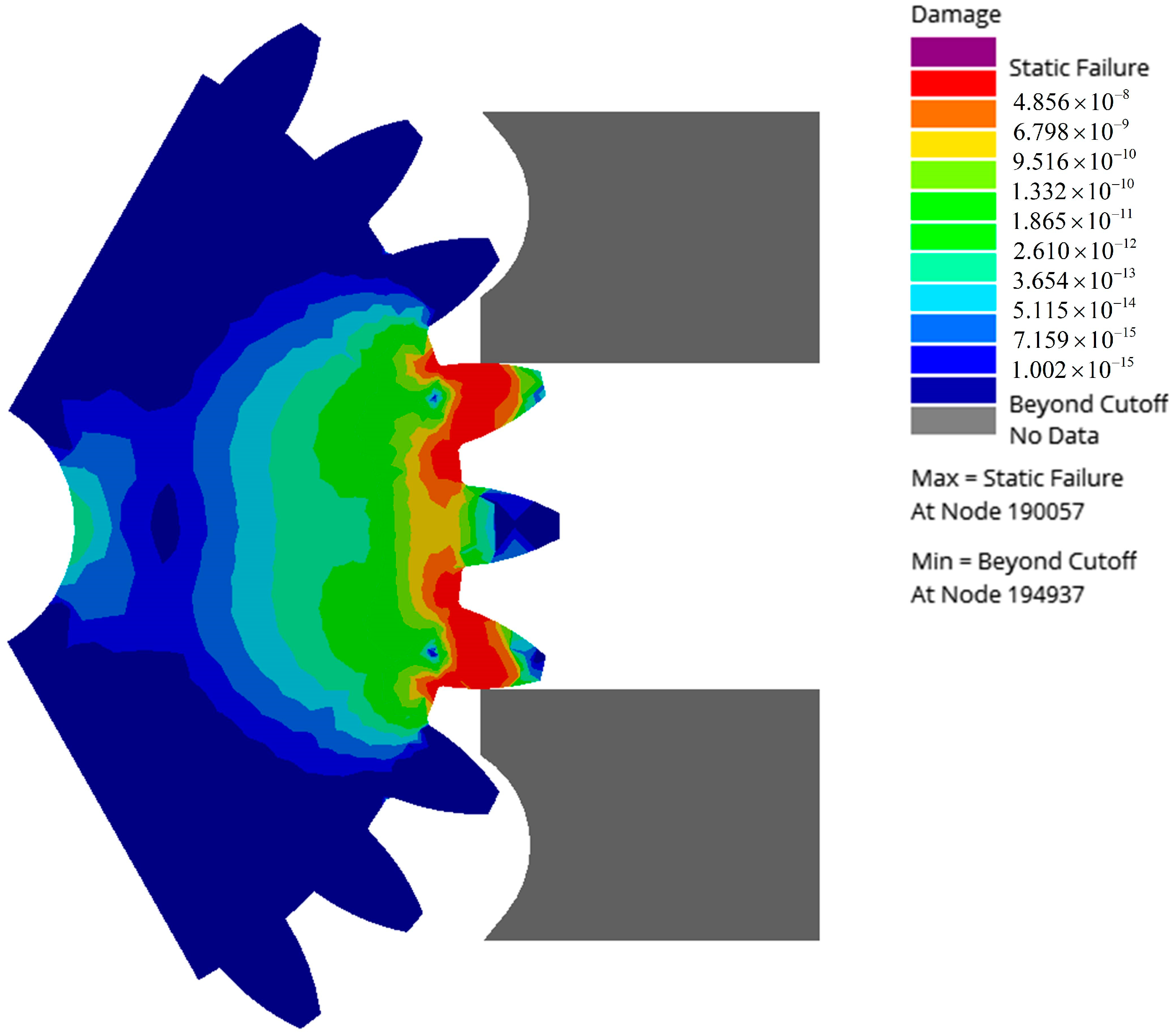
4.1. Residual Strength Model for Tooth Root Bending Strength
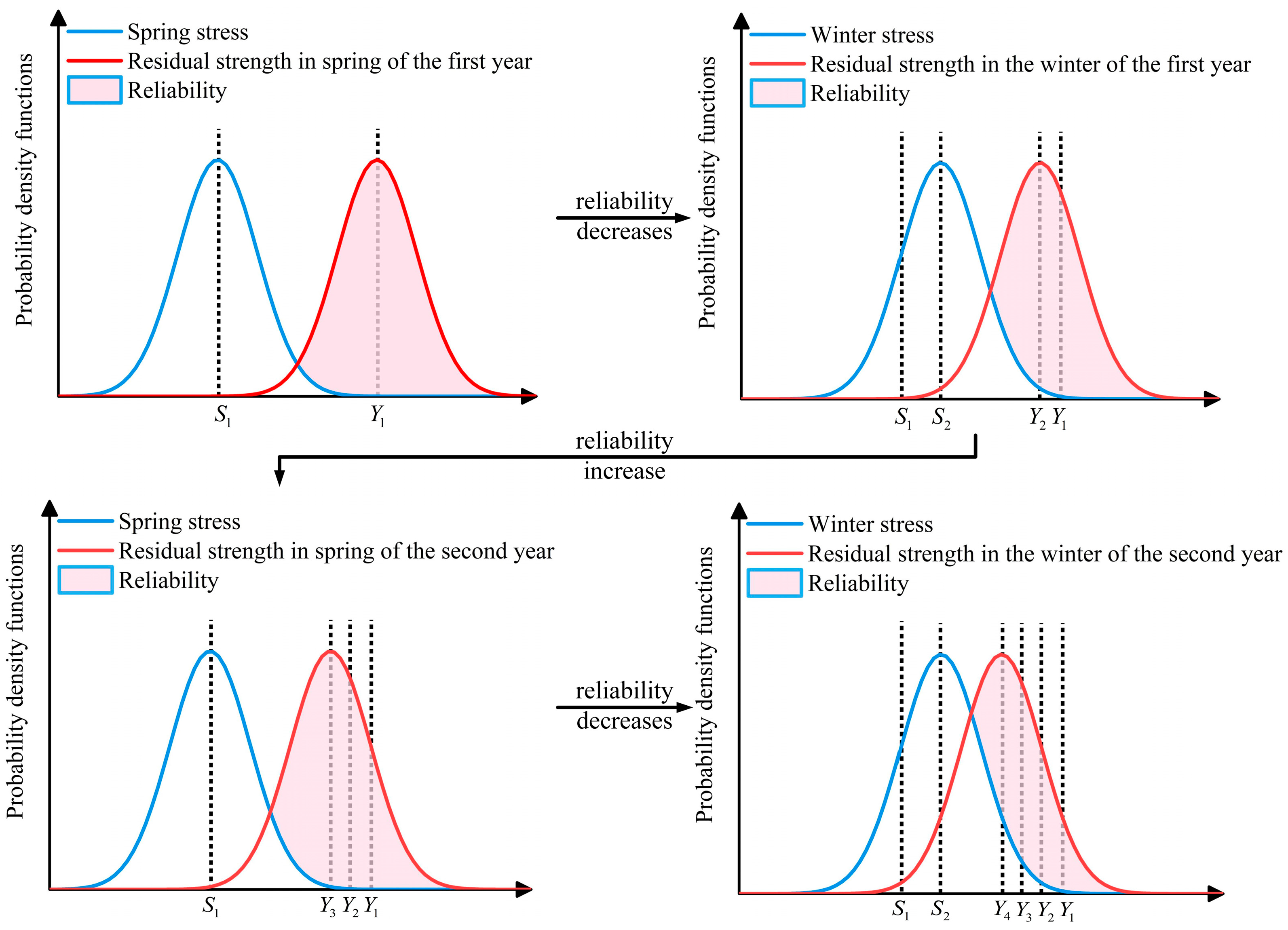
4.2. Gear Reliability Analysis Considering the Failure of Tooth Root Bending
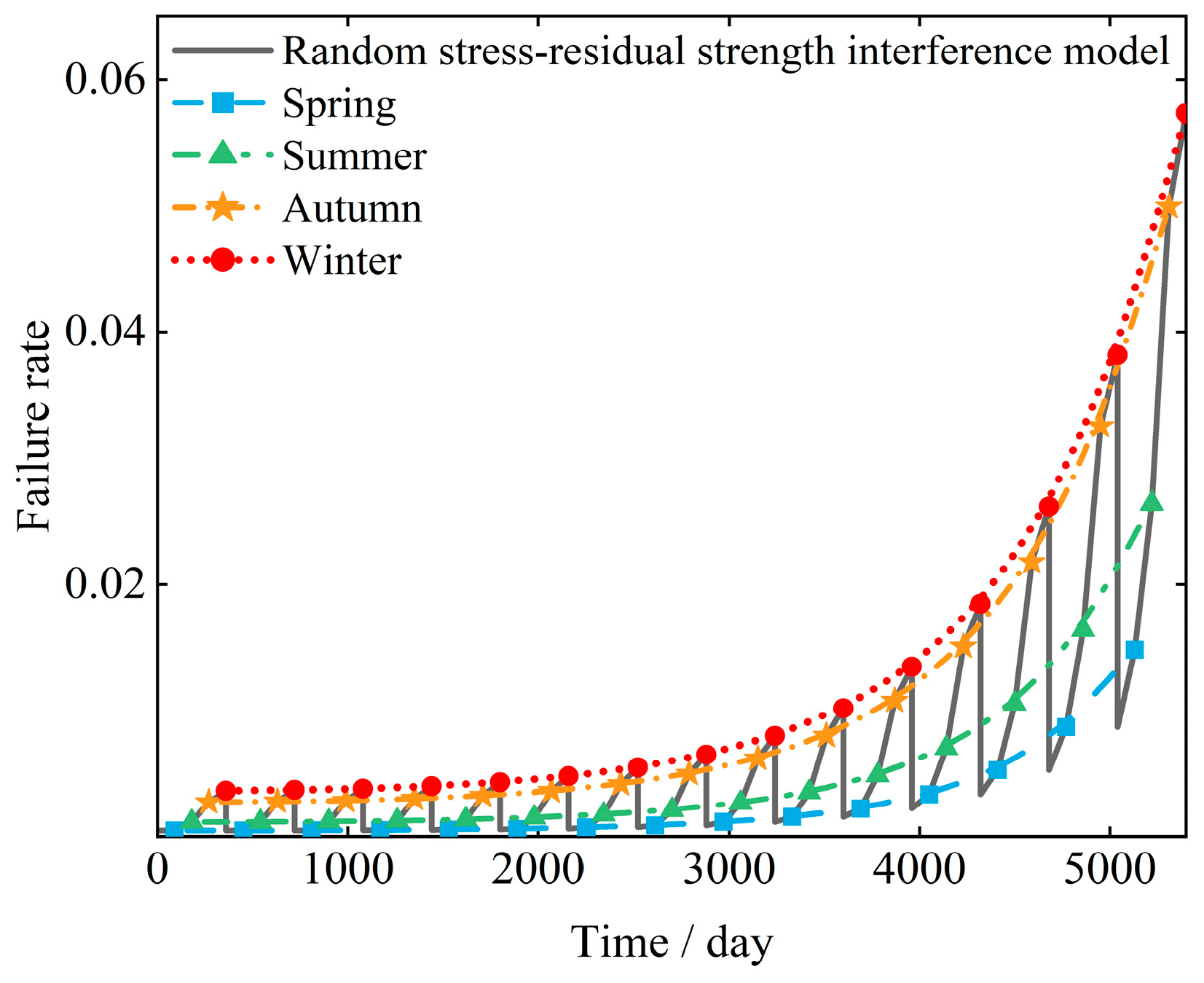
- The overall decreasing trend of reliability is determined by the degradation trend of gear strength. The gear’s reliability in each season decreases monotonically from year to year, which indicates that the reliability of the gear has decreased compared to the previous year in all seasons. Due to the sudden increase in the decay rate of the residual strength, the reliability of the gear suddenly decreases rapidly in the 15th year.
- By observing the distance between the four seasonal reliability curves, it can be found that the distance between the summer and autumn reliability curves is the largest, the distance between the spring and summer curves ranks second, and the distance between the autumn and winter curves is the smallest. It can be considered that the impact of load amplitudes in the four seasons causes a change in the distance between the reliability curves of adjacent seasons. In Table 4, it can be seen that there is a significant difference in load amplitudes between summer and autumn, resulting in a significant downward shift in the reliability curve from summer to autumn. The difference in amplitude between autumn and winter loads is the smallest, so the overall downward movement of the reliability curve from autumn to winter is relatively small.
- The difference in reliability between the four seasons is relatively small in the first few years. In the first nine years, the reliability of gears fluctuated between 1 and 0.99 per year. As the service life increases, the reliability difference of the gear in the four seasons of the same year becomes increasingly significant. In the 15th year, the reliability fluctuation range of the gear within one year is 0.99 to 0.94. This is affected by the randomness of decreasing residual gear strength. As time passes, the range of residual gear strength increases, resulting in a greater range of changes in gear reliability throughout the year.
5. Conclusions
- (1)
- The proposed residual strength model is validated using experimental data from two materials, and the calculation results showed that the proposed model has good predictive performance. In addition, by comparing its predictive performance with the classical Schaff’s model, it can be concluded that the proposed model can more accurately predict the residual strength of wind turbine gears.
- (2)
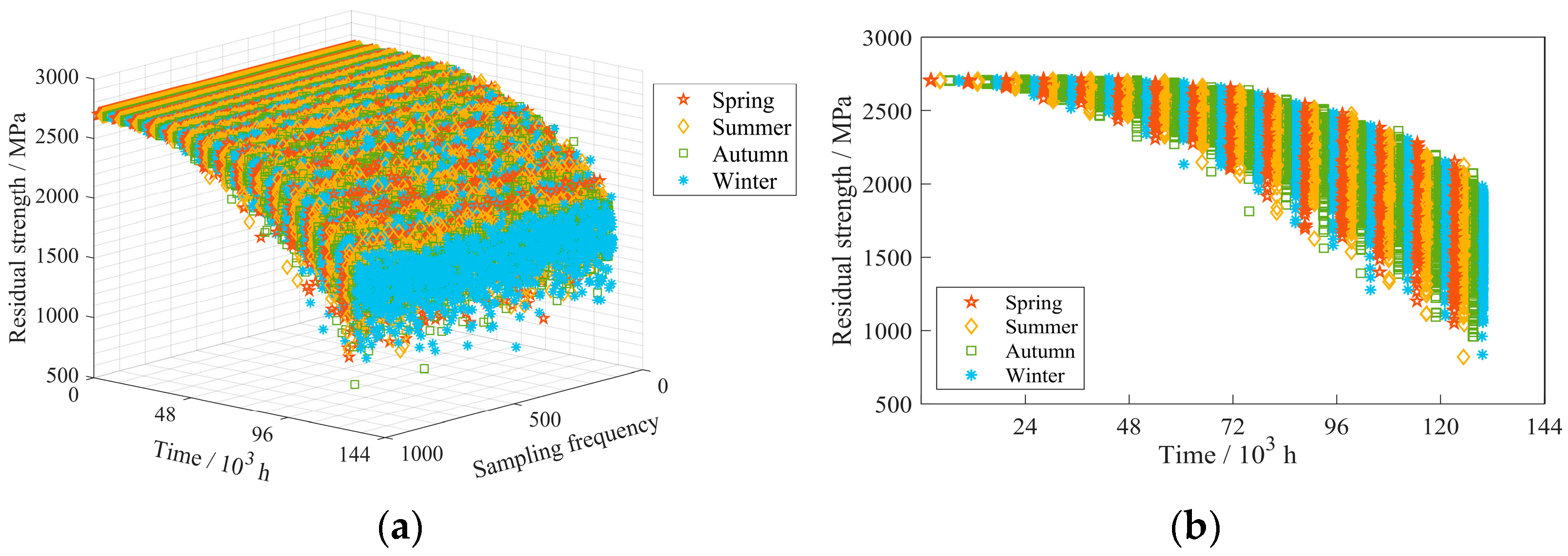
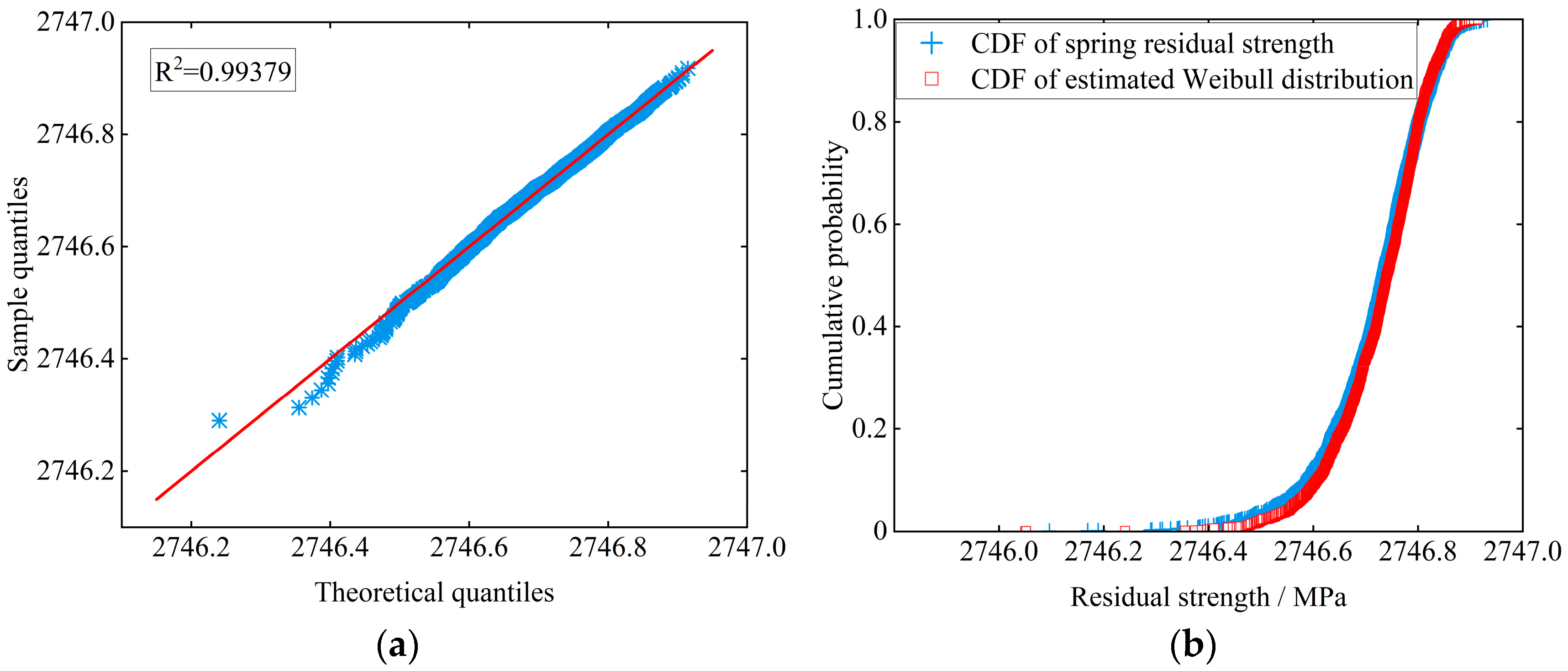
- The residual strength of the gear at a determined time point is a random variable that follows the Weibull distribution and is affected by the randomness of the load. The overall residual strength of the gear shows a decreasing trend. Moreover, the randomness of the residual strength of the gear at a certain time becomes stronger, and the range of residual strength values becomes wider as the service time increases.
- (3)
- Wind load amplitudes in each season influence the reliability of wind turbine gears. Initially, there is a small difference in reliability between seasons, but as the service time increases, the difference becomes more significant. Overall, the reliability of gears decreases monotonically over time in each season. However, there is a jump in reliability due to the effect of wind speed on the gears in different seasons.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pérez, J.M.P.; Márquez, F.P.G.; Tobias, A.; Papaelias, M. Wind turbine reliability analysis. Renew. Sustain. Energy Rev. 2013, 23, 463–472. [Google Scholar] [CrossRef]
- Kusiak, A.; Li, W.Y. The prediction and diagnosis of wind turbine faults. Renew. Energy 2011, 36, 16–23. [Google Scholar] [CrossRef]
- Chen, S.; Qiao, Z.J.; Xie, C.Y.; Zhu, R.H.; Lai, Z.H.; Xu, X.F.; Zhou, S.T. Transfer condition monitoring across wind turbines using feature alignment and parameter fine-tuning. Meas. Sci. Technol. 2023, 34, 125901. [Google Scholar] [CrossRef]
- Dui, H.; Wang, X.; Zhou, H. Redundancy-based resilience optimization of multi-component systems. Mathematics 2023, 11, 3151. [Google Scholar] [CrossRef]
- Su, H.; Zhao, Y.; Wang, X. Analysis of a state degradation model and preventive maintenance strategies for wind turbine generators based on stochastic differential equations. Mathematics 2023, 11, 2608. [Google Scholar] [CrossRef]
- Costa, Á.M.; Orosa, J.A.; Vergara, D.; Fernández-Arias, P. New tendencies in wind energy operation and maintenance. Appl. Sci. 2021, 11, 1386. [Google Scholar] [CrossRef]
- Meng, D.B.; Yang, S.Y.; De Jesus, A.M.P.; Zhu, S.P. A novel Kriging-model-assisted reliability-based multidisciplinary design optimization strategy and its application in the offshore wind turbine tower. Renew. Energy 2023, 203, 407–420. [Google Scholar] [CrossRef]
- Meng, D.B.; Yang, S.Y.; Lin, T.; Wang, J.P.; Yang, H.F.; Lv, Z.Y. RBMDO using Gaussian mixture model-based second-order mean-value saddlepoint approximation. CMES-Comp. Model. Eng. Sci. 2022, 132, 553–568. [Google Scholar] [CrossRef]
- Meng, D.B.; Yang, S.Y.; He, C.; Wang, H.T.; Lv, Z.Y.; Guo, Y.P.; Nie, P. Multidisciplinary design optimization of engineering systems under uncertainty: A review. Int. J. Struct. Integr. 2022, 13, 565–593. [Google Scholar] [CrossRef]
- Mseddi, A.; Naifar, O.; Rhaima, M.; Mchiri, L.; Makhlouf, A.B. Robust Control for Torque Minimization in Wind Hybrid Generators: An H∞ Approach. Mathematics 2023, 11, 3557. [Google Scholar] [CrossRef]
- Yan, Y. Load characteristic analysis and fatigue reliability prediction of wind turbine gear transmission system. Int. J. Fatigue 2020, 130, 105259. [Google Scholar] [CrossRef]
- Schaff, J.R.; Davidson, B.D. Life prediction methodology for composite structures. Part I—Constant amplitude and two-stress level fatigue. J. Compos. Mater. 1997, 31, 128–157. [Google Scholar] [CrossRef]
- Hahn, H.T.; Kim, R.Y. Proof testing of composite materials. J. Compos. Mater. 1975, 9, 297–311. [Google Scholar] [CrossRef]
- Chou, P.C.; Croman, R. Residual strength in fatigue based on the strength-life equal rank assumption. J. Compos. Mater. 1978, 12, 177–194. [Google Scholar] [CrossRef]
- Ganesan, C.; Joanna, P.S. Fatigue life and residual strength prediction of GFRP composites: An experimental and theoretical approach. Lat. Am. J. Solids Struct. 2018, 15, e72. [Google Scholar] [CrossRef]
- Cheng, H.C.; Hwu, F.S. Fatigue reliability analysis of composites based on residual strength. Adv. Compos. Mater. 2006, 15, 385–402. [Google Scholar] [CrossRef]
- Li, L.; Xie, L.Y.; He, X.H.; Hao, G.B. Strength degradation law of metallic material under fatigue loading. Chin. J. Mech. Eng. 2010, 32, 967–971. [Google Scholar]
- Gao, J.; An, Z. A new probability model of residual strength of material based on interference theory. Int. J. Fatigue 2019, 118, 202–208. [Google Scholar] [CrossRef]
- Jiang, C.J.; Liu, X.T.; Wang, X.L.; Wang, X.; Su, S.C. Interval dynamic reliability analysis of mechanical components under multistage load based on strength degradation. Qual. Reliab. Eng. Int. 2021, 37, 567–582. [Google Scholar] [CrossRef]
- Yang, B.; Fu, K.K.; Lee, J.; Li, Y. Artificial neural network (ANN)-based residual strength prediction of carbon fibre reinforced composites (CFRCs) after impact. Appl. Compos. Mater. 2021, 28, 809–833. [Google Scholar] [CrossRef]
- Lu, H.F.; Xu, Z.D.; Iseley, T.; Matthews, J.C. Novel data-driven framework for predicting residual strength of corroded pipelines. J. Pipeline Syst. Eng. Pract. 2021, 12, 04021045. [Google Scholar] [CrossRef]
- Miao, X.; Zhao, H. Novel method for residual strength prediction of defective pipelines based on HTLBO-DELM model. Reliab. Eng. Syst. Saf. 2023, 237, 109369. [Google Scholar] [CrossRef]
- Meng, D.B.; Yang, S.Y.; De Jesus, A.M.P.; Ferradosaet, T.F.; Zhu, S.P. A novel hybrid adaptive Kriging and water cycle algorithm for reliability-based design and optimization strategy: Application in offshore wind turbine monopile. Comput. Methods Appl. Mech. Eng. 2023, 412, 116083. [Google Scholar] [CrossRef]
- Yu, L.J.; Zhong, S.Y.; Bian, X.D.; Heilman, W.E. Climatology and trend of wind power resources in China and its surrounding regions: A revisit using Climate Forecast System Reanalysis data. Int. J. Climatol. 2016, 36, 2173–2188. [Google Scholar] [CrossRef]
- Whitworth, H.A. Evaluation of the residual strength degradation in composite laminates under fatigue loading. Compos. Struct. 2000, 48, 261–264. [Google Scholar] [CrossRef]
- Miner, M.A. Cumulative damage in fatigue. J. Appl. Mech. 1945, 12, A159–A164. [Google Scholar] [CrossRef]
- Manson, S.S.; Halford, G.R. Practical implementation of the double linear damage rule and damage curve approach for treating cumulative fatigue damage. Int. J. Fract. 1981, 17, 169–192. [Google Scholar] [CrossRef]
- Freudenthal, A.M.; Heller, R.A. On stress interaction in fatigue and a cumulative damage rule. J. Aerosp. Sci. 1959, 26, 431–442. [Google Scholar] [CrossRef]
- Zhu, S.P.; Huang, H.Z. A generalized frequency separation–strain energy damage function model for low cycle fatigue–creep life prediction. Fatigue Fract. Eng. Mater. Struct. 2010, 33, 227–237. [Google Scholar] [CrossRef]
- Zhu, S.P.; Huang, H.Z.; Ontiveros, V.; He, L.P.; Modarres, M. Probabilistic low cycle fatigue life prediction using an energy-based damage parameter and accounting for model uncertainty. Int. J. Damage Mech. 2012, 21, 1128–1153. [Google Scholar] [CrossRef]
- Risitano, A.; Risitano, G. Cumulative damage evaluation of steel using infrared thermography. Theor. Appl. Fract. Mech. 2010, 54, 82–90. [Google Scholar] [CrossRef]
- Peng, Z.C.; Huang, H.Z.; Wang, H.K.; Zhu, S.P.; Lv, Z.Q. A new approach to the investigation of load interaction effects and its application in residual fatigue life prediction. Int. J. Damage Mech. 2016, 25, 672–690. [Google Scholar] [CrossRef]
- Huang, B.X.; Wang, S.C.; Geng, S.L.; Liu, X.T. Improved numerical model for fatigue cumulative damage of mechanical structure considering load sequence and interaction. Adv. Mech. Eng. 2021, 13, 1687814021995309. [Google Scholar] [CrossRef]
- Gao, J.X.; Heng, F.; Yuan, Y.P.; Liu, Y.Y. Fatigue reliability analysis of composite material considering the growth of effective stress and critical stiffness. Aerospace 2023, 10, 785. [Google Scholar] [CrossRef]
- Ganesan, C.; Joanna, P.S. Modeling the residual strength and fatigue life of carbon fiber composites under constant amplitude loading. Mech. Adv. Mater. Struct. 2020, 27, 1840–1848. [Google Scholar] [CrossRef]
- Fu, Z.; Hu, X.; Zhang, J. A new fatigue life prediction method based on nonlinear fatigue cumulative damage generalized expression. J. Mech. Sci. Technol. 2022, 36, 205–212. [Google Scholar] [CrossRef]
- Osman, T.; Velex, P. A model for the simulation of the interactions between dynamic tooth loads and contact fatigue in spur gears. Tribol. Int. 2012, 46, 84–96. [Google Scholar] [CrossRef]
- Grbovic, A.; Rasuo, B. FEM based fatigue crack growth predictions for spar of light aircraft under variable amplitude loading. Eng. Fail. Anal. 2012, 26, 50–64. [Google Scholar] [CrossRef]
- Khan, M.A.A.; Sheikh, A.K.; Gasem, Z.M.; Asad, M. Fatigue life and reliability of steel castings through integrated simulations and experiments. Metals 2022, 12, 339. [Google Scholar] [CrossRef]
- Meng, D.B.; Lv, Z.Y.; Yang, S.Y.; Wang, H.T.; Xie, T.W.; Wang, Z.H. A time-varying mechanical structure reliability analysis method based on performance degradation. Structures 2021, 34, 3247–3256. [Google Scholar] [CrossRef]
- Ouammi, A.; Dagdougui, H.; Sacile, R.; Mimet, A. Monthly and seasonal assessment of wind energy characteristics at four monitored locations in Liguria region (Italy). Renew. Sustain. Energy Rev. 2010, 14, 1959–1968. [Google Scholar] [CrossRef]
- Wais, P. A review of Weibull functions in wind sector. Renew. Sustain. Energy Rev. 2017, 70, 1099–1107. [Google Scholar] [CrossRef]
- Altunkaynak, A.; Erdik, T.; Dabanlı, Í.; Şen, Z. Theoretical derivation of wind power probability distribution function and applications. Appl. Energy 2012, 92, 809–814. [Google Scholar] [CrossRef]
- Qian, B.Y.; Zhou, K.C.; Gao, X.X.; Liu, W. Torque transmission law of wind turbine drive system under the excitation of uneven wind load. J. Phys. Conf. Ser. 2022, 2218, 012057. [Google Scholar] [CrossRef]
- Gao, J.X. Reliability Analysis of Wind Turbine Gearbox Considering Strength Degradation and Failure Dependence. Master’s Thesis, Lanzhou University of Technology, Gansu, China, 2014. (In Chinese). [Google Scholar]
- Kebir, T.; Correia, J.; Benguediab, M.; Jesus, A.M.D. Numerical study of fatigue damage under random loading using Rainflow cycle counting. Int. J. Struct. Integr. 2021, 12, 149–162. [Google Scholar] [CrossRef]
- Jiang, S.; Li, W.; Xin, G.F.; Sheng, L.C.; Wang, Y.Q. Study on dynamic reliability of permanent magnet gear transmission system with wear and failure correlation. Eng. Fail. Anal. 2022, 131, 105802. [Google Scholar] [CrossRef]
- Nejad, A.R.; Gao, Z.; Moan, T. On long-term fatigue damage and reliability analysis of gears under wind loads in offshore wind turbine drivetrains. Int. J. Fatigue 2014, 61, 116–128. [Google Scholar] [CrossRef]
- Kroese, D.P.; Brereton, T.; Taimre, T.; Botev, Z.I. Why the Monte Carlo method is so important today. Wiley Interdiscip. Rev.-Comput. Stat. 2014, 6, 386–392. [Google Scholar] [CrossRef]
- Papadopoulos, C.E.; Yeung, H. Uncertainty estimation and Monte Carlo simulation method. Flow Meas. Instrum. 2001, 12, 291–298. [Google Scholar] [CrossRef]
- Nakazawa, M. Examining the Advantages and Disadvantages of Pilot Studies: Monte Carlo Simulations. Master’s Thesis, The University of New Mexico, Albuquerque, NM, USA, 2011. [Google Scholar]
- Huang, P.; Gu, Y.K.; Li, H.; Yazdi, M.; Qiu, G.Q. An optimal tolerance design approach of robot manipulators for positioning accuracy reliability. Reliab. Eng. Syst. Saf. 2023, 237, 109347. [Google Scholar] [CrossRef]
- Li, H.; Yazdi, M.; Huang, H.Z.; Huang, C.G.; Peng, W.; Nedjati, A.; Adesina, K.A. A fuzzy rough copula Bayesian network model for solving complex hospital service quality assessment. Complex Intell. Syst. 2023, 1–27. [Google Scholar] [CrossRef] [PubMed]
- Yazdi, M.; Mohammadpour, J.; Li, H.; Huang, H.Z.; Zarei, E.; Pirbalouti, R.G.; Adumene, S. Fault tree analysis improvements: A bibliometric analysis and literature review. Qual. Reliab. Eng. Int. 2023, 39, 1639–1659. [Google Scholar] [CrossRef]
- Yan, Y.T.; Luo, Z.Q.; Liu, Z.Y.; Liu, Z.B. Risk Assessment Analysis of Multiple Failure Modes Using the Fuzzy Rough FMECA Method: A Case of FACDG. Mathematics 2023, 11, 3459. [Google Scholar] [CrossRef]
- Yu, S.; Wang, Z.L. A general decoupling approach for time-and space-variant system reliability-based design optimization. Comput. Methods Appl. Mech. Eng. 2019, 357, 112608. [Google Scholar] [CrossRef]
- Yu, S.; Wang, Z.L.; Li, Y. Time and space-variant system reliability analysis through adaptive Kriging and weighted sampling. Mech. Syst. Signal Process. 2022, 166, 108443. [Google Scholar] [CrossRef]
- Yu, S.; Zhang, Y.W.; Li, Y.; Wang, Z.L. Time-variant reliability analysis via approximation of the first-crossing PDF. Struct. Multidiscip. Optim. 2020, 62, 2653–2667. [Google Scholar] [CrossRef]
- Yu, S.; Guo, P.; Wu, X. Adaptive first-crossing approach for life-cycle reliability analysis. Chin. J. Mech. Eng. 2023, 145, 091707. [Google Scholar] [CrossRef]
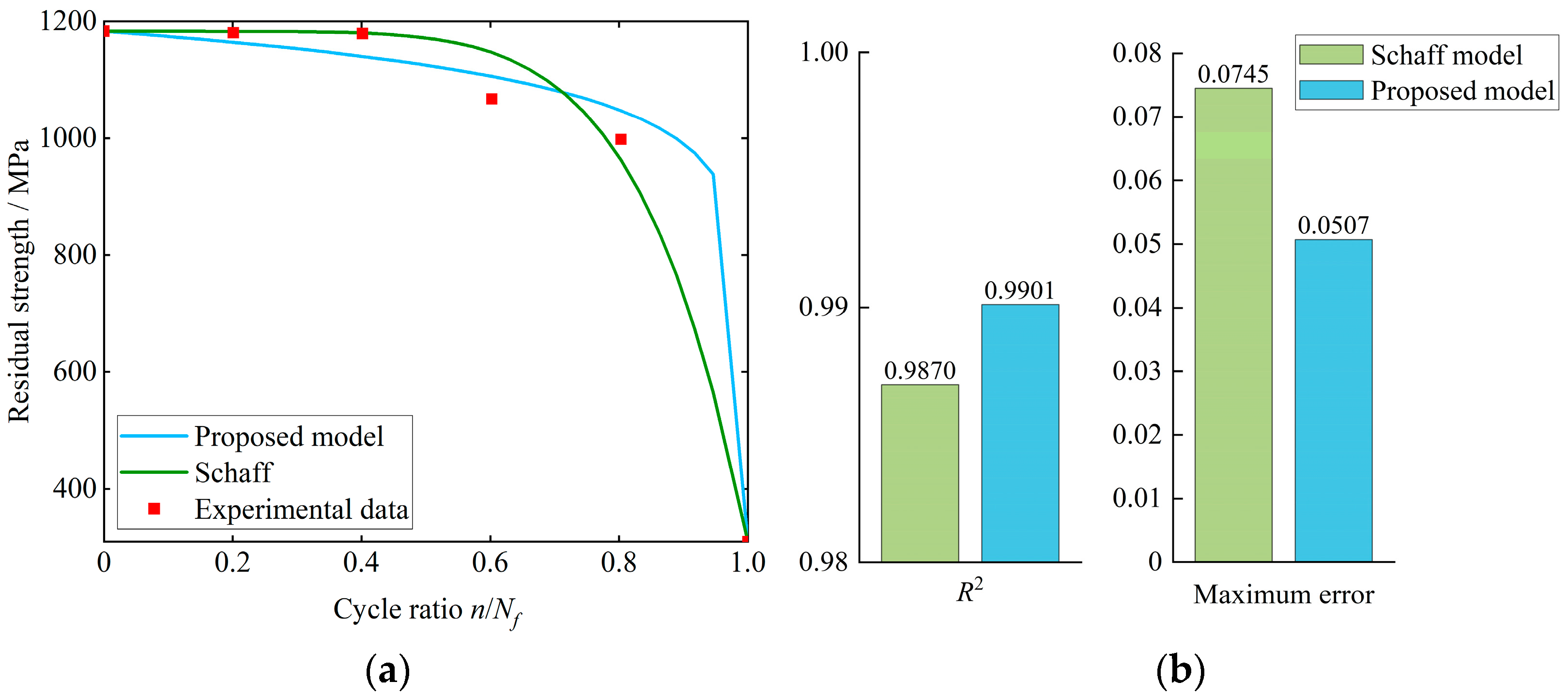

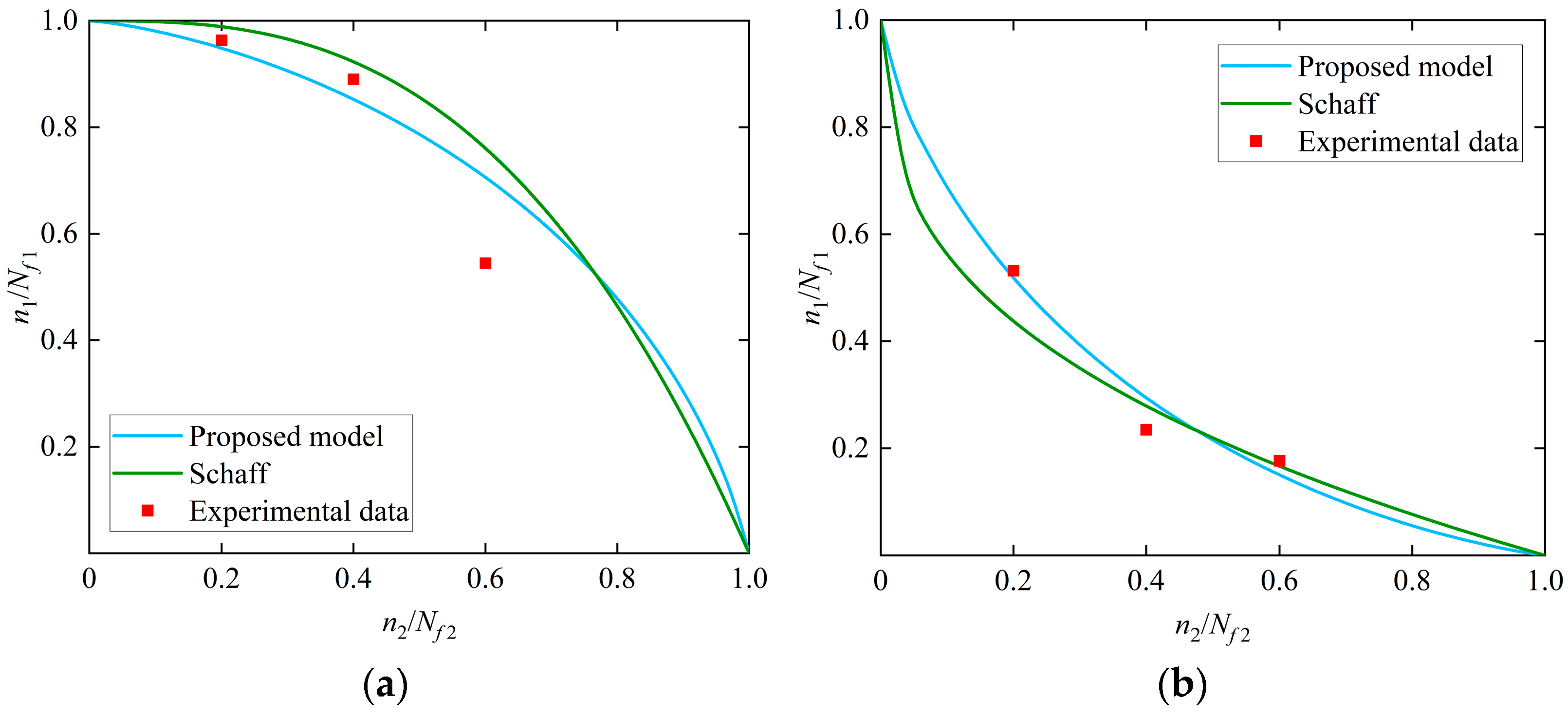
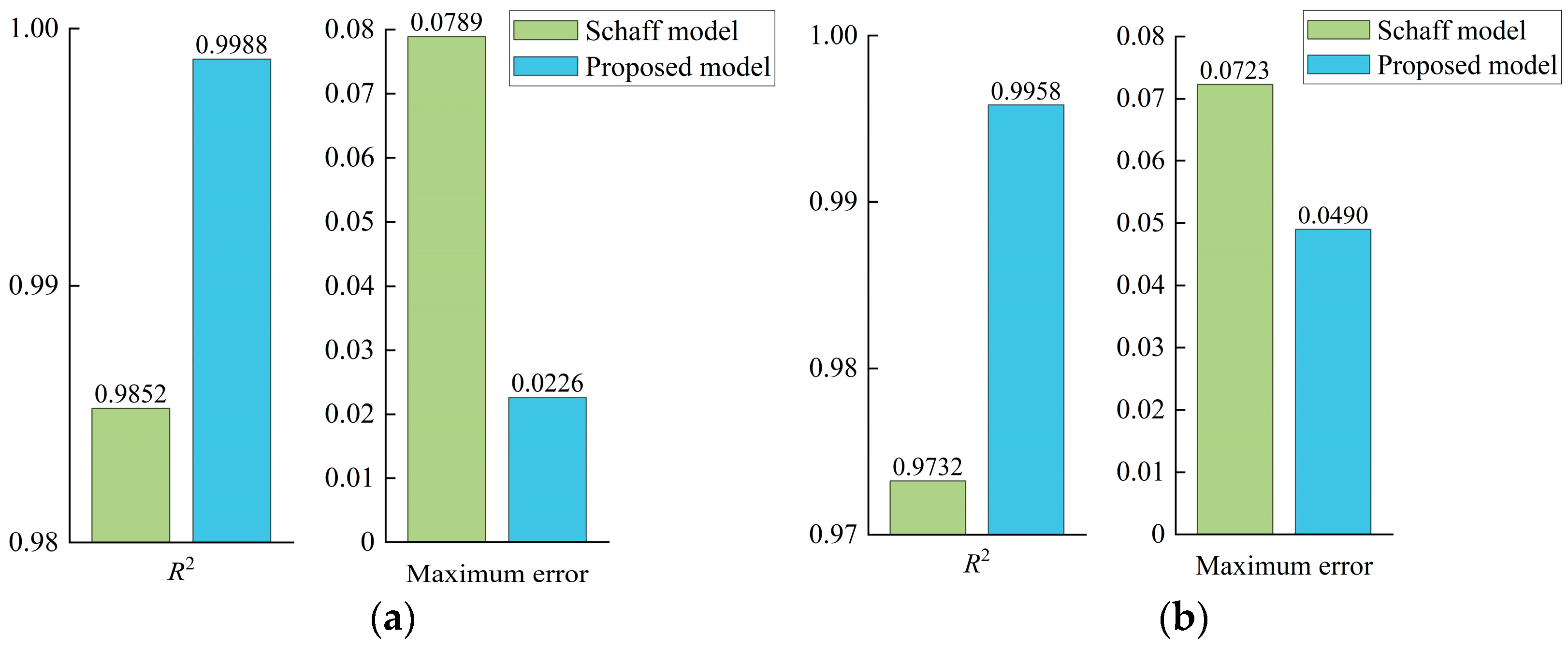




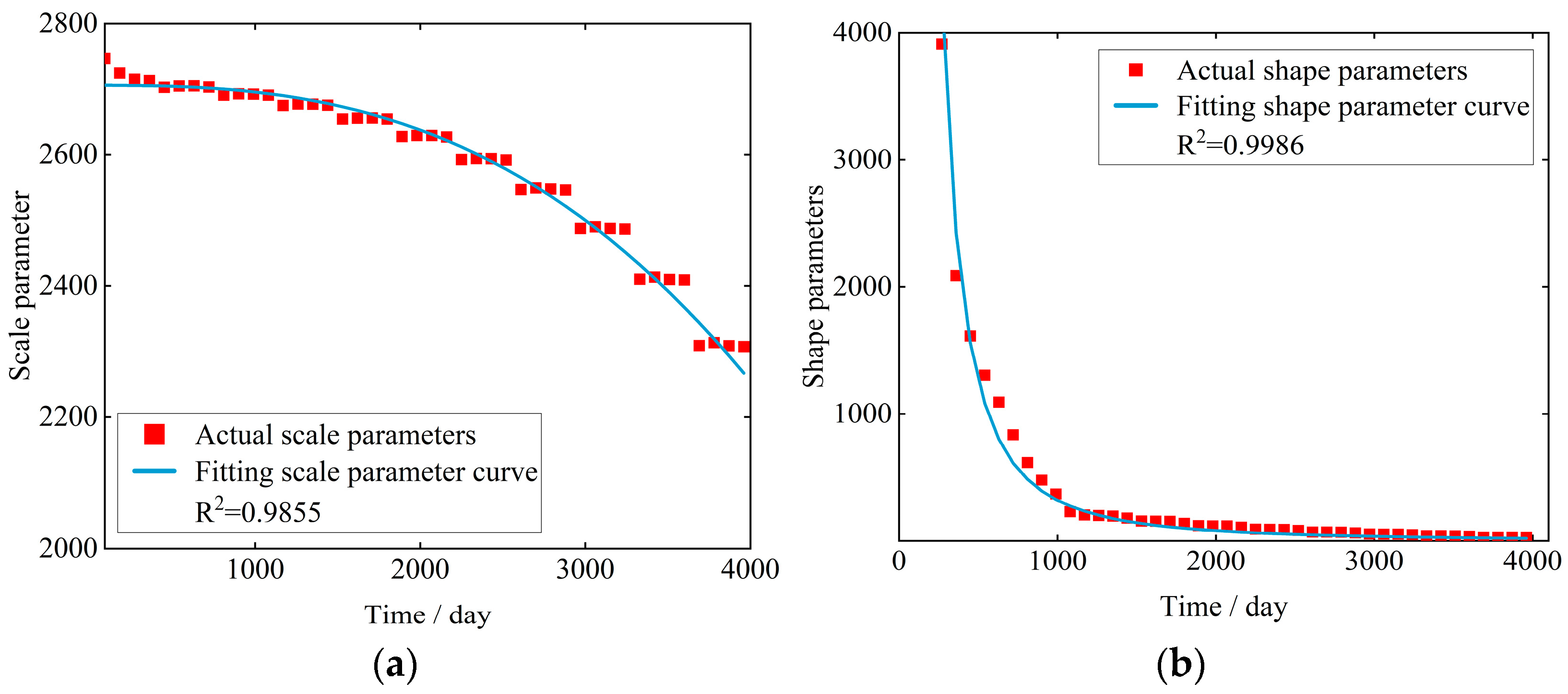

| Stress/MPa | Cycle Ratio | Cycles | Experimental Residual Strength/MPa | Schaff’s Model/MPa | Proposed Model/MPa |
|---|---|---|---|---|---|
| 310.37 | 0 | 0 | 1183.26 | 1183.26 | 1183.26 |
| 0.2 | 6970 | 1180.94 | 1183.22 | 1164.65 | |
| 0.4 | 13,940 | 1179.38 | 1180.49 | 1140.65 | |
| 0.6 | 20,970 | 1067.8 | 1147.35 | 1106.49 | |
| 0.8 | 27,900 | 998.20 | 967.76 | 1048.86 | |
| 1 | 34,866 | 310.37 | 310.37 | 310.37 |
| Stress/MPa | Loading Sequence | ||||
|---|---|---|---|---|---|
| 732→836 | Low→High | 13,000 | 0.233 | 6602 | 0.917 |
| 15,000 | 0.269 | 6501 | 0.903 | ||
| 25,000 | 0.448 | 5400 | 0.750 | ||
| 35,000 | 0.628 | 4428 | 0.615 | ||
| 45,000 | 0.807 | 3254 | 0.425 | ||
| 836→732 | High→Low | 1200 | 0.167 | 36,911 | 0.833 |
| 1800 | 0.208 | 32,450 | 0.792 | ||
| 3000 | 0.417 | 16,002 | 0.583 | ||
| 5000 | 0.694 | 6969 | 0.306 |
| Stress/MPa | Loading Sequence | ||||
|---|---|---|---|---|---|
| 150→200 | Low→High | 86,000 | 0.2 | 144,500 | 0.9633 |
| 172,000 | 0.4 | 133,500 | 0.8900 | ||
| 258,000 | 0.6 | 81,700 | 0.5447 | ||
| 200→150 | High→Low | 30,000 | 0.2 | 28,700 | 0.5319 |
| 60,000 | 0.4 | 101,050 | 0.2350 | ||
| 90,000 | 0.6 | 76,050 | 0.1769 |
| Season | Average of Wind Speed/m·s−1 | Variance of Wind Speed/m2·s−2 | Scale Parameter | Shape Parameter |
|---|---|---|---|---|
| Spring | 5.48 | 18 | 5.95 | 1.32 |
| Summer | 6.92 | 11.6 | 7.70 | 1.56 |
| Autumn | 11.81 | 26.54 | 13.28 | 1.78 |
| Winter | 8.63 | 19.12 | 9.57 | 1.51 |
| Parameters | Mean Value | Standard Error | Parameters | Mean Value | Standard Error |
|---|---|---|---|---|---|
| 1.1 | 0.036 | 2.21 | 0.073 | ||
| 1.15 | 0.035 | 1.64 | 0.066 | ||
| 1.32 | 0.02 | 0.78 | 0 | ||
| 1.01 | 0.003 | 1 | 0 |
| Season | Scale Parameter of Weibull Distribution | Shape Parameter of Weibull Distribution |
|---|---|---|
| Spring | 1.28 | 550.97 |
| Summer | 1.27 | 600.17 |
| Autumn | 1.32 | 704.99 |
| Winter | 1.25 | 679.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, J.; Liu, Y.; Yuan, Y.; Heng, F. Residual Strength Modeling and Reliability Analysis of Wind Turbine Gear under Different Random Loadings. Mathematics 2023, 11, 4013. https://doi.org/10.3390/math11184013
Gao J, Liu Y, Yuan Y, Heng F. Residual Strength Modeling and Reliability Analysis of Wind Turbine Gear under Different Random Loadings. Mathematics. 2023; 11(18):4013. https://doi.org/10.3390/math11184013
Chicago/Turabian StyleGao, Jianxiong, Yuanyuan Liu, Yiping Yuan, and Fei Heng. 2023. "Residual Strength Modeling and Reliability Analysis of Wind Turbine Gear under Different Random Loadings" Mathematics 11, no. 18: 4013. https://doi.org/10.3390/math11184013
APA StyleGao, J., Liu, Y., Yuan, Y., & Heng, F. (2023). Residual Strength Modeling and Reliability Analysis of Wind Turbine Gear under Different Random Loadings. Mathematics, 11(18), 4013. https://doi.org/10.3390/math11184013






