Surface Pencil Pair Interpolating Bertrand Pair as Common Asymptotic Curves in Euclidean 3-Space

Abstract

In this paper, we obtain the necessary and sufficient conditions of a surface pencil pair interpolating a Bertrand pair as common asymptotic curves in Euclidean 3-space ${\mathbb{E}}^3$. Afterwards, the conclusion to the ruled surface pencil pair is also obtained. Meanwhile, the epitomes are stated to emphasize that the proposed methods are effective in product manufacturing by adjusting the shapes of the surface pencil pair.

1. Introduction

An asymptotic curve on a surface is an essential geometrical characteristic that plays a major role in a variety of implementations, such as the design of hulls, car shells, knife rests, cloths, etc. In the context of geometry, an asymptotic curve is a curve constantly tangent to an asymptotic trend (direction) of the surface. It is occasionally named an asymptotic line, although it is not required to be a line. An asymptotic trend is one for which the normal curvature is identically zero. This means that, for a point on an asymptotic curve, we take the plane that affords both the surface’s normal and the curve’s tangent at this point. The intersection curve of the plane and the surface will have zero curvature at this point. Asymptotic trends can only arise if the Gaussian curvature is negative (or zero). There will be two asymptotic trends if every point has a negative Gaussian curvature; these trends are halved by the principal lines [1,2]. In practical applications, essential work has focused on the reverse problem or backward analysis: given a 3D curve, how can we define those surfaces that possess this curve as a special curve, rather than finding and assorting curves on analytical curved surfaces? Wang et al. [3] considered the issue of constructing a surface pencil from a specified spatial geodesic curve, through which each surface can be a candidate for style design. They proved the necessary and sufficient conditions for the coefficients to be content with both the geodesic and the isoparametric requirements. This scheme has been utilized by numerous researchers (see, for example, [4,5,6,7,8,9,10,11,12,13,14,15,16]).

In the context of the theory of special curves, the consistency relationship among the curves is a fascinating issue. The Bertrand curve is one of the best-known special curves. Two curves are called a Bertrand pair if there exists a consistency relationship among their principal normals at the analogical points [1,2]. The Bertrand curve can be evaluated as the popularization of the helix. The helix, as a certain type of curve, has attracted the attention of mathematicians as well as scientists because of its diverse implementations; for instance, the Bertrand curves represent special models of offset curves, which are used in computer-aided manufacturing (CAM) and computer-aided design (CAD) (see [17,18,19]). However, to our knowledge, there is no work that designs a surface pencil pair interpolating a Bertrand pair to be asymptotic curves in Euclidean 3-space ${\mathbb{E}}^3$. This paper is intended to satisfy such a requirement; we evaluate a Bertrand pair as asymptotic curves to model a surface pencil pair in ${\mathbb{E}}^3$. Moreover, a ruled surface is indispensable for various areas of CAGD; regarding the aim of this work, the conclusion to the ruled surface pencil pair is also outlined. Meanwhile, some examples are shown to depict the surface pencil and ruled surface pencil with common Bertrand asymptotic curves.

2. Preliminaries

In this section, we list the most important notations that we use in this paper [1,2]. A curve is regular if it possesses a tangent line at each point of the curve. In the following, all curves are supposed to be regular. Given a spatial curve $\mathit{\alpha }\left(s\right)$, it is expressed by arc length parameter s. We assume $\stackrel{..}{\mathit{\alpha }}\left(s\right)\ne$ 0 for all s∈$[0,L]$, since this would give a straight line. In this paper, $\stackrel{.}{\mathit{\alpha }}\left(s\right)$ and ${\mathit{\alpha }}^{\prime }\left(v\right)$ indicate the derivatives of $\mathit{\alpha }$ with respect to arc length parameter s and arbitrary parameter v, respectively. For each point of $\mathit{\alpha }\left(s\right)$, the set $\{{\mathit{\chi }}_1\left(s\right)$, ${\mathit{\chi }}_2\left(s\right)$, ${\mathit{\chi }}_3\left(s\right)\}$ is named the Serret–Frenet frame on $\mathit{\alpha }\left(s\right)$, where ${\mathit{\chi }}_1\left(s\right)=\stackrel{.}{\mathit{\alpha }}\left(s\right)$, ${\mathit{\chi }}_2\left(s\right)=\stackrel{..}{\mathit{\alpha }}\left(s\right)/∥\stackrel{..}{\mathit{\alpha }}\left(s\right)∥$ and ${\mathit{\chi }}_3\left(s\right)={\mathit{\chi }}_1\left(s\right)\times {\mathit{\chi }}_2\left(s\right)$ are the unit tangent, principal normal, and binormal vectors of the curve at the point $\mathit{\alpha }\left(s\right)$, respectively. The arc length derivative of the Serret–Frenet frame is [1,2]

$$\left(\begin{array}{c}\stackrel{.}{{\mathit{\chi }}_1}\hfill \\ \stackrel{.}{{\mathit{\chi }}_2}\hfill \\ \stackrel{.}{{\mathit{\chi }}_3}\hfill \end{array}\right)=\left(\begin{array}{ccc}0\hfill & \kappa \left(s\right)\hfill & 0\hfill \\ -\kappa \left(s\right)\hfill & 0\hfill & \tau \left(s\right)\hfill \\ 0\hfill & -\tau \left(s\right)\hfill & 0\hfill \end{array}\right)\left(\begin{array}{c}{\mathit{\chi }}_1\hfill \\ {\mathit{\chi }}_2\hfill \\ {\mathit{\chi }}_3\hfill \end{array}\right),$$

(1)

where the curvature $\kappa \left(s\right)$ and torsion $\tau \left(s\right)$ are specified by

$$\kappa \left(s\right)=∥\stackrel{..}{\mathit{\alpha }}\left(s\right)∥,\tau \left(s\right)=\frac{det(\stackrel{.}{\mathit{\alpha }}\left(s\right),\stackrel{..}{\mathit{\alpha }}\left(s\right),\stackrel{...}{\mathit{\alpha }}\left(s\right))}{{∥\stackrel{..}{\mathit{\alpha }}\left(s\right)∥}^2}.$$

In spite of the fact that the arc length parameter is simple to analyze, in the majority of feasible situations, the parameter of a specified curve is commonly not in arc length parametrization. We can symbolize the specified curve by employing arc length parametrization. Given the curve

$$\mathit{\alpha }\left(v\right)=({\alpha }_1\left(v\right),{\alpha }_2\left(v\right),{\alpha }_3\left(v\right)),0\le v\le H,$$

where the parameter v is not the arc length. The synthesis of the Serret–Frenet frame is specified by [1,2]

$${\mathit{\chi }}_1\left(v\right)=\frac{{\mathit{\alpha }}^{\prime }\left(v\right)}{∥{\mathit{\alpha }}^{\prime }\left(v\right)∥},{\mathit{\chi }}_3\left(v\right)=\frac{{\mathit{\alpha }}^{\prime }\left(v\right)\times {\mathit{\alpha }}^{″}\left(v\right)}{∥{\mathit{\alpha }}^{\prime }\left(v\right)\times {\mathit{\alpha }}^{″}\left(v\right)∥},{\mathit{\chi }}_2\left(v\right)={\mathit{\chi }}_3\left(v\right)\times {\mathit{\chi }}_1\left(v\right),{(}^{\prime }\stackrel{def}{=}\frac{d}{dv}),$$

(2)

and the Serret–Frenet formula is

$$\left(\begin{array}{c}{\mathit{\chi }}_1^{\prime }\left(v\right)\hfill \\ {\mathit{\chi }}_2^{\prime }\left(v\right)\hfill \\ {\mathit{\chi }}_3^{\prime }\left(v\right)\hfill \end{array}\right)=\left(\begin{array}{ccc}0\hfill & \kappa \left(v\right)∥{\mathit{\alpha }}^{\prime }\left(v\right)∥\hfill & 0\hfill \\ -\kappa \left(v\right)∥{\mathit{\alpha }}^{\prime }\left(v\right)∥\hfill & 0\hfill & \tau \left(v\right)∥{\mathit{\alpha }}^{\prime }\left(v\right)∥\hfill \\ 0\hfill & -\tau \left(v\right)∥{\mathit{\alpha }}^{\prime }\left(v\right)∥\hfill & 0\hfill \end{array}\right)\left(\begin{array}{c}{\mathit{\chi }}_1\left(v\right)\hfill \\ {\mathit{\chi }}_2\left(v\right)\hfill \\ {\mathit{\chi }}_3\left(v\right)\hfill \end{array}\right).$$

(3)

We utilize basic notation for the Bertrand pair from [1,2]: Let $\mathit{\alpha }\left(s\right)$ and $\widehat{\mathit{\alpha }}\left(s\right)$ be two curves in ${\mathbb{E}}^3$; ${\mathit{\chi }}_2\left(s\right)$ and ${\widehat{\mathit{\chi }}}_2\left(s\right)$ are the principal normal vectors of them, respectively; the pair {$\mathit{\alpha }\left(s\right)$, $\widehat{\mathit{\alpha }}\left(s\right)$} is named a Bertrand pair if ${\mathit{\chi }}_2\left(s\right)$ and ${\widehat{\mathit{\chi }}}_2\left(s\right)$ are linearly dependent at the congruent points. $\mathit{\alpha }\left(s\right)$ is named the Bertrand mate of $\widehat{\mathit{\alpha }}\left(\widehat{s}\right)$, and

$$\widehat{\mathit{\alpha }}\left(s\right)=\mathit{\alpha }\left(s\right)+f{\mathit{\chi }}_2\left(s\right).$$

(4)

where f is steady. Therefore, the associations of the Serret–Frenet frame of $\mathit{\alpha }\left(s\right)$ with that of $\widehat{\mathit{\alpha }}\left(s\right)$ are

$$\left(\begin{array}{c}{\widehat{\mathit{\chi }}}_1\hfill \\ {\widehat{\mathit{\chi }}}_2\hfill \\ {\widehat{\mathit{\chi }}}_3\hfill \end{array}\right)=\left(\begin{array}{ccc}cos\phi \hfill & 0\hfill & sin\phi \hfill \\ 0\hfill & 1\hfill & 0\hfill \\ -sin\phi \hfill & 0\hfill & cos\phi \hfill \end{array}\right)\left(\begin{array}{c}{\mathit{\chi }}_1\hfill \\ {\mathit{\chi }}_2\hfill \\ {\mathit{\chi }}_3\hfill \end{array}\right),$$

(5)

where $\phi$ is a constant angle.

We represent a surface M by

$$M:\mathit{y}(s,t)=\left(y_1\left(s,t\right),y_2\left(s,t\right),y_3\left(s,t\right)\right),(s,t)\in \mathbb{D}\subseteq {\mathbb{R}}^2.$$

(6)

If ${\mathit{y}}_j(s,t)=\frac{\partial \mathit{y}}{\partial j}$, the surface normal is

$$\mathit{\zeta }(s,t)={\mathit{y}}_s\wedge {\mathit{y}}_t,$$

(7)

which is perpendicular to the vectors ${\mathit{y}}_s$ and ${\mathit{y}}_t$.

Definition 1

 ([1,2]). A curve on a surface is asymptotic if and only if the binormal vector of the curve is everywhere parallel to the surface normal.

A curve $\mathit{\alpha }\left(s\right)$ on a surface $\mathit{y}(s,t)$ is an isoparametric curve if it has a stationary s or t-parameter value. In other words, there exists a parameter $t_0$ such that $\mathit{\alpha }\left(s\right)=\mathit{y}(s,t_0)$ or $\mathit{\alpha }\left(t\right)=\mathit{y}(s_0,t)$. Given a parametric curve $\mathit{\alpha }\left(s\right)$, we call it an isoasymptotic curve of the surface $\mathit{y}(s,t)$ if it is both an asymptotic and a parameter curve on $\mathit{y}(s,t)$.

3. Main Results

This section presents a new approach to constructing a surface pencil pair interpolating a Bertrand pair as common asymptotic curves in ${\mathbb{E}}^3$. To do this, we take into consideration a Bertrand pair, such that the surfaces’ tangent planes are concomitant with the curves’ osculating planes.

Let $\mathit{\alpha }\left(s\right)$ be a curve with $∥\stackrel{..}{\mathit{\alpha }}\left(s\right)∥\ne 0$; $\widehat{\mathit{\alpha }}\left(s\right)$ is the Bertrand mate of $\mathit{\alpha }\left(s\right)$, and $\{\widehat{\kappa }\left(s\right)$, $\widehat{\tau }\left(s\right)$, ${\widehat{\mathit{\chi }}}_1\left(s\right),{\widehat{\mathit{\chi }}}_2\left(s\right)$, ${\widehat{\mathit{\chi }}}_3\left(s\right)\}$ is the Frenet–Serret apparatus of $\widehat{\mathit{\alpha }}\left(s\right)$ as in Equation (1). The surface pencil M interpolating $\mathit{\alpha }\left(s\right)$ can be denoted by

$$M:\mathit{y}(s,t)=\mathit{\alpha }\left(s\right)+a(s,t){\mathit{\chi }}_1\left(s\right)+b(s,t){\mathit{\chi }}_2\left(s\right);0\le t\le T.$$

(8)

Similarly, the surface pencil $\widehat{M}$ interpolating $\widehat{\mathit{\alpha }}\left(s\right)$ is denoted by

$$\widehat{M}:\widehat{\mathit{y}}(s,t)=\widehat{\mathit{\alpha }}\left(s\right)+a(s,t){\widehat{\mathit{\chi }}}_1\left(s\right)+b(s,t){\widehat{\mathit{\chi }}}_2\left(\widehat{s}\right);0\le t\le T.$$

(9)

Here, $a(s,t)$, $b(s,t)\in C^1$ are named marching-scale functions, and $b(s,t)\ne 0$.

In order to obtain the $\widehat{M}$ interpolating $\widehat{\mathit{\alpha }}\left(s\right)$ as a mutual asymptotic curve, according to Equations (8) and (9), we examine what the marching-scale functions should fulfill. To do this, we have

$$\left.\begin{array}{c}{\widehat{\mathit{y}}}_s(s,t)=(1+a_s-b\widehat{\kappa }){\widehat{\mathit{\chi }}}_1+(b_s+a\widehat{\kappa }){\widehat{\mathit{\chi }}}_2+b\widehat{\tau }{\widehat{\mathit{\chi }}}_3,\hfill \\ {\widehat{\mathit{y}}}_t(s,t)=a_t{\widehat{\mathit{\chi }}}_1+b_t{\widehat{\mathit{\chi }}}_2,\hfill \end{array}\right\}$$

(10)

and

$$\widehat{\mathit{\zeta }}(s,t):={\widehat{\mathit{y}}}_s\times {\widehat{\mathit{y}}}_t=b\widehat{\tau }\left(b_t{\widehat{\mathit{\chi }}}_1+a_t{\widehat{\mathit{\chi }}}_2\right)+\left[(1+a_s-b\widehat{\kappa })b_t-(a\widehat{\kappa }+b_s)a_t\right]{\widehat{\mathit{\chi }}}_3\left(s\right).$$

(11)

Since $\widehat{\mathit{\alpha }}\left(s\right)$ is isoparametric on $\widehat{M}$, there exists a value $t=t_0\in [0,T]$ such that $\widehat{\mathit{y}}(s,t_0)=\widehat{\mathit{\alpha }}\left(s\right)$; in other words,

$$a(s,t_0)=b(s,t_0)=0,a_s(s,t_0)=b_s(s,t_0)=0.$$

(12)

Thus, as $t=t_0$, i.e., over $\widehat{\mathit{\alpha }}\left(s\right)$, we have

$$\widehat{\mathit{\zeta }}(s,t_0)=b_t{\widehat{\mathit{\chi }}}_3\left(s\right).$$

(13)

The coincidence of the binormal ${\widehat{\mathit{\chi }}}_3\left(s\right)$ with surface normal $\widehat{\mathit{\zeta }}(s,t_0)$ identifies $\widehat{\mathit{\alpha }}\left(s\right)$ as an asymptotic curve. We utilize {M, $\widehat{M}$} to indicate the surface pencil pair. Then, from Equations (9)–(13), we derive the following theorem.

Theorem 1.

{M, $\widehat{M}$} interpolate the Bertrand pair {$\mathit{\alpha }\left(s\right)$, $\widehat{\mathit{\alpha }}\left(s\right)$} as common asymptotic curves if and only if

$$\left.\begin{array}{c}a(s,t_0)=b(s,t_0)=0,\hfill \\ b_t(s,t_0)\ne 0,0\le t_0\le T,0\le s\le L.\hfill \end{array}\right\}$$

(14)

We call M and $\widehat{M}$, expressed by by Equations (8) and (9) and satisfying the conditions (14), an asymptotic surface pencil pair interpolating a Bertrand pair, since the common asymptotic curves are also a Bertrand pair. Any {M, $\widehat{M}$} satisfying the conditions of Equation (14) is a member of this surface pencil pair. As reported in [3], for ease of interpretation, the marching-scale functions $a(s,t)$ and $b(s,t)$ can be displayed as two factors:

$$\begin{array}{c}a(s,t)=l\left(s\right)A\left(t\right),\\ b(s,t)=m\left(s\right)B\left(t\right).\end{array}$$

(15)

$l\left(\widehat{s}\right)$, $m\left(\widehat{s}\right),A\left(t\right)$ and $B\left(t\right)$ are $C^1$ functions that do not identically vanish. Then, we can obtain the below corollary.

Corollary 1.

{M, $\widehat{M}$} interpolate the Bertrand pair {$\mathit{\alpha }\left(s\right)$, $\widehat{\mathit{\alpha }}\left(s\right)$} as common asymptotic curves if and only if

$$\left.\begin{array}{c}A\left(t_0\right)=B\left(t_0\right)=0,l\left(s\right)=const.\ne 0,m\left(s\right)=const.\ne 0,\hfill \\ \frac{dB\left(t_0\right)}{dt}=const.\ne 0,0\le t_0\le T,0\le s\le L.\hfill \end{array}\right\}$$

(16)

To confirm that {M, $\widehat{M}$} interpolate the Bertrand pair {$\mathit{\alpha }\left(s\right)$, $\widehat{\mathit{\alpha }}\left(s\right)$}, we can first design the marching-scale functions in Equation (16), and then use them in Equations (8) and (9) to specify the parameterization. For suitability in practice, the functions $a(s,t)$ and $b(s,t)$ can be moreover constrained to be in extra limited forms and still possess sufficient degrees of freedom to specify a large pencil pair interpolating the Bertrand pair {$\mathit{\alpha }\left(s\right)$, $\widehat{\mathit{\alpha }}\left(s\right)$} as common asymptotic curves. Therefore, let us assume that $a(s,t)$ and $b(s,t)$ can be displayed as follows.

(1) If

$$\left\{\begin{array}{c}a(s,t)=\underset{k=1}{\stackrel{p}{\Sigma }}{a}_{1k}l{\left(s\right)}^{k}A{\left(t\right)}^k,\\ b(s,t)=\underset{k=1}{\stackrel{p}{\Sigma }}{b}_{1k}m{\left(s\right)}^{k}B{\left(t\right)}^k,\end{array}\right.$$

(17)

then,

$$\left\{\begin{array}{c}A\left(t_0\right)=B\left(t_0\right)=0,\\ b_{11}\ne 0,m\left(s\right)\ne 0,\mathrm{and}\frac{dB\left(t_0\right)}{dt}=const.\ne 0,\end{array}\right.$$

(18)

where $l\left(s\right)$, $m\left(s\right)$, $A\left(t\right),B\left(t\right)$ $\in C^1$, $a_{ij}$, $B_{ij}\in \mathbb{R}$ $(i=1,2;j=1,2,\dots ,p)$ and $l\left(s\right)$, and $m\left(s\right)$ are not identically zero.

(2) If

$$\left\{\begin{array}{c}a(s,t)=f(\underset{k=1}{\stackrel{p}{\Sigma }}{a}_{1k}{l}^k\left(s\right)A^k\left(t\right)),\\ b(s,t)=g(\underset{k=1}{\stackrel{p}{\Sigma }}{b}_{1k}{m}^k\left(s\right)B^k\left(t\right)),\end{array}\right.$$

(19)

then

$$\left\{\begin{array}{c}A\left(t_0\right)=B\left(t_0\right)=f\left(0\right)=g\left(0\right)=0,\\ b_{11}\ne 0,\frac{dB\left(t_0\right)}{dt}=const\ne 0,m\left(s\right)\ne 0,g^{\prime }\left(0\right)\ne 0,\end{array}\right.$$

(20)

where $l\left(s\right)$, $m\left(s\right)$, $A\left(t\right),B\left(t\right)\in C^1$, $a_{ij}$, $b_{ij}\in \mathbb{R}$ $(i=1,2;j=1,2,\dots ,p)$ and $l\left(s\right)$, and $m\left(s\right)$ are not identically zero.

Since the parameters $a_{ij}$, $b_{ij}\in \mathbb{R}$ $(i=1,2;j=1,2,\dots ,p)$ control the shape of {M, $\widehat{M}$}, we can adjust these parameters to output {M, $\widehat{M}$}, which represent definite restrictions, such as conditions on the boundary, curvature, etc. The marching-scale functions in Equations (15), (17) and (19) are general for {M, $\widehat{M}$} interpolating the given Bertrand curves as common asymptotic curves. Furthermore, since there are no constraints related to the Bertrand curves in Equations (16), (18) or (20), the surface pencil pair interpolating the given Bertrand curves, acting as both isoparametric curves and asymptotic curves, can always be found by choosing suitable marching-scale functions. Furthermore, some more conditions for various types of {M, $\widehat{M}$} interpolating the given Bertrand curves can be obtained from $0\le \phi \le \frac{\pi }{2}$; in the special cases, if $\phi =0$ ($\phi =\pi /2$), then the pair {M, $\widehat{M}$} are named the oriented pair and right pair, respectively.

Example 1.

If ${\mathit{a}}_0=(0,0,0),{\mathit{a}}_1=(0,1,1)$ and ${\mathit{a}}_2=(1,2,0)$ are points in the Euclidean 3-space ${\mathbb{E}}^3$, then the quadratic Bézier curve can be specified as

$$\mathit{\alpha }\left(v\right)=b_0\left(v\right){\mathit{a}}_0+b_1\left(v\right){\mathit{a}}_1+b_2\left(v\right){\mathit{a}}_2,0\le v\le 1.$$

where

$$b_0\left(v\right)={(1-v)}^2,b_1\left(v\right)=2v(1-v),b_2\left(v\right)=v^2,$$

are the blending functions of the curve $\mathit{\alpha }\left(v\right)$. It is easy to show that

$$\kappa \left(v\right)=\frac{1}{2}\sqrt{\frac{6}{5v^2-4v+2}},\tau \left(v\right)=0.$$

After simple computation, we obtain

$${\mathit{\chi }}_1\left(v\right)=\frac{(v,1,1-2v)}{\rho },{\mathit{\chi }}_2\left(v\right)=\frac{\left(2(1-v),2-5v,-(2+v)\right)}{\sqrt{6}\rho },{\mathit{\chi }}_3\left(v\right)=(-\frac{2}{\sqrt{6}},\frac{1}{\sqrt{6}},-\frac{1}{\sqrt{6}}),$$

where $\rho \left(v\right)=\sqrt{5v^2-4v+2}$. Selecting $a(v,t)=-4vt$, $b(v,t)=-t$, $\gamma \ne 0$, and $t_0=0$. Clearly, Equation (16) is satisfied, and the parametric surface specified by Equation (8) is

$$M:\mathit{y}(v,t)=\left(v^2,2v,2v-2v^2\right)+t\left(-4v,-1,0\right)\left(\begin{array}{ccc}\frac{v}{\rho }\hfill & \frac{1}{\rho }\hfill & \frac{1-2v}{\rho }\hfill \\ \frac{2(1-v)}{\sqrt{6}\rho }\hfill & \frac{2-5v}{\sqrt{6}\rho }\hfill & \frac{-(2+v)}{\sqrt{6}\rho }\hfill \\ -\frac{2}{\sqrt{6}}\hfill & \frac{1}{\sqrt{6}}\hfill & -\frac{1}{\sqrt{6}}\hfill \end{array}\right).$$

Let $f=\sqrt{6}$ in Equation (7), and we obtain

$$\widehat{\mathit{\alpha }}\left(v\right)=(v^2-\frac{2v}{\rho },2v-\frac{(2-5v)}{\rho },2v(1-v)-\frac{(2+v)}{\rho }).$$

Via Equation (5), we find

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\chi }}}_1& =& \left(\begin{array}{c}{\mathit{\chi }}_{11}\hfill \\ {\mathit{\chi }}_{12}\hfill \\ {\mathit{\chi }}_{13}\hfill \end{array}\right)=\left(\begin{array}{c}\frac{v}{\rho }cos\phi -\frac{2}{\sqrt{6}}sin\phi \hfill \\ \frac{1}{\rho }cos\phi +\frac{1}{\sqrt{6}}sin\phi \hfill \\ \frac{1-2v}{\rho }cos\phi +\frac{1}{\sqrt{6}}sin\phi \hfill \end{array}\right),\hfill \\ & & \\ \hfill {\widehat{\mathit{\chi }}}_3& =& \left(\begin{array}{c}{\mathit{\chi }}_{31}\hfill \\ {\mathit{\chi }}_{32}\hfill \\ {\mathit{\chi }}_{33}\hfill \end{array}\right)=\left(\begin{array}{c}-\frac{v}{\rho }sin\phi -\frac{2}{\sqrt{6}}cos\phi \hfill \\ -\frac{1}{\rho }sin\phi +\frac{1}{\sqrt{6}}cos\phi \hfill \\ -\frac{(1-2v)}{\rho }sin\phi +\frac{1}{\sqrt{6}}cos\phi \hfill \end{array}\right).\hfill \end{array}$$

Then, we have

$$\widehat{M}:\widehat{\mathit{y}}(v,t)=(v^2-\frac{2v}{\rho },2v+\frac{2-3v}{\rho },2v-2v^2-\frac{(2+v)}{\rho })+t\left(-4v,-1,0\right)\left(\begin{array}{ccc}{\mathit{\chi }}_{11}\hfill & {\mathit{\chi }}_{12}\hfill & {\mathit{\chi }}_{13}\hfill \\ 0\hfill & 1\hfill & 0\hfill \\ {\mathit{\chi }}_{31}\hfill & {\mathit{\chi }}_{32}\hfill & {\mathit{\chi }}_{33}\hfill \end{array}\right).$$

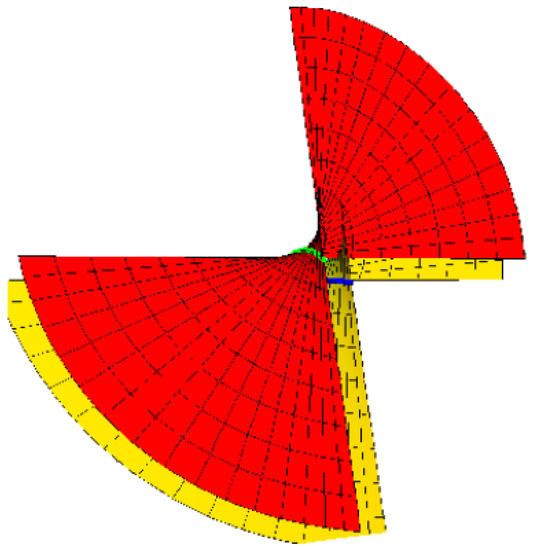
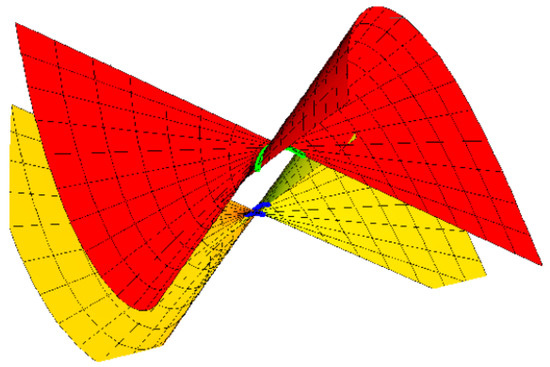
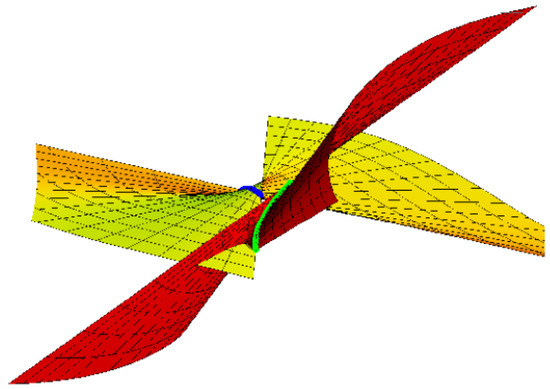
For $\beta =\gamma =-1$, the oriented pair and the right pair, respectively, are shown in Figure 1 and Figure 2, where $0\le r\le 1$, and $-15\le t\le 15$.

Figure 1. Oriented pair {M, $\widehat{M}$} with $\widehat{\mathit{\alpha }}\left(v\right)$ blue and $\mathit{\alpha }\left(v\right)$ green.

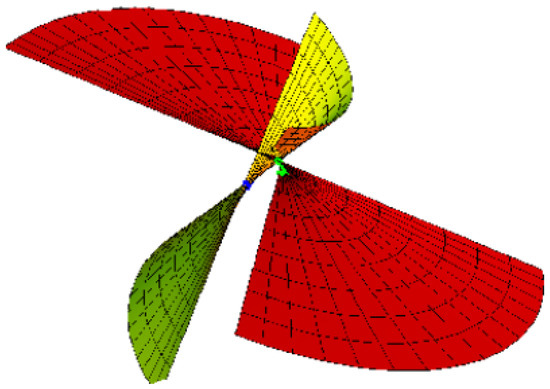
Figure 2. Right pair {M, $\widehat{M}$} with $\widehat{\mathit{\alpha }}\left(v\right)$ blue and $\mathit{\alpha }\left(v\right)$ green.

Example 2.

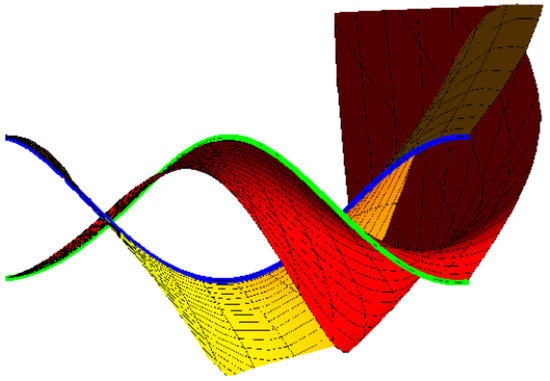
Given a helix

$$\mathit{\alpha }\left(s\right)=\frac{1}{\sqrt{2}}\left(coss,sins,s\right),0\le s\le 2\pi .$$

The Serret–Frenet frame is

$${\mathit{\chi }}_1\left(s\right)=\frac{1}{\sqrt{2}}(-sins,coss,1),{\mathit{\chi }}_2\left(s\right)=(-coss,-sins,0),{\widehat{\mathit{\chi }}}_3\left(s\right)=\frac{1}{\sqrt{2}}(sins,-coss,1).$$

Then, the parametric surface defined by Equation (8) is

$$M:\mathit{y}(s,t)=\frac{1}{\sqrt{2}}\left(coss,sins,s\right)+\left(a(s,t),b(s,t),0\right)\left(\begin{array}{ccc}\frac{-sins}{\sqrt{2}}\hfill & \frac{coss}{\sqrt{2}}\hfill & \frac{1}{\sqrt{2}}\hfill \\ -coss\hfill & -sins\hfill & 0\hfill \\ \frac{sins}{\sqrt{2}}\hfill & \frac{-coss}{\sqrt{2}}\hfill & \frac{1}{\sqrt{2}}\hfill \end{array}\right).$$

Let $f=\sqrt{2}$ in Equation (7), and we have

$$\widehat{\mathit{\alpha }}\left(s\right)=\frac{1}{\sqrt{2}}\left(-coss,-sins,s\right),0\le s\le 2\pi .$$

Via Equation (5), we find

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\chi }}}_1& =& \left(\begin{array}{c}{\mathit{\chi }}_{11}\hfill \\ {\mathit{\chi }}_{12}\hfill \\ {\mathit{\chi }}_{13}\hfill \end{array}\right)=\left(\begin{array}{c}\frac{1}{\sqrt{2}}(-cos\phi +sin\phi )sins\hfill \\ \frac{1}{\sqrt{2}}(cos\phi -sin\phi )coss\hfill \\ \frac{1}{\sqrt{2}}(cos\phi +sin\phi )\hfill \end{array}\right),\hfill \\ & & \\ \hfill {\widehat{\mathit{\chi }}}_3& =& \left(\begin{array}{c}{\mathit{\chi }}_{31}\hfill \\ {\mathit{\chi }}_{32}\hfill \\ {\mathit{\chi }}_{33}\hfill \end{array}\right)=\left(\begin{array}{c}\frac{1}{\sqrt{2}}(sin\phi +cos\phi )sins\hfill \\ \frac{1}{\sqrt{2}}(-sin\phi -cos\phi )coss\hfill \\ \frac{1}{\sqrt{2}}(cos\phi -sin\phi )\hfill \end{array}\right).\hfill \end{array}$$

Then, we have

$$\widehat{M}:\widehat{\mathit{y}}(s,t)=\frac{1}{\sqrt{2}}\left(-coss,-sins,s\right)+\left(a(s,t),b(s,t),0\right)\left(\begin{array}{ccc}{\mathit{\chi }}_{11}\hfill & {\mathit{\chi }}_{12}\hfill & {\mathit{\chi }}_{13}\hfill \\ -coss\hfill & -sins\hfill & 0\hfill \\ {\mathit{\chi }}_{31}\hfill & {\mathit{\chi }}_{32}\hfill & {\mathit{\chi }}_{33}\hfill \end{array}\right).$$

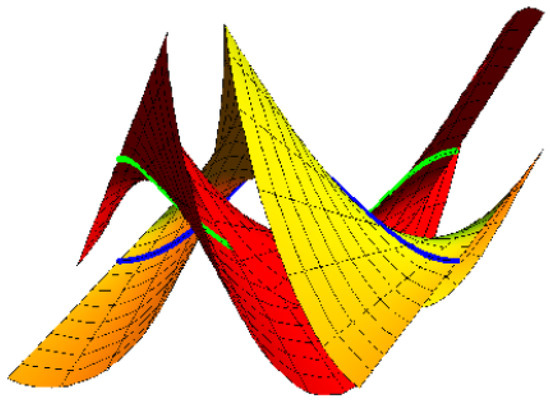
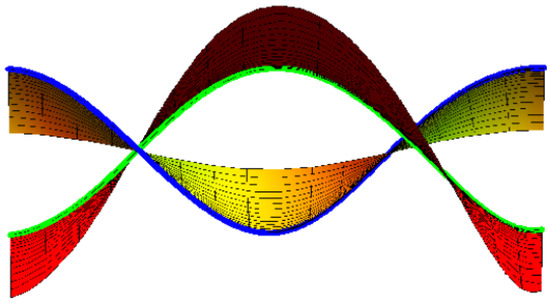
(1) If we take $a(s,t)=0$, $b(s,t)=1-cosht+\underset{k=2}{\stackrel{4}{\Sigma }}{b}_{2k}{(1-cosht)}^k$, where $t_0=0$ and $b_{2k}\in \mathbb{R}$, then Equation (18) is satisfied. The oriented pair and the right pair are identical; where $b_{2k}$ approaches zero, $0\le t\le 0.2$, and $0\le s\le 2\pi$ (Figure 3).

Figure 3. Oriented right pair {M, $\widehat{M}$} with $\widehat{\mathit{\alpha }}\left(s\right)$ blue and $\mathit{\alpha }\left(s\right)$ green.

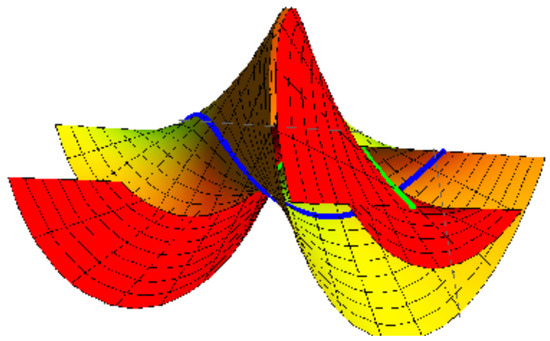
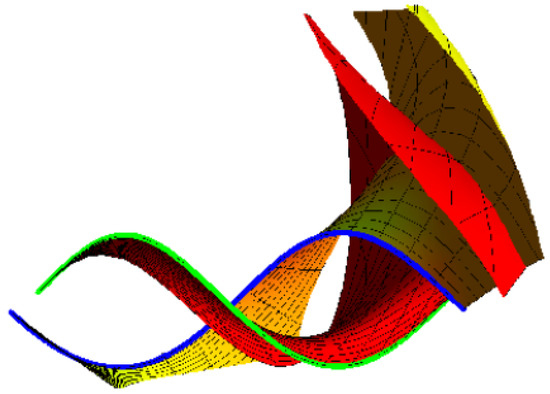
(2) If we take $a(s,t)=sin\left(\underset{k=1}{\stackrel{4}{\Sigma }}{t}^k{s}^k\right)$, $b(s,t)=\underset{k=1}{\stackrel{4}{\Sigma }}{t}^k{s}^k$, and $t_0=0$, then Equation (20) is satisfied. The oriented pair and the right pair, respectively, are shown in Figure 4 and Figure 5, where $0\le t\le 0.1$, and $0\le s\le 2\pi$.

Figure 4. Oriented pair {M, $\widehat{M}$} with $\widehat{\mathit{\alpha }}\left(s\right)$ blue and $\mathit{\alpha }\left(s\right)$ green.

Figure 5. Right pair {M, $\widehat{M}$} with $\widehat{\mathit{\alpha }}\left(s\right)$ blue and $\mathit{\alpha }\left(s\right)$ green.

Ruled Surface Family Pair with Bertrand Pair as Mutual Asymptotic Curves

Ruled surfaces are simple and common surfaces in geometric designs. Suppose that $\widehat{\mathit{y}}(s,t)$ is a ruled surface with the base $\widehat{\mathit{\alpha }}\left(s\right)$ and $\widehat{\mathit{\alpha }}\left(s\right)$ is also an isoparametric curve of $\widehat{\mathit{y}}(s,t)$; then, there exists $t_0$ such that $\widehat{\mathit{y}}(s,t_0)=\widehat{\mathit{\alpha }}\left(s\right)$. It follows that the surface can be represented as

$$\widehat{M}:\widehat{\mathit{y}}(s,t)-\widehat{\mathit{y}}(s,t_0)=(t-t_0)\widehat{\mathit{e}}\left(s\right),0\le s\le L,\mathrm{with}t,t_0\in [0,T],$$

(21)

where $\widehat{\mathit{e}}\left(s\right)$ defines the direction of the rulings. In view of Equation (9), we have

$$(t-t_0)\widehat{\mathit{e}}\left(s\right)=a(s,t){\widehat{\mathit{\chi }}}_1\left(s\right)+v(s,t){\widehat{\mathit{\chi }}}_2\left(s\right),0\le s\le L,\mathrm{with}t,t_0\in [0,T].$$

For $a(s,t)$ and $b(s,t)$, we have

$$\begin{array}{c}a(s,t)=(t-t_0)<\widehat{\mathit{e}}\left(s\right),{\widehat{\mathit{\chi }}}_1\left(s\right)>,\\ b(s,t)=(t-t_0)<\widehat{\mathit{e}}\left(s\right),{\widehat{\mathit{\chi }}}_2\left(s\right)>.\end{array}$$

(22)

The above equations are simply the necessary and sufficient conditions for which $\widehat{\mathit{y}}(s,t)$ is a ruled surface with a base $\widehat{\mathit{\alpha }}\left(s\right)$.

Now, we examine whether $\widehat{\mathit{\alpha }}\left(s\right)$ is also asymptotic on $\widehat{M}$ by employing Theorem 1. It is apparent that, in this case, it follows that

$$<\widehat{\mathit{e}}\left(s\right),{\widehat{\mathit{\chi }}}_2\left(s\right)>=det(\widehat{\mathit{e}},{\widehat{\mathit{\chi }}}_3,{\widehat{\mathit{\chi }}}_1)\ne 0.$$

(23)

Then, at any point on $\widehat{\mathit{\alpha }}\left(s\right)$, the $\widehat{\mathit{e}}$ should be in the osculating plane. Moreover, the $\widehat{\mathit{e}}$ and $\widehat{\mathit{t}}$ must not be parallel. It follows that

$$\widehat{\mathit{e}}\left(s\right)=x\left(s\right){\widehat{\mathit{\chi }}}_1\left(s\right)+y\left(s\right){\widehat{\mathit{\chi }}}_2\left(s\right),0\le s\le L.$$

(24)

Substituting Equation (24) into Equation (22), we obtain

$$tx\left(s\right)=a(s,t),\mathrm{and}ty\left(s\right)=b(s,t),\mathrm{with}y\left(s\right)\ne 0.$$

(25)

Then, the ruled surface family with the mutual geodesic $\widehat{\mathit{\alpha }}\left(s\right)$ can be specified as

$$\widehat{M}:\widehat{\mathit{y}}(s,t)=\widehat{\mathit{\alpha }}\left(s\right)+t(x\left(s\right){\widehat{\mathit{\chi }}}_1\left(s\right)+y\left(s\right){\widehat{\mathit{\chi }}}_2\left(s\right)),0\le s\le L,0\le t\le T,$$

(26)

where $x\left(s\right)$, $y\left(s\right)\ne 0$, $0\le s\le L,$ and $0\le t\le T$. However, the normal vector to $\widehat{M}$ along the curve $\widehat{\mathit{\alpha }}\left(s\right)$| is

$$\widehat{\mathit{\zeta }}(s,t_0)=y\left(s\right){\widehat{\mathit{\chi }}}_3\left(s\right),$$

(27)

which shows that $\widehat{\mathit{\alpha }}\left(s\right)$ is an asymptotic curve on $\widehat{M}$. Then, the following theorem can be stated.

Theorem 2.

The ruled surface family pair {M, $\widehat{M}$} interpolate the Bertrand pair {$\mathit{\alpha }\left(s\right)$, $\widehat{\mathit{\alpha }}\left(s\right)$} as common asymptotic curves if and only if there exists a parameter $t_0\in [0,T]$, and the functions $x\left(s\right)$, $y\left(s\right)\ne 0$, so that $\widehat{M}$ and M are, respectively, parameterized by Equation (26), and

$$M:\mathit{y}(s,t)=\mathit{\alpha }\left(s\right)+t(x\left(s\right){\mathit{\chi }}_1\left(s\right)+y\left(s\right){\mathit{\chi }}_2\left(s\right)),0\le s\le L,0\le t\le T.$$

(28)

It must be pointed out that in Equations (26) and (28), there exist two asymptotic curves crossing every point on the curves $\widehat{\mathit{\alpha }}\left(s\right)$($\mathit{\alpha }\left(s\right))$. One is $\widehat{\mathit{\alpha }}$ itself and the other is a line in the orientation $\widehat{\mathit{e}}\left(s\right)$ as given in Equation (24). Every constituent of the isoparametric ruled surface family with the mutual asymptotic $\widehat{\mathit{\alpha }}$ is established by two set functions $x\left(s\right)$, $y\left(s\right)\ne 0$.

Example 3.

In view of Example 1, for $x\left(v\right)=y\left(v\right)=-1$, the ruled oriented pair {M, $\widehat{M}$} and the ruled right pair {M, $\widehat{M}$}, respectively, are shown in Figure 6 and Figure 7, where $0\le v\le 1$, and $-4\le t\le 4$.

Figure 6. Ruled oriented pair {M, $\widehat{M}$} with $\widehat{\mathit{\alpha }}\left(v\right)$ blue and $\mathit{\alpha }\left(v\right)$ green.

Figure 7. Ruled right pair {M, $\widehat{M}$} with $\widehat{\mathit{\alpha }}\left(v\right)$ blue and $\mathit{\alpha }\left(v\right)$ green.

Example 4.

In view of Example 2, for $x\left(s\right)=y\left(s\right)=1$, the ruled oriented pair {M, $\widehat{M}$}, and the ruled right pair {M, $\widehat{M}$}, respectively, are shown in Figure 8 and Figure 9, where $-2\le t\le 2$, and $0\le s\le 2\pi$ (Figure 8).

Figure 8. Ruled oriented pair {M, $\widehat{M}$} with $\widehat{\mathit{\alpha }}\left(s\right)$ blue and $\mathit{\alpha }\left(s\right)$ green.

Figure 9. Ruled right pair {M, $\widehat{M}$} with $\widehat{\mathit{\alpha }}\left(s\right)$ blue and $\mathit{\alpha }\left(s\right)$ green.

4. Conclusions

In this work, we constructed the surface pencil pair and ruled surface pencil pair interpolating a Bertrand pair as common asymptotic curves in Euclidean 3-space ${\mathbb{E}}^3$. Moreover, some curves were selected to organize the surface pencil pair and ruled surface pencil pair that have the Bertrand pair {$\widehat{\mathit{\alpha }}\left(s\right)$, $\mathit{\alpha }\left(s\right)$} as common asymptotic curves. Hopefully, these results will be advantageous for work in computer-aided manufacturing and to those exploring manufacturing. Our results, presented in this paper, can contribute to the field of CAGD and have practical applications in CAM. The authors plan to register the study in different spaces and examine the classification of singularities as reported in [20,21,22].