Motion-Tracking Control of Mobile Manipulation Robotic Systems Using Artificial Neural Networks for Manufacturing Applications
Abstract
1. Introduction
2. Mathematical Modeling of the Mobile Manipulation Robotic System
2.1. System Description
2.2. Kinematic Modeling
2.3. Dynamic Modeling
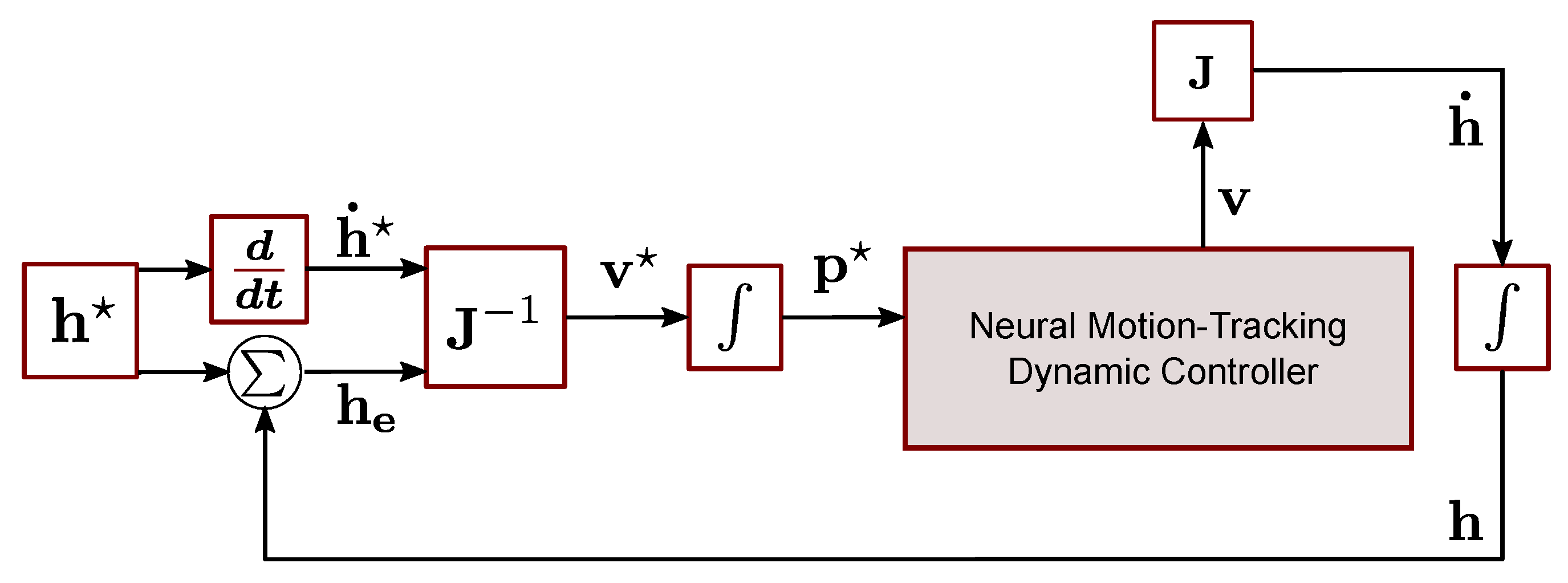
3. A Motion-Control Approach for the Mobile Manipulation Robotic System
4. Mobile Manipulation Robotic System Motion Control Using Artificial Neural Networks
5. Numeric Simulation Results
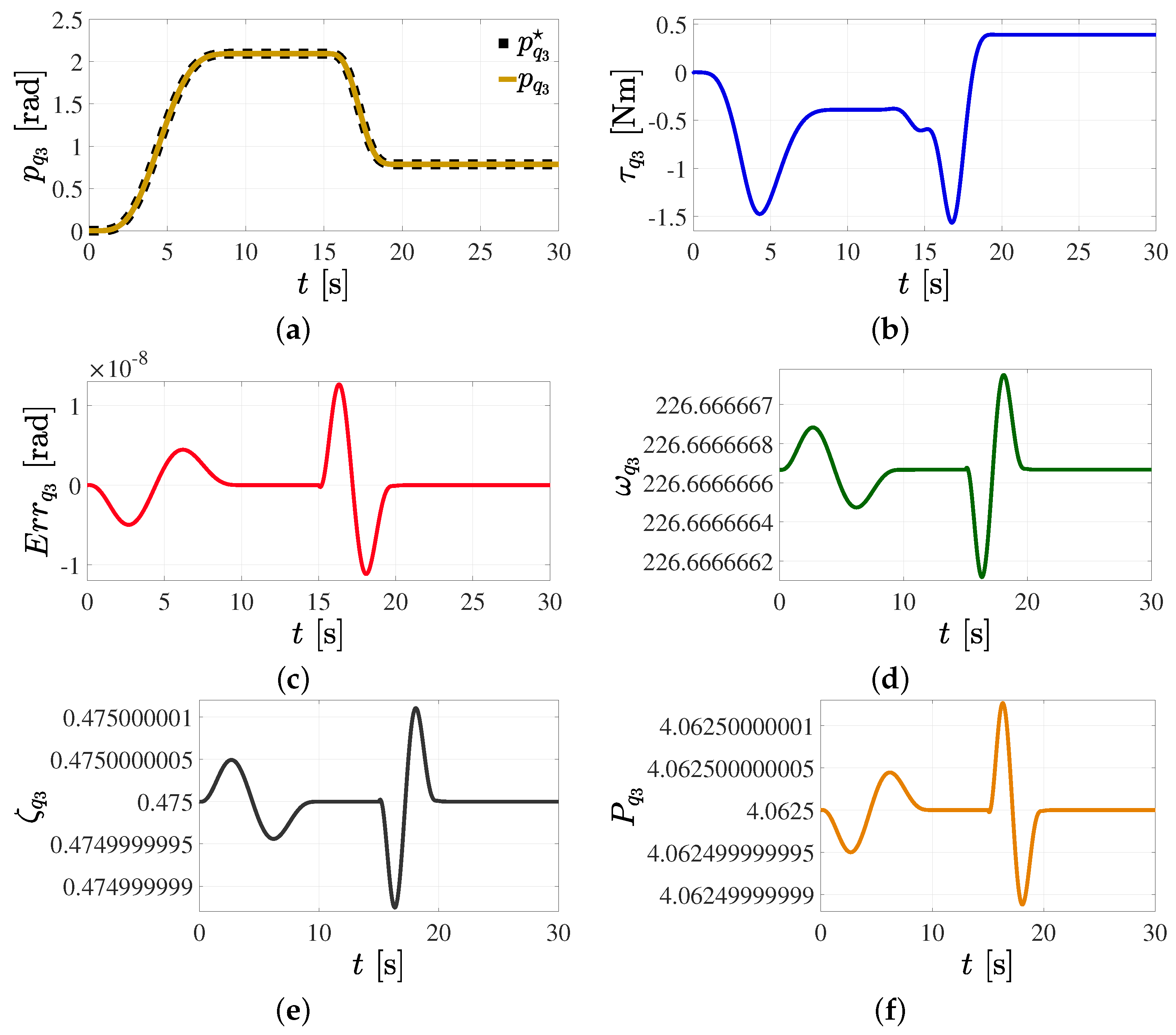
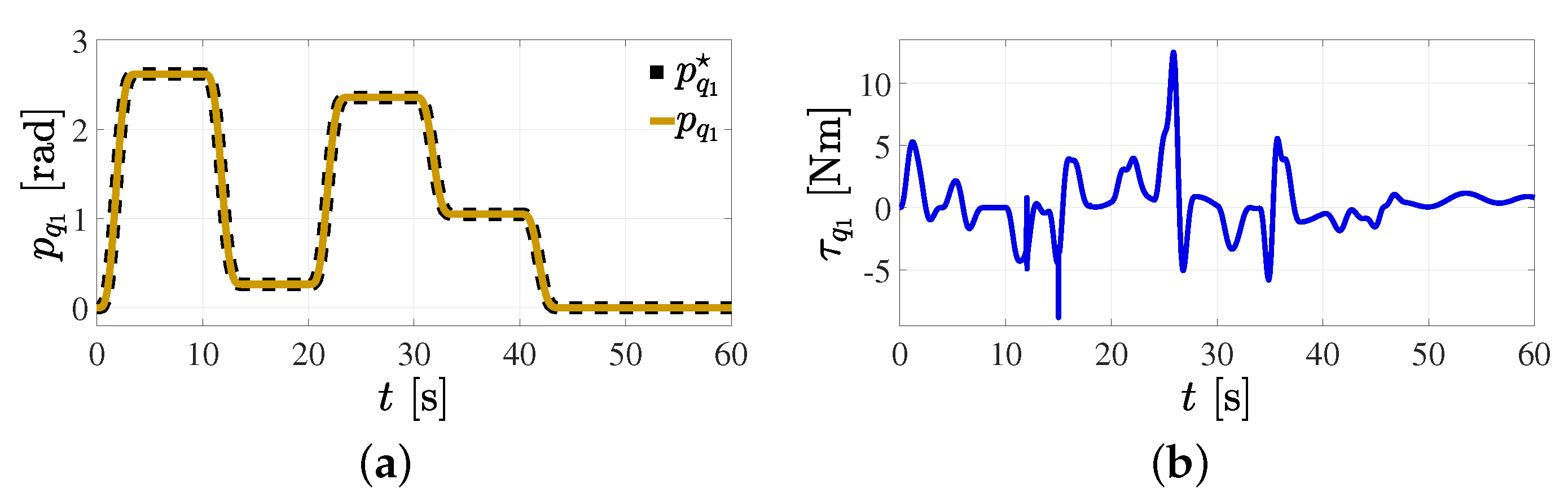
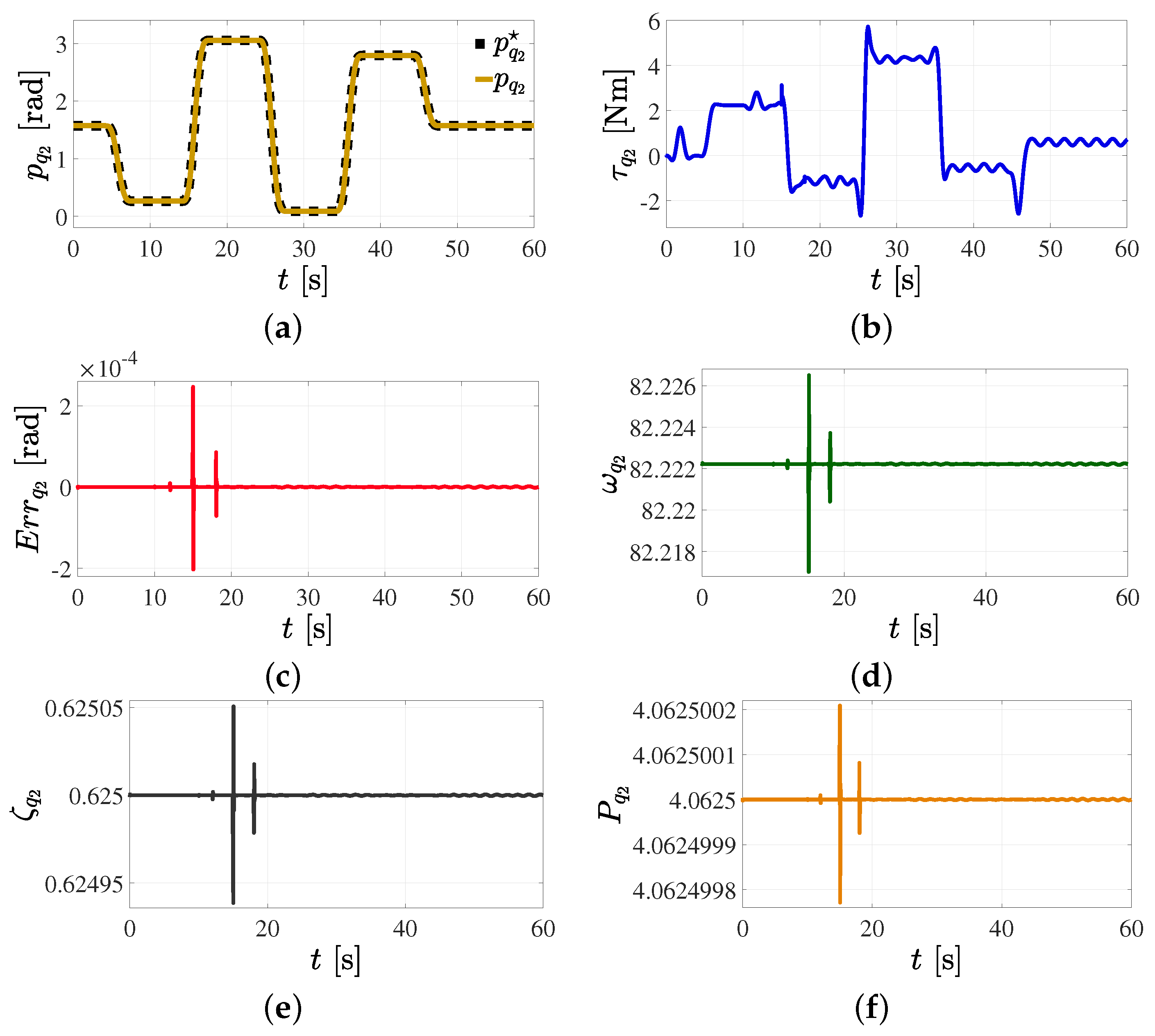
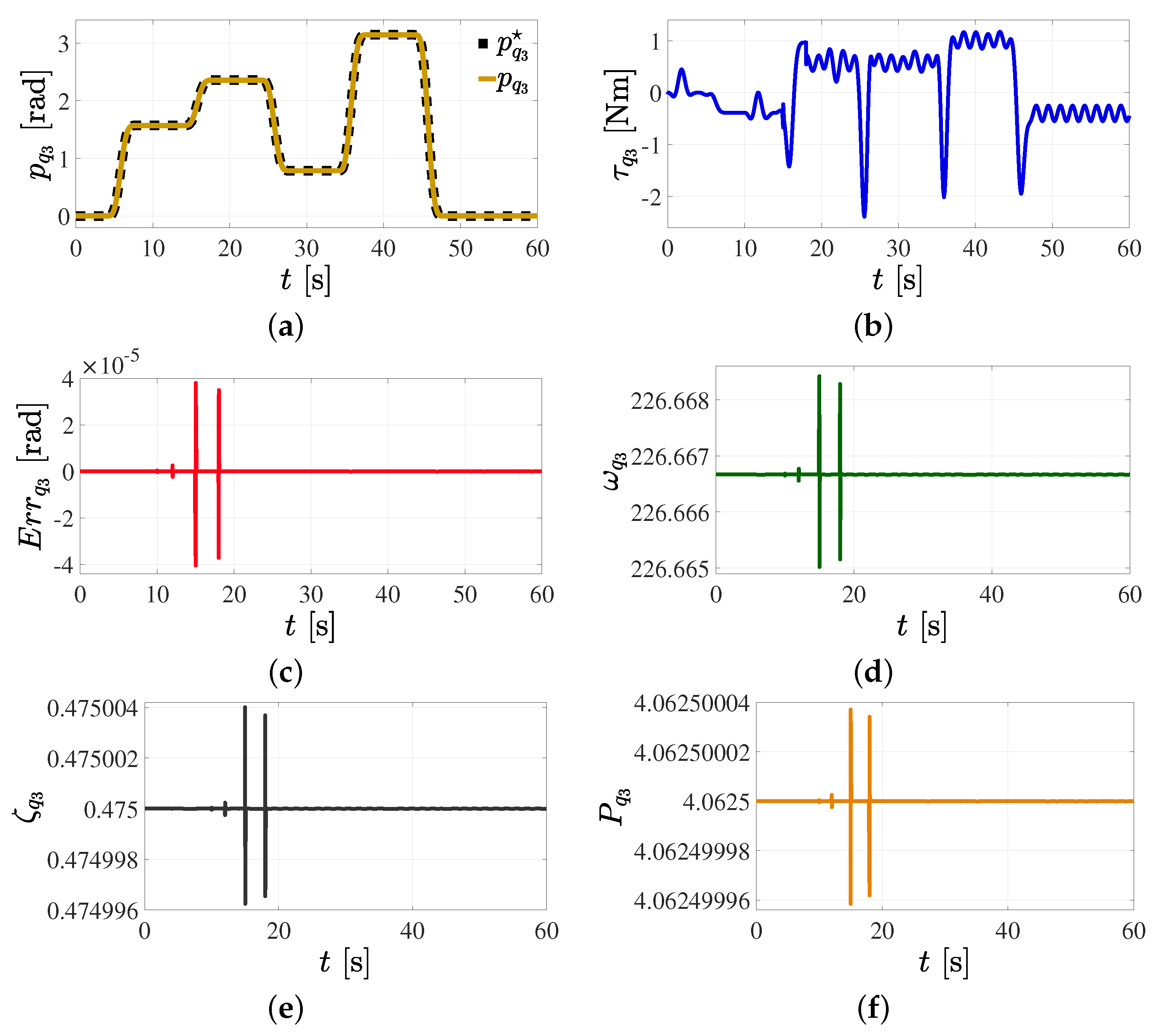
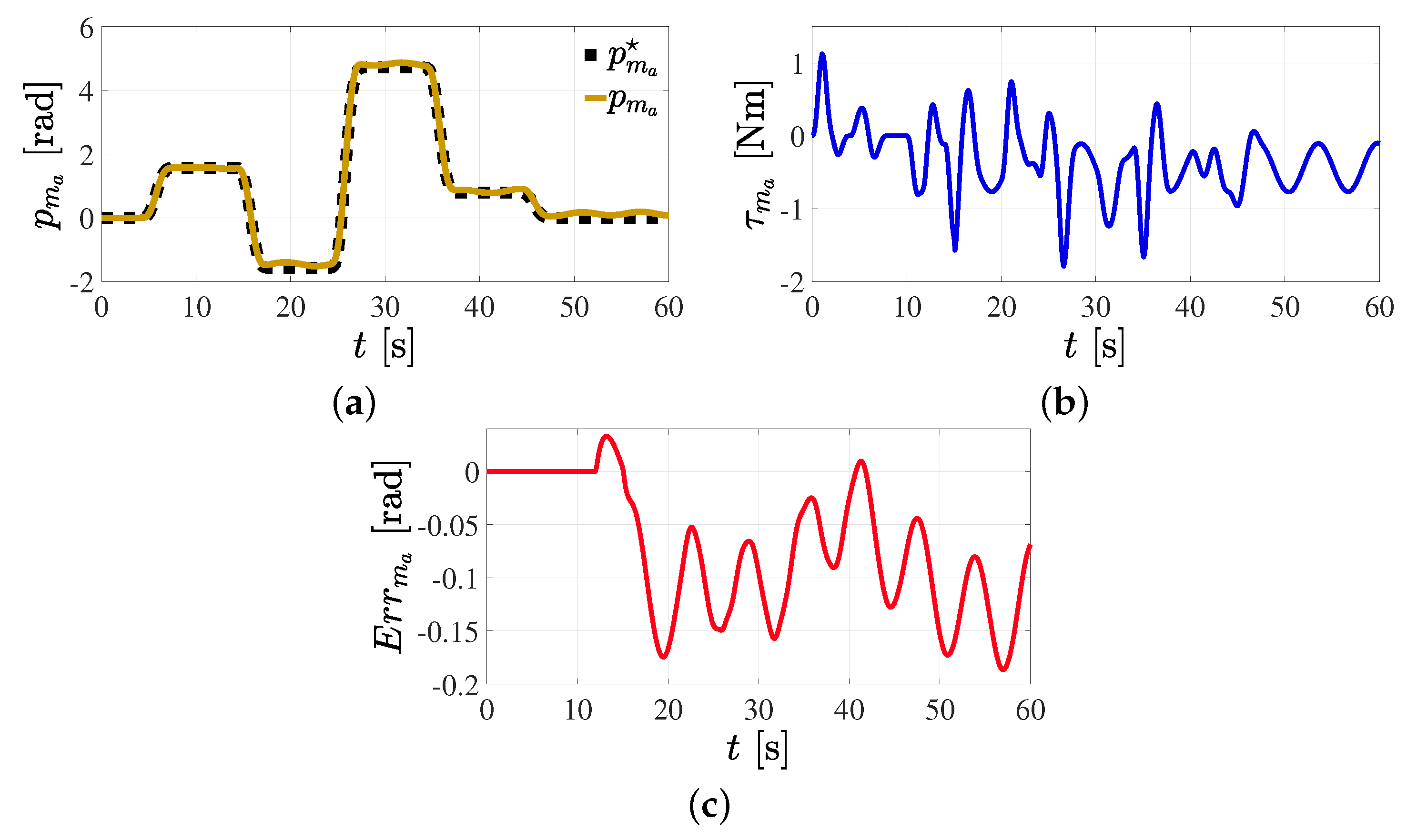
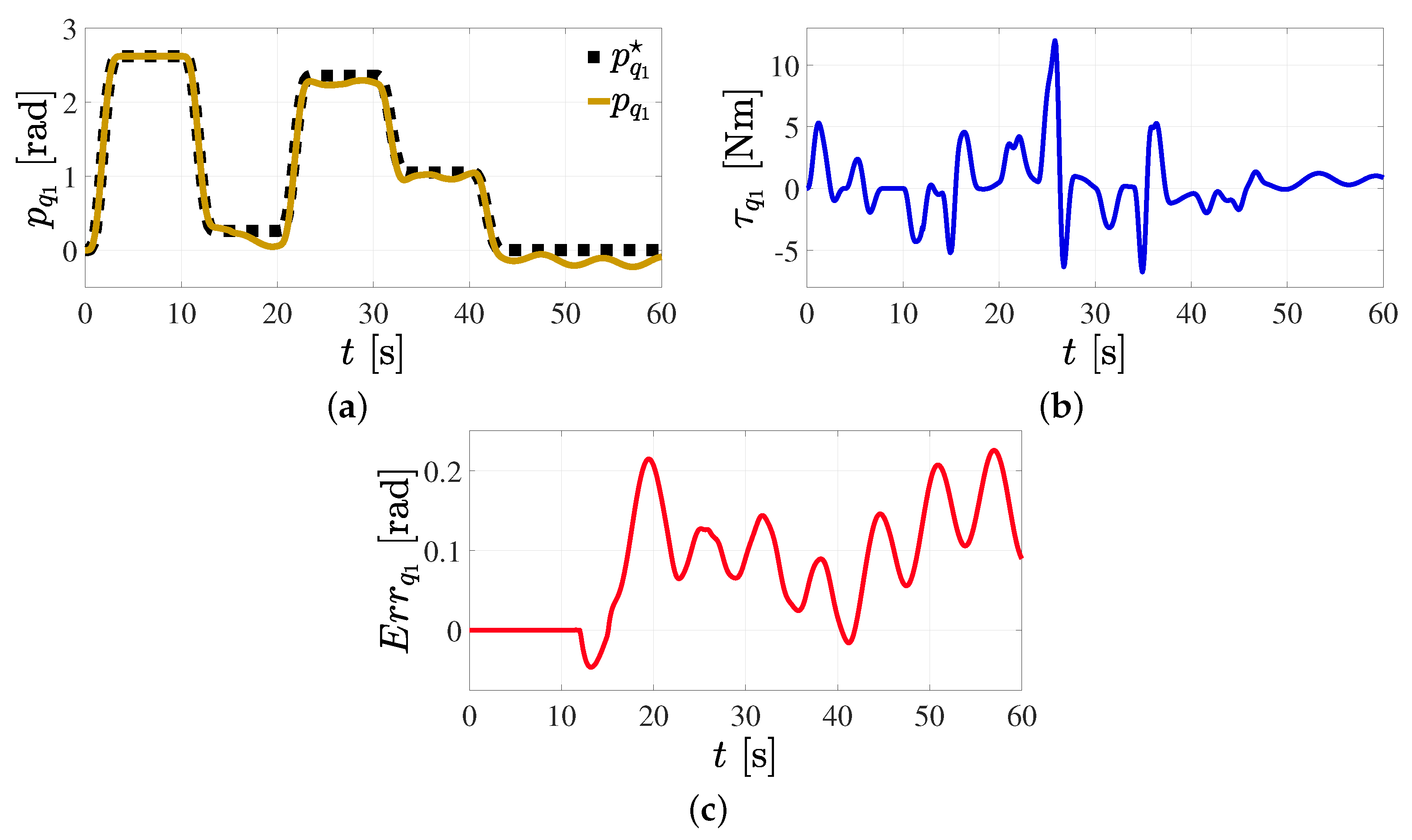
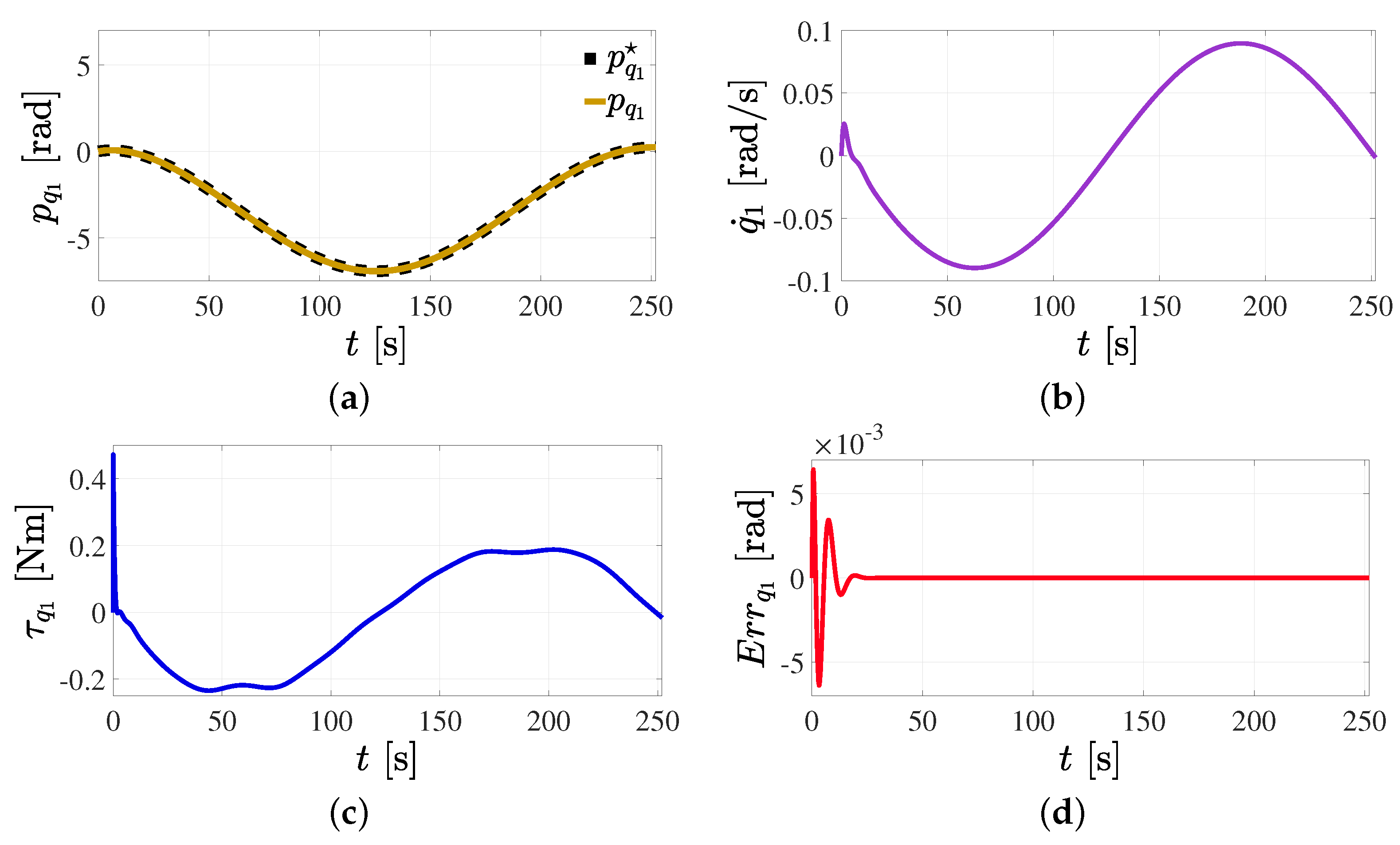
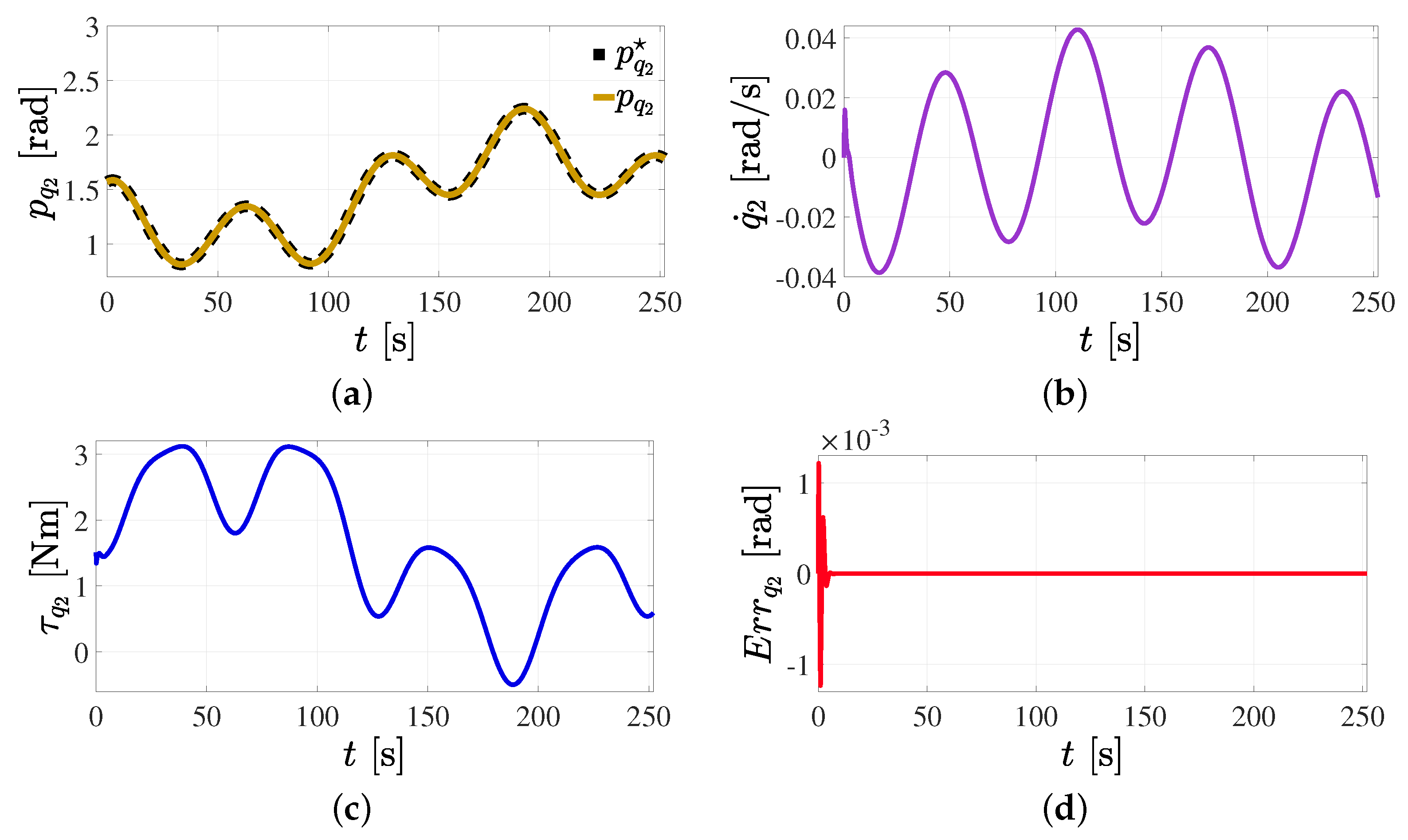
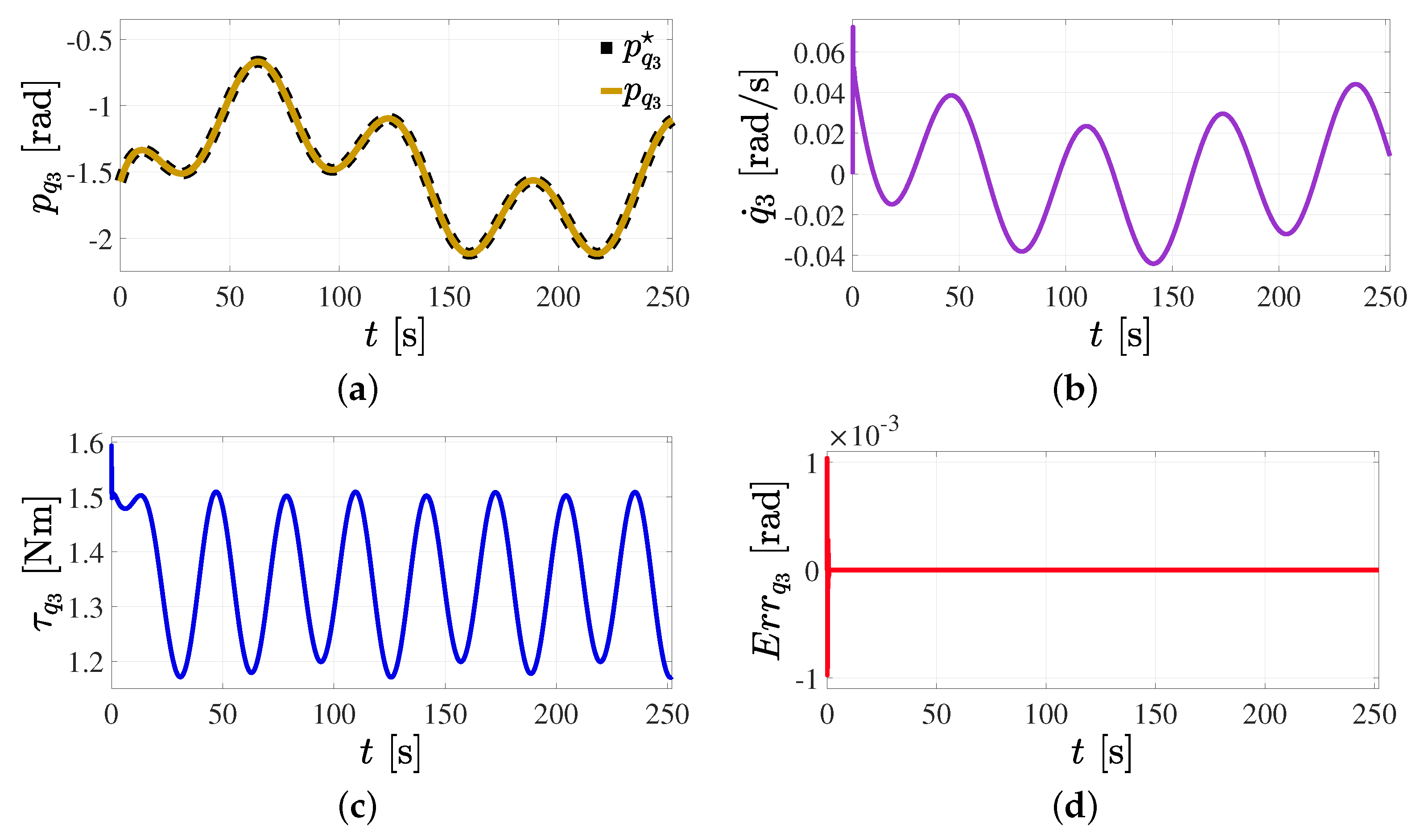
5.1. Position Reference Tracking Control in the Joint Space
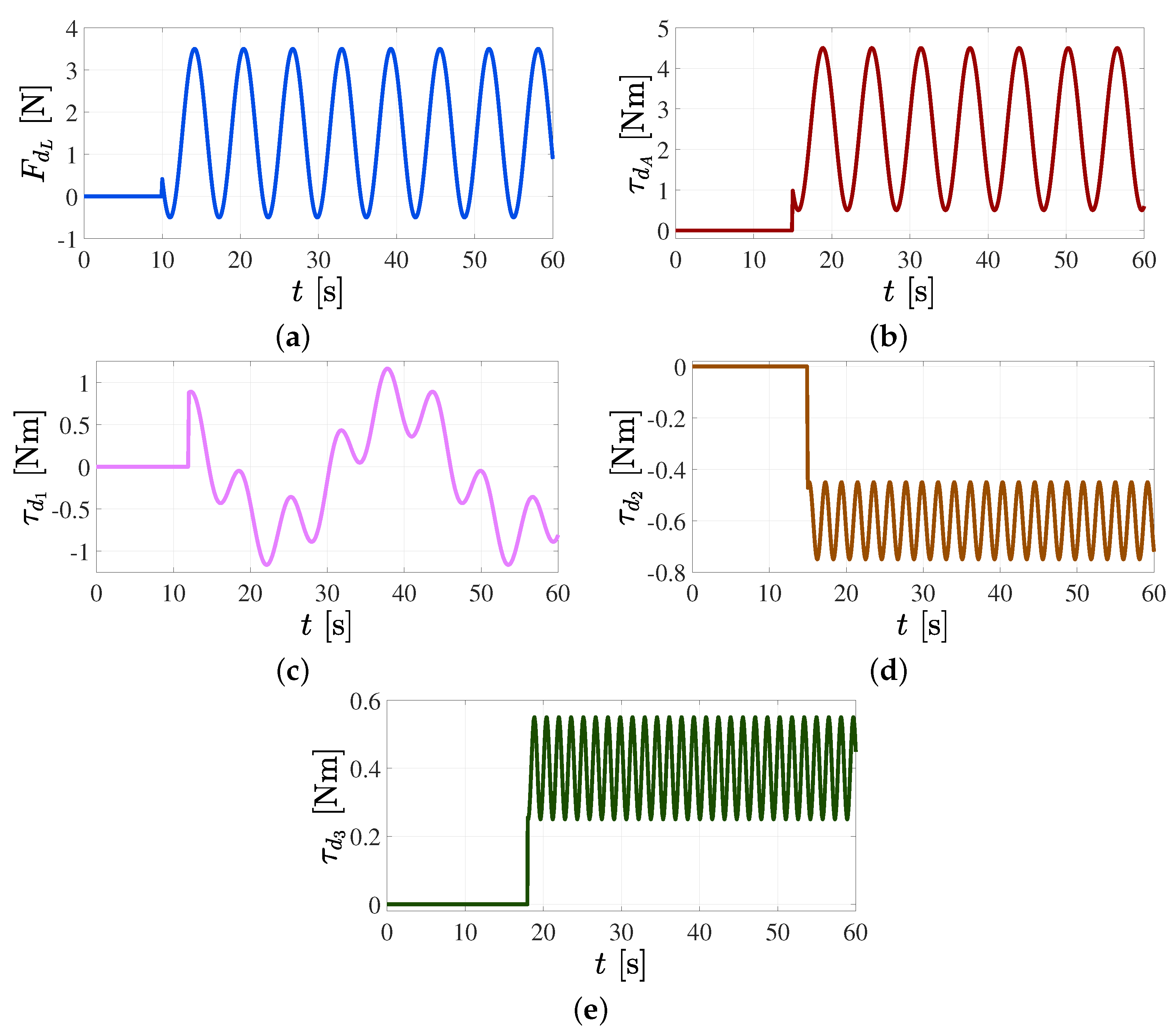
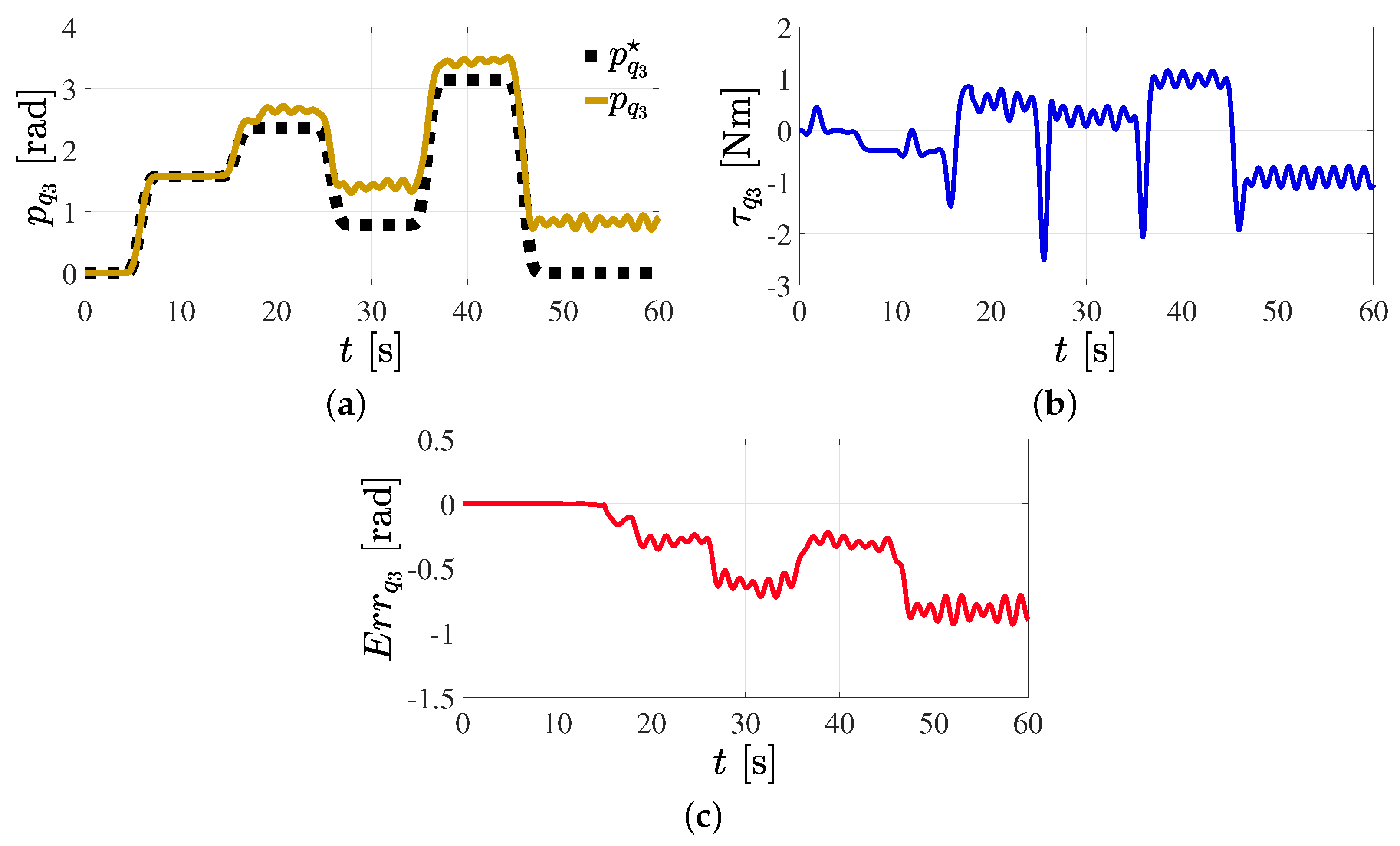
5.2. Position Reference Tracking Control in the Joint Space Subjected to External Vibratory Torques
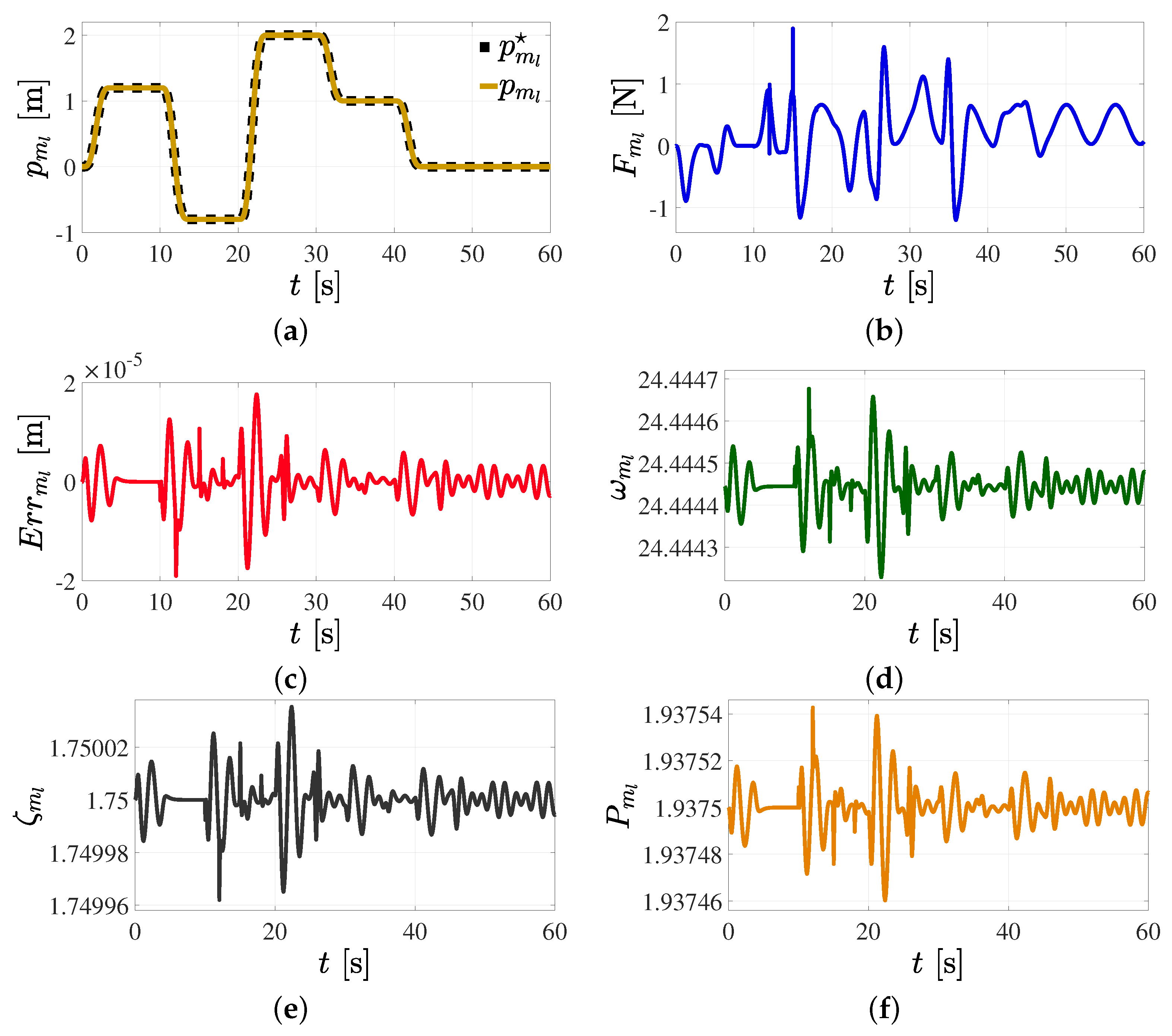
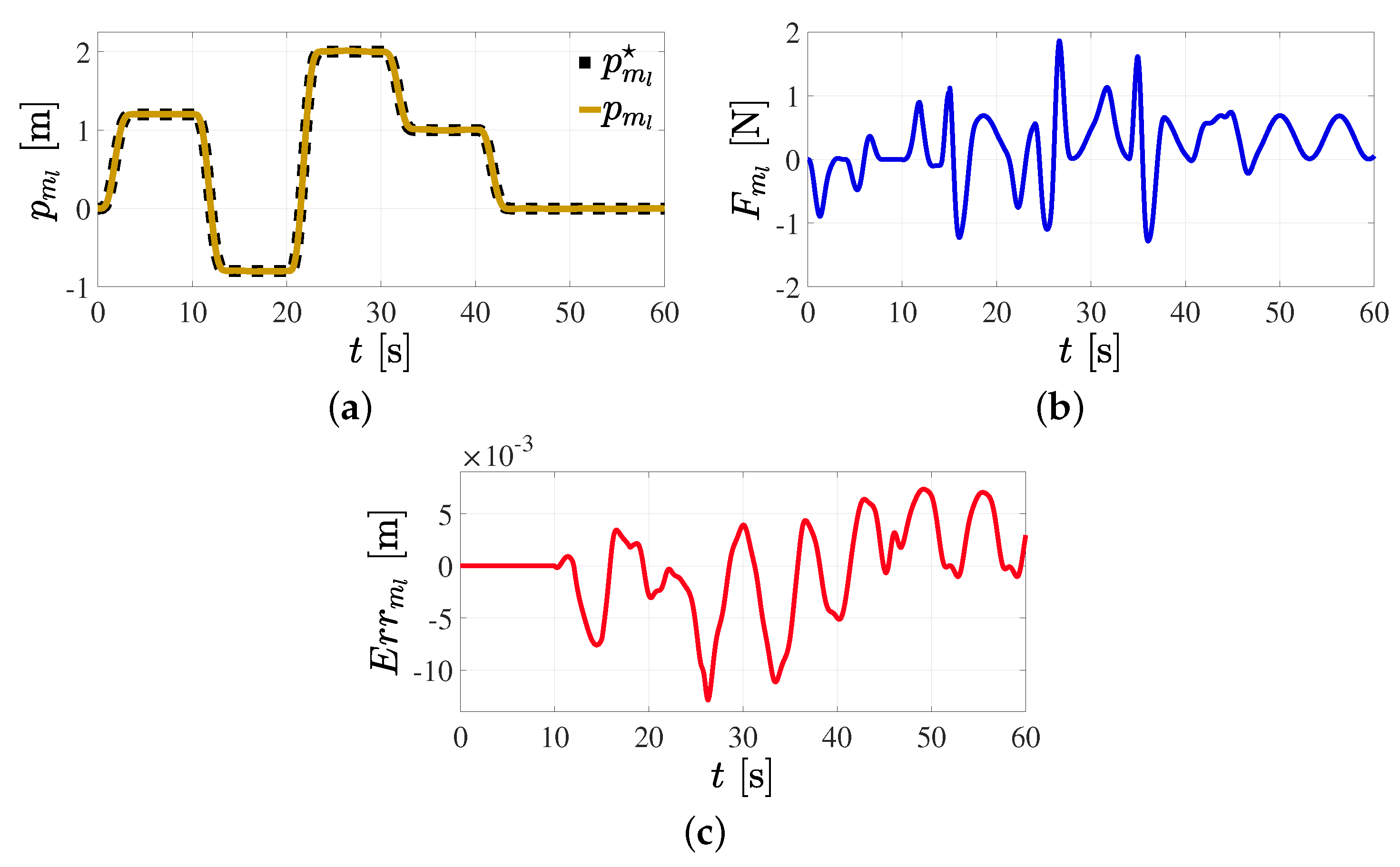
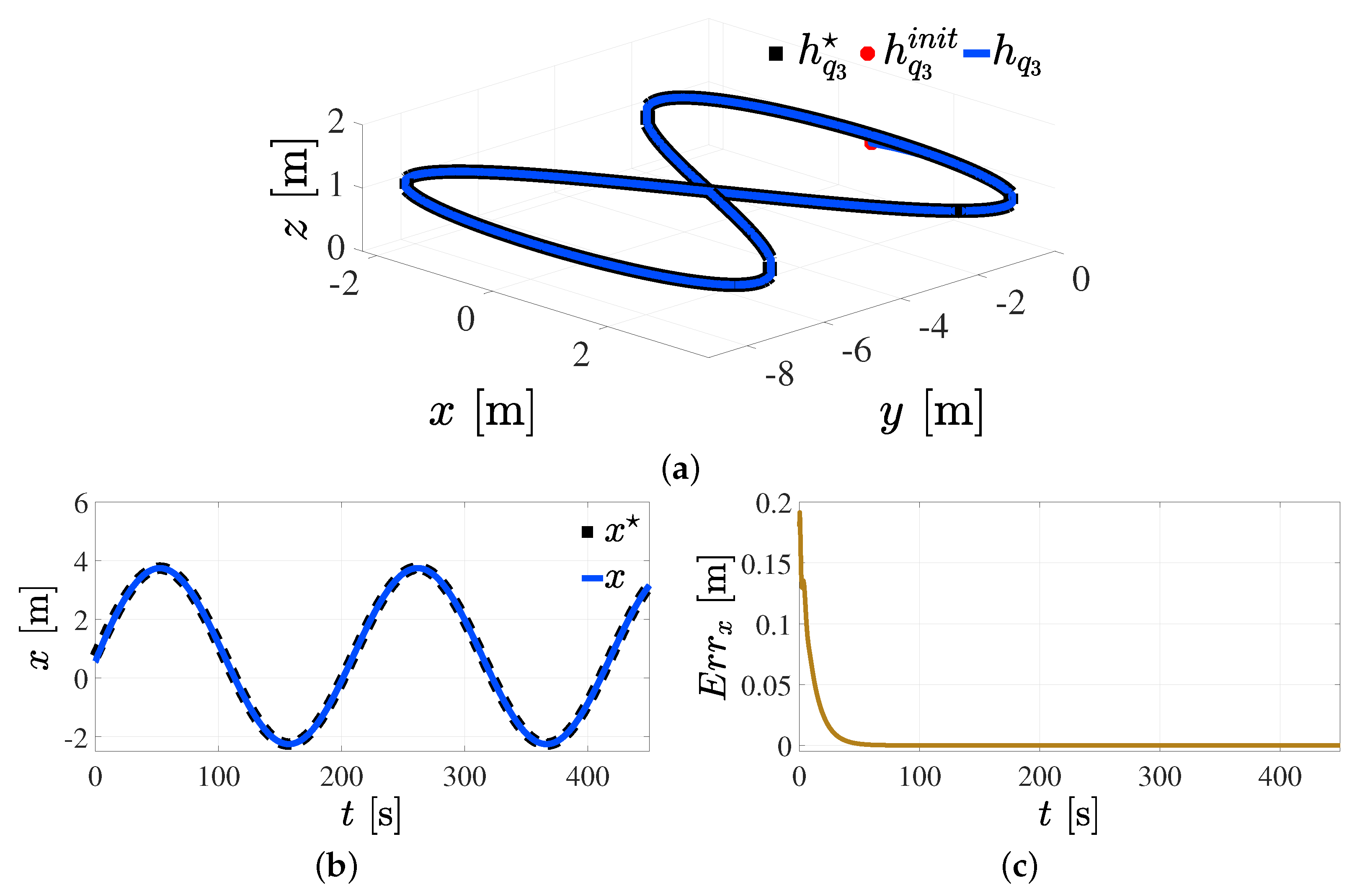
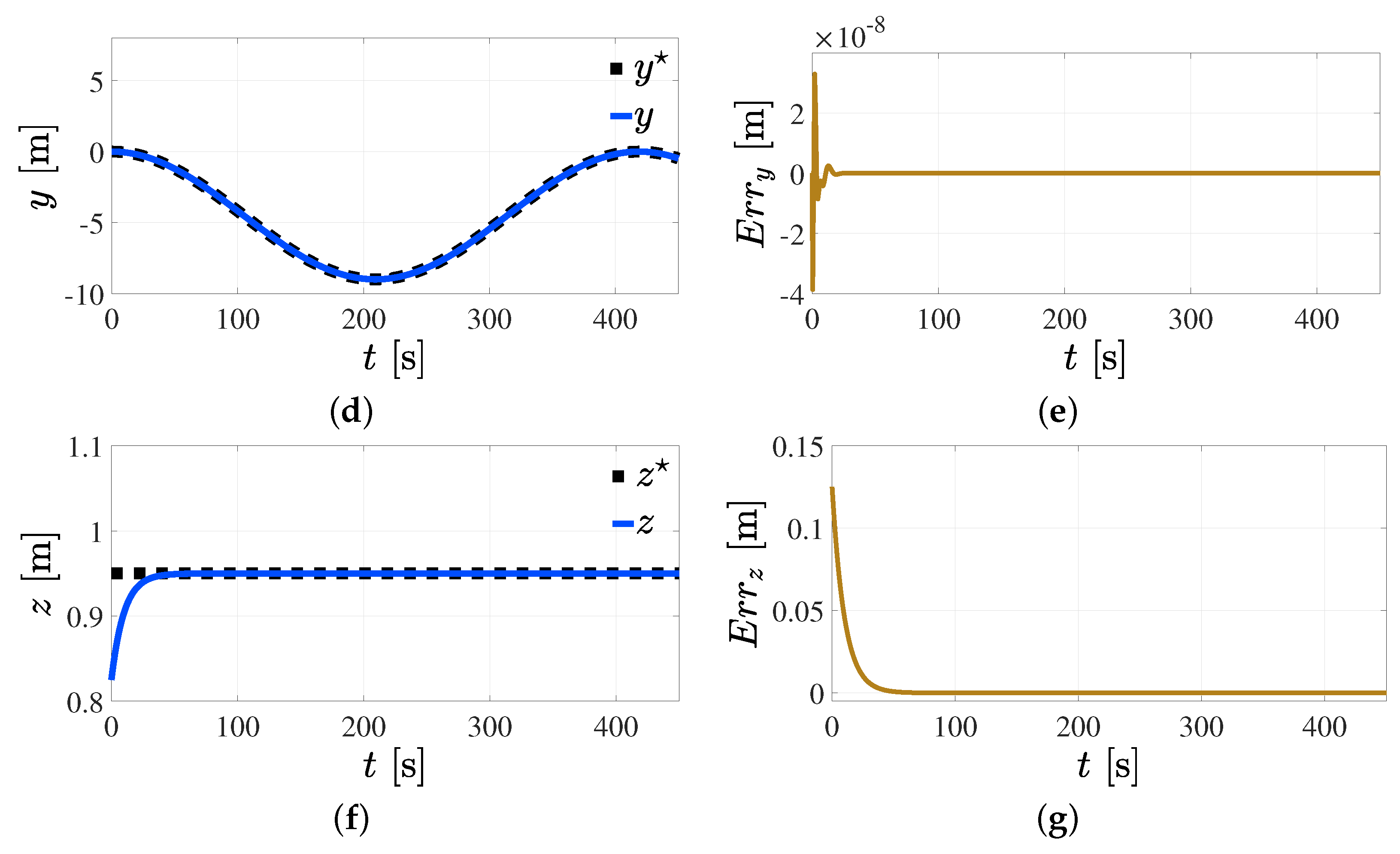
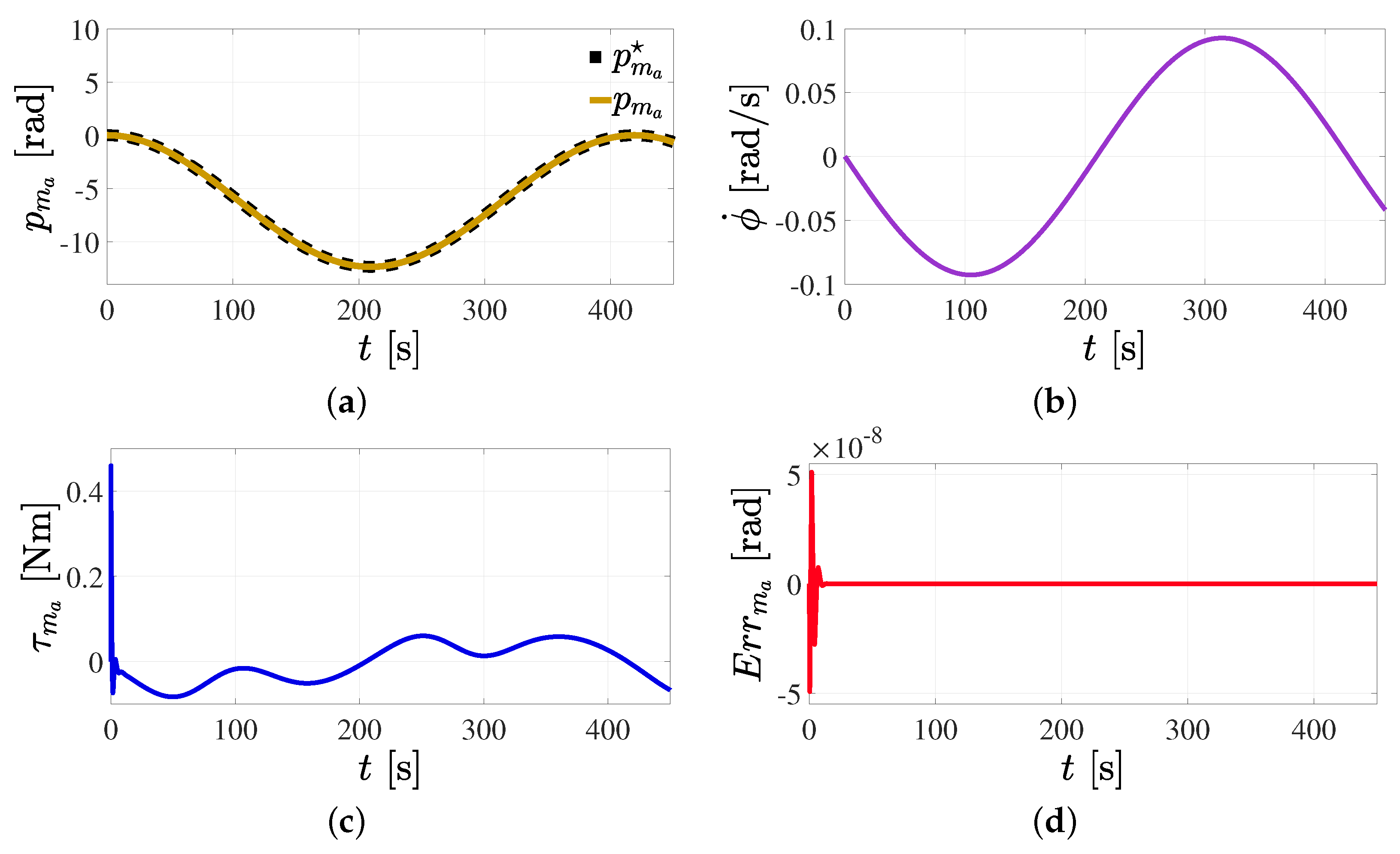
5.3. Trajectory Tracking Control in Cartesian Space
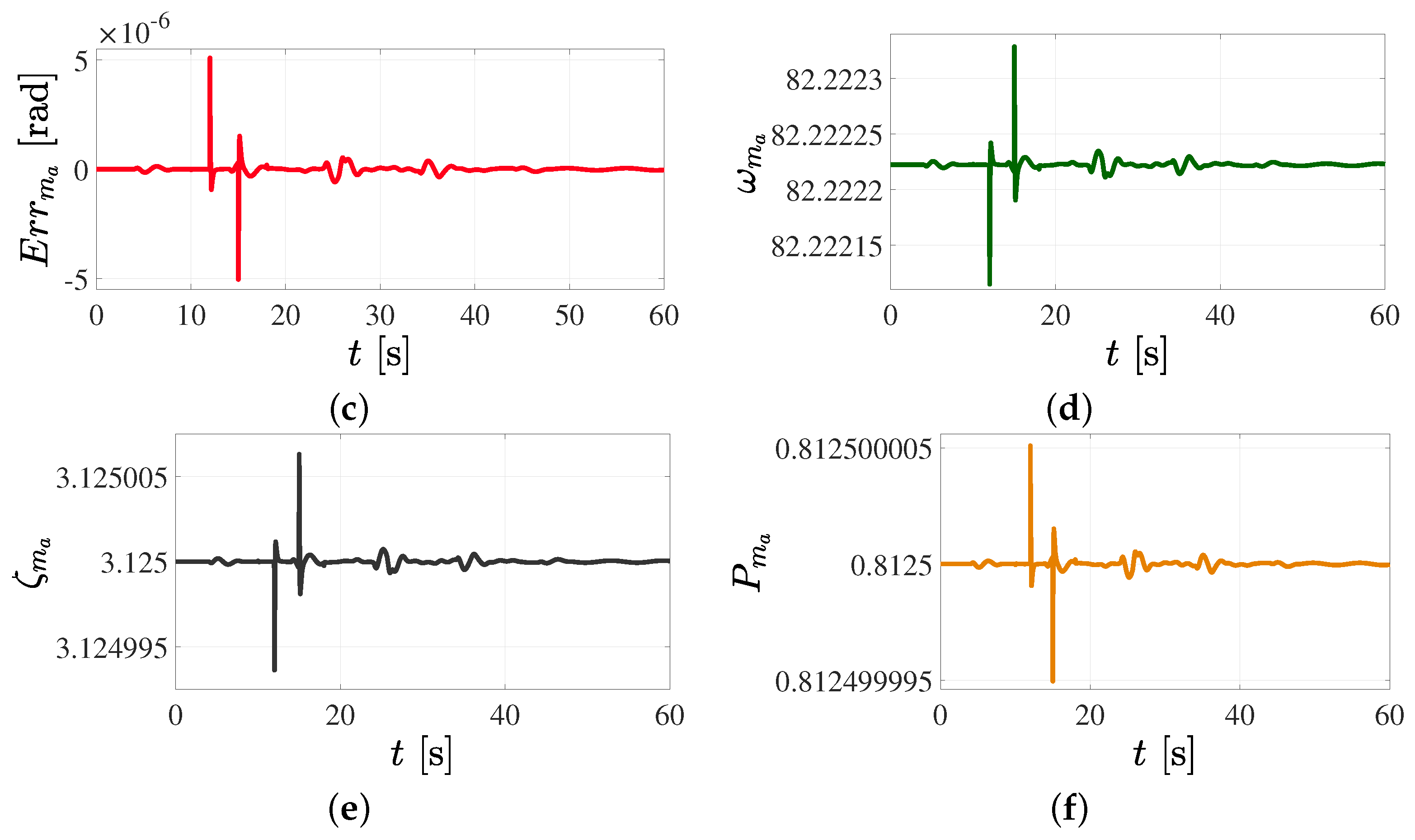
5.4. Trajectory Tracking Control in Cartesian Space with Parameter Variation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| BS-ANN | B-Spline Artificial Neural Network |
| DC | Direct Current |
| DOF | Degrees of Freedom |
| PD | Proportional Derivative |
| PID | Proportional Integral Derivative |
References
- Dörfler, K.; Dielemans, G.; Lachmayer, L.; Recker, T.; Raatz, A.; Lowke, D.; Gerke, M. Additive Manufacturing using Mobile Robots: Opportunities and Challenges for Building Construction. Cem. Concr. Res. 2022, 158, 106772. [Google Scholar] [CrossRef]
- Matheson, E.; Minto, R.; Zampieri, E.G.; Faccio, M.; Rosati, G. Human–Robot Collaboration in Manufacturing Applications: A Review. Robotics 2019, 8, 100. [Google Scholar] [CrossRef]
- Wilson, M. Industrial Robots. In Implementation of Robot Systems: An Introduction to Robotics, Automation, and Successful Systems Integration in Manufacturing; Butterworth-Heinemann: London, UK, 2014; pp. 19–38. [Google Scholar]
- Sandakalum, T.; Ang Jr, M.H. Motion Planning for Mobile Manipulators—A Systematic Review. Machines 2022, 10, 97. [Google Scholar] [CrossRef]
- Bonci, A.; Cen Cheng, P.D.; Indri, M.; Nabissi, G.; Sibona, F. Human–Robot Perception in Industrial Environments: A Survey. Sensors 2021, 21, 1571. [Google Scholar] [CrossRef]
- Yang, M.; Yang, E.; Zante, R.C.; Post, M.; Liu, X. Collaborative Mobile Industrial Manipulator: A Review of System Architecture and Applications. In Proceedings of the 2019 25th International Conference on Automation and Computing (ICAC 2019), Lancaster, UK, 5–7 September 2019; pp. 1–6. [Google Scholar]
- Li, R.; Qiao, H. A Survey of Methods and Strategies for High–Precision Robotic Grasping and Assembly Tasks—Some New Trends. IEEE/ASME Trans. Mechatronics 2019, 24, 2718–2732. [Google Scholar] [CrossRef]
- Sumanas, M.; Petronis, A.; Bucinskas, V.; Dzedzickis, A.; Virzonis, D.; Morkvenaite-Vilkonciene, I. Deep Q–Learning in Robotics: Improvement of Accuracy and Repeatability. Sensors 2022, 22, 3911. [Google Scholar] [CrossRef] [PubMed]
- Arents, J.; Greitans, M. Smart Industrial Robot Control Trends, Challenges and Opportunities within Manufacturing. Appl. Sci. 2022, 12, 937. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, Q.; Xu, W.; Wang, L.; Zhou, Z. Robot Learning towards Smart Robotic Manufacturing: A Review. Robot. Comput.-Integr. Manuf. 2022, 77, 102360. [Google Scholar] [CrossRef]
- Liu, H.; Wang, L. Remote Human–Robot Collaboration: A Cyber–Physical System Application for Hazard Manufacturing Environment. J. Manuf. Syst. 2020, 54, 24–34. [Google Scholar] [CrossRef]
- Oomen, T. Advanced Motion Control for Precision Mechatronics: Control, Identification, and Learning of Complex Systems. Ieej J. Ind. Appl. 2018, 7, 127–140. [Google Scholar] [CrossRef]
- Hamner, B.; Koterba, S.; Shi, J.; Simmons, R.; Singh, S. An Autonomous Mobile Manipulator for Assembly Tasks. Auton. Robot. 2010, 28, 131–149. [Google Scholar] [CrossRef]
- Alandoli, E.A.; Lee, T.; Vijayakumar, V.; Lin, Y.; Mohammed, M.Q. Dynamic Model and Integrated Optimal Controller of Hybrid Arms Robot for Laser Contour Machining. J. Vib. Control 2022, 29, 10775463221090000. [Google Scholar] [CrossRef]
- Jafari, D.; Vaneker, T.H.; Gibson, I. Wire and Arc Additive Manufacturing: Opportunities and Challenges to Control the Quality and Accuracy of Manufactured Parts. Mater. Des. 2021, 202, 109471. [Google Scholar] [CrossRef]
- Nagabandi, A.; Konolige, K.; Levine, S.; Kumar, V. Deep Dynamics Models for Learning Dexterous Manipulation. In Proceedings of the Conference on Robot Learning, Virtual Event, 16–18 November 2020; pp. 1101–1112. [Google Scholar]
- Billard, A.; Kragic, D. Trends and Challenges in Robot Manipulation. Science 2019, 364, eaat8414. [Google Scholar] [CrossRef]
- Kumar, M.; Shenbagaraman, V.; Shaw, R.N.; Ghosh, A. Digital Transformation in Smart Manufacturing with Industrial Robot through Predictive Data Analysis. In Machine Learning for Robotics Applications; Springer: Singapore, 2021; pp. 85–105. [Google Scholar]
- Javaid, M.; Haleem, A.; Singh, R.P.; Suman, R. Substantial Capabilities of Robotics in Enhancing Industry 4.0 Implementation. Cogn. Robot. 2021, 1, 58–75. [Google Scholar] [CrossRef]
- Beschi, M.; Mutti, S.; Nicola, G.; Faroni, M.; Magnoni, P.; Villagrossi, E.; Pedrocchi, N. Optimal Robot Motion Planning of Redundant Robots in Machining and Additive Manufacturing Applications. Electronics 2019, 8, 1437. [Google Scholar] [CrossRef]
- Bi, Z.M.; Luo, C.; Miao, Z.; Zhang, B.; Zhang, W.; Wang, L. Safety Assurance Mechanisms of Collaborative Robotic Systems in Manufacturing. Robot. Comput.-Integr. Manuf. 2021, 67, 102022. [Google Scholar] [CrossRef]
- Minniti, M.V.; Farshidian, F.; Grandia, R.; Hutter, M. Whole–Body MPC for a Dynamically Stable Mobile Manipulator. IEEE Robot. Autom. Lett. 2019, 4, 3687–3694. [Google Scholar] [CrossRef]
- Garnier, S.; Subrin, K.; Arevalo-Siles, P.; Caverot, G.; Furet, B. Mobile Robot Stability for Complex Tasks in Naval Industries. Procedia CIRP 2018, 72, 297–302. [Google Scholar] [CrossRef]
- Zacharaki, A.; Kostavelis, I.; Gasteratos, A.; Dokas, I. Safety Bounds in Human Robot Interaction: A Survey. Saf. Sci. 2020, 127, 104667. [Google Scholar] [CrossRef]
- Fareh, R.; Khadraoui, S.; Abdallah, M.Y.; Baziyad, M.; Bettayeb, M. Active Disturbance Rejection Control for Robotic Systems: A Review. Mechatronics 2021, 80, 102671. [Google Scholar] [CrossRef]
- Liu, S.; Wang, L.; Wang, X.V. Sensorless Force Estimation for Industrial Robots using Disturbance Observer and Neural Learning of Friction Approximation. Robot. Comput.-Integr. Manuf. 2021, 71, 102168. [Google Scholar] [CrossRef]
- Nikranjbar, A.; Haidari, M.; Atai, A.A. Adaptive Sliding Mode Tracking Control of Mobile Robot in Dynamic Environment using Artificial Potential Fields. J. Comput. Robot. 2018, 11, 1–14. [Google Scholar]
- Katz, D.; Horrell, E.; Yang, Y.; Burns, B.; Buckley, T.; Grishkan, A.; Zhylkovskyy, V.; Brock, O.; Learned-Miller, E. The UMass Mobile Manipulator UMan: An Experimental Platform for Autonomous Mobile Manipulation. In Workshop on Manipulation in Human Environments at Robotics: Science and Systems; University of Pennsylvania: Philadelphia, PA, USA, 2006; Available online: https://people.cs.umass.edu/~elm/papers/UMan_workshop_06.pdf (accessed on 25 June 2023).
- Ambrose, R.O.; Savely, R.T.; Goza, S.M.; Strawser, P.; Diftler, M.A.; Spain, I.; Radford, N. Mobile Manipulation using NASA’s Robonaut. In Proceedings of the IEEE International Conference on Robotics and Automation, 2004. Proceedings. ICRA’04. 2004, New Orleans, LA, USA, 26 April–1 May 2004; Volume 2, pp. 2104–2109. [Google Scholar]
- Park, D.; Hoshi, Y.; Mahajan, H.P.; Kim, H.K.; Erickson, Z.; Rogers, W.A.; Kemp, C.C. Active Robot–Assisted Feeding with a General-Purpose Mobile Manipulator: Design, Evaluation, and Lessons Learned. Robot. Auton. Syst. 2020, 124, 103344. [Google Scholar] [CrossRef]
- Yamamoto, T.; Terada, K.; Ochiai, A.; Saito, F.; Asahara, Y.; Murase, K. Development of Human Support Robot as the Research Platform of a Domestic Mobile Manipulator. Robomech J. 2019, 6, 4. [Google Scholar] [CrossRef]
- Merckaert, K.; Convens, B.; Wu, C.-j.; Roncone, A.; Nicotra, M.M.; Vanderborght, B. Real–Time Motion Control of Robotic Manipulators for Safe Human–Robot Coexistence. Robot. Comput.-Integr. Manuf. 2022, 73, 102223. [Google Scholar] [CrossRef]
- Prasad, A.; Sharma, B.; Vanualailai, J.; Kumar, S. Motion Control of an Articulated Mobile Manipulator in 3D using the Lyapunov–based Control Scheme. Int. J. Control 2022, 95, 2581–2595. [Google Scholar] [CrossRef]
- Fareh, R.; Saad, M.R.; Saad, M.; Brahmi, A.; Bettayeb, M. Trajectory Tracking and Stability Analysis for Mobile Manipulators based on Decentralized Control. Robotica 2019, 37, 1732–1749. [Google Scholar] [CrossRef]
- Brahmi, A.; Saad, M.; Brahmi, B.; Bojairami, I.E.; Gauthier, G.; Ghommam, J. Robust Adaptive Tracking Control for Uncertain Nonholonomic Mobile Manipulator. Proc. Inst. Mech. Eng. Part J. Syst. Control Eng. 2022, 236, 395–405. [Google Scholar] [CrossRef]
- Mishra, S.; Londhe, P.S.; Mohan, S.; Vishvakarma, S.K.; Patre, B. Robust Task–Space Motion Control of a Mobile Manipulator using a Nonlinear Control with an Uncertainty Estimator. Comput. Electr. Eng. 2018, 67, 729–740. [Google Scholar] [CrossRef]
- Xia, K.; Gao, H.; Ding, L.; Liu, G.; Deng, Z.; Liu, Z.; Ma, C. Trajectory Tracking Control of Wheeled Mobile Manipulator based on Fuzzy Neural Network and Extended Kalman Filtering. Neural Comput. Appl. 2018, 30, 447–462. [Google Scholar] [CrossRef]
- Mai, T. Hybrid Adaptive Tracking Control Method for Mobile Manipulator Robot based on Proportional–Integral–Derivative Technique. Proc. Inst. Mech. Eng. Part J. Mech. Eng. Sci. 2021, 235, 6463–6480. [Google Scholar] [CrossRef]
- Qin, D.; Liu, A.; Xu, J.; Zhang, W.A.; Yu, L. Learning from Human Demonstrations for Wheel Mobile Manipulator: An Unscented Model Predictive Control Approach. IEEE Trans. Neural Netw. Learn. Syst. 2022. early access. [Google Scholar] [CrossRef]
- Liu, L.; Yue, X.; Wen, H.; Hao, Z.; Wang, Z. Output Feedback Tracking Control for Nonholonomic Wheeled Mobile Manipulator Systems with Full–Output Constraints. Proc. Inst. Mech. Eng. Part J. Syst. Control Eng. 2023, 237, 09596518221141489. [Google Scholar] [CrossRef]
- Sharma, M.; Luthra, S.; Joshi, S.; Kumar, A. Implementing Challenges of Artificial Intelligence: Evidence from Public Manufacturing Sector of an Emerging Economy. Gov. Inf. Q. 2022, 39, 101624. [Google Scholar] [CrossRef]
- Arinez, J.F.; Chang, Q.; Gao, R.X.; Xu, C.; Zhang, J. Artificial Intelligence in Advanced Manufacturing: Current Status and Future Outlook. J. Manuf. Sci. Eng. 2020, 142, 110804. [Google Scholar] [CrossRef]
- Balamurugan, E.; Flaih, L.R.; Yuvaraj, D.; Sangeetha, K.; Jayanthiladevi, A.; Kumar, T.S. Use Case of Artificial Intelligence in Machine Learning Manufacturing 4.0. In Proceedings of the 2019 International conference on computational intelligence and knowledge economy (ICCIKE), Dubai, United Arab Emirates, 11–12 December 2019; pp. 656–659. [Google Scholar]
- Soori, M.; Arezoo, B.; Dastres, R. Artificial Intelligence, Machine Learning and Deep Learning in Advanced Robotics, A Review. Cogn. Robot. 2023, 3, 54–70. [Google Scholar] [CrossRef]
- Kim, S.W.; Kong, J.H.; Lee, S.W.; Lee, S. Recent Advances of Artificial Intelligence in Manufacturing Industrial Sectors: A Review. Int. J. Precis. Eng. Manuf. 2022, 23, 111–129. [Google Scholar] [CrossRef]
- Xiao, H.; Muthu, B.; Kadry, S.N. Artificial Intelligence with Robotics for Advanced Manufacturing Industry using Robot–Assisted Mixed–Integer Programming Model. Intell. Serv. Robot. 2020, 1–10. [Google Scholar] [CrossRef]
- Saridis, G. Intelligent Robotic Control. IEEE Trans. Autom. Control 1983, 28, 547–557. [Google Scholar] [CrossRef]
- de Silva, C.W. Intelligent Control of Robotic Systems with Application in Industrial Processes. Robot. Auton. Syst. 1997, 21, 221–237. [Google Scholar] [CrossRef]
- Rawat, D.; Gupta, M.K.; Sharma, A. Intelligent Control of Robotic Manipulators: A Comprehensive Review. Spat. Inf. Res. 2022, 31, 345–357. [Google Scholar] [CrossRef]
- Jin, L.; Li, S.; Yu, J.; He, J. Robot Manipulator Control using Neural Networks: A Survey. Neurocomputing 2018, 285, 23–34. [Google Scholar] [CrossRef]
- Montesinos López, O.A.; Montesinos López, A.; Crossa, J. Fundamentals of Artificial Neural Networks and Deep Learning. In Multivariate Statistical Machine Learning Methods for Genomic Prediction; Springer: Cham, Switzerland, 2022; pp. 379–425. [Google Scholar]
- Chaoui, H.; Sicard, P.; Gueaieb, W. ANN–based Adaptive Control of Robotic Manipulators with Friction and Joint Elasticity. IEEE Trans. Ind. Electron. 2009, 56, 3174–3187. [Google Scholar] [CrossRef]
- Wai, R.J. Tracking Control based on Neural Network Strategy for Robot Manipulator. Neurocomputing 2003, 51, 425–445. [Google Scholar] [CrossRef]
- Liu, Z.; Peng, K.; Han, L.; Guan, S. Modeling and Control of Robotic Manipulators Based on Artificial Neural Networks: A Review. Iran. J. Sci. Technol. Trans. Mech. Eng. 2023, 1–41. [Google Scholar] [CrossRef]
- Yen, V.T.; Nan, W.Y.; Van Cuong, P. Robust Adaptive Sliding Mode Neural Networks Control for Industrial Robot Manipulators. Int. J. Control. Autom. Syst. 2019, 17, 783–792. [Google Scholar] [CrossRef]
- Miljković, Z.; Mitić, M.; Lazarević, M.; Babić, B. Neural Network Reinforcement Learning for Visual Control of Robot Manipulators. Expert Syst. Appl. 2013, 40, 1721–1736. [Google Scholar] [CrossRef]
- Sun, Y.; Gao, Y.; Zhao, Y.; Liu, Z.; Wang, J.; Kuang, J.; Yan, F.; Liu, J. Neural Network–based Tracking Control of Uncertain Robotic Systems: Predefined–Time Nonsingular Terminal Sliding–Mode Approach. IEEE Trans. Ind. Electron. 2022, 69, 10510–10520. [Google Scholar] [CrossRef]
- Han, N.; Ren, X.; Zhang, C.; Zheng, D. Prescribed Performance Control with Input Indicator for Robot System based on Spectral Normalized Neural Networks. Neurocomputing 2022, 492, 201–210. [Google Scholar] [CrossRef]
- Yañez-Badillo, H.; Beltran-Carbajal, F.; Tapia-Olvera, R.; Favela-Contreras, A.; Sotelo, C.; Sotelo, D. Adaptive Robust Motion Control of Quadrotor Systems using Artificial Neural Networks and Particle Swarm Optimization. Mathematics 2021, 9, 2367. [Google Scholar] [CrossRef]
- Yañez-Badillo, H.; Tapia-Olvera, R.; Beltran-Carbajal, F. Adaptive Neural Motion Control of a Quadrotor UAV. Vehicles 2020, 2, 468–490. [Google Scholar] [CrossRef]
- Yañez Badillo, H.; Tapia Olvera, R.; Aguilar Mejía, O.; Beltrán Carbajal, F. Control Neuronal en Línea para Regulación y Seguimiento de Trayectorias de Posición para un Quadrotor. Rev. Iberoam. Autom. Inform. Ind. 2017, 14, 141–151. [Google Scholar] [CrossRef]
- Galvan-Perez, D.; Yañez-Badillo, H.; Beltran-Carbajal, F.; Rivas-Cambero, I.; Favela-Contreras, A.; Tapia-Olvera, R. Neural Adaptive Robust Motion–Tracking Control for Robotic Manipulator Systems. Actuators 2022, 11, 255. [Google Scholar] [CrossRef]
- Beltran-Carbajal, F.; Tapia-Olvera, R.; Valderrabano-Gonzalez, A.; Lopez-Garcia, I. Adaptive Neuronal Induction Motor Control with an 84–Pulse Voltage Source Converter. Asian J. Control 2021, 23, 1603–1616. [Google Scholar] [CrossRef]
- Beltran-Carbajal, F.; Tapia-Olvera, R.; Lopez-Garcia, I.; Guillen, D. Adaptive Dynamical Tracking Control under Uncertainty of Shunt DC Motors. Electr. Power Syst. Res. 2018, 164, 70–78. [Google Scholar] [CrossRef]
- Lin, Z.; Reay, D.S.; Williams, B.W.; He, X. Online Modeling for Switched Reluctance Motors using B–Spline Neural Networks. IEEE Trans. Ind. Electron. 2007, 54, 3317–3322. [Google Scholar] [CrossRef]
- Tapia-Olvera, R.; Beltran-Carbajal, F.; Valderrabano-Gonzalez, A. Adaptive Neural Trajectory Tracking Control for Synchronous Generators in Interconnected Power Systems. Appl. Sci. 2022, 13, 561. [Google Scholar] [CrossRef]
- Beltran-Carbajal, F.; Yañez-Badillo, H.; Tapia-Olvera, R.; Rosas-Caro, J.C.; Sotelo, C.; Sotelo, D. Neural Network Trajectory Tracking Control on Electromagnetic Suspension Systems. Mathematics 2023, 11, 2272. [Google Scholar] [CrossRef]
- Varela-Aldás, J.; Andaluz, V.H.; Chicaiza, F.A. Modelling and Control of a Mobile manipulator for Trajectory Tracking. In Proceedings of the 2018 International Conference on Information Systems and Computer Science (INCISCOS), Quito, Ecuador, 13–15 November 2018; pp. 69–74. [Google Scholar]
- Prada-Jiménez, V.; Niño-Suárez, P.A.; Mauledoux-Monroy, M.F.; Aponte-Rodríguez, J. Coupled Dynamic Model for a Mobile Manipulator. Int. J. Appl. Eng. Res. 2019, 14, 2622–2629. [Google Scholar]
- Prada-Jimenez, V.; Niáo-Suaréz, P.A.; Portilla-Flores, E.A.; Mauledoux-Monroy, M.F. Tuning a PD+ Controller by Means of Dynamic Optimization in a Mobile Manipulator with Coupled Dynamics. IEEE Access 2019, 7, 124712–124726. [Google Scholar] [CrossRef]
- Li, Z.; Ge, S.S.; Adams, M.; Wijesoma, W.S. Adaptive Robust Output–Feedback Motion/Force Control of Electrically Driven Nonholonomic Mobile Manipulators. IEEE Trans. Control Syst. Technol. 2008, 16, 1308–1315. [Google Scholar]
- Moon, F.C. Applied Dynamics: With Applications to Multibody and Mechatronic Systems; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Cortés, F.R. Dinámica de Robots Manipuladores. In Robótica: Control de Robots Manipuladores; Marcombo: Barcelona, Spain, 2020; pp. 259–263. (In Spanish) [Google Scholar]
- Li, Z.; Ming, A.; Xi, N.; Shimojo, M. Motion Control of Nonholonomic Mobile Underactuated Manipulator. In Proceedings of the Proceedings 2006 IEEE International Conference on Robotics and Automation, 2006. ICRA, Orlando, FL, USA, 15–19 May 2006; pp. 3512–3519. [Google Scholar]
- Li, Z.; Gu, J.; Ming, A.; Xu, C.; Shimojo, M. Intelligent Compliant Force/Motion Control of Nonholonomic Mobile Manipulator Working on the Nonrigid Surface. Neural Comput. Appl. 2006, 15, 204–216. [Google Scholar] [CrossRef]
- Jia, Y.; Xi, N.; Cheng, Y.; Liang, S. Coordinated Motion Control of a Nonholonomic Mobile Manipulator for Accurate Motion Tracking. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 1635–1640. [Google Scholar]
- Fliess, M.; Marquez, R.; Delaleau, E.; Sira-Ramírez, H. Correcteurs Proportionnels–Intégraux Généralisés. Esaim Control. Optim. Calc. Var. 2002, 7, 23–41. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks and Learning Machines; Pearson: London, UK, 2009. [Google Scholar]
- Bossley, K.; Brown, M.; Harris, C. Neurofuzzy Adaptive Modelling and Construction of Nonlinear Dynamical Processes. Neural Network Applications in Control; Institution of Engineering and Technology (IET): Stevenage, UK, 1995; pp. 253–292. [Google Scholar]
- Harris, C.J.; Moore, C.G.; Brown, M. Intelligent Control: Aspects of Fuzzy Logic and Neural Nets; World Scientific: London, UK, 1993. [Google Scholar]
- dos Santos Coelho, L.; Pessôa, M.W. Nonlinear Identification using a B–Spline Neural Network and Chaotic Immune Approaches. Mech. Syst. Signal Process. 2009, 23, 2418–2434. [Google Scholar] [CrossRef]
- Oliveira, T.R.; Peixoto, A.J.; Nunes, E.V. Binary Robust Adaptive Control with Monitoring Functions for Systems under Unknown High–Frequency–Gain Sign, Parametric Uncertainties and Unmodeled Dynamics. Int. J. Adapt. Control Signal Process. 2016, 30, 1184–1202. [Google Scholar] [CrossRef]
- Yao, J.; Deng, W. Active Disturbance Rejection Adaptive Control of Uncertain Nonlinear Systems: Theory and Application. Nonlinear Dynamics 2017, 89, 1611–1624. [Google Scholar] [CrossRef]
- Yang, J.; Na, J.; Gao, G. Robust Model Reference Adaptive Control for Transient Performance Enhancement. Int. J. Robust Nonlinear Control 2020, 30, 6207–6228. [Google Scholar] [CrossRef]
- Saad, D. On–Line Learning in Neural Networks; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Beltran-Carbajal, F.; Silva-Navarro, G. Output Feedback Dynamic Control for Trajectory Tracking and Vibration Suppression. Appl. Math. Model. 2020, 79, 793–808. [Google Scholar] [CrossRef]
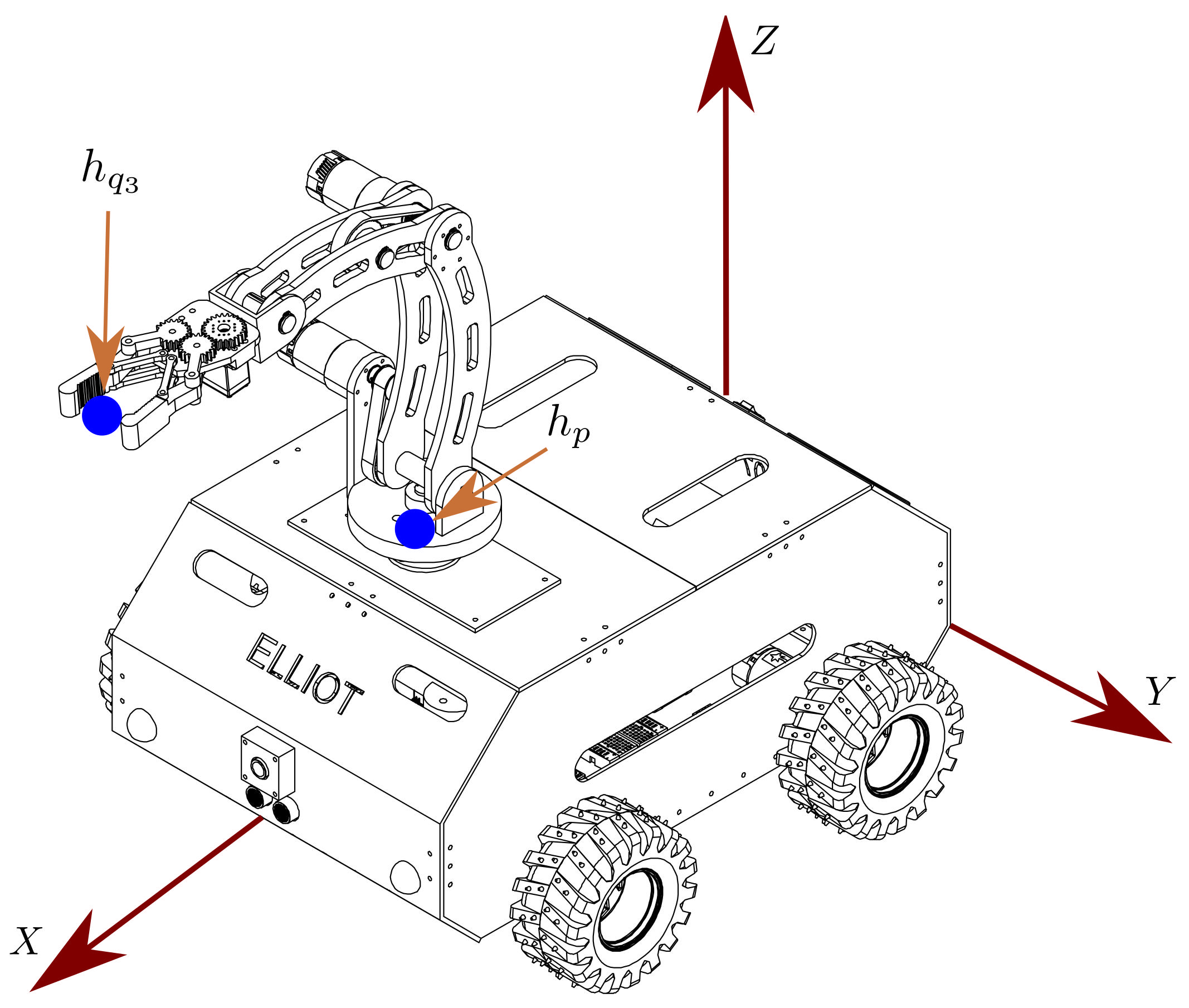
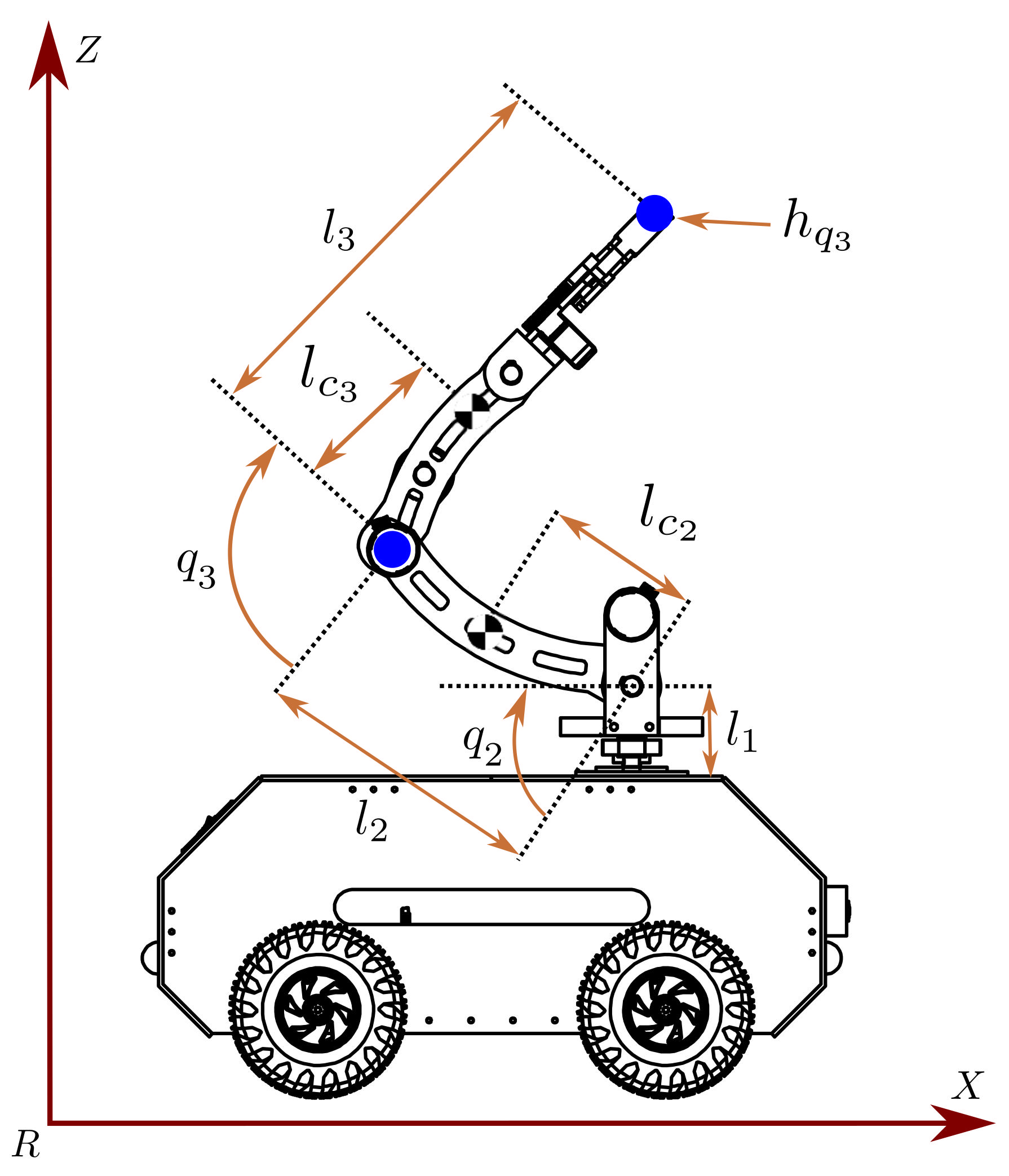
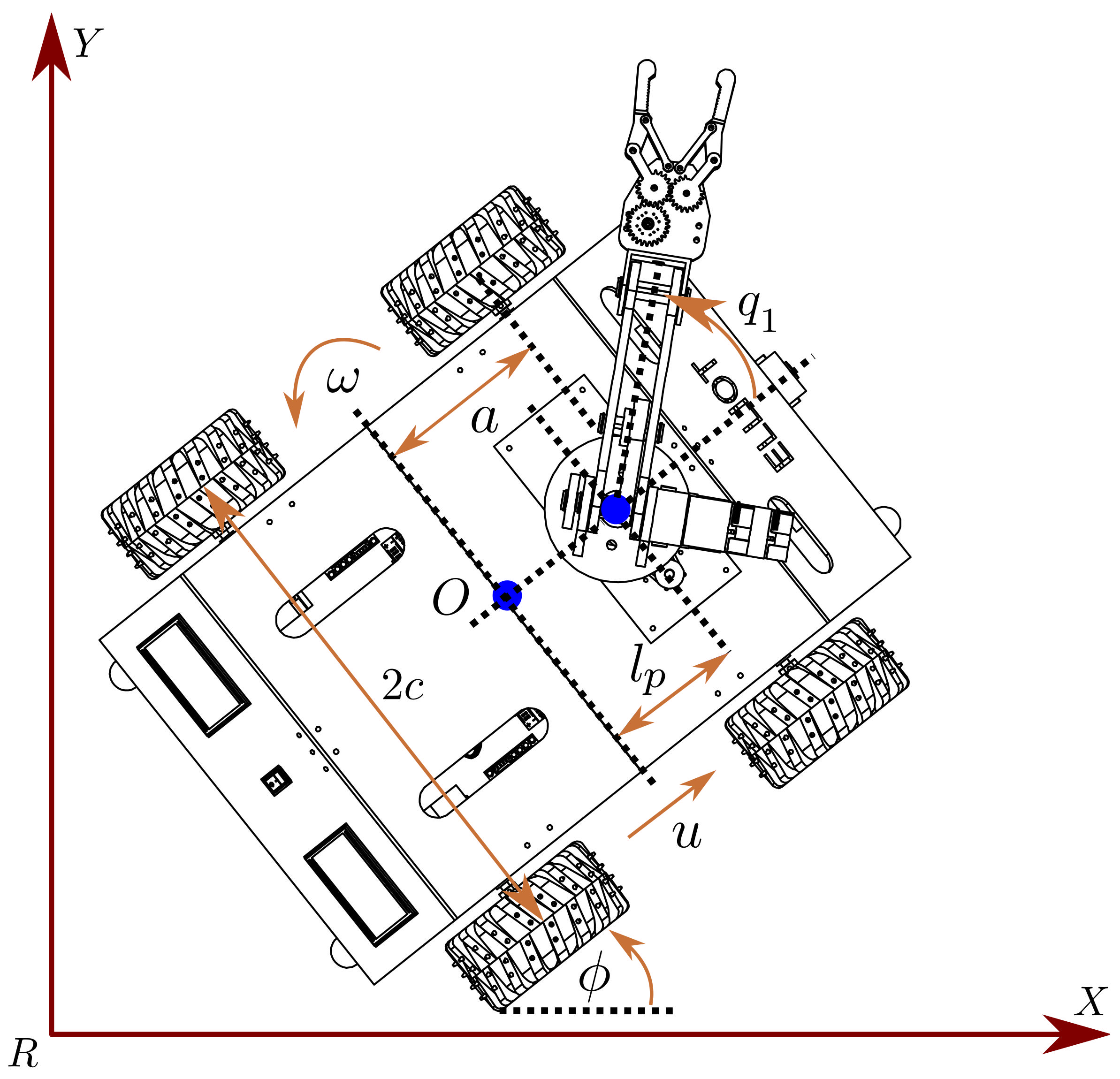
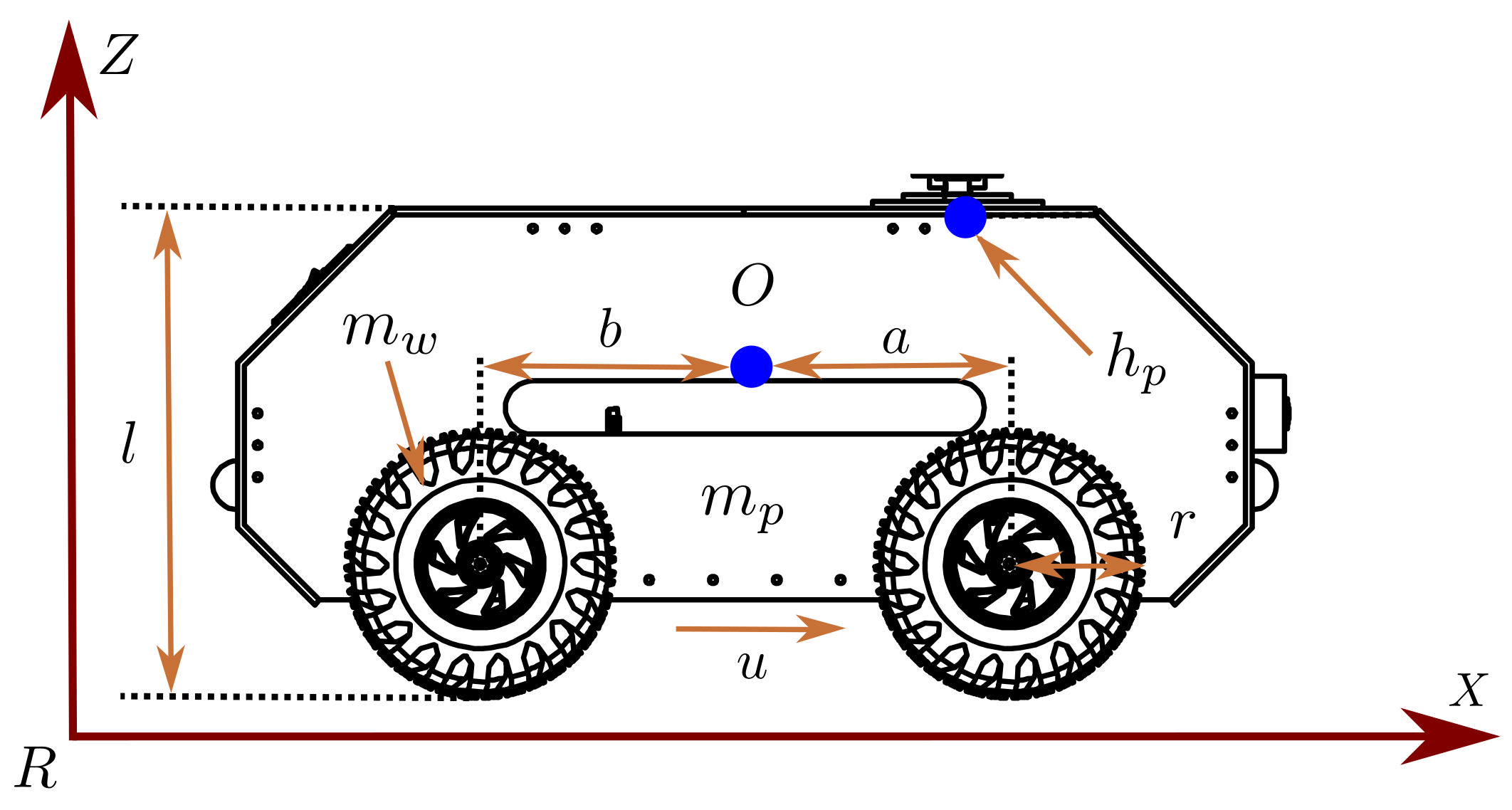





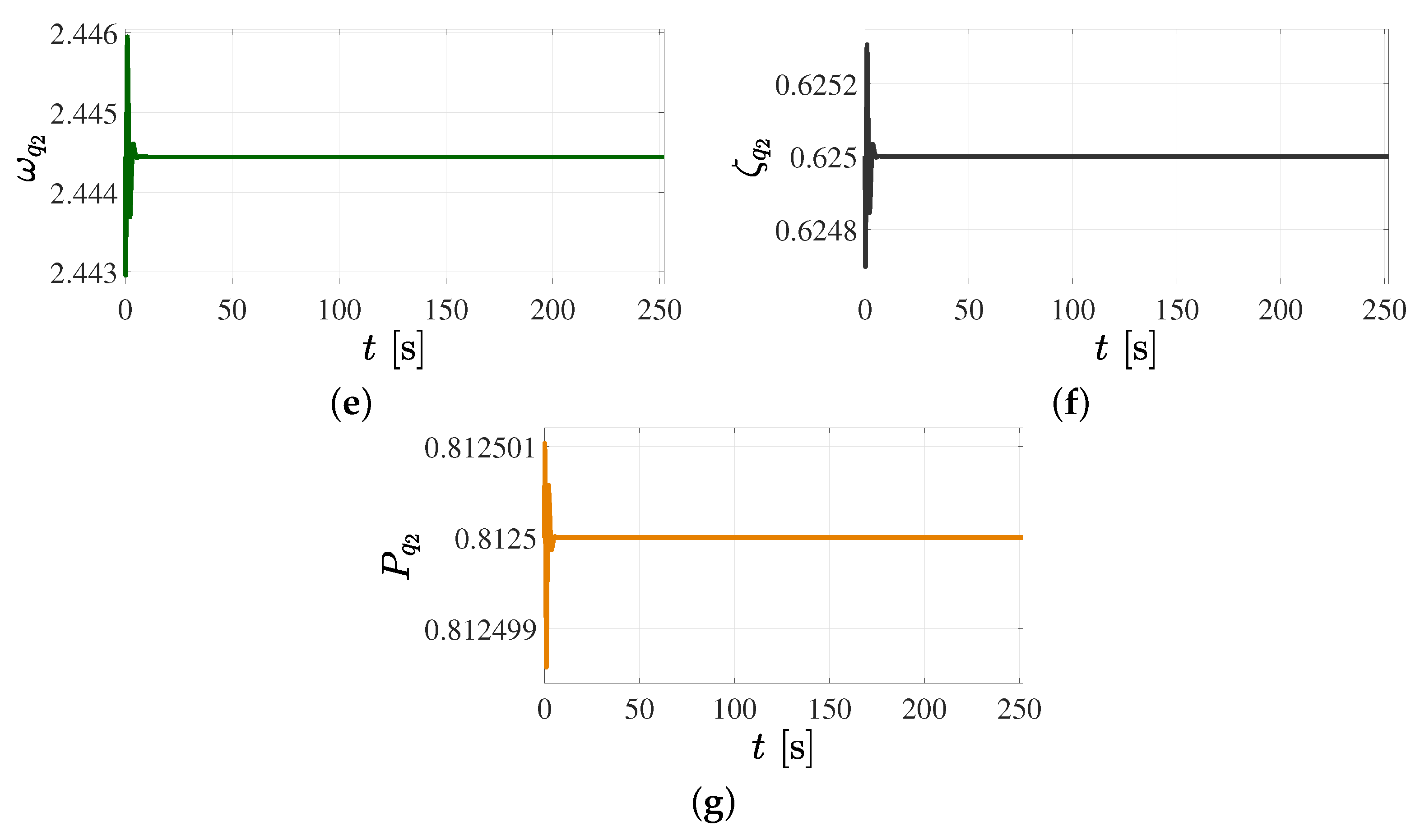


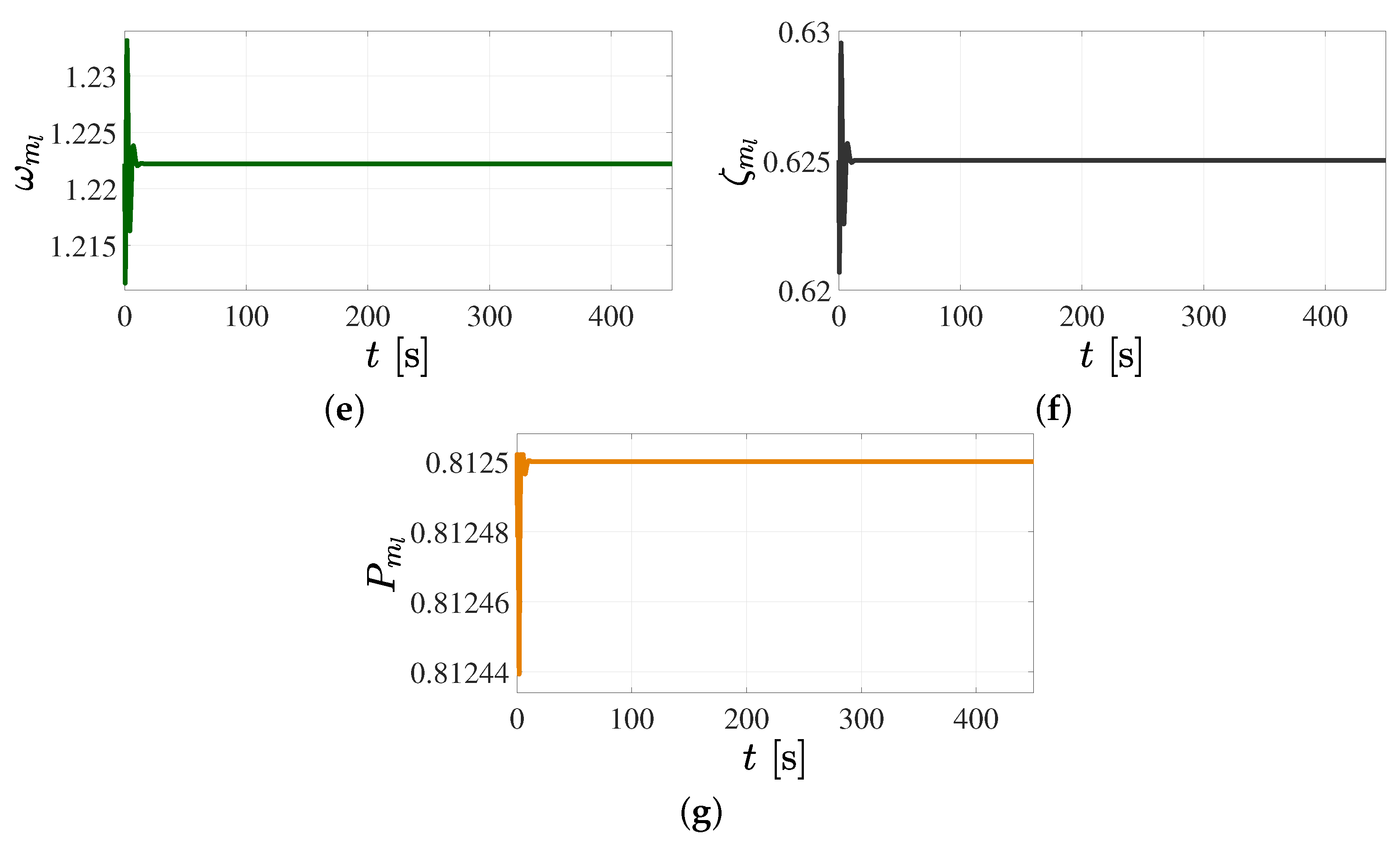





| Variable | Definition |
|---|---|
| O | Location of the mobile robot’s center of mass |
| a | Distance from the center of mass to the front axis of the mobile robot |
| b | Distance from the center of mass to the rear axis of the mobile robot |
| Distance between the wheels of the mobile robot | |
| r | Radius of each wheel of the mobile robot |
| l | Height of the mobile robot |
| Distance from the center of mass to the base of the manipulator robot | |
| First link length of the manipulator robot | |
| Second link length to the center of mass | |
| Second link length of the manipulator robot | |
| Third link length to the center of mass | |
| Third link length of the manipulator robot | |
| Mobile robot chassis mass | |
| Mass of each wheel of the mobile robot | |
| First link mass of the manipulator robot | |
| Second link mass of the manipulator robot | |
| Third link mass of the manipulator robot | |
| Moment of inertia around the Z-axis of the mobile robot | |
| Moment of inertia around the Y-axis of each wheel of the system | |
| Moment of inertia around the Z-axis of each wheel of the system | |
| Moment of inertia around the Z-axis of the first link | |
| Moment of inertia around the Y-axis of the second link | |
| Moment of inertia around the Z-axis of the second link | |
| Moment of inertia around the Y-axis of the third link | |
| Moment of inertia around the Z-axis of the third link | |
| u | Linear velocity of the mobile robot |
| Angular velocity of the mobile robot | |
| Angle of rotation in the Z-axis of the mobile robot | |
| Angle of rotation in the Z-axis of the first link | |
| Angle of rotation in the Y-axis of the second link | |
| Angle of rotation in the Y-axis of the third link | |
| XYZ position of the coupling point on the mobile robot | |
| XYZ position of the mobile manipulator robot’s end-effector | |
| g | Gravitational acceleration constant |
| R | Inertial coordinate system |
| Parameter | Quantity | Units | Description |
|---|---|---|---|
| c | 0.1920 | m | Distance from O to each side’s wheels of the robot |
| r | 0.06 | m | Radius of each wheel of the mobile robot |
| l | 0.2272 | m | Height of the mobile robot |
| 0.1 | m | Distance from O to the base of the manipulator robot | |
| 0.0645 | m | First link length of the manipulator robot | |
| 0.2031 | m | Second link length of the manipulator robot | |
| 0.3018 | m | Third link length of the manipulator robot | |
| 7.1368 | Kg | Mobile robot chassis mass | |
| 0.18 | Kg | Mass of each wheel of the mobile robot | |
| 0.7238 | Kg | First link mass of the manipulator robot | |
| 0.8524 | Kg | Second link mass of the manipulator robot | |
| 0.5085 | Kg | Third link mass of the manipulator robot | |
| 0.2308 | Kg m2 | Inertia moment in the Z-axis of the mobile robot | |
| 0.0003 | Kg m2 | Inertia moment in the Y-axis of the wheels | |
| 0.0002 | Kg m2 | Inertia moment in the Z-axis of the wheels | |
| 0.0015 | Kg m2 | Inertia moment in the Z-axis of the first link | |
| 0.0054 | Kg m2 | Inertia moment in the Y-axis of the second link | |
| 0.0013 | Kg m2 | Inertia moment in the Z-axis of the second link | |
| 0.0031 | Kg m2 | Inertia moment in the Y-axis of the third link | |
| 0.0032 | Kg m2 | Inertia moment in the Z-axis of the third link | |
| g | 9.81 | m/s2 | Gravitational acceleration constant |
| Parameter | Quantity | Units | Description |
|---|---|---|---|
| c | 0.25 | m | Distance from O to each side’s wheels of the robot |
| r | 0.075 | m | Radius of each wheel of the mobile robot |
| l | 0.4 | m | Height of the mobile robot |
| 0.27 | m | Distance from O to the base of the manipulator robot | |
| 0.2 | m | First link length of the manipulator robot | |
| 0.3 | m | Second link length of the manipulator robot | |
| 0.3 | m | Third link length of the manipulator robot | |
| 19.2372 | Kg | Mobile robot chassis mass | |
| 0.901 | Kg | Mass of each wheel of the mobile robot | |
| 3.293 | Kg | First link mass of the manipulator robot | |
| 3.436 | Kg | Second link mass of the manipulator robot | |
| 1.229 | Kg | Third link mass of the manipulator robot | |
| 0.7004 | Kg m2 | Inertia moment in the Z-axis of the mobile robot | |
| 0.0015 | Kg m2 | Inertia moment in the Y-axis of the wheels | |
| 0.0030 | Kg m2 | Inertia moment in the Z-axis of the wheels | |
| 0.0230 | Kg m2 | Inertia moment in the Z-axis of the first link | |
| 0.0457 | Kg m2 | Inertia moment in the Y-axis of the second link | |
| 0.0461 | Kg m2 | Inertia moment in the Z-axis of the second link | |
| 0.0242 | Kg m2 | Inertia moment in the Y-axis of the third link | |
| 0.0255 | Kg m2 | Inertia moment in the Z-axis of the third link |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galvan-Perez, D.; Beltran-Carbajal, F.; Rivas-Cambero, I.; Yañez-Badillo, H.; Favela-Contreras, A.; Tapia-Olvera, R. Motion-Tracking Control of Mobile Manipulation Robotic Systems Using Artificial Neural Networks for Manufacturing Applications. Mathematics 2023, 11, 3489. https://doi.org/10.3390/math11163489
Galvan-Perez D, Beltran-Carbajal F, Rivas-Cambero I, Yañez-Badillo H, Favela-Contreras A, Tapia-Olvera R. Motion-Tracking Control of Mobile Manipulation Robotic Systems Using Artificial Neural Networks for Manufacturing Applications. Mathematics. 2023; 11(16):3489. https://doi.org/10.3390/math11163489
Chicago/Turabian StyleGalvan-Perez, Daniel, Francisco Beltran-Carbajal, Ivan Rivas-Cambero, Hugo Yañez-Badillo, Antonio Favela-Contreras, and Ruben Tapia-Olvera. 2023. "Motion-Tracking Control of Mobile Manipulation Robotic Systems Using Artificial Neural Networks for Manufacturing Applications" Mathematics 11, no. 16: 3489. https://doi.org/10.3390/math11163489
APA StyleGalvan-Perez, D., Beltran-Carbajal, F., Rivas-Cambero, I., Yañez-Badillo, H., Favela-Contreras, A., & Tapia-Olvera, R. (2023). Motion-Tracking Control of Mobile Manipulation Robotic Systems Using Artificial Neural Networks for Manufacturing Applications. Mathematics, 11(16), 3489. https://doi.org/10.3390/math11163489





