Hidden Markov Model-Based Control for Cooperative Output Regulation of Heterogeneous Multi-Agent Systems under Switching Network Topology
Abstract
1. Introduction
- This paper makes a first attempt to reflect the influence of the asynchronous mode between heterogeneous MASs and observer-based distributed controllers while achieving stochastically cooperative output regulation subject to Markov jumps. Different from [22,23,25,26], the realistic case where rapid changes in the system modes of MASs affect the network topology is considered in the control design processes.
- This paper proposes a method to design a continuous-time leader–state observer capable of estimating the leader–state value for each agent under abrupt changes in both systems and network topology. Also, it introduces an alternative mechanism by integrating system-mode-dependent solutions of regulator equations into the output of the leader–state observer to reduce the complexity arising from the asynchronous controller-side mode.
- In the control design process, the asynchronous mode-dependent control gain is coupled with the system-mode-dependent Lyapunov matrix, which makes it difficult to directly use the well-known variable replacement technique [27]. For this reason, this paper suggests a suitable linear decoupling method that is capable of handling the aforementioned coupling problem.
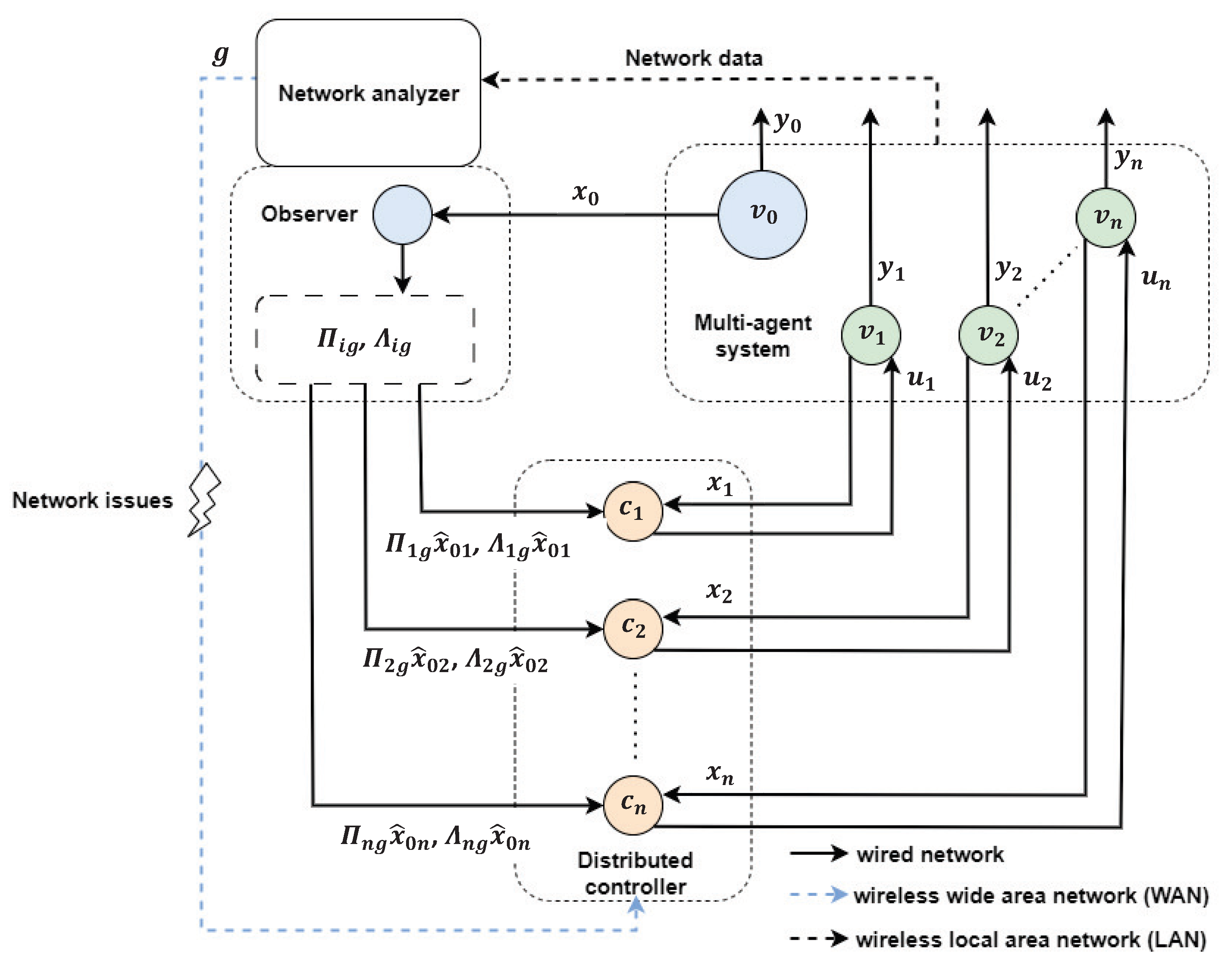
2. Preliminaries and Problem Statement
2.1. Heterogeneous Multi-Agent System Description
2.2. Communication Topology
- System (1) is stochastically stable when ,
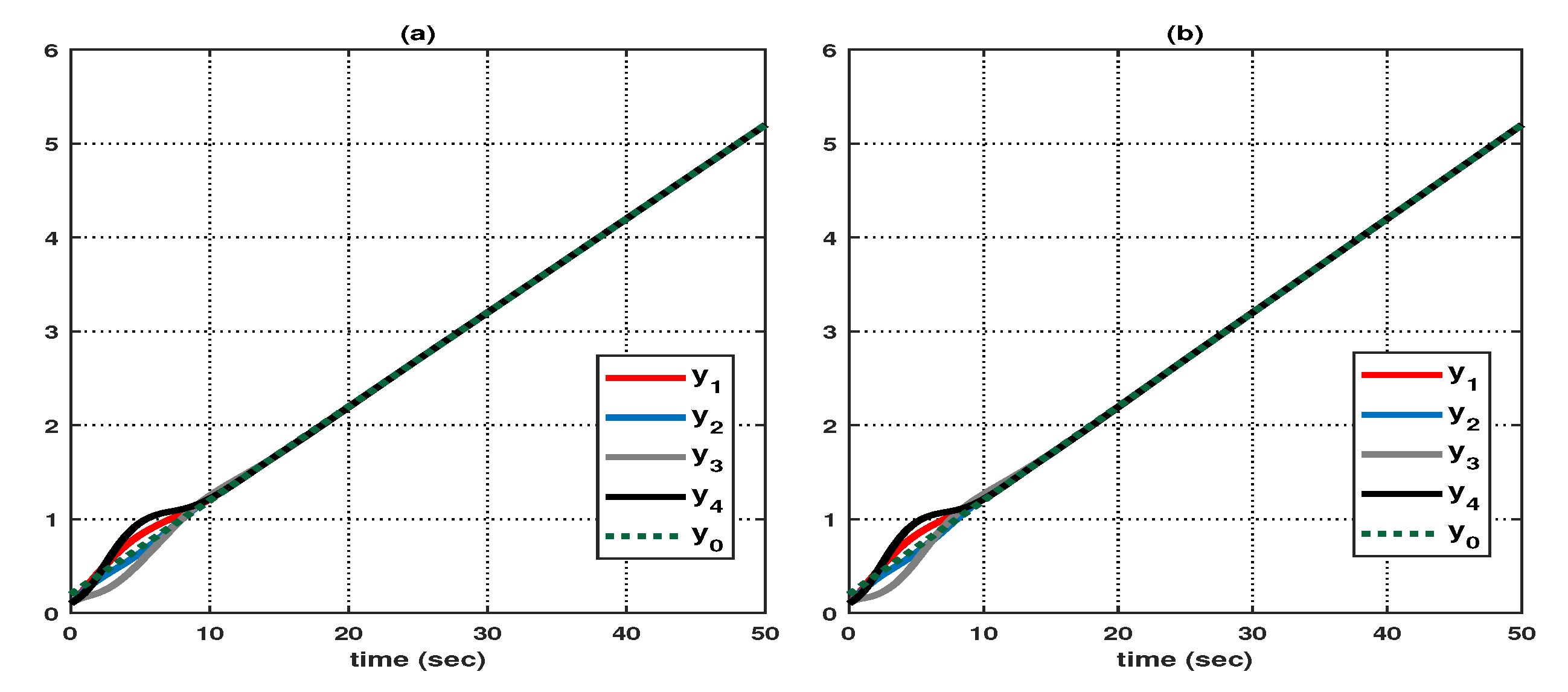
- For any initial conditions, and ,where represents the error between the output of the ith agent and the output of the leader.
3. Main Results
3.1. Leader–State Observer Design
3.2. Distributed Controller Design
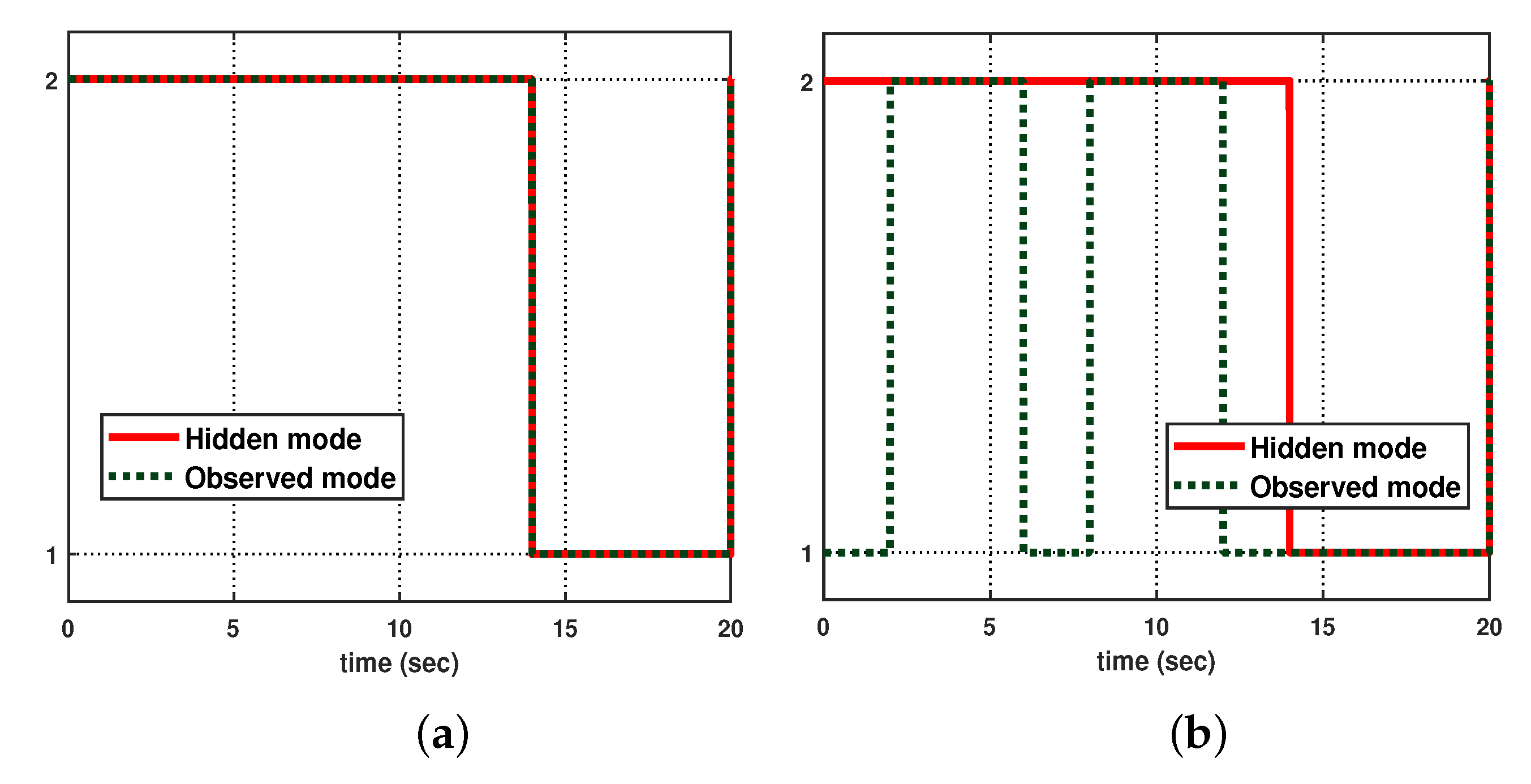
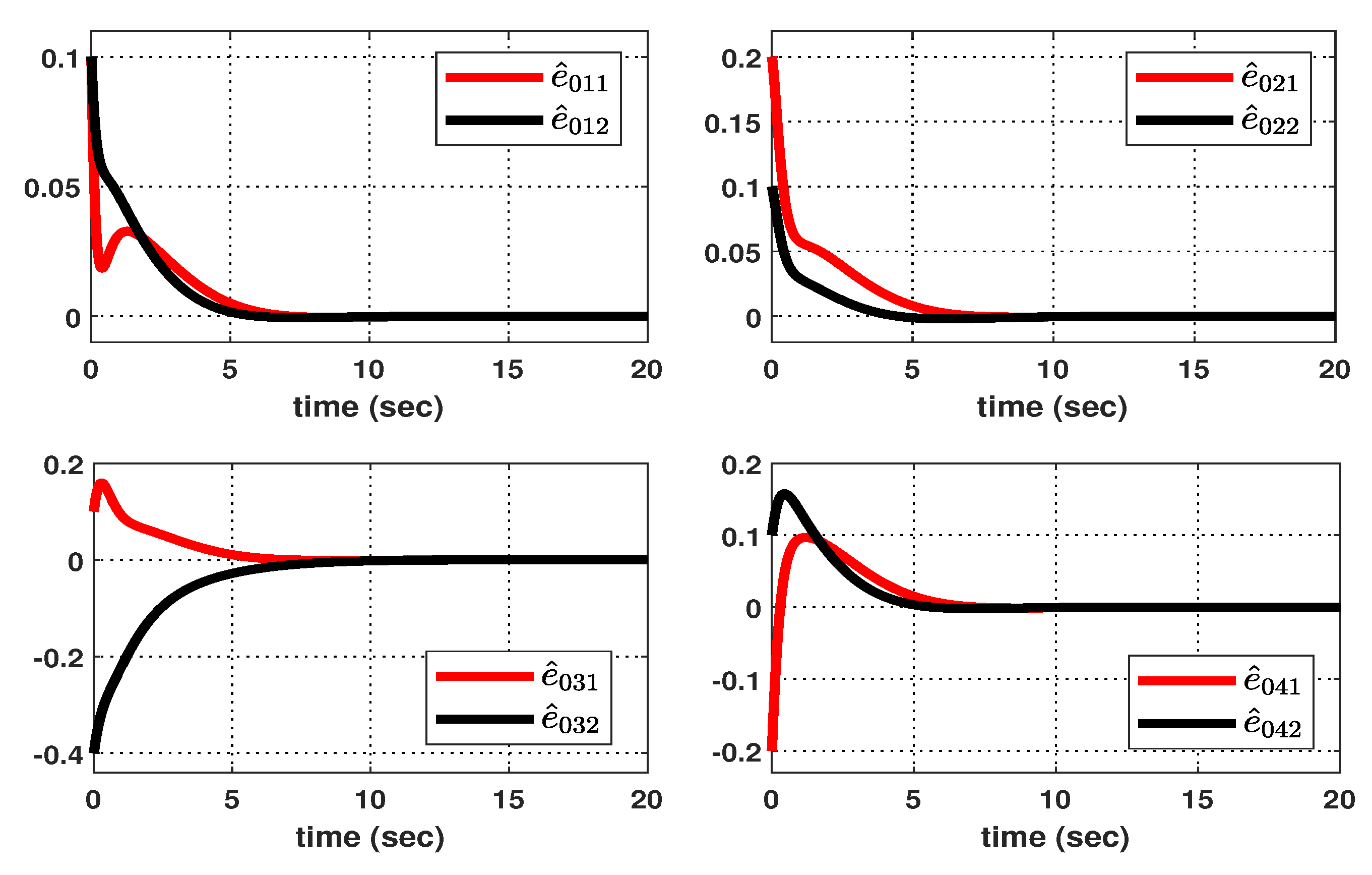
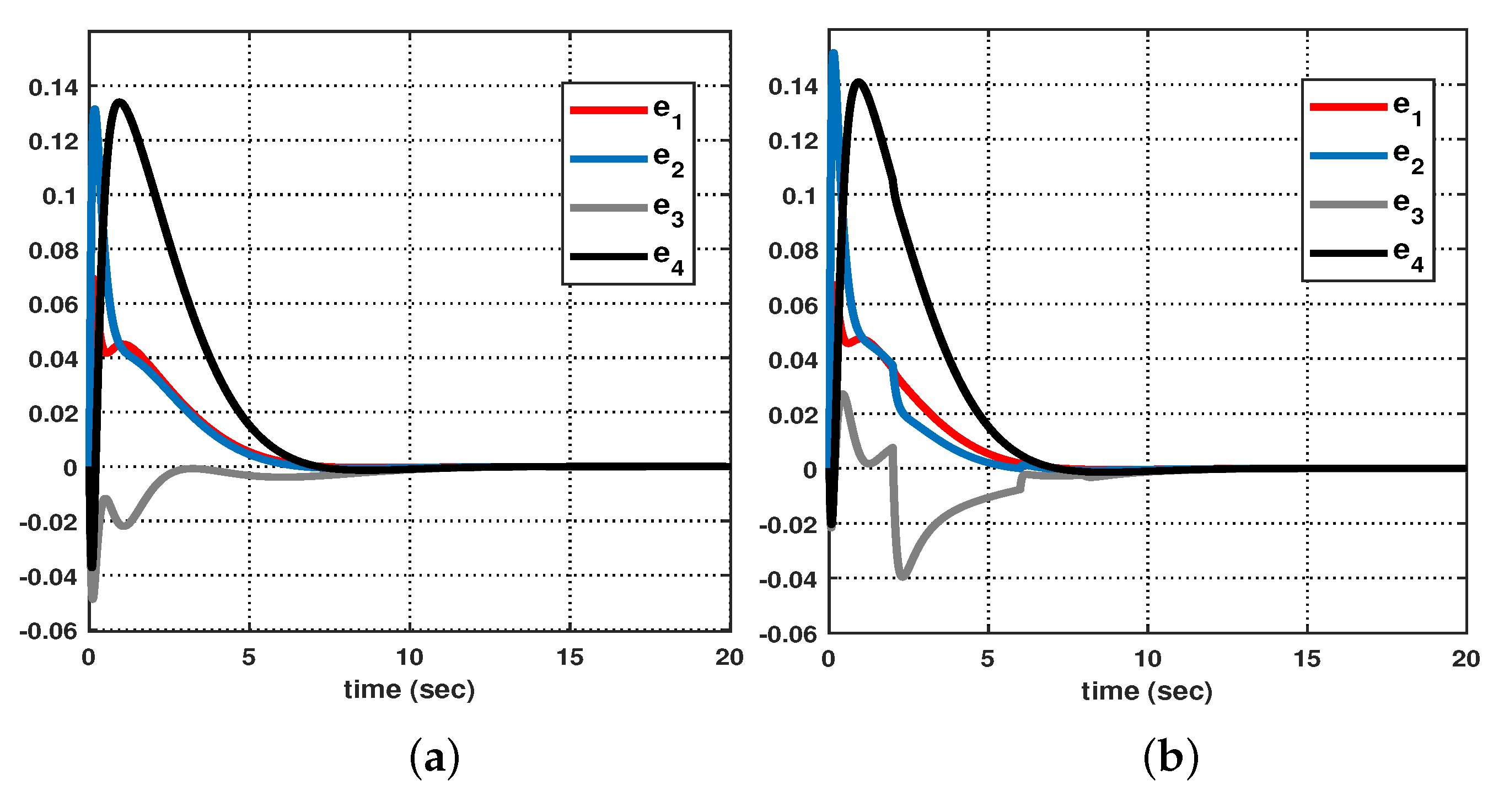
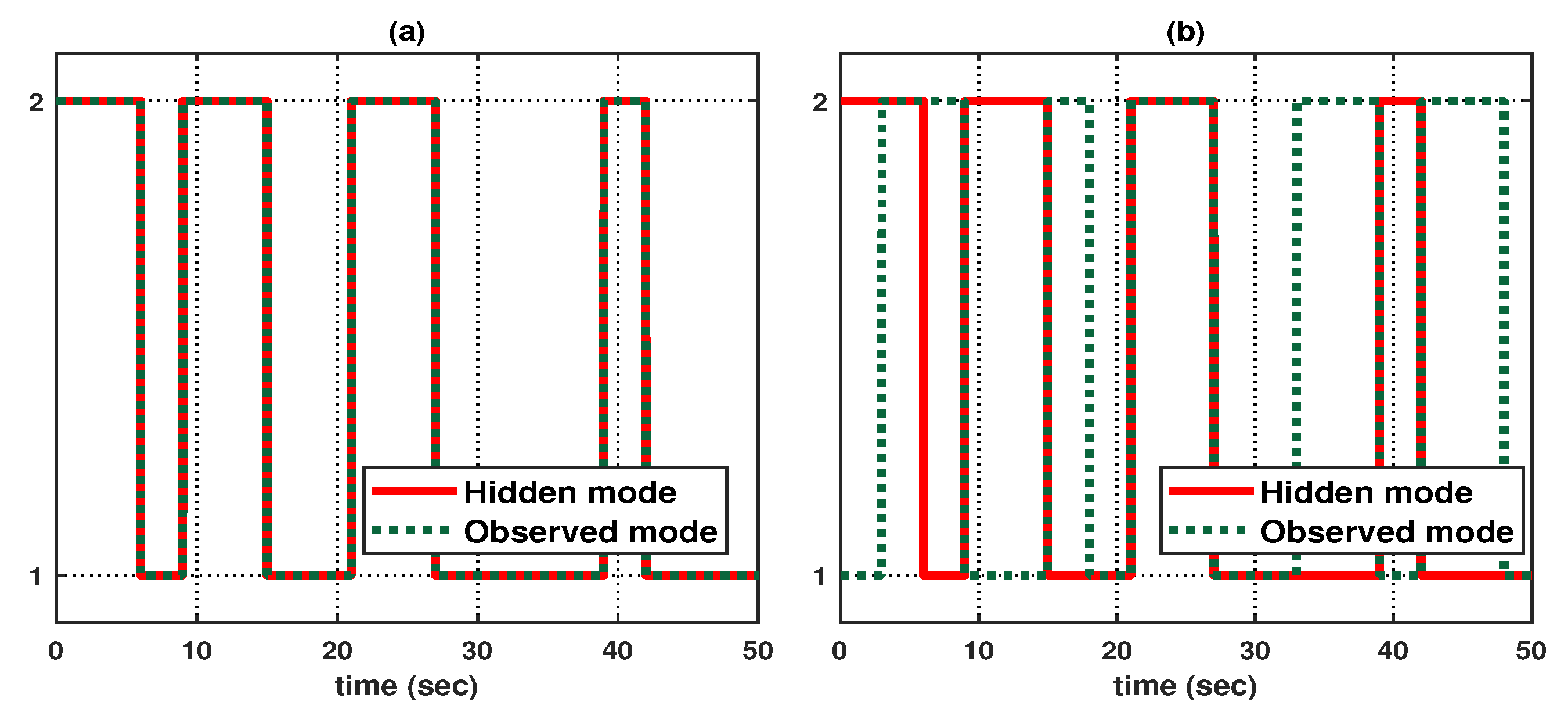
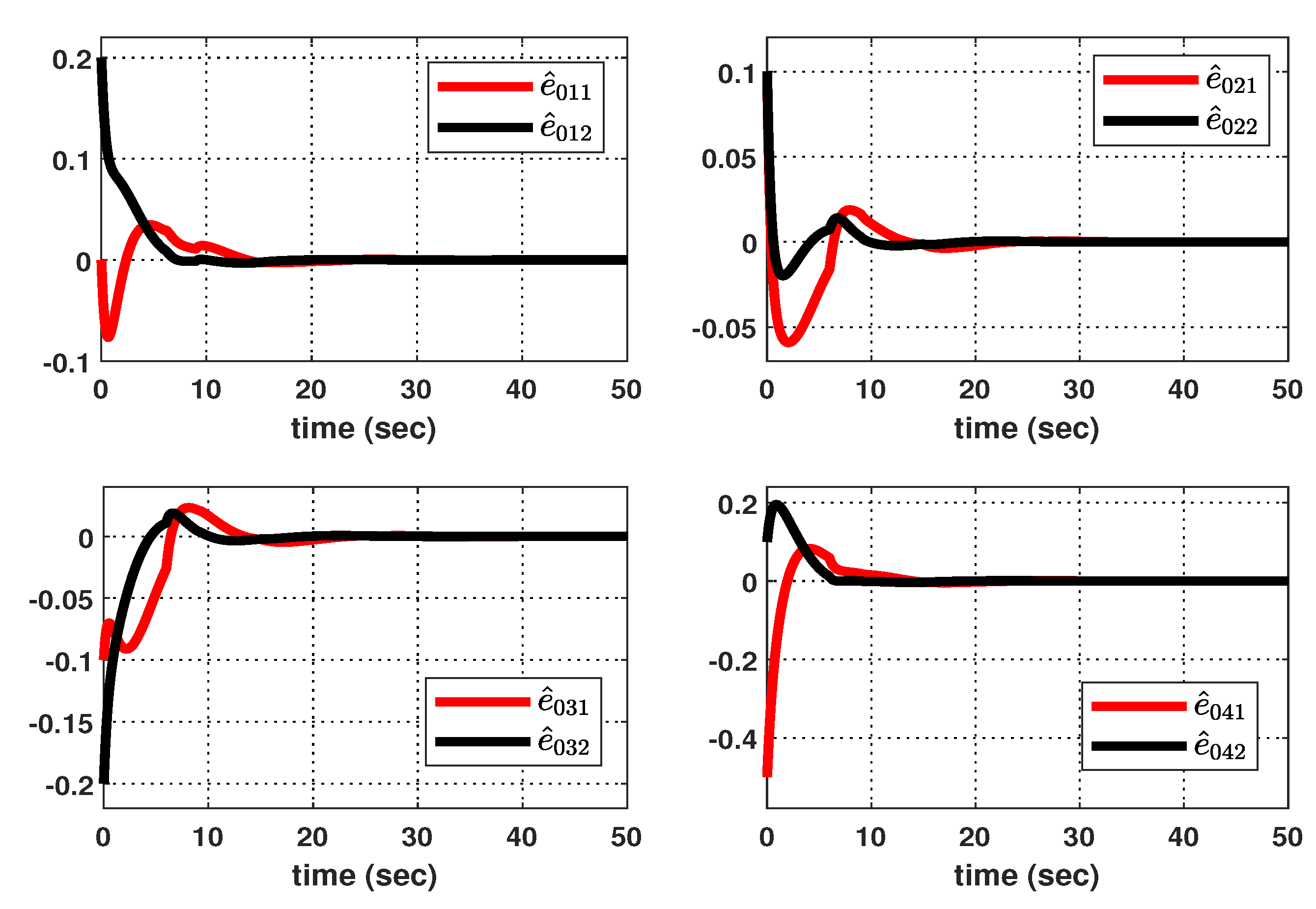
4. Illustrative Examples
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiménez, A.C.; García-Díaz, V.; Bolaños, S. A decentralized framework for multi-agent robotic systems. Sensors 2018, 18, 417. [Google Scholar] [CrossRef] [PubMed]
- Dai, S.; Wu, Z.; Zhang, P.; Tan, M.; Yu, J. Distributed Formation Control for a Multi-Robotic Fish System with Model-Based Event-Triggered Communication Mechanism. IEEE Trans. Ind. Electron. 2023, 70, 11433–11442. [Google Scholar] [CrossRef]
- Huang, Z.; Chu, D.; Wu, C.; He, Y. Path planning and cooperative control for automated vehicle platoon using hybrid automata. IEEE Trans. Intell. Transp. Syst. 2018, 20, 959–974. [Google Scholar] [CrossRef]
- Xiao, S.; Ge, X.; Han, Q.L.; Zhang, Y. Dynamic event-triggered platooning control of automated vehicles under random communication topologies and various spacing policies. IEEE Trans. Cybern. 2021, 52, 11477–11490. [Google Scholar] [CrossRef]
- Cui, J.; Liu, Y.; Nallanathan, A. Multi-agent reinforcement learning-based resource allocation for UAV networks. IEEE Trans. Wirel. Commun. 2019, 19, 729–743. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, Z.; Xiao, M. UAVs’ formation keeping control based on Multi–Agent system consensus. IEEE Access 2020, 8, 49000–49012. [Google Scholar] [CrossRef]
- Yan, Z.; Han, L.; Li, X.; Dong, X.; Li, Q.; Ren, Z. Event-Triggered formation control for time-delayed discrete-Time multi-Agent system applied to multi-UAV formation flying. J. Frankl. Inst.-Eng. Appl. Math. 2023, 360, 3677–3699. [Google Scholar] [CrossRef]
- Chen, Y.J.; Chang, D.K.; Zhang, C. Autonomous tracking using a swarm of UAVs: A constrained multi-agent reinforcement learning approach. IEEE Trans. Veh. Technol. 2020, 69, 13702–13717. [Google Scholar] [CrossRef]
- Pham, V.H.; Sakurama, K.; Mou, S.; Ahn, H.S. Distributed Control for an Urban Traffic Network. IEEE Trans. Intell. Transp. Syst. 2022, 23, 22937–22953. [Google Scholar] [CrossRef]
- Qu, Z.; Pan, Z.; Chen, Y.; Wang, X.; Li, H. A distributed control method for urban networks using multi-agent reinforcement learning based on regional mixed strategy Nash-equilibrium. IEEE Access 2020, 8, 19750–19766. [Google Scholar] [CrossRef]
- Ma, Q.; Xu, S.; Lewis, F.L.; Zhang, B.; Zou, Y. Cooperative output regulation of singular heterogeneous multiagent systems. IEEE Trans. Cybern. 2015, 46, 1471–1475. [Google Scholar] [CrossRef]
- Li, Z.; Chen, M.Z.; Ding, Z. Distributed adaptive controllers for cooperative output regulation of heterogeneous agents over directed graphs. Automatica 2016, 68, 179–183. [Google Scholar] [CrossRef]
- Hu, W.; Liu, L. Cooperative output regulation of heterogeneous linear multi-agent systems by event-triggered control. IEEE Trans. Cybern. 2016, 47, 105–116. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H.; Cai, Y.; Lu, Y. Distributed cooperative output regulation of heterogeneous linear multi-agent systems based on event-and self-triggered control with undirected topology. ISA Trans. 2020, 99, 191–198. [Google Scholar] [CrossRef] [PubMed]
- Yuan, C. Cooperative H∞ output regulation of heterogeneous parameter-dependent multi-agent systems. J. Frankl. Inst.-Eng. Appl. Math. 2017, 354, 7846–7870. [Google Scholar] [CrossRef]
- Wang, Y.; Xia, J.; Wang, Z.; Zhou, J.; Shen, H. Reliable consensus control for semi-Markov jump multi-agent systems: A leader-following strategy. J. Frankl. Inst.-Eng. Appl. Math. 2019, 356, 3612–3627. [Google Scholar] [CrossRef]
- Zhang, G.; Li, F.; Wang, J.; Shen, H. Mixed H∞ and passive consensus of Markov jump multi-agent systems under DoS attacks with general transition probabilities. J. Frankl. Inst.-Eng. Appl. Math. 2023, 360, 5375–5391. [Google Scholar] [CrossRef]
- Li, M.; Deng, F.; Ren, H. Scaled consensus of multi-agent systems with switching topologies and communication noises. Nonlinear Anal.-Hybrid Syst. 2020, 36, 100839. [Google Scholar] [CrossRef]
- Li, B.; Wen, G.; Peng, Z.; Wen, S.; Huang, T. Time-varying formation control of general linear multi-agent systems under Markovian switching topologies and communication noises. IEEE Trans. Circuits Syst. II-Express Briefs 2020, 68, 1303–1307. [Google Scholar] [CrossRef]
- Liu, Z.; Yan, W.; Li, H.; Zhang, S. Cooperative output regulation problem of discrete-time linear multi-agent systems with Markov switching topologies. J. Frankl. Inst.-Eng. Appl. Math. 2020, 357, 4795–4816. [Google Scholar] [CrossRef]
- Meng, M.; Liu, L.; Feng, G. Adaptive output regulation of heterogeneous multiagent systems under Markovian switching topologies. IEEE Trans. Cybern. 2017, 48, 2962–2971. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Li, T. Cooperative output feedback tracking control of stochastic linear heterogeneous multi-agent systems. IEEE Trans. Autom. Control 2021, 33, 7154–7180. [Google Scholar]
- Dong, S.; Chen, G.; Liu, M.; Wu, Z.G. Cooperative adaptive H∞ output regulation of continuous-time heterogeneous multi-agent Markov jump systems. IEEE Trans. Circuits Syst. II-Express Briefs 2021, 68, 3261–3265. [Google Scholar] [CrossRef]
- Nguyen, N.H.A.; Kim, S.H. Leader-following consensus for multi-agent systems with asynchronous control modes under nonhomogeneous Markovian jump network topology. IEEE Access 2020, 8, 203017–203027. [Google Scholar] [CrossRef]
- Ding, L.; Guo, G. Sampled-data leader-following consensus for nonlinear multi-agent systems with Markovian switching topologies and communication delay. J. Frankl. Inst.-Eng. Appl. Math. 2015, 352, 369–383. [Google Scholar] [CrossRef]
- Nguyen, N.H.A.; Kim, S.H. Asynchronous H∞ observer-based control synthesis of nonhomogeneous Markovian jump systems with generalized incomplete transition rates. Appl. Math. Comput. 2021, 411, 126532. [Google Scholar] [CrossRef]
- Dong, J.; Yang, G.H. Robust H2 control of continuous-time Markov jump linear systems. Automatica 2008, 44, 1431–1436. [Google Scholar] [CrossRef]
- Sakthivel, R.; Sakthivel, R.; Kaviarasan, B.; Alzahrani, F. Leader-following exponential consensus of input saturated stochastic multi-agent systems with Markov jump parameters. Neurocomputing 2018, 287, 84–92. [Google Scholar] [CrossRef]
- He, G.; Zhao, J. Cooperative output regulation of T-S fuzzy multi-agent systems under switching directed topologies and event-triggered communication. IEEE Trans. Fuzzy Syst. 2022, 30, 5249–5260. [Google Scholar] [CrossRef]
- Huang, J. Nonlinear Output Regulation: Theory and Applications; SIAM: Bangkok, Thailand, 2004. [Google Scholar]
- Yaghmaie, F.A.; Lewis, F.L.; Su, R. Output regulation of linear heterogeneous multi-agent systems via output and state feedback. Automatica 2016, 67, 157–164. [Google Scholar] [CrossRef]
- Arrifano, N.S.; Oliveira, V.A. Robust H∞ fuzzy control approach for a class of markovian jump nonlinear systems. IEEE Trans. Fuzzy Syst. 2006, 14, 738–754. [Google Scholar] [CrossRef]
- Nguyen, T.B.; Kim, S.H. Nonquadratic local stabilization of nonhomogeneous Markovian jump fuzzy systems with incomplete transition descriptions. Nonlinear Anal.-Hybrid Syst. 2021, 42, 101080. [Google Scholar] [CrossRef]
- He, S.; Ding, Z.; Liu, F. Output regulation of a class of continuous-time Markovian jumping systems. Signal Process. 2013, 93, 411–419. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, L.; De Souza, C.E. Robust control of a class of uncertain nonlinear systems. Syst. Control Lett. 1992, 19, 139–149. [Google Scholar] [CrossRef]
- Wieland, P.; Sepulchre, R.; Allgöwer, F. An internal model principle is necessary and sufficient for linear output synchronization. Automatica 2011, 47, 1068–1074. [Google Scholar] [CrossRef]
- Yan, S.; Gu, Z.; Park, J.H.; Xie, X. Distributed-delay-dependent stabilization for networked interval type-2 fuzzy systems with stochastic delay and actuator saturation. IEEE Trans. Syst. Man Cybern.-Syst. 2022, 53, 3165–3175. [Google Scholar] [CrossRef]
- Yan, S.; Gu, Z.; Park, J.H.; Xie, X. A delay-kernel-dependent approach to saturated control of linear systems with mixed delays. Automatica 2023, 152, 110984. [Google Scholar] [CrossRef]
- Zhang, T.; Li, Y. Global exponential stability of discrete-time almost automorphic Caputo–Fabrizio BAM fuzzy neural networks via exponential Euler technique. Knowl.-Based Syst. 2022, 246, 108675. [Google Scholar] [CrossRef]



| Hardware Resources | Information |
|---|---|
| Operating System | Microsoft Windows 10 Pro |
| RAM | 8 GB |
| Processor | 3.20 GHz |
| Hard Drive | 120 GB SSD |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, G.-B.; Kim, S.-H. Hidden Markov Model-Based Control for Cooperative Output Regulation of Heterogeneous Multi-Agent Systems under Switching Network Topology. Mathematics 2023, 11, 3481. https://doi.org/10.3390/math11163481
Hong G-B, Kim S-H. Hidden Markov Model-Based Control for Cooperative Output Regulation of Heterogeneous Multi-Agent Systems under Switching Network Topology. Mathematics. 2023; 11(16):3481. https://doi.org/10.3390/math11163481
Chicago/Turabian StyleHong, Gia-Bao, and Sung-Hyun Kim. 2023. "Hidden Markov Model-Based Control for Cooperative Output Regulation of Heterogeneous Multi-Agent Systems under Switching Network Topology" Mathematics 11, no. 16: 3481. https://doi.org/10.3390/math11163481
APA StyleHong, G.-B., & Kim, S.-H. (2023). Hidden Markov Model-Based Control for Cooperative Output Regulation of Heterogeneous Multi-Agent Systems under Switching Network Topology. Mathematics, 11(16), 3481. https://doi.org/10.3390/math11163481







