Author Contributions
Conceptualization, F.H. and A.Z.; writing—original draft, F.H.; formal analysis, F.H.; supervision, A.Z.; validation, F.H.; writing—reviewing and editing, F.H., A.Z. and G.H.; investigation, F.H.; visualization, F.H.; resources, F.H., A.Z. and G.H.; methodology, F.H.; software, F.H. All authors have read and agreed to the published version of the manuscript.
Figure 1.
End-view of the tilting vehicle structure.
Figure 1.
End-view of the tilting vehicle structure.
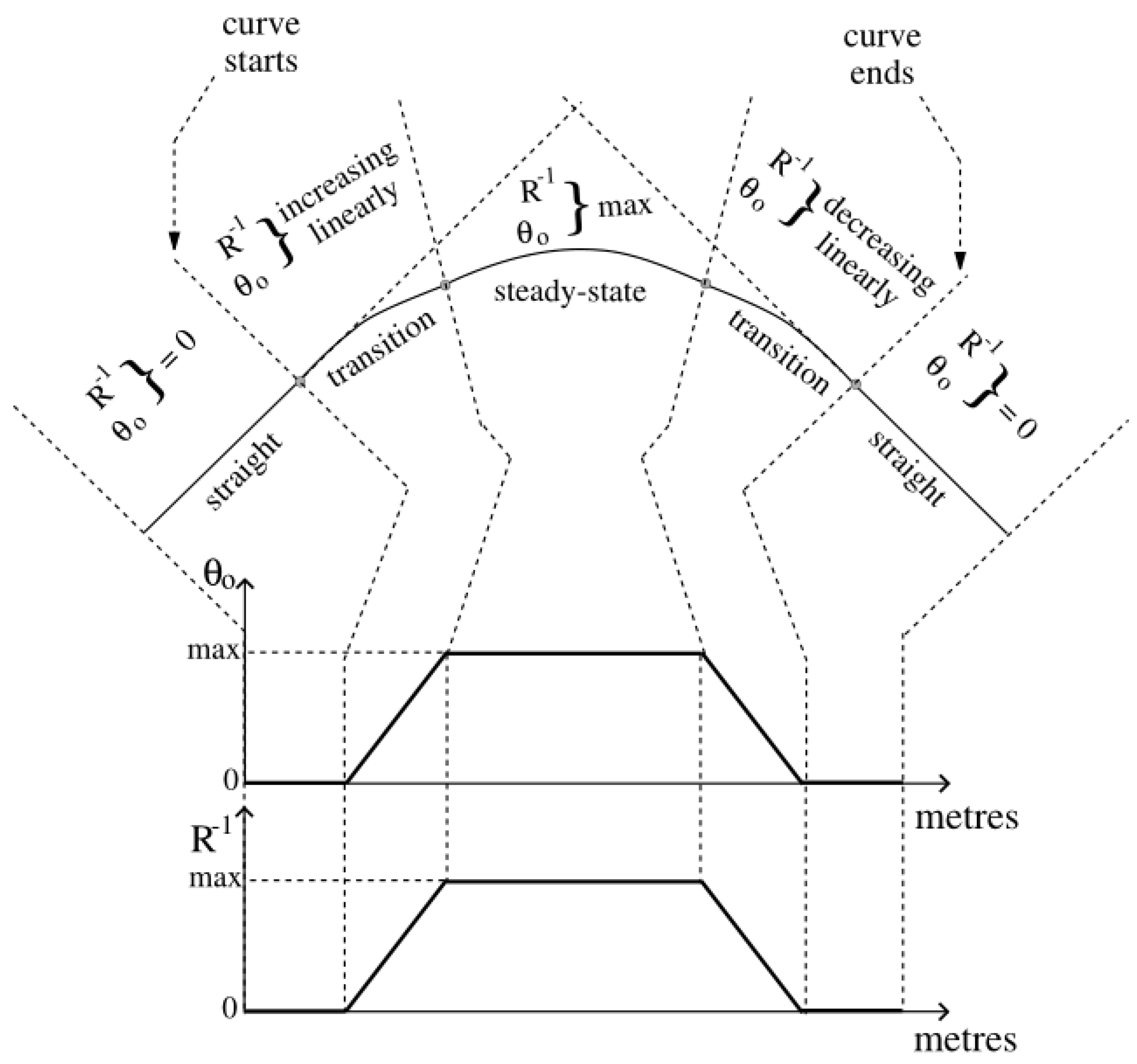
Figure 2.
Deterministic track profile representation.
Figure 2.
Deterministic track profile representation.
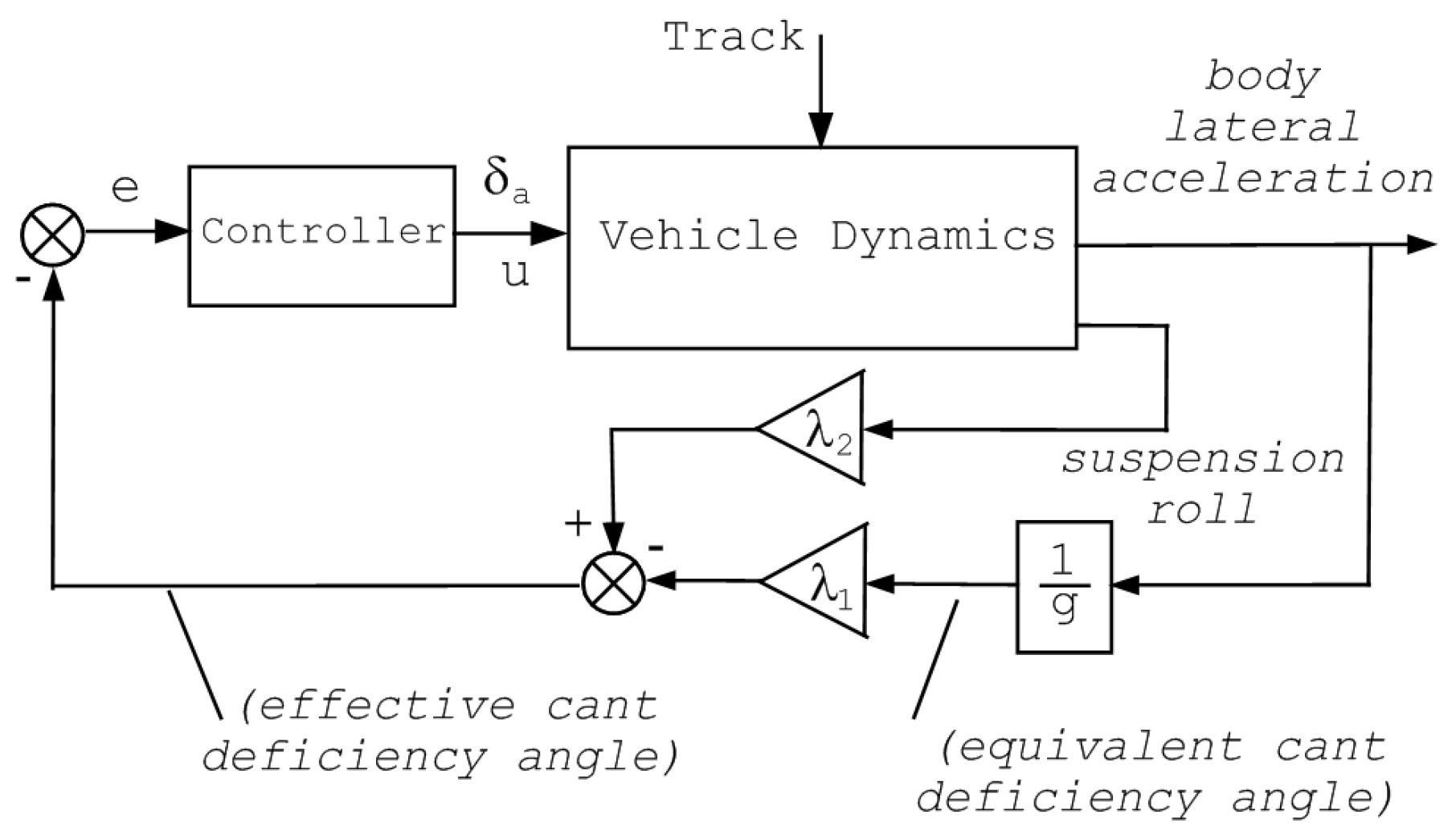
Figure 3.
Partial nulling tilt compensation control feedback setup.
Figure 3.
Partial nulling tilt compensation control feedback setup.
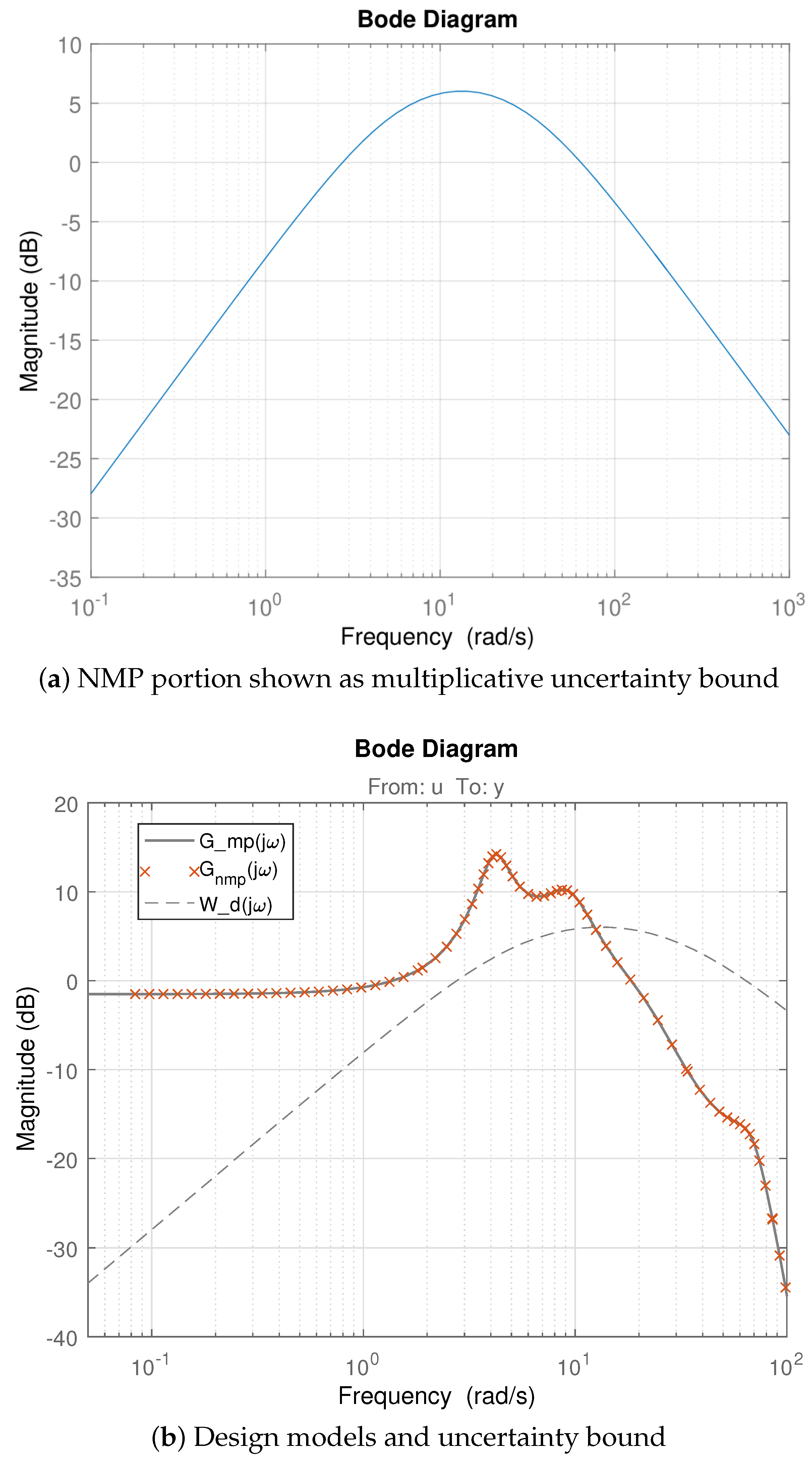
Figure 4.
Frequency response of NMP original and of MP factorized TFs.
Figure 4.
Frequency response of NMP original and of MP factorized TFs.
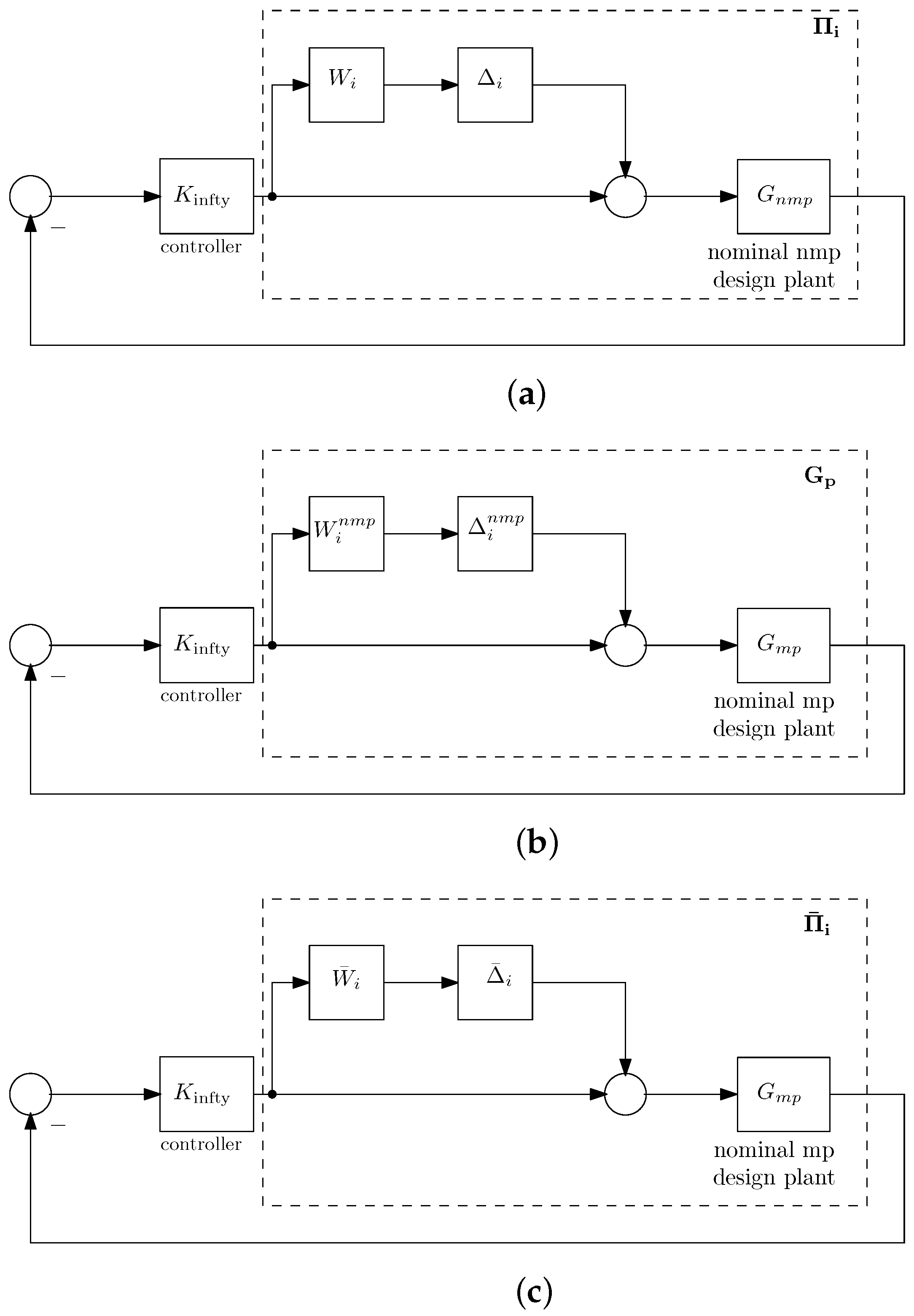
Figure 5.
Feedback setup with multiplicative uncertainty. (a) The plant family for the NMP system model. (b) The factorized nominal NMP model. (c) The overall uncertainty control feedback setup for nominal minimum phase (MP) model.
Figure 5.
Feedback setup with multiplicative uncertainty. (a) The plant family for the NMP system model. (b) The factorized nominal NMP model. (c) The overall uncertainty control feedback setup for nominal minimum phase (MP) model.
Figure 6.
Consideration of model factorization.
Figure 6.
Consideration of model factorization.
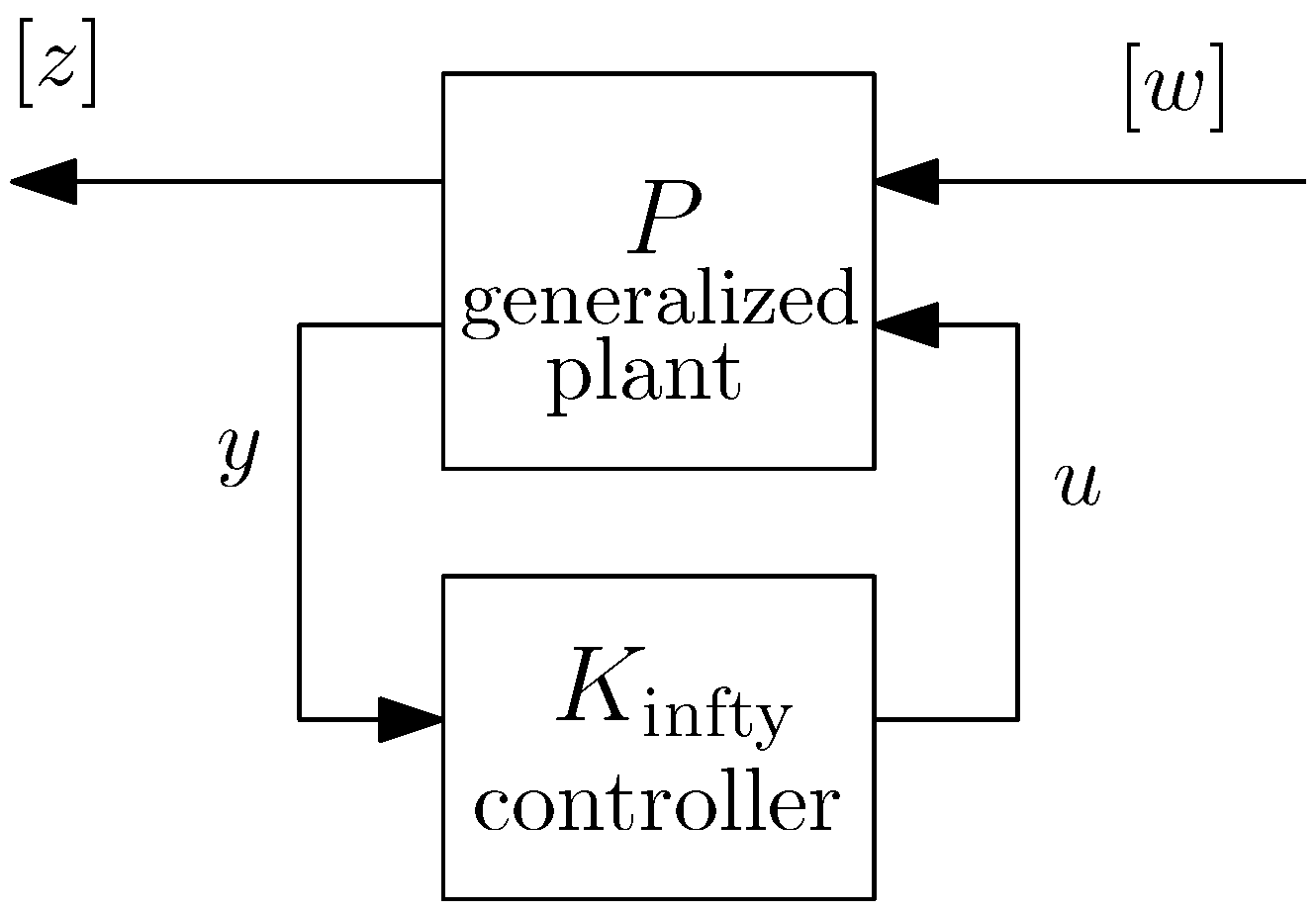
Figure 7.
Generalized regulator setup for the mixed-sensitivity design.
Figure 7.
Generalized regulator setup for the mixed-sensitivity design.
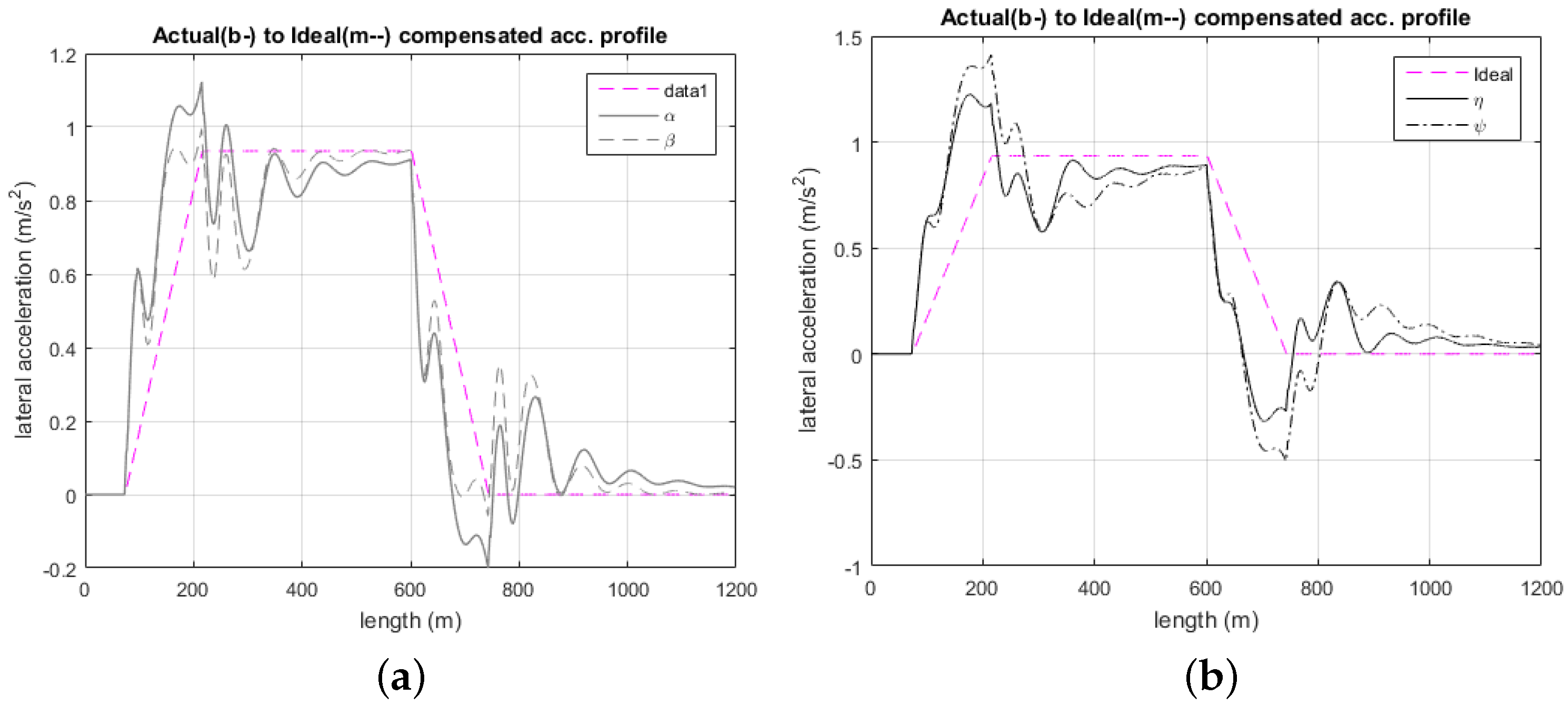
Figure 8.
Lateral acceleration plot for -() and () (a), () and () (b).
Figure 8.
Lateral acceleration plot for -() and () (a), () and () (b).
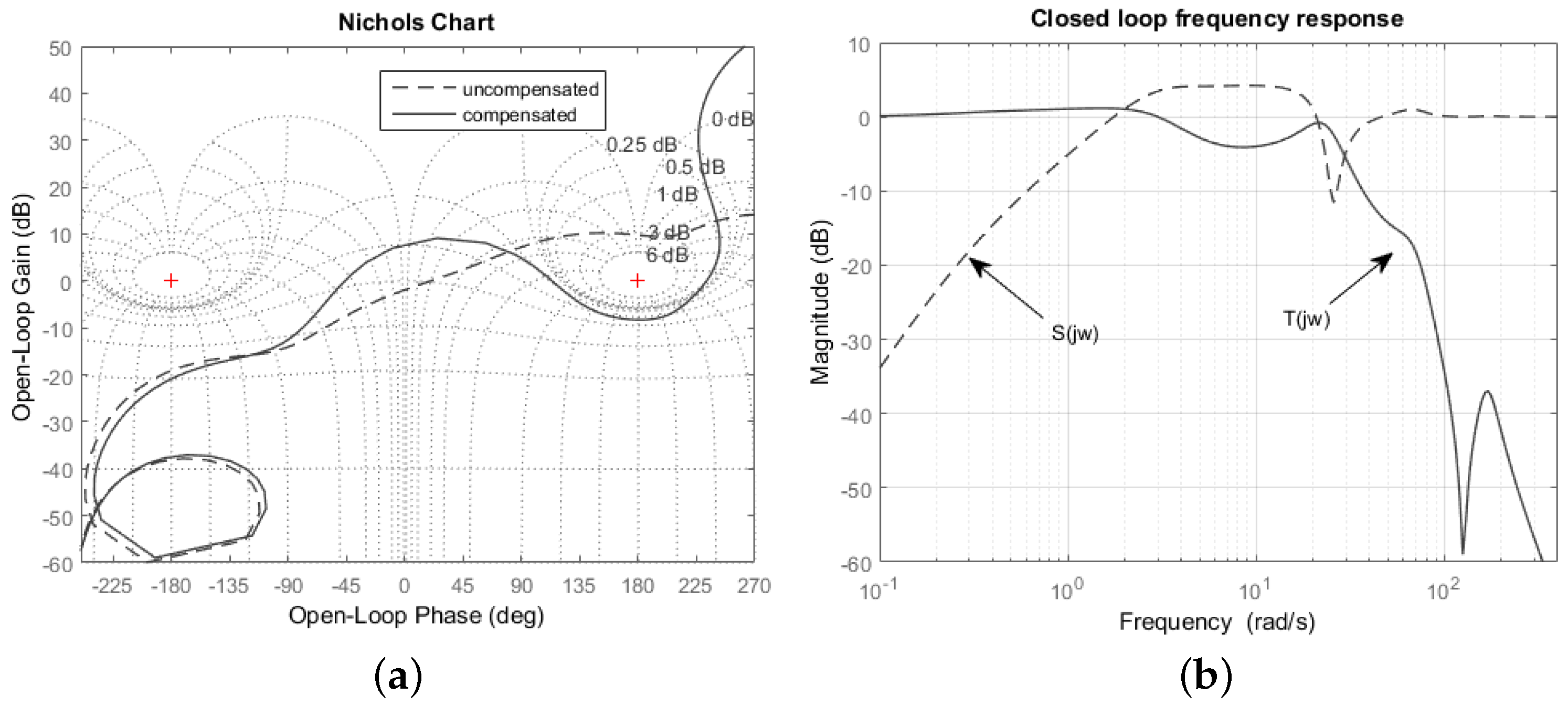
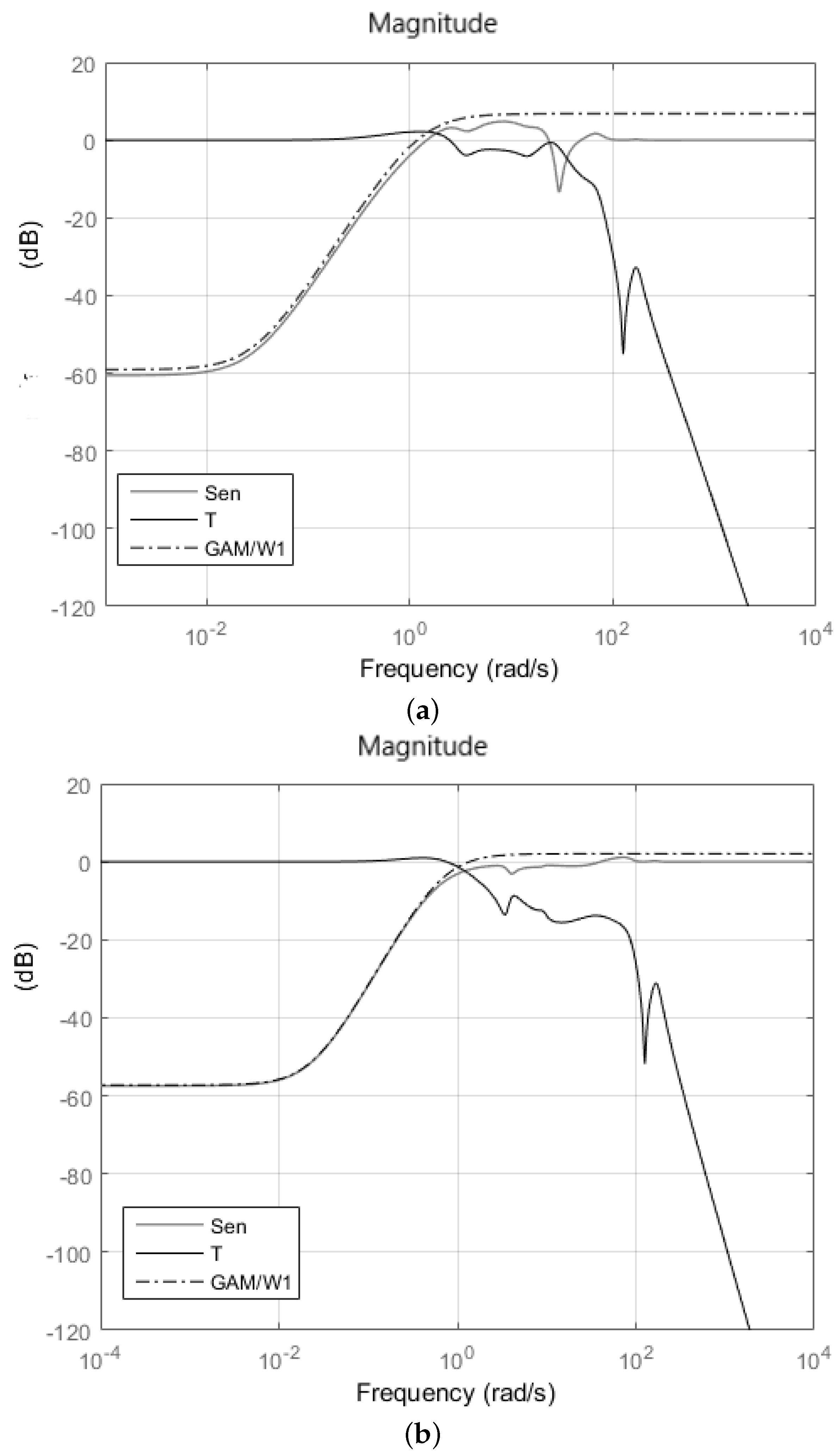
Figure 9.
Open loop (a) and closed loop (b) complementary sensitivity () and sensitivity () plots for case.
Figure 9.
Open loop (a) and closed loop (b) complementary sensitivity () and sensitivity () plots for case.
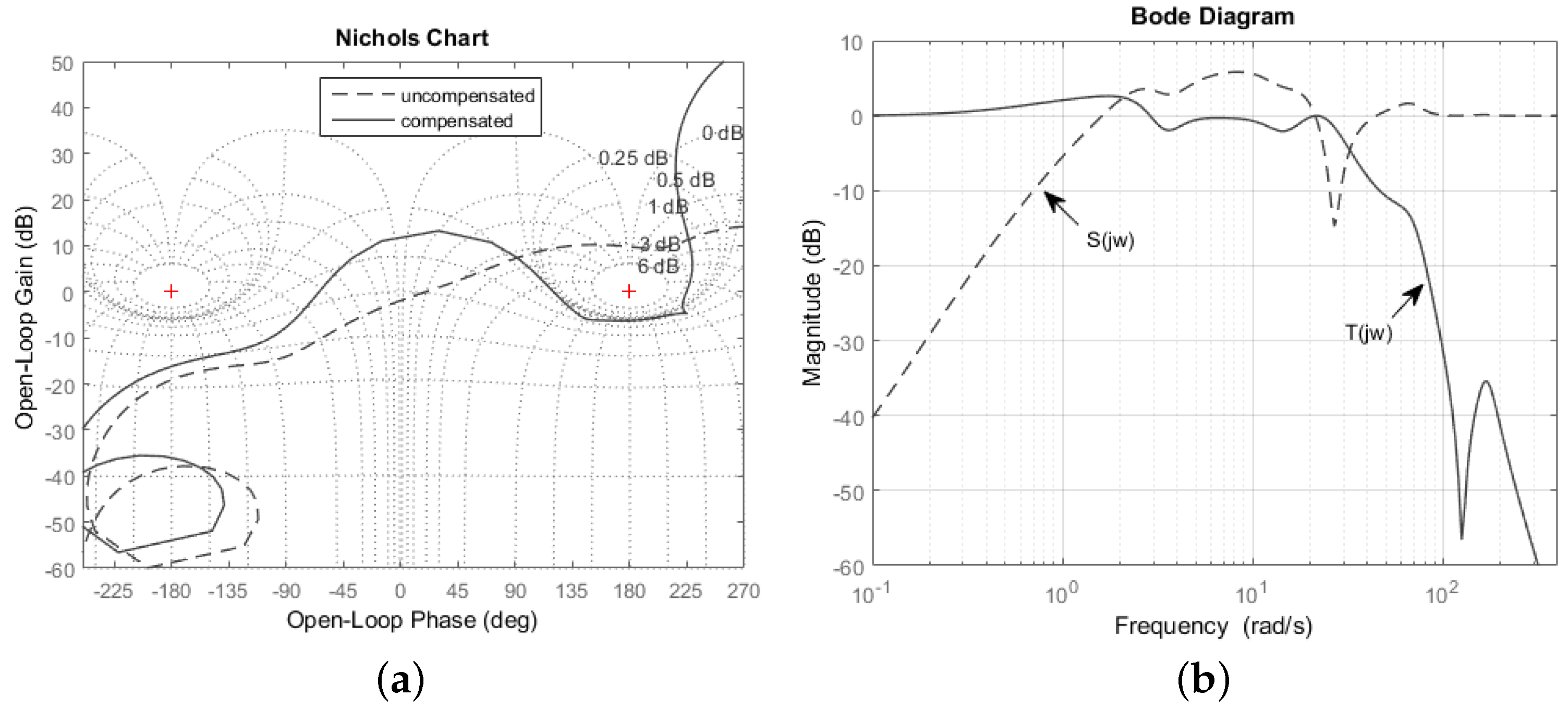
Figure 10.
Open loop (a) and closed loop (b) complementary sensitivity () and sensitivity () plots for case.
Figure 10.
Open loop (a) and closed loop (b) complementary sensitivity () and sensitivity () plots for case.
Figure 11.
Open loop (a) and closed loop (b) complementary sensitivity () and sensitivity() plots for case.
Figure 11.
Open loop (a) and closed loop (b) complementary sensitivity () and sensitivity() plots for case.
Figure 12.
Open loop (a) and closed loop (b) complementary sensitivity () and sensitivity () plots for case.
Figure 12.
Open loop (a) and closed loop (b) complementary sensitivity () and sensitivity () plots for case.
Figure 13.
Sensitivity (S), complementary sensitivity (T), and plot for (a) ; (b) .
Figure 13.
Sensitivity (S), complementary sensitivity (T), and plot for (a) ; (b) .
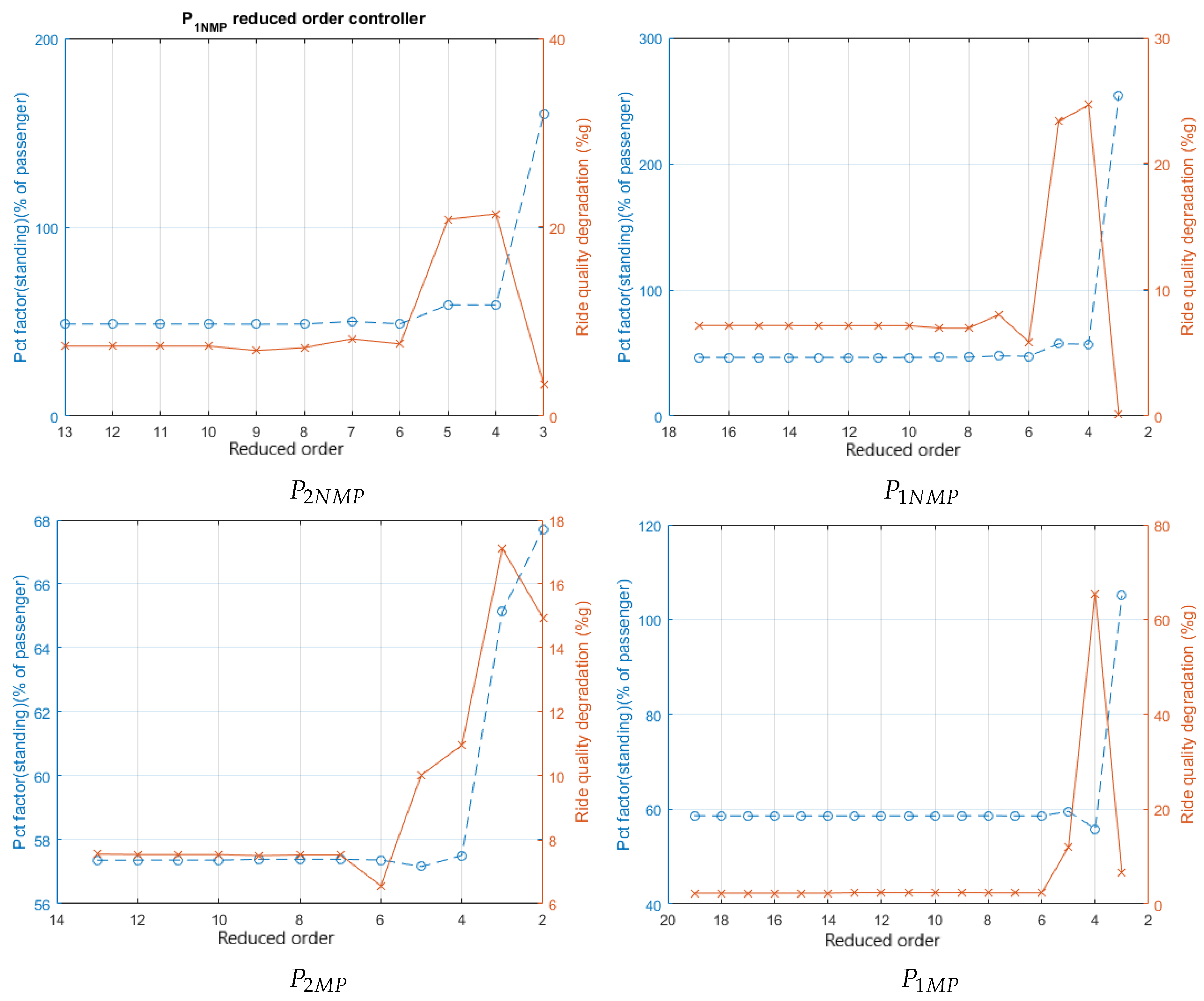
Figure 14.
Controller reduction and performance trade-off for mixed-sensitivity cases. The blue line represents factor of standing passenger, the red line represents ride quality degradation.
Figure 14.
Controller reduction and performance trade-off for mixed-sensitivity cases. The blue line represents factor of standing passenger, the red line represents ride quality degradation.
Table 1.
The track test profiles used for simulation and assessment.
Table 1.
The track test profiles used for simulation and assessment.
| Tilt Compensation | 60% | Units |
|---|
| deterministic (curved track) | | |
| maximum cant angle | | 6.00 | (degrees) |
| maximum curve radius | | 1000.00 | (m) |
| transition length | | 145.00 | (m)
@ each end |
| track length | | 1200.00 | (m) |
| stochastic (straight track) | | |
| track roughness | | 0.33 × 10 | (m) |
| track spatial spectrum | | | |
| track
length | | 1200.00 | (m) |
Table 2.
Perturbed (uncertainty) plant cases.
Table 2.
Perturbed (uncertainty) plant cases.
| Plant ID | Perturbation |
|---|
| P1 | body mass increase |
| P2 | body mass decrease |
| P3 | decrease in dynamic body mass and decrease (increase) in secondary suspension damping (stiffness) |
| P4 | increase in dynamic body mass and decrease (increase) in secondary suspension stiffness (damping) |
Table 3.
Minimization approach identifiers and weight sensitivity parameters (transfer function) for mixed-sensitivity optimization (note: rqd denotes ride quality degradation).
Table 3.
Minimization approach identifiers and weight sensitivity parameters (transfer function) for mixed-sensitivity optimization (note: rqd denotes ride quality degradation).
| Minimization ID | | | |
|---|
| | 0.9355 | not used |
| | 0.7047 | |
| | 0.5338 | not used |
| | 0.309 | |
Table 4.
Minimization approach identifiers and weight sensitivity parameters (transfer function) for mixed-sensitivity optimization for and with fixed and (note: rqd denotes ride quality degradation).
Table 4.
Minimization approach identifiers and weight sensitivity parameters (transfer function) for mixed-sensitivity optimization for and with fixed and (note: rqd denotes ride quality degradation).
| | | |
|---|
| W2 = 0.75 | | W2 = 0.5 | |
| W2 = 0.5 | | W2 = 0.1 | |
| W2 = 0.1 | | W2 = 0.05 | |
| | | |
Table 5.
Mixed-sensitivity controller performance assessment with the different time-domain optimization approaches.
Table 5.
Mixed-sensitivity controller performance assessment with the different time-domain optimization approaches.
| Deterministic (as Per Given Units) | | | | |
|---|
| Lateral accel. | RMS deviation (%g) | 2.194 | 2.064 | 2.921 | 3.474 |
| | Peak value (%g) | 11.434 | 10.137 | 12.476 | 14.388 |
| Roll gyro. | RMS deviation (rad/s) | 0.024 | 0.024 | 0.031 | 0.033 |
| | Peak value (rad/s) | 0.118 | 0.124 | 0.127 | 0.114 |
| -related | Peak jerk level (%g/s) | 6.495 | 6.279 | 8.025 | 7.933 |
| | Standing (% of passenger) | 48.703 | 46.41 | 57.359 | 58.672 |
| | Seated (% of passenger) | 13.029 | 11.912 | 15.737 | 16.832 |
| Stochastic(acceleration %g) @58 m/s 1 |
| Ride quality | Tilting train | 3.059 | 3.052 | 3.063 | 2.914 |
| | Degradation (%) | 7.413 | 7.166 | 7.55 | 2.331 |
| Performance Margins |
| Freq. resp. | Gain margin (dB) | 8.306 | 6.243 | 8.475 | 10.607 |
| | Phase margin (deg) | 52.682 | 44.513 | 41.083 | 57.123 |
| | Bandwidth (rad/s) | 1.25 | 1.23 | 0.809 | 0.723 |
| | | 1.625 | 1.952 | 1.993 | 1.535 |
| | Gamma | 1.3139 | 1.3221 | 0.8409 | 0.6412 |
Table 6.
Mixed-sensitivity controller performance assessment with the different fixed values for case.
Table 6.
Mixed-sensitivity controller performance assessment with the different fixed values for case.
| Deterministic | | | | |
|---|
| (as per Given Units) | 0.75 | 0.5 | 0.1 | HPF |
|---|
| -related | Peak jerk level (% g/s) | 6.29 | 6.674 | 9.004 | 7.140 |
| | Standing (% of passenger) | 46.341 | 48.706 | 66.045 | 52.106 |
| | Seated (% of passenger) | 11.902 | 12.786 | 20.138 | 14.124 |
| Stochastic (acceleration %g) @58 m/s 1 |
| Ride quality | Tilting train | 3.056 | 3.032 | 3.062 | 2.957 |
| | Degradation (%) | 7.306 | 6.462 | 7.52 | 3.840 |
| Performance Margins |
| Freq. resp. | Gain margin (dB) | 6.142 | 7.484 | 15.858 | 8.540 |
| | Phase margin (deg) | 44.19 | 48.263 | 65.457 | 52.718 |
| | | 1.974 | 1.736 | 1.195 | 1.596 |
| | Gamma | 1.294 | 1.112 | 0.623 | 1.446 |
Table 7.
Mixed-sensitivity controller performance assessment with the different fixed values for case.
Table 7.
Mixed-sensitivity controller performance assessment with the different fixed values for case.
| Deterministic | | | |
|---|
| (as per Given Units) | 0.5 | 0.1 | 0.05 |
|---|
| -related | Peak jerk level (% g/s) | 7.647 | 7.638 | 7.671 |
| | Standing (% of passenger) | 56.884 | 56.451 | 56.595 |
| | Seated (% of passenger) | 15.964 | 15.897 | 15.973 |
| Stochastic (acceleration %g) @58 m/s 1 |
| Ride quality | Tilting train | 3.062 | 2.961 | 3.022 |
| | Degradation (%) | 7.497 | 3.971 | 6.120 |
| Performance Margins |
| Freq. resp. | Gain margin (dB) | 8.689 | 10.299 | 10.508 |
| | Phase margin (deg) | 55.339 | 55.307 | 55.538 |
| | | 1.827 | 1.585 | 1.559 |
| | Gamma | 0.9130 | 0.6869 | 0.6752 |
Table 8.
Robust performance for standing for 8th-order controller.
Table 8.
Robust performance for standing for 8th-order controller.
| Case | P0 Nominal | P1 | P2 | P3 | P4 |
|---|
| 48.674 | 49.965 | 50.264 | 50.606 | 51.688 |
| 46.535 | 46.196 | 48.957 | 57.200 | 47.904 |
| 48.816 | 49.583 | 49.910 | 50.230 | 50.662 |
| 57.392 | 59.567 | 55.362 | 55.571 | 63.388 |
| 58.682 | 62.161 | 59.943 | 60.860 | 65.678 |
| 56.667 | 59.831 | 58.944 | 59.765 | 63.196 |
Table 9.
Robust performance for ride quality for 8th-order controller.
Table 9.
Robust performance for ride quality for 8th-order controller.
| Case | P0 Nominal | P1 | P2 | P3 | P4 |
|---|
| 7.241 | 29.453 | 14.539 | 36.730 | unstable |
| 6.966 | 24.418 | 22.475 | 92.808 | unstable |
| 6.210 | 15.509 | 17.379 | 35.497 | 69.424 |
| 7.527 | 14.288 | 4.581 | 4.168 | 29.282 |
| 2.403 | 5.866 | −0.481 | −1.253 | 10.002 |
| 4.372 | 7.692 | 2.698 | 2.137 | 13.244 |