Abstract
A blockchain-oriented continuous micropayment system forms an integral element of the digital economy, enabling seamless transactions and encouraging minor purchases. However, due to the inherent throughput constraints of blockchain, payment channels (PCs) are customarily deployed for managing high-volume transactions in an off-chain mode. Despite this, the integration of a PC necessitates a trusted intermediary to safeguard transactional security, thereby imposing an extra security assumption as only the initial and concluding transactions are visible to other system participants. To circumvent this limitation, we introduce an innovative micropayment structure utilizing lockable signatures. Each transaction within the PC coalesces into a continuous microtransaction hash-chain (CMHC), precluding unscrupulous users from accessing transactional data during the process. Additionally, all locks within the CMHC remain concealed throughout the transaction, with all information relayed in a tamper-proof manner. We provide a comprehensive security analysis and perform a gamut of evaluations. Empirical evidence indicates that our proposed system outperforms existing state-of-the-art solutions in transaction time and verification expenses. This lockable signature-dependent micropayment system not only ensures robust security but also enhances transactional speed and efficiency, thereby catalyzing the growth of the digital economy.
MSC:
68-04
1. Introduction
Blockchain, a decentralized and distributed ledger, facilitates secure and transparent transactions without necessitating intermediaries [1]. However, this technology grapples with certain challenges, such as its limited capability to handle an extensive quantity of on-chain transactions, resulting in slow transaction speeds and inflated transaction fees. Moreover, the susceptibility of the blockchain to malevolent actors aiming to distort the system or pilfer sensitive data poses a considerable risk [2,3,4,5].
Off-blockchain payment channels have been proposed as a compelling solution to enhance the scalability of blockchain technology, addressing the aforementioned limitations [6,7]. These channels empower two parties to execute continuous micropayments without individually uploading every transaction to the blockchain, thereby alleviating blockchain load, augmenting transaction speed, and diminishing transaction costs [8,9,10,11]. Consequently, off-blockchain payment channels stand to augment the efficiency and scalability of blockchain technology, broadening its applicability and accessibility.
The absence of a third-party supervisory entity overseeing transactions in micropayment via payment channels raises valid security concerns, rendering the system vulnerable to adversary attacks. For example, if Alice establishes a payment channel with Bob to conduct ‘n’ continual micropayments through a hash chain, where a small amount is any transaction under USD 10 and the total transaction amount is the sum of ‘n’ successive transactions, two potential threat scenarios could lead to losses for Alice or Bob:
- (1)
- In the midst of continual transactions, Alice or Bob could engage in deceptive or default payments, causing loss to the counterpart.
- (2)
- An external adversary could compromise the intermediate link of the continuous transactions and acquire transaction messages, incurring losses for either Alice or Bob.
Either scenario can result in losses to Alice or Bob.
To preempt such attacks, the establishment of rigorous security protocols is imperative, ensuring that all participants are credible and dependable. Two prominent solutions have been proposed to this end. The first is the network of micropayment channels introduced by Joseph Poon et al. [12], employing scripting opcodes for secure fund transfers and enforcing noncooperation through blockchain-validated multisignature transactions. The second approach is a blockchain-based micropayment scheme that leverages chameleon hash functions to establish a secure hash chain for transactions.
In this paper, we introduce a lockable signature scheme to ensure the continuity and security of micropayments. Our proposition utilizes an unnoticeable signature lock to eliminate the necessity for a trusted third-party agency during transaction processing. This offers a secure and efficient method for parties lacking mutual trust or a trading platform.
1.1. Our Main Contributions
We have engineered a state-of-the-art, rapid, and secure continuous micropayment system (CMS) employing blockchain technology and payment channels. To maintain transactional continuity, our system leverages hash chains to interlink each transaction, ensuring fluid transaction processing. Transactions are capped at amounts below USD 10, and consumers are facilitated in procuring multiple items from vendors, with the aggregate transaction amount equating to the sum of all transactions. This provision enables customers to purchase high-value items from vendors.
For bolstering system security, we have integrated a lockable signature scheme. Through the incorporation of an inconspicuous signature lock into each transaction, we deter both parties from fraudulent actions and safeguard against adversarial incursions. This obviates the requirement for a trusted third party during transactions. Our security analysis validates that our CMS is both secure and demonstrably provable.
Our CMS pioneers the integration of a concealed signature lock structure into a micropayment scheme, curbing transactional costs in off-chain payment channels. Our empirical results substantiate the efficacy of our system.
1.2. Organization
The remaining sections of this paper are arranged as follows: Section 2 familiarizes the reader with the background knowledge pertinent to this study. Section 3 elucidates the definitions of our system model. Section 4 delineates the architecture of our CMS system. In Section 5, we discuss an analysis of the CMS system model. Section 6 exhibits our experimental results. Section 7 surveys related work in this field. The paper is concluded in Section 8.
2. Preliminaries
In this section, we introduce certain useful preliminaries for our scheme.
2.1. Digital Signature
The digital signature fosters the credibility and reliability of a message. In a formal sense, it comprises the following trio of efficient algorithms, predicated on public-key cryptography:
The key generation algorithm : It takes as input the security parameter and outputs a pair of public–private keys .
The signing algorithm : It inputs a secret key and a message and outputs a signature .
The verification algorithm : It outputs 1 if is a valid signature on m under the public key , and outputs 0 otherwise.
Assume two users, Alice and Bob, serving as the sender and recipient of the signature, respectively. Alice can employ her private key to sign the message m and subsequently dispatch the obtained signature to Bob. Bob, the recipient, uses Alice’s public key to validate the received signature.
The security definitions and mathematical proofs for the digital signature have been unambiguously and explicitly established. When utilizing digital signatures to structure lockable signature schemes, it is imperative to elucidate the standard concepts of existential unforgeability and correctness of digital signatures.
The two aforementioned properties of the digital signature are
- (1)
- Existential Unforgeability: Within a signature scheme, any adversary can forge a message’s signature. However, the probability of the adversary forging successfully cannot exceed the negligible probability obtained by inputting the security parameters, even if the adversary has seen the signatures of numerous self-selected messages.
The situation where the adversary has access to all signature oracles, which is formulated as
where is an ensemble representing all plaintexts queried by the adversary.
- (2)
- Correctness: All secure signatures must be verifiable with a probability of unverifiability lower than the negligible probability obtained by the input security parameters. With an overwhelmingly high probability, all valid signatures must be verified.
2.2. Hash Function and Hash Chain
The hash function is a common term encompassing a range of functions that must meet the following conditions:
- (1)
- It can take as input a string of any length.
- (2)
- It can generate fixed-length output values.
- (3)
- Its computation time is reasonable.
A cryptographic hash function can be denoted as , capable of compressing a bit string of any length to n through function operations. Two essential properties of a secure cryptographic hash function are
- (1)
- Collision resistance: For a given set of functions , it should be computationally infeasible to find a pair of distinct strings x, y such that . More formally,where represents an adversary.
- (2)
- One-wayness: The computation process of the function should be straightforward; given a value h and computing , if x cannot be found in the computation, the cryptographic hash function is defined as a one-way function. More formally,
Hash functions can be employed in micropayment schemes to facilitate more efficient and quicker transactions. The PayWord scheme [13] generates the following hash chain:
This method ensures that the origin of each transaction remains consistent. The bank signs the transaction with its private key. Subsequent minor transactions are connected to via the hash function. Throughout the transaction, the security of each minor transaction hinges on the challenge of calculating the hash inverse function [14]. The concept of the hash chain is illustrated in Figure 1.
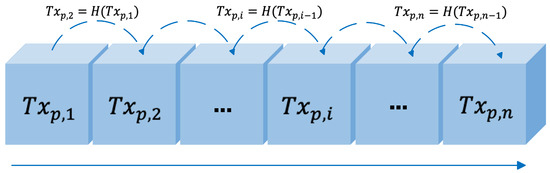
Figure 1.
The idea of hash chain.
2.3. Blockchain
The blockchain, denoted as , can be conceived as a unique form of ledger system, leveraging distributed ledger technology to store a variety of transactional data in the cloud. The decentralization of the blockchain enables trustful interactions between parties without the need for oversight from a trusted third party. By mitigating information asymmetry, the blockchain’s large-scale data technology ensures the credibility and authenticity of transactions. The blockchain’s cloud server and network equipment continuously exchange messages, allowing rapid worldwide transmission of information.
We posit an ideal function, , that maintains the blockchain , updating messages on the blockchain based on the transaction process between clients and vendors. The client generates a private key and signs each transaction with the vendor. The blockchain records the messages of the first and final transactions, denoted as and respectively. We use the symbol to replace the n-th transaction, where () and (). Any user C can send a read message to , which in turn transmits the entire blockchain transcript to user C. We have also incorporated a time lock interface into the function to set a deadline for the final transaction. If the global clock surpasses this deadline without completion of the transaction, the transaction amount is reverted to the client’s bank account.
2.4. Payment Channel
The payment channel () allows two mutually distrustful parties to transact without posting each payment message to the blockchain. To open a payment channel, two parties broadcast a funding transaction, along with their deposits, to the blockchain [15,16,17]. The capital capacity to open the is the total transaction amount between the two parties, equivalent to the sum transferred by the bank to the client. The crux of the protocol is that transacting parties can achieve a consensus on the latest fund allocation. If either party wishes to terminate the transaction, they can send a commitment to the blockchain outlining the final version of the fund distribution. Consequently, the can be closed, and the corresponding funds returned to the user. Since only the initial and final transactions are uploaded to the blockchain for opening and closing payment channels, this significantly enhances the blockchain’s throughput.
3. System Model
3.1. System Model
The CMS system model is presented in Figure 2. We provide a brief description of the role each entity plays.
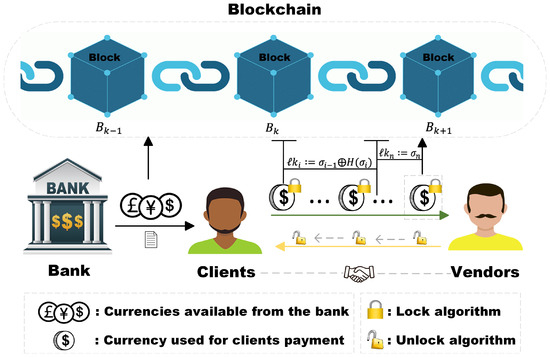
Figure 2.
The system model of the proposed CMS.
- (1)
- Bank (B): B acts as the transaction overseer and does not facilitate payment channels for users (clients and vendors) with low reputation scores. Once the transaction is initiated, the bank sends the total transaction amount and the signatures of the transaction messages (transaction amount, parts of both parties’ identification information, and send time) to the clients.
- (2)
- Clients (C): C is the initiator of the transaction. Only clients with a reputation score above 50 in their bank account can successfully start transactions. If a client engages in a fraudulent transaction during continuous micropayments, their bank account’s reputation score will be deducted according to the severity of the misconduct.
- (3)
- Vendors (V): V is the recipient of the transaction. Vendors with a credit score above 50 in their bank account can successfully accept transactions. If a vendor engages in fraudulent behavior during continuous micropayments, the bank account’s reputation score will be deducted based on the severity of the infraction.
- (4)
- Blockchain (): is used to record transactions between the two parties. Only when the transaction is successfully completed will the initial and final transaction information be uploaded and recorded successfully.
3.2. Definitions of Lockable Signatures
A lockable signature scheme () is defined in terms of public key system signature schemes, as defined below.
: The key generation algorithm takes as input the security parameter and generates a pair of public–private keys .
: The lock algorithm takes as input two pairs of secret key and message and and returns a lock . denotes the private key and message corresponding to the locked signature, and denotes the private key and message corresponding to the locking signature.
: The unlock algorithm takes as input two pairs of public key and message and , a locking signature , and a lock and outputs a locked signature .
: A lockable signature scheme is correct if for all , all pairs of messages , for all key pairs and in the image of .
3.3. Definitions of Micropayment Algorithms
We list the notations of CMS in Table 1. The system consists of the following algorithms:

Table 1.
Notations in CMS system.
: The setup algorithm takes no input other than the security parameter . It outputs the public key and the master secret key .
: The key generation algorithm takes as input the master secret key and a set of attributes and generates the public key and the secret key .
: The signature algorithm takes as input the transaction , the credibility of both parties to the transaction , and the timestep of the transaction . It outputs the first signature of the transaction , which is the signature sent by the bank to C.
: The signature algorithm takes as input the transaction and the timestep of the transaction . It outputs C’s signature for each transaction .
: The lock algorithm takes as input a locked signature and a locking signature and returns a lock .
: The unlock algorithm takes as input a locking signature ; a public key ; and a lock , and returns a locked signature .
, : The verification algorithm outputs 1 if the individual transaction signatures and transaction messages are obtained gradually by the unlocking algorithm; otherwise, it outputs 0.
3.4. Threat Model
In this segment, we delineate the security assumptions and potential threats that this scheme may encounter. Our security assumptions are as follows:
- Both parties may not be trustworthy, possessing the potential to engage in malicious actions.
- We presume that user communication occurs synchronously.
- The foundational blockchain is secure and impervious to manipulation by malicious entities.
The blockchain, featuring ideal functionality, updates in response to transactions between parties, and possesses a time-locked interface that nullifies the transaction impact on user balances upon expiration after a time duration t.
Furthermore, we delineate potential threat scenarios that our system may encounter:
Customer’s fraudulent payment: A malevolent customer may endeavor to execute a fraudulent payment, fabricating payment information without actually making the payment. They sign off the payment information, generate a signature lock, and dispatch it to the vendor via a local channel.
Provision of counterfeit goods by the vendor: A malevolent vendor might supply customers with counterfeit or worthless goods. The transaction operates on a principle of equal exchange, one item for one price. In cases where the vendor engages in fraudulent actions, the customer reserves the right to terminate the transaction.
External attack behaviors: Malicious adversaries might attempt to alter the transaction process through forgery. Adversaries strive to execute transaction information leakage attacks during a certain phase of off-chain transactions to acquire transaction information and reap illicit profits.
4. Our Construction
Initially, we present an overview of the framework (see Figure 3). Following that, we illustrate a detailed construction of the and CMS within this section.
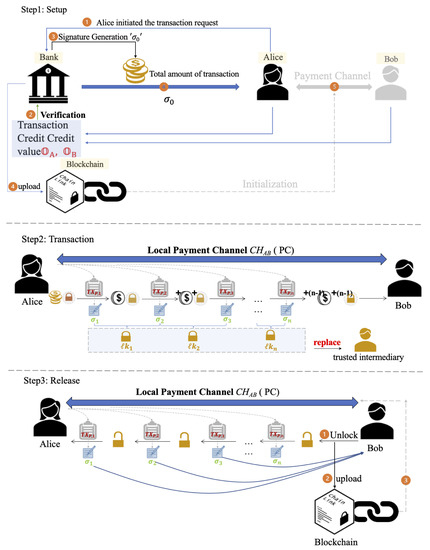
Figure 3.
The overview of the proposed CMS framework. The CMS framework process works in three steps: (1) the initiation of the transaction request and initialization process of the payment channel, (2) the generation and sending of signature locks during continuous micropayment transactions, and (3) unlocking and uploading transaction messages to the blockchain.
4.1. Framework Overview
The continuous micropayment system is designed to ensure an efficient, rapid, and secure continuous micropayment process for both parties. Rooted in blockchain technology, the use of off-chain payment channels augments the scalability of the blockchain, enabling transactions and data to be transitioned off-chain. The system encompasses a bank, clients, and vendors. The bank furnishes clients with the required total transaction amount. Each user (clients and vendors) possesses a respective reputation score within the bank. Upon receipt of the transaction request, the bank is entitled to verify the reputation score of both parties to decide if the transaction can be initiated. Continuous minor-value transactions occur between users and suppliers through transaction channels. These successive transactions could be in the form of microcoins. Each transaction is interconnected rather than independent.
The client authenticates each transaction, consequently generating a sequence of signature locks. Every transaction received by vendors incorporates a signature lock. This lock remains inconspicuous during the transaction, bolstering its security. Upon receiving the final transaction, vendors utilize the algorithm to sequentially disengage the chain of locks. Once the unlocking procedure is completed, the details of each transaction can be accessed. Ultimately, the first and last transaction data are uploaded to the blockchain.
4.2. Detailed LS
The algorithm is parameterized by a group of the order q. The group is generated by a point on an elliptic curve over the finite field of integers modulo a prime p. The algorithm makes use of a hash function . Curve coordinates and scalars are represented in bits, which is also the security parameter [18,19,20]. The LS algorithms are as follows:
- :
Select the secret key from the finite field
Compute the public key as
Select the secret key from the finite field
Compute the public key
Output and
(1)
- Select from the finite field
Compute
Compute
Compute
(2)
- Select the instance key from the finite field
Compute
Compute
Compute
Output
- :Output
- :(1)Parse asComputeOutput 1 if and only if(2)
Output 1 if for all , all pairs of messages , for all key pairs of and in the image of .
A lockable signature scheme encompasses two signatures, classified as the locking signature and the locked signature. Concurrently, the lockable signature scheme incorporates two algorithms, specifically the lock algorithm and the unlock algorithm (see Figure 4). In continual micropayment schemes, these algorithms sign two distinct yet contiguous transaction messages.
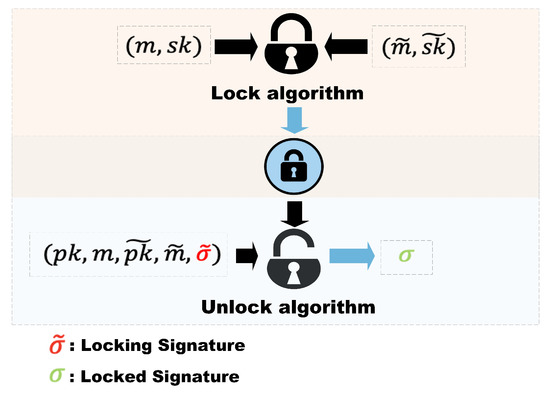
Figure 4.
The illustration of a lockable signature ().
Initially, we ascertain the transaction details, then discern the information corresponding to the locked and locking signatures, and employ the signature algorithm to generate the respective signatures. These signatures are then combined with the hash operation and linked following the procedural methodology of the hash chain. Lastly, we introduce the computation process of the lockable signatures, the two forms of which can be authenticated against distinct public keys.
An inconspicuous signature lock can be acquired by inputting the locked and locking signatures into the locking algorithm [21]. During the transaction phase, the client generates a sequence of unseen locks, with each node transaction of the hash chain being sent to the vendor via the payment channel. The vendor, through the unlocking algorithm, completes the unlocking process, thereby accessing the transaction messages and the amount for each transaction.
We define our concept of security for lockable signatures as follows. As stated previously, the lockable signature scheme incorporates two algorithms, namely, the lock algorithm and the unlock algorithm. Initially, we posit that the signature algorithms can yield deterministic signatures. Subsequently, we presume that the lock algorithm is executed sincerely in the context of security (Algorithm 1).
| Algorithm 1 The unlockability of lockable signature. |
| Input: Output:
|
(Unlockability) The unlockability embodies three features.
- (1)
- Correctness: This ensures that lockable signature schemes can be successfully unlocked at the conclusion of a series of transactions.
- (2)
- Efficiency: Lockable signatures exhibit greater efficiency during transactions compared with traditional schemes that employ a trusted third party to oversee the entire transaction process.
- (3)
- Completeness: Lockable signature schemes can deter the interruption of the transaction process by external adversaries who might initiate a transaction-intercept attack. (Adversary obtains the transaction message (time or phase) in the middle of the micropayment transaction using a hash chain. Then can trace back to the first transaction, and the account messages of transaction parties are exposed).
An adversary, , can access the transaction message (time or phase) during the micropayment transaction using a hash chain, potentially tracing back to the first transaction and exposing the account details of the transaction parties.
For the security analysis, an adversary, , can select a message pair while utilizing the secret key’s signing oracle. During the verification of unlockability, the produced signature lock is obtained by executing the lock algorithm honestly. This signature lock is revealed to the adversary, , who then returns a candidate locking signature for unlocking and retrieves the corresponding locked signature through the unlocking process. If the derived locked signature is an invalid signature for the transaction message m under the public key , the adversary, , wins.
We maintain that the lockable signature satisfies the attribute of unlockability, which implies that the adversary, , has a negligible advantage under the constraints of the given security parameters.
(Invisibility) As previously mentioned, the signature locks remain hidden during transactions [22]. The invisibility attribute ensures that both the locking signature and the locked signature remain unseen within the transaction process. In other words, the transaction details are not exposed until they are unlocked. During the security analysis, can query the signature oracle for the secret key and, subsequently, select a message pair . The lockable signature scheme is deemed to comply with the definition of invisibility, suggesting the adversary’s probability of winning approximates 1/2 (Algorithm 2).
| Algorithm 2 The invisibility of lockable signature. |
| Input:
Output:
|
4.3. Detailed CMS
A continuous micropayment system encompasses a cohort of users engaged in transactions and a blockchain-based cryptocurrency system for microtransactions. In a series of transactions, it is crucial to verify that the amount of the prior transaction has been subtracted, indicating that the previous transaction has been finalized.
The client C identifies the vendor V for the transaction and initiates the transaction request. Upon receiving the request, the bank B first validates the reputation score of both transaction parties. If either party’s reputation score falls below 50, the bank B will either issue a transaction warning or disallow the commencement of the transaction. If a credit value is needed, the bank will send the client the total transaction amount F, identification information for both parties , and a signature for the transaction messages . These transaction messages include time , reputation value , and message .
An off-chain payment channel is constructed between the client C and the vendor V. The client makes n micropayments of the amount f (which can be created via Bitcoin) to the vendor through the payment channel. In the first transactions, the client sends each transaction’s amount and the signature lock (produced by the client’s signature on the transaction via the lock algorithm) to the vendor.
In the n-th transaction, the client sends the transaction amount and the signature lock to the vendor. The difference between the n-th transaction and the first transactions lies in the construction of the signature lock .
The vendor receives each transaction through the payment channel. Through the verification algorithm () and the unlock algorithm (), the client’s signature on each transaction message is gradually obtained, and finally, each transaction message is obtained. This allows the vendor to perform verification. Any losses can be compensated at the end of the payment process. Generally speaking, if the client fails to pay in multiple transactions, the total amount received by the vendor will not match the total amount issued by the bank at the end of the transaction. The vendor can provide the voucher to the bank and receive the replenished amount. If one of the clients or vendors needs to abort the transaction in multiple consecutive transactions, the existence of the signature lock can avoid the loss of both parties after the transaction is interrupted.
The vendor can obtain a message about each transaction by progressively unlocking it. After a successful transaction, the first and last transactions are uploaded to the blockchain and used to open and close the blockchain. The blockchain is used as proof of the transaction.
5. Security Analysis
In this section, we have analyzed the security of the scheme. The scheme utilizes the notion of blind signature and some cryptographic tools to defend against the threats defined earlier.
The signature scheme we use is unforgeable and correct. Among them, unforgeability means that the adversary can return a valid signature of a selected message through access to the signature oracle. However, the adversary cannot forge a new signature on its newly selected message.
The hash function we use is proven to be efficient and secure. The collision resistance and one-wayness are two properties of the secure hash function.
The customer falsely pays. The supplier receives a series of locks to unlock and obtain signatures for transaction information, thereby obtaining transaction information from the signatures. The supplier fails to verify the transaction information, sends a verification failure flag to the bank, and freezes the funds irreversibly. At the same time, the last transaction information will not be uploaded to the blockchain, and the transaction will not be recorded and confirmed. For example, the scheme is constructed based on an ECDSA signature. Alice, as the customer, forges the i-th payment information. Alice randomly selects the private key k; calculates the public key , where G is the base point of the elliptic curve; and then selects a random number r to calculate for information i. When Alice signs the information , she randomly selects d; first calculates , where H is -3; and then calculates the signature , . Then, the obtained signature is input into the lock algorithm to generate the signature lock , which Bob receives and inputs into the unlock algorithm to obtain Alice’s signature for , verifying that . Therefore, the supplier fails to verify the transaction information, and the transaction will not be recorded and confirmed.
The supplier provides false goods. The transaction is based on the principle of one good, one price, and if the supplier engages in misconduct, the customer can terminate the transaction. A successful transaction means that the customer approves of the goods provided by the supplier. The transaction is unlocked and verified on a transaction-by-transaction basis, and after the verification is complete, the last transaction is automatically uploaded to the blockchain.
External attack behavior. Malicious adversaries would like to alter the transaction process through forged behavior. The adversary seeks to carry out transaction information leakage attacks during a certain stage of off-chain transactions in order to obtain transaction information and illegitimate profits. This scheme uses ECDSA signatures, which are tamper-proof. The digital signature lock in this scheme has concealment. Concealment ensures that the properly generated lock will not expose the locked signature and the signature used to generate the lock. When an adversary chooses to attack, they can choose two messages , randomly generate a b, and if , correctly generates a lock. If , a simulator outputs a lock. The adversary must solve the elliptic curve discrete logarithm problem to forge a valid signature. The adversary can only run the unlock algorithm using the signature on m.
6. Experiment
Our experiment comprises two phases: the off-chain transaction process and the uploading of the transaction message to the blockchain. The latter encapsulates two portions of the message, namely, the initial bank-to-client remittance message and the final transaction information from the continuous micropayment.
We conducted experiments on a local machine equipped with an Apple M1 chip 8-core processor and 16 GB memory, measuring and calculating time and overhead costs. Using Python, we evaluated the time cost of a continuous micropayment scheme where each micropayment is under USD 10. To analyze the impact of the payment amount on computational cost, we designated three payment amounts: USD 1, USD 5, and USD 10.
Simultaneously, we fixed the number of continuous transactions through the off-chain payment channel to range between 10 and 1000 times, selecting 6 fixed transaction times for statistical time cost. Hash functions form the backbone of our blockchain construction, transactions, and micropayments. Our system is built upon the underlying security of hash functions such as . Utilizing the algorithm as the hash function, the signature is randomly generated during the transaction. We executed 900 operations, and the averaged transaction time and communication cost measurements are noted in Table 2. Our measurements do not take network latency into account, but this does not represent an efficiency bottleneck in our approach.

Table 2.
Notations in LS.
During the stage, the bank is required to verify the reputation value of both transaction parties. The client needs to receive the total transaction amount, the signature, and some identification information of both parties from the bank. We used 40-bit characters to denote the bank-generated signature and found the average transaction time to be s. During the phase, users employ a signature generator to produce signatures for each transaction. Subsequently, the lock is created via the lock algorithm and transmitted to the vendor over 10,000 consecutive transactions. The measured average transaction time was s. Table 3 records the time and cost of 10,000 consecutive transactions using the off-chain channel with a transaction amount of USD 10.

Table 3.
The costs of CMS.
Upon initialization of the off-chain payment channel, both parties partake in ongoing multiple payment transactions, comprising customer C’s fund outflow and vendor B’s receipt process. Our approach accomplishes a cost-effective payment scheme while guaranteeing secure transactions. Article [23] also utilizes off-chain transactions, but their solution differs from ours by introducing off-chain committees to facilitate secure transactions.
To illustrate the efficiency of our scheme in off-chain transactions, we carried out a series of experiments. Initially, we conducted a comparative experiment utilizing a hash chain to implement continuous transactions in off-chain payment channels, employing an off-chain committee in our scheme to ensure the security of these transactions. We juxtaposed the results of the comparative experiment with our experimental findings. To ensure fairness, we compared these two schemes under the same cryptographic system. We assumed that both schemes utilized the off-chain ECDSA signature scheme, with the length of the generated signature represented by ‘’. We denoted the length of each off-chain transaction amount as ‘f’, ‘s’ as the length of the off-chain transaction serial number, ‘e’ as the number of off-chain committee members, and ‘h’ as the number of times the hash function is called. We used 10 consecutive transactions as an example.
The experiments demonstrated that under normal trading conditions without external attacks, our solution has lower costs (see Table 4). If the transaction process is subject to external attacks, the use of off-chain committees incurs additional expenses, whereas the costs of our solution remain constant under both conditions, irrespective of the presence of external attacks or not.

Table 4.
Comparison results of communication overhead.
The second part involves uploading the initial and final transaction information to the blockchain. We employed a virtual machine to construct a Hyperledger blockchain framework. Throughout the entire transaction process, the initial transaction message (total transaction, transaction number, partial identity information of both parties, bank signature) is uploaded to the blockchain. The final transaction information (single transaction amount, transaction number, customer signature) is also uploaded to the blockchain. The time taken to upload these two messages is recorded (see Figure 5, Figure 6 and Figure 7).
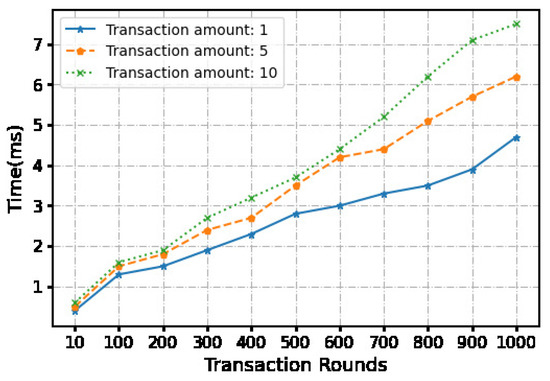
Figure 5.
Time cost of the setup phase.
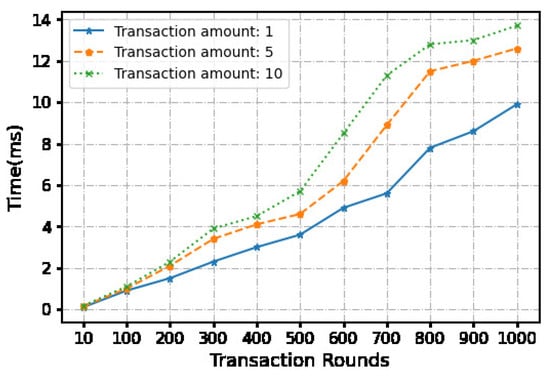
Figure 6.
Time cost of the transaction phase.
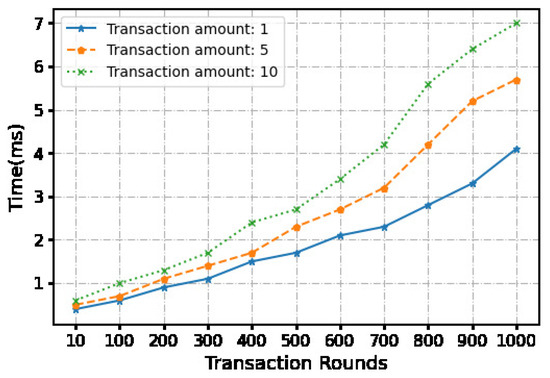
Figure 7.
Time cost of the release phase.
7. Related Work
Micropayments first emerged two decades ago, with initial micropayment transaction amounts ranging from a few cents to a few dollars [24]. Richard J. Lipton [25] proposed a micropayment system tailored for the World Wide Web. The system instituted a coin-tossing protocol to ensure transaction fairness through a third-party entity. Silvio Micali and Ronald L. Rivest [26] put forward three micropayment schemes—MR1, MR2, and MR3—aimed at enhancing the efficiency of micropayment schemes and thwarting malicious actions by individual actors. Ronald L. Rivest and Adi Shamir [27] proposed micropayment schemes named ‘PayWord’ and ‘MicroMint’, focusing on the application of hash functions to minimize the number of public key operations. Yi et al. [28] suggested three micropayment schemes grounded in hash chains and hash functions, incorporating salt into the scheme to boost payment security and eliminate scheme constraints. Quan Son Nguyen [29] presented the concept of a multidimensional hash chain and applied it to the micropayment scheme, underscoring that a multidimensional hash chain could elevate payment security and efficiency. Jie Wu et al. [30] introduced the notion of supernodes to tackle the issue of instantaneous execution capability of Lightning Network applications in micropayment systems, reducing the number of small nodes necessitating liquidation in the Lightning Network.
With the evolution and maturation of blockchain technology, an increasing number of micropayment schemes incorporating blockchain have been put forth [31]. Conrad Burchert et al. [32] proposed a micropayment channel network, introducing a new layer between the blockchain and the payment channel to address the blockchain scalability issue. Noureddine Boudriga [33] suggested a blockchain-based micropayment scheme, employing three trust models for verifying and managing the blockchain network, thereby cutting transaction verification costs and mitigating network attacks. Fatemeh Rezaeibagha and Yi Mu [34] proposed a cryptocurrency-based micropayment scheme built on the foundation of blockchain, employing the chameleon hash function to construct a flawless hash chain. Hao Lei et al. [35] suggested a multinode payment channel method based on the payment channel, reducing information transmission cost and enhancing blockchain scalability. Kao Y.C et al. [36] proposed that the leading strategy based on blockchain is the best choice for banking financial services. Using an integrated approach, this study constructs a mixed decision model for banks using the decision experiment and evaluation laboratory and multiple analytical methods. Feasible fintech strategies in existing research are summarized, and the evaluation results show that it can help banks develop a supply chain financing business. Liu et al. [37] proposed a hybrid chain model that combines PANDA and X-Alliance. This research can solve the problems of inconvenient information verification, data falsification, efficiency, safety, and cost in supply chain finance. Issa W et al. [38] reviewed blockchain-based federated learning methods for securing IoT systems. This study summarizes the relevant research content of blockchain and its application in IoT security and privacy.
8. Conclusions
In conclusion, we presented an efficient, swift, and secure continuous micropayment system in this paper. The micropayment system, underpinned by blockchain, utilizes an off-chain payment channel for transactions. Each transaction is not isolated but interconnected. Throughout the transaction process, we employ a lockable signature scheme to create a signature lock, with the lock concealed. The system can offer a fast and secure method in the absence of a trading platform and amidst mutual distrust between trading parties. This micropayment system can enhance blockchain scalability, curtail transaction time and storage duration, and decrease system computation and transmission overhead, thereby achieving rapid transactions.
Author Contributions
Investigation, W.L.; Writing—original draft, W.W.; Writing—review & editing, G.C.; Supervision, C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Macau Foundation: No.MF2102.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
No conflict of interest exists in the submission of this manuscript, and all authors for publication approve the manuscript On behalf of my co-authors, I would like to declare that the work described was research that has not been published previously, and is not under consideration for publication elsewhere, in whole or in part. All the authors listed have approved the manuscript that is enclosed.
References
- Zhang, Y.; Deng, R.H.; Liu, X.; Zheng, D. Blockchain based efficient and robust fair payment for outsourcing services in cloud computing. Inf. Sci. 2018, 462, 262–277. [Google Scholar] [CrossRef]
- Syed, T.A.; Alzahrani, A.; Jan, S.; Siddiqui, M.S.; Nadeem, A.; Alghamdi, T. A comparative analysis of blockchain architecture and its applications: Problems and recommendations. IEEE Access 2019, 7, 176838–176869. [Google Scholar] [CrossRef]
- Dai, H.N.; Zheng, Z.; Zhang, Y. Blockchain for Internet of Things: A survey. IEEE Internet Things J. 2019, 6, 8076–8094. [Google Scholar]
- Konstantinidis, I.; Siaminos, G.; Timplalexis, C.; Zervas, P.; Peristeras, V.; Decker, S. Blockchain for business applications: A systematic literature review. In Proceedings of the International Conference on Business Information Systems, Berlin, Germany, 18–20 July 2018; Springer: Cham, Switzerland, 2018; pp. 384–399. [Google Scholar]
- Pandey, A.A.; Fernandez, T.F.; Bansal, R.; Tyagi, A.K. Maintaining Scalability in Blockchain. In Proceedings of the International Conference on Intelligent Systems Design and Applications, Online, 12–14 December 2022; Springer: Cham, Switzerland, 2022; pp. 34–45. [Google Scholar]
- Li, D.; Liu, J.; Tang, Z.; Wu, Q.; Guan, Z. Agentchain: A decentralized cross-chain exchange system. In Proceedings of the 2019 18th IEEE International Conference on Trust, Security and Privacy in Computing and Communications/13th IEEE International Conference on Big Data Science and Engineering (Trustcom/BigdataSE), Rotorua, New Zealand, 5–8 August 2019; pp. 491–498. [Google Scholar]
- Ying, N.; Wu, T.W. xlumi: Payment channel protocol and off-chain payment in blockchain contract systems. arXiv 2021, arXiv:2101.10621. [Google Scholar]
- Erdin, E.; Mercan, S.; Akkaya, K. An evaluation of cryptocurrency payment channel networks and their privacy implications. arXiv 2021, arXiv:2102.02659. [Google Scholar]
- Pass, R.; Shelat, A. Micropayments for decentralized currencies. In Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security, Denver, CO, USA, 12–16 October 2015; pp. 207–218. [Google Scholar]
- Avarikioti, Z.; Thyfronitis Litos, O.S.; Wattenhofer, R. Cerberus channels: Incentivizing watchtowers for bitcoin. In Proceedings of the International Conference on Financial Cryptography and Data Security, Kota Kinabalu, Malaysia, 10–14 February 2020; Springer: Cham, Switzerland, 2020; pp. 346–366. [Google Scholar]
- Takahashi, T.; Otsuka, A. Probabilistic micropayments with transferability. In Proceedings of the European Symposium on Research in Computer Security, Online, 4–8 October 2021; Springer: Cham, Switzerland, 2021; pp. 390–406. [Google Scholar]
- Poon, J.; Dryja, T. The Bitcoin Lightning Network: Scalable Off-Chain Instant Payments. 2016, pp. 1–59. Available online: http://lightning.network/lightning-network-paper-DRAFT-0.5.pdf (accessed on 27 July 2023).
- Decker, C.; Wattenhofer, R. A fast and scalable payment network with bitcoin duplex micropayment channels. In Proceedings of the Symposium on Self-Stabilizing Systems, Edmonton, AB, Canada, 18–21 August 2015; Springer: Cham, Switzerland, 2015; pp. 3–18. [Google Scholar]
- Buldas, A.; Laanoja, R.; Truu, A. A blockchain-assisted hash-based signature scheme. In Proceedings of the Nordic Conference on Secure IT Systems, Oslo, Norway, 28–30 November 2018; Springer: Cham, Switzerland, 2018; pp. 138–153. [Google Scholar]
- Zhang, J.; Ye, Y.; Wu, W.; Luo, X. Boros: Secure and Efficient Off-Blockchain Transactions via Payment Channel Hub. IEEE Trans. Dependable Secur. Comput. 2021, 20, 407–421. [Google Scholar]
- Fazli, M.A.; Nehzati, S.M.; Salarkia, M.A. Building Stable Off-chain Payment Networks. arXiv 2021, arXiv:2107.03367. [Google Scholar]
- McCorry, P.; Möser, M.; Shahandasti, S.F.; Hao, F. Towards bitcoin payment networks. In Proceedings of the Australasian Conference on Information Security and Privacy, Melbourne, VIC, Australia, 4–6 July 2016; Springer: Cham, Switzerland, 2016; pp. 57–76. [Google Scholar]
- Doerner, J.; Kondi, Y.; Lee, E.; Shelat, A. Secure two-party threshold ECDSA from ECDSA assumptions. In Proceedings of the 2018 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 21–23 May 2018; pp. 980–997. [Google Scholar]
- Deepa, N.; Pham, Q.V.; Nguyen, D.C.; Bhattacharya, S.; Prabadevi, B.; Gadekallu, T.R.; Pathirana, P.N. A survey on blockchain for big data: Approaches, opportunities, and future directions. Future Gener. Comput. Syst. 2022, 131, 209–226. [Google Scholar]
- Boneh, D.; Lynn, B.; Shacham, H. Short signatures from the Weil pairing. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Taipei, Taiwan, 5–9 December 2001; Springer: Berlin/Heidelberg, Germany, 2001; pp. 514–532. [Google Scholar]
- Malavolta, G.; Moreno-Sanchez, P.; Schneidewind, C.; Kate, A.; Maffei, M. Anonymous Multi-Hop Locks for Blockchain Scalability and Interoperability. Cryptology ePrint Archive. 2018. Available online: https://eprint.iacr.org/2018/472.pdf (accessed on 27 July 2023).
- Thyagarajan, S.A.K.; Malavolta, G. Lockable signatures for blockchains: Scriptless scripts for all signatures. In Proceedings of the 2021 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 24–27 May 2021; pp. 37–954. [Google Scholar]
- Li, T.; Yang, A.; Weng, J.; Tong, Y.; Pei, Q. Concurrent and efficient IoT data trading based on probabilistic micropayments. Wirel. Netw. 2022, 29, 607–622. [Google Scholar] [CrossRef]
- Delmolino, K.; Arnett, M.; Kosba, A.; Miller, A.; Shi, E. Step by step towards creating a safe smart contract: Lessons and insights from a cryptocurrency lab. In Proceedings of the International Conference on Financial Cryptography and Data Security, Christ Church, Barbados, 22–26 February 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 79–94. [Google Scholar]
- Lipton, R.J.; Ostrovsky, R. Micro-payments via efficient coin-flipping. In Proceedings of the International Conference on Financial Cryptography, Anguilla, British West Indies, 23–25 February 1998; Springer: Berlin/Heidelberg, Germany, 1998; pp. 1–15. [Google Scholar]
- Micali, S.; Rivest, R.L. Micropayments revisited. In Proceedings of the Cryptographer Track at the RSA Conference, San Jose, CA, USA, 18–22 February 2002; Springer: Berlin/Heidelberg, Germany, 2002; pp. 149–163. [Google Scholar]
- Rivest, R.L.; Shamir, A. PayWord and MicroMint: Two simple micropayment schemes. In Proceedings of the International Workshop on Security Protocols, Cambridge, UK, 10–12 April 1996; Springer: Berlin/Heidelberg, Germany, 1996; pp. 69–87. [Google Scholar]
- Mu, Y.; Varadharajan, V.; Lin, Y.X. New micropayment schemes based on Pay Words. In Proceedings of the Australasian Conference on Information Security and Privacy, Brisbane, QLD, Australia, 28–30 November 1997; Springer: Berlin/Heidelberg, Germany, 1997; pp. 283–293. [Google Scholar]
- Nguyen, Q.S. Multi-dimensional hash chains and application to micropayment schemes. In Proceedings of the International Workshop on Coding and Cryptography, Bergen, Norway, 14–18 March 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 218–228. [Google Scholar]
- Wu, J.; Jiang, S. On Increasing Scalability and Liquidation of Lightning Networks for Blockchains. IEEE Trans. Netw. Sci. Eng. 2022, 9, 2589–2600. [Google Scholar]
- Nofer, M.; Gomber, P.; Hinz, O.; Schiereck, D. Blockchain. Bus. Inf. Syst. Eng. 2017, 59, 183–187. [Google Scholar]
- Burchert, C.; Decker, C.; Wattenhofer, R. Scalable funding of bitcoin micropayment channel networks. R. Soc. Open Sci. 2018, 5, 180089. [Google Scholar] [CrossRef] [PubMed]
- Boudriga, N. A resilient micro-payment infrastructure: An approach based on blockchain technology. Kuwait J. Sci. 2022, 49. [Google Scholar] [CrossRef]
- Rezaeibagha, F.; Mu, Y. Efficient micropayment of cryptocurrency from blockchains. Comput. J. 2019, 62, 507–517. [Google Scholar] [CrossRef]
- Lei, H.; Huang, L.; Wang, L.; Chen, J. MPC: Multi-node Payment Channel for Off-chain Transactions. In Proceedings of the IEEE International Conference on Communications (ICC 2022), Seoul, Republic of Korea, 16–20 May 2022; pp. 4733–4738. [Google Scholar]
- Kao, Y.C.; Shen, K.Y.; Lee, S.T.; Shieh, J.C. Selecting the Fintech Strategy for Supply Chain Finance: A Hybrid Decision Approach for Banks. Mathematics 2022, 10, 2393. [Google Scholar]
- Liu, J.; Yan, L.; Wang, D. A hybrid blockchain model for trusted data of supply chain finance. Wirel. Pers. Commun. 2021, 127, 919–943. [Google Scholar] [CrossRef] [PubMed]
- Issa, W.; Moustafa, N.; Turnbull, B.; Sohrabi, N.; Tari, Z. Blockchain-based federated learning for securing internet of things: A comprehensive survey. ACM Comput. Surv. 2023, 55, 1–43. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).