A Study of Independency on Fuzzy Resolving Sets of Labelling Graphs

Abstract

Considering a fuzzy graph G is simple and can be connected and considered as a subset $H=\left\{\left(u_1,\sigma \left(u_1\right)\right),\left(u_2,\sigma \left(u_2\right)\right),\dots \left(u_k,\sigma \left(u_k\right)\right)\right\}, \left|H\right|\ge 2$; then, every two pairs of elements of $\sigma -H$ have a unique depiction with the relation of $H$, and $H$ can be termed as a fuzzy resolving set (FRS). The minimal $H$ cardinality is regarded as the fuzzy resolving number (FRN), and it is signified by $Fr\left(G\right)$. An independence set is discussed on the FRS, fuzzy resolving domination set (FRDS), and Fuzzy modified antimagic resolving set (FMARS). In this paper, we discuss the independency of FRS and FMARS in which an application has also been developed.

1. Introduction

The graph theory has been put forward by the Fuzzy set in the 21st century. In 1986, Ref. [1] on the fuzzy graph, the authors used intuitionistic concepts. In [2], the author investigated the concept of antimagic labelling. For antimagic total labelling, all vertices and edges were labelled with values ranging from 1 to $v+e$. For G. Chartrand et al. [3], the higher dimensions and resolving numbers for multiple popular graphs were determined. In [4], the author referred to the metric aspects of a graph and its resolvability. The domination in FG was established by Gani A.N. et al. [5] in 2012, who worked with many authors and created multiple research works in FG, including works on the strengths and weaknesses of domination [6]. A.N. Gani et al. [7] identified a novel idea of fuzzy labelling. The fuzzy cut and fuzzy end nodes of the fuzzy labelling graph were established. In 2014, Ref. [8], the authors introduced the ideas of fuzzy labelling and fuzzy magic labelling (FML) graphs. FML has been defined for certain graphs, especially the path, cycle, and star graphs. Additionally, some characteristics of fuzzy bridges and cut nodes have been discussed, and the fuzzy labelling cycles have all been identified.

In 2014, Ref. [9], the authors investigated the presence of vertex total antimagic labelling (VTAL) in the Harary structure and satisfied for r-copies. In [10], we examined and presented several estimates of the antimagic chromaticlocal value for a disjointed union of several duplicates of a graph. G. Moderson, Sunil Mathew, et al. [11] evolved an FG with several uses.

Ref. [12] This article investigates how graph labelling may be used to improve network safety and network tracking, such as the channel allocation method and social media networks. Kauffman developed the FG theory from the fuzzy set in 1973, Ref. [13], and Rosenfeld enhanced it in 1975. A fuzzy set is characterized by uncertainty and ambiguity. Several real-world applications were later built using this approach by Shanmugapriya et al., and this was further expanded to resolvability in FG [14]. They also developed modified FRN and FRS features. In the context of uncertainty and ambiguity in many circumstances, a fuzzy system was designed. It was later developed by a number of researchers.

In 2020, Ref. [15], the researcher introduced and their characteristics discussed the concepts of MFRS, MFRN, and MFSRN. From [16], the characteristics of FRS and FRN are covered in this article. Additionally, it established a few theorems and properties of fuzzy resolving numbers. Additionally, some characteristics of fuzzy bridges and fuzzy cut nodes were discussed. In [17], Shanmugapriya et al. proposed a study on Fuzzy Resolving Domination Sets and Their Application in Network Theory, whose resolving set provided a foundation for this basis. In [18], the authors analysed fuzzy vertex graceful labelling on specific kinds of graphs in this paper. The author investigated a study on FDS in [19]. In [20], the researcher introduced Antimagic labelling, which occurred for some graphs with paths and cycles. Euler first proposed the graph theory in 1936, and Zadeh [21] analysed it in 1965. Some of the applications of these resolvable sets are discussed by Muhammad Faisal Nadeem and others [22,23,24].

Fuzzy sets are used in traffic light problems, the theory of networks, mathematical biological processes, drug identification, cancer diagnosis, the examination of an organizing pattern, and the picture captures [25,26]. A dynamic system of various types includes the independency of FRS, FSRS, FMARS, and so on; the illustrations are discussed in Section 5 and Section 6. Many applications make use of the clustering of sets of parameters. A vast range of data related to everyday issues can be understood using various graphs like an IFG and an NFG [27,28]. The value of membership is a unique value that varies from 0 to 1. A problem can be more easily clarified and solved promptly and precisely by being represented as a graph. A complicated problem can be represented in a basic graph theory, employing nodes and arcs with the graph theory. Additionally, we can solve many social life problems with FRS, FDS, and also the combination of both in order to obtain the unique and perfect set to rule out the problems in a different way. The resolving set in the graph theory is completely different from FRS, where it is entirely focused on unique sets, whereas the resolving set in a graph is based on the separation between vertices [29,30].

In graph theory, a revolving set of graphs have applications in network discovery, discovering drugs, robotic navigation, coin-weighing options, and mastermind games. In this article, we define the IFRDS and its number. Additionally, we specified the characteristics of IFRDS, FMARS, and a theory of network applications based on FRDS.

2. Preliminaries

In this portion, we outline a few definitions to understand the nature of the paper as discussed below.

Definition 1.

A FG $G\left(V,\sigma ,\rho \right)$ is a fuzzy relation where$\sigma$ be a function from $V to$and $\rho$ranges from $V\times V$to [0, 1] such that $\rho \left(u,y\right)\le min\{\sigma \left(u\right),\sigma \left(y\right)\}$, $\forall u,y\in V$.

Definition 2.

An FG is called as a complete fuzzy graph (CFG) if $\rho \left(u,y\right)=min\{\sigma \left(u\right),\sigma \left(y\right)\} \forall u,y\in V$ and ${\rho }^{\infty }\left(u,v\right)=\rho \left(u,y\right), \forall u,y\in V$.

Definition 3.

In an FG, an arc $(u,y)$ is represented as a strong arc if ${\rho }^{\infty }\left(u,y\right)=\rho (u,y)$.

Definition 4.

Consider a subset $H=\left\{\left(u_1,\sigma \left(u_1\right)\right), \left(u_2, \sigma \left(u_2\right)\right),\dots \left(u_k,\sigma \left(u_k\right)\right)\right\}$, $\left|H\right|\ge 2$, the representation of $\left(z,\sigma \left(z\right)\right)ϵ\sigma -H=\left\{\left(u_{k+1},\sigma \left(u_{k+1}\right)\right),\left(u_{k+2},\sigma \left(u_{k+2}\right)\right),\dots (u_n,\sigma \left(u_n\right))\right\}$ and $\left\{w\left(z,u_1\right),w\left(z,u_2\right),\dots w(z,u_k)\right\}$. If every pair word of elements in $H$ has a unique representation in order to $H$, the set is known as a FRS. The minimal size of FRS is FRN.

Definition 5.

A set Q of vertices if every vertex of $V\backslash Q$ is adjacent to any vertex of $Q$. The minimal size of this set is called the fuzzy domination number (FDN) and it is written as $F_{\gamma }\left(G\right)$.

Definition 6.

Let $S$is a FRDS if it is a subset of node of G that is both FDRS and FRS. The minimal size of $S$ is known as a fuzzy resolving domination number (FRDN) which was written as ${ F}_{\gamma r}\left(G\right)$.

Definition 7.

A modified fuzzy labelling (MFL) graph, $\left|V\right|\ne \varnothing ,$ σ be a function from V to [0, 1] and μ ranges from $VXV$ to [0, 1] so that $\mu \left(u,y\right)<max\left\{\sigma \left(u\right),\sigma \left(y\right)\right\}$ and it is written as ${FA}_m\left(G\right)$.

Definition 8.

A modified fuzzy antimagic labelling graph (MFAL), $\left|V\right|=\varnothing$, σ is a function from $V$ to [0, 1] and function μ that ranges from $VXV$ to [0, 1]. If the collection of edge or node weights is ${FA}_m\left(W\right)=\left\{w_t\left(x\right)\right\}=\left\{az,\left(a+d\right)z,\dots \right\}$, are distinct for some integers a and d, where a is the minimum edge or vertex weight and d is the difference between the every edge or vertex weight then it is known as a modified fuzzy antimagic labelling graph.

Definition 9.

Consider fuzzy graph, if the modified representations of all the elements in σ − H with regard to are all distinct, a proper subset of H of σ, $2\le \left|H\right|\le n-1$ is known as the MFRS of G. The modified fuzzy resolving number (MFRN) of G denoted as ${Fr}_m\left(G\right)$.

Definition 10.

The fuzzy modified graceful labelling graph whose memberships value of a vertex is represented $\sigma \left(x\right)=\sum \mu (E\left(e)\right),$ then,  $\mu \left(u,y\right)<max\left\{\sigma \left(u\right),\sigma \left(y\right)\right\}$, and it is denoted as ${FG}_m\left(G\right)$.

3. Independent Fuzzy Resolving Set (IFRS)

The subset $F$ is called an independent FRS if $F$ is an FRS and also an independent set. The minimal cardinality of $F$ is known as an independent FRN, which can be written as $FIr\left(G\right)$.

Let $F$ be an independent fuzzy super resolving set FSRS if $F$ is an independent set and also an FSRS. The lowest size of $F$ is regarded as an independent FSRN which can be written as $SIr\left(G\right)$.

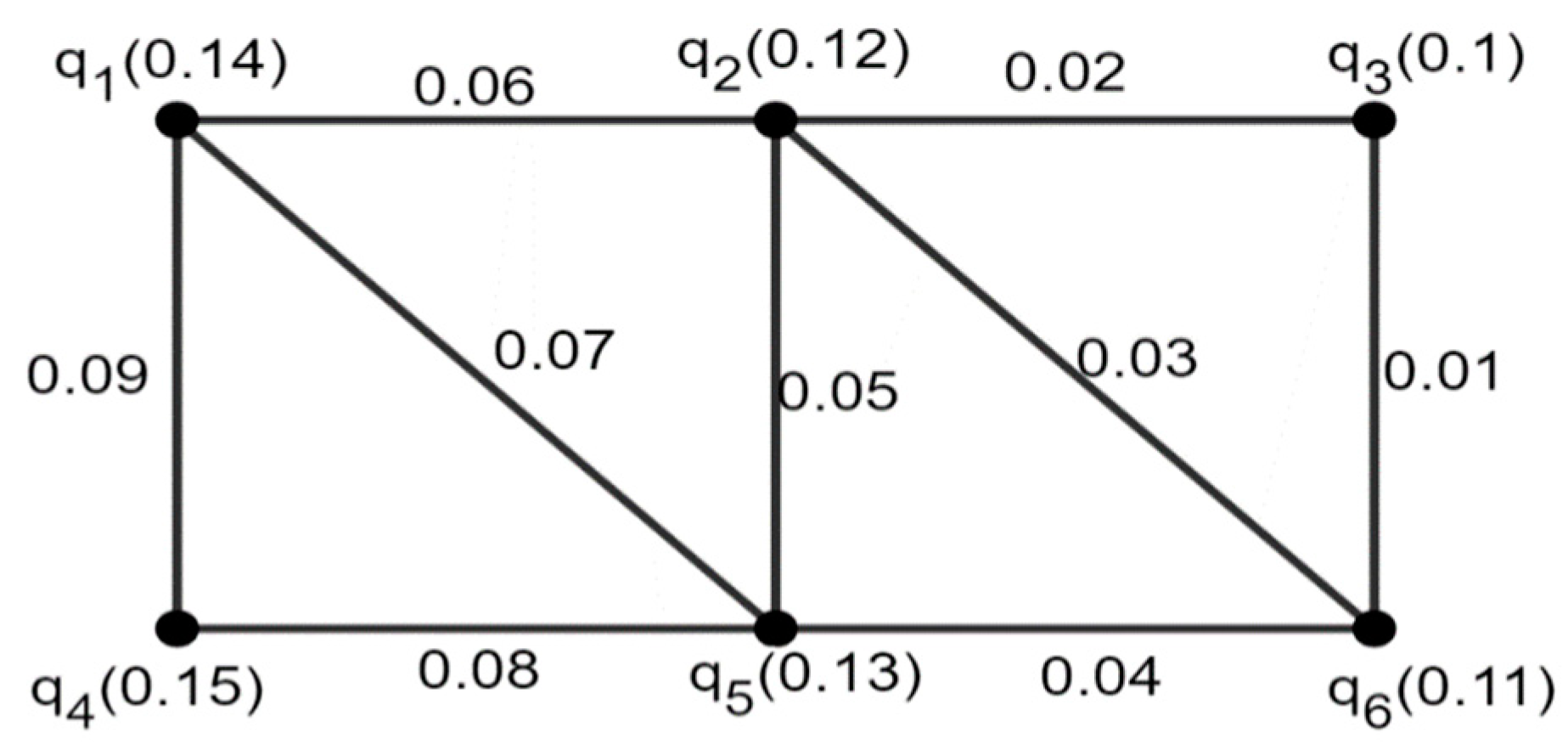
3.1. Theorem: On $K_{n,n}$ Fuzzy Graph, $FIr\left(G\right)\le n$

Proof. 

(i) Consider $FIr\left(G\right)>n$, then at least one or more pairs of vertices are adjacent which leads to a contradiction in the definition of Independent sets. Hence, $FIr\left(G\right)$ cannot be greater than $n$.

(ii)

Consider $FIr\left(G\right)<n$, then there is a possibility that all the vertices are not adjacent to each other and also an FRS. Hence, $FIr\left(G\right)<n$.

(iii)

If, $FIr\left(G\right)=n$, then there is an equal chance that not all the vertices are adjacent to each other. We can find an independent set and FRS using a strong arc. Hence, $FIr\left(G\right)=n$ completes the observation. □

3.2. Theorem: If $G$ Is a CFG, Then, $FIr\left(G\right)$ Does Not Exist

Proof. 

Consider $G$ is a CFG and $F$ is an IFRS, then by the definition of CFG, all the vertices are connected internally. If we find $V-F$, then all the vertices in the set are connected by a pair of edges. This gives us no chance to find the independent set in a CFG. Hence, $FIr\left(G\right)$ does not exist. □

3.3. Theorem: An Union of Two IFRS Need Not Be an IFRS But an Intersection of Two IFRS May Be an IFRS

Proof. 

Let any two IFRSs of an FG $\mathrm{G}$ have a cardinality $\mathrm{n}\ge 3.$ The union of both these sets may include adjacent vertices or not which implies that the union of two IFRSs need not to be an independent set. Similarly, the intersection of two IFRSs can be an independent set with respect to the FRS. □

3.4. Remark

For every IFRS, it is true that $Fr\left(G\right)\le FIr\left(G\right).$

3.5. Theorem: Every $Fr\left(G\right)$ Does Not Have to Be a $FIr\left(G\right)$ But Every $FIr\left(G\right)$ Is $Fr\left(G\right)$

Proof. 

The obtained FRS may or may not be a fuzzy independent set, so it is not obvious to say that every FRS is also an IFRS. However, by the definition of IFRS, it is obvious that every IFRS is also an FRS. Hence, every FRS does not have to be an IFRS. □

3.6. Discussion

For every simple connected fuzzy graph, 2$\le FIr\left(G\right)\le n-1.$

4. Independent Fuzzy Resolving Domination Set (IFRDS)

Authors should discuss the results and how they can be interpreted from the perspective of previous studies and on the working hypotheses. The findings and their implications should be discussed in the broadest context possible. Future research directions may also be highlighted.

Let $F$ be a subset of $G$ and $F$ be an FRDS and also an independent set, then $F$ is represented IFRDS and the lowest size of $F$ is known as a fuzzy resolving independent domination number (IFRDN) which is written as ${FI}_{\gamma r}\left(G\right).$

4.1. Theorem: If $G$ Is a CFG, Then, ${ FI}_{\gamma r}\left(G\right)$ Does Not Exist

Proof. 

Consider $G$ is a CFG and $F$ is an IFRDS, then by the definition of CFG, all the vertices are connected internally. If we find $V-F$, then all the vertices in the set are connected by a pair of edges. This gives us no chance to find the independent set in a CFG. Hence, ${FI}_{\gamma r}\left(G\right)$ does not exist. □

4.2. Theorem: An IFRDS Is Always an FRDS But FRDS Need Not Have to Be an IFRDS

Proof. 

Let $H=\{{\sigma }_1,{\sigma }_2,\dots {\sigma }_l$} be an FRDS and, here, $l$ is the FRDN of $G$ since $l$ is the lowest size of $H.$ Similarly, we can obtain different resolving dominating subsets containing the vertices of $G$ and the FRDN will be different according to each subset of $G$. The independent set of all these resolving subsets might or might not be the same for resolving domination subsets of the same graph $G$. Hence, FRDS need not be an IFRDS of $G$. □

Now, let $H$ be an IFRDS of $G$. It is clear to observe that the subset of a resolving FG can have the same independent resolving domination subsets. Hence, the IFRDS and FRDS of $G$ are same.

4.3. Theorem: Consider $\mathrm{G}$ as a Star FG and If μ Is Not Constant for All the Nodes, Then, IFRDS Exists and ${FI}_{\gamma r}\left(G\right)=$ 2

Proof. 

Consider that $G$ is a star FG from which all the nodes are powerful. Additionally, since $\mu$ is not constant, every edge has a separate membership value. It is obvious that an independent FDS can be obtained with the size of two. Considering that each representations values are unique, we can also discover an FRS. Hence, an IFRDN is ${FI}_{\gamma r}\left(G\right)=2$. □

4.4. Theorem: The Union and Intersection of Two IFRDS May Not Be an IFRDS

Proof. 

Let $R_1=\{u,v\}$ and $R_2=\left\{w,x\right\}$ be the two independent fuzzy resolving domination sets with respect to $G$ which states that they are both FRS and FDS, respectively. However, the combination of these both sets may or may not be independent sets similarly for intersection. Hence, ${ R}_1\cup R_2$ and $R_1\cap R_2$ is need not be an IFRDS. □

4.5. Discussion

For every simple connected fuzzy graph, 2$\le {FI}_{\gamma r}\left(G\right)\le n-1.$

5. Fuzzy Modified Labelling Resolving Set

Considering the ordered fuzzy, odified labelling subset $S=\{\left(u_1,\sigma \left(u_1\right)\right),\left(u_2,\sigma \left(u_2\right)\right),\dots ,\left(u_k,\sigma \left(u_k\right)\right)\},$ |S| ≥ 2 and (z, σ(z)$)\in \sigma -S=\left\{\left(u_{k+1},{\sigma (u}_{k+1}\right)\right),(u_{k+2},{\sigma (u}_{k+2}\left)\right),\dots ,(u_n,{\sigma (u}_n)\left)\right\}$ and $\left\{W\left(z,u_1\right),W\left(z,u_2\right),\dots W\left(z,u_k\right)\right\},$ the set is said to be FMLRS. The FMLRN is expressed as $F_{mr}\left(G\right)$, S and is known as the FSRS of the modified if every two elements have unique representations with regard to S. The minimum cardinality is said to be the FSRN of $G$, which is denoted as ${FS}_r\left(G\right)$.

5.1. Fuzzy Modified Antimagic Lableling Resolving Set

Figure 1 shows a fuzzy modified antimagic triangular ladder graph.

The connectedness matrix for the above graph is,

$$\left|\begin{array}{cccccc}-& 0.06& 0.02& 0.09& 0.08& 0.04\\ 0.06& -& 0.02& 0.06& 0.06& 0.04\\ 0.02& 0.02& -& 0.02& 0.02& 0.02\\ 0.09& 0.06& 0.02& -& 0.08& 0.04\\ 0.08& 0.06& 0.02& 0.08& -& 0.04\\ 0.04& 0.04& 0.02& 0.04& 0.04& -\end{array}\right|$$

$$H_1=\left\{q_1,q_2\right\}, then \sigma -H_1=\{q_3,q_4,q_5,q_6\}$$

$$H_1/q_3=\left\{\mu \left(q_1,q_3\right),\mu (q_2,q_3)\right\}=(0.02,0.02)$$

$$H_1{/q}_4=\left(\mathrm{0.09,0.06}\right)$$

$$H_1{/q}_5=\left(\mathrm{0.08,0.06}\right)$$

$$H_1{/q}_6=\left(\mathrm{0.04,0.04}\right)$$

$$\mathrm{FRS}=\left\{\left\{q_1,q_2\right\},\left\{q_3,q_4\right\},\left\{q_4,q_5\right\},\left\{q_1,q_3\right\},\left\{q_1,q_4\right\}\right\},\left\{q_1,q_5\right\},\left\{q_1,q_6\right\},\left\{q_2,q_4\right\},\left\{q_4,q_6\right\}.$$

For this graph, $Fr\left(G\right)$ = 2.

Fuzzy independent resolving set = $\left\{\left\{q_3,q_4\right\},\left\{q_1,q_3\right\},\left\{q_1,q_6\right\},\left\{q_2,q_4\right\},\left\{q_4,q_6\right\}\right\}$.

$$FIr\left(G\right)=2$$

5.1.1. Theorem

Let FMA (G) with Vertex Set 4 and $G^{\mathrm{*}}$ be a cycle if μ is not fixed. Then, $F{A}_{mr}\left(G\right)$ = 2.

5.1.2. Result

σ − S does not necessarily need to be a resolving set of G if S is a resolving set of G in an FMA (G).

Every fuzzy modified antimagic graph has an FMARS of G, but FMARS does not need to be a fuzzy modified antimagic graph.

5.1.3. Theorem: The MFRN of G Is 2 If G Is an FMA Labelling Four Cycle

Proof. 

If G is a fuzzy modified antimagic labelling four cycles, then the modified fuzzy resolving set of cardinality 2 exists. As a result, the concept of the modified fuzzy resolving set, $F{A}_{mr}\left(G\right)=$ 2. □

5.2. Modified Fuzzy Graceful Lableling Resolving (FMGLR) Set

5.2.1. Lemma

A union of two MFGLR sets need not be an MFGIR set but an intersection of the two MFGIR sets can be an MFGR set.

Every MFGLRS $\left(G\right)$ does not have to be modified graceful independent fuzzy resolving (G) but every $\mathrm{M}\mathrm{F}\mathrm{G}\mathrm{I}\mathrm{R}\left(G\right)$ is MFGLR $\left(G\right)$.

5.2.2. Theorem: The Modified Fuzzy Graceful Resolving Number of G Is Two If G Is an FMG Labelling

Proof. 

Let G be fuzzy modified graceful labelling and then the modified fuzzy resolving set of cardinality two exists. As a result, the concept of the modified fuzzy resolving set is $F{A}_{mr}\left(G\right)=$ 2. □

5.2.3. Theorem: If H Is the Aconnected FRS of a Modified Fuzzy Graceful Labelling Graph G, Then H Is an FSRS of G

Proof. 

A bijection from the set of every vertex and edge of G to [0, 1] and ${\mu }^{\omega }$(u, v) < ${\sigma }^{\omega }$ (u) $\bigvee {\sigma }^{\omega }$ (v) exists by definition. Let H = {${\sigma }_1$, ${\sigma }_2$, … ${\sigma }_k$} represent G, which is an FRS, then each distinct representation of ${\sigma }_i$/H exists for i = r + 1, r + 2, … n. For i = 1, 2, … r, σ($v_i$) = ${\mu }^{\infty }$($v_i$, $v_i$) and are all distinct in a fuzzy labelling graph G. As a result, G is a fuzzy resolving set of H. □

5.2.4. Theorem: The Resolving Number of a Modified Fuzzy Graceful Labelling of the Wheel Graph Is ‘2’

Proof. 

Let G be a fuzzy labelling wheel graph and let the membership values of the edges be ${\gamma }_1$ > ${\gamma }_2$ > … > ${\gamma }_n$. Now, let $\mu (u,v)$ = ${\gamma }_1$ and $\mu (w,v)$ = ${\gamma }_2$ where $v$ is the centre node. Since $uv \mathrm{and} vw$ are the two edges with a maximum edge weight, any path from $u \mathrm{and} w$ together with vertices $v_i$ for $v_i$ ≠ $u,w$, have a membership value μ($v_i$, v), which are all distinct for a fuzzy graceful labelling graph. Additionally, therefore, the illustration of $\sigma -H$ in relation to $H=\left\{\right(u, \sigma \left(u\right)), (w, \sigma \left(w\right)\left)\right\}$ are all distinct. Hence, the fuzzy resolving number of the modified fuzzy graceful labelling wheel graph is ‘2’. □

Illustration:

The connected matrix of the modified fuzzy graceful labelling wheel graph:

$$\left[\begin{array}{ccc}\begin{array}{cc}-& 0.9\\ 0.9& -\end{array}& \begin{array}{cc}0.4& 0.4\\ 0.8& 0.5\end{array}& \begin{array}{cc}0.7& 0.9\\ 0.7& 1\end{array}\\ \begin{array}{cc}0.4& 0.8\\ 0.4& 0.5\end{array}& \begin{array}{cc}-& 0.5\\ 0.5& -\end{array}& \begin{array}{cc}0.7& 0.8\\ 0.5& 0.4\end{array}\\ \begin{array}{cc}0.7& 0.7\\ 0.9& 1\end{array}& \begin{array}{cc}0.7& 0.5\\ 0.8& 0.4\end{array}& \begin{array}{cc}-& 0.7\\ 0.7& -\end{array}\end{array}\right]$$

$$H_1=\left\{q_1,q_2\right\}, then \sigma -H_1=\{q_3,q_4,q_5,q_6\}$$

$$F{G}_{mr}\left(G\right)=2.$$

6. Application

Consider any social network with a multiple number of nodes and the links connecting them. Fuzzy graphs play a significant part in application-based challenges that arise in real life, although recent research has focused solely on application development [31,32]. The vertices represent the different social network units, and the edges represent the strength of the signal passing through them [33]. The vertex sets are chosen randomly and are checked for fuzzy the resolving set using a strong fuzzy arc. The obtained fuzzy resolving set is the set that is enough to provide signals to all the other networks. Domination is a key factor in determining which specific sets will be helpful in solving social network challenges. Moreover, resolving sets makes it possible to recognize a set’s unique qualities in comparison to all other vertices. We can then find the one and only set by combining these two sets; this is a more efficient method to address the issue [34,35]. With the IFRDS principle, we can locate an appropriate set in any network connection for further approaches. Additionally, if we consider the transport routes of many rural villages, we can easily identify the best route for using social service places like hospitals, schools, and municipalities using FRS. Similar to the dominance set, the Independence set is important when determining the non-adjacent vertices of the sets, which is useful in solving many social problems [36,37]. In order to find the different schools or hospitals which are not connected in the rural areas, we can use the independency method along with the domination set to find the best sets for the people who are living there long-term without any technological development. The combination of the above three sets enables us to obtain a convenient output for social network problems or social-related queries. We are also working on the programming of FRS in order to find the FRS sooner in case of large data in the large sense of social networks. It can also be used in data processing units which are useful for a future generation of people to identify particular sets to rule out their problems. It is difficult to identify the unique set in large networks with a membership value, and so it leads to a bigger evaluation of the FRS which may or may not be perfect. In addition to this, we can also find FDS, IFRDS and so on with the easy evaluation of FRS [38]. Additionally, in the medical field, the combination of different drugs can be evaluated using FRS or FRDS in order to find the mixture of some drugs which are useful for certain diseases. With the unique characteristics of all drugs, we can always find the best solution to cure the person with certain medical conditions. The application of FRS in real life offers a more substantial and practical means of finding a solution that is accurate. It can also be applied to transportation issues, and we are still exploring many applications that could be built on it. These days, social networks are large enough to encompass all other networks, and there are numerous ways to interact with them in a beneficial way. We can also break up large amounts of data into smaller chunks, as in a hypergraph, and then use those segments to quickly retrieve the specific solution to a given issue. Even if the problem is more complicated, we can utilize coding or other mathematical programming to obtain the answers, which could be a very effective way to obtain the right answer. In control mechanics, many research papers are developed with fuzzy logic as they are very efficient for use in a dynamic way. We can easily design the electronic device by loops and formulate the problem using fuzzy logic and proceed with FRS. In terms of applications, fuzzy graphs cover real-life problems, and it is a more significant way to process problems. Nowadays, there are many methods to solve real-life problems using graph theory, fuzzy logic, intuitionistic sets, modelling, neutrosophic sets, etc.

7. Conclusions

In this paper, IFRDS, IFRS, and FMARS of FG have been discussed, as well as the properties based on them. A number of real-world issues are significantly impacted by the use of FRDS, and this also aids in choosing a precise set that can be useful for the issue and provide an ideal remedy. We hope to look into more facets of FRS in the future.