A New Efficient Method for Absolute Value Equations

Abstract

In this paper, the two-step method is considered with the generalized Newton method as a predictor step. The three-point Newton–Cotes formula is taken as a corrector step. The proposed method’s convergence is discussed in detail. This method is very simple and therefore very effective for solving large systems. In numerical analysis, we consider a beam equation, transform it into a system of absolute value equations and then use the proposed method to solve it. Numerical experiments show that our method is very accurate and faster than already existing methods.

1. Introduction

Suppose an AVE of the form

$$Ax-\left|x\right|=b,$$

(1)

where $A\in {\mathbb{R}}^{n\times n}$, $x,b\in {\mathbb{R}}^n$ and $\left|·\right|$ represents an absolute value. The AVE

$$Ax+B\left|x\right|=b$$

(2)

is the generalized form of Equation (1) for $B\in {\mathbb{R}}^{n\times n}$, which was first presented by Rohn [1]. The AVE Equation (1) has many applications in pure and applied sciences [2]. It is difficult to find the exact solution of Equation (1) because of the absolute values of x. For some works on this aspect, we refer to [3,4,5]. Many iterative methods were proposed to study the AVE Equation (1), for example [6,7,8,9,10,11,12,13,14,15].

Nowadays, the two-step techniques are very poplar for solving AVE Equation (1). Liu [16,17] presented two-step iterative methods to solve AVEs. Khan et al. [18] have suggested a new method based on a generalized Newton’s technique and Simpson’s rule for solving AVEs. Shi et al. [19] have developed a two-step Newton-type method with linear convergence for AVEs. Noor et al. [20] have suggested minimization techniques for AVEs and discussed the convergence of these techniques under some suitable conditions. In [21], the two-step Gauss quadrature method was suggested for solving AVEs. When the coefficient matrix A in the AVE Equation (1) has the Toeplitz structure, Gu et al. [22] suggested the nonlinear CSCS-like method and the Picard–CSCS method for solving this problem.

In this paper, the Newton–Cotes open method along with the generalized Newton technique [23] is suggested to solve Equation (1). This new method is straightforward and very effective. The proposed method’s convergence is proved under the condition that $\parallel A^{-1}\parallel <\frac{1}{10}$ in Section 3. To prove the effectiveness, we consider several examples in Section 4. The main aim of this new method is to obtain the solution of (1) in a few iterations with good accuracy. This new method successfully solves large systems of AVEs. In most cases, this new method requires just one iteration to find the approximate solution of Equation (1) with accuracy up to ${10}^{-13}$. The following notations are used. Let $sign\left(x\right)$ be a vector with entries $1,0,-1$, based on the associated entries of x. The generalized Jacobian $\sigma \left|x\right|$ of $\left|x\right|$ based on a subgradient [24,25] of the entries of $\left|x\right|$ is the diagonal matrix D given by

$$D\left(x\right)=\sigma \left|x\right|=diag\left(sign\left(x\right)\right).$$

(3)

$svd\left(A\right)$ denotes the n singular values of A, $\parallel A\parallel ={\left(\lambda \right)}^{\frac{1}{2}}$ represents the 2-norm of A and $\lambda$ is the maximum eigenvalue of $A^{T}A$ in absolute. $\parallel x\parallel =\sqrt{(x^T,x)}$ is the 2-norm of the vector x; for more detail, see [26].

2. Proposed Method

We develop a new two-step (NTS) method for AVE Equation (1) in this section. Let

$$J\left(x\right)=Ax-\left|x\right|-b.$$

(4)

Then, $J^{\prime }\left(x\right)$ is given by:

$$J^{\prime }\left(x\right)=\sigma \left(J\left(x\right)\right)=A-D\left(x\right).$$

(5)

Consider the predictor step as:

$${\gamma }^k={\left(A-D\left(x^k\right)\right)}^{-1}b.$$

(6)

Let v be the solution of Equation (1). To construct the corrector step, we proceed as follows:

$${\int }_u^v{J}^{\prime }\left(x\right)dx=J\left(v\right)-J\left(u\right)=-J\left(u\right).$$

(7)

Now, using the three-point Newton–Cotes formula, we have

$${\int }_u^v{J}^{\prime }\left(x\right)dx=\frac{1}{3}\left[2J^{\prime }\left(\frac{3u+v}{4}\right)-J^{\prime }\left(\frac{u+v}{2}\right)+2J^{\prime }\left(\frac{u+3v}{4}\right)\right](v-u).$$

(8)

From Equations (7) and (8), we have

$$-J\left(u\right)=\frac{1}{3}\left[2J^{\prime }\left(\frac{3u+v}{4}\right)-J^{\prime }\left(\frac{u+v}{2}\right)+2J^{\prime }\left(\frac{u+3v}{4}\right)\right](v-u).$$

(9)

Thus,

$$v=u-3{\left[2J^{\prime }\left(\frac{3u+v}{4}\right)-J^{\prime }\left(\frac{u+v}{2}\right)+2J^{\prime }\left(\frac{u+3v}{4}\right)\right]}^{-1}J\left(u\right).$$

(10)

From Equation (10), the NTS method can be written as (Algorithm 1):

Algorithm 1: NTS Method

1: Choose $x^0\in {\mathbb{R}}^n$. 2: For k, calculate ${\gamma }^k={\left(A-D\left(x^k\right)\right)}^{-1}b.$ 3: Using Step 2, calculate $x^{k+1}=x^k-3{\left[2J^{\prime }\left(\frac{3x^k+{\gamma }^k}{4}\right)-J^{\prime }\left(\frac{x^k+{\gamma }^k}{2}\right)+2J^{\prime }\left(\frac{x^k+3{\gamma }^k}{4}\right)\right]}^{-1}J\left(x^k\right).$ 4: If $\left|\left|x^{k+1}-x^k\right|\right|<tol$, then stop. Otherwise, go to step 2.

3. Convergence

Now, we examine the convergence of the NTS method. The predictor step

$${\gamma }^k={\left(A-D\left(x^k\right)\right)}^{-1}b$$

(11)

is well defined; see Lemma 2 [23]. To prove that

$$2J^{\prime }\left(\frac{3x^k+{\gamma }^k}{4}\right)-J^{\prime }\left(\frac{x^k+{\gamma }^k}{2}\right)+2J^{\prime }\left(\frac{x^k+3{\gamma }^k}{4}\right)$$

(12)

is nonsingular, first we consider

$${\varphi }^k=\frac{3x^k+{\gamma }^k}{4},{\delta }^k=\frac{x^k+{\gamma }^k}{2},{\tau }^k=\frac{x^k+3{\gamma }^k}{4}.$$

(13)

Now

$$\begin{array}{cc}\hfill & 2J^{\prime }\left(\frac{3x^k+{\gamma }^k}{4}\right)-J^{\prime }\left(\frac{x^k+{\gamma }^k}{2}\right)+2J^{\prime }\left(\frac{x^k+3{\gamma }^k}{4}\right)\hfill \\ \hfill =& 2A-2D\left(\frac{3x^k+{\gamma }^k}{4}\right)-A+D\left(\frac{x^k+{\gamma }^k}{2}\right)+2A-D\left(\frac{x^k+3{\gamma }^k}{4}\right)\hfill \\ \hfill =& 3A-2D\left({\varphi }^k\right)+D\left({\delta }^k\right)-2D\left({\tau }^k\right),\hfill \end{array}$$

where $D\left({\varphi }^k\right)$, $D\left({\delta }^k\right)$ and $D\left({\tau }^k\right)$ are diagonal matrices defined in Equation (3).

Lemma 1.

If $svd\left(A\right)>1$, then ${\left(3A-2D\left({\varphi }^k\right)+D\left({\delta }^k\right)-2D\left({\tau }^k\right)\right)}^{-1}$ exists for any diagonal matrix D defined in Equation (3).

Proof. 

If $3A-2D\left({\varphi }^k\right)+D\left({\delta }^k\right)-2D\left({\tau }^k\right)$ is singular, then

$$\left(3A-2D\left({\varphi }^k\right)+D\left({\delta }^k\right)-2D\left({\tau }^k\right)\right)u=0$$

(14)

for some $u\ne 0$. As $svd\left(A\right)>1$, therefore, using Lemma 1 [23], we have

$$\begin{array}{cc}\hfill u^{T}u<u^T{A}^{T}Au=& \frac{1}{9}{u}^T\left(\left(2D\left({\varphi }^k\right)-D\left({\delta }^k\right)+2D\left({\tau }^k\right)\right)\left(2D\left({\varphi }^k\right)-D\left({\delta }^k\right)+2D\left({\tau }^k\right)\right)\right)u\hfill \\ \hfill =& \frac{1}{9}{u}^T\left(4D\left({\varphi }^k\right)D\left({\varphi }^k\right)-4D\left({\varphi }^k\right)D\left({\delta }^k\right)+8D\left({\varphi }^k\right)D\left({\tau }^k\right)+D\left({\delta }^k\right)D\left({\delta }^k\right)\right.\hfill \\ \hfill & \left.-4D\left({\delta }^k\right)D\left({\tau }^k\right)+4D\left({\tau }^k\right)D\left({\tau }^k\right)\right)u\hfill \\ \hfill \le & \frac{1}{9}{u}^T\left(9\right)u\hfill \\ \hfill =& u^{T}u,\hfill \end{array}$$

which is a contradiction, hence $3A-2D\left({\varphi }^k\right)+D\left({\delta }^k\right)-2D\left({\tau }^k\right)$ is nonsingular.   □

Lemma 2.

If $svd\left(A\right)>1$, then the sequence of the NTS method is well defined and bounded with an accumulation point $\tilde{x}$ such that

$$\tilde{x}=\tilde{x}-3{\left(2J^{\prime }\left({\varphi }^k\right)-J^{\prime }\left({\delta }^k\right)+2J^{\prime }\left({\tau }^k\right)\right)}^{-1}J\left(\tilde{x}\right),$$

(15)

or it is equivalent to

$$\left(2J^{\prime }\left({\varphi }^k\right)-J^{\prime }\left({\delta }^k\right)+2J^{\prime }\left({\tau }^k\right)\right)\tilde{x}=\left(2J^{\prime }\left({\varphi }^k\right)-J^{\prime }\left({\delta }^k\right)+2J^{\prime }\left({\tau }^k\right)\right)\tilde{x}-3J\left(\tilde{x}\right).$$

(16)

Hence, there exists an accumulation point $\tilde{x}$ with

$$\left(A-\tilde{D}\left(\tilde{x}\right)\right)\tilde{x}=b,$$

(17)

for some diagonal matrix $\tilde{D}$ whose diagonal entries are 0 or $\pm 1$ depending on whether the corresponding component of $\tilde{x}$ is zero, positive, or negative as defined in (3).

Proof. 

The proof is the same as given in [23]. Thus, it is skipped.   □

Theorem 1.

If $\left|\left|{\left(2J^{\prime }\left({\varphi }^k\right)-J^{\prime }\left({\delta }^k\right)+2J^{\prime }\left({\tau }^k\right)\right)}^{-1}\right|\right|<\frac{1}{9}$, then the NTS method converges to a solution v of Equation (1).

Proof. 

Consider

$$\begin{array}{cc}\hfill x^{k+1}-v& =x^k-3{\left(2J^{\prime }\left({\varphi }^k\right)-J^{\prime }\left({\delta }^k\right)+2J^{\prime }\left({\tau }^k\right)\right)}^{-1}J\left(x^k\right)-v\hfill \\ \hfill & =x^k-v-3{\left(2J^{\prime }\left({\varphi }^k\right)-J^{\prime }\left({\delta }^k\right)+2J^{\prime }\left({\tau }^k\right)\right)}^{-1}J\left(x^k\right).\hfill \end{array}$$

It is seen that

$$\left(2J^{\prime }\left({\varphi }^k\right)-J^{\prime }\left({\delta }^k\right)+2J^{\prime }\left({\tau }^k\right)\right)\left(x^{k+1}-v\right)=\left(2J^{\prime }\left({\varphi }^k\right)-J^{\prime }\left({\delta }^k\right)+2J^{\prime }\left({\tau }^k\right)\right)\left(x^k-v\right)-3J\left(x^k\right).$$

(18)

As the solution to Equation (1) is v, therefore

$$J\left(v\right)=Av-\left|v\right|-b=0.$$

(19)

From Equations (18) and (19), we have

$$\begin{array}{cc}\hfill & \left(2J^{\prime }\left({\varphi }^k\right)-J^{\prime }\left({\delta }^k\right)+2J^{\prime }\left({\tau }^k\right)\right)\left(x^{k+1}-v\right)\hfill \\ \hfill =& \left(2J^{\prime }\left({\varphi }^k\right)-J^{\prime }\left({\delta }^k\right)+2J^{\prime }\left({\tau }^k\right)\right)\left(x^k-v\right)-3J\left(x^k\right)+3J\left(v\right)\hfill \\ \hfill =& \left(2J^{\prime }\left({\varphi }^k\right)-J^{\prime }\left({\delta }^k\right)+2J^{\prime }\left({\tau }^k\right)\right)\left(x^k-v\right)-3\left(J\left(x^k\right)-J\left(v\right)\right)\hfill \\ \hfill =& \left(2J^{\prime }\left({\varphi }^k\right)-J^{\prime }\left({\delta }^k\right)+2J^{\prime }\left({\tau }^k\right)\right)\left(x^k-v\right)-3\left(A{x}^k-\left|x^k\right|-Av+\left|v\right|\right)\hfill \\ \hfill =& \left(2J^{\prime }\left({\varphi }^k\right)-J^{\prime }\left({\delta }^k\right)+2J^{\prime }\left({\tau }^k\right)-3A\right)\left(x^k-v\right)+3\left(\left|x^k\right|-\left|v\right|\right)\hfill \\ \hfill =& \left(-2D\left({\varphi }^k\right)+D\left({\delta }^k\right)-2D\left({\tau }^k\right)\right)\left(x^k-v\right)+3\left(\left|x^k\right|-\left|v\right|\right).\hfill \end{array}$$

It follows that

$$\begin{array}{cc}\hfill x^{k+1}-v=& {\left(2J^{\prime }\left({\varphi }^k\right)-J^{\prime }\left({\delta }^k\right)+2J^{\prime }\left({\tau }^k\right)\right)}^{-1}\left[\left(-2D\left({\varphi }^k\right)+D\left({\delta }^k\right)-2D\left({\tau }^k\right)\right)\left(x^k-v\right)\right.\hfill \\ \hfill & \left.+3\left(\left|x^k\right|-\left|v\right|\right)\right].\hfill \end{array}$$

Thus, we know

$$\begin{array}{cc}\hfill \left|\left|x^{k+1}-v\right|\right|=& \left|\left|{\left(2J^{\prime }\left({\varphi }^k\right)-J^{\prime }\left({\delta }^k\right)+2J^{\prime }\left({\tau }^k\right)\right)}^{-1}\left[\left(-2D\left({\varphi }^k\right)+D\left({\delta }^k\right)-2D\left({\tau }^k\right)\right)\left(x^k-v\right)\right.\right.\right.\hfill \\ \hfill & \left.\left.\left.+3\left(\left|x^k\right|-\left|v\right|\right)\right]\right|\right|.\hfill \end{array}$$

This leads to

$$\begin{array}{cc}\hfill \left|\left|x^{k+1}-v\right|\right|\le & \left|\left|{\left(2J^{\prime }\left({\varphi }^k\right)-J^{\prime }\left({\delta }^k\right)+2J^{\prime }\left({\tau }^k\right)\right)}^{-1}\right|\right|\left|\left|\left[\left(-2D\left({\varphi }^k\right)+D\left({\delta }^k\right)-2D\left({\tau }^k\right)\right)\left(x^k-v\right)\right.\right.\right.\hfill \\ \hfill & \left.\left.\left.+3\left(\left|x^k\right|-\left|v\right|\right)\right]\right|\right|\hfill \\ \hfill \le & \left|\left|{\left(2J^{\prime }\left({\varphi }^k\right)-J^{\prime }\left({\delta }^k\right)+2J^{\prime }\left({\tau }^k\right)\right)}^{-1}\right|\right|\left[\left|\left|-2D\left({\varphi }^k\right)+D\left({\delta }^k\right)-2D\left({\tau }^k\right)\right|\right|\left|\left|x^k-v\right|\right|\right.\hfill \\ \hfill & \left.+3\left|\left|\left|x^k\right|-\left|v\right|\right|\right|\right].\hfill \end{array}$$

(20)

Since $D\left({\varphi }^k\right)$, $D\left({\delta }^k\right)$ and $D\left({\tau }^k\right)$ are diagonal matrices, therefore

$$\left|\left|-2D\left({\varphi }^k\right)+D\left({\delta }^k\right)-2D\left({\tau }^k\right)\right|\right|\le 3,$$

(21)

We also use the Lipchitz continuity (see Lemma 5 [23]), that is

$$\left|\left|\left|x^k\right|-\left|v\right|\right|\right|\le 2\left|\left|x^k-v\right|\right|.$$

(22)

From Equations (20)–(22), we have

$$\begin{array}{cc}\hfill \left|\left|x^{k+1}-v\right|\right|& \le ∥{\left(2J^{\prime }\left({\varphi }^k\right)-J^{\prime }\left({\delta }^k\right)+2J^{\prime }\left({\tau }^k\right)\right)}^{-1}∥\left[3∥x^k-v∥+6∥x^k-v∥\right]\hfill \\ \hfill & =9\left|\left|{\left(2J^{\prime }\left({\varphi }^k\right)-J^{\prime }\left({\delta }^k\right)+2J^{\prime }\left({\tau }^k\right)\right)}^{-1}\right|\right|\left|\left|x^k-v\right|\right|\hfill \\ \hfill & <\left|\left|x^k-v\right|\right|.\hfill \end{array}$$

(23)

In Equation (23), the supposition $\left|\left|{\left(2J^{\prime }\left({\varphi }^k\right)-J^{\prime }\left({\delta }^k\right)+2J^{\prime }\left({\tau }^k\right)\right)}^{-1}\right|\right|<\frac{1}{9}$ is used. Hence $x^k$ converges linearly to the solution of Equation (1).   □

Lemma 3.

Let $\left|\left|A^{-1}\right|\right|<\frac{1}{10}$ and $D\left({\varphi }^k\right)$, $D\left({\delta }^k\right)$, $D\left({\tau }^k\right)$ be non-zeros. Then, for any b, the NTS method converges to the unique solution of Equation (1) for any initial guess $x^0\in {\mathbb{R}}^n$.

Proof. 

Since $\left|\left|A^{-1}\right|\right|<\frac{1}{10}$, therefore, Equation (1) is uniquely solvable for any b see ([2], Proposition 4). Since $A^{-1}$ exists, therefore, by Lemma 2.3.2 [26], we have

$$\begin{array}{cc}\hfill & \left|\left|{\left(2J^{\prime }\left({\varphi }^k\right)-J^{\prime }\left({\delta }^k\right)+2J^{\prime }\left({\tau }^k\right)\right)}^{-1}\right|\right|\hfill \\ \hfill =& \left|\left|3A-2D\left({\tau }^k\right)+D\left({\delta }^k\right)-2D\left({\tau }^k\right)\right|\right|\hfill \\ \hfill \le & \frac{\left|\left|{\left(3A\right)}^{-1}\right|\right|\left|\left|-2D\left({\varphi }^k\right)+D\left({\delta }^k\right)-2D\left({\tau }^k\right)\right|\right|}{1-\left|\left|{\left(3A\right)}^{-1}\right|\right|\left|\left|-2D\left({\varphi }^k\right)+D\left({\delta }^k\right)-2D\left({\tau }^k\right)\right|\right|}\hfill \\ \hfill \le & \frac{\frac{1}{3}\left|\left|A^{-1}\right|\right|3}{1-\frac{1}{3}\left|\left|A^{-1}\right|\right|3}\hfill \\ \hfill <& \frac{\frac{1}{10}}{1-\frac{1}{10}}=\frac{1}{9}.\hfill \end{array}$$

Hence, by Theorem 1, the NTS method converges to the unique solution of Equation (1).   □

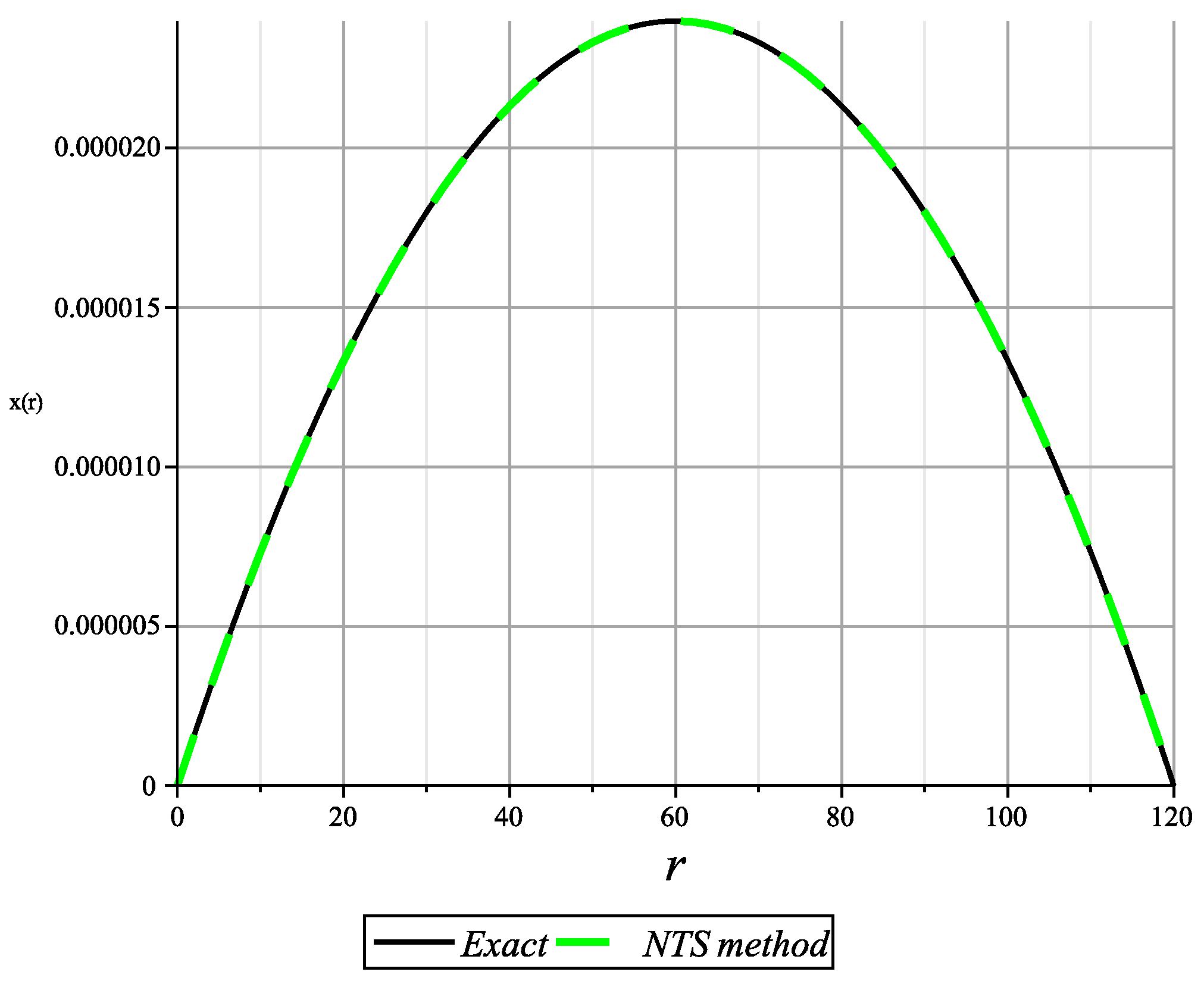
4. Numerical Result

In the section, several examples are taken to prove the efficiency of the suggested method. We use Matlab R2021a with a core (TM) i5@ 1.70 GHz. The CPU time in seconds, number of iterations and 2-norm of residuals are denoted by time, K and RES, respectively.

Example 1

([9]). Consider

$$A=tridiag\left(-1.5,4,-0.5\right)\in {\mathbb{R}}^{s\times s},x\in {\mathbb{R}}^{s}andb={\left(1,2,\cdots ,s\right)}^T.$$

(24)

A comparison of the NTS method with the MSOR-like method [9], generalized Newton method (GNM) [23] and RIM [11] is given in

Table 1. NTS method verses MSOR-like method and RIM.

Method	s	1000	2000	3000	4000	5000	6000
	K	24	25	25	25	25	25
RIM	CPU	7.084206	54.430295	150.798374	321.604186	581.212038	912.840059
	RES	7.6844 × 10${}^{-7}$	4.9891 × 10${}^{-7}$	6.3532 × 10${}^{-7}$	7.6121 × 10${}^{-7}$	8.8041 × 10${}^{-7}$	9.9454 × 10${}^{-7}$
	K	30	31	32	32	33	33
MSOR-Like	CPU	0.0067390	0.0095621	0.0215634	0.0541456	0.0570134	0.0791257
	RES	5.5241 × 10${}^{-7}$	7.0154 × 10${}^{-7}$	5.8684 × 10${}^{-7}$	9.0198 × 10${}^{-7}$	5.6562 × 10${}^{-7}$	7.4395 × 10${}^{-7}$
	K	5	5	5	5	5	5
GNM	CPU	0.0059651	0.007333	0.0115038	0.0330345	0.0551818	0.0783684
	RES	3.1777 × 10${}^{-10}$	7.8326 × 10${}^{-9}$	2.6922 × 10${}^{-10}$	3.7473 × 10${}^{-9}$	8.3891 × 10${}^{-9}$	5.8502 × 10${}^{-8}$
	K	1	1	1	1	1	2
NTS method	CPU	0.001816	0.003410	0.018771	0.0326425	0.031539	0.069252
	RES	9.6317 × 10${}^{-12}$	2.3697 × 10${}^{-11}$	4.1777 × 10${}^{-11}$	6.2756 × 10${}^{-11}$	8.20814 × 10${}^{-11}$	5.9998 × 10${}^{-11}$

.

Table 1 shows that the NTS method finds the solution of Equation (1) very quickly. The RES of the NTS method shows that the new method is more accurate than all the methods stated in Table 1.

Example 2

([16]). Consider

$$A=round(s\times (eye(s,s)-0.02\times (2\times rand(s,s)-1)\left)\right).$$

(25)

Choose a random $x\in {\mathbb{R}}^s$ and $b=Ax-\left|x\right|$.

We compare the NTS method with INM [7], the GQ method [21] and TSI [16] in

Table 2. Numerical results for Example 2.

Method	s	200	400	600	800	1000
	K	3	3	3	4	4
TSI	RES	7.6320 × 10${}^{-12}$	9.0622 × 10${}^{-12}$	1.9329 × 10${}^{-11}$	4.0817 × 10${}^{-11}$	7.1917 × 10${}^{-11}$
	CPU	0.031619	0.120520	0.32591	0.83649	1.00485
	K	3	3	3	4	4
INM	RES	2.1320 × 10${}^{-12}$	6.6512 × 10${}^{-12}$	3.0321 × 10${}^{-11}$	2.0629 × 10${}^{-11}$	8.0150 × 10${}^{-11}$
	CPU	0.012851	0.098124	0.156810	0.638421	1 0.982314
	K	2	2	2	2	2
GQ method	RES	2.1415 × 10${}^{-12}$	4.4320 × 10${}^{-12}$	1.0515 × 10${}^{-11}$	1.9235 × 10${}^{-11}$	2.8104 × 10${}^{-11}$
	CPU	0.013145	0.038734	0.162439	0.204578	0.276701
	K	1	1	1	1	2
NTS method	RES	1.0637 × 10${}^{-12}$	4.0165 × 10${}^{-12}$	1.0430 × 10${}^{-11}$	2.0644 × 10${}^{-11}$	2.1660 × 10${}^{-11}$
	CPU	0.012832	0.071124	0.153001	0.201356	0.274165

.

It is clear that the NTS method converges in one iteration in most cases. The other two methods require at least three iterations to find the solution of Equation (1) to achieve the given accuracy.

Example 3

([7]). Let

$$A=tridiag(-1,8,-1)\in {\mathbb{R}}^{s\times s},b=Ae-\left|e\right|fore={\left(-1,1,-1,\cdots ,\right)}^T\in {\mathbb{R}}^s,$$

(26)

where the initial vector is taken from [7].

We compare the NTS method with GGS [8], MGS [6] and Method II [7].

As seen in

Table 3. Comparison of NTS method with GGS, MGS and Method II.

Methods	s	1000	2000	3000	4000	5000
	K	11	11	11	11	11
GGS	RES	2.4156 × 10${}^{-9}$	2.7231 × 10${}^{-9}$	3.1872 × 10${}^{-9}$	3.2167 × 10${}^{-9}$	3.4538 × 10${}^{-9}$
	CPU	0.514656	1.045221	1.153442	1.843198	5.652411
	K	7	8	8	8	8
MGS	RES	6.7056 × 10${}^{-9}$	7.30285 × 10${}^{-10}$	7.6382 × 10${}^{-10}$	9.57640 × 10${}^{-10}$	8.52425 × 10${}^{-10}$
	CPU	0.215240	0.912429	0.916788	1.503518	4.514201
	K	6	6	6	6	6
Method II	RES	3.6218 × 10${}^{-8}$	5.1286 × 10${}^{-8}$	6.2720 × 10${}^{-8}$	7.2409 × 10${}^{-8}$	8.0154 × 10${}^{-8}$
	CPU	0.238352	0.541264	0.961534	1.453189	2.109724
	K	1	1	1	1	1
NTS method	RES	4.9774 × 10${}^{-15}$	7.0304 × 10${}^{-15}$	8.6069 × 10${}^{-15}$	9.9363 × 10${}^{-15}$	1.1107 × 10${}^{-14}$
	CPU	0.204974	0.321184	0.462869	0.819503	1.721235

, the suggested method approximates the solution of Equation (1) in just one iteration. The residual shows that the NTS method is very accurate.

Example 4.

Consider the beam equation of the form

$$\frac{d^{2}x}{d{r}^2}-\left|x\right|=\frac{Sx}{EM}-\frac{qr\left(r-L\right)}{2EM},$$

(27)

with boundary conditions

$$x\left(0\right)=0,x\left(L\right)=0,$$

(28)

where $L=120in.$ is the length of the beam, the modulus of elasticity $E=3\times {10}^{7}lb/in{.}^2$, the intensity of uniform load $q=100lb/ft$, the stress at the ends is 1000 lb and the central moment of inertia $M=625in{.}^4$.

We use FDM to discretize this equation. A comparison of the NTS method with the solution by Maple is illustrated in Figure 1.

Figure 1 shows the effectiveness and accuracy of the NTS method. Clearly, the deflection of the beam is maximum at the center.

Example 5

([20]). Consider an AVE of the form

$$a_{ii}=4s,a_{i,i+1}=a_{i+1,i}=s,a_{ij}=0.5,i=1,2,\cdots ,s.$$

(29)

Choose a constant vector b, and the initial guess is taken from [20]. A comparison of the NTS method with MM [20] and MMSGP [1] is presented in

Table 4. The numerical results for Example 5.

		MMSGP			MM			NTS Method
s	K	CPU	RES	K	CPU	RES	K	CPU	RES
2	24	0.005129	5.6800 × 10${}^{-7}$	2	0.029965	1.2079 × 10${}^{-12}$	1	0.0032321	1.7763 × 10${}^{-15}$
4	37	0.008701	9.7485 × 10${}^{-7}$	4	0.027864	5.5011 × 10${}^{-8}$	1	0.008621	3.5527 × 10${}^{-15}$
8	45	0.009217	5.5254 × 10${}^{-7}$	6	0.045387	6.9779 × 10${}^{-8}$	1	0.004120	2.9296 × 10${}^{-14}$
16	66	0.012458	5.8865 × 10${}^{-7}$	7	0.356930	2.0736 × 10${}^{-8}$	1	0.006156	8.4072 × 10${}^{-14}$
32	55	0.031597	8.2514 × 10${}^{-7}$	8	0.033277	4.9218 × 10${}^{-8}$	1	0.005108	2.1645 × 10${}^{-13}$
64	86	0.085621	7.6463 × 10${}^{-7}$	9	0.185753	9.0520 × 10${}^{-9}$	1	0.008120	1.0088 × 10${}^{-12}$
128	90	0.521056	6.3326 × 10${}^{-7}$	9	0.452394	1.7912 × 10${}^{-8}$	1	0.362162	2.2822 × 10${}^{-12}$

.

We observe that the NTS method is very successful for solving Equation (1). Furthermore, the NTS method is very consistent when n increases (large systems), whereas the other two methods need more iterations.

5. Conclusions

In this paper, we have used a two-step method for AVEs. In this new method, a three-point Newton–Cotes open formula is taken as a corrector step, while a generalized Newton method is taken as the predictor. The local convergence of the NTS method is proved in Section 2. Theorem 1 proves the linear convergence of the proposed method. A comparison shows that this method is very accurate and converges in just one iteration in most cases. This idea can be used to solve generalized AVEs and also to find all solutions of AVEs in the future.