Design of a Fixed-Time Stabilizer for Uncertain Chaotic Systems Subject to External Disturbances
Abstract
1. Introduction
- It designs a fixed-time controller for the stabilization of perturbed chaotic systems based on a new sliding mode surface.
- It suggests a method to determine a boundary for the fixed-time stability of uncertain chaotic systems with external disturbances that is independent of the initial conditions.
- It derives the required conditions to achieve the fixed-time stability.
2. Preliminaries and System Description
3. Sliding Surface and Controller Design
- constructing a suitable nonsingular terminal sliding surface.
- building a robust fixed-time control law to guarantee the existence of the sliding motion in a given setting time.
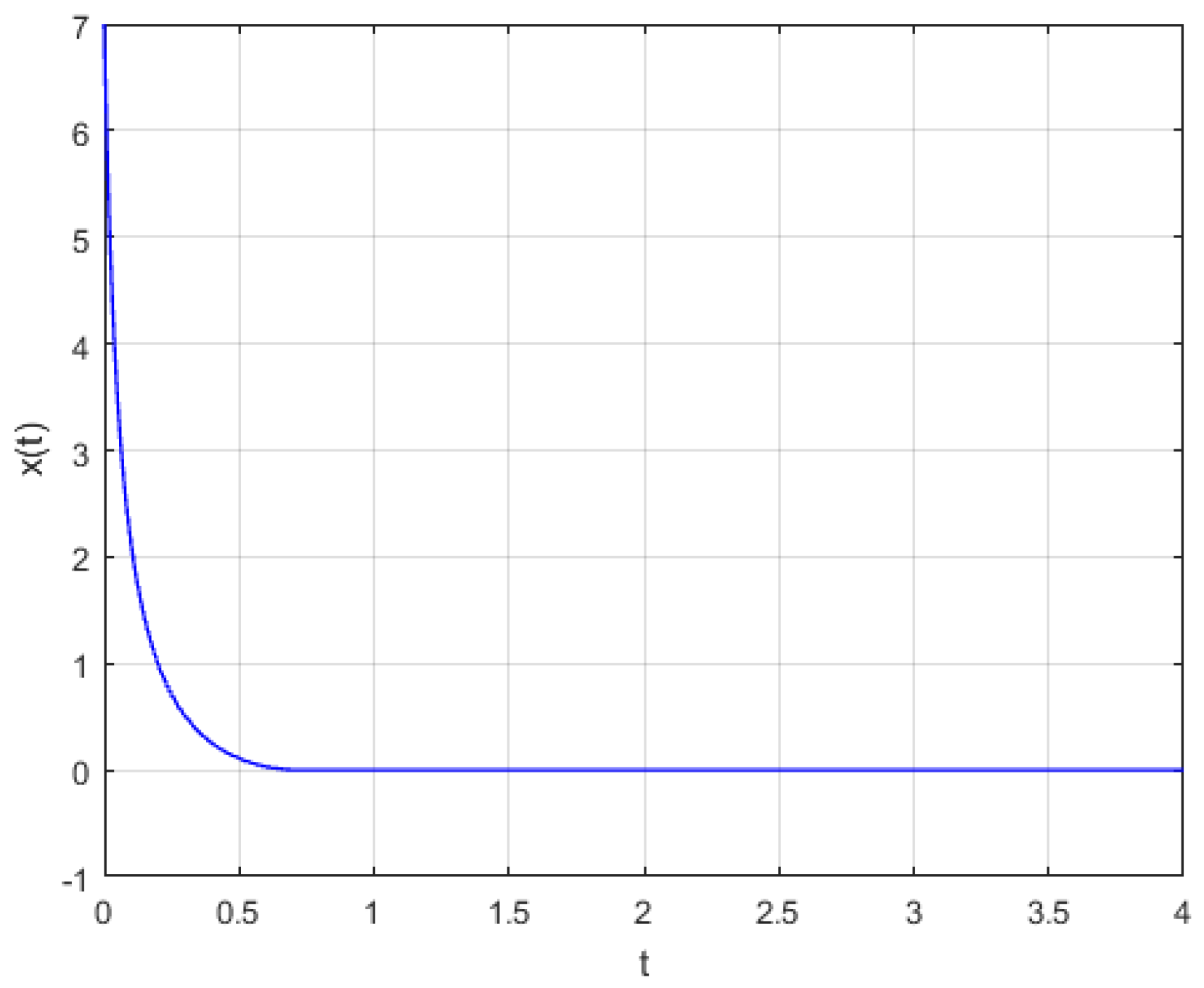
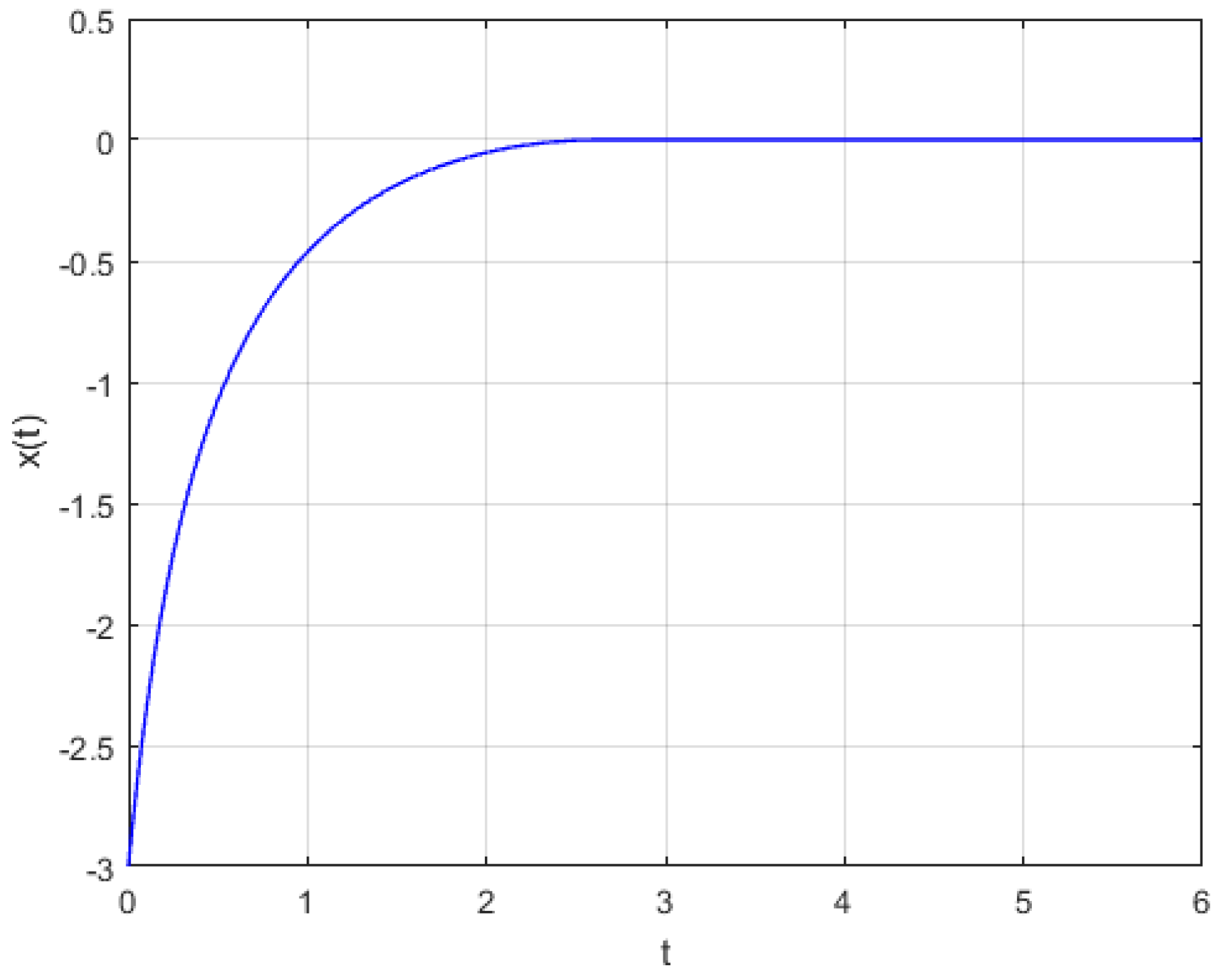
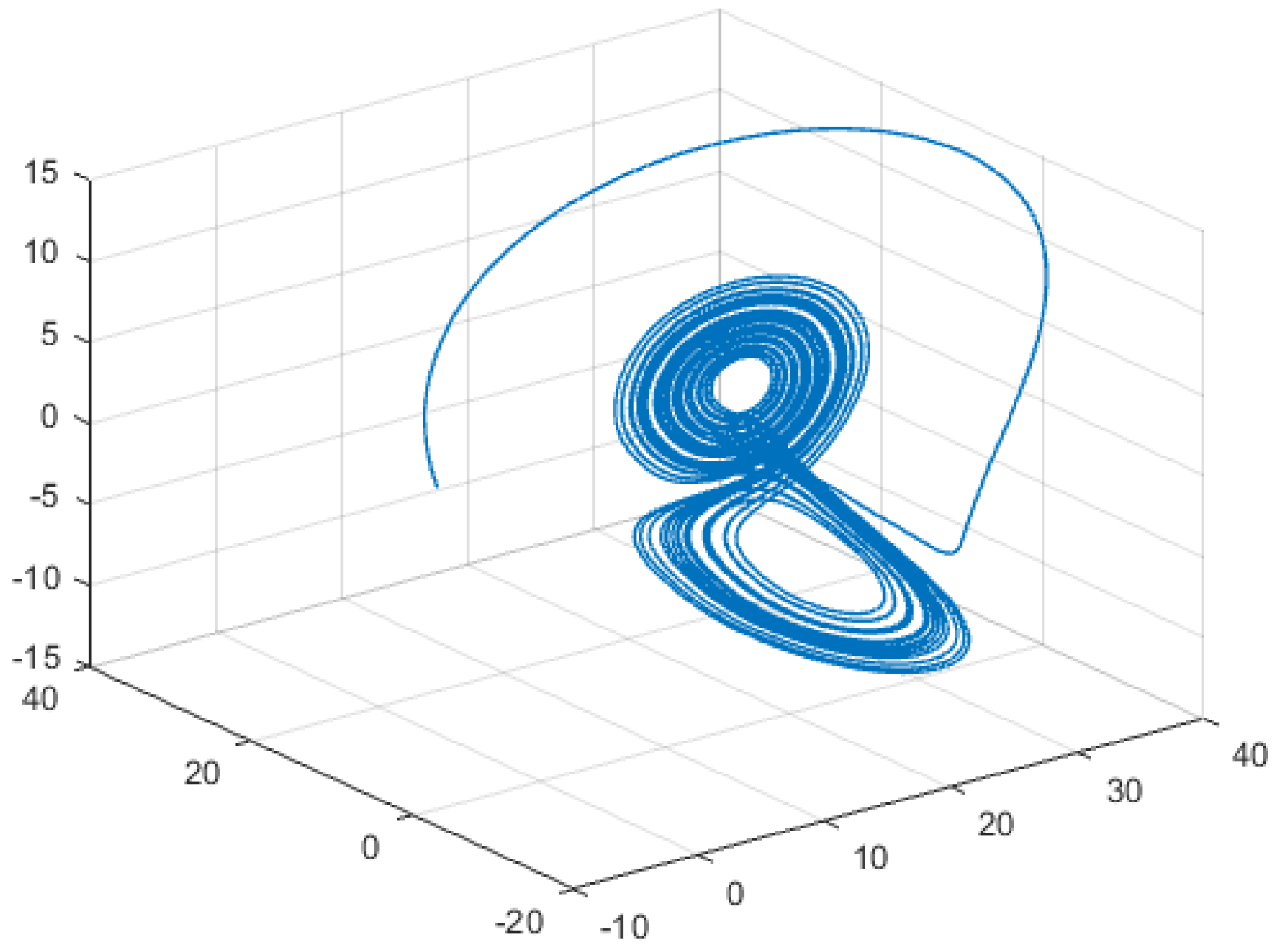
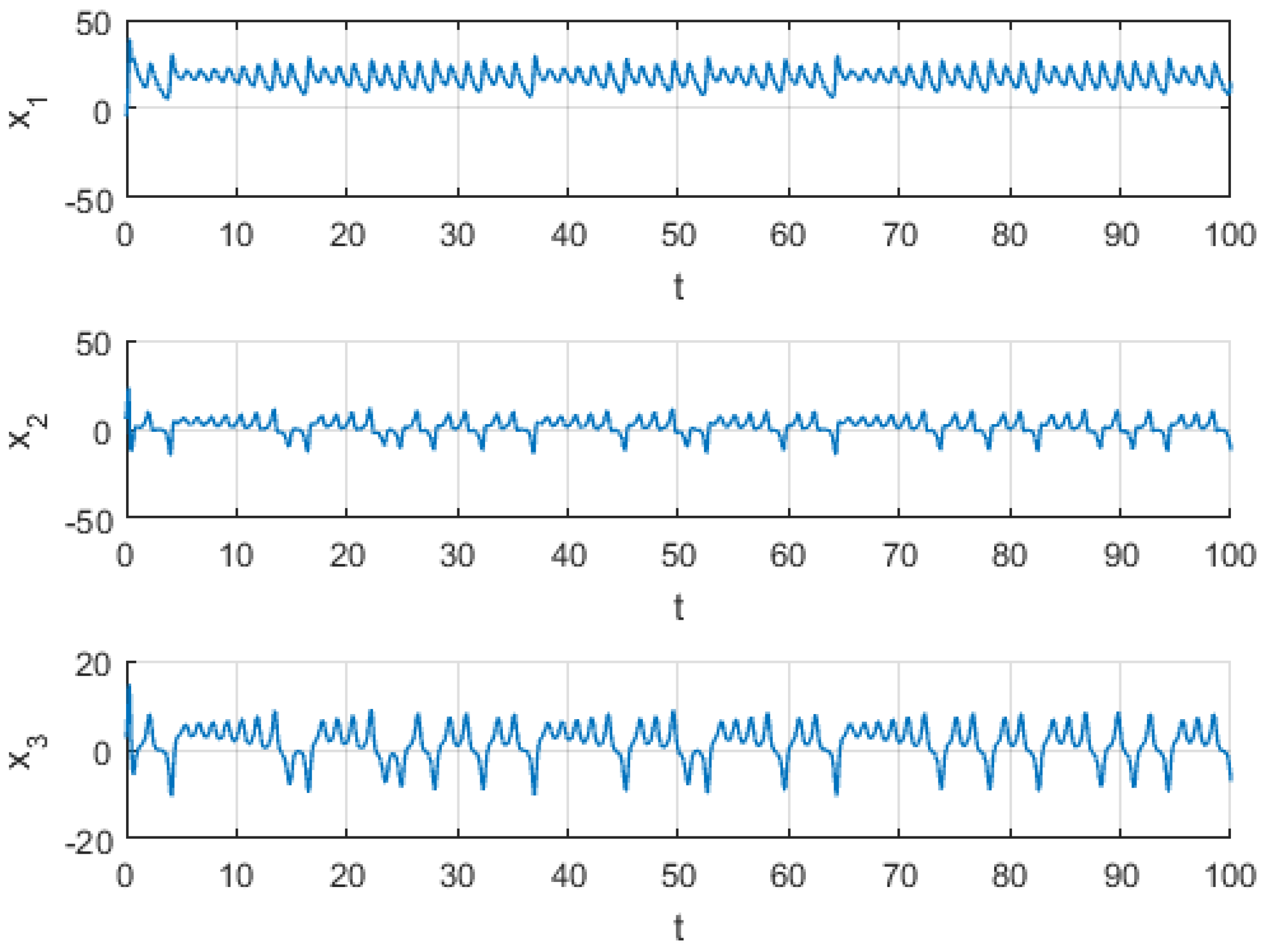
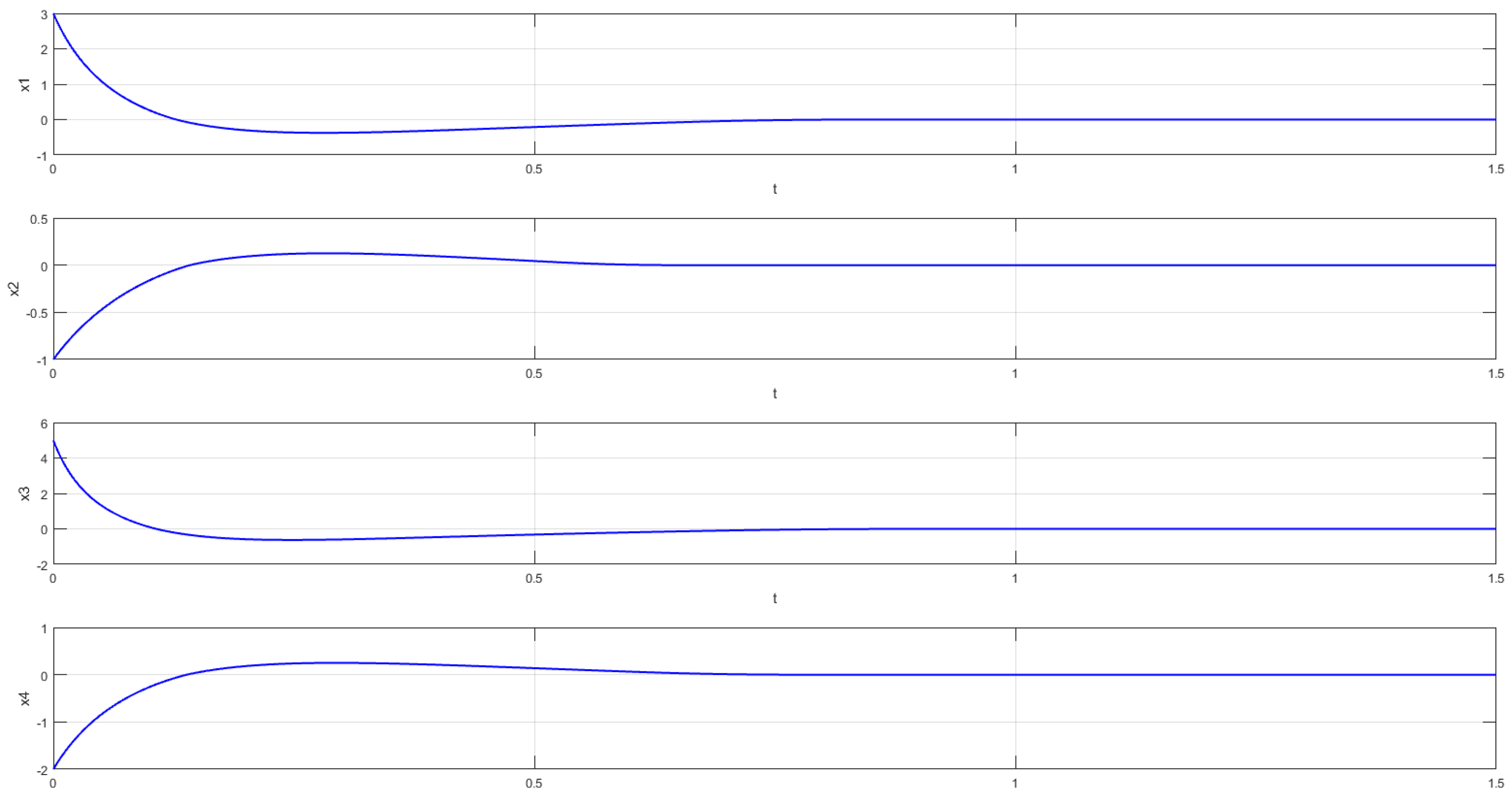
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mirrezapour, S.Z.; Zare, A.; Hallaji, M. A new fractional sliding mode controller based on nonlinear fractional-order proportional integral derivative controller structure to synchronize fractional-order chaotic systems with uncertainty and disturbances. J. Vib. Control 2022, 28, 773–785. [Google Scholar] [CrossRef]
- Jiang, X.; Xu, X.; Liang, C.; Liu, H.; Atindana, A.V. Robust controller design of a semi-active quasi-zero stiffness air suspension based on polynomial chaos expansion. J. Vib. Control 2023, 10775463231153706. [Google Scholar] [CrossRef]
- Xie, Z.; Sun, J.; Tang, Y.; Tang, X.; Simpson, O.; Sun, Y. A K-SVD Based Compressive Sensing Method for Visual Chaotic Image Encryption. Mathematics 2023, 11, 1658. [Google Scholar] [CrossRef]
- Sheng, Z.; Li, C.; Gao, Y.; Li, Z.; Chai, L. A Switchable Chaotic Oscillator with Multiscale Amplitude/Frequency Control. Mathematics 2023, 11, 618. [Google Scholar] [CrossRef]
- May, R.M. Deterministic models with chaotic dynamics. Nature 1975, 256, 165–166. [Google Scholar] [CrossRef]
- Ott, E.; Grebogi, C.; Yorke, J.A. Controlling chaos. Phys. Rev. Lett. 1990, 64, 1196–1199. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821–824. [Google Scholar] [CrossRef]
- Lin, W.; Qian, C. Adding one power integrator: A tool for global stabilization of high-order lower-triangular systems. Syst. Control. Lett. 2000, 39, 339–351. [Google Scholar] [CrossRef]
- Bernstein, S.P.; Bernstein, D.S. Finite-Time Stability of Continuous Autonomous Systems. SIAM J. Control. Optim. 2000, 38, 751–766. [Google Scholar]
- Aghababa, M.P.; Khanmohammadi, S.; Alizadeh, G. Finite-time synchronization of two different chaotic systems with unknown parameters via sliding mode technique. Appl. Math. Model. 2011, 35, 3080–3091. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear Feedback Design for Fixed-Time Stabilization of Linear Control Systems. IEEE Trans. Autom. Control 2012, 57, 2106–2110. [Google Scholar] [CrossRef]
- Polyakov, A.; Efimov, D.; Perruquetti, W. Finite-time and fixed-time stabilization: Implicit Lyapunov function approach. Automatica 2015, 51, 332–340. [Google Scholar] [CrossRef]
- Luo, R.; Zeng, Y. The control of chaotic systems with unknown parameters and external disturbance via backstepping-like scheme. Complexity 2016, 21, 573–583. [Google Scholar] [CrossRef]
- Shi, K.; Tang, Y.; Liu, X.; Zhong, S. Non-fragile sampled-data robust synchronization of uncertain delayed chaotic Lurie systems with randomly occurring controller gain fluctuation. ISA Trans. 2017, 66, 185–199. [Google Scholar] [CrossRef]
- Luo, R.; Su, H. Finite-time control and synchronization of a class of systems via the twisting controller. Chin. J. Phys. 2017, 55, 2199–2207. [Google Scholar] [CrossRef]
- Zhang, T.; Xia, M.; Yi, Y. Adaptive neural dynamic surface control of strict-feedback nonlinear systems with full state constraints and unmodeled dynamics. Automatica 2017, 81, 232–239. [Google Scholar] [CrossRef]
- Nafia, N.; El Kari, A.; Ayad, H.; Mjahed, M. Robust Interval Type-2 Fuzzy Sliding Mode Control Design for Robot Manipulators. Robotics 2018, 7, 40. [Google Scholar] [CrossRef]
- Matouk, A.E. Dynamics and control in a novel hyperchaotic system. Int. J. Dyn. Control 2019, 7, 241–255. [Google Scholar] [CrossRef]
- Kim, Y.; Oh, T.H.; Park, T.; Lee, J.M. Backstepping control integrated with Lyapunov-based model predictive control. J. Process Control 2019, 73, 137–146. [Google Scholar] [CrossRef]
- Rabiee, H.; Ataei, M.; Ekramian, M. Continuous nonsingular terminal sliding mode control based on adaptive sliding mode disturbance observer for uncertain nonlinear systems. Automatica 2019, 109, 108515. [Google Scholar] [CrossRef]
- Runzi, L.; Huang, M.; Su, H. Robust Control and Synchronization of 3-D Uncertain Fractional-Order Chaotic Systems with External Disturbances via Adding One Power Integrator Control. Complexity 2019, 2019, 8417536. [Google Scholar]
- Ma, H.; Liang, H.; Zhou, Q.; Ahn, C.K. Adaptive Dynamic Surface Control Design for Uncertain Nonlinear Strict-Feedback Systems With Unknown Control Direction and Disturbances. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 506–515. [Google Scholar] [CrossRef]
- Li, Z.W. Fixed-Time and Finite-Time Synchronization for a Class of Output-Coupling Complex Networks via Continuous Control. Int. J. Commun. Netw. Syst. Sci. 2019, 12, 151–169. [Google Scholar] [CrossRef]
- Yin, X.; She, J.; Liu, Z.; Wu, M.; Kaynak, O. Chaos suppression in speed control for permanent-magnet-synchronous-motor drive system. J. Frankl. Inst. 2020, 357, 13283–13303. [Google Scholar] [CrossRef]
- Rashidnejad, Z.; Karimaghaee, P. Synchronization of a class of uncertain chaotic systems utilizing a new finite-time fractional adaptive sliding mode control. Chaos Solitons Fractals X 2020, 5, 100042. [Google Scholar] [CrossRef]
- Chen, C.; Li, L.; Peng, H.; Yang, Y.; Mi, L.; Zhao, H. A new fixed-time stability theorem and its application to the fixed-time synchronization of neural networks. Neural Netw. 2020, 123, 412–419. [Google Scholar] [CrossRef]
- Su, H.; Luo, R.; Fu, J.; Huang, M. Fixed time stability of a class of chaotic systems with disturbances by using sliding mode control. ISA Trans. 2021, 118, 75–82. [Google Scholar] [CrossRef] [PubMed]
- Tong, D.; Xu, C.; Chen, Q.; Zhou, W. Sliding mode control of a class of nonlinear systems. J. Frankl. Inst. 2020, 357, 1560–1581. [Google Scholar] [CrossRef]
- Xiong, X.; Yang, X.; Cao, J.; Tang, R. Finite-time control for a class of hybrid systems via quantized intermittent control. Sci. China Inf. Sci. 2020, 63, 192201. [Google Scholar] [CrossRef]
- Shi, K.; Jun, w.; Zhong, S.; Tang, Y.; Cheng, J. Hybrid-driven finite-time H∞ sampling synchronization control for coupling memory complex networks with stochastic cyber attacks. Neurocomputing 2020, 387, 241–254. [Google Scholar] [CrossRef]
- Hua, L.; Zhong, S.; Shi, K.; Zhang, X. Further results on finite-time synchronization of delayed inertial memristive neural networks via a novel analysis method. Neural Netw. 2020, 127, 47–57. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Li, X.; Nieto, J.J. Finite-time stability and stabilization for time-varying systems. Chaos Solitons Fractals 2021, 148, 111076. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X.; Liu, S. Finite-time stability of ABC type fractional delay difference equations. Chaos Solitons Fractals 2021, 152, 111430. [Google Scholar] [CrossRef]
- Su, H.; Luo, R.; Huang, M.; Fu, J. Robust Fixed Time Control of a Class of Chaotic Systems with Bounded Uncertainties and Disturbances. Int. J. Control. Autom. Syst. 2022, 20, 813–822. [Google Scholar] [CrossRef]
- Kavikumar, R.; Kaviarasan, B.; Lee, Y.-G.; Kwon, O.-M.; Sakthivel, R.; Choi, S.-G. Robust dynamic sliding mode control design for interval type-2 fuzzy systems. Discret. Contin. Dyn. Syst. S 2022, 15, 1839–1858. [Google Scholar] [CrossRef]
- Luo, D.; Tian, M.; Zhu, Q. Some results on finite-time stability of stochastic fractional-order delay differential equations. Chaos Solitons Fractals 2022, 158, 111996. [Google Scholar] [CrossRef]
- He, X.; Li, X.; Song, S. Finite-time stability of state-dependent delayed systems and application to coupled neural networks. Neural Netw. 2022, 154, 303–309. [Google Scholar] [CrossRef] [PubMed]
- Gokul, P.; Rakkiyappan, R. New finite-time stability for fractional-order time-varying time-delay linear systems: A Lyapunov approach. J. Frankl. Inst. 2022, 359, 7620–7631. [Google Scholar]
- Long, S.; Zhou, L.; Zhong, S.; Liao, D. An improved result for the finite-time stability of the singular system with time delay. J. Frankl. Inst. 2022, 359, 9006–9021. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhao, J.; Sun, Z.-Y. Fast finite time stability of stochastic nonlinear systems. J. Frankl. Inst. 2022, 359, 9039–9055. [Google Scholar] [CrossRef]
- Michalak, A. Finite-time and fixed-time stability analysis for time-varying systems: A dual approach. J. Frankl. Inst. 2022, 359, 10676–10687. [Google Scholar] [CrossRef]
- Liu, J.X.; Wang, Z.X.; Lei, T.F.; Yin, W.J. Finite-time chaotic synchronization control of permanent magnet synchronous motor. Small Spec. Electr. Mach. 2019, 47, 45–53. [Google Scholar]
- Yang, X.H.; Liu, X.P.; Hu, L.L.; Xu, S.P. Robust sliding mode mariable structure synchronization control of chaos in permanent magnet synchronous motor. Modul. Mach. Tool Autom. Manuf. Tech. 2012, 8, 93–95. [Google Scholar]
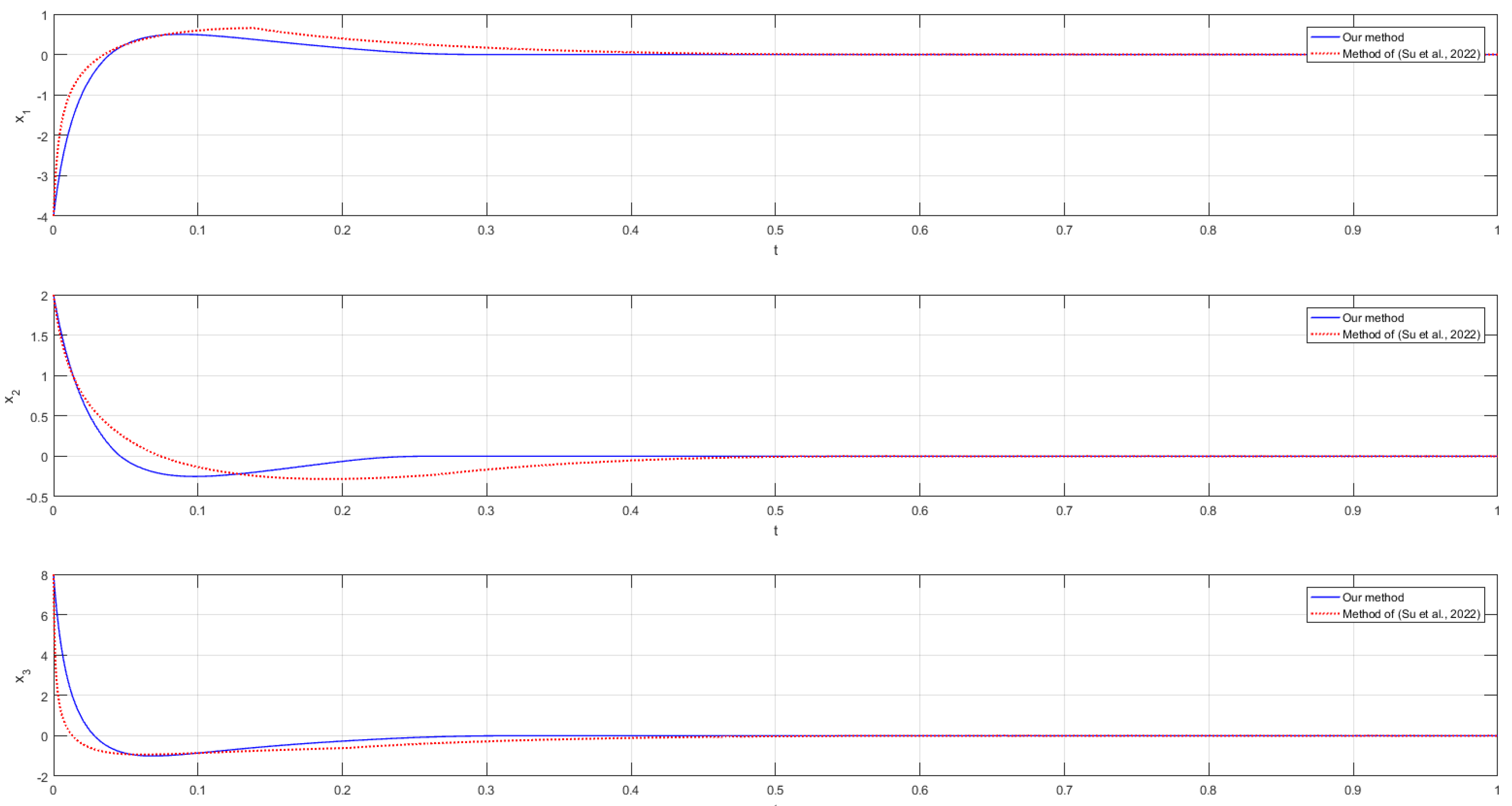
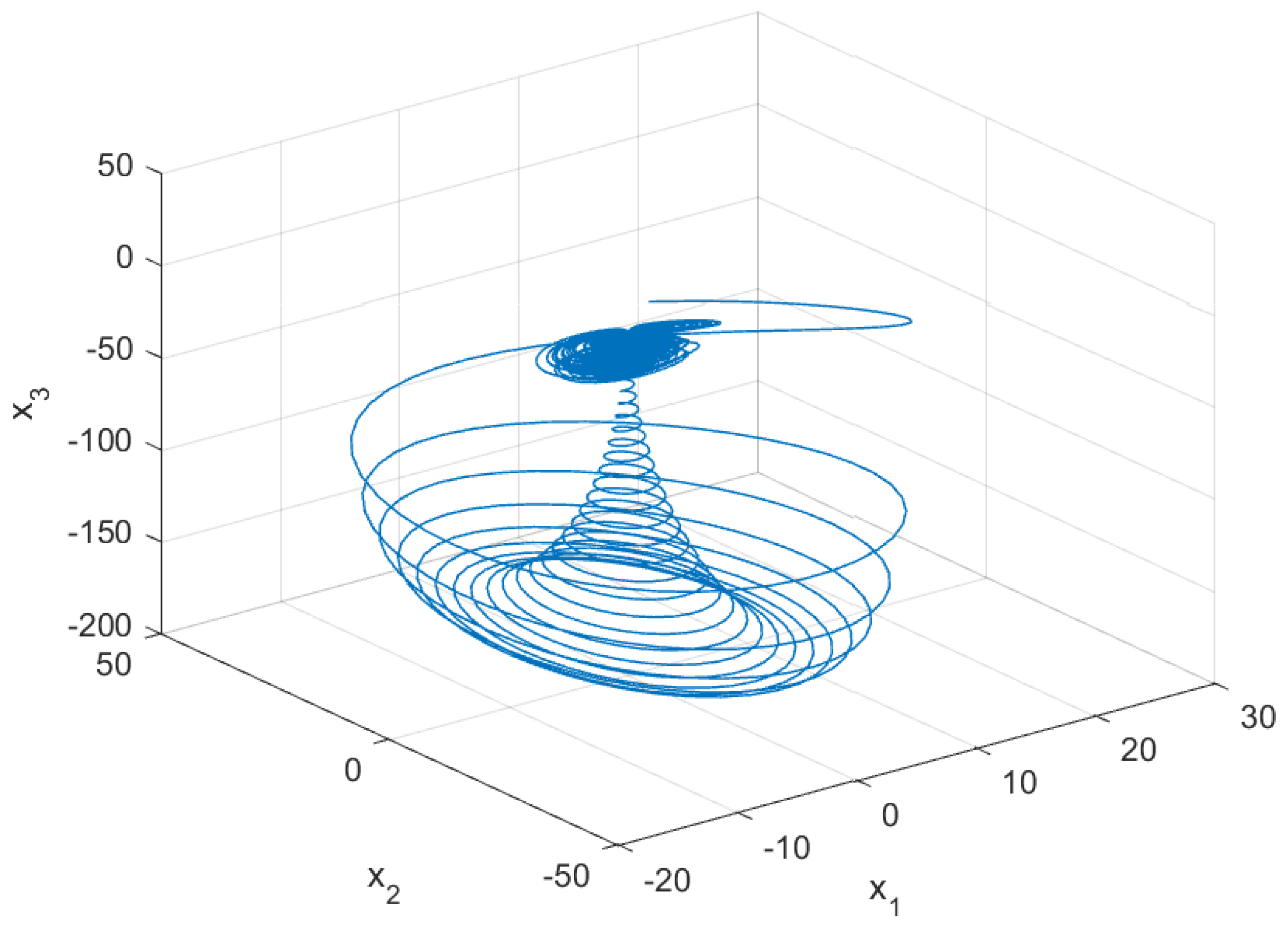

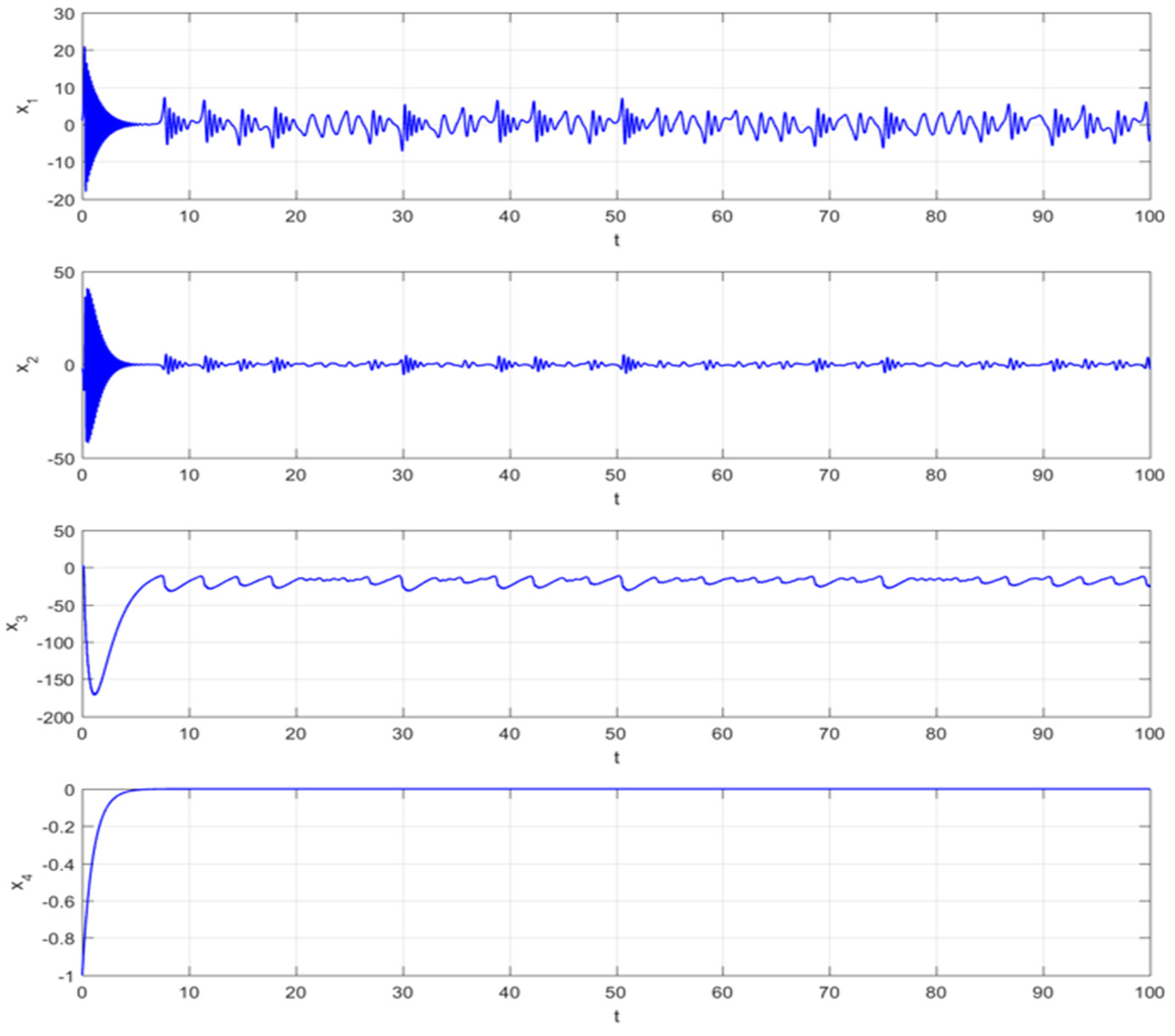
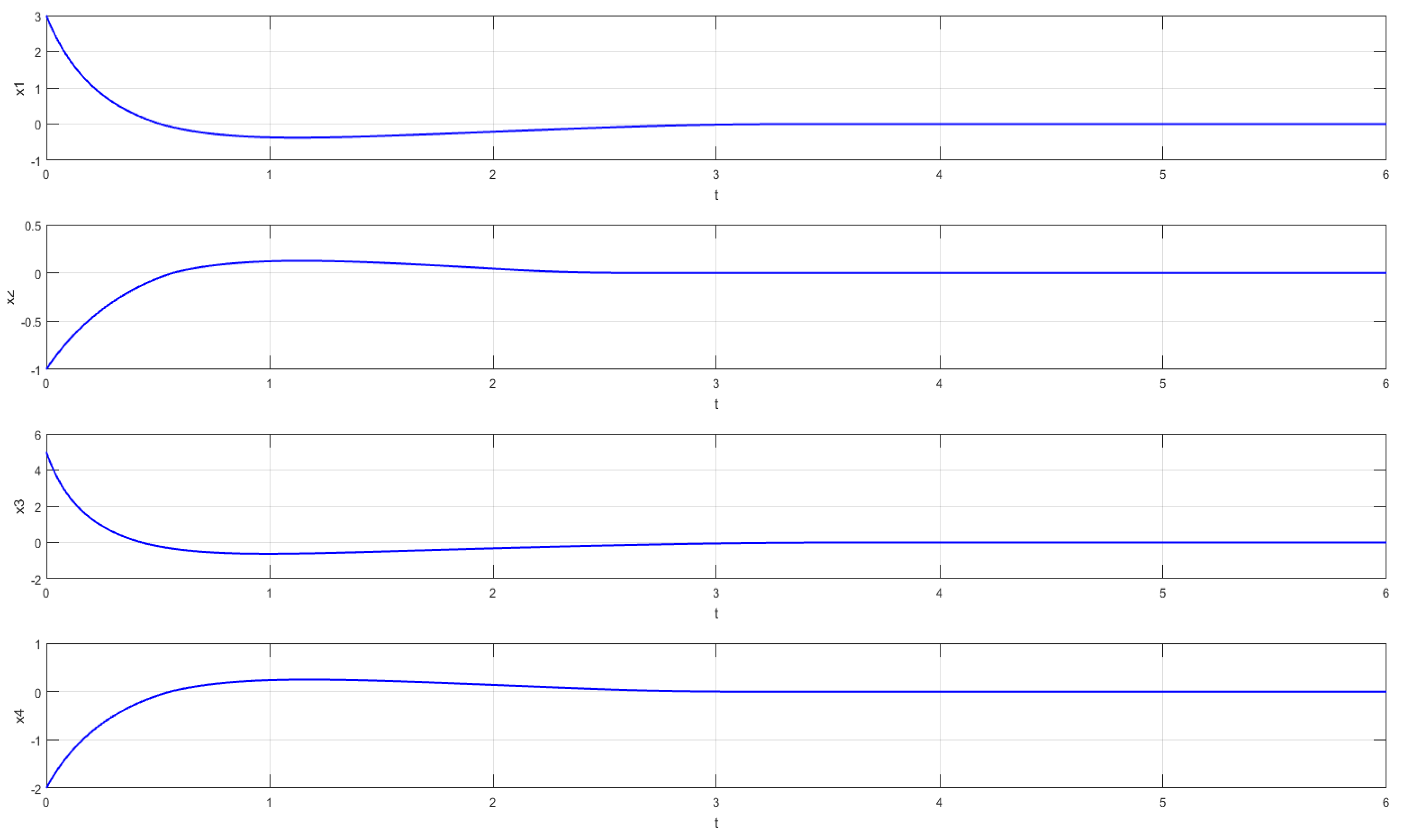
| Method | Time (s) | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1 |
|---|---|---|---|---|---|---|---|
| Our method | −4 | 0.1638 | −3.9031 × 10−18 | −3.9031 × 10−18 | −3.9031 × 10−18 | −3.9031 × 10−18 | |
| 2 | −0.0652 | 1.0503 × 10−19 | 1.0503 × 10−19 | 1.0503 × 10−19 | 1.0503 × 10−19 | ||
| 8 | −0.2688 | 4.5794 × 10−17 | 4.5794 × 10−17 | 4.5794 × 10−17 | 4.5794 × 10−17 | ||
| Method of Ref [34] | −4 | 0.3975 | 0.0525 | 0.002 | −2.4926 × 10−4 | −2.6047 × 10−5 | |
| 2 | −0.2800 | −0.0507 | −1.8392 × 10−4 | 1.4824 × 10−5 | 2.0169 × 10−5 | ||
| 8 | −0.6131 | −0.1117 | −0.0031 | −1.4171 × 10−4 | 1.7504 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rezaie, A.; Mobayen, S.; Ghaemi, M.R.; Fekih, A.; Zhilenkov, A. Design of a Fixed-Time Stabilizer for Uncertain Chaotic Systems Subject to External Disturbances. Mathematics 2023, 11, 3273. https://doi.org/10.3390/math11153273
Rezaie A, Mobayen S, Ghaemi MR, Fekih A, Zhilenkov A. Design of a Fixed-Time Stabilizer for Uncertain Chaotic Systems Subject to External Disturbances. Mathematics. 2023; 11(15):3273. https://doi.org/10.3390/math11153273
Chicago/Turabian StyleRezaie, Amir, Saleh Mobayen, Mohammad Reza Ghaemi, Afef Fekih, and Anton Zhilenkov. 2023. "Design of a Fixed-Time Stabilizer for Uncertain Chaotic Systems Subject to External Disturbances" Mathematics 11, no. 15: 3273. https://doi.org/10.3390/math11153273
APA StyleRezaie, A., Mobayen, S., Ghaemi, M. R., Fekih, A., & Zhilenkov, A. (2023). Design of a Fixed-Time Stabilizer for Uncertain Chaotic Systems Subject to External Disturbances. Mathematics, 11(15), 3273. https://doi.org/10.3390/math11153273









