Endomorphism Spectra of Double-Edge Fan Graphs

Abstract

There are six classes of endomorphisms for a graph. The sets of these endomorphisms form a chain under the inclusion of sets. In order to systematically study these endomorphisms, Böttcher and Knauer defined the concepts of the endomorphism spectrum and endomorphism type of a graph in 1992. In this paper, based on the property and structure of the endomorphism monoids of graphs, six classes of endomorphisms of double-edge fan graphs are described. In particular, we give the endomorphism spectra and endomorphism types of double-edge fan graphs.

1. Introduction

The endomorphism monoid of a graph is a generalization of the automorphism group of a graph. In recent years, the endomorphism monoids of graphs have attracted the attention of many scholars, and many meaningful results related to the endomorphism monoids of graphs have been obtained (cf. [1,2,3,4,5]). Some combinatorial counting problems related to the endomorphisms of graphs are some of the research hotspots in this field. In order to reveal the combinatorial counting properties of six kinds of endomorphisms of graphs at a deeper level, in [6], Böttcher and Knauer put forward the definition of the endomorphism spectrum and endomorphism type of graphs. In [7], the endomorphism types of bipartite graphs with diameter three and girth six were studied by Fan. In [8], Hou, Luo and Cheng gained the endomorphism spectrum and endomorphism type of $\overline{P_n}$ by exploring the endomorphism of $\overline{P_n}$, where $\overline{P_n}$ is defined as the complement of a path $P_n$. In [9], Hou and Gu characterized the endomorphisms of fan graphs. The endomorphism types and endomorphism spectra of fan graphs were obtained. In [10], the endomorphisms of double fan graphs were studied, and the endomorphism types of double fan graphs were given.

Given a graph, we can define its six classes of endomorphisms. The endomorphism spectrum of a graph is a six-tuple related to the number of its endomorphisms. The endomorphism type of a graph is an integer from 0 to 31. In this paper, we investigate six classes of endomorphisms of double-edge fan graphs and give the endomorphism spectra and endomorphism types of double-edge fan graphs.

2. Preliminary Concepts

All graphs we consider are finite, undirected and simple. Let us suppose that G is a graph. The vertex set of G is denoted by $V\left(G\right)$, and the edge set of G is denoted by $E\left(G\right)$. If two vertices $a_1$ and $a_2$ are adjacent in G, the edge connecting $a_1$ and $a_2$ is denoted by $\{a_1,a_2\}$, and $\{a_1,a_2\}\in E\left(G\right)$. Subgraph H of G is called induced subgraph of G if for any $h_1,h_2\in V\left(H\right)$, $\{h_1,h_2\}\in E\left(H\right)$, if and only if $\{h_1,h_2\}\in E\left(G\right)$. A graph G is called a complete graph if for any $g_1,g_2\in V\left(G\right)$, $\{g_1,g_2\}\in E\left(G\right)$. A complete graph with n vertices is denoted by $K_n$. A graph $F_n$ is called fan graph if it results from the joining of $P_n$ and a vertex.

Let us suppose that X and Y are two graphs. Let g be a mapping from $V\left(X\right)$ to $V\left(Y\right)$. g is a homomorphism if $\{s,t\}\in E\left(X\right)$ implies that $\left\{g\right(s),g(t\left)\right\}\in E\left(Y\right)$. A homomorphism g is half-strong if $\left\{g\right(u),g(v\left)\right\}\in E\left(Y\right)$ implies that there exist $s,t\in V\left(X\right)$ with $g\left(u\right)=g\left(s\right)$ and $g\left(v\right)=g\left(t\right)$ such that $\{s,t\}\in E\left(X\right)$. A homomorphism g is locally strong if $\left\{g\right(u),g(v\left)\right\}\in E\left(Y\right)$ implies that for every $s\in g^{-1}\left(g\left(u\right)\right)$ there exists $t\in g^{-1}\left(g\left(v\right)\right)$ such that $\{s,t\}\in E\left(X\right)$; it is analogous for every preimage of $g\left(v\right)$ (the subgraph of X induced by $g^{-1}\left(g\left(u\right)\right)\cup g^{-1}\left(g\left(v\right)\right)$ contains no isolated vertices). A homomorphism g is quasi-strong if $\left\{g\right(u),g(v\left)\right\}\in E\left(Y\right)$ implies that there exists $s\in g^{-1}\left(g\left(u\right)\right)$ adjacent to every vertex of $g^{-1}\left(g\left(v\right)\right)$; it is analogous for the preimage of $g\left(v\right)$. A homomorphism g is strong if $\left\{g\right(u),g(v\left)\right\}\in E\left(Y\right)$ implies that every preimage of $g\left(u\right)$ is adjacent to every preimage of $g\left(v\right)$ (the subgraph of X induced by $g^{-1}\left(g\left(u\right)\right)\cup g^{-1}\left(g\left(v\right)\right)$ is a complete bipartite graph). A homomorphism g is an isomorphism if g is bijective and $g^{-1}$ is a homomorphism. If g is a homomorphism (isomorphism) from X to itself, then it is called an endomorphism (automorphism) of X.

We denote the sets of all endomorphisms, half-strong endomorphisms, locally strong endomorphisms, quasi-strong endomorphisms, strong endomorphisms and automorphisms for a graph G by $End\left(G\right)$, $hEnd\left(G\right)$, $lEnd\left(G\right)$, $qEnd\left(G\right)$, $sEnd\left(G\right)$ and $Aut\left(G\right)$, respectively. Obviously,

$$Aut\left(G\right)\subseteq sEnd\left(G\right)\subseteq qEnd\left(G\right)\subseteq lEnd\left(G\right)\subseteq hEnd\left(G\right)\subseteq End\left(G\right).$$

Let us suppose that G is a graph; then, the six-tuple

$$\begin{array}{c}\left(\right|End\left(G\right)|,|hEnd\left(G\right)|,|lEnd\left(G\right)|,|qEnd\left(G\right)|,|sEnd\left(G\right)|,|Aut\left(G\right)\left|\right)\hfill \end{array}$$

is called the endomorphism spectrum of G, and we denote it by $EndospecG$. The integer ${\mathsf{\Sigma }}_{i=1}^5{s}_i{2}^{i-1}$ is called the endomorphism type of G, where $s_i\in \{0,1\}$; $s_i=0$ shows that the ith element is equal to the $(i+1)$th element in $EndospecG$, and $s_i=1$, otherwise. We denote it by $EndotypeG$.

Let $f\in End\left(G\right)$ and $H\subseteq V\left(G\right)$. We denote by ${f|}_H$ the restriction of f on H and by $I_f$ the endomorphic image of G under f. The endomorphic kernel ${\rho }_f$ induced by f is an equivalence relation on $V\left(G\right)$ such that $(s,t)\in {\rho }_f$ if and only if $f\left(s\right)=f\left(t\right)$ for any $s,t\in V\left(G\right)$. We denote by ${\left[s\right]}_{{\rho }_f}$ the equivalence class of s under ${\rho }_f$.

For concepts and terms related to graph theory and semigroup theory not listed in this paper, please read the relevant references [11,12,13,14].

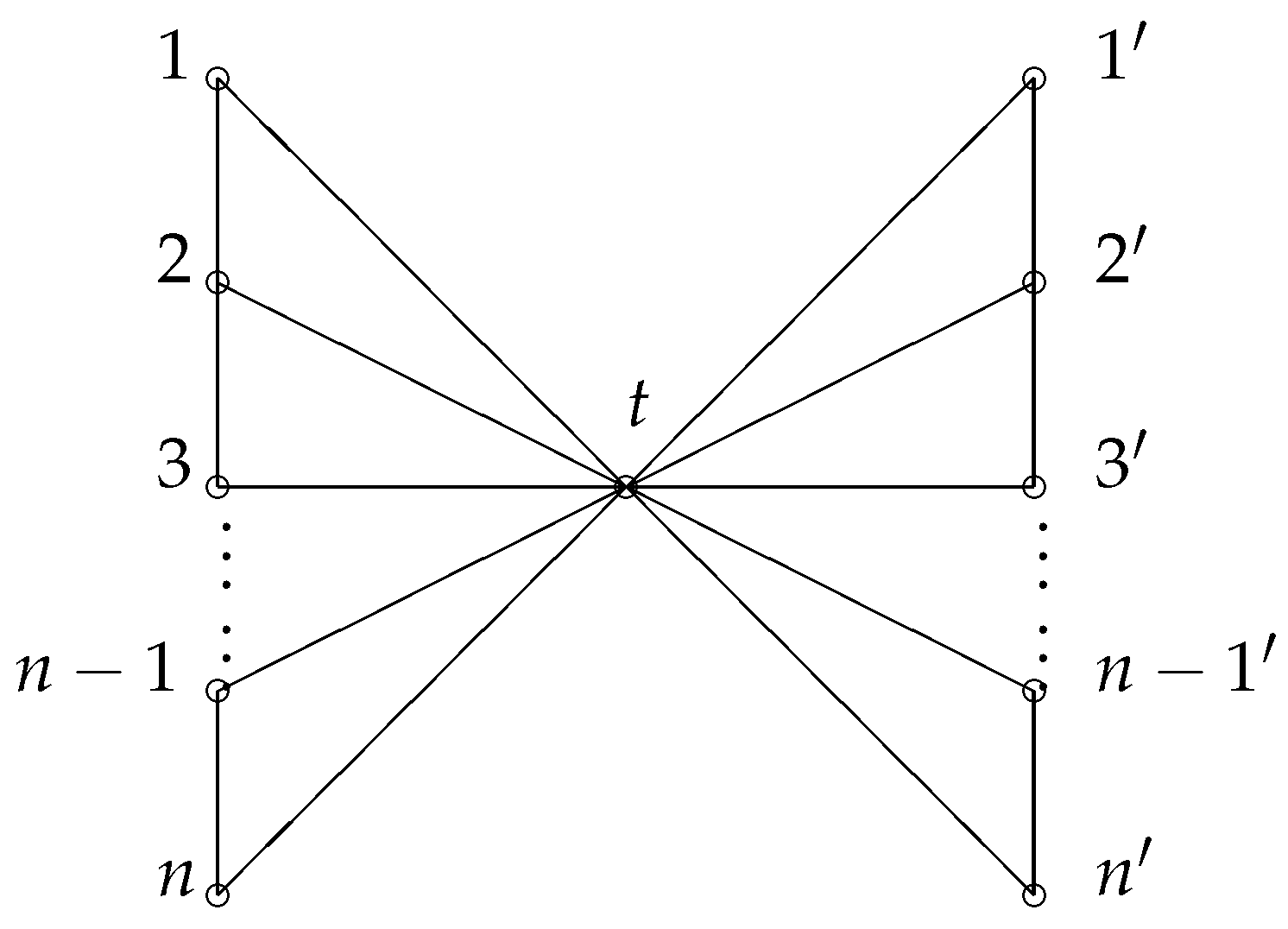
3. Endomorphism Spectra of Double-Edge Fan Graphs

Let $D{E}_n$ be a double-edge fan graph (see Figure 1). We denote $A=\left\{1,2,\dots ,n\right\}$, $B=\left\{1,3,5,\dots \right\}$ and $C=\left\{2,4,6\dots \right\}$. We denote $A^{\prime }=\left\{1^{\prime },2^{\prime },\dots ,n^{\prime }\right\}$, $B^{\prime }=\left\{1^{\prime },3^{\prime },5^{\prime },\dots \right\}$ and $C^{\prime }=\left\{2^{\prime },4^{\prime },6^{\prime }\dots \right\}$. We denote by $P_n$, $P_n^{\prime }$, $F_n$ and $F_n^{\prime }$ the subgraph of $D{E}_n$ induced by A, $A^{\prime }$, $A\cup \left\{t\right\}$ and $A^{\prime }\cup \left\{t\right\}$, respectively.

Lemma 1

([15]). Let G be a graph and $f\in End\left(G\right)$. Then, $f\in hEnd\left(G\right)$ if and only if $I_f$ is an induced subgraph of G.

Lemma 2.

Let $f\in End\left(D{E}_n\right)$. Then, the following apply:

(1) 

$f\left(t\right)\ne f\left(i\right)$ for any $i\in A\cup A^{\prime }$.

(2) 

If $f\left(t\right)=t$, then $f\left(A\right)\subseteq A$ or $f\left(A\right)\subseteq A^{\prime }$, $f\left(A^{\prime }\right)\subseteq A$ or $f\left(A^{\prime }\right)\subseteq A^{\prime }$.

(3) 

If $f\left(t\right)\ne t$ , then $I_f\cong K_3$ or $I_f\cong F_3$.

Proof. 

(1) Note that $\{t,i\}\in E\left(D{E}_n\right)$ for any $i\in A\cup A^{\prime }$. If $f\left(t\right)=f\left(i\right)$, then $f\left(t\right)$ forms a loop in $D{E}_n$, which is a contradiction.

(2) If $f\left(t\right)=t$, then we have $f\left(A\right)\subseteq A$ or $f\left(A\right)\subseteq A^{\prime }$. Otherwise, there are $u,v\in A$ such that $f\left(u\right)\in A$ and $f\left(v\right)\in A^{\prime }$. Since $P_n$ is connected, there exists a path from u to v in $P_n$. Thus, there exists a path from $f\left(u\right)$ to $f\left(v\right)$ in $f\left(P_n\right)$. Note that every path from $f\left(u\right)$ to $f\left(v\right)$ must contain t. Hence, there exists $w\in A$ such that $f\left(w\right)=f\left(t\right)=t$. This contradicts (1). It is similar for $f\left(A^{\prime }\right)\subseteq A$ or $f\left(A^{\prime }\right)\subseteq A^{\prime }$.

(3) If $f\left(t\right)\ne t$, then $f\left(t\right)=k$ for some $k\in A\cup A^{\prime }$. Since $\{t,i\}\in E\left(D{E}_n\right)$ for any $i\in A\cup A^{\prime }$, $\{f\left(t\right),f\left(i\right)\}=\{k,f\left(i\right)\}\in E\left(D{E}_n\right)$. Note that $d\left(k\right)\le 3$. If $\left|V\left(I_f\right)\right|=3$, then $I_f\cong K_3$. If $\left|V\left(I_f\right)\right|=4$, then $I_f\cong F_3$. □

Lemma 3.

$End\left(D{E}_n\right)=hEnd\left(D{E}_n\right)$ if and only if $n\le 3$.

Proof. 

Necessity. We just need to verify that $End\left(D{E}_n\right)\ne hEnd\left(D{E}_n\right)$ for any $n\ge 4$. Let f be a mapping on $V\left(D{E}_n\right)$ defined by

$$f\left(x\right)=\left\{\begin{array}{c}1,x\in B,\hfill \\ 2,x\in C,\hfill \\ 3,x\in B^{\prime },\hfill \\ 4,x\in C^{\prime },\hfill \\ t,x=t.\hfill \end{array}\right.$$

Then, $f\in End\left(D{E}_n\right)$. Clearly, $\left\{2,3\right\}\in E\left(I_f\right)$, $f^{-1}\left(2\right)=C$, $f^{-1}\left(3\right)=B^{\prime }$. Note that there exist no $c\in C$ and $b^{\prime }\in B^{\prime }$ such that $\{c,b^{\prime }\}\in E\left(D{E}_n\right)$. Then, $f\notin hEnd\left(D{E}_n\right)$. Therefore, $End\left(D{E}_n\right)\ne hEnd\left(D{E}_n\right)$.

Sufficiency. Let $n\le 3$ and $f\in End\left(D{E}_n\right)$. If $f\left(t\right)\ne t$, then $I_f\cong K_3$ or $I_f\cong F_3$ by Lemma 2 (3). Note that both $K_3$ and $F_3$ are induced subgraphs of $D{E}_n$. By Lemma 1, $f\in hEnd\left(D{E}_n\right)$.

If $f\left(t\right)=t$, then $f\left(i\right)\ne t$ for $i\in A\cup A^{\prime }$ by Lemma 2 (1). Thus, $f\left(A\right)\subseteq A$ or $f\left(A\right)\subseteq A^{\prime }$, $f\left(A^{\prime }\right)\subseteq A$ or $f\left(A^{\prime }\right)\subseteq A^{\prime }$. Let $\{f\left(i\right),f\left(j\right)\}\in E\left(D{E}_n\right)$ for some $i,j\in V\left(D{E}_n\right)$. If $t\in {\left[i\right]}_{{\rho }_f}$, then $\{t,j\}\in E\left(D{E}_n\right)$. If $t\in {\left[j\right]}_{{\rho }_f}$, then $\{t,i\}\in E\left(D{E}_n\right)$. Now, we suppose that $t\notin {\left[i\right]}_{{\rho }_f}\cup {\left[j\right]}_{{\rho }_f}$. Then, $f\left(t\right)\ne f\left(k\right)$ for any $k\in {\left[i\right]}_{{\rho }_f}\cup {\left[j\right]}_{{\rho }_f}$. If ${\left[i\right]}_{{\rho }_f}\cap A\ne ⌀$ and ${\left[j\right]}_{{\rho }_f}\cap A\ne ⌀$, then there exist $u\in {\left[i\right]}_{{\rho }_f}\cap A$ and $v\in {\left[j\right]}_{{\rho }_f}\cap A$ such that $\{u,v\}\in E\left(D{E}_n\right)$, since $f\left(A\right)$ is connected. If ${\left[i\right]}_{{\rho }_f}\cap A^{\prime }\ne ⌀$ and ${\left[j\right]}_{{\rho }_f}\cap A^{\prime }\ne ⌀$, then there exist $u\in {\left[i\right]}_{{\rho }_f}$ and $v\in {\left[j\right]}_{{\rho }_f}$ such that $\{u,v\}\in E\left(D{E}_n\right)$. Without loss of generality, let us suppose that ${\left[i\right]}_{{\rho }_f}\subseteq A$ and ${\left[j\right]}_{{\rho }_f}\subseteq A^{\prime }$, then $f\left(A\right)\cap f\left(A^{\prime }\right)=⌀$. Note that $\left|f\right(A\left)\right|\ge 2$ and $\left|f\right(A^{\prime }\left)\right|\ge 2$; thus, $n\ge 3$. This is a contradiction. Therefore, $f\in hEnd\left(D{E}_n\right)$. □

Lemma 4.

$$\left|End\left(D{E}_n\right)\right|=\left\{\begin{array}{c}4{\left((n+1)2^{n-1}-(2n-1)\left({}_{\frac{n-1}{2}}^{n-1}\right)\right)}^2+16(n-1)\hfill \\ +2(n-2)\left({\left(2^{\frac{n+1}{2}}+2^{\frac{n-1}{2}}-4\right)}^2+8\left(2^{\frac{n+1}{2}}+2^{\frac{n-1}{2}}-4\right)+8\right),ifnisodd,\hfill \\ 4{\left((n+1)2^{n-1}-n\left({}_{\frac{n}{2}}^n\right)\right)}^2+16(n-1)\hfill \\ +2(n-2)\left(4{\left(2^{\frac{n}{2}}-2\right)}^2+16\left(2^{\frac{n}{2}}-2\right)+8\right),ifniseven.\hfill \end{array}\right.$$

Proof. 

Let $f\in End\left(D{E}_n\right)$. There are two cases.

(1) $f\left(t\right)=t$. By Lemma 2 (2), $f\left(A\right)\subseteq A$ or $f\left(A\right)\subseteq A^{\prime }$, $f\left(A^{\prime }\right)\subseteq A$ or $f\left(A^{\prime }\right)\subseteq A^{\prime }$. Clearly, there are ${\left|End\left(P_n\right)\right|}^2$ endomorphisms of $D{E}_n$ satisfying $f\left(A\right)\subseteq A$ and $f\left(A^{\prime }\right)\subseteq A^{\prime }$. Analogously, there are ${\left|End\left(P_n\right)\right|}^2$ endomorphisms for the cases of $f\left(A\right)\subseteq A$ and $f\left(A^{\prime }\right)\subseteq A$, $f\left(A\right)\subseteq A^{\prime }$ and $f\left(A^{\prime }\right)\subseteq A^{\prime }$, and $f\left(A\right)\subseteq A^{\prime }$ and $f\left(A^{\prime }\right)\subseteq A$. Thus, we obtain $4{\left|End\left(P_n\right)\right|}^2$ endomorphisms satisfying $f\left(t\right)=t$. It is known from [16] that

$$\left|End\left(P_n\right)\right|=\left\{\begin{array}{c}(n+1)2^{n-1}-(2n-1)\left({}_{\frac{n-1}{2}}^{n-1}\right),ifnisodd,\hfill \\ (n+1)2^{n-1}-n\left({}_{\frac{n}{2}}^n\right),ifniseven.\hfill \end{array}\right.$$

(2) $f\left(t\right)\ne t$. By Lemma 2 (3), there are two cases.

(i) Let us assume that $I_f\cong K_3$. Then, $\left|f(A\cup A^{\prime })\right|=2$, and ${\rho }_f=\{\left\{t\right\},C\cup C^{\prime },B\cup B^{\prime }\}$ or ${\rho }_f=\{\left\{t\right\},C\cup B^{\prime },B\cup C^{\prime }\}$. There are $2(n-1)$ subgraphs Y in $D{E}_n$ such that $Y\cong K_3$. Let K be a subgraph of $D{E}_n$ such that $K\cong K_3$ and $V\left(K\right)=\left\{t,i,i+1\right\}$ for some $i\in A$. Since $f\left(t\right)\ne t$, $f\left(t\right)\in \{i,i+1\}$. Furthermore, there are two methods to map ${\rho }_f\backslash \left\{t\right\}$ to $V\left(X\right)\backslash \left\{f\right(t\left)\right\}$. Hence, we obtain $16(n-1)$ endomorphisms satisfying $f\left(t\right)\ne t$ and $I_f\cong K_3$. (ii) Let us assume that $I_f\cong F_3$. Then, $\left|f(A\cup A^{\prime })\right|=3$, and there are $2(n-2)$ subgraphs Y in $D{E}_n$ such that $Y\cong F_3$. Let F be a subgraph of $D{E}_n$ satisfying $F\cong F_3$ and $V\left(F\right)=\left\{t,j-1,j,j+1\right\}$ for some $j\in A\cup A^{\prime }$. Note that $f\left(t\right)\ne t$ and $\{f\left(t\right),k\}\in E\left(D{E}_n\right)$ for any $k\in V\left(F\right)\backslash \left\{f\right(t\left)\right\}$. Hence, $f\left(t\right)=j$. Since $f\left(t\right)\ne f\left(i\right)$ for any $i\in A\cup A^{\prime }$, $f(A\cup A^{\prime })\subseteq \{j-1,j+1,t\}$. There are four cases.

Case 1. Let us assume that $\left|f\left(A\right)\right|=3$ and $\left|f\left(A^{\prime }\right)\right|=3$.

If n is odd, then $\left|B\right|=\left|B^{\prime }\right|=\frac{n+1}{2}$ and $\left|C\right|=\left|C^{\prime }\right|=\frac{n-1}{2}$. Since $\left|f\left(A\right)\right|=3$, $f\left(B\right)=t$ or $f\left(C\right)=t$. If $f\left(B\right)=t$, then $f^{-1}(j-1)\subseteq C$ and $f^{-1}(j+1)\subseteq C$. Note that we have $2^{\frac{n-1}{2}}-2$ methods to divide set C into two non-empty subsets, $C_1$ and $C_2$. Clearly, there are $2^{\frac{n-1}{2}}-2$ methods to map $\{C_1,C_2\}$ to $\{j-1,j+1\}$. If $f\left(C\right)=t$, then $f^{-1}(j-1)\subseteq B$ and $f^{-1}(j+1)\subseteq B$. Similarly, we have $2^{\frac{n+1}{2}}-2$ methods to divide set B into two non-empty subsets, $B_1$ and $B_2$. Clearly, there are $2^{\frac{n+1}{2}}-2$ methods to map $\{B_1,B_2\}$ to $\{j-1,j+1\}$. Thus, there are $2^{\frac{n+1}{2}}+2^{\frac{n-1}{2}}-4$ ways to map A to $\{j-1,j+1,t\}$. Analogously, there are $2^{\frac{n+1}{2}}+2^{\frac{n-1}{2}}-4$ ways to map $A^{\prime }$ to $\{j-1,j+1,t\}$. Therefore, there are $2(n-2){\left(2^{\frac{n+1}{2}}+2^{\frac{n-1}{2}}-4\right)}^2$ endomorphisms in this case.

Similarly, if n is even, we can obtain $8(n-2){\left(2^{\frac{n}{2}}-2\right)}^2$ endomorphisms.

Case 2. Let us assume that $\left|f\left(A\right)\right|=3$ and $\left|f\left(A^{\prime }\right)\right|=2$.

If n is odd, then $\left|B\right|=\left|B^{\prime }\right|=\frac{n+1}{2}$ and $\left|C\right|=\left|C^{\prime }\right|=\frac{n-1}{2}$. Since $\left|f\left(A\right)\right|=3$, there are $2^{\frac{n+1}{2}}+2^{\frac{n-1}{2}}-4$ ways to map A to $\{j-1,j+1,t\}$ by Case 1. Since $\left|f\left(A^{\prime }\right)\right|=2$, $f\left(A^{\prime }\right)=\{j-1,t\}$ or $f\left(A^{\prime }\right)=\{j+1,t\}$. Now, we have two methods to map $\{B^{\prime },C^{\prime }\}$ to $\{j-1,t\}$ or $\{j+1,t\}$. Therefore, there are $8(n-2)\left(2^{\frac{n+1}{2}}+2^{\frac{n-1}{2}}-4\right)$ endomorphisms in this case.

Similarly, if n is even, we can obtain $16(n-2)\left(2^{\frac{n}{2}}-2\right)$ endomorphisms.

Case 3. Let us assume that $\left|f\left(A\right)\right|=2$ and $\left|f\left(A^{\prime }\right)\right|=3$.

If n is odd, we can obtain $8(n-2)\left(2^{\frac{n+1}{2}}+2^{\frac{n-1}{2}}-4\right)$ endomorphisms by Case 2. If n is even, we can obtain $16(n-2)\left(2^{\frac{n}{2}}-2\right)$ endomorphisms.

Case 4. Let us assume that $\left|f\left(A\right)\right|=2$ and $\left|f\left(A^{\prime }\right)\right|=2$.

Clearly, $f\left(A\right)=\{j-1,t\}$ and $f\left(A^{\prime }\right)=\{j+1,t\}$, or $f\left(A\right)=\{j+1,t\}$ and $f\left(A^{\prime }\right)=\{j-1,t\}$. If $f\left(A\right)=\{j-1,t\}$ and $f\left(A^{\prime }\right)=\{j+1,t\}$, then there are two methods to map $\{B,C\}$ to $\{j-1,t\}$, and there are two methods to map $\{B^{\prime },C^{\prime }\}$ to $\{j+1,t\}$. Analogously, if $f\left(A\right)=\{j+1,t\}$ and $f\left(A^{\prime }\right)=\{j-1,t\}$, then there are also four methods to map A to $\{j+1,t\}$ and to map $A^{\prime }$ to $\{j-1,t\}$. Hence, we obtain $16(n-2)$ endomorphisms.

From the above discussion, the result of Lemma 4 can be obtained. □

Lemma 5.

Let $D{E}_n$ be a double-edge fan graph with $n\ge 4$. Then, $\left|hEnd\left(D{E}_n\right)\right|=\left|End\left(D{E}_n\right)\right|-4\left({\displaystyle \sum _{\begin{array}{c}2\le i,j\le n-2\\ 4\le i+j\le n\end{array}}}\left(n-i-j+1\right)\frac{\left|Hom(P_n,P_i)\right|}{n-i+1}·\frac{\left|Hom(P_n,P_j)\right|}{n-j+1}\right)$, where $\left|Hom(P_n,P_k)\right|=k·2^{n-1}-$${\displaystyle \sum _{i=0}^{n-2}}{2}^{n-1-i}{\displaystyle \sum _{j\in Z}}\left(\left(\begin{array}{c}i\\ \lceil \frac{i}{2}\rceil -j(k+1)\end{array}\right)-\left(\begin{array}{c}i\\ \lfloor \frac{i+k-1}{2}\rfloor -j(k+1)\end{array}\right)\right)$.

Proof. 

Let $f\in End\left(D{E}_n\right)$ for some $n\ge 4$. If $f\left(t\right)\ne t$, then $I_f\cong K_3$ or $I_f\cong F_3$. Thus, $I_f$ is an induced subgraph of $D{E}_n$. By Lemma 1, $f\in hEnd\left(D{E}_n\right)$.

If $f\left(t\right)=t$, then $f\left(A\right)\subseteq A$ or $f\left(A\right)\subseteq A^{\prime }$, $f\left(A^{\prime }\right)\subseteq A$ or $f\left(A^{\prime }\right)\subseteq A^{\prime }$. Then, $f\notin hEnd\left(D{E}_n\right)$ if and only if $f\left(A\right)=V\left(P_i\right)$, with $2\le i\le n-2$; $f\left(A^{\prime }\right)=V\left(P_j\right)$, with $2\le j\le n-2$; and $f(A\cup A^{\prime })=V\left(P_{i+j}\right)$, with $V\left(P_{i+j}\right)=V\left(P_i\right)\cup V\left(P_j\right)$. Clearly, there are $2(n-i-j+1)$ subgraphs in $D{E}_n$ isomorphic to $P_{i+j}$. Then, there are $\frac{\left|Hom(P_n,P_i)\right|}{n-i+1}$ ways to map A to $V\left(P_i\right)$, and there are $\frac{\left|Hom(P_n,P_j)\right|}{n-j+1}$ ways to map A to $V\left(P_j\right)$. Thus, there are $4\left({\displaystyle \sum _{\begin{array}{c}2\le i,j\le n-2\\ 4\le i+j\le n\end{array}}}\left(n-i-j+1\right)\frac{\left|Hom(P_n,P_i)\right|}{n-i+1}·\frac{\left|Hom(P_n,P_j)\right|}{n-j+1}\right)$ endomorphisms, which are not half-strong.

It is known from [16] that

$\left|Hom(P_n,P_k)\right|=k·2^{n-1}-{\displaystyle \sum _{i=0}^{n-2}}{2}^{n-1-i}{\displaystyle \sum _{j\in Z}}\left(\left(\begin{array}{c}i\\ \lceil \frac{i}{2}\rceil -j(k+1)\end{array}\right)-\left(\begin{array}{c}i\\ \lfloor \frac{i+k-1}{2}\rfloor -j(k+1)\end{array}\right)\right)$, where Z is a set of integers.

From the above discussion, the result of Lemma 5 can be obtained. □

Lemma 6.

$hEnd\left(D{E}_n\right)=lEnd\left(D{E}_n\right)$ if and only if $n=2$.

Proof. 

Necessity. We just need to verify that $hEnd\left(D{E}_n\right)\ne lEnd\left(D{E}_n\right)$ when $n\ge 3$. Let f be a mapping on $V\left(D{E}_n\right)$ defined by

$$f\left(x\right)=\left\{\begin{array}{c}3,x=1,\hfill \\ i,x=i^{\prime },wherei=1,2,\dots ,n,\hfill \\ x,otherwise.\hfill \end{array}\right.$$

Then, $f\in hEnd\left(D{E}_n\right)$. Clearly, $\left\{1,2\right\}\in E\left(I_f\right)$, $f^{-1}\left(1\right)=\left\{1^{\prime }\right\}$, $f^{-1}\left(2\right)=\left\{2^{\prime },2\right\}$. Note that $\{1^{\prime },2\}\notin E\left(D{E}_n\right)$; then, $f\notin lEnd\left(D{E}_n\right)$. Therefore, $hEnd\left(D{E}_n\right)\ne lEnd\left(D{E}_n\right)$.

Sufficiency. Let $f\in hEnd\left(D{E}_2\right)\backslash Aut\left(D{E}_2\right)$. Then, $I_f\cong K_3$, ${\rho }_f=\{\left[t\right],[1,1^{\prime }],[2,2^{\prime }]\}$ or ${\rho }_f=\{\left[t\right],[1,2^{\prime }],[2,1^{\prime }]\}$. If ${\rho }_f=\{\left[t\right],[1,1^{\prime }],[2,2^{\prime }]\}$, then the subgraphs of $D{E}_n$ induced by $\left\{1,1^{\prime }\right\}\cup \left\{2,2^{\prime }\right\}$, $\left\{1,1^{\prime }\right\}\cup \left\{t\right\}$ or $\left\{2,2^{\prime }\right\}\cup \left\{t\right\}$ have no isolated vertices. If ${\rho }_f=\{\left[t\right],[1,2^{\prime }],[2,1^{\prime }]\}$, then the subgraphs of $D{E}_n$ induced by $\left\{1,2^{\prime }\right\}\cup \left\{2,1^{\prime }\right\}$, $\left\{1,2^{\prime }\right\}\cup \left\{t\right\}$ or $\left\{2,1^{\prime }\right\}\cup \left\{t\right\}$ have no isolated vertices. Therefore, $f\in lEnd\left(D{E}_n\right)$. □

Lemma 7.

Let $f\in End\left(D{E}_n\right)$ and $n\ge 4$. If $f\left(t\right)=t$, then $f\in lEnd\left(D{E}_n\right)$ if and only if one of the following conditions holds:

(1) 

${f|}_A\in lEnd\left(P_n\right)$ and ${f|}_{A^{\prime }}\in lEnd\left(P_n^{\prime }\right)$, or ${f|}_A\in lHom(P_n,P_n^{\prime })$ and ${f|}_{A^{\prime }}\in lHom(P_n^{\prime },P_n)$;

(2) 

$f\left(A\right)=f\left(A^{\prime }\right)$, ${f|}_A\in lHom(P_n,P)$ and ${f|}_{A^{\prime }}\in lHom(P_n^{\prime },P)$, where P is a subgraph of $D{E}_n$ induced by $f\left(A\right)$;

(3) 

${f|}_A\in lHom(P_n,P_i)$ and ${f|}_{A^{\prime }}\in lHom(P_n^{\prime },P_j)$, where $V\left(P_i\right),V\left(P_j\right)\subset A$ or $V\left(P_i\right)$, $V\left(P_j\right)\subset A^{\prime }$, $V\left(P_i\right)\cap V\left(P_j\right)=⌀$, and the subgraph of $D{E}_n$ induced by $V\left(P_i\right)\cup V\left(P_j\right)$ is disconnected.

Proof. 

Necessity. Let $f\in lEnd\left(D{E}_n\right)$. Since $f\left(t\right)=t$, by Lemma 2 (2), $f\left(A\right)\subseteq A$ or $f\left(A\right)\subseteq A^{\prime }$, $f\left(A^{\prime }\right)\subseteq A$ or $f\left(A^{\prime }\right)\subseteq A^{\prime }$.

(1) Let us assume that $f\left(A\right)\subseteq A$ and $f\left(A^{\prime }\right)\subseteq A^{\prime }$. Let $a,b\in V\left(I_{{f|}_A}\right)$ be such that $\{a,b\}\in E\left(I_{{f|}_A}\right)$. Since $f\in lEnd\left(D{E}_n\right)$, for every $\overline{a}\in f^{-1}\left(a\right)$, there exists $\overline{b}\in f^{-1}\left(b\right)$ such that $\left\{\overline{a},\overline{b}\right\}\in E\left(P_n\right)$, and it is similar for the preimage of b. Note that ${f|}_A^{-1}\left(a\right)=f^{-1}\left(a\right)\subseteq A$ and ${f|}_A^{-1}\left(b\right)=f^{-1}\left(b\right)\subseteq A$. Then, ${f|}_A\in lEnd\left(P_n\right)$. In the same way, we can obtain ${f|}_{A^{\prime }}\in lEnd\left(P_n^{\prime }\right)$. Similarly, if $f\left(A\right)\subseteq A^{\prime }$ and $f\left(A^{\prime }\right)\subseteq A$, then ${f|}_A\in lHom(P_n,P_n^{\prime })$ and ${f|}_{A^{\prime }}\in lHom(P_n^{\prime },P_n)$.

(2) Let us assume that $f\left(A\right)=f\left(A^{\prime }\right)\subseteq A$ or $f\left(A\right)=f\left(A^{\prime }\right)\subseteq A^{\prime }$. Let P be a subgraph of $D{E}_n$ induced by $f\left(A\right)$. Let $a,b\in V\left(P\right)$ be such that $\{a,b\}\in E\left(P\right)$. Since $f\in lEnd\left(D{E}_n\right)$, the subgraph of $D{E}_n$ induced by $f^{-1}\left(a\right)\cup f^{-1}\left(b\right)$ contains no isolated vertices. Since ${f|}_A^{-1}\left(a\right)=f^{-1}\left(a\right)\cap A$ and ${f|}_A^{-1}\left(b\right)=f^{-1}\left(b\right)\cap A$ (${f|}_{A^{\prime }}^{-1}\left(a\right)=f^{-1}\left(a\right)\cap A^{\prime }$ and ${f|}_{A^{\prime }}^{-1}\left(b\right)=f^{-1}\left(b\right)\cap A^{\prime }$), the subgraph of $D{E}_n$ induced by ${f|}_A^{-1}{\left(a\right)\cup f|}_A^{-1}\left(b\right)$ and ${f|}_{A^{\prime }}^{-1}{\left(a\right)\cup f|}_{A^{\prime }}^{-1}\left(b\right)$ contains no isolated vertices. Then, ${f|}_A\in lHom(P_n,P)$ and ${f|}_{A^{\prime }}\in lHom(P_n^{\prime },P)$.

(3) Let us assume that $f\left(A\right),f\left(A^{\prime }\right)\subseteq A$ or $f\left(A\right),f\left(A^{\prime }\right)\subseteq A^{\prime }$, but $f\left(A\right)\ne f\left(A^{\prime }\right)$. Since $f\in lEnd\left(D{E}_n\right)$, it is easy to obtain ${f|}_A\in lHom(P_n,P_i)$ and ${f|}_{A^{\prime }}\in lHom(P_n^{\prime },P_j)$, where $V\left(P_i\right),V\left(P_j\right)\subset A$ or $V\left(P_i\right),V\left(P_j\right)\subset A^{\prime }$, $V\left(P_i\right)\cap V\left(P_j\right)=⌀$ and the subgraph of $D{E}_n$ induced by $V\left(P_i\right)\cup V\left(P_j\right)$ is disconnected.

Sufficiency. Let $f\in End\left(D{E}_n\right)$ and $a,b\in V\left(I_f\right)$ be such that $\left\{a,b\right\}\in E\left(I_f\right)$.

(1) Let us suppose that ${f|}_A\in lEnd\left(P_n\right)$ and ${f|}_{A^{\prime }}\in lEnd\left(P_n^{\prime }\right)$. Note that $f\left(t\right)=t$. If $a=t$, then $f^{-1}\left(a\right)=t$. Clearly, $\{t,s\}\in E\left(D{E}_n\right)$ for any $s\in f^{-1}\left(b\right)$. If $b=t$, then $f^{-1}\left(b\right)=t$. Clearly, $\{t,s\}\in E\left(D{E}_n\right)$ for any $s\in f^{-1}\left(a\right)$. If $a\ne t$ and $b\ne t$, then $a,b\in A$ or $a,b\in A^{\prime }$. If $a,b\in A$, then for every $\overline{a}\in f{{|}_A}^{-1}\left(a\right)$, there exists $\overline{b}\in f{{|}_A}^{-1}\left(b\right)$ such that $\left\{\overline{a},\overline{b}\right\}\in E\left(P_n\right)$, and it is similar for the preimage of b. Thus, $f{{|}_A}^{-1}\left(a\right)=f^{-1}\left(a\right)\subseteq A$ and $f{{|}_A}^{-1}\left(b\right)=f^{-1}\left(b\right)\subseteq A$. Analogously, if $a,b\in A^{\prime }$, then $f{{|}_{A^{\prime }}}^{-1}\left(a\right)=f^{-1}\left(a\right)\subseteq A^{\prime }$ and $f{{|}_{A^{\prime }}}^{-1}\left(b\right)=f^{-1}\left(b\right)\subseteq A^{\prime }$. Therefore, $f\in lEnd\left(D{E}_n\right)$. Similarly, if ${f|}_A\in lHom(P_n,P_n^{\prime })$ and ${f|}_{A^{\prime }}\in lHom(P_n^{\prime },P_n)$, then $f\in lEnd\left(D{E}_n\right)$.

(2) Let us suppose that $f\left(A\right)=f\left(A^{\prime }\right)$, ${f|}_A\in lHom(P_n,P)$ and ${f|}_{A^{\prime }}\in lHom(P_n^{\prime },P)$, where P is a subgraph of $D{E}_n$ induced by $f\left(A\right)$. If $a=t$, then $f^{-1}\left(a\right)=t$. Clearly, $\{t,s\}\in E\left(D{E}_n\right)$ for any $s\in f^{-1}\left(b\right)$. If $b=t$, then $f^{-1}\left(b\right)=t$. Clearly, $\{t,s\}\in E\left(D{E}_n\right)$ for any $s\in f^{-1}\left(a\right)$. If $a\ne t$ and $b\ne t$, then $a,b\in A$ or $a,b\in A^{\prime }$. Since ${f|}_A\in lHom(P_n,P)$ and ${f|}_{A^{\prime }}\in lHom(P_n^{\prime },P)$, the subgraphs of $D{E}_n$, which is induced by ${f|}_A^{-1}{\left(a\right)\cup f|}_A^{-1}\left(b\right)$ and ${f|}_{A^{\prime }}^{-1}{\left(a\right)\cup f|}_{A^{\prime }}^{-1}\left(b\right)$, contain no isolated vertices. Since ${f|}_A^{-1}{\left(a\right)\cup f|}_{A^{\prime }}^{-1}\left(a\right)=f^{-1}\left(a\right)$ and ${f|}_A^{-1}{\left(b\right)\cup f|}_{A^{\prime }}^{-1}\left(b\right)=f^{-1}\left(b\right)$, the subgraph of $D{E}_n$, which is induced by $f^{-1}\left(a\right)\cup f^{-1}\left(b\right)$, contains no isolated vertices. Therefore, $f\in lEnd\left(D{E}_n\right)$.

(3) Let us suppose that $f\left(t\right)=t$, ${f|}_A\in lHom(P_n,P_i)$ and ${f|}_{A^{\prime }}\in lHom(P_n^{\prime },P_j)$, where $V\left(P_i\right),V\left(P_j\right)\subset A$ or $V\left(P_i\right),V\left(P_j\right)\subset A^{\prime }$, $V\left(P_i\right)\cap V\left(P_j\right)=⌀$ and the subgraph of $D{E}_n$ induced by $V\left(P_i\right)\cup V\left(P_j\right)$ is disconnected. Then, it is a routine matter to verify that $f\in lEnd\left(D{E}_n\right)$. □

Lemma 8.

Let $f\in End\left(D{E}_n\right)$ and $n\ge 4$. If $f\left(t\right)\ne t$, then $f\in lEnd\left(D{E}_n\right)$ if and only if one of the following conditions holds:

(1) 

$I_f\cong K_3$;

(2) 

n is odd; $I_f\cong F_3$; and ${\rho }_f=\{\left[t\right],C\cup C^{\prime },B_1\cup B_1^{\prime },B_2\cup B_2^{\prime }\}$ or ${\rho }_f=\{\left[t\right],C\cup C^{\prime },B_1\cup B_2^{\prime },B_2\cup B_1^{\prime }\}$, where $B_1=\{1,5,9,\dots \}$, $B_2=\{3,7,11,\dots \}$, $B_1^{\prime }=\{1^{\prime },5^{\prime },9^{\prime },\dots \}$ and $B_2^{\prime }=\{3^{\prime },7^{\prime },{11}^{\prime },\dots \}$.

Proof. 

Necessity. Let $f\in lEnd\left(D{E}_n\right)$. Since $f\left(t\right)\ne t$, $I_f\cong K_3$ or $I_f\cong F_3$ by Lemma 2 (3).

Let us assume that $I_f\cong F_3$. If n is even, then $2/|n-1$, and ${f|}_A$ and ${f|}_{A^{\prime }}$ is not a complete folding. Thus, f is not locally strong according to [17].

If n is odd, then $2|n-1$. We only need to prove that $f\notin lEnd\left(D{E}_n\right)$ when ${\rho }_f\ne \{\left[t\right],C\cup C^{\prime },B_1\cup B_1^{\prime },B_2\cup B_2^{\prime }\}$ and ${\rho }_f\ne \{\left[t\right],C\cup C^{\prime },B_1\cup B_2^{\prime },B_2\cup B_1^{\prime }\}$. Without loss of generality, we suppose that ${\rho }_f=\left\{\left[t\right],B\cup B^{\prime },C_1\cup C_1^{\prime },C_2\cup C_2^{\prime }\right\}$, where $C_1=\{2,6,10,\dots \}$, $C_2=\{4,8,12,\dots \}$, $C_1^{\prime }=\{2^{\prime },6^{\prime },{10}^{\prime },\dots \}$, $C_2^{\prime }=\{4^{\prime },8^{\prime },{12}^{\prime },\dots \}$. Note that $\{f\left(B\right),f\left(C_2\right)\}\in E\left(I_f\right)$, but $1\in B$ is an isolated vertex of $B\cup C_2$. Thus, f is not locally strong.

Sufficiency. (1) If $I_f\cong K_3$, then ${\rho }_f=\left\{\left[t\right],C\cup C^{\prime },B\cup B^{\prime }\right\}$ or ${\rho }_f=\left\{\left[t\right],C\cup B^{\prime },B\cup C^{\prime }\right\}$. It is easy to verify that $f\in lEnd\left(D{E}_n\right)$.

(2) Let us suppose that $V\left(F_3\right)=\{j-1,j,j+1,t\}$ for some $j\in A\cup A^{\prime }$. Since $f\left(t\right)\ne t$, then $f\left(t\right)=j$. If ${\rho }_f=\{\left[t\right],C\cup C^{\prime },B_1\cup B_1^{\prime },B_2\cup B_2^{\prime }\}$, then $f\left(C\right)=f\left(C^{\prime }\right)=t$, $f\left(B_1\right)=j-1$ and $f\left(B_2\right)=j+1$, or $f\left(B_1\right)=j+1$ and $f\left(B_2\right)=j-1$. It is not difficult to check that $f\in lEnd\left(D{E}_n\right)$. If ${\rho }_f=\{\left[t\right],C\cup C^{\prime },B_1\cup B_2^{\prime },B_2\cup B_1^{\prime }\}$, then a similar argument shows that $f\in lEnd\left(D{E}_n\right)$. □

Lemma 9.

Let $n\ge 4$.

(1) 

If n is odd, then $$\begin{gathered} \left|lEnd\left(D{E}_n\right)\right|=8{\left({\sum }_{l\mid (n-1)}\left(n-l\right)\right)}^2+8{\sum }_{l\mid (n-1)}\left(n-l\right)+24n-32 \\ +16\left({\displaystyle \sum _{\begin{array}{c}2\le i,j\le n-3\\ 4<i+j\le n-1\\ i-1\mid n-1,j-1\mid n-1\end{array}}}{\displaystyle \sum _{k=1}^{n-i-j}}\left(n-(i+j+k)+1\right)\right) \end{gathered}$$;

(2) 

If n is even, then $$\begin{gathered} \left|lEnd\left(D{E}_n\right)\right|=8{\left({\sum }_{l\mid (n-1)}\left(n-l\right)\right)}^2+8{\sum }_{l\mid (n-1)}\left(n-l\right)+16(n-1)+ \\ 16\left({\displaystyle \sum _{\begin{array}{c}2\le i,j\le n-3\\ 4<i+j\le n-1\\ i-1\mid n-1,j-1\mid n-1\end{array}}}{\displaystyle \sum _{k=1}^{n-i-j}}\left(n-(i+j+k)+1\right)\right) \end{gathered}$$, where ∣ means divisible.

Proof. 

Let $f\in lEnd\left(D{E}_n\right)$. If $f\left(t\right)=t$, then there exist three cases by Lemma 7.

Case 1. Let us assume that ${f|}_A\in lEnd\left(P_n\right)$ and ${f|}_{A^{\prime }}\in lEnd\left(P_n^{\prime }\right)$, or ${f|}_A\in lHom(P_n,P_n^{\prime })$ and ${f|}_{A^{\prime }}\in lHom(P_n^{\prime },P_n)$. If ${f|}_A\in lEnd\left(P_n\right)$ and ${f|}_{A^{\prime }}\in lEnd\left(P_n^{\prime }\right)$, then there are $|lEnd\left(P_n\right){|}^2$ ways to map $P_n$ to $P_n$ and to map $P_n^{\prime }$ to $P_n$. Analogously, if ${f|}_A\in lHom(P_n,P_n^{\prime })$ and ${f|}_{A^{\prime }}\in lHom(P_n^{\prime },P_n)$, then there are $|lEnd\left(P_n\right){|}^2$ ways to map $P_n$ to $P_n^{\prime }$ and to map $P_n^{\prime }$ to $P_n$. It is known from [17] that $\left|lEnd\left(P_n\right)\right|=2{\sum }_{l\mid (n-1)}(n-l)$. Thus, we obtain $8{\left({\sum }_{l\mid (n-1)}\left(n-l\right)\right)}^2$ locally strong endomorphisms.

Case 2. Let us assume that $f\in lEnd\left(D{E}_n\right)$, satisfying Lemma 7 (2). If $P\subseteq P_n$, then there are $2\left|lEnd\right(P_n\left)\right|$ ways to map $P_n$ and $P_n^{\prime }$ to P. Analogously, if $P\subseteq P_n^{\prime }$, then there are $2\left|lEnd\right(P_n\left)\right|$ ways to map $P_n$ and $P_n^{\prime }$ to P. Thus, we obtain $8{\sum }_{l\mid (n-1)}\left(n-l\right)$ locally strong endomorphisms.

Case 3. Let us assume that $f\in lEnd\left(D{E}_n\right)$, satisfying Lemma 7 (3). Then, there are $\frac{\left|lEn{d}_i(P_n)\right|}{n-i+1}$ ways to map A to fixed $P_i$, and there are $\frac{\left|lEn{d}_j(P_n)\right|}{n-j+1}$ ways to map $A^{\prime }$ to fixed $P_j$. There are $2{\displaystyle \sum _{k=1}^{n-i-j}}\left(n-(i+j+k)+1\right)$ subgraphs in $P_n$ and $P_n^{\prime }$ isomorphic to $P_i\cup P_j$. It is known from [17] that $\left|lEn{d}_i(P_n)\right|=2(n-i+1)$. Thus, we have

$$16\left(\sum _{\begin{array}{c}2\le i,j\le n-3\\ 4<i+j\le n-1\\ i-1\mid n-1,j-1\mid n-1\end{array}}\sum _{k=1}^{n-i-j}\left(n-(i+j+k)+1\right)\right)$$

locally strong endomorphisms.

If $f\left(t\right)\ne t$, then there exist two cases by Lemma 8.

Case 4. Let us assume that $I_f\cong K_3$. Then, we have $16(n-1)$ locally strong endomorphisms by Lemma 4.

Case 5. Let us assume that $f\in lEnd\left(D{E}_n\right)$, satisfying Lemma 8(2). Then, ${\rho }_f=\{\left[t\right],C\cup C^{\prime },B_1\cup B_1^{\prime },B_2\cup B_2^{\prime }\}$ or ${\rho }_f=\{\left[t\right],C\cup C^{\prime },B_1\cup B_2^{\prime },B_2\cup B_1^{\prime }\}$. Let us suppose that $V\left(F_3\right)=\{j-1,j,j+1,t\}$ for some $j\in A\cup A^{\prime }$. Since $f\left(t\right)\ne t$, $f\left(t\right)=j$. Then, $f\left(C\right)=f\left(C^{\prime }\right)=t$. Note that there are two methods to map $\{B_1,B_2\}$ to $\{j-1,j+1\}$; there are two methods to map $\{B_1^{\prime },B_2^{\prime }\}$ to $\{j-1,j+1\}$; and there are $2(n-2)$ subgraphs of $D{E}_n$ induced by $F_3$. Thus, we obtain $8(n-2)$ locally strong endomorphisms.

From the above discussion, the result of Lemma 9 can be obtained. □

Lemma 10.

$lEnd\left(D{E}_n\right)\ne qEnd\left(D{E}_n\right)$.

Proof. 

Let f be a mapping on $V\left(D{E}_n\right)$ defined by

$$f\left(x\right)=\left\{\begin{array}{c}{1}^{\prime },x\in B\cup B^{\prime },\hfill \\ 2^{\prime },x\in C\cup C^{\prime },\hfill \\ x,x=t.\hfill \end{array}\right.$$

Then, $f\in lEnd\left(D{E}_n\right)\backslash qEnd\left(D{E}_n\right)$. Thus, $lEnd\left(D{E}_n\right)\ne qEnd\left(D{E}_n\right)$. □

Lemma 11.

$qEnd\left(D{E}_n\right)=Aut\left(D{E}_n\right)$ if and only if $n\notin \{3,4\}$.

Proof. 

Necessity. We just need to prove that $qEnd\left(D{E}_n\right)\ne Aut\left(D{E}_n\right)$ when $n\in \{3,4\}$. Let f be a mapping on $V\left(D{E}_4\right)$ defined by

$$f\left(x\right)=\left\{\begin{array}{c}1,x=3,\hfill \\ x,otherwise.\hfill \end{array}\right.$$

Then, $f\in sEnd\left(D{E}_3\right)$. Hence, $f\in qEnd\left(D{E}_3\right)$. Note that $f\left(1\right)=f\left(3\right)=1$. Then, $f\notin Aut\left(D{E}_3\right)$. Therefore, $qEnd\left(D{E}_3\right)\ne Aut\left(D{E}_3\right)$.

Let f be a mapping on $V\left(D{E}_4\right)$ defined by

$$f\left(x\right)=\left\{\begin{array}{c}1,x=3,\hfill \\ 2,x=4,\hfill \\ x,otherwise.\hfill \end{array}\right.$$

Then, $f\in qEnd\left(D{E}_4\right)$. Note that $f\left(1\right)=f\left(3\right)=1$, and $f\left(2\right)=f\left(4\right)=2$. Then, $f\notin Aut\left(D{E}_4\right)$. Therefore, $qEnd\left(D{E}_4\right)\ne Aut\left(D{E}_4\right)$.

Sufficiency. Let $n=2$; then, it is easy to see that $qEnd\left(D{E}_2\right)=Aut\left(D{E}_2\right)$.

Let $n\ge 5$ and $f\in qEnd\left(D{E}_n\right)\backslash Aut\left(D{E}_n\right)$. Then, there exist $i,j\in V\left(D{E}_n\right)$ such that $f\left(i\right)=f\left(j\right)$. Clearly, $i,j\ne t$. There are two cases.

(1) One between i and j is in A, and the other is in $A^{\prime }$. Then, there exists $k\in A\cup A^{\prime }$ such that $\{f\left(i\right),f\left(k\right)\}\in E\left(D{E}_n\right)$. Since $f\in qEnd\left(D{E}_n\right)$, there exists $\overline{k}\in f^{-1}\left(f\left(k\right)\right)$ such that $\overline{k}$ is adjacent to both i and j. This is impossible.

(2) $i,j\in A$, or $i,j\in A^{\prime }$. Without loss of generality, we suppose that $i,j\in A$. Then, there are two cases.

Case 1. $\left|f\right(A\left)\right|=2$. Then, there exists $k\in A$ such that $\{f\left(k\right),f\left(i\right)\}\in E\left(I_f\right)$. Then, either $f^{-1}\left(f\left(k\right)\right)=B$ and $f^{-1}\left(f\left(i\right)\right)=C$ are true, or $f^{-1}\left(f\left(k\right)\right)=C$ and $f^{-1}\left(f\left(i\right)\right)=B$ are true. Note that $n\ge 5$. Then, $\left|B\right|\ge 3$. Since $f\in qEnd\left(D{E}_n\right)$, there exists $c\in C$ such that $\{c,b\}\in E\left(D{E}_n\right)$ for any $b\in B$. This contradicts that c is adjacent to at most two vertices of B.

Case 2. $\left|f\right(A\left)\right|\ge 3$. If $f\left(i\right)$ is the middle point in image $f\left(A\right)$, then there exist $f\left(u\right),f\left(v\right)\in f\left(A\right)$ such that $\left\{f\left(i\right),f\left(u\right)\right\}\in E\left(I_{{f|}_A}\right)$ and $\left\{f\left(i\right),f\left(v\right)\right\}\in E\left(I_{{f|}_A}\right)$. Since $f\in qEnd\left(D{E}_n\right)$, there exists $\overline{u}\in f^{-1}\left(f\left(u\right)\right)$ such that $\{\overline{u},i\}\in E\left(D{E}_n\right)$ and $\{\overline{u},j\}\in E\left(D{E}_n\right)$, and there exists $\overline{v}\in f^{-1}\left(f\left(v\right)\right)$ such that $\{\overline{v},i\}\in E\left(D{E}_n\right)$ and $\{\overline{v},j\}\in E\left(D{E}_n\right)$. So, $\left\{i,j,\overline{u},\overline{v}\right\}$ form cycle $C_4$. This contradicts that the subgraph of $D{E}_n$ induced by A is a path. If $f\left(i\right)$ is the end point in image $f\left(A\right)$, then there is exactly one vertex $f\left(w\right)\in f\left(A\right)$ such that $\left\{f\left(i\right),f\left(w\right)\right\}\in E\left(I_{{f|}_A}\right)$. But there still exists one vertex $f\left(k\right)\in f\left(A\right)$ such that $\left\{f\left(w\right),f\left(k\right)\right\}\in E\left(I_{{f|}_A}\right)$, since $\left|f\left(A\right)\right|\ge 3$. Since $f\in qEnd\left(D{E}_n\right)$, there exists $\overline{w}\in f^{-1}\left(f\left(w\right)\right)$ such that $\{\overline{w},i\}\in E\left(D{E}_n\right)$ and $\{\overline{w},j\}\in E\left(D{E}_n\right)$, and there exists $\overline{k}\in f^{-1}\left(f\left(k\right)\right)$ such that $\{\overline{w},\overline{k}\}\in E\left(D{E}_n\right)$ . Then, $\overline{w}$ is adjacent to at least three vertices of set A. This is impossible.

Consequently, $qEnd\left(D{E}_n\right)=Aut\left(D{E}_n\right)$ for $n\ge 5$. □

Lemma 12.

$\left|Aut\left(D{E}_n\right)\right|=8$.

Proof. 

Let $f\in Aut\left(D{E}_n\right)$, then $f\left(t\right)=t$. If $f\left(A\right)=A$ and $f\left(A^{\prime }\right)=A^{\prime }$, then there are four automorphisms in this case. Analogously, there are also four automorphisms such that $f\left(A\right)=A^{\prime }$ and $f\left(A^{\prime }\right)=A$. Therefore, $\left|Aut\left(D{E}_n\right)\right|=8$. □

Now, we obtain the main theorems of this paper.

Theorem 1. 

$$Endospec\left(D{E}_n\right)=\left\{\begin{array}{ll}(32,32,32,8,8,8),\hfill & n=2,\\ (232,232,136,72,72,8),\hfill & n=3,\\ (1296,1280,224,144,8,8),\hfill & n=4,\\ (A_1\left(n\right),B_1\left(n\right),C_1\left(n\right),8,8,8),\hfill & n\ge 5,andnisodd,\hfill \\ (A_2\left(n\right),B_2\left(n\right),C_2\left(n\right),8,8,8),\hfill & n\ge 5,andniseven.\hfill \end{array}\right.$$

where$A_1\left(n\right)=4{((n+1)2^{n-1}-(2n-1)\left({}_{\frac{n-1}{2}}^{n-1}\right))}^2+2(n-2)({(2^{\frac{n+1}{2}}+2^{\frac{n-1}{2}}-4)}^2+8(2^{\frac{n+1}{2}}+2^{\frac{n-1}{2}}-4)+8)+16(n-1)$;

$A_2\left(n\right)=4{\left((n+1)2^{n-1}-n\left({}_{\frac{n}{2}}^n\right)\right)}^2+2(n-2)\left(4{\left(2^{\frac{n}{2}}-2\right)}^2+16\left(2^{\frac{n}{2}}-2\right)+8\right)+16(n-1)$;

$B_1\left(n\right)=A_1\left(n\right)-4\left({\displaystyle \sum _{\begin{array}{c}2\le i,j\le n-2\\ 4\le i+j\le n\end{array}}}\left(n-i-j+1\right)\frac{\left|Hom(P_n,P_i)\right|}{n-i+1}·\frac{\left|Hom(P_n,P_j)\right|}{n-j+1}\right)$;

$B_2\left(n\right)=A_2\left(n\right)-4\left({\displaystyle \sum _{\begin{array}{c}2\le i,j\le n-2\\ 4\le i+j\le n\end{array}}}\left(n-i-j+1\right)\frac{\left|Hom(P_n,P_i)\right|}{n-i+1}·\frac{\left|Hom(P_n,P_j)\right|}{n-j+1}\right)$;

$C_1\left(n\right)=16\left({\displaystyle \sum _{\begin{array}{c}2\le i,j\le n-3\\ 4<i+j\le n-1\\ i-1\mid n-1,j-1\mid n-1\end{array}}}{\displaystyle \sum _{k=1}^{n-i-j}}\left(n-(i+j+k)+1\right)\right)+8{\left({\sum }_{l\left|\right(n-1)}\left(n-l\right)\right)}^2+8{\sum }_{l\mid (n-1)}\left(n-l\right)+24n-32$;

$C_2\left(n\right)=16\left({\displaystyle \sum _{\begin{array}{c}2\le i,j\le n-3\\ 4<i+j\le n-1\\ i-1\mid n-1,j-1\mid n-1\end{array}}}{\displaystyle \sum _{k=1}^{n-i-j}}\left(n-(i+j+k)+1\right)\right)+8{\left({\sum }_{l\left|\right(n-1)}\left(n-l\right)\right)}^2+8{\sum }_{l\mid (n-1)}\left(n-l\right)+16(n-1)$, where ∣ means divisible;

$|Hom(P_n,P_k)|=-{\displaystyle \sum _{i=0}^{n-2}}{2}^{n-1-i}{\displaystyle \sum _{j\in Z}}\left(\left(\begin{array}{c}i\\ \lceil \frac{i}{2}\rceil -j(k+1)\end{array}\right)-\left(\begin{array}{c}i\\ \lfloor \frac{i+k-1}{2}\rfloor -j(k+1)\end{array}\right)\right)+k·2^{n-1}$, where Z is the set of integers.

Proof. 

This follows immediately from Lemmas 3–6, 9, 11 and 12. □

Theorem 2. 

$$Endotype\left(D{E}_n\right)=\left\{\begin{array}{ll}4,\hfill & n=2,\hfill \\ 22,\hfill & n=3,\hfill \\ 15,\hfill & n=4,\hfill \\ 7,\hfill & n\ge 5.\hfill \end{array}\right.$$

Proof. 

This follows immediately from Theorem 1. □

4. Conclusions

In this paper, we give the endomorphism spectra and endomorphism types of double-edge fan graphs by studying six classes of endomorphisms.

The purpose of this paper is to establish the relation between the algebraic theory of semigroups and graph theory to study the combinatorial counting properties of graphs using the algebraic properties of the endomorphic monoids of graphs. In the future, we will stick to research in this field and reveal more combinatorial properties of the endomorphism monoids of graphs.