Generalized Connectivity of the Mycielskian Graph under g-Extra Restriction

Abstract

The g-extra connectivity is a very important index to evaluate the fault tolerance, reliability of interconnection networks. Let g be a non-negative integer, G be a connected graph with vertex set V and edge set E, a subset $S\subseteq V$ is called a g-extra cut of G if the graph induced by the set $G-S$ is disconnected and each component of $G-S$ has at least $g+1$ vertices. The g-extra connectivity of G, denoted as ${\kappa }_g\left(G\right)$, is the cardinality of the minimum g-extra cut of G. Mycielski introduced a graph transformation to discover chromatic numbers of triangle-free graphs that can be arbitrarily large. This transformation converts a graph G into a new compound graph called $\mu \left(G\right)$, also known as the Mycielskian graph of G. In this paper, we study the relationship on g-extra connectivity between the Mycielskian graph $\mu \left(G\right)$ and the graph G. In addition, we show that ${\kappa }_3\left(\mu \left(G\right)\right)=2{\kappa }_1\left(G\right)+1$ for ${\kappa }_1\left(G\right)\le min\{4,\lfloor \frac{n}{2}\rfloor \}$, and prove the bounds of ${\kappa }_{2g+1}\left(\mu \left(G\right)\right)$ for $g\ge 2$.

1. Introduction

With the rise and swift progress of high-performance parallel computer technology, there is increasing focus on interconnection networks that exhibit strong performance. A well-designed topological structure offers significant benefits in enhancing reliability. When designing the network’s topological structure, fault tolerance is a fundamental consideration. This means that the interconnection network should be able to operate effectively even when certain nodes and edges fail, ensuring that it retains specific network properties. Moreover, the topological structure of an interconnection network can be modeled as an undirected graph $G=(V,E)$, where every vertex of V corresponds to a processor, and each edge of E corresponds to a communication link. Then many computer scientists and engineers use some parameters of graph theory to design and analyzing topological structures of interconnection networks, such as the connectivity. In order to design the topological structure of a network with good performance, the fault-tolerance must be considered. This means that the network should be able to function effectively even if certain nodes and edges fail, while still maintaining specific network properties. Additionally, the structure of an interconnection network can be represented as an undirected graph $G=(V,E)$, where each vertex in V represents a processor, and each edge in E represents a communication link. Therefore, many computer scientists and engineers utilize various parameters from graph theory to design and analyze the topological structures of interconnection networks, including connectivity.

The connectivity is a crucial measure of fault-tolerance in an interconnection network. Generally, a higher connectivity indicates better fault-tolerance. Let $F\subseteq V\left(G\right)$, F is called a cut set of G if the graph obtained by removing F is disconnected or trivial. The connectivity of a graph G, denoted by $\kappa \left(G\right)$, is the minimum number of elements of all cut set of G. A graph G is said to be k-connected if $\kappa \left(G\right)\ge k$.

To analyze disconnected graphs resulting from a vertex-cut in more detail, Harary [1] proposed investigating the conditional connectivities while imposing additional constraints on the vertex-cut F and/or the component of $G-F$. A notion concerning the number of vertices of each component associated with the disconnected graph $G-F$ was first introduced by Fábrega and Fiol [2]. Let g be a non-negative integer, $G=(V,E)$ be a connected graph, a subset $S\subseteq V$ is a g-extra cut of G if the graph induced by the set $V-S$ is disconnected and each component of $G-S$ has at least $g+1$ vertices. The g-extra connectivity of G, denoted as ${\kappa }_g\left(G\right)$, is the cardinality of the minimum g-extra cut of G. When $g=0$, we will write for short $\kappa \left(G\right)$ instead of ${\kappa }_0\left(G\right)$. The exploration of the g-extra connectivity has achieved much progress, see [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20].

Many researchers are interested with chromatic number without small circles, see [21,22]. To search for arbitrarily large chromatic numbers of triangle-free graphs, Mycielski [23] introduced a graph transformation that converts a graph G into a new compound graph $\mu \left(G\right)$. This transformed graph is known as the Mycielskian graph of G, as depicted below. For a graph $G=(V,E)$, the graph $\mu \left(G\right)$ with $V\left(\mu \left(G\right)\right)=V\cup V^{\prime }\cup \left\{u\right\}$, $E\left(\mu \left(G\right)\right)=E\cup \left\{x{y}^{\prime }\right|xy\in E\}\cup \left\{y^{\prime }u\right|y^{\prime }\in V^{\prime }\}$, where $V^{\prime }=\left\{x^{\prime }\right|x\in V\}$. We call the vertex $x^{\prime }$ is the twin of the vertex x (and x is also the twin of $x^{\prime }$). Morever, the set $F^{\prime }$ ($F^{\prime }\subseteq V^{\prime }$) is called the twin of F (and F is also the twin of $F^{{}^{\prime }}$) for some $F\subseteq V$. The vertex u is called as the root of $\mu \left(G\right)$. For instance, the Mycielskian graph of a path of order n is showed in Figure 1.

Recently, Chang et al. [24] have verified that $\kappa \left(\mu \right(G\left)\right)\ge \mu \left(G\right)+1$ if a graph G has no isolated vertices. In 2008, Raj and Balakrishnan [25] have studied the edge-connectivity $\lambda \left(\mu \right(G\left)\right)$ and the vertex-connectivity $\kappa \left(\mu \right(G\left)\right)$. In 2016, Guo and Liu [26] have shown that if G is a connected graph, then $\mu \left(G\right)$ is super-$\lambda$ if and only if $G\ncong K_2$, and $\mu \left(G\right)$ is super-$\kappa$ if and only if $\delta \left(G\right)<2\kappa \left(G\right)$. In addition, Guo et al. [27] derived the Mycielskian graph of a digraph in terms of the vertex(arc) connectivity. Recently, the relationship between the 3-connectivity of G has been established and generalized 3-connectivity of the Mycielskian graph $\mu \left(G\right)$ has been study by Li et al. [28], i.e., ${\kappa }_3\left(\mu \left(G\right)\right)\ge {\kappa }_3\left(G\right)+1$. Moreover, they determined the generalized 3-connectivity of the Mycielskian graph of the tree $T_n$, the complete graph $K_n$ and the complete bipartite graph $K_{a,b}$. Now, the results on some graph parameters of the Mycielskian graphs have been obtained, see [29,30,31,32,33].

In this paper, we will discuss the relationship between the g-extra connectivity of $\mu \left(G\right)$ and G. In addition, we show that ${\kappa }_3\left(\mu \left(G\right)\right)=2{\kappa }_1\left(G\right)+1$ for ${\kappa }_1\left(G\right)\le min\{4,\lfloor \frac{n}{2}\rfloor \}$, and propose the bounds of ${\kappa }_{2g+1}\left(\mu \left(G\right)\right)$ for $(g\ge 2)$.

2. Terminology and Notations

All graphs are simple, connected, finite and undirected in following section. For graph theoretical symbols and terminology not expounded here, we use for reference [34]. For a graph G, let V and E represent the set of vertices and the set of edges of G. Let G and H be two graphs, H is called the subgraph of G subject to $V\left(H\right)\subseteq V\left(G\right)$, $E\left(H\right)\subseteq E\left(G\right)$. For any vertex subset X of the graph G, the graph $G-X$ is the subgraph of G obtained by deleting all the vertices of X together with the edges incident with them from G. In case $X=\left\{v\right\}$, we simply write $G-v$ instead of $G-X$. For a vertex $u\in V\left(G\right)$, the neighborhood of u in G, denoted by $N_G\left(u\right)$, is the set of vertices adjacent to u in G. For a subset $X\subseteq V\left(G\right)$, the neighborhood of X in G is defined as $N_G\left(X\right)={\bigcup }_{u\in X}{N}_G\left(u\right)-X$. The degree of u in G is denoted by $de{g}_G\left(u\right)=\left|N_G\left(u\right)\right|$. We also denote the minimum degree $\delta \left(G\right)=min\left\{de{g}_G\left(u\right)\right|u\in V\left(G\right)\}$.

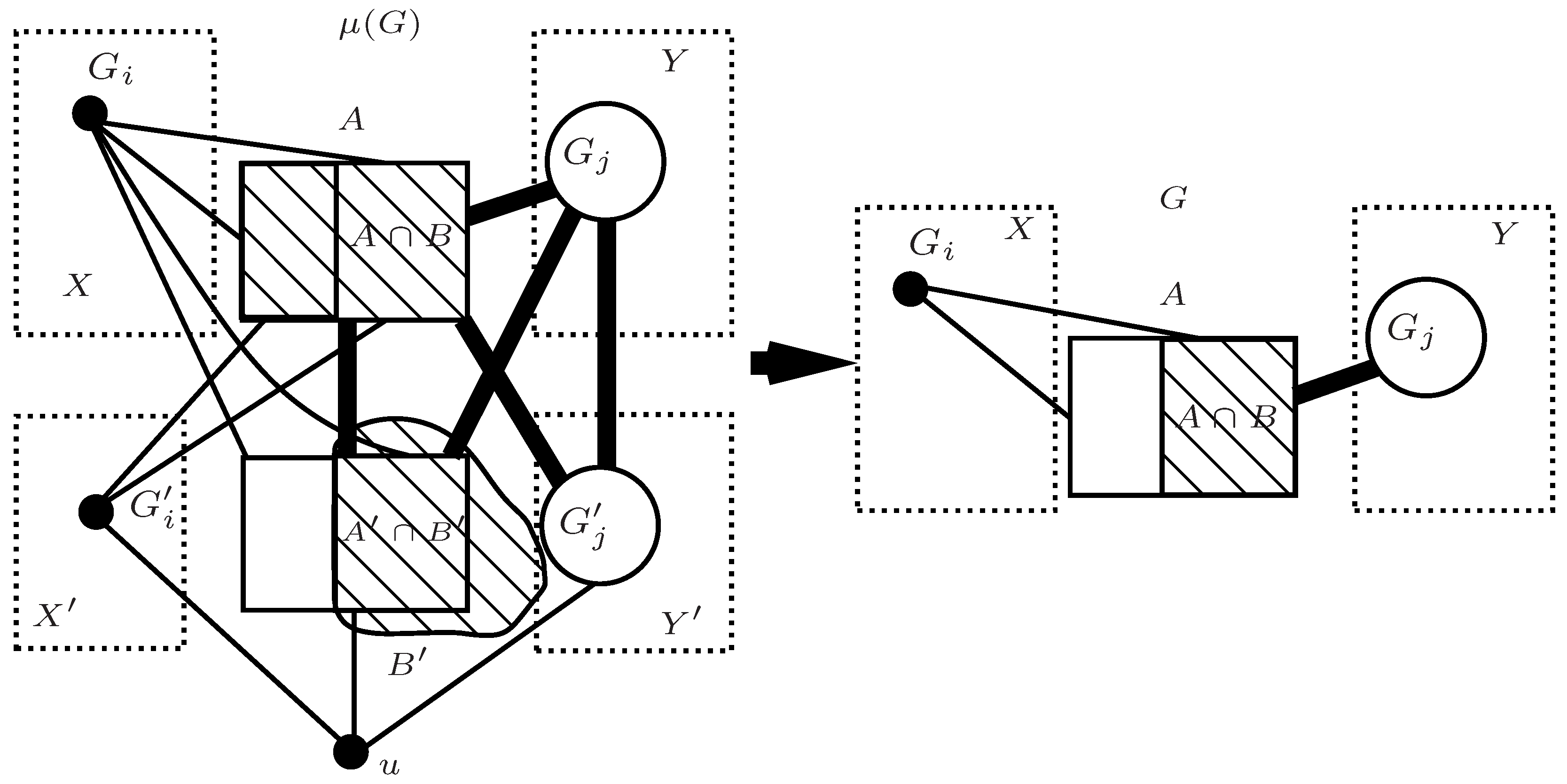
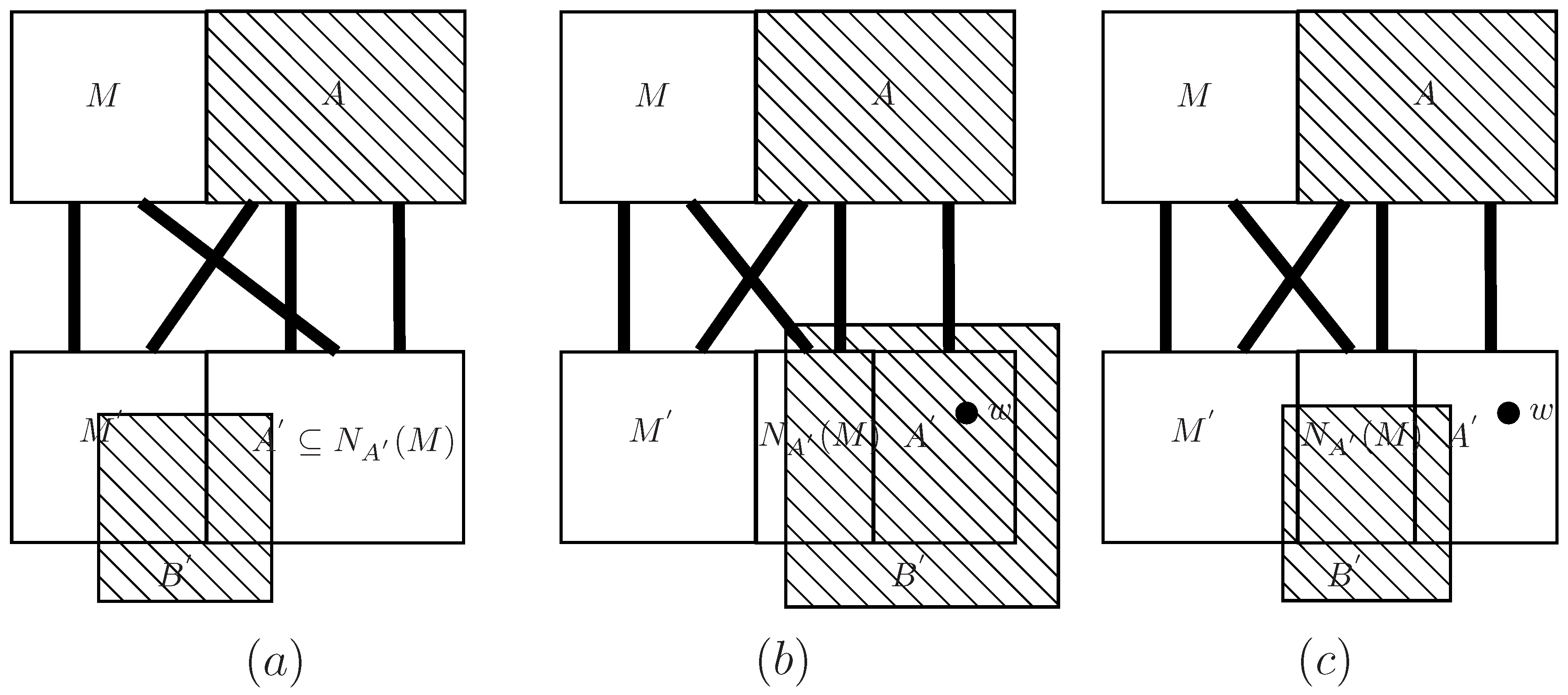
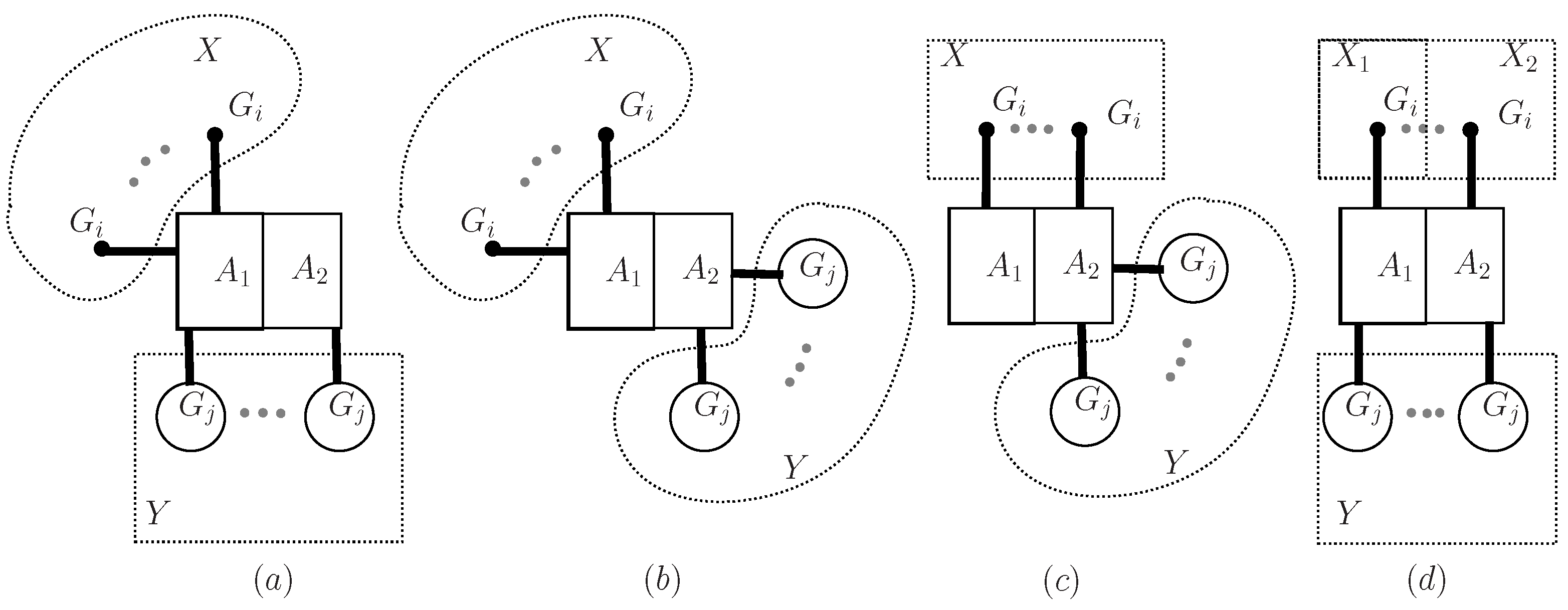
3. Main Results

In this section, we determine the relationship between ${\kappa }_g\left(\mu \left(G\right)\right)$ and ${\kappa }_g\left(G\right)$ for $g\ge 0$.

Balakrishnan [25] have the following conclusions.

Lemma 1

([25]). If G is a connected graph, then $\kappa \left(\mu \right(G\left)\right)=min\left\{\delta \right(G)+1,2\kappa (G)+1\}.$

For a graph G, in view of the fact ${\kappa }_0\left(G\right)=\kappa \left(G\right)$ and Lemma 1, the relationship between ${\kappa }_g\left(\mu \left(G\right)\right)$ and ${\kappa }_g\left(G\right)$ is immediately obtained for $g\ge 0$.

Theorem 1.

If G is a connected graph, then ${\kappa }_0\left(\mu \left(G\right)\right)=min\{\delta \left(G\right)+1,2{\kappa }_0\left(G\right)+1\}.$

Next, we investigate the relationship between ${\kappa }_g\left(\mu \left(G\right)\right)$ and ${\kappa }_g\left(G\right)$ for $g\ge 1$.

Lemma 2.

Let F be a vertex cut of G, and $G_1,G_2,\dots ,G_r$$(r\ge 2)$ be all components of $G-F$.

(1)

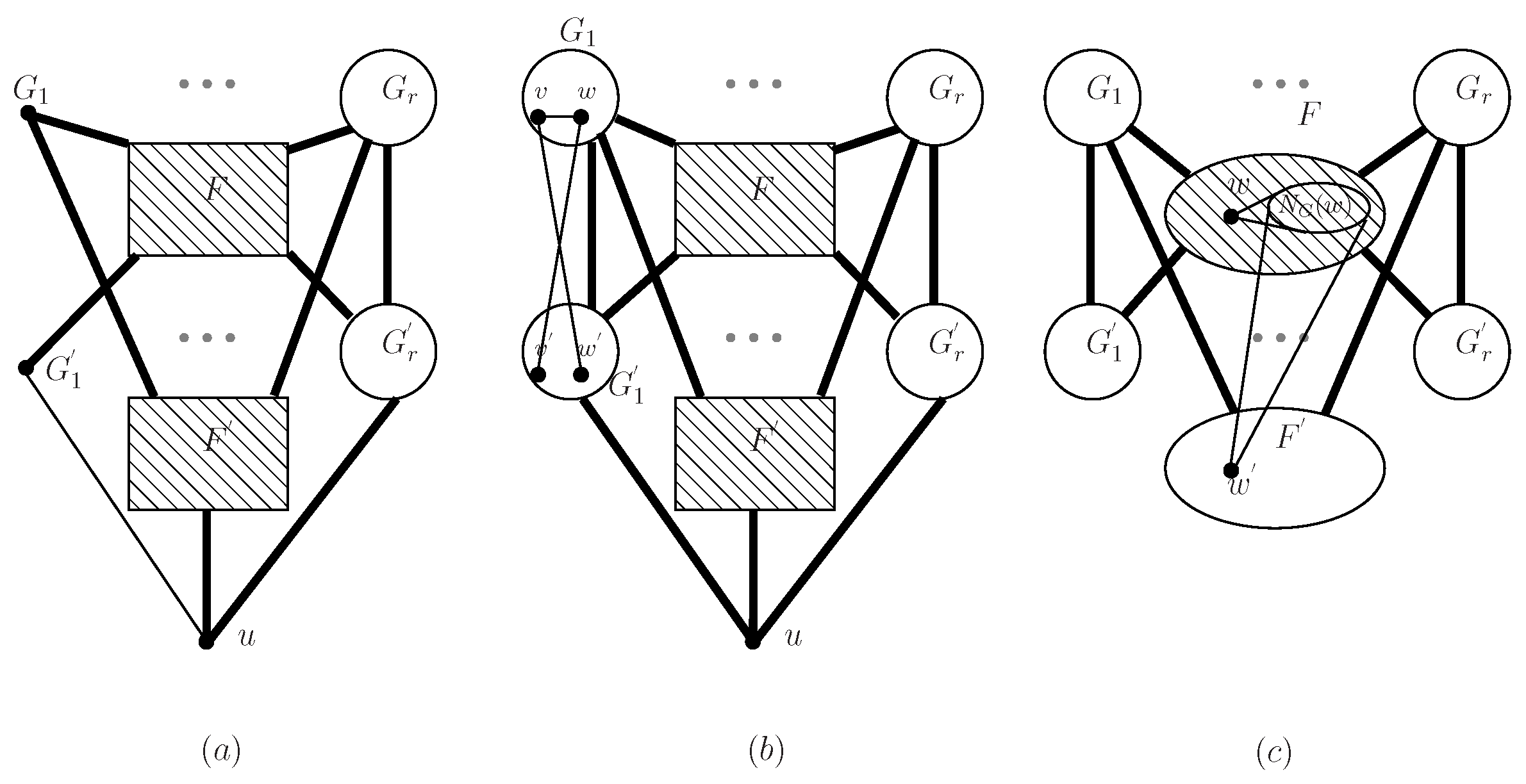
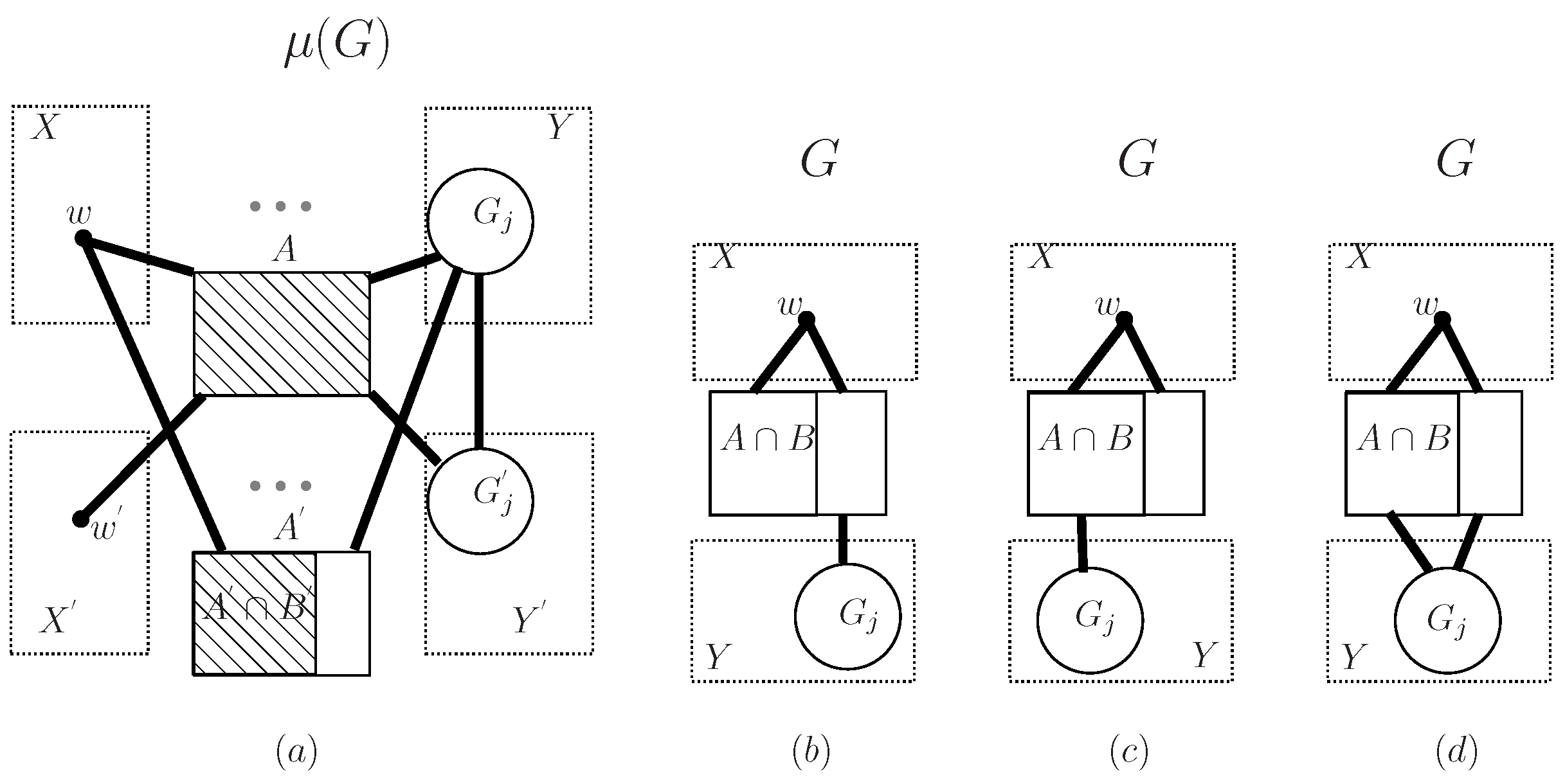
If there exists some $G_i$$(1\le i\le r)$ such that $|G_i|=1$, then $\mu \left(G\right)-(F\cup F^{\prime })$ ($F^{\prime }$ be the twin of F) is disconnected and the smallest component is the isolated vertex $G_i$.

(2)

If $|G_i|\ge 2$ for any $G_i$$(1\le i\le r)$, then $G_i$ is connected to $G_i^{\prime }$ in $\mu \left(G\right)-(F\cup F^{\prime })$ (where $G_i^{\prime }$ and $F^{\prime }$ be the twin of $G_i$ and F, respectively).

(3)

If there exists one vertex w such that $w\in F$ and $N_G\left(w\right)\subseteq F$, then $\mu \left(G\right)-(F\cup \{u\left\}\right)$ is disconnected and $w^{\prime }$ ($w^{\prime }$ is the twin of w) is an isolated vertex.

Proof of Lemma 2.

(1) As there exists some $G_i$$(1\le i\le r)$ such that $|G_i|=1$, without loss of generality, we set $|G_1|=1$. By the construction of $\mu \left(G\right)$, $N_{\mu \left(G\right)}\left(G_1\right)\subseteq (F\cup F^{\prime })$ (see Figure 2a). Then $\mu \left(G\right)-(F\cup F^{\prime })$ is disconnected and $G_1$ is the smallest component.

(2)

In this situation, $|G_i|\ge 2$ for any $G_i$$(1\le i\le r)$, there exists one edge $(v,w)\in E\left(G_i\right)$. By the construction of $\mu \left(G\right)$, $(v^{\prime },w)\in E\left(\mu \left(G\right)\right)$ and $(v,w^{\prime })\in E\left(\mu \left(G\right)\right)$ (see Figure 2b). Then $G_i$ is connected to $G_i^{\prime }$ in $(\mu \left(G\right)-(F\cup F^{\prime }))$.

(3)

In this situation, there exists one vertex w such that $w\in F$ and $N_G\left(w\right)\subseteq F$. By the construction of $\mu \left(G\right)$, $w^{\prime }$ is the twin of w, and $N_{\mu \left(G\right)}\left(w^{\prime }\right)\subseteq (F\cup \left\{u\right\})$ (see Figure 2c). Then $\mu \left(G\right)-(F\cup \{u\left\}\right)$ is disconnected and $w^{\prime }$ is an isolated vertex.

□

Figure 2. An illustration of the proof of Lemma 2.

Figure 2. An illustration of the proof of Lemma 2.

Theorem 2.

Let G be a connected graph with n vertices such that ${\kappa }_1\left(G\right)\le min\{4,\lfloor \frac{n}{2}\rfloor \}$. Then

$${\kappa }_3\left(\mu \left(G\right)\right)=2{\kappa }_1\left(G\right)+1.$$

Proof of Theorem 2.

According to the definition of ${\kappa }_1\left(G\right)$, there exists a set $F\subseteq V$ with $\left|F\right|={\kappa }_1\left(G\right)$ such that $G-F$ is disconnected and each component of $G-F$ has at least 2 vertices. Let $F^{\prime }$ be the twin of F. Then $\mu \left(G\right)-(F\cup F^{\prime }\cup \left\{u\right\})$ (u is the root vertex of $\mu \left(G\right)$) is disconnected and each the rest of component has at least 4 vertices. Therefore, ${\kappa }_3\left(\mu \left(G\right)\right)\le 2{\kappa }_1\left(G\right)+1$.

Next, we show ${\kappa }_3\left(\mu \left(G\right)\right)\ge 2{\kappa }_1\left(G\right)+1$. Conversely, we assume that ${\kappa }_3\left(\mu \left(G\right)\right)\le 2{\kappa }_1\left(G\right)$. Let S be a vertex set of $\mu \left(G\right)$ with $\left|S\right|\le 2{\kappa }_1\left(G\right)$, we need show it is a contradiction. Without loss of generality, let $S\cap V=A$, $S\cap V^{\prime }=B^{\prime }$ and $G_1,G_2,\dots ,G_r$$(r\ge 2)$ be all components of $G-A$. The following two cases will be discussed.

Case 1. $u\notin S$.

Subcase 1.1 $G-A$ is connected.

Let $M=G-A$, where $M^{\prime }$ and $A^{\prime }$ are the twins of M and A, severally. We consider the situations as follow.

If $(M^{\prime }\cup N_{A^{\prime }}\left(M\right))\subseteq B^{\prime }$, then $\mu \left(G\right)-S$ is disconnected (see Figure 3a). Thus, $2{\kappa }_1\left(G\right)\ge \left|S\right|=|A\cup B^{\prime }|\ge |A\cup M^{\prime }\cup N_{A^{\prime }}\left(M\right)|\ge n+1$, which contradicts with ${\kappa }_1\left(G\right)\le \lfloor \frac{n}{2}\rfloor$.

If $(M^{\prime }\cup N_{A^{\prime }}\left(M\right))⊈B^{\prime }$, then there exists at least one vertex w such that $w\in (M^{\prime }\cup N_{A^{\prime }}\left(M\right))$ and $w\notin B^{\prime }$. Since the root vertex u is adjacent to all vertices of $V^{\prime }$ and w is connected to the connected component M, $\mu \left(G\right)-S$ is connected (see Figure 3b), a contradiction.

Subcase 1.2 $G-A$ is disconnected and each component of $G-A$ has at least two vertices.

Clearly, $|V\cap S|=\left|A\right|\ge {\kappa }_1\left(G\right)$, and $|B^{\prime }|\le {\kappa }_1\left(G\right)$. By Lemma 2$\left(2\right)$, $G_i$ is connected to $G_i^{\prime }$ ($G_i^{\prime }$ is the twin of $G_i$), and $G_i^{\prime }$ is connected to the root vertex u, then $\mu \left(G\right)-S$ is connected, a contradiction.

Subcase 1.3 $G-A$ is disconnected and at least one component is an isolated vertex.

Let $X=\left\{G_i\right|\left|G_i\right|=1,1\le i\le r\}$ and $Y=\left\{G_j\right|\left|G_j\right|\ge 2,1\le j\le r\}$. We distinguish between the following two situations.

If $N_{A^{\prime }}\left(G_i\right)\subseteq (A^{\prime }\cap B^{\prime })$ for some $G_i\in X$. By Lemma 2 $\left(1\right)$, $G_i$$(G_i\in X)$ is an isolated vertex in $\mu \left(G\right)-S$, which contradicts with the definition of ${\kappa }_3\left(\mu \left(G\right)\right)$.

Next, we suppose that $N_{A^{\prime }}\left(G_i\right)⊈(A^{\prime }\cap B^{\prime })$ for any $G_i\in X$, then it implies $G_i$ connected to $A^{\prime }-(A^{\prime }\cap B^{\prime })$ for any $G_i\in X$. First, we consider $N_{A^{\prime }}\left(G_j\right)\subseteq (A^{\prime }\cap B^{\prime })$ for some $G_j\in Y$, it implies $N_A\left(G_j\right)\subseteq (A\cap B)$ for some $G_j$ ($G_j\in Y$) in graph G, then every component of $G-(A\cap B)$ has at least two vertices (see Figure 4). So $|A\cap B|\ge {\kappa }_1\left(G\right)$. If $\left|A\right|\le {\kappa }_1\left(G\right)-1$, then it contradicts with $|A\cap B|\le \left|A\right|\le {\kappa }_1\left(G\right)-1$. If $\left|A\right|\ge {\kappa }_1\left(G\right)$, then $\left|S\right|=\left|A\right|+|B^{\prime }|+|\left\{u\right\}|>|A|+|A^{\prime }\cap B^{\prime }|+|\left\{u\right\}|\ge 2{\kappa }_1\left(G\right)+1$, which contradicts with $\left|S\right|\le 2{\kappa }_1\left(G\right)$. Second, $N_{A^{\prime }}\left(G_j\right)⊈(A^{\prime }\cap B^{\prime })$, it implies $G_j$ connected to $A^{\prime }-(A^{\prime }\cap B^{\prime })$ for any $G_j$ ($G_j\in Y$). By the construction of $\mu \left(G\right)$, all components of $G-A$ are connected to $A^{\prime }-(A^{\prime }\cap B^{\prime })$, and $A^{\prime }-(A^{\prime }\cap B^{\prime })$ is connected to the root vertex u, then $\mu \left(G\right)-S$ is connected, a contradiction.

Case 2. $u\in S$.

Subcase 2.1 $G-A$ is connected.

Let $M=G-A$.

If $A^{\prime }\subseteq N_{A^{\prime }}\left(M\right)$, then $\mu \left(G\right)-S$ is connected (see Figure 5a), a contradiction.

If $A^{\prime }⊈N_{A^{\prime }}\left(M\right)$. By the construction of $\mu \left(G\right)$, all vertices in $(A^{\prime }-N_{A^{\prime }}\left(M\right))$ are connected to A. If $(A^{\prime }-N_{A^{\prime }}\left(M\right))\subseteq B^{\prime }$, then $\mu \left(G\right)-S$ is connected (see Figure 5b). If $(A^{\prime }-N_{A^{\prime }}\left(M\right))⊈B^{\prime }$, then there exists at least one vertex w such that $w\in (A^{\prime }-N_{A^{\prime }}\left(M\right))$ and $w\notin B^{\prime }$. Thus, $\mu \left(G\right)-S$ is disconnected and the smallest component is the vertex w (see Figure 5c), a contradiction.

Subcase 2.2 $G-A$ is disconnected and every component of $G-A$ has at least two vertices.

Clearly, $|V\cap S|=\left|A\right|\ge {\kappa }_1\left(G\right)$, and $|V^{\prime }\cap S|=|B^{\prime }|\le {\kappa }_1\left(G\right)-1$.

Subcase 2.2.1 $A^{\prime }\cap B^{\prime }=\varnothing$.

By Lemma 2 $\left(3\right)$, we have the following fact.

Fact 1. All vertices of A are adjacent to some components of $G-A$.

If there exists one component, say $G_1$, such that $N_A\left(G_1\right)=A$, then $G_1$ is connected to all vertices of $A^{\prime }$ (see Figure 6a). By Fact 1, all vertices of $A^{\prime }$ are adjacent to some components of $G-A$, then $\mu \left(G\right)-S$ is connected, a contradiction.

Otherwise, $N_A\left(G_i\right)⊊A$ for any $G_i$ of $G-A$.

Let $G_1,G_2,\dots ,G_t$$(t<r)$ be some components of $G-A$ such that $N_A\left(G_1\right)\cup N_A\left(G_2\right)\dots \cup N_A\left(G_t\right)=A_1$$(A_1\subseteq A)$, and $N_A\left(G_{t+1}\right)\cup N_A\left(G_{t+2}\right)\dots \cup N_A\left(G_{r-1}\right)=A_2$$(A_1\cap A_2=\varnothing )$. If there exists the component $G_r$ of $G-A$ such that $N_A\left(G_r\right)\cap A_1\ne \varnothing$ and $N_A\left(G_r\right)\cap A_2\ne \varnothing$, by the construction of $\mu \left(G\right)$, $G_r$ connected to $A_1^{\prime }$ and $A_2^{\prime }$, then $\mu \left(G\right)-S$ is connected. So, $N_A\left(G_r\right)\cap A_1\ne \varnothing$ and $N_A\left(G_r\right)\cap A_2=\varnothing$ or $N_A\left(G_r\right)\cap A_1=\varnothing$ and $N_A\left(G_r\right)\cap A_2\ne \varnothing$ or $N_A\left(G_r\right)\cap A_1=\varnothing$ and $N_A\left(G_r\right)\cap A_2=\varnothing$. Then we have the following fact.

Fact 2. There exist some components $G_1,G_2,\dots ,G_t$$(t<r)$ of $G-A$ such that $(N_A\left(G_1\right)\cup N_A\left(G_2\right),\dots ,\cup N_A\left(G_t\right))\bigcap (N_A\left(G_{t+1}\right)\cup N_A\left(G_{t+2}\right),\dots ,\cup N_A\left(G_r\right))=\varnothing$.

By Fact 2, we decompose the set A into $A_1$ and $A_2$, then some components of $G-A$ are connected to $A_1$, and the remaining components of $G-A$ are connected to $A_2$. By the construction of G, $G-A_1$ is disconnected and each component has at least two vertices, then $|A_1|\ge {\kappa }_1\left(G\right)$. By the same reason, $|A_2|\ge {\kappa }_1\left(G\right)$ (see Figure 6b). So, $\left|A\right|>|A_1|+|A_2|\ge 2{\kappa }_1\left(G\right)$, which contradicts with $\left|A\right|\le \left|S\right|-\left|\left\{u\right\}\right|\le 2{\kappa }_1\left(G\right)-1$.

Subcase 2.2.2 $A^{\prime }\cap B^{\prime }\ne \varnothing$.

If there exists one component, say $G_1$, such that $N_{A^{\prime }}\left(G_1\right)\subseteq (A^{\prime }\cap B^{\prime })$, then $N_A\left(G_1\right)\subseteq (A\cap B)$, and each component of $G-(A\cap B)$ has at least two vertices in G. Clearly, $|A\cap B|\ge {\kappa }_1\left(G\right)$, which contradicts with $|A\cap B|\le |B^{\prime }|\le {\kappa }_1\left(G\right)-1$. Otherwise, $N_{A^{\prime }}\left(G_1\right)⊈(A^{\prime }\cap B^{\prime })$, it implies $G_i$ is connected to $A^{\prime }-(A^{\prime }\cap B^{\prime })$ for any $G_i$. By the same reason with the Subcase $2.2.1$ (the vertex set $A^{\prime }-(A^{\prime }\cap B^{\prime })$ in Subcase 2.2.2 is the same as the vertex set $A^{\prime }$ in Subcase $2.2.1$).

Subcase 2.3 $G-A$ is disconnected and at least one component is an isolated vertex.

Let $X=\left\{G_i\right|\left|G_i\right|=1,1\le i\le r\}$ and $Y=\left\{G_j\right|\left|G_j\right|\ge 2,1\le j\le r\}$.

Subcase 2.3.1 $A^{\prime }\cap B^{\prime }=\varnothing$.

If there exists one vertex $w^{\prime }$ such that $w^{\prime }\in X^{\prime }$ and $w^{\prime }\notin B^{\prime }$, then $\mu \left(G\right)-S$ is disconnected and $w^{\prime }$ is an isolated vertex in $\mu \left(G\right)-S$, which contradicts with the definition of ${\kappa }_3\left(\mu \left(G\right)\right)$. Then we have the following fact.

Fact 3. $X^{\prime }\subseteq B^{\prime }$.

If there exists one component $G_t$ of $G-A$ such that $N_A\left(G_t\right)=A$, then $G_t$ is connected to all vertices of $A^{\prime }$. By Fact 1, all vertices of $A^{\prime }$ are adjacent to some components of $G-A$, then $\mu \left(G\right)-S$ is connected, a contradiction.

Otherwise, $N_A\left(G_t\right)⊊A$ for any $G_t$ of $G-A$.

By Fact 2, we decompose the set A into $A_1$ and $A_2$, then some components of $G-A$ are connected to $A_1$ and the remaining components of $G-A$ are connected to $A_2$. We consider the following four situations.

If each component $G_i$$(G_i\subseteq X)$ and some components $G_j$$(G_j\subseteq Y)$ are connected to $A_1$, and the remaining components of Y are connected to $A_2$ (see Figure 7a). By the construction of G, we know that $G-A_2$ is disconnected and each component of $G-A_2$ has at least two vertices, then $|A_2|\ge {\kappa }_1\left(G\right)$. By the same reason, $|A_1|+|X|\ge {\kappa }_1\left(G\right)$. By Facts 1 and 3,

$$\left|S\right|=\left|A\right|+|B^{\prime }|+|\left\{u\right\}|\ge \left|A\right|+|X^{\prime }|+|\left\{u\right\}|=|A_1|+|A_2|+|X|+|\left\{u\right\}|\ge 2{\kappa }_1\left(G\right)+1,$$

which contradicts with $\left|S\right|\le 2{\kappa }_1\left(G\right)$.

If each component $G_i$$(G_i\subseteq X)$ is connected to $A_1$, and each component $G_j$$(G_j\subseteq Y)$ is connected to $A_2$ (see Figure 7b). By the same reason with the previous situation, then $|A_2|\ge {\kappa }_1\left(G\right)$. If $|A_1|+|X|\le 3$, then $\mu \left(G\right)-S$ is disconnected and $(A_1^{\prime }\cup X)$$\left(\right|A_1^{\prime }\cup X|=|A_1|+|X|\le 3)$ is one component of $\mu \left(G\right)-S$, which contradicts with the definition of ${\kappa }_3\left(\mu \left(G\right)\right)$. So, we have $|A_1|+|X|\ge 4$. And by Facts 1 and 3,

$$\left|S\right|=\left|A\right|+|B^{\prime }|+|\left\{u\right\}|\ge \left|A\right|+|X^{\prime }|+|u|=|A_1|+|A_2|+|X|+|\left\{u\right\}|\ge {\kappa }_1\left(G\right)+5,$$

which contradicts with $\left|S\right|\le 2{\kappa }_1\left(G\right)$ and ${\kappa }_1\left(G\right)\le 4$.

If some component $G_i$$(G_i\subseteq X)$ are connected to $A_1$ such that the remaining components of X are connected to $A_2$, and each component $G_j$$(G_j\subseteq Y)$ in connected to $A_2$ (see Figure 7c). By the same reason with the previous situation. Thus, $\left|S\right|\ge {\kappa }_1\left(G\right)+5$, which contradicts with $\left|S\right|\le 2{\kappa }_1\left(G\right)$ and ${\kappa }_1\left(G\right)\le 4$.

If some components $G_i$$(G_i\subseteq X)$ are connected to $A_1$ such that the remaining components of X are connected to $A_2$, and some components $G_j$$(G_j\subseteq Y)$ are connected to $A_1$ such that the remaining components of Y are connected to $A_2$ (see Figure 7d). Let $X_1=\left\{G_i\right|G_i\in X,N_G\left(G_i\right)\subseteq A_1\}$ and $X_2=X-X_1=\left\{G_i\right|G_i\in X,N_G\left(G_i\right)\subseteq A_2\}$. By the construction of G, $G-A_1-X_1$ is disconnected and each component has at least two vertices, then $|A_1|+|X_1|\ge {\kappa }_1\left(G\right)$. By the same reason, $|A_2|+|X_2|\ge {\kappa }_1\left(G\right)$. And by Facts 1 and 3,

$$\left|S\right|=\left|A\right|+|B^{\prime }|+|\left\{u\right\}|\ge \left|A\right|+|X^{\prime }|+|u|=|A_1|+|A_2|+|X_1|+|X_2|+|\left\{u\right\}|\ge 2{\kappa }_1\left(G\right)+1,$$

which contradicts with $\left|S\right|\le 2{\kappa }_1\left(G\right)$.

Subcase 2.3.2 $A^{\prime }\cap B^{\prime }\ne \varnothing$.

If there exists one vertex w ($w\in X$) such that $N_{A^{\prime }}\left(w\right)\subseteq (A^{\prime }\cap B^{\prime })$, then $\mu \left(G\right)-S$ is disconnected and w is an isolated vertex in $\mu \left(G\right)-S$ (see Figure 8a), which contradicts the definition of ${\kappa }_3\left(\mu \left(G\right)\right)$.

Otherwise, we suppose that $N_{A^{\prime }}\left(G_i\right)⊈(A^{\prime }\cap B^{\prime })$ for any $G_i$ ($G_i\in X$), it implies $G_i$ connected to $A-(A\cap B)$ for any $G_i$ ($G_i\in X$). Next, we consider the following three situations.

If $N_{A^{\prime }}\left(G_j\right)\subseteq (A^{\prime }-(A^{\prime }\cap B^{\prime }))$ for some $G_j$ ($G_j\in Y$), it implies $N_A\left(G_j\right)\subseteq (A-(A\cap B))$ for some $G_j$ ($G_j\in Y$), then each component of $G-(A-(A\cap B\left)\right)$ has at least two vertices in G (see Figure 8b). So, $|A-(A\cap B)|\ge {\kappa }_1\left(G\right)$. If $\left|A\right|\le {\kappa }_1\left(G\right)-1$, then it contradicts with $|A-(A\cap B)|<\left|A\right|\le {\kappa }_1\left(G\right)-1$. If $\left|A\right|\ge {\kappa }_1\left(G\right)$, and $\left|S\right|=\left|A\right|+|B^{\prime }|+|\left\{u\right\}|>|A|+|A^{\prime }-(A^{\prime }\cap B^{\prime })|+|\left\{u\right\}|\ge 2{\kappa }_1\left(G\right)+1$, which contradicts with $\left|S\right|\le 2{\kappa }_1\left(G\right)$.

If $N_{A^{\prime }}\left(G_j\right)\subseteq (A^{\prime }\cap B^{\prime })$ for some $G_j$ ($G_j\in Y$), it implies $N_A\left(G_j\right)\subseteq (A\cap B)$ for some $G_j$ ($G_j\in Y$), and so every component of $G-(A\cap B)$ has at least two vertices in G (see Figure 8c). So, $|A\cap B|\ge {\kappa }_1\left(G\right)$. If $\left|A\right|\le {\kappa }_1\left(G\right)-1$, then it contradicts with $|A\cap B|<\left|A\right|\le {\kappa }_1\left(G\right)-1$. If $\left|A\right|\ge {\kappa }_1\left(G\right)$, then $\left|S\right|=\left|A\right|+|B^{\prime }|+|\left\{u\right\}|>|A|+|A^{\prime }\cap B^{\prime }|+|\left\{u\right\}|\ge 2{\kappa }_1\left(G\right)+1$, which contradicts with $\left|S\right|\le 2{\kappa }_1\left(G\right)$.

If $N_{A^{\prime }}\left(G_j\right)\cap (A^{\prime }-(A^{\prime }\cap B^{\prime }))\ne \varnothing$ and $N_{A^{\prime }}\left(G_j\right)\cap (A^{\prime }\cap B^{\prime })\ne \varnothing$ for any $G_j$ ($G_j\in Y$) (see Figure 8d). By the same reason with the Subcase $2.3.1$ (the vertex set $A^{\prime }-(A^{\prime }\cap B^{\prime })$ in Subcase $2.3.2$ is the same as the vertex set $A^{\prime }$ in Subcase $2.3.1$). □

Theorem 3.

Let G be a connected graph with n vertices and g be a non-integer with $g\ge 2$. Then

$$3\le {\kappa }_{2g+1}\left(\mu \left(G\right)\right)\le 2{\kappa }_g\left(G\right)+1.$$

Proof of Theorem 3.

The upper bound is similar to that the upper bound of the Theorem 2.

Next, we show ${\kappa }_{2g+1}\left(\mu \left(G\right)\right)\ge 3$. Assume, to the contrary, that ${\kappa }_{2g+1}\left(\mu \left(G\right)\right)\le 2$. Let S be an vertex set of $\mu \left(G\right)$ with $\left|S\right|\le 2$. The following two cases will be discussed.

Case 1. $u\notin S$.

By the construction of $\mu \left(G\right)$, we consider the following three situations.

If $|S\cap V|=2$ and $|S\cap V{}^{\prime }|=0$, then $G-S$ is connected to $V{}^{\prime }$ and $V{}^{\prime }$ is connected to the root vertex u, so $\mu \left(G\right)-S$ is connected, a contradiction.

If $|S\cap V|=0$ and $|S\cap V{}^{\prime }|=2$, then $V{}^{\prime }-S$ is connected to V and $V{}^{\prime }-S$ is connected to the root vertex u, so $\mu \left(G\right)-S$ is connected, a contradiction.

If $|S\cap V|=1$ and $|S\cap V{}^{\prime }|=1$. By Lemma 2 (1) and $\left(2\right)$, then $\mu \left(G\right)-S$ is connected or $\mu \left(G\right)-S$ is disconnected and there exists at least one component is an isolated vertex, a contradiction.

Case 2. $u\in S$.

By the construction of $\mu \left(G\right)$, we consider the following two situations.

If $|S\cap V|=0$ and $|S\cap V{}^{\prime }|=1$, then $V{}^{\prime }-S$ is connected to V. So $\mu \left(G\right)-S$ is connected, a contradiction.

If $|S\cap V|=1$ and $|S\cap V{}^{\prime }|=0$, then $\mu \left(G\right)-S$ is connected or $\mu \left(G\right)-S$ is disconnected and there exists at least one component, which is an isolated vertex, a contradiction. □

Furthermore, for $g\ge 2$, we give an example to show that the lower bounds are sharp of Theorem 3.

Example 1.

For $g\ge 2$, let $Q_i$$(1\le i\le 6)$ be a clique such that $|Q_1|=|Q_6|=g$ and $|Q_j|\ge g+1$$(2\le j\le 5)$. Let $Q^{*}$ be the graph with the vertex set $V\left(Q^{*}\right)=V\left(Q_1\right)\cup \dots \cup V\left(Q_6\right)\cup \left\{v\right\}\cup \left\{w\right\}$ and the edge set $E\left(Q^{*}\right)=E\left(Q_1\right)\cup \dots \cup E\left(Q_6\right)\cup E\left(K_{\left|V\right(Q_1\left)\right|,\left|v\right|}\right)\cup E\left(K_{\left|V\right(Q_2\left)\right|,\left|v\right|}\right)\cup E\left(K_{\left|V\right(Q_3\left)\right|,\left|v\right|}\right)\cup E\left(K_{\left|V\right(Q_4\left)\right|,\left|w\right|}\right)\cup E\left(K_{\left|V\right(Q_5\left)\right|,\left|w\right|}\right)\cup E\left(K_{\left|V\right(Q_6\left)\right|,\left|w\right|}\right)\cup \left\{vw\right\}$, (see Figure 9). The removal of v and $V\left(Q_1\right)$ of $Q^{*}$, results in a graph with three components $Q_2$, $Q_3$ and $(\left\{w\right\}\cup Q_4\cup Q_5\cup Q_6)$, and so ${\kappa }_g\left(Q^{*}\right)=g+1$. The removal of v, w and u (u is the root of $\mu \left(Q^{*}\right)$) of $\mu \left(M^{*}\right)$, results in a graph is disconnected, and so ${\kappa }_g(\mu \left(Q^{*}\right)=3$. Hence, the upper bound of Theorem 3 is sharp.

4. Conclusions

In this paper, we investigate the relationship on the g-extra connectivity between the Mycielskian graph $\mu \left(G\right)$ and the original graph G. In addition, we show that ${\kappa }_3\left(\mu \left(G\right)\right)=2{\kappa }_1\left(G\right)+1$ for ${\kappa }_1\left(G\right)\le min\{4,\lfloor \frac{n}{2}\rfloor \}$, and propose the bounds of ${\kappa }_{2g+1}\left(\mu \left(G\right)\right)$ for $g\ge 2$. The existence g-extra connectivity is still open. Next, we will investigate the g-good-neighbor connectivity and structural connectivity of the Mycielskian graph.