High-Performance Time Series Anomaly Discovery on Graphics Processors
Abstract
1. Introduction
- We perform a thorough review of works related to discord-based approaches to discovering time series anomalies and their parallelization for diverse hardware platforms.
- Based on MERLIN [7], we introduce the parallel algorithm PALMAD (parallel arbitrary length MERLIN-based anomaly discovery) for the discovery of arbitrary length discords on a graphics processor. As per the review above, PALMAD is the sole parallel algorithm capable of discovering all discords with lengths within a specified range, rather than discords of a specific length. In our algorithm, we employ our derived recurrent formulas on mean values and standard deviations of subsequences to avoid redundant calculations and utilize array-based data structures to provide efficient parallel processing.
- We carry out extensive experiments to evaluate our algorithm over five real-world and two synthetic time series against two state-of-the-art parallel analogs that discover discords of a specific length. To provide a fair comparison, we limit the range of discord lengths by one discord and measure the average running time to discover one discord. In the experiments, PALMAD significantly outran its closest rival in terms of the average running time to discover one discord: by at least two times and three orders of magnitude in the case of the real and synthetic time series, respectively.
- We apply PALMAD to anomaly discovery in a real-world time series from a smart heating control system, employing our proposed discord heatmap technique to illustrate the results. In addition, we establish a repository [17] that contains the algorithm’s source code, data, etc., to facilitate the reproducibility of our study.
2. Related Work
| Algorithm | Year | Ancestor (If Any) and Approach |
|---|---|---|
| HOTSAX [4] | 2005 |
|
| WAT [22,23] | 2006 2007 |
|
| DRAG [8] | 2007 |
|
| iSAX [20] HOT-iSAX [21] | 2008 2011 |
|
| BitClusterDiscord [26] | 2013 |
|
| RRA [28] | 2015 | |
| HashDD [24] | 2016 |
|
| HDD-MBR [25] | 2018 |
|
| Matrix profile (MP) [32] | 2018 | Discords are discovered as a by-product of MP |
| Son [30] | 2020 | |
| MERLIN [7] | 2020 |
|
| HST [27] | 2022 |
|
| MERLIN++ [33] | 2023 |
|
3. Preliminaries
3.1. Notation and Definitions
3.2. MERLIN and DRAG Algorithms
| Algorithm 1 MERLIN (in T, , , ; out) |
|
| Algorithm 2 DRAG (in T, m, r; out) | |
Phase 1. Select candidates
| Phase 2. Refine discords
|
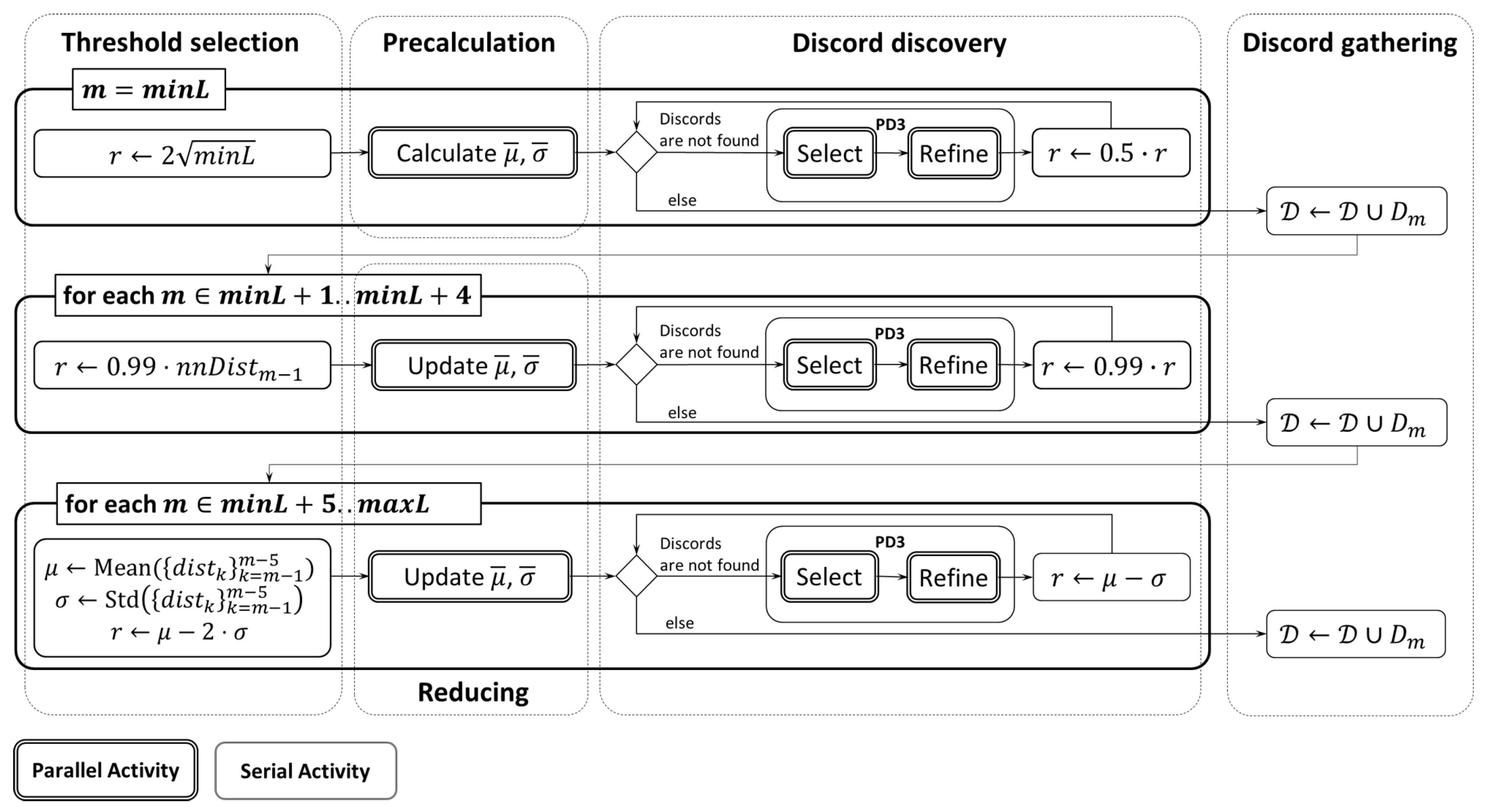
4. Arbitrary Length Discord Discovery with GPU
4.1. General Architecture
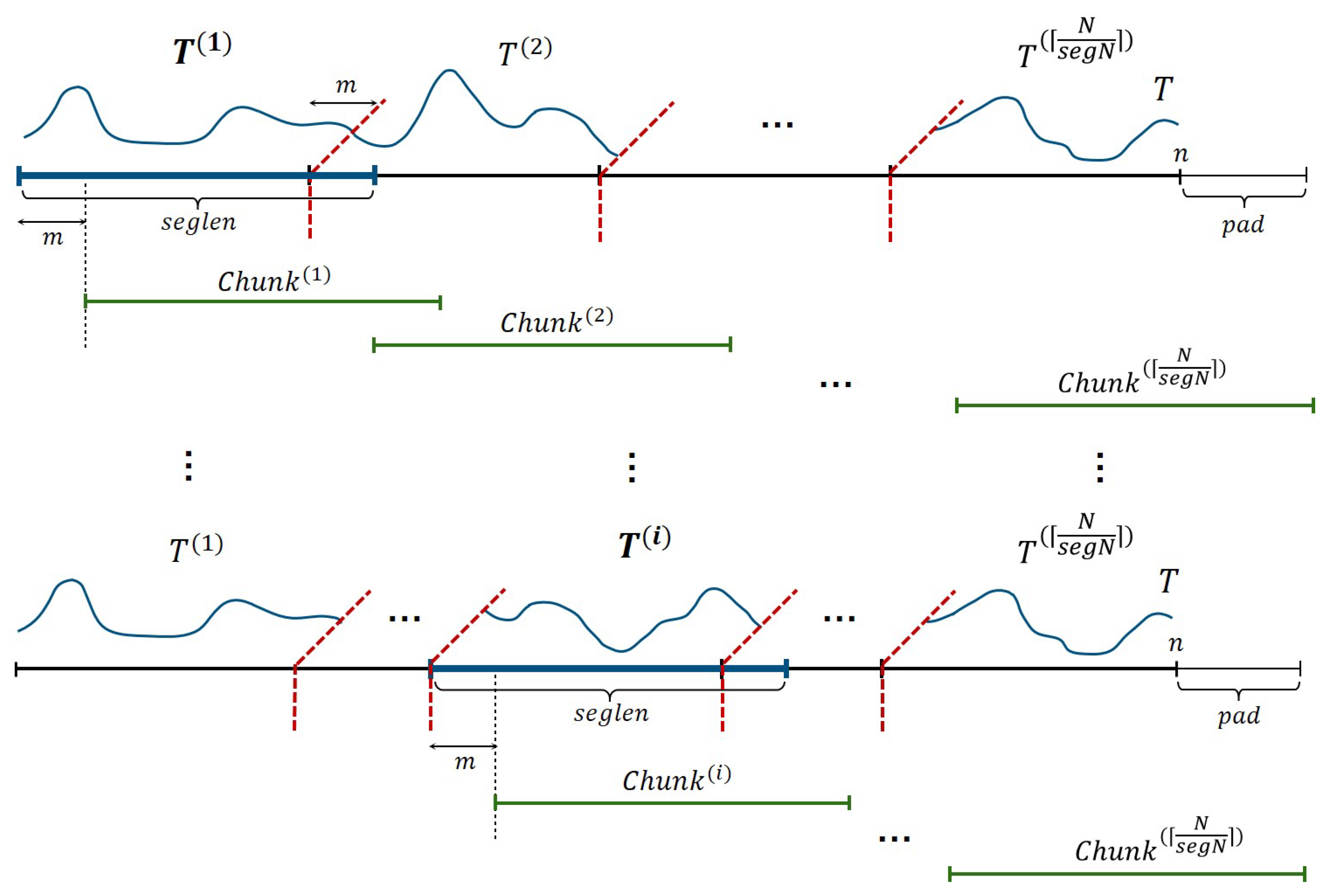
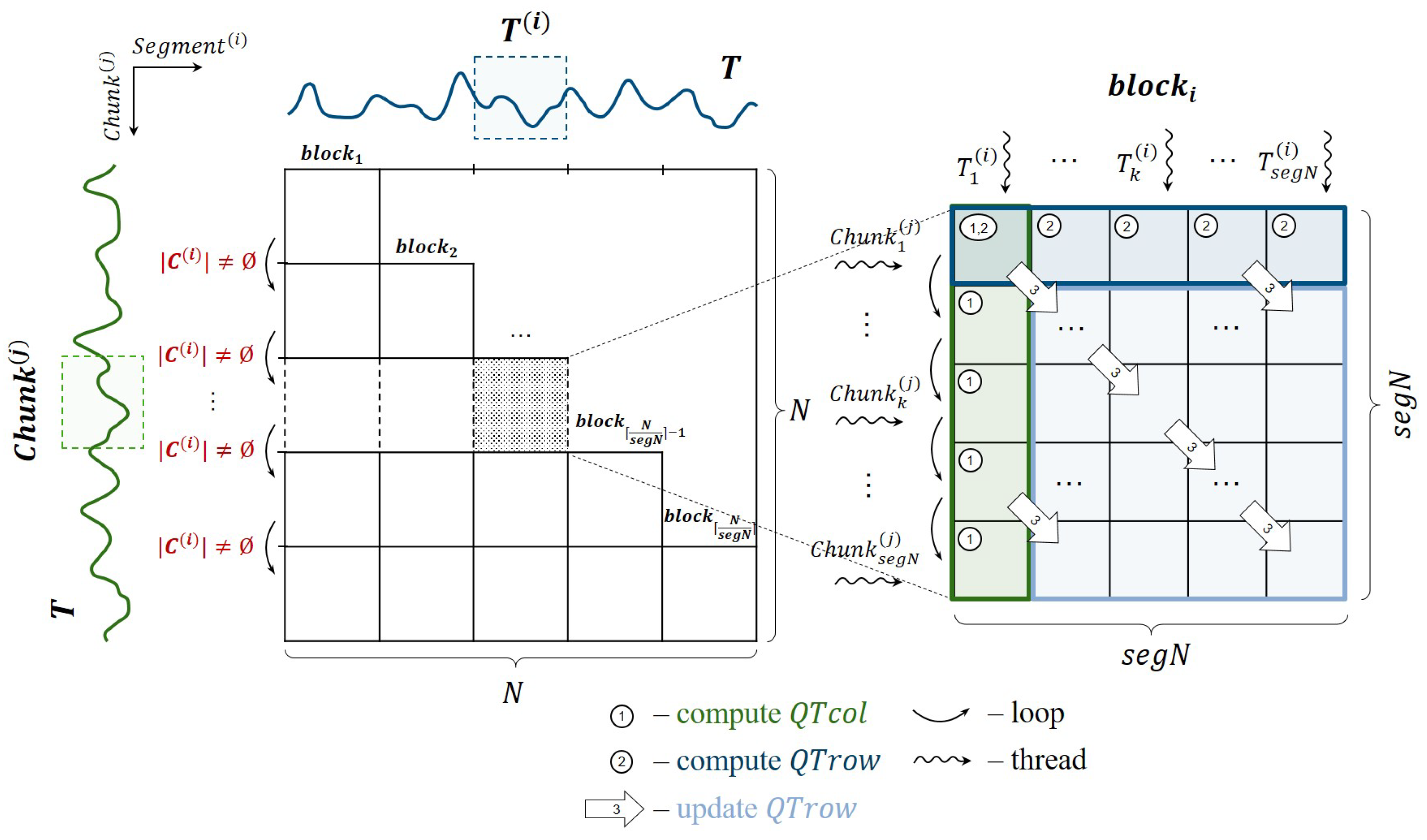
4.2. Data Layout
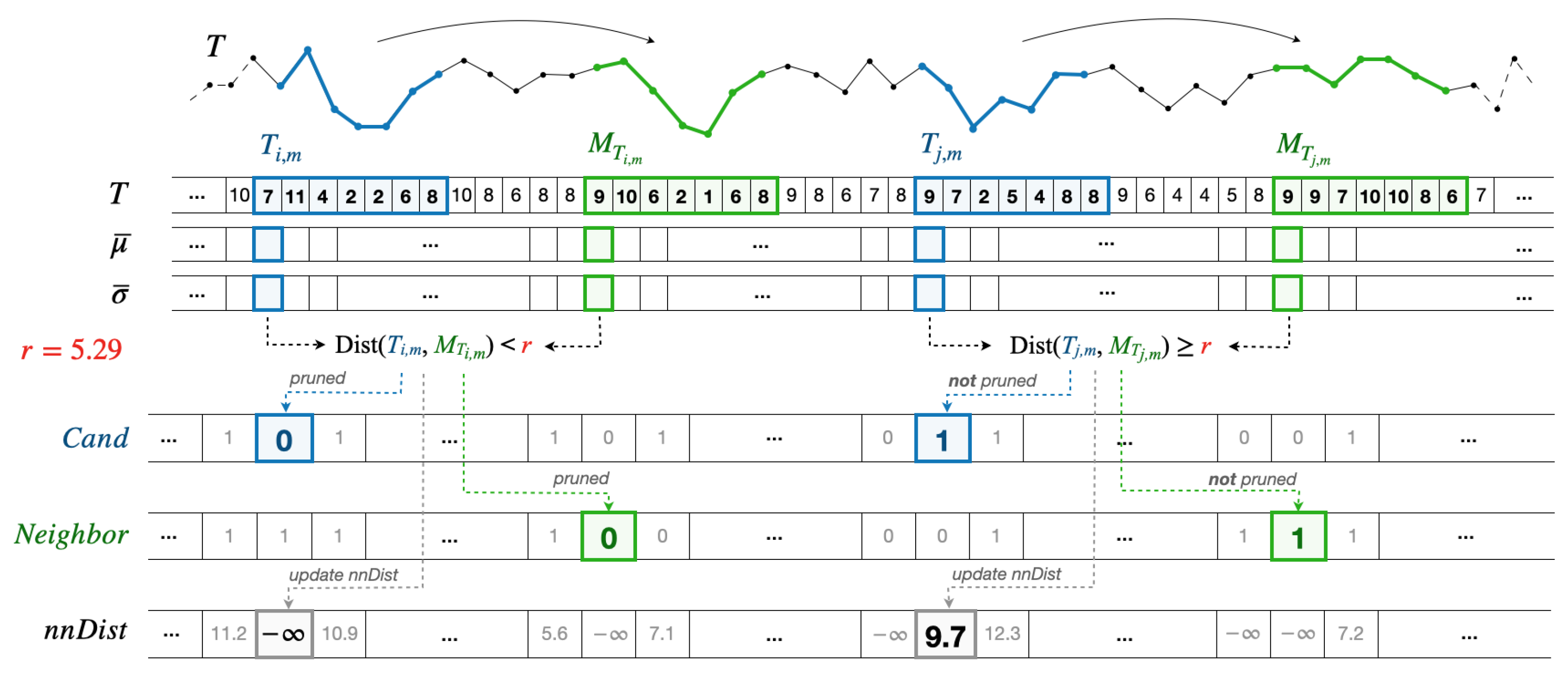
4.3. Parallelization of Candidate Selection
| Algorithm 3 PD3select (in T, m, r; out) |
|
4.4. Parallelization of Discord Refinement
| Algorithm 4 PD3refine (in T, m, r; out) |
|
5. Experimental Evaluation
5.1. The Experimental Setup
5.2. Results and Discussion
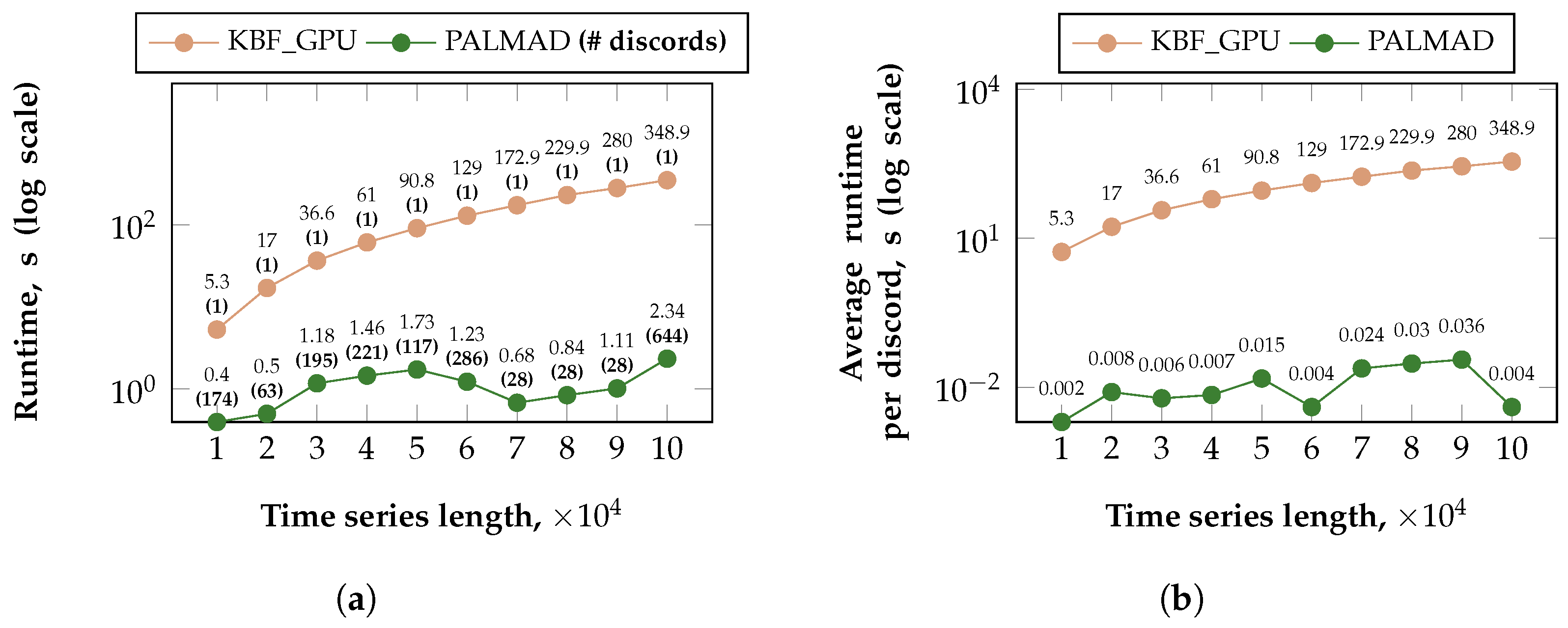
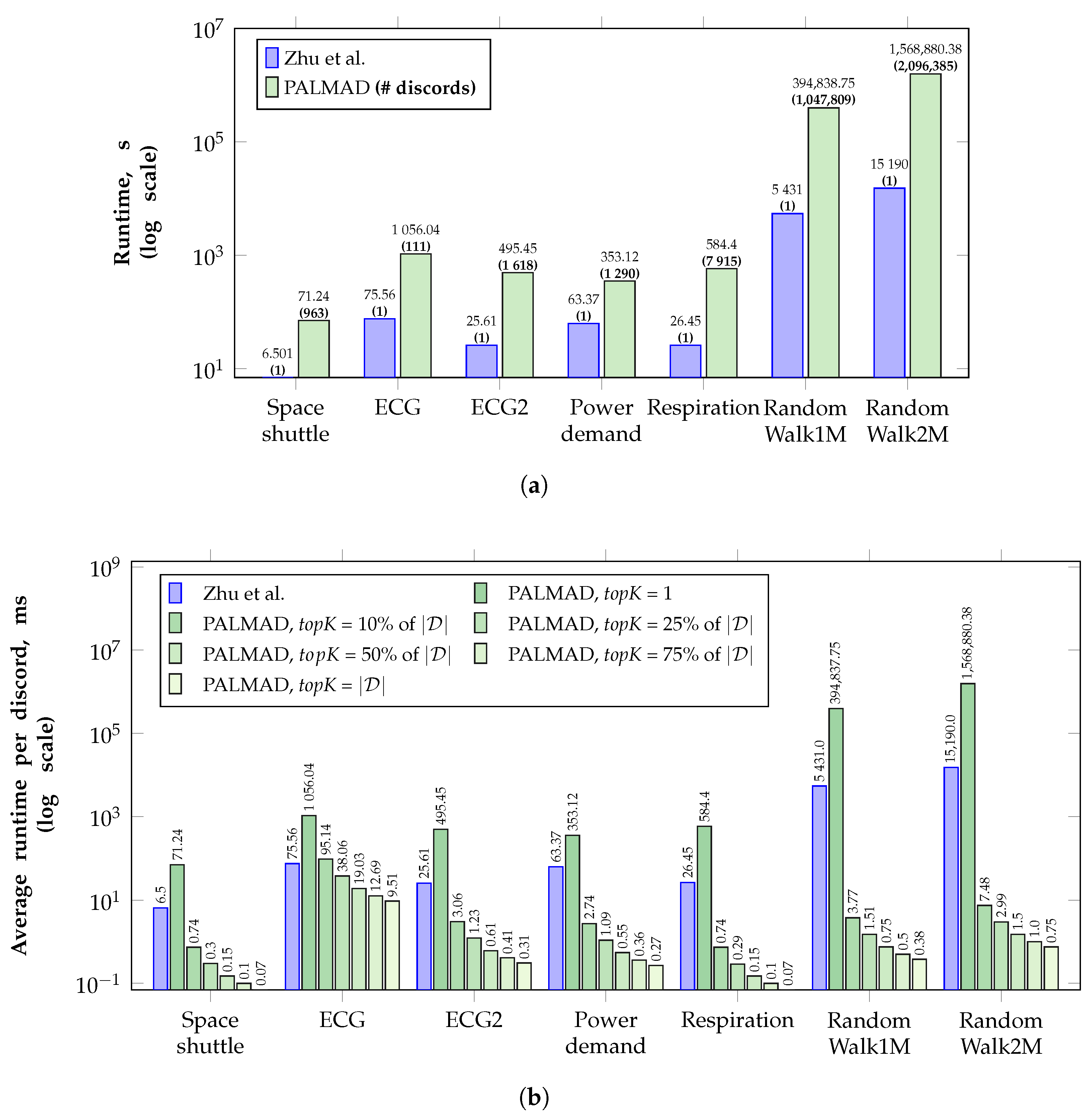
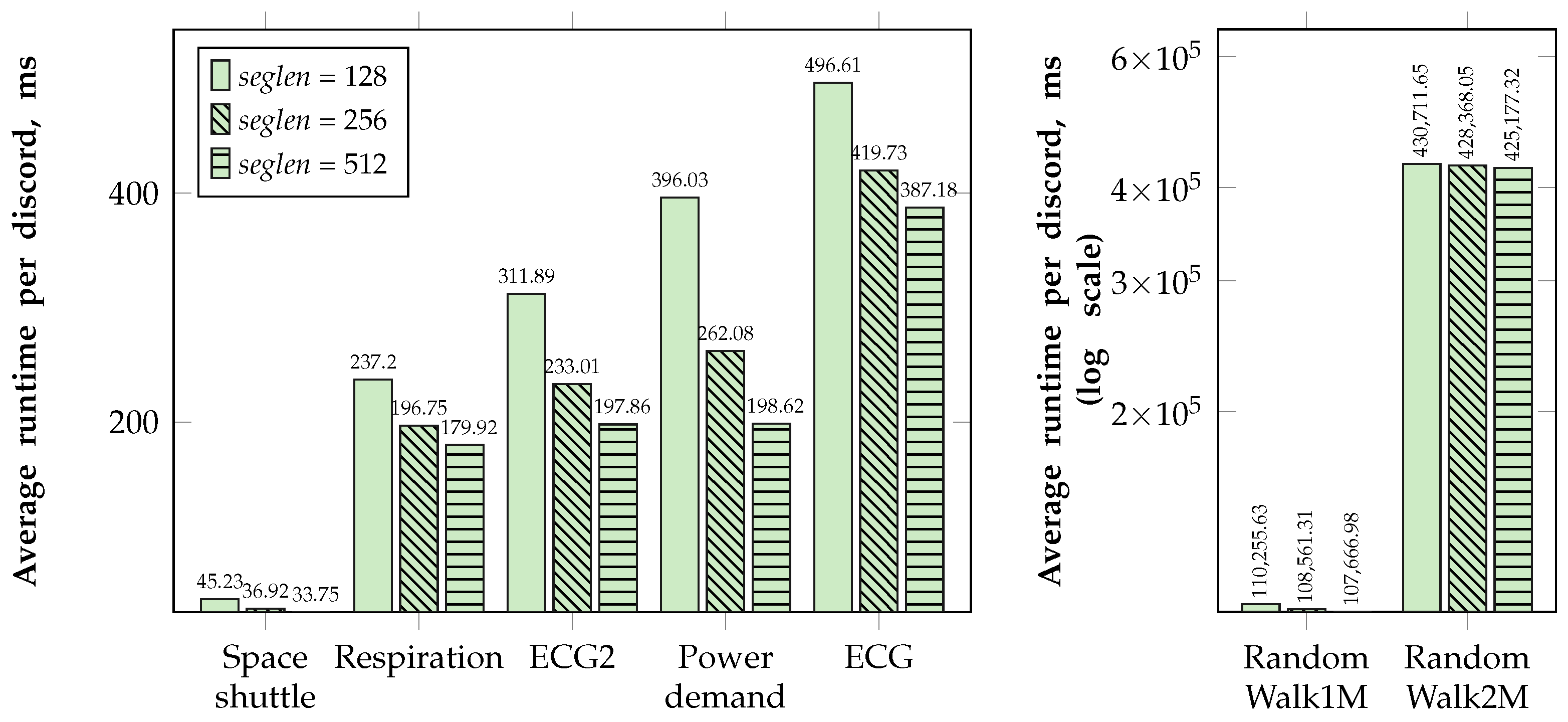
5.2.1. Comparison with Analogs
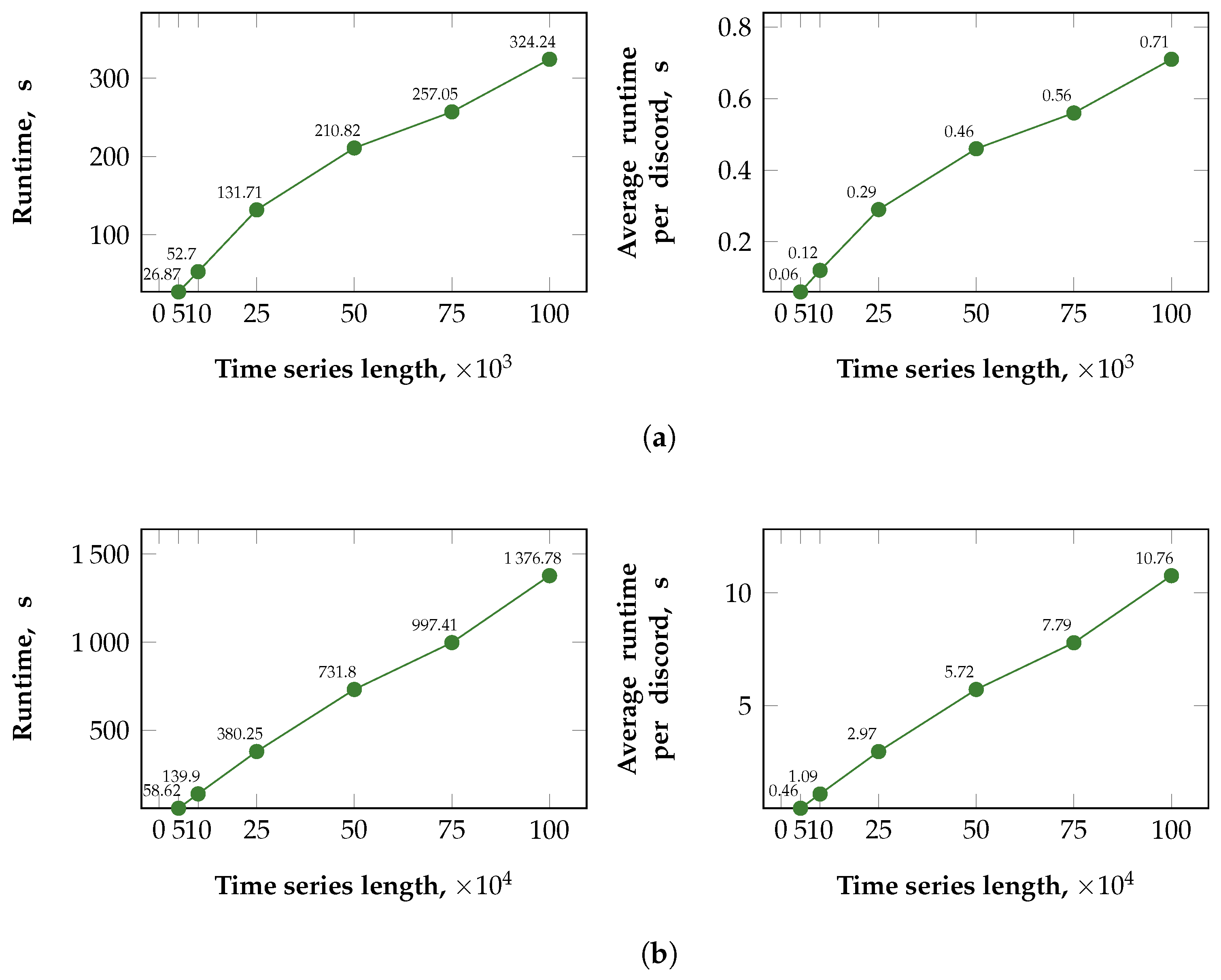
5.2.2. Scalability of PALMAD
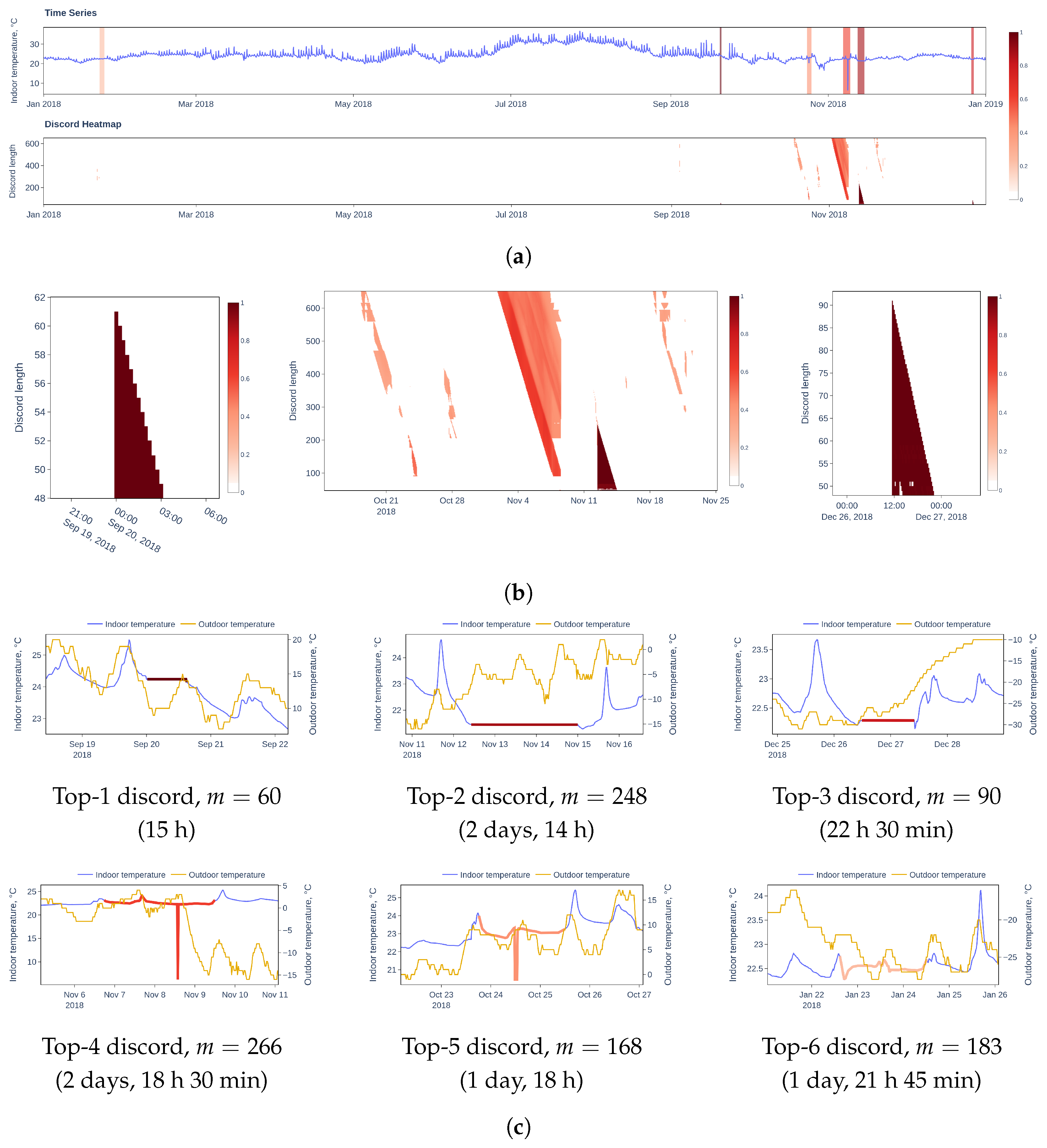
6. Case Study
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Blázquez-García, A.; Conde, A.; Mori, U.; Lozano, J.A. A Review on Outlier/Anomaly Detection in Time Series Data. ACM Comput. Surv. 2021, 54, 56. [Google Scholar] [CrossRef]
- Choi, K.; Yi, J.; Park, C.; Yoon, S. Deep Learning for Anomaly Detection in Time-Series Data: Review, Analysis, and Guidelines. IEEE Access 2021, 9, 120043–120065. [Google Scholar] [CrossRef]
- Schmidl, S.; Wenig, P.; Papenbrock, T. Anomaly Detection in Time Series: A Comprehensive Evaluation. Proc. VLDB Endow. 2022, 15, 1779–1797. [Google Scholar] [CrossRef]
- Lin, J.; Keogh, E.J.; Fu, A.W.; Herle, H.V. Approximations to magic: Finding unusual medical time series. In Proceedings of the 18th IEEE Symposium on Computer-Based Medical Systems (CBMS 2005), Dublin, Ireland, 23–24 June 2005; IEEE Computer Society: Washington, DC, USA, 2005; pp. 329–334. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. 2009, 41, 15. [Google Scholar] [CrossRef]
- Chandola, V.; Cheboli, D.; Kumar, V. Detecting Anomalies in a Time Series Database. Retrieved from the University of Minnesota Digital Conservancy. 2009. Available online: https://hdl.handle.net/11299/215791 (accessed on 12 April 2022).
- Nakamura, T.; Imamura, M.; Mercer, R.; Keogh, E.J. MERLIN: Parameter-free discovery of arbitrary length anomalies in massive time series archives. In Proceedings of the 20th IEEE International Conference on Data Mining (ICDM 2020), Sorrento, Italy, 17–20 November 2020; pp. 1190–1195. [Google Scholar] [CrossRef]
- Yankov, D.; Keogh, E.J.; Rebbapragada, U. Disk aware discord discovery: Finding unusual time series in terabyte sized datasets. In Proceedings of the 7th IEEE International Conference on Data Mining (ICDM 2007), Omaha, NE, USA, 28–31 October 2007; IEEE Computer Society: Washington, DC, USA, 2007; pp. 381–390. [Google Scholar] [CrossRef]
- Kraeva, Y.; Zymbler, M.L. Scalable algorithm for subsequence similarity search in very large time series data on cluster of Phi KNL. In Communications in Computer and Information Science, Proceedings of the Data Analytics and Management in Data Intensive Domains—20th International Conference (DAMDID/RCDL 2018), Moscow, Russia, 9–12 October 2018; Manolopoulos, Y., Stupnikov, S.A., Eds.; Revised Selected Papers; Springer: Berlin/Heidelberg, Germany, 2018; Volume 1003, pp. 149–164. [Google Scholar] [CrossRef]
- Zymbler, M. A parallel discord discovery algorithm for time series on many-core accelerators. Numer. Methods Program. 2019, 20, 211–223. (In Russian) [Google Scholar] [CrossRef]
- Zymbler, M.; Kraeva, Y. Discovery of time series motifs on Intel many-core systems. Lobachevskii J. Math. 2019, 40, 2124–2132. [Google Scholar] [CrossRef]
- Zymbler, M.; Grents, A.; Kraeva, Y.; Kumar, S. A parallel approach to discords discovery in massive time series data. Comput. Mater. Contin. 2021, 66, 1867–1878. [Google Scholar] [CrossRef]
- Zymbler, M.; Polyakov, A.; Kipnis, M. Time series discord discovery on Intel many-core systems. In Communications in Computer and Information Science, Proceedings of the 13th International Conference (PCT 2019), Kaliningrad, Russia, 2–4 April 2019; Sokolinsky, L., Zymbler, M., Eds.; Revised Selected Papers; Springer: Cham, Switzerland, 2019; Volume 1063, pp. 168–182. [Google Scholar] [CrossRef]
- Zymbler, M.; Kraeva, Y. Parallel algorithm for time series motif discovery on graphics processor. Comput. Math. Softw. Eng. 2020, 9, 17–34. (In Russian) [Google Scholar] [CrossRef]
- Zymbler, M.; Ivanova, E. Matrix profile-based approach to industrial sensor data analysis inside RDBMS. Mathematics 2021, 9, 2146. [Google Scholar] [CrossRef]
- Zymbler, M.; Goglachev, A. Fast summarization of long time series with graphics processor. Mathematics 2022, 10, 1781. [Google Scholar] [CrossRef]
- Kraeva, Y.; Zymbler, M. PALMAD: Parallel MERLIN-Based Anomaly Discovery Algorithm for GPU. 2022. Available online: https://github.com/kraevaya/PALMAD (accessed on 1 December 2022).
- Lin, J.; Keogh, E.J.; Lonardi, S.; Chiu, B.Y. A symbolic representation of time series, with implications for streaming algorithms. In Proceedings of the 8th ACM SIGMOD Workshop on Research Issues in Data Mining and Knowledge Discovery (DMKD 2003), San Diego, CA, USA, 13 June 2003; ACM: New York, NY, USA, 2003; pp. 2–11. [Google Scholar] [CrossRef]
- Fredkin, E. Trie memory. Commun. ACM 1960, 3, 490–499. [Google Scholar] [CrossRef]
- Shieh, J.; Keogh, E.J. iSAX: Indexing and mining terabyte sized time series. In Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Las Vegas, NV, USA, 24–27 August 2008; ACM: New York, NY, USA, 2008; pp. 623–631. [Google Scholar] [CrossRef]
- Buu, H.T.Q.; Anh, D.T. Time series discord discovery based on iSAX symbolic representation. In Proceedings of the 3rd International Conference on Knowledge and Systems Engineering (KSE 2011), Hanoi, Vietnam, 14–17 October 2011; IEEE Computer Society: Washington, DC, USA, 2011; pp. 11–18. [Google Scholar] [CrossRef]
- Bu, Y.; Leung, O.T.; Fu, A.W.; Keogh, E.J.; Pei, J.; Meshkin, S. WAT: Finding top-k discords in time series database. In Proceedings of the 7th SIAM International Conference on Data Mining, Minneapolis, MN, USA, 26–28 April 2007; pp. 449–454. [Google Scholar] [CrossRef]
- Fu, A.W.; Leung, O.T.; Keogh, E.J.; Lin, J. Finding time series discords based on Haar transform. In Proceedings of the 2nd International Conference on Advanced Data Mining and Applications (ADMA 2006), Xi’an, China, 14–16 August 2006; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4093, pp. 31–41. [Google Scholar] [CrossRef]
- Thuy, H.T.T.; Anh, D.T.; Chau, T.N.V. An effective and efficient hash-based algorithm for time series discord discovery. In Proceedings of the 2016 3rd National Foundation for Science and Technology Development Conference on Information and Computer Science (NICS), Danang, Vietnam, 14–16 September 2016; pp. 85–90. [Google Scholar] [CrossRef]
- Chau, P.M.; Duc, B.M.; Anh, D.T. Discord detection in streaming time series with the support of R-tree. In Proceedings of the 2018 International Conference on Advanced Computing and Applications (ACOMP), Ho Chi Minh City, Vietnam, 27–29 November 2018; pp. 96–103. [Google Scholar] [CrossRef]
- Li, G.; Bräysy, O.; Jiang, L.; Wu, Z.; Wang, Y. Finding time series discord based on bit representation clustering. Knowl.-Based Syst. 2013, 54, 243–254. [Google Scholar] [CrossRef]
- Avogadro, P.; Dominoni, M.A. A fast algorithm for complex discord searches in time series: HOT SAX Time. Appl. Intell. 2022, 52, 10060–10081. [Google Scholar] [CrossRef]
- Senin, P.; Lin, J.; Wang, X.; Oates, T.; Gandhi, S.; Boedihardjo, A.P.; Chen, C.; Frankenstein, S. Time series anomaly discovery with grammar-based compression. In Proceedings of the 18th International Conference on Extending Database Technology (EDBT 2015), Brussels, Belgium, 23–27 March 2015; OpenProceedings.org: Konstanz, Germany, 2015; pp. 481–492. [Google Scholar] [CrossRef]
- Keogh, E.J.; Chakrabarti, K.; Pazzani, M.J.; Mehrotra, S. Dimensionality reduction for fast similarity search in large time series databases. Knowl. Inf. Syst. 2001, 3, 263–286. [Google Scholar] [CrossRef]
- Son, N.T. An improvement of disk aware discord discovery algorithm for discovering time series discord. In Proceedings of the 2020 5th International Conference on Green Technology and Sustainable Development (GTSD), Ho Chi Minh City, Vietnam, 27–28 November 2020; pp. 19–23. [Google Scholar] [CrossRef]
- Mueen, A.; Nath, S.; Liu, J. Fast approximate correlation for massive time-series data. In Proceedings of the ACM SIGMOD International Conference on Management of Data (SIGMOD 2010), Indianapolis, IN, USA, 6–10 June 2010; ACM: New York, NY, USA, 2010; pp. 171–182. [Google Scholar] [CrossRef]
- Yeh, C.M.; Zhu, Y.; Ulanova, L.; Begum, N.; Ding, Y.; Dau, H.A.; Zimmerman, Z.; Silva, D.F.; Mueen, A.; Keogh, E.J. Time series joins, motifs, discords and shapelets: A unifying view that exploits the matrix profile. Data Min. Knowl. Discov. 2018, 32, 83–123. [Google Scholar] [CrossRef]
- Nakamura, T.; Mercer, R.; Imamura, M.; Keogh, E.J. MERLIN++: Parameter-free discovery of time series anomalies. Data Min. Knowl. Discov. 2023, 37, 670–709. [Google Scholar] [CrossRef]
- Orchard, M.T. A fast nearest-neighbor search algorithm. In Proceedings of the 1991 International Conference on Acoustics, Speech, and Signal Processing (ICASSP ‘91), Toronto, ON, Canada, 14–17 May 1991; IEEE Computer Society: Washington, DC, USA, 1991; pp. 2297–2300. [Google Scholar] [CrossRef]
- Wang, J.T.; Wang, X.; Lin, K.D.; Shasha, D.E.; Shapiro, B.A.; Zhang, K. Evaluating a Class of Distance-Mapping Algorithms for Data Mining and Clustering. In Proceedings of the 5th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 15–18 August 1999; ACM: New York, NY, USA, 1999; pp. 307–311. [Google Scholar] [CrossRef]
- Pearson, K. The problem of the random walk. Nature 1905, 72, 294. [Google Scholar] [CrossRef]
- de Supinski, B.R.; Scogland, T.R.W.; Duran, A.; Klemm, M.; Bellido, S.M.; Olivier, S.L.; Terboven, C.; Mattson, T.G. The Ongoing Evolution of OpenMP. Proc. IEEE 2018, 106, 2004–2019. [Google Scholar] [CrossRef]
- Reyes, R.; López-Rodríguez, I.; Fumero, J.J.; de Sande, F. A preliminary evaluation of OpenACC implementations. J. Supercomput. 2013, 65, 1063–1075. [Google Scholar] [CrossRef]
- Yankov, D.; Keogh, E.J.; Rebbapragada, U. Disk aware discord discovery: Finding unusual time series in terabyte sized datasets. Knowl. Inf. Syst. 2008, 17, 241–262. [Google Scholar] [CrossRef]
- Wu, Y.; Zhu, Y.; Huang, T.; Li, X.; Liu, X.; Liu, M. Distributed discord discovery: Spark based anomaly detection in time series. In Proceedings of the 2015 IEEE 17th International Conference on High Performance Computing and Communications, 2015 IEEE 7th International Symposium on Cyberspace Safety and Security, and 2015 IEEE 12th International Conference on Embedded Software and Systems, New York, NY, USA, 24–26 August 2015; pp. 154–159. [Google Scholar] [CrossRef]
- Huang, T.; Zhu, Y.; Mao, Y.; Li, X.; Liu, M.; Wu, Y.; Ha, Y.; Dobbie, G. Parallel discord discovery. In Proceedings of the Advances in Knowledge Discovery and Data Mining—20th Pacific-Asia Conference (PAKDD 2016), Auckland, New Zealand, 19–22 April 2016; Springer: Berlin/Heidelberg, Germany, 2016; Volume 9652, pp. 233–244. [Google Scholar] [CrossRef]
- Zimmerman, Z.; Kamgar, K.; Senobari, N.S.; Crites, B.; Funning, G.J.; Brisk, P.; Keogh, E.J. Matrix profile XIV: Scaling time series motif discovery with GPUs to break a quintillion pairwise comparisons a day and beyond. In Proceedings of the ACM Symposium on Cloud Computing (SoCC 2019), Santa Cruz, CA, USA, 20–23 November 2019; ACM: New York, NY, USA, 2019; pp. 74–86. [Google Scholar] [CrossRef]
- Pfeilschifter, G. Time Series Analysis with Matrix Profile on HPC Systems. Master’s Thesis, Department of Informatics, Technical University of Munich, Munich, Germany, 2019. [Google Scholar]
- Thuy, T.T.H.; Anh, T.D.; Chau, T.N.V. A new discord definition and an efficient time series discord detection method using GPUs. In Proceedings of the 2021 3rd International Conference on Software Engineering and Development (ICSED 2021), Xiamen, China, 19–21 November 2021; pp. 63–70. [Google Scholar] [CrossRef]
- Zhu, B.; Jiang, Y.; Gu, M.; Deng, Y. A GPU acceleration framework for motif and discord based pattern mining. IEEE Trans. Parallel Distrib. Syst. 2021, 32, 1987–2004. [Google Scholar] [CrossRef]
- Dean, J.; Ghemawat, S. MapReduce: Simplified data processing on large clusters. In Proceedings of the 6th Symposium on Operating System Design and Implementation (OSDI 2004), San Francisco, CA, USA, 6–8 December 2004; USENIX Association: Berkeley, CA, USA, 2004; pp. 137–150. [Google Scholar]
- Snir, M. Technical perspective: The future of MPI. Commun. ACM 2018, 61, 105. [Google Scholar] [CrossRef]
- Imani, S.; Keogh, E.J. Matrix profile XIX: Time series semantic motifs: A new primitive for finding higher-level structure in time series. In Proceedings of the 2019 IEEE International Conference on Data Mining (ICDM 2019), Beijing, China, 8–11 November 2019; pp. 329–338. [Google Scholar] [CrossRef]
- Imani, S.; Madrid, F.; Ding, W.; Crouter, S.E.; Keogh, E.J. Introducing time series snippets: A new primitive for summarizing long time series. Data Min. Knowl. Discov. 2020, 34, 1713–1743. [Google Scholar] [CrossRef]
- Zhu, Y.; Imamura, M.; Nikovski, D.; Keogh, E.J. Introducing time series chains: A new primitive for time series data mining. Knowl. Inf. Syst. 2019, 60, 1135–1161. [Google Scholar] [CrossRef]
- Zhu, Y.; Yeh, C.M.; Zimmerman, Z.; Kamgar, K.; Keogh, E.J. Matrix profile XI: SCRIMP++: Time series motif discovery at interactive speeds. In Proceedings of the IEEE International Conference on Data Mining (ICDM 2018), Singapore, 17–20 November 2018; IEEE Computer Society: Washington, DC, USA, 2018; pp. 837–846. [Google Scholar] [CrossRef]
- Wei, L.; Keogh, E.; Xi, X. SAXually Explicit Images: Finding Unusual Shapes. In Proceedings of the 6th International Conference on Data Mining (ICDM’06), Hong Kong, China, 18–22 December 2006; pp. 711–720. [Google Scholar] [CrossRef]
- Huang, T.; Zhu, Y.; Wu, Y.; Shi, W. J-distance discord: An improved time series discord definition and discovery method. In Proceedings of the 2015 IEEE International Conference on Data Mining Workshop (ICDMW), Atlantic City, NJ, USA, 14–17 November 2015; pp. 303–310. [Google Scholar] [CrossRef]
- Kirk, D.B. NVIDIA CUDA software and GPU parallel computing architecture. In Proceedings of the 6th International Symposium on Memory Management (ISMM 2007), Montreal, QC, Canada, 21–22 October 2007; ACM: New York, NY, USA, 2007; pp. 103–104. [Google Scholar] [CrossRef]
- Kraeva, Y.; Zymbler, M. A parallel discord discovery algorithm for a graphics processor. Pattern Recognit. Image Anal. 2023, 33, 101–112. [Google Scholar] [CrossRef]
- Keogh, E.J.; Lin, J.; Fu, A.W. HOT SAX: Efficiently finding the most unusual time series subsequence. In Proceedings of the 5th IEEE International Conference on Data Mining (ICDM 2005), Houston, TX, USA, 27–30 November 2005; IEEE Computer Society: Washington, DC, USA, 2005; pp. 226–233. [Google Scholar] [CrossRef]
- Ferrell, B.; Santuro, S. NASA Shuttle Valve Data. 2005. Available online: https://www.cs.fit.edu/~pkc/nasa/data/ (accessed on 19 March 2022).
- Goldberger, A.L.; Amaral, L.A.N.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet components of a new research resource for complex physiologic signals. Circulation 2000, 101, 215–220. [Google Scholar] [CrossRef]
- Koski, A. Primitive coding of structural ECG features. Pattern Recognit. Lett. 1996, 17, 1215–1222. [Google Scholar] [CrossRef]
- van Wijk, J.J.; van Selow, E.R. Cluster and calendar based visualization of time series data. In Proceedings of the IEEE Symposium on Information Visualization 1999 (INFOVIS’99), San Francisco, CA, USA, 24–29 October 1999; IEEE Computer Society: Washington, DC, USA, 1999; pp. 4–9. [Google Scholar] [CrossRef]
- Dolganina, N.; Ivanova, E.; Bilenko, R.; Rekachinsky, A. HPC resources of South Ural State University. In Communications in Computer and Information Science, Proceedings of the 16th International Conference on Parallel Computational Technologies (PCT 2022), Dubna, Russia, 29–31 March 2022; Sokolinsky, L., Zymbler, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2022; Volume 1618, pp. 43–55. [Google Scholar] [CrossRef]
- Voevodin, V.V.; Antonov, A.S.; Nikitenko, D.A.; Shvets, P.A.; Sobolev, S.I.; Sidorov, I.Y.; Stefanov, K.S.; Voevodin, V.V.; Zhumatiy, S.A. Supercomputer Lomonosov-2: Large scale, deep monitoring and fine analytics for the user community. Supercomput. Front. Innov. 2019, 6, 4–11. [Google Scholar] [CrossRef]
- Zymbler, M.; Kraeva, Y.; Latypova, E.; Kumar, S.; Shnayder, D.; Basalaev, A. Cleaning Sensor Data in Smart Heating Control System. In Proceedings of the 2020 Global Smart Industry Conference (GloSIC 2020), Chelyabinsk, Russia, 17–19 November 2020; pp. 375–381. [Google Scholar] [CrossRef]
- Kraeva, Y. Anomaly detection in sensor data using parallel computing. Comput. Math. Softw. Eng. 2023, 9, 47–61. (In Russian) [Google Scholar] [CrossRef]
- Madrid, F.; Imani, S.; Mercer, R.; Zimmerman, Z.; Senobari, N.S.; Keogh, E.J. Matrix Profile XX: Finding and Visualizing Time Series Motifs of All Lengths using the Matrix Profile. In Proceedings of the 2019 IEEE International Conference on Big Knowledge (ICBK 2019), Beijing, China, 10–11 November 2019; pp. 175–182. [Google Scholar]
- Weather for 243 Countries of the World: Chelyabinsk. 2022. Available online: https://rp5.ru/Weather_in_Chelyabinsk/ (accessed on 17 November 2022).

| Algorithm | Year | Platform | Serial Ancestor (If Any) or Approach | |
|---|---|---|---|---|
| Hardware | Software | |||
| DRAG [39] | 2008 | Simulation of MapReduce | DRAG [8] | |
| DDD [40] | 2015 | HPC cluster | Spark | |
| PDD [41] | 2016 | HPC cluster | Spark | |
| GPU-STAMP [32] | 2018 | GPU | CUDA | Matrix profile [32] |
| SCAMP [42] | 2019 | GPU | CUDA | |
| MP-HPC [43] | 2019 | HPC cluster | MPI | |
| Zymbler et al. [10,13] | 2019 | Many-core CPU GPU | OpenMP OpenACC | HOTSAX [4] |
| Zymbler et al. [12] | 2021 | HPC cluster of many-core CPU | MPI OpenMP | DRAG [8] |
| KBF_GPU [44] | 2021 | GPU | CUDA | Brute-force search for K-distance discord [44] |
| Zhu et al. [45] | 2021 | GPU | CUDA | Computational patterns |
| Time Series | Length | Discord Length | Domain |
|---|---|---|---|
| Space shuttle | 50,000 | 150 | Measurements of a sensor on the NASA spacecraft |
| ECG | 45,000 | 200 | Electrocardiogram of an adult patient |
| ECG-2 | 21,600 | 400 | |
| Koski-ECG | 100,000 | 458 | |
| Respiration | 24,125 | 250 | Human breathing by chest expansion |
| Power demand | 33,220 | 750 | Annual energy consumption of an office |
| RandomWalk1M | 512 | Synthetic time series | |
| RandomWalk2M | 2 × | 512 |
| Specifications | GPU-SUSU | GPU-MSU |
|---|---|---|
| Brand and Product Line | NVIDIA Tesla | |
| Model | V100 | P100 |
| # cores | 5120 | 3584 |
| Core frequency, GHz | 1.3 | 1.19 |
| Memory, Gb | 32 | 16 |
| Peak performance (double precision), TFLOPS | 7 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zymbler, M.; Kraeva, Y. High-Performance Time Series Anomaly Discovery on Graphics Processors. Mathematics 2023, 11, 3193. https://doi.org/10.3390/math11143193
Zymbler M, Kraeva Y. High-Performance Time Series Anomaly Discovery on Graphics Processors. Mathematics. 2023; 11(14):3193. https://doi.org/10.3390/math11143193
Chicago/Turabian StyleZymbler, Mikhail, and Yana Kraeva. 2023. "High-Performance Time Series Anomaly Discovery on Graphics Processors" Mathematics 11, no. 14: 3193. https://doi.org/10.3390/math11143193
APA StyleZymbler, M., & Kraeva, Y. (2023). High-Performance Time Series Anomaly Discovery on Graphics Processors. Mathematics, 11(14), 3193. https://doi.org/10.3390/math11143193







