Bifurcation Analysis in a Harvested Modified Leslie–Gower Model Incorporated with the Fear Factor and Prey Refuge

Abstract

Fear and prey refuges are two significant topics in the ecological community because they are closely associated with the connectivity of natural resources. The effect of fear on prey populations and prey refuges (proportional to both the prey and predator) is investigated in the nonlinear-type predator-harvested Leslie–Gower model. This type of prey refuge is much more sensible and realistic than the constant prey refuge model. Because there is less research on the dynamics of this type of prey refuge, the current study has been considered to strengthen the existing literature. The number and stability properties of all positive equilibria are examined. Since the calculations for the determinant and trace of the Jacobian matrix are quite complicated at these equilibria, the stability of certain positive equilibria is evaluated using a numerical simulation process. Sotomayor’s theorem is used to derive a precise mathematical confirmation of the appearance of saddle-node bifurcation and transcritical bifurcation. Furthermore, numerical simulations are provided to visually demonstrate the dynamics of the system and the stability of the limit cycle is discussed with the help of the first Lyapunov number. We perform some sensitivity investigations on our model solutions in relation to three key model parameters: the fear impact, prey refuges, and harvesting. Our findings could facilitate some biological understanding of the interactions between predators and prey.

1. Introduction

Several researchers have explored the dynamical intricacy of interacting prey–predator models in depth to comprehend the species’ long-term behavior. A wide range of models have been developed to investigate the dynamic relationship between prey and their specialist predators. These models rely on the mathematical formulation by Lotka and Volterra. It should be noted, however, that certain models are classified as Gause-type models [1,2,3,4]. The Leslie–Gower form relies on the premise that a predator’s population reduction and the per-capita availability of its prey are inversely correlated. As a matter of fact, Leslie [5] established a predator–prey model in which the carrying capacity of the predator’s habitat is inversely correlated with the amount of prey. Leslie and Gower [6] and Pielou [7] have also examined an intriguing approach to predator dynamics. Similar to this, the researchers investigated the Leslie–Gower model, taking into account the effects of other ecological aspects, including harvesting, the Allee effect, prey refuges, and cooperative hunting. The functional response, or the interaction term, is another crucial element of population dynamics. Several ecologists and biologists have modified and analyzed various functional responses in the literature, including the Holling, ratio-dependent, Beddington–DeAngelis, and Crowley–Martin responses. For instance, the predator–prey model that states the predator eats its preferred food (prey) in a ratio-dependent manner was taken into consideration by the authors of [8]. They carefully examined how the Allee factor and the fear factor affect the size of the prey population. Also, they showed that the model under consideration experiences a number of bifurcations, which include saddle-node bifurcation, Hopf bifurcation, and Bogdanov–Takens bifurcation. Local and global stability analysis for the Leslie–Gower model and its modified model have been carried out by many researchers [9,10,11].

Despite the fact that some ecologists and biologists agree that prey–predator interactions are inadequately defined solely by regular predation and that a certain amount of fear must be assumed, few mathematical models have been constructed to quantify the possibility that fear factors influence the size of the prey population. This is partly due to the absence of specific experimental data illustrating how populations of terrestrial vertebrates can be impacted by fear [12,13]. Zanette et al. [14] just finished manipulating song sparrows throughout the course of a mating season to see if the assumed predation risk may impact reproduction despite the lack of direct killing. Fear may also have an impact on a juvenile prey’s physiological state, which might reduce its odds of surviving to adulthood. Birds, for instance, have predator defenses that they activate when they hear a predator, and when they are breeding they will leave their nests as soon as a threat is detected. Such anti-predator behavior can have long-term detrimental impacts on reproduction and population growth, even though it may enhance the probability of survival. Recent mathematical research has investigated the various changes in dynamical behavior that the fear effect might bring about in prey–predator models [15]. The modified Leslie–Gower model was employed by the authors in [16] to explore how fear affects the population of prey. They looked into the existence of different bifurcation behaviors and showed that the system experiences a series of dynamic behavior switches as the cost of fear rises, which eventually cause the prey population to go extinct while the predators survive because alternative prey is abundant. In [17], the authors studied the modified Leslie–Gower model with the impact of the fear effect and nonlinear harvesting in both prey and predators. Up until certain thresholds, it is seen that the fear rate stabilizes the system; after that, it causes prey extinction.

The prey refuge helps to safeguard prey to some extent and improves species coexistence by lowering the risk of extinction caused by predation. The refuge lowers prey–predator interactions and increases prey survival from extinction, according to a wide range of observational and empirical evidence [18,19]. Prey refuges have also been the subject of several theoretical investigations into their impacts, and it has generally been shown that they promote persistence by stabilizing the prey–predator relationship [20]. According to some empirical research, refuges can save prey from going extinct by stabilizing the community equilibrium and lowering the predator–prey interactions’ tendency to oscillate. Most recently, Al-Salti et al. [15] considered and studied the prey–predator model in regards to a refuge factor with a variable carrying capacity. Further, from the perspective of fulfilling human requirements, fishing, forestry, and animal management frequently practice population harvesting and the exploitation of biological resources. There is considerable interest in using bioeconomic modeling to shed light on the scientific administration of natural resources like fisheries and forests with regard to protection for the future benefit of humankind. Hence, we consider prey refuges in the harvested predator–prey model in this study.

Inspired by the existing literature, this work uses the nonlinear, harvested modified Leslie-Gower model with Holling type II interaction. Further, the study examines the results of including a fear of predation and refuge to balance out predation. To the extent of our knowledge, there is less research concerning the modified Leslie–Gower model with predator harvesting, a refuge factor proportional to both species, and a fear factor on the prey population. The conditions for various local bifurcation occurrences are described. The suggested model is illustrated by extensive numerical computations in terms of phase portraits and bifurcation diagrams. In this article, we studied details of methods followed by [21,22].

In this study, we will address the following three important aims:

i

To explore how the prey population fear and prey refuge impact the dynamical behavior in the proposed system. The prey refuge considered here depends on both the prey and predator and this paper shows how it impacts long-term survival.

ii

To investigate the necessary parametric conditions for the existence of equilibrium points, local and global stability, and bifurcation around the coexisting equilibrium point.

iii

To determine whether the system solution is close to a coexisting equilibrium point or exhibits periodic oscillations by examining the initial sizes of predators and prey.

The paper is structured as follows. In Section 2, we give a deep formulation of a mathematical model to consider in this work. Basic properties such as positive invariance, boundedness, and persistence are provided in Section 3. The conditions for the existence and local and global stability of all possible equilibria are given in Section 4. The conditions for the occurrence of various bifurcation behavior in the proposed model are in Section 5.

2. Mathematical Formulation

First, the Leslie–Gower models are formulated with coupled, nonlinear ordinary differential equations, which illustrate the interaction between prey and their specialist predators in the form below:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \dot{x}=r_{1}x\left(1-\frac{x}{K_1}\right)-exy,}\hfill \\ {\displaystyle \dot{y}=r_{2}y\left(1-\frac{y}{bx}\right)}\hfill \\ x\left(0\right)\ge 0,y\left(0\right)\ge 0.\hfill \end{array}\right.\end{array}$$

(1)

It is considered that prey grow logistically and have a linear increase in their intake rate with food density, where a denotes the attack rate. Also, $\frac{dy}{dt}=r_{2}y(1-\frac{y}{bx})$ denotes the growth of the predator population is of the logistic form, but the traditional $K_2$, which assesses the carrying capacity determined by the available resources in the ecosystem, is $K_2=bx$, proportional to the number of prey (b is the ratio of prey to predators). The Lesie–Gower term in this equation is denoted by $y/bx$. It assesses the decline in the predator population brought on by the scarcity (per capita $y/x$) of the prey. If there is an extreme shortage, y can search for other species, but this will restrict its growth because its preferred food (x) is not widely accessible. A positive constant might be added to the denominator to solve this problem. Then, the model becomes the modified Leslie–Gower model [23]. Some recent studies on Leslie–Gower models are cited in [16]. In this work, we confine ourselves to the modified Leslie–Gower model, which is of the form

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \dot{x}=r_{1}x\left(1-\frac{x}{K_1}\right)-exy,}\hfill \\ {\displaystyle \dot{y}=r_{2}y\left(1-\frac{y}{n+bx}\right)}\hfill \\ x\left(0\right)\ge 0,y\left(0\right)\ge 0.\hfill \end{array}\right.\end{array}$$

(2)

The modified Leslie–Gower model is obtained by adding a positive constant n to the denominator in the second equation of model (1).

2.1. Fear Effect on Prey Population

Model (2) with the assumption that the presence of predators causes fear in the prey population is provided by

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \dot{x}=\frac{r_{0}x}{1+ky}-d_{0}x-\frac{r_1{x}^2}{K_1}-exy,}\hfill \\ {\displaystyle \dot{y}=r_{2}y\left(1-\frac{y}{n+bx}\right)}\hfill \\ x\left(0\right)\ge 0,y\left(0\right)\ge 0.\hfill \end{array}\right.\end{array}$$

(3)

Here, we multiplied the function $f(k,y)=\frac{1}{1+ky}$ in the birth rate of the prey population due to fear induced by predators, where k is the amount of anti-predator defense due to fear [16,17]. Hence, the function $f(k,y)=\frac{1}{1+ky}$ meets a biological meaning and needs to satisfy the following conditions:

$$\begin{array}{ccc}\hfill f(0,y)=1,& f(k,0)=1,& \underset{k\to \infty }{lim}f(k,y)=0,\hfill \\ \hfill \underset{y\to \infty }{lim}f(k,y)=0,& \frac{\partial f(k,y)}{\partial k}<0,& \frac{\partial f(k,y)}{\partial y}<0.\hfill \end{array}$$

The above biological assumptions are given in Appendix A. For other important results on considering fear levels in prey–predator dynamics, see [24,25,26,27].

2.2. Harvesting in Predator Population

In the disciplines of fisheries, forestry, and wildlife management, using biological resources and harvesting species are common practices. It is important to note that harvesting is continuing for a long time before the extinction of the population. Harvesting can be implemented in three ways: (a) a constant-yield $H\left(y\right)=$ constant, (b) a constant-effort $H\left(y\right)=qEy$, or (c) a Michaelis–Menten type $H\left(y\right)=\frac{qEy}{cE+ly}$. The modified Leslie–Gower model with a nonlinear harvesting rate in predators is demonstrated below:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \dot{x}=\frac{r_{0}x}{1+ky}-d_{0}x-\frac{r_1{x}^2}{K_1}-exy,}\hfill \\ {\displaystyle \dot{y}=r_{2}y\left(1-\frac{y}{bx}\right)-\frac{qEy}{cE+ly}}\hfill \\ x\left(0\right)\ge 0,y\left(0\right)\ge 0.\hfill \end{array}\right.\end{array}$$

(4)

A version of the model (4) without the fear effect has been studied in [28]. In constant effort harvesting, y is finite and fixed or as the $y\to \infty$ if E is finite and fixed. Hence, the significance of choosing nonlinear harvesting is that the unrealistic features have been removed such that $\frac{qEy}{cE+ly}\to \frac{qy}{c}$ as $E\to \infty$ and $\frac{qEy}{cE+ly}\to \frac{qE}{l}$ as $y\to \infty$. Nonlinear harvesting is more realistic from an economic and biological point of view than other types of harvesting.

2.3. Prey Refuge

Next, taking into account prey refuges proportional to both populations brings our model system closer to reality since, in certain natural systems, prey refuges may be impacted by the size of both predators and prey. In light of this, the current work attempts to examine how refuges and harvesting affect a Holling type II prey–predator model [29]. However, research into the Leslie–Gower model with group defense is infrequent. Sokol and Howell [30] proposed a modified Leslie–Gower predator–prey system with group defense. Prey refuges were included in the model investigated in [30], and the spatial component revealed that species distributions are highly susceptible to group defense compared to prey refuges [31].

Model (4) includes a prey refuge that is proportional to both populations, i.e., the refuge size is $\mu xy$ from the predator, with $\mu \in [0,1]$. The incorporation of a prey refuge allows $(1-\mu y)x$ of the prey to be accessible for the predator to hunt [10]. To guarantee that the allowable range of the refuge is $0\le (1-\mu y)\le 1$ for a realistic biosystem [32], we only permit those tiny values of $\mu$ such that $(1-\mu y)\ge 0$, i.e., $y\le \frac{1}{\mu }$. Next, model (4) is provided by

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \dot{x}=\frac{r_{0}x}{1+ky}-d_{1}x-\frac{r_1}{K_1}{x}^2-\frac{e(1-\mu y)xy}{1+m(1-\mu y)x},}\hfill \\ {\displaystyle \dot{y}=r_{2}y\left(1-\frac{y}{n+bx(1-\mu y)}\right)-\frac{qEy}{cE+ly},}\hfill \\ x\left(0\right)\ge 0,y\left(0\right)\ge 0,\hfill \end{array}\right.\end{array}$$

(5)

where x and y stand for the prey and generalist predator densities, respectively, at time t; $r_0$ and $d_1$ are the growth and death rate of the prey population; $K_1$ is the prey’s carrying capacity; the term $y/(1+mx)$ is the Holling type II function [2,33,34] where $m>0$ represents a reduction in the predation rate at high predator densities due to mutual interference among the predators while searching for food or m is the product of the feeding rate and processing time, i.e., processing and searching for food are mutually exclusive events; and $r_2$ denotes the growth rate of the predator population size. The biological meaning of all parameters are presented in

Table 1. Biological meaning of the parameters.

Parameter	Value
$r_0$	Birth rate of prey
b	Conversion factor of prey into predator
k	The level of fear
n	Positive constant (alternative food for predator)
d	Natural death rate of predator
q	Catchability coefficient
m	Half saturation constant
$K_1$	Environmental carrying capacity
E	External effort devoted to harvesting
e	The effort of capture rate
c	Positive constant
$r_2$	Intrinsic growth rate of predator
l	Positive constant

.

By considering $a_1=\frac{r_1}{K_1}$, $a_2=\frac{r_2}{b}$, $\alpha =\frac{qE}{l}$ and $\beta =\frac{cE}{l}$, then the model with fewer parameters takes the following form:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \dot{x}=\frac{r_{0}x}{1+ky}-d_{1}x-a_1{x}^2-\frac{e(1-\mu y)xy}{1+m(1-\mu y)x}:={\widehat{F}}_1(x,y),}\hfill \\ {\displaystyle \dot{y}=y\left(r_2-\frac{a_{2}y}{n+x(1-\mu y)}\right)-\frac{\alpha y}{\beta +y}:={\widehat{F}}_2(x,y),}\hfill \\ x\left(0\right)\ge 0,y\left(0\right)\ge 0,\hfill \end{array}\right.\end{array}$$

(6)

where $x\left(0\right)=x_0$ and $y\left(0\right)=y_0$ are the initial conditions for model (6). Hereafter, we consider model (6) for analysis in the below sections.

3. Some Preliminaries

In this section, we provide some preliminaries, such as the existence, positivity, persistence, and boundedness of the solution for model (6). The persistence in a predator–prey model plays a significant role in mathematical ecology that guarantees the long-term existence of all species. Here, we have demonstrated the persistence criterion using the average Lyapunov function [35].

3.1. Existence and Positive Invariance

Let $\widehat{X}={(x,y)}^t$, $F={\mathbb{R}}^2\to {\mathbb{R}}^2$, $\widehat{F}={({\widehat{F}}_1,{\widehat{F}}_2)}^t$, and model (6) is given as

$$\begin{array}{c}\hfill \frac{d\widehat{X}}{dt}=\widehat{F}\left(\widehat{X}\right),\end{array}$$

(7)

where ${\widehat{F}}_i\in C^{\infty }\left(\mathbb{R}\right)$ and $i=1,2$. Since $\widehat{F}$ is a smooth function of the variables $(x,y)$ in the positive quadrant $\Omega =\{(x,y);x>0,y>0\}\subset {\mathbb{R}}_{+}^2$, where $\widehat{F}$ is Lipschitzian function of two variables, the local existence and uniqueness of the solution set the hold on the $\Omega$.

3.2. Persistence

Let us consider

$$\begin{array}{c}\hfill P(x,y)=x^{p_1}{y}^{p_2},\end{array}$$

(8)

where $p_1$ and $p_2$ are positive constants. Now, define the function $\Phi$ as:

$$\begin{array}{ccc}\hfill \Phi (x,y)& =& \frac{\dot{P}(x,y)}{P(x,y)}={\gamma }_1\frac{\dot{x}}{x}+{\gamma }_2\frac{\dot{y}}{y}\hfill \\ & =& {\gamma }_1\left({\displaystyle \frac{r_0}{1+ky}-d_1-a_{1}x-\frac{e(1-\mu y)y}{1+m(1-\mu y)x}}\right)+{\gamma }_2\left({\displaystyle r_2-\frac{a_{2}y}{n+x(1-\mu y)}-\frac{\alpha }{\beta +y}}\right).\hfill \end{array}$$

Now, $\Phi (0,0)={\gamma }_1{r}_0-{\gamma }_1{d}_1+{\gamma }_2{r}_2-{\gamma }_2\frac{\alpha }{\beta }>0$, if ${\gamma }_1{r}_0+{\gamma }_2{r}_2>{\gamma }_1{d}_1+{\gamma }_2\frac{\alpha }{\beta }$.

$$\begin{array}{ccc}\hfill \Phi (\overline{x},0)& =& {\gamma }_1\left(r_0-d_1-a_1\overline{x}\right)+{\gamma }_2\left(r_2-\frac{\alpha }{\beta }\right)\hfill \\ & =& {\gamma }_2\left(r_2-\frac{\alpha }{\beta }\right)>0,\mathrm{if}{r}_2>\frac{\alpha }{\beta }.\hfill \end{array}$$

Hence, the solution of model (6) is permanent if ${\gamma }_1{r}_0+{\gamma }_2{r}_2>{\gamma }_1{d}_1+{\gamma }_2\frac{\alpha }{\beta }$ and $r_2>\frac{\alpha }{\beta }$ are satisfied.

3.3. Positivity and Uniform Boundedness

Theorem 1.

Every solution of model (6) with initial conditions $x\left(t\right)>0$ and $y\left(t\right)>0$ exists in the interval $[0,+\infty )$, for all $t\ge 0$.

Proof. 

The given initial condition for model (6) ensures that a unique solution $\left(x\right(t),y(t\left)\right)$ exists and is defined on the interval $[0,\xi )$, where $0<\xi \le +\infty$. This is due to the fact that the right-hand side of model (6) is continuously differentiable and locally Lipschitz in the domain ${\mathbb{R}}_{+}^2$, ensuring the existence and uniqueness of the solution.

From model (6), we have

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle x\left(t\right)=x\left(0\right)exp\left[{\int }_0^t\left\{\frac{r_{0}x}{1+ky}-d_{1}x-a_1{x}^2-\frac{e(1-\mu y)xy}{1+m(1-\mu y)x}\right\}d\theta \right]>0,}\hfill \\ {\displaystyle y\left(t\right)=y\left(0\right)exp\left[{\int }_0^t\left\{y\left(r_2-\frac{a_{2}y}{n+x(1-\mu y)}\right)-\frac{\alpha y}{\beta +y}\right\}d\theta \right]>0.}\hfill \end{array}\right.\end{array}$$

(9)

□

It can be concluded that model (6) is positively invariant for all $t\ge 0$.

Theorem 2.

All solutions starting in ${\mathbb{R}}_{+}^2$ are uniformly bounded.

Proof. 

From model (6),

$$\begin{array}{ccc}\hfill \frac{dx}{dt}& \le & \frac{r_{0}x}{1+ky}-d_{1}x-a_1{x}^2\hfill \\ & \le & r_{0}x-d_{1}x-a_1{x}^2\hfill \\ & =& x(r_0-d_1-a_{1}x),\hfill \end{array}$$

and it is clear that $x\left(t\right)\le \frac{r_0-d_1}{a_1}:=M_1$ as $t\to \infty$, since it is considered that the intrinsic growth rate of the prey size should be positive, i.e., $r_0-d_1>0$.

Then, using the maximum $M_1$ in the second equation of model (6), we have

$$\begin{array}{c}\hfill \frac{dy}{dt}\le y\left(r_2-\frac{a_{2}y}{n+M_1{\mu }_{1}y}-\frac{\alpha }{\beta +y}\right),\end{array}$$

where ${\mu }_1=1-\mu y>0$. Then, from the above inequality, we have

$$\begin{array}{c}\hfill y\left(t\right)\le \frac{n+{\mu }_1{M}_1-\alpha }{r_2{a}_2}:=M_2 \mathrm{as} t\to \infty ,\end{array}$$

which ensures the boundedness of the solutions. □

4. Equilibria and Their Stability

This section investigates the equilibria points’ existence in the proposed model and provides a qualitative assessment of their stability. To obtain the equilibria of model (6), we need to solve the prey and predator nullcline equation, which is

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \frac{r_0}{1+ky}-d_1-a_{1}x-\frac{e(1-\mu y)y}{1+m(1-\mu y)x}=0,}\hfill \\ {\displaystyle r_2-\frac{a_{2}y}{n+x(1-\mu y)}-\frac{\alpha }{\beta +y}=0.}\hfill \end{array}\end{array}$$

(10)

We can see that model (6) possesses the following equilibria:

1. The trivial equilibrium $E_0(0,0)$ always exists.

2. The predator-free equilibrium $\widehat{E}(\widehat{x},0)$ always exists, where $\widehat{x}=\frac{r_0-d_1}{a_1}$, i.e., $r_0>d_1$.

3. The prey-free equilibrium is denoted by $\overline{E}(0,\overline{y})$, where $\overline{y}$ is calculated by solving the quadratic equation below:

$$a_2{\overline{y}}^2+(a_2\beta -r_{2}n)\overline{y}+\alpha n-r_{2}n\beta =0.$$

(11)

Hence, if $r_2>\frac{\alpha }{\beta }$ then (11) has at least one positive root. Then, the model possesses a prey-free equilibrium point.

4. Now, we are interested in the coexistence equilibrium point $E^{*}(x^{*},y^{*})$, where $x^{*}$ is calculated from the second equation of (10), which is

$$x^{*}=\frac{A_1+A_2{y}^{*}+A_3{y^{*}}^2}{A_4+A_5{y}^{*}+A_6{y^{*}}^2},$$

(12)

where $A_1=\alpha n-r_2\beta n$, $A_2=a_2\beta -r_{2}n$, $A_3=a_2$, $A_4=r_2\beta -\alpha$, $A_5=r_2-r_2\beta \mu +\alpha \mu$, $A_6=-r_2\mu ,$ and $y^{*}$ is calculated from the following equation:

$$\begin{array}{c}\hfill B_1{y}^7+B_2{y}^6+B_3{y}^5+B_4{y}^4+B_5{y}^3+B_6{y}^2+B_{7}y+B_8=0,\end{array}$$

(13)

where

$$\begin{array}{ccc}\hfill B_1& =& A_6^{2}ek{y}^7\mu ,\hfill \\ \hfill B_2& =& a_1{A}_3^{2}km\mu +A_{6}k(2A_{5}e+A_3{d}_{1}m)\mu +A_6^{2}e(-k+\mu ),\hfill \\ \hfill B_3& =& A_6\left(-a_1{A}_{3}k+A_2{d}_{1}k\mu m-d_1{A}_{3}km+A_3{d}_1\mu m+2A_{4}ek\mu +2A_{5}e(\mu -k)-A_3\mu m{r}_0\right)\hfill \\ & & +a_1{A}_{3}m\left(2A_{2}k\mu +A_3(\mu -k)\right)+A_{5}k\mu \left(A_3{d}_{1}m+A_{5}e\right)-A_6^2\left(d_{1}k+e\right),\hfill \\ \hfill B_4& =& -a_1\left(A_3\left(-2A_{1}k\mu m+2A_{2}km+A_{5}k-2A_2\mu m+A_6\right)+A_{2}k\left(A_6-A_2\mu m\right)+A_3^{2}m\right)\hfill \\ & & -A_6\left(2A_5\left(d_{1}k+e\right)+m\left(-A_1{d}_{1}k\mu +A_2{d}_{1}k-A_2{d}_1\mu +A_3{d}_1+A_2\mu r_0-A_3{r}_0\right)+2A_{4}e(k-\mu )\right)\hfill \\ & & +A_2{A}_5{d}_{1}k\mu m+A_3{A}_4{d}_{1}k\mu m-A_3{A}_5{d}_{1}km+A_6^2\left(r_0-d_1\right)\hfill \\ & & +A_3{A}_5{d}_1\mu m+2A_4{A}_{5}ek\mu -A_5^{2}ek+A_5^{2}e\mu -A_3{A}_5\mu m{r}_0,\hfill \\ \hfill B_5& =& -a_1\left(A_2^{2}m(k-\mu )+A_2\left(k\left(A_5-2A_1\mu m\right)+A_6\right)+A_3\left(2m\left(A_{1}k-A_1\mu +A_2\right)+A_{4}k+A_5\right)+A_1{A}_{6}k\right)\hfill \\ & & -A_5\left(m\left(-A_1{d}_{1}k\mu +A_2{d}_{1}k-A_2{d}_1\mu +A_3{d}_1+A_2\mu r_0-A_3{r}_0\right)+2A_6\left(d_1-r_0\right)+2A_{4}e(k-\mu )\right)\hfill \\ & & -A_5^2\left(d_{1}k+e\right)+A_2{A}_4{d}_{1}k\mu m-A_3{A}_4{d}_{1}km-A_1{A}_6{d}_{1}km-2A_6{A}_4{d}_{1}k+A_3{A}_4{d}_1\mu m\hfill \\ & & +A_1{A}_6{d}_1\mu m-A_2{A}_6{d}_{1}m+A_4^{2}ek\mu -2A_6{A}_{4}e-A_3{A}_4\mu m{r}_0-A_1{A}_6\mu m{r}_0+A_2{A}_{6}m{r}_0,\hfill \\ \hfill B_6& =& -a_1\left(A_2\left(2A_{1}m(k-\mu )+A_{4}k+A_5\right)+A_1\left(k\left(A_5-A_1\mu m\right)+A_6\right)+A_2^{2}m+A_3\left(2A_{1}m+A_4\right)\right)\hfill \\ & & -2A_5{A}_4\left(d_{1}k+e\right)+A_1{A}_4{d}_{1}k\mu m-A_{5}m\left(A_1{d}_1(k-\mu )+A_2\left(d_1-r_0\right)+A_1\mu r_0\right)\hfill \\ & & -A_2{A}_4{d}_{1}km+A_2{A}_4{d}_1\mu m-A_3{A}_4{d}_{1}m-A_1{A}_6{d}_{1}m-A_5^2\left(d_1-r_0\right)-2A_6{A}_4{d}_1\hfill \\ & & -A_4^{2}ek+A_4^{2}e\mu -A_2{A}_4\mu m{r}_0+A_3{A}_{4}m{r}_0+A_1{A}_{6}m{r}_0+2A_6{A}_4{r}_0,\hfill \\ \hfill B_7& =& -a_1{A}_1\left(A_{1}m(k-\mu )+A_{4}k+A_5\right)-a_1{A}_2\left(2A_{1}m+A_4\right)-A_4^2\left(d_{1}k+e\right)\hfill \\ & & -A_1{A}_{4}m\left(d_1(k-\mu )+\mu r_0\right)-A_2{A}_{4}m\left(d_1-r_0\right)\hfill \\ & & -A_1{A}_{5}m\left(d_1-r_0\right)-2A_5{A}_4\left(d_1-r_0\right),\hfill \\ \hfill B_8& =& -\left(A_{1}m+A_4\right)\left(a_1{A}_1-A_4\left(r_0-d_1\right)\right).\hfill \end{array}$$

Here, the coefficients $B_i,i=1,2,\dots ,8$ in equation (13) are influenced by the system parameters. The analytical expression for equilibria to the aforementioned model is extremely challenging. By solving numerically, one can derive the coexistence equilibrium $E^{*}$. Then, we have the following lemma on the existence of various equilibria.

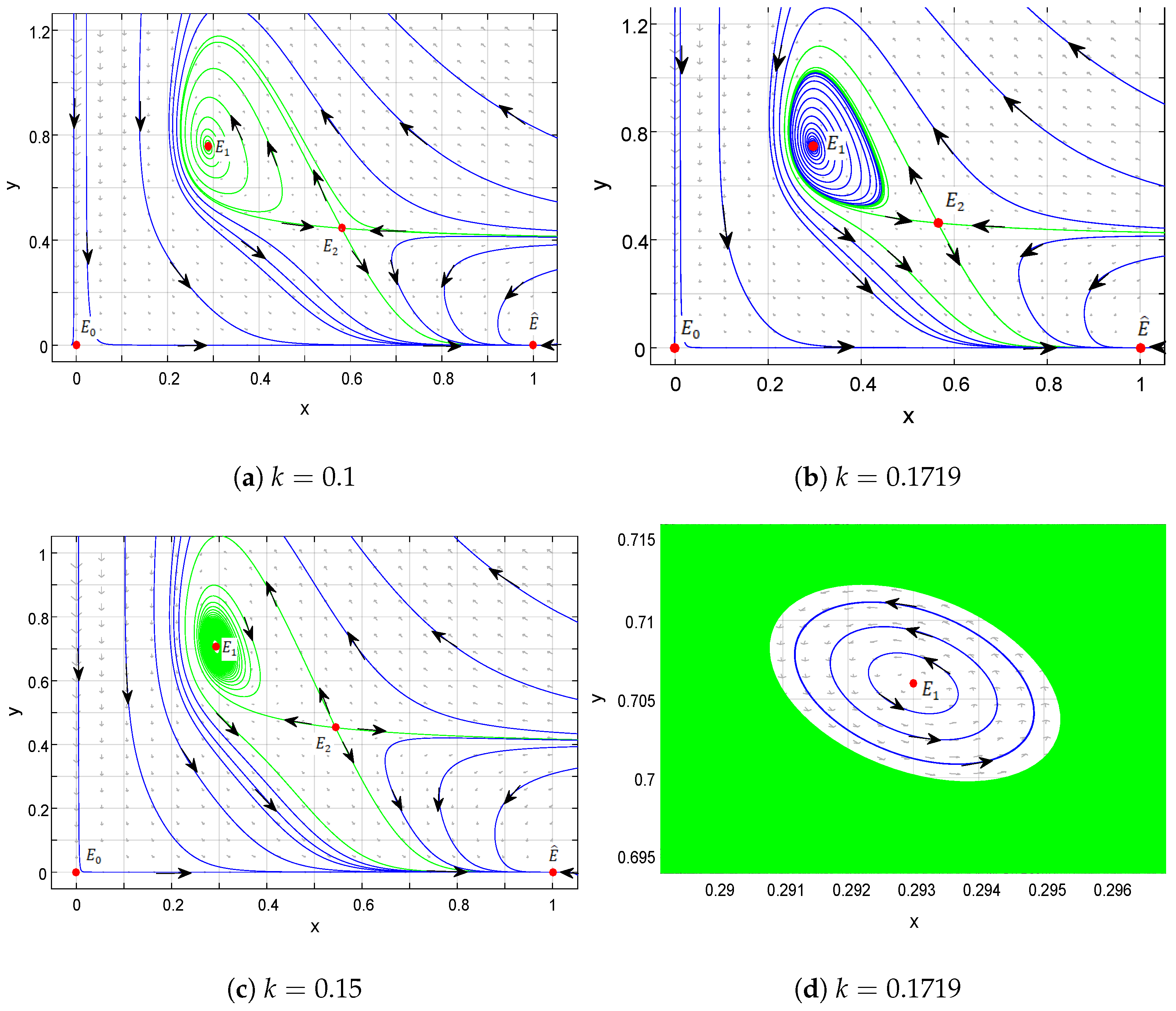
Remark 1.

For model (6), $E_0$ and $\widehat{E}$ always exist. $\overline{E}$ exists if $r_2>\frac{\alpha }{\beta }$ holds. From Descartes’s rule of sign changes, it is clear that $B_1>0$ and $B_8<0$ if $a_1{A}_1>A_4(r_0-d_1)$. Then, (13) has at least one positive root. Furthermore, the number of sign changes in (13) can determine the number of coexistence equilibria of model (6), and it is also necessary that $x^{*}>0$. Equation (13) has exactly one positive root if there is only one sign change occurring in the coefficients $B_i$. Hereafter, we consider that if model (6) has two coexistence equilibria they are named $E_1$ and $E_2$. If it has only one coexistence equilibrium, it is named $E_1$.

Furthermore, the nullcline plot illustrates how the number of equilibria varies by varying the fear parameter with the other parameters held constant. For the choice of fixed parameter values k, for instance, Figure 1 illustrates the existence of two, one, and no interior equilibrium points for model (6). For the choice of fixed parameter values $r_0=1.01$, $d=0.01$, $a_1=1$, $e=0.85635$, $\mu =0.015$, $m=0.015$, $r_2=2.60$, $a_2=0.4142$, $n=0.01$, $\alpha =1.475193$, and $\beta =0.2$ and varying the fear parameter k, model (6) has the two interior equilibrium points $E_1=(0.28693,0.79719)$ and $E_2=(0.60581,0.44076)$ for $k=0.05$, unique equilibrium $E_1=(0.37126,0.52976)$ for $k=0.4093$, and no equilibria for $k=0.5$. Similar changes in the number of equilibria can occur by varying both the prey refuge $\mu$ and harvesting parameter $\alpha$.

4.1. Local Stability

We now examine the local stability properties around the equilibria for model (6). For any given equilibrium $(x,y)$, the Jacobian matrix is

$$\begin{array}{c}\hfill J=\left[\begin{array}{cc}x\frac{\partial f_1}{\partial x}+f_1& x\frac{\partial f_1}{\partial y}\\ y\frac{\partial f_2}{\partial x}& y\frac{\partial f_2}{\partial y}+f_2\end{array}\right],\end{array}$$

(14)

where

$$\begin{array}{ccc}& & f_1=\frac{r_0}{1+ky}-d_1-a_{1}x-\frac{e(1-\mu y)y}{1+m(1-\mu y)x},\hfill \\ & & f_2=r_2-\frac{a_{2}y}{n+x(1-\mu y)}-\frac{\alpha }{\beta +y},\hfill \\ & & \frac{\partial f_1}{\partial x}=\frac{emy{(1-\mu y)}^2}{{(mx(1-\mu y)+1)}^2}-a_1,\hfill \\ & & \frac{\partial f_1}{\partial y}=\frac{2e\mu y-e}{mx(1-\mu y)+1}-\frac{e\mu mxy(1-\mu y)}{{(mx(1-\mu y)+1)}^2}-\frac{k{r}_0}{{(ky+1)}^2},\hfill \\ & & \frac{\partial f_2}{\partial x}=\frac{a_{2}y(1-\mu y)}{{(n+x(1-\mu y))}^2},\hfill \\ & & \frac{\partial f_2}{\partial y}=-\frac{a_2(n+x)}{n+x(1-\mu y)}+\frac{\alpha }{{(\beta +y)}^2}.\hfill \end{array}$$

The local stability properties of the equilibria $E_0$, $\widehat{E}$, and $\overline{E}$ are stated in the following theorem.

Theorem 3.

For model (6),

1. 

$E_0$ is saddle if $r_2<\frac{\alpha }{\beta }$, otherwise it is unstable.

2. 

$\widehat{E}$ is stable if $r_2<\frac{\alpha }{\beta }$ and $r_0-d_1<2a_1$, otherwise it is saddle.

3. 

$\overline{E}$ is

i. 

stable if $\frac{r_0}{1+k\overline{y}}<d_1+e(1-\mu \overline{y})\overline{y}$ and $r_2<\frac{2a_2\overline{y}}{n}+\frac{\alpha \beta }{{(\overline{y}+\beta )}^2}$.

ii. 

saddle if $\frac{r_0}{1+k\overline{y}}<d_1+e(1-\mu \overline{y})\overline{y}$ and $r_2>\frac{2a_2\overline{y}}{n}+\frac{\alpha \beta }{{(\overline{y}+\beta )}^2}$ (or) $\frac{r_0}{1+k\overline{y}}>d_1+e(1-\mu \overline{y})\overline{y}$ and $r_2<\frac{2a_2\overline{y}}{n}+\frac{\alpha \beta }{{(\overline{y}+\beta )}^2}$.

iii. 

unstable if $\frac{r_0}{1+k\overline{y}}>d_1+e(1-\mu \overline{y})\overline{y}$ and $r_2>\frac{2a_2\overline{y}}{n}+\frac{\alpha \beta }{{(\overline{y}+\beta )}^2}$.

Proof. 

The Jacobian matrices calculated at $E_0$, $\widehat{E}$, and $\overline{E}$ are

$$\begin{array}{ccc}\hfill J_{E_0}& =& \left(\begin{array}{cc}{r}_0-d_1& 0\\ 0& r_2-\frac{\alpha }{\beta }\end{array}\right),J_{\widehat{E}}=\left(\begin{array}{cc}{r}_0-d_1-2a_1& -\widehat{x}\left(\frac{e}{1+m}+k{r}_0\right)\\ 0& r_2-\frac{\alpha }{\beta }\end{array}\right),\hfill \\ \hfill J_{\overline{E}}& =& \left(\begin{array}{cc}\frac{r_0}{1+k\overline{y}}-d_1-e(1-\mu \overline{y})\overline{y}& 0\\ \frac{{\overline{y}}^2(1-\mu \overline{y})a_2}{n^2}& r_2-\frac{2a_2\overline{y}}{n}-\frac{\alpha \beta }{{(\overline{y}+\beta )}^2}\end{array}\right).\hfill \end{array}$$

The eigenvalues of the $J_{E_0}$ is $r_0-d_1$ and $r_2-\frac{\alpha }{\beta }$. The eigenvalue of $J_{\widehat{E}}$ is $r_0-d_1-2a_1$ and $r_2-\frac{\alpha }{\beta }$. The eigenvalues of $J_{\overline{E}}$ are $\frac{r_0}{1+k\overline{y}}-d_1-e(1-\mu \overline{y})\overline{y}$ and $r_2-\frac{2a_2\overline{y}}{n}-\frac{\alpha \beta }{{(\overline{y}+\beta )}^2}$. □

The following theorem provides the conditions for the local asymptotic stability of an arbitrary interior equilibrium point $E^{*}$.

Theorem 4.

The coexistence equilibrium $E^{*}$ is locally asymptotically stable if and only if $Tr\left(J_{E^{*}}\right)<0$ and $Det\left(J_{E^{*}}\right)>0$.

Proof. 

The Jacobian matrix at $E^{*}$ is given by

$$\begin{array}{c}\hfill J_{E^{*}}=\left(\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right),\end{array}$$

(15)

where

$$\begin{array}{ccc}& & {\displaystyle a_{11}=\frac{em{x}^{*}{y}^{*}{(1-\mu y^{*})}^2}{{(m{x}^{*}(1-\mu y^{*})+1)}^2}-a_1{x}^{*},}\hfill \\ & & {\displaystyle a_{12}=\frac{2e\mu x^{*}{y}^{*}-e{x}^{*}}{m{x}^{*}(1-\mu y^{*})+1}-\frac{e\mu m{x^{*}}^2{y}^{*}(1-\mu y^{*})}{{(m{x}^{*}(1-\mu y^{*})+1)}^2}-\frac{k{r}_0{x}^{*}}{{(k{y}^{*}+1)}^2},}\hfill \\ & & {\displaystyle a_{21}=\frac{a_2{y^{*}}^2(1-\mu y^{*})}{{(n+x^{*}(1-\mu y^{*}))}^2},}\hfill \\ & & {\displaystyle a_{22}=-\frac{a_2{y}^{*}(n+x^{*})}{n+x^{*}(1-\mu y^{*})}+\frac{\alpha y^{*}}{{(\beta +y^{*})}^2}.}\hfill \end{array}$$

The characteristic polynomial of $J_{E^{*}}$ is given by

$$\begin{array}{c}\hfill {\lambda }^2-Tr\left(J_{E^{*}}\right)\lambda +Det\left(J_{E^{*}}\right)=0,\end{array}$$

(16)

where $Tr\left(J_{E^{*}}\right)=a_{11}+a_{22}$ and $Det\left(J_{E^{*}}\right)=a_{11}{a}_{22}-a_{12}{a}_{21}$. □

Furthermore, the dynamical behaviors are summarized in

Table 2. Existence and stability conditions of equilibria for model (6).

	Equilibrium and Coordinate	Feasibility Condition	Stability Status
(i)	$E_0(0,0)$	always	saddle
(ii)	$\widehat{E}(\widehat{x},0)$	always	stable
			if $r_2<\frac{\alpha }{\beta }$ and $r_0-d_1<2a_1$
(iii)	$\overline{E}(0,\overline{y})$	$r_2>\frac{\alpha }{\beta }$	stable if
			$\frac{r_0}{1+k\overline{y}}<d_1+e(1-\mu \overline{y})\overline{y}$ and
			$r_2<\frac{2a_2\overline{y}}{n}+\frac{\alpha \beta }{{(\overline{y}+\beta )}^2}$
(iv)	$E^{*}(x^{*},y^{*})$	at least one sign change	$Tr\left(J_{E^{*}}\right)<0$ and
		in coefficients $B_i$ in (13)	$Det\left(J_{E^{*}}\right)>0$
		and $x^{*}>0$

.

Then, we conclude that $E_0$ and $\widehat{E}$ always exist, i.e., the birth rate of the prey population $r_0$ is always greater than $d_1$. Additionally, if $\widehat{E}$ exists and is stable it violates the condition for the existence of $\overline{E}$. Moreover, the relationship between the effects of other parameters has been discussed in the numerical simulations section.

4.2. Global Stability

Local stability only guarantees the behavior of the system in the small neighbourhood of an equilibrium point. It does not provide information about the long-term behavior of the system or its stability properties over the entire state space. In contrast, global stability refers to the property of a dynamical system where all trajectories, regardless of their initial conditions, converge to a stable equilibrium point. In this subsection, we concentrate on the global coexistence property of the arbitrary coexistence equilibrium point $E^{*}$. The global stability properties of model (6) are attained by considering a suitable Lyapunov function. The Lyapunov function used in this article has been widely considered in [32,36,37]. From Remark 1, if model (6) has exactly one coexistence equilibrium point $E_1(x_1,y_1)$ then we have the following results for the globally asymptotically stable condition for $E_1(x_1,y_1)$.

Theorem 5.

If $r_0-d_1>0$ and $a_1{D}_1>em{y}_1(1-\mu y_1)(1-\mu y)$ is satisfied, then the coexistence equilibrium $E_1$ is globally asymptotically stable.

Proof. 

Let us take the suitable Lyapunov function $V(x,y):{\mathbb{R}}_{+}^2\to \mathbb{R}$ as follows:

$$\begin{array}{c}\hfill V(x,y)=V_1\left(x\right)+\Omega V_2\left(y\right),\end{array}$$

(17)

where $V_1\left(x\right)=x-x_1-x_{1}ln(x/x_1)$ and $V_2\left(y\right)=y-y_1-y_{1}ln(y/y_1)$. The positive constant $\Omega$ is defined below. Both functions are well defined and continuous on ${\mathbb{R}}_{+}^2$. $V(x,y)$ is positive in ${\mathbb{R}}_{+}^2$ except at $E_1(x_1,y_1)$ and $V(x,y)=0$ at $E_1(x_1,y_1)$. Moreover, $\frac{\partial V_1\left(x\right)}{\partial x}>0$ for $x>x_1$, $\frac{\partial V_1\left(x\right)}{\partial x}<0$ for $x<x_1$, and $\frac{\partial V_2\left(y\right)}{\partial y}>0$ for $y>y_1$, $\frac{\partial V_2\left(y\right)}{\partial y}<0$ when $y<y_1$. The time derivative of $V_1$ and $V_2$ at the solutions of model (6) after using $E_1$ is

$$\begin{array}{ccc}\hfill \frac{d{V}_1}{dt}& =& (x-x_1)\frac{\dot{x}}{x}\hfill \\ & =& (x-x_1)\left(\frac{r_0}{1+ky}-d_1-a_{1}x-\frac{e(1-\mu y)y}{1+m(1-\mu y)x}\right)\hfill \\ & =& (x-x_1)\left(\frac{r_0}{1+ky}-\frac{r_0}{1+k{y}_1}-a_{1}x+a_1{x}_1-\frac{e(1-\mu y)y}{1+m(1-\mu y)x}+\frac{e(1-\mu y_1)y_1}{1+m(1-\mu y_1)x_1}\right).\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill \frac{d{V}_2}{dt}& =& (y-y_1)\frac{\dot{y}}{y}\hfill \\ & =& (y-y_1)\left(r_2-\frac{a_{2}y}{n+x(1-\mu y)}-\frac{\alpha }{\beta +y}\right)\hfill \\ & =& (y-y_1)\left(\frac{a_2{y}_1}{n+x_1(1-\mu y_1)}-\frac{a_{2}y}{n+x(1-\mu y)}-\frac{\alpha }{\beta +y_1}+\frac{\alpha }{\beta +y}\right).\hfill \end{array}$$

(19)

We define $D_1=(1+m(1-\mu y)x)(1+m(1-\mu y_1)x_1)$ and $D_2=(n+x(1-\mu y))$$(n+x_1(1-\mu y_1))$. By substituting (18) and (19), we obtain

$$\begin{array}{ccc}\hfill \frac{dV}{dt}& =& (x-x_1)\left(\frac{r_0}{1+ky}-\frac{r_0}{1+k{y}_1}-a_{1}x+a_1{x}_1-\frac{e(1-\mu y)y}{1+m(1-\mu y)x}+\frac{e(1-\mu y_1)y_1}{1+m(1-\mu y_1)x_1}\right)\hfill \\ & & +\Omega (y-y_1)\left(r_2-\frac{a_{2}y}{n+x(1-\mu y)}-\frac{\alpha }{\beta +y}\right)\hfill \\ & =& (x-x_1)\left(\frac{-r_{0}k}{(1+ky)(1+k{y}_1)}(y-y_1)-a_1(x-x_1)\right.\hfill \\ & & +\frac{1}{D_1}\left((-e(1+m{x}_1)+e\mu (1+m)(y+y_1)-em{\mu }^2{x}_1{y}_{1}y)(y-y_1)\right.\hfill \\ & & \left.\left.+\left(em{y}_1(1-\mu y_1)(1-\mu y)\right)(x-x_1)\right)\right)\hfill \\ & & +(y-y_1)(-\alpha \Omega (y-y_1)-\frac{\Omega }{D_2}(a_2(n+x_1)(y-y_1)+a_2{y}_1(1-\mu y)(x-x_1))).\hfill \end{array}$$

(20)

Choosing $\Omega$ such that

$$\begin{array}{c}\hfill \Omega =\frac{D_2}{a_2{y}_1(1-\mu y_1)}\left(\frac{-r_{0}k}{(1+ky)(1+k{y}_1)}+\frac{(-e(1+m{x}_1)+e\mu (1+m)(y+y_1)-em{\mu }^2{x}_1{y}_{1}y)}{D_1}\right),\end{array}$$

(21)

we obtain

$$\begin{array}{c}\hfill \frac{dV}{dt}=-\left(-a+\frac{em{y}_1(1-\mu y_1)(1-\mu y)}{D_1}\right){(x-x_1)}^2-\left(\alpha \Omega +\frac{a_2(n+x_1)\Omega }{D_2}\right){(y-y_1)}^2.\end{array}$$

(22)

We can see that the coefficient of ${(y-y_1)}^2<0$ and it is necessary to have a negative in the coefficient of ${(x-x_1)}^2$; for this, we have

$$\begin{array}{c}\hfill -a_1+\frac{em{y}_1(1-\mu y_1)(1-\mu y)}{(1+m(1-\mu y)x)(1+m(1-\mu y_1)x_1)}\le -a_1+\frac{em{y}_1(1-\mu y_1)}{(1+m(1-\mu y_1)x_1)}.\end{array}$$

(23)

Clearly, V is positive definite for $(x,y)\in {\mathbb{R}}_{+}^2\backslash (x_1,y_1)$. Since the quadratic form (23) in the previous equation is positively defined, every trajectory in the positive quadrant other than $(x_1,y_1)$ has $\frac{dV}{dt}<0$. As a result, if the condition is met then $E_1$ is globally asymptotically steady: $\frac{dV}{dt}{|}_{(x_1,y_1)}=0$. Then, the Lyapunov function V constructed here follows the Lyapunov–Lasalle’s invariance principle [38]. □

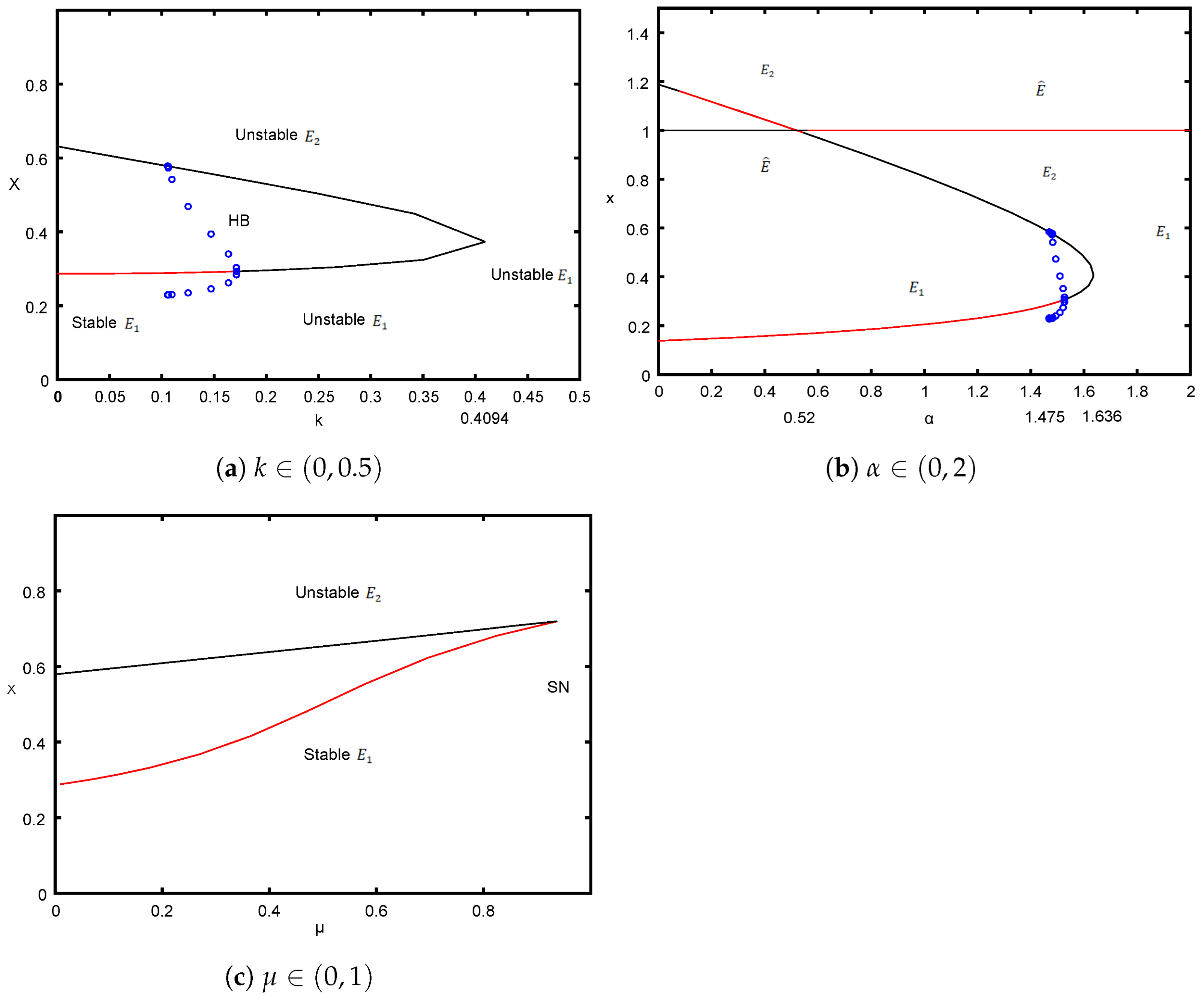
5. Bifurcation Analysis

The study of dynamical systems that undergo abrupt qualitative changes in behavior due to changes in their parameter values is the focus of the mathematical field of bifurcation. For further information on the foundations of local bifurcation analysis, see [21,22,39]. In this section, the parametric conditions for the occurrence of various bifurcation behavior for model (6) is discussed here, which is saddle-node, transcritical, and Hopf bifurcation near $E^{*}$ by varying the fear, refuge, and harvesting parameter.

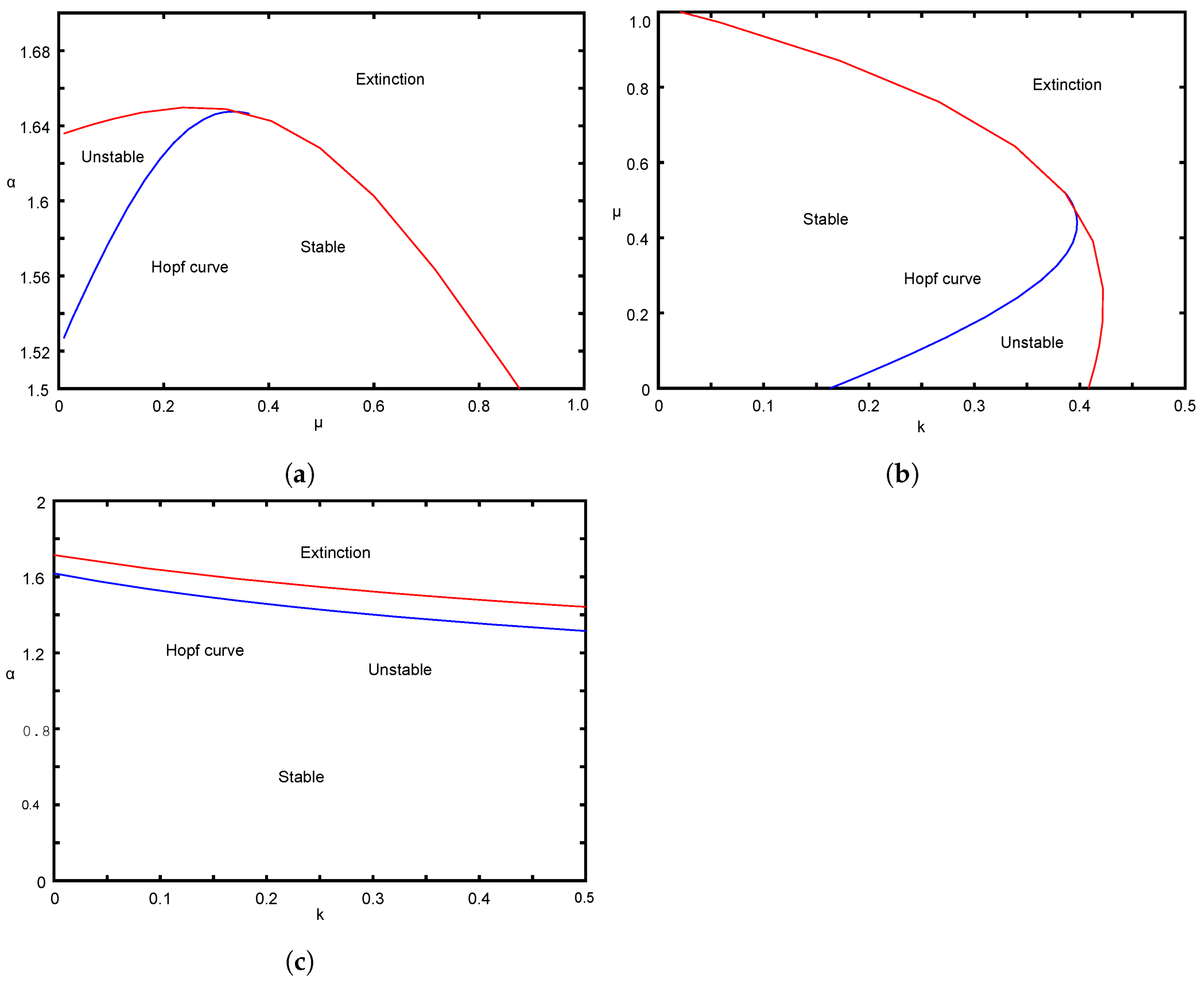
5.1. Hopf Bifurcation

In this subsection, we provide the condition for the existence of Hopf bifurcation around the arbitrary interior equilibrium $E^{*}$, and the stability of the Hopf bifurcation is discussed with the help of the value of the first Lyapunov coefficient.

Theorem 6.

The interior equilibrium $E^{*}$ undergoes Hopf bifurcation if $Tr\left(J_{E^{*}}\right)=0$ and $Det\left(J_{E^{*}}\right)>0$.

Theorem 7.

Assume that the system has an interior equilibrium $E^{*}$ and satisfies Theorem 6; then, $E^{*}$ changes its stability via Hopf bifurcation at some threshold $k=k_{HB}$ and satisfies $\frac{d}{dk}Tr\left[E^{*}\right]{|}_{k=k_{HB}}\ne 0$.

Proof. 

We must confirm the Hopf bifurcation’s transversality condition in order to guarantee the stability changes induced by nondegenerate Hopf bifurcation. Clearly,

$$\begin{array}{c}\hfill \frac{d}{dk}Tr\left[E^{*}\right]{|}_{k=k_{HB}}=(-\frac{r_0{y}^{*}}{{(k{y}^{*}+1)}^2})\ne 0.\end{array}$$

(24)

When the parametric limitation $Tr\left[E^{*}\right]=0$ and the aforementioned transversality requirement are both met then $E^{*}$ loses stability via Hopf bifurcation. □

5.2. Stability of Limit Cycle

To analyze the stability direction of the limit cycle, we proceed to compute the first Lyapunov number $l_1$ at the equilibrium point $E^{*}$ of model (6).

To begin with, we shift the equilibrium E of model (6) to $(0,0)$ by applying $x=\widehat{x}-x^{*}$ and $y=\widehat{y}-y^{*}$. This yields model (6) in a neighborhood of the origin as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{\widehat{x}}={\widehat{a}}_{10}\widehat{x}+{\widehat{a}}_{01}\widehat{y}+{\widehat{a}}_{20}{\widehat{x}}^2+{\widehat{a}}_{11}\widehat{x}\widehat{y}+{\widehat{a}}_{02}{\widehat{y}}^2+{\widehat{a}}_{30}{\widehat{x}}^3+{\widehat{a}}_{21}{\widehat{x}}^2\widehat{y}+{\widehat{a}}_{12}\widehat{x}{\widehat{y}}^2+{\widehat{a}}_{03}{\widehat{y}}^3,\\ \dot{\widehat{y}}={\widehat{b}}_{10}\widehat{x}+{\widehat{b}}_{01}\widehat{y}+{\widehat{b}}_{20}{\widehat{x}}^2+{\widehat{b}}_{11}\widehat{x}\widehat{y}+{\widehat{b}}_{02}{\widehat{y}}^2+{\widehat{b}}_{30}{\widehat{x}}^3+{\widehat{b}}_{21}{\widehat{x}}^2\widehat{y}+{\widehat{b}}_{12}\widehat{x}{\widehat{y}}^2+{\widehat{b}}_{03}{\widehat{y}}^3,\end{array}\right.\end{array}$$

(25)

Since model (6) exhibits the Hopf bifurcation, we have $({\widehat{a}}_{10}+{\widehat{b}}_{01}=0)$ and $\Delta ={\widehat{a}}_{10}{\widehat{b}}_{01}-{\widehat{a}}_{01}{\widehat{b}}_{10}>0$. The coefficients ${\widehat{a}}_{ij}$ and ${\widehat{b}}_{ji}$ are determinant by

$$\begin{array}{ccc}& & {\displaystyle {\widehat{a}}_{10}=\frac{em{x}^{*}{y}^{*}{(1-\mu y^{*})}^2}{{(m{x}^{*}(1-\mu y^{*})+1)}^2}-a_1{x}^{*},}\hfill \\ & & {\displaystyle {\widehat{a}}_{01}=-\frac{k_{HB}{r}_0{x}^{*}}{{(1+k_{HB}{y}^{*})}^2}-\frac{em{x^{*}}^2{y}^{*}\mu (1-\mu y^{*})}{{(1+m{x}^{*}(1-\mu y^{*}))}^2}+\frac{2e{x}^{*}{y}^{*}\mu -e{x}^{*}}{1+m{x}^{*}(1-\mu y^{*})}}\hfill \\ & & {\widehat{a}}_{20}=-a_1-\frac{em{y}^{*}{(\mu y^{*}-1)}^2}{{(m{x}^{*}(\mu y^{*}-1)-1)}^3},\hfill \\ & & {\widehat{a}}_{11}=\frac{e(-\mu y^{*}(m{x}^{*}+2)+m{x}^{*}+1)}{{(m{x}^{*}(\mu y^{*}-1)-1)}^3}-\frac{k_{HB}{r}_0}{{(k_{HB}{y}^{*}+1)}^2},\hfill \\ & & {\widehat{a}}_{02}=\frac{k_{HB}^2{r}_0{x}^{*}}{{(k_{HB}{y}^{*}+1)}^3}-\frac{e\mu x^{*}(m{x}^{*}+1)}{{(m{x}^{*}(\mu y^{*}-1)-1)}^3},\hfill \\ & & {\widehat{a}}_{30}=\frac{e{m}^2{y}^{*}{(\mu y^{*}-1)}^3}{{(m(x^{*}-\mu x^{*}{y}^{*})+1)}^4},\hfill \\ & & {\widehat{a}}_{21}=\frac{em(\mu y^{*}-1)(m{x}^{*}(\mu y^{*}-1)+3\mu y^{*}-1)}{{(m(x^{*}-\mu x^{*}{y}^{*})+1)}^4},\hfill \\ & & {\widehat{a}}_{12}=\frac{e\mu (m{x}^{*}(m{x}^{*}(\mu y^{*}-1)+2\mu y^{*})+1)}{{(m(x^{*}-\mu x^{*}{y}^{*})+1)}^4}+\frac{k_{HB}^2{r}_0}{{(k_{HB}{y}^{*}+1)}^3},\hfill \\ & & {\widehat{a}}_{03}=x^{*}\left(\frac{e{\mu }^{2}m{x}^{*}(m{x}^{*}+1)}{{(m(x^{*}-\mu x^{*}{y}^{*})+1)}^4}-\frac{k_{HB}^3{r}_0}{{(k_{HB}{y}^{*}+1)}^4}\right),\hfill \\ & & {\displaystyle {\widehat{b}}_{10}=\frac{a_2{y^{*}}^2(1-\mu y^{*})}{{(n+x^{*}(1-\mu y^{*}))}^2},}\hfill \\ & & {\displaystyle {\widehat{b}}_{01}=-\frac{a_2{y}^{*}(n+x^{*})}{{(n+x^{*}(1-\mu y^{*}))}^2}+\frac{\alpha y^{*}}{{(\beta +y^{*})}^2},}\hfill \\ & & {\widehat{b}}_{20}=-\frac{a_2{y^{*}}^2{(1-\mu y^{*})}^2}{{(n+x^{*}(1-\mu y^{*}))}^3},\hfill \\ & & {\widehat{b}}_{11}=\frac{a_2{y}^{*}\left(-3\mu y^{*}(n+x^{*})+2(n+x^{*})+{\mu }^2{x}^{*}{y^{*}}^2\right)}{{(n-\mu x^{*}{y}^{*}+x^{*})}^3},\hfill \\ & & {\widehat{b}}_{02}=\frac{\alpha \beta }{{(\beta +y^{*})}^3}-\frac{a_2{(n+x^{*})}^2}{{(n-\mu x^{*}{y}^{*}+x^{*})}^3},\hfill \\ & & {\widehat{b}}_{30}=\frac{a_2{y^{*}}^2{(1-\mu y^{*})}^3}{{(n+x^{*}(1-\mu y^{*}))}^4},\hfill \\ & & {\widehat{b}}_{21}=\frac{a_2{y}^{*}(\mu y^{*}-1)(n(2-4\mu y^{*})+\mu x^{*}{y}^{*}(\mu y^{*}-3)+2x^{*})}{{(n-\mu x^{*}{y}^{*}+x^{*})}^4},\hfill \\ & & {\widehat{b}}_{12}=-\frac{a_2(n+x^{*})(\mu y^{*}(3n+x^{*})-n-x^{*})}{{(n-\mu x^{*}{y}^{*}+x^{*})}^4},\hfill \\ & & {\widehat{b}}_{03}=-\frac{a_2\mu x^{*}{(n+x^{*})}^2}{{(n-\mu x^{*}{y}^{*}+x^{*})}^4}-\frac{\alpha \beta }{{(\beta +y^{*})}^4}.\hfill \end{array}$$

Then, the quantity $l_1$ says the stability of the limit cycle for model (6) is given by

$$\begin{array}{ccc}& & l_1=\frac{-3\pi }{2{\widehat{a}}_{01}{\Delta }^{3/2}}\left\{\left[{\widehat{a}}_{10}{\widehat{b}}_{10}({\widehat{a}}_{11}^2+{\widehat{a}}_{11}{\widehat{b}}_{02}+{\widehat{a}}_{02}{\widehat{b}}_{11})+{\widehat{a}}_{10}{\widehat{a}}_{01}({\widehat{b}}_{11}^2+{\widehat{a}}_{20}{\widehat{b}}_{11}+{\widehat{a}}_{11}{\widehat{b}}_{02})\right.\right.\hfill \\ & & +{\widehat{b}}_{10}^2({\widehat{a}}_{11}{\widehat{a}}_{02}+2{\widehat{a}}_{02}{\widehat{b}}_{02})-2{\widehat{a}}_{10}{\widehat{b}}_{10}({\widehat{b}}_{02}^2-{\widehat{a}}_{20}{\widehat{a}}_{02})-2{\widehat{a}}_{10}{\widehat{a}}_{01}({\widehat{a}}_{20}^2-{\widehat{a}}_{20}{\widehat{a}}_{02})\hfill \\ & & -{\widehat{a}}_{01}^2(2{\widehat{a}}_{20}{\widehat{b}}_{20}+{\widehat{b}}_{11}{\widehat{b}}_{20})+({\widehat{a}}_{01}{\widehat{b}}_{10}-2{\widehat{b}}_{10}^2)({\widehat{b}}_{11}{\widehat{b}}_{02}-{\widehat{b}}_{11}{\widehat{a}}_{20})]\hfill \\ & & \left.-({\widehat{a}}_{10}^2+{\widehat{a}}_{01}{\widehat{b}}_{10})\left[3({\widehat{b}}_{10}{\widehat{b}}_{03}-{\widehat{a}}_{01}{\widehat{a}}_{30})+2{\widehat{a}}_{10}({\widehat{a}}_{21}+{\widehat{b}}_{12})+({\widehat{b}}_{10}{\widehat{a}}_{12}-{\widehat{a}}_{01}{\widehat{b}}_{21})\right]\right\}.\hfill \end{array}$$

A supercritical Hopf bifurcation destabilizes the equilibrium $E^{*}$ when $l_1<0$, whereas a subcritical Hopf bifurcation occurs when $l_1>0$. Since the above expression for the first Lyapunov number $l_1$ is complex, we cannot determine the sign of $l_1$ from the above expression analytically. As a result, we have found it in the numerical part at the Hopf bifurcation point.

5.3. Nonexistence of Periodic Solution

Now, we will express model (6) as $\frac{d\widehat{x}}{dt}=\widehat{F}\left(\widehat{X}\right)$, where $\widehat{X}=(x,y)$ and $\widehat{F}=({\widehat{F}}_1,{\widehat{F}}_2)$. Here, ${\widehat{F}}_1,{\widehat{F}}_2\in C^{\infty }\left(\mathbb{R}\right)$, where ${\widehat{F}}_1=\frac{r_{0}x}{1+ky}-d_{1}x-a_1{x}^2-\frac{e(1-\mu y)xy}{1+m(1-\mu y)x}$ and ${\widehat{F}}_2=r_{2}y-\frac{a_2{y}^2}{n+x(1-\mu y)}-\frac{\alpha y}{\beta +y}$. Let $\widehat{H}(x,y)=\frac{1}{xy}$ be a continuously differentiable function for $(x,y)\in \Phi$.

$$\begin{array}{ccc}\hfill ▽·\left(H\widehat{F}\right)& =& \frac{\partial }{\partial x}\left(\frac{r_0}{y(1+ky)}-\frac{d_1}{y}-\frac{a_{1}x}{y}-\frac{e(1-\mu y)}{1+m(1-\mu y)x}\right)\hfill \\ & & +\frac{\partial }{\partial y}\left(\frac{r_2}{x}-\frac{a_{2}y}{x(n+x(1-\mu y\left)\right)}-\frac{\alpha }{x(\beta +y)}\right)\hfill \\ & =& -\frac{a}{y}+\frac{em{(1-\mu y)}^2}{{(1+m(1-\mu y)x)}^2}-\frac{a_2(n+x)}{x{(n+x(1-\mu y))}^2}+\frac{\alpha }{x{(y+\beta )}^2}<0.\hfill \end{array}$$

(26)

According to Bedixson–Dulac’s criterion for the nonexistence of periodic orbits [40], if $▽·\left(H\widehat{F}\right)<0$ then the present system does not exhibit any periodic orbits.

5.4. Transcritical Bifurcation

Next, we discuss the possibility of the existence of transcritical bifurcation in this subsection. We know model (6) has the boundary equilibrium $\overline{E}(\widehat{x},0)$. Also, when $\alpha ={\alpha }_{TC}=r_2\beta$, $\widehat{E}$ coincides with arbitrary $E^{*}$. By taking $\alpha$ as the bifurcation parameter, we use Sotomayor’s Theorem [39] to check model (6) undergoes a transcritical bifurcation. According to [39], $Det\left(J_{\widehat{E}}\right)={\lambda }_1{\lambda }_2=0$. Let $\widehat{F}={({\widehat{F}}_1,{\widehat{F}}_2)}^T$; the Jacobian $J_{\widehat{E}}$ at $\widehat{E}$ is given by

$$\begin{array}{c}\hfill J_{\widehat{E}}=Dg\left(\overline{E}\right)=\left(\begin{array}{cc}{r}_0-d_1-2a_1& -\widehat{x}\left(k{r}_0+\frac{e}{1+m}\right)\\ 0& 0\end{array}\right).\end{array}$$

Clearly, $Det\left(J_{\widehat{E}}\right)=0$ at $\alpha ={\alpha }_{TC}=r_2\beta$, which has a simple zero eigenvalue. Also, let the matrices $J_{\widehat{E}}$ and ${J_{\widehat{E}}}^T$ have the eigenvectors $\Theta ={({\theta }_1,{\theta }_2)}^T$ and $\Phi ={({\varphi }_1,{\varphi }_2)}^T$ for the zero eigenvalue, which yields

$$\begin{array}{cc}\hfill \Theta =& {\left(\widehat{x}\left(k{r}_0+\frac{e}{1+m}\right),r_0-d_1-2a_1\right)}^T,\Phi ={\left(0,1\right)}^T.\hfill \end{array}$$

Furthermore, we can obtain ${\widehat{F}}_{\mu }(\widehat{E};{\alpha }_{TC})=\left(\begin{array}{c}0\\ -\frac{y}{y+\beta }\end{array}\right){|}_{(\widehat{x},0)}.$

Now,

$$\begin{array}{cc}\hfill {\Omega }_1=& {\Phi }^T{\widehat{F}}_{\alpha }(\widehat{E};{\alpha }_{TC})=0,\hfill \end{array}$$

(27)

and also

$$\begin{array}{c}\hfill D{\widehat{F}}_{\alpha }(\widehat{E};{\alpha }_{TC})\Theta =\left(\begin{array}{cc}0& 0\\ 0& \frac{-\frac{\beta }{{(y+\beta )}^2}}{{(y+m_t)}^3}\end{array}\right)\left(\begin{array}{c}0\\ 1\end{array}\right){|}_{(\widehat{x},0)}=\left(\begin{array}{c}0\\ -\frac{1}{\beta }\end{array}\right).\end{array}$$

(28)

Therefore,

$$\begin{array}{cc}\hfill {\Omega }_2=& {\Phi }^{T}D\widehat{F}(\widehat{E};{\alpha }_{TC})\Theta =-\frac{1}{\beta }\ne 0,\hfill \end{array}$$

(29)

Similarly,

$$\begin{array}{cc}\hfill D^2\widehat{F}(\widehat{E};{\alpha }_{TC})(\Theta ,\Theta )=& \left(\begin{array}{c}\frac{{\partial }^2{f}_1}{\partial x^2}{\theta }_1^2+2\frac{{\partial }^2{f}_1}{\partial x\partial y}{\theta }_1{\theta }_2+\frac{{\partial }^2{f}_1}{\partial y^2}{\theta }_2^2\\ \frac{{\partial }^2{f}_2}{\partial x^2}{\theta }_1^2+2\frac{{\partial }^2{\theta }_2}{\partial x\partial y}{\theta }_1{\theta }_2+\frac{{\partial }^2{f}_2}{\partial y^2}{\theta }_2^2\end{array}\right)\hfill \\ \hfill =& \left(\begin{array}{c}{\eta }_1{\theta }_1^2+2{\eta }_2{\theta }_1{\theta }_2+{\eta }_3{\theta }_2^2\\ {\eta }_4{\theta }_1^2+2{\eta }_5{\theta }_1{\theta }_2+{\eta }_6{\theta }_2^2\end{array}\right),\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill {\eta }_1& =-2a_1,{\eta }_2=-\frac{e}{m\widehat{x}+1}+\frac{em\widehat{x}}{{(m\widehat{x}+1)}^2}-k{r}_0,\hfill \\ \hfill {\eta }_3& =\widehat{x}\left(\frac{2e\mu }{m\widehat{x}+1}-\frac{2e\mu m\widehat{x}}{{(m\widehat{x}+1)}^2}+2k^2{r}_0\right),\hfill \\ \hfill {\eta }_4& =0,{\eta }_5=0,{\eta }_6=\frac{2{\alpha }_{Tc}}{{\beta }^2}-\frac{2a_2}{n+\widehat{x}},\hfill \end{array}$$

and also

$$\begin{array}{ccc}\hfill {\Omega }_3& =& {\Phi }^T{D}^2\widehat{F}(\widehat{E};{\alpha }_{TC})(\Theta ,\Theta )\hfill \\ & =& \left(\begin{array}{cc}{\varphi }_1& {\varphi }_2\end{array}\right)\left(\begin{array}{c}{\eta }_1{\theta }_1^2+{\eta }_2{\theta }_1{\theta }_2+{\eta }_3{\theta }_2^2\\ {\eta }_4{\theta }_1^2+{\eta }_5{\theta }_1{\theta }_2+{\eta }_6{\theta }_2^2\end{array}\right)\hfill \\ & =& \left(\frac{2{\alpha }_{Tc}}{{\beta }^2}-\frac{2a_2}{n+\widehat{x}}\right){\left(r_0-d_1-2a_1\right)}^2.\hfill \end{array}$$

(30)

Hence, ${\Omega }_3\ne 0$ if both ${\alpha }_{Tc}\ne \frac{a_2{\beta }^2}{n+\overline{x}}$ and $r_0\ne d_1+2a_1$ are satisfied. Thus, from Sotomayor’s Theorem model (6) admits a transcritical bifurcation near $\widehat{E}$ at ${\alpha }_{TC}$, if ${\Omega }_1=0$ and ${\Omega }_{2,3}\ne 0$.

5.5. Saddle-Node Bifurcation

Next, we provide the parametric condition for the occurrence of saddle-node bifurcation in the following.

Theorem 8.

If $Det\left(J_{E^{*}}\right)=0$ at a critical threshold $\mu ={\mu }_{SN}$, then model (6) admits saddle-node bifurcation at $E^{*}$.

Proof. 

Let us take a bifurcation parameter $\mu$ and apply Sotomayor’s Theorem [39] to show model (6) admits a saddle-node bifurcation at the arbitrary equilibrium point $E^{*}$. According to [39], since $Det\left(J_{E^{*}}\right)={\lambda }_1{\lambda }_2=0$, then either ${\lambda }_1$ or ${\lambda }_2$ must be zero and the other less than zero. Also, $Tr\left(J_{E^{*}}\right)<0$. Let $\widehat{F}={({\widehat{F}}_1,{\widehat{F}}_2)}^T$; then, matrix $J_{E^{*}}$ is written as

$$\begin{array}{c}\hfill J_{E^{*}}=\left(\begin{array}{cc}{\widehat{a}}_{11}& {\widehat{a}}_{12}\\ {\widehat{a}}_{21}& {\widehat{a}}_{22}\end{array}\right).\end{array}$$

where

$$\begin{array}{ccc}& & {\displaystyle {\widehat{a}}_{11}=\frac{em{x}^{*}{y}^{*}{(1-{\mu }_{SD}{y}^{*})}^2}{{(m{x}^{*}(1-{\mu }_{SD}{y}^{*})+1)}^2}-a_1{x}^{*},}\hfill \\ & & {\displaystyle {\widehat{a}}_{12}=\frac{2e{\mu }_{SD}{x}^{*}{y}^{*}-e{x}^{*}}{m{x}^{*}(1-{\mu }_{SD}{y}^{*})+1}-\frac{e{\mu }_{SD}m{x^{*}}^2{y}^{*}(1-{\mu }_{SD}{y}^{*})}{{(m{x}^{*}(1-{\mu }_{SD}{y}^{*})+1)}^2}-\frac{k{r}_0{x}^{*}}{{(k{y}^{*}+1)}^2},}\hfill \\ & & {\displaystyle {\widehat{a}}_{21}=\frac{a_2{y^{*}}^2(1-{\mu }_{SD}{y}^{*})}{{(n+x^{*}(1-{\mu }_{SD}{y}^{*}))}^2},}\hfill \\ & & {\displaystyle {\widehat{a}}_{22}=-\frac{a_2{y}^{*}(n+x^{*})}{n+x^{*}(1-{\mu }_{SD}{y}^{*})}+\frac{\alpha y^{*}}{{(\beta +y^{*})}^2}.}\hfill \end{array}$$

Let ${\mu }_{SD}$ be the critical value, such that $J_{E^{*}}$ has the eigenvalue zero, such that $Det\left(J_{E^{*}}\right)=0$ at ${\mu }_{SD}$. Also, let the matrices $J_{E^{*}}$ and ${J_{E^{*}}}^T$ have the eigenvectors $\Theta ={({\theta }_1,{\theta }_2)}^T$ and $\Phi ={({\varphi }_1,{\varphi }_2)}^T$ for the zero eigenvalue, which gives $\Theta ={\left(-{\widehat{a}}_{22},{\widehat{a}}_{21}\right)}^T$ and $\Phi ={\left({\widehat{a}}_{22},-{\widehat{a}}_{12}\right)}^T$. Furthermore, we obtain get

$$\begin{array}{c}\hfill {\widehat{F}}_m(E^{*};{\mu }_{SD})=\left(\begin{array}{c}{\widehat{b}}_{11}\\ {\widehat{b}}_{12}\end{array}\right),\end{array}$$

where

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\widehat{b}}_{11}=\frac{e{x}^{*}{y^{*}}^2}{{(1+m{x}^{*}(1-{\mu }_{SD}{y}^{*}))}^2},}\hfill \\ {\displaystyle {\widehat{b}}_{12}=\frac{a_2{x}^{*}{y^{*}}^3}{{(n+x^{*}(1-\mu y^{*}))}^2}.}\hfill \end{array}\end{array}$$

Now,

$$\begin{array}{cc}\hfill {\Omega }_1=& {\Phi }^T{\widehat{F}}_{\mu }(E^{*};{\mu }_{SD})={\widehat{a}}_{22}{\widehat{b}}_{11}-{\widehat{a}}_{12}{\widehat{b}}_{12}.\hfill \end{array}$$

(31)

Therefore, ${\Omega }_1\ne 0$ at $\mu ={\mu }_{SD}$, and also

$$\begin{array}{cc}\hfill D^2\widehat{F}(E^{*};{\mu }_{SD})(\Theta ,\Theta )=& \left(\begin{array}{c}\frac{{\partial }^2{f}_1}{\partial x^2}{\theta }_1^2+2\frac{{\partial }^2{f}_1}{\partial x\partial y}{\theta }_1{\theta }_2+\frac{{\partial }^2{f}_1}{\partial y^2}{\theta }_2^2\\ \frac{{\partial }^2{f}_2}{\partial x^2}{\theta }_1^2+2\frac{{\partial }^2{f}_2}{\partial x\partial y}{\theta }_1{\theta }_2+\frac{{\partial }^2{f}_2}{\partial y^2}{\theta }_2^2\end{array}\right)\hfill \\ \hfill =& \left(\begin{array}{c}{\epsilon }_1{\theta }_1^2+2{\epsilon }_2{\theta }_1{\theta }_2+{\epsilon }_3{\theta }_2^2\\ {\epsilon }_4{\theta }_1^2+2{\epsilon }_5{\theta }_1{\theta }_2+{\epsilon }_6{\theta }_2^2\end{array}\right),\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill {\epsilon }_1& =-2a_1-\frac{2em{y}^{*}{({\mu }_{SD}{y}^{*}-1)}^2}{{(m{x}^{*}({\mu }_{SD}{y}^{*}-1)-1)}^3},\hfill \\ \hfill {\epsilon }_2& =\frac{e(-{\mu }_{SD}{y}^{*}(m{x}^{*}+2)+m{x}^{*}+1)}{{(m{x}^{*}({\mu }_{SD}{y}^{*}-1)-1)}^3}-\frac{k{r}_0}{{(k{y}^{*}+1)}^2},\hfill \\ \hfill {\epsilon }_3& =\frac{2k^2{r}_0{x}^{*}}{{(k{y}^{*}+1)}^3}-\frac{2e{\mu }_{SD}{x}^{*}(m{x}^{*}+1)}{{(m{x}^{*}({\mu }_{SD}{y}^{*}-1)-1)}^3},\hfill \\ \hfill {\epsilon }_4& =-\frac{2a_2{y^{*}}^2{(1-{\mu }_{SD}{y}^{*})}^2}{{(n+x^{*}(1-{\mu }_{SD}{y}^{*}))}^3},\hfill \\ \hfill {\epsilon }_5& =\frac{a_2{y}^{*}\left(-3{\mu }_{SD}{y}^{*}(n+x^{*})+2(n+x^{*})+{\mu }_{SD}^2{x}^{*}{y^{*}}^2\right)}{{(n-{\mu }_{SD}{x}^{*}{y}^{*}+x^{*})}^3},\hfill \\ \hfill {\epsilon }_6& =\frac{2\alpha \beta }{{(\beta +y^{*})}^3}-\frac{2a_2{(n+x^{*})}^2}{{(n-{\mu }_{SD}{x}^{*}{y}^{*}+x^{*})}^3},\hfill \end{array}$$

and also

$$\begin{array}{c}\hfill {\Omega }_2={\Phi }^T{D}^2\widehat{F}(E^{*};{\mu }_{SD})(\Theta ,\Theta )=\left(\begin{array}{cc}{\varphi }_1& {\varphi }_2\end{array}\right)\left(\begin{array}{c}{\epsilon }_1{\theta }_1^2+{\epsilon }_2{\theta }_1{\theta }_2+{\epsilon }_3{\theta }_2^2\\ {\epsilon }_4{\theta }_1^2+{\epsilon }_5{\theta }_1{\theta }_2+{\epsilon }_6{\theta }_2^2\end{array}\right)\ne 0.\end{array}$$

(32)

According to Sotomayor’s Theorem, the system exhibits a saddle-node bifurcation around $E^{*}(x^{*},y^{*})$ at $\mu ={\mu }_{SD}$ if ${\Omega }_1\ne 0$ and ${\Omega }_2\ne 0$. To confirm ${\Omega }_1,{\Omega }_2\ne 0$, we calculated it numerically. Thus, it can be inferred that the variation of the parameter $\mu$ across the critical threshold $\mu ={\mu }_{SD}$ results in a change in the number of interior equilibria of model (6) from zero to one to two. □

6. Numerical Simulations

The dynamic nature of the proposed model that corresponds to changes in the fear, prey refuge, and harvesting parameters cannot be expressed explicitly or analyzed analytically. Therefore, numerical simulations are required to comprehend the model’s dynamics, which were carried out with the help of XPPAUT [41] and PPLANE [42] software. Let us consider the model parameters as follows:

In order to check the effect of fear, the prey refuge, and harvesting in the considered model (6), we consider the fixed parameter values in

Table 3. Fixed parameter values.

Parameter	Value	Parameter	Value
$r_0$	1.01	m	0.015
k	0.1	$r_2$	2.60
d	0.01	$a_2$	0.4142
$a_1$	1	n	0.01
e	0.85635	$\alpha$	1.475193
$\mu$	0.01	$\beta$	0.2

and vary the k, $\mu$, and $\alpha$. The dynamics of the model are analyzed using phase portraits and one- or two-parameter bifurcation diagrams, as discussed below.

6.1. Effect of Fear in Prey Population

For model (6) with the fixed parameters in Table 3, varying the fear parameter k exhibits complex behavior. For instance, the numbers for the existence of interior equilibria are shown using nullcline analysis (see Figure 1). To verify whether the species can coexist for a long period of time, it is crucial to examine the local stability of the equilibria. If $k=0.1$, the system has four equilibrium points: $E_0(0,0)$ is unstable, $\widehat{E}=(1,0)$ is unstable, $E_1(0.2884,0.75692)$ is a spiral sink that satisfies Theorem 4 and whose eigenvalues are ${\lambda }_{1,2}=-0.066223\pm 0.81822i$, and $E_2(0.58067,0.44519)$ is a saddle point, which is shown in Figure 2a. If $k=0.15$, the equilibrium point $E_1(0.29127,0.72082)$ is a spiral sink surrounded by an unstable limit cycle, as shown in Figure 2b. On further increasing $k_{HB}=0.1719$, the equilibrium $E_1(0.293,0.70599)$ is a center, which is shown in Figure 2c. Then, the eigenvalues are ${\lambda }_{1,2}=\pm 0.75151$, which satisfies Theorem 6, and $\frac{d}{dk}Tr\left[E_1\right]{|}_{k=k_{HB}}=(-\frac{r_0{y}_1}{{(k_{HB}{y}_1+1)}^2})=-0.567061\ne 0$. Also, the unstable periodic solution collides with the saddle point. The local amplification near the interior equilibrium point $E_1$ of Figure 2c is shown in Figure 2d. It is clear there exists a Hopf bifurcation on varying f. It is clear that the eigenvalues of the Jacobian matrix at $E_1(0.293,0.70599)$ are ${\lambda }_{1,2}=\pm 0.70599$ and it also satisfies the transversality condition of Theorem 7. Further, we found the first Lyapunov coefficient is $l_1=75.1529\pi >0$, and it is clear that the existing limit cycle is unstable.

6.2. Effect of Harvesting

Further, it is necessary to verify the effect of harvesting the predator population in the system dynamics. We fix all other parameters as in Table 3 and vary the harvesting parameter $\alpha$. For the smaller value of $\alpha =0.1$, the system has the following equilibrium points: $E_0(0,0)$, $\widehat{E}(1,0)$, $E_1(0.14202,0.91344)$, and $E_2(1.1536,-0.16237)$ (see Figure 3a). In $E_2$, the predator population size is negative and it is biologically meaningless. And on increasing ${\alpha }_{TC}=0.52$, the equilibrium $E_2$ and $\widehat{E}$ collide with each other and exchange their stability properties, which ensure the existence of transcritical bifurcation (see Figure 3b). We have exactly one coexistence equilibrium point $E_1(0.16494,0.88891)$, which satisfies Theorem 5. Then, $E_1$ is globally asymptotically stable and also clearly shown in Figure 3b. If $\alpha =1.475$, $E_1(0.28834,0.75698)$ is a spiral sink and its eigenvalues are ${\lambda }_{1,2}=-0.066458\pm 0.81845i$ (see Figure 3c), and for $\alpha =1.527$ the equilibrium point $E_1$ becomes the center and its eigenvlues are ${\lambda }_{1,2}=\pm 0.74182i$ (see Figure 3d). This existence of transcritical bifurcation is verified from the quantities ${\Omega }_1=0$, ${\Omega }_2=-5\ne 0$, and ${\Omega }_3=-25.1798\ne 0$ by the Sotomayor theorem.

6.3. Effect of Prey Refuge

The phenomena of the existence of one, two, and no equilibria can also occur for the refuge parameter by fixing the parameters in Table 3 and varying the refuge parameter. If $\mu =0.2$, model (6) has four equilibria, $E(0,0)$, $\widehat{E}(1,0)$, $E_1(0.34004,0.81828)$, and is a spiral sink, whose eigenvalues are ${\lambda }_{1,2}=-0.27115\pm 0.772464$, and $E_2(1,0)$ is a saddle point (see Figure 4a). If ${\mu }_{SN}=0.9374$, the number of interior equilibria is reduced to one and it is a saddle point $E_1(0.71968,0.56214)$ whose eigenvalues are ${\lambda }_1=-0.69553$ and ${\lambda }_2=0.021212$ (see Figure 4b), which ensures the occurrence of saddle bifurcation for the parameter $\mu$. And the quantities ${\Omega }_1=0.196311\ne 0$ and ${\Omega }_2=-1.51299\ne 0$ ensure the existence of saddle-node bifurcation for model (6) by using the Sotomayor theorem.

For a clear view of such a critical transaction, the one-parameter bifurcation by varying $k\in (0,0.5)$, $\alpha \in (0,1)$, and $\mu \in (0,2)$ is shown in Figure 5a–c, and all other parameters are fixed as in Table 3. One of the prominent phenomena of the ecological system is extinction criteria and it also necessary to show the dynamics of model (6) with the combination of this parameter. We plotted the two-parameter bifurcation diagrams in Figure 6a–c. The extinction region, the stable and unstable region of the interior equilibria with the particular choice of parameter values, is clearly shown. Further, it is necessary to show how the model studied in this article differs from other earlier works. We compared some works from the existing literature in

Table 4. Earlier works on Leslie–Gower model.

Reference	Prey Refuge	Fear Effect	Harvesting	Functional Response
[16]	×	√	×	Holling IV
[17]	Constant	√	√	Holling II
[43]	×	√	×	Holling IV
This paper	Both prey and predator	√	√	Holling II

. The extinction of the population for the particular choice of k, $\mu$, $\alpha$, and other values is fixed as in Table 3 and is shown in Figure 7a–c.

The dynamics of model (2), the model with fear, in which the predator consumes the prey in the form of a Holling type II interaction, were examined by the authors in [16]. Transcritical bifurcation, Hopf bifurcation, and Bogdanov–Takens bifurcation are all present in the under-considered model. The authors of [17] looked at nonlinear harvesting in both species, prey refuges, and fear in the prey population. They demonstrated how the model experiences transcritical and saddle-node bifurcations. Mukherjee [43] investigated that the modified Leslie–Gower model with Holling type IV interaction, used to study the fear impact on a predator–prey system, experiences similar sorts of bifurcations. In this study, we examined the modified Leslie–Gower model with nonlinear harvesting in the predator population, fear in the prey population, and a prey refuge proportional to both species. We showed that model (6) exhibits saddle-node bifurcation, transcritical bifurcation, Hopf bifurcation, the extinction of species, and cusp-type dynamics. Since the computation approach offers fascinating details about how ecological systems function, there are significant drawbacks because (a) nonlinearity in the system frequently results in highly sensible solutions to variations in system parameters and (b) we frequently lack knowledge of true parameter values. This suggests that the specific decisions we produced regarding the values of the parameters and the precise structure of functional relationships may have significantly influenced the results. Analytical methods are precise and broad but only work with very basic models. But even the simplest model’s formal analysis can serve as an initial guide for particular ideas that are easily evaluated through numerical simulations.

7. Conclusions

In this study, we studied the influence of fear in the prey population, the refuge effect proportional to both prey and predators, and nonlinear harvesting in the predator population. We have assumed that prey ensures the admissible range of a refuge $0\le (1-\mu y)\le 1$ in our considered model. We also took into account a consideration of nonlinear harvesting in the predator population. To analyze the effect of this biological situation, we considered the modified Leslie–Gower model, where the prey consumes its favorite food in the form of a Holling type II interaction term. It is important in ecology that the predator can switch over to other food in the abundance of its favorite prey. The existence of all biologically feasible equilibria has been investigated in order to analyze the local dynamics of the considered model. The local stability analysis was carried out in order to show the long-term coexistence of populations, which was analyzed with the help of eigenvalues of the corresponding Jacobian matrices of the equilibria. Further, we took the conventional Lyapunov function to derive the analytical condition for the global stability of the coexisting equilibrium point. The complex dynamical behavior of the model was discussed in terms of bifurcation analysis and extinction of populations, since both play a crucial role in conserving the populations in the ecological system. We showed the occurrence of saddle bifurcation, transcritical bifurcation, and Hopf bifurcation by varying the fear parameter k, refuge parameter $\mu$, and harvesting parameter $\alpha$. 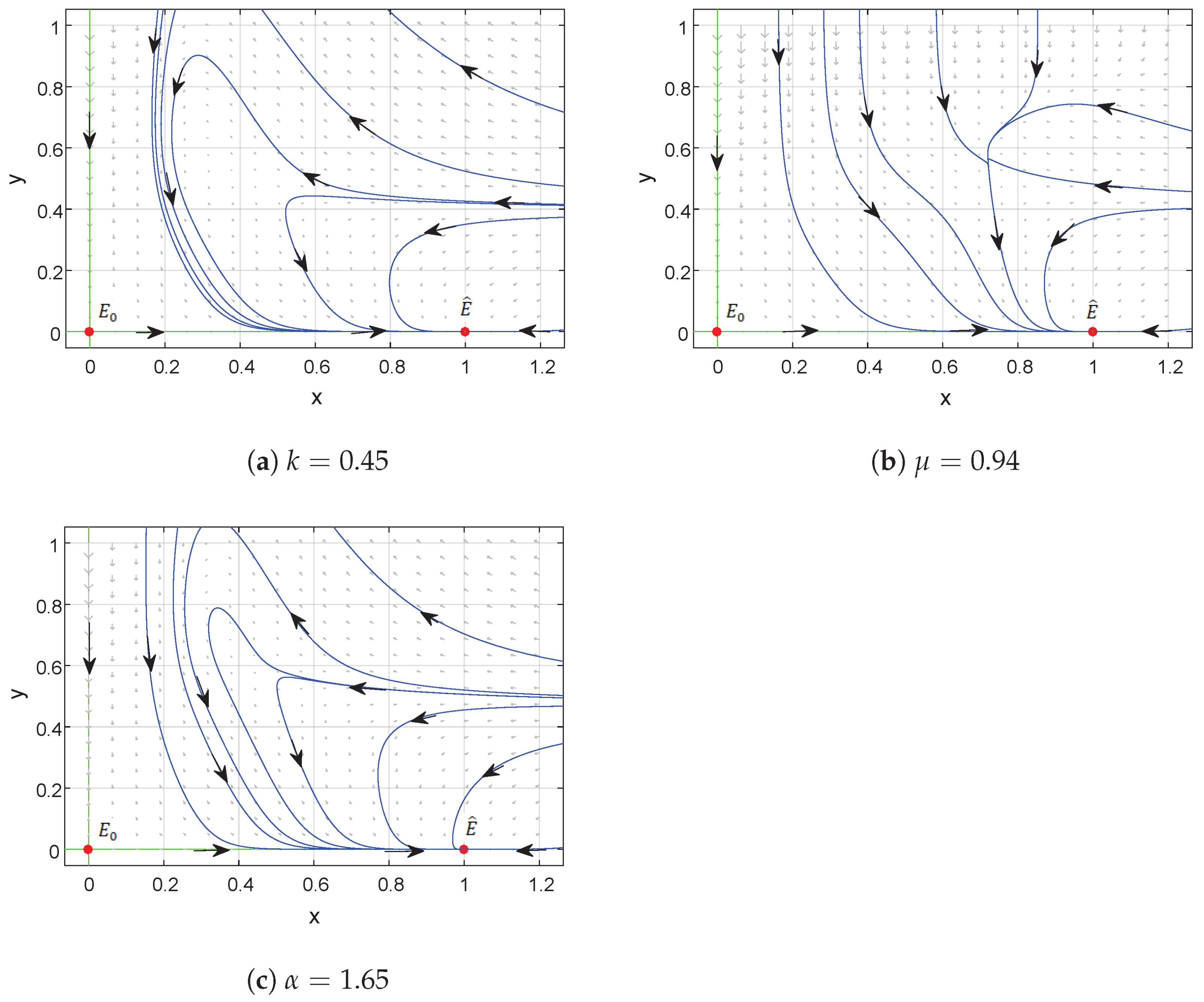The occurrence of transcritical and saddle-node bifurcation was verified with the help of normal form theory [39] and we also showed that the existence of subcritical Hopf bifurcation is confirmed with the help of calculating the first Lyapunov number, i.e., the unstable limit cycle. We also showed that the population becomes extinct by increasing this parameter at a certain critical threshold.

When studying interactions between prey and predators or other ecological systems, achieving sustainability is of utmost importance. This is often accomplished by establishing a stable limit cycle, which helps to maintain the system’s long-term stability. But in our proposed model we found the coexisting equilibrium surrounded by an unstable limit cycle. So it is necessary to allow small fluctuations in the populations inside the limit cycle, otherwise it leads to the extinction of species. Enhancing the biological realism of the studied model is one of the challenges for future research. Biological systems are more complex and it is difficult to study their underlying mechanisms. It is necessary to study our model by considering various functional responses and possibly extend it to the food chain model.