Abstract
In this article, we investigate the behavior of vehicle platoons operating in a predecessor-following configuration, implemented through sampled-data control systems. Our primary focus is to examine the potential influence of the sampling time on the string stability of the platoon. To address this, we begin by designing a string-stable platoon in continuous time. Subsequently, we consider the controller discretization process and proceed to simulate and implement the designed control strategy on an experimental platform at a scaled-down level. Through experimental testing and some theoretical results, we analyze the effects of different sampling times on the string stability performance of the platoon. We observe that an inappropriate selection of the sampling time can lead to a degradation in string stability within the platoon, making the choice of the sampling time crucial in maintaining the desired string stability properties. These findings highlight the importance of carefully considering the sampling time in the implementation of control systems for platooning applications.
MSC:
93-05
1. Introduction
In recent years, the field of intelligent transportation systems (ITS) has grown significantly thanks to advancements in wireless communication, data processing, control systems, and artificial intelligence algorithms, among other areas [1,2,3]. One specific area of ITS research is cooperative adaptive cruise control systems, which enable vehicles to navigate at a cruise speed that adapts to the speed of preceding vehicles. Using information sent wirelessly by other vehicles can improve the goal of maintaining a desired inter-vehicle distance between them [4]. A well-designed ITS system with these features can allow a platoon of vehicles to navigate cooperatively and efficiently, resulting in reduced fuel usage, pollutant emissions, travel times, and improved transport safety [5]. By utilizing these technologies, we can create a smarter transportation infrastructure that meets the needs of modern society.
Naturally, in platooning applications, each vehicle’s control system must achieve internal stability, the desired cruise speed, and maintain the desired distance between vehicles. However, there is an additional requirement when designing these control systems, which relates to how transient errors caused by external stimuli or disturbances propagate to the vehicles further back in the platoon. If these errors are amplified along the chain of vehicles, the platoon will exhibit erratic and dangerous behavior, which will worsen if more vehicles are added to the platoon. In this case, the platoon is said to be string-unstable. On the other hand, if the system is string-stable, the errors will be reduced or remain bounded as they propagate along a platoon, regardless of its length, reducing the danger in navigation and allowing more vehicles to be added without compromising performance [6]. The importance of string stability in platooning has motivated researchers to obtain conditions on the design parameters of controllers that guarantee it. It has been found that these conditions depend on many factors, such as the topology of the communication between vehicles, the type of information that is sent, the spacing policy between vehicles, the quality of the communication channels, and the dynamic characteristics of the vehicles, among others [6,7,8].
Initially, most of the results related to string stability in platooning have been derived for continuous-time frameworks (see, for instance, [6,7,9,10]). However, in recent years, there has been a growing interest in studying platoons within a discrete-time setting. This is because a crucial aspect of many control systems is their practical implementation using computer-based control and, consequently, the use of a discrete-time framework. Additionally, the implementation of digital wireless communications among vehicles in the context of platooning further justifies the use of discrete-time analysis. As a result, a variety of digital technologies have gained attention in the field of platooning, with the ultimate aim of transforming it into a practical reality [11,12,13].
When implementing sampled-data control in platooning, it is crucial to carefully evaluate the impact of the sampling process on the system’s performance. It is widely acknowledged that selecting an inappropriate sampling time in a feedback loop can result in the loss of internal stability [14]. However, the effect of the sampling time on string stabilization in platooning has received limited attention from researchers thus far. Instead, most studies in this area have primarily focused on addressing the challenges posed by unreliable communication links and utilizing discrete-time control techniques for platooning analysis. For instance, Ref. [15] employs Model Predictive Control (MPC) to handle switching communication topologies in a platooning setting, providing stability and string stability results. In [16], a sampled-data-based MPC-like control method is proposed to achieve string stability in platoons subject to disturbances and saturation constraints. Similarly, Ref. [17] considers platooning with non-ideal communications using LQR control, allowing for dealing with transmissions of data that are samples of the real acceleration of vehicles. In [18], platooning control using sampled positions of vehicles was investigated, focusing on the input-to-state stability of the multi-agent system instead of string stability. Various aspects of platooning under unreliable communication links, such as random data loss, have been studied in the literature, including a discrete-time approach. For instance, in this context, researchers have explored mean square stabilization [19] and string stability [20,21,22], the employment of data-loss compensation strategies [23], and also estimation techniques to deal with data loss [24,25]. Platooning with communication links subject to malicious attacks is studied in, for instance, [26,27], which naturally considers sampled systems. The authors of [28] investigate event-triggered platooning control for random communication topologies and different spacing policies but do not provide explicit string stability results. In [29], the authors primarily focus on sampled-data control of vehicular platoons, specifically considering undirected communication topology and analog fading networking, while omitting detailed analysis of string stability. Earlier works addressing sampling and platooning can be found in [30,31,32]. These works provide several insights into the relationships between sampling and important aspects of vehicular platooning. However, most of the previous works do not thoroughly consider the effect that varying the sampling time has on the scalability properties of a platoon, particularly its string stability.
On the other hand, experimental validation in vehicular platooning is a challenging but important task. In both continuous and discrete-time literature results, some works obtained analytical expressions for the string stability conditions and sometimes complemented them with simulations to verify their consistency [9,10]. In other cases, the analysis has been reduced to numerical studies only [20,23,33]. In very few cases, there is experimental validation of the results, mainly due to cost limitations associated with implementing the techniques on real vehicles, which limits the size of the platoon [34]. However, some studies use scale experimental platforms to test the proposed algorithms [24,35,36,37,38]. In the realm of platooning research, most analytical findings have been derived within the continuous-time framework despite the practical implementation necessitating the use of sampled-data control systems. Consequently, the selection of an appropriate sampling time becomes a fundamental yet critical task. The lack of results concerning the interplay between the sampling time and string stability further complicates this task.
The previous literature review reveals a noticeable gap in the literature relating sampling time and string stability. Motivated by this, in this work, we aim to investigate whether the choice of sample time can impact the string stability property in a real implementation. To achieve this, we first design a string-stable platoon using a continuous-time setting. Next, we adapt the continuous-time design to a sample-data feedback control framework and simulate the behavior of the platoon for different sampling times. We chose sampling times that guarantee internal stability for the feedback system, enabling us to assess the string stability property separately from any internal instability concerns. We also provide theoretical results that motivate the design of platooning experiments. Finally, we implement this sample-data control scheme on the scaled-down experimental platform, PL-TOON [39]. Our simulation results and experimental findings provide empirical evidence that the selection of sample time can indeed influence the string stability property of a platoon. These results highlight the need for a deeper analysis of the relationship between sampling time and string stabilization, incorporating both theoretical and practical analyses. Our results are an initial step towards a derivation of necessary and sufficient conditions on the sample time for string stability. This is necessary to ensure the proper functioning of platoons in practical applications.
2. Problem Formulation
2.1. Preliminaries and Notation
Throughout the manuscript, we consider most of the standard systems and control literature notation. For a signal of the continuous time variable , we denote , with as its Laplace transform. If the transfer function of a single-input single-output LTI continuous time system is given by , we denote its -norm as
with . Analogously, for discrete time, we use horizontal bars to denote the discrete-time version of signals , of a continuous-time signal . The respective -transform of is given by , , and the sampled equivalent or discrete-time implementation of a continuous-time transfer function is given by , with its respective -norm given by
We base the following analysis on theoretical results for platooning that were provided for continuous-time models (see, e.g., [40]). However, when implementing control algorithms on real hardware, mostly through the use of digital micro-controllers, sensors, and actuators, it is often necessary to convert most, if not all, signals to their sampled-based versions. In the following, we will consider that digital controllers will be implemented using discrete-time approximations of continuous-time controllers and that continuous-time plants will be shifted to their zero-order hold (ZOH) equivalents, which is one of the most common approaches for dealing with discrete-time control implementations [14].
2.2. Platooning Setup
In this work, we consider a one-dimensional platoon consisting of vehicles. Each vehicle is labelled with an index and is equipped with a controller that aims to maintain a desired inter-vehicle distance while following the vehicle in front, with the exception of the leader vehicle (), which operates independently from the rest of the platoon. To aid in accomplishing this task, each vehicle utilizes wireless communication to transmit pertinent information to the subsequent vehicles. We assume that the platoon adopts a predecessor-following configuration; that is, each vehicle receives information only from its predecessor. This configuration is illustrated in Figure 1, where denotes the inter-vehicle distance between vehicle i and its predecessor. Here, we consider that each vehicle in the platoon is capable of measuring its own position, , and its own speed, . Each vehicle also obtains its predecessor position, . Hence, each vehicle has access to the inter-vehicle distance
where is the length of the predecessor vehicle.

Figure 1.
Vehicle platoon with a predecessor-following topology.
We assume that the platoon under study is composed of a set of homogeneous agents, and, thus, each agent has the same dynamical behavior. Specifically, we consider a continuous-time linear-time-invariant (LTI) system to model the dynamics of each agent, characterized by the transfer function , which is assumed to be strictly proper. Additionally, all vehicles are equipped with an identical local stabilizing controller described by the LTI system .
In this context, the local control loop is designed to track the predecessor vehicle and keep the inter-vehicle distance as close as possible to a predefined reference signal denoted by . In order to reduce the risk of collisions, it is prudent to set a larger distance reference when the vehicle is operating at high speeds. Conversely, for low-speed navigation, it is advisable to maintain a smaller reference distance. This approach aims for both safety and efficient operation. Hence, it is common to set as
where is the velocity of the vehicle i, is a constant that defines the minimum desired distance, and is the time headway constant, which is a design parameter. This spacing policy has been widely studied, and it is known as the constant time headway spacing policy (see, e.g., [6,40]).
2.3. Controller Design for String Stability
Since the goal is to follow a given reference, the tracking error is defined as
and given the previous setup, we can use Laplace domain analysis and the fact that , , and to conclude that
which implies then that
where is the transfer function
with . This shows that the local control in each vehicle can be written equivalently as the feedback loop depicted in Figure 2, where corresponds to the closed-loop transfer function.
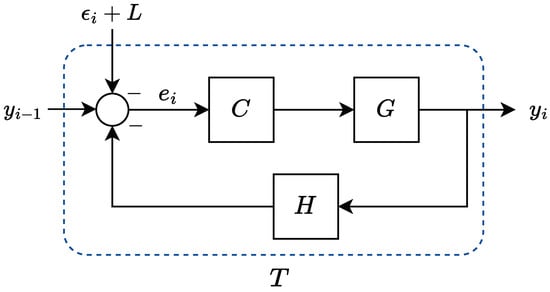
Figure 2.
Feedback control loop for the position in each vehicle. The time headway spacing policy is included in H.
As a primary goal, each local controller must be designed to stabilize the feedback loop and achieve zero tracking error in a steady state. In the platooning problem context, the position becomes a ramp signal in steady state; hence, to perform the tracking task with zero stationary error, it is required that has at least double integration [41].
Aside from the primary objective of tracking the predecessor, it is crucial to design the controller in such a way that it achieves the property of string stability. This property is related to the amplification of the effect of a disturbance on an individual vehicle as it propagates through the chain of vehicles. We use the following definition for string stability [42]:
Definition 1.
Let be a sequence of stable transfer functions. The sequence is said to be string-stable if there exists , independent of , such that for all n. The sequence will be called string-unstable otherwise.
Numerous research efforts have been devoted to comprehending and enhancing control designs aimed at ensuring string stability. These efforts encompass various aspects, including communication topologies, vehicle models, information flow, and other relevant assumptions.
In order to contextualize platooning and the scalability of a multi-vehicle configuration in both continuous and discrete-time frameworks, with respect to the previous definition, we can recall the following lemmas [9,43].
Lemma 1.
Let be a real rational scalar function of the complex variable s. Suppose that and also that T is stable (analytic in the closed right half complex plane). Then,
Lemma 2.
Let be a real rational scalar function of . Suppose that and also that is stable (analytic in the closed unit disk). Then,
The previous lemmas establish that any stable complementary sensitivity function relating to standard control loops must attain a magnitude greater than 1 for some frequency (either or ) whenever there is double integration in the open loop. Indeed, in continuous time, double integration in the product implies that , and, in discrete time, double integration in the product implies that . As mentioned above, double integration is needed for tracking constant speeds and inter-vehicle distances in the formation control of platooning systems. Now, it is possible to show in both cases that , which then implies that and must be greater than 1 for some frequency. Given this observation, it is clear that the absence of measures to prevent the effect of the double integration in the local closed loops will imply string instability of the multi-agent system according to Definition 1 since the cascading effect of disturbances at a particular vehicle will affect the vehicle k positions behind it through a multiple of [9]. Hence, given the problem setup in this paper, string stability is achieved in continuous time if and only if and for a discrete-time setting (see, e.g., [6,20,23]).
2.4. Problem of Interest
While the topic of platooning string stabilization has been extensively investigated in continuous-time scenarios, the exploration and understanding of its implementation in discrete time remain relatively limited. The effect of implementing platooning controllers in discrete time on the property of string stability is still not well-understood.
Indeed, one notable challenge in discrete-time implementation arises from the practical limitation imposed on the choice of the sample time, a critical parameter in discrete-time implementations. However, the influence of this parameter on string stability has not been thoroughly examined. The effect of the sample time choice may be further compounded by the practical inability to instantaneously measure velocity and acceleration, which are commonly assumed to be available to controllers in many continuous-time designs [6]. These assumptions, however, are not always feasible in practice.
With the aim of reducing this gap, in this paper, we examine the impact that the choice of the sample time, inherent in the discrete-time implementation, can have on the crucial property of string stability. In order to do so, we first design a string-stable controller within a continuous-time framework. Then, we obtain a discrete-time representation of such a design to implement in practice. Finally, we implement the case study on the scale-down experimental platform PL-TOON [39] and verify whether the string stability property is preserved or not for different sampling times.
3. Materials and Methods
3.1. PL-TOON Experimental Platform
We use the PL-TOON platform [39] for the experimental implementation, with 5 homogeneous agents. The agents on the platform are mounted on rails, which simplifies the control problem to one dimension, eliminating the need to deal with lateral control issues. By reducing the system to a one-dimensional setting, the focus can be placed primarily on assessing the string stability of the platoon without the influence introduced by lateral control challenges.
Regarding the capabilities of the agents, each agent on the platform is equipped with a DC motor and two sensors. The first sensor is a frontal time-of-flight sensor, specifically the VL53L0X, which measures the distance to the preceding vehicle. The second sensor is an optical sensor called ANDS3080, which is used for independent velocity estimation. The primary microcontroller unit used for each vehicle is the ESP32, which offers wireless capabilities for broadcasting data to other agents. The experimental platform is illustrated in Figure 3. In our previous work [39], a complete description of the PL-TOON platform can be found.

Figure 3.
Three agents of the PL-TOON experimental platform.
In platooning studies, it is common to model the vehicle dynamics as simple integrator [9,20], or as a second-order system with integration [24,34]. For the experimental platform, each agent’s movement is governed by the DC motor dynamics. A common model for these motors is given by
where represents the velocity of the agent i, denotes its acceleration, and is the motor input, which is given by the local controller. and are constant parameters that depend on the agent mass and friction coefficient. From (10), we obtain the transfer function
where and correspond to the Laplace transform of the velocity and input, respectively. Furthermore, due to Laplace properties, we have , where is the position of the agent in the Laplace domain. Hence, it is reasonable to describe the following model for the position
We perform standard system identification techniques for the first-order model in (11). Specifically, the convergence rate of the system is easily deduced from the step response of the system, as well as the DC gain [44]. From this, we experimentally obtain the values of and . It is worth noting that, while all agents on the platform have the same design and share the same components, there may be slight variations in these parameters for each individual agent.
It is important to note that, in our setup, the transfer function between two consecutive inter-vehicle distances is equivalent to the transfer function between two consecutive vehicle positions. This means that we can describe the platoon using either the absolute positions or the inter-vehicle distances , and the closed-loop transfer function T, as well as the criterion for string stability, remains the same. This is particularly relevant for the real implementation as the PL-TOON experimental platform does not have the capability to directly measure the absolute position of each agent, but it can measure . Nevertheless, it is worth mentioning that the absolute position of each agent can be inferred by considering the initial positions, the sampled distance measurement between vehicles, and the length of each agent L, which is the same for all agents and given by .
3.2. Continuous-Time Controller Design
We use a proportional-integrative (PI) controller for each agent, which is one of the most common types of controllers in practice, and is able to achieve string stability for our platooning setup. This type of controller incorporates integration, which, combined with the integrator of the plant , enables tracking of ramp references. The continuous-time PI controller is designed to ensure internal stability for T, zero stationary error, and also string stability. This last criterion requires .
Given the system model, we set as a desired constant time headway policy and design the PI controller as
with and . This yields
and is such that . This continuous-time design is verified in Matlab 2023a considering vehicles, obtaining the tracking errors reported in Figure 4. It is clear that the platoon is string-stable since the error magnitude is reduced as i increases, as expected.
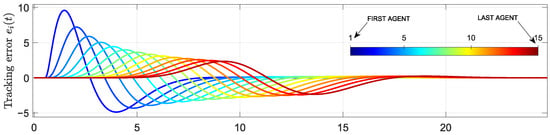
Figure 4.
Tracking errors for the string-stable continuous-time platoon of size 15. The first agent is represented by darker blue, while the last agent corresponds to the dark red curve.
3.3. Discrete-Time Implementation
Although the vehicle dynamics are described in continuous time, and the design of both the spacing policy and the controller is typically completed in continuous time as well, the actual implementation requires both the controller and the spacing policy to be implemented in discrete time. This means that, in practice, the control loop is a sampled-data control system.
The sampled-data control system is obtained using a standard zero-order hold approach, with sampling time . The zero-order hold discrete time equivalent of can be computed as [14]
The control algorithm implementation in each agent was carried out using a PID control library developed for the Arduino IDE, whose coding environment is compatible with ESP32. This library approximates the continuous-time designed controller using a digital controller, namely , based on the forward Euler discretization. That is
with , and where z is the variable in the -transform domain.
On the other hand, the velocity is measured considering the current and past positions as
where refers to the discrete-time index. Hence, the reference in discrete time is given by
Note that, given , the equivalent discrete-time version of is given by
which is a backward Euler approximation of .
In Figure 5, the equivalent sampled control scheme is depicted. To convert the controller output into a continuous-time signal for the plant, the zero-order hold method is employed. This method, part of the digital/analog block, is widely utilized in practice. The measurements are consistently sampled at a constant rate denoted by in the analog/digital device. Then, the equivalent sampled-data closed-loop transfer function is given by
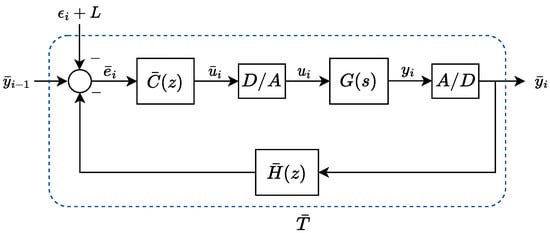
Figure 5.
Feedback control loop implementation in discrete time. Both the controller and the time headway block are implemented digitally, whereas the input and output of are converted to the appropriate time domain using a digital-to-analog converter (D/A) and an analog-to-digital converter (A/D), respectively.
Some insight into the role of the sample time on string stability can be obtained from . Indeed, from (12), we have that expanded through partial fraction decomposition is
which yields
Consequently, from (14), we obtain that
Although the combined effect that the three transfer functions , and have on the closed-loop dynamics may be hard to assess by inspection, we can explore the effect of the sample time and the time headway constant on the locations of the poles of . Figure 6 shows the locations of the closed-loop poles of the sampled-time closed loop for 4 values of and h varying from 0 to 1 with and . We can see that, as and h increase, the closed loop may become internally unstable. Interestingly, it may be argued that the most impactful of the three parameters is as its frequency response, in (18), varies considerably as h and change, as opposed to those of and , in (15) and (21), respectively, which remain less perturbed. We will explore this further with the following derivations.
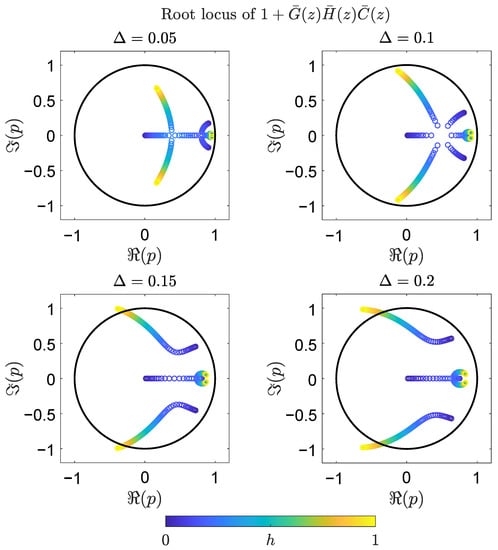
Figure 6.
Pole locations of the closed-loop sampled-time transfer function for varying h with 4 values of the sample time . (Top left) (s); (top right) (s); (bottom left) (s); (bottom right) (s).
To shed light on the possibility of the configuration being string-stable for some sampling time , we will focus our attention on computing when we have in the feedback loop, as in Figure 5. Its value is due to the implications that may have on T given Lemma 2, which also depends on . Indeed Lemma 2 provides a Bode-type integral restriction to a closed loop that satisfies , which is a well-known fundamental limit in control theory (see, e.g., [43]). In our setup, the local closed loops at each vehicle must satisfy to achieve predecessor tracking (zero tracking error to constant references in steady state), which is the first goal of platooning. Hence, this integral provides valuable information regarding the potential for to exceed 1 for certain values of , which implies string instability. The following proposition establishes a relationship between and the sampling time, offering insights into the influence of the sampling time on the string stability given Lemma 2.
Proposition 1.
Let be the transfer function of the discrete-time loop in Figure 5, and then
Proof.
Noting that
we can now compute
where
As mentioned after Lemmas 1 and 2, has, at most, two poles at , in particular with and finite. We can now compute
and it is possible to write
which implies that has two zeros at , and, hence, . Therefore, as , we obtain
□
Given Lemma 2, the previous result establishes that the closed-loop transfer function that must be analyzed to verify the string stability of a cascade interconnection of vehicles satisfies the Bode-type integral condition
We can conclude that the effect of increasing the sampling time has a potentially detrimental effect on the string stability property of the interconnected sampled system. As grows, the right side of (29) approaches 0, which in turn makes it more likely that for some value of . In particular, note that is positive in , which then implies that, although the integral is greater than a negative value that is small in magnitude, may be positive in a sub-interval of . On the other hand, increasing h should have a positive effect on achieving string stability, which is well-known in the continuous-time case [40] but seems to remain true for the sampled data case. As discussed before, increasing both the sampling time and the time headway constant has a negative effect on the internal stability of the closed loop, so care must be taken in order to design these parameters. Note that we cannot conclude string stability from the condition in (29) as the bound for the Bode integral being negative does not prevent from having an infinity norm greater than 1. However, the result does suggest that having and such that is large should contribute positively towards achieving string stability.
Figure 7 shows different Bode plots as the value of h varies from 0 to 1 for fixed values of C(s), G(s), which have been transformed accordingly for . It is possible to see that, for (s), there exists a minimum value of for which any achieves for For (s), we see that there is a range of values of h that achieve string stability, but, as h grows, . For , we again have . Similar behaviors occur for larger , with certain resonance phenomena arising around the higher values of the frequency range. This behavior will become evident in some of the experimental results (Figure 8).
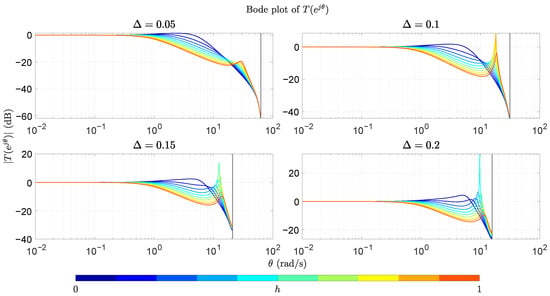
Figure 7.
Magnitude plots for the transfer function for varying h with 4 values of the sample time . (Top left) (s); (top right) (s); (bottom left) (s); (bottom right) (s).
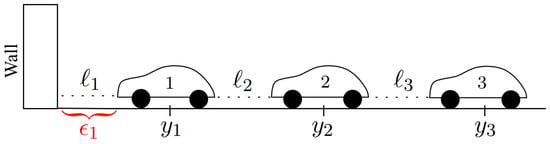
Figure 8.
Setup of the experiment to perform showing 3 PL-TOON agents. The platoon starts in formation with the desired distance between vehicles and then the setpoint changes its value periodically, which provokes a tracking error in the first vehicle that then propagates to the rest of the platoon.
4. Simulation and Experimental Results
In this section, we report the results obtained via simulations, which will then be corroborated by using the PL-TOON platform.
4.1. Experiment Description
The experiment to evaluate the string stability of the platoon consists of five agents in formation, with the first agent of the platoon facing a wall. At the start, all agents are set to be at rest and in the desired formation. To introduce a disturbance, the distance setpoint of the first car, denoted as , is varied every 30 s. The remaining values for are held constant at 20 cm. As a result, the first agent accelerates to achieve the new desired position, yielding a transient tracking error. This transient error subsequently propagates to the following vehicles in the platoon. Figure 3 provides a visual representation of the platoon configuration for this experimental setup.
In order to observe the effect of the sample time Δ in the string-stable behavior of the vehicles, we perform the experiment and collect data multiple times for different sample time values. The minimum sampling rate of the distance sensor is 20 ms, and, hence, we cannot go below this sample time value since a new measurement will not be available. On the other hand, we set 0.20 s as the upper limit for the sample time since it is sufficient to observe the effect on string stability without compromising internal stability. Thus, we repeat the experiment for sample time values within 0.02 and 0.20 s. Except for the sampling time, all other parameters involved in the control loop and its implementation remain invariant.
It is worth mentioning that conducting experiments with a larger number of agents, such as 10, 20, or more, could provide even clearer evidence of string stability/instability. However, practical challenges arise when attempting to perform experiments with such a significant number of agents due to technical and financial constraints. This situation further emphasizes the limitations faced when trying to analyze string stability in real-world scenarios.
4.2. Simulation Results
For the simulation results, we calculate the discrete-time closed-loop transfer function considering three different sampling times, , , and .
In the case of , we have
yielding . Hence, the platoon remains string-stable for this sample time. This is observed in Figure 9, where the behavior of a platoon of five vehicles is simulated.
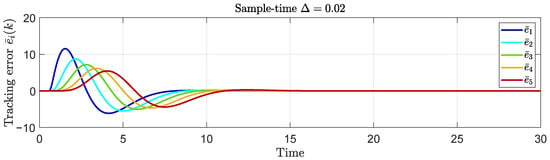
Figure 9.
Simulation results for the tracking error for the vehicle platoon with a sampling time s.
For , we have
which also leads to a string-stable platoon since . This is depicted in Figure 10; however, it can also be observed that the performance of the platoon is deteriorated, compared to the case with , due to the ripple and higher amplitudes exhibited by the tracking errors.
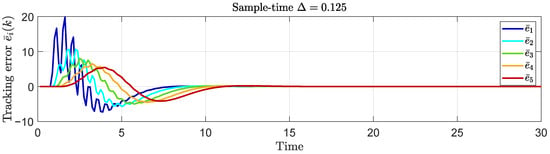
Figure 10.
Simulation results for the tracking error for the vehicle platoon with a sampling time s.
Finally, for , we have
For this case, we have , and, hence, the platoon becomes string-unstable. The platoon behavior is shown in Figure 11, where it is clear that the errors are increasing along the string of vehicles. We can observe in this example that string stability is lost due to the inappropriate sampling time choice. Note that the amplitudes of the errors also increase considerably for this case, reaching values near 50. The oscillatory behavior of each error is also undesired, and it is also a consequence of the sampling time choice. Nevertheless, each vehicle in the platoon reaches its references and the tracking errors converge to zero given that the loss of string stability does not imply the loss of internal stability.
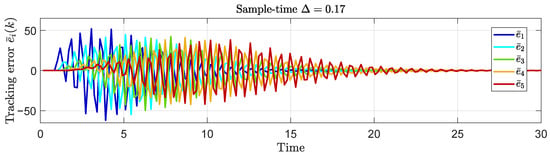
Figure 11.
Simulation results for the tracking error for the vehicle platoon with a sampling time s.
4.3. Experimental Results
It is important to mention that the simulation results and the experimental results were not the same for the same design parameters. This could be due to differences in the actual dynamics of the cars compared to the proposed simplified model. Additionally, there may be non-linear phenomena that were not modeled and could influence the discrepancy between the experimental and simulated results. However, the design parameters were slightly adjusted to clearly observe the same qualitative behavior that demonstrates the effect of the sampling time. Thus, the controller maintains the same parameters as in the simulation, but the experimental value for the parameter h is instead of 0.6. Furthermore, instead of using (s), an experimental value of (s) is used, and, instead of using (s), (s) is used experimentally. We also consider additional values of in the experimental setup. In Figure 12, the tracking errors are shown for different values of . The effect of the sampling time in the platoon behavior can be observed as well, where the amplitude of the errors starts to increase along with . The behavior of the transient is also affected by the sample time, where, for larger values of , the response of the vehicles is much more oscillatory and faster than for smaller values of . Next, we will focus on three values similar to those used for the simulation results and analyze the corresponding graphs in more detail.
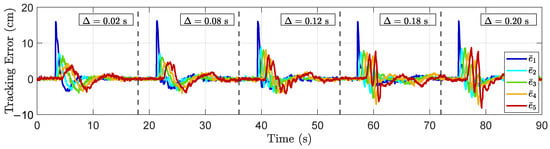
Figure 12.
Tracking error for the experimental vehicle platoon with different sample times in the range – s.
We begin by using a sampling time of (s). The results for the tracking errors are shown in Figure 13, where it can be inferred, by visual inspection, that the platoon exhibits string-stable behavior since the errors are not being amplified as it propagates along the vehicles. Therefore, we can conclude that the string stability property of the platoon, designed in a continuous-time framework, is preserved in the discrete-time implementation for this particular sampling time.
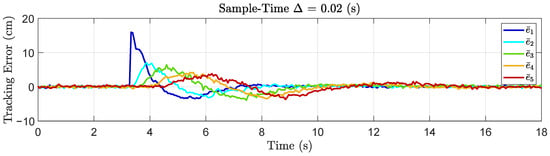
Figure 13.
Tracking error for the experimental vehicle platoon with a sampling time (s).
Then, we increase the sampling time to (s), and the corresponding results are depicted in Figure 14. In this scenario, it is evident that the error amplitudes are higher compared to the previous case with (s). Additionally, there is a notorious presence of oscillations in the tracking errors. Nonetheless, it is not evident in this case whether the platoon is string-stable or not. At first glance, it appears that the error is not being amplified at each agent. However, due to the small size of the platoon, it is not possible to confidently determine this solely through visual inspection. It is plausible that, with the addition of more agents to the platoon, the tracking error might exhibit clear string-unstable behavior for this particular sample time.
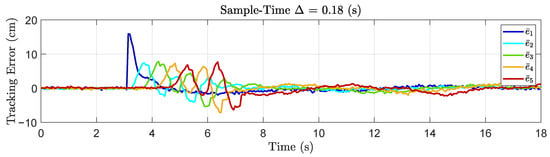
Figure 14.
Tracking error for the experimental vehicle platoon with a sampling time (s).
Lastly, we conduct the experiment using a sampling time of (s). The results of the platoon tracking error under this sample time are illustrated in Figure 15. We observe here a greater amplification in the error signals and a higher prevalence of oscillations. In this scenario, the presence of string instability can be stated with more confidence as the error amplifies in the agents while propagating through the platoon. This can be observed by comparing the magnitudes of the errors when they are negative, wherein the magnitudes are higher than those of their preceding agents.
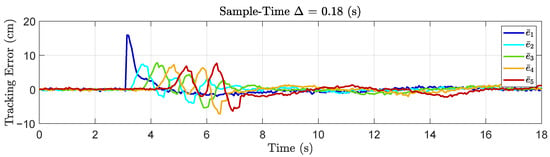
Figure 15.
Tracking error for the experimental vehicle platoon with a sampling time (s).
In Table 1, we present the integral of the squared error for our experimental results. We can clearly observe that the first agent is the most affected by the disturbance in all cases, which is reasonable for small platoons. When , we can see that the error tends to decrease, reaching values more than three times lower than the error of the first car. We can infer with some confidence that this is stable string behavior. However, for , we notice that, while the error of the second car is considerably lower than that of the first car, the errors of the remaining cars do not exhibit a consistent trend of increase or decrease. This lack of consistent behavior can be attributed to the unclear string stability for this particular value of . It is probably influenced by the fact that agents’ models are not exactly the same and, hence, the small variations in the agent’s models could have an impact in each case. Only by experimentally adding more vehicles could we determine instability. In the last case (), as the error increases from the second car to the last, it clearly indicates unstable string behavior.

Table 1.
Comparison of the ISE index for the tracking error for different sample times.
Our simulation and experimental results suggest that there is a critical value for the choice of , below which string stability is achieved. It is important to mention that, in the previous analysis, for all the reported choices of , internal stability and zero steady-state error are achieved. Thus, the analysis focuses solely on string stability. Certainly, a poor choice of sampling time can also deteriorate the performance of the controller and even cause internal instability, as illustrated in the previous section, but this is well-known in the literature on sampled data feedback control and not a consequence of the string stabilization analysis.
5. Conclusions and Future Work
Our study examined the dynamics of vehicle platoons operating in a predecessor-following configuration using sampled-data control systems. The key objective was to assess the impact of the sampling time on the string stability of the platoon. Starting with the design of a string-stable platoon in continuous time, we then discretized the controller and simulated the resulting sampled data control system. Finally, we implemented the control strategy on a scaled-down experimental platform. Through simulation and real experimentation, we analyzed the effects of varying sampling times on the platoon’s string stability performance. Our findings indicate that an improper selection of the sampling time could significantly undermine the platoon’s string stability. Our results also suggest that there is a critical choice of the sample time below which string stability is guaranteed. Thus, careful consideration of the sampling time is essential in ensuring the desired string stability properties when implementing control systems for platooning applications. This study provides valuable insights into the relationship between sampling time and the stability of vehicle platoons.
Future research in this field entails conducting a more comprehensive theoretical analysis to elucidate the impact of sampling on string stability and obtaining necessary and sufficient conditions on the sampling time to preserve string stability. Studying the effect of non-uniform sampling is also part of future work, as well as platoons of vehicles moving beyond a one-dimensional setting.
Author Contributions
Conceptualization, F.J.V.; methodology, F.J.V.; software, F.I.V. and A.A.P.; validation, F.I.V.; formal analysis, all authors; investigation, all authors; resources, F.J.V. and A.A.P.; data curation, F.I.V. and F.J.V.; writing—original draft preparation, all authors; writing—review and editing, all authors; visualization, all authors; supervision, F.J.V.; project administration, F.J.V.; funding acquisition, F.J.V. and A.A.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been funded by UTFSM, ANID FONDECYT 11221365 grant, and CORFO Project 14ENI226865.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank Felipe Ulloa of UAI for their valuable technical support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liang, K.Y.; Mårtensson, J.; Johansson, K.H. Heavy-duty vehicle platoon formation for fuel efficiency. IEEE Trans. Intell. Transp. Syst. 2015, 17, 1051–1061. [Google Scholar] [CrossRef]
- Jia, D.; Lu, K.; Wang, J.; Zhang, X.; Shen, X. A survey on platoon-based vehicular cyber-physical systems. IEEE Commun. Surv. Tutorials 2015, 18, 263–284. [Google Scholar] [CrossRef]
- Bonnet, C.; Fritz, H. Fuel Consumption Reduction in a Platoon: Experimental Results with Two Electronically Coupled Trucks at Close Spacing; Technical Report, SAE Technical Paper; SAE International: Warrendale, PA, USA, 2000. [Google Scholar]
- Shladover, S.E.; Nowakowski, C.; Lu, X.Y.; Ferlis, R. Cooperative adaptive cruise control: Definitions and operating concepts. Transp. Res. Rec. 2015, 2489, 145–152. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, G.; Barth, M.J. A review on cooperative adaptive cruise control (CACC) systems: Architectures, controls, and applications. In Proceedings of the IEEE 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 2884–2891. [Google Scholar]
- Feng, S.; Zhang, Y.; Li, S.E.; Cao, Z.; Liu, H.X.; Li, L. String stability for vehicular platoon control: Definitions and analysis methods. Annu. Rev. Control 2019, 47, 81–97. [Google Scholar] [CrossRef]
- Stüdli, S.; Seron, M.M.; Middleton, R.H. From vehicular platoons to general networked systems: String stability and related concepts. Annu. Rev. Control 2017, 44, 157–172. [Google Scholar] [CrossRef]
- Balador, A.; Bazzi, A.; Hernandez-Jayo, U.; de la Iglesia, I.; Ahmadvand, H. A survey on vehicular communication for cooperative truck platooning application. Veh. Commun. 2022, 35, 100460. [Google Scholar] [CrossRef]
- Middleton, R.H.; Braslavsky, J.H. String instability in classes of linear time invariant formation control with limited communication range. IEEE Trans. Autom. Control. 2010, 55, 1519–1530. [Google Scholar] [CrossRef]
- Van Nunen, E.; Reinders, J.; Semsar-Kazerooni, E.; Van De Wouw, N. String stable model predictive cooperative adaptive cruise control for heterogeneous platoons. IEEE Trans. Intell. Veh. 2019, 4, 186–196. [Google Scholar] [CrossRef]
- Ge, X.; Han, Q.L.; Ding, D.; Zhang, X.M.; Ning, B. A survey on recent advances in distributed sampled-data cooperative control of multi-agent systems. Neurocomputing 2018, 275, 1684–1701. [Google Scholar] [CrossRef]
- Ge, X.; Han, Q.L.; Ding, L.; Wang, Y.L.; Zhang, X.M. Dynamic event-triggered distributed coordination control and its applications: A survey of trends and techniques. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 3112–3125. [Google Scholar] [CrossRef]
- Zhang, X.M.; Han, Q.L.; Ge, X.; Ning, B.; Zhang, B.L. Sampled-data control systems with non-uniform sampling: A survey of methods and trends. Annu. Rev. Control 2023, 55, 70–91. [Google Scholar] [CrossRef]
- Åström, K.J.; Wittenmark, B. Computer-Controlled Systems: Theory and Design; Courier Corporation: Chelmsford, MA, USA, 2013. [Google Scholar]
- Wang, P.; Deng, H.; Zhang, J.; Wang, L.; Zhang, M.; Li, Y. Model predictive control for connected vehicle platoon under switching communication topology. IEEE Trans. Intell. Transp. Syst. 2021, 23, 7817–7830. [Google Scholar] [CrossRef]
- Feng, S.; Sun, H.; Zhang, Y.; Zheng, J.; Liu, H.X.; Li, L. Tube-based discrete controller design for vehicle platoons subject to disturbances and saturation constraints. IEEE Trans. Control. Syst. Technol. 2019, 28, 1066–1073. [Google Scholar] [CrossRef]
- Ma, F.; Wang, J.; Zhu, S.; Gelbal, S.Y.; Yang, Y.; Aksun-Guvenc, B.; Guvenc, L. Distributed control of cooperative vehicular platoon with nonideal communication condition. IEEE Trans. Veh. Technol. 2020, 69, 8207–8220. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, C.; Xie, X. Platooning control of vehicular systems by using sampled positions. IEEE Trans. Circuits Syst. II Express Briefs, 2023; early access. [Google Scholar] [CrossRef]
- Gordon, M.A.; Vargas, F.J.; Peters, A.A. Mean square stability conditions for platoons with lossy inter-vehicle communication channels. Automatica 2023, 147, 110710. [Google Scholar] [CrossRef]
- Vargas, F.J.; Maass, A.I.; Peters, A.A. String stability for predecessor following platooning over lossy communication channels. In Proceedings of the 23rd International Symposium on Mathematical Theory of Networks and Systems (MNTS), Hong Kong, China, 16–20 July 2018; pp. 834–837. [Google Scholar]
- Li, Z.; Hu, B.; Li, M.; Luo, G. String stability analysis for vehicle platooning under unreliable communication links with event-triggered strategy. IEEE Trans. Veh. Technol. 2019, 68, 2152–2164. [Google Scholar] [CrossRef]
- Zhao, C.; Cai, L.; Cheng, P. Stability analysis of vehicle platooning with limited communication range and random packet losses. IEEE Internet Things J. 2020, 8, 262–277. [Google Scholar] [CrossRef]
- Gordon, M.A.; Vargas, F.J.; Peters, A.A. Comparison of simple strategies for vehicular platooning with lossy communication. IEEE Access 2021, 9, 103996–104010. [Google Scholar] [CrossRef]
- Villenas, F.I.; Vargas, F.J.; Peters, A.A. A Kalman-Based Compensation Strategy for Platoons Subject to Data Loss: Numerical and Empirical Study. Mathematics 2023, 11, 1228. [Google Scholar] [CrossRef]
- Acciani, F.; Frasca, P.; Heijenk, G.; Stoorvogel, A.A. Stochastic string stability of vehicle platoons via cooperative adaptive cruise control with lossy communication. IEEE Trans. Intell. Transp. Syst. 2021, 23, 10912–10922. [Google Scholar] [CrossRef]
- Li, Z.; Hu, B.; Yang, Z. Co-design of distributed event-triggered controller for string stability of vehicle platooning under periodic jamming attacks. IEEE Trans. Veh. Technol. 2021, 70, 13115–13128. [Google Scholar] [CrossRef]
- Zhao, N.; Zhao, X.; Chen, M.; Zong, G.; Zhang, H. Resilient distributed event-triggered platooning control of connected vehicles under denial-of-service attacks. IEEE Trans. Intell. Transp. Syst. 2023, 24, 6191–6202. [Google Scholar] [CrossRef]
- Xiao, S.; Ge, X.; Han, Q.L.; Zhang, Y. Dynamic event-triggered platooning control of automated vehicles under random communication topologies and various spacing policies. IEEE Trans. Cybern. 2021, 52, 11477–11490. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.; Liu, Y.; Li, Z.; Nabin, M.H. Cooperative spacing sampled control of vehicle platoon considering undirected topology and analog fading networks. IEEE Trans. Intell. Transp. Syst. 2022, 23, 18478–18491. [Google Scholar] [CrossRef]
- Kianfar, R.; Falcone, P.; Fredriksson, J. A control matching model predictive control approach to string stable vehicle platooning. Control. Eng. Pract. 2015, 45, 163–173. [Google Scholar] [CrossRef]
- Dolk, V.S.; Ploeg, J.; Heemels, W.M.H. Event-triggered control for string-stable vehicle platooning. IEEE Trans. Intell. Transp. Syst. 2017, 18, 3486–3500. [Google Scholar] [CrossRef]
- Thormann, S.; Schirrer, A.; Jakubek, S. Safe and efficient cooperative platooning. IEEE Trans. Intell. Transp. Syst. 2020, 23, 1368–1380. [Google Scholar] [CrossRef]
- Murillo, A.; Vargas, F.; Peters, A. Effects of speed saturation in a predecessor-following vehicle platoon. In Proceedings of the 2019 IEEE CHILEAN Conference on Electrical, Electronics Engineering, Information and Communication Technologies (CHILECON), Valparaiso, Chile, 13–27 November 2019; pp. 1–7. [Google Scholar]
- Naus, G.J.L.; Vugts, R.P.A.; Ploeg, J.; van de Molengraft, M.J.G.; Steinbuch, M. String-Stable CACC Design and Experimental Validation: A Frequency-Domain Approach. IEEE Trans. Veh. Technol. 2010, 59, 4268–4279. [Google Scholar] [CrossRef]
- Segata, M.; Bloessl, B.; Joerer, S.; Sommer, C.; Gerla, M.; Cigno, R.L.; Dressler, F. Toward communication strategies for platooning: Simulative and experimental evaluation. IEEE Trans. Veh. Technol. 2015, 64, 5411–5423. [Google Scholar] [CrossRef]
- Johnson, M.; Hayes, M.J. String Stability Experimentation using a Low-Cost Mobile Robotic Testbed. In Proceedings of the 2019 30th Irish Signals and Systems Conference (ISSC), Maynooth, Ireland, 17–18 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Qin, W.B.; Orosz, G. Experimental Validation of String Stability for Connected Vehicles Subject to Information Delay. IEEE Trans. Control. Syst. Technol. 2020, 28, 1203–1217. [Google Scholar] [CrossRef]
- Escobar, C.; Vargas, F.J.; Peters, A.A.; Carvajal, G. A Cooperative Control Algorithm for Line and Predecessor Following Platoons Subject to Unreliable Distance Measurements. Mathematics 2023, 11, 801. [Google Scholar] [CrossRef]
- Peters, A.A.; Vargas, F.J.; Garrido, C.; Andrade, C.; Villenas, F. PL-TOON: A Low-Cost Experimental Platform for Teaching and Research on Decentralized Cooperative Control. Sensors 2021, 21, 2072. [Google Scholar] [CrossRef]
- Klinge, S.; Middleton, R.H. Time headway requirements for string stability of homogeneous linear unidirectionally connected systems. In Proceedings of the 48h IEEE Conference on Decision and Control (CDC) Held Jointly with 2009 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009; pp. 1992–1997. [Google Scholar] [CrossRef]
- Goodwin, G.C.; Graebe, S.F.; Salgado, M.E.; Elsley, G. Control System Design; Prentice Hall: Upper Saddle River, NJ, USA, 2001; Volume 240. [Google Scholar]
- Peters, A.A.; Middleton, R.H.; Mason, O. Leader tracking in homogeneous vehicle platoons with broadcast delays. Automatica 2014, 50, 64–74. [Google Scholar] [CrossRef]
- Seron, M.M.; Braslavsky, J.H.; Goodwin, G.C. Fundamental Limitations in Filtering and Control; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Badillo, D.; Huidobro, C.; Villenas, F.; Peters, A.; Vargas, F. Sensor Calibration and Filtering for an Agent of the PL-TOON Platooning Platform. In Proceedings of the 2021 IEEE CHILEAN Conference on Electrical, Electronics Engineering, Information and Communication Technologies (CHILECON), Virtual, 6–9 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).