A Cubic Class of Iterative Procedures for Finding the Generalized Inverses
Abstract
1. Introduction
2. Iterative Scheme
3. Convergence Behavior
4. Variants of the New Family (4)
5. Numerical Testing
Study of Different Parametric Values
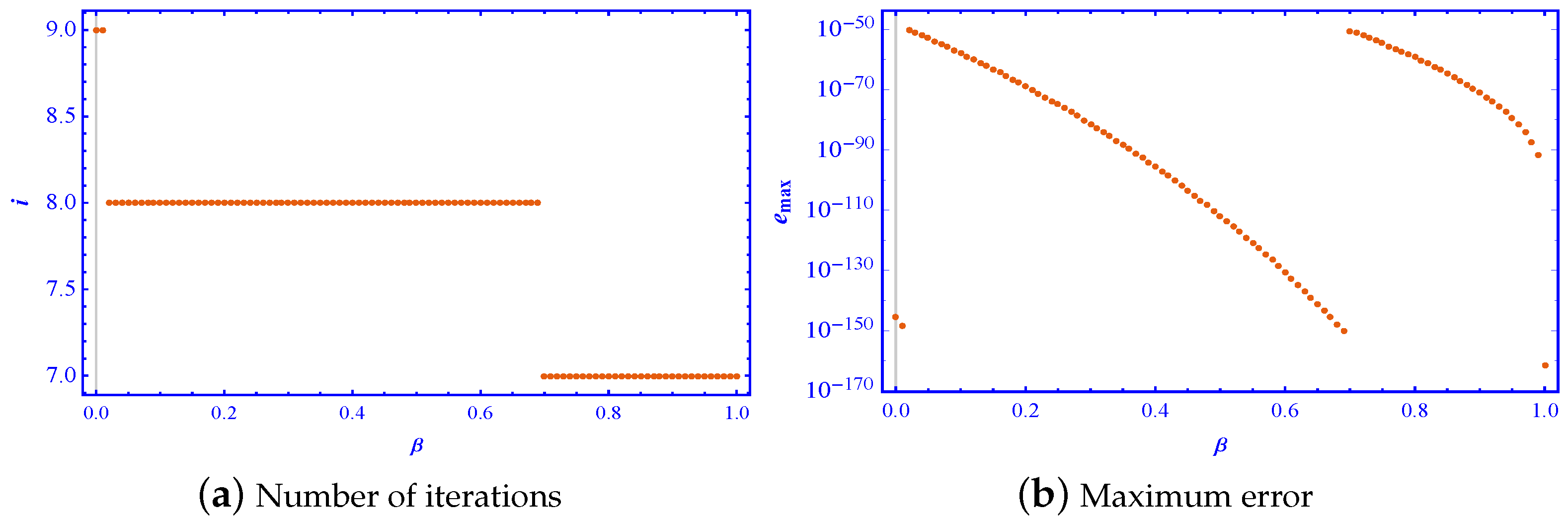
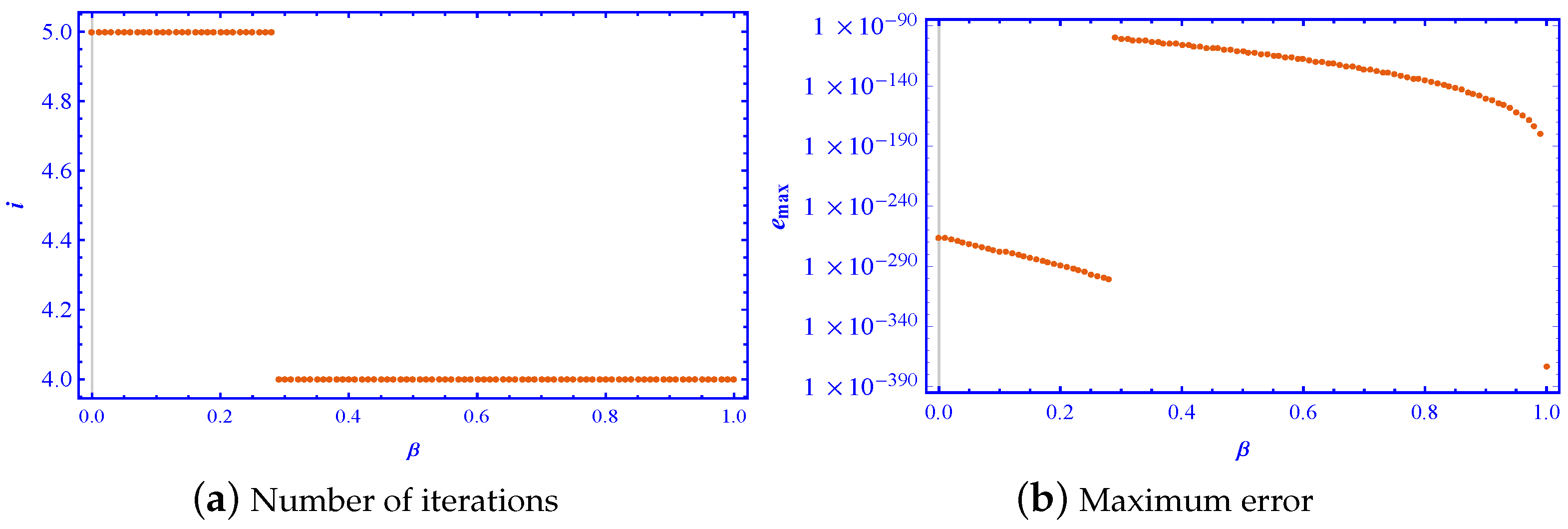
- The graph of the number of iterations shows that, as the value of increased, the number of iterations did not necessarily decrease. In fact, it can be observed that the presented scheme used fewer iterations for values of close to one compared to values of close to zero, indicating that the scheme converged faster for higher values of .
- To achieve a more precise matrix inverse, the maximum error norm should be lower. However, it was observed that the scheme (4), which resulted in fewer iterations as depicted in Figure 4 and Figure 6, corresponded to a higher error norm. Nevertheless, when the accuracy of the solutions obtained from each iterative method was evaluated for a particular iteration, it was found that the scheme with that required fewer iterations yielded a comparatively more accurate and precise matrix inverse.
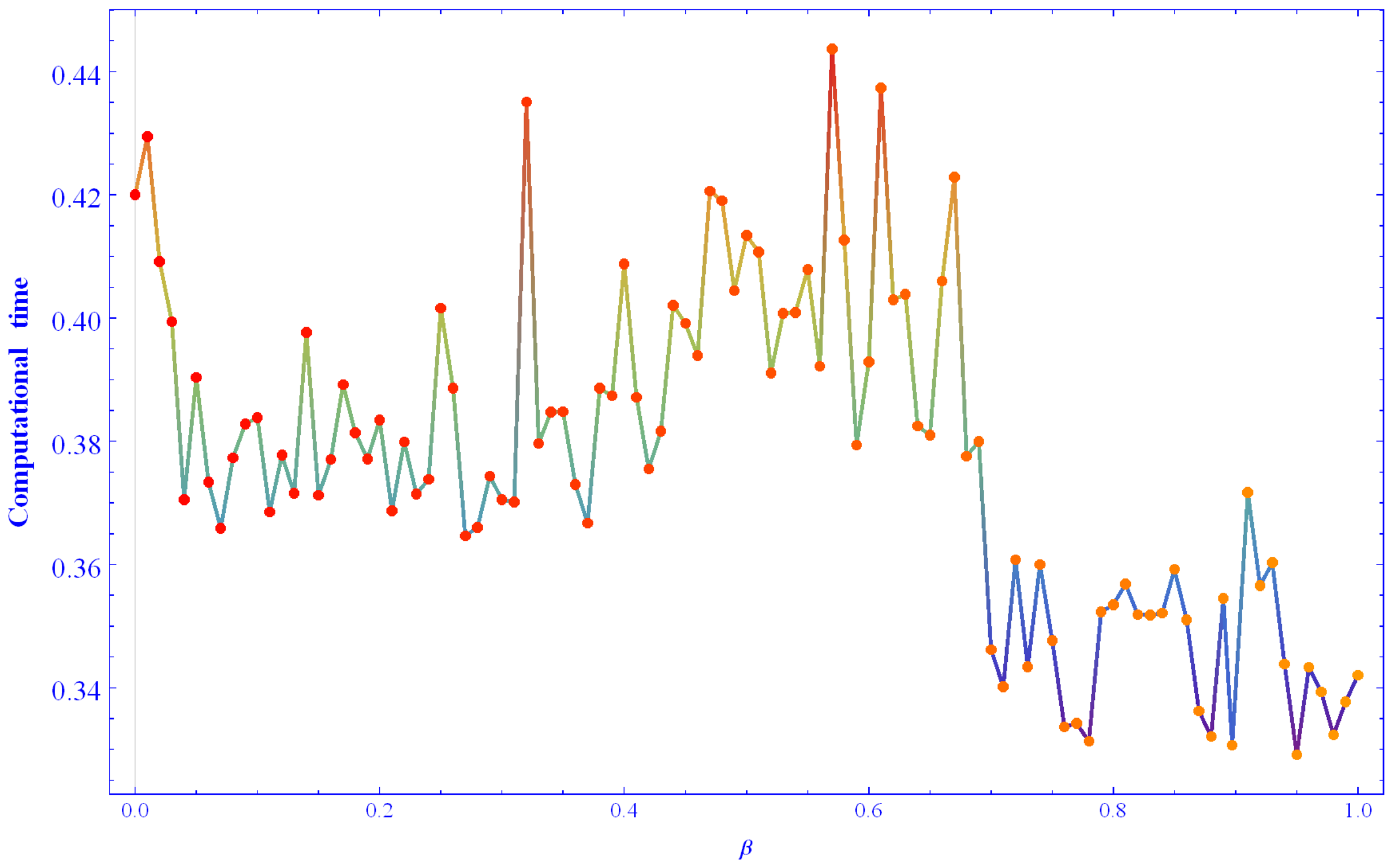
- On the other hand, the same trend did not necessarily hold for a computational time, due to fluctuations. For example, for matrix of (25), the time taken for computation with a close to one was comparatively less than the near to zero. However, such behavior of was not observed for the matrix in (26). Therefore, the computational time varied depending on the characteristics of the matrices used.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stanimirović, P.S.; Chountasis, S.; Pappas, D.; Stojanović, I. Removal of blur in images based on least squares solutions. Math. Methods Appl. Sci. 2013, 36, 2280–2296. [Google Scholar] [CrossRef]
- Meister, S.; Stockburger, J.T.; Schmidt, R.; Ankerhold, J. Optimal control theory with arbitrary superpositions of waveforms. J. Phys. A Math. Theor. 2014, 47, 495002. [Google Scholar] [CrossRef]
- Wang, J.Z.; Williamson, S.J.; Kaufman, L. Magnetic source imaging based on the minimum-norm least-squares inverse. Brain Topogr. 1993, 5, 365–371. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.; Wang, X.; Zhang, G.; Zhou, X. Effective algorithms of the Moore–Penrose inverse matrices for extreme learning machine. Intell. Data Anal. 2015, 19, 743–760. [Google Scholar] [CrossRef]
- Pavlíková, S.; Ševčovič, D. On the Moore–Penrose pseudo-inversion of block symmetric matrices and its application in the graph theory. Linear Algebra Appl. 2023, 673, 280–303. [Google Scholar] [CrossRef]
- Feliks, T.; Hunek, W.P.; Stanimirović, P.S. Application of generalized inverses in the minimum-energy perfect control theory. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 4560–4575. [Google Scholar] [CrossRef]
- Doty, K.L.; Melchiorri, C.; Bonivento, C. A theory of generalized inverses applied to robotics. Int. J. Robot. Res. 1993, 12, 1–19. [Google Scholar] [CrossRef]
- Soleimani, F.; Stanimirović, P.S.; Soleymani, F. Some matrix iterations for computing generalized inverses and balancing chemical equations. Algorithms 2015, 8, 982–998. [Google Scholar] [CrossRef]
- Moore, E.H. On the reciprocal of the general algebraic matrix. Bull. Am. Math. Soc. 1920, 26, 394–395. [Google Scholar]
- Penrose, R. A generalized inverse for matrices. Math. Proc. Camb. Philos. Soc. 1955, 51, 406–413. [Google Scholar] [CrossRef]
- Rado, R. Note on generalized inverses of matrices. Math. Proc. Camb. Philos. Soc. 1956, 52, 600–601. [Google Scholar] [CrossRef]
- Ben-Israel, A. Generalized inverses of matrices: A perspective of the work of Penrose. Math. Proc. Camb. Philos. Soc. 1986, 100, 407–425. [Google Scholar] [CrossRef]
- Lee, M.; Kim, D. On the use of the Moore–Penrose generalized inverse in the portfolio optimization problem. Finance Res. Lett. 2017, 22, 259–267. [Google Scholar] [CrossRef]
- Kučera, R.; Kozubek, T.; Markopoulos, A.; Machalová, J. On the Moore–Penrose inverse in solving saddle-point systems with singular diagonal blocks. Numer. Linear Algebra Appl. 2012, 19, 677–699. [Google Scholar] [CrossRef]
- Kyrchei, I. Weighted singular value decomposition and determinantal representations of the quaternion weighted Moore–Penrose inverse. Appl. Math. Comput. 2017, 309, 1–16. [Google Scholar] [CrossRef]
- Long, J.; Peng, Y.; Zhou, T.; Zhao, L.; Li, J. Fast and Stable Hyperspectral Multispectral Image Fusion Technique Using Moore–Penrose Inverse Solver. Appl. Sci. 2021, 11, 7365. [Google Scholar] [CrossRef]
- Zhuang, G.; Xia, J.; Feng, J.E.; Wang, Y.; Chen, G. Dynamic compensator design and Hinf admissibilization for delayed singular jump systems via Moore–Penrose generalized inversion technique. Nonlinear Anal. Hybrid Syst. 2023, 49, 101361. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, Q.M.J.; Yang, Y.; Akilan, T. Multimodel Feature Reinforcement Framework Using Moore–Penrose Inverse for Big Data Analysis. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5008–5021. [Google Scholar] [CrossRef]
- Castaño, A.; Fernández-Navarro, F.; Hervás-Martínez, C. PCA-ELM: A Robust and Pruned Extreme Learning Machine Approach Based on Principal Component Analysis. Neural Process. Lett. 2013, 37, 377–392. [Google Scholar] [CrossRef]
- Lauren, P.; Qu, G.; Zhang, F.; Lendasse, A. Discriminant document embeddings with an extreme learning machine for classifying clinical narratives. Neurocomputing 2018, 277, 129–138. [Google Scholar] [CrossRef]
- Koliha, J.; Djordjević, D.; Cvetković, D. Moore–Penrose inverse in rings with involution. Linear Algebra Its Appl. 2007, 426, 371–381. [Google Scholar] [CrossRef]
- Jäntschi, L. The Eigenproblem Translated for Alignment of Molecules. Symmetry 2019, 11, 1027. [Google Scholar] [CrossRef]
- Baksalary, O.M.; Trenkler, G. The Moore–Penrose inverse: A hundred years on a frontline of physics research. Eur. Phys. J. H 2021, 46, 9. [Google Scholar] [CrossRef]
- Hornick, M.; Tamayo, P. Extending Recommender Systems for Disjoint User/Item Sets: The Conference Recommendation Problem. IEEE Trans. Know. Data Eng. 2012, 24, 1478–1490. [Google Scholar] [CrossRef]
- Chatterjee, S.; Thakur, R.S.; Yadav, R.N.; Gupta, L. Sparsity-based modified wavelet de-noising autoencoder for ECG signals. Signal Process. 2022, 198, 108605. [Google Scholar] [CrossRef]
- Shinozaki, N.; Sibuya, M.; Tanabe, K. Numerical algorithms for the Moore–Penrose inverse of a matrix: Direct methods. Ann. Inst. Stat. Math. 1972, 24, 193–203. [Google Scholar] [CrossRef]
- Katsikis, V.N.; Pappas, D.; Petralias, A. An improved method for the computation of the Moore–Penrose inverse matrix. Appl. Math. Comput. 2011, 217, 9828–9834. [Google Scholar] [CrossRef]
- Stanimirović, I.P.; Tasić, M.B. Computation of generalized inverses by using the LDL* decomposition. Appl. Math. Lett. 2012, 25, 526–531. [Google Scholar] [CrossRef]
- Stanimirović, P.S.; Petković, M.D. Gauss—Jordan elimination method for computing outer inverses. Appl. Math. Comput. 2013, 219, 4667–4679. [Google Scholar] [CrossRef]
- Schultz, G. Iterative berechung der reziproken matrix. ZAMM Z. Angew. Math. Mech. 1933, 13, 57–59. [Google Scholar] [CrossRef]
- Ben-Israel, A.; Greville, T.N. Generalized Inverses: Theory and Applications; Springer: New York, NY, USA, 2003. [Google Scholar]
- Pan, V.; Schreiber, R. An improved Newton iteration for the generalized inverse of a matrix, with applications. SIAM J. Sci. Statist. Comput. 1991, 12, 1109–1130. [Google Scholar] [CrossRef]
- Kaur, M.; Kansal, M.; Kumar, S. An Efficient Matrix Iterative Method for Computing Moore–Penrose Inverse. Mediterr. J. Math. 2021, 18, 1–21. [Google Scholar] [CrossRef]
- Li, W.; Li, Z. A family of iterative methods for computing the approximate inverse of a square matrix and inner inverse of a non-square matrix. Appl. Math. Comput. 2010, 215, 3433–3442. [Google Scholar] [CrossRef]
- Petković, M.D. Generalized Schultz iterative methods for the computation of outer inverses. Comput. Math. Appl. 2014, 67, 1837–1847. [Google Scholar] [CrossRef]
- Stanimirović, P.S.; Soleymani, F. A class of numerical algorithms for computing outer inverses. J. Comput. Appl. Math. 2014, 263, 236–245. [Google Scholar] [CrossRef]
- Liu, X.; Jin, H.; Yu, Y. Higher-order convergent iterative method for computing the generalized inverse and its application to Toeplitz matrices. Linear Algebra Appl. 2013, 439, 1635–1650. [Google Scholar] [CrossRef]
- Soleymani, F.; Stanimirović, P.S. A higher order iterative method for computing the Drazin inverse. Sci. World J. 2013, 2013, 708647. [Google Scholar] [CrossRef]
- Soleymani, F.; Stanimirović, P.S.; Ullah, M.Z. An accelerated iterative method for computing weighted Moore–Penrose inverse. Appl. Math. Comput. 2013, 222, 365–371. [Google Scholar] [CrossRef]
- Sun, L.; Zheng, B.; Bu, C.; Wei, Y. Moore–Penrose inverse of tensors via Einstein product. Linear Multilinear Algebra 2016, 64, 686–698. [Google Scholar] [CrossRef]
- Ma, H.; Li, N.; Stanimirović, P.S.; Katsikis, V.N. Perturbation theory for Moore–Penrose inverse of tensor via Einstein product. Comput. Appl. Math. 2019, 38, 111. [Google Scholar] [CrossRef]
- Liang, M.; Zheng, B. Further results on Moore–Penrose inverses of tensors with application to tensor nearness problems. Comput. Math. Appl. 2019, 77, 1282–1293. [Google Scholar] [CrossRef]
- Huang, B. Numerical study on Moore–Penrose inverse of tensors via Einstein product. Numer. Algorithms 2021, 87, 1767–1797. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Y.; Tan, N.; Cai, B. Zhang neural network solving for time-varying full-rank matrix Moore–Penrose inverse. Computing 2011, 92, 97–121. [Google Scholar] [CrossRef]
- Wu, W.; Zheng, B. Improved recurrent neural networks for solving Moore–Penrose inverse of real-time full-rank matrix. Neurocomputing 2020, 418, 221–231. [Google Scholar] [CrossRef]
- Miao, J.M. General expressions for the Moore–Penrose inverse of a 2 × 2 block matrix. Linear Algebra Appl. 1991, 151, 1–15. [Google Scholar] [CrossRef]
- Kyrchei, I.I. Determinantal representations of the Moore–Penrose inverse over the quaternion skew field and corresponding Cramer’s rules. Linear Multilinear Algebra 2011, 59, 413–431. [Google Scholar] [CrossRef]
- Wojtyra, M.; Pekal, M.; Fraczek, J. Utilization of the Moore–Penrose inverse in the modeling of overconstrained mechanisms with frictionless and frictional joints. Mech. Mach. Theory 2020, 153, 103999. [Google Scholar] [CrossRef]
- Zhuang, H.; Lin, Z.; Toh, K.A. Blockwise Recursive Moore–Penrose Inverse for Network Learning. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 3237–3250. [Google Scholar] [CrossRef]
- Sharifi, M.; Arab, M.; Haghani, F.K. Finding generalized inverses by a fast and efficient numerical method. J. Comput. Appl. Math. 2015, 279, 187–191. [Google Scholar] [CrossRef]
- Li, H.B.; Huang, T.Z.; Zhang, Y.; Liu, X.P.; Gu, T.X. Chebyshev-type methods and preconditioning techniques. Appl. Math. Comput. 2011, 218, 260–270. [Google Scholar] [CrossRef]
- Chun, C. A geometric construction of iterative functions of order three to solve nonlinear equations. Comput. Math. Appl. 2007, 53, 972–976. [Google Scholar] [CrossRef]
- Altman, M. An optimum cubically convergent iterative method of inverting a linear bounded operator in Hilbert space. Pac. J. Math. 1960, 10, 1107–1113. [Google Scholar] [CrossRef]
- Trott, M. The Mathematica Guidebook for Programming; Springer: New York, NY, USA, 2013. [Google Scholar]
- Matrix Market. Available online: https://math.nist.gov/MatrixMarket (accessed on 24 April 2023).

| Method | i | Time | |||||
|---|---|---|---|---|---|---|---|
| SM [30] | 21 | 0 | 0 | 2.0001 | 277.203 | ||
| CM [51] | 14 | 0 | 0 | 3.0000 | 194.312 | ||
| MP [51] | 13 | 0 | 0 | 3.0000 | 194.325 | ||
| HM [51] | 12 | 0 | 0 | 3.0000 | 179.031 | ||
| NM1 (18) | 12 | 0 | 0 | 3.0000 | 174.985 | ||
| NM2 (19) | 12 | 0 | 0 | 3.0000 | 171.470 | ||
| HP4 [53] | 11 | 0 | 0 | 4.0000 | 155.702 |
| Method | i | Time | |||||
|---|---|---|---|---|---|---|---|
| SM [30] | 25 | 0 | 0 | 2.0000 | 1644.86 | ||
| CM [51] | 16 | 0 | 0 | 3.0000 | 1680.99 | ||
| MP [51] | 15 | 0 | 0 | 3.0000 | 1153.19 | ||
| HM [51] | 14 | 0 | 0 | 3.0000 | 941.094 | ||
| NM1 (18) | 13 | 0 | 0 | 3.0000 | 793.515 | ||
| NM2 (19) | 13 | 0 | 0 | 3.0000 | 817.546 | ||
| HP4 [53] | 13 | 0 | 0 | 4.0000 | 831.734 |
| Method | i | Time | |||||
|---|---|---|---|---|---|---|---|
| SM [30] | 16 | 0 | 0 | 2.0000 | 128.719 | ||
| CM [51] | 10 | 0 | 0 | 3.0068 | 63.071 | ||
| MP [51] | 10 | 0 | 0 | 3.0015 | 66.297 | ||
| HM [51] | 9 | 0 | 0 | 3.0671 | 109.813 | ||
| NM1 (18) | 9 | 0 | 0 | 3.0589 | 54.781 | ||
| NM2 (19) | 9 | 0 | 0 | 3.0493 | 61.610 | ||
| HP4 [53] | 8 | 0 | 0 | 4.1557 | 54.875 |
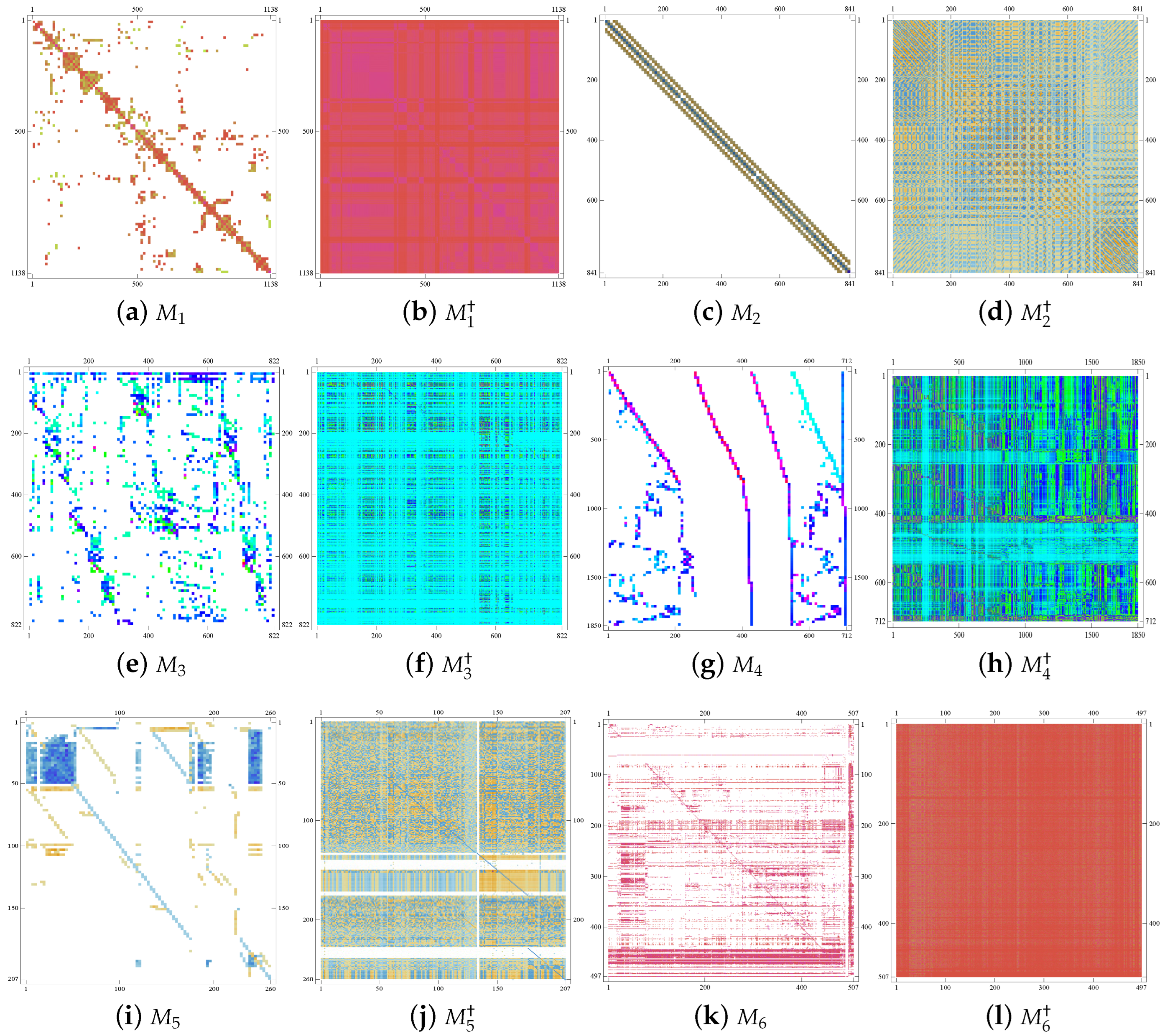
| Name of Problem | Description | |
|---|---|---|
| 1138 BUS | Order: , rank =1138, condition number (est.): 1 (+2) | |
| YOUNG1C | Order: , rank = 841, condition number (est.): 2.9 (+2) | |
| BP600 | Order: , rank = 822, condition number (est.): 5.1 (+06) | |
| ILLC1850 | Order: , rank = 712 | |
| WM3 | Order: , rank = 207 | |
| BEAUSE | Order: , rank = 459 |
| Method | i | Time | |||||
|---|---|---|---|---|---|---|---|
| SM [30] | 51 | 113.688 | |||||
| CM [51] | 32 | 71.687 | |||||
| MP [51] | 30 | 68.750 | |||||
| HM [51] | 28 | 63.297 | |||||
| NM1 (18) | 26 | 51.437 | |||||
| NM2 (19) | 27 | 53.750 | |||||
| HP4 [53] | 26 | 42.548 | |||||
| SM [30] | 21 | 47.203 | |||||
| CM [51] | 14 | 34.015 | |||||
| MP [51] | 13 | 31.344 | |||||
| HM [51] | 12 | 28.749 | |||||
| NM1 (18) | 11 | 21.016 | |||||
| NM2 (19) | 11 | 21.781 | |||||
| HP4 [53] | 11 | 20.843 | |||||
| SM [30] | 46 | 131.891 | |||||
| CM [51] | 29 | 57.125 | |||||
| MP [51] | 27 | 49.343 | |||||
| HM [51] | 26 | 48.515 | |||||
| NM1 (18) | 24 | 25.845 | |||||
| NM2 (19) | 24 | 25.844 | |||||
| HP4 [53] | 23 | 26.984 | |||||
| SM [30] | 26 | 117.156 | |||||
| CM [51] | 16 | 67.656 | |||||
| MP [51] | 15 | 66.499 | |||||
| HM [51] | 15 | 66.439 | |||||
| NM1 (18) | 13 | 54.313 | |||||
| NM2 (19) | 14 | 56.781 | |||||
| HP4 [53] | 13 | 55.281 | |||||
| SM [30] | 27 | 3.009 | |||||
| CM [51] | 17 | 2.094 | |||||
| MP | 16 | 2.048 | |||||
| HM [51] | 15 | 1.922 | |||||
| NM1 (18) | 14 | 1.890 | |||||
| NM2 (19) | 14 | 1.891 | |||||
| HP4 [53] | 14 | 1.806 | |||||
| SM [30] | 36 | 18.656 | |||||
| CM [51] | 23 | 12.688 | |||||
| MP [51] | 21 | 12.094 | |||||
| HM [51] | 20 | 12.094 | |||||
| NM1 (18) | 19 | 11.652 | |||||
| NM2 (19) | 19 | 11.922 | |||||
| HP4 [53] | 18 | 10.982 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kansal, M.; Kaur, M.; Rani, L.; Jäntschi, L. A Cubic Class of Iterative Procedures for Finding the Generalized Inverses. Mathematics 2023, 11, 3031. https://doi.org/10.3390/math11133031
Kansal M, Kaur M, Rani L, Jäntschi L. A Cubic Class of Iterative Procedures for Finding the Generalized Inverses. Mathematics. 2023; 11(13):3031. https://doi.org/10.3390/math11133031
Chicago/Turabian StyleKansal, Munish, Manpreet Kaur, Litika Rani, and Lorentz Jäntschi. 2023. "A Cubic Class of Iterative Procedures for Finding the Generalized Inverses" Mathematics 11, no. 13: 3031. https://doi.org/10.3390/math11133031
APA StyleKansal, M., Kaur, M., Rani, L., & Jäntschi, L. (2023). A Cubic Class of Iterative Procedures for Finding the Generalized Inverses. Mathematics, 11(13), 3031. https://doi.org/10.3390/math11133031







