Derivative-Free Families of With- and Without-Memory Iterative Methods for Solving Nonlinear Equations and Their Engineering Applications
Abstract
:1. Introduction
2. Construction of New Iterative Schemes and Their Convergence Analysis
Parametric Family of Three-Point With-Memory Method and Its Convergence Analysis
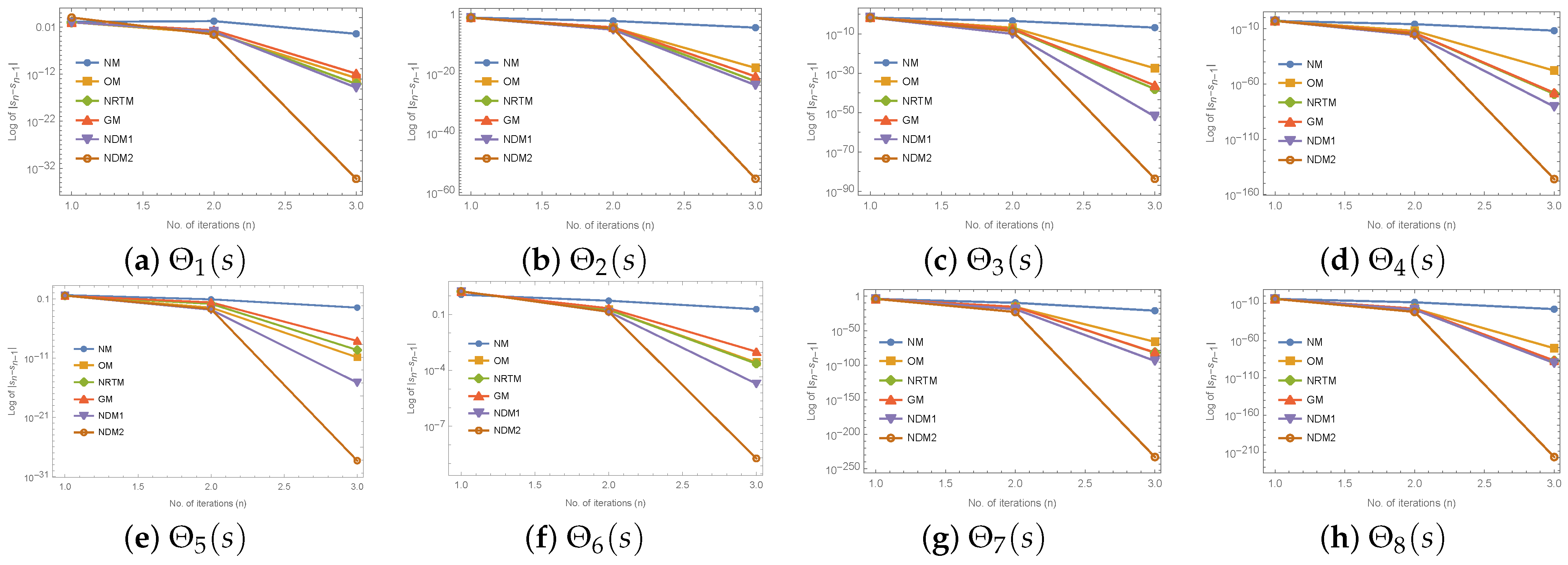
3. Numerical Discussion
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GM | Grau fifth-order method |
| NM | Newton–Raphson method |
| NDM1 | Newly developed method 1 (without memory, Equation (3)) |
| NDM2 | Newly developed method 2 (with memory, Equation (19)) |
| NRTM | Nouri fifth-order method (Equation (35)) |
| OM | Ostrowski’s method |
| COC | Computational rate of convergence |
| The following constants were used in this manuscript: | |
| c | speed of light |
| P | Planck constant |
| For the authors, the following abbreviations were used: | |
| E.S. | Ekta Sharma |
| L.J. | Lorentz Jäntschi |
| S.K.M. | Shubham Kumar Mittal |
| S.P. | Sunil Panday |
| D.-M.J. | Dan-Marian Joița |
| L.L.P. | Lavinia Lorena Pruteanu |
References
- Behbahan, A.S.; Alizadeh, A.a.; Mahmoudi, M.; Shamsborhan, M.; Al-Musawi, T.J.; Pasha, P. A new Adomian decomposition technique for a thermal analysis forced non-Newtonian magnetic Reiner-Rivlin viscoelastic fluid flow. Alex. Eng. J. 2023, 80, 48–57. [Google Scholar] [CrossRef]
- Fika, P. Approximation of the Tikhonov regularization parameter through Aitken’s extrapolation. Appl. Numer. Math. 2023, 190, 270–282. [Google Scholar] [CrossRef]
- Gutierrez, C.; Gutierrez, F.; Rivara, M.C. Complexity of the bisection method. Theor. Comput. Sci. 2007, 382, 131–138. [Google Scholar] [CrossRef]
- Sharma, H.; Kansal, M. A modified Chebyshev–Halley-type iterative family with memory for solving nonlinear equations and its stability analysis. Math. Methods Appl. Sci. 2023, 46, 12549–12569. [Google Scholar] [CrossRef]
- Petković, I.; Herceg, D. Computers in mathematical research: The study of three-point root-finding methods. Numer. Algorithms 2020, 84, 1179–1198. [Google Scholar] [CrossRef]
- Lu, Y.; Tang, Y. Solving Fractional Differential Equations Using Collocation Method Based on Hybrid of Block-pulse Functions and Taylor Polynomials. Turk. J. Math. 2021, 45, 1065–1078. [Google Scholar] [CrossRef]
- Assari, P.; Dehghan, M. A meshless local Galerkin method for solving Volterra integral equations deduced from nonlinear fractional differential equations using the moving least squares technique. Appl. Numer. Math. 2019, 143, 276–299. [Google Scholar] [CrossRef]
- Farhood, A.K.; Mohammed, O.H. Homotopy perturbation method for solving time-fractional nonlinear Variable-Order Delay Partial Differential Equations. Partial. Differ. Equ. Appl. Math. 2023, 7, 100513. [Google Scholar] [CrossRef]
- Argyros, I.K.; Sharma, D.; Argyros, C.I.; Parhi, S.K.; Sunanda, S.K.; Argyros, M.I. Extended three step sixth order Jarratt- like methods under generalized conditions for nonlinear equations. Arab. J. Math. 2022, 11, 443–457. [Google Scholar] [CrossRef]
- Temple, B.; Young, R. Inversion of a non-uniform difference operator and a strategy for Nash–Moser. Methods Appl. Anal. 2022, 29, 265–294. [Google Scholar] [CrossRef]
- Pho, K.H. Improvements of the Newton–Raphson method. J. Comput. Appl. Math. 2022, 408, 114106. [Google Scholar] [CrossRef]
- Argyros, I.K.; George, S. Local convergence of osada’s method for finding zeros with multiplicity. In Understanding Banach Spaces; Sáanchez, D.G., Ed.; Nova Science Publishers: Hauppauge, NY, USA, 2019; pp. 147–151. Available online: http://idr.nitk.ac.in/jspui/handle/123456789/14597 (accessed on 11 October 2023).
- Postigo Beleña, C. Ostrowski’s Method for Solving Nonlinear Equations and Systems. J. Mech. Eng. Autom. 2023, 13, 1–6. [Google Scholar] [CrossRef]
- Ivanov, S.I. General Local Convergence Theorems about the Picard Iteration in Arbitrary Normed Fields with Applications to Super–Halley Method for Multiple Polynomial Zeros. Mathematics 2020, 8, 1599. [Google Scholar] [CrossRef]
- Coclite, G.M.; Fanizzi, A.; Lopez, L.; Maddalena, F.; Pellegrino, S.F. Numerical methods for the nonlocal wave equation of the peridynamics. Appl. Numer. Math. 2020, 155, 119–139. [Google Scholar] [CrossRef]
- Darvishi, M.T.; Barati, A. A fourth-order method from quadrature formulae to solve systems of nonlinear equations. Appl. Math. Comput. 2007, 188, 257–261. [Google Scholar] [CrossRef]
- Nisha, S.; Parida, P.K. Super-Halley method under majorant conditions in Banach spaces. Cubo (Temuco) 2020, 22, 55–70. [Google Scholar] [CrossRef]
- Putri, R.Y.; Wartono, W. Modifikasi metode Schroder tanpa turunan kedua dengan orde konvergensi empat. Aksioma J. Mat. Dan Pendidik. Mat. 2020, 11, 240–251. [Google Scholar] [CrossRef]
- Sharma, J.R.; Kumar, D.; Argyros, I.K. An efficient class of Traub-Steffensen-like seventh order multiple-root solvers with applications. Symmetry 2019, 11, 518. [Google Scholar] [CrossRef]
- Jamaludin, N.A.A.; Nik Long, N.M.A.; Salimi, M.; Sharifi, S. Review of Some Iterative Methods for Solving Nonlinear Equations with Multiple Zeros. Afr. Mat. 2019, 30, 355–369. [Google Scholar] [CrossRef]
- Traub, J.F. Iterative Methods for the Solution of Equations; American Mathematical Society: Providence, RI, USA, 1982; Volume 312. [Google Scholar]
- Ostrowski, A.M. Solution of Equations in Euclidean and Banach Spaces; Academic Press: Cambridge, MA, USA, 1973; Available online: https://cir.nii.ac.jp/crid/1130282272784494208 (accessed on 11 October 2023).
- Kumar, M.; Singh, A.K.; Srivastava, A. A new fifth-order derivative free Newton-type method for solving nonlinear equations. Appl. Math. Inf. Sci. 2015, 9, 1507. [Google Scholar]
- Choubey, N.; Jaiswal, J.P. A derivative-free method of eighth-order for finding simple root of nonlinear equations. Commun. Numer. Anal. 2015, 2, 90–103. [Google Scholar] [CrossRef]
- Sharma, E.; Panday, S.; Dwivedi, M. New Optimal Fourth Order Iterative Method for Solving Nonlinear Equations. Int. J. Emerging Technol. 2020, 11, 755–758. Available online: https://www.researchtrend.net/ijet/pdf/New%20Optimal%20Fourth%20Order%20Iterative%20Method%20for%20Solving%20Nonlinear%20Equations%20Ekta%20Sharma%202481.pdf (accessed on 11 October 2023).
- Panday, S.; Sharma, A.; Thangkhenpau, G. Optimal fourth and eighth-order iterative methods for non-linear equations. J. Appl. Math. Comput. 2022, 69, 953–971. [Google Scholar] [CrossRef]
- Singh, M.K.; Singh, A.K. The optimal order Newton’s like methods with dynamics. Mathematics 2021, 9, 527. [Google Scholar] [CrossRef]
- Solaiman, O.S.; Hashim, I. Optimal eighth-order solver for nonlinear equations with applications in chemical engineering. Intell. Autom. Soft Comput. 2020, 13, 87–93. [Google Scholar] [CrossRef]
- Chanu, W.H.; Panday, S. Excellent Higher Order Iterative Scheme for Solving Non-linear Equations. Iaeng Int. J. Appl. Math. 2022, 52, 1–7. Available online: https://www.iaeng.org/IJAM/issues_v52/issue_1/IJAM_52_1_18.pdf (accessed on 11 October 2023).
- Nouri, K.; Ranjbar, H.; Torkzadeh, L. Two High Order Iterative Methods for Roots of Nonlinear Equations. Punjab Univ. J. Math. 2020, 51. Available online: http://journals.pu.edu.pk/journals/index.php/pujm/article/viewFile/3339/1452 (accessed on 11 October 2023).
- Grau, M.; Díaz-Barrero, J.L. An improvement of the Euler–Chebyshev iterative method. J. Math. Anal. Appl. 2006, 315, 1–7. [Google Scholar] [CrossRef]
- Neta, B. A new derivative-free method to solve nonlinear equations. Mathematics 2021, 9, 583. [Google Scholar] [CrossRef]
- Chanu, W.H.; Panday, S.; Thangkhenpau, G. Development of Optimal Iterative Methods with Their Applications and Basins of Attraction. Symmetry 2022, 14, 2020. [Google Scholar] [CrossRef]
- Thangkhenpau, G.; Panday, S.; Mittal, S.K.; Jäntschi, L. Novel Parametric Families of with and without Memory Iterative Methods for Multiple Roots of Nonlinear Equations. Mathematics 2023, 11, 2036. [Google Scholar] [CrossRef]
- Lotfi, T.; Soleymani, F.; Noori, Z.; Kılıçman, A.; Khaksar Haghani, F. Efficient iterative methods with and without memory possessing high efficiency indices. Discret. Dyn. Nat. Soc. 2014, 2014, 912796. [Google Scholar] [CrossRef]
- Džunić, J. On efficient two-parameter methods for solving nonlinear equations. Numer. Algorithms 2013, 63, 549–569. [Google Scholar] [CrossRef]
- Maroju, P.; Magreñán, Á.A.; Motsa, S.S.; Sarría, Í. Second derivative free sixth order continuation method for solving nonlinear equations with applications. J. Math. Chem. 2018, 56, 2099–2116. [Google Scholar] [CrossRef]
- Weerakoon, S.; Fernando, T. A variant of Newton’s method with accelerated third-order convergence. Appl. Math. Lett. 2000, 13, 87–93. [Google Scholar] [CrossRef]
| Method | COC | ||||
|---|---|---|---|---|---|
| NM | |||||
| OM | |||||
| NRTM | |||||
| GM | |||||
| NDM1 ( = 1, = 1) | |||||
| NDM2 |
| Method | COC | ||||
|---|---|---|---|---|---|
| NM | |||||
| OM | |||||
| NRTM | |||||
| GM | |||||
| NDM1 ( = 1, = 1) | |||||
| NDM2 |
| Method | COC | ||||
|---|---|---|---|---|---|
| NM | |||||
| OM | |||||
| NRTM | |||||
| GM | |||||
| NDM1 ( = 1, = 1) | |||||
| NDM2 |
| Method | COC | ||||
|---|---|---|---|---|---|
| NM | |||||
| OM | |||||
| NRTM | |||||
| GM | |||||
| NDM1 ( = 1, = 1) | |||||
| NDM2 |
| Method | COC | ||||
|---|---|---|---|---|---|
| NM | |||||
| OM | |||||
| NRTM | |||||
| GM | |||||
| NDM1 ( = , = ) | |||||
| NDM2 |
| Method | COC | ||||
|---|---|---|---|---|---|
| NM | |||||
| OM | |||||
| NRTM | |||||
| GM | |||||
| NDM1 ( = , = ) | |||||
| NDM2 |
| Method | COC | ||||
|---|---|---|---|---|---|
| NM | |||||
| OM | |||||
| NRTM | |||||
| GM | |||||
| NDM1 ( = 1, = 1) | |||||
| NDM2 |
| Method | COC | ||||
|---|---|---|---|---|---|
| NM | |||||
| OM | |||||
| NRTM | |||||
| GM | |||||
| NDM1 ( = 1, = 1) | |||||
| NDM2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, E.; Panday, S.; Mittal, S.K.; Joița, D.-M.; Pruteanu, L.L.; Jäntschi, L. Derivative-Free Families of With- and Without-Memory Iterative Methods for Solving Nonlinear Equations and Their Engineering Applications. Mathematics 2023, 11, 4512. https://doi.org/10.3390/math11214512
Sharma E, Panday S, Mittal SK, Joița D-M, Pruteanu LL, Jäntschi L. Derivative-Free Families of With- and Without-Memory Iterative Methods for Solving Nonlinear Equations and Their Engineering Applications. Mathematics. 2023; 11(21):4512. https://doi.org/10.3390/math11214512
Chicago/Turabian StyleSharma, Ekta, Sunil Panday, Shubham Kumar Mittal, Dan-Marian Joița, Lavinia Lorena Pruteanu, and Lorentz Jäntschi. 2023. "Derivative-Free Families of With- and Without-Memory Iterative Methods for Solving Nonlinear Equations and Their Engineering Applications" Mathematics 11, no. 21: 4512. https://doi.org/10.3390/math11214512
APA StyleSharma, E., Panday, S., Mittal, S. K., Joița, D.-M., Pruteanu, L. L., & Jäntschi, L. (2023). Derivative-Free Families of With- and Without-Memory Iterative Methods for Solving Nonlinear Equations and Their Engineering Applications. Mathematics, 11(21), 4512. https://doi.org/10.3390/math11214512







