Mathematical Modelling of Fused Deposition Modeling (FDM) 3D Printing of Poly Vinyl Alcohol Parts through Statistical Design of Experiments Approach
Abstract
1. Introduction
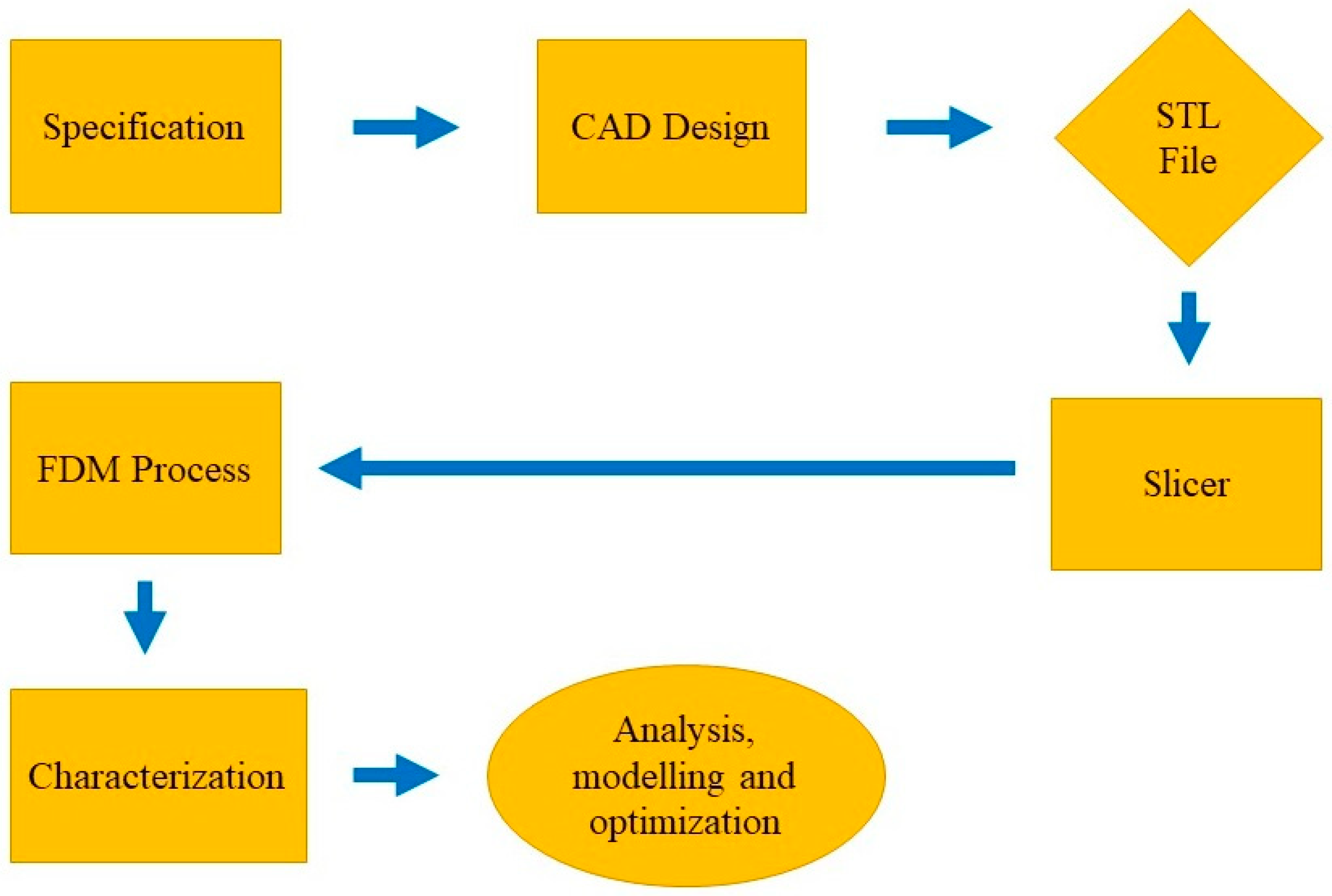
2. Methodology and Experimental Work
2.1. Methodology
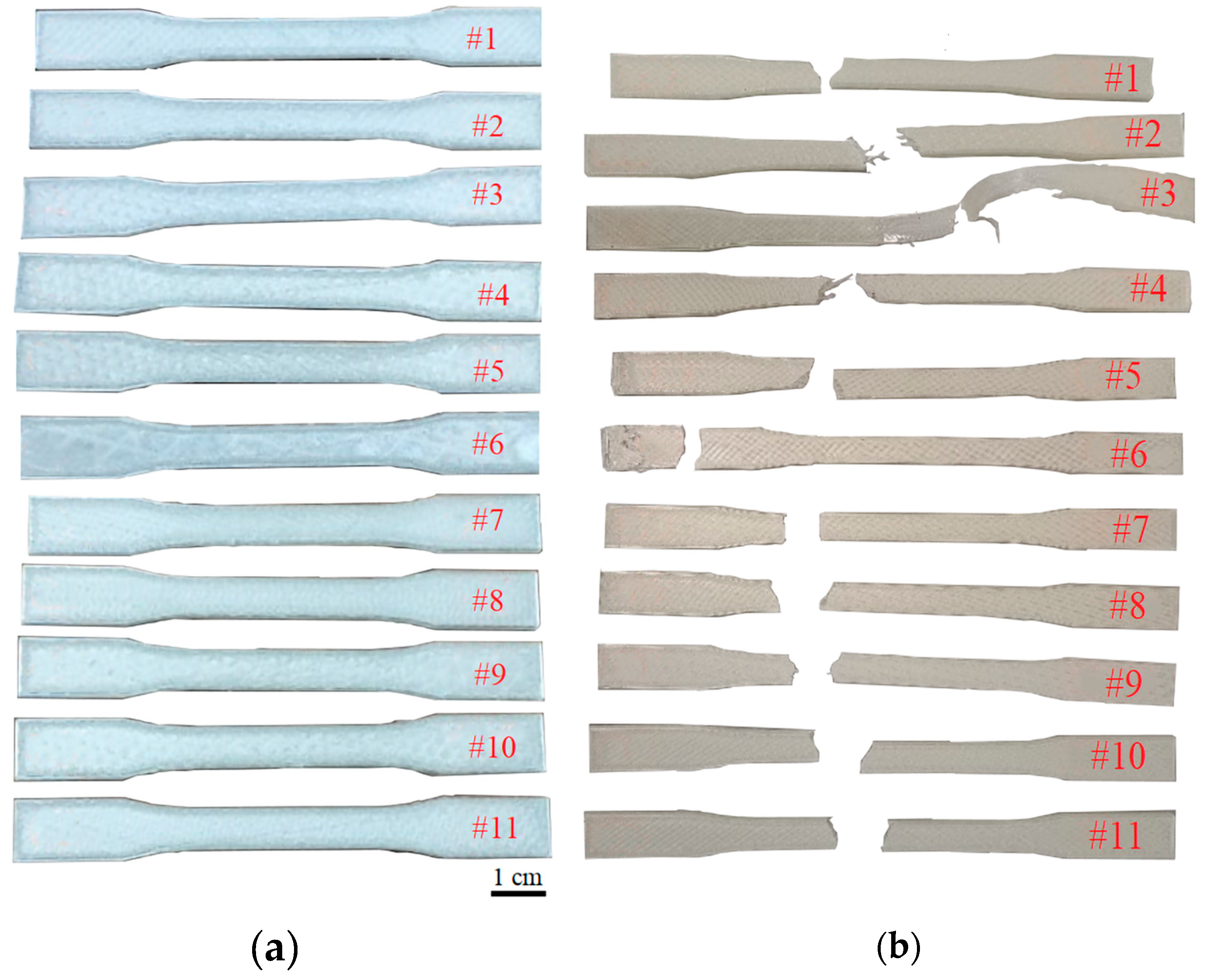
2.2. Experimental Work
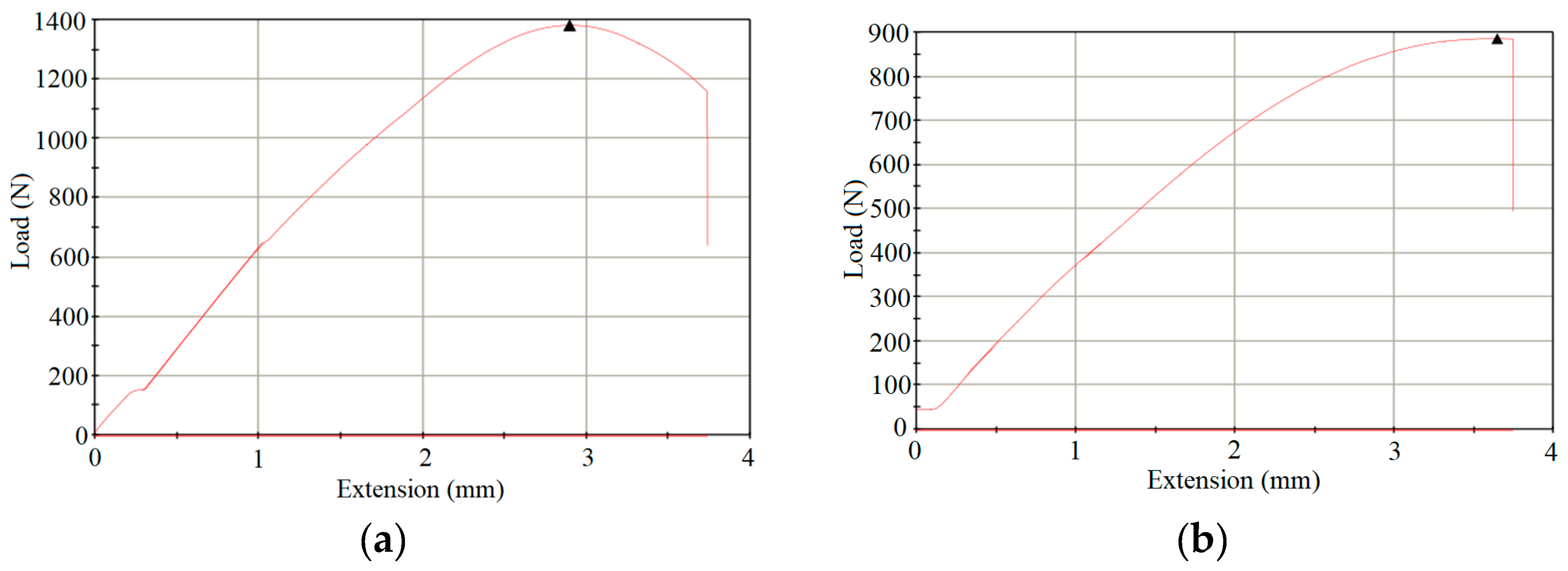
3. Result and Discussion
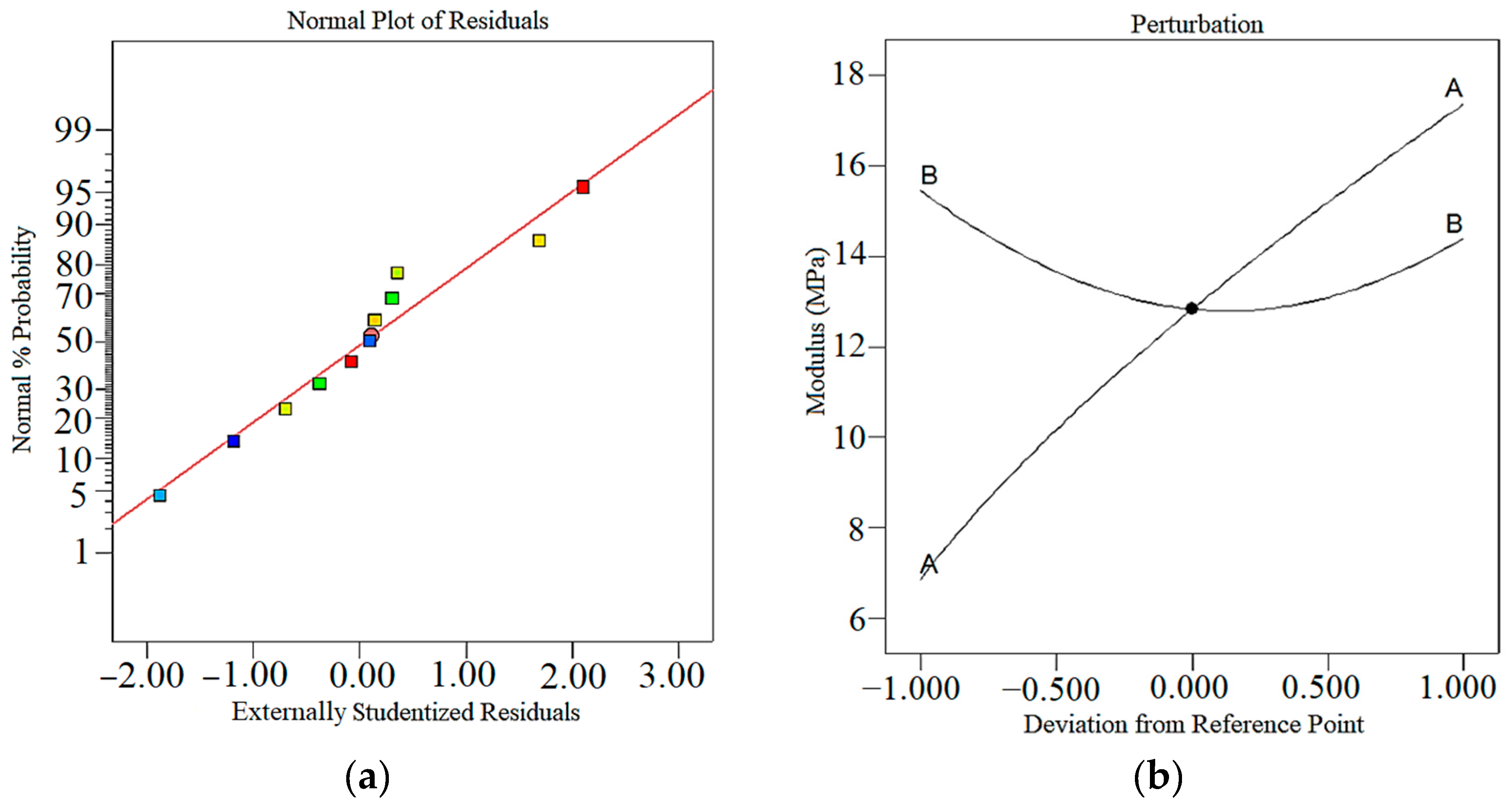
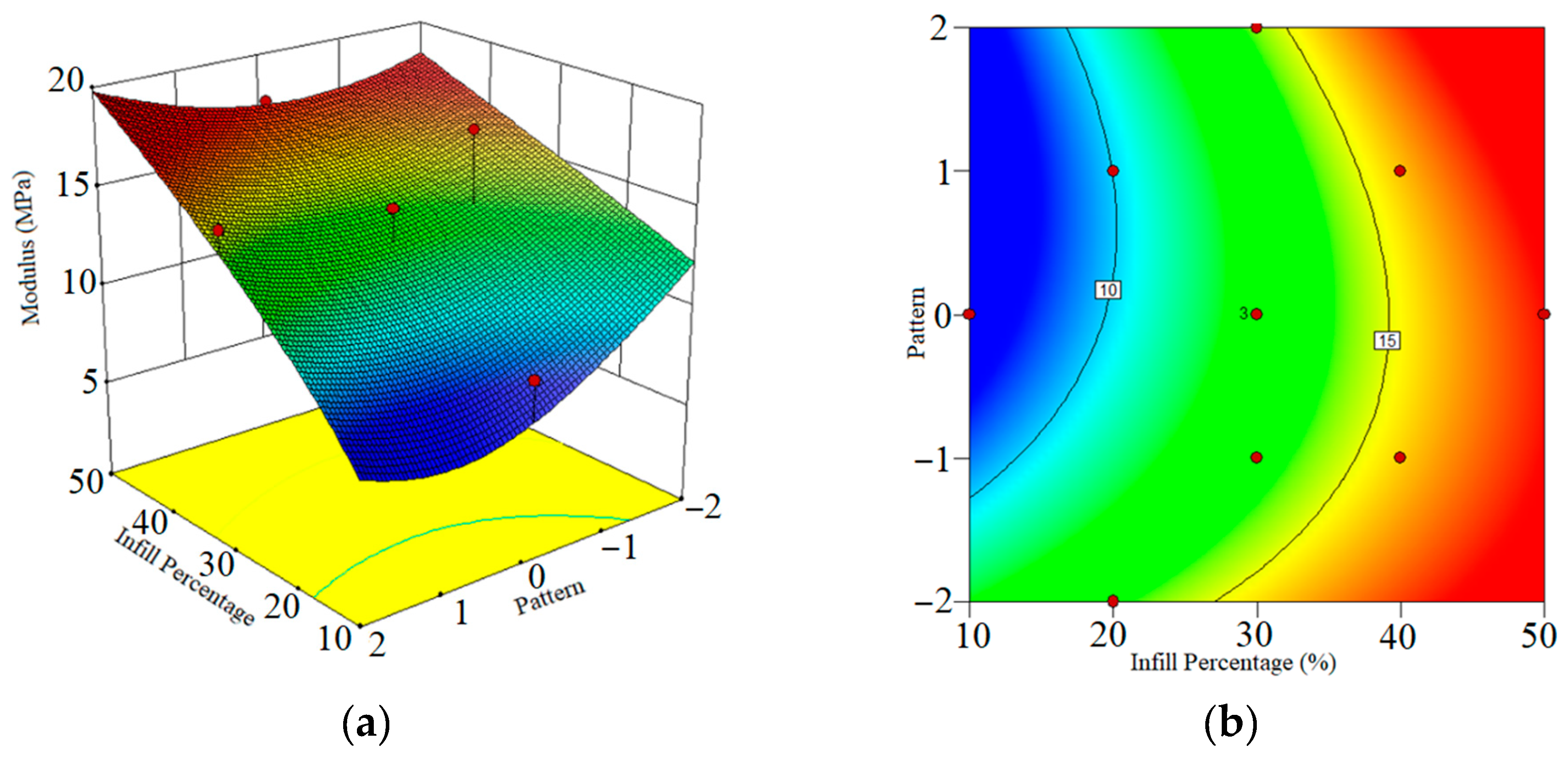
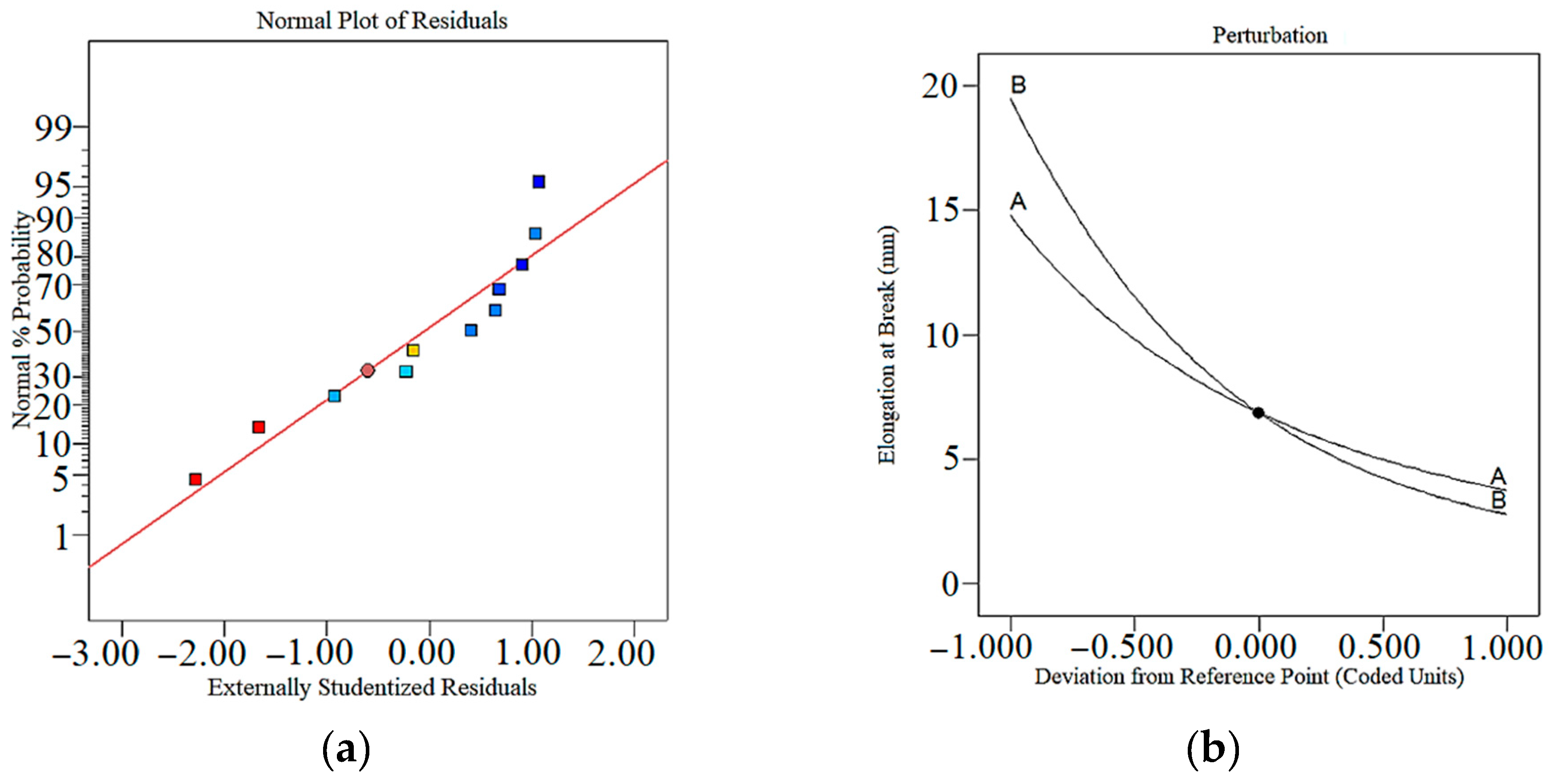
3.1. Modulus
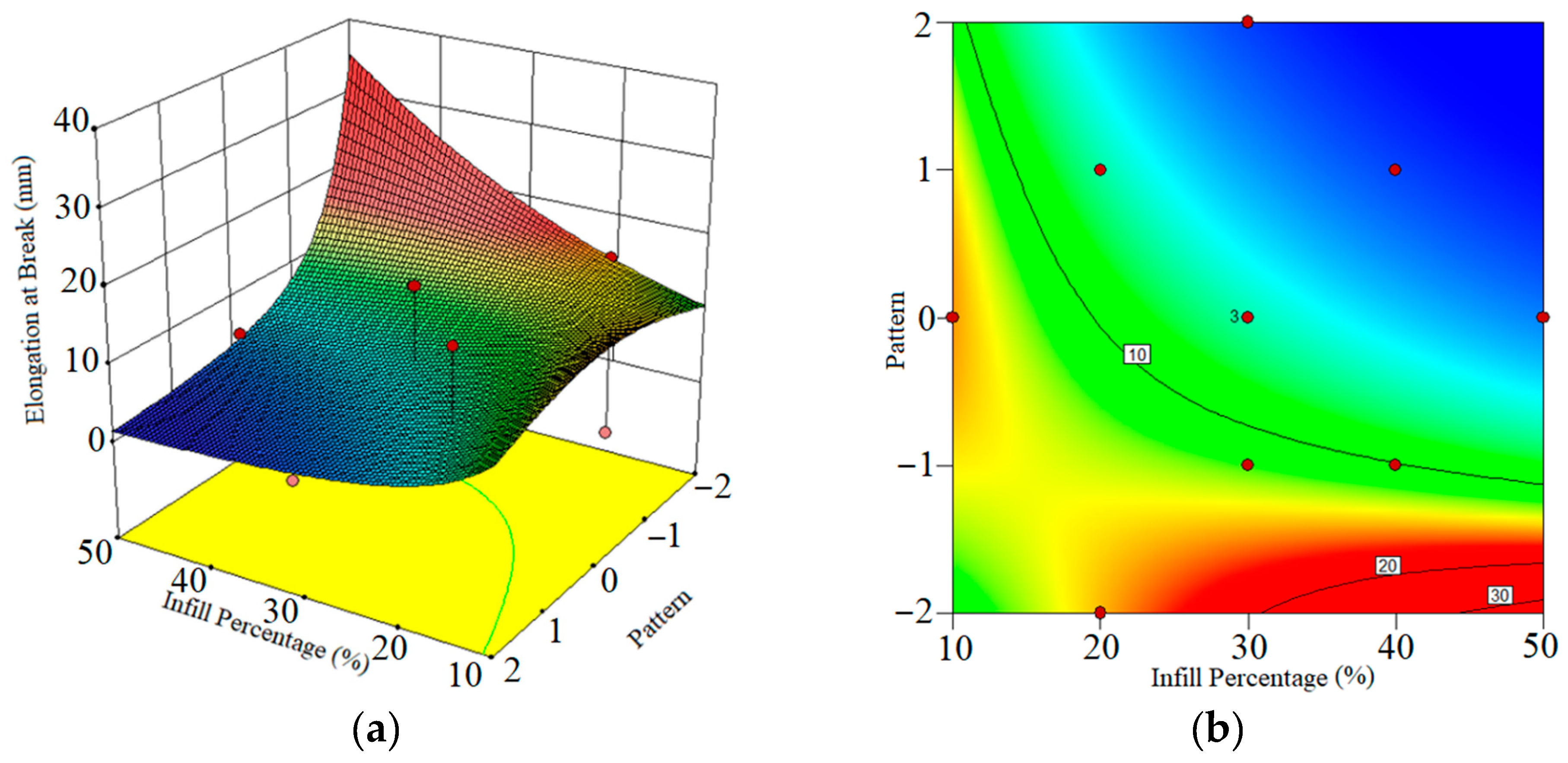
3.2. Elongation at Break
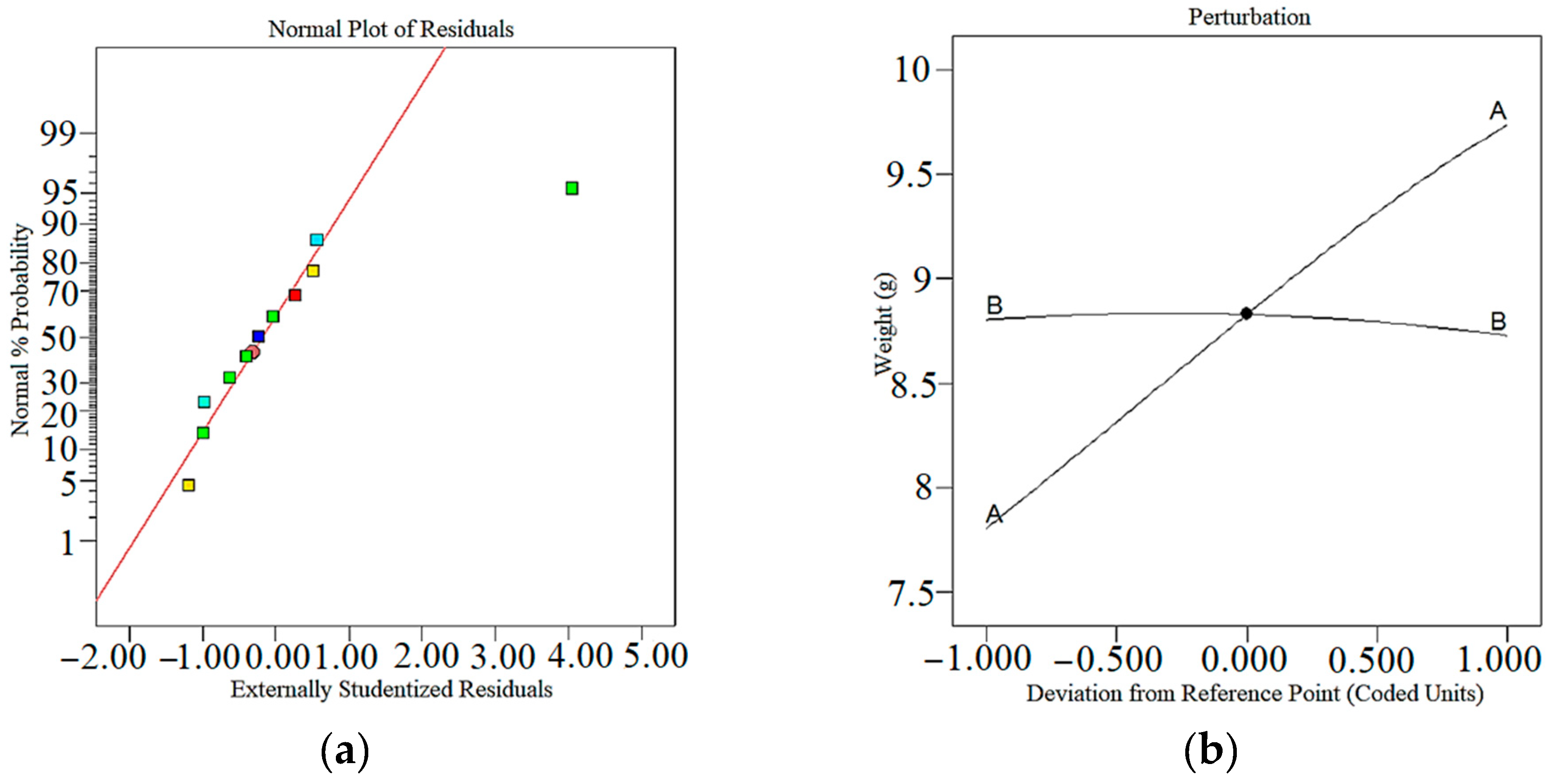
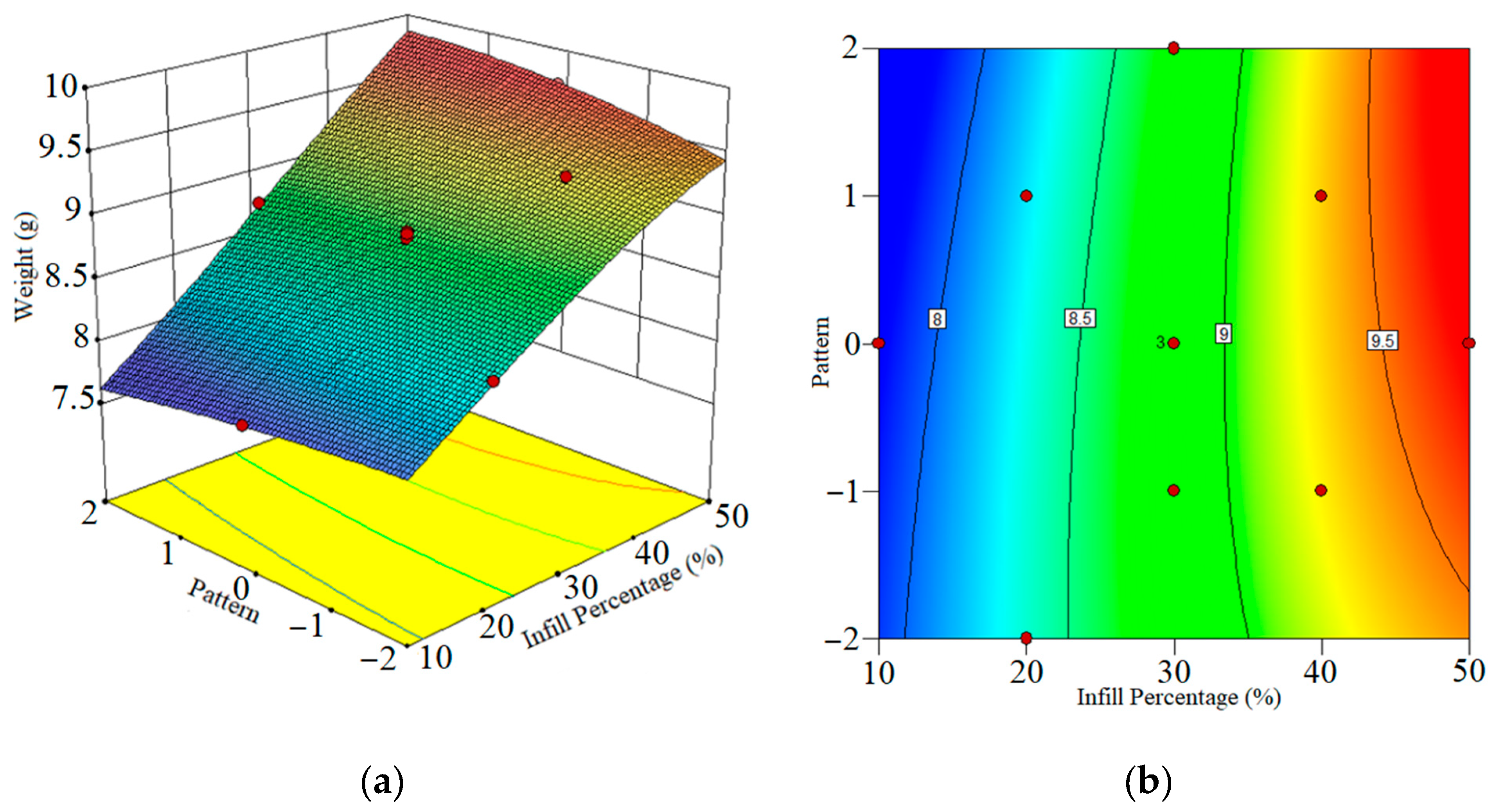
3.3. Weight
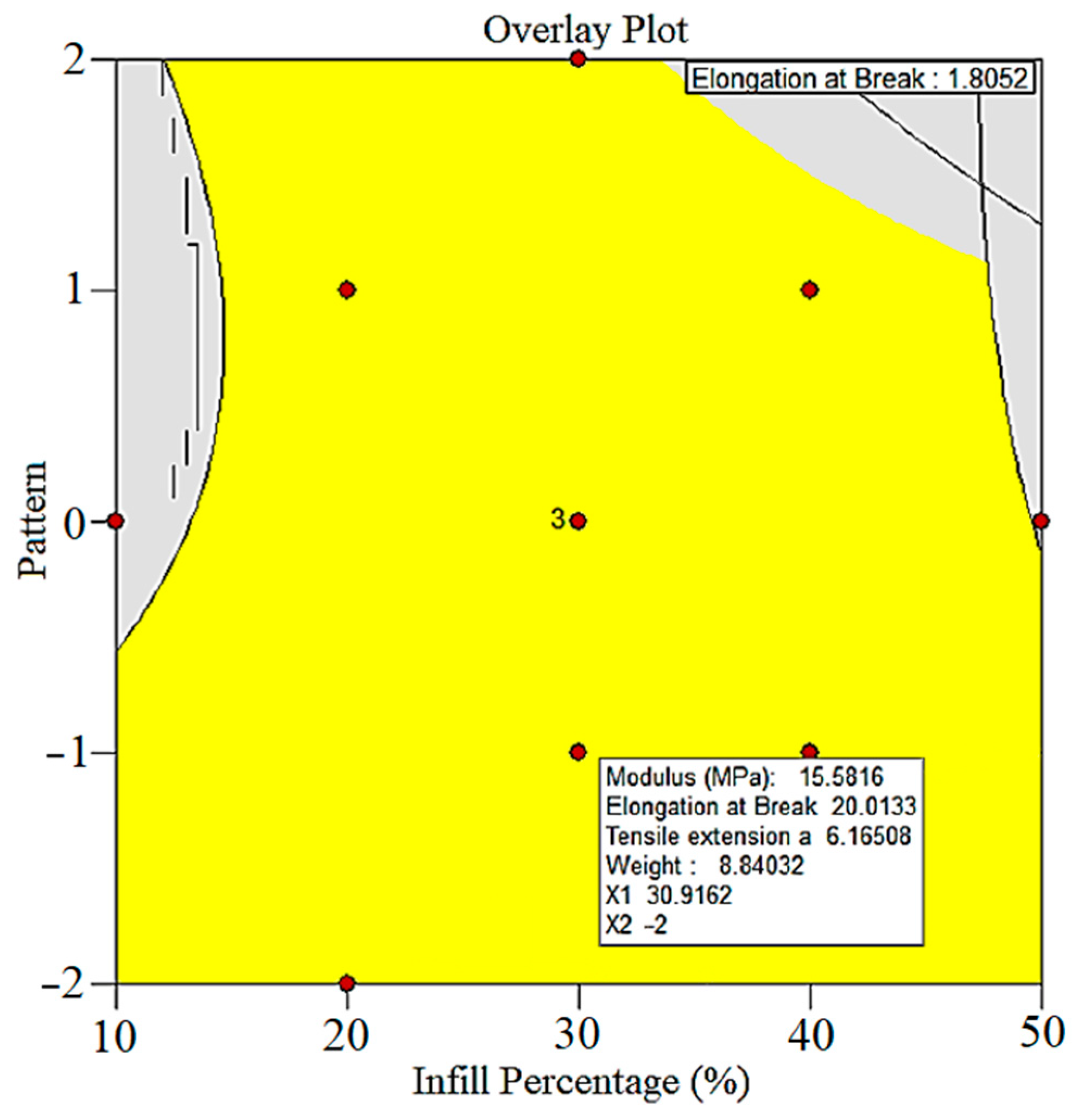
4. Optimization
5. Conclusions
- (1)
- The 3D printer could print the PVA filament properly by considering five different patterns.
- (2)
- The maximum modulus for the sample is 17.519 MPa, and this phenomenon is due to the cohesion of the melted material, which increases this parameter. So, by increasing the IP, the modulus increased.
- (3)
- The triangle pattern with 20% IP had a maximum elongation at break (17.026 mm). In this kind of sitting, the sample had more elongation because of the geometry and the IP percent.
- (4)
- Based on the statistical modeling and RSM design, the overlay plot was designed to show the optimum situations for the input parameters.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FDM | Fused Deposition Modeling |
| RSM | Response Surface Methodology |
| DOE | Design of Experiment |
| ANOVA | Analysis of Variance |
| PVA | Polyvinyl Alcohol |
| ABS | Acrylonitrile Butadiene Styrene |
| CFRP | Carbon-Fiber-Reinforced Plastic |
| IP | Infill Percentage |
References
- Muscolino, E.; Di Stefano, A.B.; Trapani, M.; Sabatino, M.A.; Giacomazza, D.; Alessi, S.; Cammarata, E.; Moschella, F.; Cordova, A.; Toia, F.; et al. κ-Carrageenan and PVA blends as bioinks to 3D print scaffolds for cartilage reconstruction. Int. J. Biol. Macromol. 2022, 222, 1861–1875. [Google Scholar] [CrossRef] [PubMed]
- Meiabadi, M.S.; Moradi, M.; Karamimoghadam, M.; Ardabili, S.; Bodaghi, M.; Shokri, M.; Mosavi, A.H. Modeling the Producibility of 3D Printing in Polylactic Acid Using Artificial Neural Networks and Fused Filament Fabrication. Polymers 2021, 13, 3219. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Li, Q.; Li, J. Shrinkage and mechanical properties optimization of spray-based 3D printed concrete by PVA fiber. Mater. Lett. 2022, 319, 132253. [Google Scholar] [CrossRef]
- Saviano, M.; Bowles, B.J.; Penny, M.R.; Ishaq, A.; Muwaffak, Z.; Falcone, G.; Russo, P.; Hilton, S.T. Development and analysis of a novel loading technique for FDM 3D printed systems: Microwave-assisted impregnation of gastro-retentive PVA capsular devices. Int. J. Pharm. 2022, 613, 121386. [Google Scholar] [CrossRef]
- Shahrjerdi, A.; Karamimoghadam, M.; Bodaghi, M. Enhancing Mechanical Properties of 3D-Printed PLAs via Optimization Process and Statistical Modeling. J. Compos. Sci. 2023, 7, 151. [Google Scholar] [CrossRef]
- Moradi, M.; Karami Moghadam, M.; Shamsborhan, M.; Bodaghi, M.; Falavandi, H. Post-Processing of FDM 3D-Printed Polylactic Acid Parts by Laser Beam Cutting. Polymers 2020, 12, 550. [Google Scholar] [CrossRef]
- Sun, X.; Zhou, J.; Wang, Q.; Shi, J.; Wang, H. PVA fibre reinforced high-strength cementitious composite for 3D printing: Mechanical properties and durability. Addit. Manuf. 2022, 49, 102500. [Google Scholar] [CrossRef]
- Kim, Y.T.; Ahmadianyazdi, A.; Folch, A. A ‘print–pause–print’ protocol for 3D printing microfluidics using multimaterial stereolithography. Nat. Protoc. 2023, 18, 1243–1259. [Google Scholar] [CrossRef]
- Li, M.; Zhou, S.; Cheng, L.; Mo, F.; Chen, L.; Yu, S.; Wei, J. 3D Printed Supercapacitor: Techniques, Materials, Designs, and Applications. Adv. Funct. Mater. 2023, 33, 2208034. [Google Scholar] [CrossRef]
- Li, Q.; Chen, T.; Liang, J.; Zhang, C.; Li, J.; Zhou, Y.; Sun, X. Manufacturing of ceramic cores: From hot injection to 3D printing. J. Mater. Sci. Technol. 2023, 134, 95–105. [Google Scholar] [CrossRef]
- Mirkhalaf, M.; Men, Y.; Wang, R.; No, Y.; Zreiqat, H. Personalized 3D printed bone scaffolds: A review. Acta Biomater. 2023, 156, 110–124. [Google Scholar] [CrossRef]
- Liu, B.; Liu, X.; Li, G.; Geng, S.; Li, Z.; Weng, Y.; Qian, K. Study on anisotropy of 3D printing PVA fiber reinforced concrete using destructive and non-destructive testing methods. Case Stud. Constr. Mater. 2022, 17, e01519. [Google Scholar] [CrossRef]
- Moradi, M.; Karami Moghadam, M.; Shamsborhan, M.; Bodaghi, M. The Synergic Effects of FDM 3D Printing Parameters on Mechanical Behaviors of Bronze Poly Lactic Acid Composites. J. Compos. Sci. 2020, 4, 17. [Google Scholar] [CrossRef]
- Imanian, M.E.; Biglari, F.R. Modeling and prediction of surface roughness and dimensional accuracy in SLS 3D printing of PVA/CB composite using the central composite design. J. Manuf. Process. 2022, 75, 154–169. [Google Scholar] [CrossRef]
- Zieliński, P.S.; Gudeti, P.K.R.; Rikmanspoel, T.; Włodarczyk-Biegun, M.K. 3D printing of bio-instructive materials: Toward directing the cell. Bioact. Mater. 2023, 19, 292–327. [Google Scholar] [CrossRef] [PubMed]
- Wei, Q.; Zhou, J.; An, Y.; Li, M.; Zhang, J.; Yang, S. Modification, 3D printing process and application of sodium alginate based hydrogels in soft tissue engineering: A review. Int. J. Biol. Macromol. 2023, 232, 123450. [Google Scholar] [CrossRef] [PubMed]
- Padhi, S.K.; Sahu, R.K.; Mahapatra, S.S.; Das, H.C.; Sood, A.K.; Patro, B.; Mondal, A.K. Optimization of fused deposition modeling process parameters using a fuzzy inference system coupled with Taguchi philosophy. Adv. Manuf. 2017, 5, 231–242. [Google Scholar] [CrossRef]
- Gardan, J.; Makke, A.; Recho, N. Improving the fracture toughness of 3D printed thermoplastic polymers by fused deposition modeling. Int. J. Fract. 2018, 210, 1–15. [Google Scholar] [CrossRef]
- Peng, A.; Xiao, X.; Yue, R. Process parameter optimization for fused deposition modeling using response surface methodology combined with fuzzy inference system. Int. J. Adv. Manuf. Technol. 2014, 73, 87–100. [Google Scholar] [CrossRef]
- Sajan, N.; John, T.D.; Sivadasan, M.; Singh, N.K. An investigation on circularity error of components processed on Fused Deposition Modeling (FDM). Mater Today Proc. 2018, 5, 1327–1334. [Google Scholar] [CrossRef]
- Gautam, R.; Idapalapati, S.; Feih, S. Printing and characterisation of Kagome lattice structures by fused deposition modelling. Mater. Des. 2018, 137, 266–275. [Google Scholar] [CrossRef]
- Ning, F.; Cong, W.; Wei, J.; Wang, S.; Zhang, M. Additive Manufacturing of CFRP Composites Using Fused Deposition Modeling: Effects of Carbon Fiber Content and Length. In Proceedings of the ASME 2015 International Manufacturing Science and Engineering Conference, Charlotte, NC, USA, 8–12 June 2015; Volume 1. [Google Scholar]
- Komarasamy, M.; Wang, T.; Liu, K.; Reza-Nieto, L.; Mishra, R.S. Hierarchical multi-phase microstructural architecture for exceptional strength-ductility combination in a complex concentrated alloy via high-temperature severe plastic deformation. Scr. Mater. 2019, 162, 38–43. [Google Scholar] [CrossRef]
- Taherzadehboroujeni, M.; Kalhor, R.; Fahs, G.B.; Moore, R.B.; Case, S.W. Accelerated testing method to estimate the long-term hydrostatic strength of semi-crystalline plastic pipes. Polym. Eng. Sci. 2020, 60, 879–888. [Google Scholar] [CrossRef]
- Ghennai, W.; Boussaid, O.; Bendjama, H.; Haddag, B.; Nouari, M. Experimental and numerical study of DC04 sheet metal behaviour—Plastic anisotropy identification and application to deep drawing. Int. J. Adv. Manuf. Technol. 2019, 100, 361–371. [Google Scholar] [CrossRef]
- Alatefi, M.; Al-Ahmari, A.M.; AlFaify, A.Y.; Saleh, M. A Framework for Multivariate Statistical Quality Monitoring of Additive Manufacturing: Fused Filament Fabrication Process. Processes 2023, 11, 1216. [Google Scholar] [CrossRef]
- Turner, B.N.; Strong, R.; Gold, S.A. A review of melt extrusion additive manufacturing processes: I. Process design and modeling. Rapid Prototyp. J. 2014, 20, 192–204. [Google Scholar] [CrossRef]
- Qattawi, A. Investigating the effect of fused deposition modeling processing parameters using Taguchi design of experiment method. J. Manuf. Process. 2018, 36, 164–174. [Google Scholar]
- Idà, E.; Nanetti, F.; Mottola, G. An Alternative Parallel Mechanism for Horizontal Positioning of a Nozzle in an FDM 3D Printer. Machines 2022, 10, 542. [Google Scholar] [CrossRef]
- Ong, J.J.; Castro, B.M.; Gaisford, S.; Cabalar, P.; Basit, A.W.; Pérez, G.; Goyanes, A. Accelerating 3D printing of pharmaceutical products using machine learning. Int. J. Pharm. X 2022, 4, 100120. [Google Scholar] [CrossRef]
- Kadam, V.; Kumar, S.; Bongale, A.; Wazarkar, S.; Kamat, P.; Patil, S. Enhancing surface fault detection using machine learning for 3D printed products. Appl. Syst. Innov. 2021, 4, 34. [Google Scholar] [CrossRef]
- Panwar, V.; Sharma, D.K.; Kumar, K.P.; Jain, A.; Thakar, C. Experimental investigations and optimization of surface roughness in turning of en 36 alloy steel using response surface methodology and genetic algorithm. Mater. Today Proc. 2021, 46, 6474–6481. [Google Scholar] [CrossRef]
- Abdellatief, M.; Elemam, W.E.; Alanazi, H.; Tahwia, A.M. Production and optimization of sustainable cement brick incorporating clay brick wastes using response surface method. Ceram. Int. 2023, 49, 9395–9411. [Google Scholar] [CrossRef]
- Mohammed, B.S.; Adamu, M. Mechanical performance of roller compacted concrete pavement containing crumb rubber and nano silica. Constr. Build. Mater. 2018, 159, 234–251. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C.; Vining, G.G.; Borror, C.M.; Kowalski, S.M. Response surface methodology: A retrospective and literature survey. J. Qual. Technol. 2004, 36, 53–77. [Google Scholar] [CrossRef]
- Bezerra, M.A.; Santelli, R.E.; Oliveira, E.P.; Villar, L.S.; Escaleira, L.A. Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta 2008, 76, 965–977. [Google Scholar] [CrossRef]

| Variable | Notation | Unit | −2 | −1 | 0 | 1 | 2 |
|---|---|---|---|---|---|---|---|
| Infill Percentage | IP | % | 10 | 20 | 30 | 40 | 50 |
| Pattern | W | - | Cubic | Gyroid | Tri-Hexagonal | Triangle | Grid |
| No. | Input Variables | Responses | ||||||
|---|---|---|---|---|---|---|---|---|
| Infill Percentage | Pattern | Modulus (MPa) | Elongation at Break (mm) | Weight (g) | ||||
| Actual | Relative Error % | Actual | Relative Error % | Actual | Relative Error % | |||
| 1 | 30 | Grid | 15.561 | 7.52 | 1.871 | −48.12 | 8.74 | 0.22 |
| 2 | 40 | Triangle | 15.696 | −0.31 | 1.80 | −59.44 | 9.3 | −0.32 |
| 3 | 30 | Cubic | 17.414 | 21.59 | 3.731 | −200.07 | 8.71 | −1.37 |
| 4 | 30 | Tri-Hexagon | 14.492 | 13.02 | 2.806 | 73.24 | 8.89 | 0.78 |
| 5 | 30 | Tri-Hexagon | 9.609 | 33.54 | 4.818 | −144.64 | 8.83 | 0.11 |
| 6 | 10 | Tri-Hexagon | 8.939 | 23.18 | 3.741 | −294.91 | 7.81 | 0.12 |
| 7 | 50 | Tri-Hexagon | 17.519 | 0.91 | 4.358 | 13.97 | 9.72 | −0.10 |
| 8 | 20 | Gyroid | 12.726 | −9.27 | 14.279 | 0.06 | 8.39 | 0.23 |
| 9 | 20 | Triangle | 8.049 | −24.75 | 17.026 | 58.98 | 8.22 | −0.24 |
| 10 | 30 | Tri-Hexagon | 12.763 | −0.47 | 16.851 | 59.34 | 8.87 | 0.56 |
| 11 | 40 | Cubic | 14.739 | −5.83 | 3.581 | −183.24 | 9.32 | 0.64 |
| Source | Sum of Squares | df | Mean Square | F Value | p-Value Prob > F |
|---|---|---|---|---|---|
| Model | 5664.59 | 5 | 1132.92 | 1.87 | 0.2550 |
| A-IP | 5395.16 | 1 | 5395.16 | 8.89 | 0.0307 |
| B-Pattern | 67.32 | 1 | 67.32 | 0.11 | 0.7526 |
| AB | 49.64 | 1 | 49.64 | 0.082 | 0.7864 |
| A2 | 1.55 | 1 | 1.55 | 2.547 × 10−3 | 0.9617 |
| B2 | 359.98 | 1 | 359.98 | 0.59 | 0.4760 |
| Residual | 3034.79 | 5 | 606.96 | ||
| Lack of Fit | 2143.83 | 3 | 714.61 | 1.60 | 0.4063 |
| Pure Error | 890.95 | 2 | 445.48 | ||
| Cor Total | 8699.37 | 10 |
| Source | Sum of Squares | df | Mean Square | F Value | p-Value Prob > F |
|---|---|---|---|---|---|
| Model | 0.13 | 5 | 0.025 | 0.61 | 0.6992 |
| A-IP | 0.038 | 1 | 0.038 | 0.92 | 0.3818 |
| B-Pattern | 0.075 | 1 | 0.075 | 1.82 | 0.2353 |
| AB | 8.564 × 10−3 | 1 | 8.564 × 10−3 | 0.21 | 0.6674 |
| A2 | 1.255 × 10−4 | 1 | 1.255 × 10−4 | 3.050 × 10−3 | 0.9581 |
| B2 | 1.383 × 10−3 | 1 | 1.383 × 10−3 | 0.034 | 0.8618 |
| Residual | 0.21 | 5 | 0.041 | ||
| Lack of Fit | 0.14 | 3 | 0.048 | 1.53 | 0.4193 |
| Pure Error | 0.063 | 2 | 0.031 | ||
| Cor Total | 0.33 | 10 |
| Source | Sum of Squares | df | Mean Square | F Value | p-Value Prob > F |
|---|---|---|---|---|---|
| Model | 8.050 × 10−6 | 5 | 1.610 × 10−6 | 123.12 | <0.0001 |
| A-IP | 7.529 × 10−6 | 1 | 7.529 × 10−6 | 575.76 | <0.0001 |
| B-Pattern | 9.611 × 10−9 | 1 | 9.611 × 10−9 | 0.73 | 0.4304 |
| AB | 2.714 × 10−8 | 1 | 2.714 × 10−8 | 2.08 | 0.2093 |
| A2 | 1.995 × 10−7 | 1 | 1.995 × 10−7 | 15.26 | 0.0113 |
| B2 | 1.011 × 10−8 | 1 | 1.011 × 10−8 | 0.77 | 0.4195 |
| Residual | 6.538 × 10−8 | 5 | 1.308 × 10−8 | ||
| Lack of Fit | 6.075 × 10−8 | 3 | 2.025 × 10−8 | 8.74 | 0.1044 |
| Pure Error | 4.633 × 10−9 | 2 | 2.317 × 10−9 | ||
| Cor Total | 8.115 × 10−6 | 10 |
| Parameters/ Responses | Name | Goal | Lower Limit | Upper Limit | Importance |
|---|---|---|---|---|---|
| Parameters | A: IP | is in range | 10 | 50 | 3 |
| B: Pattern | is in range | −2 | 2 | 3 | |
| Responses | Modulus | maximize | 8.049 | 17.519 | 3 |
| Elongation at Break | maximize | 1.805 | 17.027 | 3 | |
| Weight | minimize | 7.81 | 9.72 | 3 |
| No. | IP (%) | Pattern | Desirability | Modulus (MPa) | Elongation at Break (mm) | Weight (g) |
|---|---|---|---|---|---|---|
| 1 | 30.916 | −2.000 | 0.818 | 15.582 | 20.014 | 8.840 |
| 2 | 31.104 | −2.000 | 0.817 | 15.610 | 20.131 | 8.848 |
| 3 | 33.000 | −2.000 | 0.809 | 15.894 | 21.346 | 8.923 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moradi, M.; Karamimoghadam, M.; Meiabadi, S.; Casalino, G.; Ghaleeh, M.; Baby, B.; Ganapathi, H.; Jose, J.; Abdulla, M.S.; Tallon, P.; et al. Mathematical Modelling of Fused Deposition Modeling (FDM) 3D Printing of Poly Vinyl Alcohol Parts through Statistical Design of Experiments Approach. Mathematics 2023, 11, 3022. https://doi.org/10.3390/math11133022
Moradi M, Karamimoghadam M, Meiabadi S, Casalino G, Ghaleeh M, Baby B, Ganapathi H, Jose J, Abdulla MS, Tallon P, et al. Mathematical Modelling of Fused Deposition Modeling (FDM) 3D Printing of Poly Vinyl Alcohol Parts through Statistical Design of Experiments Approach. Mathematics. 2023; 11(13):3022. https://doi.org/10.3390/math11133022
Chicago/Turabian StyleMoradi, Mahmoud, Mojtaba Karamimoghadam, Saleh Meiabadi, Giuseppe Casalino, Mohammad Ghaleeh, Bobymon Baby, Harikrishna Ganapathi, Jomal Jose, Muhammed Shahzad Abdulla, Paul Tallon, and et al. 2023. "Mathematical Modelling of Fused Deposition Modeling (FDM) 3D Printing of Poly Vinyl Alcohol Parts through Statistical Design of Experiments Approach" Mathematics 11, no. 13: 3022. https://doi.org/10.3390/math11133022
APA StyleMoradi, M., Karamimoghadam, M., Meiabadi, S., Casalino, G., Ghaleeh, M., Baby, B., Ganapathi, H., Jose, J., Abdulla, M. S., Tallon, P., Shamsborhan, M., Rezayat, M., Paul, S., & Khodadad, D. (2023). Mathematical Modelling of Fused Deposition Modeling (FDM) 3D Printing of Poly Vinyl Alcohol Parts through Statistical Design of Experiments Approach. Mathematics, 11(13), 3022. https://doi.org/10.3390/math11133022











