Performance of an Adaptive Optimization Paradigm for Optimal Operation of a Mono-Switch Class E Induction Heating Application
Abstract
1. Introduction
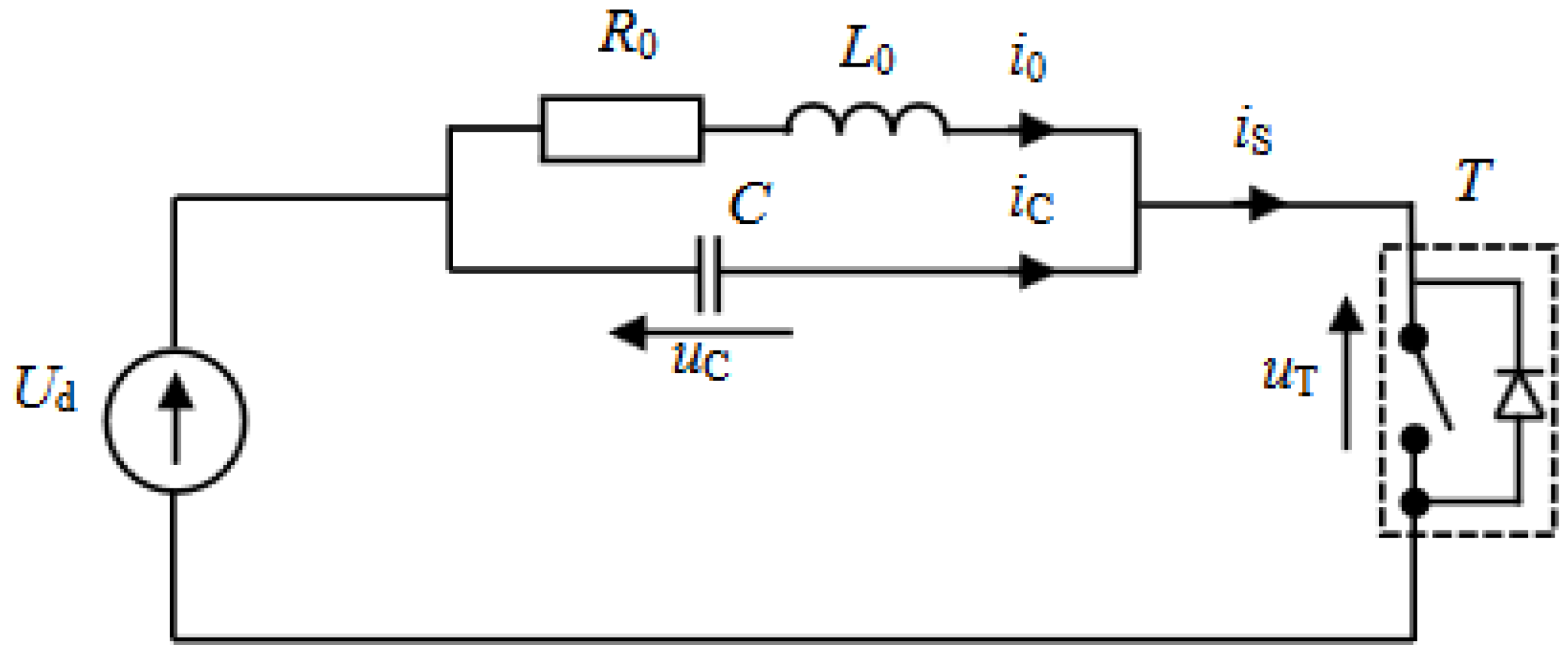
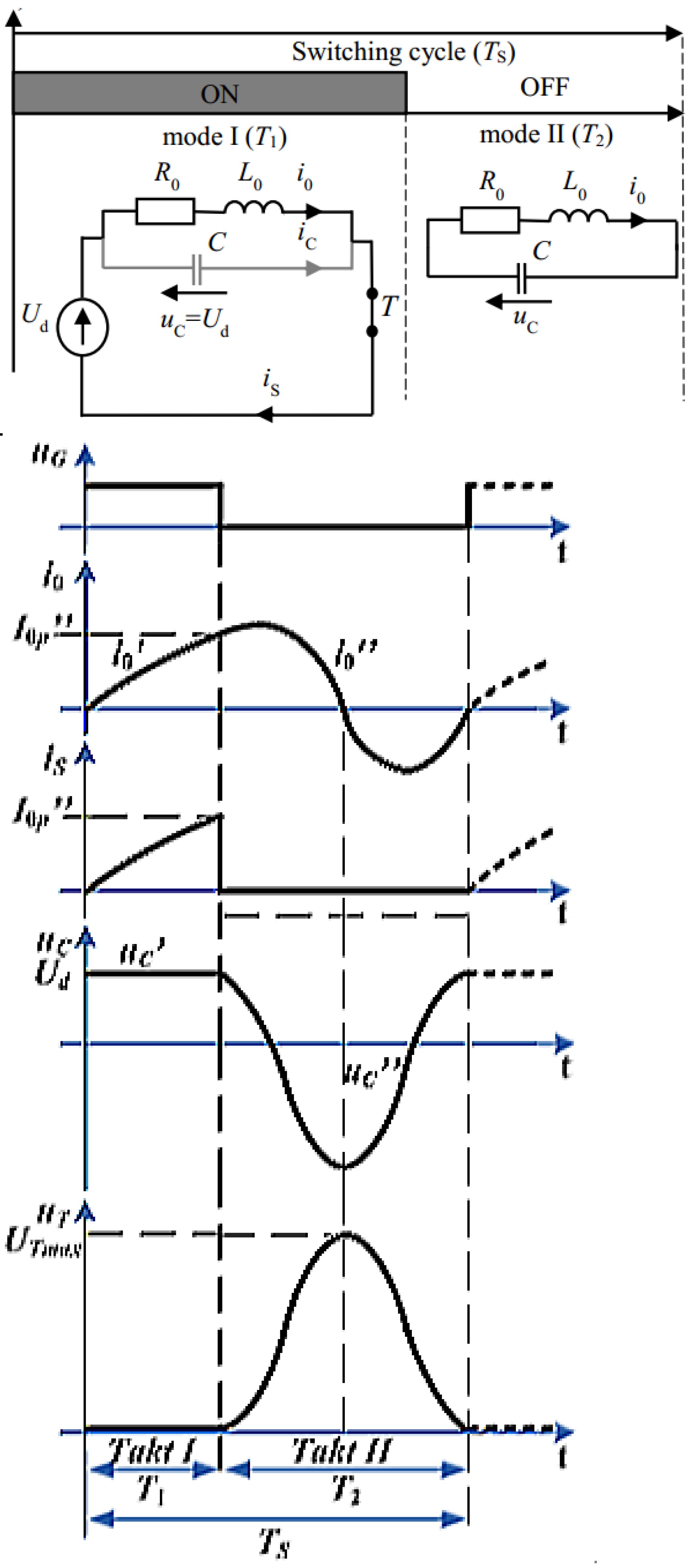
2. Basic Philosophy of Mono-Switch E Class Inverter
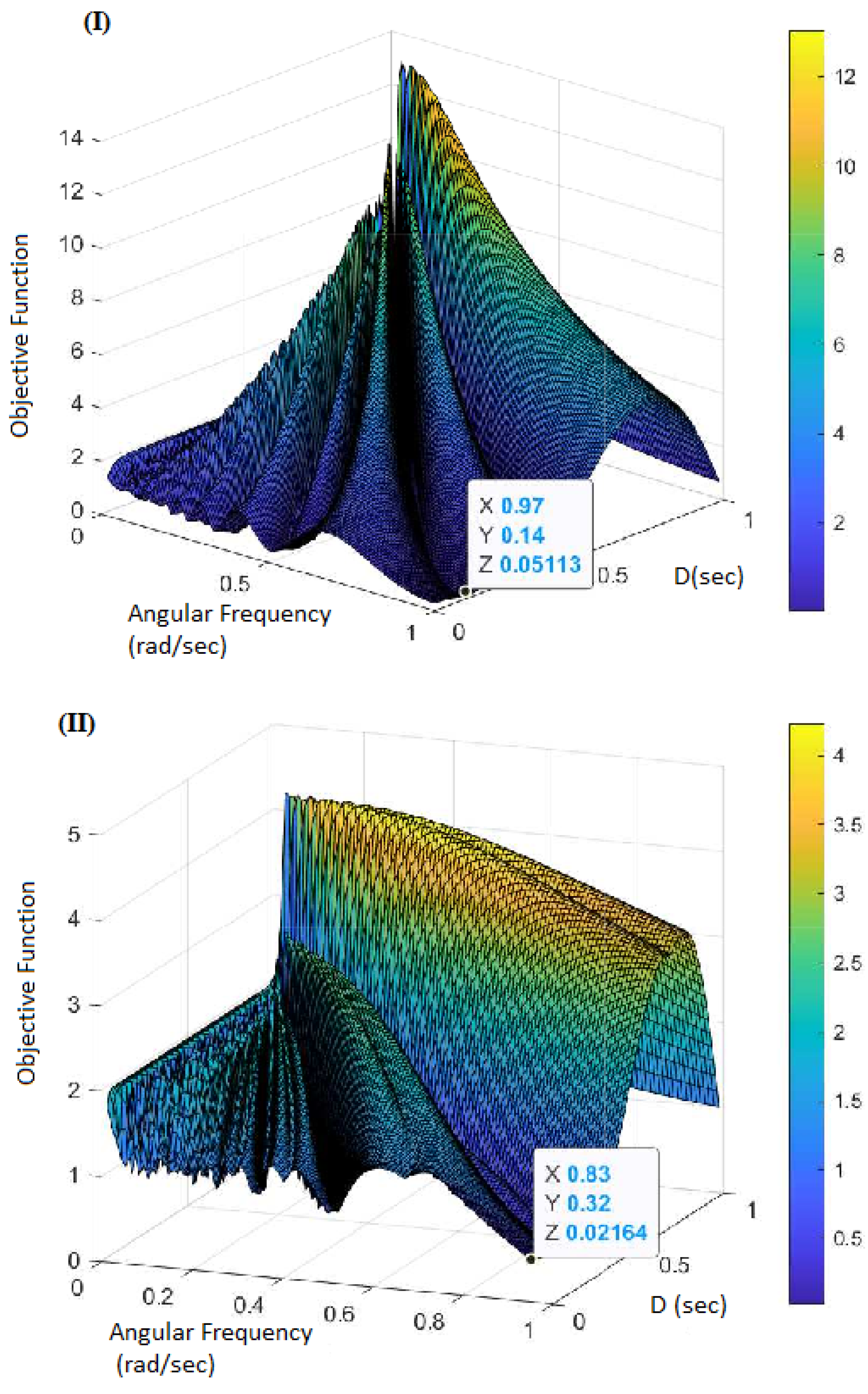
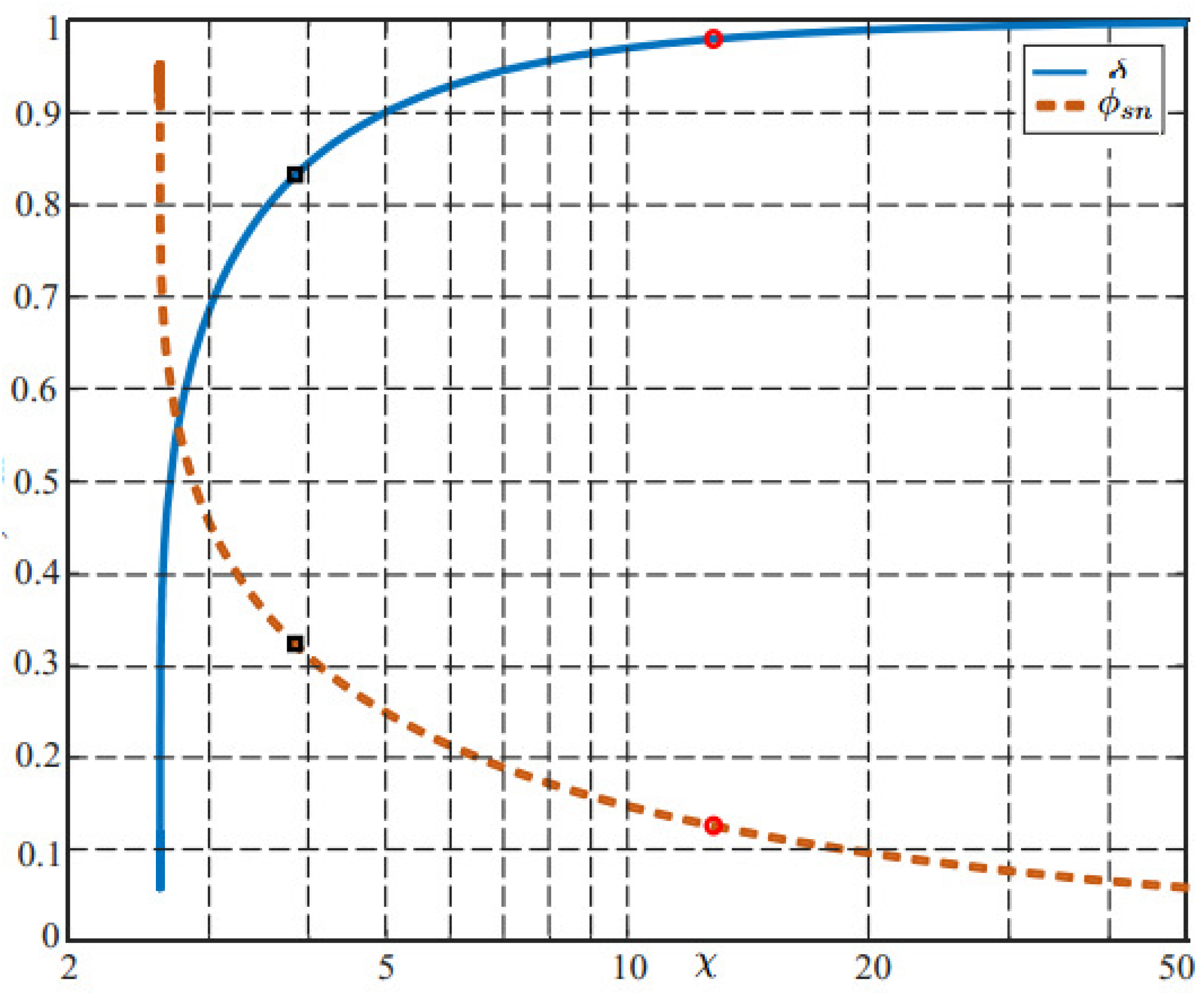
- Scenario-I: = MH, C = MF, = M, = , and = THz;
- Scenario-II: = MH, C = MF, = M, = , and = THz.
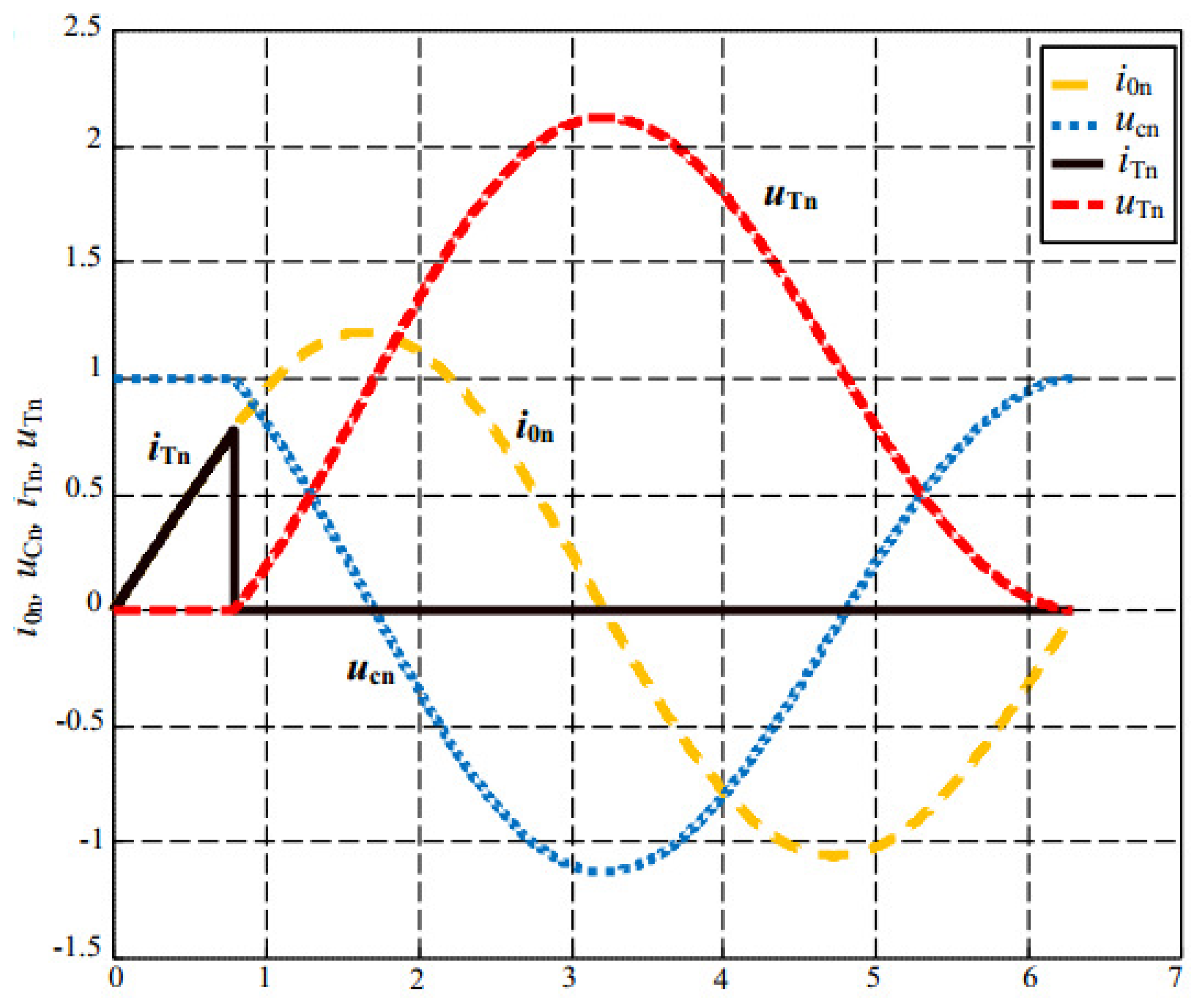
- (a): = , = , y = , = 3,731,886 rad/s, and = kHz, s, s;
- (b): = , = , y = , = 2,588,401 rad/s, and = 2,588,986,505 rad/s, s, s.
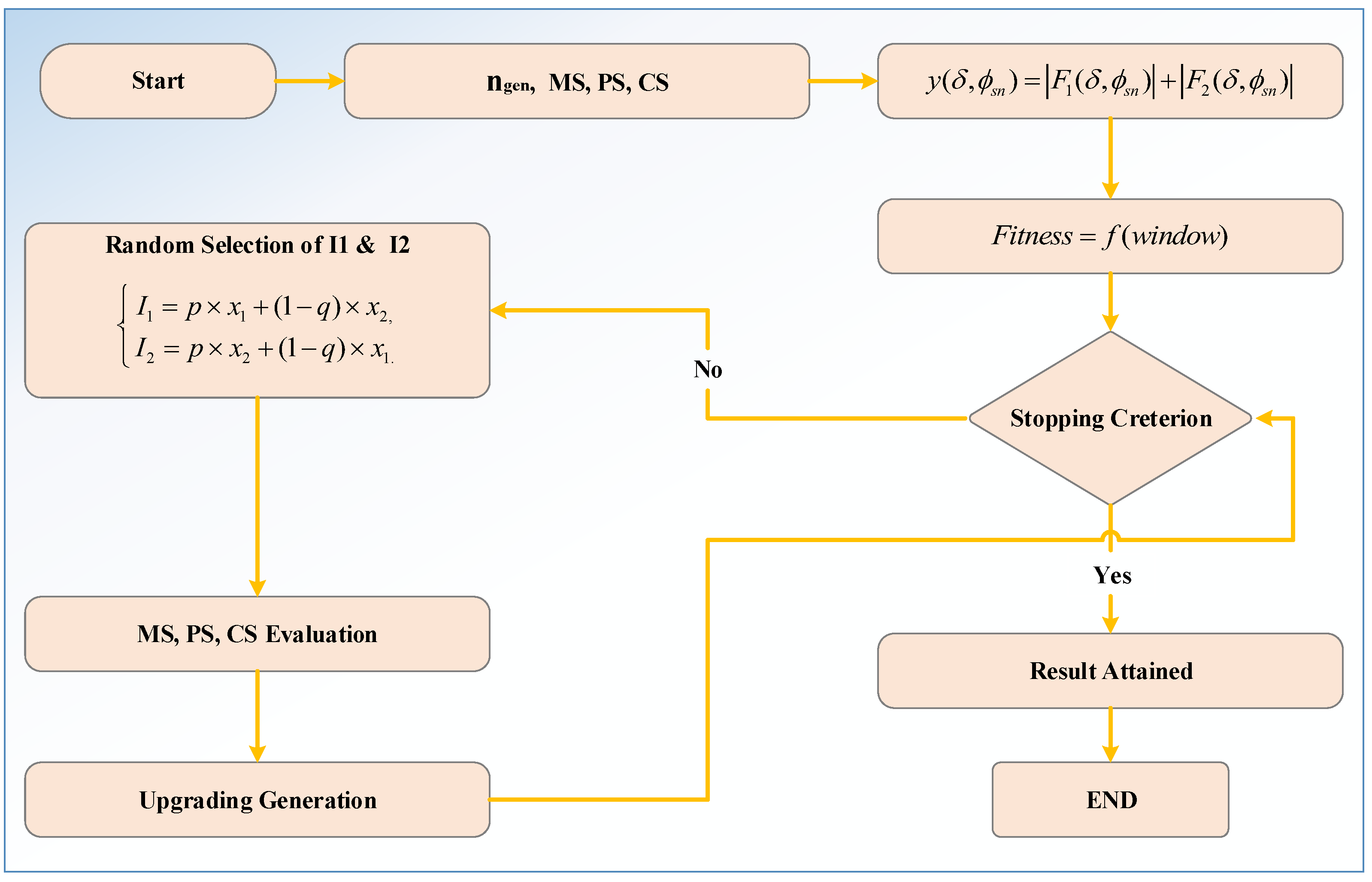
3. Proposed Adaptive Computing Paradigm
3.1. BWS Biological Lifespan
3.1.1. Breeding Mechanism of BWS-Based Optimization
Logical Steps in ABWOA
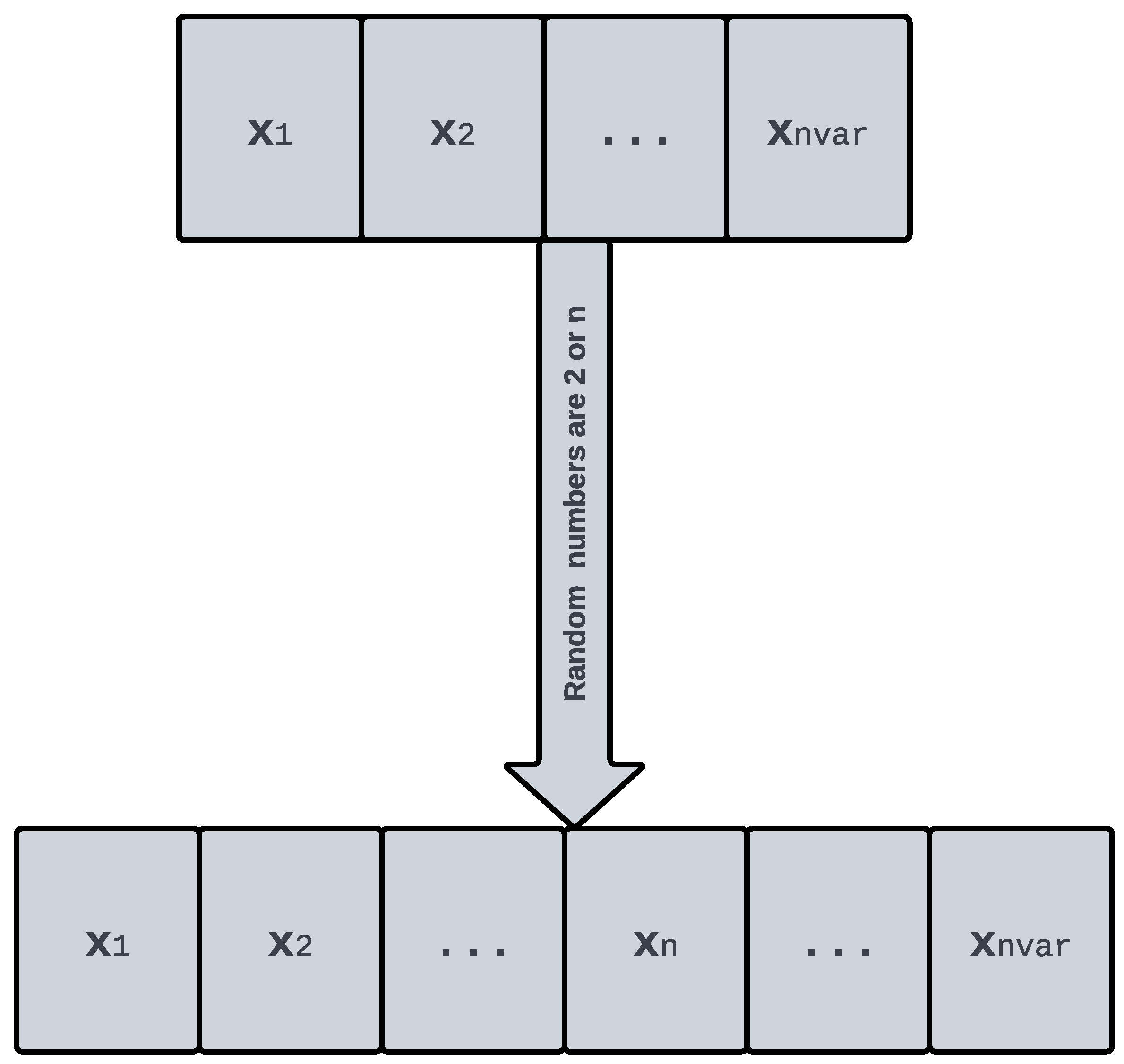
3.1.2. Adjusting the Configuration
- The proportion of participants who should take part in reproducing is equal to the PS. By regulating the progeny produced, this variable increases diversity and opens up more avenues for inquiry;
- The cannibal function eliminates undesirable members of the colony based on the value of the governing factor, CS. The exploitation stage’s effectiveness can be improved by setting the appropriate level for this option;
- PS denotes the percentage of individuals who mutate. Each variable can direct the search individuals’ movement from the global to the localized phase, propelling it closer to the ideal alternative.
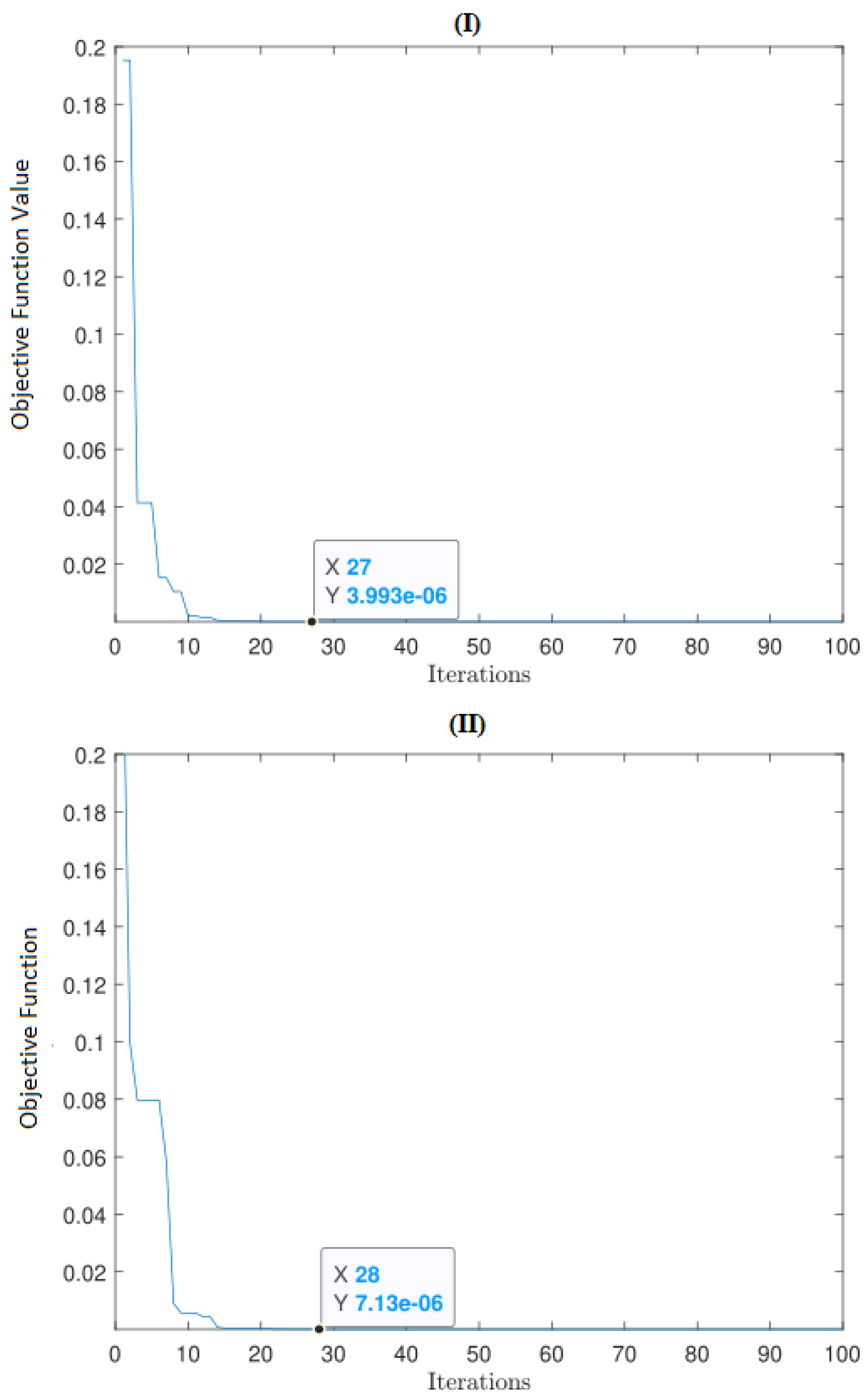
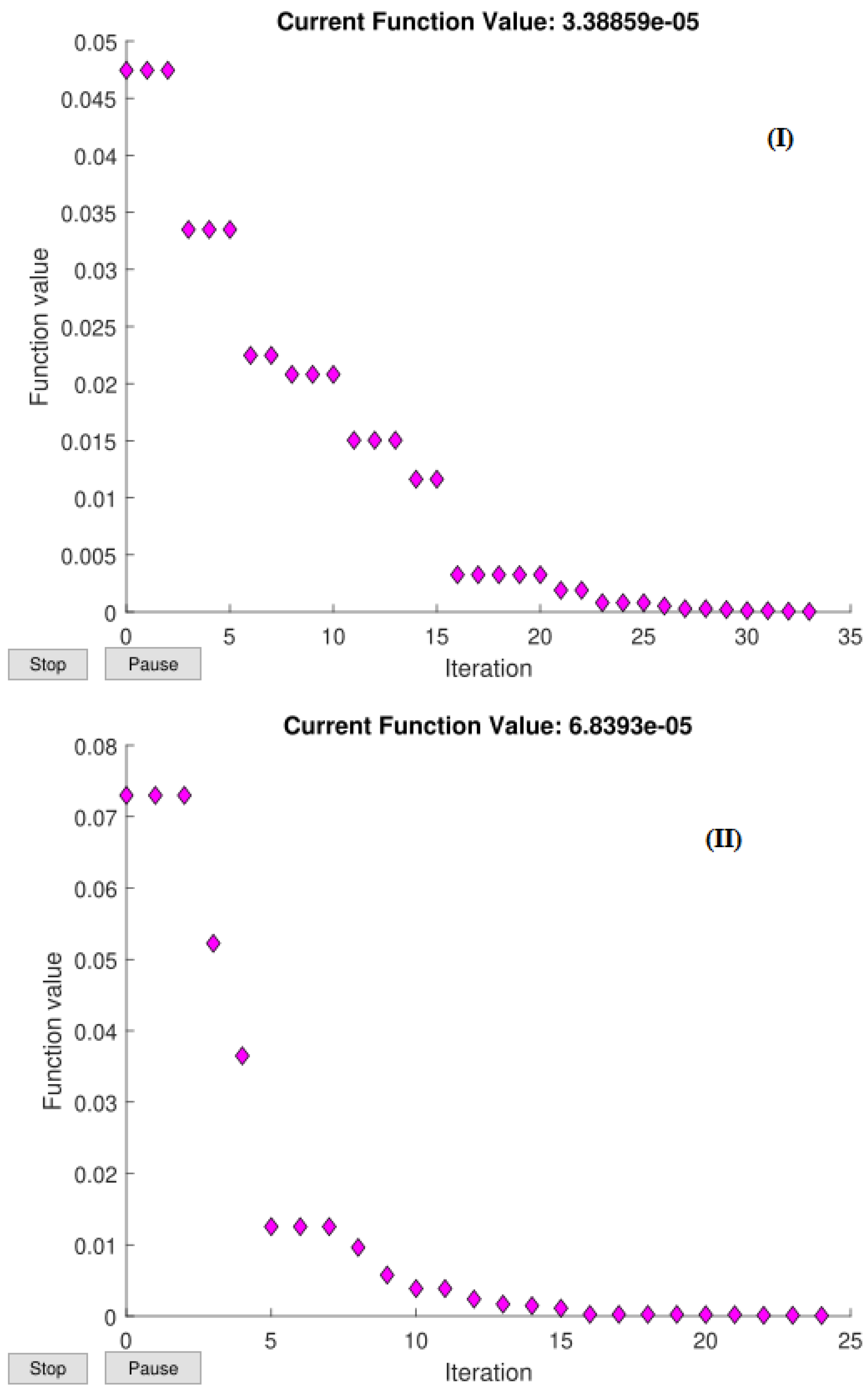
4. Simulation and Results
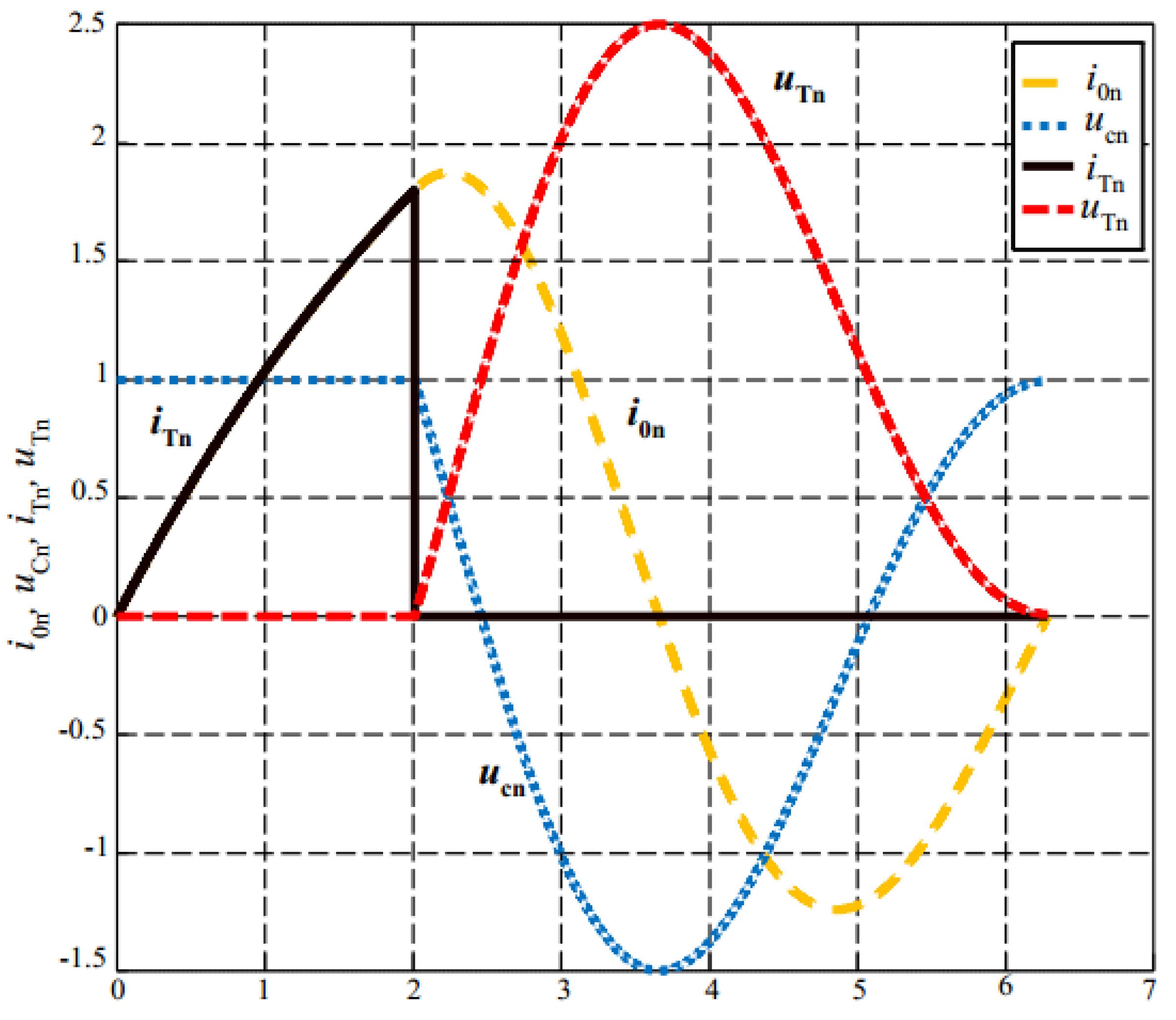
- (a): = , = , y = , = 3,721,985 rad/s, and = kHz, s, s;
- (b): = , = , y = , = 2,622,943 rad/s, and = kHz, s, s.
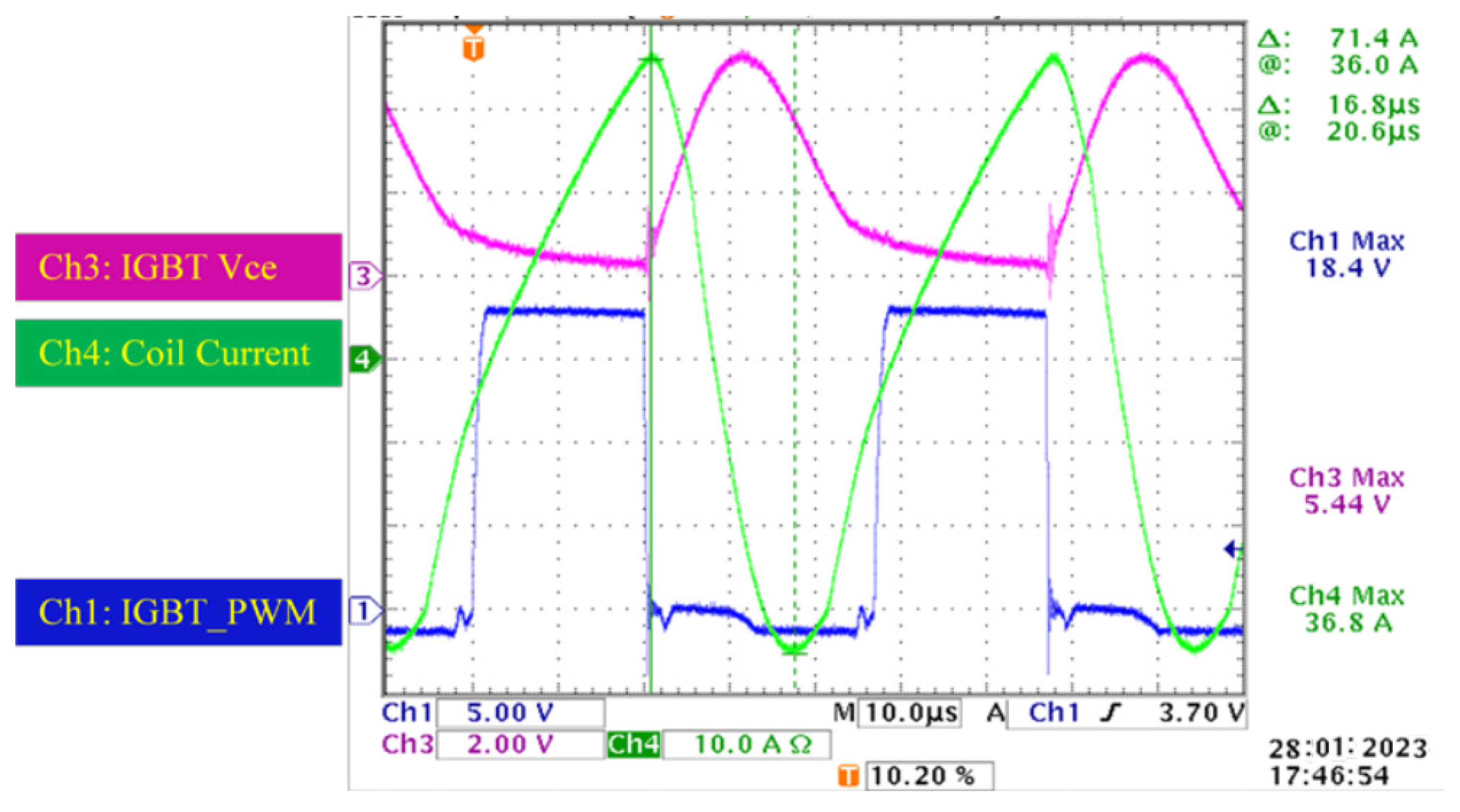
5. Practical Validation of Results
6. Conclusions
- The discussed inverter can perform optimally in class E at a substantially higher rate than is usually demonstrated in investigations;
- A well-tuned mechanism ensures maximum inverter performance and reduced energy fluctuations at the power-electronic converter;
- The adoption of a modern generational converter, such as a SiC semiconductor, mitigates the need for high voltage demand;
- The proposed tailored ABWOA scheme method enhances the resolution of real-world issues. The advancements in induction cooking pots are promising and can lead to enhanced culinary experiences, increased ease of use, reduced energy consumption, and heightened ecological viability;
- Future research in this field should focus on integrating a greater number of non-linear constraints to attain superior and high-quality optimal solutions.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ayub, M.A.; Aziz, S.; Liu, Y.; Peng, J.; Yin, J. Design and Control of Novel Single-Phase Multilevel Voltage Inverter Using MPC Controller. Sustainability 2023, 15, 860. [Google Scholar] [CrossRef]
- Rasachak, S.; Khan, R.S.U.; Kumar, L.; Zahid, T.; Ghafoor, U.; Selvaraj, J.; Nasrin, R.; Ahmad, M.S. Effect of tin oxide/black paint coating on absorber plate temperature for improved solar still production: A controlled indoor and outdoor investigation. Int. J. Photoenergy 2022, 2022, 6902783. [Google Scholar] [CrossRef]
- Guillen, P.; Sarnago, H.; Lucia, O.; Burdio, J.M. Series-Resonant Matrix Inverter with Asymmetrical Modulation for Improved Power Factor Correction in Flexible Induction Heating Appliances. IEEE Trans. Ind. Electron. 2022, 70. [Google Scholar] [CrossRef]
- Plumed, E.; Lope, I.; Acero, J.; Burdío, J.M. Domestic induction heating system with standard primary inductor for reduced-size and high distance cookware. IEEE Trans. Ind. Appl. 2022, 58, 7562–7571. [Google Scholar] [CrossRef]
- Salvi, B.; Porpandiselvi, S.; Vishwanathan, N. A Three Switch Resonant Inverter for Multiple Load Induction Heating Applications. IEEE Trans. Power Electron. 2022, 37, 12108–12117. [Google Scholar] [CrossRef]
- Qais, M.; Loo, K.; Liu, J.; Lai, C.M. Least Mean Square Based Fuzzy C-Means Clustering for Load Recognition of Induction Heating. IEEE Trans. Instrum. Meas. 2022. [Google Scholar] [CrossRef]
- Oncu, S.; Unal, K.; Tuncer, U. Laboratory setup for teaching resonant converters and induction heating. Eng. Sci. Technol. Int. J. 2022, 28, 101012. [Google Scholar] [CrossRef]
- Jang, E.; Kwon, M.J.; Park, S.M.; Ahn, H.M.; Lee, B.K. Analysis and Design of Flexible-Surface Induction-Heating Cooktop with GaN-HEMT-based Multiple Inverter System. IEEE Trans. Power Electron. 2022, 37, 12865–12876. [Google Scholar] [CrossRef]
- Edrisian, A.; Goudarzi, A.; Ebadian, M. Investigating the effect of high level of wind penetration on voltage stability by quasi-static time-domain simulation (QSTDS). Int. J. Renew. Energy Res. 2014, 4, 355–362. [Google Scholar]
- Edrisian, A.; Goudarzi, A.; Ebadian, M.; Swanson, A.G.; Mahdiyan, D. Assessing the effective parameters on operation improvement of SCIG based wind farms connected to network. Int. J. Renew. Energy Res. 2016, 6, 585–592. [Google Scholar]
- Geetha, V.; Pushpavalli, M.; Abirami, P.; Sivagami, P.; Harikrishnan, R. Virtual Plan of the Domestic Enlistment Warming Framework to Reproduce Electromagnetic Boundaries. In Advancement in Materials, Manufacturing and Energy Engineering; Springer: Berlin/Heidelberg, Germany, 2022; Volume I, pp. 575–584. [Google Scholar]
- Goudarzi, A.; Kazemi, M. DC Optimal Power Flow through the Linear Programming—In Context of Smart Grid. In Proceedings of the 24th Southern African Universities Power Engineering Conference, Vereeniging, South Africa, 26–28 January 2016. [Google Scholar]
- Ke, G.; Chen, Q.; Zhang, S.; Xu, X.; Xu, L. A Single-Ended Hybrid Resonant Converter with High Misalignment Tolerance. IEEE Trans. Power Electron. 2022, 37, 12841–12852. [Google Scholar] [CrossRef]
- Wang, S.; Izaki, K.; Hirota, I.; Yamashita, H.; Omori, H.; Nakaoka, M. Induction-heated cooking appliance using new quasi-resonant ZVS-PWM inverter with power factor correction. IEEE Trans. Ind. Appl. 1998, 34, 705–712. [Google Scholar] [CrossRef]
- Nosan, M.; Pavko, L.; Fisgar, M.; Kolar, M.; Genorio, B. Improving Electroactivity of N-Doped Graphene Derivatives with Electrical Induction Heating. ACS Appl. Energy Mater. 2022, 5, 9571–9580. [Google Scholar] [CrossRef]
- Aziz, S.; Hasan, K.; Yaqub, R.; Ahmad, S.; Faiz, M.T. Identifying Unusual Charging Patterns of Electric Vehicles Using Artificial Intelligence. In Proceedings of the 2022 IEEE PES 14th Asia-Pacific Power and Energy Engineering Conference (APPEEC), Melbourne, Australia, 20–23 November 2022; pp. 1–6. [Google Scholar]
- Yin, Y.; Zhang, N.; Zhang, J.; Li, Z.; Jia, Z. Thermal optimization of single crystal fiber manufacturing based on heat loss compensation. Appl. Therm. Eng. 2022, 201, 117741. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, J.; Mao, L.; Zhao, J.; Jiang, Z.; Qu, K. ZVS Operation of Class-E Inverter Based on Secondary Side Zero Compensation Switching at Variable Coupling Coefficient in WPT. IEEE Trans. Ind. Appl. 2021, 58, 1022–1031. [Google Scholar] [CrossRef]
- Karafil, A.; Ozbay, H.; Oncu, S. Comparison of regular and irregular 32 pulse density modulation patterns for induction heating. IET Power Electron. 2021, 14, 78–89. [Google Scholar] [CrossRef]
- Lundström, F.; Frogner, K.; Andersson, M. Numerical modelling of CFRP induction heating using temperature-dependent material properties. Compos. Part Eng. 2021, 220, 108982. [Google Scholar] [CrossRef]
- Villa, J.; Navarro, D.; Dominguez, A.; Artigas, J.I.; Barragan, L.A. Vessel Recognition in Induction Heating Appliances—A Deep-Learning Approach. IEEE Access 2021, 9, 16053–16061. [Google Scholar] [CrossRef]
- Gillani, F.; Zahid, T.; Bibi, S.; Khan, R.S.U.; Bhutta, M.R.; Ghafoor, U. Parametric Optimization for Quality of Electric Discharge Machined Profile by Using Multi-Shape Electrode. Materials 2022, 15, 2205. [Google Scholar] [CrossRef]
- Maier, H.R.; Razavi, S.; Kapelan, Z.; Matott, L.S.; Kasprzyk, J.; Tolson, B.A. Introductory overview: Optimization using evolutionary algorithms and other metaheuristics. Environ. Model. Softw. 2019, 114, 195–213. [Google Scholar] [CrossRef]
- Aziz, S.; Irshad, M.; Haider, S.A.; Wu, J.; Deng, D.N.; Ahmad, S. Protection of a smart grid with the detection of cyber-malware attacks using efficient and novel machine learning models. Front. Energy Res. 2022, 10, 1102. [Google Scholar] [CrossRef]
- Ahmed, I.; Alvi, U.E.H.; Basit, A.; Khursheed, T.; Alvi, A.; Hong, K.S.; Rehan, M. A novel hybrid soft computing optimization framework for dynamic economic dispatch problem of complex non-convex contiguous constrained machines. PLoS ONE 2022, 17, e0261709. [Google Scholar] [CrossRef]
- Li, M.; Wang, G.G.; Yu, H. Sorting-based discrete artificial bee colony algorithm for solving fuzzy hybrid flow shop green scheduling problem. Mathematics 2021, 9, 2250. [Google Scholar] [CrossRef]
- Ahmed, I.; Rao, A.R.; Shah, A.; Alamzeb, E.; Khan, J.A. Performance of various metaheuristic techniques for economic dispatch problem with valve point loading effects and multiple fueling options. Adv. Electr. Eng. 2014, 2014, 765053. [Google Scholar] [CrossRef]
- Ahmed, I.; Rehan, M.; Basit, A.; Hong, K.S. Greenhouse gases emission reduction for electric power generation sector by efficient dispatching of thermal plants integrated with renewable systems. Sci. Rep. 2022, 12, 12380. [Google Scholar] [CrossRef]
- Ahmed, I.; Basit, A.; Rehan, M.; Hong, K.S. Multi-objective whale optimization approach for cost and emissions scheduling of thermal plants in energy hubs. Energy Rep. 2022, 8, 9158–9174. [Google Scholar] [CrossRef]
- Ahmed, I.; Rehan, M.; Basit, A.; Malik, S.H.; Hong, K.S. Multi-area economic emission dispatch for large-scale multi-fueled power plants contemplating inter-connected grid tie-lines power flow limitations. Energy 2022, 261, 125178. [Google Scholar] [CrossRef]
- Zhang, R.; Li, G.; Bu, S.; Aziz, S.; Qureshi, R. Data-driven cooperative trading framework for a risk-constrained wind integrated power system considering market uncertainties. Int. J. Electr. Power Energy Syst. 2023, 144, 108566. [Google Scholar] [CrossRef]
- Li, J.; An, Q.; Lei, H.; Deng, Q.; Wang, G.G. Survey of lévy flight-based metaheuristics for optimization. Mathematics 2022, 10, 2785. [Google Scholar] [CrossRef]
- Darvay, Z.; Illés, T.; Rigó, P.R. Predictor-corrector interior-point algorithm for P*(κ)-linear complementarity problems based on a new type of algebraic equivalent transformation technique. Eur. J. Oper. Res. 2022, 298, 25–35. [Google Scholar] [CrossRef]
- Qi, R.; Li, J.Q.; Wang, J.; Jin, H.; Han, Y.Y. QMOEA: A Q-learning-based multiobjective evolutionary algorithm for solving time-dependent green vehicle routing problems with time windows. Inf. Sci. 2022, 608, 178–201. [Google Scholar] [CrossRef]
- Essa, K.S.; Diab, Z.E. Magnetic data interpretation for 2D dikes by the metaheuristic bat algorithm: Sustainable development cases. Sci. Rep. 2022, 12, 14206. [Google Scholar] [CrossRef]
- Li, Q.; Li, D.; Zhao, K.; Wang, L.; Wang, K. State of health estimation of lithium-ion battery based on improved ant lion optimization and support vector regression. J. Energy Storage 2022, 50, 104215. [Google Scholar] [CrossRef]
- Wang, Y.; Li, K.; Wang, G.G. Combining key-points-based transfer learning and hybrid prediction strategies for dynamic multi-objective optimization. Mathematics 2022, 10, 2117. [Google Scholar] [CrossRef]
- Bogonikolos, N.; Metai, E.; Tsiomos, K. Centralized and Decentralized Optimization Approaches for Energy Management within the VPP. In Virtual Power Plant Solution for Future Smart Energy Communities; CRC Press: Boca Raton, FL, USA, 2022; pp. 145–154. [Google Scholar]
- Askarzadeh, A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Comput. Struct. 2016, 169, 1–12. [Google Scholar] [CrossRef]
- Zhang, R.; Aziz, S.; Farooq, M.U.; Hasan, K.N.; Mohammed, N.; Ahmad, S.; Ibadah, N. A wind energy supplier bidding strategy using combined ega-inspired hpsoifa optimizer and deep learning predictor. Energies 2021, 14, 3059. [Google Scholar] [CrossRef]
- Meng, A.; Wang, H.; Aziz, S.; Peng, J.; Jiang, H. Kalman filtering based interval state estimation for attack detection. Energy Procedia 2019, 158, 6589–6594. [Google Scholar] [CrossRef]
- Lucía, O.; Burdío, J.; Millán, I.; Acero, J.; Llorente, S. Efficiency optimization of half-bridge series resonant inverter with asymmetrical duty cycle control for domestic induction heating. In Proceedings of the 2009 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009; pp. 1–6. [Google Scholar]
- Souley, M.; Egalon, J.; Caux, S.; Pateau, O.; Lefèvre, Y.; Maussion, P. Optimization of the settings of multiphase induction heating system. IEEE Trans. Ind. Appl. 2013, 49, 2444–2450. [Google Scholar] [CrossRef]
- Omori, H.; Yamashita, H.; Nakaoka, M.; Maruhashi, T. A novel type induction-heating single-ended resonant inverter using new bipolar Darlington-Transistor. In Proceedings of the 1985 IEEE Power Electronics Specialists Conference, Toulouse, France, 24–28 June 1985; pp. 590–599. [Google Scholar]
- Zhou, Z.; Anwar, G.A.; Dong, Y. Performance-based bi-objective retrofit optimization of building portfolios considering uncertainties and environmental impacts. Buildings 2022, 12, 85. [Google Scholar] [CrossRef]
- Meraihi, Y.; Gabis, A.B.; Ramdane-Cherif, A.; Acheli, D. A comprehensive survey of Crow Search Algorithm and its applications. Artif. Intell. Rev. 2021, 54, 2669–2716. [Google Scholar] [CrossRef]
- Anwar, G.A.; Hussain, M.; Akber, M.Z.; Khan, M.A.; Khan, A.A. Sustainability-Oriented Optimization and Decision Making of Community Buildings under Seismic Hazard. Sustainability 2023, 15, 4385. [Google Scholar] [CrossRef]
- Ahmed, I.; Hasan, S.R.; Ashfaq, B.; Raza, M.; Mukhtar, S. Adaptive Swarm Intelligence-Based Optimization Approach for Smart Grids Power Dispatch. In Proceedings of the 2022 International Conference on Emerging Technologies in Electronics, Computing and Communication (ICETECC), Jamshoro, Pakistan, 7–9 December 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Mustafa, F.E.; Ahmed, I.; Basit, A.; Malik, S.H.; Mahmood, A.; Ali, P.R. A review on effective alarm management systems for industrial process control: Barriers and opportunities. Int. J. Crit. Infrastruct. Prot. 2023, 41, 1043. [Google Scholar] [CrossRef]
- Ahmed, I.; Rehan, M.; Basit, A.; Tufail, M.; Hong, K.S. A Dynamic Optimal Scheduling Strategy for Multi-Charging Scenarios of Plug-in-Electric Vehicles over a Smart Grid. IEEE Access 2023, 11, 28992–29008. [Google Scholar] [CrossRef]
- Ahmed, I.; Rehan, M.; Hong, K.S.; Basit, A. A Consensus-based Approach for Economic Dispatch considering Multiple Fueling Strategy of Electricity Production Sector over a Smart Grid. In Proceedings of the 2022 13th Asian Control Conference (ASCC), Jeju, Republic of Korea, 4–7 May 2022. [Google Scholar] [CrossRef]
- Schraft, H.A.; Bilbrey, C.; Olenski, M.; DiRienzo, N.; Montiglio, P.O.; Dornhaus, A. Injected serotonin decreases foraging aggression in black widow spiders (Latrodectus hesperus), but dopamine has no effect. Behav. Process. 2023, 204, 104802. [Google Scholar] [CrossRef] [PubMed]
- Hayyolalam, V.; Kazem, A.A.P. Black widow optimization algorithm: A novel meta-heuristic approach for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2020, 87, 103249. [Google Scholar] [CrossRef]
- McCowan, C.; Garb, J.E. Recruitment and diversification of an ecdysozoan family of neuropeptide hormones for black widow spider venom expression. Gene 2014, 536, 366–375. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aziz, S.; Lai, C.-M.; Loo, K.H. Performance of an Adaptive Optimization Paradigm for Optimal Operation of a Mono-Switch Class E Induction Heating Application. Mathematics 2023, 11, 3020. https://doi.org/10.3390/math11133020
Aziz S, Lai C-M, Loo KH. Performance of an Adaptive Optimization Paradigm for Optimal Operation of a Mono-Switch Class E Induction Heating Application. Mathematics. 2023; 11(13):3020. https://doi.org/10.3390/math11133020
Chicago/Turabian StyleAziz, Saddam, Cheung-Ming Lai, and Ka Hong Loo. 2023. "Performance of an Adaptive Optimization Paradigm for Optimal Operation of a Mono-Switch Class E Induction Heating Application" Mathematics 11, no. 13: 3020. https://doi.org/10.3390/math11133020
APA StyleAziz, S., Lai, C.-M., & Loo, K. H. (2023). Performance of an Adaptive Optimization Paradigm for Optimal Operation of a Mono-Switch Class E Induction Heating Application. Mathematics, 11(13), 3020. https://doi.org/10.3390/math11133020







