Assessing the Risk of APOE-ϵ4 on Alzheimer’s Disease Using Bayesian Additive Regression Trees
Abstract
1. Introduction
- We apply the BART method to a non-parametric AFT model for right-censored data;
- We infer the causal effect of - on AD at both population and individual levels under the potential outcome framework;
- We explore heterogeneous evidence of the causal effect and identify important variables associated with the causal effect.
2. Model and Methods
2.1. Notation
2.2. Non-parametric Accelerated Failure Time BART Model
| Algorithm 1 Bayesian algorithm for the AFT-BART model. |
Input: Data , , initial values for , , , the on the residual, , and other parameters variables .
Output: New values of , , , and , . |
2.3. Onset Probability Analysis
| Algorithm 2 Bayesian back-fitting algorithm for updating BART |
Input: Data , , initial values for , , , and other parameters/variables .
Output: New values of , , . |
2.4. Posterior Inference Statistics
| Algorithm 3 Effect Estimation of - on AD |
Input: Two data sets in total, n training samples in each. , ; , .
Output: and CI of age at onset, and CI of onset risk, evidence for heterogeneity of treatment effect . |
3. Application
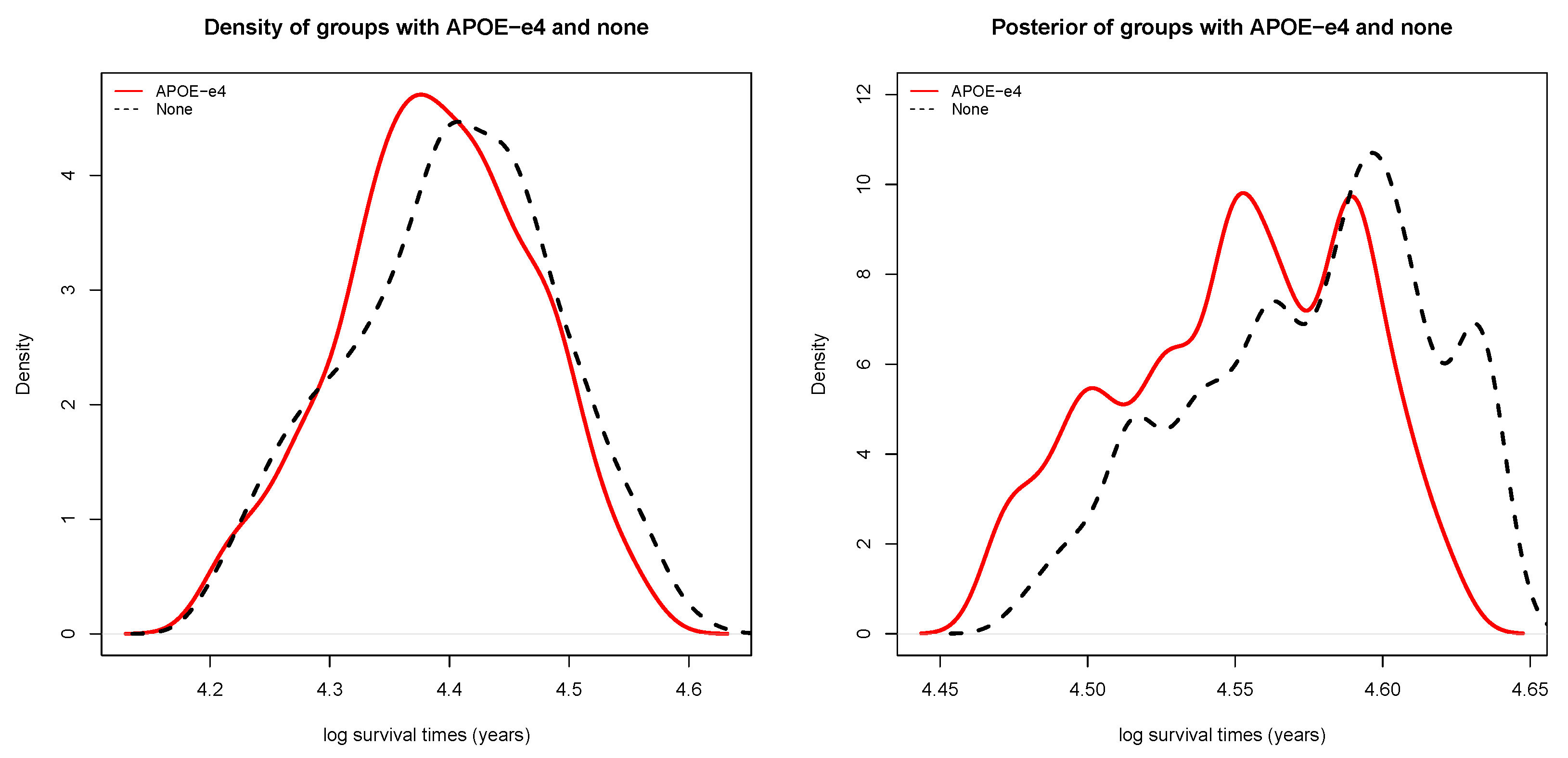
3.1. Overall Causal Effect of Patients at Onset
3.2. Distribution of Causal Effect for Patients
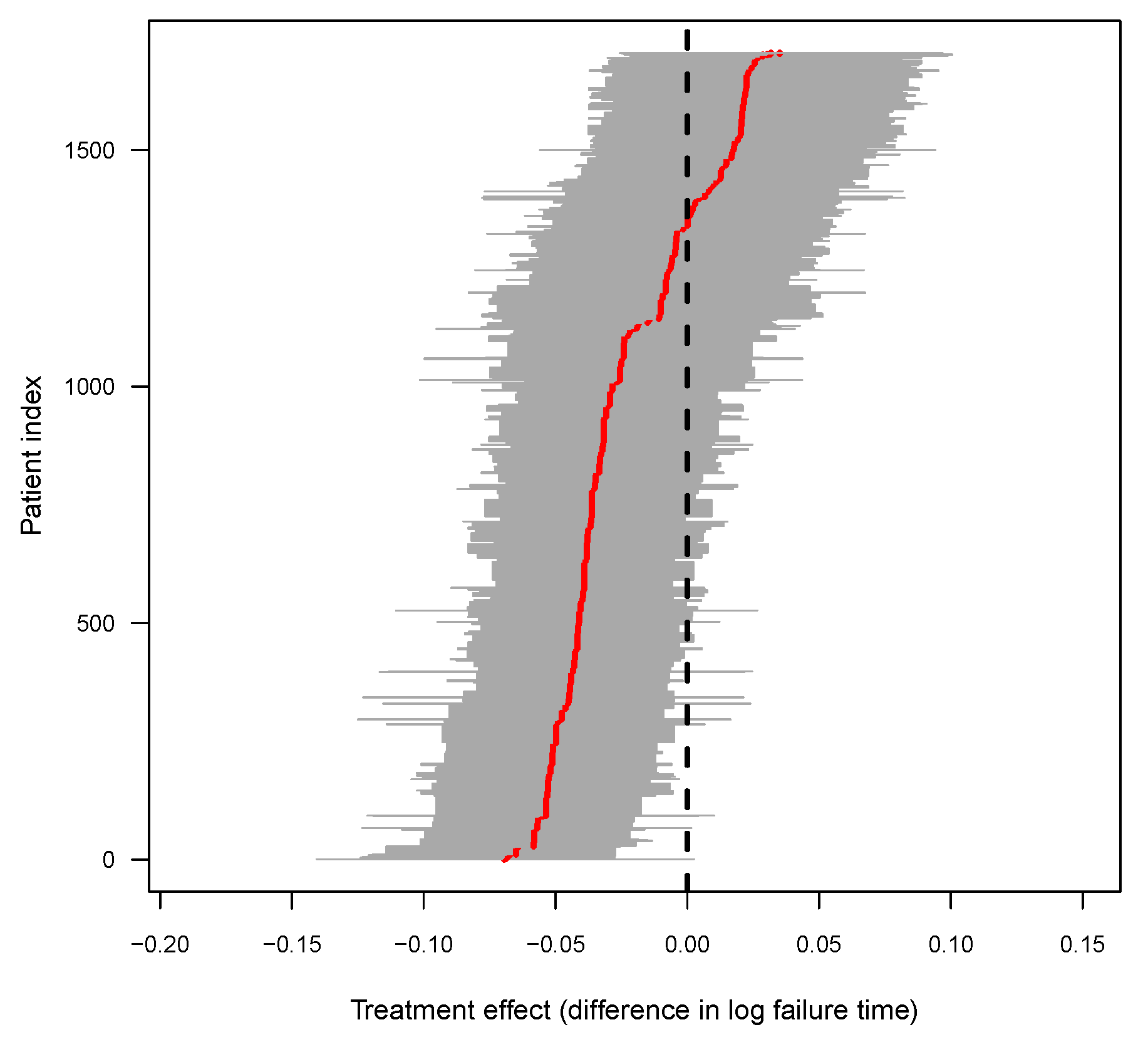
3.3. Individualized Treatment Effect
3.4. Covariate-Specific Treatment Effects
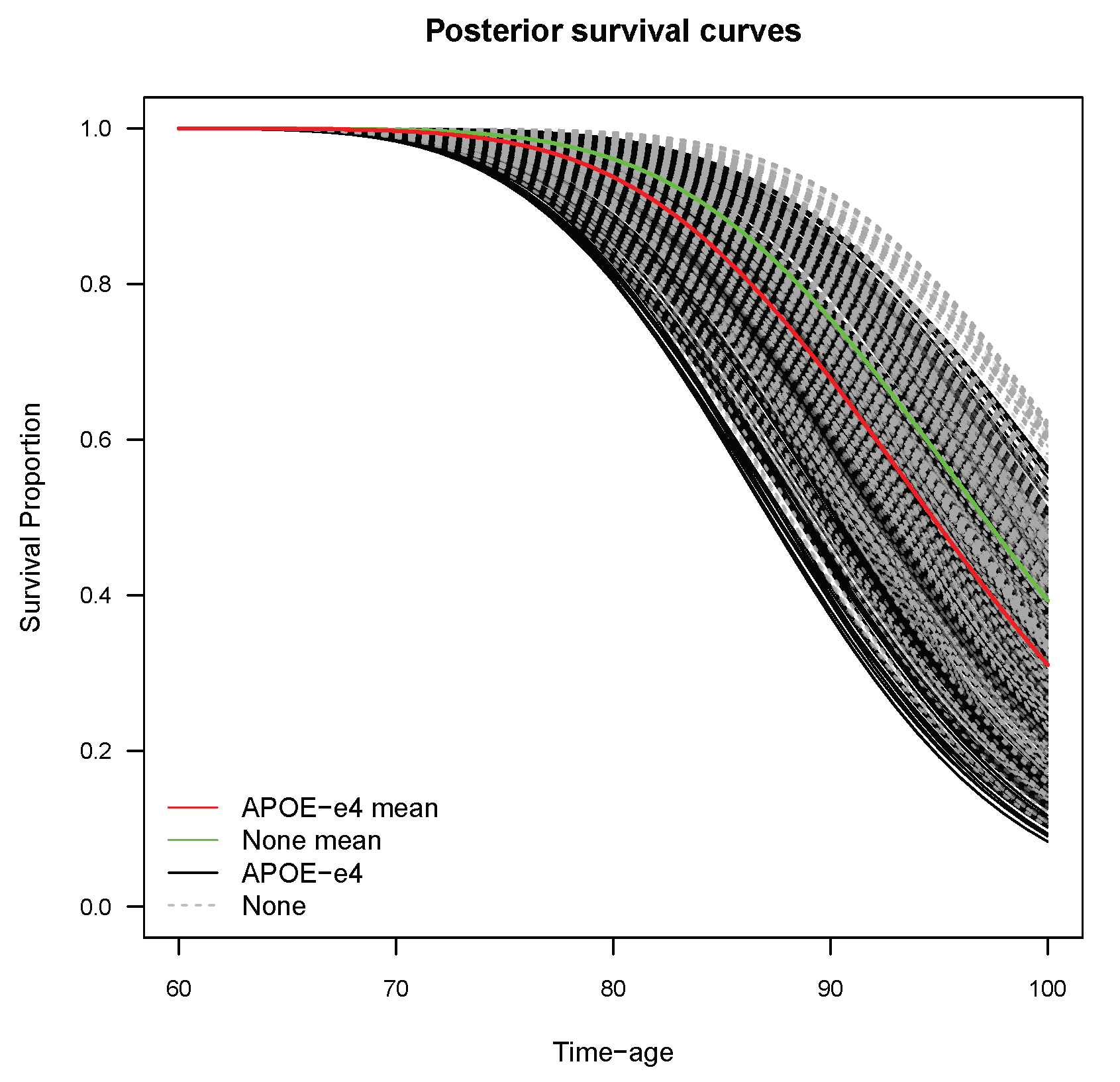
3.5. Individual Survival Curves
3.6. Evidence for Heterogeneous Treatment Effects
3.7. Important Factors
4. Discussion
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Implementation
- install.packages("devtools")
- library(devtools)
- install_github("nchenderson/AFTrees")
- library(caret)
- library(AFTrees)
- source("SurvivalProb-AD.R")
- # loading data ...
- set.seed(1)
- data <- read.csv(’AD_Data.csv’)
- censor_data <- data
- n <- nrow(censor_data)
- d <- 3
- X <- cbind(censor_data$X.1, censor_data$X.2, censor_data$X.3)
- # treatment indicators
- W <- censor_data$G_i
- Y <- censor_data$Y
- status <- censor_data$delta
- # prepare data
- colnames(X) <- colnames(X, do.NULL = FALSE, prefix = "x")
- AD_data <- data.frame(X, W = W, Y = Y, status = status)
- n <- nrow(AD_data)
- # data split
- set.seed(10)
- fold_idx <- createFolds(y = AD_data$W, k=3)
- for(i in 1:3){
- cat("\n NO.", i, "fold analysis ...\n")
- train_data <- AD_data[-fold_idx[[i]], ]
- est_data <- AD_data[fold_idx[[i]], ]
- # IndivAFT ...
- bart.tot <- IndivAFT(x.train = as.matrix(xtrain),
- y.train = train_data$Y,
- status = train_data$status,
- Trt = xtrain$W,
- x.test = as.matrix(xtest),
- ntree = 200,
- ndpost = 1000,
- nskip = 5000)
- ite <- colMeans(bart.tot$Theta.test)
- }
References
- Evans, D.A.; Funkenstein, H.H.; Albert, M.S.; Scherr, P.A.; Cook, N.R.; Chown, M.J.; Hebert, L.E.; Hennekens, C.H.; Taylor, J.O. Prevalence of Alzheimer’s disease in a community population of older persons: Higher than previously reported. JAMA 1989, 262, 2551–2556. [Google Scholar] [CrossRef]
- Corder, E.H.; Saunders, A.M.; Strittmatter, W.J.; Schmechel, D.E.; Gaskell, P.C.; Small, G.W.; Roses, A.D.; Haines, J.L.; Pericak-Vance, M.A. Gene dose of apolipoprotein e type 4 allele and the risk of alzheimer’s disease in late onset families. Science 1993, 261, 921–923. [Google Scholar] [CrossRef] [PubMed]
- Ortega-Rojas, J.; Arboleda-Bustos, C.E.; Guerrero, E.; Neira, J.; Arboleda, H. Genetic Variants and Haplotypes of TOMM40, APOE, and APOC1 are Related to the Age of Onset of Late-onset Alzheimer Disease in a Colombian Population. Alzheimer Dis. Assoc. Disord. 2022, 36, 29–35. [Google Scholar] [CrossRef] [PubMed]
- Corder, E.H.; Saunders, A.M.; Risch, N.J.; Strittmatter, W.J.; Schmechel, D.E.; Gaskell, P.C., Jr.; Rimmler, J.B.; Locke, P.A.; Conneally, P.M.; Schmader, K.E.; et al. Protective effect of apolipoprotein E type 2 allele for late onset Alzheimer’ disease. Nat. Genet. 1994, 7, 180–184. [Google Scholar] [CrossRef] [PubMed]
- Farrer, L.A.; Cupples, L.A.; Haines, J.L.; Hyman, B.; Kukull, W.A.; Mayeux, R.; Myers, R.H.; Pericak-Vance, M.A.; Risch, N.; van Duijn, C.M. Effects of age, sex and ethnicity on the association between apolipoprotein E genotype and Alzheimer’ disease. A meta analysis. APOE and Alzheimer’ disease Meta Analysis Consortium. JAMA 1997, 278, 1349–1356. [Google Scholar] [CrossRef] [PubMed]
- Gatz, M.; Reynolds, C.A.; Fratiglioni, L.; Johansson, B.; Mortimer, J.A.; Berg, S.; Fiske, A.; Pedersen, N.L. Role of genes and environments for explaining Alzheimer’ disease. Arch. Gen. Psychiatry 2006, 63, 168–174. [Google Scholar] [CrossRef] [PubMed]
- Robins, C.; Wingo, A.P.; Meigs, J.; Duong, D.; Cutler, D.J.; De Jager, P.L.; Lah, J.J.; Bennett, D.A.; Seyfried, N.T.; Wingo, T.S.; et al. Identifying novel causal genes and proteins in Alzheimer’s disease. Alzheimer’s Dement. 2020, 16, e043523. [Google Scholar] [CrossRef]
- Zhang, W.; Jiao, B.; Xiao, T.; Liu, X.; Liao, X.; Xiao, X.; Guo, L.; Yuan, Z.; Yan, X.; Tang, B.; et al. Association of rare variants in neurodegenerative genes with familial Alzheimer’s disease. Ann. Clin. Transl. Neurol. 2020, 7, 1985–1995. [Google Scholar] [CrossRef]
- Rubin, D.B. Estimating causal effects of treatments in randomized and nonrandomized studies. J. Educ. Psychol. 1974, 66, 688–701. [Google Scholar] [CrossRef]
- Nguyen, T.L.; Collins, G.S.; Landais, P.; Manach, Y.L. Counterfactual clinical prediction models could help to infer individualized treatment effects in randomized controlled trials - An illustration with the International Stroke Trial. J. Clin. Epidemiol. 2020, 125, 47–56. [Google Scholar] [CrossRef]
- Dorresteijn, J.A.N.; Visseren, F.L.J.; Ridker, P.M.; Wassink, A.M.J.; Paynter, N.P.; Steyerberg, E.W.; van der Graaf, Y.; Cook, N.R. Estimating treatment effects for individual patients based on the results of randomised clinical trials. BMJ 2011, 343, d5888. [Google Scholar] [CrossRef] [PubMed]
- Jennifer, L.H. Bayesian nonparametric modeling for causal inference. J. Comput. Graph. Stat. 2011, 20, 217–240. [Google Scholar] [CrossRef]
- Chipman, H.A.; George, E.I.; Mcculloch, R.E. BART: Bayesian additive regression trees. Ann. Appl. Stat. 2010, 4, 266–298. [Google Scholar] [CrossRef]
- Henderson, N.C.; Louis, T.A.; Rosner, G.L.; Varadhan, R. Individualized treatment effects with censored data via fully nonparametric Bayesian accelerated failure time models. Biostatistics 2018, 21, 5–68. [Google Scholar] [CrossRef]
- Bonato, V.; Baladandayuthapani, V.; Broom, B.M.; Sulman, E.P.; Aldape, K.D.; Do, K.A. Bayesian ensemble methods for survival prediction in gene expression data. Bioinformatics 2011, 27, 359–367. [Google Scholar] [CrossRef]
- Sparapani, R.A.; Logan, B.R.; Mcculloch, R.E.; Laud, P.W. Nonparametric survival analysis using bayesian additive regression trees (BART). Stat. Med. 2016, 35, 2741–2753. [Google Scholar] [CrossRef]
- Basak, P.; Linero, A.; Sinha, D.; Lipsitz, S. Semiparametric analysis of clustered interval-censored survival data using soft Bayesian additive regression trees (SBART). Biometrics 2022, 78, 880–893. [Google Scholar] [CrossRef]
- Tan, Y.V.; Roy, J. Bayesian additive regression trees and the General BART model. Stat. Med. 2019, 38, 5048–5069. [Google Scholar] [CrossRef]
- Albert, J.H.; Chib, S. Bayesian analysis of binary and polychotomous response data. Publ. Am. Stat. Assoc. 1993, 88, 669–679. [Google Scholar] [CrossRef]
- Hill, J.; Linero, A.; Murray, J. Bayesian Additive Regression Trees: A Review and Look Forward. Annu. Rev. Stat. Its Appl. 2021, 7, 251–278. [Google Scholar] [CrossRef]
- Mayeux, R.; Reitz, C.; Brickman, A.M.; Haan, M.N.; Manly, J.J.; Glymour, M.M.; Weiss, C.C.; Yaffe, K.; Middleton, L.; Hendrie, H.C.; et al. Operationalizing diagnostic criteria for Alzheimer’s disease and other age-related cognitive impairment—Part 1. Alzheimers Dement. 2011, 7, 15–34. [Google Scholar] [CrossRef] [PubMed]
- González Burchard, E.; Borrell, L.N.; Choudhry, S.; Naqvi, M.; Tsai, H.J.; Rodriguez-Santana, J.R.; Chapela, R.; Rogers, S.D.; Mei, R.; Rodriguez-Cintron, W.; et al. Latino populations: A unique opportunity for the study of race, genetics, and social environment in epidemiological research. Am. J. Public Health 2005, 95, 2161–2168. [Google Scholar]
- Tang, M.X.; Stern, Y.; Marder, K.; Bell, K.; Gurl, B.; Lantigua, R.; Andrews, H.; Feng, L.; Tycko, B.; Mayeux, R. The APOE-e4 allele and the risk of Alzheimer disease among African Americans, whites, and Hispanics. JAMA 1998, 279, 751–755. [Google Scholar] [CrossRef]
- Sparapani, R.; Spanbauer, C.; McCulloch, R. Nonparametric machine learning and efficient computation with Bayesian additive regression trees: The BART R Package. J. Stat. Softw. 2021, 97, 1–66. [Google Scholar] [CrossRef]
- Zhang, W.; Le, T.D.; Liu, L.; Zhou, Z.; Li, J. Mining heterogeneous causal effects for personalized cancer treatment. Bioinformatics 2017, 33, 2372–2378. [Google Scholar] [CrossRef] [PubMed]



| Characteristic | - Carriers | Non-Carriers | Total | |||
|---|---|---|---|---|---|---|
| Total. | 453 | 1252 | 1705 | |||
| Onset age—no. (%) | ||||||
| 60∼70 | 22 | (5) | 60 | (5) | 82 | (5) |
| 70∼80 | 192 | (42) | 429 | (34) | 621 | (36) |
| 80∼90 | 203 | (45) | 591 | (47) | 794 | (47) |
| 36 | (8) | 172 | (14) | 208 | (12) | |
| Sex—no.(%) | ||||||
| male | 155 | (34) | 432 | (35) | 587 | (34) |
| female | 298 | (66) | 820 | (65) | 1118 | (66) |
| Educational—no. (%) | ||||||
| <−0.9 | 94 | (21) | 266 | (21) | 360 | (21) |
| −0.9∼0.5 | 242 | (53) | 620 | (50) | 862 | (51) |
| 0.5∼2.0 | 117 | (26) | 366 | (29) | 483 | (28) |
| Race—no. (%) | ||||||
| Race-1 | 113 | (25) | 425 | (34) | 538 | (32) |
| Race-2 | 174 | (38) | 363 | (29) | 537 | (31) |
| Race-3 | 161 | (36) | 441 | (35) | 602 | (35) |
| Race-4 | 5 | (1) | 23 | (2) | 28 | (2) |
| Methods | Mean | ||
|---|---|---|---|
| AFT-BART | |||
| AFT | |||
| Two-AFT | |||
| SCT |
| Value | Mean | ||
|---|---|---|---|
| Risk diff | |||
| Gene prob | |||
| None prob |
| Significant | Not Significant | |||
|---|---|---|---|---|
| Characteristic | Count | Percentage (%) | Count | Percentage (%) |
| Total | 515 | 30 | 1190 | 70 |
| Sex—no. (%) | ||||
| male | 171 | 33 | 415 | 35 |
| female | 344 | 67 | 774 | 65 |
| Education—no. (%) | ||||
| <−0.9 | 116 | 23 | 244 | 21 |
| −0.9∼0.5 | 259 | 50 | 603 | 51 |
| 0.5∼2.0 | 140 | 27 | 343 | 29 |
| Race—no. (%) | ||||
| Race-1 | 138 | 27 | 400 | 34 |
| Race-2 | 176 | 34 | 361 | 30 |
| Race-3 | 191 | 37 | 411 | 35 |
| Race-4 | 10 | 2 | 18 | 2 |
| Measurement | Posterior Probabilities | - | None |
|---|---|---|---|
| Onset age | |||
| Onset probability | |||
| 0 | 0 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, Y.; Liang, B. Assessing the Risk of APOE-ϵ4 on Alzheimer’s Disease Using Bayesian Additive Regression Trees. Mathematics 2023, 11, 3019. https://doi.org/10.3390/math11133019
Xia Y, Liang B. Assessing the Risk of APOE-ϵ4 on Alzheimer’s Disease Using Bayesian Additive Regression Trees. Mathematics. 2023; 11(13):3019. https://doi.org/10.3390/math11133019
Chicago/Turabian StyleXia, Yifan, and Baosheng Liang. 2023. "Assessing the Risk of APOE-ϵ4 on Alzheimer’s Disease Using Bayesian Additive Regression Trees" Mathematics 11, no. 13: 3019. https://doi.org/10.3390/math11133019
APA StyleXia, Y., & Liang, B. (2023). Assessing the Risk of APOE-ϵ4 on Alzheimer’s Disease Using Bayesian Additive Regression Trees. Mathematics, 11(13), 3019. https://doi.org/10.3390/math11133019





