Simple and Robust Boolean Operations for Triangulated Surfaces ^†

Abstract

Boolean operations on geometric models are important in numerical simulation and serve as essential tools in the fields of computer-aided design and computer graphics. The accuracy of these operations is heavily influenced by finite precision arithmetic, a commonly employed technique in geometric calculations, which introduces numerical approximations. To ensure robustness in Boolean operations, numerical methods relying on rational numbers or geometric predicates have been developed. These methods circumvent the accumulation of rounding errors during computation, thus preserving accuracy. Nonetheless, it is worth noting that these approaches often entail more intricate operation rules and data structures, consequently leading to longer computation times. In this paper, we present a straightforward and robust method for performing Boolean operations on both closed and open triangulated surfaces. Our approach aims to eliminate errors caused by floating-point operations by relying solely on entity indexing operations, without the need for coordinate computation. By doing so, we ensure the robustness required for Boolean operations. Our method consists of two main stages: (1) Firstly, candidate triangle intersection pairs are identified using an octree data structure, and then parallel algorithms are employed to compute the intersection lines for all pairs of triangles. (2) Secondly, closed or open intersection rings, sub-surfaces, and sub-blocks are formed, which is achieved entirely by cleaning and updating the mesh topology without geometric solid coordinate computation. Furthermore, we propose a novel method based on entity indexing to differentiate between the union, subtraction, and intersection of Boolean operation results, rather than relying on inner and outer classification. We validate the effectiveness of our method through various types of Boolean operations on triangulated surfaces.

1. Introduction

Numerical modeling methods have garnered extensive usage within the engineering domain. Ensuring the precision of these models necessitates the construction of accurate geometric representations. The construction of geometric models commonly employs various techniques such as boundary representation (B-Rep) [1], wireframe representation [2], and voxel representation [3]. Among these, B-Rep is the predominant method employed for constructing geometric models, primarily relying on parametric surfaces such as non-uniform rational basis spline (NURBS) surfaces or discrete surfaces. The discrete surface represents the decomposition of a specific surface domain, with polygonal meshes, particularly triangular meshes, emerging as the favored form of representation.

In the majority of cases, triangular meshes are typically expected to maintain manifold characteristics. However, certain situations, such as dynamic collisions or extensive deformations, may lead to the loss of this property. To restore manifoldness to such meshes, mesh reconstruction becomes necessary [4]. Mesh reconstruction involves employing Boolean operations, which aim to obtain the union, subtraction, and intersection of geometric models in order to reconstruct the desired geometric models.

Boolean operations on geometric models are a core element in the field of computer-aided design and graphics, and are the basic algorithms for constructing solid geometric models. They are used in the construction industry [5], manufacturing industry [6,7], computer vision [8,9,10], graphics [11,12], and other scientific research fields [13,14]. Boolean operations are needed to combine and truncate geometric models to generate complex 3D models; therefore, Boolean operations have important research significance.

Various implementations of Boolean operations can be found in the literature, which can be broadly classified based on three main properties: the type of input data, the type of computation, and the type of output data [15]. Input models encompass a range of sources, including those generated by B-Rep based on NURBS surfaces [16,17], curved surfaces [18], and polygonal meshes [15,19,20], which can be manifold or non-manifold [21]. Most methods focus on performing Boolean operations on manifold surfaces. In terms of computation, Tayebi et al. [16] categorized them into four distinct categories: exact arithmetic methods [19], approximate arithmetic methods [22], interval computation methods, and volumetric methods [23,24]. Among these computation types, exact arithmetic methods and interval computation methods directly calculate Booleans on the initial surfaces, while the other two methods employ indirect approaches.

During the implementation of direct Boolean operations for mesh models, two crucial procedures significantly impact the effectiveness and efficiency of the overall algorithm. The first procedure involves robustly obtaining intersection lines and loops of all intersected entities in the quickest manner possible. The key aspect of this procedure lies in accurately identifying all potentially intersected entities within a short timeframe to minimize computational costs. Numerous techniques have been developed to achieve this objective, including binary space partitions (BSP) [19], octree [15], OBB trees [25], bipartite graph structure [26], and tracking neighbors [18,27]. The second key procedure pertains to correctly assembling and distinguishing the union, subtraction, and intersection of intersected models. The most straightforward approach is to perform an inside/outside classification [28], which involves examining the location of vertices or facets within the resulting volumes. Different algorithms for direct Boolean operations devise their solutions for addressing these two aforementioned challenges.

One of the primary challenges encountered in implementing Boolean operations is the utilization of finite precision arithmetic. In geometric calculations, floating-point arithmetic is commonly employed for computing point coordinates [29,30,31]. Nonetheless, owing to the finite precision nature of floating-point arithmetic, the introduction of rounding errors and loss of precision becomes inevitable [32,33]. Consequently, when calculating and comparing intersection points, small errors may arise, leading to slight deviations from the actual intersection position. These errors may accumulate and produce larger errors in subsequent calculations, thus affecting the final result.

To address this issue, researchers have employed different approaches. One method involves using rational numbers to represent point coordinates, enabling accurate representation of point locations and ensuring topological correctness of the calculation results [34]. For instance, Hu et al. [32] combined exact rational number calculations with geometric tolerance to robustly solve problems such as self-intersections and gaps in Boolean operations. Trettner et al. [35] and Nehring-Wirxel et al. [36] introduced homogeneous integer coordinates to ensure the accuracy of Boolean operations. However, it is important to note that rational number calculations involve more complex arithmetic rules and data structures, resulting in slower computations compared to floating-point arithmetic, typically by 1 to 2 orders of magnitude. Another alternative approach is to use implicit representation, where the position of a point is described based on specific properties and relationships of the geometry, rather than directly representing the coordinate values. This approach circumvents precision issues inherent in floating-point arithmetic. For example, Attene et al. [37] and Diazzi et al. [38] employ the concept of indirect geometric predicates to handle intersections, ensuring the robustness and speed of Boolean operations.

Many novel studies about Boolean operations on polygonal meshes have been presented. For example, Feito [39] introduced an efficient and robust approach for regularized Boolean operations on triangular meshes, encompassing union, subtraction, and intersection operations. This method proves particularly useful in constructing computational models with complex meshes. Gao [40] developed a rasterization-based algorithm, leveraging a many-core GPU, to perform Boolean operations on arbitrarily closed polygons. The algorithm demonstrates higher computational efficiency when handling polygons with a large number of vertices. Qin [41] proposed a fast method for triangle intersection in Boolean operations involving geometric models with triangle meshes. This method, based on the intersection distance criterion, finds utility in modeling underground space engineering. Wang [42] constructed a complex geological model using a robust Boolean operations method. The method prioritizes the robustness of geometric calculations, addressing calculation errors and data inaccuracies. Furthermore, the well-known library CGAL [43] and various open-source packages such as MeshLab [44], OpenFlipper [45], and MEPP [46], also offer robust implementations of Boolean operations. These resources provide additional tools and functionality for reliably performing Boolean operations.

When devising algorithms to address specific problems, it is often the case that faster and more efficient algorithms tend to possess higher complexity compared to slower ones. This observation holds for Boolean operations performed on triangular meshes. In this paper, we aim to strike a relative balance between efficiency and complexity in the algorithms we propose. We seek to develop a simple and robust approach for Boolean operations that also exhibits satisfactory efficiency. Here are several key highlights of our method:

(1)

An octree-based method for locating and searching possible intersecting triangle pairs is proposed, and a parallel algorithm is used to calculate the intersection lines of candidate intersecting triangle pairs.

(2)

An entity index-based method is proposed to obtain intersection rings of triangular surfaces, create sub-surfaces and sub-blocks, and distinguish between merging, intersecting, and subtracting volumes of two intersecting surfaces.

(3)

Through these techniques, we reduce computational effort, enhance robustness, and cater to a wide range of triangulated surface Boolean operations.

The rest of this paper is organized as follows. Section 2 presents the details of the proposed algorithm. Section 3 utilizes five examples to demonstrate the effectiveness of the proposed method. Section 4 discusses the advantages and limitations of the proposed method and future research directions. Section 5 summarizes the work of this paper.

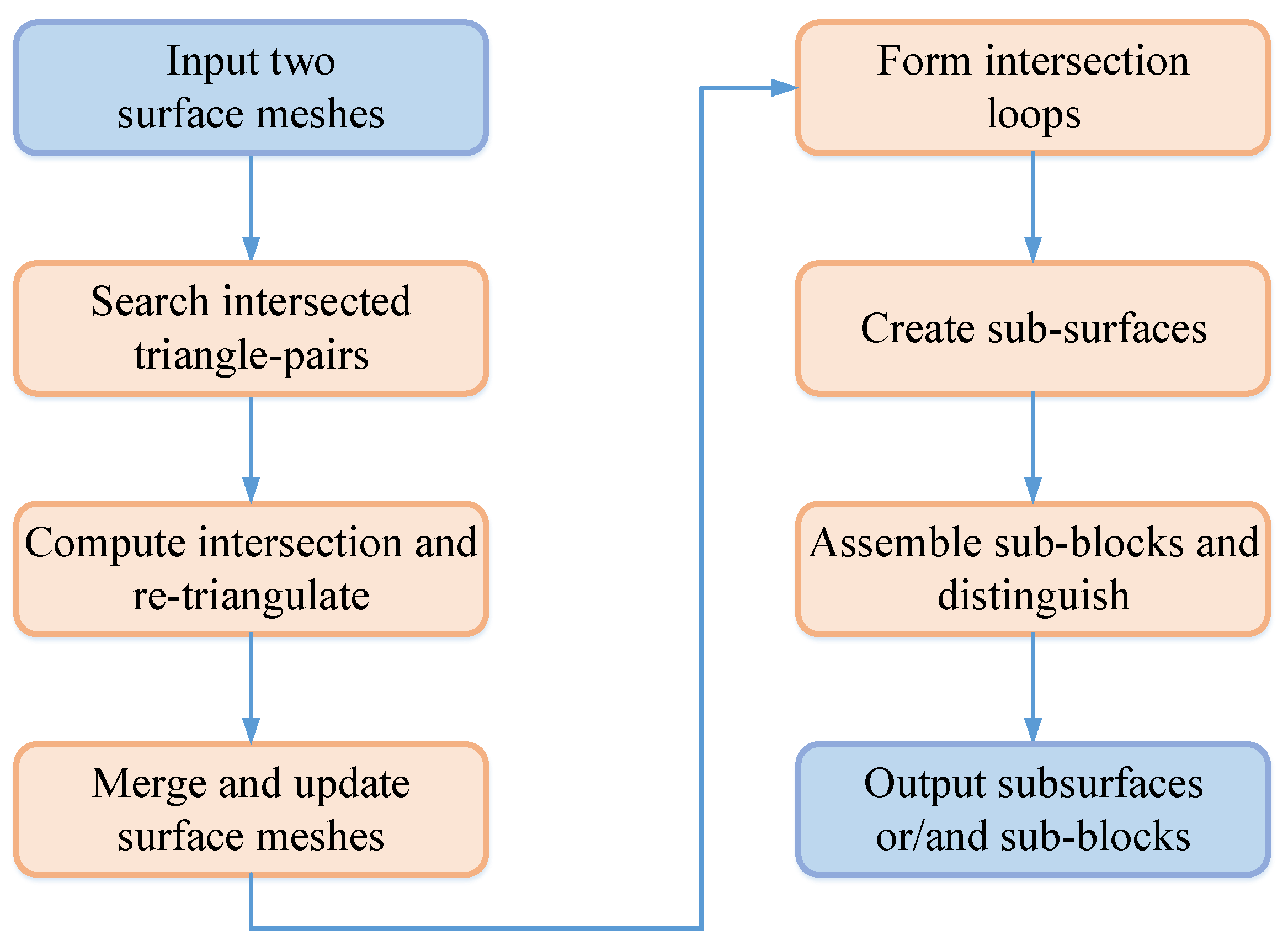
2. The Proposed Method

2.1. Overview

In the context of Boolean operations, floating-point arithmetic is commonly used for calculating intersection point coordinates. However, the finite precision of floating-point arithmetic introduces rounding errors and loss of precision. This can result in calculated results that slightly deviate from the actual intersection locations. The accumulation of errors during subsequent calculations can impact the final results. To address this issue, researchers have explored methods to reduce numerical approximation errors. Some approaches involve using rational arithmetic and geometric predicates instead of floating-point arithmetic. However, these alternative methods often involve complex arithmetic procedures and data structures.

This paper presents a straightforward and reliable approach for performing Boolean operations. The proposed method eliminates the need for geometric coordinate calculations by utilizing entity indexing, thus mitigating the accumulation of numerical approximation errors. By focusing on mesh topology elimination and updates, the method constructs intersecting rings, generates sub-surfaces, assembles blocks, and distinguishes between different types of volumes. It is specifically designed to handle Boolean operations on triangulated surfaces, including open and closed surfaces, as well as surfaces that combine both open and closed regions. It is important to note that the triangulated surfaces used in the computation should be populated and free from self-intersections.

The proposed method can be summarized into six steps, as depicted in Figure 1. These steps can be categorized into two distinct states: the first state involves computations for entity coordinates, while the second state focuses on operations related to entity indexes. In the first state, the method initially searches for intersected triangle pairs. Once identified, it calculates the intersection lines for each pair of triangles. Subsequently, re-triangulation and updates are performed on the resulting surface meshes. The second stage of the method solely operates on the indexes of entities. It involves forming intersection loops, creating sub-surfaces, and assembling and distinguishing sub-blocks based on the entity indexes.

Step 1: The first step of the proposed method involves searching for candidate intersected triangle pairs. To optimize computational efficiency, a robust and rapid search algorithm is employed to identify potentially intersected triangles. In this study, we utilize the octree structure [47], which enables efficient location and identification of these candidate pairs.

Step 2: Once the candidate intersected triangle pairs have been identified, the next step is to compute the intersection line for each pair. To achieve this, we adopt the algorithm developed by Möller [48], known for its robustness and efficiency. In scenarios where a large number of triangle pairs require intersection calculations, parallel computation techniques based on OpenMP [49] are implemented to enhance performance.

Step 3: After calculating the intersection lines, the next task is to merge and renumber all vertices, as well as update and clear the meshes. The intersection process generates new vertices, while the intersected triangles undergo re-triangulation. To ensure a valid topology, all vertices are merged and renumbered, and all triangles are updated accordingly. This step guarantees the maintenance of a consistent and accurate mesh representation.

Step 4: The fourth step of the proposed method involves connecting the computed intersection lines into closed or open loops. After computing the intersections for each pair of triangles, a set of discrete edges is obtained. These edges need to be connected to form closed or open-oriented loops. If there is no closed loop present on an intersected surface, it indicates that no closed block bounded by triangular facets will be formed.

Step 5: The next step is to obtain sub-surfaces based on the closed loops. A sub-surface comprises the closed loop and all of its incident triangles. The edges of a closed loop are designated as the advancing front, and a new surface is “grown” based on the topology until the number of faces in the sub-surface ceases to increase.

Step 6: Finally, the method proceeds to assemble and distinguish sub-blocks. Sub-blocks can be easily created by assembling related sub-surfaces. Additionally, the boundary closed loops generated in Step 4 can be utilized to represent sub-surfaces. Assembling and distinguishing operations are performed based on these boundary-closed loops.

2.2. Data Structure and Notation

In this section, we introduce notations for various geometric entities and define additional properties, such as direction, for some of them.

Definition 1.

Directed edge is a segment with a specified direction. It consists of two vertices, where the first vertex is referred to as the head and the second vertex as the tail.

Definition 2.

Orientated loop is a collection of connected directed edges that can be either closed or open. It can also be represented as an ordered set of vertices. If two oriented loops have the same vertices but in opposite order, they are defined as twins.

Definition 3.

Normalized face is a coplanar polygon with a defined normal. In the context of this paper, a normalized face refers to either a triangle or a polygon.

To facilitate the description of our algorithm in the subsequent sections, we adopt several common geometric objects and allocate arrays to store the corresponding geometric entities.

The “m_aVerts” array comprises vertices representing the intersections and mergers of triangle pairs. It is necessary to verify and renumber all the vertices in this array.

The “m_aEdges” array consists of edges that represent the intersection lines resulting from the intersection of all triangle pairs. The head and tail attributes of each edge in this array are updated following the merging and renumbering of all vertices.

The “m_aLoops” array stores closed or open intersection loops. The ordered set of vertices within each loop must have their IDs updated to reflect the changes.

The “m_aPolys” array contains polygons that are the outcome of intersecting triangle pairs. Each polygon in this array will be decomposed into new triangles through polygon triangulation.

The “m_aTrgls” array is composed of triangles that have been updated through the intersection and merging operations. These triangles originate from two sources: (1) the original triangles that do not intersect with others, and (2) the newly generated triangles resulting from re-triangulating the polygons obtained from intersecting triangle pairs.

The “m_aSurfs” array contains surfaces representing sub-surfaces that have been created. Each sub-surface in this array is associated with one or more boundary sub-loops, which are prepared for the assembly of sub-blocks.

The “m_aBlocks” array stores assembled sub-blocks, encompassing the collected sub-surfaces.

2.3. Details of the Proposed Method

In this section, we will provide a comprehensive and detailed description of the six steps involved in our approach. Each step will be discussed individually, highlighting its purpose and methodology. Furthermore, we will explain several procedures, including the clearing of the triangular mesh and the creation of sub-surfaces and sub-blocks. To facilitate understanding and implementation, we will accompany these procedures with pseudocode examples, illustrating the specific algorithms and logic employed.

2.3.1. Searching Intersected Triangle Pairs

Before calculating the intersection between any pair of triangles, it is essential to identify which pairs have the potential to intersect. One straightforward but inefficient approach is to conduct a bounding box intersection test between each triangle on a surface and every other triangle. To enhance efficiency, we employ an octree data structure to locate and identify candidate triangle pairs that may intersect.

Given two surface meshes, S${}_A$ and S${}_B$, compute their smallest AABBs denoted as Box${}_A$ and Box${}_B$, respectively, and then calculate the intersection Box${}_{AB}$ of Box${}_A$ and Box${}_B$ (Box${}_{AB}$ = Box${}_A$∩Box${}_B$); check each triangle of S${}_A$ and S${}_B$ whether it is outside of the volume Box${}_{AB}$, and divide S${}_A$ and S${}_B$ into two sub-arrays where S${}_{Aout}$ + S${}_{Ain}$ = S${}_A$, S${}_{Bout}$ + S${}_{Bin}$ = S${}_B$; and then extend the volume Box${}_{AB}$ into a cube to be an AABB for the triangles from both S${}_{Ain}$ and S${}_{Bin}$ (S${}_{Ain}$∪S${}_{Bin}$).

To construct the octree, we begin with a bounding cube as the root node. This root node is then recursively subdivided into eight octants, creating a hierarchical structure. At each interior node of the octree, we keep track of the number of triangles that intersect it from two different sets, denoted as N${}_a$ and N${}_b$, corresponding to the triangles from S${}_{Ain}$ and S${}_{Bin}$, respectively. The recursion process continues until certain termination conditions are met, at which point a node becomes a leaf node. The termination conditions are as follows:

(1)

The depth of the node reaches a user-specified maximum depth;

(2)

Both N${}_a$ and N${}_b$ less than a given allowable number;

(3)

N${}_a$ or N${}_b$ is zero.

To determine whether a triangle from either S${}_{Ain}$ or S${}_{Bin}$ is contained within a node of the octree, a straightforward approach is to conduct an intersection test between the bounding box of the triangle and the node of the octree. If the bounding box and the node intersect, it can be inferred that the triangle is inside the node. It is important to note that a triangle may intersect multiple nodes within the octree. To mitigate the computational cost of calculating the bounding box for each triangle individually, we optimize the process by precomputing the bounding boxes for all triangles in S${}_{Ain}$ and S${}_{Bin}$ beforehand. By calculating these bounding boxes in advance, we can reuse them when necessary, eliminating the need for repeated computations during the intersection tests.

2.3.2. Intersecting of Triangles and Re-Triangulating

The intersection of triangles is a task that has been extensively studied, and Möller [48] has developed a robust and efficient algorithm along with its corresponding code for this purpose. In this paper, we directly utilize Möller’s work as our chosen method for performing triangle intersection calculations.

Given the scenario where a substantial number of triangle pairs require intersection calculations, it becomes crucial to employ an effective parallel strategy. In this step, the intersection calculation for each pair of triangles is independent, enabling us to utilize the OpenMP API [49] to parallelize the computations.

  #pragma omp parallel for

for each pair of triangles $p_i$ {

  Calculate the intersection of $p_i$;

  Save the intersection edge of $p_i$ if it exists;

}

Once the intersection calculation for all triangle pairs is completed, it is common for individual intersected triangles to contain multiple intersection edges within them. This occurs because a triangle may intersect with several other triangles, resulting in the division of the original triangle into multiple sub-polygons along these intersection edges. To generate these sub-polygonal faces for a given triangle, denoted as $T_i$, we follow a series of steps. First, we identify all the intersection edges associated with $T_i$. Then, we connect these edges to form one or more open or closed loops. Finally, we iteratively divide the newly formed polygons using any remaining unused intersection loops until all loops of $T_i$ are utilized. This process is illustrated in Figure 2.

As mentioned above, the resulting polygonal faces from the intersection of triangles need to be decomposed into triangles for easier manipulation of the surface mesh in subsequent steps. This can be achieved using an ear-clipping algorithm [50]. However, before applying the ear-clipping algorithm, it is necessary to perform some preprocessing steps due to its validity for planar and counter-clockwise polygons. The partitioning of a polygon P into triangles can be obtained through the following three steps:

Step 1: Compute the local coordinate system of P and transform P into its local representation, denoted as $P^{\prime }$;

Step 2: Determine the orientation of $P^{\prime }$ by evaluating the order of its vertices as either counterclockwise (CCW) or clockwise (CW). If the orientation is CW, reverse the order of vertices in $P^{\prime }$ to ensure it is CCW;

Step 3: Generate the polygon triangulation $T^{\prime }$ of $P^{\prime }$ via ear-clipping and then directly obtain T for P according to $P^{\prime }$, because the topologies of T and $T^{\prime }$ are exactly the same while the coordinates of vertices differ (Figure 2d).

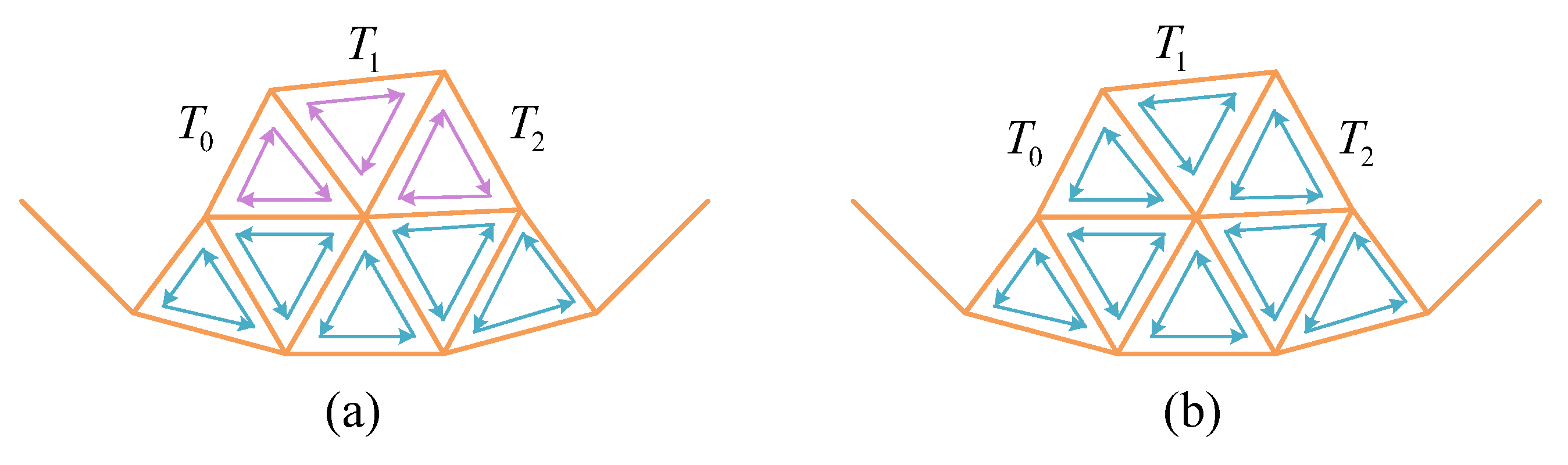
2.3.3. Merging and Updating

After intersecting pairs of triangles, new vertices are generated, and the original intersected triangles are replaced with re-triangulated triangles. To ensure a valid topology for subsequent operations, the surfaces need to be merged and updated. The following steps are performed to achieve this:

(1)

All vertices are merged and renumbered;

(2)

The vertex indexes are updated for each triangle and loop;

(3)

Each triangle and loop are checked to identify if there are any vertices with the same index;

(4)

The newly generated triangles are reversed (Figure 3).

After the clearing process, several requirements need to be satisfied: there should be no duplicate vertices, no degenerate triangles, no identical vertices within a loop, and no duplicate edges.

Apart from merging and renumbering vertices, clearing the topology is essential for subsequent procedures such as connecting loops and creating sub-surfaces. In Figure 3, (a) represents the original triangular meshes with three invalid faces that share edges with their adjacent triangles, while (b) shows the cleared version after addressing these issues.

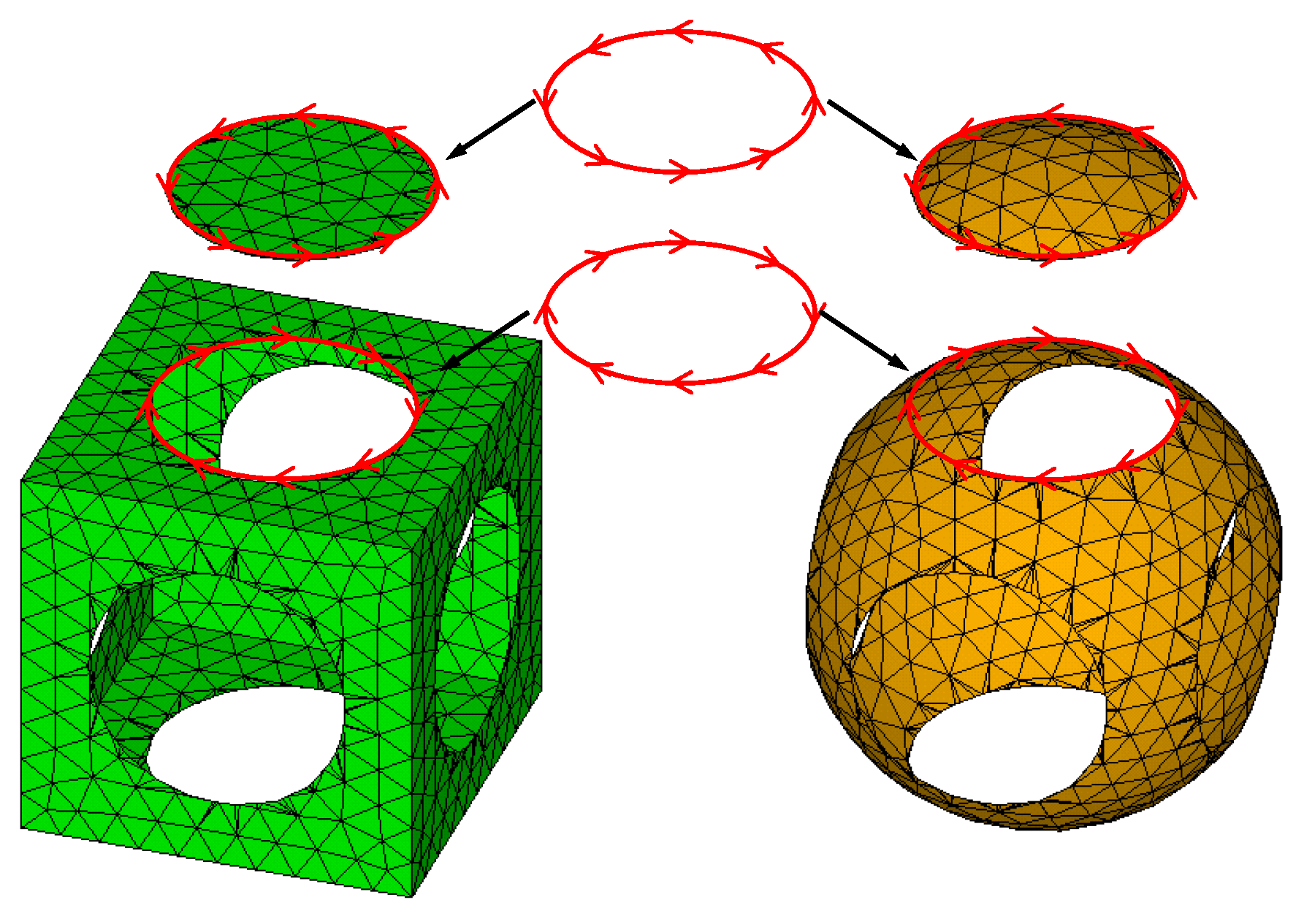
2.3.4. Forming Intersection Loops

As defined in Section 2.2, Oriented loop is a set of connected directed edges, which can be closed as a cycle or open as a polyline. An open loop is an intersection loop in which either the first or the last vertex is shared only by one intersection edge, while each of the other vertices is shared by two edges. A close loop is an intersection loop in which each vertex is shared by at least two intersection edges. We classify the closed intersection loops into hard closed and soft closed:

Hard closed loop is characterized by each vertex being shared exclusively by two intersection edges. For example, Figure 4a exhibits six instances of hard closed loops.

Soft closed loop is identified by the first and last vertices being shared by more than two intersection edges, while each intermediate vertex is shared by two edges. Figure 4b illustrates four occurrences of soft closed loops.

Only closed intersection loops, which include both hard closed and soft closed loops, are eligible for the creation of sub-surfaces, as mentioned in Section 2.3.5. Loops, whether closed or open, can be formed by directly connecting the head of one edge with the tail of another edge, or vice versa. The process of assembling these loops continues until no more connected edges can be found. The resulting closed or open loops can be visualized as a collection of edges and can also be represented as an ordered set of vertices. When working with an original surface, multiple loops may be present. To determine whether a loop is closed or open, one simply needs to compare the head of the first edge with the tail of the last edge.

2.3.5. Creating Sub-Surfaces

Assuming that there is at least one closed loop in the original surface, the process of creating sub-surfaces begins by selecting a closed loop. Each sub-surface consists of the closed loop and the triangles that are incident to it. The edges of the closed loop are designated as the advancing edge front, which gradually expands or “grows” until the number of faces in the sub-surface no longer increases. The growth of the advancing edge front is guided by the topology of the updated surface. To determine the next face in the growing process, a search is performed among the incident faces of the advancing front edge. After each growth step, all advancing front edges must be updated to prepare for the subsequent expansion until a complete sub-surface is formed. The growing process continues until all closed loops have been utilized, at which point the growth terminates (refer to Algorithm 1).

Algorithm 1 Create Sub-surfaces from Closed Loops

Input:  A set of closed loops stored in m_aLoops and a triangular surface S Output:  A set of sub-surfaces stored in m_aSurfs  1: for loop $L_i$ in m_aLoops do  2:    create a new empty surface $newSf$;  3:    copy and add $L_i$ as a boundary loop into $newSf$;  4:    while the number of triangles of $newSf$ increases do  5:      for edge $e_j$ of loop $L_i$ do  6:         let $egHead$ and $egTail$ be the first and second vertices of $e_j$;  7:         for triangle $T_k$ in m_aTrgls do  8:           let nID[3] denote the 3 vertices of $T_k$;  9:           if (nID[1] = $egHead$ and nID[0] = $egTail$) or (nID[2] = $egHead$ and nID[1] = $egTail$) or (nID[0] = $egHead$ and nID[2] = $egTail$) then 10:              add 3 edges of $T_k$ into loop $L_i$ as new advancing front; 11:              add triangle $T_k$ into $newSf$; break; 12:           end if 13:         end for 14:         update loop $L_i$ by removing any pair of opposite edges; 15:      end for 16:    end while 17:    add $newSf$ into m_aSurfs; 18: end for

In general, an original surface can give rise to multiple sub-surfaces, which can be classified as either public or private.

Definition 4.

Private sub-surface: a sub-surface is considered private when it contains only one closed loop. In this case, the sub-surface is exclusively owned by that loop.

Definition 5.

Public sub-surface: a sub-surface is deemed public when it contains more than one closed loop. In such instances, multiple closed loops share the same sub-surface. It is worth noting that if a public sub-surface is generated from an original open surface, it must also include a closed boundary loop in addition to the intersecting closed loop(s).

Definition 6.

Sub-surface owner: the sub-surface owner refers to either the single closed loop that possesses a private sub-surface or the collection of multiple closed loops that share a public sub-surface.

Remark 1.

There can be no more than one public sub-surface present.

Remark 2.

There is always at least one private sub-surface in the overall structure.

2.3.6. Assembling and Distinguishing Sub-Blocks

(1)

Assembling All Possible Sub-Blocks

After intersecting two original surfaces, S${}_A$ and S${}_B$, a set of sub-surfaces is obtained. Let us consider a sub-surface, $SS$, from the original surface S${}_A$, which consists of n closed loops denoted as $L_i$ ($i=0,\dots ,n-1$). This implies that there are n owners who share the sub-surface SS. If we can identify n private surfaces from the original surface S${}_B$, with each private sub-surface solely owned by the corresponding closed-loop $L_i$, it becomes possible to assemble a sub-block. This sub-block comprises the sub-surface $SS$ from surface S${}_A$ and the n private surfaces from surface S${}_B$. The process of assembling sub-blocks is detailed in Algorithm 2. Furthermore, several conclusions can be drawn regarding the assembly of sub-blocks.

Algorithm 2 Create Sub-blocks From Sub-surfaces

Input:  A set of sub-surfaces stored in m_aSurfs Output:  A set of sub-blocks stored in m_aBlocks  1: while all sub-surfaces in m_aSurfs are not tested completely do  2:    find a untested sub-surface $startSS$ as the starting one;  3:    set $startSS$ as being tested;  4:    if $startSS$ is a public sub-surface with boundary loop(s) then  5:      continue;  6:    end if  7:    create a new empty sub-block $newBlk$;  8:    add $startSS$ into $newBlk$;  9:    for the $i^{th}$ closed loop $L_i$ in $startSS$ do 10:      for each sub-surface $S{S}_i$ in m_aSurfs do 11:         if ($S{S}_i$ is untested and also owned only by $L_i$) and ($S{S}_i$ and $startSS$ not come from same surface) then 12:           set $S{S}_i$ as being tested; 13:           add $S{S}_i$ into $newBlk$; break; 14:         end if 15:      end for 16:    end for 17:    add $newBlk$ into m_aBlocks; 18: end while.

Remark 3.

A private sub-surface can be utilized either once or twice in the process of assembling sub-blocks.

Remark 4.

A public sub-surface, which does not include a boundary loop, can also be employed once or twice in the assembly of sub-blocks.

Remark 5.

A public sub-surface that includes a boundary loop, generated from an original open surface, cannot be used to assemble sub-blocks. This is due to the inability to find a sub-surface that is also owned by the boundary closed loop in the intersected original surface.

(2)

Distinguishing

Based on Algorithm 2, we can generate all possible sub-blocks. Now, the question arises: given two blocks B${}_A$ and B${}_B$ (Figure 5a), how do we differentiate between their union, intersection, and subtraction? To address this problem, we have developed a novel and straightforward method, which is outlined in Figure 6. The specific flow of this method is presented to provide a solution.

Step 1: To determine the non-subtraction (union and intersection) between blocks, we rely on the orientation of closed intersection loops during the assembly of sub-blocks.

However, at this stage, we can only identify whether sub-blocks are subtracted; we cannot clearly distinguish whether they form a union or intersection.

Let us consider a sub-block SB, which consists of a total of n closed loops denoted as $L_i$ ($i=0,\dots ,n-1$). Each closed loop $L_i$ has two opposing versions: $L_i^{+}$ represents the loop with its original orientation, while $L_i^{-}$ represents the loop with the same vertices as $L_i^{+}$ but with the opposite orientation (as illustrated in Figure 7). These two loops, $L_i^{+}$ and $L_i^{-}$, are referred to as twins in Section 2.2. The loop $L_i$ either owns or shares two sub-surfaces, denoted as SS${}_{L_i}^A$ and SS${}_{L_i}^B$, originating from two different original surfaces, S${}_A$ and S${}_B$, respectively. To determine the sub-block SB, we can apply the following conditions:

Case 1: if SS${}_{L_i}^A$ and SS${}_{L_i}^B$ are owned or shared by $L_i^{+}$ and $L_i^{-}$, respectively, or if SS${}_{L_i}^A$ and SS${}_{L_i}^B$ are owned or shared by $L_i^{-}$ and $L_i^{+}$, respectively, then the sub-block SB is union or intersection volume.

Case 2: if both SS${}_{L_i}^A$ and SS${}_{L_i}^B$ are owned or shared by $L_i^{+}$, or if both SS${}_{L_i}^A$ and SS${}_{L_i}^B$ are owned or shared by $L_i^{-}$, then the sub-block SB is subtraction volume.

Step 2: To distinguish between the union and intersection operations, we follow the following approach.

As previously mentioned, we denote (B${}_A$∪B${}_B$), (B${}_A$∩B${}_B$), (B${}_A$−B${}_B$), and (B${}_B$−B${}_A$) as the union, intersection, and subtraction operations between a pair of blocks B${}_A$ and B${}_B$. It is evident that the relationship (B${}_A$∩B${}_B$) ≤ (B${}_A$∪B${}_B$) holds. The exception to this relationship occurs only when B${}_A$ and B${}_B$ coincide, which can be identified and addressed separately, and thus does not need to be considered at this stage. Consequently, we conclude that (B${}_A$∩B${}_B$) < (B${}_A$∪B${}_B$). The aforementioned result establishes that the intersection operation between two blocks is consistently smaller in size than their corresponding union operation. Furthermore, it indicates that the minimum coordinates of all vertices within the intersection are never smaller than those of the union, while the maximum coordinates of the intersection are never larger than those of the union. Consequently, the minimum and maximum coordinates of the vertices obtained from both the union and intersection are precisely equal to those derived solely from the union.

Thus, we can distinguish the union and the intersection by following three sub-procedures.

Step 2-1: By sorting all vertices, we can easily obtain the maximum and minimum coordinates of both the intersection and union, denoted as $N_{max}^{Total}$ and $N_{min}^{Total}$, respectively, (Figure 6). These coordinates can be stored during the merging and updating of vertices.

Step 2-2: To identify the union volume, we compare the maximum and minimum coordinates of each candidate union sub-block, denoted as $N_{max}^{SB}$ and $N_{min}^{SB}$, respectively (Figure 6). If these coordinates match the values obtained in Step 2-1, then it signifies the presence of only union volume (Figure 5c).

Step 2-3: The remaining sub-block(s) are considered to be the intersection volume (Figure 5c).

It is important to note that these procedures are not applicable in special cases where mesh B${}_A$ is contained within B${}_B$ or vice versa. These exceptional cases should be handled separately during the preprocessing stage.

Step 3: Determine all subtractions

After classifying the union and intersection, the subtractions (B${}_A$−B${}_B$) and (B${}_B$−B${}_A$) can be easily determined: define all sub-surfaces that comprise the only union volume as outer ones, while those from the intersection volume(s) as inner, for each undistinguished sub-block,

(1) Identify the sub-surfaces within the sub-block. If any of the sub-surfaces belong to the original block B${}_A$ and are classified as outer surfaces, then the sub-block is considered as part of the (B${}_A$−B${}_B$) subtraction operation. Otherwise, if the sub-surfaces belong to the original block B${}_B$ and are classified as outer surfaces, the sub-block is considered as part of the (B${}_B$−B${}_A$) subtraction operation.

(2) Similarly, if any of the sub-surfaces within the sub-block are classified as inner surfaces (part of the intersection volume), and they belong to the original block B${}_A$, then the sub-block is considered as part of the (B${}_B$−B${}_A$) subtraction operation. Conversely, if the inner sub-surface(s) belong to the original block B${}_B$, the sub-block is considered as part of the (B${}_A$−B${}_B$) subtraction operation.

After distinguishing the subtractions, all triangles within the inner sub-surfaces of the subtraction operations are reversed. This ensures a valid topology for the entire mesh model and ensures that the normals of all facets are oriented outward.

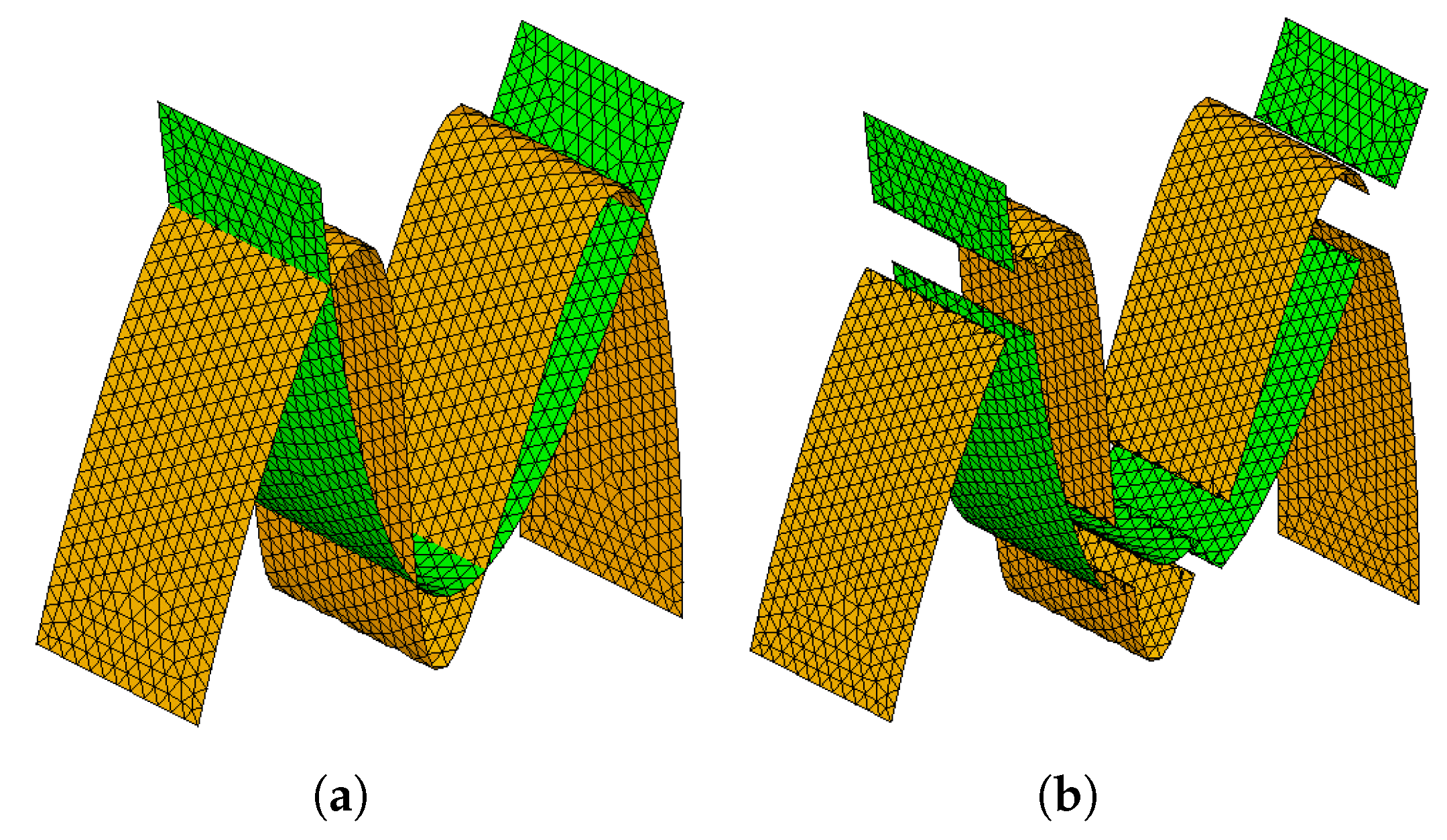
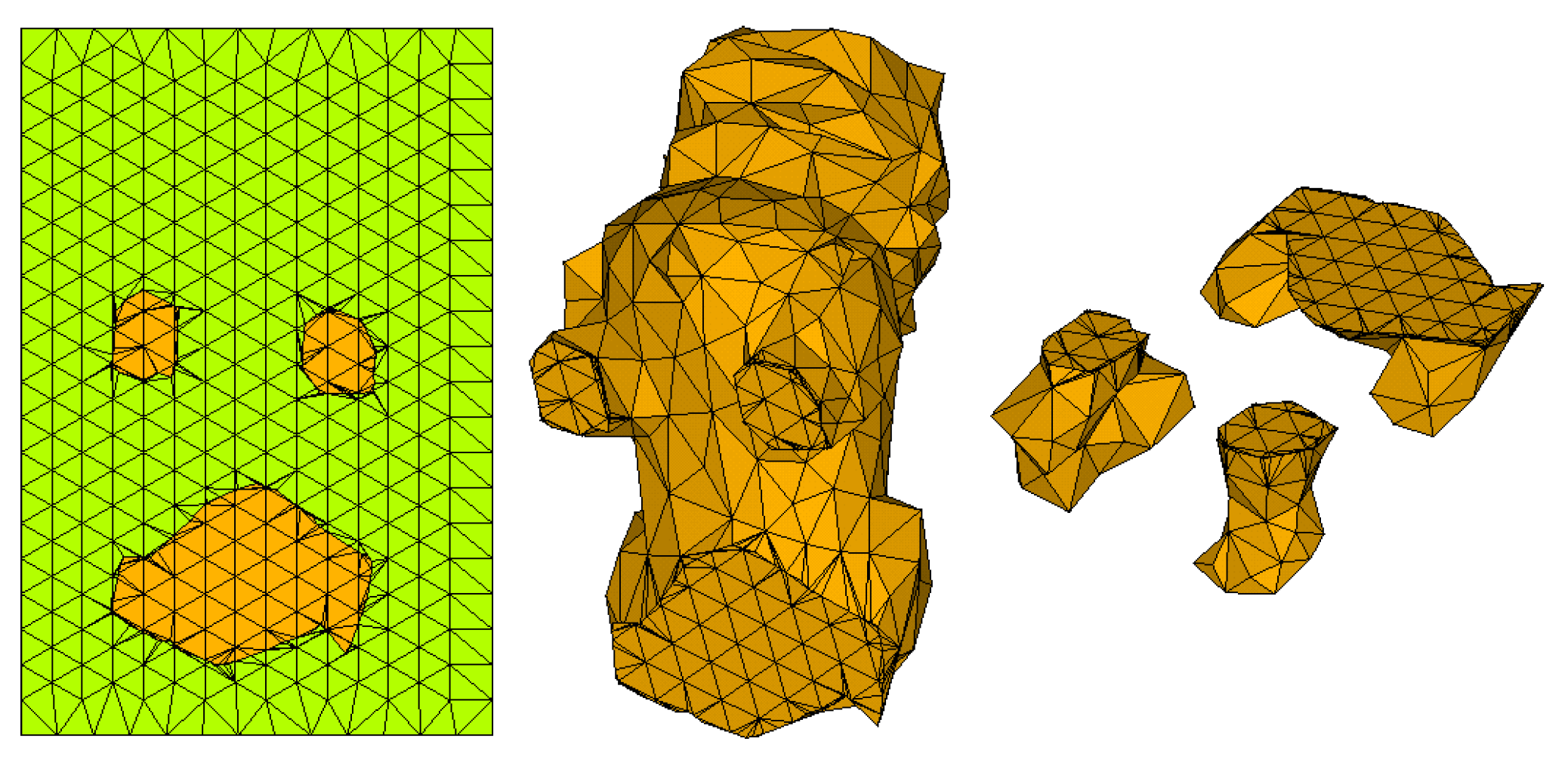
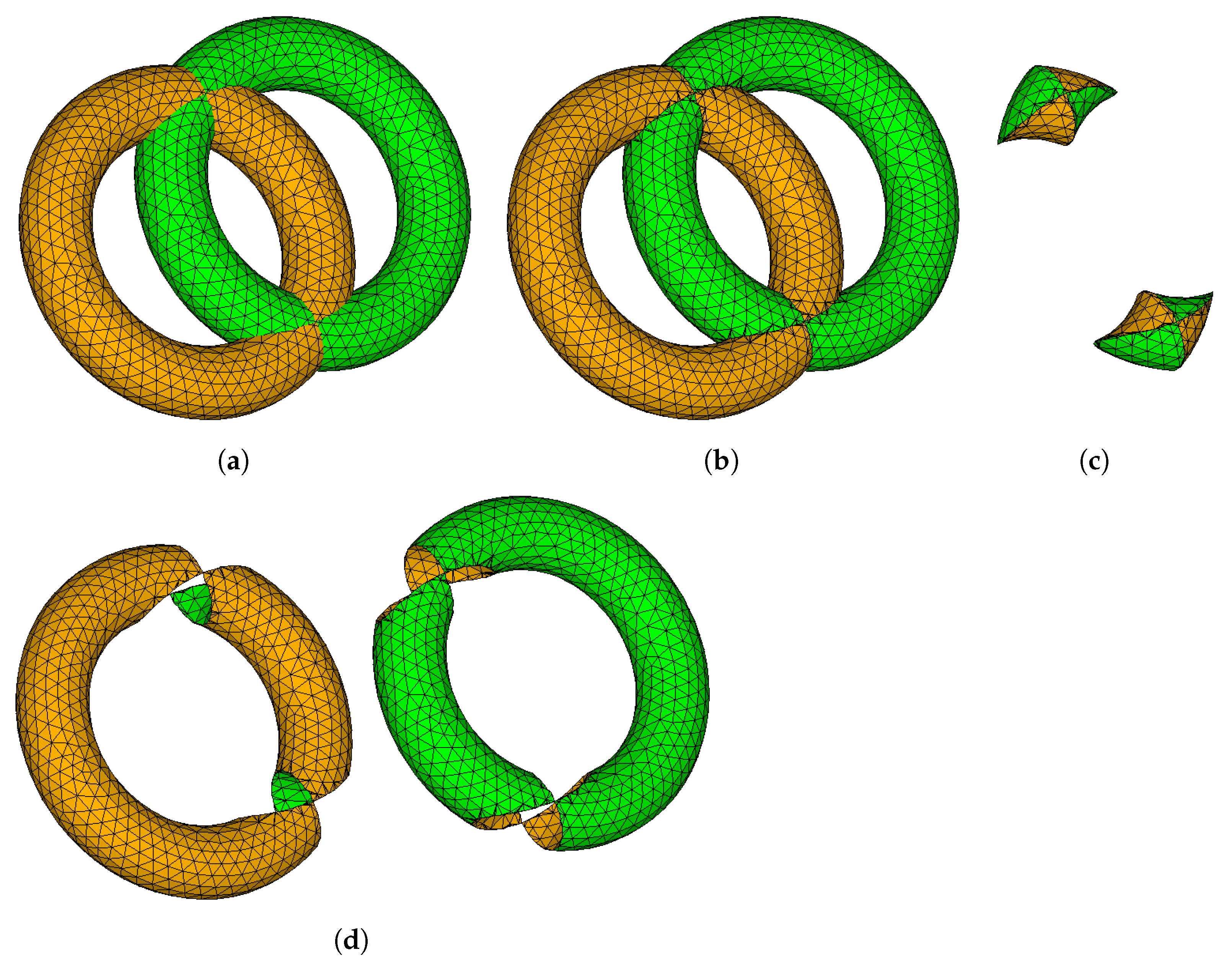
3. Results

As outlined in Section 1, our objective is to execute Boolean operations on a pair of surfaces. These surfaces can either be open or closed. In this section, we demonstrate the Boolean operations for various pairs of surfaces, encompassing open-and-open scenarios (Figure 8), open-and-closed scenarios (Figure 9 and Figure 10), as well as closed-and-closed scenarios (Figure 11 and Figure 12). Through these examples, we aim to showcase the effectiveness of our approach.

The intersection of a pair of open triangulated surfaces is tested in Figure 8. Before considering the boundary outer loops of the original surfaces, four open intersection loops can be formed for each surface, and then the boundary loop is divided into five closed loops; therefore, five corresponding sub-surfaces can be created for each surface.

To evaluate the Boolean operations between an open surface and a closed surface, we conduct a division of a planar meshed surface using a triangulated Chinese lion model. The Chinese lion model (Figure 9) is sourced from http://shapes.aim-at-shape.net/, accessed on 1 June 2013. As depicted in Figure 9, three closed loops can be identified in both the Chinese lion and the surface. Figure 10 illustrates the division results, where four sub-surfaces are generated for each original surface, and the lion model is partitioned into four sub-blocks. These outcomes demonstrate the successful execution of the Boolean operations and the creation of distinct sub-surfaces and sub-blocks.

To test the Boolean operations on two closed surfaces, we provide examples of such operations using a pair of cylinders (Figure 11) and a pair of toruses (Figure 12). When computing the intersection edges of triangles for the cylinders, we observe the formation of four soft closed intersection loops (as defined in Section 2.3.4). These soft closed loops exhibit the characteristic that both the first and last vertices are shared by four intersection edges. Utilizing these soft closed loops, we can create four sub-surfaces for each cylinder and subsequently assemble and distinguish sub-blocks, including union, intersection, and subtractions, based on the sub-surfaces. Figure 12 illustrates the Boolean operations performed on a pair of toruses with identical inner radii. The process is similar to that of the cylinders but slightly more intricate. In these examples, only soft closed loops are generated. However, Figure 5 provides a simple example where hard closed loops are obtained.

4. Discussion

4.1. Comparative Analysis with Other Methods

4.1.1. Advantages of the Proposed Algorithm

This paper presents a straightforward and reliable algorithm for conducting Boolean operations on manifold triangulated surfaces, while the algorithm does not account for self-intersecting meshes, it demonstrates its effectiveness in handling diverse types of triangulated surfaces. The proposed algorithm offers several notable advantages, including simplicity, improved computational efficiency, and enhanced robustness. It introduces a dependable approach for executing Boolean operations and finds applicability across various scenarios involving triangulated surfaces. The subsequent analysis provides a comprehensive comparison highlighting the specific improvements achieved by the proposed algorithm in contrast to commonly employed algorithms.

(1) The proposed algorithm offers reduced computational effort and improved computational efficiency for Boolean operations on geometric models. Traditionally, obtaining the intersection lines and intersection rings of intersecting entities is a crucial step. In this paper, an octree-based method is employed to locate and search intersecting triangle pairs, while a parallel algorithm is used to compute the intersection lines of these pairs.

Compared to algorithms based on BSP [19], the octree algorithm addresses the efficiency problem caused by unnecessary partitioning during BSP tree construction. Additionally, the octree algorithm overcomes the limitation of BSP trees, which can only perform Boolean operations on two models. The proposed method leverages the octree algorithm to reduce the overall computational effort required for Boolean operations when obtaining candidate intersecting triangle pairs of triangulated surfaces. Furthermore, the use of a parallel algorithm enhances the computational efficiency when calculating the intersection lines of intersecting triangle pairs.

(2) The proposed algorithm enhances the robustness of Boolean operations by addressing the correct assembly and differentiation of merge, subtraction, and intersection regions in intersecting models. Once the intersection lines of triangulated surfaces are obtained, the subsequent task is to accurately determine these regions. In this paper, a solid index-based method is introduced to create sub-surfaces, sub-blocks, and other entities by manipulating the mesh topology through elimination and updates. Building upon this approach, the direction of directed rings on the newly generated sub-surfaces is utilized to identify the merge, intersection, and subtraction regions resulting from the Boolean operation. A previously proposed method, called BoolSurf, by Riso et al. [51], enables Boolean operations between shapes bounded by freely intersecting curves on any surface, including open surfaces. However, BoolSurf relies on standard floating-point arithmetic, which introduces numerical approximation errors during computation. Additionally, it employs traditional inner and outer classification methods to distinguish the outcomes of merging, intersecting, and subtracting operations.

In contrast, our method improves the Boolean operation process by introducing an entity index-based approach that eliminates the need for coordinate calculations, thereby avoiding numerical approximation errors and enhancing the robustness of Boolean operations. Moreover, the entity index-based method is employed to accurately differentiate between merge, intersection, and subtraction regions, eliminating the requirement for an extensive point or face calculations based on the position of the entity model using traditional classification methods of inner and outer regions.

(3) The proposed method achieves a balance between computational efficiency and computational accuracy. The widely recognized computational geometry library CGAL utilizes rational number arithmetic for exact computations, ensuring high robustness by avoiding rounding errors in floating-point arithmetic [43,52]. However, the reliance on rational number arithmetic introduces complexity to the computation process. Additionally, CGAL requires the input model to be converted to Nef polygons, which involves a complex data structure and imposes a substantial memory footprint at runtime [53].

In contrast, our method improves upon the necessity of rational number arithmetic for computing intersection coordinates, thereby enhancing robustness. Instead of relying on rational number arithmetic, we employ the entity indexing method for Boolean operations. Notably, our method does not impose any additional requirements on the input model and avoids the need for excessive preprocessing. As a result, our approach strikes a favorable balance between computational efficiency and computational accuracy.

(4) The proposed algorithm extends the range of geometric models to which Boolean operations can be applied. Diazzi et al. [38] introduced a method that utilizes indirect geometric predicates to generate a convex polyhedral mesh representing the internal volume of a triangular input surface. This method explicitly defines the solid model based on the geometric properties of the input polygons. Employing an implicit approach avoids the need for coordinate calculations during Boolean operations and minimizes the occurrence of numerical approximation errors. However, this method is limited in its ability to handle Boolean operations on open surfaces.

In contrast to the Boolean method based on indirect geometric predicates proposed by Diazzi et al. [38], our proposed method is not restricted to specific surface types or combinations. The algorithm we present is effective and applicable regardless of whether it involves open surfaces, closed surfaces, or a combination of both. This versatility is particularly valuable in fields such as computational and aided design, computer graphics, and numerical simulation, where complex geometric processing and analysis are required. By extending the applicability of Boolean operations to a wider range of geometric models, our method offers increased flexibility and utility in various domains.

4.1.2. Disadvantages of the Proposed Algorithm

Although the triangulated surface Boolean algorithm proposed in this paper shows good robustness in handling various types of flow triangulated surfaces, it is necessary to acknowledge its drawbacks and challenges.

(1) The proposed method introduces a complex data structure and involves numerous judgments and checks during the computation process. In contrast to the floating-point arithmetic-based method BoolSurf [51], the entity index-based Boolean operation presented in this paper necessitates the construction and management of intricate data structures to represent surface relationships. Consequently, this leads to computational and memory overheads. Although coordinate computation is not required for creating sub-surfaces and sub-blocks, determining the merge, intersection, and subtraction regions of the model after Boolean operations entail a substantial amount of judgment and checking.

(2) The proposed method has difficulties in dealing with models with defective inputs. In comparison to Boolean methods based on indirect geometric predicates [38], the entity index-based approach may encounter difficulties when dealing with complex geometric scenarios or inputs that contain defects. These defects include self-intersecting surfaces, non-manifold surfaces, and surfaces with voids or gaps. Ensuring the correctness of Boolean operations in such cases may require additional processing and repair steps. These additional steps introduce complexity and implementation challenges to the algorithm.

(3) The entity index-based Boolean operation method may face performance and scalability challenges as the size of geometric data increases. When dealing with high-resolution grids, the proposed method requires significant memory and computational resources for constructing and maintaining data structures. The judgment and checking processes performed on a large number of triangular surfaces contribute to increased execution time. To address performance challenges, researchers have proposed various techniques. For instance, Cherchi et al. [33] introduced an improved mesh arrangement method and a new internal and external classification system based on exact ray projection. This approach aimed to enhance the efficiency of triangular mesh Boolean operations, particularly for interactive applications. However, it still exhibits limitations when applied to very high-resolution meshes, typically exceeding 200K triangles. In light of the rapid development of computer technology, parallel strategies utilizing multicore GPUs hold significant potential in improving computational efficiency. For example, Xiao et al. [54] developed a multi-core GPU-based triangle intersection algorithm capable of detecting around 1.5 billion triangle pairs in less than 0.5 s.

4.2. Outlook and Future Work

Boolean operations on triangulated surfaces play a crucial role in computer-aided design, computer vision and graphics, and numerical simulation. These operations enable the manipulation of complex geometries by performing merging, intersection, and subtraction operations. The application of Boolean operations has a significant impact on various industries, including aerospace, automotive, architecture, medical, agricultural, and entertainment. By leveraging Boolean operations, designers and engineers can enhance their design capabilities and create intricate and customized objects. This, in turn, contributes to improved product design and development processes. Overall, Boolean operations on triangulated surfaces offer numerous benefits across various fields, enabling advanced design capabilities, cost-effective manufacturing processes, sophisticated simulations, and a deeper understanding of real-world phenomena.

Although the proposed algorithm in this paper exhibits good robustness, it also has some limitations and areas for further improvement. In future research, the focus will be on enhancing the proposed method by simplifying the data structure and reducing the computational overhead caused by numerous judgments and checks, while still maintaining the robustness of Boolean operations. Additionally, further research is needed to address specific challenges associated with trigonometric surfaces, such as complex topological relationships, self-intersections, defects, and other special cases that commonly occur in practical applications. Developing strategies to handle these scenarios will enhance the algorithm’s versatility and make it more applicable in real-world situations.

Furthermore, it is crucial to explore the integration of the proposed algorithms with existing efficient data structures, parallel algorithms, and optimization techniques. This integration can significantly improve the computational efficiency and scalability of the algorithm, particularly when dealing with large-scale triangulated surfaces or high-resolution models. The ability to process such data in real-time and interactive applications is essential for practical implementation.

In conclusion, future research endeavors will focus on simplifying the algorithm, addressing complex geometric scenarios, and integrating it with efficient data structures, parallel algorithms, and optimization techniques. These advancements will contribute to improving the overall performance and scalability of the proposed method, thus enhancing its applicability in various domains.

5. Conclusions

This paper presents simple and robust algorithms for Boolean operations in geometric modeling. The proposed algorithms are validated using various pairs of surfaces, including open–open, open–closed, and closed–closed cases. Our approach utilizes exact arithmetic methods for computation and employs octree for efficient triangle location and intersection detection. Furthermore, a parallel algorithm is utilized to calculate the intersection lines of triangles. We classify intersection loops into open, hard closed, and soft closed categories, and use them to create sub-surfaces by expanding from the closed intersection loops. Sub-blocks are then easily assembled based on the boundary loops of sub-surfaces and distinguished by comparing the minimum and maximum coordinates of the updated vertices.

Our approach consists of two stages. The first stage involves calculating intersection lines for triangles and subsequently merging and updating the resulting surfaces. This stage requires coordinate calculations to handle geometric entities. In the second stage, we focus on forming intersection loops, creating sub-surfaces, assembling sub-blocks, and distinguishing between them. Unlike the first stage, this stage operates solely on the cleared and updated topology of triangular meshes without involving coordinate computations of geometric entities. We have demonstrated the effectiveness of our approach through several test examples.

While the proposed triangular surface Boolean algorithm demonstrates robustness in handling a wide range of triangular surfaces without self-intersection, such as open and closed surfaces, it may encounter challenges when dealing with complex geometric problems or defective inputs. Additionally, as geometric data scales up, Boolean methods based on entity indexes may experience performance and scalability issues. Future research will focus on addressing Boolean operations for triangulated surfaces with complex topological relations, self-intersections, defects, and other special cases. This will involve incorporating efficient data structures, parallel computing, and optimization algorithms to enhance the computational efficiency and scalability of the proposed algorithms.