Modelling Fractional Advection–Diffusion Processes via the Adomian Decomposition
Abstract
1. Introduction
2. Preliminaries and Notations
- Properties
3. Basic Idea of the Adomian Decomposition Method
4. Physical Interpretation: Anomalous Advection Diffusion–Reaction Processes within Saturated Multiphase Porous Media
5. The Fractional Advection–Diffusion Equation Model and Its Solution by ADM
6. Calibration
7. Numerical Implementation
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Salomoni, V.A.; De Marchi, N. A fractional approach to fluid flow and solute transport within deformable saturated porous media. Int. J. Comput. Mater. Sci. Eng. 2022, 11, 2250003. [Google Scholar] [CrossRef]
- Goldsztein, G.H. Solute transport in porous media. Media with capillaries as voids. SIAM J. Appl. Math. 2008, 68, 1203–1222. [Google Scholar] [CrossRef]
- Zhang, H.; Jeng, D.S.; Barry, D.A.; Seymour, B.R.; Li, L. Solute transport in nearly saturated porous media under landfill clay liners: A finite deformation approach. J. Hydrol. 2013, 479, 189–199. [Google Scholar] [CrossRef]
- Zou, L.; Jing, L.; Cvetkovic, V. Modeling of solute transport in a 3D rough-walled fracture–matrix system. Transp. Porous Media 2017, 116, 1005–1029. [Google Scholar] [CrossRef]
- Tate, M.K.; Knothe, U. An ex vivo model to study transport processes and fluid flow in loaded bone. J. Biomech. 2000, 33, 247–254. [Google Scholar] [CrossRef] [PubMed]
- Wang, L. Solute transport in the bone lacunar-canalicular system (LCS). Curr. Osteoporos. Rep. 2018, 16, 32–41. [Google Scholar] [CrossRef]
- Majorana, C.; Salomoni, V. Parametric analyses of diffusion of activated sources in disposal forms. J. Hazard. Mater. 2004, 113, 45–56. [Google Scholar] [CrossRef]
- Biot, M.A. General theory of three-dimensional consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Biot, M.A. General solutions of the equations of elasticity and consolidation for a porous material. J. Appl. Mech. 1956, 23, 91–96. [Google Scholar] [CrossRef]
- Lewis, R.; Schretler, B. The Finite Element Method in the Static and Dynamic Deformation and Consolidation of Porous Media; Wiley: Chichester, UK, 1998. [Google Scholar]
- Borja, R.I. Cam-Clay plasticity. Part V: A mathematical framework for three-phase deformation and strain localization analyses of partially saturated porous media. Comput. Methods Appl. Mech. Eng. 2004, 193, 5301–5338. [Google Scholar] [CrossRef]
- Coussy, O. Poromechanics; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- De Boer, R. Trends in Continuum Mechanics of Porous Media; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005; Volume 18. [Google Scholar]
- Fomin, S.A.; Chugunov, V.A.; Hashida, T. Non-Fickian mass transport in fractured porous media. Adv. Water Resour. 2011, 34, 205–214. [Google Scholar] [CrossRef]
- Zhou, H.; Yang, S.; Zhang, S. Modeling non-Darcian flow and solute transport in porous media with the Caputo–Fabrizio derivative. Appl. Math. Model. 2019, 68, 603–615. [Google Scholar] [CrossRef]
- Sultana, F.; Singh, D.; Pandey, R.K.; Zeidan, D. Numerical schemes for a class of tempered fractional integro-differential equations. Appl. Numer. Math. 2020, 157, 110–134. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley & Sons: Hoboken, NJ, USA, 1993. [Google Scholar]
- Prakash, P.; Sahadevan, R. Lie symmetry analysis and exact solution of certain fractional ordinary differential equations. Nonlinear Dyn. 2017, 89, 305–319. [Google Scholar] [CrossRef]
- Jannelli, A.; Ruggieri, M.; Speciale, M.P. Numerical solutions of space-fractional advection-diffusion equations with nonlinear source term. Appl. Numer. Math. 2020, 155, 93–102. [Google Scholar] [CrossRef]
- Bira, B.; Mandal, H.; Zeidan, D. Exact solution of the time fractional variant Boussinesq-Burgers equations. Appl. Math. 2021, 66, 437–449. [Google Scholar] [CrossRef]
- Mandal, H.; Bira, B.; Zeidan, D. Power series solution of time-fractional Majda-Biello system using lie group analysis. In Proceedings of the International Conference on Fractional Differentiation and its Applications (ICFDA), Amman, Jordan, 16–18 July 2018. [Google Scholar]
- Deng, Z.Q.; Singh, V.P.; Bengtsson, L. Numerical solution of fractional advection-dispersion equation. J. Hydraul. Eng. 2004, 130, 422–431. [Google Scholar] [CrossRef]
- Kumar, S.; Zeidan, D. An efficient Mittag-Leffler kernel approach for time-fractional advection-reaction-diffusion equation. Appl. Numer. Math. 2021, 170, 190–207. [Google Scholar] [CrossRef]
- Yavuz, M.; Ozdemir, N. An integral transform solution for fractional Advection-Diffusion problem. In Proceedings of the International Conference on Mathematical Studies and Applications, Karaman, Turkey, 4–6 October 2018. [Google Scholar]
- Sousa, E. Finite difference approximations for a fractional advection diffusion problem. J. Comput. Phys. 2009, 228, 4038–4054. [Google Scholar] [CrossRef]
- Chen, C.M.; Liu, F.; Turner, I.; Anh, V. A Fourier method for the fractional diffusion equation describing sub-diffusion. J. Comput. Phys. 2007, 227, 886–897. [Google Scholar] [CrossRef]
- Shen, S.; Liu, F. Error analysis of an explicit finite difference approximation for the space fractional diffusion equation with insulated ends. Anziam J. 2004, 46, C871–C887. [Google Scholar] [CrossRef]
- Tadjeran, C.; Meerschaert, M.M.; Scheffler, H.P. A second-order accurate numerical approximation for the fractional diffusion equation. J. Comput. Phys. 2006, 213, 205–213. [Google Scholar] [CrossRef]
- Tadjeran, C.; Meerschaert, M.M. A second-order accurate numerical method for the two-dimensional fractional diffusion equation. J. Comput. Phys. 2007, 220, 813–823. [Google Scholar] [CrossRef]
- Yuste, S.B.; Acedo, L. An explicit finite difference method and a new von Neumann-type stability analysis for fractional diffusion equations. SIAM J. Numer. Anal. 2005, 42, 1862–1874. [Google Scholar] [CrossRef]
- Yuste, S.B. Weighted average finite difference methods for fractional diffusion equations. J. Comput. Phys. 2006, 216, 264–274. [Google Scholar] [CrossRef]
- Liu, F.; Zhuang, P.; Anh, V.; Turner, I.; Burrage, K. Stability and convergence of the difference methods for the space–time fractional advection–diffusion equation. Appl. Math. Comput. 2007, 191, 12–20. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Tadjeran, C. Finite difference approximations for fractional advection–dispersion flow equations. J. Comput. Appl. Math. 2004, 172, 65–77. [Google Scholar] [CrossRef]
- Li, C.; Cai, M. Theory and Numerical Approximations of Fractional Integrals and Derivatives; SIAM: Philadelphia, PA, USA, 2019. [Google Scholar]
- Pinnola, F.P.; Vaccaro, M.S.; Barretta, R.; Marotti de Sciarra, F. Random vibrations of stress-driven nonlocal beams with external damping. Meccanica 2021, 56, 1329–1344. [Google Scholar] [CrossRef]
- Barretta, R.; Marotti de Sciarra, F.; Pinnola, F.P.; Vaccaro, M.S. On the nonlocal bending problem with fractional hereditariness. Meccanica 2022, 57, 807–820. [Google Scholar] [CrossRef]
- Wang, Q. Numerical solutions for fractional KdV–Burgers equation by Adomian decomposition method. Appl. Math. Comput. 2006, 182, 1048–1055. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z. Numerical solutions of the space-time fractional advection-dispersion equation. Numer. Methods Partial Differ. Equ. Int. J. 2008, 24, 1416–1429. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z. Analytical approach to linear fractional partial differential equations arising in fluid mechanics. Phys. Lett. A 2006, 355, 271–279. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z. Analytical solution of a time-fractional Navier–Stokes equation by Adomian decomposition method. Appl. Math. Comput. 2006, 177, 488–494. [Google Scholar] [CrossRef]
- Ray, S.S.; Bera, R. Solution of an extraordinary differential equation by Adomian decomposition method. J. Appl. Math. 2004, 2004, 331–338. [Google Scholar] [CrossRef]
- Sweilam, N.; Khader, M.; Al-Bar, R. Numerical studies for a multi-order fractional differential equation. Phys. Lett. A 2007, 371, 26–33. [Google Scholar] [CrossRef]
- Abbasbandy, S. A new application of He’s variational iteration method for quadratic Riccati differential equation by using Adomian’s polynomials. J. Comput. Appl. Math. 2007, 207, 59–63. [Google Scholar] [CrossRef]
- Hashim, I.; Abdulaziz, O.; Momani, S. Homotopy analysis method for fractional IVPs. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 674–684. [Google Scholar] [CrossRef]
- Deng, W.; Hesthaven, J.S. Local discontinuous Galerkin methods for fractional diffusion equations. ESAIM Math. Model. Numer. Anal. Modél. Mathémat. Anal. Numér. 2013, 47, 1845–1864. [Google Scholar] [CrossRef]
- Rawashdeh, E. Numerical solution of fractional integro-differential equations by collocation method. Appl. Math. Comput. 2006, 176, 1–6. [Google Scholar] [CrossRef]
- Ray, S.S.; Bera, R. An approximate solution of a nonlinear fractional differential equation by Adomian decomposition method. Appl. Math. Comput. 2005, 167, 561–571. [Google Scholar]
- González, J.R.; Guerrero, L.H.; Alzate, P.P.C. Solution of nonlinear equation representing a generalization of the Black–Scholes model using ADM. Contemp. Eng. Sci. 2017, 10, 621–629. [Google Scholar] [CrossRef]
- Akgül, A.; Aliyu, A.I.; Inc, M.; Yusuf, A.; Baleanu, D. Approximate solutions to the conformable Rosenau-Hyman equation using the two-step Adomian decomposition method with Pad é approximation. Math. Methods Appl. Sci. 2020, 43, 7632–7639. [Google Scholar] [CrossRef]
- Ziane, D.; Baleanu, D.; Belghaba, K.; Cherif, M.H. Local fractional Sumudu decomposition method for linear partial differential equations with local fractional derivative. J. King Saud Univ. Sci. 2019, 31, 83–88. [Google Scholar] [CrossRef]
- Khan, H.; Shah, R.; Kumam, P.; Baleanu, D.; Arif, M. An efficient analytical technique, for the solution of fractional-order telegraph equations. Mathematics 2019, 7, 426. [Google Scholar] [CrossRef]
- Yunus, A.O.; Olayiwola, M.O.; Omoloye, M.A.; Oladapo, A.O. A fractional order model of lassa disease using the Laplace-adomian decomposition method. Healthc. Anal. 2023, 3, 100167. [Google Scholar] [CrossRef]
- Ali, R.; Ghosh, U.N.; Mandi, L.; Chatterjee, P. Application of Adomian decomposition method to study collision effect in dusty plasma in the presence of polarization force. Indian J. Phys. 2023, 97, 2209–2216. [Google Scholar] [CrossRef]
- Abdel-Salam, E.; Nouh, M.; Alali, E. On the Solution of the Variable Order Time Fractional Schrödinger Equation. Trends Sci. 2022, 19, 6183. [Google Scholar] [CrossRef]
- Jiao, Y.; Yamamoto, Y.; Dang, C.; Hao, Y. An aftertreatment technique for improving the accuracy of Adomian’s decomposition method. Comput. Math. Appl. 2002, 43, 783–798. [Google Scholar] [CrossRef]
- Jiao, Y.C.; Dang, C.; Yamamoto, Y. An extension of the decomposition method for solving nonlinear equations and its convergence. Comput. Math. Appl. 2008, 55, 760–775. [Google Scholar] [CrossRef]
- Abuasad, S.; Hashim, I.; Abdul Karim, S.A. Modified fractional reduced differential transform method for the solution of multiterm time-fractional diffusion equations. Adv. Math. Phys. 2019, 2019, 5703916. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- El-Sayed, A.; Gaber, M. The Adomian decomposition method for solving partial differential equations of fractal order in finite domains. Phys. Lett. A 2006, 359, 175–182. [Google Scholar] [CrossRef]
- Salomoni, V. A mathematical framework for modelling 3D coupled THM phenomena within saturated porous media undergoing finite strains. Compos. Part B: Eng. 2018, 146, 42–48. [Google Scholar] [CrossRef]
- Salomoni, V.A.L.; De Marchi, N. Numerical Solutions of Space-Fractional Advection–Diffusion–Reaction Equations. Fractal Fract. 2022, 6, 21. [Google Scholar] [CrossRef]
- Hikal, M.; Ibrahim, M.A. On Adomian’s decomposition method for solving a fractional advection-dispersion equation. Int. J. Pure Appl. Math. 2015, 104, 43–56. [Google Scholar] [CrossRef]
- Cherruault, Y. Convergence of Adomian’s method. Kybernetes 1989, 18, 31–38. [Google Scholar] [CrossRef]
- Cherruault, Y.; Adomian, G. Decomposition methods: A new proof of convergence. Math. Comput. Model. 1993, 18, 103–106. [Google Scholar] [CrossRef]
- Abbaoui, K.; Cherruault, Y. New ideas for proving convergence of decomposition methods. Comput. Math. Appl. 1995, 29, 103–108. [Google Scholar] [CrossRef]
- Himoun, N.; Abbaoui, K.; Cherruault, Y. New results of convergence of Adomian’s method. Kybernetes 1999, 28, 423–429. [Google Scholar] [CrossRef]
- Cherruault, Y.; Saccomandi, G.; Some, B. New results for convergence of Adomian’s method applied to integral equations. Math. Comput. Model. 1992, 16, 85–93. [Google Scholar] [CrossRef]
- Cherruault, Y.; Adomian, G.; Abbaoui, K.; Rach, R. Further remarks on convergence of decomposition method. Int. J. Bio-Med. Comput. 1995, 38, 89–93. [Google Scholar] [CrossRef] [PubMed]
- Ouedraogo, R.; Cherruault, Y.; Abbaoui, K. Convergence of Adomian’s method applied to algebraic equations. Kybernetes 2000, 29, 1298–1305. [Google Scholar] [CrossRef]
- Babolian, E.; Biazar, J.; Vahidi, A. The decomposition method applied to systems of Fredholm integral equations of the second kind. Appl. Math. Comput. 2004, 148, 443–452. [Google Scholar] [CrossRef]
- Bakodah, H. A comparison study between a Chebyshev collocation method and the Adomian decomposition method for solving linear system of Fredholm integral equations of the second kind. J. King AbdulAziz Univ. 2012, 24, 49–59. [Google Scholar] [CrossRef]
- Yee, E. Application of the decomposition method to the solution of the reaction-convection-diffusion equation. Appl. Math. Comput. 1993, 56, 1–27. [Google Scholar] [CrossRef]
- Abdelrazec, A.; Pelinovsky, D. Convergence of the Adomian decomposition method for initial-value problems. Numer. Methods Partial Differ. Equ. 2011, 27, 749–766. [Google Scholar] [CrossRef]
- Raza, A.; Farid, S.; Amir, M.; Yasir, M.; Danyal, R. A Study on Convergence Analysis of Adomian Decomposition Method Applied to Different linear and non-linear Equations. Int. J. Sci. Eng. Res. 2020, 11, 22. [Google Scholar]
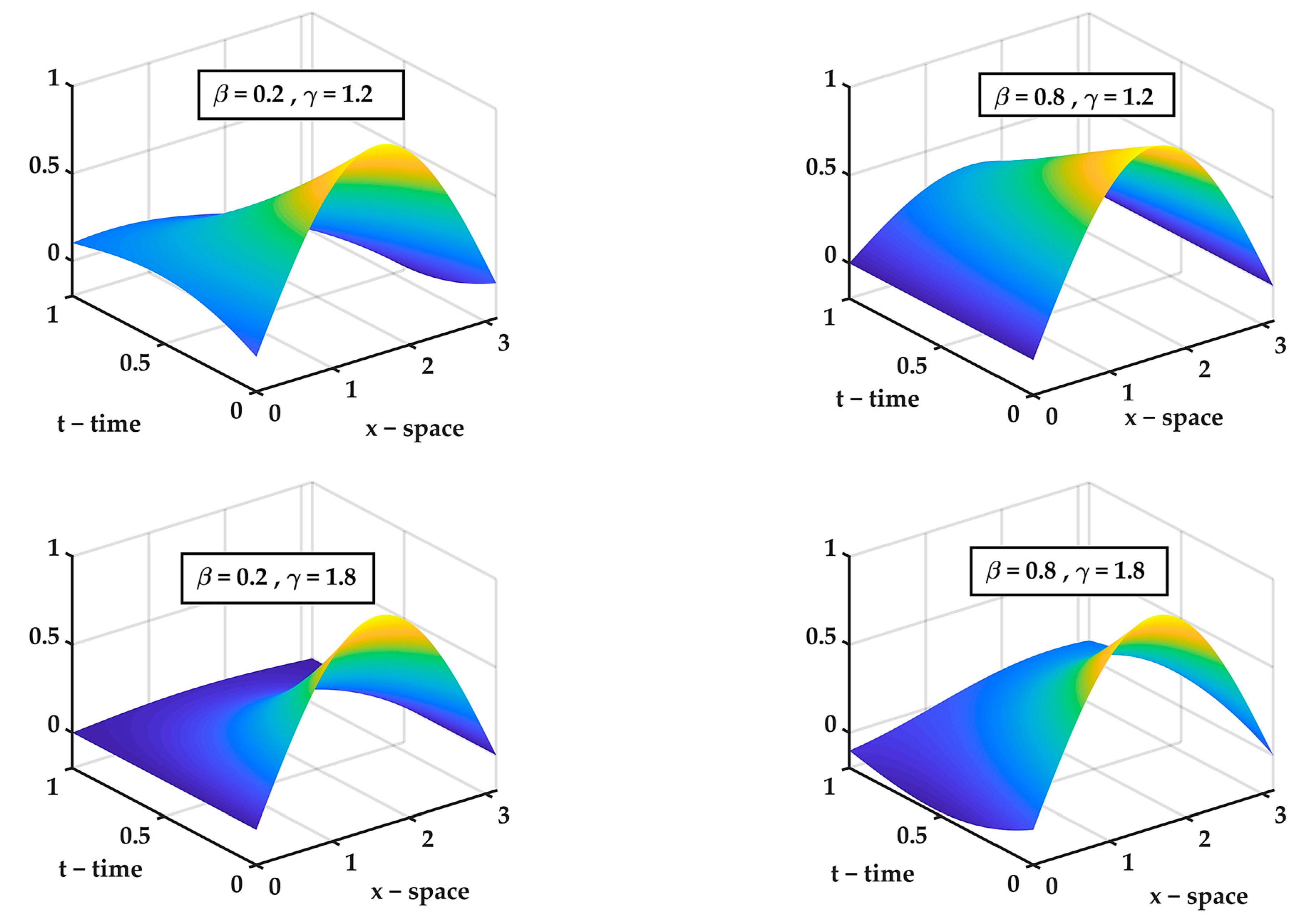


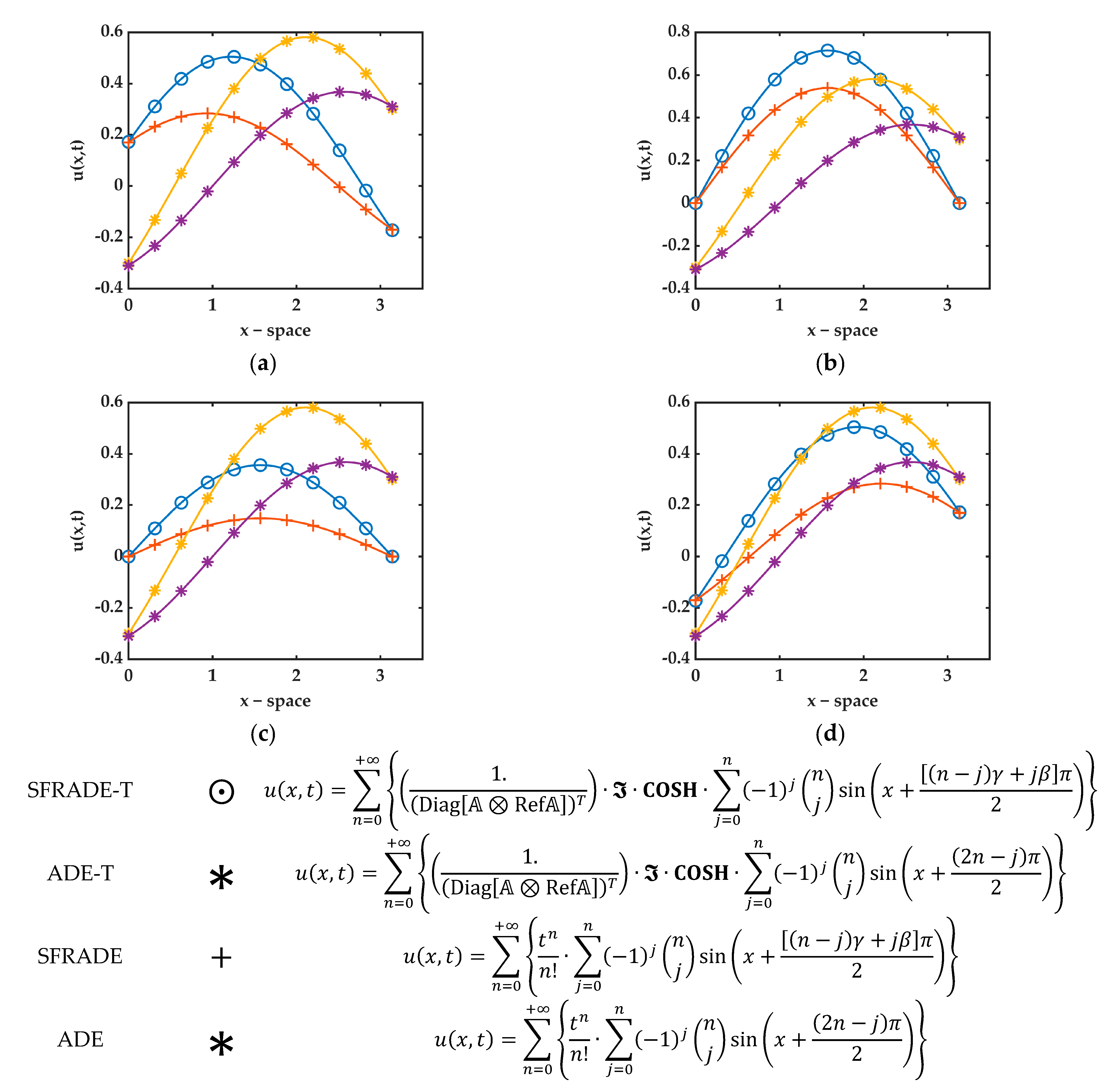
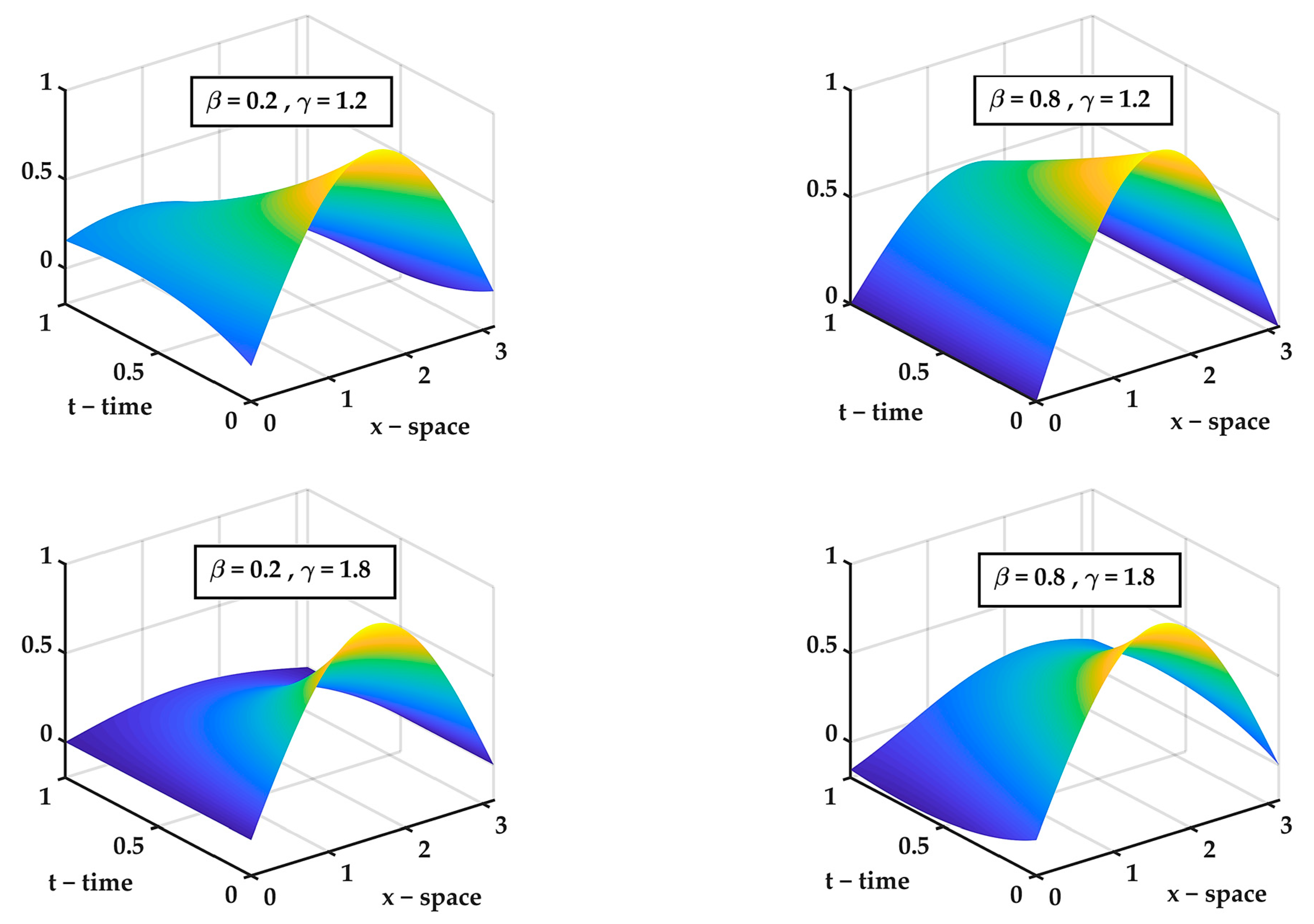
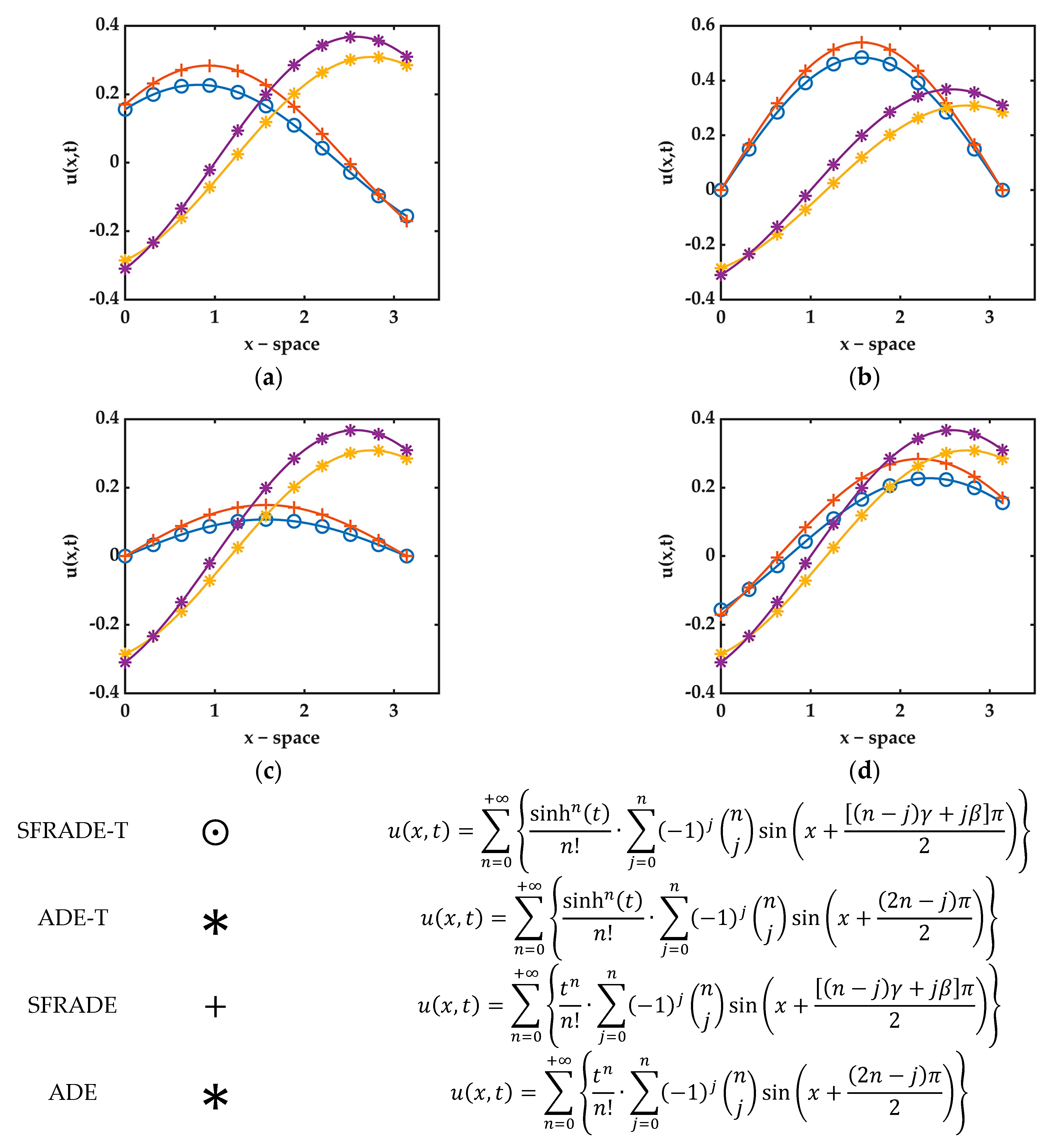
, |
| ADE | Advection–Diffusion Equation | |
| ADE-T | Advection–Diffusion Equation-Time dependent advective and diffusive terms | |
| SFRADE | Space FRactional Advection–Diffusion Equation | |
| SFRADE-T | Space FRactional Advection–Diffusion Equation-Time dependent advective and diffusive terms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antonini, A.; Salomoni, V.A.L. Modelling Fractional Advection–Diffusion Processes via the Adomian Decomposition. Mathematics 2023, 11, 2657. https://doi.org/10.3390/math11122657
Antonini A, Salomoni VAL. Modelling Fractional Advection–Diffusion Processes via the Adomian Decomposition. Mathematics. 2023; 11(12):2657. https://doi.org/10.3390/math11122657
Chicago/Turabian StyleAntonini, Alberto, and Valentina Anna Lia Salomoni. 2023. "Modelling Fractional Advection–Diffusion Processes via the Adomian Decomposition" Mathematics 11, no. 12: 2657. https://doi.org/10.3390/math11122657
APA StyleAntonini, A., & Salomoni, V. A. L. (2023). Modelling Fractional Advection–Diffusion Processes via the Adomian Decomposition. Mathematics, 11(12), 2657. https://doi.org/10.3390/math11122657







