Distributed Finite-Time Coverage Control of Multi-Quadrotor Systems with Switching Topology †
Abstract
1. Introduction
2. Preliminaries
2.1. Graph Theory
2.2. Locational Optimization
2.3. Quaternion-Based Rotation
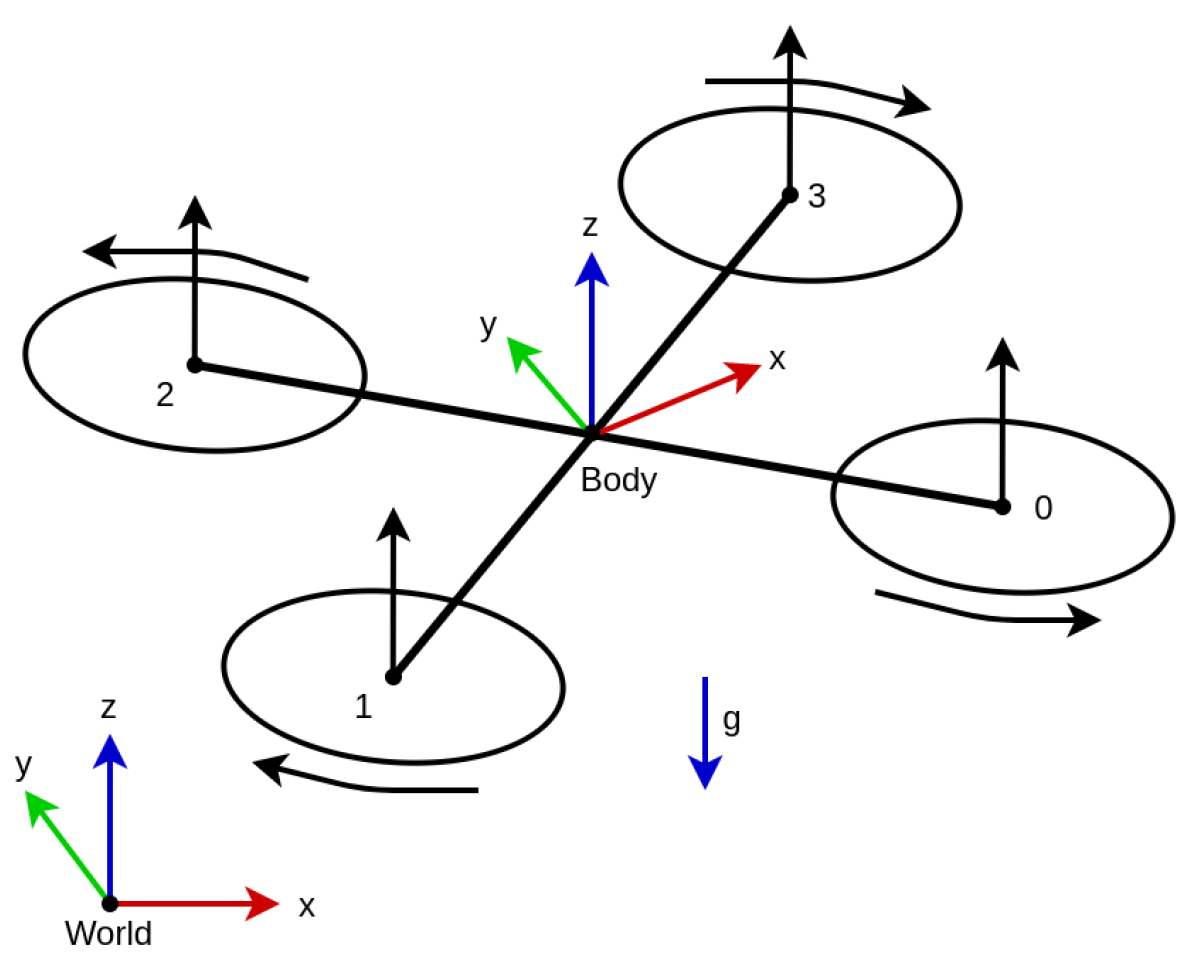
3. Problem Formulation
4. Finite-Time Control Design
4.1. Translation Control with Fixed Topology
4.2. Translation Control with Switching Topology
4.3. Rotation Control
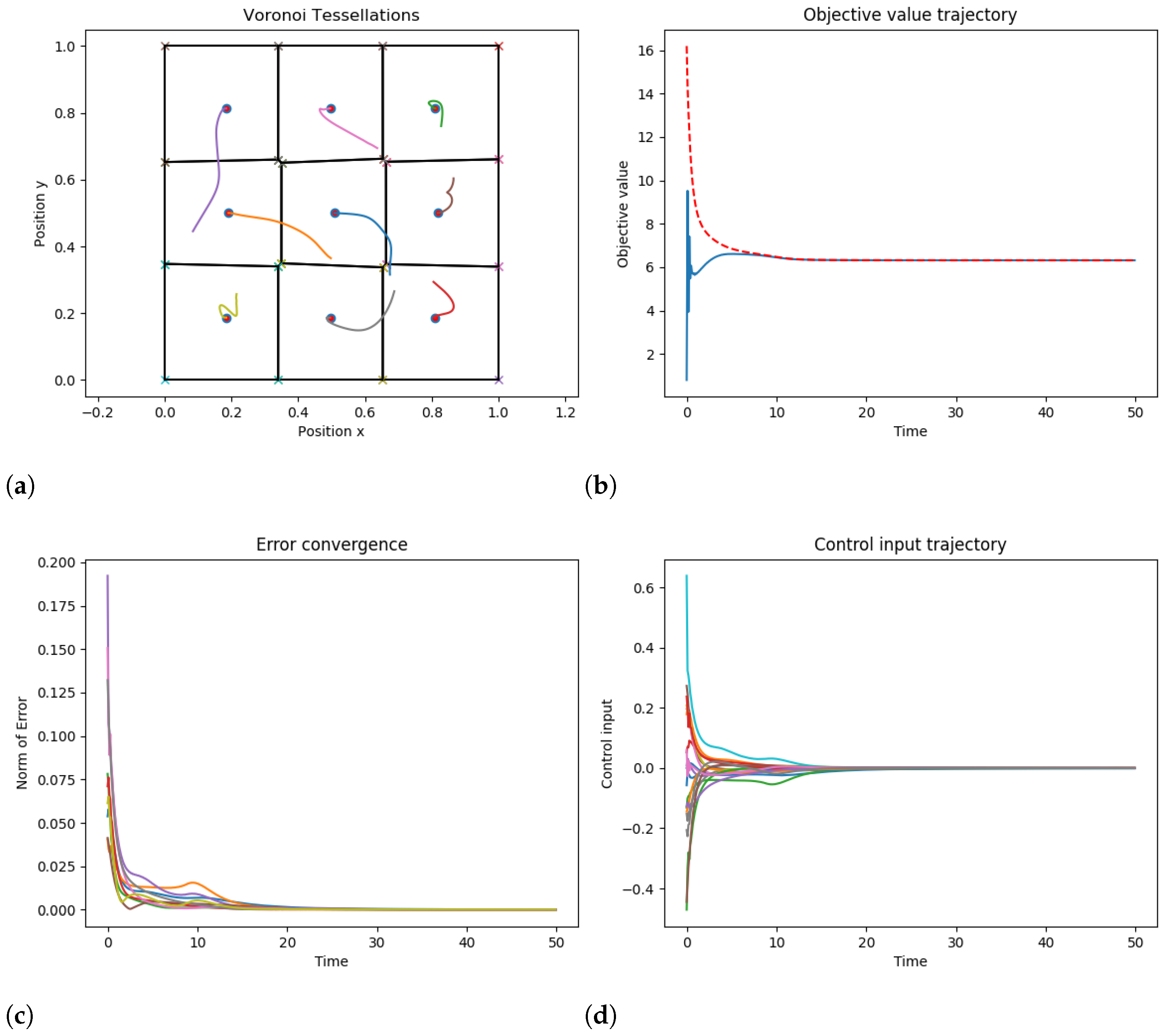
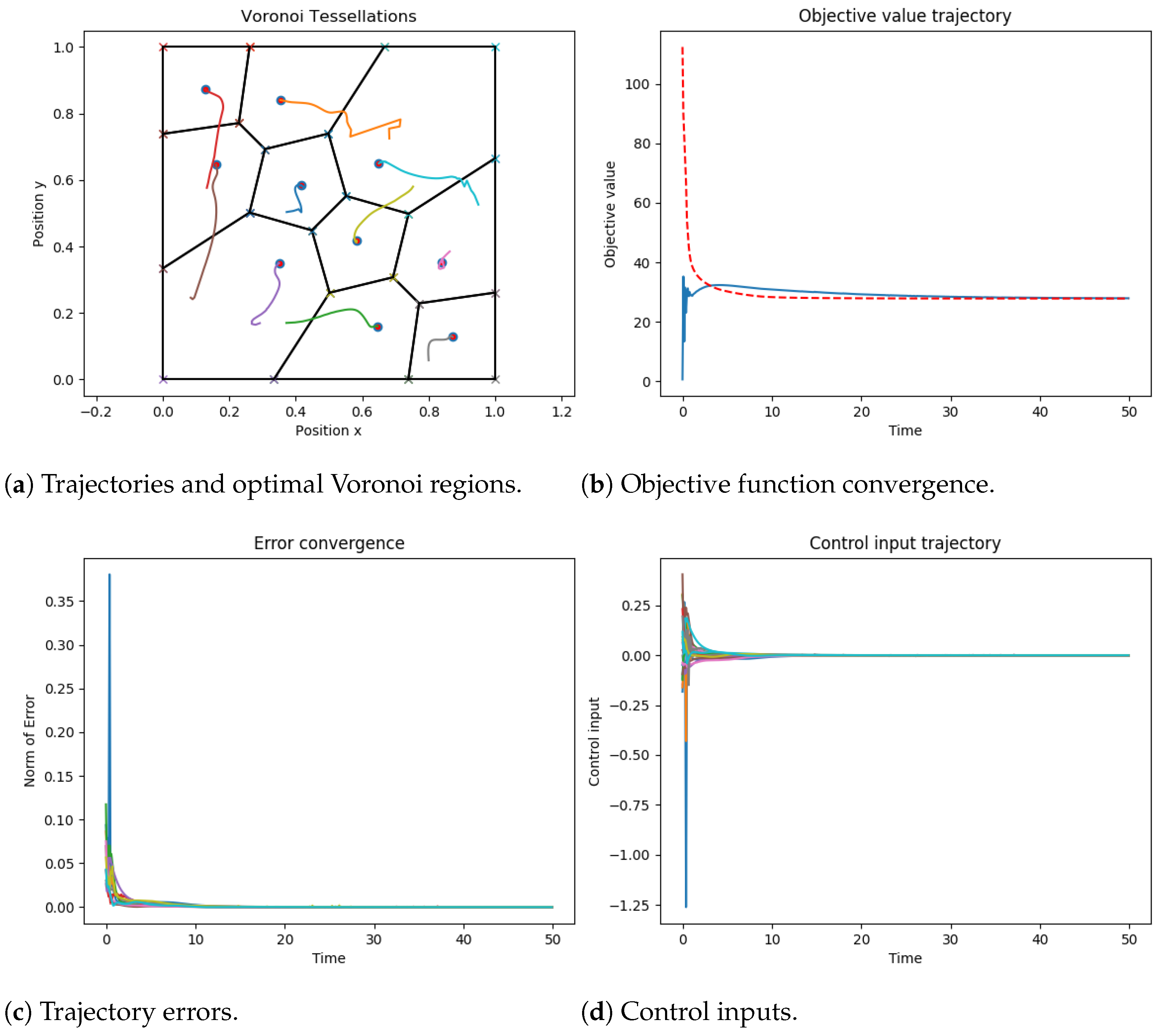
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Carron, A.; Zeilinger, M.N. Model Predictive Coverage Control. IFAC-PapersOnLine 2020, 53, 6107–6112. [Google Scholar] [CrossRef]
- Mei, Y.; Lu, Y.H.; Hu, Y.C.; Lee, C.S. Deployment strategy for mobile robots with energy and timing constraints. Proc.-IEEE Int. Conf. Robot. Autom. 2005, 2005, 2816–2821. [Google Scholar] [CrossRef]
- Tsouros, D.C.; Bibi, S.; Sarigiannidis, P.G. A Review on UAV-Based Applications for Precision Agriculture. Information 2019, 10, 349. [Google Scholar] [CrossRef]
- Zhang, J.; Tnunay, H.; Wang, C.; Lyu, X.; Ding, Z. Distributed Coverage Optimization and Control with Applications to Precision Agriculture. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 6836–6841. [Google Scholar] [CrossRef]
- Okabe, A.; Suzuki, A. Locational optimization problems solved through Voronoi diagrams. Eur. J. Oper. Res. 1997, 98, 445–456. [Google Scholar] [CrossRef]
- Okabe, A.; Boots, B.; Sugihara, K.; Chiu, S.N. Spatial Tessellations: Concepts and Applications of Voronoi Diagrams, 2nd ed.; Wiley Series in Probability and Statistics; Wiley: New York, NY, USA, 1995; Volume 26, p. 79. [Google Scholar] [CrossRef]
- Pavone, M.; Arsie, A.; Frazzoli, E.; Bullo, F. Distributed Algorithms for Environment Partitioning in Mobile Robotic Networks. IEEE Trans. Autom. Control 2011, 56, 1834–1848. [Google Scholar] [CrossRef]
- Cortes, J.; Martinez, S.; Karatas, T.; Bullo, F. Coverage Control for Mobile Sensing Networks. IEEE Trans. Robot. Autom. 2004, 20, 243–255. [Google Scholar] [CrossRef]
- Salhi, S. Facility Location: A Survey of Applications and Methods. J. Oper. Res. Soc. 1996, 47, 1421–1422. [Google Scholar] [CrossRef]
- Lee, S.G.; Diaz-Mercado, Y.; Egerstedt, M. Multirobot Control Using Time-Varying Density Functions. IEEE Trans. Robot. 2015, 31, 489–493. [Google Scholar] [CrossRef]
- Cortés, J.; Martínez, S.; Bullo, F. Spatially-distributed coverage optimization and control with limited-range interactions. ESAIM-Control. Optim. Calc. Var. 2005, 11, 691–719. [Google Scholar] [CrossRef]
- Pimenta, L.C.; Kumar, V.; Mesquita, R.C.; Pereira, G.A. Sensing and coverage for a network of heterogeneous robots. In Proceedings of the IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 3947–3952. [Google Scholar] [CrossRef]
- Gusrialdi, A.; Hatanaka, T.; Fujita, M. Coverage control for mobile networks with limited-range anisotropic sensors. In Proceedings of the IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 4263–4268. [Google Scholar] [CrossRef]
- Parapari, H.F.; Abdollahi, F.; Menhaj, M.B. Coverage control in non-convex environment considering unknown non-convex obstacles. In Proceedings of the 2014 2nd RSI/ISM International Conference on Robotics and Mechatronics, ICRoM 2014, Tehran, Iran, 15–17 October 2014; pp. 119–124. [Google Scholar] [CrossRef]
- Kantaros, Y.; Thanou, M.; Tzes, A. Distributed coverage control for concave areas by a heterogeneous Robot-Swarm with visibility sensing constraints. Automatica 2015, 53, 195–207. [Google Scholar] [CrossRef]
- Schwager, M.; Slotine, J.J.; Rus, D. Decentralized, adaptive control for coverage with networked robots. In Proceedings of the IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 3289–3294. [Google Scholar] [CrossRef]
- Martinez, S. Distributed interpolation schemes for field estimation by mobile sensor networks. IEEE Trans. Control Syst. Technol. 2010, 18, 491–500. [Google Scholar] [CrossRef]
- Schwager, M.; Vitus, M.P.; Powers, S.; Rus, D.; Tomlin, C.J. Robust adaptive coverage control for robotic sensor networks. IEEE Trans. Control Netw. Syst. 2017, 4, 462–476. [Google Scholar] [CrossRef]
- Kantaros, Y.; Zavlanos, M.M. Distributed communication-aware coverage control by mobile sensor networks. Automatica 2016, 63, 209–220. [Google Scholar] [CrossRef]
- Wang, P.; Song, C.; Liu, L. Coverage Control for Mobile Sensor Networks with Unknown Terrain Roughness and Time-varying Delays. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Tamba, T.A. Optimizing the Area Coverage of Networked UAVs using Multi-Agent Reinforcement Learning. In Proceedings of the 2021 International Conference on Instrumentation, Control, and Automation (ICA), Bandung, Indonesia, 25–27 August 2021; pp. 197–201. [Google Scholar] [CrossRef]
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Xiao, F.; Wang, L.; Chen, J.; Gao, Y. Finite-time formation control for multi-agent systems. Automatica 2009, 45, 2605–2611. [Google Scholar] [CrossRef]
- Khoo, S.; Xie, L.; Man, Z. Robust finite-time consensus tracking algorithm for multirobot systems. IEEE/ASME Trans. Mechatron. 2009, 14, 219–228. [Google Scholar] [CrossRef]
- Du, H.; Yang, C.; Jia, R. Finite-time formation control of multiple mobile robots. In Proceedings of the 6th Annual IEEE International Conference on Cyber Technology in Automation, Control and Intelligent Systems, IEEE-CYBER 2016, Chengdu, China, 19–22 June 2016; pp. 416–421. [Google Scholar] [CrossRef]
- Wang, J.; Liang, H.; Sun, Z.; Zhang, S.; Liu, M. Finite-time control for spacecraft formation with dual-number-based description. J. Guid. Control. Dyn. 2012, 35, 950–962. [Google Scholar] [CrossRef]
- Zuo, Z.; Tie, L. A new class of finite-time nonlinear consensus protocols for multi-agent systems. Int. J. Control 2014, 87, 363–370. [Google Scholar] [CrossRef]
- Zuo, Z. Nonsingular fixed-time consensus tracking for second-order multi-agent networks. Automatica 2015, 54, 305–309. [Google Scholar] [CrossRef]
- Wang, C.; Tnunay, H.; Zuo, Z.; Lennox, B.; Ding, Z. Fixed-Time Formation Control of Multirobot Systems: Design and Experiments. IEEE Trans. Ind. Electron. 2019, 66, 6292–6301. [Google Scholar] [CrossRef]
- Tnunay, H.; Moussa, K.; Hably, A.; Marchand, N. Distributed Finite-time Coverage Control of Multi-quadrotor Systems. In Proceedings of the IECON 2022—48th Annual Conference of the IEEE Industrial Electronics Society, Brussels, Belgium, 17–20 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Abdulghany, A.R. Generalization of parallel axis theorem for rotational inertia. Am. J. Phys. 2017, 85, 791–795. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Brescianini, D.; Hehn, M.; D’Andrea, R. Nonlinear Quadrocopter Attitude Control; Technical Report; ETH Zürich, Departement Maschinenbau und Verfahrenstechnik: Zürich, Swizerland, 2013; pp. 1–21. [Google Scholar] [CrossRef]
- Meier, L.; Honegger, D.; Pollefeys, M. PX4: A node-based multithreaded open source robotics framework for deeply embedded platforms. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 6235–6240. [Google Scholar] [CrossRef]
- Lim, J. Mavros_Controllers—Aggressive Trajectory Tracking Using Mavros for PX4 Enabled Vehicles. 2019. Available online: https://scholar.google.co.kr/citations?view_op=view_citation&hl=en&user=NOdnT3EAAAAJ&citation_for_view=NOdnT3EAAAAJ:zYLM7Y9cAGgC (accessed on 10 January 2023). [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tnunay, H.; Moussa, K.; Hably, A.; Marchand, N. Distributed Finite-Time Coverage Control of Multi-Quadrotor Systems with Switching Topology. Mathematics 2023, 11, 2621. https://doi.org/10.3390/math11122621
Tnunay H, Moussa K, Hably A, Marchand N. Distributed Finite-Time Coverage Control of Multi-Quadrotor Systems with Switching Topology. Mathematics. 2023; 11(12):2621. https://doi.org/10.3390/math11122621
Chicago/Turabian StyleTnunay, Hilton, Kaouther Moussa, Ahmad Hably, and Nicolas Marchand. 2023. "Distributed Finite-Time Coverage Control of Multi-Quadrotor Systems with Switching Topology" Mathematics 11, no. 12: 2621. https://doi.org/10.3390/math11122621
APA StyleTnunay, H., Moussa, K., Hably, A., & Marchand, N. (2023). Distributed Finite-Time Coverage Control of Multi-Quadrotor Systems with Switching Topology. Mathematics, 11(12), 2621. https://doi.org/10.3390/math11122621








