On Correspondences between Feedforward Artificial Neural Networks on Finite Memory Automata and Classes of Primitive Recursive Functions

Abstract

When realized on computational devices with finite quantities of memory, feedforward artificial neural networks and the functions they compute cease being abstract mathematical objects and turn into executable programs generating concrete computations. To differentiate between feedforward artificial neural networks and their functions as abstract mathematical objects and the realizations of these networks and functions on finite memory devices, we introduce the categories of general and actual computabilities and show that there exist correspondences, i.e., bijections, between functions computable by trained feedforward artificial neural networks on finite memory automata and classes of primitive recursive functions.

1. Introduction

An offspring of McCollough and Pitts’ research on foundations of cybernetics [1], artificial neural networks (ANNs) entered mainstream machine learning after the discovery of backpropagation by Rumelhart, Hinton, and Williams [2]. ANNs proved to be universal approximators of different classes of functions when no limits are imposed on the number of artificial neurons in any layer (arbitrary width) or on the number of hidden layers (arbitrary depth) and even with bounded widths and depths (e.g., [3,4,5]). ANNs cease being abstract mathematical objects when implemented in specific programming languages on computational devices with finite quantities of internal and external memory, to which we interchangeably refer in our article as finite memory devices (FMDs) and finite memory automata (FMA). To differentiate between functions computable by ANNs in principle and functions computable by ANNs realized on FMA, we introduce the categories of general and actual computabilities and show that there exist correspondences, i.e., bijections, between functions computable by trained feedforward ANNs (FANNs) on FMA and classes of primitive recursive functions.

Our article is organized as follows. In Section 2, we expound the terms, definitions, and notational conventions for functions and predicates espoused in this article and define the term finite memory automaton. In Section 3, we explicate the categories of general and actual computabilities and elucidate their similarities and differences. In Section 4, we formalize FANNs in terms of recursively defined functions. In Section 5, we present primitive recursive techniques to pack finite sets and Cartesian powers thereof into Gödel numbers. In Section 6, we use the set packing techniques of Section 5 to show that functions computable by trained FANNs implemented on FMA can be archived into natural numbers. In Section 7, we show how such archives can be used to define primitive recursive functions corresponding to functions computable by FANNs. In Section 8, we discuss theoretical and practical reasons for separating computability into the general and actual categories and pursue some implications of the theorems proved in Section 7. In Section 9, we summarize our conclusions. For the reader’s convenience, Appendix A gives supplementary definitions, results, and examples that are referenced in the main text when relevant.

2. Preliminaries

2.1. Functions and Predicates

If f is a function, $dom\left(f\right)$ and $codom\left(f\right)$ denote the domain and the co-domain of f, respectively. Statements such as $f:S\mapsto R$ abbreviate the logical conjunction $dom\left(f\right)=S\wedge codom\left(f\right)=R$. A function f is partial on a set S if $dom\left(f\right)$ is a proper subset of S, i.e., $dom\left(f\right)\subset S$. Thus, if $S=\mathbb{N}=\{0,1,2,\dots \}$ and $f\left(x\right)=x^{1/3}$, then f is partial on S, because $dom\left(f\right)=\left\{i^3\right|i\in \mathbb{N}\}\subset \mathbb{N}$. If S and R are sets, then $S=R$ is logically equivalent to the logical conjunction $S\subseteq R\wedge R\subseteq S$, i.e., S is a subset of R, and vice versa. If f is partial on S and $z\in S$, the following statements are equivalent: (1) $z\in dom\left(f\right)$; (2) f is defined on z; (3) $f\left(z\right)$ is defined; and (4) $f\left(z\right)\downarrow$. The following statements are also equivalent: (1) $z\notin dom\left(f\right)$; (2) f is undefined on z; (3) $f\left(z\right)$ is undefined; and (4) $f\left(z\right)\uparrow$. If f is partial on S and $dom\left(f\right)=S$, then f is total on S. Thus, $f\left(x\right)=x+1$ is total on $\mathbb{N}$. When $f:S\mapsto R$ is a bijection, i.e., f is injective (one-to-one) and surjective (onto), f is a correspondence between S and R.

If S is a set, then $\left|S\right|$ is the cardinality of S, i.e., the number of elements in S. S is finite if and only if (iff) $\left|S\right|\in \mathbb{N}$. For $n>0$, $S^n$ is the n-th Cartesian power of S, i.e., $S^n=\left\{(s_0,\dots ,s_{n-1})\right|s_i\in S,0\le i\le n-1\}$ $=\left\{(s_1,\dots ,s_n)\right|s_i\in S,1\le i\le n\}$ Thus, if $f:{\mathbb{R}}^2\mapsto \mathbb{N}$, $dom\left(f\right)=\left\{(x_1,x_2)\right|x_1,x_2\in \mathbb{R}\}$. The symbol $\overrightarrow{x}$ is a sequence of numbers, i.e., a vector, from a set S, i.e., $\overrightarrow{x}=(x_0,x_1,\dots ,x_{n-1})=(x_1,x_2,\dots ,x_n)\in S^n$; $\left(\right)$ is the empty sequence. If $\overrightarrow{x}\in S^n$, its individual elements are ${\overrightarrow{x}}_0=x_0$, ${\overrightarrow{x}}_1=x_1$, $\dots ,$${\overrightarrow{x}}_{n-1}=x_{n-1}$ or, equivalently, ${\overrightarrow{x}}_1=x_1$, ${\overrightarrow{x}}_2=x_2$, $\dots ,$${\overrightarrow{x}}_n=x_n$. If $dom\left(f\right)\subseteq S^n$ and $\overrightarrow{x}\in S^n$, $f\left(\overrightarrow{x}\right)$ = $f\left(({\overrightarrow{x}}_0,\dots ,{\overrightarrow{x}}_{n-1})\right)$ = $f(x_0,\dots ,x_{n-1})$ = $f(x_1,\dots ,x_n)$. If $f:dom\left(f\right)\mapsto codom\left(f\right)$ is a bijection, the inverse of f is $f^{-1}:codom\left(f\right)\mapsto dom\left(f\right)$. When the arguments of f are evident, f or $f(·)$ abbreviate $f\left(\overrightarrow{x}\right)$, $f(x_0,\dots ,x_{n-1})$, or $f(x_1,\dots ,x_n)$

A total function $P:S^n\mapsto \{0,1\}$ is a predicate if, for any $\overrightarrow{x}\in S^n$, $P\left(\overrightarrow{x}\right)=1$ or $P\left(\overrightarrow{x}\right)=0$, where 1 arbitrarily designates the logical truth and 0 designates a logical falsehood. The symbols ¬, ∧, ∨, →, respectively, refer to logical not, logical and, logical or, and logical implication. We abbreviate $P\left(\overrightarrow{x}\right)=1$ to $P\left(\overrightarrow{x}\right)$ and $P\left(\overrightarrow{x}\right)=0$ to $\neg P\left(\overrightarrow{x}\right)$. If P and Q are predicates, then $\neg P\vee Q$ is logically equivalent to $P\to Q$, i.e., $\neg P\vee Q\equiv P\to Q$. For clarity, sub-predicates of compound predicates may be included in matching pairs of $\left\{\right\}$. Thus, if a compound predicate P consists of predicates $P_1$, $P_2$, $P_3$, and $P_4$, it can be defined as $P\equiv \{\{P_1\to P_2\}\wedge \{P_3\vee P_4\}\}$. The symbols ∃ and ∀ refer to the logical existential (there exists) and universal (for all) quantifiers, respectively. Thus, the statement $(\exists \overrightarrow{x}\in S^n)P\left(\overrightarrow{x}\right)$ is logically equivalent to the statement that $P\left(\overrightarrow{x}\right)$ holds for at least one $\overrightarrow{x}$ in $dom\left(P\right)$, while the statement $(\forall \overrightarrow{x}\in S^n)P\left(\overrightarrow{x}\right)$ is logically equivalent to the statement that $P\left(\overrightarrow{x}\right)$ holds for all $\overrightarrow{x}$ in $dom\left(P\right)$.

2.2. Finite Memory Automata

A finite memory device $D_j$ is a physical or abstract automaton with a finite quantity of internal and external memory and an automated capability of executing programs, i.e., finite sequences of instructions written in a formalism, e.g., a programming language for $D_j$, and stored in the finite memory of $D_j$. Since bijections exist between expressions over any finite alphabet, i.e., a finite set of symbols or signs, and subsets of $\mathbb{N}$ [6], we call the memory of $D_j$ numerical memory. The numerical memory consists of registers, each of which is a sequence of numerical unit cells, e.g., digital array cells, mechanical switches, and finite state machine tape cells. The quantity of numerical memory is the product of the number of registers and the number of unit cells in each register, i.e., this quantity is a natural number.

A cell holds exactly one elementary sign from a finite alphabet, e.g., { “.”, “0”, “1”, “2”, “3”, “4”, “5”, “6”, “7”, “8”, “9” }, or is empty. The sign of the empty cell is unique and is not an elementary sign. A number sign is a sequence of elementary signs in consecutive cells of a register with no empty cells to the left of the first elementary sign and possibly some empty cells to the right of the rightmost elementary sign. Thus, if “|” is the empty sign on $D_j$, the alphabet is { “.”, “-”, “0”, “1”, “2”, “3”, “4”, “5”, “6”, “7”, “8”, “9” }, and each register on $D_j$ has seven cells, then “3.1||||”, “3.14|||”, “3.141||”, “3.1415|”, and “3.14159” are number signs conventionally interpreted as the real numbers 3.1, 3.14, 3.141, 3.1415, and 3.14159, respectively. An arbitrary number sign interpretation is fixed a priori for a given alphabet and $D_j$ and does not change from sign to sign. Thus, if the alphabet is { “,”, “0”, “f0”, “ff0”, “fff0”, “ffff0”, “fffff0”, “ffffff0”, “fffffff0”, “ffffffff0”, “fffffffff0” } and the interpretation is such that “,” is interpreted as the decimal point, “0” as 0, “f0” as 1, “ff0” as 2, “fff0” as 3, etc., “*” is the empty sign, and each sign is read left to right, then, if each register on $D_j$ has twenty three cells, the sign “f0,ffff0f0ffff0ff0f0***” is interpreted as 1.41421.

A real number x is signifiable on $D_j$ iff a register on $D_j$ can hold its sign. Put another way, a number is signifiable on $D_j$ if, in a programming language L for $D_j$, the number’s sign can be assigned to a variable, i.e., stored in a designated register. When x is signifiable on $D_j$, we say that x is simply signifiable. A set or a sequence of numbers is signifiable if each number in the set or sequence is signifiable.

${\Delta }_j>0$ is the smallest positive signifiable real number on $D_j$ iff for any signifiable x, there is no signifiable y such that $x<y<x+{\Delta }_j$. The finite set of real numbers in the closed interval between 0 and 1 signifiable on $D_j$ is

$$R_{0,1}^j\equiv \{x\in \mathbb{R}|x=i{\Delta }_j<1\}\cup \left\{1\right\},i\in \mathbb{N}.$$

(1)

We note, in passing, a notational convention in Equation (1) to which we adhere in our article: if $D_j$ is an FMA, then the Latin letter j in subscripts or superscripts of symbols is used to emphasize that they are defined with respect to $D_j$. Thus, if $D_j$ and $D_k$ are two FMDs with different quantities of numerical memory, ${\Delta }_j\ne {\Delta }_k$.

Lemma 1.

If $z=i{\Delta }_j$ is a maximal element of $\{x\in \mathbb{R}|x=i{\Delta }_j<1\}$ and $y=(i+1){\Delta }_j$, then $y\ge 1$.

Proof. 

If $y\in R_{0,1}^j$, then $y=1$, because 1 is the only number in $R_{0.1}^j$ greater than z. If $y\notin R_{0,1}^j$, then $y>1$ and $z<1<y$.    □

A corollary of Lemma 1 is that if $a,b$ are signifiable, $a<b$, then

$$R_{a,b}^j\equiv \{x\in \mathbb{R}|x=a+i{\Delta }_j<b\}\cup \left\{b\right\},i\in \mathbb{N},$$

(2)

is the finite set of signifiable numbers in the closed interval from a to b such that there exists no signifiable number between any two consecutive members of $R_{a,b}^j$ when the latter is sorted in non-descending order.

Lemma 2.

If $a,b$ are signifiable and $b-a\ge {\Delta }_j$, there exists a bijection ${\psi }_{a,b}^j$: $R_{a,b}^j$↦$Z_{a,b}^j$ = $\{0,\dots ,z\}\subset \mathbb{N}$, $z>0$, where $a+z{\Delta }_j\ge b$. If $a+z{\Delta }_j$ is signifiable, it is the smallest signifiable number $\ge b$.

Proof. 

Let

$${\psi }_{a,b}^j\left(x\right)=\left\{\begin{array}{cc}k\hfill & \mathrm{if}x=a+k{\Delta }_j<b,\hfill \\ z\hfill & \mathrm{if}\{\{x=a+z{\Delta }_j=b\}\vee \hfill \\ \hfill & \{a+(z-1){\Delta }_j<x=b<a+z{\Delta }_j\}\}.\hfill \end{array}\right.$$

(3)

Let $r\in Z_{a,b}^j$. If $r=z$, then ${\psi }_{a,b}^j\left(x\right)=r$, for $x=a+z{\Delta }_j=b$ or $a+(z-1){\Delta }_j<x=b<a+z{\Delta }_j$. If $r<z$, then ${\psi }_{a,b}^j\left(x\right)=r$, for $x=a+r{\Delta }_j$. Let ${\psi }_{a,b}^j\left(x\right)={\psi }_{a,b}^j\left(y\right)=r$. If $r=z$, then $x=a+r{\Delta }_j=y=b$ or $a+(r-1){\Delta }_j<x=b=y<a+r{\Delta }_j$. If $r<z$, then $x=a+r{\Delta }_j=y$. Let $a+z{\Delta }_j$ be signifiable. If $a+z{\Delta }_j=b$, it is vacuously the smallest signifiable number $\ge b$. If $a+z{\Delta }_j>b$, then, since $a+(z-1){\Delta }_j<b<a+z{\Delta }_j$, the assertion that $0<b-(a+(z-1){\Delta }_j)<{\Delta }_j$ or $0<a+z{\Delta }_j-b<{\Delta }_j$ leads to a contradiction.    □

A corollary of Lemma 2 is that ${{\psi }_{a,b}^j}^{-1}:Z_{a,b}^j\mapsto R_{a,b}^j$ is

$${{\psi }_{a,b}^j}^{-1}\left(k\right)=\left\{\begin{array}{cc}x\hfill & \mathrm{if}x=a+k{\Delta }_j<b,\hfill \\ b\hfill & \mathrm{if}\{\{b=a+k{\Delta }_j\}\vee \hfill \\ \hfill & \{a+(k-1){\Delta }_j<b<a+k{\Delta }_j\}\}.\hfill \end{array}\right.$$

(4)

Lemmas 1 and 2 draw on the empirically verifiable fact manifested by division underflow errors in modern programming languages: given an FMD $D_j$ and two signifiable real numbers a and b, with $a<b$, the set of signifiable real numbers in the closed interval between a and b is a proper finite subset of the set of real numbers $\mathbb{R}$. Thus, bijections are possible between $R_{a,b}^j$ and finite subsets of $\mathbb{N}$. While these bijections may differ from FMA to FMA in that they depend on the exact quantity of memory on a given FMA, they differ only in terms of the cardinalities of their domains and co-domains: the larger the quantity of memory, the greater the cardinality. A constructive interpretation of Lemmas 1 and 2 is that if we take two signifiable real numbers a and b such that $b-a\ge {\Delta }_j$, we can effectively enumerate the elements of $Z_{a,b}^j$ by iteratively adding increasing integer multiples of ${\Delta }_j$ to a until we reach b, i.e., $a+z{\Delta }_j=b$, or go slightly above it, i.e., $a+(z-1){\Delta }_j<b<a+z{\Delta }_j$, for $z>0$.

To map the elements of $R_{a,b}^j$ to ${\mathbb{N}}^{+}=\{1,2,3,\dots \}$, we define the bijection ${\mu }_{a,b}^j\left(x\right):R_{a,b}^j\mapsto I_{a,b}^j=\left\{z+1|z\in Z_{a,b}^j\right\}$ and its inverse ${{\mu }_{a,b}^j\left(x\right)}^{-1}:I_{a,b}^j\mapsto R_{a,b}^j$ as

$$\begin{array}{ccc}{\mu }_{a,b}^j\left(x\right)\hfill & =\hfill & {\psi }_{a,b}^j\left(x\right)+1;\hfill \\ {{\mu }_{a,b}^j}^{-1}\left(k\right)\hfill & =\hfill & {{\psi }_{a,b}^j}^{-1}(k-1),k>0.\hfill \end{array}$$

(5)

If we abbreviate ${\mu }_{0,1}^j$, ${{\mu }_{0,1}^j}^{-1}$, ${\psi }_{0,1}^j$, ${{\psi }_{0,1}^j}^{-1}$, $R_{0,1}^j$, and $Z_{0,1}^j$, $I_{0,1}^j$ to $\mu$, ${\mu }^{-1}$, $\psi$, ${\psi }^{-1}$, R, Z, and I, respectively, and let ${\Delta }_j=0.2$, we have the following example.

Example 1.

$$\begin{array}{c}R=\{0,0.2,0.4,0.6,0.8,1\};Z=\{0,1,2,3,4,5\};I=\{1,2,3,4,5,6\};\hfill \\ \psi \left(0\right)=0,\psi \left(0.2\right)=1,\psi \left(0.4\right)=2,\psi \left(0.6\right)=3,\psi \left(0.8\right)=4,\psi \left(1\right)=5;\hfill \\ {\psi }^{-1}\left(0\right)=0,{\psi }^{-1}\left(1\right)=0.2,{\psi }^{-1}\left(2\right)=0.4,{\psi }^{-1}\left(3\right)=0.6,{\psi }^{-1}\left(4\right)=0.8,{\psi }^{-1}\left(5\right)=1;\hfill \\ \mu \left(0\right)=1,\mu \left(0.2\right)=2,\mu \left(0.4\right)=3,\mu \left(0.6\right)=4,\mu \left(0.8\right)=5,\mu \left(1\right)=6;\hfill \\ {\mu }^{-1}\left(1\right)=0,{\mu }^{-1}\left(2\right)=0.2,{\mu }^{-1}\left(3\right)=0.4,{\mu }^{-1}\left(4\right)=0.6,{\mu }^{-1}\left(5\right)=0.8,{\mu }^{-1}\left(6\right)=1.\hfill \end{array}$$

For ${\Delta }_j=0.3$, we have another example.

Example 2.

$$\begin{array}{c}R=\{0,0.3,0.6,0.9,1\};Z=\{0,1,2,3,4\};I=\{1,2,3,4,5\};\hfill \\ \psi \left(0\right)=0,\psi \left(0.3\right)=1,\psi \left(0.6\right)=2,\psi \left(0.9\right)=3,\psi \left(1\right)=4;\hfill \\ {\psi }^{-1}\left(0\right)=0,{\psi }^{-1}\left(1\right)=0.3,{\psi }^{-1}\left(2\right)=0.6,{\psi }^{-1}\left(3\right)=0.9,{\psi }^{-1}\left(4\right)=1;\hfill \\ \mu \left(0\right)=1,\mu \left(0.3\right)=2,\mu \left(0.6\right)=3,\mu \left(0.9\right)=4,\mu \left(1\right)=5;\hfill \\ {\mu }^{-1}\left(1\right)=0,{\mu }^{-1}\left(2\right)=0.3,{\mu }^{-1}\left(3\right)=0.6,{\mu }^{-1}\left(4\right)=0.9,{\mu }^{-1}\left(5\right)=1.\hfill \end{array}$$

3. Computability: General vs. Actual

Computability theory lacks a uniform, commonly accepted formalism for computable, partially computable, and primitive recursive functions. The treatment of such functions in our article is based, in part, on the formalism by Davis, Sigal, and Weyuker (Chapters 2 and 3 in [7]), which has, in turn, much in common with Kleene’s formalism (Chapter 9 in  [8]). Alternative treatments include [9], where primitive recursive functions are formalized as loop programs consisting of assignment and iteration statements similar to DO statements in FORTRAN, and [10], where $\lambda$-calculus is used. These symbolically different treatments have one feature in common: computable, partially computable, and primitive recursive functions operate on natural numbers and the underlying automata, explicit or implicit, on which these functions can, in principle, be executed if implemented as programs in some formalism, have access to infinite numerical memory. To distinguish computability in principle from computability on finite memory automata, we introduce the categories of general and actual computabilities.

3.1. General Computability

As our formalism in this section, we use the programming language $\mathcal{L}$ developed in Chapter 2 in [7] and subsequently used in that book to define partially computable, computable, and primitive recursive functions and to prove various properties thereof. An $\mathcal{L}$ program $\mathcal{P}$ is a finite sequence of $\mathcal{L}$ instructions. The unique variable Y is designated as the output variable where the output of $\mathcal{P}$ on a given input is stored. $X_1,X_2,\dots$ designate input variables, and $Z_1,Z_2,\dots$ refer to internal variables, i.e., variables in $\mathcal{P}$ that are not input variables. No bounds are imposed on the magnitude of natural numbers assigned to variables. $\mathcal{L}$ has conditional dispatch instructions; line labels; elementary arithmetic operations on and comparisons of natural numbers; and macros, i.e., statements expandable into primitive $\mathcal{L}$ instructions.

A computation of $\mathcal{P}$ on some input $\overrightarrow{x}\in {\mathbb{N}}^m$, $m>0$, is a finite sequence of snapshots $(s_1,\dots ,s_k)$, where each snapshot $s_{1\le i\le k}$, $k>0$, specifies the number of the instruction in $\mathcal{P}$ to be executed and the value of each variable in $\mathcal{P}$. The snapshot $s_1$ is the initial snapshot, where the values of all input variables are set to their initial values, the program instruction counter is set to 1, i.e., the number of the first instruction in $\mathcal{P}$, and the values of all the other variables in $\mathcal{P}$ are set to 0. The snapshot $s_k$ in $(s_1,\dots ,s_k)$ is a terminal snapshot, where the instruction counter is set to the number of the instructions in $\mathcal{P}$ plus 1. Not all snapshot sequences are computations. If $(s_1,s_2,\dots ,s_k)$ is a computation of $\mathcal{P}$ on $\overrightarrow{x}\in {\mathbb{N}}^m$, i.e., $X_1=x_1$, $X_2=x_2$, …, $X_m=x_m$, then there is a function that, given the text of $\mathcal{P}$ and a snapshot $s_{1\le i<k}$ in the computation, generates the next snapshot $s_{i+1}$ of the computation. This function can verify if $(s_1,\dots ,s_k)$ constitutes the computation of $\mathcal{P}$ on $\overrightarrow{x}$. The existence of such functions implies that each instruction in $\mathcal{L}$ is interpreted unambiguously. If some program $\mathcal{P}$ in $\mathcal{L}$ takes m inputs and the values of the input variables are $X_1=x_1$, $X_2=x_2$, …, $X_m=x_m$, then

$${\mathsf{\Psi }}_{\mathcal{P}}^{\left(m\right)}(x_1,x_2,\dots ,x_m)=\left\{\begin{array}{cc}Y\mathrm{in}{s}_k\hfill & \mathrm{if}\exists \mathrm{a}\mathrm{computation}(s_1,\dots ,s_k),k\ge 1,\hfill \\ \uparrow \hfill & otherwise\hfill \end{array}\right.$$

(6)

denotes the value of Y in the terminal snapshot $s_k$ if there exists a computation $(s_1,\dots ,s_k)$ of $\mathcal{P}$ on $(x_1,x_2,\dots ,x_m)$ and is undefined otherwise.

Definition 1.

A function $f:{\mathbb{N}}^m\mapsto \mathbb{N}$, $m\in {\mathbb{N}}^{+}$, is partially computable if f is partial and there is an $\mathcal{L}$ program $\mathcal{P}$ such that Equation (7) holds.

$$(\forall \overrightarrow{x}\in {\mathbb{N}}^m)f\left(\overrightarrow{x}\right)={\mathsf{\Psi }}_{\mathcal{P}}^{\left(m\right)}\left(\overrightarrow{x}\right)$$

(7)

Equation (7) is interpreted so that $f\left(\overrightarrow{x}\right)\downarrow$ iff ${\mathsf{\Psi }}_{\mathcal{P}}^{\left(m\right)}\left(\overrightarrow{x}\right)\downarrow$ and $f\left(\overrightarrow{x}\right)\uparrow$ iff ${\mathsf{\Psi }}_{\mathcal{P}}^{\left(m\right)}\left(\overrightarrow{x}\right)\uparrow$.

Definition 2.

A function $f:{\mathbb{N}}^m\mapsto \mathbb{N}$, $0<m\in \mathbb{N}$, is computable if it is total, i.e., $(\forall \overrightarrow{x}\in {\mathbb{N}}^m)f\left(\overrightarrow{x}\right)\downarrow$, and partially computable.

Let $f:{\mathbb{N}}^k\mapsto \mathbb{N}$ and $g_i:{\mathbb{N}}^n\mapsto \mathbb{N}$, $1\le i\le k$, $n\in {\mathbb{N}}^{+}$. Then, $h:{\mathbb{N}}^n\mapsto \mathbb{N}$ is obtained by composition from $f,g_1,\dots ,g_k$ if

$$h(x_1,\dots ,x_n)=f(g_1(x_1,\dots ,x_n),\dots ,g_k(x_1,\dots ,x_n)).$$

(8)

Let $k\in \mathbb{N}$, $n\in {\mathbb{N}}^{+}$, and $\varphi :{\mathbb{N}}^2\mapsto \mathbb{N}$, $f:{\mathbb{N}}^n\mapsto \mathbb{N}$, $g:{\mathbb{N}}^{n+2}\mapsto \mathbb{N}$ be total. If h is obtained from $\varphi$ by the recurrences in (9) or from f and g by the recurrences in (10), then h is obtained from $\varphi$ or from f and g by primitive recursion or simply by recursion. The recurrences in (10) are isomorphic to Gödel’s recurrences (Section 2, Equation (2) in [6]) where he introduces the concept of recursively defined number-theoretic function. The three functions in (11) are the initial functions.

$$\begin{array}{ccc}h\left(0\right)\hfill & =\hfill & k,\hfill \\ h(t+1)\hfill & =\hfill & \varphi (t,h(t\left)\right)\hfill \end{array}$$

(9)

$$\begin{array}{ccc}h(x_1,\dots ,x_n,0)\hfill & =\hfill & f(x_1,\dots ,x_n),\hfill \\ h(x_1,\dots ,x_n,t+1)\hfill & =\hfill & g(t,h(x_1,\dots ,x_n,t),x_1,\dots ,x_n)\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill & s\left(x\right)=x+1;\hfill & \\ \hfill & n\left(x\right)=0;\hfill & \\ \hfill & u_i^n(x_1,\dots ,x_n)=x_i,1\le i\le n,\hfill & \end{array}$$

(11)

Definition 3.

A function is primitive recursive if it can be obtained from the initial functions by a finite number of applications of composition and recursion in (8)–(10).

An implication of Definition 3 is that if f is a primitive recursive function, then there is a sequence of functions $(f_1,\dots ,f_n=f)$, $n>0$, where every function in the sequence is an initial function or is obtained from the previous functions in the sequence by composition or recursion.

A class $\mathcal{C}$ of total functions is primitive recursively closed (PRC) if the initial functions are in it and any function obtained from the functions in $\mathcal{C}$ by composition or recursion is also in $\mathcal{C}$. It has been shown (Chapter 3 in [7]) that (1) the class of computable functions is PRC; (2) the class of primitive recursive functions is PRC; and (3) a function is primitive recursive iff it belongs to every PRC class. A corollary of (3) is that every primitive recursive function is computable.

If $\mathcal{C}$ includes all functions of a certain type, we refer to it as the class of those functions, e.g., the class of partially computable functions, the class of computable functions, the class of primitive recursive functions, etc. When we say that ${\mathcal{C}}^{\prime }$ is a class of functions of a certain type, we mean that ${\mathcal{C}}^{\prime }\subseteq \mathcal{C}$, where $\mathcal{C}$ is the class of functions of that type.

3.2. Actual Computability

In general, the FMA defined in Section 2.2 is different from the finite state automata of classical computability theory, because the latter, e.g., a Turing machine (TM), do not impose any limitations on memory. A TM becomes an FMA iff the number of cells on its tape where it reads and writes symbols is finite. Analogously, a finite state automaton (FSA) of classical computability is an FMA iff there is a limit, expressed as a natural number, on the length of the input tape from which the FSA reads sign sequences over a given alphabet.

As is the case with general computability, we let $P_L^j$ be a L program, i.e., a finite sequence of unambiguous instructions in a programming language L for an FMD $D_j$. Thus, if $D_j$ is a physical computer with an operating system, e.g., Linux, a programming language for $D_j$ can be Lisp, C, Perl, Python, etc. If $D_j$ is an abstract FMA, e.g., a TM with a finite number of cells on its tape, then $D_j$ is programmed with the standard quadruple formalism (Chapter 6 in  [7]). If $D_j$ is a mechanical device, then we assume that there is a formalism that consists of instructions such as “set switch i to position p”, “turn handle full circle clockwise t times”, etc. A state of $D_j$ while executing $P_L^j$ on some input $\overrightarrow{x}$ includes the number of the instruction in $P_L^j$ to execute next and, depending on $D_j$, may include the contents of each register, the signs on the finite input tape, or the state of each mechanical switch. As we did with general computability, we call such a state a snapshot of $D_j$ for $P_L^j\left(\overrightarrow{x}\right)$ and define a computation of $P_L^j\left(\overrightarrow{x}\right)$ on $D_j$ to be a finite sequence of snapshots $(s_1,\dots ,s_k)$, $k\ge 1$, where each subsequent snapshot is computed from the previous snapshot, the initial snapshot $s_1$ has the values of all the variables in $P_L^j$ appropriately specified and the instruction counter of $P_L^j$ set to 1, and the terminal snapshot $s_k$ has the instruction counter set to the number of the instructions in $P_L^j$ plus 1. We let

$${\mathsf{\Psi }}_{P_L^j}^{\left(n\right)}\left(\overrightarrow{x}\right)$$

denote the number sign corresponding to the output of $P_L^j\left(\overrightarrow{x}\right)$ executed on $D_j$. It is irrelevant to our discussion where this number sign is stored (e.g., in a register, a section of a finite tape, or the sequence of the positions of the mechanical switches examined left to right or right to left, etc.) so long as it is understood that the output, whenever there is a computation, is unambiguously interpreted as a real number according to an interpretation fixed a priori.

Definition 4.

A partial function $f:{\mathbb{R}}^m\mapsto \mathbb{R}$, $m\in {\mathbb{N}}^{+}$, is actually partially computable on $D_j$ if Equation (12) holds.

$$(\forall \overrightarrow{x}\in {\mathbb{R}}^m)f\left(\overrightarrow{x}\right)={\mathsf{\Psi }}_{P_L^j}^{\left(m\right)}\left(\overrightarrow{x}\right).$$

(12)

Equation (12) of actual computability is interpreted so that $f\left(\overrightarrow{x}\right)\downarrow$ iff ${\mathsf{\Psi }}_{\mathcal{P}}^{\left(m\right)}\left(\overrightarrow{x}\right)\downarrow$, i.e., $f\left(\overrightarrow{x}\right)=z$ iff ${\mathsf{\Psi }}_{\mathcal{P}}^{\left(m\right)}\left(\overrightarrow{x}\right)=z$, for any $\overrightarrow{x}\in {\mathbb{R}}^m$ and $z\in \mathbb{R}$ signifiable on $D_j$, and $f\left(\overrightarrow{x}\right)\uparrow$ iff ${\mathsf{\Psi }}_{\mathcal{P}}^{\left(m\right)}\left(\overrightarrow{x}\right)\uparrow$. However, unlike Equation (7) of general computability, which is defined only on natural numbers and every natural number is signifiable by implication, in actual computability, we have to make provisions for non-signifiable real numbers. Toward that end, we introduce the following inequality, which holds when a non-signifiable number is encountered during a computation of $P_L^j\left(\overrightarrow{x}\right)$.

$$(\exists \overrightarrow{x}\in {\mathbb{R}}^m)f\left(\overrightarrow{x}\right)\ne {\mathsf{\Psi }}_{P_L^j}^{\left(m\right)}\left(\overrightarrow{x}\right).$$

(13)

Inequality (13) can be illustrated with two examples. Let $D_j$ have two cells per register, let $f:{\mathbb{N}}^2\mapsto \mathbb{N}$ be $f(x_1,x_2)=x_1+x_2$, and let $P_L^j(x_1,x_2)$ be a program that implements f, i.e., adds two number signs of $x_1$ and $x_2$ and puts the number sign of $x_1+x_2$ in a designated output register. Let number signs be interpreted in standard decimal notation. Furthermore, if some number x is not signifiable on $D_j$, only the first two elementary signs of the number sign of x are placed into a register, i.e., number signs are truncated to fit into registers, as is common in many programming languages. Then, after “100” is truncated to “10”,

$$f(99,1)=100\ne {\mathsf{\Psi }}_{P_L^j}^{\left(2\right)}(99,1)=10,$$

and

$$f(213,13)=226\ne {\mathsf{\Psi }}_{P_L^j}^{\left(2\right)}(213,13)=34,$$

because 213 is not signifiable on $D_j$ and is truncated to “21.” In both cases, $f(x_1,x_2)$, as a mathematical object, is total, and there is a computation of $P_L^j(x_1,x_2)$ on $x_1=99,x_2=1$ and $x_1=213,x_2=13$, but during both computations, non-signifiable numbers, i.e., 100 and 213, are encountered.

Definition 5.

A function $f:{\mathbb{R}}^m\mapsto \mathbb{R}$, $m\in {\mathbb{N}}^{+}$, is actually computable on $D_j$ if it is total, i.e., $(\forall \overrightarrow{x}\in {\mathbb{R}}^m)f\left(\overrightarrow{x}\right)\downarrow$, and actually partially computable.

A program $P_L^j$ that implements an actually computable $f\left(\overrightarrow{x}\right)$ is guaranteed to have a computation for any signifiable $\overrightarrow{x}$. However, Inequality (13) may still hold if a non-signifiable number is produced during a computation. Functions can be defined for a specific $D_j$ so that they deal only with signifiable numbers, e.g., whose domains and codomains are, respectively, finite signifiable proper subsets of ${\mathbb{R}}^m$ and $\mathbb{R}$. The next definition characterizes these functions.

Definition 6.

A function $f:{\mathbb{R}}^m\mapsto \mathbb{R}$, $m\in {\mathbb{N}}^{+}$, is absolutely actually computable on $D_j$ if it is actually computable and Inequality (13) holds for no computation of $P_L^j\left(\overrightarrow{x}\right)$, where $\overrightarrow{x}$ is signifiable on $D_j$.

An implication of Definitions 4–6 is that if $f:{\mathbb{N}}^m\mapsto \mathbb{N}$ satisfies Definition 4, it is partially computable according to Definition 1, and if it satisfies Definitions 5 or 6, it is computable according to Definition 2, because, if no memory limitations are placed on registers, every natural number is signifiable.

We call an FMD $D_j$ sufficiently significant if three conditions are satisfied. First, a programming language L for $D_j$ exists with the same control structures as the programming language $\mathcal{L}$ described in Section 3.1 such that L (1) is capable of signifying a finite subset of $\mathbb{R}$ and (2) capable of specifying the following operations on numbers: addition, subtraction, multiplication, division, assignment, i.e., setting the value of a register to a number sign, comparison, i.e., $a=b$, $a<b$, $a>b$, $a\le b$, $a\ge b$, on any signifiable a and b, and the truncation of the signs of non-signifiable numbers to fit them into registers. Second, the finite memory of $D_j$ suffices to hold L programs of length $\le N\in {\mathbb{N}}^{+}$, where the length of the program is the number of instructions in it. Third, the finite memory of $D_j$ suffices, in addition to holding a program of at most N instructions, to hold number signs in $K\in {\mathbb{N}}^{+}$ registers.

Lemma 3.

Let an FMA $D_j$ be sufficiently significant with $K\ge 7$, $a,b$ signifiable, $b-a\ge {\Delta }_j$, and let $a+z{\Delta }_j$, $z>0$, be the smallest signifiable number greater than or equal to b. Let ${\mu }_{a,b}^j$: $R_{a,b}^j$↦$I_{a,b}^j$ be the bijection in (5). Let $P_L^j\left(x\right)$, $x\in R_{a,b}^j$, be a program for $D_j$ that iterates from a to $a+z{\Delta }_j\ge b$ in positive unit integer increments of ${\Delta }_j$ until k or z that satisfies the conditions in (3) is encountered, and the length of $P_L^j$$\le N$. Then, ${\mu }_{a,b}^j$ is absolutely actually computable.

Proof. 

Since $a,b$, and $a+z{\Delta }_j$ are signifiable, so are $dom\left({\mu }_{a,b}^j\right)$ and $codom\left({\mu }_{a,b}^j\right)$. The finite memory of $D_j$ suffices to hold $P_L^j$, and $P_L^j$ needs access to five signifiable numbers to iterate over $dom\left({\mu }_{a,b}^j\right)$: a, b, i, ${\Delta }_j$, $a+i{\Delta }_j$. Since $K\ge 7$, the signs of these numbers are placed in registers ${\rho }_1$, ${\rho }_2$, ${\rho }_3$, ${\rho }_4$, and ${\rho }_5$. After $x\in dom\left({\mu }_{a,b}^j\right)$ is placed in register ${\rho }_6$, $P_L^j$ sets ${\rho }_3$ to 0. If $x<b$, $P_L^j$ goes into a while loop with the condition of ${\rho }_5<{\rho }_2$, i.e., $a+i{\Delta }_j<b$. Inside the loop, when ${\rho }_5={\rho }_6$, ${\rho }_3$ is incremented by 1 and placed into the output register ${\rho }_7$, and $P_L^j$ exits. Otherwise, the loop continues with ${\rho }_3$ incremented by 1. If $x=b$, $P_L^j$ goes into a while loop with the condition of ${\rho }_5\le {\rho }_2$, i.e., $a+i{\Delta }_j\le b$, and keeps incrementing ${\rho }_3$ by 1 inside the loop. After the loop terminates, ${\rho }_3$ is incremented by 1 and placed into the output register ${\rho }_7$, and $P_L^j$ exits.    □

A corollary of Lemma 3 is that ${{\mu }_{a,b}^j}^{-1}$ is absolutely actually computable.

4. A Recursive Formalization of Feedforward Artificial Neural Networks

A trained feedforward artificial neural network (FANN) $N_z^j$ implemented in a programming language L on a sufficiently significant FMA $D_j$ is a finite set of artificial neurons, each of which is connected to a finite number of the neurons in the same set through the synapses, i.e., directed weighted edges (See Figure 1). The neurons are organized into $k+1$ layers $E_0,E_1,\dots ,E_k$, with $E_0$ being the input layer; $E_k$ being the output layer; and $E_e$, $0<e<k$, being the hidden layers. We let $E_z^j$ denote the number of layers in $N_z^j$ and $n_{z,i}^{j,e}$ refer to the i-th neuron in layer $E_e$ in $N_z^j$. We abbreviate $n_{z,i}^{j,e}$ to $n_i^e$, because $n_i^e$ always refers to a unique neuron in $N_z^j$. The function $n{n}_z^j\left(e\right):\mathbb{N}\mapsto {\mathbb{N}}^{+}$ specifies the number of neurons in layer $E_e$ of $N_z^j$ and is abbreviated $nn\left(e\right)$.

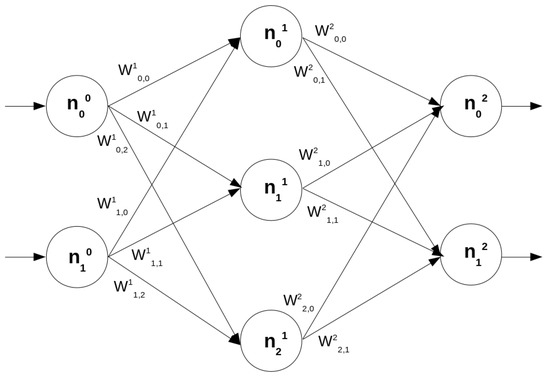
Figure 1. A 3-layer fully connected feedforward artificial neural network (FANN); layer 0 includes the neurons $n_0^0$ and $n_1^0$; layer 1 includes the neurons $n_0^1$, $n_1^1$, and $n_2^1$; layer 2 includes the neurons $n_0^2$ and $n_1^2$; the two arrows coming into $n_0^0$ and $n_1^0$ signify that layer 0 is the input layer; the two arrows going out of $n_0^2$ and $n_1^2$ signify that layer 2 is the output layer; $w_{i,j}^e$, $0<e<3$, is the weight of the synapse from $n_i^{e-1}$ to $n_j^e$, e.g., $w_{0,0}^1$ is the weight of the synapse from $n_0^0$ to $n_0^1$ and $w_{2,1}^2$ is the weight of the synapse from $n_2^1$ to $n_1^2$.

We assume that $N_z^j$ is trained, i.e., the synapse weights are fixed automatically or manually, and fully connected, i.e., there is a synapse from every neuron in layer $E_{e-1}$ to every neuron in layer $E_e$. Each synapse has a weight, i.e., a signifiable real number, associated with it. We let $w_{i,j}^e$, $0<e<E_z^j$, denote the weight of the synapse from $n_i^{e-1}$ to $n_j^e$ (see Figure 1) and ${\overrightarrow{w}}^e$ refer to a vector of all synaptic weights between $E_{e-1}$ and $E_e$. We define ${\overrightarrow{w}}^0=\left(\right)$. Thus, for the FANN $N_z^j$ in Figure 1, ${\overrightarrow{w}}^1=\left(w_{0,0}^1,w_{0,1}^1,w_{0,2}^1,w_{1,0}^1,w_{1,1}^1,w_{1,2}^1\right)$ and ${\overrightarrow{w}}^2=\left(w_{0,0}^2,w_{0,1}^2,w_{1,0}^2,w_{1,1}^2,w_{2,0}^2,w_{2,1}^2\right)$. We assume, without loss of generality, that all numbers in ${\overrightarrow{w}}^e$ are in $R_{0,1}^j$ defined in (1), because, if that is not the case, they can be so scaled, nor is there any loss of generality associated with the assumption of full connectivity, because partial connectivity can be defined by setting the weights of the appropriate synapses to 0.

If $R_{0,1}^j$ is abbreviated to $R_{0,1}$, each $n_i^e$ in $N_z^j$, $e>0$, computes an activation function

$${\alpha }_i^e\left({\overrightarrow{a}}^{e-1},{\overrightarrow{w}}^e\right):{R_{0,1}}^{nn(e-1)}\mapsto R_{0,1},$$

(14)

where ${\overrightarrow{a}}^{e-1}$ is the vector of the activations, i.e., real signifiable numbers, of the neurons in layer $E_{e-1}$. For $e=0$,

$${\alpha }_i^0(\overrightarrow{x},())={\overrightarrow{x}}_i,$$

(15)

where $\overrightarrow{x}\in {R_{0,1}}^{nn\left(0\right)}$ and ${\overrightarrow{x}}_i\in R_{0,1}$, $0\le i<nn\left(0\right)$. Thus, if $nn\left(0\right)=3$, as in Figure 1, then, given the input $\overrightarrow{x}=(x_0,x_1,x_2)=(0.0,0.3,0.6)$, ${\alpha }_0^0(\overrightarrow{x},())={\overrightarrow{x}}_0=x_0=0.0$, ${\alpha }_1^0(\overrightarrow{x},())={\overrightarrow{x}}_1=x_1=0.3$, ${\alpha }_2^0(\overrightarrow{x},())={\overrightarrow{x}}_2=x_2=0.6$. Since $N_z^j$ is implemented on a sufficiently significant $D_j$, all activation functions ${\alpha }_i^e(·)$ are absolutely actually computable. It is irrelevant to our discussion whether the activation functions are the same, e.g., sigmoid, for all or some neurons, or each neuron has its own activation function.

The term feedforward means that the activations of the neurons are computed layer by layer from the input layer to the output layer, because the activation functions of the neurons in the next layer require only the weights of the synapses connecting the next layer with the previous one and the activation values, i.e., the outputs of the activation functions of the neurons in the previous layer. To define the activation vectors of individual layers, let

$$\begin{array}{ccc}{\overrightarrow{a}}^0\hfill & =\hfill & \left({\alpha }_0^0\left(\overrightarrow{x},\left(\right)\right),\dots {\alpha }_{nn\left(0\right)-1}^0\left(\overrightarrow{x},\left(\right)\right)\right),\hfill \\ {\overrightarrow{a}}^e\hfill & =\hfill & \left({\alpha }_0^e\left({\overrightarrow{a}}^{e-1},{\overrightarrow{w}}^e\right),\dots ,{\alpha }_{nn\left(e\right)-1}^e\left({\overrightarrow{a}}^{e-1},{\overrightarrow{w}}^e\right)\right),\hfill \end{array}$$

(16)

where $0<e<E_z^j$ and $\overrightarrow{x}$ is an input vector. For each $N_z^j$, we define the absolutely actually computable function that $N_z^j$ computes as

$$\begin{array}{ccc}{f}_z^j(\overrightarrow{x},0)\hfill & =\hfill & \overrightarrow{x},\hfill \\ f_z^j(\overrightarrow{x},e+1)\hfill & =\hfill & \left({\alpha }_0^{e+1}\left(f_z^j\left(\overrightarrow{x},e\right),{\overrightarrow{w}}^{e+1}\right),\dots ,{\alpha }_{nn(e+1)-1}^{e+1}\left(f_z^j\left(\overrightarrow{x},e\right),{\overrightarrow{w}}^{e+1}\right)\right).\hfill \end{array}$$

(17)

If $e>E_z^j-1$, let $f(\overrightarrow{x},e)=\left(\right)$. The function $f_z^j$ in (17) computes the feedforward activation of $N_z^j$ layer by layer, i.e., $f(\overrightarrow{x},0)={\overrightarrow{a}}^0,f(\overrightarrow{x},1)={\overrightarrow{a}}^1,\dots ,f(\overrightarrow{x},E_z^j-1)={\overrightarrow{a}}^{E_z^j-1}$. For example, if $\overrightarrow{x}=(x_0,x_1)\in {R_{0,1}}^2$ is the input to $N_z^j$ in Figure 1,

$$\begin{array}{ccc}{f}_z^j(\overrightarrow{x},0)\hfill & =\hfill & {\overrightarrow{a}}^0=\overrightarrow{x};\hfill \\ f_z^j(\overrightarrow{x},1)\hfill & =\hfill & \left({\alpha }_0^1\left(f_z^j\left(\overrightarrow{x},0\right),{\overrightarrow{w}}^1\right),{\alpha }_1^1\left(f_z^j\left(\overrightarrow{x},0\right),{\overrightarrow{w}}^1\right),{\alpha }_2^1\left(f_z^j\left(\overrightarrow{x},0\right),{\overrightarrow{w}}^1\right)\right)\hfill \\ \hfill & =\hfill & \left({\alpha }_0^1\left({\overrightarrow{a}}^0,{\overrightarrow{w}}^1\right),{\alpha }_1^1\left({\overrightarrow{a}}^0,{\overrightarrow{w}}^1\right),{\alpha }_2^1\left({\overrightarrow{a}}^0,{\overrightarrow{w}}^1\right)\right)\hfill \\ \hfill & =\hfill & {\overrightarrow{a}}^1\in {R_{0,1}^j}^3;\hfill \\ f_z^j(\overrightarrow{x},2)\hfill & =\hfill & \left({\alpha }_0^2\left(f_z^j\left(\overrightarrow{x},1\right),{\overrightarrow{w}}^2\right)\right),{\alpha }_1^2\left(f_z^j\left(\overrightarrow{x},1\right),{\overrightarrow{w}}^2\right))\hfill \\ \hfill & =\hfill & \left({\alpha }_0^2\left({\overrightarrow{a}}^1,{\overrightarrow{w}}^2\right),{\alpha }_1^2\left({\overrightarrow{a}}^1,{\overrightarrow{w}}^2\right)\right)\hfill \\ \hfill & =\hfill & {\overrightarrow{a}}^2\in {R_{0,1}^j}^2.\hfill \end{array}$$

5. Finite Sets as Gödel Numbers

Our primitive recursive techniques to pack finite sets and Cartesian powers thereof into Gödel numbers in this section rely, in part, on our previous work on primitive recursive characteristics of chess [11], which, in turn, was based on several functions shown to be primitive recursive in [7]. For the reader’s convenience, Appendix A.1 in Appendix A gives the functions shown to be primitive recursive in [7] and gives the necessary auxiliary definitions and theorems. Appendix A.2 in Appendix A gives the functions or variants thereof shown to be primitive recursive in [11]. When we use the functions from [7,11] in this section, we refer to their definitions in the above two sections of Appendix A as necessary.

Let G be a Gödel number (G-number) as defined in (A8). The primitive recursive predicate $GP$ in (18) uses the bounded existential quantification of a primitive recursive predicate defined in (A2) and the primitive recursive functions ${\left(x\right)}_i$ and $Lt\left(x\right)$, respectively, defined in (A9) and (A10).

$$\begin{array}{ccc}GP\left(G\right)\hfill & \equiv \hfill & \{Lt\left(G\right)>0\}\wedge \{\{Lt\left(G\right)=1\wedge Lt\left({\left(G\right)}_1\right)>0\}\vee \hfill \\ \hfill & \hfill & \{{(\forall t)}_{\le Lt\left(G\right)}\{\{t>1\}\to \{\{Lt\left({\left(G\right)}_t\right)=Lt\left({\left(G\right)}_1\right)\}\wedge \{Lt\left({\left(G\right)}_t\right)>0\}\}\}\}\}\hfill \end{array}$$

(18)

The logical structure of $GP$ is $G{P}_1\wedge \{G{P}_2\vee G{P}_3\}$, where $G{P}_1$, $G{P}_2$, and $G{P}_3$ are

$$\begin{array}{ccc}G{P}_1\hfill & \equiv \hfill & \left\{Lt\right(G)>0\};\hfill \\ G{P}_2\hfill & \equiv \hfill & \{Lt\left(G\right)=1\wedge Lt\left({\left(G\right)}_1\right)>0\};\hfill \\ G{P}_3\hfill & \equiv \hfill & {(\forall t)}_{\le Lt\left(G\right)}\{\{t>1\}\to \{\{Lt\left({\left(G\right)}_t\right)=Lt\left({\left(G\right)}_1\right)\}\wedge \{Lt\left({\left(G\right)}_t\right)>0\}\}\}.\hfill \end{array}$$

The predicate $GP$ holds for G-numbers with at least one element and whose elements themselves have the same length, i.e., the same number of elements, greater than 0. Thus, $GP\left(\right[\left[1\right]\left]\right)$, $GP\left(\right[\left[1\right],\left[2\right],\left[3\right]\left]\right)$, and $GP\left(\right[[1,2],[3,4],[5,6]\left]\right)$, but $\neg GP\left(\right[\left[0\right]\left]\right)$ and $\neg GP\left(\right[\left[1\right],[3,4,5],[11,10]\left]\right)$.

Let G be a G-number, the predicate ${\in }_g$ be as defined in  (A13), the function $s\left(t\right)$ be as defined in (11), and the function $x{\otimes }_{l}y$ be as defined in (A15), and let

$$\begin{array}{ccc}\tau {\chi }_0(G,0)\hfill & =\hfill & 1,\hfill \\ \tau {\chi }_0(G,t+1)\hfill & =\hfill & \left[\left[{\left(G\right)}_{s\left(t\right)}\right]\right]{\otimes }_l\tau {\chi }_0(G,t).\hfill \end{array}$$

Then, the primitive recursive function

$${\tau }_0\left(G\right)=\left\{\begin{array}{cc}\tau {\chi }_0(G,Lt\left(G\right))\hfill & \mathrm{if}Lt\left(G\right)>0\wedge 0{\notin }_{g}G,\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(19)

turns a G-number into another G-number whose elements are the elements of the original G-number G, each of which is placed into a G-number whose length is 1. Thus, ${\tau }_0\left([11,13]\right)=[\left[11\right],\left[13\right]]$. In general, if $G=[g_1,\dots ,g_n]$, $Lt\left(G\right)>0$, $0{\notin }_{g}G$, i.e., $g_i\ne 0$, for $1\le i\le n$, then ${\tau }_0\left(G\right)=[\left[g_1\right],\dots ,\left[g_n\right]]$.

Let $g\in \mathbb{N}$, G be a G-number, the function $x{\otimes }_{r}y$ be defined in (A16), and

$$\begin{array}{ccc}\tau {\chi }_1(g,G,0)\hfill & =\hfill & 1,\hfill \\ \tau {\chi }_1(g,G,t+1)\hfill & =\hfill & \left[\left[g\right]{\otimes }_r\left[{\left(G\right)}_{s\left(t\right)}\right]\right]{\otimes }_l\tau {\chi }_1(g,G,t).\hfill \end{array}$$

Then, the primitive recursive function

$${\tau }_1(g,G)=\left\{\begin{array}{cc}\tau {\chi }_1(g,G,Lt\left(G\right))\hfill & \mathrm{if}g>0\wedge GP\left(G\right),\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(20)

adds g to each element of G. Thus, ${\tau }_1(1,[\left[2\right],\left[3\right]])=[[1,2],[1,3]]$ and ${\tau }_1(3,[[1,2],[4,5]])=[[3,1,2],[3,4,5]]$.

Let $G_1$ and $G_2$ be two G-numbers, and let

$$\begin{array}{ccc}\tau {\chi }_2(G_1,G_2,0)\hfill & =\hfill & 1,\hfill \\ \tau {\chi }_2(G_1,G_2,t+1)\hfill & =\hfill & {\tau }_1({\left(G_1\right)}_{s\left(t\right)},G_2){\otimes }_l\tau {\chi }_2(G_1,G_2,t).\hfill \end{array}$$

Then, the primitive recursive function

$${\tau }_2(G_1,G_2)=\left\{\begin{array}{cc}\tau {\chi }_2(G_1,G_2,Lt\left(G_1\right))\hfill & \mathrm{if}0{\notin }_g{G}_1\wedge GP\left(G_2\right)\wedge Lt\left(G_1\right)>0,\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(21)

adds each element of $G_1$ to each element of $G_2$. Thus,

$$\begin{array}{ccc}{\tau }_2(\left[1\right],[\left[2\right],\left[3\right]])\hfill & =\hfill & \left[\right[1,2],[1,3\left]\right];\hfill \\ {\tau }_2([1,2],[[4,5],[6,7]])\hfill & =\hfill & \left[\right[1,4,5],[1,6,7],[2,4,5],[2,6,7\left]\right].\hfill \end{array}$$

Let G be a G-number, and let

$$\begin{array}{ccc}\tau {\chi }_3(G,0)\hfill & =\hfill & {\tau }_0\left(G\right),\hfill \\ \tau {\chi }_3(G,t+1)\hfill & =\hfill & {\tau }_2(G,{\tau }_3(G,t)).\hfill \end{array}$$

Then, the primitive recursive function

$${\tau }_3(G,t)=\left\{\begin{array}{cc}\tau {\chi }_3(G,t)\hfill & \mathrm{if}0{\notin }_{g}G\wedge Lt\left(G\right)>0,\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(22)

computes, for $t\in {\mathbb{N}}^{+}$, a Gödel number whose components are Gödel numbers representing all sequences of $t+1$ elements of G. Thus,

$$\begin{array}{ccc}{\tau }_3([1,2],1)\hfill & =\hfill & \left[\right[1,1],[1,2],[2,1],[2,2\left]\right].\hfill \end{array}$$

Let $S=\{a_1,a_2,\dots ,a_n\}\subset {\mathbb{N}}^{+}$, $S\ne \varnothing$, and $G=[a_1,\dots ,a_n]$. An induction on t shows that, for $t>0$, ${\tau }_3(G,t-1)$ is a G-number representation of $S^t$ in the sense that $(a_{i_1},\dots ,a_{i_t})\in S^t$ iff $[a_{i_1},\dots ,a_{i_t}]{\in }_g{\tau }_3(G,t-1)$.

If $D_j$ is an FMA, we let

$$G_{a,b}^j=ggn\left(1,\left|R_{a,b}^j\right|,1\right),$$

(23)

where $R_{a,b}^j$ is defined in (2) and $ggn(·)$ is defined in (A17). If we recall from Lemma 2 and (5) that ${\mu }_{a,b}^j$: $R_{a,b}^j$↦$I_{a,b}^j$ = $\{1,\dots ,z+1\}$, where $a+z{\Delta }_j$ is the smallest signifiable real number $\ge b$ on $D_j$, we observe that $G_{a,b}^j$ is a G-number representation of $I_{a,b}^j$. Thus, if we return to Example 2 and use the accessor function ${\left(x\right)}_i$ in (A9), then for $G_{0,1}^j=[1,2,3,4,5]$, we have

$$\begin{array}{ccccc}\mu \left(0\right)\hfill & =\hfill & 1\hfill & =\hfill & {\left(G_{0,1}^j\right)}_1;\hfill \\ \mu \left(0.3\right)\hfill & =\hfill & 2\hfill & =\hfill & {\left(G_{0,1}^j\right)}_2;\hfill \\ \mu \left(0.6\right)\hfill & =\hfill & 3\hfill & =\hfill & {\left(G_{0,1}^j\right)}_3;\hfill \\ \mu \left(0.9\right)\hfill & =\hfill & 4\hfill & =\hfill & {\left(G_{0,1}^j\right)}_4;\hfill \\ \mu \left(1\right)\hfill & =\hfill & 5\hfill & =\hfill & {\left(G_{0,1}^j\right)}_5.\hfill \end{array}$$

In general, for $x\in R_{a,b}^j$,

$$\begin{array}{cccc}{\mu }_{a,b}^j\left(x\right)\hfill & =t\hfill & =\hfill & {\left(G_{a,b}^j\right)}_t\in I_{a,b}^j\hfill \\ \\ {{\mu }_{a,b}^j}^{-1}\left({\left(G_{a,b}^j\right)}_t\right)\hfill & \hfill & =\hfill & x.\hfill \end{array}$$

Let, for $t>1$, ${\tau }_3$ in (22), and $x\dot{-}y$ in (A4),

$$G_{a,b}^{t,j}={\tau }_3\left(G_{a,b}^j,t\dot{-}\right),$$

(24)

and, in particular, for $a=0$ and $b=1$, let

$$G_{0,1}^{t,j}={\tau }_3\left(G_{0,1}^j,t\dot{-}\right).$$

(25)

Then, $G_{0,1}^{t,j}$ is a G-number representation of ${I_{0,1}^j}^t$, i.e., the t-th Cartesian power of $I_{0,1}^j$. Since both ${\tau }_3$ and ∸ are primitive recursive functions, $G_{a,b}^{t,j}\in \mathbb{N}$ and $G_{0,1}^{t,j}\in \mathbb{N}$ are primitive recursively computable.

Example 3.

Let $R=\{0,0.3,0.6,0.9,1\}$, $I=\{1,2,3,4,5\}$ and $t=2$. Then,

$$\begin{array}{ccc}{G}_{0,1}^{2,j}\hfill & =\hfill & {\tau }_3(G_{0,1}^2,2\dot{-}1)\hfill \\ \hfill & =\hfill & {\tau }_3\left(ggn\right(1,\left|R\right|,1),1),1)\hfill \\ \hfill & =\hfill & {\tau }_3([1,2,3,4,5],1)\hfill \\ \hfill & =\hfill & \left[\right[1,1],[1,2],[1,3],[1,4],[1,5],\hfill \\ \hfill & \hfill & [2,1],[2,2],[2,3],[2,4],[2,5],\hfill \\ \hfill & \hfill & [3,1],[3,2],[3,3],[3,4],[3,5],\hfill \\ \hfill & \hfill & [4,1],[4,2],[4,3],[4,4],[4,5],\hfill \\ \hfill & \hfill & [5,1],[5,2],[5,3],[5,4],[5,5]].\hfill \end{array}$$

We note that $(x,y)\in I^2$ iff $[x,y]\in G_{0,1}^{2,j}$.

Let $\overrightarrow{x}\in {R_{a,b}^j}^t$, $t>0$, $\tilde{x}{\in }_g{G}_{a,b}^{t,j}$, and let ${\eta }_{a,b}^{t,j}:{R_{a,b}^j}^t\mapsto \mathbb{N}$ and ${\zeta }_{a,b}^{t,j}:\mathbb{N}\mapsto {R_{a,b}^j}^t$ be defined as

$$\begin{array}{ccc}{\eta }_{a,b}^{t,j}\left(\overrightarrow{x}\right)\hfill & =\hfill & \left[{\mu }_{a,b}^j\left({\overrightarrow{x}}_0\right),\dots {\mu }_{a,b}^j\left({\overrightarrow{x}}_{t-1}\right)\right]=\tilde{x};\hfill \\ \\ {\zeta }_{a,b}^{t,j}\left(\tilde{x}\right)\hfill & =\hfill & \left({{\mu }_{a,b}^j}^{-1}\left({\left(\tilde{x}\right)}_1\right),\dots ,{{\mu }_{a,b}^j}^{-1}\left({\left(\tilde{x}\right)}_t\right)\right).\hfill \end{array}$$

(26)

If $R_{a,b}^j$ is signifiable, ${\eta }_{a,b}^{t,j}\left(\overrightarrow{x}\right)=\tilde{x}$ iff ${\zeta }_{a,b}^{t,j}\left(\tilde{x}\right)=\overrightarrow{x}$, for any $\overrightarrow{x}\in {R_{a,b}^j}^t$. If $\tilde{x}$ is not signifiable, ${\eta }_{a,b}^{t,j}$ and ${\zeta }_{a,b}^{t,j}$ are actually computable; if $\tilde{x}$ is signifiable, the functions are absolutely actually computable.

Example 4.

To continue with Example 3, if $\overrightarrow{x}=(0.9,0.6)\in {R_{0,1}}^2$ and $\tilde{x}=[4,3]\in G_{0,1}^{2,j}$, then, if we abbreviate ${\eta }_{0,1}^2$, ${\zeta }_{0,1}^2$ to ${\eta }^2$, ${\zeta }^2$, we have

$$\begin{array}{ccccccc}{\eta }^2\left(\overrightarrow{x}\right)\hfill & =\hfill & \left(\mu \right(0.9),\mu (0.6\left)\right)\hfill & \hfill & & =\hfill & [4,3];\hfill \\ \\ {\zeta }^2\left(\tilde{x}\right)\hfill & =\hfill & ({\mu }^{-1}\left({\left(\tilde{x}\right)}_1\right),{\mu }^{-1}\left(\left({\tilde{x}}_2\right)\right))\hfill & =\hfill & ({\mu }^{-1}\left(4\right),{\mu }^{-1}\left(3\right))\hfill & =\hfill & (0.9,0.6).\hfill \end{array}$$

6. Numbers ${\mathbf{\Omega }}_{\mathbf{z},\mathbf{i}}^{\mathbf{j},\mathbf{e}}$ and ${\mathbf{\Omega }}_{\mathbf{z}}^{\mathbf{j}}$: Packing FANNs into Natural Numbers

Let us assume that ${\mu }_{0,1}^j$ is absolutely actually computable on a sufficiently significant FMA $D_j$ and abbreviate ${\mu }_{0,1}^j$ to $\mu$, ${\zeta }_{0,1}^{t,j}$ to ${\zeta }^t$, and $G_{0,1}^{t,j}$ in (25) to $G^t$. Let $⟨x,y⟩$ be as defined in (A5) and $Lt\left(x\right)$ be as defined in (A10). Then, for each input neuron $n_i^0$ in an FANN $N_z^j$, let

$$\begin{array}{ccc}{\mathsf{\Omega }}_{z,i}^{j,0}={\mathsf{\Omega }}_i^0=\hfill & \hfill & \\ \\ [⟨{\left(G^{nn\left(0\right)}\right)}_1,\mu \left({\alpha }_i^0\left({\zeta }^{nn\left(0\right)}\left({\left(G^{nn\left(0\right)}\right)}_1\right),\left(\right)\right)\right)⟩,\hfill & \hfill & \\ \\ \dots ,\hfill & \hfill & \\ \\ ⟨{\left(G^{nn\left(0\right)}\right)}_{Lt\left(G^{nn\left(0\right)}\right)},\mu \left({\alpha }_i^0\left({\zeta }^{nn\left(0\right)}\left({\left(G^{nn\left(0\right)}\right)}_{Lt\left(G^{nn\left(0\right)}\right)}\right),\left(\right)\right)\right)⟩].\hfill & \hfill & \end{array}$$

(27)

We recall that $E_z^j>0$ is the number of layers in $N_z^j$. Then, for a hidden or output neuron $n_i^e$, $0<e<E_z^j$, let

$$\begin{array}{ccc}{\mathsf{\Omega }}_{z,i}^{j,e}={\mathsf{\Omega }}_i^e=\hfill & \hfill & \\ \\ [⟨{\left(G^{nn(e-1)}\right)}_1,\mu \left({\alpha }_i^e\left({\zeta }^{nn(e-1)}\left({\left(G^{nn(e-1)}\right)}_1\right),{\overrightarrow{w}}^e\right)\right)⟩,\hfill & \hfill & \\ \\ \dots ,\hfill & \hfill & \\ \\ ⟨{\left(G^{nn(e-1)}\right)}_{Lt\left(G^{nn(e-1)}\right)},\mu \left({\alpha }_i^e\left({\zeta }^{nn(e-1)}\left({\left(G^{nn(e-1)}\right)}_{Lt\left(G^{nn(e-1)}\right)}\right),{\overrightarrow{w}}^e\right)\right)⟩].\hfill & \hfill & \end{array}$$

(28)

For an FANN $N_z^j$ on $D_j$ and $E=E_z^j-1$, let

$$\begin{array}{ccc}{\mathsf{\Omega }}_z^j\hfill & =\hfill & \left[⟨0,\left[{\mathsf{\Omega }}_0^0,\dots ,{\mathsf{\Omega }}_{nn\left(0\right)-1}^0\right]⟩,\dots ,⟨E,\left[{\mathsf{\Omega }}_0^E,\dots ,{\mathsf{\Omega }}_{nn\left(E\right)-1}^E\right]⟩\right].\hfill \end{array}$$

(29)

An implication of the definitions of $⟨x,y⟩$ in (A5) and the G-number in (A8) is that ${\mathsf{\Omega }}_z^j$ is unique for $N_z^j$, because the only way for another FANN $N_k^j$ on $D_j$ to have ${\mathsf{\Omega }}_k^j={\mathsf{\Omega }}_z^j$ is for $N_k^j$ to have the same number of layers, the same number of neurons in each layer, the same activation function in each neuron, and the same synapse weights between the same neurons, i.e., $N_k^j=N_z^j$. Appendix A.3 in Appendix A gives several examples of how the $\mathsf{\Omega }$ numbers are computed for $N_z^j$ in Figure 1.

Lemma 4.

Let ${\mu }_{0,1}^j$ be absolutely actually computable on a sufficiently significant FMA $D_j$ and let $N_z^j$ be an FANN implemented on $D_j$. Let $0\le i<nn\left(0\right)$, $0\le k<nn\left(e\right)$, $0<e<E_z^j$, and $G_{0,1}^{t,j}$ in (25) be signifiable on $D_j$. Then, ${\mathsf{\Omega }}_{z,i}^{j,0}={\mathsf{\Omega }}_i^0\in \mathbb{N}$ and ${\mathsf{\Omega }}_{z,i}^{j,e}={\mathsf{\Omega }}_i^e\in \mathbb{N}$.

Proof. 

We abbreviate ${\mu }_{0,1}^j$ to $\mu$, ${\zeta }_{0,1}^t$ to ${\zeta }^t$, and $G_{0,1}^{t,j}$ to $G^t$, and let

$$\begin{array}{ccc}{z}_0\hfill & =\hfill & \mu \left({\alpha }_i^0\left({\zeta }^{nn\left(0\right)}\left({\left(G^{nn\left(0\right)}\right)}_{t_0}\right),\left(\right)\right)\right);\hfill \\ z_e\hfill & =\hfill & \mu \left({\alpha }_k^e\left({\zeta }^{nn(e-1)}\left({\left(G^{nn(e-1)}\right)}_{t_{e-1}}\right),{\overrightarrow{w}}^e\right)\right),\hfill \end{array}$$

where $0<t_0\le nn\left(0\right)$ and $0<t_{e-1}\le nn(e-1)$. Since $\mu$ is absolutely actually computable and $G^t$ signifiable, ${\zeta }^{nn\left(0\right)},{\zeta }^{nn\left(1\right)},\dots ,{\zeta }^{nn(e-1)}$ are absolutely actually computable. Thus, $z_0,z_e\in \mathbb{N}$. The statement of the lemma then follows from the definitions of $⟨x,y⟩$ in (A5) and the G-number in (A8).    □

7. FANNs and Primitive Recursive Functions

For $0\le e<E_z^j$, $0\le i<nn\left(e\right)$, $x\in \mathbb{N}$, let

$$\begin{array}{ccc}{\tilde{\alpha }}_i^e\left(x\right)\hfill & =\hfill & r\left(asc\left(x,{\left(r\left(asc\left(e,{\mathsf{\Omega }}_z^j\right)\right)\right)}_{i+1}\right)\right),\hfill \end{array}$$

(30)

where $r(·)$ and $asc(·)$ are defined in (A6) and (A19), respectively. An example of computing ${\tilde{\alpha }}_i^e$ is given at the end of Appendix A.3 in the Appendix A.

Lemma 5.

Let ${\mu }_{0,1}^j$, abbreviated as μ, be absolutely actually computable on a sufficiently significant FMA $D_j$ and let $N_z^j$ be an FANN implemented on $D_j$. Let $G_{0,1}^t$ in (25), abbreviated as $G^t$, be signifiable. Let $0\le e<E_j^z$, ${\eta }_{0,1}^{t,j}\left(\overrightarrow{x}\right)={\eta }^t\left(\overrightarrow{x}\right)=\tilde{x}$ = $\left[\mu \left({\overrightarrow{a}}_0^e\right),\dots ,\mu \left({\overrightarrow{a}}_{nn\left(e\right)-1}^e\right)\right]\in \mathbb{N}$, where ${\overrightarrow{a}}^e$ is defined in (16). Then,

$${\tilde{\alpha }}_i^e\left(\tilde{x}\right)=\left\{\begin{array}{cc}\mu \left({\alpha }_i^0\left({\zeta }^{nn\left(0\right)}\left({\left(G^{nn\left(0\right)}\right)}_t\right),{\overrightarrow{w}}^0\right)\right)\hfill & \mathit{if}e=0,\hfill \\ \\ \mu \left({\alpha }_i^e\left({\zeta }^{nn(e-1)}\left({\left(G^{nn(e-1)}\right)}_t\right),{\overrightarrow{w}}^e\right)\right)\hfill & \mathit{if}e>0,\hfill \end{array}\right.$$

where $t=asx\left(\tilde{x},G^{nn\left(0\right)}\right)$, for $1\le t\le Lt\left(G^{nn\left(0\right)}\right)$ and $e=0$; $t=asx\left(\tilde{x},G^{nn(e-1)}\right)$, for $1\le t\le Lt\left(G^{nn(e-1)}\right)$ and $e>0$; and $asx$ is as defined in (A18).

Proof. 

By (28)–(30) and (A18), we have

$$\begin{array}{ccc}{\tilde{\alpha }}_i^e\left(\tilde{x}\right)\hfill & =\hfill & r\left(asc\left(\tilde{x},{\left(r\left(asc\left(e,{\mathsf{\Omega }}_z^j\right)\right)\right)}_{i+1}\right)\right)\hfill \\ \hfill & =\hfill & r\left(asc\left(\tilde{x},{\left(r\left(⟨e,\left[{\mathsf{\Omega }}_0^e,\dots ,{\mathsf{\Omega }}_{nn\left(e\right)-1}^e\right]⟩\right)\right)}_{i+1}\right)\right)\hfill \\ \hfill & =\hfill & r\left(asc\left(\tilde{x},{\left(\left[{\mathsf{\Omega }}_0^e,\dots ,{\mathsf{\Omega }}_{nn\left(e\right)-1}^e\right]\right)}_{i+1}\right)\right)\hfill \\ \hfill & =\hfill & r\left(asc\left(\tilde{x},{\mathsf{\Omega }}_i^e\right)\right)\hfill \end{array}$$

If $e=0$, then $t=asx\left(\tilde{x},G^{nn\left(0\right)}\right)$, for $1\le t\le Lt\left(G^{nn\left(0\right)}\right)$. Thus,

$$\begin{array}{ccccc}{\tilde{\alpha }}_i^e\left(\tilde{x}\right)\hfill & =\hfill & r\left(asc\left(\tilde{x},{\mathsf{\Omega }}_i^e\right)\right)\hfill & =\hfill & \mu \left({\alpha }_i^0\left({\zeta }^{nn\left(0\right)}\left(\tilde{x}\right)\right),\left(\right)\right).\hfill \end{array}$$

If $e>0$, then $t=asx\left(\tilde{x},G^{nn(e-1)}\right)$, for $1\le t\le Lt\left(G^{nn(e-1)}\right)$. Thus,

$$\begin{array}{ccccc}{\tilde{\alpha }}_i^e\left(\tilde{x}\right)\hfill & =\hfill & r\left(asc\left(\tilde{x},{\mathsf{\Omega }}_i^e\right)\right)\hfill & =\hfill & \mu \left({\alpha }_i^e\left({\zeta }^{nn(e-1)}\left(\tilde{x}\right)\right),{\overrightarrow{w}}^e\right).\hfill \end{array}$$

   □

If $e=0$ and ${\left(G^{nn\left(0\right)}\right)}_t=\tilde{x}$, for $0<t\le Lt\left(G^{nn\left(0\right)}\right)$, let

$$\begin{array}{ccc}{\tilde{a}}^0\hfill & =\hfill & \left[{\tilde{\alpha }}_0^0\left(\tilde{x}\right),\dots ,{\tilde{\alpha }}_{nn\left(0\right)-1}^0\left(\tilde{x}\right)\right].\hfill \end{array}$$

(31)

If $0<e<E_z^j$ and ${\left(G^{nn(e-1)}\right)}_t=\tilde{x}$, for $0<t\le Lt\left(G^{nn(e-1)}\right)$, let

$$\begin{array}{ccc}{\tilde{a}}^e\hfill & =\hfill & \left[{\tilde{\alpha }}_0^e\left(\tilde{x}\right),\dots ,{\tilde{\alpha }}_{nn\left(e\right)-1}^e\left(\tilde{x}\right)\right].\hfill \end{array}$$

(32)

Theorem 1.

Let $N_z^j$ be an FANN with $E_z^j>0$ layers on a sufficiently significant FMA $D_j$, and let $f_z^j(\overrightarrow{x},e)$ in (17) be absolutely actually computable. Let ${\mu }_{0,1}^j(·)$ be absolutely actually computable and $G_{0,1}^{t,j}$, for $t\in \left\{nn\left(e\right)\right|0\le e<E_z^j\}$, be signifiable. Then, if $\tilde{x}=\left[{\mu }_{0,1}^j\left({\overrightarrow{x}}_0\right),\dots ,{\mu }_{0,1}^j\left({\overrightarrow{x}}_{nn\left(0\right)-1}\right)\right]={\tilde{a}}^0={\eta }_{0,1}^{nn\left(0\right),j}\left(\overrightarrow{x}\right)$, where ${\eta }_{0,1}^{t,j}$ is defined in (26), there exists a primitive recursive function ${\tilde{f}}_z^j(\tilde{x},e)$ such that

$$\begin{array}{ccc}{f}_z^j(\overrightarrow{x},e)={\overrightarrow{a}}^e\hfill & \mathit{iff}\hfill & {\tilde{f}}_z^j(\tilde{x},e)={\tilde{a}}^e.\hfill \end{array}$$

Proof. 

Let us abbreviate $f_z^j$ to f, ${\mu }_{0,1}^j$ to $\mu$, ${{\mu }_{0,1}^j}^{-1}$ to ${\mu }^{-1}$, ${\eta }_{0,1}^{t,j}$ to ${\eta }^t$, ${\zeta }_{0,1}^{t,j}$ to ${\zeta }^t$, and $G_{0,1}^{t,j}$ to $G^t$. Since $G^t$ is signifiable, ${\zeta }^t$ and ${\eta }^t$ are absolutely actually computable. Let

$$\begin{array}{ccc}{\tilde{f}}_z^j(\tilde{x},0)\hfill & =\hfill & \tilde{x},\hfill \\ {\tilde{f}}_z^j(\tilde{x},e+1)\hfill & =\hfill & \left[{\tilde{\alpha }}_0^{e+1}\left({\tilde{f}}_z^j\left(\tilde{x},e\right)\right),\dots ,{\tilde{\alpha }}_{nn(e+1)-1}^{e+1}\left({\tilde{f}}_z^j\left(\tilde{x},e\right)\right)\right].\hfill \end{array}$$

Let us abbreviate ${\tilde{f}}_z^j$ to $\tilde{f}$, and let $e=0$. Then $f(\overrightarrow{x},0)={\overrightarrow{a}}^0=\overrightarrow{x}$ and $\tilde{f}(\tilde{x},0)=\tilde{x}$. We observe that

$$\begin{array}{ccc}\tilde{x}\hfill & =\hfill & \left[\mu \left({\overrightarrow{x}}_0\right),\dots ,\mu \left({\overrightarrow{x}}_{nn\left(0\right)-1}\right)\right]\hfill \\ \hfill & =\hfill & \left[\mu \left({\alpha }_0^0\left(\overrightarrow{x},\left(\right)\right)\right),\dots ,\mu \left({\alpha }_{nn\left(0\right)-1}^0\left(\overrightarrow{x},\left(\right)\right)\right)\right]\hfill \\ \hfill & =\hfill & {\eta }^{nn\left(0\right)}\left(\overrightarrow{x}\right).\hfill \end{array}$$

Since $\mu$ is an absolutely actually computable bijection,

$$\begin{array}{ccc}\overrightarrow{x}\hfill & =\hfill & ({\mu }^{-1}\left(\mu \left({\overrightarrow{x}}_0\right)\right),\dots ,{\mu }^{-1}\left(\mu \left({\overrightarrow{x}}_{nn\left(0\right)-1}\right)\right)\hfill \\ \hfill & =\hfill & \left({\mu }^{-1}\left({\left(\tilde{x}\right)}_1\right),\dots ,{\mu }^{-1}\left({\left(\tilde{x}\right)}_{nn\left(0\right)}\right)\right)\hfill \\ \hfill & =\hfill & {\zeta }^{nn\left(0\right)}\left(\tilde{x}\right).\hfill \end{array}$$

By (26), ${\eta }^{nn\left(0\right)}\left(\overrightarrow{x}\right)=\tilde{x}$ iff ${\zeta }^{nn\left(0\right)}\left(\tilde{x}\right)=\overrightarrow{x}$. Thus, $f(\overrightarrow{x},0)={\overrightarrow{a}}^0$ iff $\tilde{f}(\tilde{x},0)=\tilde{x}$.

Let $e=1$. Then,

$$\begin{array}{ccc}f(\overrightarrow{x},1)\hfill & =\hfill & {\overrightarrow{a}}^1\hfill \\ \hfill & =\hfill & \left({\alpha }_0^1\left({\overrightarrow{a}}^0,{\overrightarrow{w}}^1\right),\dots ,{\alpha }_{nn\left(1\right)-1}^1\left({\overrightarrow{a}}^0,{\overrightarrow{w}}^1\right)\right)\hfill \\ \hfill & =\hfill & \left({\alpha }_0^1\left(\overrightarrow{x},{\overrightarrow{w}}^1\right),\dots ,{\alpha }_{nn\left(1\right)-1}^1\left(\overrightarrow{x},{\overrightarrow{w}}^1\right)\right).\hfill \end{array}$$

By Lemma 5,

$$\begin{array}{ccc}\tilde{f}(\tilde{x},1)\hfill & =\hfill & \left[{\tilde{\alpha }}_0^1\left(\tilde{f}\left(\tilde{x},0\right)\right),\dots ,{\tilde{\alpha }}_{nn\left(1\right)-1}^1\left(\tilde{f}\left(\tilde{x},0\right)\right)\right]\hfill \\ \hfill & =\hfill & \left[{\tilde{\alpha }}_0^1\left(\tilde{x}\right),\dots ,{\tilde{\alpha }}_{nn\left(1\right)-1}^1\left(\tilde{x}\right)\right]\hfill \\ \hfill & =\hfill & \left[\mu \left({\alpha }_0^1\left(\overrightarrow{x},{\overrightarrow{w}}^1\right)\right),\dots ,\mu \left({\alpha }_{nn\left(1\right)-1}^1\left(\overrightarrow{x},{\overrightarrow{w}}^1\right)\right)\right]\hfill \\ \hfill & =\hfill & \left[\mu \left({\alpha }_0^1\left({\overrightarrow{a}}^0,{\overrightarrow{w}}^1\right)\right),\dots ,\mu \left({\alpha }_{nn\left(1\right)-1}^1\left({\overrightarrow{a}}^0,{\overrightarrow{w}}^1\right)\right)\right]\hfill \\ \hfill & =\hfill & \left[\mu \left({\overrightarrow{a}}_0^1,\right),\dots ,\mu \left({\overrightarrow{a}}_{nn\left(1\right)-1}^1\right)\right]\hfill \\ \hfill & =\hfill & {\tilde{a}}^1={\eta }^{nn\left(1\right)}\left({\overrightarrow{a}}^1\right).\hfill \end{array}$$

Since $\mu$ is an absolutely actually computable bijection,

$${\overrightarrow{a}}^1=\left({\mu }^{-1}\left(\mu \left({\left({\tilde{a}}^1\right)}_1\right)\right),\dots ,{\mu }^{-1}\left(\mu \left({\left({\tilde{a}}^1\right)}_{nn\left(1\right)}\right)\right)\right),$$

whence, since ${\zeta }^{nn\left(1\right)}\left({\tilde{a}}^1\right)={\overrightarrow{a}}^1$ iff ${\eta }^{nn\left(1\right)}\left({\overrightarrow{a}}^1\right)={\tilde{a}}^1$, $f(\overrightarrow{x},1)={\overrightarrow{a}}^1$ iff $\tilde{f}(\tilde{x},1)={\tilde{a}}^1$.

Let us assume $f(\overrightarrow{x},e)={\overrightarrow{a}}^e$ iff $\tilde{f}(\tilde{x},e)={\tilde{a}}^e$ for $e\ge 1$. Then,

$$\begin{array}{ccc}f(\overrightarrow{x},e+1)\hfill & =\hfill & {\overrightarrow{a}}^{e+1}\hfill \\ \hfill & =\hfill & ({\alpha }_0^{e+1}\left(f\left(\overrightarrow{x},e\right),{\overrightarrow{w}}^{e+1}\right),\dots ,{\alpha }_{nn(e+1)-1}^{e+1}\left(f\left(\overrightarrow{x},e\right),{\overrightarrow{w}}^{e+1}\right)\hfill \\ \hfill & =\hfill & \left({\alpha }_0^{e+1}\left({\overrightarrow{a}}^e,{\overrightarrow{w}}^{e+1}\right),\dots ,{\alpha }_{nn(e+1)-1}^{e+1}\left({\overrightarrow{a}}^e,{\overrightarrow{w}}^{e+1}\right)\right),\hfill \end{array}$$

and

$$\begin{array}{ccc}\tilde{f}(\tilde{x},e+1)\hfill & =\hfill & \left[{\tilde{\alpha }}_0^{e+1}\left(\tilde{f}\left(\tilde{x},e\right)\right),\dots ,{\tilde{\alpha }}_{nn(e+1)-1}^{e+1}\left(\tilde{f}\left(\tilde{x},e\right)\right)\right]\hfill \\ \hfill & =\hfill & \left[{\tilde{\alpha }}_0^{e+1}\left({\tilde{a}}^e\right),\dots ,{\tilde{\alpha }}_{nn(e+1)-1}^{e+1}\left({\tilde{a}}^e\right)\right]\hfill \\ \hfill & =\hfill & \left[\mu \left({\alpha }_0^{e+1}\left({\overrightarrow{a}}^e,{\overrightarrow{w}}^{e+1}\right)\right),\dots ,\mu \left({\alpha }_{nn(e+1)-1}^{e+1}\left({\overrightarrow{a}}^e,{\overrightarrow{w}}^{e+1}\right)\right)\right]\hfill \\ \hfill & =\hfill & {\eta }^{nn(e+1)}\left({\overrightarrow{a}}^{e+1}\right).\hfill \end{array}$$

Then,

$${\overrightarrow{a}}^{e+1}=\left({\mu }^{-1}\left(\mu \left({\left({\tilde{a}}^{e+1}\right)}_1\right)\right),\dots ,{\mu }^{-1}\left(\mu \left({\left({\tilde{a}}^{e+1}\right)}_{nn(e+1)}\right)\right)\right),$$

whence, by induction, since ${\zeta }^{nn(e+1)}\left({\tilde{a}}^{e+1}\right)={\overrightarrow{a}}^{e+1}$ iff ${\eta }^{nn(e+1)}\left({\overrightarrow{a}}^{e+1}\right)={\tilde{a}}^{e+1}$, $f(\overrightarrow{x},e+1)={\overrightarrow{a}}^{e+1}$ iff $\tilde{f}(\tilde{x},e+1)={\tilde{a}}^{e+1}$.    □

Let, for $\overrightarrow{x}\in {R_{0,1}^j}^{nn\left(0\right)}$ and $E_z^j>0$,

$$A_z^j\left(\overrightarrow{x}\right)=f_z^j(\overrightarrow{x},E_z^j-1),$$

(33)

and, for $\tilde{x}={\eta }^{nn\left(0\right)}\left(\overrightarrow{x}\right)$, let

$${\tilde{A}}_z^j\left(\overrightarrow{x}\right)={\tilde{f}}_z^j(\tilde{x},E_z^j\dot{-}1).$$

(34)

Then, $A_z^j\left(\overrightarrow{x}\right)$ is the absolutely actually computable function computed by $N_z^j$ and, by Theorem 1, ${\tilde{A}}_z^j$ is primitive recursive. We are now in a position to prove the final theorem of this article.

Theorem 2.

Let

$${\mathcal{N}}_j=\left\{N_1^j,N_2^j,\dots ,N_k^j\right\},k\in {\mathbb{N}}^{+},$$

(35)

be the set of FANNs implemented on a sufficiently significant FMA $D_j$, and let

$${\mathcal{A}}_j=\left\{A_1^j,A_2^j,\dots ,A_k^j\right\},k\in {\mathbb{N}}^{+},$$

(36)

be the set of corresponding absolutely actually computable functions of the FANNs in ${\mathcal{N}}_j$, as defined in (33). There exists a bijection between ${\mathcal{N}}_j$ and a class of primitive recursive functions.

Proof. 

Let

$${\mathcal{O}}_j=\left\{{\mathsf{\Omega }}_1^j,{\mathsf{\Omega }}_2^j,\dots ,{\mathsf{\Omega }}_k^j\right\},k\in {\mathbb{N}}^{+},$$

(37)

be the set of the numbers ${\mathsf{\Omega }}_z^j$ defined in (28), each of which uniquely corresponds to $N_z^j\in {\mathcal{N}}_j$. Let

$${\mathcal{F}}_j=\left\{{\tilde{A}}_1^j,{\tilde{A}}_2^j,\dots ,{\tilde{A}}_k^j\right\},k\in {\mathbb{N}}^{+},$$

(38)

be a class of primitive recursive functions, one function per each ${\mathsf{\Omega }}_z^j\in {\mathcal{O}}_z$, as defined in (34). We observe that

$$\left|{\mathcal{N}}_j\right|=\left|{\mathcal{A}}_j\right|=\left|{\mathcal{O}}_j\right|=\left|{\mathcal{F}}_j\right|=k.$$

Let ${\lambda }_1:{\mathcal{N}}_j\mapsto {\mathcal{A}}_j$, ${\lambda }_2:{\mathcal{A}}_j\mapsto {\mathcal{O}}_j$, and ${\lambda }_3:{\mathcal{O}}_j\mapsto {\mathcal{F}}_j$ be defined as

$$\begin{array}{ccc}{\lambda }_1^j\left(N_j\right)\hfill & =\hfill & A_z^j;\hfill \\ {\lambda }_2^j\left(A_z^j\right)\hfill & =\hfill & {\mathsf{\Omega }}_z^j;\hfill \\ {\lambda }_3^j\left({\mathsf{\Omega }}_z^j\right)\hfill & =\hfill & {\tilde{A}}_z^j.\hfill \end{array}$$

Then, ${\lambda }_j:{\mathcal{N}}_j\mapsto {\mathcal{F}}_j$, defined as

$${\lambda }_j\left(N_z^j\right)={\lambda }_3^j\left({\lambda }_2^j\left({\lambda }_1^j\left(N_z^j\right)\right)\right),$$

(39)

is a bijection.    □

8. Discussion

The definition of the finite memory device or automation (FMD or FMA) in Section 2.2 has four main implications. First, a physical or abstract automaton is an FMD when its memory amount is quantifiable as a natural number. Second, characters and strings are not necessary, because bijections exist between any finite alphabet of symbols and natural numbers and, through Gödel numbering, between any strings over a finite alphabet and natural numbers, hence the term numerical memory used in the article. Third, an FSA of classical computability becomes an FMA when the quantity of its internal and external memory is finite, i.e., there is an upper bound in the form of a natural number on the quantity of the machine’s memory. It is irrelevant for the scope of this investigation whether the input tape of an FSA, the input and output tapes of such FSA modifications as the Mealy and Moore machines (Chapter 2 in [12]) or the finite state transducers (Chapter 3 in [13]), and the input tape and the stack of a pushdown automaton (PDA) (Chapter 5 in [12]) are considered internal or external memory. Fourth, a universal Turing machine (UTM) (Chapter 6 in [7]) is an FMA when the number of its tape cells is bounded by a natural number, which a fortiori makes any physical computer an FMA. Thus, only one type of universal computer is needed to define all FMA it can simulate.

Consider a universal computer $UC$ capable of executing the universal L program $U_1$ constructed to prove the Universality Theorem (Theorem 3.1, Chapter 3 in [7]). The computer $UC$, equivalent to a UTM, takes an arbitrary L program P, an input to that program in the form of a natural number stored in its input register $X_1$, which can be a Gödel number encoding an array of numbers, executes P on $X_1$ by encoding the memory of P as another Gödel number and returns the output of P as a natural number, which can also be a Gödel number encoding a sequence of natural numbers, saved in its output register Y. Since characters and character sequences can be bijectively mapped to natural numbers, $UC$ can simulate any FSA or a modification thereof, e.g., a Mealy machine, a Moore machine, a finite state transducer, or a PDA. Technically speaking, there is no need to distinguish between the Mealy and Moore machines, because they are equivalent (Theorems 2.6, 2.7, Chapter 2 in [12]). When a limit is placed on the numerical memory of $UC$ by way of the number of registers it can use and the size of the numbers signifiable in them, the input and output registers included, $UC$ immediately becomes an FMD and so a fortiori any device that $UC$ is capable of simulating.

The separation of computability into the two overlapping categories, general and actual, is necessary for theoretical and practical reasons. A theoretical reason, generally accepted in classical computability theory, is that it is of no advantage to put any memory limitations on automata or on the a priori counts of unit time steps that automata may take to execute programs that implement functions in order to show that those functions are computable. Were it not the case, we would not be able to investigate what is computable in principle. Rogers [10] succinctly expresses this point of view:

                 "[w]e thus require that a computation

                  terminate after some finite number

                  of steps; we do not insist on an a

                  priori ability to estimate this number."

An implication of the above assumption is that an automaton, explicit or implicit, on which the said computation is executed has access to, literally, astronomical quantities of numerical memory. For a thought experiment, consider an automaton programmable in $\mathcal{L}$ of Chapter 2 of [7] that we used in Section 3.1, and let a program $P_{\mathcal{L}}^j\left(n\right)$, $n\in {\mathbb{N}}^{+}$, compute the G-number of the sequence $(1,\dots ,n)$, i.e., the function computed by $P_{\mathcal{L}}^j$ is $f\left(n\right)=[1,\dots ,n]$, as defined in (A8). Then, $f\left(n\right)$ is a primitive recursive function and, hence, computable in the general sense of Definition 2. Thus, $f\left(n\right)$ is signifiable for any $n\in {\mathbb{N}}^{+}$ on the automaton. In particular, if n is the Eddington number, i.e., $n={10}^{80}\in {\mathbb{N}}^{+}$, estimating the number of hydrogen atoms in the observable universe [14], there is a computation and, by implication, a variable in $P_{\mathcal{L}}^j$ to which the G-number of $(1,2,\dots ,{10}^{80})$ can be assigned.

The foregoing paragraph brings us to a practical reason for separating computability into the general and actual categories: it is of little use for an applied scientist who wants to implement a number-theoretic function f in a programming language L for an FMA $D_j$ to know that f is generally computable and the L program can, therefore, compute, in principle, some characteristic of arbitrarily large natural numbers, e.g., the Eddington number. If no natural number greater than some $n\in \mathbb{N}$ is signifiable on $D_j$, the scientist must make provisions in the program for the non-signifiable numbers in order to achieve feasible results with absolutely actually computable functions.

Theorem 1 shows that the computation of a trained FANN on a finite memory device can be packed into a unique natural number. Once packed, the natural number can be used as an archive, after a fashion, to look up natural numbers that correspond, in the bijective sense of the term, to the real vectors computed by the function $A_z^z$ of an FANN $N_z^j$ implemented on the device. The correspondence is such that for any signifiable $\overrightarrow{x}$, the output of $N_z^j$, i.e., $A_z^j\left(\overrightarrow{x}\right)=\overrightarrow{a}$, corresponds to the natural number $\tilde{a}$ computed by the primitive recursive function ${\tilde{A}}_z^j$, i.e., ${\tilde{A}}_z^j\left(\tilde{x}\right)=\tilde{a}$, and the input $\overrightarrow{x}$ corresponds to the natural number $\tilde{x}$. Thus, $A_z^j\left(\overrightarrow{x}\right)=\overrightarrow{a}$ iff ${\tilde{A}}_z^j\left(\tilde{x}\right)=\tilde{a}$. Furthermore, the function ${\tilde{A}}_z^j$ is computable in the general sense and is absolutely actually computable on any FMA where the natural number ${\mathsf{\Omega }}_z^j$ is signifiable.

A correspondence established in Theorem 2 should be construed so that the uniqueness of ${\mathsf{\Omega }}_z^j$ does not imply the uniqueness of $A_z^j$ because the same function can be computed by different FANNs. What it implies is that, for any two different FANNs $N_n^j$ and $N_m^j$, $n\ne m$ (e.g., different numbers of layers or different numbers of nodes in a layer or different activation functions or different weights), implemented on the same FMA $D_j$, ${\mathsf{\Omega }}_n^j\ne {\mathsf{\Omega }}_m^j$. However, it may be the case that $A_m^j\left(\overrightarrow{x}\right)=A_n^j\left(\overrightarrow{x}\right)$ for any signifiable $\overrightarrow{x}$, and consequently, ${\tilde{A}}_m^j\left(\tilde{x}\right)={\tilde{A}}_n^j\left(\tilde{x}\right)$.

9. Conclusions

To differentiate between feedforward artificial neural networks and their functions as abstract mathematical objects and the realizations of these networks and functions on finite memory devices, we introduced the categories of general and actual computability. We showed that correspondences are possible between trained feedforward artificial neural networks on finite memory devices and classes of primitive recursive functions. We argued that there are theoretical and practical reasons why computability should be separated into these categories. The categories are overlapping in the sense that some functions belong in both categories.

Appendix A.1. Primitive Recursive Functions and Predicates

In this section, we define several functions shown to be primitive recursive in [7]. All smallcase variables in this section, e.g, x, y, z, t, n, and m, with and without subscripts, refer to natural numbers and the term number is synonymous with the term natural number.

The expression

$${(\exists t)}_{\le z}P(t,x_1,\dots ,x_n)$$

(A1)

is called the bounded existential quantification of the predicate P and holds iff $P(t,x_1,\dots ,x_n)=1$ for at least one t such that $0\le t\le z$. The expression

$${(\forall t)}_{\le z}P(t,x_1,\dots ,x_n)$$

(A2)

is called a bounded universal quantification of P and holds iff $P(t,x_1,\dots ,x_n)=1$ for every t such that $0\le t\le z$. If $P(t,x_1,\dots ,x_n)$ is a predicate and z is a number, then

$$x={\displaystyle \underset{t\le z}{min}}\left\{P(t,x_1,\dots ,x_n)\right\}$$

(A3)

is called the bounded minimalization of P and defines the smallest number t for which P holds or 0 if there is no such number. It is shown in [7] that (1) the predicates $x=y$, $x\ne y$, $x<y$, $x>y$, $x\le y$, $x\ge y$, and $x|y$, i.e., x divides y, are primitive recursive; (2) a finite logical combination of primitive recursive predicates is primitive recursive; and (3) if a predicate $P(·)$ is primitive recursive, then so are its negation, its bounded minimalization, and its bounded universal and existential quantifications.

Let

$$x\dot{-}y=\left\{\begin{array}{cc}x-y\hfill & \mathrm{if}x\ge 0,\hfill \\ 0\hfill & \mathrm{if}x<y.\hfill \end{array}\right.$$

(A4)

The pairing function of natural numbers x and y, $⟨x,y⟩:\mathbb{N}\to \mathbb{N}$, is

$$\begin{array}{ccc}\hfill & ⟨x,y⟩=z,\hfill & \end{array}$$

(A5)

where

$$\begin{array}{cc}\hfill & z=2^x(2y+1)\dot{-}1;\hfill \\ \\ \hfill & \gamma \left(d\right)\equiv \left\{2^d\right|(z+1)\wedge {(\forall c)}_{\le z+1}\{2^c\nmid (z+1)\vee c\le d\}\};\hfill & \\ \\ \hfill & x={\displaystyle \underset{d\le z+1}{min}}\gamma \left(d\right);\hfill & \\ \\ \hfill & y=\frac{1}{2}\left(\frac{z+1}{2^x}\dot{-}1\right).\hfill & \end{array}$$

For any number z, there are unique x and y such that $⟨x,y⟩=z$. For example, if $z=27$, then

$$\begin{array}{ccc}\hfill & x={\displaystyle \underset{d\le 28}{min}}\gamma \left(d\right)=2;\hfill & \\ \\ \hfill & y=\frac{1}{2}\left(\frac{28}{2^2}\dot{-}1\right)=3;\hfill & \\ \\ \hfill & ⟨2,3⟩=2^2(2·3+1)\dot{-}1=27.\hfill & \end{array}$$

The functions $l\left(z\right)$ and $r\left(z\right)$

$$\begin{array}{cc}\hfill l\left(z\right)& ={\displaystyle \underset{x\le z}{min}}\left\{{(\exists y)}_{\le z}\{z=⟨x,y⟩\}\right\}\hfill \\ \\ \hfill r\left(z\right)& ={\displaystyle \underset{y\le z}{min}}\left\{{(\exists x)}_{\le z}\{z=⟨x,y⟩\}\right\}\hfill \end{array}$$

(A6)

return the left and right components of any number z so that $⟨l\left(z\right),r\left(z\right)⟩=z$. Thus, if $z=27=⟨2,3⟩$, then $l\left(z\right)=2$, $r\left(z\right)=3$.

The symbol $p_n$ refers to the n-th prime, i.e., $p_1=2$, $p_2=3$, $p_3=5$, etc., and $p_0=0$, by definition. The primes are computed by the following primitive recursive function.

$$\pi \left(i\right)=p_i.$$

(A7)

Thus, $\pi \left(0\right)=0$, $\pi \left(1\right)=2$, $\pi \left(2\right)=3$, $\pi \left(3\right)=5$, $\pi \left(4\right)=7$, $\pi \left(5\right)=11$, etc. If $(a_1,\dots ,a_n)$ is a sequence of numbers, the function

$$[a_1,\dots ,a_n]=\prod _{i=1}^n\pi {\left(i\right)}^{a_i}$$

(A8)

computes the Gödel number (G-number) of this sequence. The G-number of the empty number sequence $\left(\right)$ is 1. Thus, the G-number of $(3,101,7891,1,43)$ is $[3,101,7891,1,43]=2^3·3^{101}·5^{7891}·7^1·{11}^{43}$.

If $x=[a_1,\dots ,a_n]$, the accessor function

$${\left(x\right)}_i={\displaystyle \underset{t\le x}{min}}\{\neg \left\{\pi {\left(i\right)}^{t+1}\right|x\}\}$$

(A9)

returns the i-th element of x. Thus, if $x=[1,7,13]$, then ${\left(x\right)}_1=1$, ${\left(x\right)}_2=7$, ${\left(x\right)}_3=13$, and ${\left(x\right)}_j=0$ for $j=0$ or $j>3$.

The length of a Gödel number x is the position of the last non-zero prime power in x. Specifically, if $x=[a_1,a_2,\dots ,a_n]$, its length is computed by the function $Lt(·)$ defined as

$$Lt\left(x\right)={\displaystyle \underset{i\le x}{min}}\{{\left(x\right)}_i\ne 0\wedge {(\forall j)}_{\le x}\{\{j>i\}\to \{{\left(x\right)}_j=0\}\}\}.$$

(A10)

Thus, $Lt\left(540\right)=Lt\left(\right[2,3,1\left]\right)=3$. $Lt\left([a_1,\dots ,a_n]\right)=n$ iff $a_n\ne 0$, $[{\left(x\right)}_1,\dots ,{\left(x\right)}_n]=x$ when $Lt\left(x\right)=n$, and $Lt\left(0\right)=Lt\left(1\right)=0$. $Lt\left([x_1,x_2,\dots ,x_n]\right)=Lt\left([x_1,x_2,\dots ,x_n,0,\dots ,0]\right)$, where $x_n\ne 0$.

The function $\lfloor x/y\rfloor$ returns the integer part of the quotient $x/y$. Thus, $\lfloor 7/2\rfloor =3$, $\lfloor 2/5\rfloor =0$, $\lfloor 8/5\rfloor =1$, and $\lfloor x/0\rfloor =0$ for any number x.

Appendix A.2. Gödel Number Operators

The functions in this section or variants thereof were shown to be primitive recursive in [11]. The function

$$set(b,i,v)=\left\{\begin{array}{cc}\lfloor \frac{b}{\pi {\left(i\right)}^{{\left(b\right)}_i}}\rfloor ·\pi {\left(i\right)}^v\hfill & \mathrm{if}1\le i\le Lt\left(b\right)\wedge b>1\wedge v>0,\hfill \\ \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(A11)

assigns the value of the i-th element of the G-number b to v. Thus, if $b=[1,2]=2^1{3}^2=18$, $i=1$, and $v=3$, then

$$set([1,2],1,3)=\lfloor \frac{b}{\pi {\left(1\right)}^{{\left(b\right)}_1}}\rfloor ·\pi {\left(1\right)}^3=\lfloor \frac{[1,2]}{2^{{\left([1,2]\right)}_1}}\rfloor ·2^3=\lfloor \frac{2^1·3^2}{2^1}\rfloor ·2^3=[3,2]=72.$$

The function $cnt(·)$ in (A12), where $s\left(t\right)=t+1$ is one of the three initial functions defined in (11) and ${\left(x\right)}_i$ is defined in (A9), returns the count of occurrences of x in y. Thus, if $y=[1,2,1,3]$, then $\mathtt{c}\mathtt{n}\mathtt{t}(1,y)=2$. A convention in (A12) and other equations in this section is that the name of auxiliary functions end in “x”.

$$cnt(x,y)=\left\{\begin{array}{cc}cntx(x,y,Lt(y\left)\right)\hfill & \mathrm{if}y>1,\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(A12)

$$\begin{array}{ccc}cntx(x,y,0)\hfill & =\hfill & 0,\hfill \\ cntx(x,y,t+1)\hfill & =\hfill & cntxx(x,y,t,cntx(x,y,t\left)\right).\hfill \end{array}$$

$$cntxx(x,y,t,c)=\left\{\begin{array}{cc}1+c\hfill & \mathrm{if}{\left(y\right)}_{s\left(t\right)}=x,\hfill \\ c\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

If y is a G-number, then the predicate

$$x{\in }_{g}y\equiv cnt(x,y)\ne 0$$

(A13)

holds if x is an element of y. Thus, $1{\in }_g[3,4,1,5]$, but $1{\notin }_g[3,4,2,5]$. The function

$$rap(x,y)=\left\{\begin{array}{cc}y·{\left\{\pi (\mathtt{L}\mathtt{t}\left(y\right)+1)\right\}}^x\hfill & \mathrm{if}x>0\wedge y>1\wedge 0{\notin }_{g}y,\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(A14)

appends x to the right of the rightmost element of y. Thus,

$$\begin{array}{ccc}rap(1,[1\left]\right)\hfill & =\hfill & \left[1\right]·{\left\{\pi (Lt\left(\left[1\right]\right)+1)\right\}}^1=\left[1\right]·{\left\{\pi \left(2\right)\right\}}^1\hfill \\ \hfill & =\hfill & 2^1·3^1=[1,1];\hfill \\ rap(8,[2,3,5\left]\right)\hfill & =\hfill & [2,3,5]·{\left\{\pi \left(4\right)\right\}}^8\hfill \\ \hfill & =\hfill & [2,3,5,8];\hfill \\ rap(5,set([10,3],1,2\left)\right)\hfill & =\hfill & rap(5,[2,3\left]\right)\hfill \\ \hfill & =\hfill & [2,3,5].\hfill \end{array}$$

Let

$$\begin{array}{ccc}lc(x_1,x_2,0)\hfill & =\hfill & x_2,\hfill \\ lc(x_1,x_2,t+1)\hfill & =\hfill & rap({\left(x_1\right)}_{s\left(t\right)},lc(x_1,x_2,t)).\hfill \end{array}$$

Then, the function

$$x{\otimes }_{l}y=\left\{\begin{array}{cc}lc(x,y,Lt(x\left)\right)\hfill & \mathrm{if}x>1\wedge y>1\wedge 0{\notin }_{g}x\wedge 0{\notin }_{g}y,\hfill \\ x\hfill & \mathrm{if}x>1\wedge y=1\wedge 0{\notin }_{g}x,\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(A15)

places all numbers in y, in order, to the left of the first number in x, while the function

$$x{\otimes }_{r}y=\left\{\begin{array}{cc}y{\otimes }_{l}x\hfill & \mathrm{if}x>1\wedge y>1\wedge 0{\notin }_{g}x\wedge 0{\notin }_{g}y,\hfill \\ x\hfill & \mathrm{if}x>1\wedge y=1\wedge 0{\notin }_{g}x,\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(A16)

places all numbers of y, in order, to the right of the rightmost number in x. We refer to the function in (A15) as left concatenation and to the function in (A16) as right concatenation. Thus, $[3,5]{\otimes }_l[7,11]=[7,11,3,5]$; $[3,5]{\otimes }_r[7,11]=[3,5,7,11]$; $[2,3]{\otimes }_l\left[1\right]=[1,2,3]$; $[2,3]{\otimes }_r\left[1\right]=[2,3,1]$.

Let

$$\begin{array}{ccc}gnx(l,u,k,0)\hfill & =\hfill & \left[l\right],\hfill \\ gnx(l,u,k,t+1)\hfill & =\hfill & gnxx(l,u,k,gnx(l,u,k,t),t);\hfill \end{array}$$

$$gnxx(l,u,k,z,t)=\left\{\begin{array}{cc}z{\otimes }_r[l+s\left(t\right)k]\hfill & \mathrm{if}l+s\left(t\right)k\le u,\hfill \\ z\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Then, for $l>0$ and $u>0$, the function

$$ggn(l,u,k)=\left\{\begin{array}{cc}gnx(l,u,k,s(u\dot{-}l\left)\right)\hfill & \mathrm{if}k>0\wedge {(\exists t)}_{\le u}\{l+tk=u\wedge t>0\},\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(A17)

generates a G-number whose numbers start at l and go to u in positive integer increments of k. Thus, $ggn(1,2,1)=[1,2]$; $ggn(1,2,2)=0$; $ggn(1,3,1)=[1,2,3]$; $ggn(1,3,2)=[1,3]$; $ggn(1,3,3)=0$. The abbreviation $ggn$ stands for generator of Gödel numbers.

The function

$$asx(x,y)={\displaystyle \underset{t\le Lt\left(y\right)}{min}}\{t>0\wedge x=l\left({\left(y\right)}_t\right)\}$$

(A18)

returns the smallest index t of $⟨i,j⟩\in y$ such that $x=i$. Thus, if

$$y=[⟨10,100⟩,⟨20,200⟩,⟨30,300⟩],$$

then $asx(10,y)=1$, $asx(20,y)=2$, $asx(30,y)=3$. The function

$$\mathtt{a}\mathtt{s}\mathtt{c}(x,y)={\left(y\right)}_{\mathtt{a}\mathtt{s}\mathtt{x}(x,y)}$$

(A19)

returns the pair from y at the index t returned by $asx(·)$. Thus, if

$$y=[⟨10,100⟩,⟨20,200⟩,⟨30,300⟩],$$

then

$$\begin{array}{ccccccc}asc(10,y)\hfill & =\hfill & {\left(y\right)}_{asx(10,y)}\hfill & =\hfill & {\left(y\right)}_1\hfill & =\hfill & ⟨10,100⟩;\hfill \\ asc(20,y)\hfill & =\hfill & {\left(y\right)}_{asx(20,y)}\hfill & =\hfill & {\left(y\right)}_2\hfill & =\hfill & ⟨20,200⟩;\hfill \\ asc(30,y)\hfill & =\hfill & {\left(y\right)}_{asx(30,y)}\hfill & =\hfill & {\left(y\right)}_3\hfill & =\hfill & ⟨30,200⟩;\hfill \\ asc(13,y)\hfill & =\hfill & {\left(y\right)}_{asx(13,y)}\hfill & =\hfill & {\left(y\right)}_0\hfill & =\hfill & 0.\hfill \end{array}$$

Appendix A.3. Examples of Ω Numbers

Let us abbreviate $G_{0,1}^{t,j}$ in (25) to $G^t$ and consider the FANN in Figure 1. Let us assume that, as in Example 3, $R=\{0,0.3,0.6,0.9,1\}$, $I=\{1,2,3,4,5\}$ and $t=2$, and

$$\begin{array}{ccc}{G}_{0,1}^{2,j}\hfill & =\hfill & G^2\hfill \\ \hfill & =\hfill & \left[\right[1,1],[1,2],[1,3],[1,4],[1,5],\hfill \\ \hfill & \hfill & [2,1],[2,2],[2,3],[2,4],[2,5],\hfill \\ \hfill & \hfill & [3,1],[3,2],[3,3],[3,4],[3,5],\hfill \\ \hfill & \hfill & [4,1],[4,2],[4,3],[4,4],[4,5],\hfill \\ \hfill & \hfill & [5,1],[5,2],[5,3],[5,4],[5,5]].\hfill \end{array}$$

In other words, $G^2$ is a G-number such that $[x_1,x_2]{\in }_g{G}^2$ iff $(x_1,x_2)\in I^2$. $G^3$, whose definition we omit for space reasons, is a G-number whose length is 125 such that $[x_1,x_2,x_3]{\in }_g{G}^3$ iff $(x_1,x_2,x_3)\in I^3$, e.g., $[1,2,3]{\in }_g{G}^3$ iff $(1,2,3)\in I^3$. We can compute ${\mathsf{\Omega }}_i^e$ for the FANN $N_z^j$ in Figure 1 as follows.

$$\begin{array}{c}{\mathsf{\Omega }}_0^0=\left[⟨{\left(G^2\right)}_1,\mu \left({\alpha }_0^0\left({\zeta }^2\left({\left(G^2\right)}_1\right),\left(\right)\right)\right)⟩,\dots ,⟨{\left(G^2\right)}_{25},\mu \left({\alpha }_0^0\left({\zeta }^2\left({\left(G^2\right)}_{25}\right),\left(\right)\right)\right)⟩\right];\hfill \\ {\mathsf{\Omega }}_1^0=\left[⟨{\left(G^2\right)}_1,\mu \left({\alpha }_1^0\left({\zeta }^2\left({\left(G^2\right)}_1\right),\left(\right)\right)\right)⟩,\dots ,⟨{\left(G^2\right)}_{25},\mu \left({\alpha }_1^0\left({\zeta }^2\left({\left(G^2\right)}_{25}\right),\left(\right)\right)\right)⟩\right];\hfill \\ {\mathsf{\Omega }}_0^1=\left[⟨{\left(G^2\right)}_1,\mu \left({\alpha }_0^1\left({\zeta }^2\left({\left(G^2\right)}_1\right),{\overrightarrow{w}}^1\right)\right)⟩,\dots ,⟨{\left(G^2\right)}_{25},\mu \left({\alpha }_0^1\left({\zeta }^2\left({\left(G^2\right)}_{25}\right),{\overrightarrow{w}}^1\right)\right)⟩\right];\hfill \\ {\mathsf{\Omega }}_1^1=\left[⟨{\left(G^2\right)}_1,\mu \left({\alpha }_1^1\left({\zeta }^2\left({\left(G^2\right)}_1\right),{\overrightarrow{w}}^1\right)\right)⟩,\dots ,⟨{\left(G^2\right)}_{25},\mu \left({\alpha }_1^1\left({\zeta }^2\left({\left(G^2\right)}_{25}\right),{\overrightarrow{w}}^1\right)\right)⟩\right];\hfill \\ {\mathsf{\Omega }}_2^1=\left[⟨{\left(G^2\right)}_1,\mu \left({\alpha }_2^1\left({\zeta }^2\left({\left(G^2\right)}_1\right),{\overrightarrow{w}}^1\right)\right)⟩,\dots ,⟨{\left(G^2\right)}_{25},\mu \left({\alpha }_2^1\left({\zeta }^2\left({\left(G^2\right)}_{25}\right),{\overrightarrow{w}}^1\right)\right)⟩\right];\hfill \\ {\mathsf{\Omega }}_0^2=\left[⟨{\left(G^3\right)}_1,\mu \left({\alpha }_0^2\left({\zeta }^3\left({\left(G^3\right)}_1\right),{\overrightarrow{w}}^2\right)\right)⟩,\dots ,⟨{\left(G^3\right)}_{125},\mu \left({\alpha }_0^2\left({\zeta }^3\left({\left(G^3\right)}_{125}\right),{\overrightarrow{w}}^2\right)\right)⟩\right];\hfill \\ {\mathsf{\Omega }}_1^2=\left[⟨{\left(G^3\right)}_1,\mu \left({\alpha }_1^2\left({\zeta }^3\left({\left(G^3\right)}_1\right),{\overrightarrow{w}}^2\right)\right)⟩,\dots ,⟨{\left(G^3\right)}_{125},\mu \left({\alpha }_1^2\left({\zeta }^3\left({\left(G^3\right)}_{125}\right),{\overrightarrow{w}}^2\right)\right)⟩\right].\hfill \end{array}$$

We can compute individual elements of ${\mathsf{\Omega }}_i^e$. For example, since ${\left(G^2\right)}_{17}=[4,2]$,

$$\begin{array}{ccc}{\left({\mathsf{\Omega }}_0^0\right)}_{17}\hfill & =\hfill & ⟨{\left(G^2\right)}_{17},\mu \left({\alpha }_0^0\left({\zeta }^2\left({\left(G^2\right)}_{17}\right),\left(\right)\right)\right)⟩\hfill \\ \hfill & =\hfill & ⟨[4,2],\mu \left({\alpha }_0^0\left({\zeta }^2\left([4,2]\right),\left(\right)\right)\right)⟩\hfill \\ \hfill & =\hfill & ⟨[4,2],\mu \left({\alpha }_0^0\left((0.9,0.3),\left(\right)\right)\right)⟩\hfill \\ \hfill & =\hfill & ⟨[4,2],\mu \left(0.9\right)⟩\hfill \\ \hfill & =\hfill & ⟨[4,2],4⟩\in \mathbb{N}.\hfill \end{array}$$

Since ${\left(G^2\right)}_{12}=[3,2]$,

$$\begin{array}{ccc}{\left({\mathsf{\Omega }}_0^1\right)}_{12}\hfill & =\hfill & ⟨{\left(G^2\right)}_{12},\mu \left({\alpha }_0^1\left({\zeta }^2\left({\left(G^2\right)}_{12}\right),{\overrightarrow{w}}^1\right)\right)⟩\hfill \\ \hfill & =\hfill & ⟨[3,2],\mu \left({\alpha }_0^1\left({\zeta }^2\left([3,2]\right),{\overrightarrow{w}}^1\right)\right)⟩\hfill \\ \hfill & =\hfill & ⟨[3,2],\mu \left({\alpha }_0^1\left((0.6,0.3),{\overrightarrow{w}}^1\right)\right)⟩\hfill \\ \hfill & =\hfill & ⟨[3,2],z⟩\in \mathbb{N},\hfill \end{array}$$

where $z=\mu \left({\alpha }_0^1\left((0.6,0.3),{\overrightarrow{w}}^1\right)\right)\in I$. We know that $[2,3,4]{\in }_g{G}^3$ because $(2,3,4)\in I^3$. Thus, ${\left(G^3\right)}_t=[2,3,4]$, for $1\le t\le 125$. Let us therefore assume, for the sake of this example, that ${\left(G^3\right)}_{35}=[2,3,4]$. Then,

$$\begin{array}{ccc}{\left({\mathsf{\Omega }}_1^2\right)}_{35}\hfill & =\hfill & ⟨{\left(G^3\right)}_{35},\mu \left({\alpha }_1^2\left({\zeta }^3\left({\left(G^3\right)}_{35}\right),{\overrightarrow{w}}^2\right)\right)⟩\hfill \\ \hfill & =\hfill & ⟨[2,3,4],\mu \left({\alpha }_1^2\left({\zeta }^3\left([2,3,4]\right),{\overrightarrow{w}}^2\right)\right)⟩\hfill \\ \hfill & =\hfill & ⟨[2,3,4],\mu \left({\alpha }_1^2\left((0.3,0.6,0.9),{\overrightarrow{w}}^2\right)\right)⟩\hfill \\ \hfill & =\hfill & ⟨[2,3,4],\mu \left({\alpha }_1^2\left((0.3,0.6,0.9),{\overrightarrow{w}}^2\right)\right)⟩\hfill \\ \hfill & =\hfill & ⟨[2,3,4],z⟩\in \mathbb{N},\hfill \end{array}$$

where $z=\mu \left({\alpha }_1^2\left((0.3,0.6,0.9),{\overrightarrow{w}}^2\right)\right)\in I$.

Using (29), we can compute ${\mathsf{\Omega }}_z^j$ for the FANN $N_z^j$ in Figure 1 with the $\mathsf{\Omega }$ numbers as

$$\begin{array}{ccc}{\mathsf{\Omega }}_z^j\hfill & =\hfill & \left[⟨0,\left[{\mathsf{\Omega }}_0^0,{\mathsf{\Omega }}_1^0\right]⟩,⟨1,\left[{\mathsf{\Omega }}_0^1,{\mathsf{\Omega }}_1^1,{\mathsf{\Omega }}_2^1\right]⟩,⟨2,\left[{\mathsf{\Omega }}_0^2,{\mathsf{\Omega }}_1^2\right]⟩\right].\hfill \end{array}$$

From ${\mathsf{\Omega }}_z^j$ above, we can compute all ${\tilde{\alpha }}_i^e$ defined in (30) for $N_z^j$ in Figure 1. For example, since ${\left(G^2\right)}_{12}=[3,2]$,

$$\begin{array}{ccc}{\tilde{\alpha }}_1^1\left([3,2]\right)\hfill & =\hfill & r\left(asc\left(x,{\left(r\left(asc\left(1,{\mathsf{\Omega }}_z^j\right)\right)\right)}_2\right)\right)\hfill \\ \hfill & =\hfill & r\left(asc\left([3,2],{\mathsf{\Omega }}_1^1\right)\right)\hfill \\ \hfill & =\hfill & r\left(⟨{\left(G^2\right)}_{12},\mu \left({\alpha }_1^1\left({\zeta }^2\left({\left(G^2\right)}_{12}\right),{\overrightarrow{w}}^1\right)\right)⟩\right)\hfill \\ \hfill & =\hfill & \mu \left({\alpha }_1^1\left({\zeta }^2\left({\left(G^2\right)}_{12}\right),{\overrightarrow{w}}^1\right)\right)\hfill \\ \hfill & =\hfill & \mu \left({\alpha }_1^1\left({\zeta }^2\left([3,2]\right),{\overrightarrow{w}}^1\right)\right)\hfill \\ \hfill & =\hfill & \mu \left({\alpha }_1^1\left(\left(0.6,0.3\right),{\overrightarrow{w}}^1\right)\right)\in I.\hfill \end{array}$$