A New Entropy Stable Finite Difference Scheme for Hyperbolic Systems of Conservation Laws
Abstract
1. Introduction
2. Construction of One-Dimensional High-Order ES Scheme
2.1. The EC Schemes
2.1.1. The EC Schemes for Shallow Water Equations
2.1.2. Entropy Conservative Schemes for Euler Equations
2.2. The High-Order EC Scheme
2.3. High-Order ES Scheme
2.4. The Temporal Discretization
2.5. Summary of the Proposed Scheme
3. Extension to a Two-Dimensional System
3.1. The Two-Dimensional SWEs
3.2. The Two-Dimensional Euler Equations
4. Numerical Results
4.1. The SWEs
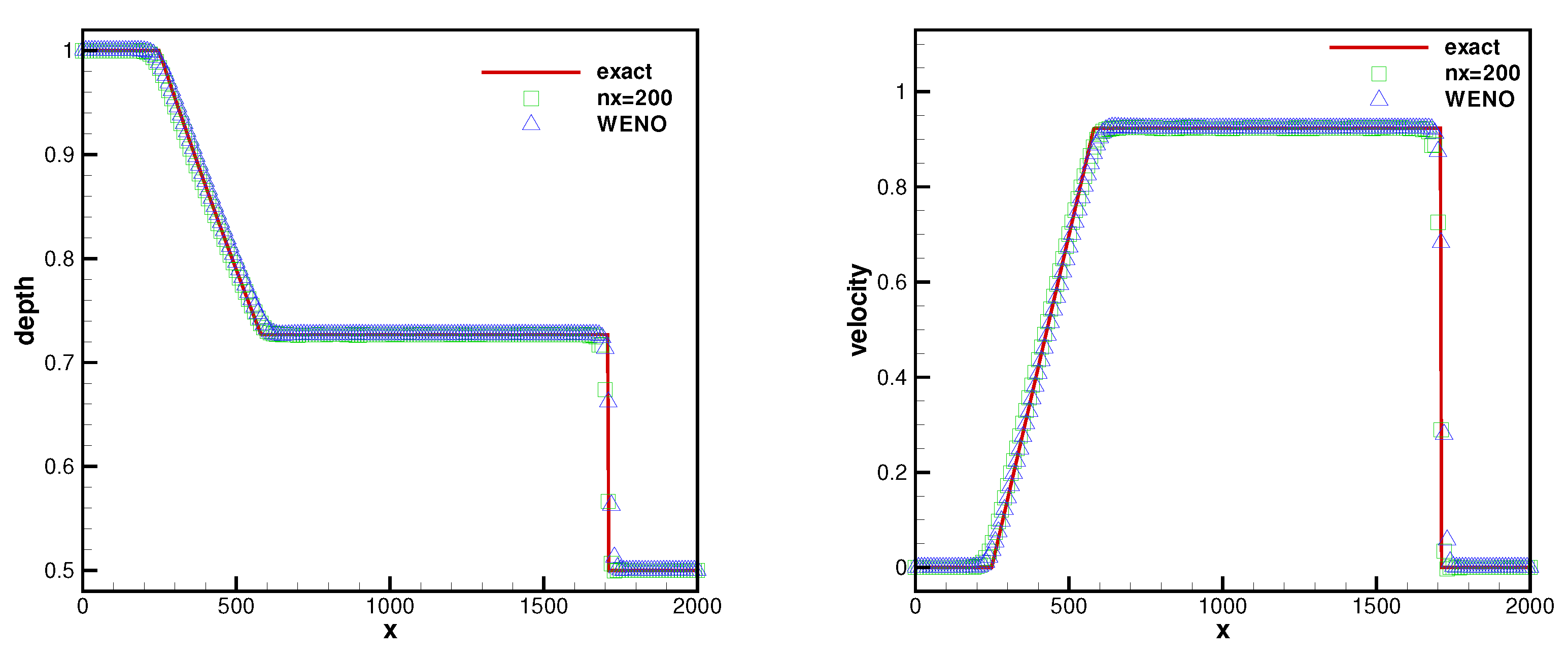
4.1.1. Example 1
4.1.2. Example 2
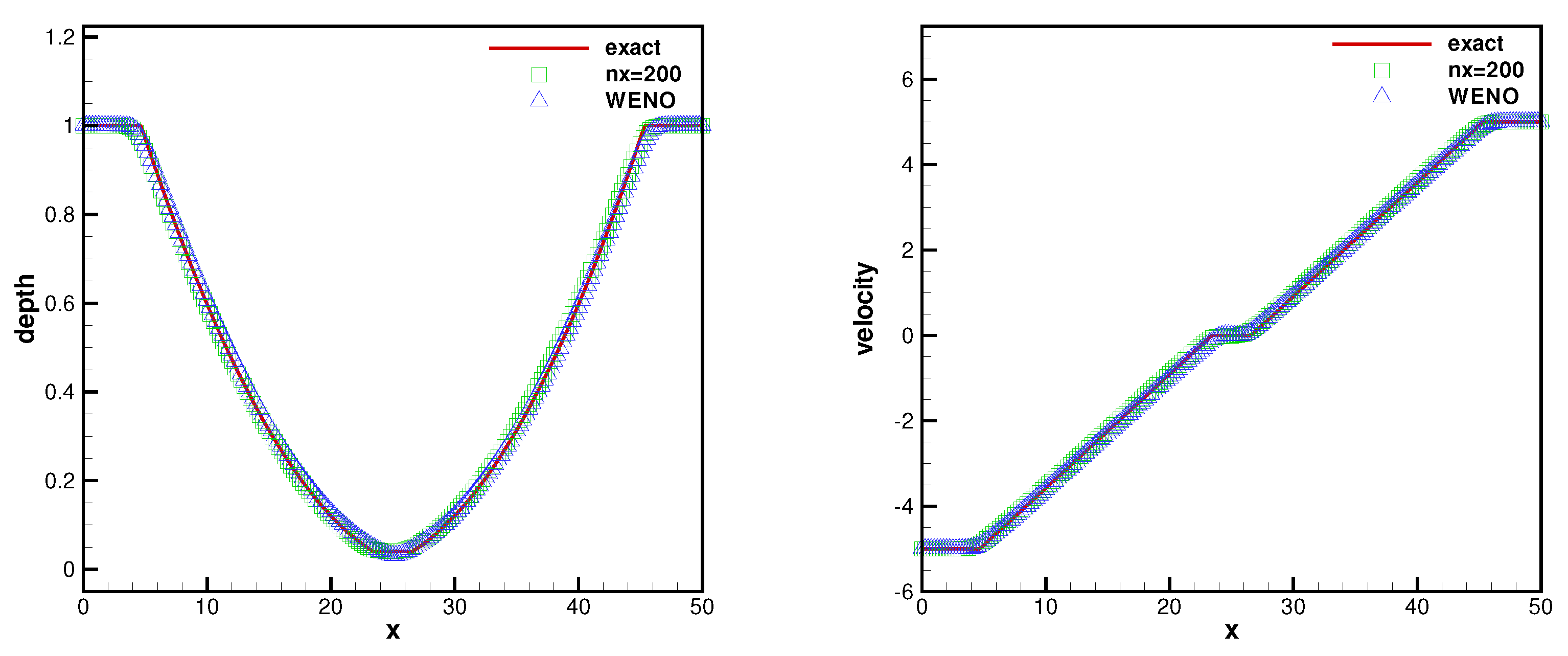
4.1.3. Example 3
4.1.4. Example 4
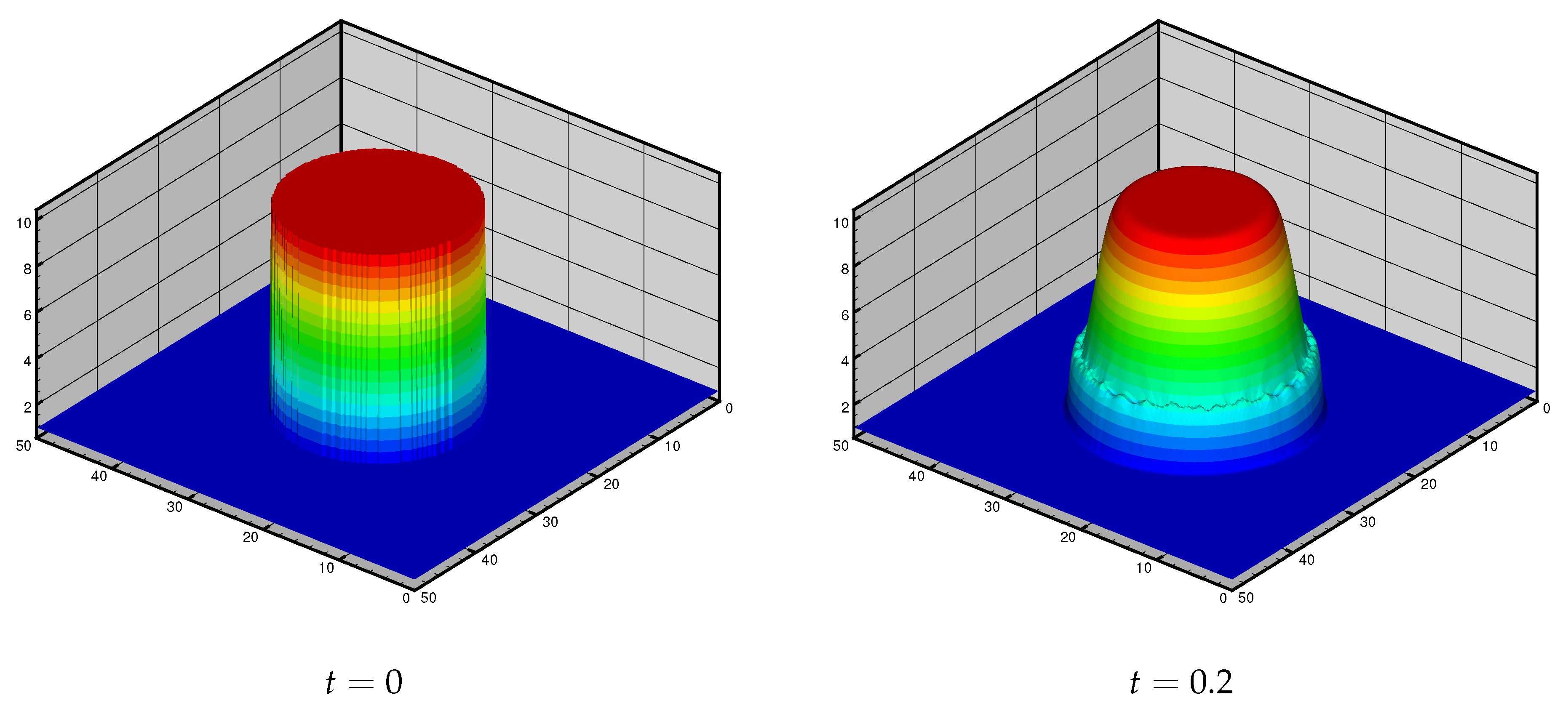
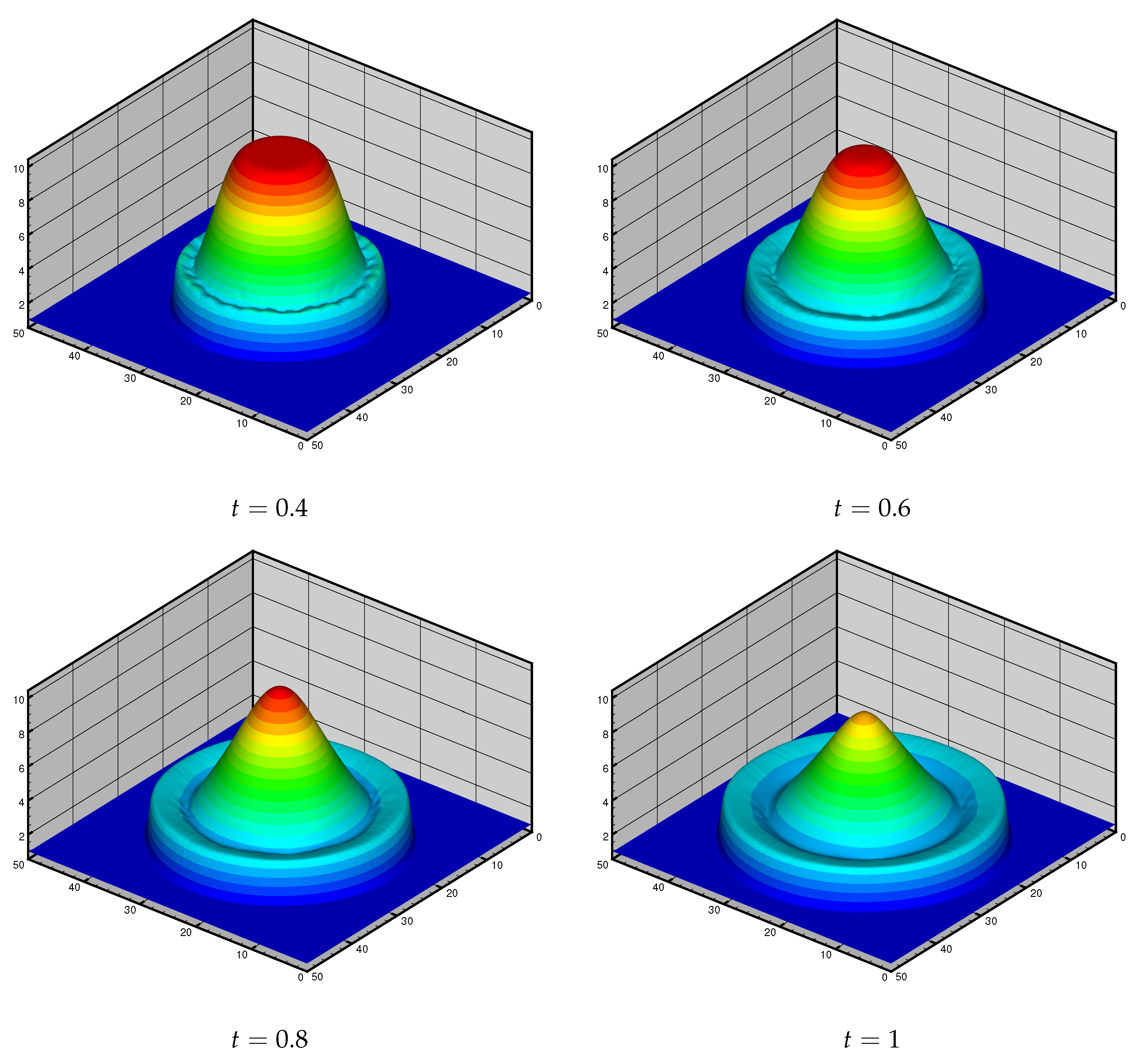
4.1.5. Example 5: Circular Dam Break Problem
4.2. The Euler Equations of Gas Dynamics
4.2.1. Testing the Order of Accuracy
4.2.2. Sod Problem
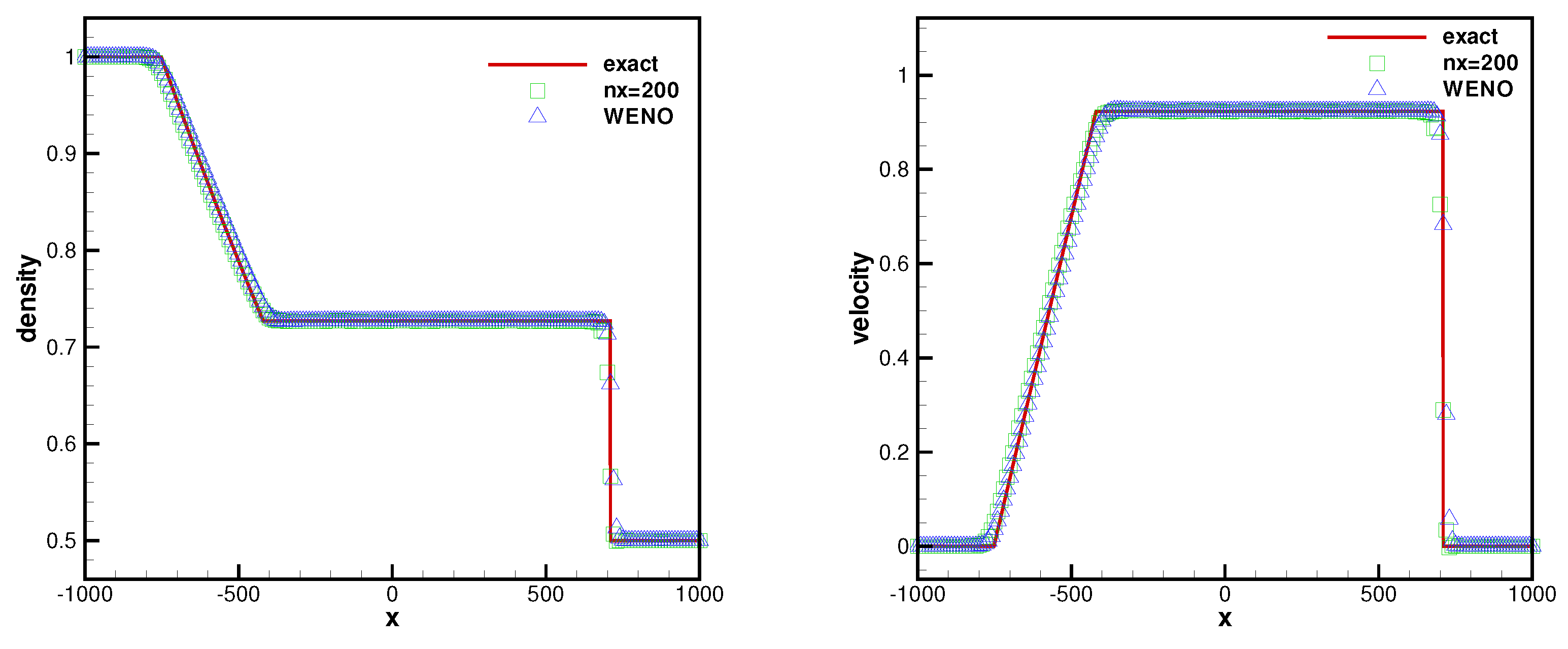
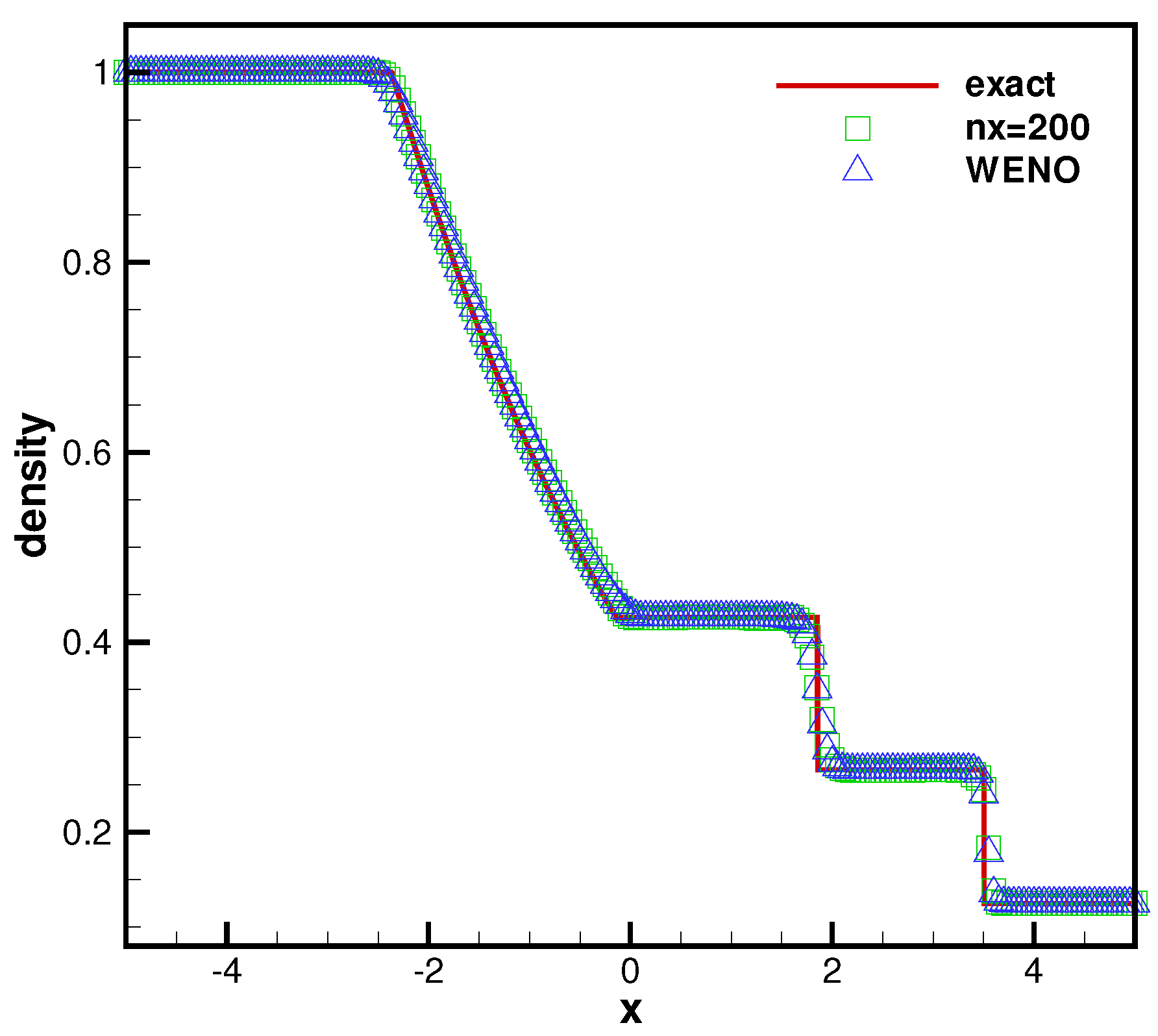
4.2.3. Lax Problem
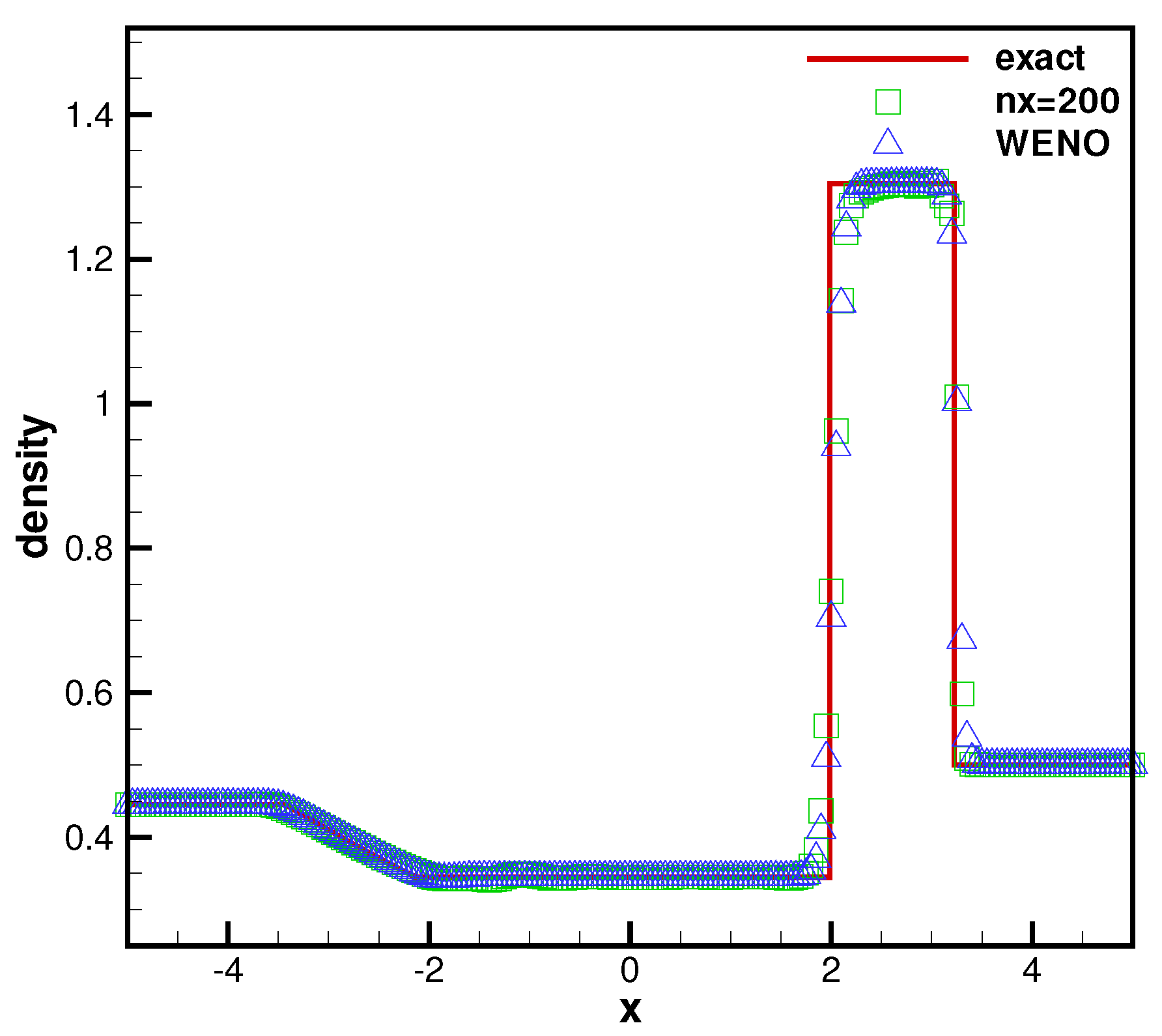
4.2.4. Shu–Osher Problem
4.2.5. 123 Problem
4.2.6. Modified Shock/Turbulence Interaction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bradford, S.F.; Sanders, B.F. Finite volume model for shallow water flooding of arbitrary topography. J. Hydraul. Eng. 2002, 128, 289–298. [Google Scholar] [CrossRef]
- Gottardi, G.; Venutelli, M. Central scheme for the two-dimensional dam-break flow simulation. Adv. Water Resour. 2004, 27, 259–268. [Google Scholar] [CrossRef]
- Vreugdenhil, C.B. Numerical Methods for Shallow-Water Flow; Springer: Dordrecht, The Netherlands, 1995; pp. 15–25. [Google Scholar]
- Perthame, B.; Simeoni, C. A kinetic scheme for the Saint-Venant system with a source term. Calcolo 2001, 38, 201–231. [Google Scholar] [CrossRef]
- Xu, K. A well-balanced gas-kinetic scheme for the shallow-water equations with source terms. J. Comput. Phys. 2002, 178, 533–562. [Google Scholar] [CrossRef]
- Kurganov, A.; Levy, D. Central-upwind schemes for the Saint-Venant system. Math. Model. Numer. Anal. 2002, 36, 397–425. [Google Scholar] [CrossRef]
- Vukovic, S.; Sopta, L. ENO and WENO schemes with the exact conservation property for one-dimensional shallow water equations. J. Comput. Phys. 2002, 179, 593–621. [Google Scholar] [CrossRef]
- Vukovic, S.; Crnjaric-Zic, N.; Sopta, L. WENO schemes for balance laws with spatially varying flux. J. Comput. Phys. 2004, 199, 87–109. [Google Scholar] [CrossRef]
- Xing, Y.L.; Shu, C.-W. High order finite difference WENO schemes with the exact conservation property for the shallow water equations. J. Comput. Phys. 2005, 208, 206–227. [Google Scholar] [CrossRef]
- Noelle, S.; Pankratz, N.; Puppo, G.; Natvig, J. Well-balanced finite volume schemes of arbitrary order of accuracy for shallow water flows. J. Comput. Phys. 2006, 213, 474–499. [Google Scholar] [CrossRef]
- Xing, Y.L.; Shu, C.-W. High order well-balanced finite volume WENO schemes and discontinuous Galerkin methods for a class of hyperbolic systems with source terms. J. Comput. Phys. 2006, 214, 567–598. [Google Scholar] [CrossRef]
- Noelle, S.; Xing, Y.; Shu, C.-W. High-order well-balanced finite volume WENO schemes for shallow water equation with moving water. J. Comput. Phys. 2007, 226, 29–58. [Google Scholar] [CrossRef]
- Li, G.; Lu, C.; Qiu, J. Hybrid well-balanced WENO schemes with different indicators for shallow water equations. J. Sci. Comput. 2012, 51, 527–559. [Google Scholar] [CrossRef]
- Li, G.; Caleffi, V.; Qi, Z.K. A well-balanced finite difference WENO scheme for shallow water flow model. Appl. Math. Comput. 2015, 265, 1–16. [Google Scholar] [CrossRef]
- Zhu, Q.; Gao, Z.; Don, W.S.; Lv, X. Well-balanced hybrid compact-WENO scheme for shallow water equations. Appl. Numer. Math. 2017, 112, 65–78. [Google Scholar] [CrossRef]
- Li, J.J.; Li, G.; Qian, S.G.; Gao, J.M. High-order well-balanced finite volume WENO schemes with conservative variables decomposition for shallow water equations. Adv. Appl. Math. Mech. 2021, 13, 827–849. [Google Scholar]
- Caleffi, V. A new well-balanced Hermite weighted essentially non-oscillatory scheme for shallow water equations. Int. J. Numer. Methods Fluids 2011, 67, 1135–1159. [Google Scholar] [CrossRef]
- Russo, G. Central schemes for balance laws. In Proceedings of the VIII International Conference on Nonlinear Hyperbolic Problems, Magdeburg, Germany, 28 February–3 March 2000. [Google Scholar]
- Touma, R.; Khankan, S. Well-balanced unstaggered central schemes for one and two-dimensional shallow water equation systems. Appl. Math. Comput. 2012, 218, 5948–5960. [Google Scholar] [CrossRef]
- Ern, A.; Piperno, S.; Djadel, K. A well-balanced Runge-Kutta discontinuous Galerkin method for the shallow-water equations with flooding and drying. Int. J. Numer. Methods Fluids 2008, 58, 1–25. [Google Scholar] [CrossRef]
- Xing, Y. Exactly well-balanced discontinuous Galerkin methods for the shallow water equations with moving water equilibrium. J. Comput. Phys. 2014, 257, 536–553. [Google Scholar] [CrossRef]
- Li, G.; Song, L.N.; Gao, J.M. High order well-balanced discontinuous Galerkin methods based on hydrostatic reconstruction for shallow water equations. J. Comput. Appl. Math. 2018, 340, 546–560. [Google Scholar] [CrossRef]
- Vignoli, G.; Titarev, V.A.; Toro, E.F. ADER schemes for the shallow water equations in channel with irregular bottom elevation. J. Comput. 2008, 227, 2463–2480. [Google Scholar] [CrossRef]
- Navas-Montilla, A.; Murillo, J. Energy balanced numerical schemes with very high order. The Augmented Roe Flux ADER scheme. Application to the shallow water equations. J. Comput. Phys. 2015, 290, 188–218. [Google Scholar] [CrossRef]
- Gassner, G.J.; Winters, A.R.; Kopriva, D.A. A well balanced and entropy conservative discontinuous Galerkin spectral element method for the shallow water equations. Appl. Math. Comput. 2016, 272, 291–308. [Google Scholar] [CrossRef]
- Berthon, C.; Chalons, C. A fully well-balanced, positive and entropy-satisfying Godunov-type method for the shallow-water equations. Math. Comput. 2016, 85, 1281–1307. [Google Scholar] [CrossRef]
- Yuan, X.H. A well-balanced element-free Galerkin method for the nonlinear shallow water equations. Appl. Math. Comput. 2018, 331, 46–53. [Google Scholar] [CrossRef]
- Li, G.; Li, J.J.; Qian, S.G.; Gao, J.M. A well-balanced ADER discontinuous Galerkin method based on differential transformation procedure for shallow water equations. Appl. Math. Comput. 2021, 395, 125848. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Yang, L.M.; Shu, C.; Zhang, H.W. Three-dimensional high-order least square-based finite difference-finite volume method on unstructured grids. Phys. Fluids 2020, 32, 123604. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Shu, C.; Yang, L.M.; Liu, Y.G.; Liu, W.; Zhang, Z.L. High-order implicit RBF-based differential quadrature-finite volume method on unstructured grids: Application to inviscid and viscous compressible flows. J. Comput. Phys. 2023, 478, 111962. [Google Scholar] [CrossRef]
- Jitendra; Chaurasiya, V.; Rai, K.N.; Singh, J. Legendre wavelet residual approach for moving boundary problem with variable thermal physical properties. Int. J. Nonlinear Sci. Numer. Simul. 2022, 23, 947–956. [Google Scholar]
- Chaurasiya, V.; Jain, A.; Singh, J. Numerical study of a non-linear porous sublimation problem with temperature-dependent thermal conductivity and Concentration-Dependent Mass Diffusivity. ASME J. Heat Mass Transf. 2023, 145, 072701. [Google Scholar] [CrossRef]
- Chaudhary, R.K.; Chaurasiya, V.; Singh, J. Numerical estimation of temperature response with step heating of a multi-layer skin under the generalized boundary condition. J. Therm. Biol. 2022, 108, 103278. [Google Scholar] [CrossRef]
- Fjordholm, U.S.; Mishra, S.; Tadmor, E. The numerical viscosity of entropy stable schemes for systems of conservation laws. I. Math. Comput. 1987, 49, 91–103. [Google Scholar]
- Duan, J.M.; Tang, H.Z. High-order accurate entropy stable finite difference schemes for the shallow water magneto-hydrodynamics. J. Comput. Phys. 2021, 431, 110136. [Google Scholar] [CrossRef]
- Winters, A.R.; Gassner, G.J. A comparison of two entropy stable discontinuous Galerkin spectral element approximations for the shallow water equations with non-constant topography Author links open overlay panel. J. Comput. Phys. 2015, 301, 357–376. [Google Scholar] [CrossRef]
- Wintermeyer, N.; Winters, A.R.; Gassner, G.J.; Kopriva, D.A. An entropy stable nodal discontinuous Galerkin method for the two dimensional shallow water equations on unstructured curvilinear meshes with discontinuous bathymetry. J. Comput. Phys. 2017, 340, 200–242. [Google Scholar] [CrossRef]
- Wintermeyer, N.; Winters, A.R.; Gassner, G.J.; Warburton, T. An entropy stable discontinuous Galerkin method for the shallow water equations on curvilinear meshes with wet/dry fronts accelerated by GPUs. J. Comput. Phys. 2018, 375, 447–480. [Google Scholar] [CrossRef]
- Wen, X.; Don, W.S.; Gao, Z.; Xing, Y.L. Entropy stable and well-balanced discontinuous Galerkin methods for the nonlinear shallow water equations. J. Sci. Comput. 2020, 83, 66. [Google Scholar] [CrossRef]
- Liu, Q.S.; Liu, Y.Q.; Feng, J.H. The scaled entropy variables reconstruction for entropy stable schemes with application to shallow water equations. Comput. Fluids 2019, 192, 104266. [Google Scholar] [CrossRef]
- Ismail, F.; Roe, P.L. Affordable, entropy-consistent Euler flux functions II: Entropy production at shocks. J. Comput. Phys. 2009, 228, 5410–5436. [Google Scholar] [CrossRef]
- Lefloch, P.G.; Mercier, J.M.; Rohde, C. Fully discrete entropy conservative schemes of arbitrary order. SIAM J. Numer. Anal. 2002, 40, 1968–1992. [Google Scholar] [CrossRef]
- Fjordholm, U.S.; Mishra, S.; Tadmor, E. Arbitrarily high-order accurate entropy stable essentially non-oscillatory schemes for systems of conservation laws. SIAM J. Numer. Anal. 2012, 50, 544–573. [Google Scholar] [CrossRef]
- Fjordholm, U.S.; Mishra, S.; Tadmor, E. ENO reconstruction and ENO interpolation are stable. Found. Comput. Math. 2013, 13, 139–159. [Google Scholar] [CrossRef]
- Biswas, B.; Dubey, R.K. Low dissipative entropy stable schemes using third order WENO and TVD reconstructions. Adv. Comput. Math. 2018, 44, 1153–1181. [Google Scholar] [CrossRef]
- Alcrudo, F.; Garcia-Navarro, P. A high-resolution Godunov-type scheme in finite volumes for the 2D shallow-water equations. Int. J. Numer. Methods Fluids 1993, 16, 489–505. [Google Scholar] [CrossRef]
- Qiu, J.; Shu, C.-W. Hermite WENO schemes and their application as limiters for Runge–Kutta discontinuous Galerkin method: One-dimensional case. J. Comput. Phys. 2003, 193, 115–135. [Google Scholar] [CrossRef]
- Sod, G. A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws. J. Comput. Phys. 1978, 27, 1–31. [Google Scholar] [CrossRef]
- Shu, C.-W.; Osher, S. Efficient implementation of essentially non-oscillatory shock capturing schemes. J. Comput. Phys. 1988, 77, 439–471. [Google Scholar] [CrossRef]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Toro, E.F.; Titarev, V.A. TVD fluxes for the high-order ADER schemes. J. Sci. Comput. 2005, 24, 285–309. [Google Scholar] [CrossRef]
- Jiang, G.S.; Shu, C.-W. Efficient Implementation of weighted ENO Schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef]
- Balsara, D.S.; Shu, C.-W. Monotonicity preserving weighted essentially non-oscillatory schemes with increasingly high order of accuracy. J. Comput. Phys. 2000, 160, 405–452. [Google Scholar] [CrossRef]




| Cells | Order | Order | Order | |||
|---|---|---|---|---|---|---|
| 25 | 7.1557 × 10 | 5.4250 × 10 | 4.6434 × 10 | |||
| 50 | 1.4620 × 10 | 2.29 | 5.0198 × 10 | 3.43 | 5.4977 × 10 | 3.08 |
| 100 | 3.2688 × 10 | 5.48 | 1.1626 × 10 | 5.43 | 1.2667 × 10 | 5.44 |
| 200 | 1.2699 × 10 | 4.69 | 5.8475 × 10 | 4.31 | 5.2894 × 10 | 4.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Zhou, X.; Li, G.; Qian, S.; Niu, Q. A New Entropy Stable Finite Difference Scheme for Hyperbolic Systems of Conservation Laws. Mathematics 2023, 11, 2604. https://doi.org/10.3390/math11122604
Zhang Z, Zhou X, Li G, Qian S, Niu Q. A New Entropy Stable Finite Difference Scheme for Hyperbolic Systems of Conservation Laws. Mathematics. 2023; 11(12):2604. https://doi.org/10.3390/math11122604
Chicago/Turabian StyleZhang, Zhizhuang, Xiangyu Zhou, Gang Li, Shouguo Qian, and Qiang Niu. 2023. "A New Entropy Stable Finite Difference Scheme for Hyperbolic Systems of Conservation Laws" Mathematics 11, no. 12: 2604. https://doi.org/10.3390/math11122604
APA StyleZhang, Z., Zhou, X., Li, G., Qian, S., & Niu, Q. (2023). A New Entropy Stable Finite Difference Scheme for Hyperbolic Systems of Conservation Laws. Mathematics, 11(12), 2604. https://doi.org/10.3390/math11122604







