Comparative Study of Type-1 and Interval Type-2 Fuzzy Logic Systems in Parameter Adaptation for the Fuzzy Discrete Mycorrhiza Optimization Algorithm

Abstract

The Fuzzy Discrete Mycorrhiza Optimization (FDMOA) Algorithm is a new hybrid optimization method using the Discrete Mycorrhiza Optimization Algorithm (DMOA) in combination with type-1 or interval type-2 fuzzy logic system. In this new research, when using T1FLS, membership functions are defined by type-1 fuzzy sets, which allows for a more flexible and natural representation of uncertain and imprecise data. This approach has been successfully applied to several optimization problems, such as in feature selection, image segmentation, and data clustering. On the other hand, when DMOA is using IT2FLS, membership functions are represented by interval type-2 fuzzy sets, which allows for a more robust and accurate representation of uncertainty. This approach has been shown to handle higher levels of uncertainty and noise in the input data and has been successfully applied to various optimization problems, including control systems, pattern recognition, and decision-making. Both DMOA using T1FLS and DMOA using IT2FLS have shown better performance than the original DMOA algorithm in many applications. The combination of DMOA with fuzzy logic systems provides a powerful and flexible optimization framework that can be adapted to various problem domains. In addition, these techniques have the potential to more efficiently and effectively solve real-world problems.

1. Introduction

Heuristic methods involve searching for solutions through trial and error, while metaheuristics are considered more advanced because they use information and solution selection to guide the search process [1]. Most metaheuristics imitate nature, specifically biological systems that have evolved over time due to natural selection [2]. For instance, ticks rely on temperature and body odor as important indicators, while bats use air compression waves to echo in caves. These unique traits have inspired algorithms that imitate nature and have gained popularity in various fields, such as fuzzy systems, neural networks, machine learning, artificial intelligence, computational intelligence, and engineering. These applications often require sophisticated optimization algorithms due to their involvement in nonlinear optimization [1,3,4].

Algorithms are used to solve optimization problems, but uncertainty in the real world can make this search more complicated. To address this, an optimal and robust design is aimed to find the best possible solutions. Solutions that are optimal but not robust are not practical in the real world [1,5,6,7].

This study proposes a new optimization algorithm called the Mycorrhiza Optimization Algorithm (MOA), which is inspired by the symbiotic relationship between plant roots and fungi shown in Figure 1. The algorithm aims to optimize resource allocation and communication through biochemical signals that alert the organisms to predators or other dangers.

Maximizing or minimizing is a technique that has been used for a long time to achieve optimized results. It is a common practice in everyday life and can be applied to various areas such as time, money, and resources. As a result, optimization is becoming increasingly important [8].

Symbiotic fungi have been thought to help plants migrate to land by improving the search for mineral nutrients and exchanging them for photosynthetic organic carbon. Nowadays, plant–fungal symbioses are common and varied. Recent findings suggest that early terrestrial plants had access to a range of possible fungal associations and that these associations were influenced by changes in atmospheric CO₂ concentrations.

The relationship between soil-dwelling filamentous fungi and plants is one of the most significant examples of natural symbiosis, following mitochondria and plastids. Most land-based plants, including many agricultural crops, form close symbiotic relationships with fungi. These mutually beneficial partnerships are believed to have played a vital role in the evolution and diversity of land plants. In plants with roots, this relationship is known as “mycorrhiza,” while in plants without roots that have intracellular fungal structures resembling those in rooted plants, such as coils and arbuscules, it is called “mycorrhiza-like.”

Fungal mycelium can spread extensively through soil, and the relationships between fungi and host plants are often widespread, leading to the development of Mycorrhiza Networks (MN). These networks consist of uninterrupted fungal mycelia that connect two or more plants, regardless of whether they are of the same or different species. This allows MN to integrate numerous plant and fungal species, which interact, give feedback, and adapt, creating a complex adaptive social network. It is becoming increasingly clear that MN has an impact on member plants and fungi and involves communication between plants and fungi through biochemical signaling, resource transfers, or the influence of electrical signals.

Plants and fungi respond quickly to communication through MN, which can be described as behavioral responses. This approach allows us to view MN in terms of plant behavior.

A design approach for the algorithm involves five phases that incorporate a simulation of the ecosystem that exists between plants and the mycorrhizal fungal network. The five phases are colonization, mutualism, pollination, resource exchange, and plant defense. The Lotka–Volterra system of equations is utilized in three of these phases, which involve discrete equations. In the pollination phase, Levy’s flight equation can be used, but other equations can also be used.

The main contribution of this research is enhancing the ability of the Discrete Mycorrhizal Optimization Algorithm (DMOA) in conjunction with the type-1 fuzzy logic system (T1FLS) and interval type-2 fuzzy logic system (IT2FLS) to obtain better results than those found by only using the original algorithm and how finally the results of the DMOA together with the IT2FLS were the best of all, which is what we expected, due to the ability of IT2FLSs of handling higher degrees of uncertainty

The article is organized as follows, in Section 1 we make an introduction to the Discrete Mycorrhizal Optimization Algorithm, in Section 2 we make a description of the concept of optimization and what it actually represents for an algorithm, Section 3 shows the basics of the T1FLS and IT2FLS, Section 4 shows a brief history of the developed algorithms in relation to the plants, in Section 5 we present the method with which we developed this investigation, in Section 6 we present the results by means of tables and graphs, and in Section 7 we present the conclusions of this investigation.

2. Optimization

The term “optimization” refers to the process of selecting the best possible option among several viable options while keeping a set of constraints in mind. Optimization theory is an example of how humans seek perfection by teaching how to define and achieve an optimal outcome. Through optimization, the aim is to enhance system performance towards the optimal point(s) [9]. Depending on the theoretical or practical aspect, optimization can be considered a component of applied or numerical mathematics or a computer-based system design method [10]. The analytical solution of an optimization problem relies on the shape of the criterion and constraint functions [11]. The simplest form of the general optimization problem is the unconstrained optimization issue, where decision variables have no restrictions, and calculus can be applied for analysis. Another relatively simple form is when all the constraints can be expressed as equality relationships.

Humans have the ability to comprehend, analyze, improve, and learn from the processes that occur around them. Animals, too, continue to improve the processes in which they are involved, whether consciously or unconsciously. Monkeys are known to create tools. The crow has been taught to collect trash in exchange for food. Over time, moths have developed techniques to avoid bats. During the drought season, an elephant herd can find water. Even trees in the tropics grow tall in order to compete for sunlight. There are numerous examples.

The improvement of processes in living creatures over time is a result of their behavior and evolution, rather than their intelligence. As time passes, methods are refined to produce better techniques and outcomes. Scholars and researchers have examined these tendencies toward process optimization and developed evolutionary optimization algorithms (EOAs) based on them. DMOA is one such EOA, where plants compete for sunlight and mycorrhizae compete for resources such as water, carbon, and zinc. The behavior patterns of these organisms are modeled in this algorithm [12].

The application of engineering practice, artificial intelligence, and managerial decision-making all include extensive research into optimization issues. The optimization problem gets more complicated as manufacturing size grows. The intricacy of the old exact algorithms based on derivative approaches limits their use in small-scale situations even though they can offer the exact answer to a problem [13].

Additionally, the problem that needs to be solved must have a model that is continuous and derivable; global optimization cannot be achieved for multi-peak, substantially nonlinear, or problems that are evolving dynamically [14]. As a result, solving global optimization problems via conventional techniques becomes very difficult.

Particle swarm optimization (PSO) [15], bat algorithm (BA) [16], JADE [17], cuckoo optimization algorithm (COA) [18], and flower pollination algorithm (FPA) [19] are examples of bioinspired intelligent optimization algorithms that have been proposed to solve complex optimization problems. The following algorithms simulate group behaviors and natural phenomena, such as the crow search algorithm (CSA) [20], grey wolf optimizer (GWO) [21], teaching–learning-based optimization (TLBO) [22], symbiotic organisms search (SOS) [23], and elephant herding optimization (EHO) [24]. Other cases are the YUKI algorithm, which is an innovative technique used to reduce the search space in specific problems. It involves creating a smaller local search area and simultaneously allocating two parts of the population for exploration and exploitation. This allows for the optimization of the search for interesting and promising solutions within the context of the problem being addressed [25,26,27], and the snake optimizer algorithm (SO) to address a diverse set of optimization tasks that mimics the special mating behavior of snakes. Each snake (male/female) struggles to have the best mate if the existing food is sufficient and the temperature is low, the algorithm mimics and mathematically models such behaviors and patterns of foraging and reproduction in a simple and efficient way [28]. These are only a few of the innovative intelligence algorithms that have been developed in the last five years. No intelligent algorithm, however, is capable of resolving every optimization issue. As a result, the freshly proposed or newly discovered algorithms have a wide range of application history.

Optimization is not restricted to a particular discipline such as applied mathematics, engineering, medicine, economics, computer science, or operations research. It has become a crucial tool in all areas of study. Advancements in developing novel algorithms and theoretical methods have enabled optimization to evolve in multiple directions, with a specific emphasis on artificial intelligence. This includes fields such as deep learning, machine learning, computer vision, fuzzy logic systems, and quantum computing [29,30].

Optimization has experienced a consistent expansion over the last five decades. Contemporary society not only exists in a fiercely competitive setting but also has to contemplate sustainable growth and conservation of resources. Therefore, it is crucial to optimally plan, design, operate, and manage resources and assets. Initially, the focus was on optimizing each operation independently. However, the present inclination is towards an integrated approach that encompasses synthesis and design, design and control, production planning, scheduling, and control [31].

Optimization has been evolving in recent years to the point that now provides general solutions to linear, nonlinear, unbounded, and constrained optimization problems. These problems are part of the mathematical programming area and can be divided into two classes: linear and nonlinear programming problems. Genetic algorithms and simulated annealing are two key methodologies that have been receiving increasing attention in real applications. The rapid development of technology has offered users a plethora of optimization codes with diverse degrees of rigor and complexity that can help in solving real-world problems. It is also possible to extend the capabilities of existing methods by integrating the features of two or more optimization methods to achieve a more efficient hybrid optimization algorithm [32]. However, there is no single method that can solve all specific problems of No Free Lunch (NFL) [33], and research is still ongoing to develop optimization methods that can solve them all.

Optimization methods have particular applications and are not applicable to every problem. It is necessary to recognize a problem as an optimization problem, or else other artificial intelligence techniques with specific specializations may be more appropriate.

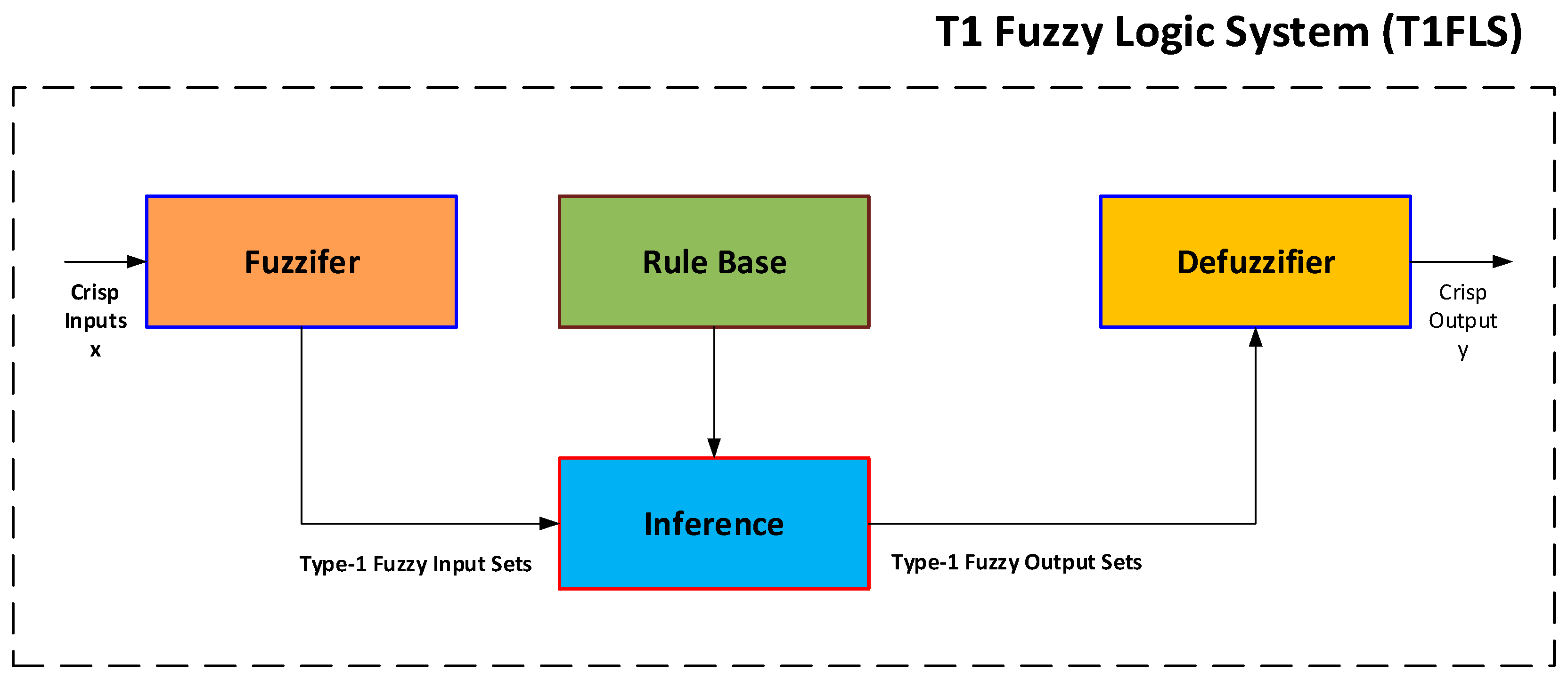
3. Fuzzy Logic Systems

Fuzzy logic is a mathematical method that was introduced by Lotfi A. Zadeh in the 1960s [34] and is based on the theory of fuzzy sets. This theory proposes that an element can partially belong to a set, unlike in classical set theory where an element either belongs or does not belong to a set. This allows for an efficient way to work with uncertainties and to condition knowledge in the form of rules towards a quantitative level that can be processed by computers. Fuzzy logic is based on the way that people make decisions based on imprecise and linguistic information. Fuzzy sets are mathematical concepts for representing vagueness and imprecise information. The concept of fuzzy set membership is used to determine how much observation is within a set. Fuzzy logic deals with uncertainty in reasoning and utilizes concepts, principles, and methods developed within it.

Fuzzy logic is a computational technique that imitates the way humans think. Humans can make decisions based on vague information, such as determining if a room is hot without knowing the exact temperature. Fuzzy logic attempts to simulate this behavior of the human brain by using logical expressions that consider “degrees of truth” instead of the classic terms “true” or “false”. Equation (1) shows the equation for type-1 fuzzy logic systems (T1FLS), and Figure 2 shows the general scheme for T1FLS.

The theory of fuzzy sets, developed by L. Zadeh, allows modeling the uncertainty that occurs in biological and social systems. Fuzzy logic is a theory dealing with uncertainty in reasoning and utilizes concepts, principles, and methods developed within it [35,36].

$$A=\left\{\left(x,{\mu }_A\left(x\right)\right)\left|x\in X\right.\right\}$$

(1)

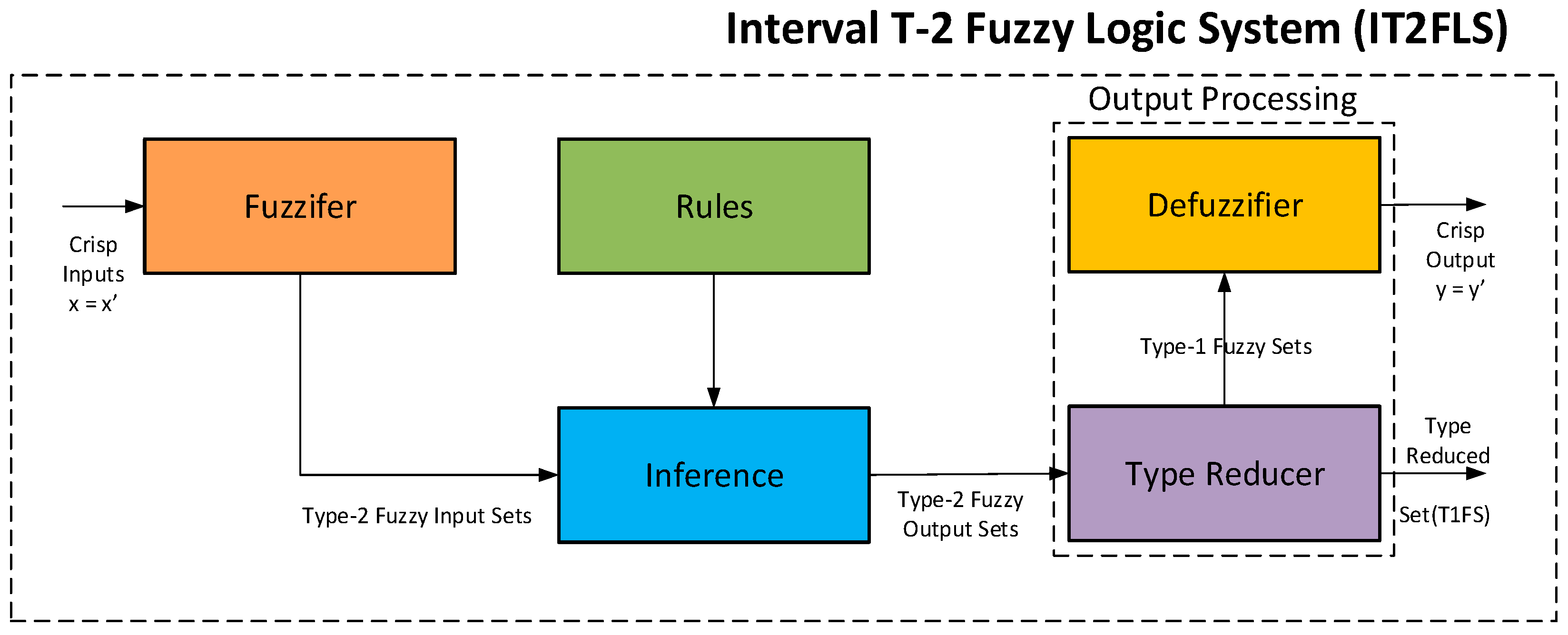
Interval Type-2 Fuzzy Logic System

Zadeh introduced the concept of type-2 fuzzy sets as an extension of fuzzy sets, specifically type-1 fuzzy sets, according to [37]. Type-2 fuzzy sets are characterized by having fuzzy membership degrees [38], which can be any subset of [0, 1] of the primary membership. Additionally, for each primary membership, there is a corresponding secondary membership that defines the possibilities of the primary membership, and this secondary membership can range “between 0 and 1” as noted in [39]. Type-1 fuzzy sets are a special case of type-2 fuzzy sets, where the secondary membership function consists of a single element, the unit. The use of type-2 fuzzy sets enables us to manage linguistic uncertainty, such as the fact that “words can mean different things to different people”. Higher types of fuzzy relations, including type-2, increase fuzziness in relationships and can lead to greater logical processing of imprecise information, as stated in [40].

Interval type-2 fuzzy sets (IT2FLS) are a mathematical framework that builds on the original concepts of fuzzy sets, providing a means to account for uncertainty in models. Recent years have seen significant progress in this area. An IT2FLS can be defined mathematically, as shown in [41,42]. A fuzzy set is a way to express the degree of truth for an element belonging to a set in a non-deterministic manner that allows for imprecision and uncertainty. In this context, a type-2 fuzzy set, denoted by Ã, is characterized by a type-2 membership function $\left(x,u\right)$ where $x\in X$, $u\in J_x\subseteq \left[0,1\right]$, and $0\le \left(x,u\right)\le 1$ defined in Equation (2) and Figure 3.

Fuzziness (entropy) is usually considered in measuring uncertainty for type-1 fuzzy sets, while for IT2FLS, centroid, and other measures are used to measure uncertainty.

$$\tilde{A}=\left\{\left(\left(x,u\right),1\right)|\forall x\in X,\forall u\in J_x\subseteq \left[0,1\right]\right\}$$

(2)

4. Related Work

Nature-inspired optimization algorithms, such as particle Swarm Optimization (PSO) [43], flower pollination algorithm (FPA) [19,44], ant colony optimization (ACO) [45], artificial bee colony (ABC) [46], firefly algorithm (FA) [47], etc., have demonstrated flexibility, efficiency, and adaptability, in solving a wide spectrum of problems in real world applications, their merits and successes have inspired researchers to continuously develop these algorithms innovative.

For these reasons, it is proposed to develop an algorithm inspired by plants and how they adapt to physiological changes, survival, and growth through communication and the exchange of resources that are transferred through a fungal network. The proposed metaheuristics have a stochastic basis, that is, probabilistic, and the randomness rules are combined to imitate the process that inspires the algorithm.

Plant-inspired algorithms exist in the literature, it has been shown that plants exhibit intelligent behaviors “Plant intelligence-based metaheuristic optimization algorithms” [48], such as the one based on plant defense mechanism “A New Bio-inspired Optimization Algorithm Based on the Self-defense Mechanisms of Plants” [49], Flower Pollination Algorithm (FPA) “Fuzzy Flower Pollination Algorithm to Solve Control Problems” [50], Plant Growth Optimization (PGO) “A Global Optimization Algorithm Based on Plant Growth Theory: Plant Growth Optimization” [51].

Plants are highly successful in colonizing many habitats and represent approximately 99% of the planet’s eukaryotic biomass. They have evolved a variety of mechanisms to solve problems such as foraging and reproductive strategies. Plants sense environmental conditions and take measures to adapt to changing environments, such as searching for light and nutrients, to defend themselves against herbivores and other attackers. Although plants do not have a brain or central nervous system, they can sense environmental conditions and take “adaptive” measures that allow them to adjust to environmental changes. Plant adaptations are special features that improve their chances of survival and evolve over a long period of time. Examples of plant adaptations include:

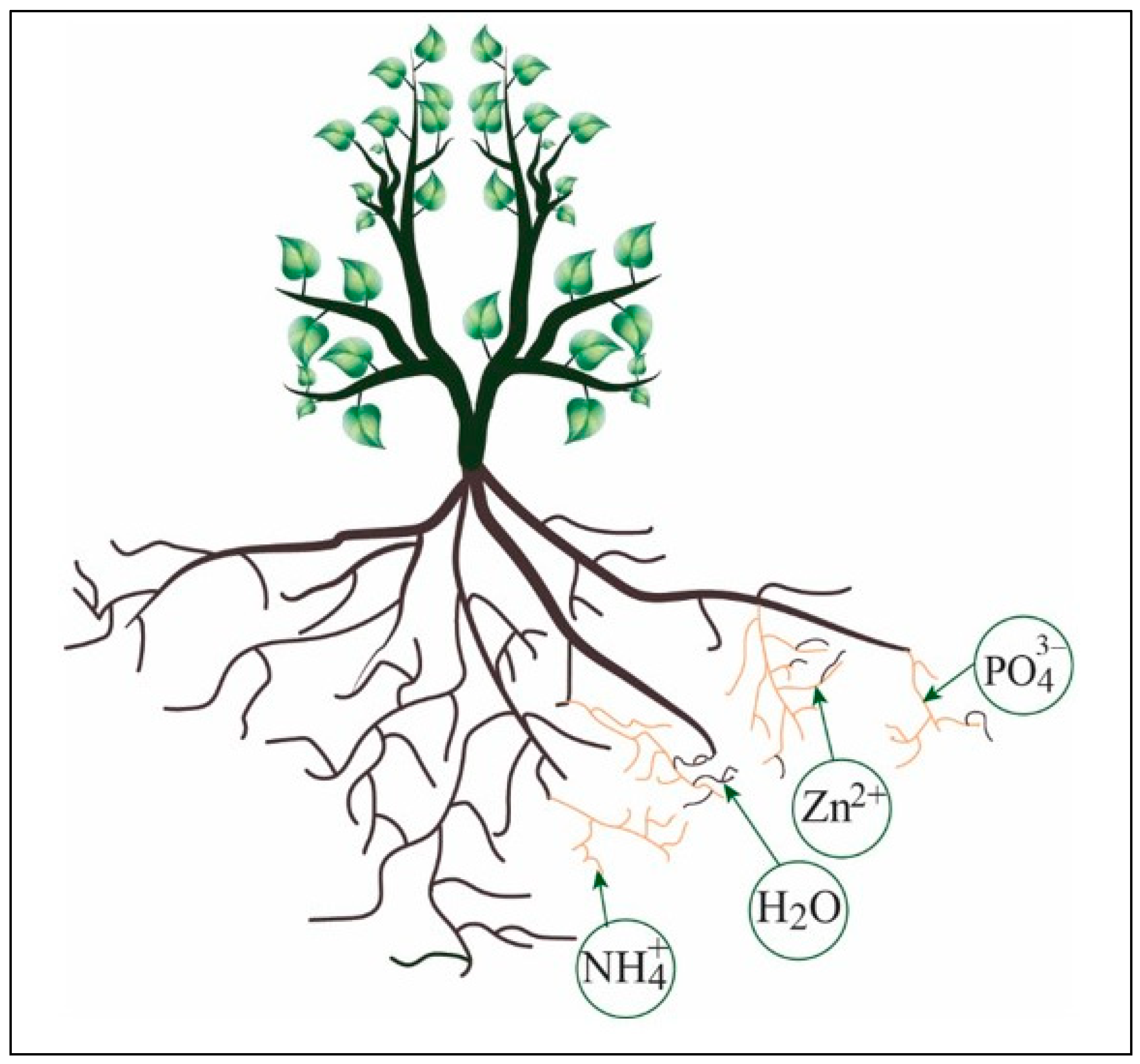
• Foraging for light, water, and other nutrients;
• The ability to defend themselves against herbivores and other attackers;
• The ability to “remember” past events.

Plants and algae use photosynthesis to convert carbon dioxide and water into organic compounds, especially carbohydrates, using energy from sunlight and releasing oxygen as waste. Although plants are not known for their ability to move, they can move in response to various stimuli, but much more slowly than animals. Plants and algae are photosynthetic organisms that account for almost 50% of the photosynthesis that occurs on Earth. Photosynthesis is the process by which light energy is converted to chemical energy, whereby carbon dioxide and water are converted into organic molecules. Plants can move in response to a variety of stimuli, which include:

• Light (phototropism), plants constantly monitor their visible environment.
• Gravity (geotropism), the plant’s root network also moves, and the root tips respond to gravity.
• Water (hydrotropism), which is the response of plant growth to water.
• Touch (thigmotropism), many plants respond to the sense of touch, such as the tendrils of climbing plants, vines, or bindweed.

With plant propagation algorithms, plants have a propagation process, such as seed dispersal and root propagation. The invasive weed optimization algorithm (IWO), based on the colonization behavior of weeds, was put forward by Mehrabian and Lucas (2006) [52]. The paddy field algorithm was first proposed by Premaratne, Samarabandu, and Sidhu (2009) [53], and is inspired by aspects of the plant reproduction cycle, focusing on pollination and seed dispersal process. Although many plants are propagated using seeds, some employ a system of “runners” or horizontal stems that grow outward from the base of the plant. The strawberry plant algorithm is inspired by the propagation of plants through seeds and stolons [54]. In the plant growth simulation algorithm (PGSA), inspired by the light foraging process, an important aspect of plant growth is that the initial plant stem eventually gives rise to branches and leaves as it is growing [55].

Despite the wide variety of plants and associated plant behaviors that occur in the natural world, little inspiration has so far been taken from these mechanisms for the design of computational algorithms.

So far, there is no algorithm with the characteristics that mimic the behavior of an ecosystem such as a forest and specifically in the understory, i.e., the behavior between tree roots and a fungal network.

5. Proposed Method

The novel DMOA algorithm is inspired by the nature of the Mycorrhiza Network (MN) and plant roots with this close interaction between these two organisms (plant roots and MN fungal network), a symbiosis is generated, and it has been found that in this relationship [56,57,58,59,60]:

• There is communication among plants, which may or may not be of the same species, through a fungal network (MN).
• There is an exchange of resources among plants through the fungal network (MN).
• There is a defense behavior against predators that can be insects or animals, for the survival of the whole habitat (plants and fungi).
• The colonization of a forest through a fungal network (MN) thrives much more than in a forest where there is no exchange of resources (see Figure 4).

This new optimization method FDMOA inspired by the symbiosis of plants and the Mycorrhizal Network uses the six discrete Lotka–Volterra system equations (DLVSE), these equations model the understory ecosystem where plant roots and the MN have a symbiotic relationship. With Equations (3) and (4) in predator–predator model, biochemical signals that travel through the MN alert all the plants that are connected to this network to the danger of predators, fires, floods, etc., with Equations (5) and (6) in the cooperative model, it transfers resources from plants to other growing plants and from plants to the MN, all these resources travel through the MN and Equations (7) and (8) competitive model, it competes for habitat resources with respect to other plants for obtaining sunlight to perform photosynthesis that is converted into carbon that they share with the MN, the water and minerals that the MN obtains are shared with the plants.

It has been demonstrated that the algorithm has a fast convergence and therefore a low computational cost, the three biological operators represented by DLVSE are the defense model, the cooperative model and the competitive model, initially we have two populations (plants and MN), both populations are obtained by generating random numbers, we obtain the best fitness of each population, these values are the input to the parameters a (population grow rate x) and d (population grow rate y) of the DLVSE equation system, the result of Equation (9) (iterations), is the input for the fuzzy systems T1FLS and IT2FLS, the parameterization of the membership functions are modified with values provided by the FDMOA algorithm, the output of the fuzzy system is the parameter xi (growth rates of the populations x in time t) that influence in a determinant way the convergence of the algorithm, then the biological operator resource exchange (cooperative model) and its result has inference in one of the two biological operators (defensive model or competitive model) based on a random outcome 1 or 2, with this we try to simulate what happens in an ecosystem where these events of defense against predators and competition for resources such as water, carbon, zinc, etc. Then the fitness is evaluated, the population and fitness are updated, and the stop condition is verified, if it is higher the algorithm is terminated, otherwise the process continues with the fuzzy systems process. The sequence of the FDMOA algorithm can be seen in Algorithm 1 showing the pseudocode and Figure 5 illustrating the flowchart of the FDMOA algorithm.

Algorithm 1: Fuzzy Discrete Mycorrhiza Optimization Algorithm (FDMOA)

1:  Objective min or max f(x), x = (x1, x2,…, xd)  2:  Define parameters (a, b, c, d, e, f, x, y)  3:  Initialize a population of n plants and mycorrhiza with random solutions  4:  Find the best solution fit in the initial population  5:  while (t < maxIter)  6:  for i = 1:n (for n plants and Mycorrhiza population)  7:  $X_p=abs\left(FitA\right)$  8:  $X_m=abs\left(FitB\right)$  9:  end for  10:  $a=minor{X}_p$  11:  $d=minor{X}_m$  12:  Apply (LV-Cooperative Model)  13:  $x_i^{t+1}=\frac{\left({ax}_i-b{x}_i{y}_i\right)}{\left(1-g{x}_i\right)}$  14:  $y_i^{t+1}=\frac{\left({dy}_i+e{x}_i{y}_i\right)}{\left(1+h{y}_i\right)}$  15:  if $x_i<y_i$  16:  $x^t=x_i$  17:  else  18:  $x^t=y_i$  19:  end if  20:  rand ([1 2])  21:  if (rand = 1)  22:  Apply (LV-Predator-Prey Model)  23:  $x_i^{t+1}=a{x}_i\left(1-x_i\right)-b{x}_i{y}_i$  24:  $y_i^{t+1}=d{x}_i{y}_i-g{y}_i$  25:  else  26:  Apply (LV-Competitive Model)  27:  $x_i^{t+1}=\frac{\left({ax}_i-b{x}_i{y}_i\right)}{\left(1+g{x}_i\right)}$  28:  $y_i^{t+1}=\frac{\left({dy}_i-e{x}_i{y}_i\right)}{\left(1+h{y}_i\right)}$  29:  end if  30:  Evaluate new solutions.  31:  T1FLS-IT2FLS Architecture  32:  Evaluate Error  33:  Error minor?  34:  Update T1FLS-IT2FLS Architecture.  35:  Find the current best FLS-Architecture solution.  36:  end while

All the parameters in Algorithm 1, have been obtained from the literature [61,62,63,64] and are sensitive to the results obtained in this investigation, the only parameters that we experiment that move in an important way the generation of new values are the parameters a and d that we mentioned previously, the parameter xi generated by the fuzzy systems, is the parameter that moves the fuzzy system towards the convergence, we have to investigate in depth each one of the parameters to see its incidence in the results; this investigation will be reason to make another article.

By dynamic adaptation of parameters in this method we refer to the change in the parameter values of the membership functions of the T1FLS and IT2FLS fuzzy systems in each iteration with the purpose of improving the performance and precision of the algorithm.

This new optimization method inspired by the symbiosis of plants and the Mycorrhiza Network, the FDMOA algorithm uses the discrete Lotka–Volterra system equations (DLVSE), it has been demonstrated that the algorithm has fast convergence and therefore a low computational cost, the three biological operators represented by DLVSE are the defense model, cooperative model, and competitive model, initially we have two populations (plants and MN), we obtain the best fitness of each population, the result of Equation (9) (iterations), is the input for the fuzzy systems T1FLS and IT2FLS, the parameterization of the membership functions are modified with values provided by the FDMOA algorithm, the output of the fuzzy system is the parameter xi (grow rates of populations x at time t) that influence of determinant form in the convergence of the algorithm, then the biological operator resource exchange (cooperative model) and its result has inference in one of the two biological operators (defense model or competitive model) based on a random result 1 or 2, with this we try to simulate what happens in an ecosystem where these events of defense against predators and competition for resources such as water, carbon, zinc, etc., then the fitness is evaluated, the population and fitness are updated, the stop condition is checked, if it is higher the algorithm is terminated, otherwise the process continues in the fuzzy systems step. The sequence of the FDMOA algorithm can be seen in the pseudocode of Algorithm 1 and in the flowchart of Figure 5.

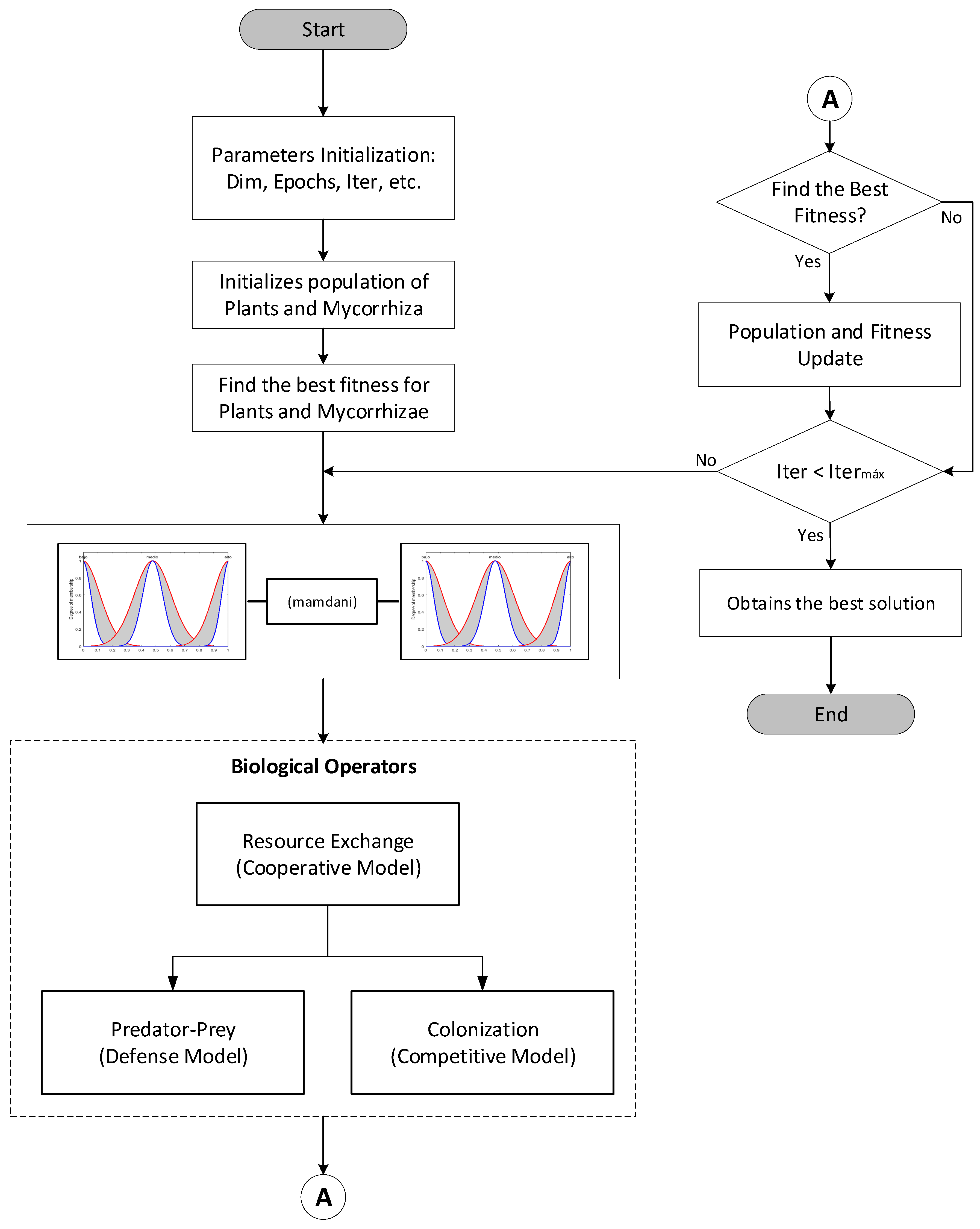
5.1. Discrete Mycorrhiza Optimization Algorithm

The mycorrhizal associations between plants and fungi have significant impacts on the ecosystem at a large scale. This is mostly due to the fact that most plants tend to form these associations, which are believed to have originated in ancient times and helped plants colonize the land. The symbiosis between plants and fungi is a many-to-many relationship, meaning that plants can form associations with a wide variety of fungal species, and fungal species can colonize many different plant species. While most mycorrhizal fungi have a broad range of hosts and form diffuse mutualisms, some are specialists that only occur in one host.

It is now understood that the Mycorrhiza Network (MN) can impact various aspects of plant life, including establishment, survival, physiology, growth, and chemical defense. This impact is thought to occur because MN serves as a pathway for exchanging stress molecules and resources between plants. For instance, the most common method for mycorrhizal fungal colonization of regenerating plants in their natural environment is believed to be through anastomosis with pre-existing MN of established plants. The colonization of seedlings by MN enables them to obtain enough nutrients from the soil for the growth of their roots and shoots, leading to their survival.

The behavior of living things in nature has inspired researchers in computer science to develop new optimization algorithms, with a focus on the relationship that mycorrhiza fungi have developed with the roots of plants, specifically trees. The colonization of trees on the earth would not have occurred except for the mycorrhiza fungal networks through their roots. To date, 100,000 species of fungi are known, but it is possible that there are more. This relationship between fungi and plants is an example of symbiosis, where there is a mutual exchange of resources between the two organisms, with fungi providing plants with nitrates and phosphates necessary for their growth in exchange for carbon dioxide carried out through photosynthesis, resulting in mutual benefit and improved biological fitness for both plant and fungus [65].

Symbiosis refers to a close and ongoing biological interaction between different species of organisms. In the case of fungi, they reside either on the surface of the roots or within the bark of plant roots, as illustrated in Figure 4. This interaction involves an exchange of resources between the fungi and plants, where the fungi provide nitrates and phosphates that are essential for plant growth in return for carbon dioxide produced through photosynthesis. This leads to a mutually beneficial relationship, or mutualism, where both the plant and fungus benefit and enhance their biological fitness [66,67,68].

In Figure 4 we can see that a mycorrhiza is a symbiotic relationship between roots (1) and fungi (2) that involves the exchange of plant and tree sugars for moisture and nutrients acquired by fungal filaments (3) from the soil. By extending the root systems of trees, mycorrhizae significantly improve their absorptive capacity, expanding their ability to gather essential resources.

5.2. Discrete Lotka–Volterra System Equation

The discrete Lotka–Volterra system equations (DLVSE) used in this research are Linear Equations (3)–(8) which are described below:

Equations (3) and (4) [61,62], were used to develop the biological operator (predator–prey model) within the algorithm.

Equations (5) and (6) [63], were used to develop the biological operator (cooperative model) in the algorithm.

Equations (7) and (8) [63,64], were used to develop the biological operator (competitive model) in the algorithm.

$$x_i^{t+1}=\frac{\left({ax}_i-b{x}_i{y}_i\right)}{\left(1-g{x}_i\right)}$$

(3)

$$y_i^{t+1}=\frac{\left({dy}_i+e{x}_i{y}_i\right)}{\left(1+h{y}_i\right)}$$

(4)

$$x_i^{t+1}=a{x}_i\left(1-x_i\right)-b{x}_i{y}_i$$

(5)

$$y_i^{t+1}=d{x}_i{y}_i-g{y}_i$$

(6)

$$x_i^{t+1}=\frac{\left({ax}_i-b{x}_i{y}_i\right)}{\left(1+g{x}_i\right)}$$

(7)

$$y_i^{t+1}=\frac{\left({dy}_i-e{x}_i{y}_i\right)}{\left(1+h{y}_i\right)}$$

(8)

5.3. FDMOA Parameters

Table 1. FDMOA parameters.

Parameter	Description	Value
DMOA—Parameters:
$x_i^{t+1}$	Population x at time t
$y_i^{t+1}$	Population y at time t
$x_i$	Grow rates of populations x at time t
$y_i$	Grow rates of populations y at time t
t	time
a	Population growth rate x	0.01
b	Influence of population x on itself	0.02
g	Influence of population y on population x	0.06
d	Population growth rate y	0
e	Influence of population x on population y	1.7
h	Influence of population y on itself	0.09
x	Initial population in x	0.0002
y	Initial population in y	0.0006
In the absence of population x = 0, In the absence of population y = 0
a, b, c, d, e and f—are positive constants
Population	Population size	20
Populations	Number of populations	2
Dimensions	Dimensions size	30, 50, 100
Epochs	Number of epochs	30
Iterations	Iteration’s size	30, 50, 100, 500

provides all the parameters that are used in the FDMOA algorithm, such as populations, dimensions, epochs, iterations, etc. These parameters are fixed, but we also consider some parameters as dynamic, as is explained later.

5.4. FDMOA Pseudocode

Algorithm 1 shows the pseudocode of the logic and structure of the FDMOA optimization algorithm.

5.5. FDMOA Flowchart

Figure 5 shows the process flow diagram of the FDMOA optimization algorithm.

5.6. Mathematical Functions

Table 2. 36 Mathematical functions.

F	Function	Range	Nature
F1	Sphere	[−5.12, 5.12]	U
F2	Rosenbrock	[−5, 10]	U
F3	Griewank	[−600, 600]	M
F4	Rastrigin	[−5.12, 5.12]	M
F5	Ackley	[−32.768, 32.768]	M
F6	Dixon-Price	[−10, 10]	U
F7	Michalewicz	[0, π]	M
F8	Powell	[−4, 5]	U
F9	RHE: Rotate Hyper Ellipsoid	[−65.536, 65.536]	U
F10	Shwefel	[−500, 500]	M
F11	Styblinski–Tang	[−5, 5]	U
F12	SDP: Sum Different Powers	[−1, 1]	M
F13	Sum Squares	[−10, 10]	U
F14	Trid	[−d2, d2]	U
F15	Zakharov	[−5, 10]	U
F16	Bukin No 6	[−15, −5]	U
F17	Cross-in-Tray	[−10, 10]	M
F18	Drop-Wave	[−5.12. 5.12]	M
F19	Eggholder	[−5.12, 5.12]	M
F20	Beale	[−4.5, 4.5]	U
F21	Holder Table	[−10, 10]	M
F22	Branin	[−5, 10]	M
F23	Levy	[−10, 10]	M
F24	Levy 13	[−10, 10]	M
F25	Schaffer 2	[−100, 100]	M
F26	Schaffer 4	[−100, 100]	M
F27	Shubert	[−10, 10]	M
F28	Bohachevsky 1	[−100, 100]	M
F29	Bohachevsky 2	[−100, 100]	M
F30	Bohachevsky 3	[−100, 100]	M
F31	Booth	[−10, 10]	U
F32	Matyas	[−10, 10]	U
F33	Mccormick	[−1.5, 4]	U
F34	Easom	[−100, 100]	U
F35	Goldstein–Price	[−2, 2]	M
F36	Three-Hump Camel	[−5, 5]	M
U	Unimodal
M	Multimodal

contains the 36 mathematical functions with which we performed all the experimentation in this article: function number (F), function name, range, and nature (U: unimodal or M: multimodal).

Figure 6, Figure 7, Figure 8 and Figure 9 represent the graphical schemes of the 36 different mathematical functions (CEC2013) and Figure 10 shows the 36 mathematical functions, mentioned in Table 2, which we are using for the experimentation of the DMOA algorithm, in the figures we can find the function number (F), the image of the function.

Sphere function is a convex and unimodal function, which means that it has a single global minimum, optimization algorithms usually have no problem finding the global minimum. Rosenbrock function is a non-convex function with a long narrow valley leading to the global minimum. Griewank function is a multimodal function with multiple local minima, it presents a challenging optimization landscape with oscillations. Rastrigin function is a highly multimodal function with a rough landscape, its optimization challenges arise from the presence of many local minima. Ackley function is a multimodal function with a complex landscape, its optimization challenges stem from the trade-off between exploration and exploitation. Dixon-Price function is a unimodal function with multiple local minima. Michalewicz function is a multimodal function with a complex landscape, it tests the ability of an optimization algorithm to handle high-dimensional problems with intricate relationships between variables. Powell function is a mathematical function with multiple local minima, its optimization challenges stem from its high dimensionality and the presence of local minima. The Rotate Hyper-Ellipsoid function is a smooth elongated function used to evaluate optimization algorithms. Schwefel function has a very rough landscape with multiple local minima, Figure 6.

Styblinski-Tang function is a unimodal function with many local minima. Sum Different Powers function is a multimodal function with multiple local minima, it presents challenges in optimization due to its hilly landscape and the presence of local minima. Sum Squares function is a convex and unimodal function, optimization algorithms usually have no problems finding the global minimum. Trid function is a unimodal function with multiple local minima. Zakharov function is a unimodal function with multiple local minima, its optimization problems arise from its hilly landscape and the presence of local minima. Bukin No 6 function is a unimodal function with multiple local minima, its optimization problems arise from the complexity and irregularity of the environment. Cross-in-Tray function is a multimodal function with multiple local minima, its optimization problems lie in the presence of many local minima and in the complexity of the environment. Drop-Wave function is a multimodal function with a challenging optimization landscape, it has a global minimum in a narrow region surrounded by many local minima. Eggholder function is a multimodal function with a complex landscape, its optimization problems arise from the presence of multiple local minima and intricate relationships between variables. Beale function is a unimodal function with multiple local minima, optimization algorithms face the challenge of efficiently exploring the search space, Figure 7.

Holder Table function is a multimodal function with multiple local minima, it has a complex and irregular landscape with distinct peaks and valleys. Branin function is a multimodal function with multiple local minima. Levy function is a multimodal function with a complex and challenging landscape. Levy 13 function is a multimodal function with multiple local minima, it presents optimization challenges due to its complex and irregular landscape. Shaffer 2 function is a multimodal function with multiple local minima, it has a complex and hilly landscape, which makes it challenging for optimization algorithms. Shaffer function 4 is a multimodal function with multiple local minima, it has a complex and irregular landscape. Shubert function is a multimodal function with a highly oscillatory landscape, it has multiple local minima and a global minimum. Bohachevsky 1 function is a multimodal function with multiple local minima, it has a complex and irregular landscape. Bohachevsky function 2 is a multimodal function with multiple local minima, it has a complex and irregular landscape. Bohachevsky function 3 is a multimodal function with multiple local minima, it presents optimization challenges due to its complex and irregular landscape, Figure 8.

Booth function is a unimodal function with multiple local minima, it has a simple but narrow valley landscape. Matyas function is a unimodal function with multiple local minima, it has a bowl-shaped landscape. McCormick function is a unimodal function with multiple local minima, it has a complex and irregular landscape. The Easom function is a unimodal function with multiple local minima, it has a sharp, narrow peak surrounded by a hilly landscape. The Goldstein-Price function is a multimodal function with multiple local minima, it has a complex and oscillatory landscape. Three-Hump Camel function is a multimodal function with multiple local minima, it has three distinct peaks and valleys, Figure 9.

Table 3. Rules IF THEN for T1FLS and IT2FLS.

N	Rules If Then
1	if (iter is Low) then (xi is High)
2	if (iter is Medium) then (xi is Medium)
3	if (iter is High) then (xi is Low)

shows the three fuzzy IF THEN rules that were used for both the T1FLS and IT2FLS fuzzy systems.

Equation (9) shows the way to calculate the “iteration” variable:

$$Iteration=\frac{Current\hspace{1em}Iteration}{Total\hspace{1em}Iterations}$$

(9)

Figure 11 shows the architecture for T1FLS Fis-fisGau318 with parameter adaptation, an input with three Gaussian functions and output also with three Gaussian functions using the Mamdani method, Gaussian membership function “Low” with blue color, Gaussian membership function “Medium” with orange color and Gaussian memebership function “High” with yellow color, “iter” is the number of iteration parameters and xi is a DLVSE parameter indicating grow rates of populations x at time t.

Figure 12 shows the architecture for the IT2FLS FIS-it2_gausS01 with parameter adaptation, an input with three Gaussian functions, and an output also with three Gaussian type-2 functions using the Mamdani method, in the three Gaussian membership functions Low, Medium and High, the red line is the value of the upper membership function (UMF), the blue line is the value of the lower membership function (LMF) and the The internal part of the membership function with the gray color is called the footprint of uncertainty (FOU).

Figure 13 shows the architecture for IT2FLS FIS-it2_3gausS6523 optimized with the DMOA algorithm.

Figure 14 shows the Gaussian Membership Function with the uncertainty in the standard deviation that is used in the design of architecture of the interval type-2 fuzzy logic system. Within the framework of the three Gaussian membership functions, namely Low, Medium, and High, the upper membership function (UMF) is represented by the red line, while the lower membership function (LMF) is represented by the blue line. The gray-colored region within the membership function is referred to as the footprint of uncertainty (FOU).

Equations (10)–(13) represent the type-2 Gaussian equations.

$${\mu }_{\tilde{F}}=⌈{\underset{¯}{\mu }}_{\tilde{F}}\left(x\right),{\overline{\mu }}_{\tilde{F}}\left(x\right)=igaussstype2\left(x,\left[{\sigma }_1,{\sigma }_2,m\right]\right)⌉$$

(10)

$${\mu }_{\tilde{F}}=exp⌈-\frac{1}{2}{\left(\frac{x-m}{\tilde{\sigma }}\right)}^2⌉,\tilde{\sigma }\in \left[{\sigma }_1,{\sigma }_2\right]$$

(11)

$${\overline{\mu }}_{\tilde{F}}\left(x\right)=exp⌈-\frac{1}{2}{\left(\frac{x-m}{{\sigma }_2}\right)}^2⌉$$

(12)

$${\underset{¯}{\mu }}_{\tilde{F}}\left(x\right)=exp⌈-\frac{1}{2}{\left(\frac{x-m}{{\sigma }_1}\right)}^2⌉$$

(13)

Table 4. Fuzzy systems configuration T1FLS and IT2FLS.

T1FLS = “fisGau318”	[System]
	Name = “fisGau318”
	Type = “mamdani”
	Version = 2.0
	NumInputs = 1
	NumOutputs = 1
	NumRules = 3
	AndMethod = “min”
	OrMethod = “max”
	ImpMethod = “min”
	AggMethod = “max”
	DefuzzMethod = “centroid”
IT2FLS = “it2_3gausS6523”	[System]
	Name = “it2_3gausS6523”
	Type = “mamdani”
	Version = 2.0
	NumInputs = 1
	NumOutputs = 1
	NumRules = 3
	AndMethod = “min”
	OrMethod = “max”
	ImpMethod = “min”
	AggMethod = “max”
	DefuzzMethod = “centroid”

shows the configuration of the two type-1 and type-2 fuzzy systems that are compared in this investigation.

6. Results

Table 5. Mean and standard deviation for T1FLS and for 30, 50, and 100 dimensions.

N	T1FLS-DMOAx30		T1FLS-DMOAx50		T1FLS-DMOAx100
	Mean	SD	Mean	SD	Mean	SD
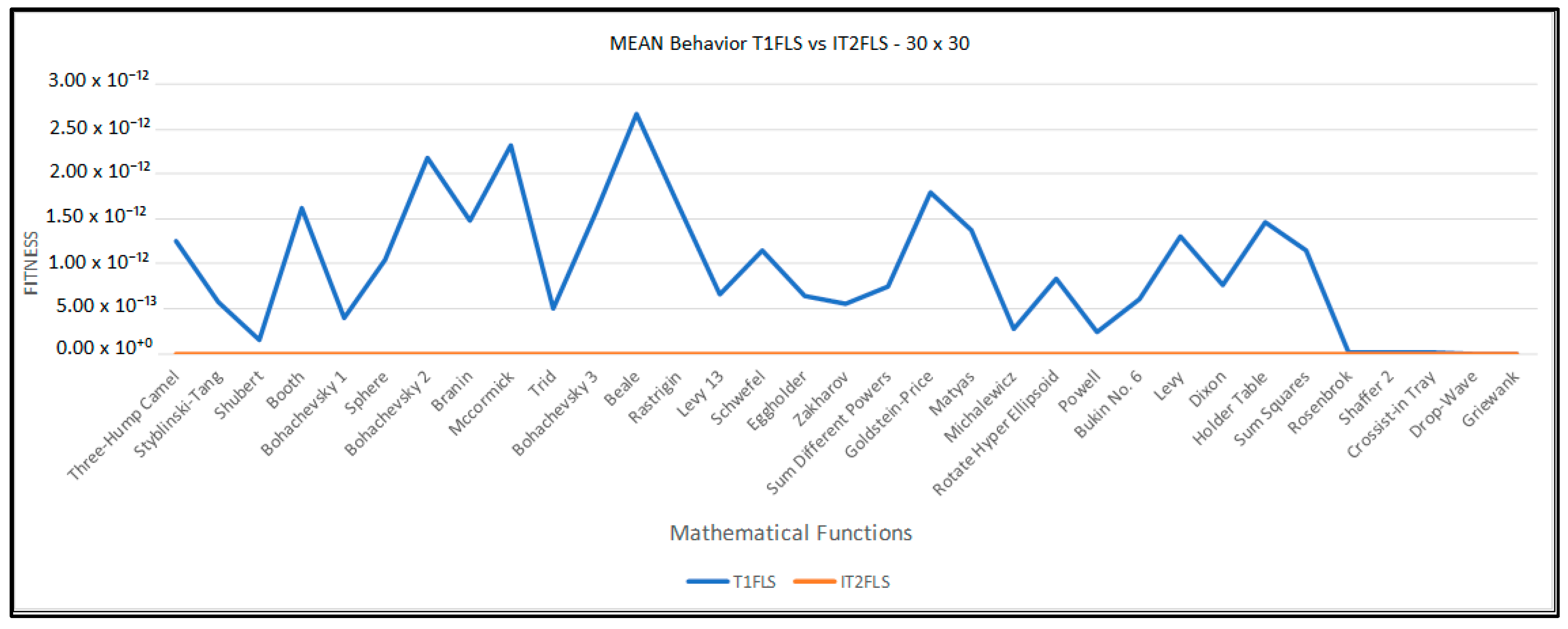
1	1.04 × 10−12	2.82 × 10−12	1.30 × 10−12	3.49 × 10−12	3.86 × 10−12	1.66 × 10−11
2	2.91 × 10−15	6.07 × 10−15	7.96 × 10−16	2.01 × 10−15	7.39 × 10−15	2.63 × 10−14
3	5.62 × 10−17	2.12 × 10−16	1.90 × 10−16	5.43 × 10−16	3.01 × 10−14	8.31 × 10−14
4	1.64 × 10−12	4.37 × 10−12	8.02 × 10−13	1.60 × 10−12	8.71 × 10−13	3.38 × 10−12
5	2.14 × 10−9	1.79 × 10−9	2.48 × 10−9	1.35 × 10−8	1.93 × 10−8	1.30 × 10−8
6	7.54 × 10−13	1.88 × 10−12	1.47 × 10−12	3.39 × 10−12	7.90 × 10−13	2.03 × 10−12
7	2.63 × 10−13	4.95 × 10−13	1.46 × 10−12	4.47 × 10−12	2.13 × 10−12	6.74 × 10−12
8	2.39 × 10−13	6.15 × 10−13	1.45 × 10−12	4.24 × 10−12	8.91 × 10−13	2.71 × 10−12
9	8.35 × 10−13	2.23 × 10−12	1.01 × 10−12	2.80 × 10−12	5.46 × 10−13	1.17 × 10−12
10	1.14 × 10−12	3.03 × 10−12	9.81 × 10−13	2.42 × 10−12	9.03 × 10−13	1.97 × 10−12
11	5.77 × 10−13	1.16 × 10−12	4.46 × 10−13	7.81 × 10−13	1.22 × 10−12	3.91 × 10−12
12	7.45 × 10−13	1.58 × 10−12	6.76 × 10−15	1.34 × 10−14	2.71 × 10−20	7.10 × 10−20
13	1.15 × 10−12	3.55 × 10−12	1.48 × 10−12	3.89 × 10−12	2.11 × 10−12	5.48 × 10−12
14	4.96 × 10−13	1.20 × 10−12	1.99 × 10−12	7.02 × 10−12	4.24 × 10−13	8.07 × 10−13
15	5.46 × 10−13	1.12 × 10−12	4.11 × 10−13	9.33 × 10−13	1.28 × 10−13	2.52 × 10−13
16	6.03 × 10−13	1.28 × 10−12	5.79 × 10−13	1.11 × 10−12	5.58 × 10−13	1.19 × 10−12
17	1.62 × 10−15	3.07 × 10−15	5.12 × 10−16	8.36 × 10−16	4.69 × 10−16	1.66 × 10−15
18	4.31 × 10−17	9.02 × 10−17	1.46 × 10−16	3.83 × 10−16	8.38 × 10−17	2.94 × 10−16
19	6.38 × 10−13	1.80 × 10−12	4.32 × 10−12	1.65 × 10−11	9.12 × 10−13	1.68 × 10−12
20	2.66 × 10−12	6.49 × 10−12	7.51 × 10−13	1.86 × 10−12	7.58 × 10−13	1.62 × 10−12
21	1.46 × 10−12	7.82 × 10−12	4.73 × 10−13	2.32 × 10−12	2.98 × 10−14	6.60 × 10−14
22	1.47 × 10−12	2.63 × 10−12	8.50 × 10−13	3.52 × 10−12	1.09 × 10−12	3.49 × 10−12
23	1.30 × 10−12	3.46 × 10−12	5.72 × 10−13	1.03 × 10−12	3.76 × 10−13	8.72 × 10−13
24	6.63 × 10−13	1.39 × 10−12	3.60 × 10−12	1.83 × 10−11	2.26 × 10−12	7.21 × 10−12
25	1.65 × 10−15	5.19 × 10−15	1.43 × 10−15	4.36 × 10−15	6.01 × 10−16	1.50 × 10−15
26	2.40 × 10−8	1.36 × 10−8	1.79 × 10−8	1.05 × 10−8	1.87 × 10−8	9.88 × 10−9
27	1.57 × 10−13	2.55 × 10−13	3.87 × 10−13	8.95 × 10−13	2.11 × 10−12	7.50 × 10−12
28	3.95 × 10−13	9.97 × 10−13	4.16 × 10−13	8.78 × 10−13	4.11 × 10−12	9.48 × 10−12
29	2.18 × 10−12	6.80 × 10−12	2.97 × 10−13	6.44 × 10−13	6.45 × 10−13	1.02 × 10−12
30	1.56 × 10−12	3.32 × 10−12	4.08 × 10−13	7.22 × 10−13	2.99 × 10−13	5.03 × 10−13
31	1.61 × 10−12	3.89 × 10−12	2.99 × 10−12	1.13 × 10−11	9.34 × 10−13	2.65 × 10−12
32	1.37 × 10−12	3.30 × 10−12	1.67 × 10−13	4.69 × 10−13	1.71 × 10−13	5.44 × 10−13
33	2.32 × 10−12	6.87 × 10−12	1.76 × 10−12	4.06 × 10−12	1.33 × 10−12	3.02 × 10−12
34	1.09 × 10−20	3.96 × 10−20	3.74 × 10−20	1.16 × 10−19	5.56 × 10−20	2.29 × 10−19
35	1.79 × 10−12	5.13 × 10−12	3.83 × 10−13	7.54 × 10−13	4.14 × 10−13	8.86 × 10−13
36	1.25 × 10−12	3.25 × 10−12	6.11 × 10−13	1.02 × 10−12	1.55 × 10−12	4.83 × 10−12

shows the mean and standard deviation of T1FLS-fisGau318 for 30, 50, and 100 dimensions, for the 36 mathematical functions in Table 3.

Table 6. Mean and standard deviation for IT2FLS and for 30, 50, and 100 dimensions.

N	IT2FLS-DMOAx30		IT2FLS-DMOAx50		IT2FLS-DMOAx100
	Mean	SD	Mean	SD	Mean	SD
1	5.39 × 10−20	1.18 × 10−19	3.76 × 10−20	9.84 × 10−20	3.97 × 10−20	6.97 × 10−20
2	9.69 × 10−22	2.04 × 10−21	7.56 × 10−22	9.99 × 10−22	7.99 × 10−22	1.81 × 10−21
3	1.02 × 10−22	2.36 × 10−22	1.81 × 10−22	4.36 × 10−22	6.00 × 10−21	1.10 × 10−20
4	3.27 × 10−20	6.48 × 10−20	4.19 × 10−20	8.97 × 10−20	6.70 × 10−20	1.42 × 10−19
5	1.79 × 10−18	1.30 × 10−18	2.80 × 10−18	5.28 × 10−18	6.42 × 10−18	4.23 × 10−18
6	1.75 × 10−20	4.76 × 10−20	2.80 × 10−20	3.96 × 10−20	5.60 × 10−20	7.87 × 10−20
7	2.57 × 10−20	3.54 × 10−20	5.97 × 10−20	1.20 × 10−19	6.67 × 10−20	2.76 × 10−19
8	2.08 × 10−20	4.94 × 10−20	7.59 × 10−20	2.55 × 10−19	5.84 × 10−20	1.36 × 10−19
9	2.51 × 10−20	6.85 × 10−20	4.39 × 10−20	7.03 × 10−20	3.56 × 10−20	6.70 × 10−20
10	3.24 × 10−20	6.93 × 10−20	4.86 × 10−20	8.13 × 10−20	3.56 × 10−20	6.07 × 10−20
11	8.33 × 10−20	1.64 × 10−19	4.14 × 10−20	6.42 × 10−20	6.20 × 10−20	8.90 × 10−20
12	2.89 × 10−20	4.59 × 10−20	1.64 × 10−20	5.89 × 10−20	6.23 × 10−24	4.84 × 10−24
13	1.25 × 10−20	1.78 × 10−20	5.64 × 10−20	9.65 × 10−20	1.70 × 10−20	2.93 × 10−20
14	4.10 × 10−20	7.01 × 10−20	2.63 × 10−20	4.20 × 10−20	3.15 × 10−20	6.48 × 10−20
15	3.07 × 10−20	4.41 × 10−20	2.63 × 10−20	4.71 × 10−20	4.77 × 10−20	8.87 × 10−20
16	2.01 × 10−20	5.14 × 10−20	2.11 × 10−20	2.65 × 10−20	2.86 × 10−20	3.96 × 10−20
17	7.19 × 10−22	1.03 × 10−21	1.06 × 10−21	1.78 × 10−21	8.02 × 10−22	1.53 × 10−21
18	2.19 × 10−22	5.72 × 10−22	1.78 × 10−22	7.21 × 10−22	5.96 × 10−23	1.08 × 10−22
19	3.19 × 10−20	6.17 × 10−20	2.90 × 10−20	5.45 × 10−20	3.73 × 10−20	4.39 × 10−20
20	3.29 × 10−20	5.28 × 10−20	3.47 × 10−20	5.03 × 10−20	2.33 × 10−20	3.70 × 10−20
21	1.37 × 10−20	4.70 × 10−20	6.02 × 10−21	1.12 × 10−20	1.78 × 10−20	4.97 × 10−20
22	4.76 × 10−20	1.54 × 10−19	6.65 × 10−20	1.92 × 10−19	1.49 × 10−20	2.85 × 10−20
23	1.82 × 10−20	3.14 × 10−20	1.05 × 10−19	1.74 × 10−19	1.84 × 10−20	3.05 × 10−20
24	3.25 × 10−20	6.89 × 10−20	3.34 × 10−20	6.81 × 10−20	2.24 × 10−20	4.26 × 10−20
25	9.69 × 10−22	2.29 × 10−21	9.72 × 10−22	2.36 × 10−21	3.30 × 10−22	6.23 × 10−22
26	6.05 × 10−18	4.05 × 10−18	7.26 × 10−18	5.36 × 10−18	7.70 × 10−18	5.55 × 10−18
27	7.03 × 10−20	1.14 × 10−19	4.36 × 10−20	8.94 × 10−20	1.53 × 10−20	2.38 × 10−20
28	5.67 × 10−20	1.09 × 10−19	4.68 × 10−20	1.01 × 10−19	4.93 × 10−20	8.81 × 10−20
29	4.76 × 10−20	9.85 × 10−20	3.95 × 10−20	6.92 × 10−20	3.25 × 10−20	5.28 × 10−20
30	3.38 × 10−20	6.08 × 10−20	3.06 × 10−20	6.69 × 10−20	2.19 × 10−20	4.23 × 10−20
31	6.30 × 10−20	7.13 × 10−20	5.60 × 10−20	1.23 × 10−19	2.12 × 10−20	3.97 × 10−20
32	2.71 × 10−20	6.28 × 10−20	4.81 × 10−20	9.99 × 10−20	2.56 × 10−20	4.14 × 10−20
33	4.24 × 10−20	8.03 × 10−20	2.74 × 10−20	4.33 × 10−20	2.55 × 10−20	3.25 × 10−20
34	4.68 × 10−24	2.31 × 10−24	6.08 × 10−24	3.46 × 10−24	4.96 × 10−24	2.05 × 10−24
35	2.81 × 10−20	4.92 × 10−20	2.64 × 10−20	3.01 × 10−20	1.23 × 10−19	3.19 × 10−19
36	9.93 × 10−20	2.71 × 10−19	6.27 × 10−20	1.32 × 10−19	2.53 × 10−20	4.93 × 10−20

shows the mean and SD for IT2FLS-it2_3gausS6523 optimized with the DMOA algorithm for 30, 50, and 100 dimensions.

Comparison

Table 7. Hypothesis Test T1FLS vs. IT2FLS—30 dimensions.

	T1FLS		IT2FLS		Hypothesis Test
No	fisGau318 30		it2_3gausS01 30
	Mean	SD	Mean	SD	Z	E
1	1.04 × 10−12	2.82 × 10−12	1.44 × 10−12	4.82 × 10−12	−0.94	N
2	2.91 × 10−15	6.07 × 10−15	2.93 × 10−15	7.79 × 10−15	−2.08	Y
3	5.62 × 10−17	2.12 × 10−16	5.54 × 10−16	2.08 × 10−15	1.96	N
4	1.64 × 10−12	4.37 × 10−12	2.83 × 10−12	1.09 × 10−11	−0.99	N
5	2.14 × 10−9	1.79 × 10−9	1.14 × 10−9	1.08 × 10−9	−2.8	Y
6	7.54 × 10−13	1.88 × 10−12	2.47 × 10−13	5.68 × 10−13	−0.04	N
7	2.63 × 10−13	4.95 × 10−13	1.46 × 10−12	5.09 × 10−12	1.62	N
8	2.39 × 10−13	6.15 × 10−13	5.53 × 10−13	2.02 × 10−12	0.77	N
9	8.35 × 10−13	2.23 × 10−12	4.85 × 10−13	1.16 × 10−12	−0.35	N
10	1.14 × 10−12	3.03 × 10−12	3.49 × 10−13	6.59 × 10−13	0.09	N
11	5.77 × 10−13	1.16 × 10−12	1.20 × 10−12	3.45 × 10−12	0.29	N
12	7.45 × 10−13	1.58 × 10−12	9.57 × 10−13	3.18 × 10−12	−0.31	N
13	1.15 × 10−12	3.55 × 10−12	6.23 × 10−13	2.15 × 10−12	−0.84	N
14	4.96 × 10−13	1.20 × 10−12	2.39 × 10−13	4.22 × 10−13	1.54	N
15	5.46 × 10−13	1.12 × 10−12	2.30 × 10−13	3.98 × 10−13	1.15	N
16	6.03 × 10−13	1.28 × 10−12	8.31 × 10−13	2.34 × 10−12	0.92	N
17	1.62 × 10−15	3.07 × 10−15	3.09 × 10−15	1.38 × 10−14	0.63	N
18	4.31 × 10−17	9.02 × 10−17	9.31 × 10−16	3.65 × 10−15	1.47	N
19	6.38 × 10−13	1.80 × 10−12	3.87 × 10−13	7.05 × 10−13	−1.15	N
20	2.66 × 10−12	6.49 × 10−12	3.41 × 10−13	6.03 × 10−13	−1.1	N
21	1.46 × 10−12	7.82 × 10−12	1.97 × 10−14	3.75 × 10−14	−0.96	N
22	1.47 × 10−12	2.63 × 10−12	2.22 × 10−12	9.69 × 10−12	−2.15	Y
23	1.30 × 10−12	3.46 × 10−12	8.46 × 10−13	2.37 × 10−12	0.78	N
24	6.63 × 10−13	1.39 × 10−12	9.68 × 10−13	3.02 × 10−12	0.69	N
25	1.65 × 10−15	5.19 × 10−15	1.79 × 10−15	7.18 × 10−15	−0.68	N
26	2.40 × 10−8	1.36 × 10−8	1.44 × 10−8	7.47 × 10−9	−3.81	Y
27	1.57 × 10−13	2.55 × 10−13	3.18 × 10−13	7.86 × 10−13	−0.24	N
28	3.95 × 10−13	9.97 × 10−13	1.13 × 10−13	1.47 × 10−13	−0.66	N
29	2.18 × 10−12	6.80 × 10−12	2.05 × 10−12	5.11 × 10−12	−1.61	N
30	1.56 × 10−12	3.32 × 10−12	1.37 × 10−12	3.86 × 10−12	−1.97	Y
31	1.61 × 10−12	3.89 × 10−12	2.26 × 10−13	4.34 × 10−13	−0.07	N
32	1.37 × 10−12	3.30 × 10−12	4.40 × 10−13	1.22 × 10−12	−1.25	N
33	2.32 × 10−12	6.87 × 10−12	1.45 × 10−12	6.94 × 10−12	−0.97	N
34	1.09 × 10−2⁰	3.96 × 10−2⁰	2.25 × 10−2⁰	6.20 × 10−2⁰	0.98	N
35	1.79 × 10−12	5.13 × 10−12	3.85 × 10−13	5.53 × 10−13	−1.1	N
36	1.25 × 10−12	3.25 × 10−12	4.75 × 10−13	1.30 × 10−12	−1.31	N

shows the hypothesis test between T1FLS and IT2FLS fuzzy systems with parameter adaptation and 30 dimensions where the IT2FLS (Not optimized) was better in 5 of 36 mathematical functions.

Figure 15 and Figure 16 show the behaviors of the mean and standard deviation of the two types of fuzzy systems T1FLS vs. IT2FLS for 30 dimensions.

Table 8. Convergence of T1FDMOA (T1FLS).

T1DMOA
N	Rosenbrock	Griewank	Rastrigin	Ackley	Dixon
1	2.36 × 10−14	1.16 × 10−15	2.02 × 10−11	6.60 × 10−9	8.45 × 10−12
2	1.70 × 10−14	1.84 × 10−16	1.30 × 10−11	6.38 × 10−9	6.47 × 10−12
3	1.43 × 10−14	1.32 × 10−16	6.56 × 10−12	5.63 × 10−9	1.57 × 10−12
4	1.39 × 10−14	7.92 × 10−17	2.57 × 10−12	5.20 × 10−9	8.69 × 10−13
5	7.44 × 10−15	6.08 × 10−17	1.40 × 10−12	4.58 × 10−9	7.23 × 10−13
6	3.49 × 10−15	1.79 × 10−17	1.11 × 10−12	3.00 × 10−9	6.88 × 10−13
7	2.25 × 10−15	1.35 × 10−17	8.16 × 10−13	2.82 × 10−9	6.56 × 10−13
8	2.07 × 10−15	1.13 × 10−17	7.81 × 10−13	2.52 × 10−9	5.66 × 10−13
9	1.23 × 10−15	8.50 × 10−18	6.32 × 10−13	2.50 × 10−9	5.20 × 10−13
10	4.85 × 10−16	6.81 × 10−18	6.01 × 10−13	2.05 × 10−9	5.07 × 10−13
11	3.92 × 10−16	4.42 × 10−18	3.02 × 10−13	1.99 × 10−9	3.95 × 10−13
12	3.77 × 10−16	3.11 × 10−18	2.84 × 10−13	1.96 × 10−9	3.30 × 10−13
13	2.16 × 10−16	1.56 × 10−18	2.63 × 10−13	1.94 × 10−9	1.80 × 10−13
14	1.38 × 10−16	1.19 × 10−18	2.48 × 10−13	1.78 × 10−9	1.63 × 10−13
15	1.07 × 10−16	8.77 × 10−19	9.11 × 10−14	1.70 × 10−9	9.61 × 10−14
16	8.13 × 10−17	7.96 × 10−19	7.89 × 10−14	1.52 × 10−9	9.49 × 10−14
17	8.07 × 10−17	5.67 × 10−19	6.61 × 10−14	1.41 × 10−9	9.39 × 10−14
18	7.83 × 10−17	3.79 × 10−19	4.30 × 10−14	1.32 × 10−9	8.95 × 10−14
19	6.97 × 10−17	3.46 × 10−19	2.72 × 10−14	1.21 × 10−9	5.51 × 10−14
20	6.69 × 10−17	2.09 × 10−19	2.01 × 10−14	1.14 × 10−9	5.21 × 10−14
21	3.75 × 10−17	1.90 × 10−19	2.01 × 10−14	1.10 × 10−9	1.50 × 10−14
22	1.67 × 10−17	1.63 × 10−19	8.26 × 10−15	1.01 × 10−9	1.12 × 10−14
23	1.63 × 10−17	1.62 × 10−19	3.35 × 10−15	9.97 × 10−10	9.05 × 10−15
24	5.22 × 10−18	1.09 × 10−19	2.88 × 10−15	9.87 × 10−10	8.08 × 10−15
25	1.13 × 10−19	5.59 × 10−20	2.81 × 10−15	9.40 × 10−10	7.59 × 10−15
26	9.94 × 10−20	4.94 × 10−20	7.21 × 10−16	6.83 × 10−10	1.19 × 10−16
27	4.94 × 10−20	1.37 × 10−20	5.87 × 10−16	5.36 × 10−10	8.47 × 10−17
28	2.38 × 10−20	5.92 × 10−21	3.10 × 10−16	5.13 × 10−10	3.28 × 10−17
29	5.52 × 10−22	2.01 × 10−21	6.27 × 10−18	2.08 × 10−10	2.82 × 10−18
30	2.18 × 10−22	1.90 × 10−21	9.69 × 10−21	2.35 × 10−16	5.76 × 10−20

shows the convergence of the T1FDMOA method for 30 dimensions of the mathematical Rosenbrock, Griewank, Rastrigin, Ackley, and Dixon functions.

Table 9. Convergence of IT2FDMOA (IT2FLS).

	IT2DMOA
N	Rosenbrock	Griewank	Rastrigin	Ackley	Dixon
1	1.10 × 10−20	1.15 × 10−21	3.30 × 10−19	7.33 × 10−18	2.56 × 10−19
2	2.53 × 10−21	6.51 × 10−22	1.50 × 10−19	3.44 × 10−18	7.39 × 10−20
3	2.14 × 10−21	2.49 × 10−22	8.57 × 10−20	3.18 × 10−18	3.87 × 10−20
4	1.89 × 10−21	1.92 × 10−22	7.09 × 10−20	2.91 × 10−18	3.20 × 10−20
5	1.73 × 10−21	1.79 × 10−22	5.33 × 10−20	2.70 × 10−18	2.72 × 10−20
6	1.60 × 10−21	1.40 × 10−22	4.24 × 10−20	2.56 × 10−18	1.75 × 10−20
7	1.57 × 10−21	7.15 × 10−23	4.15 × 10−20	2.41 × 10−18	1.53 × 10−20
8	1.33 × 10−21	5.31 × 10−23	3.40 × 10−20	2.07 × 10−18	1.00 × 10−20
9	1.29 × 10−21	4.75 × 10−23	2.41 × 10−20	2.03 × 10−18	8.16 × 10−21
10	9.88 × 10−22	3.73 × 10−23	2.26 × 10−20	1.86 × 10−18	7.74 × 10−21
11	7.09 × 10−22	3.61 × 10−23	2.03 × 10−20	1.81 × 10−18	6.86 × 10−21
12	6.90 × 10−22	3.13 × 10−23	1.34 × 10−20	1.62 × 10−18	5.37 × 10−21
13	4.46 × 10−22	2.70 × 10−23	1.16 × 10−20	1.55 × 10−18	4.83 × 10−21
14	2.83 × 10−22	2.62 × 10−23	1.08 × 10−20	1.48 × 10−18	4.62 × 10−21
15	2.25 × 10−22	2.54 × 10−23	1.04 × 10−20	1.45 × 10−18	4.03 × 10−21
16	1.82 × 10−22	2.31 × 10−23	9.73 × 10−21	1.43 × 10−18	3.72 × 10−21
17	1.47 × 10−22	2.04 × 10−23	8.79 × 10−21	1.41 × 10−18	2.84 × 10−21
18	9.52 × 10−23	1.97 × 10−23	6.98 × 10−21	1.35 × 10−18	2.63 × 10−21
19	8.76 × 10−23	1.95 × 10−23	6.55 × 10−21	1.33 × 10−18	1.62 × 10−21
20	5.84 × 10−23	1.23 × 10−23	5.24 × 10−21	1.26 × 10−18	1.16 × 10−21
21	3.47 × 10−23	7.12 × 10−24	4.86 × 10−21	1.26 × 10−18	1.14 × 10−21
22	3.12 × 10−23	5.57 × 10−24	4.16 × 10−21	1.13 × 10−18	5.58 × 10−22
23	3.05 × 10−23	5.30 × 10−24	3.13 × 10−21	1.05 × 10−18	2.14 × 10−22
24	9.22 × 10−24	4.56 × 10−24	3.07 × 10−21	1.03 × 10−18	1.80 × 10−22
25	5.51 × 10−24	3.73 × 10−24	2.86 × 10−21	9.60 × 10−19	8.63 × 10−23
26	4.24 × 10−24	3.27 × 10−24	2.07 × 10−21	8.09 × 10−19	7.28 × 10−23
27	2.44 × 10−24	2.50 × 10−24	1.64 × 10−21	7.61 × 10−19	3.99 × 10−23
28	3.98 × 10−25	2.49 × 10−24	5.63 × 10−22	7.07 × 10−19	2.67 × 10−23
29	1.39 × 10−25	1.04 × 10−24	2.11 × 10−22	6.77 × 10−19	1.28 × 10−23
30	4.22 × 10−26	1.17 × 10−25	1.96 × 10−22	1.88 × 10−19	6.05 × 10−24

shows the convergence of the IT2FDMOA method for 30 dimensions of the mathematical Rosenbrock, Griewank, Rastrigin, Ackley, and Dixon function.

In Figure 17, we can see how the two methods T1FDMOA and IT2FDMOA converge for the Rosenbrock mathematical function, in Figure 18 and Figure 19 we can see separately the two methods so that we can clearly observe the convergence and the exploration and exploitation phases of each of them, both methods tend to 0 but never reach the value of the same mathematical function.

Figure 20 illustrates the convergence of the T1FDMOA and IT2FDMOA methods for the Dixon–Price mathematical function. Figure 21 and Figure 22 present a separate visualization of each method, enabling a clear observation of their convergence as well as the exploration and exploitation phases. Although both methods approach but do not reach a value of 0, this behavior is consistent with the characteristics of the Dixon–Price function.

Figure 23 showcases the convergence of the T1FDMOA and IT2FDMOA methods for the Ackley mathematical function. Figure 24 and Figure 25 provide individual depictions of each method, facilitating a distinct analysis of their convergence and the exploration and exploitation phases. As with the previous case, both methods approach but do not reach a value of 0, which aligns with the nature of the Ackley function.

6.1. Hypothesis Test

Equation (14) represents the hypothesis test for two independent samples of 30 experiments, the Null Hypothesis Equation (15) and the Alternate Hypothesis Equation (16), with which comparisons were performed between DMOA-T1FLS and DMOA-IT2FLS, where our claim is that the DMOA-IT2FLS method is better than the DMOA-T1FLS method, Figure 26 shows the left-tailed hypothesis test plot.

$$z=\frac{({\overline{x}}_1-{\overline{x}}_2)}{\sqrt{\frac{{\sigma }_1^2}{n_1}+\frac{{\sigma }_2^2}{n_2}}}$$

(14)

$$H_0:{\mu }_1\ge {\mu }_2$$

(15)

$$H_a:{\mu }_1<{\mu }_2\hspace{1em}claim$$

(16)

Where ${\overline{x}}_1$ is the mean of sample 1, ${\overline{x}}_2$ mean of sample 2, ${\sigma }_1$ standard deviation of sample 1, ${\sigma }_2$ standard deviation of sample 2, $n_1$ number of sample data 1, $n_2$ number of sample data 2.

Significance level α = 0.05, confidence level = 95%, confidence level = 1 − α; 1 − 0.05 = 0.95 or 95%, since the p-value is less than 0.05, the null hypothesis is rejected.

Comparison

Table 10. Hypothesis test T1FLS vs. IT2FLS—30 dimensions.

No	T1FLS		IT2FLS		Hypothesis Test
	fisGau318 30		it2_3gausS6523 30
	Mean	SD	Mean	SD	Z	E
1	1.04 × 10−12	2.82 × 10−12	5.39 × 10−20	1.18 × 10−19	−2.12	Y
2	2.91 × 10−15	6.07 × 10−15	9.69 × 10−22	2.04 × 10−21	−2.76	Y
3	5.62 × 10−17	2.12 × 10−16	1.02 × 10−22	2.36 × 10−22	−1.52	N
4	1.64 × 10−12	4.37 × 10−12	3.27 × 10−20	6.48 × 10−20	−2.16	Y
5	2.14 × 10−9	1.79 × 10−9	1.79 × 10−18	1.30 × 10−18	−6.88	Y
6	7.54 × 10−13	1.88 × 10−12	1.75 × 10−20	4.76 × 10−20	−2.31	Y
7	2.63 × 10−13	4.95 × 10−13	2.57 × 10−20	3.54 × 10−20	−3.06	Y
8	2.39 × 10−13	6.15 × 10−13	2.08 × 10−20	4.94 × 10−20	−2.24	Y
9	8.35 × 10−13	2.23 × 10−12	2.51 × 10−20	6.85 × 10−20	−2.16	Y
10	1.14 × 10−12	3.03 × 10−12	3.24 × 10−20	6.93 × 10−20	−2.16	Y
11	5.77 × 10−13	1.16 × 10−12	8.33 × 10−20	1.64 × 10−19	−2.86	Y
12	7.45 × 10−13	1.58 × 10−12	2.89 × 10−20	4.59 × 10−20	−2.72	Y
13	1.15 × 10−12	3.55 × 10−12	1.25 × 10−20	1.78 × 10−20	−1.86	Y
14	4.96 × 10−13	1.20 × 10−12	4.10 × 10−20	7.01 × 10−20	−2.37	Y
15	5.46 × 10−13	1.12 × 10−12	3.07 × 10−20	4.41 × 10−20	−2.8	Y
16	6.03 × 10−13	1.28 × 10−12	2.01 × 10−20	5.14 × 10−20	−2.71	Y
17	1.62 × 10−15	3.07 × 10−15	7.19 × 10−22	1.03 × 10−21	−3.03	Y
18	4.31 × 10−17	9.02 × 10−17	2.19 × 10−22	5.72 × 10−22	−2.75	Y
19	6.38 × 10−13	1.80 × 10−12	3.19 × 10−20	6.17 × 10−20	−2.03	Y
20	2.66 × 10−12	6.49 × 10−12	3.29 × 10−20	5.28 × 10−20	−2.36	Y
21	1.46 × 10−12	7.82 × 10−12	1.37 × 10−20	4.70 × 10−20	−1.07	N
22	1.47 × 10−12	2.63 × 10−12	4.76 × 10−20	1.54 × 10−19	−3.22	Y
23	1.30 × 10−12	3.46 × 10−12	1.82 × 10−20	3.14 × 10−20	−2.15	Y
24	6.63 × 10−13	1.39 × 10−12	3.25 × 10−20	6.89 × 10−20	−2.74	Y
25	1.65 × 10−15	5.19 × 10−15	9.69 × 10−22	2.29 × 10−21	−1.82	Y
26	2.40 × 10−8	1.36 × 10−8	6.05 × 10−18	4.05 × 10−18	−10.17	Y
27	1.57 × 10−13	2.55 × 10−13	7.03 × 10−20	1.14 × 10−19	−3.54	Y
28	3.95 × 10−13	9.97 × 10−13	5.67 × 10−20	1.09 × 10−19	−2.28	Y
29	2.18 × 10−12	6.80 × 10−12	4.76 × 10−20	9.85 × 10−20	−1.84	Y
30	1.56 × 10−12	3.32 × 10−12	3.38 × 10−20	6.08 × 10−20	−2.7	Y
31	1.61 × 10−12	3.89 × 10−12	6.30 × 10−20	7.13 × 10−20	−2.38	Y
32	1.37 × 10−12	3.30 × 10−12	2.71 × 10−20	6.28 × 10−20	−2.39	Y
33	2.32 × 10−12	6.87 × 10−12	4.24 × 10−20	8.03 × 10−20	−1.94	Y
34	1.09 × 10−20	3.96 × 10−20	4.68 × 10−24	2.31 × 10−24	−1.58	N
35	1.79 × 10−12	5.13 × 10−12	2.81 × 10−20	4.92 × 10−20	−2.01	Y
36	1.25 × 10−12	3.25 × 10−12	9.93 × 10−20	2.71 × 10−19	−2.22	Y
						33

shows the hypothesis test for 30 dimensions of the fuzzy systems T1FLS with parameter adaptation and optimized IT2FLS was better in 33 out of 36 mathematical functions. In the hypothesis tests in Table 10,

Table 11. Hypothesis test T1FLS vs. IT2FLS—50 dimensions.

	T1FLS		IT2FLS		Hypothesis Test
No	fisGau318 50		it2_3gausS6523 50
	Mean	SD	Mean	SD	Z	E
1	1.30 × 10−12	3.49 × 10−12	3.76 × 10−20	9.84 × 10−20	−2.04	Y
2	7.96 × 10−16	2.01 × 10−15	7.56 × 10−22	9.99 × 10−22	−2.17	Y
3	1.90 × 10−16	5.43 × 10−16	1.81 × 10−22	4.36 × 10−22	−1.92	Y
4	8.02 × 10−13	1.60 × 10−12	4.19 × 10−20	8.97 × 10−20	−2.74	Y
5	2.48 × 10−9	1.35 × 10−8	2.80 × 10−18	5.28 × 10−18	−1	N
6	1.47 × 10−12	3.39 × 10−12	2.80 × 10−20	3.96 × 10−20	−2.38	Y
7	1.46 × 10−12	4.47 × 10−12	5.97 × 10−20	1.20 × 10−19	−1.78	Y
8	1.45 × 10−12	4.24 × 10−12	7.59 × 10−20	2.55 × 10−19	−1.88	Y
9	1.01 × 10−12	2.80 × 10−12	4.39 × 10−20	7.03 × 10−20	−1.97	Y
10	9.81 × 10−13	2.42 × 10−12	4.86 × 10−20	8.13 × 10−20	−2.22	Y
11	4.46 × 10−13	7.81 × 10−13	4.14 × 10−20	6.42 × 10−20	−3.13	Y
12	6.76 × 10−15	1.34 × 10−14	1.64 × 10−20	5.89 × 10−20	−2.76	Y
13	1.48 × 10−12	3.89 × 10−12	5.64 × 10−20	9.65 × 10−20	−2.09	Y
14	1.99 × 10−12	7.02 × 10−12	2.63 × 10−20	4.20 × 10−20	−1.55	N
15	4.11 × 10−13	9.33 × 10−13	2.63 × 10−20	4.71 × 10−20	−2.41	Y
16	5.79 × 10−13	1.11 × 10−12	2.11 × 10−20	2.65 × 10−20	−2.87	Y
17	5.12 × 10−16	8.36 × 10−16	1.06 × 10−21	1.78 × 10−21	−3.36	Y
18	1.46 × 10−16	3.83 × 10−16	1.78 × 10−22	7.21 × 10−22	−2.09	Y
19	4.32 × 10−12	1.65 × 10−11	2.90 × 10−20	5.45 × 10−20	−1.44	N
20	7.51 × 10−13	1.86 × 10−12	3.47 × 10−20	5.03 × 10−20	−2.21	Y
21	4.73 × 10−13	2.32 × 10−12	6.02 × 10−21	1.12 × 10−20	−1.12	N
22	8.50 × 10−13	3.52 × 10−12	6.65 × 10−20	1.92 × 10−19	−1.32	N
23	5.72 × 10−13	1.03 × 10−12	1.05 × 10−19	1.74 × 10−19	−3.06	Y
24	3.60 × 10−12	1.83 × 10−11	3.34 × 10−20	6.81 × 10−20	−1.08	N
25	1.43 × 10−15	4.36 × 10−15	9.72 × 10−22	2.36 × 10−21	−1.8	Y
26	1.79 × 10−8	1.05 × 10−8	7.26 × 10−18	5.36 × 10−18	−9.35	Y
27	3.87 × 10−13	8.95 × 10−13	4.36 × 10−20	8.94 × 10−20	−2.37	Y
28	4.16 × 10−13	8.78 × 10−13	4.68 × 10−20	1.01 × 10−19	−2.6	Y
29	2.97 × 10−13	6.44 × 10−13	3.95 × 10−20	6.92 × 10−20	−2.53	Y
30	4.08 × 10−13	7.22 × 10−13	3.06 × 10−20	6.69 × 10−20	−3.09	Y
31	2.99 × 10−12	1.13 × 10−11	5.60 × 10−20	1.23 × 10−19	−1.46	N
32	1.67 × 10−13	4.69 × 10−13	4.81 × 10−20	9.99 × 10−20	−1.95	Y
33	1.76 × 10−12	4.06 × 10−12	2.74 × 10−20	4.33 × 10−20	−2.37	Y
34	3.74 × 10−20	1.16 × 10−19	6.08 × 10−24	3.46 × 10−24	−1.76	Y
35	3.83 × 10−13	7.54 × 10−13	2.64 × 10−20	3.01 × 10−20	−2.78	Y
36	6.11 × 10−13	1.02 × 10−12	6.27 × 10−20	1.32 × 10−19	−3.27	Y
						29

and

Table 12. Hypothesis test T1FLS vs. IT2FLS—100 dimensions.

	T1FLS		IT2FLS		Hypothesis Test
No	fisGau318 100		it2_3gausS6523 100
	Mean	SD	Mean	SD	Z	E
1	3.86 × 10−12	1.66 × 10−11	3.97 × 10−20	6.97 × 10−20	−1.27	N
2	7.39 × 10−15	2.63 × 10−14	7.99 × 10−22	1.81 × 10−21	−1.54	N
3	3.01 × 10−14	8.31 × 10−14	6.00 × 10−21	1.10 × 10−20	−1.98	Y
4	8.71 × 10−13	3.38 × 10−12	6.70 × 10−20	1.42 × 10−19	−1.41	N
5	1.93 × 10−8	1.30 × 10−8	6.42 × 10−18	4.23 × 10−18	−8.11	Y
6	7.90 × 10−13	2.03 × 10−12	5.60 × 10−20	7.87 × 10−20	−2.13	Y
7	2.13 × 10−12	6.74 × 10−12	6.67 × 10−20	2.76 × 10−19	−1.73	Y
8	8.91 × 10−13	2.71 × 10−12	5.84 × 10−20	1.36 × 10−19	−1.8	Y
9	5.46 × 10−13	1.17 × 10−12	3.56 × 10−20	6.70 × 10−20	−2.55	Y
10	9.03 × 10−13	1.97 × 10−12	3.56 × 10−20	6.07 × 10−20	−2.51	Y
11	1.22 × 10−12	3.91 × 10−12	6.20 × 10−20	8.90 × 10−20	−1.71	Y
12	2.71 × 10−20	7.10 × 10−20	6.23 × 10−24	4.84 × 10−24	−2.09	Y
13	2.11 × 10−12	5.48 × 10−12	1.70 × 10−20	2.93 × 10−20	−2.11	Y
14	4.24 × 10−13	8.07 × 10−13	3.15 × 10−20	6.48 × 10−20	−2.88	Y
15	1.28 × 10−13	2.52 × 10−13	4.77 × 10−20	8.87 × 10−20	−2.78	Y
16	5.58 × 10−13	1.19 × 10−12	2.86 × 10−20	3.96 × 10−20	−2.57	Y
17	4.69 × 10−16	1.66 × 10−15	8.02 × 10−22	1.53 × 10−21	−1.54	N
18	8.38 × 10−17	2.94 × 10−16	5.96 × 10−23	1.08 × 10−22	−1.56	N
19	9.12 × 10−13	1.68 × 10−12	3.73 × 10−20	4.39 × 10−20	−2.98	Y
20	7.58 × 10−13	1.62 × 10−12	2.33 × 10−20	3.70 × 10−20	−2.57	Y
21	2.98 × 10−14	6.60 × 10−14	1.78 × 10−20	4.97 × 10−20	−2.47	Y
22	1.09 × 10−12	3.49 × 10−12	1.49 × 10−20	2.85 × 10−20	−1.71	Y
23	3.76 × 10−13	8.72 × 10−13	1.84 × 10−20	3.05 × 10−20	−2.36	Y
24	2.26 × 10−12	7.21 × 10−12	2.24 × 10−20	4.26 × 10−20	−1.71	Y
25	6.01 × 10−16	1.50 × 10−15	3.30 × 10−22	6.23 × 10−22	−2.19	Y
26	1.87 × 10−8	9.88 × 10−9	7.70 × 10−18	5.55 × 10−18	−10.36	Y
27	2.11 × 10−12	7.50 × 10−12	1.53 × 10−20	2.38 × 10−20	−1.54	N
28	4.11 × 10−12	9.48 × 10−12	4.93 × 10−20	8.81 × 10−20	−2.37	Y
29	6.45 × 10−13	1.02 × 10−12	3.25 × 10−20	5.28 × 10−20	−3.45	Y
30	2.99 × 10−13	5.03 × 10−13	2.19 × 10−20	4.23 × 10−20	−3.25	Y
31	9.34 × 10−13	2.65 × 10−12	2.12 × 10−20	3.97 × 10−20	−1.93	Y
32	1.71 × 10−13	5.44 × 10−13	2.56 × 10−20	4.14 × 10−20	−1.72	Y
33	1.33 × 10−12	3.02 × 10−12	2.55 × 10−20	3.25 × 10−20	−2.41	Y
34	5.56 × 10−20	2.29 × 10−19	4.96 × 10−24	2.05 × 10−24	−1.33	N
35	4.14 × 10−13	8.86 × 10−13	1.23 × 10−19	3.19 × 10−19	−2.56	Y
36	1.55 × 10−12	4.83 × 10−12	2.53 × 10−20	4.93 × 10−20	−1.76	Y
						29

, our claim is that the results of the experiments performed with optimized IT2FLS are better than the experiments performed with T1FLS with parameter adaptation.

Figure 27 and Figure 28 show the behaviors of the mean and standard deviation of the two types of fuzzy systems T1FLS vs. IT2FLS, for 30 dimensions.

Comparison Table 11 shows the hypothesis test for 50 dimensions of the fuzzy systems T1FLS with parameter adaptation and optimized IT2FLS was better in 29 out of 36 mathematical functions.

Figure 29 and Figure 30 show the behaviors of the mean and standard deviation of the two types of fuzzy systems T1FLS vs. IT2FLS, for 50 dimensions and 30 iterations.

Comparison Table 12 shows the hypothesis test for 100 dimensions of the fuzzy systems T1FLS with parameter adaptation and optimized IT2FLS was better in 29 out of 36 mathematical functions.

Figure 31 and Figure 32 show the behaviors of the mean and standard deviation of the two types of fuzzy systems T1FLS vs. IT2FLS for 100 dimensions.

6.2. Discussion of Results

The use of metaheuristics in model optimization is a constant in all research works in artificial intelligence. In this research, we used the DMOA optimization algorithm, T1FLS and IT2FLS fuzzy systems with parameter adaptation, 36 mathematical functions, from CEC-2013 (Table 2) to measure their performance capabilities, and hypothesis testing was performed to test the optimization capability.

When evaluating the results of the hypothesis tests T1FLS and IT2FLS fuzzy systems for 30 dimensions, both with parameter adaptation in Table 7, the results favor the T1FLS fuzzy system in 31 out of 36 mathematical functions evaluated, however when optimizing the parameters of the membership functions of the fuzzy IT2FLS system for 30 dimensions the results of the hypothesis tests favor IT2FLS in 33 out of 36 hypothesis tests in Table 10, and for 50 dimensions the hypothesis tests favor IT2FLS in 29 out of 36 hypothesis tests in Table 11 and finally for 100 dimensions the results favor IT2FLS in 29 out of 36 hypothesis tests in Table 12.

6.3. Programming Environment

The language used in the programming of the DMOA algorithm is MATLAB R2017b and the equipment where the programming and experiments were carried out is a Desktop Computer Intel Core i5 4460S 2.90 GHz., RAM memory DDR3 16 Gb, Intel HD Graphics 4600, and Operating System Windows 10 Professional.

7. Conclusions

As we have already mentioned, the DMOA is a metaheuristic that simulates a biological system that exists in nature, where there is diversity of plants, and where there is communication among plants and the Mycorrhiza Network. To model this ecosystem, the discrete Lotka–Volterra models can be used: the defense model that simulates emergency situations that can manifest in the ecosystem, the cooperative model that simulates the exchange of resources such as CO₂, water, nitrogen, phosphorus, potassium, etc., and the competitive model that represents how the Mycorrhizal Network can be extended by adding other plants competing in the habitat for resources and how within the network larger plants and the Mycorrhiza Network offer resources to growing plants.

Experiments and statistical tests were carried out with the DMOA optimization algorithm with 36 CEC-2013 mathematical functions, as can be seen in Table 2. The configuration of the parameters significantly affects the performance of the algorithm and therefore its convergence and it is very important to find the relationship between parameter values and convergence rate and adjust them for better performance. The statistical tests carried out tell us that when we optimize the parameters of the membership functions of the IT2FLS fuzzy systems with the DMOA algorithm, we obtain better results than the T1FLS fuzzy systems with parameter adaptation: in 33 of 36 statistical tests for 30 dimensions, shown in Table 10, in 29 of 36 statistical tests for 50 dimensions (shown in Table 11) and in 29 of 36 tests for 100 dimensions (shown in Table 12). In summary, of 108 statistical tests carried out in 91 tests, the IT2FLS fuzzy systems optimized with the DMOA algorithm are better, which is in 84.25% of the cases.

We have previously applied the DMOA algorithm in the optimization of the architecture of a non-linear autoregressive neural network for Mackey–Glass time series prediction [69], and in this article in the adaptation of the parameters of the fuzzy systems T1FLS and IT2FLS. Additionally, hypothesis tests were carried out and the results obtained in both investigations were favorable for the DMOA optimization algorithm. In the near future, we plan to conduct research applying the CMOA (Continuous Mycorrhiza Optimization Algorithm) and DMOA in the optimization of the architecture of a long short-term memory (LSTM) neural network. We also plan to solve control problems with the two algorithms (CMOA-DMOA) and systems: type-1 fuzzy logic system (T1FLS), interval type-2 fuzzy logic system (IT2FLS) and generalized type-2 fuzzy logic system (GT2FLS). In addition, experiments with the mathematical functions of CEC-2017 and CEC-2019 are also planned. These two optimization methods, CMOA and DMOA, can be very useful in the optimization of neural networks and fuzzy systems architectures in an efficient way due to their fast convergence, as we have already seen with NARNN neural networks and IT2FLS fuzzy systems, and for this reason we expect to obtain good results in the future research works that we intend to perform.