1. Introduction
One of the critical challenges in any business is determining the right price for individual products and services as pricing plays a significant role in strengthening a company’s competitive power. Therefore, a company requires pricing strategies to improve profitability [
1,
2]. The first factor that a company should consider is how customers will react to the pricing of various goods and services [
3]. The pricing strategy includes a range of factors such as demand, cost, margin, market share, customer loyalty, and product life cycle. To consider these factors and to make pricing decisions successfully for the effective operation of the companies, most of them have attempted to construct systematic price decision support tools using price optimisation models [
4]. For instance, the retail industry has been actively using price optimisation models to determine their prices, inventory levels, and assortment [
5]. Two main categories of price optimisation models in the retail industry have been studied in detail. The first category has been developed for the fashion industry, which has the characteristic that product inventory is highly perishable at the end of the season [
6,
7]. The capacity and price policy properties, in this case, are similar to those used in the airline or hotel industries [
5]. Another category of price optimisation models developed for the retail industry is to consider unlimited inventory capabilities [
8,
9,
10]. Usually, online and offline Fast Moving Consumer Goods (FMCG) companies deal with products with a short shelf life and high turnover rates because of their high customer demands. Thus, demand forecasting plays an essential role in companies’ sales and operation planning (S&OP) [
11] when it comes to determining the price.
In the FMCG industry, in contrast to the fashion industry, the customer’s response to a price change is more important than inventory management as inventory can be continually replenished. In this case, the demand for goods is usually independent over time as customers purchase products repeatedly. Although there is enough transactional sales data in the FMCG industry, it is not easy to predict demand or reflect the exact reaction of customers to products as there are demand correlation issues [
12,
13]. Demand correlation in the retail industry measures how changes in demand for one product affect demand for another. These include factors such as seasonality, consumer trends, inflation, and recession. The income effect also is another important factor in changing demand. The income effect is the resulting change in demand for goods or services due to an increase or decrease in a consumer’s purchasing power or real income in microeconomics [
14]. In the FMCG industry, demand correlation exists in various types. For instance, within a product category, the sales of one product usually decrease when the price of other goods decreases. This is called the substitution effect. Another type of demand correlation is a complementary effect. That is if the price of one product decreases, the sales of related products increase, i.e., pasta and pasta sauce, wine and cheese [
15,
16,
17]. In addition, the sale of one product can be affected by the competitor’s price. This is called the competition effect [
18]. In general, estimating demand for each product taking into account these correlations is complicated as it should deal with multiple products [
11]. The more effect factors needed to predict demand, the more variables and price combinations should be considered. This can result in an exponential number of variables and a higher degree of model complexity.
In papers [
19,
20], some models for demand prediction in multiple products with a substitution effect have been developed. In these models, it is assumed that every customer prefers a specific product based on individual consumer choices. This means every customer associates a utility function with each product [
21,
22]; thus, the choice probabilities should be determined. In this case, the customer’s choice becomes an essential element of the formulation, and the demand process depends on a whole vector of prices, including the price of substitute products. If the distribution of utilities across the customers is known, the Multinomial Logit (MNL) model or the Locational Choice (LC) model can be used to calculate the purchase probability of a product and substitution probability in case the product is not on the shelf. The MNL model assumes that the customer purchases a substitute based on the market share of the products if the preferred product is not on the shelf [
21,
23]. On the other hand, the LC model assumes that the customer purchases a substitute that is the most similar to the preferred product [
20]. Furthermore, in [
19], the Exogenous Demand (ED) model was applied for the substitution effect. In this model, the share of customers with a favorite product and the probability of buying another product if the favored product is not in the assortment are defined. The ED model is more flexible for substitution than the MNL and the LC models; however, it is more challenging to be utilised due to the number of parameters [
22]. Although these models and research works have performed quite well in some applications, finding individual customer preferences and the segmentation of the customers appropriately is challenging in real-world situations. Thus, the calculation of accurate substitution probabilities can not be guaranteed.
Once demand correlation considering various effects has been calculated demand prediction and price optimisation models are constructed and solved. Some researchers have applied data-driven machine learning approaches to the demand prediction model. For instance, Islam et al. [
24] used the Relational Regressor Chain (RRC) method together with traditional time series methods. Makridakis et al. [
25] presented the background, data, and characteristics of the Makridakis 5 (M5) competition that forecast demand for items on sale at Walmart. Chawla et al. [
26] performed demand forecasting by applying an Artificial Neural Network (ANN) method to the same Walmart data used for the M5 competition. Punia et al. [
27] attempted to forecast demand by applying a prediction method that combines Long Short Term Memory (LSTM) networks and Random Forest (RF) to actual multichannel retail data. Vairagade et al. [
28] also applied RF and ANN to Supply Chain Management (SCM).
To solve the price optimisation model, various methods have been applied. For instance, Akçay et al. solved the optimisation problem for multiple products using dynamic programming (DP) [
29]. Although the results were promising for this particular application, the model complexity increases when the effect in optimisation model results in an exponential number of variables. Some researchers have proposed to apply more efficient approaches to reduce the number of operations and thus execution time. Caro et al. [
6] used Mixed Integer Programming (MIP) to compensate for the higher degree of complexity. They applied approximate formulations in which future sales are replaced by their expected values. Ferreira et al. [
5] applied Integer Programming (IP) to solve the optimisation problem for substitute products using a reference price metric.
Although the models and methods described above have demonstrated some promising results, their applications to real-world situations are not always possible due to the curse of dimensionality and time complexity. Thus, it is essential to design techniques that can be executed on the available computer resources within a reasonable time while considering both various business rules and optimisation processes.
In this paper, we extend the study of the retailer in the FMCG industry aiming to provide an efficient price optimisation model that can be applied to business operations in a computationally effective manner. More specifically, we investigate the demand prediction and the price optimisation of multiple products considering the combination of price changes of products to reflect the effect of the substitution within the product category. The customers’ responses to the different price ranges using real-world transactional sales data are also studied. A significant part of this research is associated with the substitution effect and has been conducted to estimate demand in the retail industry. This research is more focused on the price-based substitution effect than the assortment-based substitution effect.
The main contributions of this paper are:
investigating demand prediction models for multiple products with substitution effect and proposing a new demand prediction procedure;
utilising data-driven machine learning approaches in demand forecasting;
studying price optimisation models for the retailer that reflects all price changes of products and constructing a novel price optimisation procedure;
applying the proposed demand prediction and price optimisation procedures to real-world transaction data.
The rest of the paper is organised as follows.
Section 2 presents the data collection and how to identify the key factors for the demand prediction model using Exploratory Data Analysis (EDA).
Section 3 and
Section 4 describe the demand prediction and price optimisation models, respectively, as well as the experimental results of the models.
Section 5 presents the discussion and conclusion.
2. Data Set
This section provides information about the data set used in our experiments followed by the description of processing and analysing data.
2.1. Data Description
Three years of transaction data on products sold in US supermarket chains were taken from the Dunnhumby website and used as a sample for this study (Dunnhumby’s ‘Breakfast at the Frat: A Time Series Analysis’). The data consists of three tables in total (in CSV format): the product table that provides product information such as product name, description, subcategory, brand, and size; the transaction table that contains weekly unit sales, sales amounts, number of visitors, number of visiting households, base price, actual sales price at the shelf, and promotion information for each product; and finally, the store table that has information such as store type, store size, parking lot size, and average sales amount.
The data contains the sales histories of four product categories during 156 weeks from 2009 to 2011 in 4 US states, 51 cities, and 79 stores. These categories are bag snacks, cold cereal, frozen pizza, and oral hygiene products. Each category has sales of the top three products for each of the top five brands—a total of 15 products. Among these categories, cold cereal is selected as a sample in our experiments due to the following reasons: it has the most frequent purchases, the appropriate number of subcategories, and a relatively wide range of discount frequencies and depths. In addition, products in this category are known to represent the characteristics of essential consumer goods in the FMCG industry and are less affected by time series (e.g., seasonal and monthly effects).
The cold cereal category consists of five brands (Kellogg, Post, General MI, Quaker, and Private Label). As Quaker brand products have a shorter sales period than other products, it is not easy to use the products of this brand for modeling. Thus, we remove them from the data and consider only sales data from 12 products representing four brands. Furthermore, as the sales periods are slightly different for each product, 104 weeks of data, the two years from 8 July 2009, are used for developing the demand prediction model. In addition, one of the Cincinnati stores (Store id = 25,027) is selected as a sample since this store has a relatively large amount of transactional sales data.
Moreover, the products of each brand have different market shares, but at the same time, sales of products are greatly affected by price changes caused by discounts or promotions. As the discount period and depth vary from brand to brand, how the price change of one product affects the sales of other products should be measured, for instance, using transaction data. As a result, weekly sales of each product are widely distributed according to brand loyalty, discount rate, and substitution effect. In the following, exploratory data analysis is done to measure and examine own-product price elasticity, cross-product price elasticity, and seasonal effects in detail.
2.2. Data Preprocessing
First, the three tables (the transaction data, product information, and store information) are combined into one table. Then, missing values and outliers are scanned. There are no significant outliers in the sample; however, missing values occurred due to differences in product sales periods when generating the price combination variable of products within a product category. We impute the missing values using Random Forest, when implementing the demand prediction model.
Next, we create various derivative variables such as discount rate, unit price, relative price, and successive discount periods. Since the price variable has a significant impact on sales, some derivative variables related to price are created. In addition, we calculate the discount rate using the base and actual selling prices (DISCOUNT_RATE). The unit price is also created by calculating the selling price per unit—in this case, usually per ounce (UNIT_PRICE). Note that the relative prices within product categories have been frequently used as reference prices in previous studies [
5]; thus, we calculate these values by dividing the price of each product by the average of the prices of all products in the product category (RELATIVE_PRICE). As most product discounts do not stop after just one week but last for several consecutive weeks, new variables are created by calculating consecutive discount weeks (DISCOUNT_WEEKS) and consecutive nondiscount weeks (NO_DISCOUNT_WEEKS). Variables such as YEAR, MONTH, and WEEK are also newly created to understand the influence of time series factors such as trends and seasonality.
Furthermore, we create various discount-type variables (DISCOUNT_TYPE2). They include NO if the product is not discounted at all, UNSUPPORTED if the discount is put in place without other promotion, and SUPPORTED if the discount is supported simultaneously with promotions such as display and feature.
2.3. Exploratory Data Analysis (EDA)
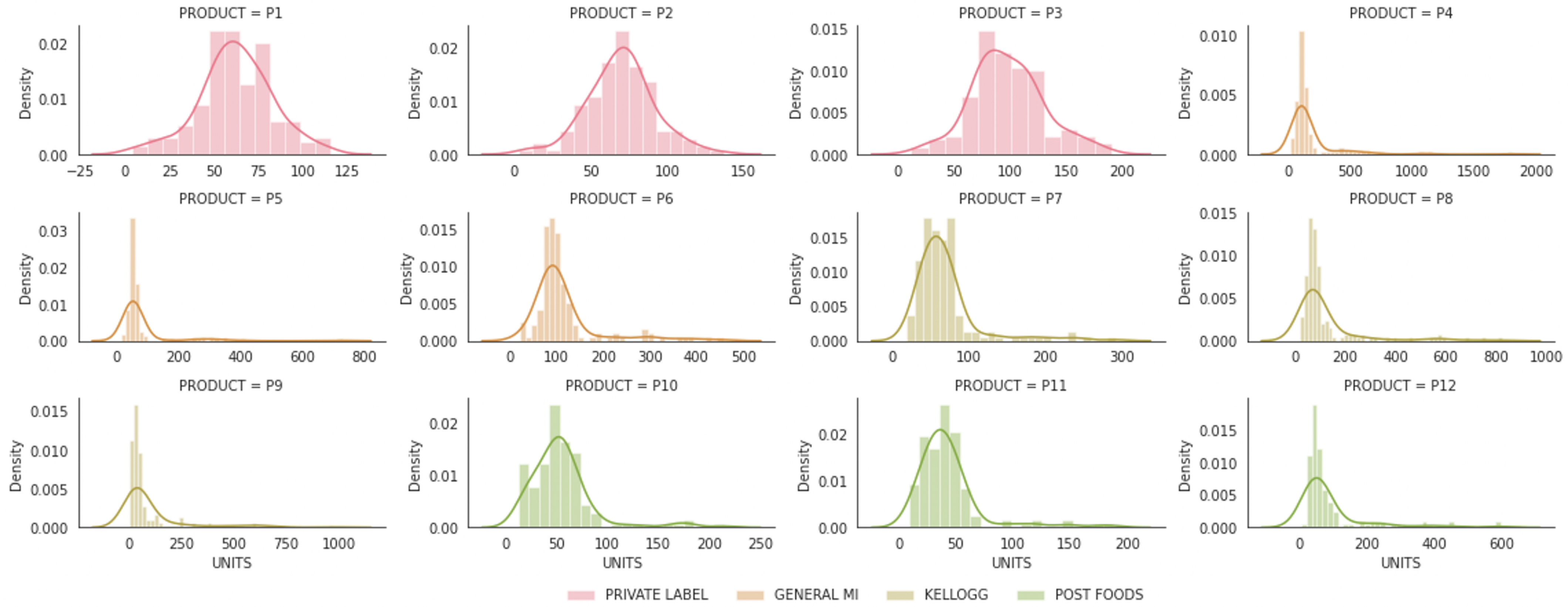
To get more insight into customer response to price changes and features that affect sales, and also to calculate price sensitivity and substitution effect, we conduct EDA. Univariate analysis shows the distribution of prices, discount rates, promotions, and sales of each product. Each product has a different price, discount rate, discount frequency, and promotional frequency. Since the sales distribution of most products has a long right tail, indicating that the sales of products increased dramatically during discount periods (see
Figure 1), we apply log transformation to variables such as sales units, sales amount, and price. This allows us to calculate price elasticity efficiently as well as to improve the prediction accuracy of the demand prediction model.
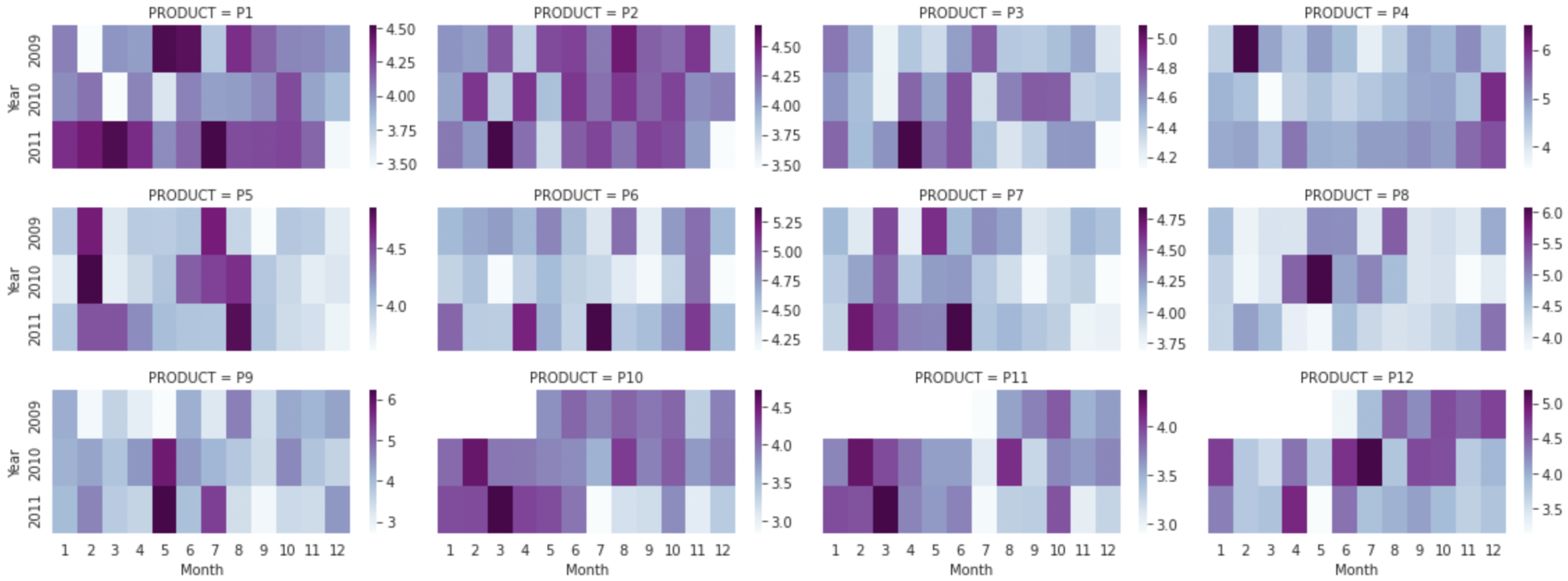
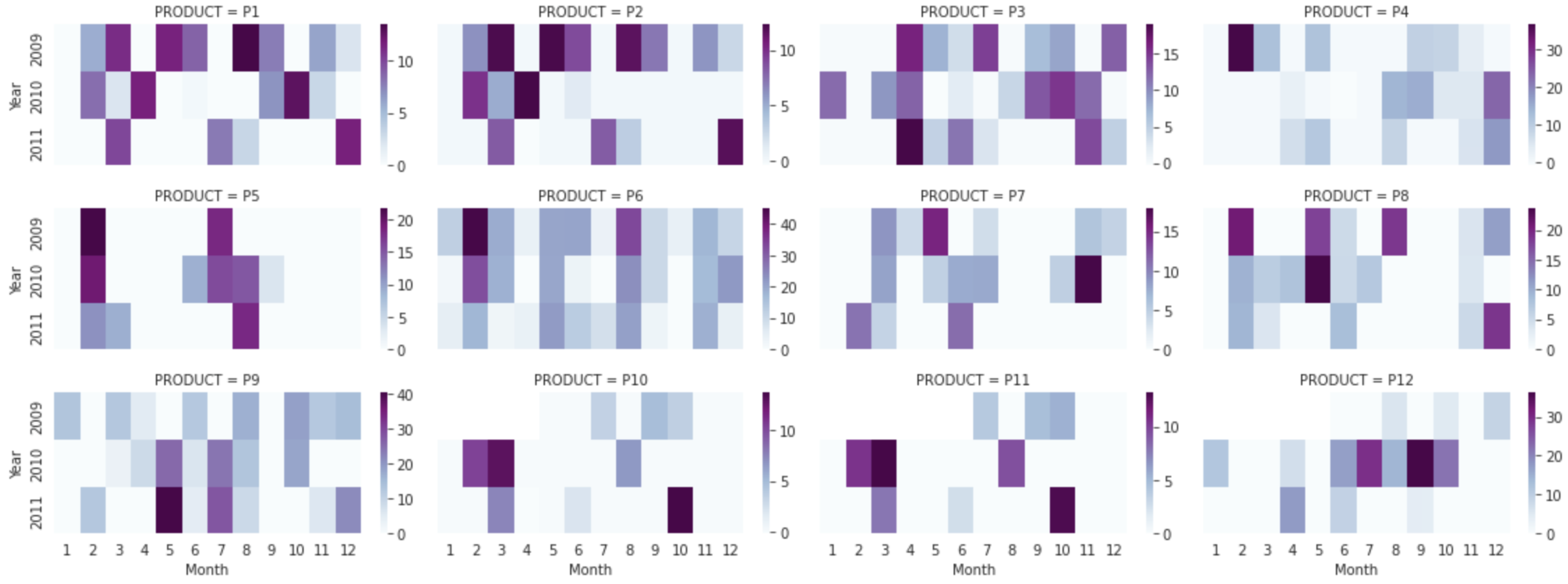
Furthermore, we apply the well-known demand forecasting approach, time series analysis, to investigate trends, seasonality, and cycles. The results show that there is no distinct seasonality, and the hypothesis that the sales of FMCG industry products are time-independent is satisfied. The results of heatmap are illustrated in
Figure 2 and
Figure 3. It can be seen that there is no special monthly effect on sales and discount rates. The darker the color in the heat map graph below, the higher the month’s sales volume (see
Figure 2). For instance, months with high sales are a darker color in the graph, but each product has a different month with high sales. Consequently, the heatmap graph shows no patterns in which the sales of a particular month were steadily higher or lower.
To assess whether there is an autocorrelation with past sales of products, we utilize Autocorrelation Function (ACF) and Partial Autocorrelation Function (PACF). The ACF indicates the correlation coefficient between the current time series and the
kth time leg, and the PACF shows a partial correlation between the current time series and the
kth time lag. Since the results are very similar for ACF and PACF, we only include the results of the ACF (see
Figure 4). If the height of the bar is significant in the positive or negative direction, then there is a substantial correlation between the time lag and the current time series. The ACF starts with a lag of 0, which is the correlation of the time series with itself and therefore results in a correlation of 1. The shaded area represents the 95% confidence interval and indicates the significance threshold. For instance, lags within the shaded area are insignificant, and lags outside the shaded area are statistically significant. The results show that most products have a significant correlation with time lag 1 or lag 2. However, none of ACF and PACF graphs show significant correlation with time lags 12 and 24, which means that there is no specific seasonality (i.e., they did not cross the 5% confidence boundary for auto correlation).
Next, we study the variables affecting sales—as they are essential input variables for the demand prediction model—and select candidate features. We apply the correlation analysis for this purpose. The results of our analysis show that sales of each product were most affected by price and discount. Promotions such as displays and features were also strongly correlated with product sales.
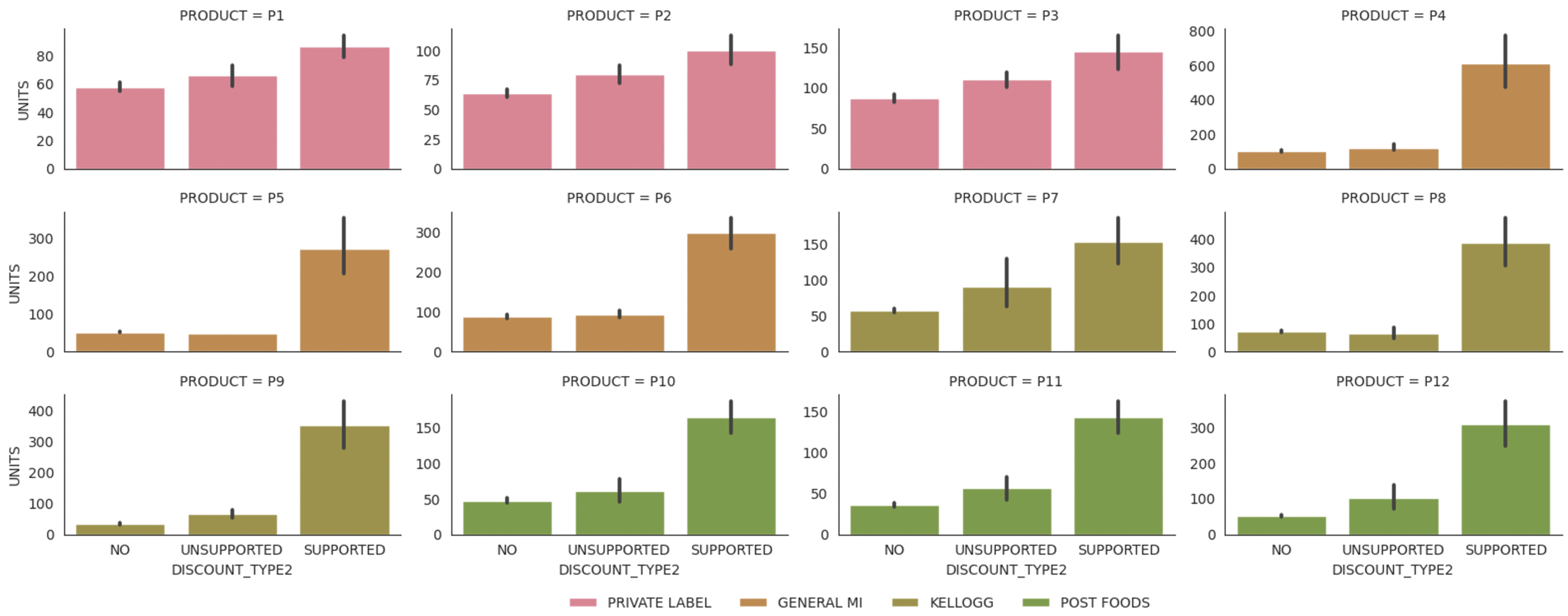
Figure 5 shows the product sales when there is no discount (NO), a price discount without promotion (UNSUPPORTED), and a price discount with the promotion such as display and feature promotion (SUPPORTED). The graph presents that if the discounts are supported together with the promotions (SUPPORTED), product sales increase sharply compared to if they are not discounted (NO) or discounted without promotions (UNSUPPORTED).
Furthermore, we examine the relationship between sales, prices, and discounts in more detail using regression analysis. The price sensitivity of each product is assumed to be equal to its own-product price elasticity, and a product with high price elasticity is considered to be a product with high price sensitivity. Indeed, it is expected that products with high price elasticity are more critical in the demand forecasting model. Many studies used a log-log linear regression function to calculate the own-product price elasticity for a particular period [
30,
31]. In this case, the own-product price elasticity is the same as the
value (slope) of the regression function (see Equation (
1)) as it represents the change in the sales of one product divided by the price change.
where:
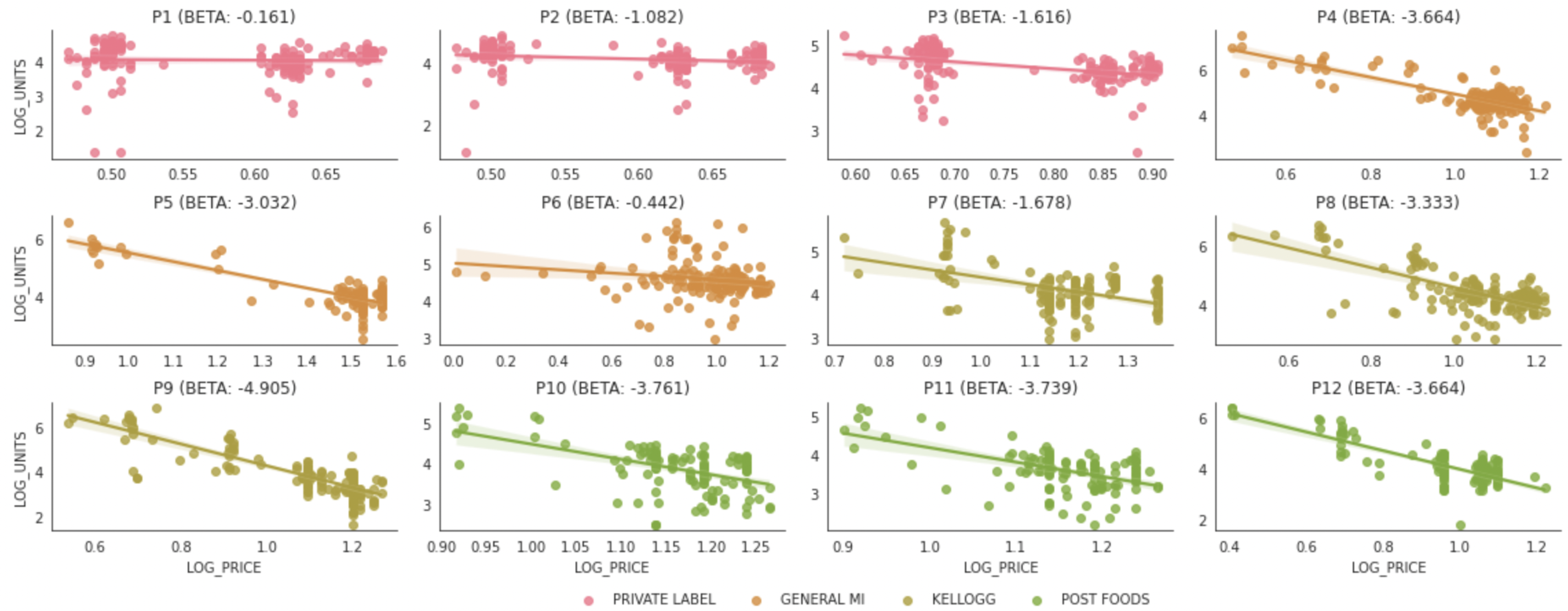
Moreover, the results of our analysis (given in
Figure 6) reveal that each product had different price elasticity. In this figure, the larger the slope in the negative direction, the more significant the change in sales volume. For example, product P9 has a slope of −4.905, showing that its changes in product sales from changes in price are much greater than for other products. As expected for a product with high price elasticity, the higher the discount rate, the more sales increase.
In addition, the cross-product price elasticity was used to identify the substitution effect of two products in many studies [
32]. Like the own-product price elasticity, the log-log linear regression function is used to calculate the cross-product price elasticity of two products A and B for a particular period. That is, the (
1) can be reformulated as (
2) to see how product B’s sales change as product A’s price changes, and vice versa.
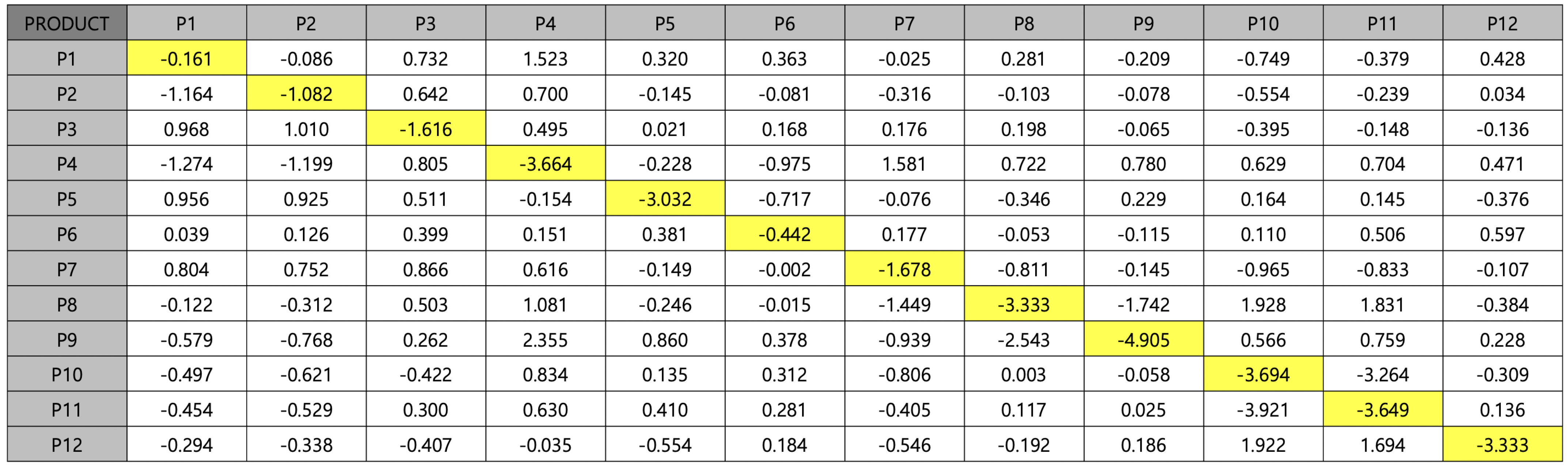
Using these equations, we calculate the cross-product price elasticity matrix,
Figure 7. This matrix shows which/how price changes in some products had more significant impacts on the sales of other products. The diagonal of this matrix represents the own-product price elasticity of each product, and the larger the negative value, the higher the price elasticity. Asymmetric cross-product price elasticity between two products is also given in the matrix. This means that price changes of one product have a greater impact on the sales of other products, while conversely, some products are more affected by price changes of other products. The cross-product price elasticity results have the advantage of showing the influence of each product pair. However, there is the limitation that they show the substitution effect only between two products. The results of this matrix show that it is not desirable to assume a specific mathematical model for substitution effects as the price change of each product has different effects on other products. Therefore, we focus on demand prediction and price optimisation models that reflect the substitution effect through machine learning data-driven methods.
3. Demand Prediction Models
One of the most critical factors of price optimisation is to obtain demand forecasts that match changes in a product price. One needs to understand how a product’s demand changes with different pricing options. As mentioned above, there are different factors that can affect prediction of demand. We study demand prediction models that consider the substitution effect. To reflect this effect, demand prediction models should include the price changes of all the products in the product category as input. We utilise the candidate variables selected through EDA and the prices of all products within the product category as input variables for demand prediction.
In this section, we present a framework that selects each product’s best demand prediction model among the candidate models. The demand prediction model selected as best for each product will then automatically become the input of the price optimisation model. To select the best model for each product, we compare the benchmark models with the candidate demand prediction models.
3.1. Existing Models
Among existing demand prediction models, the simple average, simple median, naïve Bayes, and seasonal naïve models are commonly used in most studies [
33,
34,
35]. Thus, we consider these models as benchmarks for our study.
The simple average model uses the average of the sales historical data to forecast all future values, and defined as
where:
Like the simple average model, the simple median model uses the median value of the sales historical data to forecast all future values, and given as
The naïve model utilises the value of the last observation to forecast all future values and is defined as
where
is the last observed value of time T period data.
The seasonal naïve model works well in data that have seasonal components. While the naïve model uses the most current value as a predictor, the seasonal naïve model predicts the value of the last observation from the previous season. For example, when we want to forecast monthly data, the seasonal naïve model predicts the May of this year as the data value of the May of the previous year. The seasonal naïve model is defined as
where
m is the seasonal period and
Note that the seasonal Naïve model is used to check if the seasonality improves the model performance.
The first demand prediction model used in our comparison is the ARIMA, where time series elements are included as primary input variables. As no seasonality was observed in the FMCG industry dataset, the ARIMA model is used and tested. The ARIMA model is a generalisation of the Auto Regressive Moving Averages model, that explains the current time series values using past observations and errors. ARIMA is a model that integrates the Auto Regressive (AR) and Moving Averages (MA) models. The ARIMA model has three parameters
—the
p-order of the AR (
p) model, the
q-order of the MA (
q) model, and the number of differences (
d-order) as follows:
Parameters
p,
d, and
q could be manually identified using the ACF and PACF graphs above but instead we use a hyperparameter tuning method to find the optimal parameters by programming (Python coding) as this allows the analysis to be automated. Then, the forecast at time
t,
, using the ARIMA is given by
where:
The MLR model uses the prices of all the products and other critical features as identified through the EDA for forecasting demand. We apply the log-log linear regression to estimate the demand for one product, that is
where:
For other machine learning models, K-Neighbours, Decision Tree, Random Forest, Extremely Randomised Tree, GBM, Light GBM, Histogram-based GBM, and XGBoost, we apply hyperparameter tuning to find the optimal parameters. More precisely, during the model training and testing process, various parameter combinations are tested to find the most robust demand forecasting model. In addition, a grid search method to implement one of the time-series cross-validation techniques, rolling forecasting, is utilised in the tuning procedure.
The
K-Neighbours regression algorithm is a supervised learning, a nonparametric algorithm that regresses using labeled data. It is commonly used for demand forecasting in the retail industry, as it has no assumptions about the underlying distribution of the data, is robust to outliers, and is easy to implement [
36,
37,
38].
The Decision Tree model has been the most widely used in the field of data science because it has fast, easy-to-interpret, and strong predictive performance [
39]. The ‘training’ of this model is carried out by dividing the data set for learning into subsets according to the appropriate partitioning rule. However, they also have the disadvantage that there can easily be overfitting when new data is predicted [
40].
One of the typical methods to prevent such overfitting is Random Forest, which employs the ensemble technique. Random Forest is an algorithm that creates multiple decision trees and determines the results using the voting method. Random Forest composes the forest using bootstrap aggregation, called the ‘begging’ algorithm [
41]. Several studies conducted retail demand forecasting using Random Forest, as it can handle missing values, nonlinear relationships, large data sets, and is robust to overfitting [
28,
42].
The Randomised Trees model, also known as the Extra Trees model, increases randomness by randomly dividing each candidate feature in the forest tree—that is, the model randomly selects independent variables at each node [
43].
Unlike the Random Forest model, Gradient Boosting creates a tree sequentially in a way that compensates for the error of the previous tree [
44]. Therefore, the Gradient Boosting model has no randomness, as the next tree is affected by the outcome of the previous tree. Compared to the ‘bagging’ algorithm that only controls high variance in the model, the ‘boosting’ algorithm is known to control both bias and variance [
45]. Several studies used Gradient Boosting for forecasting demand, as it is more robust to noisy data and uses less memory [
46,
47].
XGBoost (Extreme Gradient Boosting) [
48], LightGBM developed by Microsoft [
49], and Histogram-based Gradient Boosting [
50] are the most popular Gradient Boosting implementation libraries. XGBoost is a scalable and highly accurate gradient-boosting machine learning library. XGBoost shows faster computational performance because the trees are built in parallel rather than sequentially as they are in Gradient Boosting. In addition, XGBoost has the advantage of minimising overfitting by fine-tuning more diverse parameters through hyperparameter tuning.
Despite XGBoost’s excellent prediction performance, it has the disadvantage of requiring an extended learning time [
48]. In comparison, LightGBM has the advantage of fast speed and low memory usage, and its accuracy is not much different from XGBoost [
49]. Histogram-based Gradient Boosting reduces the split points to consider by binning the input sample with an integer value of bin (histogram, typically 255 bins). As a result, the number of candidates to split is significantly reduced compared to sorted continuous values because the algorithms utilise data structures based on integers [
50] (see
Table 1).
3.2. Selection of Variables
We use the historical transaction data without assuming consumer preference or utility being utilised. Since the prices of all products in a product category have to be used as inputs to a demand prediction model to reflect the substitution effects, we consider the price combination of all products within a product category.
In the benchmark and ARIMA models, only the historical sales data is used, while all the candidate variables and the prices of all products are used in other models. The candidate variables that have the most significant impact on the sales of the products are selected through univariate, bivariate, correlation, and time series analysis. They include the key variables highly correlated with product sales such as price, discount rates, promotion type, and time-related variables like month and week. The time lags are also selected as a candidate variable, as there is an autocorrelation with lags 1 and 2 through time series analysis in the EDA process. In addition, previous discounts, discount weeks, and no discount weeks are selected, see
Table 2.
3.3. Validation of Models
We use the time-series cross-validation technique for model validation. Compared to general cross-validation techniques that randomly separate training data and test data to validate model performance, time-series cross-validation techniques have the characteristic of separating training data and test data by taking the training data from one time period and the test data from a subsequent time period. For more robust model evaluation, we apply a rolling forecasting method, which sequentially separates historical data into several pairs of train-test sets and considers the average value of prediction errors for each test set as the final model performance. Furthermore, we utilise the expanding window technique to expand the training data sequentially, but the test data is used only for a fixed period.
3.4. Evaluation and Comparison of Models
To compare the models, we apply the Root Mean Square Percentage Error (RMSPE) to report the difference between the actual and the predicted values at all times, defined as
where:
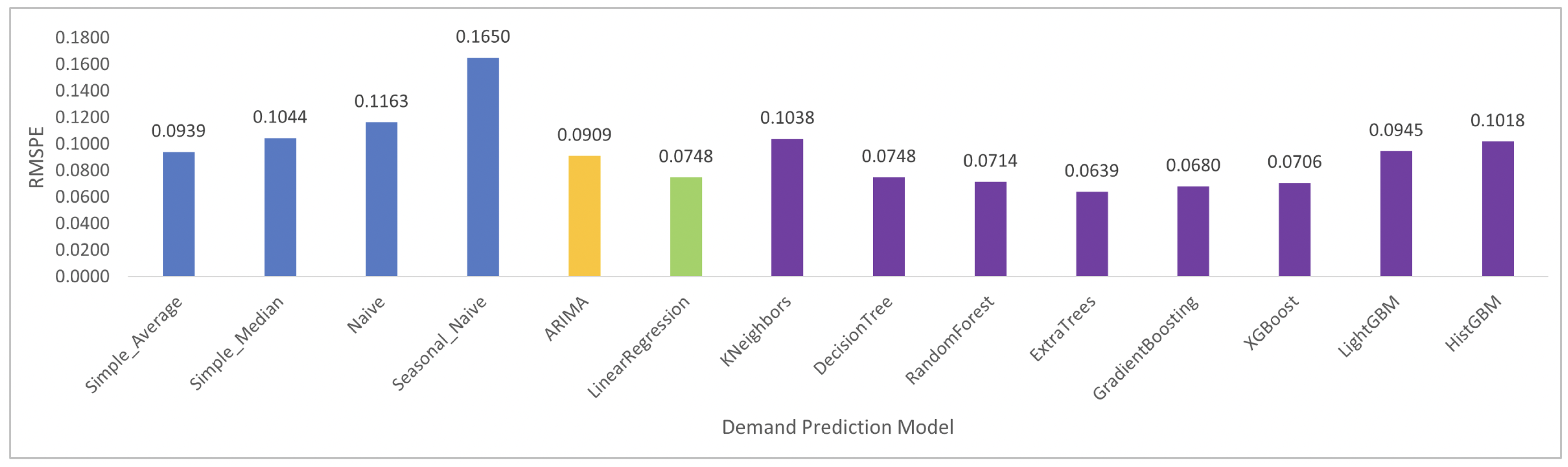
Next, we present and discuss the results obtained by the models mentioned above. After testing all candidate demand prediction models, the best model—the one that minimised prediction error—is selected for each individual product. For instance for the product (P4), the results are given in
Figure 8. We can see that the prediction errors of most candidate machine learning models, Random Forest, Extra Tree, Gradient Boosting, XGBoost, and Decision Tree as well as MLR, are lower than those produced by the ARIMA and the benchmark models. Overall, these machine learning models show an improvement in RMSPE score of between 2% to 16% over the benchmark models. The best model with the lowest value of the RMSPE score is Extra Trees (0.0639), which shows a performance improvement of about 3% over the Simple Average model (0.0939) and about 10% over the Seasonal Naïve model (0.1650).
The final results with all products are presented in
Table 3. In this table, the first column indicates the product name, the second column shows the best model for the corresponding product, and the last two columns present the best parameters and scores. The ‘n_estimators’ parameter in the third column indicates the number of trees in the forest and this value could be 100, 500, or 1000. Likewise the ‘max_depth’ parameter represents the maximum number of levels in each decision tree and this was tested at values of 3, 4, or 5 for hyperparameter tuning. Moreover there is no one correct answer for these parameters as the decision is more experimental than theoretical. Therefore, we need to test various combinations of the parameter options to see which gets the best results. The best score is the RMSPE value of the best model of each product, that is, the model with the lowest prediction error.
We can see from this table that mostly machine learning models are selected as the best model for each product. These results also confirm that the accuracy of the models reflecting the substitution effect (machine learning models) is higher than the models with no substitution effect (ARIMA and benchmark models).
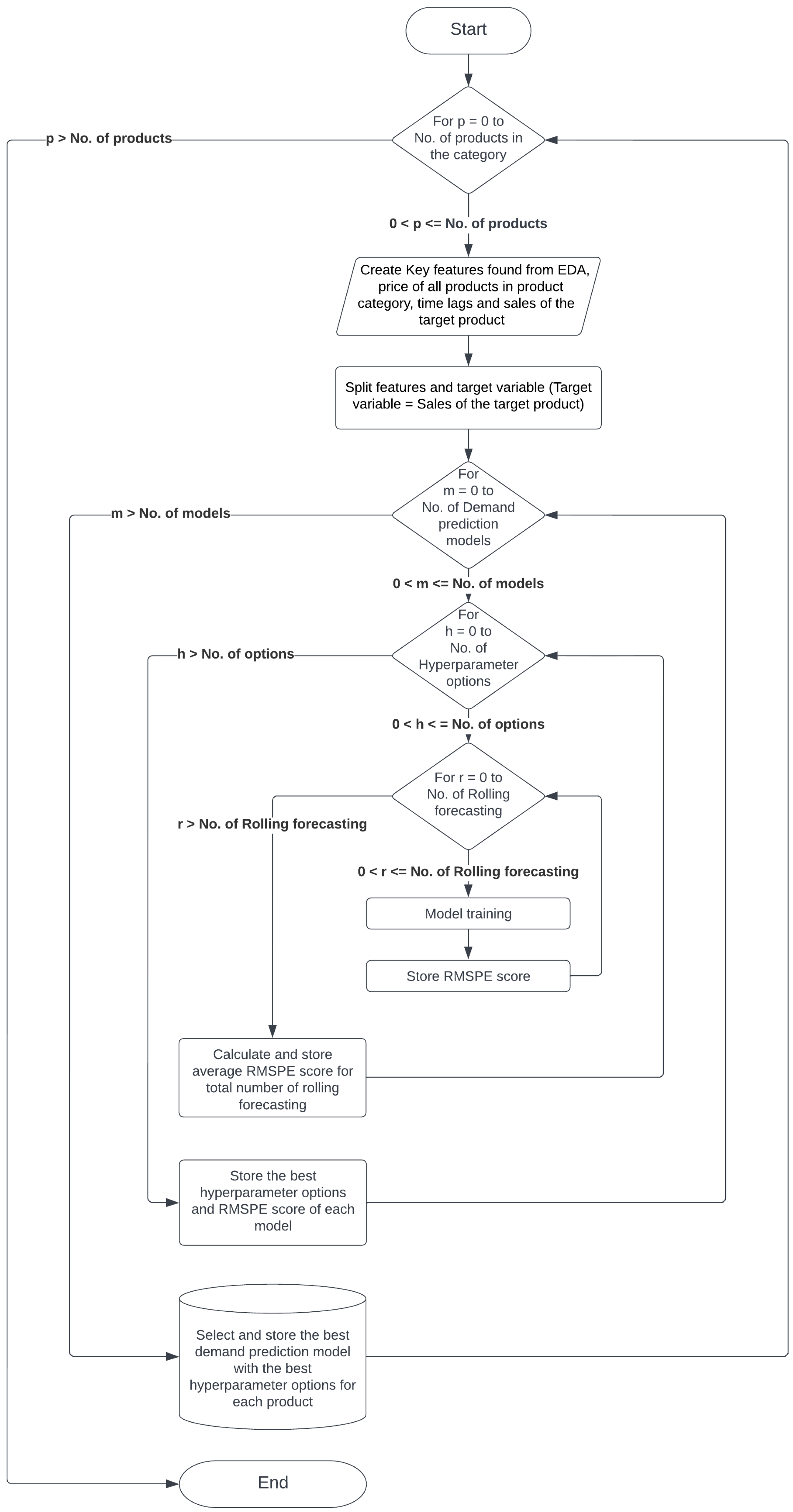
3.5. The Proposed Demand Prediction Procedure
Following our observations and experiments, next we propose a procedure for best demand prediction. Denote the number of products by
p (also used for the number of iterations), the number of demand prediction models by
m, the number of hyperparameter options for each product by
h, and the number of possible rolling forecasting windows
r. To find the best demand prediction model for each product, one should follow the following procedure (illustrated also in
Figure 9):
- 1.
Start modelling for the first product on the product list p (p = 1–12);
- 2.
Generate input data including key features, price of all products, time lags, and sales of the target product from the database;
- 3.
Split features and target variable;
- 4.
Select the individual demand prediction model from the predefined model set m (m = 1–14);
- 5.
Select the hyperparameter option combination from the predefined parameter set h (h is different depends on the model);
- 6.
Increase the rolling forecasting windows from 52 weeks to [the total number of weeks of each product − test weeks];
- 7.
Perform the demand prediction model training with selected demand prediction model, hyperparameter option and rolling forecasting window obtained in steps 4–6;
- 8.
Calculate and store RMSPE score from the model validation process using (
9);
- 9.
After finishing the rolling forecasting loop, calculate and store the average RMSPE score of all the rolling forecasting for selected hyperparameter option;
- 10.
After finishing the hyperparameter option loop, store the best hyperparameter option with the lowest RMSPE score for selected demand prediction model;
- 11.
After finishing the demand prediction model loop, store the best demand prediction model with the best hyperparameter option for selected product;
- 12.
After finishing the product loop, print the best demand prediction model for all the products.
Figure 9.
The proposed demand prediction procedure.
Figure 9.
The proposed demand prediction procedure.
Note that the demand forecasting for each product is performed using the best demand prediction model for that product. In addition, the demand prediction results reflecting all the product price combinations (where K is the number of products in the category, and N is the number of discount rate options) are taken from the model and are used to reflect the substitution effect. These demand forecast results will be the key input for the price optimisation model.
4. Price Optimisation Models
The final price optimisation model should be as accurate as possible and be feasible within affordable system performance. The core input to the price optimisation model is demand forecasts reflecting the substitution effect. Another important key is solving the curse of dimensionality caused by the substitution effect of considering the price combination of all products in the product category. The final output of the price optimisation model is the optimal discount rate for individual products selected from a set of discount rate options (e.g., {0%, 25%, 50%}).
Furthermore, any business rules and limitations associated with the industry must be investigated and applied to the price optimisation model. Most business rules have to be created based on the business strategy already used by the retail company. The company can also develop new strategies and business rules using the insights gained from the EDA.
In this paper, we concentrate more on a model that can reduce the number of combinations and thus execution time using Constraints Programming (CP) techniques, as, in essence, this is a typical combinatorial optimisation problem. We use the best demand prediction model, for each product with different price combinations of products in the product category, constructed in the previous section. Furthermore, we add several business rules as constraints.
In the following, we first describe a basic price optimisation model that reflects the substitution effect. After determining the input variables, decision variables, parameters, and objective function, we evaluate the model from various viewpoints. Then, we add several business rules that may arise in FMCG industries to this price optimisation model as constraints and formulate two price optimisation models named Model 1 and Model 2. Finally, we compare the models through computing simulations to assess how the combinations and execution times vary when the number of products, discount rates, and constraints are changed.
4.1. Basic Model
To formulate the basic model, we use products for sale in the cold cereal product category from the data set described in
Section 2. Recall that the number of discount rate options determines the number of price combinations for products within a product category and thus has a significant impact on system performance and execution time. Therefore, the basic price optimisation model allows us to check changes in system performance based on the number of discount rate options. Note that it is assumed there are a limited number of discount rate options.
Using each product’s underlying price and cost, the product margin is calculated by applying each product’s selected discount rate. Then, in the objective function, the total profit for the product is estimated by applying the calculated margin to the demand values from the demand prediction model. The goal of the basic model is to find a single set of discount rate options that maximise profit. The optimal discount rate selected for each product allows the store to maximise its overall weekly profit.
We use the following notations to form the model.
Formulation
The objective of this model is to determine the discount rate options for each product that maximises the weekly profit of all products into the product category. The price, cost, and discount rate of each product are entered in the model as an inputs. The margin [base price ∗ (1 − discount rate) − cost)] is then calculated from these values to obtain a solution to the objective function. This is followed by calculating profit from the product margin and the demand forecast value. Therefore, the demand forecasts need to be generated as many times as the discount rate combinations of all products.
subject to
The number of demand forecast values to be generated by the demand prediction model is . For example, if twelve products and three discount rate options are applied, a total of = 6,377,292 demand forecasts should be calculated. However, if the number of products or discount rate options increases, the number of demand forecast values to be generated will also increase exponentially. This then leads to a sharp increase in model execution time and makes demand prediction impossible due to system performance limitations.
In the objective function (
10), the binary decision variables
can have
combinations. Therefore, only one combination among the total
cases should have a value of 1 (as a binary value), and the remaining combinations must have zero value. In conclusion, the combination of value with 1 should be the final optimal solution.
Constraint (
11) ensures that only one combination has a value of 1. In other words, only one of the
combinations should be selected, and the selected combination becomes the optimal solution of the objective function as the one that maximises profit. Constraint (
12) assumes a business rule that says there should be at least four discount products every week. This number can be changed depending on the purpose or characteristics of the business. Similarly, Constraint (
13) requires that no more than six products be discounted every week in the product category. Again this can be arbitrarily adjusted in a real-world situation.
Constraint (
14) implies that all demand forecasts for each product must be greater than or equal to 0 in all combinations. It means the model will not consider returns or refunds for products. Constraints (
15) and (
16) ensure the range of the variables.
Next, using 12 products from the cereal category and three discount rate options (0%, 25%, and 50%) we present the model performance and its final optimal solution. Note that the base price of each product is gained from the transaction data set. However, the cost of each product should be assumed as the data provides no cost information. In this case, the number of combinations of the discount rate of all products is 531,441 per product. In
Table 4, we provide the values of the parameters used for model simulation.
To obtain the results of this model, we follow the following process:
- 1.
Demand prediction and model training:
Train the selected best demand prediction model for individual product in the product category;
Identify the demand prediction error of each model through validation process;
Identify the impact of variables on sales by producing the feature importance score;
- 2.
Generate new input data:
- 3.
Demand forecasting:
- 4.
Price optimisation:
The results obtained using the above process are given in
Table 5. From the results, we can see that the optimal solution produces the optimal discount rate for each product. According to the constraints of this model, the number of products to be discounted is limited to between four and six. For example, only four products should be discounted from 25% to 50% to maximise profits, and the optimal profit is expected to be
$2456.
Next, we consider two models by adding some business rules that may arise in FMCG industries to the basic price optimisation model as constraints. This gives insight into how business rules should be applied in real-world operating environments to perform demand forecasting and price optimisation models more efficiently.
4.2. Model 1
In this model, the aim is to reduce the number of price combinations. Thus, in addition to constraints that limit the total number of discounted products in the category, we add Constraints (
17) to (
24) to limit the number of discounted products in the same brand from one to a maximum of two—that is, the objective function of Model 1 is the same as the objective of the basic model, given in (
10), and Constraints (
11) to (
16) are hold. The additional constraints are defined as follows:
4.3. Model 2
In Model 2, we try to reduce the number of price combinations much more than the basic price optimisation model and Model 1 by fine-tuning the constraints. Similar to Model 1, the objective function of Model 2 is the same as the objective of the basic model, given in (
10), and Constraints (
11) to (
16) are hold. The additional constraints are defined as follows:
To limit the number of products that can be discounted to five, we define Constraint (
25). To set a different number of products to be discounted for each brand, we have the following: brands 1 and 4 allowed only one product to be discounted—Constraints (
26) and (
31)—while brands 2 and 3 allowed one to two products to be discounted—Constraints (
27) to (
30). In addition, some products are limited to fixed discount rates. For example, the model considers products 1, 7, and 11 to be non-discountable—Constraint (
32), and product 4 to be limited to a 50% discount rate—Constraints (
33). Of course, these business rules can be changed and adjusted as much as possible in the real-world business environment.
Next, we describe the proposed price optimisation procedure followed by the comparison of these three models.
4.4. The Proposed Price Optimisation Procedure
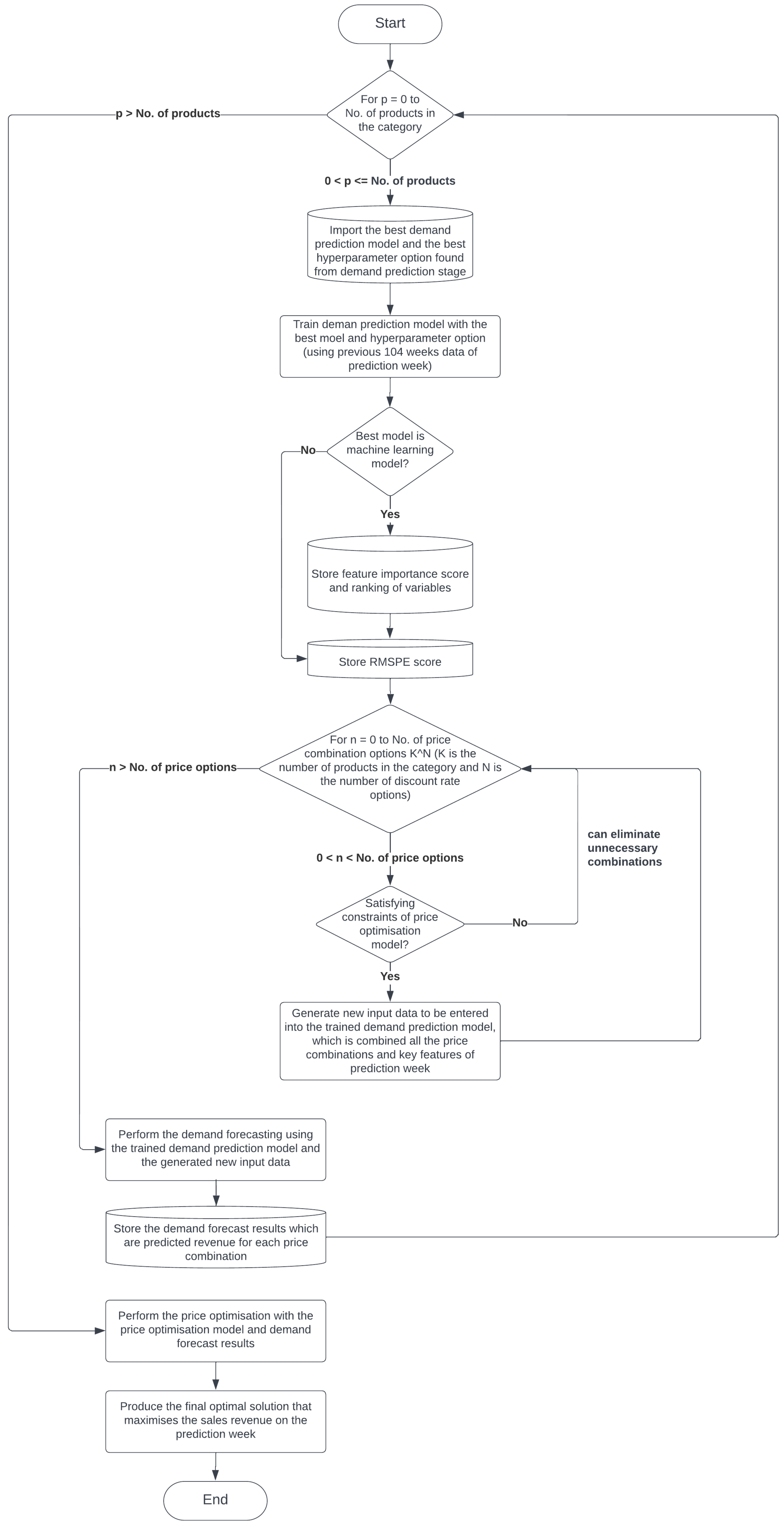
The proposed price optimisation procedure is designed to reflect the substitution effect and reduce the number of iterations significantly. The execution time also can be reduced drastically by applying the constraints listed in step 7 to the price optimisation model, as it can help avoid unnecessary demand forecasting, which is the most time-consuming task. Let the number of iterations to be determined by the number of products p, and n be the number of price combination options. Then, the proposed price optimisation procedure is as follows:
- 1.
Start modelling for the first product on the product list p (p = 1–12);
- 2.
Import the best demand prediction model and the best hyperparameter option for selected product;
- 3.
Train the best demand prediction model with the best hyperparameter option using the previous 104 weeks of the prediction week;
- 4.
Store the feature importance scores and rankings if the best demand prediction model is machine learning model;
- 5.
Calculate and store the RMSPE score using the formula (
9);
- 6.
Generate price combination options (K is the number of products in the product category and N is the number of discount rate options) in the loop;
- 7.
Generate new input data to be entered into the demand forecasting only if the selected price combination satisfy Constraints (
11)–(
16), (
17)–(
24), or (
25)–(
33) of the price optimisation model;
- 8.
After finishing the price combination options loop, perform the demand forecasting for the selected product using the selected best demand prediction model and generated new input data within the loop;
- 9.
Store the demand forecast results which are the predicted sales for each price combination;
- 10.
After finishing the product loop, perform the price optimisation with the price optimisation model: Constraint (
10) and generated demand forecast results;
- 11.
Produce the final optimal discount rate for all the products in the product category that maximise the sales revenue on the prediction week.
This procedure is also depicted in
Figure 10.
4.5. Evaluation and Comparison of Models
In this section, we present the results of the basic price optimisation model and the models with constraints by applying the proposed price optimisation procedure. We test the total number of price combinations for demand prediction, the number of search spaces, and the execution time for demand prediction and price optimisation.
The number of products is tested by comparing nine products from three brands with twelve products from four brands since each brand has three products and less than six products are too small to see the effects of substitution. The number of discount rates is simulated by increasing from two to five, taking the computing power into account. Demand prediction and price optimisation models are performed using Python programs on Google Colab notebook. Moreover, price optimisation models are implemented using Python mip packages. Google Colab notebook hardware specifications are as follows: CPU with Intel(R) Xeon(R) CPU @ 2.30 GHz; the number of CPU and threads per core is 2; Memory is 13 GB and Disk Space is 108 GB.
In
Table 6, the results of the basic price optimisation model are presented. The first column in the table is the number of products, and the second column is the number of discount rate options. The third column represents the total number of all possible price combinations. Other columns represent the reductions in price combinations, demand prediction time, and price optimisation time as each model is applied to the simulation. Results from this table show that the total number of price combinations increases exponentially as the number of products in the category and the number of discount rates increases. As a result, the execution time of the demand prediction model is much longer than the price optimisation model, and the model can not be executed due to insufficient computational capability when applying 12 products and 5 discount rates.
The results obtained for Models 1 and 2 are given in
Table 7 and
Table 8, respectively. From
Table 7, it can be observed that the number of search spaces is reduced by approximately 50% or more from those in the basic price optimisation model as additional constraints were added to the model. As a result, both the demand prediction model and price optimisation model have reduced execution times. However, due to insufficient computational capability, the model would not be applicable to 12 products and 5 discount rates. The results from
Table 8 indicate that the number of search spaces dramatically decreased through fine-tuning the constraints. As a result, the demand prediction model could obtain forecast values in around 2.5 h for approximately 3 billion price combinations. Moreover, the price optimisation model could now run in seconds.
In summary, the results from
Table 6,
Table 7 and
Table 8 clearly show that adjusting the constraints can reduce the number of search spaces for the total number of price combinations. Indeed, it is impossible to reduce the model execution time in any other way than by constraints, as price optimisation requires forecast values from the demand prediction model. Nevertheless, fine-tuning constraints that represent various business rules can dramatically reduce the number of search spaces and hence execution time for demand prediction and price optimisation. This can be seen clearly in
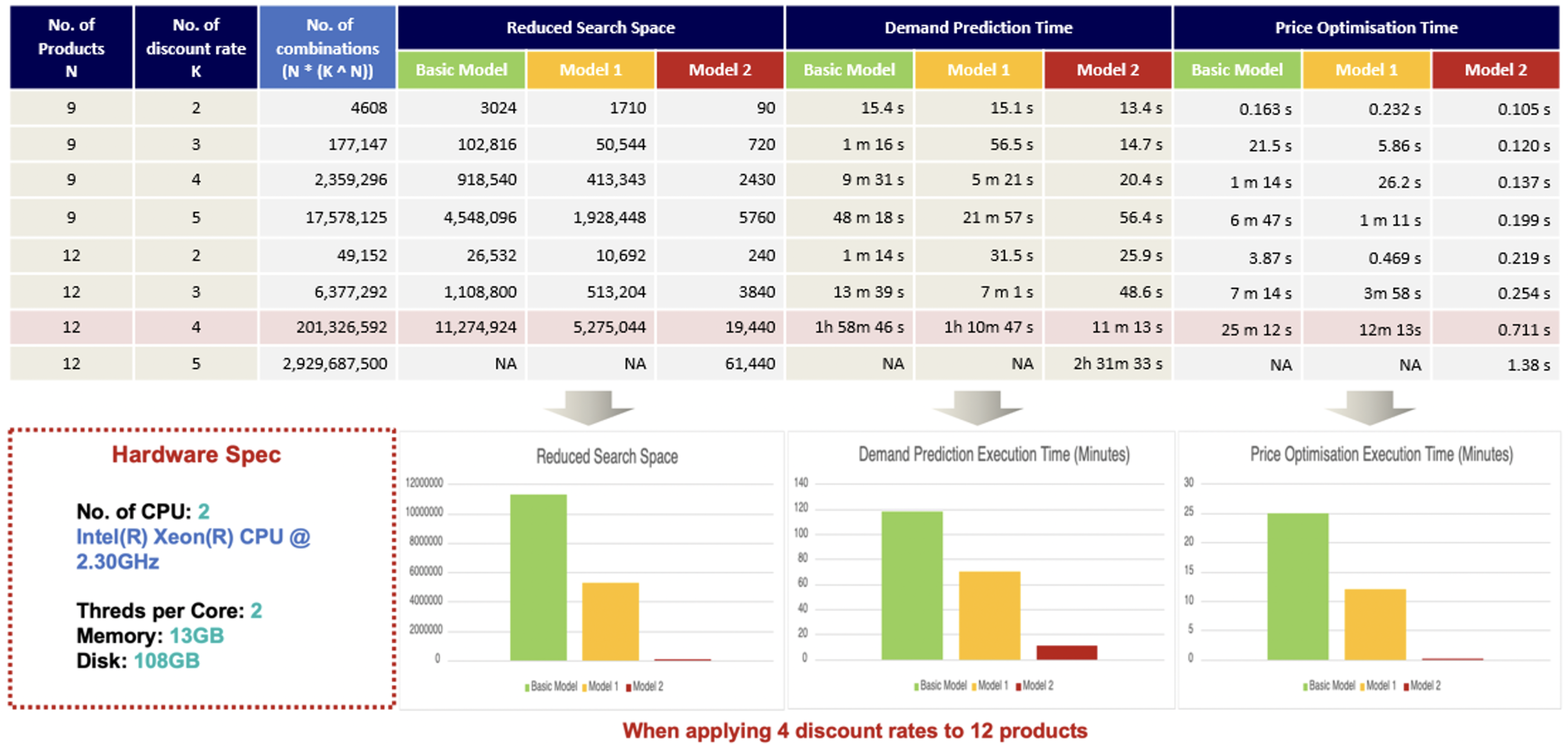
Figure 11.
The first column in this figure is the number of products, and the second column is the number of discount rate options. The third column represents the total number of all possible price combinations. Other columns represent the reduced price combinations, demand prediction time, and price optimisation time when each model is applied to the simulation. We can see that as more detailed business rules are applied, the number of search spaces and the execution time reduces drastically. For example, when applying four discount rates to 12 products, the search space can be reduced from 201,326,592 to 19,440 combinations if model 2 is used. Since the real-world business environment uses more rather than fewer business rules, the proposed algorithm can be used as an effective tool in demand forecasting and price optimisation for retail stores. Furthermore, demand forecasting takes much longer to run than price optimisation. For example, it takes 2.5 h as compared to just 1.38 s when applying 12 products and five discount rate options to model 2.
5. Discussion and Conclusions
Determining the optimal price of products is one of the best tools that strengthen the company’s competitiveness. Recently, the retail industry has been actively using price optimisation models to determine price, inventory level, and an assortment of products. In Fast Moving Consumer Goods (FMCG) industries with infinite inventory capacity, short shelf life, and high turnover rates, fast pricing plays an essential role in maximising sales and profits. However, there is only a limited number of research conducted on price optimisation models in the FMCG industries as it is not easy to detect, calculate, and reflect the substitution effect in the model.
In this paper, we have studied various demand prediction and price optimisation models and have developed new procedures for both models reflecting the demand correlation structure. In the proposed models, the substitution effect among products within the category has been considered. First, key features that affect product sales, price elasticity of products, and the substitution effect between products were identified through Exploratory Data Analysis (EDA). Then, demand prediction model was developed by including the price of all products and the critical features as input variables. The time series and some machine learning approaches with hyperparameter tuning and rolling forecasting methods have been applied to select each product’s best demand forecast. The best demand forecast reflecting the substitution effect was used as core input for the price optimisation model.
The developed procedure is a constraint programming model that identified only one price combination that maximises profit out of the many price combinations. The results showed that by including constraints representing various business rules in the proposed price optimisation procedure, the number of iterations and execution time can be significantly reduced. For instance, when applying 12 products and four discount rates, the price combinations to be performed decreased from 11,274,924 (basic model) to 19,440 (Model 2). Under the same conditions, the execution time for the demand prediction was reduced from 1 h 58 min 46 s (basic model) to 11 min 13 s (Model 2), and for the price optimisation from 25 min 12 s (basic model) to 0.711 s (Model 2).
The main goal of this study was to propose a systematic price decision support tool to perform the demand prediction and price optimisation models within an acceptable time frame. As the number of products in the category and discount rates increases, the number of input data combinations to be predicted increases exponentially. To solve this problem, we reduced the search space through the constraints before performing demand prediction and price optimisation. The more detailed constraints were applied, the more drastically reduced the number of price combinations.
Compared to most models reflecting the substitution effect with the consumer choice model or customer utility functions, this study intuitively reflects the substitution effect considering all possible price combinations of products in the product category using the data-driven method without assuming that the retailer knows the consumer’s preference for each product. Because consumer preferences for products are not easy to calculate accurately and may change over time, developed procedures will be beneficial for retailers who want to optimise prices using only available data without the assumption of consumer preference.
Another advantage of this study is that the best demand prediction model for each product can be updated after testing emerging superior models without modifying the price optimisation model structure. In summary, the systematic price decision support tool presented in this paper will enable the supply chain managers to identify the optimal discount rate for individual products in a timely manner, resulting in a net profit increase.
One of the limitations of this study is that only the assumed product cost was input into the model without considering other costs, such as promotion cost. Optimal profit is determined by selecting one value that maximises profits among all the price combinations during the sales week. Therefore, the optimal profit of the basic model is higher than that of Model 1 or Model 2, as the basic model has the highest number of price combinations. However, the study is not aimed at finding the highest optimal profit but at determining how the price combinations and execution time change based on the number of products, the number of discount rates, and the constraints required by the actual retail business. Therefore, rather than comparing the optimal profits for each case, we could simulate how retailers can maximise profits by adjusting discount rate options and business constraints using actual data in the future stage.
At this stage, we focused on developing systematic demand prediction and price optimisation procedures reflecting the substitution effects and the price changes of all the products and checking their effectiveness and availability in the retail industry. As future research, we aim to measure how much revenue can be improved by applying these procedures to the actual retail store and data. This approach also can be applied to various stores and cities to determine if the proposed procedures is robust to location change and store’s characteristics.
Another research that needs to be further developed in the future is to construct more accurate demand prediction and price optimisation models. This can be achieved by trying to stack or blend methods to enforce multiple machine learning approaches for demand prediction. Furthermore, the complement effect and/or competitive effect can be considered in future research. The income effect can also be encompassed in the model upon availability of information on consumer income data. Building an optimised computing environment that can reduce model performance time will also be an ongoing task.