Distributed Disturbance Observer-Based Containment Control of Multi-Agent Systems via an Event-Triggered Approach

Abstract

This paper studies the containment control problem of linear multi-agent systems (MASs) subject to external disturbances, where the communication graph is a directed graph with the followers being undirected connections. In order to save communication costs and energy consumption, a distributed disturbance observer-based event-triggered controller is employed based on the relative outputs of neighboring followers. Compared with conventional controllers, our observer-based controller utilizes the relative outputs of neighboring followers at the same triggered instant. Furthermore, it is shown that Zeno behavior can be avoided. Finally, the validity of our proposed methodology is demonstrated by a simulation example.

1. Introduction

Distributed cooperative control of multi-agent systems (MASs) has drawn a great deal of attention, mainly due to its wide applications in engineering systems, such as robotic systems, power sharing in DC microgrids and so forth. A rich body of results about the cooperative control of MASs has been reported, such as consensus control, leader-following tracking control and containment control [1,2,3,4,5,6,7,8]. Although there are many studies on leaderless consensus control and one-leader tracking control, in some practical applications, multiple leaders can complete certain tasks that are difficult for a single agent to complete. In the presence of multiple leaders, the containment control problem has been investigated, that is, all followers tend to the convex hull spanned by all the leaders. There is increasing research on the containment control of different MASs, including simple MASs of double-integrator MASs [9]; homogeneous linear MASs [6]; homogeneous discrete MASs [7]; and heterogeneous high-order MASs [10].

Note that disturbance widely exists in engineering applications and is usually unavoidable. In engineering, a system often works in an environment with various disturbances, which have a certain impact on the control accuracy, while the cooperative control of MASs has strict requirements on the control accuracy. Therefore, how to deal with the interference problem has always been the key to the control design of MASs. Some methods of disturbance rejection have been proposed, including anti-interference methods, disturbance observers, output regulation, and so on [11,12,13,14,15,16]. In [11], distributed event-based consensus protocols based on the disturbance observer are proposed for MASs with matched disturbances. In [13], a disturbance observer is designed for MASs under deterministic disturbances. Under the state or relative state measurements, disturbance rejection is used to estimate the disturbances [17,18,19,20]. However, when the state information is not available, it is necessary to design the output feedback control protocol [21,22]. Therefore, it is of great significance to use the output feedback method to study the containment control problem with external disturbances.

Nowadays, most communication networks between MASs are wireless communication. However, continuous communications among neighboring agents may be equipped with simple embedded microprocessors. High-frequency continuous sampling not only causes high system energy consumption but also leads to bandwidth constraints. Event-triggered control provides an effective strategy to solve this problem [23,24,25,26,27,28,29,30,31]. In this control strategy, by designing a reasonable trigger strategy, the amount of communication and data updates is reduced, but satisfactory performance is still maintained. Among them, the event-triggered strategy was first applied to MASs in the literature [23]. The consensus problem was addressed in [24,25,27,28,32,33] by using the event-triggered control strategy, and some papers considered leader-following consensus and other issues [34,35], while this paper focuses on its application to containment control problems (see [21,34,36,37]).

Enlightened by the above observations, we integrate a disturbance observer and distributed event-triggered output feedback controller for the containment control problem of linear MASs subject to external disturbances. The main contributions of this paper are at least threefold:

(1)

Compared with the works on the consensus [13], this work considers the containment control problem of linear MASs subject to external disturbances;

(2)

Compared with most existing strategies [13,38], and based on the event-triggered strategy, the containment control problem can be solved for linear MASs without the need for continuous communications;

(3)

The proposed disturbance observer-based event-triggered control uses the relative output information of each agent.

2. Preliminaries and Problem Formulation

2.1. Notations

Let ${\mathbf{0}}_m$ and ${\mathbf{0}}_{M\times M}$ be the $m\times 1$ column vector of all zeros and the $M\times M$ matrix of all zeros, respectively. For a matrix X, $X^T$ stands for its transpose, and $\parallel X\parallel$ denotes its Euclidean norm. For a square real matrix, $Z>0(Z\ge 0)$ means that Z is a positive definite (semi-definite), and $\lambda \left(Z\right)$ represents its eigenvalues. ⊗ stands for the matrix Kronecker product.

2.2. Graph Theory

A directed graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$, where $\mathcal{V}=\{1,2,\cdots ,N\}$, $\mathcal{E}\subset \mathcal{V}\times \mathcal{V}$ are the node set and the edge set, respectively. For an edge, $(i,j)\in \mathcal{E}$ means i is a neighbor of j. The self-loop is not considered in this paper, that is, $(i,i)\notin \mathcal{E}$ for any $i\in \mathcal{V}$. For an undirected graph, $(i,j)\in \mathcal{E}$ implies $(j,i)\in \mathcal{E}$. A directed path from node i to node j is a sequence of nodes of the form $i,...,j$.

A weighted adjacency matrix $\mathcal{A}=\left[a_{ij}\right]\in {\mathbb{R}}^{N\times N}$ is given by $a_{ij}=0$, $a_{ij}>0$ if $(i,j)\in \mathcal{E}$. The Laplacian matrix of $\mathcal{G}$ is defined as $L=\left[l_{ij}\right]\in {\mathbb{R}}^{N\times N}$, where $l_{ii}={\sum }_{j\ne i}{a}_{ij}$ and $l_{ij}=-a_{ij}$, where $i\ne j$.

In this paper, suppose that there are $M(M<N)$ followers and $N-M$ leaders. Let $\mathfrak{L}\triangleq \{M+1,...,N\}$ and $\mathfrak{F}\triangleq \{1,...,M\}$ denote the leader set and the follower set, respectively. The communication topology among the N agents is represented by a directed graph ${\mathcal{G}}_{\mathfrak{F}\cup \mathfrak{L}}$. Note that, here, the leaders do not receive any information. Thus, the Laplacian matrix of ${\mathcal{G}}_{\mathfrak{F}\cup \mathfrak{L}}$ can be partitioned as $L\triangleq \left[\begin{array}{cc}{L}_{\mathfrak{F}}& L_{\mathfrak{L}}\\ {\mathbf{0}}_{(N-M)\times M}& {\mathbf{0}}_{(N-M)\times (N-M)}\end{array}\right]$, where $L_{\mathfrak{F}}\in {\mathbb{R}}^{M\times M}$ and $L_{\mathfrak{L}}\in {\mathbb{R}}^{M\times (N-M)}$.

2.3. Problem Statement

Consider N agents of a linear MAS with a directed graph ${\mathcal{G}}_{\mathfrak{F}\cup \mathfrak{L}}$. The dynamics of the ith agent are described as follows:

$$\begin{array}{cc}\hfill {\dot{x}}_i& =A{x}_i+B{u}_i+D{d}_i,i\in \mathfrak{F},\hfill \end{array}$$

(1a)

$$\begin{array}{cc}\hfill {\dot{x}}_i& =A{x}_i,i\in \mathfrak{L},\hfill \end{array}$$

(1b)

$$\begin{array}{cc}\hfill y_i& =C{x}_i,i\in \mathfrak{F}\cup \mathfrak{L}.\hfill \end{array}$$

(1c)

where $x_i\in {\mathbb{R}}^n$, $u_i\in {\mathbb{R}}^m$ and $y_i\in {\mathbb{R}}^q$ are the ith agent’s state, control input and output state, respectively. A, B, C and D are known constant matrices of appropriate dimensions. $d_i\in {\mathbb{R}}^n$ is a disturbance whose dynamics are given as

$${\dot{d}}_i=S{d}_i,i\in \mathfrak{F},$$

(2)

with S being a known constant matrix.

To proceed, we also need the assumption and Lemma as follows.

Assumption 1

([11]). $(A,B)$ is stabilizable, and $(A,C)$ is detectable.

Assumption 2

([11]). The disturbance is matched, i.e., there exists a matrix F, such that $D=BF$.

Assumption 3

([11]). The eigenvalues of the matrix S are on the imaginary axis, and the pair $(S,D)$ is observable.

Remark 1.

In some cases, Assumption 2 regarding matched disturbances can be relaxed, as based on output regulation theory [13], mismatched disturbances under uncertain conditions can be transformed into matched disturbances. Assumption 3 is typically used for disturbance rejection. Assume that $(S,D)$ is observable, as any unobservable component will not affect the system state.

Definition 1

((Containment control problem) [6]). Given the MASs (1) and a directed graph ${\mathcal{G}}_{\mathfrak{F}\cup \mathfrak{L}}$, find a certain distributed controller so that the followers asymptotically converge to the convex hull spanned by the states of the leaders, that is, ${lim}_{t\to \infty }\parallel x_{\mathfrak{F}}\left(t\right)+(L_{\mathfrak{F}}^{-1}{L}_{\mathfrak{L}}\otimes I_n)x_{\mathfrak{L}}\left(t\right)\parallel =0$.

Assumption 4

([6]). Under the digraph ${\mathcal{G}}_{\mathfrak{F}\cup \mathfrak{L}}$, for each follower $i\in \mathfrak{F}$, there exists at least one leader $k\in \mathfrak{L}$ that has a directed path to the follower.

Lemma 1

([6]). Under Assumption 4, all the eigenvalues of $L_{\mathfrak{F}}$ have positive real parts, $-L_{\mathfrak{F}}^{-1}{L}_{\mathfrak{L}}$ is non-negative and $-L_{\mathfrak{F}}^{-1}{L}_{\mathfrak{L}}{\mathit{1}}_{N-M}={\mathit{1}}_M$.

3. Main Results

Assume that the states and relative input measurements are not available for all the followers; then, each follower can only obtain the relative output measurements. Let ${\phi }_i$ be the relative output measurements of ith follower as follows:

$${\phi }_i\left(t\right)=\sum _{j\in \mathfrak{F}\cup \mathfrak{L}}{a}_{ij}(y_i\left(t\right)-y_j\left(t\right)),$$

(3)

Similarly, the relative input measurements of the ith follower are as follows:

$${\chi }_i\left(t\right)=\sum _{j\in \mathfrak{F}\cup \mathfrak{L}}{a}_{ij}(x_i\left(t\right)-x_j\left(t\right)).$$

(4)

By (3) and (4), we have ${\phi }_i\left(t\right)=C{\chi }_i\left(t\right)$.

Let $x_{\mathfrak{F}}\triangleq {[x_1^T,x_2^T,...,x_M^T]}^T\in {\mathbb{R}}^{nM}$, $x_{\mathfrak{L}}\triangleq {[x_{M+1}^T,x_{M+2}^T,...,x_N^T]}^T\in {\mathbb{R}}^{n(N-M)}$ and $\chi \triangleq {[{\chi }_1^T,{\chi }_2^T,...,{\chi }_M^T]}^T\in {\mathbb{R}}^{nM}$. Then, it follows that the definition of the relative input measurements vector can be written as

$$\chi \left(t\right)=(L_{\mathfrak{F}}\otimes I_n)x_{\mathfrak{F}}+(L_{\mathfrak{L}}\otimes I_n)x_{\mathfrak{L}}.$$

(5)

Note that the followers can only obtain the relative output measurements. Based on the relative output information, we propose a distributed disturbance observer-based event-triggered containment controller for agent $i\in \mathfrak{F}$ with form

$$\begin{array}{cc}\hfill & {\dot{\widehat{d}}}_i=S{\widehat{d}}_i+G{\phi }_i\left(t_k^i\right),\hfill \\ \hfill & w_i=F{\widehat{d}}_i+E{\phi }_i\left(t_k^i\right),\hfill \\ \hfill & u_i=-w_i,i\in \mathfrak{F},t\in [t_k^i,t_{k+1}^i),\hfill \end{array}$$

(6)

where ${\widehat{d}}_i\in {\mathbb{R}}^s$ and $w_i\in {\mathbb{R}}^m$ are the estimates of the disturbance and the output variable, respectively. $S,G,F$ and E are gain matrices to be determined, and $t_k^i$ is the kth event-triggered instant of agent $i\in \mathfrak{F}$. The next event-triggered instant $\{t_k^i,k=0,1,...\}$ is defined by $t_{k+1}^i\triangleq min\{t>t_k^i\mid f_i(e_i,{\chi }_i)>0\}$, where the triggering function $f_i(·)$ is to be designed later, and the measurement error $e_i\left(t\right)$ for agent $i\in \mathfrak{F}$ is defined as

$$e_i\left(t\right)={\chi }_i\left(t_k^i\right)-{\chi }_i\left(t\right),t\in [t_k^i,t_{k+1}^i).$$

When the triggering condition is satisfied, an event at $t=t_k^i$ is triggered for agent $i\in \mathfrak{F}$, and $e_i\left(t\right)$ is reset to zero.

Remark 2.

Compared with the general MASs studied in the literature [33], this paper studies the MASs under the condition of disturbance and adopts the distributed event-triggered controller based on disturbance observers to solve the containment control problem. Many works in the literature do not consider the situation of systems with unknown disturbance, which occurs in most practical engineering applications, making the problem more complex. This article is closer to the complexity of the actual situation and more challenging.

Remark 3.

With the event-triggered strategy introduced in controller (6), this paper shows that the containment control problem can be solved. For agent i, the event-triggered instants are $\{t_k^i,k=0,1,...\}$. At each event-triggered instant, ${\phi }_i\left(t\right)$ is sampled by agent i, and its controller is updated accordingly. Noted that in (6), for agent i, all of the outputs required from its neighbors’ output are included in ${\phi }_i\left(t\right)$, which is only updated at its event-triggered instants.

Define ${\epsilon }_i={\widehat{d}}_i-d_i$, $i\in \mathfrak{F}$. It follows from (1)–(6) that

$$\begin{array}{cc}\hfill {\dot{x}}_i& =A{x}_i+B{u}_i+D{d}_i=A{x}_i-B{w}_i+D{d}_i\hfill \\ & =A{x}_i-BF{\widehat{d}}_i-BEC({\chi }_i+e_i)+D{d}_i\hfill \\ & =A{x}_i-BF{\epsilon }_i-BEC{\chi }_i-BEC{e}_i.\hfill \end{array}$$

For $i\in \mathfrak{F}\cup \mathfrak{L}$,

$$\begin{array}{cc}\hfill {\dot{x}}_{\mathfrak{F}}=& (I_{\mathfrak{F}}\otimes A)x_{\mathfrak{F}}-(I_{\mathfrak{F}}\otimes BF)\epsilon \hfill \\ & -(I_{\mathfrak{F}}\otimes BEC)\chi -(I_{\mathfrak{F}}\otimes BEC)e\hfill \\ \hfill {\dot{x}}_{\mathfrak{L}}=& (I_{\mathfrak{L}}\otimes A)x_{\mathfrak{L}},\hfill \end{array}$$

(7)

where $e\triangleq {[e_1^T,e_2^T,...,e_N^T]}^T\in {\mathbb{R}}^{nN}$, and $\epsilon \triangleq {[{\epsilon }_1^T,{\epsilon }_2^T,...,{\epsilon }_N^T]}^T\in {\mathbb{R}}^{sN}$.

Using (7) for (5), it follows that

$$\begin{array}{cc}\hfill \dot{\chi }=& (L_{\mathfrak{F}}\otimes I_N){\dot{x}}_{\mathfrak{F}}+(L_{\mathfrak{L}}\otimes I_N){\dot{x}}_{\mathfrak{L}}\hfill \\ \hfill =& (L_{\mathfrak{F}}\otimes I_N)[(I_{\mathfrak{F}}\otimes A)x_{\mathfrak{F}}-(I_{\mathfrak{F}}\otimes BF)\epsilon \hfill \\ & -(I_{\mathfrak{F}}\otimes BEC)\chi -(I_{\mathfrak{F}}\otimes BEC)e]+(L_{\mathfrak{L}}\otimes I_N)(I_{\mathfrak{L}}\otimes A)x_{\mathfrak{L}}\hfill \\ \hfill =& (I_{\mathfrak{F}}\otimes A-L_{\mathfrak{F}}\otimes BEC)\chi -(L_{\mathfrak{F}}\otimes BF)\epsilon -(L_{\mathfrak{F}}\otimes BEC)e.\hfill \end{array}$$

(8)

Using (1) and (6), one can obtain that

$$\begin{array}{cc}\hfill \dot{\epsilon }=& {\dot{\widehat{d}}}_i-{\dot{d}}_i\hfill \\ \hfill =& (I_{\mathfrak{F}}\otimes S)\epsilon -(L_{\mathfrak{F}}\otimes GC)(\chi +e).\hfill \end{array}$$

(9)

Next, Algorithm 1 is presented with procedure of controller implementation.

Algorithm 1. Distributed Disturbance Observer-based Event-triggered Control Algorithm

Under Assumptions 1–4, for disturbance signals in (2), the distributed disturbance observer-based event-triggered controller (6) can be constructed using the following form:

(i) Solve the following Linear matrix inequality (LMI): $$A^{T}P+PA-\theta PB{B}^{T}P+\kappa I<0.$$ (10) to obtain one solution $P>0$. Then, choose the matrix $EC=B^{T}P$.

(ii) Take a symmetric matrix $\widehat{P}\in {\mathbb{R}}^{s\times s}>0$, $S^T\widehat{P}+\widehat{P}S=-I$.

(iii) Select positive constants $\kappa ,\theta$ as the gains to be designed in the proof of Theorem 1.

Theorem 1.

Under Assumptions 1–4, consider the MAS (1) and disturbance signals (2) with the distributed disturbance observer-based event-triggered controller (6) using Algorithm 1, where the triggered times $t_k^i$ is determined:

$$t_{k+1}^i\triangleq min\{t>t_k^i|\parallel e_i\parallel ={\gamma }_i\parallel {\chi }_i\parallel \},$$

(11)

where ${\gamma }_i=\frac{{\sigma }_i}{{\rho }_3{\overline{\lambda }}^2}$ and the gains ${\rho }_3,{\sigma }_i$ will be defined in the proof. Then, protocol (6) solves the containment control problem.

Proof of Theorem 1.

Let $\eta ={[{\chi }^T,{\epsilon }^T]}^T$. Construct the following Lyapunov function candidate:

$$V={\eta }^T\overline{P}\eta ,$$

(12)

where $\overline{P}\triangleq \left[\begin{array}{cc}{I}_{\mathfrak{F}}\otimes P& 0\\ 0& \omega I_{\mathfrak{F}}\otimes \widehat{P}\end{array}\right]>0$, $\omega >0$ will be determined later. Evidently, $\overline{P}$ is definite-positive, so V is also definite-positive.

The time derivative of $V\left(t\right)$ along the trajectory of (8) and (9) is given by

$$\begin{array}{cc}\hfill & \dot{V}\left(t\right)\hfill \\ \hfill =& {\chi }^T[I_{\mathfrak{F}}\otimes (A^{T}P+PA)-2(L_{\mathfrak{F}}\otimes PB{B}^{T}P)]\chi \hfill \\ & -e^T(L_{\mathfrak{F}}\otimes PB{B}^{T}P)\chi -{\chi }^T(L_{\mathfrak{F}}\otimes PB{B}^{T}P)e\hfill \\ & -{\epsilon }^T(L_{\mathfrak{F}}\otimes D^{T}P)\chi -{\chi }^T(L_{\mathfrak{F}}\otimes PD)\epsilon \hfill \\ & -\omega {\epsilon }^T(I_{\mathfrak{F}}\otimes (S^T\widehat{P}+\widehat{P}S))\epsilon \hfill \\ & -\omega e^T(L_{\mathfrak{F}}\otimes C^T{G}^T\widehat{P})\epsilon -\omega {\chi }^T(L_{\mathfrak{F}}\otimes C^T{G}^T\widehat{P})\epsilon \hfill \\ & -\omega {\epsilon }^T(L_{\mathfrak{F}}\otimes \widehat{P}GC)\chi -\omega {\epsilon }^T(L_{\mathfrak{F}}\otimes \widehat{P}GC)e.\hfill \end{array}$$

(13)

Under Assumption 4 and Lemma 1, choose a unitary matrix $U\in {\mathbb{C}}^{M\times M}$, $U^H{L}_{\mathfrak{F}}U=\Lambda$, where $\Lambda$ is an upper-triangular matrix with ${\lambda }_i,i=1,...,M$, as its diagonal entries.

Let $\xi \triangleq (U^H\otimes I_n)\chi ={[{\xi }_1^T,{\xi }_2^T,...,{\xi }_M^T]}^T\in {\mathbb{R}}^{nM}$, $\overline{\epsilon }=(U^H\otimes I_s)\epsilon ={[{\overline{\epsilon }}_1^T,{\overline{\epsilon }}_2^T,...,{\overline{\epsilon }}_M^T]}^T\in {\mathbb{R}}^{sM}$ and $\overline{e}=(U^T\otimes I_n)e={[{\overline{e}}_1^T,{\overline{e}}_2^T,...,{\overline{e}}_M^T]}^T\in {\mathbb{R}}^{nM}$.

Then, it follows from (13) that

$$\begin{array}{cc}\hfill & \dot{V}\left(t\right)\hfill \\ \hfill =& {\xi }^T[I_{\mathfrak{F}}\otimes (A^{T}P+PA)-2(\Lambda \otimes PB{B}^{T}P)]\xi \hfill \\ & -{\overline{e}}^T(\Lambda \otimes PB{B}^{T}P)\xi -{\xi }^T(\Lambda \otimes PB{B}^{T}P)\overline{e}\hfill \\ & -{\overline{\epsilon }}^T(\Lambda \otimes D^{T}P)\xi -{\xi }^T(\Lambda \otimes PD)\overline{\epsilon }-\omega {\epsilon }^T\epsilon \hfill \\ & -\omega {\overline{e}}^T(\Lambda \otimes C^T{G}^T\widehat{P})\overline{\epsilon }-\omega {\xi }^T(\Lambda \otimes C^T{G}^T\widehat{P})\overline{\epsilon }\hfill \\ & -\omega {\overline{\epsilon }}^T(\Lambda \otimes \widehat{P}GC)\xi -\omega {\overline{\epsilon }}^T(\Lambda \otimes \widehat{P}GC)\overline{e}\hfill \\ \hfill =& \sum _{i=1}^M{\xi }_i^T(A^{T}P+PA-2{\lambda }_{i}PB{B}^{T}P){\xi }_i\hfill \\ & -\sum _{i=1}^M{\overline{e}}_i^T\left({\lambda }_{i}PB{B}^{T}P\right){\xi }_i-\sum _{i=1}^M{\xi }_i^T\left({\lambda }_{i}PB{B}^{T}P\right){\overline{e}}_i\hfill \\ & -\sum _{i=1}^M{\lambda }_i{\overline{\epsilon }}_i^T(D^{T}P+\omega \widehat{P}GC){\xi }_i-\sum _{i=1}^M{\lambda }_i{\xi }_i^T(PD+\omega C^T{G}^T\widehat{P}){\overline{\epsilon }}_i\hfill \\ & -\omega \sum _{i=1}^M{\overline{e}}_i^T\left({\lambda }_i{C}^T{G}^T\widehat{P}\right){\overline{\epsilon }}_i-\omega \sum _{i=1}^M{\overline{\epsilon }}_i^T\left({\lambda }_i\widehat{P}GC\right){\overline{e}}_i-\omega {\epsilon }^T\epsilon .\hfill \end{array}$$

(14)

For any $x,y\in {\mathbb{R}}^n$ and $\beta >0$, we use Young’s inequalities $x^{T}y\le \frac{\beta }{2}{\parallel x\parallel }^2+\frac{1}{2\beta }{\parallel y\parallel }^2$ ([24]), yields,

$$\begin{array}{cc}\hfill & -{\overline{e}}_i^T\left({\lambda }_{i}PB{B}^{T}P\right){\xi }_i\hfill \\ \hfill \le & \frac{{\lambda }_i\parallel PB{B}^{T}P\parallel }{2{\beta }_1}\parallel {\xi }_i{\parallel }^2+\frac{{\beta }_1{\lambda }_i\parallel PB{B}^{T}P\parallel }{2}{\parallel {\overline{e}}_i\parallel }^2.\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & -{\xi }_i^T\left({\lambda }_{i}PB{B}^{T}P\right){\overline{e}}_i\hfill \\ \hfill \le & \frac{{\lambda }_i\parallel PB{B}^{T}P\parallel }{2{\beta }_1}\parallel {\overline{e}}_i{\parallel }^2+\frac{{\beta }_1{\lambda }_i\parallel PB{B}^{T}P\parallel }{2}{\parallel {\xi }_i\parallel }^2.\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & -{\lambda }_i{\overline{\epsilon }}_i^T(D^{T}P+\omega \widehat{P}GC){\xi }_i\hfill \\ \hfill \le & \frac{{\lambda }_i\parallel D^{T}P+\omega \widehat{P}GC\parallel }{2{\beta }_2}\parallel {\xi }_i{\parallel }^2+\frac{{\beta }_2{\lambda }_i\parallel D^{T}P+\omega \widehat{P}GC\parallel }{2}{\parallel {\overline{\epsilon }}_i\parallel }^2,\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & -{\lambda }_i{\xi }_i^T(PD+\omega C^T{G}^T\widehat{P}){\overline{\epsilon }}_i\hfill \\ \hfill \le & \frac{{\lambda }_i\parallel PD+\omega C^T{G}^T\widehat{P}\parallel }{2{\beta }_2}\parallel {\overline{\epsilon }}_i{\parallel }^2+\frac{{\beta }_2{\lambda }_i\parallel PD+\omega C^T{G}^T\widehat{P}\parallel }{2}{\parallel {\xi }_i\parallel }^2,\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & -{\overline{e}}_i^T\left({\lambda }_i{C}^T{G}^T\widehat{P}\right){\overline{\epsilon }}_i\hfill \\ \hfill \le & \frac{{\lambda }_i\parallel C^T{G}^T\widehat{P}\parallel }{2{\beta }_3}\parallel {\overline{\epsilon }}_i{\parallel }^2+\frac{{\lambda }_i{\beta }_3\parallel C^T{G}^T\widehat{P}\parallel }{2}{\parallel {\overline{e}}_i\parallel }^2,\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & -{\overline{\epsilon }}_i^T\left({\lambda }_i\widehat{P}GC\right){\overline{e}}_i\hfill \\ \hfill \le & \frac{{\lambda }_i\parallel \widehat{P}GC\parallel }{2{\beta }_3}\parallel {\overline{e}}_i{\parallel }^2+\frac{{\lambda }_i{\beta }_3\parallel \widehat{P}GC\parallel }{2}{\parallel {\overline{\epsilon }}_i\parallel }^2,\hfill \end{array}$$

(20)

where ${\beta }_1$, ${\beta }_2$ and ${\beta }_3$ are positive constants.

Let $\underline{\lambda }={min}_{i=1,...,M}\left\{Re\left({\lambda }_i\right)\right\}$ and $\overline{\lambda }={max}_{i=1,...,M}\left\{Re\left({\lambda }_i\right)\right\}$, where ${\lambda }_i,i=\{1,...,M\}$ are the eigenvalues of $L_{\mathfrak{F}}$. When $0<\theta \le 2\underline{\lambda }$ and under Algorithm 1, it follows from (7), (15)–(20) that

$$\begin{array}{cc}\hfill & \dot{V}\left(t\right)\hfill \\ \hfill \le & -\kappa \sum _{i=1}^M\parallel {\xi }_i{\parallel }^2-\omega \sum _{i=1}^M\parallel {\overline{\epsilon }}_i{\parallel }^2+\sum _{i=1}^M{\rho }_1{\lambda }_i^2{\parallel {\xi }_i\parallel }^2\hfill \\ & +{\rho }_2{\overline{\lambda }}^2\sum _{i=1}^M\parallel {\overline{\epsilon }}_i{\parallel }^2+\sum _{i=1}^M{\rho }_3{\overline{\lambda }}^2{\parallel {\overline{e}}_i\parallel }^2\hfill \\ \hfill =& -\sum _{i=1}^M(\kappa -{\rho }_1)\parallel {\chi }_i{\parallel }^2-\sum _{i=1}^M(\omega -{\rho }_2{\overline{\lambda }}^2)\parallel {\epsilon }_i{\parallel }^2+\sum _{i=1}^M{\rho }_3{\overline{\lambda }}^2{\parallel e_i\parallel }^2,\hfill \end{array}$$

(21)

where ${\rho }_1=\frac{\parallel PB{B}^{T}P\parallel }{2{\beta }_1}+\frac{{\beta }_1\parallel PB{B}^{T}P\parallel }{2}+\frac{\parallel D^{T}P+\omega \widehat{P}GC\parallel }{2{\beta }_2}+\frac{{\beta }_2\parallel PD+\omega C^T{G}^T\widehat{P}\parallel }{2}$, ${\rho }_2=\frac{{\beta }_2\parallel D^{T}P+\omega \widehat{P}GC\parallel }{2}+\frac{{\lambda }_i\parallel PD+\omega C^T{G}^T\widehat{P}\parallel }{2{\beta }_2}+\frac{\parallel C^T{G}^T\widehat{P}\parallel }{2{\beta }_3}+\frac{{\beta }_3\parallel \widehat{P}GC\parallel }{2}$ and ${\rho }_3=\frac{{\beta }_1\parallel PB{B}^{T}P\parallel }{2}+\frac{\parallel PB{B}^{T}P\parallel }{2{\beta }_1}+\frac{{\beta }_3\parallel C^T{G}^T\widehat{P}\parallel }{2}+\frac{\parallel \widehat{P}GC\parallel }{2{\beta }_3}$.

Then, by choosing ${\sigma }_i$ and $\kappa$, the following condition is enforced:

$$\parallel e_i{\parallel }^2\le \frac{{\sigma }_i}{{\rho }_3{\overline{\lambda }}^2}{\parallel {\chi }_i\parallel }^2,$$

where choosing $0<{\sigma }_i<\kappa -{\rho }_1$. It is noted that ${\gamma }_i=\sqrt{\frac{{\sigma }_i}{{\rho }_3{\overline{\lambda }}^2}}$, and choosing ${\sigma }_i<{\rho }_3{\overline{\lambda }}^2$, so ${\gamma }_i<1$ can be guaranteed.

From (21) and choosing $\omega \gg 0$ such that $\omega \ge {\rho }_2{\overline{\lambda }}^2$, one can obtain that

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)\le & -\sum _{i=1}^N(\kappa -{\rho }_1-{\sigma }_i){\parallel {\chi }_i\parallel }^2\hfill \\ & -(\omega -{\rho }_2{\overline{\lambda }}^2)\sum _{i=1}^N{\parallel {\epsilon }_i\parallel }^2\le 0.\hfill \end{array}$$

Thus, by the definition of $V\left(t\right)$, $\dot{V}\left(t\right)=0$ implies that ${\chi }_i\left(t\right)=0$. According to [39], it implies that ${lim}_{t\to \infty }\parallel x_{\mathfrak{F}}\left(t\right)+(L_{\mathfrak{F}}^{-1}{L}_{\mathfrak{L}}\otimes I_n)x_{\mathfrak{L}}\left(t\right)\parallel =0$. Therefore, the containment control problem stated in Definition 1 is solved. □

Feasibility Analysis

In this section, the development analyzes the feasibility of the proposed controller (6) by excluding Zeno behavior (i.e., in the event time defined in (11) within a finite time interval, an infinite number of triggers occur). The result is summarized in the following theorem.

Theorem 2.

Consider the linear MAS (1), controller (6) and triggering condition (11). No agent will exhibit Zeno behavior.

Proof of Theorem 2.

Without loss of generality, to prove that the Zeno behavior does not exist, it is only necessary to prove that $\tau \triangleq t_{k+1}^i-t_k^i>0$ has a positive lower bound.

According to the definition of $e_i\left(t\right)$, there exists $\mid \parallel {\chi }_i\left(t_k^i\right)\parallel -\parallel {\chi }_i\left(t\right)\parallel \mid \le \parallel e_i\left(t\right)\parallel$. Using (11), we have

$$\frac{\parallel {\chi }_i\left(t_k^i\right)\parallel }{1+{\gamma }_i}\le \parallel {\chi }_i\left(t\right)\parallel \le \frac{\parallel {\chi }_i\left(t_k^i\right)\parallel }{1-{\gamma }_i}.$$

(22)

By substituting (8) with the time derivative of $\parallel e_i\left(t\right)\parallel$ over the interval $[t_k^i,t_{k+1}^i)$, we can obtain that

$$\begin{array}{cc}\hfill & \frac{d}{dt}\parallel e_i\left(t\right)\parallel \hfill \\ \hfill \le & \parallel {\dot{e}}_i\left(t\right)\parallel =\parallel -{\dot{\chi }}_i\left(t\right)\parallel \hfill \\ \hfill =& \parallel -A{\chi }_i+BEC\sum _{j\in {\mathcal{N}}_i}{a}_{ij}({\chi }_i-{\chi }_j)+BF\sum _{j\in {\mathcal{N}}_i}{a}_{ij}({\epsilon }_i-{\epsilon }_j)\hfill \\ & +BEC\sum _{j\in {\mathcal{N}}_i}{a}_{ij}(e_i-e_j)\parallel \hfill \\ \hfill \le & \parallel A+BEC\left(\right|{\mathcal{N}}_i|+1)\parallel \parallel e_i\left(t\right)\parallel +\parallel BF\left(\right|{\mathcal{N}}_i|+1)\parallel \parallel {\epsilon }_i\left(t\right)\parallel \hfill \\ & +\parallel A{\chi }_i\left(t_k^i\right)+BEC\sum _{j\in {\mathcal{N}}_i}{a}_{ij}({\chi }_i\left(t_k^i\right)-{\chi }_j\left(t_k^i\right))\parallel .\hfill \end{array}$$

(23)

From (23), we can obtain that $\parallel e_i\left(t\right)\parallel$ will not approach zero unless $\parallel {\epsilon }_i\left(t\right)\parallel$ approaches zero, which implies the existence of $0<R<\infty$, such that $\frac{\parallel {\epsilon }_i\left(t\right)\parallel }{\parallel e_i\left(t\right)\parallel }<R$. Substituting (5) and (9) into (23), one has

$$\frac{d}{dt}\parallel e_i\left(t\right)\parallel \le {\zeta }_i\parallel e_i\left(t\right)\parallel +{\varphi }_k^i,$$

(24)

where ${\zeta }_i=\parallel A+BEC\left(\right|{\mathcal{N}}_i|+1)\parallel$ and ${\varphi }_k^i=\parallel BF\left(\right|{\mathcal{N}}_i|+1)\parallel R+{max}_{t\in [t_k^i,t_{k+1}^i]}\parallel A{\chi }_i\left(t_k^i\right)+BEC{\sum }_{j\in {\mathcal{N}}_i}{a}_{ij}({\chi }_i\left(t_k^i\right)-{\chi }_j\left(t_k^i\right))\parallel$

Then, it follows that

$$\parallel e_i\left(t\right)\parallel \le \frac{{\varphi }_k^i}{{\zeta }_i}\left[exp\left({\zeta }_i(t-t_k^i)\right)-1\right].$$

(25)

At this point, we need to present a sufficient condition $\parallel e_i\left(t\right)\parallel \le \frac{{\gamma }_i}{\sqrt{2+2{\gamma }_i^2}}\parallel {\chi }_i\left(t_k^i\right)\parallel$ that ensures that the triggering condition (11) holds.

Let $s_k^i=\frac{{\gamma }_i}{\sqrt{2+2{\gamma }_i^2}}\parallel {\chi }_i\left(t_k^i\right)\parallel$. Using (24) gives

$$\parallel e_i\left(t_{k+1}^i\right)\parallel =s_k^i\le \frac{{\varphi }_k^i}{{\zeta }_i}\left[exp\left({\zeta }_i(t_{k+1}^i-t_k^i)\right)-1\right],$$

which yields $t_{k+1}^i-t_k^i\ge (1/{\zeta }_i)ln({\zeta }_i{s}_k^i/{\varphi }_k^i+1)$.

Next, we will discuss two cases.

The first case is when ${\chi }_i\left(t_k^i\right)\ne 0$. Since ${\chi }_i\left(t_k^i\right)\ne 0$, it can be seen that $s_k^i>0$. Thus, $t_{k+1}^i-t_k^i=(1/{\zeta }_i)ln({\zeta }_i{s}_k^i/{\varphi }_k^i+1)>0$.

The second case is when ${\chi }_i\left(t_k^i\right)=0$ as $k\to \infty$. Then, from (22), one has ${\chi }_i\left(t\right)=0$, and thus,

$$\begin{array}{cc}\hfill {\dot{\chi }}_i=& A{\chi }_i+BEC\sum _{j\in {\mathcal{N}}_i}{a}_{ij}({\chi }_i-{\chi }_j)-BF\sum _{j\in {\mathcal{N}}_i}{a}_{ij}({\epsilon }_i-{\epsilon }_j)\hfill \\ & +BEC\sum _{j\in {\mathcal{N}}_i}{a}_{ij}({\chi }_i\left(t_k^i\right)-{\chi }_j\left(t_{k\left(t\right)}^i\right))\hfill \\ \hfill =& 0.\hfill \end{array}$$

(26)

By simple transposition (22), we obtain

$$\underset{k\to \infty }{lim}\frac{\parallel {\chi }_i\left(t\right)\parallel }{\parallel {\chi }_i\left(t_k^i\right)\parallel }\le \frac{1}{1-{\gamma }_i}.$$

(27)

In light of (26), we obtain

$${\varphi }_k^i\le {\zeta }_i\parallel {\chi }_i\left(t\right)\parallel +\frac{2-{\gamma }_i}{1-{\gamma }_i}{\zeta }_i\parallel {\chi }_i\left(t\right)\parallel .$$

(28)

According to (27) and (28), the same as those in [24,40], we have

$$\underset{k\to \infty }{lim}(t_{k+1}^i-t_k^i)\ge \frac{1}{{\zeta }_i}ln(\frac{{\gamma }_i(2-{\gamma }_i)}{(1-{\gamma }_i)\sqrt{2+2{\gamma }_i^2}}+1).$$

Consequently, Zeno behavior is excluded for all the agents. □

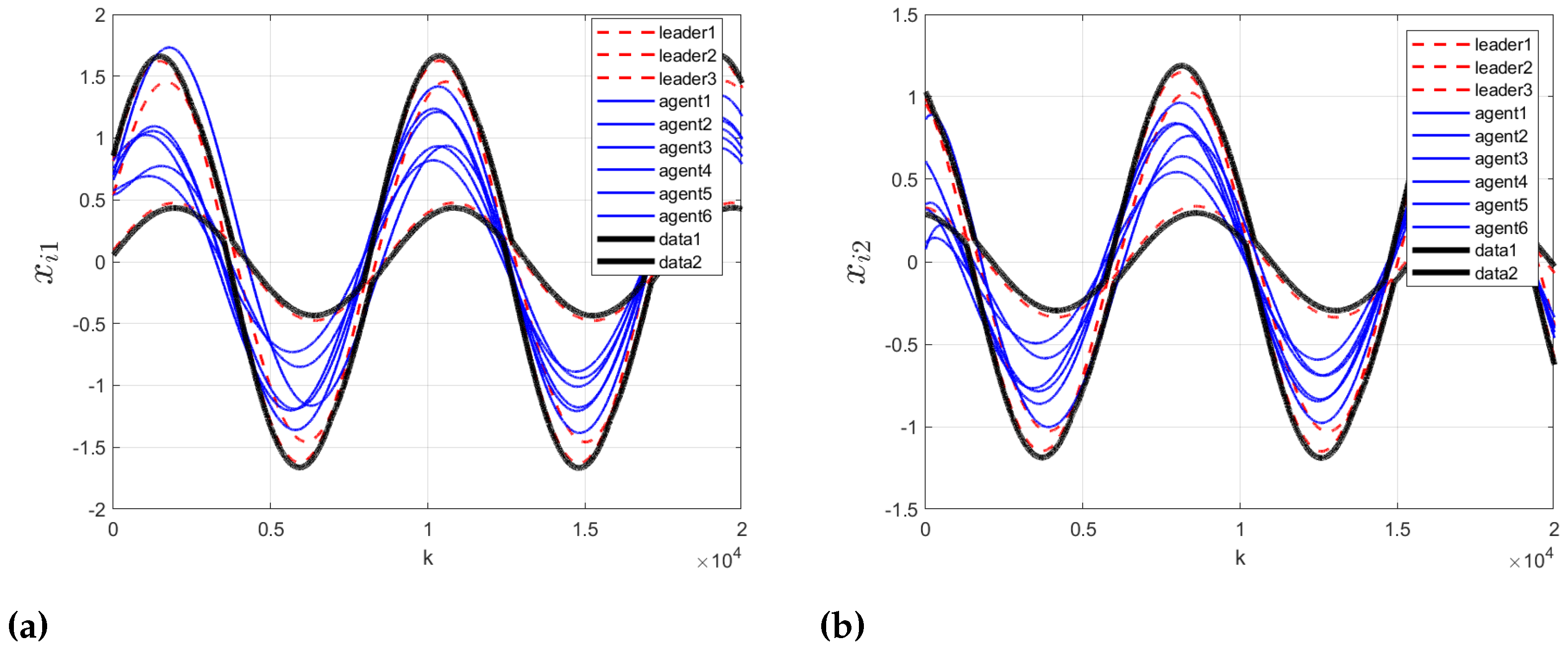
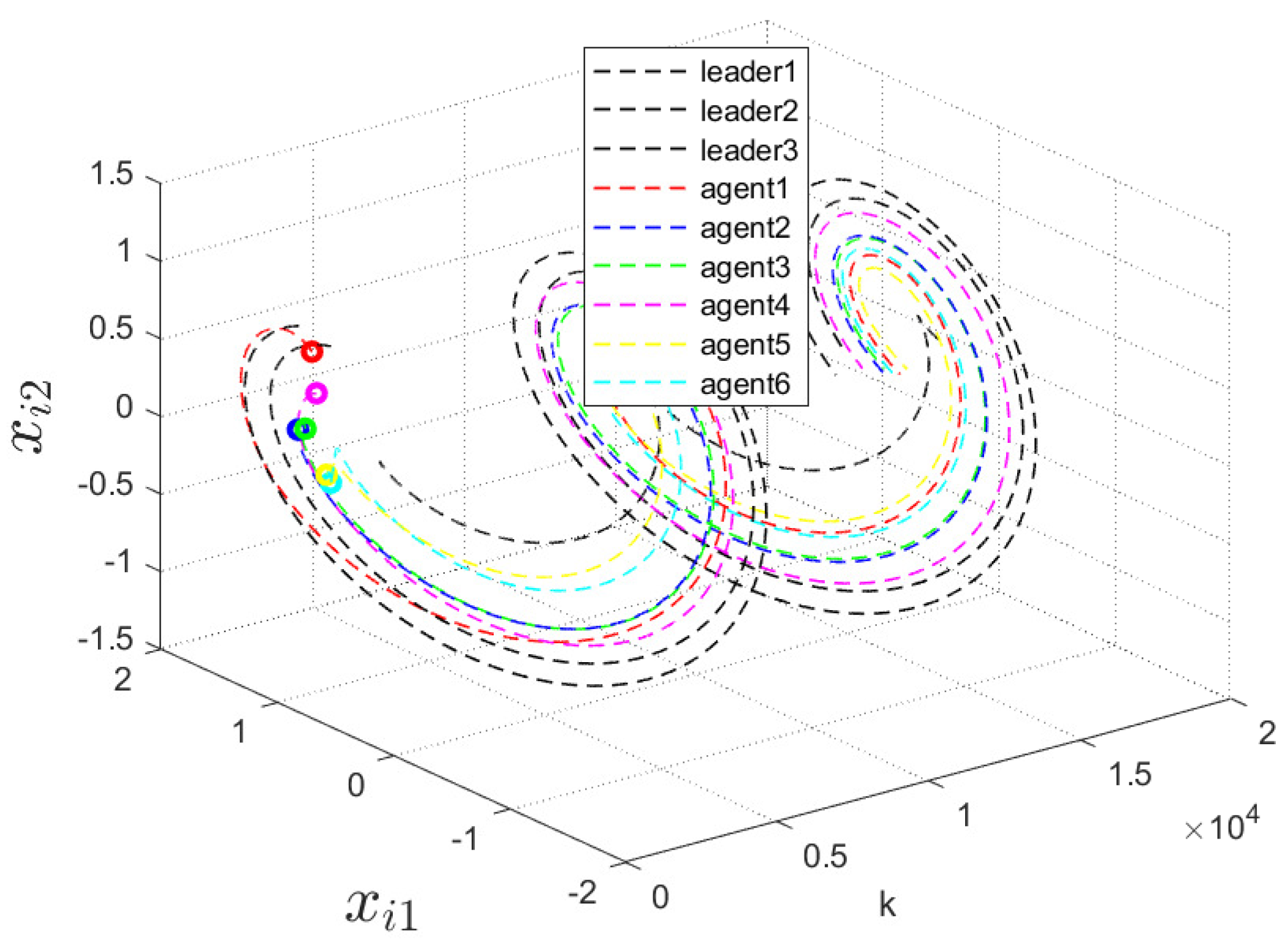
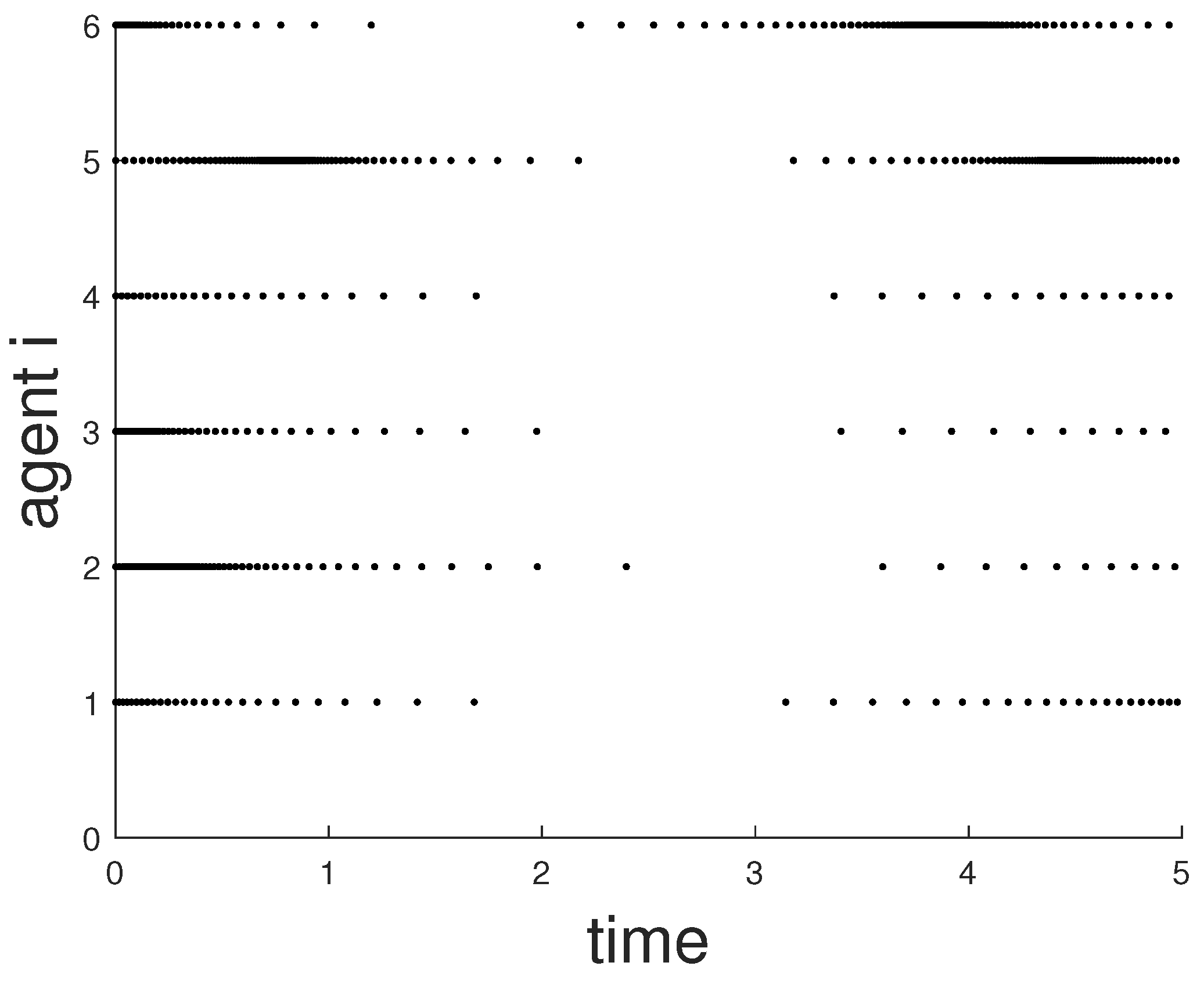
4. Simulation

For illustration, consider an MAS with the communication graph ${\mathcal{G}}_{\mathfrak{F}\cup \mathfrak{L}}$, where there are six followers $\{1-6\}\in \mathfrak{F}$ and three leaders $\{7-9\}\in \mathfrak{L}$. Assume the dynamics matrices of (1) are:

$$\begin{array}{cc}\hfill & A=\left[\begin{array}{cc}0& 1\\ -0.5& 0\end{array}\right],B=\left[\begin{array}{c}0\\ 1\end{array}\right],\hfill \\ & C=\left[\begin{array}{cc}1& 0\end{array}\right],D=\left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right].\hfill \end{array}$$

(29)

By solving the LMI (10) and the equation in Algorithm 1, the feedback gain matrices $S,F,G$ and E satisfy the condition (6)

$$\begin{array}{cc}\hfill & S=\left[\begin{array}{cc}0& 1\\ 0& -2\end{array}\right],F=\left[\begin{array}{cc}0& 1\end{array}\right],\hfill \\ & G=\left[\begin{array}{c}-2\\ -3.5\end{array}\right],E=\left[\begin{array}{c}1\end{array}\right].\hfill \end{array}$$

(30)

The initial conditions of the closed-loop system are randomly chosen. The other parameters are set as follows, $\kappa =4.6$, ${\sigma }_i=0.999$ and ${\gamma }_i=0.08$, for all $i=1,...,6$.

The communication graph ${\mathcal{G}}_{\mathfrak{F}\cup \mathfrak{L}}$ can be given by Figure 1, where nodes 7, 8 and 9 are the three leaders and the others are followers. The red dotted line represents the directed communication connection from the leader to the corresponding follower, and the black solid line represents the communication connection between the followers. Then, matrices $L_{\mathfrak{F}}$ and $L_{\mathfrak{L}}$ are as follows:

$$L_{\mathfrak{F}}=\left[\begin{array}{cccccc}3& 0& 0& -1& -1& -1\\ -1& 1& 0& 0& 0& 0\\ -1& -1& 2& 0& 0& 0\\ -1& 0& 0& 2& 0& 0\\ 0& 0& 0& -1& 2& 0\\ 0& 0& 0& 0& -1& 2\end{array}\right],L_{\mathfrak{L}}=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 1\\ 0& 1& 0\\ 1& 0& 0\end{array}\right].$$

The trajectory of the follower is represented by the solid line and that of the leader is represented by the dashed line in Figure 2, which can be clearly obtained in Definition 1, i.e., the containment control problem is indeed solved.

Through the three-dimensional effect diagram in Figure 3, the movement trajectories of six agents and three leaders over time can be more clearly seen.

Moreover, the triggering times of six followers are presented in Figure 4. As can be seen, it can effectively reduce the communication among agents.

5. Conclusions

In this paper, we have considered the containment control of MASs with external disturbances. First, a novel disturbance observer-based control has been developed by the output feedback control. Then, in order to save communication costs and energy consumption, our controller is combined with the event-triggered control. It has been shown that Zeno behavior can be excluded for the proposed controller. Here, we have only considered matched disturbances. Future work will be devoted to investigating the containment control problem with mismatched disturbances. In the meantime, this paper does not consider MASs in the presence of deception attack effects, but attacks often happen [41,42,43]. In the future, we will consider the containment control problem under deception attacks.