Systems of Linear Equations with Non-Negativity Constraints: Hyper-Rectangle Cover Theory and Its Applications

Abstract

In this paper, a novel hyper-rectangle cover theory is developed. Two important concepts, the cover order and the cover length, are introduced. We construct a specific échelon form of the matrix in the same manner as that employed to determine the rank of the matrix to obtain the cover order of any given matrix. Using the properties of the cover order, we obtain the necessary and sufficient conditions for the existence and uniqueness of the solutions for linear equations system with non-negativity constraints on variables for both homogeneous and nonhomogeneous cases. In addition, we apply the cover theory to analyze some typical problems in linear algebra and optimization with non-negativity constraints on variables, including linear programming (LP) problems and non-negative least squares (NNLS) problems. For LP problems, the three possible behaviours of the solutions are studied through cover theory. On the other hand, we develop a method to obtain the cover length of the covered variable. In this process, we discover the relationship between the cover length determination problem and the NNLS problem. This enables us to obtain an analytical optimal value for the NNLS problem.

1. Introduction

The problems with non-negativity constraints on variables play a prominent role in engineering, physics, chemistry, computer science, and economics. These problems with non-negative constraints often appear as (1) finding solutions for systems of linear equations, (2) solving LP problems, and (3) finding solutions for NNLS problems [1].

The analysis of systems of linear equations is a fundamental part of linear algebra, and forms the core of mathematical modelling of many different branches of science and engineering such as, to name but a few, electric circuits, communications, radars, optics, controls, etc. [2,3,4,5,6]. Lately, it has also been used to model the outbreak of COVID-19 and calcium diffusion [7,8,9]. Thus, methods for finding the solutions of linear equations system also play an important role in various applications [10]. Some mature methods have been developed to analyze and solve systems of linear equations without non-negativity constraints on the variables [11,12,13]. However, with non-negativity constraints added to the variables, the analysis of the solutions to the linear equations becomes harder [14]. For such problems, the classical analysis for the existence of non-negative solutions is mainly based on Farkas’ lemma [15]. In terms of uniqueness, there is no direct characterization in the general case. It is also noted that the analysis of non-negative solutions to the system of homogeneous or nonhomogeneous linear equations is mostly concerned with investigating other associated problems rather than addressing the problem in a direct way. Thus, a new approach is needed for the analysis of systems of linear equations with non-negativity constraints on the variables.

LP problems arise in many applications [16]. Many problems can be reformulated as linear programs both in theory and in practice so that fast algorithms can be applied [17,18,19,20]. Dantzig developed the simplex method in 1947, which was the first efficient method for solving LP problems and has been widely accepted as a computational tool [21,22,23]. Geometrically, the procedure of the simplex method involves moving one feasible solution to another and, for each step, the value of the objective function improves. This continues until the optimum objective is reached. It would thus be desirable if we can determine the optimal solution directly rather than moving through the feasible solutions for matrices with some specific structures. In this paper, we propose a new systematic procedure for solving the LP problem by applying cover theory using a transformed objective function.

The problem of NNLS is a type of least squares problem with non-negativity constraints on variables, which arises in applications throughout science and engineering. Various methods have been proposed to solve this kind of problems, and they can normally be divided into three classes: active-set methods [24,25,26], iterative methods [27,28], and other methods [29,30,31,32]. The first technique to solve the NNLS problem was proposed by Lawson and Hanson in [33], which is a typical active-set method, and the corresponding algorithm is named lsqnonneg in Matlab. This commonly used algorithm always converges and terminates in finite steps; however, there is no upper limit on the possible number of iterations that the algorithm might need to reach the point of the optimum value. In contrast to active-set methods, iterative methods enable one to incorporate multiple active constraints at each iteration. Since most existing algorithms for solving the NNLS problem are based on numerical analysis, we are motivated to propose a method to solve it from the matrix perspective by applying the techniques we developed in cover theory. More specifically, we solve the problem by investigating the structure of the matrix itself so as to obtain the analytical optimal value of NNLS problem.

Overview of the Paper

In this paper, we establish the novel hyper-rectangle cover theory for which we obtain the necessary and sufficient conditions that guarantee the existence and the uniqueness of the solution for a system of linear equations with non-negativity constraints on variables. A specific échelon form of the matrix is introduced and based on this form, and an efficient method is developed to determine the cover order for any given matrix. Moreover, we investigate in detail the structures of the échelon form in various cases leading to the development of feasible solutions for the system of linear equations with non-negativity constraints on variables. Parallel investigations are carried out for the LP problems. Based on the échelon form and the corresponding results on the system of linear equations with non-negative constraints, we also analyze the various possibilities of the solution for an LP problem. Finally, we develop a method to determine the cover length of the covered variables, establishing their strong relationship with the optimal objective value of NNLS problems. Based on this relationship, a new method is derived to obtain the analytical optimal value of NNLS problems.

Notation: Most notations used throughout this paper are standard: column vectors and matrices are denoted by boldface lowercase and uppercase characters, respectively; the matrix transpose is denoted by ${(·)}^T$; ${\mathbb{R}}_{+}^N$ denotes the set of all the $N\times 1$ vectors with all entries being non-negative.

2. Concept of Hyper-Rectangle Cover

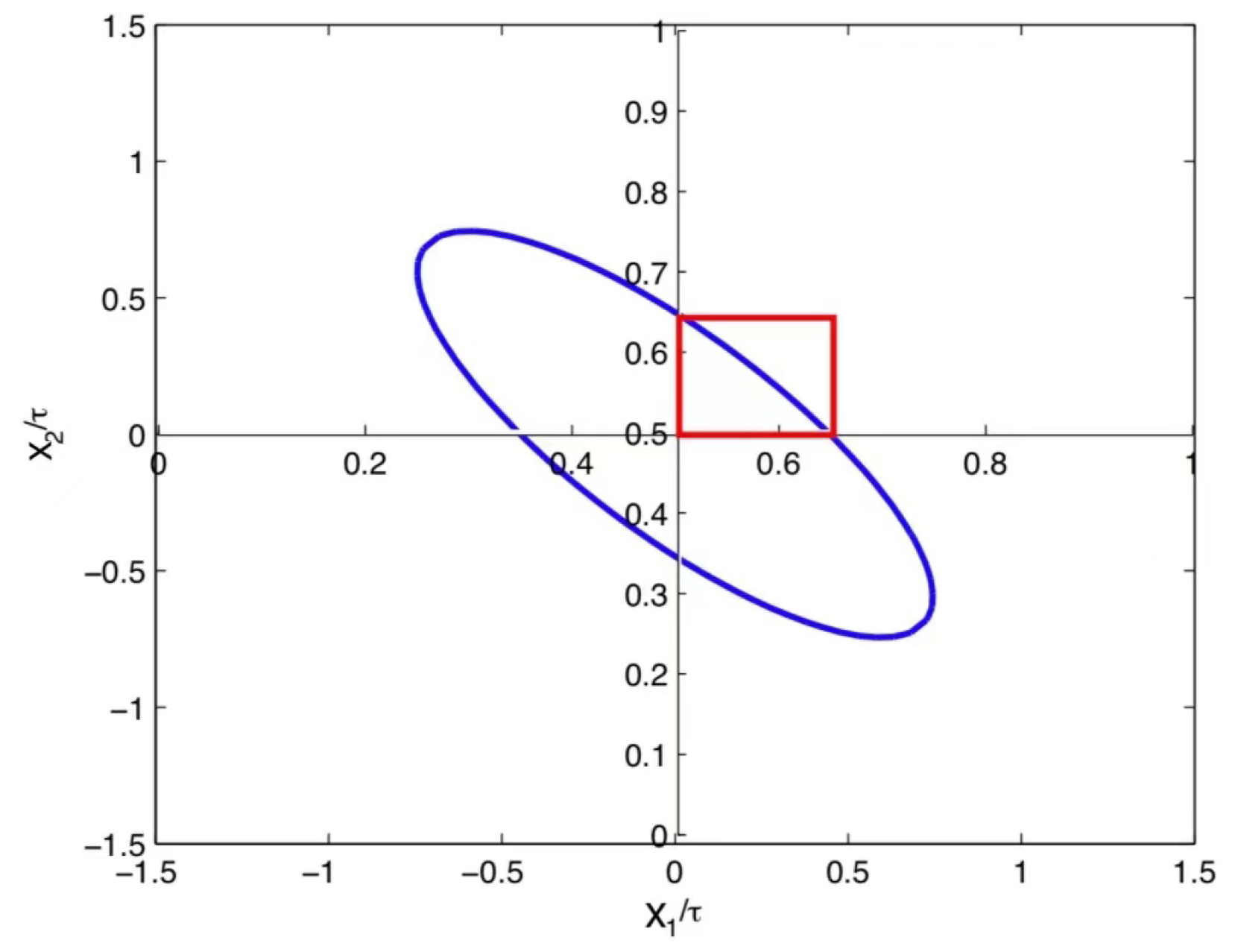
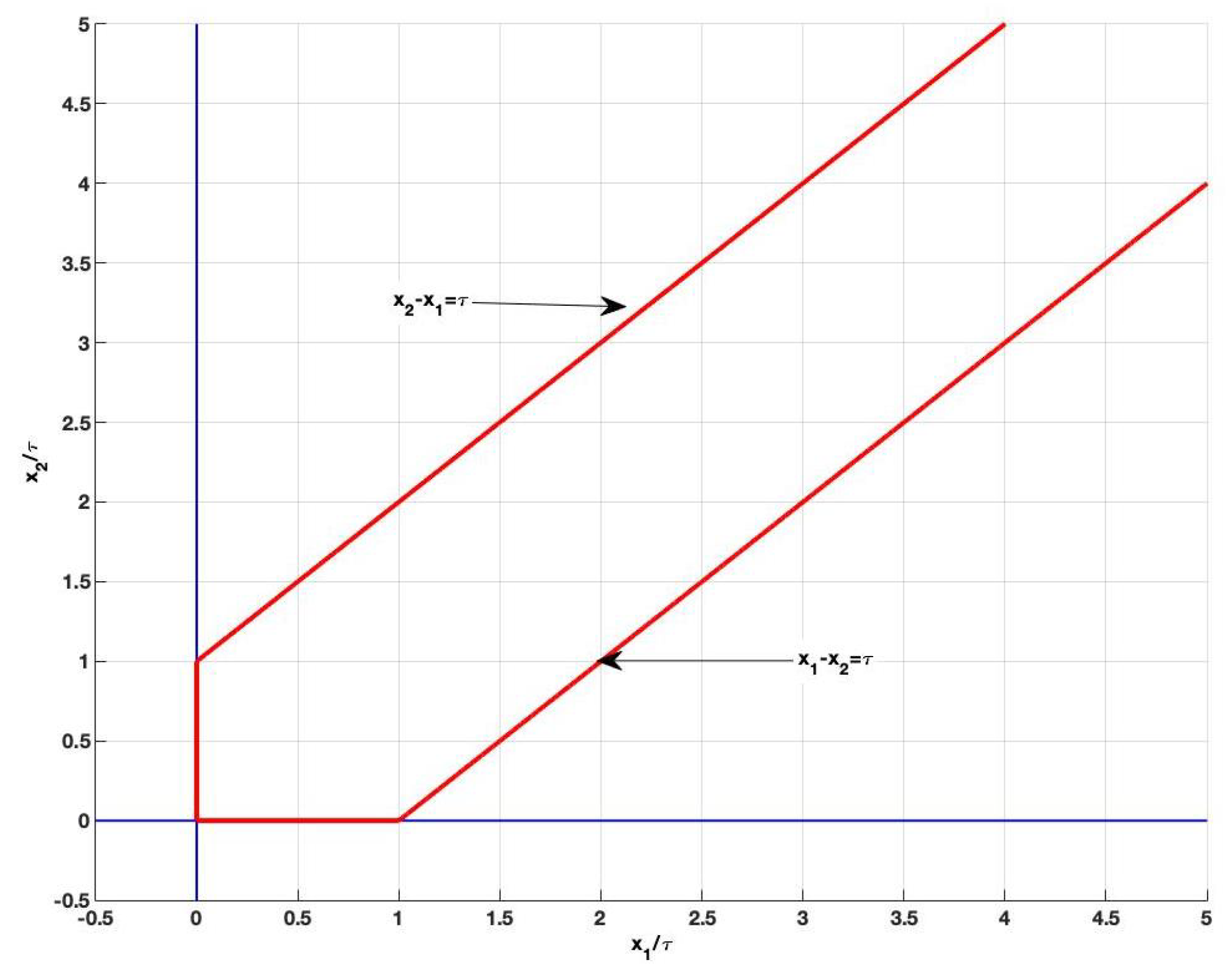
In this section, we formally give the definition of hyper-rectangle cover [34,35].

Definition 1. 

Given a matrix $\mathbf{A}\in {\mathbb{R}}^{M\times N}$ and $\mathbf{x}\in {\mathbb{R}}_{+}^N$, $x_n$ is the n-th element in $\mathbf{x}$ for index $n\in \left\{1,2,\cdots ,N\right\}$. Let $c_n\left(x_n\right)$ denote the smallest number $c_n$ such that

$$\left\{\mathbf{x}\in {\mathbb{R}}_{+}^N:{\mathbf{x}}^T{\mathbf{A}}^T\mathbf{A}\mathbf{x}\le 1\right\}\subseteq \left\{\mathbf{x}\in {\mathbb{R}}_{+}^N:x_n\le c_n\right\}$$

(1)

We say that $x_n$ is a covered variable if $c_n\left(x_n\right)$ is finite and we refer to $c_n\left(x_n\right)$ as the cover length of the covered variable $x_n$. The cover order of $\mathbf{A}$, denoted by $R_c\left(\mathbf{A}\right)$, is the number of indices $n\in \{1,2,\cdots ,N\}$ for which $c_n\left(x_n\right)<\infty$. We say that $\mathbf{A}$ has full cover if $R_c\left(\mathbf{A}\right)=N$ and has zero cover if $R_c\left(\mathbf{A}\right)=0$.

The following nontrivial examples may serve as illustrations of the definitions of cover order and cover length.

Example 1. 

Suppose that $\mathbf{A}=\left(\begin{array}{cc}1& 2\\ 2& 1\end{array}\right)$, and we have ${\mathbf{A}}^T\mathbf{A}=\left(\begin{array}{cc}5& 4\\ 4& 5\end{array}\right)$. For this matrix, $\left\{\mathbf{x}\in {\mathbb{R}}_{+}^2:{\mathbf{x}}^T{\mathbf{A}}^T\mathbf{A}\mathbf{x}\le {\tau }^2\right\}$ is an ellipse in the whole plane, which is shown in Figure 1, and the part which is located in the non-negative domain is fully covered by a rectangle. Thus, $x_1$ and $x_2$ are both covered in this example.

Example 2. 

Consider $\mathbf{A}=\left(\begin{array}{cc}1& -1\end{array}\right)$ and ${\mathbf{A}}^T\mathbf{A}=\left(\begin{array}{cc}1& -1\\ -1& 1\end{array}\right)$; for this case, the feasible set determined by ${\mathbf{x}}^T{\mathbf{A}}^T\mathbf{A}\mathbf{x}={\left(x_1-x_2\right)}^2\le {\tau }^2$ is shown in Figure 2 and is open and unbounded with respect to both $x_1$ and $x_2$. Hence, $R_c\left(\mathbf{A}\right)=0$.

From the above examples, we can find that the cover order $R_c\left(\mathbf{A}\right)$ and the cover length $c_i\left(x_i\right)$ represent the maximal dimension and minimal side lengths of the hyper-rectangle that covers $\left\{\mathbf{x}:\mathbf{x}\in {\mathbb{R}}_{+}^N,{\mathbf{x}}^T{\mathbf{A}}^T\mathbf{A}\mathbf{x}\le {\tau }^2\right\}$ respectively.

3. Systems of Linear Equations with Non-Negativity Constraints on Solutions

3.1. Homogeneous Systems of Linear Equations

In this section, we present an important result in cover theory, allowing us to determine if a column vector in $\mathbf{A}$ or the corresponding variable $x_i$ in $\mathbf{A}\mathbf{x}$ is covered or not. Furthermore, this result provides us with a method of investigating the non-negative solution to a system of linear equations. Let us first introduce the definition of a convex cone [36].

Definition 2. 

A set $\mathcal{C}\subseteq {\mathbb{R}}^M$ is a convex cone if $\alpha \mathbf{x}+\beta \mathbf{y}\in \mathcal{C}$ for all $\mathbf{x},\mathbf{y}\in \mathcal{C}$ and $\alpha ,\beta >0$.

A cone $\mathcal{C}$ is polyhedral if it is the conic combination of finitely many vectors, i.e., there is a set of vectors $\{{\mathbf{a}}_1,\cdots ,{\mathbf{a}}_N\}$, so that $\mathcal{C}=\{{\mathbf{a}}_1{u}_1+{\mathbf{a}}_2{u}_2+\cdots {\mathbf{a}}_N{u}_N|{\mathbf{a}}_i\in {\mathbb{R}}^M,u_i\in {\mathbb{R}}^{+}\}$. The polyhedral cone $\mathcal{C}$ is a closed convex cone.

With the above definition, we are now able to obtain the following result:

Theorem 1. 

Let $\mathbf{A}$ be an $M\times N$ real matrix. Then, the i-th column of $\mathbf{A}$, or the i-th variable $x_i$ associated with the i-th column vector ${\mathbf{a}}_i$ in $\mathbf{A}\mathbf{x}$, is covered if and only if $\mathbf{A}\mathbf{x}\ne \mathbf{0}$ for any $\mathbf{x}\in {\mathbb{R}}_{+}^N$ with $x_i>0$.

Proof. 

Necessity: Here, by assuming that $x_i$ is covered in $\mathbf{A}\mathbf{x}$, we need to show that for any $\mathbf{x}\in {\mathbb{R}}_{+}^N$ with $x_i>0$, we have $\mathbf{A}\mathbf{x}\ne \mathbf{0}$. Suppose that this statement was not true. Then, there exists ${\mathbf{x}}_0\in {\mathbb{R}}_{+}^N$ with $x_{0,i}>0$ such that $\mathbf{A}{\mathbf{x}}_0=\mathbf{0}$, where $x_{0,i}$ is the i-th element in ${\mathbf{x}}_0$. As a consequence, for any positive number $p>0$, we would also have $\mathbf{A}\left(p{\mathbf{x}}_0\right)=\mathbf{0}$, implying that $p{x}_{0,i}$ is not bounded if for any given $\tau >0$, $0={\left(p{\mathbf{x}}_0\right)}^T{\mathbf{A}}^T\mathbf{A}\left(p{\mathbf{x}}_0\right)\le \tau$. This contradicts the assumption that $x_i$ is covered in $\mathbf{A}\mathbf{x}$. Therefore, the necessary condition is true.

Sufficiency: For $x_i>0$, the quadratic form ${\mathbf{x}}^T{\mathbf{A}}^T\mathbf{A}\mathbf{x}$ can be rewritten as: ${\mathbf{x}}^T{\mathbf{A}}^T\mathbf{A}\mathbf{x}=\parallel {\overline{\mathbf{A}}}_i{\overline{\mathbf{x}}}_i+{\mathbf{a}}_i{x}_i{\parallel }^2=x_i^2{\parallel {\overline{\mathbf{A}}}_i\mathbf{u}+{\mathbf{a}}_i\parallel }^2$, where $\mathbf{u}=\frac{{\overline{\mathbf{x}}}_i}{x_i}$, ${\overline{\mathbf{A}}}_i$ is the $M\times (N-1)$ sub-matrix formed by deleting the i-th column from $\mathbf{A}$ and $\mathbf{u}\ge \mathbf{0}$. Consider the set $\left\{{\overline{\mathbf{A}}}_i\mathbf{u}:\mathbf{u}\in {\mathbb{R}}_{+}^{N-1}\right\}$. It is a closed convex cone according to Definition 2, and the function $\parallel {\overline{\mathbf{A}}}_i\mathbf{u}+{\mathbf{a}}_i{\parallel }^2$ is convex; thus, the minimum of $\parallel {\overline{\mathbf{A}}}_i\mathbf{u}+{\mathbf{a}}_i{\parallel }^2$ exists, i.e., there exists a ${\mathbf{u}}_0\ge \mathbf{0}$ such that $\parallel {\overline{\mathbf{A}}}_i{\mathbf{u}}_0+{\mathbf{a}}_i{\parallel }^2\le {\parallel {\overline{\mathbf{A}}}_i\mathbf{u}+{\mathbf{a}}_i\parallel }^2$, for any $\mathbf{u}\in {\mathbb{R}}_{+}^{N-1}$. In fact, $\parallel {\overline{\mathbf{A}}}_i{\mathbf{u}}_0+{\mathbf{a}}_i\parallel \ne 0$. Otherwise, if $x_{0,i}=1,x_{0,k}=u_{0,k}$, for $k=1,2,\cdots ,i-1$, and $x_{0,k}=u_{0,k-1}$, for $k=i+1,\cdots ,N$, then, we have ${\overline{\mathbf{A}}}_i{\mathbf{u}}_0+{\mathbf{a}}_i=\mathbf{A}{\mathbf{x}}_0=\mathbf{0}$, which contradicts the assumption. Now for any given positive real value $\tau$, if we let ${\mathbf{x}}^T{\mathbf{A}}^T\mathbf{A}\mathbf{x}\le {\tau }^2$, then, we have $x_i^2{\parallel {\overline{\mathbf{A}}}_i{\mathbf{u}}_0+{\mathbf{a}}_i\parallel }^2\le {\mathbf{x}}^T{\mathbf{A}}^T\mathbf{A}\mathbf{x}\le {\tau }^2$. Hence, we obtain $0<x_i<\frac{\tau }{\parallel {\overline{\mathbf{A}}}_i{\mathbf{u}}_0+{\mathbf{a}}_i\parallel }$, i.e., $x_i$ is covered in $\mathbf{A}\mathbf{x}$.

Thus, the proof of Theorem 1 is complete.    □

  From Theorem 1, the following results can be obtained.

Corollary 1. 

Let $\mathbf{A}$ be an $M\times N$ real matrix, and let ${\overline{\mathbf{A}}}_j$ be the $M\times (N-1)$ sub-matrix formed by deleting the j-th column from $\mathbf{A}$. Then, the following statements are true:

1. 

A system of homogeneous linear equations, $\mathbf{A}\mathbf{x}=\mathbf{0}$, has a nonzero solution in ${\mathbb{R}}_{+}^N$ if and only if $\mathbf{A}$ does not have full cover.

2. 

Let the j-th column of $\mathbf{A}$ be covered. Then, any column of ${\overline{\mathbf{A}}}_j$ is covered in ${\overline{\mathbf{A}}}_j$ if and only if it, as a column of $\mathbf{A}$, is also covered in $\mathbf{A}$.

3. 

If the i-th column of $\mathbf{A}$ is covered, then it is also covered in ${\overline{\mathbf{A}}}_j$ for $j\ne i$.

4. 

A full column rank matrix $\mathbf{A}$ always has full cover.

For a homogeneous system of linear equations with non-negative constraints on solutions, it is important to determine the necessary and sufficient condition which guarantees the existence of nonzero solutions. The direct determination of whether the system has nonzero solution is not simple [14,37]. Here, Theorem 1 makes a statement paralleled to the first statement of Corollary 1, providing us with the condition for the existence of nonzero solutions for the system.

3.2. Nonhomegeneous Systems of Linear Equations with Non-Negativity Constraints on Solutions

Nonhomogeneous systems of linear equations with non-negativity constraints on solutions are frequently encountered in the field of signal and image processing, multispectral data handling, fibre optics, etc. [38,39,40]. The classical way for determining the existence of non-negative solution is based on Farkas’ lemma [15]. According to Farkas’ lemma, given a problem of linear equations with non-negativity constraints on the variables, there exists another problem associated with it such that the original problem has a solution in the required domain if and only if the associated problem has no solution. Thus, this lemma provides an indirect way to check the existence of non-negative solutions to a nonhomogeneous system of linear equations.

In the following, based on the cover theory, we will derive the direct necessary and sufficient conditions for the existence and the uniqueness of non-negative solutions of the aforementioned system.

Existence of non-negative solutions:

Theorem 2. 

Let $\mathbf{A}\in {\mathbb{R}}^{M\times N}$ and $\mathbf{b}\in {\mathbb{R}}^M$. Then, there exists an $\mathbf{x}\in {\mathbb{R}}_{+}^N$ such that $\mathbf{A}\mathbf{x}=\mathbf{b}$ if and only if the cover order of the augmented matrix $\tilde{\mathbf{A}}=\left(\mathbf{A},-\mathbf{b}\right)$ is less than or equal to that of $\mathbf{A}$.

Proof. 

Let us rewrite the linear equations $\mathbf{A}\mathbf{x}=\mathbf{b}$ as $\tilde{\mathbf{A}}\tilde{\mathbf{x}}=\mathbf{0}$, where $\tilde{\mathbf{A}}=\left(\mathbf{A},-\mathbf{b}\right)$ and $\tilde{\mathbf{x}}=\left(\mathbf{x},{\tilde{x}}_{N+1}\right)$. First we prove the sufficiency: Under the assumption $R_c\left(\tilde{\mathbf{A}}\right)\le R_c\left(\mathbf{A}\right)$, by Statement 2 of Corollary 1, we can claim that ${\tilde{x}}_{N+1}$ is not covered in $\tilde{\mathbf{A}}\tilde{\mathbf{x}}$. Since $\tilde{\mathbf{A}}$ does not have full cover, then by Theorem 1, there exists an ${\tilde{\mathbf{x}}}_0=({\mathbf{x}}_0,{\tilde{x}}_{0,N+1})\in {\mathbb{R}}_{+}^{N+1}$ with ${\tilde{x}}_{0,N+1}>0$, where ${\tilde{x}}_{0,N+1}$ is the $(N+1)$-th element of ${\tilde{\mathbf{x}}}_0$, such that $\tilde{\mathbf{A}}{\tilde{\mathbf{x}}}_0=\mathbf{0}$. Hence, we have $\mathbf{A}{\mathbf{x}}_0=\mathbf{b}{\tilde{x}}_{0,N+1}$, implying that ${\mathbf{x}}_0/{\tilde{x}}_{0,N+1}$ is a solution of $\mathbf{A}\mathbf{x}=\mathbf{b}$. Therefore, the sufficient condition is true.

To prove the necessary condition, we assume that the system of linear equations $\mathbf{A}\mathbf{x}=\mathbf{b}$ has a solution in ${\mathbb{R}}_{+}^N$, i.e., there exists an ${\mathbf{x}}_0\in {\mathbb{R}}_{+}^N$ such that $\mathbf{A}{\mathbf{x}}_0=\mathbf{b}$. Then, by Theorem 1, the $(N+1)$-th column vector of $\tilde{\mathbf{A}}$ is not covered. In addition, by Statement 3) of Corollary 1, we know that if ${\tilde{\mathbf{a}}}_i$, the i-th column vector of $\tilde{\mathbf{A}}$, $i\in \{1,\cdots ,N\}$, is covered in $\tilde{\mathbf{A}}$, then ${\tilde{\mathbf{a}}}_i$, being a column vector of $\mathbf{A}$, is also covered in $\mathbf{A}$. Therefore, the inequality $R_c\left(\tilde{\mathbf{A}}\right)\le R_c\left(\mathbf{A}\right)$ holds. This completes the proof of Theorem 2.    □

Theorem 2 provides us with the regularization condition for non-negative solutions for a systems of linear algebraic equations. It is interesting to point out that in some application of systems of ordinary differential equations, there are parallel regularizations that provide non-negative solutions [41,42].

Uniqueness of non-negative solutions:

With the definition of convex cone in Definition 2, let us first introduce Carathéordory’s theorem [15]:

Lemma 1 (Carathéordory’s theorem). 

Let $\mathcal{S}\subseteq {\mathbb{R}}^M$ be a finite set, and let $\mathbf{y}\in {\mathbb{R}}^M$. If $\mathbf{y}\in \mathrm{cone}\mathcal{S}$, then there exists a linearly independent set $\mathcal{T}$ such that $\mathbf{y}\in \mathrm{cone}\mathcal{T}$.

By applying Carathéordory’s theorem, we are able to show the necessary and sufficient condition for the uniqueness of non-negative solution to a nonhomogeneous system of linear equations. This is stated in the following theorem:

Theorem 3. 

Let $\mathbf{A}\in {\mathbb{R}}^{M\times N}$ and $\mathbf{b}\in {\mathbb{R}}^M$. Then, $\mathbf{A}\mathbf{x}=\mathbf{b}$ has a unique solution $\mathbf{x}$ in ${\mathbb{R}}_{+}^N$, if and only if $R_c\left(\tilde{\mathbf{A}}\right)\le R_c\left(\mathbf{A}\right)$ and $R_c\left(\tilde{\mathbf{A}}\right)+R_r\left(\overline{\mathbf{A}}\right)=N$, where $R_r\left(\overline{\mathbf{A}}\right)$ is the rank of $\overline{\mathbf{A}}$, and $\overline{\mathbf{A}}={\left\{{\mathbf{a}}_i\right\}}_{i\in \overline{\mathcal{N}}}$, with $\overline{\mathcal{N}}$ being a set consisting of all the column indices of $\mathbf{A}$ not covered in $\tilde{\mathbf{A}}$.

Proof. 

Sufficiency: Let $\overline{R_c}\left(\tilde{\mathbf{A}}\right)$ be the number of uncovered column vectors in $\tilde{\mathbf{A}}$. Thus, we have $R_c\left(\tilde{\mathbf{A}}\right)+\overline{R_c}\left(\tilde{\mathbf{A}}\right)=N+1$, and under the assumption $R_c\left(\tilde{\mathbf{A}}\right)+R_r\left(\overline{\mathbf{A}}\right)=N$, we have $\overline{R_c}\left(\tilde{\mathbf{A}}\right)=R_r\left(\overline{\mathbf{A}}\right)+1$. In addition, since $R_c\left(\tilde{\mathbf{A}}\right)\le R_c\left(\mathbf{A}\right)$, we can obtain $\overline{R_c}\left(\tilde{\mathbf{A}}\right)=\left|\overline{\mathcal{N}}\right|+1$ and, as a result, $R_r\left(\overline{\mathbf{A}}\right)=\left|\overline{\mathcal{N}}\right|$. Therefore, all the column vectors ${\left\{{\mathbf{a}}_i\right\}}_{i\in \overline{\mathcal{N}}}$ are linearly independent in ${\mathbb{R}}^M$. As a consequence, $\mathbf{A}\mathbf{x}=\mathbf{b}$ has a unique solution in ${\mathbb{R}}_{+}^N$.

Necessity: According to the property of $R_c\left(\tilde{\mathbf{A}}\right)$ and the definition of $\overline{\mathbf{A}}$, we have $R_c\left(\tilde{\mathbf{A}}\right)+R_r\left(\overline{\mathbf{A}}\right)\le N$. Considering $R_c\left(\tilde{\mathbf{A}}\right)+R_r\left(\overline{\mathbf{A}}\right)<N$, in this case, we have $R_r\left(\overline{\mathbf{A}}\right)<|\overline{\mathcal{N}|}$. Then, for all $i\in \overline{\mathcal{N}}$, there are ${\mu }_i\in \mathbb{R}$ (not all 0) such that ${\sum }_{i\in \overline{\mathcal{N}}}{\mu }_i{\mathbf{a}}_i=\mathbf{0}$ and there are ${\lambda }_i\ge 0$ such that ${\sum }_{i\in \overline{\mathcal{N}}}{\lambda }_i{\mathbf{a}}_i=\mathbf{b}$. In addition, there is a real number $\alpha$ such that ${\lambda }_i+\alpha {\mu }_i>0$ for all $i\in \overline{\mathcal{N}}$. Let us assume that ${\mathbf{x}}_0\in {\mathbb{R}}_{+}^N$ is the unique solution of $\mathbf{A}\mathbf{x}=\mathbf{b}$, where $x_{0,i}={\lambda }_i+\alpha {\mu }_i$, for $i\in \overline{\mathcal{N}}$ and $x_{0,i}=0$, for $i\in \{1,2,\cdots ,N\}\setminus \overline{\mathcal{N}}$, then we have $\mathbf{A}{\mathbf{x}}_0=\mathbf{b}$. As Carathéordory’s theorem states, we are able to find a linearly independent subset ${\left\{{\mathbf{a}}_i\right\}}_{i\in \tilde{\mathcal{N}}}$ of ${\left\{{\mathbf{a}}_i\right\}}_{i\in \overline{\mathcal{N}}}$. Let $\tilde{\mathcal{N}}$ be the set consisting of the linearly independent column indices of ${\left\{{\mathbf{a}}_i\right\}}_{i\in \overline{\mathcal{N}}}$, and $|\tilde{\mathcal{N}}|<|\overline{\mathcal{N}}|$. Then there is another solution ${\mathbf{x}}_1\in {\mathbb{R}}_{+}^N$ such that $\mathbf{A}{\mathbf{x}}_1=\mathbf{b}$ and $x_{1,i}=0$, for $i\in \{1,2,\cdots ,N\}\setminus \tilde{\mathcal{N}}$, where the number of zero element in ${\mathbf{x}}_1$ is larger than that in ${\mathbf{x}}_0$. This contradicts the assumption that ${\mathbf{x}}_0$ is the unique solution of $\mathbf{A}\mathbf{x}=\mathbf{b}$. Therefore, $R_c\left(\tilde{\mathbf{A}}\right)+R_r\left(\overline{\mathbf{A}}\right)=N$ must be satisfied to guarantee the uniqueness of the solution. Thus, the proof of Theorem 3 is complete.    □

4. Cover Order

In this section, we develop a specific échelon form of a matrix that can be used to determine the cover order of any given matrix. Some special properties of cover order are also explored.

4.1. Cover Order Determination

Let ${\mathbb{R}}_{++}^N$ denote the set of $N\times 1$ vectors with all entries being positive. The vector $\mathbf{x}$, of which the elements are all positive, is called a positive vector. Similarly, let ${\mathbb{R}}_{+}^N$, ${\mathbb{R}}_{--}^N$, and ${\mathbb{R}}_{-}^N$, respectively, denote a non-negative, a negative, and a nonpositive set of $N\times 1$ vectors. We first present some related results in the following lemmas which are useful for our derivation of the cover order of a real matrix.

Lemma 2 

([13]). Let $\mathbb{S}$ be a subspace of ${\mathbb{R}}^N$ and ${\mathbb{S}}^{\perp }$ be the orthogonal complementary subspace of $\mathbb{S}$. Then,

1. 

$\mathbb{S}\cap {\mathbb{R}}_{+}^N=\varnothing$ if and only if ${\mathbb{S}}^{\perp }\cap {\mathbb{R}}_{++}^N\ne \varnothing$.

2. 

$\mathbb{S}\cap {\mathbb{R}}_{++}^N=\varnothing$ if and only if ${\mathbb{S}}^{\perp }\cap {\mathbb{R}}_{+}^N\ne \varnothing$.

Denoting the row space of $\mathbf{A}$ by ${\mathbb{S}}_{\mathbf{A}}$ and the orthogonal complement to this row space by ${\mathbb{S}}_{\mathbf{A}}^{\perp }$, and using Lemma 2, we have the following [34]:

Lemma 3. 

Let ${\mathbb{R}}_{+}^N\left(K\right)$ denote the set of all the non-negative vectors with K positive entries. Specifically, ${\mathbb{R}}_{+}^N\left(0\right)$ denotes the set $\left\{{\mathbf{0}}_{N\times 1}\right\}$. For any $\mathbf{A}\in {\mathbb{R}}^{M\times N}$, the cover order of $\mathbf{A}$ is equal to ${max}_{{\mathbb{S}}_{\mathbf{A}}\cap {\mathbb{R}}_{+}^N\left(K\right)\ne \varnothing }K$.

Lemma 3 shows us the necessary and sufficient condition for determining the cover order of a matrix. Now, we show an important property of cover order in the following:

Theorem 4. 

Given an $M\times N$ real matrix $\mathbf{A}$ and given an invertible $M\times M$ real matrix $\mathbf{T}$, let $\mathbf{B}=\mathbf{TA}$, then we have $R_c\left(\mathbf{B}\right)=R_c\left(\mathbf{A}\right)$.

Proof. 

Let us consider ${\mathbf{x}}^T{\mathbf{B}}^T\mathbf{B}\mathbf{x}$, which is equivalent to ${\mathbf{x}}^T\left({\mathbf{A}}^T{\mathbf{T}}^T\mathbf{T}\mathbf{A}\right)\mathbf{x}$ according to the assumption. Suppose that ${\lambda }_{\min }$ and ${\lambda }_{\max }$ are the minimum eigenvalue and the maximum eigenvalue of ${\mathbf{T}}^T\mathbf{T}$, respectively, since ${\mathbf{T}}^T\mathbf{T}$ is a real symmetric matrix, then by Rayleigh–Ritz theorem [43], we have $\forall \mathbf{x}\in {\mathbb{R}}^n$, and the inequalities ${\lambda }_{\min }·{\mathbf{x}}^T\mathbf{x}\le {\mathbf{x}}^T{\mathbf{T}}^T\mathbf{T}\mathbf{x}\le {\lambda }_{\max }·{\mathbf{x}}^T\mathbf{x}$ hold. Letting $\mathbf{y}=\mathbf{Ax}$, we have ${\lambda }_{\min }·{\mathbf{y}}^T\mathbf{y}\le {\mathbf{y}}^T{\mathbf{T}}^T\mathbf{T}\mathbf{y}\le {\lambda }_{\max }·{\mathbf{y}}^T\mathbf{y}$, i.e.,

$$\begin{array}{c}\hfill {\lambda }_{\min }·{\mathbf{x}}^T{\mathbf{A}}^T\mathbf{A}\mathbf{x}\le {\mathbf{x}}^T{\mathbf{A}}^T{\mathbf{T}}^T\mathbf{T}\mathbf{A}\mathbf{x}\le {\lambda }_{\max }·{\mathbf{x}}^T{\mathbf{A}}^T\mathbf{A}\mathbf{x}\end{array}$$

(2)

Then, using the left-hand side inequality ${\lambda }_{\min }·{\mathbf{x}}^T{\mathbf{A}}^T\mathbf{A}\mathbf{x}\le {\mathbf{x}}^T{\mathbf{B}}^T\mathbf{B}\mathbf{x}$ in Equation (2) and the definition of cover order in Definition 1, we have:

$$\begin{array}{ccc}\hfill \left\{\mathbf{x}\in {\mathbb{R}}_{+}^N:{\mathbf{x}}^T{\mathbf{B}}^T\mathbf{B}\mathbf{x}\le 1\right\}& \subseteq & \left\{\mathbf{x}\in {\mathbb{R}}_{+}^N:{\mathbf{x}}^T{\mathbf{A}}^T\mathbf{A}\mathbf{x}\le \frac{1}{{\lambda }_{min}}\right\}\hfill \\ & \subseteq & \left\{\mathbf{x}\in {\mathbb{R}}_{+}^N:x_{k_i}\le \frac{c_{k_i}}{{\lambda }_{min}},i=1,\cdots ,R_c\left(\mathbf{A}\right)\right\}\hfill \end{array}$$

(3)

where $k_i\in \{1,2,\cdots ,N\}$ and $c_{k_i}$ are positive real numbers. Then, by the definition of cover order in Definition 1, we know that at least $R_c\left(\mathbf{A}\right)$ variables in $\mathbf{x}$ associated with the column vectors in $\mathbf{B}\mathbf{x}$ are covered. Thus, we have $R_c\left(\mathbf{A}\right)\le R_c\left(\mathbf{B}\right)$.

According to the right-hand side inequality in Equation (2), we have:

$$\begin{array}{ccc}\hfill \left\{\mathbf{x}\in {\mathbb{R}}_{+}^N:{\mathbf{x}}^T{\mathbf{A}}^T\mathbf{A}\mathbf{x}\le \frac{1}{{\lambda }_{max}}\right\}& \subseteq & \left\{\mathbf{x}\in {\mathbb{R}}_{+}^N:{\mathbf{x}}^T{\mathbf{B}}^T\mathbf{B}\mathbf{x}\le 1\right\}\hfill \\ & \subseteq & \left\{\mathbf{x}:0\le x_{k_i}\le c_{k_i},i=1,\cdots ,R_c\left(\mathbf{B}\right)\right\}\hfill \end{array}$$

(4)

Similarly, at least $R_c\left(\mathbf{B}\right)$ variables in $\mathbf{x}$ associated with the column vectors in $\mathbf{A}\mathbf{x}$ are covered. Thus, we have $R_c\left(\mathbf{A}\right)\ge R_c\left(\mathbf{B}\right)$.

Hence, we can conclude that, if det$\left(\mathbf{T}\right)\ne 0$ and $\mathbf{B}=\mathbf{TA}$, then $R_c\left(\mathbf{A}\right)=R_c\left(\mathbf{B}\right)$.    □

Theorem 4 carries important implications. It states that the cover order of a matrix is invariant under any row transformation. From Lemma 3, we know that if we are able to find non-negative vectors in ${\mathbb{S}}_{\mathbf{A}}$, then the cover order of $\mathbf{A}$ is equal to the largest number of the positive entries of these vectors. Thus, Theorem 4 together with Lemma 3 implicitly suggests that we can perform a series of linear elementary row transformations and column permutations to determine the cover order of the matrix. This indeed leads us to the development of a straightforward procedure transforming $\mathbf{A}$ into an échelon form for the evaluation of its cover order.

4.2. Procedure of the Échelon Transformation

An échelon form of a rectangular matrix [1] has the following structures:

Definition 3 (échelon form). 

A rectangular matrix is in échelon form (or row échelon form) if it has the following three properties:

(a)

All nonzero rows are above any rows of all zeros.

(b)

Each leading entry of a row is in a column to the right of the leading entry of the row above it.

(c)

All entries in a column below a leading entry are zeros.  

Our procedure of échelon transformation can now be laid out as follows:

1.

The Échelon Form of $\mathbf{A}$. Given an $M\times N$ real matrix $\mathbf{A}$, we can find matrices ${\mathbf{E}}_{\mathbf{0}}$ and ${\mathbf{P}}_{\mathbf{0}}$ such that [1]:

$${\mathbf{E}}_0\mathbf{A}{\mathbf{P}}_0=\left(\begin{array}{cc}\mathbf{I}& {\mathbf{B}}_0\\ \mathbf{0}& \mathbf{0}\end{array}\right)$$

(5)

where $\mathbf{I}\in {\mathbb{R}}^{R_r\times R_r}$ and ${\mathbf{B}}_{\mathbf{0}}\in {\mathbb{R}}^{R_r\times (N-R_r)}$ with $R_r$ being the rank of the matrix $\mathbf{A}$. Here, ${\mathbf{E}}_{\mathbf{0}}$ and ${\mathbf{P}}_{\mathbf{0}}$ are, respectively, the elementary transformation and the permutation matrices, either of which may be made up of a product of simpler elementary and permutation matrices. The right side of Equation (5) conforms with the description of échelon form; thus, Equation (5) is an échelon transformation of $\mathbf{A}$. Note that the échelon transformation of $\mathbf{A}$ is not unique; we can choose different ${\mathbf{E}}_0$ and ${\mathbf{P}}_0$, arriving at different values of ${\mathbf{B}}_0$.

2.

The Cover Order. Without loss of generality, we can assume that $\mathbf{A}$ has full rank. In particular, from Theorem 1 and Lemma 3, if the initial échelon transformation of $\mathbf{A}$ in Equation (5) results in every entry in some row of ${\mathbf{B}}_0$ being positive, then $R_c\left(\mathbf{A}\right)=N$, i.e., $\mathbf{A}$, has full cover. On the other hand, if every entry in some column of ${\mathbf{B}}_0$ is negative, then $R_c\left(\mathbf{A}\right)=0$. However, if the cover order of $\mathbf{A}$ is not immediately obvious from the structure of ${\mathbf{B}}_0$ resulted from the initial échelon transformation, we need the following steps of structural arrangement to determine the cover order.

(1)

Structure Arrangement. Search for all non-negative rows in ${\mathbf{B}}_0$ and select the one which has the greatest number of positive elements. Move this selected row to the first row and assume that it contains $N_1$ positive entries. By performing the row and column permutation, we can always ensure the identity matrix structure ahead and let the following statements hold:

$$b_{11},b_{12},\cdots ,b_{1N_1}>0,b_{1(N_1+1)},\cdots ,b_{1(N-M)}=0$$

(6)

where $b_{1i}$, $i=1,\cdots ,N-M$ are the elements in the first row of the new structure of ${\mathbf{B}}_0$. Ignoring the above first $N_1$ columns in new ${\mathbf{B}}_0$, we find all non-negative rows in the remaining part of it and choose the row with the largest number of positive elements. Moving this row to the second row and assuming that it contains $N_2$ positive entries in the remaining $N-M-N_1$ columns, we have:

$$b_{2(N_1+1)},b_{2(N_1+2)},\cdots ,b_{2(N_1+N_2)}>0,b_{2(N_1+N_2+1)},\cdots ,b_{2(N-M)}=0$$

(7)

where $b_{2i}$, $i=N_1+1,\cdots ,N-M$, are the elements in the second row of the new form of ${\mathbf{B}}_0$ after the above steps. By arranging the following rows similarly, after s times, we obtain:

$$\begin{array}{c}\hfill b_{11},b_{12},\cdots ,b_{1N_1}>0,b_{1(N_1+1)},\cdots ,b_{1(N-M)}=0\\ \hfill b_{2(N_1+1)},b_{2(N_1+2)},\cdots ,b_{2(N_1+N_2)}>0,b_{2(N_1+N_2+1)},\cdots ,b_{2(N-M)}=0\\ \hfill ⋮\\ \hfill b_{s(N_1+N_2+\cdots +N_{s-1}+1)},\cdots ,b_{s(N_1+\cdots +N_s)}>0,b_{s(N_1+N_2+\cdots +N_s+1)},\cdots ,b_{s(N-M)}=0\end{array}$$

(8)

where $b_{ij}$ in Equation (8), $i=1,2,\cdots ,s$, $j=1,2,\cdots ,N-M$, and $s\le M$, are the elements in the first s rows of the structure of ${\mathbf{B}}_{\mathbf{0}}$ after s times transformation. The procedure ends when one of the following two cases happens:

(a)

${\sum }_{i=1}^s{N}_i=N-M$, in which case $\mathbf{A}$ has full cover.

(b)

There is no non-negative row vector in the row space of the ${\mathbf{B}}_0$ after s times of transformation.

Let:

$$\overline{\mathbf{B}}=\left(\begin{array}{ccc}{b}_{s+1,N_1+\cdots +N_s+1}& \cdots & b_{s+1,N-M}\\ ⋮& \ddots & ⋮\\ b_{M,N_1+\cdots +N_s+1}& \cdots & b_{M,N-M}\end{array}\right)$$

(9)

(2)

Cover Order. At the end of the above structural arrangement, we arrive at the conclusion that the cover order of $\mathbf{A}$ is $R_c\left(\mathbf{A}\right)={\sum }_{i=1}^s{N}_i+s$ and $s\le M$.

The next theorem states the property of the final échelon form of the matrix from which the cover order of $\mathbf{A}$ can be deduced.

Theorem 5. 

For any $M\times N$ real matrix $\mathbf{A}$, there exists an elementary matrix $\mathbf{E}$ and a permutation matrix $\mathbf{P}$ such that $\mathbf{E}\mathbf{A}\mathbf{P}=\left(\mathbf{I},\mathbf{B}\right)$, where $\mathbf{I}\in {\mathbb{R}}^{R_r\times R_r}$, $\mathbf{B}\in {\mathbb{R}}^{R_r\times (N-R_r)}$, and $R_r$ is the rank of the matrix $\mathbf{A}$. Then $\mathbf{B}$ either:

1. 

Contains at least one non-negative row;

2. 

Contains at least one negative column vector, or there exists one nonpositive column vector, but the same row position where the zero lies will be negative in some other columns of $\mathbf{B}$.

Proof. 

We shall prove the result by induction. Without loss of generality, we can assume that the matrix $\mathbf{A}$ has full rank. Indeed, the proof is based on the following steps: (i) Iteration $N-M=1$, i.e., $\mathbf{EAP}=(\mathbf{I},\mathbf{b})$, where $\mathbf{b}\in {\mathbb{R}}^M$. If $\mathbf{b}$ contains at least one positive element, then $\mathbf{A}$ has full cover. If $\mathbf{b}$ is a negative vector, then $\mathbf{A}$ has zero cover. If $\mathbf{b}$ is a nonpositive vector, then the cover order of $\mathbf{A}$ equals the number of zero terms. (ii) The result holds true for iteration $N-M=K+1$ given that it holds true for iteration $N-M=K$. We prove the desired result in the following:

Suppose that for $N-M=K$, the above conclusion holds, i.e., if $R_c\left(\mathbf{A}\right)>0$, then $\mathbf{A}$ can be transformed into $\left(\mathbf{I},\mathbf{B}\right)$. Let $b_{ij}$ be the $ij$-th element in $\mathbf{B}$, for $i=1,2,\cdots ,M$, $j=1,\cdots ,K$. We have Equation (8) hold and $R_c\left(\mathbf{A}\right)={\sum }_{i=1}^s{N}_i+s$. In addition, let $\overline{\mathbf{B}}$ be the form in Equation (9) with $K=N-M$, and $\overline{\mathbf{B}}$ either contains at least one negative column or has one nonpositive column, but the position where the zero lies will be negative in some other column of $\overline{\mathbf{B}}$. In the following, we will prove that if the above conclusion holds for $N-M=K$, then this conclusion will also hold when $N-M=K+1$.

When $N-M=K+1$, we can assume that $\mathbf{A}=\left(\mathbf{I},{\mathbf{b}}_1,\cdots ,{\mathbf{b}}_K,{\mathbf{b}}_{K+1}\right)$, where $\mathbf{I}\in {\mathbb{R}}^{M\times M}$ and ${\mathbf{b}}_i\in {\mathbb{R}}^M$, for $i=1,\cdots ,K+1$. Without considering the ${\mathbf{b}}_{K+1}$, we denote the remaining part in $\mathbf{A}$ as $\overline{\mathbf{A}}$, which equals $(\mathbf{I},{\mathbf{b}}_1,\cdots ,{\mathbf{b}}_K)$. According to the assumption for $N-M=K$, $\overline{\mathbf{A}}$ can be transformed into échelon form and we let $R_c\left(\overline{\mathbf{A}}\right)={\sum }_{i=1}^s{N}_i+s$. By considering the corresponding ${\mathbf{b}}_{K+1}$ with the échelon form of $\overline{\mathbf{A}}$ (apply the same row permutation to ${\mathbf{b}}_{K+1}$ as $\overline{\mathbf{A}}$ permutes in the échelon transformation and we still use ${\mathbf{b}}_{K+1}$ to denote it after the permutation), we can notice that if $b_{1,K+1}>0$, $R_c\left(\mathbf{A}\right)={\sum }_{i=1}^s{N}_i+s+1$. If $b_{1,K+1}=0$, we can perform the following process from the second row. Therefore, in the following, we will consider the case when $b_{1,K+1}<0$. According to Theorem 4 and Lemma 3, the following steps can be taken to make the first row nonpositive and move it to the last row without affecting the cover order of $\mathbf{A}$.

Step 1

Let $m=max\left\{-\frac{b_{j1}}{b_{11}},\cdots ,-\frac{b_{j,K+1}}{b_{1,K+1}}\right\}$, where $b_{j1}{b}_{11}<0$,⋯, $b_{j,K+1}{b}_{1,K+1}<0$. Multiply the first row of $\mathbf{A}$ with m, and add the product to i-th row, for $i=2,3,\cdots ,M$. We will have ${\mathbf{A}}_{\left(1\right)}$.

Step 2

Use (-1) times the first row of ${\mathbf{A}}_{\left(1\right)}$ to obtain ${\mathbf{A}}_{\left(2\right)}$.

Step 3

Let $t_2=\frac{b_{2,K+1}}{b_{1,K+1}}+m,t_3=\frac{b_{3,K+1}}{b_{1,K+1}}+m,\cdots ,t_M=\frac{b_{M,K+1}}{b_{1,K+1}}+m$ and let ${\mathbf{a}}_j^T$ be the j-th row of ${\mathbf{A}}_{\left(2\right)}$. Then by adding ${\mathbf{a}}_1^T{t}_j$ to the j-the row in ${\mathbf{A}}_{\left(2\right)}$, where $j=2,3,\cdots ,M$. We will have ${\mathbf{A}}_{\left(3\right)}$.

Step 4

Multiplying the first row of ${\mathbf{A}}_{\left(3\right)}$ with $-\frac{1}{b_{1,K+1}}$ and exchanging the position of the first column with the last column, we will obtain ${\mathbf{A}}_{\left(4\right)}$.

Step 5

Permuting the rows and columns so that the first row in the right-hand side of ${\mathbf{A}}_{\left(4\right)}$ is moved to the last row, as well as securing the left-hand side identity matrix structure. After this, we will have ${\mathbf{A}}_{\left(5\right)}$.

Step 6

Without considering the last column of ${\mathbf{A}}_{\left(5\right)}$, rearranging the rows and columns of the first $(M+K)$ columns of it, we will obtain a new échelon form matrix ${\overline{\mathbf{A}}}_{\left(5\right)}$ and $R_c\left({\overline{\mathbf{A}}}_{\left(5\right)}\right)={\sum }_{i=1}^{s^{\left(2\right)}}{N}_i^{\left(2\right)}+s^{\left(2\right)}$. By considering the corresponding ${\overline{\mathbf{b}}}_{K+1}$ with the échelon form of ${\overline{\mathbf{A}}}_{\left(5\right)}$, we can notice that if ${\overline{b}}_{1,K+1}>0$, then $R_c\left(\mathbf{A}\right)={\sum }_{i=1}^{s^{\left(2\right)}}{N}_i^{\left(2\right)}+s^{\left(2\right)}+1$. If ${\overline{b}}_{1,K+1}<0$, we can repeat the above steps.

Finally, after either t times transformation, there exists one $b_{1,K+1}>0$, such that the first row of the new matrix is non-negative and $R_c\left(\mathbf{A}\right)={\sum }_{i=1}^{s^{\left(t\right)}}{N}_i^{\left(t\right)}+s^{\left(t\right)}+1$, or $R_c\left(\mathbf{A}\right)=0$ and there exists at least one column ($(K+1)$-th column of $\mathbf{A}$) which is negative.    □

An important indication given by Theorem 5 is that when the first scenario occurs, then the cover order of $\mathbf{A}$ can be determined by the steps as shown in the above échelon transformation; otherwise, $R_c\left(\mathbf{A}\right)=0$.

4.3. Some Properties of the Échelon Form

We observe from the results of échelon transformation that the final échelon form of a matrix is not unique, and under different circumstances, different forms may be required. It is thus interesting to investigate the specific échelon form for special cases, especially for a low-rank matrix $\mathbf{A}$.

1.

Let $\mathbf{A}\in {\mathbb{R}}^{M\times N}$ and $R_r\left(\mathbf{A}\right)=2$. If $\mathbf{A}$ has full cover, then $\mathbf{A}$ can be transformed into:

$$\mathbf{A}\to \left(\begin{array}{cc}{\mathbf{I}}_2& {\mathbf{B}}_{2\times (N-2)}\\ {\mathbf{0}}_{(M-2)\times 2}& {\mathbf{0}}_{(M-2)\times (N-2)}\end{array}\right)$$

(10)

where $\mathbf{B}$ is a non-negative matrix.

Proof. 

Without loss of generality, suppose that $M=R_r\left(\mathbf{A}\right)=2$. If $\mathbf{A}$ has full cover, then by Theorem 5, $\mathbf{A}$ can be transformed into:

$$\left(\begin{array}{cccccc}1& 0& b_{11}& b_{12}& \cdots & b_{1,(N-2)}\\ 0& 1& b_{21}& b_{22}& \cdots & b_{2,(N-2)}\end{array}\right)$$

where $b_{11},b_{12},\cdots ,b_{1,(N-2)}>0$. If $b_{2i}<0$, where $i\in \{1,\cdots ,N-2\}$, let:

$$t=\underset{i\in \{1,\cdots ,N-2\}}{max}\left\{-\frac{b_{2i}}{b_{1i}},b_{2i}<0\right\}=-\frac{b_{2j}}{b_{1j}}$$

Using t times the first row of $\mathbf{A}$ and adding the product to the second row of it, in the next step, multiply the first row of the above matrix with $\frac{1}{b_{1j}}$ and exchange the first column with the j-th column so that the identity matrix structure in the left-hand side part can be guaranteed. After these steps, we obtain a matrix $\mathbf{B}$ which has two non-negative row vectors.    □

2.

For a rank-2 matrix $\mathbf{A}$, we also have the following property:

Theorem 6. 

Let $\mathbf{A}\in {\mathbb{R}}^{M\times N}$ and $R_r\left(\mathbf{A}\right)=2$. Then $\mathbf{A}$ has zero cover if and only if it can be transformed into the form:

$$\mathbf{E}\mathbf{A}\mathbf{P}=\left(\begin{array}{ccc}{\mathbf{I}}_2& {\mathbf{B}}^{+}& {\mathbf{B}}^{-}\\ {\mathbf{0}}_{\left(N-2\right)\times 2}& \mathbf{0}& \mathbf{0}\end{array}\right)$$

(11)

where all the elements in ${\mathbf{B}}^{+}$ are non-negative, while the elements in ${\mathbf{B}}^{-}$ are all nonpositive. Specifically, ${\mathbf{B}}^{-}$ contains at least one column which is a negative vector, or two non-negative vectors with their negative terms lie in different rows.

Proof. 

Without loss of generality, we can assume that $\mathbf{A}$ has full rank.

Sufficiency:  Given a zero-cover matrix $\mathbf{A}$, then by Theorem 5, it can be transformed into $(\mathbf{I},\mathbf{B})$, with $b_{ij}$ being the $ij$-th element in $\mathbf{B}$, where $i\in \{1,2\}$, $j\in \{1,\cdots ,N-2\}$. Let $t={max}_{i\in \{1,\cdots ,N-2\}}\{-\frac{b_{2i}}{b_{1i}},b_{1i}{b}_{2i}<0\}=-\frac{b_{2j}}{b_{1j}}$. We multiply the first row of the above transformed matrix with t, and add the product to the second row. Then, we multiply the first row of the resulting matrix with $\frac{1}{b_{1j}}$ and exchange the first column with the j-th column to ensure that the left-hand side part remains an identity matrix. This results in a matrix of the form:

$$\begin{array}{c}\hfill \left(\begin{array}{cccccccc}1& 0& \frac{b_{11}}{b_{1j}}& & \cdots & \frac{1}{b_{1j}}& \cdots & \frac{b_{1,N-2}}{b_{1j}}\\ 0& 1& b_{21}-b_{11}\frac{b_{2j}}{b_{1j}}& & \cdots & -\frac{b_{2j}}{b_{1j}}& \cdots & b_{2,N-2}-b_{1,N-2}\frac{b_{2j}}{b_{1j}}\end{array}\right)\end{array}$$

If $b_{1i}>0$ and $i\in \{1,\cdots ,N-2\}$, then $b_{2i}-b_{1i}\frac{b_{2j}}{b_{1j}}=b_{1i}\left(\frac{b_{2i}}{b_{1i}}-\frac{b_{2j}}{b_{1j}}\right)>0$. If $b_{1i}<0$, then for those $b_{2i}<0$, we have $b_{2i}-b_{1i}\frac{b_{2j}}{b_{1j}}<0$, and if $b_{2i}>0$, the sign of $\left(b_{2i}-b_{1i}\frac{b_{2j}}{b_{1j}}\right)$ is uncertain. After the above steps, and by performing some certain column permutations, the matrix $\mathbf{A}$ can be transformed into the form $\left(\mathbf{I},{\mathbf{B}}_{\left(1\right)},{\mathbf{B}}_{\left(2\right)},{\mathbf{B}}_{\left(3\right)}\right)$, where ${\mathbf{B}}_{\left(1\right)}$ is a non-negative matrix, ${\mathbf{B}}_{\left(3\right)}$ is a nonpositive matrix, and the elements in the first row of ${\mathbf{B}}_{\left(2\right)}$ are all negative, while the elements in the second row of it are all positive. To simplify the discussion, we can write the above matrix as $(\mathbf{I},{\mathbf{B}}^{\left(1\right)})$, with $b_{ij}^{\left(1\right)}$ being the $ij$-th element in ${\mathbf{B}}^{\left(1\right)}$, where $i\in \{1,2\}$, $j\in \{1,\cdots ,N-2\}$. Then, we let $m={max}_{i\in \{1,\cdots ,N-2\}}\{-\frac{b_{1i}^{\left(1\right)}}{b_{2i}^{\left(1\right)}},b_{2i}^{\left(1\right)}{b}_{1i}^{\left(1\right)}<0\}=-\frac{b_{1s}^{\left(1\right)}}{b_{2s}^{\left(1\right)}}$. We multiply the second row of the above matrix by m and add the product to the first row. Then, multiplying the second row of the resulting matrix with $\frac{1}{b_{2s}^{\left(1\right)}}$ and exchanging the second column with the s-th column so that the identity matrix structure on the left-hand part can be ensured, we arrive at the following matrix:

$$\begin{array}{c}\hfill \left(\begin{array}{cccccccc}1& 0& b_{11}^{\left(1\right)}-b_{21}^{\left(1\right)}\frac{b_{1s}^{\left(1\right)}}{b_{2s}^{\left(1\right)}}& & \cdots & -\frac{b_{1s}^{\left(1\right)}}{b_{2s}^{\left(1\right)}}& \cdots & b_{1,N-2}^{\left(1\right)}-b_{2,N-2}^{\left(1\right)}\frac{b_{1s}^{\left(1\right)}}{b_{2s}^{\left(1\right)}}\\ 0& 1& \frac{b_{21}^{\left(1\right)}}{b_{2s}^{\left(1\right)}}& & \cdots & \frac{1}{b_{2s}^{\left(1\right)}}& \cdots & \frac{b_{2,N-1}^{\left(1\right)}}{b_{2s}^{\left(1\right)}}\end{array}\right)\end{array}$$

In the above matrix, we have if $b_{2i}^{\left(1\right)}>0$, where $i\in \{1,\cdots ,N-2\}$, then $b_{1i}^{\left(1\right)}-b_{2i}^{\left(1\right)}\frac{b_{1s}^{\left(1\right)}}{b_{2s}^{\left(1\right)}}>0$, and if $b_{2i}^{\left(1\right)}<0$, then $b_{1i}^{\left(1\right)}-b_{2i}^{\left(1\right)}\frac{b_{1s}^{\left(1\right)}}{b_{2s}^{\left(1\right)}}<0$. As a result, if $\mathbf{A}$ has zero cover, then it can be transformed into the right-hand side form in Equation (11).

Necessity: Suppose that $\mathbf{A}$ can be transformed into the form in Equation (11). Then, consider the case when ${\mathbf{B}}^{-}$ contains two nonpositive vectors having their negative terms in different rows. Then $\mathbf{Ax}=\mathbf{0}$ can be written as:

$$\left(\begin{array}{ccccc}{\mathbf{I}}_{2\times 2}& {\mathbf{B}}^{+}& {\overline{\mathbf{B}}}^{-}& {\mathbf{b}}_1& {\mathbf{b}}_2\\ {\mathbf{0}}_{\left(N-2\right)\times 2}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\end{array}\right)\times {\left(u_1,u_2,{\mathbf{x}}^{+},{\mathbf{x}}^{-},v_1,v_2\right)}^T=\mathbf{0}$$

where ${\mathbf{b}}_1={\left(b_1,0\right)}^T,{\mathbf{b}}_2={\left(0,b_2\right)}^T$, and $b_1,b_2$ are negative, and ${\overline{\mathbf{B}}}^{-}$ is the matrix formed by deleting ${\mathbf{b}}_1$ and ${\mathbf{b}}_2$ from ${\mathbf{B}}^{-}$. Then we will have:

$$\left(\begin{array}{c}{u}_1\\ u_2\end{array}\right)=\left(\begin{array}{c}{v}_1\\ v_2\end{array}\right)-{\mathbf{B}}^{+}{\mathbf{x}}^{+}-{\overline{\mathbf{B}}}^{-}{\mathbf{x}}^{-}$$

Now, since $\mathbf{x}$ is the solution and must be positive, we can let the elements in ${\mathbf{x}}^{+}$ and ${\mathbf{x}}^{-}$ take any positive value. If we let $v_1$ and $v_2$ be positive and large enough, we can still obtain positive $u_1$ and $u_2$. In this case, all elements in $\mathbf{x}$ are positive and satisfy the equation $\mathbf{Ax}=\mathbf{0}$. By Theorem 1, $\mathbf{A}$ has zero cover.

This completes the proof of the theorem.    □

5. Cover Order and Linear Programming

In this part, we present a systematic procedure using the concept of hyper-rectangle cover for solving LP problems.

5.1. Linear Programming (LP) Problem

The LP problem [16], in general, can be stated as:

$$\begin{array}{cc}\hfill min& {\mathbf{c}}^T\mathbf{x}\\ \hfill \mathrm{subject}\mathrm{to}& \mathbf{Ax}=\mathbf{b}\\ \hfill & \mathbf{x}\ge \mathbf{0}\end{array}$$

(12)

where $\mathbf{A}\in {\mathbb{R}}^{M\times N}$, with $M<N$, $\mathbf{b}\in {\mathbb{R}}^M$, and $\mathbf{c},\mathbf{x}\in {\mathbb{R}}^N$. We can assume that $\mathbf{A}$ has full rank in general since redundant or inconsistent linear equations can always be detected and removed. The feasibility set of the above LP problem is:

$${\mathcal{F}}_1=\left\{\mathbf{x}\in {\mathbb{R}}_{+}^N:\mathbf{Ax}=\mathbf{b}\right\}\subset {\mathbb{R}}_{+}^N$$

(13)

From the necessary and sufficient condition for the existence of non-negative solution for a nonhomogeneous system of linear equations developed in Theorem 2, we can directly obtain the necessary and sufficient condition that guarantees the nonempty feasibility set of the LP problem. This is stated in the following theorem:

Theorem 7. 

The feasibility set ${\mathcal{F}}_1$ of the LP problem is nonempty iff $R_c\left(\tilde{\mathbf{A}}\right)\le R_c\left(\mathbf{A}\right)$, where $\tilde{\mathbf{A}}=(\mathbf{A},-\mathbf{b})$.

Letting $z={\mathbf{c}}^T\mathbf{x}$; then, by adding the objective function into the constraints, the above LP problem can be restated as:

$$\begin{array}{cc}\hfill min& z\\ \hfill \mathrm{subject}\mathrm{to}& \left(\begin{array}{c}\mathbf{A}\\ {\mathbf{c}}^T\end{array}\right)\mathbf{x}=\left(\begin{array}{c}\mathbf{b}\\ z\end{array}\right)\\ \hfill & \mathbf{x}\ge \mathbf{0}\end{array}$$

(14)

We denote $\left(\begin{array}{c}\mathbf{A}\\ {\mathbf{c}}^T\end{array}\right)$ as ${\mathbf{A}}_c$, $\left(\begin{array}{cc}\mathbf{A}& -\mathbf{b}\\ {\mathbf{c}}^T& -z\end{array}\right)$ as $\mathbf{A}\left(z\right)$. By applying the échelon transformation to $\mathbf{A}\left(z\right)$ without changing the position of the last row and the last column, we have:

$$\mathbf{A}\left(z\right)\to \left(\begin{array}{ccc}{\mathbf{I}}_{(M+1)\times (M+1)}& {\mathbf{B}}_{(M+1)\times (N-M-1)}& \mathbf{f}z+\mathbf{g}\end{array}\right)$$

(15)

where $\mathbf{f}$ and $\mathbf{g}$ are $(M+1)\times 1$ column vectors. To simplify the analysis, in the following, we separate $\mathbf{A}\left(z\right)$ into two parts and let:

$$\tilde{\mathbf{A}}=\left(\begin{array}{cc}{\mathbf{I}}_{(M+1)\times (M+1)}& {\mathbf{B}}_{(M+1)\times (N-M-1)}\end{array}\right)\mathrm{and}\tilde{\mathbf{b}}=\mathbf{f}z+\mathbf{g}$$

(16)

We have the following observations:

Property 1. 

From Theorem 2, in order to have a nonempty feasibility set for this LP problem, adding $\tilde{\mathbf{b}}$ to the right-hand side of $\tilde{\mathbf{A}}$ should not increase the cover order of $\tilde{\mathbf{A}}$. In other words, the cover order of $\mathbf{A}\left(z\right)$ should be less than or equal to the cover order of ${\mathbf{A}}_c$.

Property 2. 

In a minimization problem, if the uncovered variable has a negative coefficient in the objective function and has negative or zero coefficients in all constraints in the échelon form, then the objective function is unbounded over the feasible region.

5.2. Three Possibilities of the Solution

Based on Property 1, we now analyze the possibilities of the solutions and the optimal value of the objective function of the LP problem under the three conditions: (1) $\tilde{\mathbf{A}}$ has full cover; (2) $0<R_c\left(\tilde{\mathbf{A}}\right)<N$; (3) $\tilde{\mathbf{A}}$ has zero cover, resulting in the following theorem:

Theorem 8. 

For the LP problem given by Equation (14): If $\tilde{\mathbf{A}}$ has full cover and the matrix $\mathbf{B}$ in $\tilde{\mathbf{A}}$ is a non-negative matrix, then the LP problem has optimal solution if and only if ${\tilde{b}}_i=f_{i}z+g_i\le 0$, $i=1,2,\cdots ,R_r$. By solving these inequalities, we will have the range of z, which is:

$$\begin{array}{c}\hfill max\left\{-\frac{g_i}{f_i^{(+)}},i\in \{1,\cdots ,R_r\}\right\}\le z\le min\left\{-\frac{g_i}{f_i^{(-)}},i\in \{1,\cdots ,R_r\}\right\},\end{array}$$

(17)

where $f_i^{(+)}$ and $f_i^{(-)}$ are the positive and negative terms in the first $R_r$ elements of $\tilde{\mathbf{b}}$, respectively.

Proof. 

The proof of the above theorem follows directly from Property 1.    □

It should be noted that if the constraint of z in Theorem 8 is contradictory, i.e., if

$$\begin{array}{c}\hfill min\left\{-\frac{g_i}{f_i^{(-)}},i\in \{1,\cdots ,R_r\}\right\}<max\left\{-\frac{g_i}{f_i^{(+)}},i\in \{1,\cdots ,R_r\}\right\},\end{array}$$

(18)

then the feasibility set of this linear program is empty: i.e., ${\mathcal{F}}_1=\varnothing$. In other words, we are not able to find any feasible solution to this LP problem in this case. In addition, if there is no lower bound of z, i.e., $max\left\{-\frac{g_i}{f_i^{(+)}},i\in \{1,\cdots ,R_r\}\right\}$ in Equation (17) can be negative infinity, then the objective function in this minimization problem is unbounded.

By the same argument, obtaining the maximum value of z can also be achieved by solving the above inequalities. The maximum value will then be:

$$\begin{array}{c}\hfill maxz=min\{-\frac{g_i}{f_i^{(-)}},i\in \{1,\cdots ,R_r\}\}.\end{array}$$

(19)

If $\tilde{\mathbf{A}}$ has full cover, but the matrix $\mathbf{B}$ is not a non-negative matrix, then let $\mathcal{I}\subseteq \{1,\cdots ,R_r\}$ be the index set of the non-negative rows in $\tilde{\mathbf{A}}$. According to the assumption in échelon transformation, the first non-negative row vector in $\tilde{\mathbf{A}}$ contains the largest number of positive terms and the number is $N_1$. Then the optimal value of the LP problem can be obtained by performing the following steps.

Cover Method (Minimization Form)

Step 1.

Solving $f_{i}z+g_i\le 0$, for $i\in \mathcal{I}$ and a candidate minimal value of z is:

$$z_0=max\left\{-\frac{g_i}{f_i^{(-)}},i\in \mathcal{I}\right\}=-\frac{g_s}{f_s^{(-)}}$$

Step 2.

If $z_0$ satisfies:

$$max\left\{-\frac{g_k}{f_k^{(-)}},k\in \{1,\cdots ,R_r\}\setminus \mathcal{I}\right\}\le z_0\le min\left\{-\frac{g_k}{f_k^{(+)}},k\in \{1,\cdots ,R_r\}\setminus \mathcal{I}\right\}$$

then the process ends and the optimal value is obtained, which is

$$z_{min}=z_0=max\left\{-\frac{g_i}{f_i^{(-)}},i\in \mathcal{I}\right\}$$

Otherwise, there exist some $k\in \{1,\cdots ,R_r\}\setminus \mathcal{I}$ such that $f_k{z}_0+g_k>0$, i.e., we have $R_c\left(\mathbf{A}\left(z\right)\right)>R_c\left({\mathbf{A}}_c\right)$, then the process continues.

Step 3.

Choose column $j_k$ to pivot in (i.e., introduce into the basis variable) by:

$$-\frac{b_{1,j_k}}{b_{k,j_k}}=min\left\{-\frac{b_{1j}}{b_{kj}},b_{kj}<0,1\le j\le N_1\right\}$$

Step 4.

Choose row $\overline{k}$ to pivot in (i.e., drop from the basis variable) by:

$$\frac{f_{\overline{k}}{z}_0+g_{\overline{k}}}{b_{\overline{k},j_k}}=min\left\{\frac{f_k{z}_0+g_k}{b_{k{j}_k}},b_{kj}<0,f_k{z}_0+g_k>0\right\}$$

Step 5.

Replace the $\overline{k}$-th column with the $(M+j_k)$-th column and re-establish the échelon form.

Step 6.

If the matrix $\mathbf{B}$ is a non-negative matrix in the new échelon form, then the process ends and the optimal value is obtained, which is

$$z_0=max\left\{-\frac{g_i^{new}}{f_i^{(-)new}},i\in \{1,2,\cdots ,R_r\}\right\}$$

Otherwise, the process continues.

Step 7.

Return to step 1.

The whole pivot process each time is performed by using $-\frac{b_{i,j_k}}{b_{\overline{k}},j_k}$ times the $\overline{k}$-th row in $\tilde{\mathbf{A}}$, and adding the product into i-th row, for $i=1,2,\cdots ,R_r$. Then we divide the $\overline{k}$-th row with $b_{\overline{k},j_k}$, and the $(M+j_k)$-th column becomes ${\mathbf{e}}_{\overline{k}}$. Next, we exchange the position of the $(M+j_k)$-th column and the $\overline{k}$-th column. After this process, $f_{\overline{k}}z+g_{\overline{k}}$ is negative and the structure of the identity matrix ahead is reserved. The above computational procedures of the cover method in solving the LP problem can be summarized in the flow chart of Figure 3.

This simple step-by-step method provides an attractive alternative approach to the LP problem.

The following example provides a clear illustration of the cover method procedure. Here, $\tilde{\mathbf{A}}$ has full cover but the matrix $\mathbf{B}$ in $\tilde{\mathbf{A}}$ is not a non-negative matrix.

Example 3. 

$$\begin{array}{cc}\hfill min& -x_1-x_2\\ & 2x_1+x_2+x_3=12\\ & x_1+2x_2+x_4=9\\ & x_1,x_2,x_3,x_4\ge 0\end{array}$$

Letting $z={\mathbf{c}}^T\mathbf{x}$ and adding the objective function into the constraints, we will have the following augmented matrix:

$$\begin{array}{c}\hfill \tilde{\mathbf{A}}\left(z\right)=\left(\begin{array}{ccccc}2& 1& 1& 0& -12\\ 1& 2& 0& 1& -9\\ -1& -1& 0& 0& -z\end{array}\right)\end{array}$$

Applying the échelon transformation to $\tilde{\mathbf{A}}\left(z\right)$ without changing the position of the last column, we have

$$\begin{array}{c}\hfill \tilde{\mathbf{A}}\left(z\right)\to \left(\begin{array}{ccccc}1& 0& 0& 1& -9-z\\ 0& 1& 0& -1& 9+2z\\ 0& 0& 1& 1& -21-3z\end{array}\right)\end{array}$$

Since we exchange the position of the first two rows during this transformation, the corresponding positions of variables are also exchanged. According to Theorem 8, in order to have the feasible solutions for this LP problem, the following two conditions should be satisfied at the same time: $-9-z\le 0$ and $-21-3z\le 0$. By solving these two inequalities, we will have a candidate optimal value of z, which is $z_0=max\{-9,-7\}=-7$. Since $z_0\le min\left\{-\frac{g_2}{f_2}\right\}=-\frac{9}{2}$, then the optimal value of the objective function is $z^{*}=-7$, and the corresponding optimal solution is ${\mathbf{x}}^{*}={(5,2,0,0)}^T$.

Similarly, for the case when $0<R_c\left(\tilde{\mathbf{A}}\right)<N$, we can also apply the above procedures to obtain the optimal value of the objective function and the optimal solution towards the LP problem by changing the definition of the index set $\mathcal{I}$ and the range of k. For this case, we consider $i\in \mathcal{J}$, and $\mathcal{J}\subseteq \{1,\cdots ,s\}$ is the index set of the non-negative rows in the first s rows of $\tilde{\mathbf{A}}$, where s is obtained through the échelon transformation, and $k\in \{1,2,\cdots ,s\}\setminus \mathcal{J}$.

For the zero-cover matrix, the status of the solution for the LP problem is given in the following theorem.

Theorem 9. 

For a full rank matrix $\tilde{\mathbf{A}}$, if it has zero cover, then the LP problem is feasible but unbounded.

Proof. 

Since adding any column to the right-hand side of a zero-cover matrix will still arrive at a matrix with zero-cover, the feasibility set ${\mathcal{F}}_1$ is always nonempty in this case. However, according to Theorem 5, a zero-cover matrix can be transformed into a structure which has at least one negative column or has one nonpositive column, but the same row position where the zero lies will be negative in some other column(s) of this structure. Thus, by Property 2, the objective function is unbounded over the feasible domain for the case when $\tilde{\mathbf{A}}$ has zero cover.    □

5.3. Feasible Solutions for the LP Problem

With the échelon form and the specific structure of the zero-cover matrix, we are able to obtain a series of feasible solutions for any given LP problem. The detailed process is given in the following:

As we know, $\left(\tilde{\mathbf{A}},\tilde{\mathbf{b}}\right)$ is an échelon form matrix, where $\tilde{\mathbf{A}}\in {\mathbb{R}}^{(M+1)\times N}$ and $\tilde{\mathbf{b}}\in {\mathbb{R}}^{M+1}$. Then the échelon form can be divided into the following blocks:

$$\begin{array}{c}\hfill \left(\tilde{\mathbf{A}},\tilde{\mathbf{b}}\right)=\left(\begin{array}{ccccc}{\mathbf{I}}_s& \mathbf{0}& {\mathbf{B}}^{\left(1\right)}& {\mathbf{B}}^{\left(3\right)}& {\tilde{\mathbf{b}}}^{\left(1\right)}\\ \mathbf{0}& {\mathbf{I}}_{(M+1-s)}& {\mathbf{B}}^{\left(2\right)}& {\mathbf{B}}^{\left(4\right)}& {\tilde{\mathbf{b}}}^{\left(2\right)}\end{array}\right),\end{array}$$

(20)

where s is obtained through échelon transformation. Then by Theorem 1, in the system $\left(\tilde{\mathbf{A}},\tilde{\mathbf{b}}\right)\mathbf{x}=\mathbf{0}$, $\mathbf{x}\ge \mathbf{0}$, the covered variables $x_i$ are all zeros. As a result, we can ignore those covered column vectors in $\left(\tilde{\mathbf{A}},\tilde{\mathbf{b}}\right)$, which correspond to $\left(\begin{array}{cc}{\mathbf{I}}_s& {\mathbf{B}}^{\left(1\right)}\\ \mathbf{0}& {\mathbf{B}}^{\left(2\right)}\end{array}\right)$. In Equation (20), since ${\mathbf{B}}^{\left(3\right)}$ is a zero matrix and ${\tilde{\mathbf{b}}}^{\left(1\right)}$ is a zero vector, we only need to consider the remaining part of $\left(\tilde{\mathbf{A}},\tilde{\mathbf{b}}\right)$ which is $\left({\mathbf{I}}_{(M+1-s)},{\mathbf{B}}^{\left(4\right)},{\tilde{\mathbf{b}}}^{\left(2\right)}\right)$. Let us denote this part as $\left(\overline{\mathbf{A}},\overline{\mathbf{b}}\right)=\left(\mathbf{I},\overline{\mathbf{B}},\overline{\mathbf{b}}\right)=\left({\mathbf{I}}_{(M+1-s)},{\mathbf{B}}^{\left(4\right)},{\tilde{\mathbf{b}}}^{\left(2\right)}\right)$. The cover order of this matrix is zero. Thus, in order to obtain the feasible solution for the LP problem, we only need to solve the following system of linear equations, where the non-negative vector $\overline{\mathbf{x}}$ is the uncovered part in $\mathbf{x}$:

$$\left(\mathbf{I},\overline{\mathbf{B}},\overline{\mathbf{b}}\right)\overline{\mathbf{x}}=\mathbf{0}$$

(21)

For simplicity of discussion, we can assume that $\mathbf{I}\in {\mathbb{R}}^{m\times m}$, $\overline{\mathbf{B}}\in {\mathbb{R}}^{m\times (n-m)}$, and $\overline{\mathbf{b}}\in {\mathbb{R}}^m$. From Theorem 5, we know that the zero-cover matrix can be transformed to the form which contains at least one negative column, or has one nonpositive column, but the row position where the zero lies will be negative in some other column of the matrix. Without loss of generality, we can assume that the negative column appears in the first column of $\overline{\mathbf{B}}$, i.e., ${\left({\overline{b}}_{11},{\overline{b}}_{21},\cdots ,{\overline{b}}_{m1}\right)}^T$ is a negative column vector. Then the following procedure enables us to obtain a series of feasible solutions to the LP problem.

Suppose that $\overline{\mathbf{x}}={\left({\overline{x}}_1,\cdots ,{\overline{x}}_m,{\overline{x}}_{m+1},{\overline{x}}_{m+2}\cdots ,{\overline{x}}_n,{\overline{x}}_{n+1}\right)}^T$, where ${\overline{x}}_1,\cdots ,{\overline{x}}_m$ correspond to the column vectors in the $m\times m$ identity matrix, ${\overline{x}}_{m+1},{\overline{x}}_{m+2},\cdots ,{\overline{x}}_n$ correspond to the column vectors in $\overline{\mathbf{B}}$, and ${\overline{x}}_{n+1}$ corresponds to $\overline{\mathbf{b}}$ in the multiplication $\left(\mathbf{I},\overline{\mathbf{B}},\overline{\mathbf{b}}\right)\overline{\mathbf{x}}$. Then, by Equation (21), the first m elements in $\overline{\mathbf{x}}$ can be expressed as a linear combination of ${\overline{x}}_{m+1},\cdots ,{\overline{x}}_{n+1}$:

$$\begin{array}{c}\hfill {\overline{x}}_1=-{\overline{b}}_{11}{\overline{x}}_{m+1}-{\overline{b}}_{12}{\overline{x}}_{m+2}-\cdots -{\overline{b}}_{1(n-m)}{\overline{x}}_n-{\overline{b}}_1{\overline{x}}_{n+1}\\ \hfill ⋮\\ \hfill {\overline{x}}_m=-{\overline{b}}_{m1}{\overline{x}}_{m+1}-{\overline{b}}_{m2}{\overline{x}}_{m+2}-\cdots -{\overline{b}}_{m(n-m)}{\overline{x}}_n-{\overline{b}}_m{\overline{x}}_{n+1}\end{array}$$

(22)

In order to obtain a linearly independent feasible solution set, we first let the vector ${\left({\overline{x}}_{m+1},\cdots ,{\overline{x}}_{n+1}\right)}^T$ be a set of linearly independent vectors ${\left(L,1,0,\cdots ,0\right)}^T$, ${(L,0,1,\cdots ,0)}^T$, ⋯, ${(L,0,0,\cdots ,1)}^T$ successively. In addition, in order to satisfy the non-negativity constraints on the variable ${\overline{x}}_i$, $i=1,\cdots ,n+1$, we let:

$$\begin{array}{c}\hfill L=max\left\{-\frac{{\overline{b}}_{i2}}{{\overline{b}}_{11}},-\frac{{\overline{b}}_{i3}}{{\overline{b}}_{21},},\cdots ,-\frac{{\overline{b}}_{i(n-m)}}{{\overline{b}}_{m1}},-\frac{{\overline{b}}_i}{{\overline{b}}_{i1}}\right\},i=1,2,\cdots ,m\end{array}$$

(23)

We can then obtain a set of linear independent basic feasible solutions:

$$\begin{array}{c}\hfill {\mathbf{\alpha }}_1={\left(-{\overline{b}}_{11}L-{\overline{b}}_{12},\cdots ,-{\overline{b}}_{m1}L-{\overline{b}}_{m2},L,1,0,\cdots ,0\right)}^T\\ \hfill {\mathbf{\alpha }}_2={\left(-{\overline{b}}_{11}L-{\overline{b}}_{13},\cdots ,-{\overline{b}}_{m1}L-{\overline{b}}_{m3},L,0,1,\cdots ,0\right)}^T\\ \hfill ⋮\\ \hfill {\mathbf{\alpha }}_{n-m-1}={\left(-{\overline{b}}_{11}L-{\overline{b}}_{1n},\cdots ,-{\overline{b}}_{m1}L-{\overline{b}}_{mn},L,0,0,\cdots ,1,0\right)}^T\\ \hfill {\mathbf{\alpha }}_{n-m}={\left(-{\overline{b}}_{11}L-{\overline{b}}_1,\cdots ,-{\overline{b}}_{m1}L-{\overline{b}}_m,L,0,0,\cdots ,0,1\right)}^T\end{array}$$

(24)

Any convex combination of those basic feasible solutions, i.e.,

$$\begin{array}{c}\hfill \overline{\mathbf{x}}=k_1{\mathbf{\alpha }}_1+k_2{\mathbf{\alpha }}_2+\cdots +k_{n-m}{\mathbf{\alpha }}_{n-m}\end{array}$$

where the real numbers $k_i$ satisfy $k_i\ge 0$ and $k_1+\cdots +k_{n-m}=1$, is thus a solution of Equation (21). By padding the covered variables into $\overline{\mathbf{x}}$, we obtain a series of feasible solutions to the LP problem.

5.4. The Simplex Method and the Cover Method

In 1947, Dantzig developed an algorithm to solve the LP problem efficiently, called the simplex method.

The LP problem is to find the extreme point of this polytope where the objective function is the smallest (or largest) in value if such an extreme point exists. By moving along the edge of the polytope, the simplex method identifies these extreme points with better objective values. The process continues until the optimum objective value is reached, or an unbounded edge is visited. For an LP problem having a nonempty feasible region, the algorithm always terminates because of the finite number of extreme points in the polytope. In practice, the simplex method has shown remarkable efficiency. However, in 1972, Klee and Minty gave an example, the Klee–Minty cube [44], showing that the worst-case complexity of the simplex method is exponential time.

While the simplex method regards the objective value z in the canonical tableau of the LP problem as a variable, the cover method treats it as a constant. Given a linear program, the cover method first rewrites an LP problem into the form of Equation (14), and then $\mathbf{A}\left(z\right)$ is transformed into its échelon form. At this stage, if the matrix $\mathbf{B}$ in this échelon form is a non-negative matrix, then the optimum objective value can be determined directly according to Theorem 8. Thus, the computational complexity of this case is almost entirely determined by the complexity of échelon transformation. In the following, we will review the échelon transformation and analyze its computation complexity.

Consider a full rank matrix $\mathbf{A}\in {\mathbb{R}}^{M\times N}$ with $M<N$. The complexity of transforming $\mathbf{A}$ into an échelon form is $\mathcal{O}\left(M^{2}N\right)$. In the structure arrangement process of the échelon transformation, the row having the greatest number of nonzero elements is moved to the first row, while the nonzero elements in this row have been moved to the left side of $\mathbf{B}$. Meanwhile, the corresponding column permutation such that the identity matrix structure could be preserved is performed. Thus, the selection of the row having the greatest number of nonzero elements is completed. The next step takes away the columns of $\mathbf{A}$ corresponding to these nonzero elements in the first row and performs an échelon transformation on the remaining part of $\mathbf{A}$. Such an iteration of échelon transformation, each time taking a lower complexity, continues until the desired form is achieved. The complexity of the structural arrangement process is $\mathcal{O}\left(M^2(N-M)\right)$. Thus, the computation complexity of échelon transformation in solving this type of LP problem by cover method is $\mathcal{O}\left(M^{2}N\right)$.

It is observed, however, that if the matrix $\mathbf{B}$ is not a non-negative matrix, then the cover method for solving the LP problem will involve pivoting steps for which the complexity of the algorithm is no longer polynomial.

6. Cover Length

We first encountered the concept of cover length in Definition 1. In this section, we propose a method to determine the cover length of the covered variable $x_i$ associated with the i-th column vector $a_i$ in $\mathbf{A}\mathbf{x}$. In addition, we find a strong relationship between the problem of cover length determination and the non-negative least square (NNLS) problem such that we can obtain an analytical result of the NNLS problem by simply determining the cover length of the corresponding variable. We also include a discussion of the various algorithms for solving the NNLS problem and the cover length method developed here.

6.1. Determination of Cover Length

In general, the cover length is obtained by solving the following optimization problem:

Problem 1. 

Let $\mathbf{A}\in {\mathbb{R}}^{M\times N}$, $\mathbf{x}={\left\{x_1,x_2,\cdots ,x_N\right\}}^T\in {\mathbb{R}}_{+}^N$ and $x_N$ be covered in $\mathbf{A}\mathbf{x}$.

$$\begin{array}{cc}\hfill max& x_N\\ \hfill \mathrm{subject}\mathrm{to}& {\mathbf{x}}^T{\mathbf{A}}^T\mathbf{A}\mathbf{x}\le 1\end{array}$$

(25)

where $x_n\ge 0$ for $n=1,2,\cdots ,N$.

The maximum value of $x_N$ within the constraints is the cover length of the covered variable $x_N$. To solve the above optimization problem, let us form a Lagrangian function: $L(\mathbf{x},\mathsf{\lambda })=-x_N-{\sum }_{n=1}^N{\lambda }_n{x}_n+{\lambda }_{N+1}({\mathbf{x}}^T{\mathbf{A}}^T\mathbf{A}\mathbf{x}-1)/2$, where ${\lambda }_n>0$ for $n=1,2,\cdots ,N+1$. Then, the necessary and sufficient condition for ${\mathbf{x}}^{*}$ to be an optimal solution is that the following Karush–Kuhn–Tucker (KKT) condition must be satisfied:

$$\begin{array}{c}\hfill {\nabla L(\mathbf{x},\mathsf{\lambda })|}_{\mathbf{x}={\mathbf{x}}^{*},\mathsf{\lambda }={\mathsf{\lambda }}^{*}}=-{\mathbf{e}}_N-{\mathsf{\lambda }}^{*}+{\lambda }_{N+1}^{*}{\mathbf{A}}^T\mathbf{A}{\mathbf{x}}^{*}=\mathbf{0}\\ \hfill x_n^{*}{\lambda }_n^{*}=0\mathrm{for}n=1,2,\cdots ,N\\ \hfill {\lambda }_{N+1}^{*}\left({\left({\mathbf{x}}^{*}\right)}^T{\mathbf{A}}^T\mathbf{A}{\mathbf{x}}^{*}-1\right)=0\\ \hfill {\left({\mathbf{x}}^{*}\right)}^T{\mathbf{A}}^T\mathbf{A}{\mathbf{x}}^{*}\le 1\\ \hfill {\mathbf{x}}^{*}\ge \mathbf{0}\\ \hfill {\lambda }_{N+1}^{*}\ge 0,{\mathsf{\lambda }}^{*}\ge \mathbf{0}\end{array}$$

(26)

where the non-negative vector ${\mathsf{\lambda }}^{*}\in {\mathbb{R}}_{+}^N$ is associated with the optimal vector ${\mathbf{x}}^{*}$ such that $L({\mathbf{x}}^{*},{\mathsf{\lambda }}^{*})$ is a stationary point of $L(\mathbf{x},\mathsf{\lambda })$. On the other hand, we notice that

$${\mathbf{x}}^T{\mathbf{A}}^T\mathbf{A}\mathbf{x}=p_{NN}{\left(x_N+\frac{{\overline{\mathbf{p}}}_N^T{\overline{\mathbf{x}}}_N}{p_{NN}}\right)}^2+{\overline{\mathbf{x}}}_N^T\left({\overline{\mathbf{P}}}_{NN}-\frac{{\overline{\mathbf{p}}}_N{\overline{\mathbf{p}}}_N^T}{p_{NN}}\right){\overline{\mathbf{x}}}_N$$

(27)

where $\mathbf{P}={\mathbf{A}}^T\mathbf{A}$ is an $N\times N$ positive semidefinite (PSD) matrix, $p_{NN}$ is the $NN$-th element in $\mathbf{P}$, ${\overline{\mathbf{P}}}_{NN}$ is the $(N-1)\times (N-1)$ sub-matrix of $\mathbf{P}$ by deleting the N-th row and N-th column from it, ${\overline{\mathbf{p}}}_N$ is the $(N-1)\times 1$ vector generated by deleting the N-th entry from the N-th row of $\mathbf{P}$, and ${\overline{\mathbf{x}}}_N$ denotes the $(N-1)\times 1$ vector obtained by deleting the N-th entry from $\mathbf{x}$. Therefore, we can represent the KKT condition alternatively as:

$$\begin{array}{c}\hfill -{\overline{\mathsf{\lambda }}}_N^{*}+{\lambda }_{N+1}^{*}\left(\left(x_N^{*}+\frac{{\overline{\mathbf{p}}}_N^T{\overline{\mathbf{x}}}_N^{*}}{p_{NN}}\right){\overline{\mathbf{p}}}_N+\left({\mathbf{P}}_{NN}-\frac{{\overline{\mathbf{p}}}_N{\overline{\mathbf{p}}}_N^T}{p_{NN}}\right){\overline{\mathbf{x}}}_N^{*}\right)=\mathbf{0}\\ \hfill -1-{\lambda }_N^{*}+{\lambda }_{N+1}^{*}\left(p_{NN}{x}_N^{*}+{\overline{\mathbf{p}}}_N^T{\overline{\mathbf{x}}}_N^{*}\right)=0\\ \hfill x_n^{*}{\lambda }_n^{*}=0\\ \hfill {\lambda }_{N+1}^{*}\left({\left({\mathbf{x}}^{*}\right)}^T{\mathbf{A}}^T\mathbf{A}{\mathbf{x}}^{*}-1\right)=0\\ \hfill {\left({\mathbf{x}}^{*}\right)}^T{\mathbf{A}}^T\mathbf{A}{\mathbf{x}}^{*}\le 1\\ \hfill {\mathbf{x}}^{*}\ge \mathbf{0}\\ \hfill {\lambda }_{N+1}^{*}\ge 0,{\mathsf{\lambda }}^{*}\ge \mathbf{0}\end{array}$$

(28)

Here, ${\overline{\mathsf{\lambda }}}_N^{*}$ and ${\overline{\mathbf{x}}}_N^{*}$ denote, respectively, the $(N-1)\times 1$ vectors obtained by deleting the N-th entry from ${\mathsf{\lambda }}^{*}$ and ${\mathbf{x}}^{*}$. Since $x_N^{*}\ne 0$, we have ${\lambda }_{N+1}^{*}\ne 0$, and, thus, $x_N^{*}={\lambda }_{N+1}^{*}$. Using the KKT condition, the solution to Problem 1 is given in the following theorem:

Theorem 10. 

Let $\mathbf{A}$ be an $M\times N$ real matrix with its rank being R. Then, $x_n$ is covered in $\mathbf{A}\mathbf{x}$ if and only if there exists an invertible principal sub-matrix ${\mathbf{P}}_{i_1{i}_2\cdots i_r}$ of order r in ${\mathbf{A}}^T\mathbf{A}$ that includes the $nn$-th element ${\left[{\mathbf{A}}^T\mathbf{A}\right]}_{nn}$, such that the following two conditions are satisfied simultaneously:

1. 

${\mathbf{P}}_{i_1{i}_2\cdots i_r|i_j=n}^{-1}{\mathbf{e}}_j\ge \mathbf{0}$ and ${\left[{\mathbf{P}}_{i_1{i}_2\cdots i_r|i_j=n}^{-1}{\mathbf{e}}_j\right]}_j>0$;

2. 

$\det \left({\mathbf{P}}_{i_1\cdots i_r|i_j=n\to k}\right)\ge 0$ for $k\in \{1,\cdots ,N\}\setminus \{i_1,\cdots ,i_r\}$, where ${\mathbf{P}}_{i_1\cdots i_r|i_j=n\to k}$ is the sub-matrix of ${\mathbf{A}}^T\mathbf{A}$ by replacing the old row: $\left(p_{n,i_1},\cdots ,p_{n,i_r}\right)$ in ${\mathbf{P}}_{i_1\cdots i_r|i_j=n}$ with the new row $(p_{k,i_1},\cdots ,p_{k,i_r})$.

Then the cover length is given by $c_n\left(x_n\right)=\sqrt{{\left[{\left({\mathbf{P}}_{i_1{i}_2\cdots i_r|i_j=n}\right)}^{-1}\right]}_{nn}}$.

Proof. 

The KKT condition of Problem 1 can be simplified as: $\mathbf{P}\mathbf{x}=\mathbf{b},\mathbf{x}\ge \mathbf{0},\mathbf{b}\ge \mathbf{0},b_N>0$ and $x_i{b}_i=0$ for $i=1,2,\cdots ,N-1$, where $\mathbf{b}\in {\mathbb{R}}_{+}^N$. Let $\overline{\mathcal{N}}$ be the set consisting of all the indices of $x_i$ which are all positive in the variable $\mathbf{x}$. Denoting the cardinality of a set as $|·|$, we are able to find an $|\overline{\mathcal{N}}|\times |\overline{\mathcal{N}}|$ sub-matrix $\overline{\mathbf{P}}$ of $\mathbf{P}$, such that $\overline{\mathbf{P}}\overline{\mathbf{x}}={\mathbf{e}}_{|\overline{\mathcal{N}|}}$ with all $x_i$ in $\overline{\mathbf{x}}$ being uncovered variables in $\mathbf{x}$ and ${\overline{x}}_{|\overline{\mathcal{N}|}}=x_N$, i.e., the last entry in $\overline{\mathbf{x}}$ is equivalent to the last one in $\mathbf{x}$. Then there exists a full column rank matrix $\mathbf{T}\in {\mathbb{R}}^{|\overline{\mathcal{N}}|\times r}$, where $r\le |\overline{\mathcal{N}}|$, containing ${\overline{\mathbf{P}}}_{|\overline{\mathcal{N}|}}$ in $\overline{\mathbf{P}}$. Without loss of generality, we can let $\mathbf{T}=\left\{{\mathbf{t}}_1,\cdots ,{\mathbf{t}}_{r-1},{\overline{\mathbf{P}}}_{|\overline{\mathcal{N}}|}\right\}$ and we will have $\mathbf{T}\tilde{\mathbf{x}}={\mathbf{e}}_{|\overline{\mathcal{N}|}}$, where $\tilde{\mathbf{x}}\in {\mathbb{R}}_{+}^r$ and ${\tilde{x}}_r>0$. This can be proved in the following: Let $\mathbf{T}$ be the smallest set containing ${\overline{\mathbf{P}}}_{|\overline{\mathcal{N}}|}$, s.t. ${\mathbf{e}}_{|\overline{\mathcal{N}|}}\in \mathrm{cone}\mathbf{T}$, where $\mathrm{cone}\mathbf{T}=\mathrm{cone}\left\{{\mathbf{t}}_1,\cdots ,{\mathbf{t}}_{\mathrm{r}-1},{\overline{\mathbf{P}}}_{|\overline{\mathcal{N}}|}\right\}=$$\{{\theta }_1{\mathbf{t}}_1+\cdots +{\theta }_{r-1}{\mathbf{t}}_{r-1}+{\theta }_r{\overline{\mathbf{P}}}_{|\overline{\mathcal{N}}|}|{\theta }_i\ge 0\mathrm{for}i=1,\cdots ,r\}$. Then $\mathbf{T}$ is linearly independent; otherwise, there are ${\mu }_j\in \mathbb{R}$ (not all 0), s.t. ${\sum }_{j=1}^{r-1}{\mu }_j{\mathbf{t}}_j+{\mu }_r{\overline{\mathbf{P}}}_{|\overline{\mathcal{N}}|}=\mathbf{0}$. And there are ${\lambda }_j\ge 0$, s.t. ${\sum }_{j=1}^{r-1}{\lambda }_j{\mathbf{t}}_j+{\lambda }_r{\overline{\mathbf{P}}}_{|\overline{\mathcal{N}}|}={\mathbf{e}}_{|\overline{\mathcal{N}|}}$, where ${\lambda }_r>0$. Then, we have ${\sum }_{j=1}^{r-1}(\alpha {\mu }_j+{\lambda }_j){\mathbf{t}}_j+(\alpha {\mu }_r+{\lambda }_r){\overline{\mathbf{P}}}_{|\overline{\mathcal{N}}|}={\mathbf{e}}_{|\overline{\mathcal{N}|}}$. If ${\mu }_r\ge 0$, then let $\alpha ={max}_{1\le j\le r-1}\{-\frac{{\lambda }_j}{{\mu }_j},{\mu }_j>0\}=-\frac{{\lambda }_i}{{\mu }_i}$. Thus, for every $1\le j\le r-1$, ${\lambda }_j+\alpha {\mu }_j\ge 0$ and ${\lambda }_i+\alpha {\mu }_i=0$. Then, we can have a new $\tilde{\mathbf{x}}\in {\mathbb{R}}^{r-1}$ with the last element of it, which is ${\lambda }_r+\alpha {\mu }_r$, being positive, while the others are $r-2$ elements, which are expressed as ${\lambda }_j+\alpha {\mu }_j$, being non-negative. When ${\mu }_r<0$, we let $\alpha ={max}_{1\le j\le r-1}\{-\frac{{\lambda }_j}{{\mu }_j},{\mu }_j>0\}=-\frac{{\lambda }_i}{{\mu }_i}$. Then, we have a new $\tilde{\mathbf{x}}\in {\mathbb{R}}^{r-1}$ with the last element of it being positive while the others are non-negative in the same manner as the case when ${\mu }_r\ge 0$. As a result, we can always find a smaller set $\tilde{\mathbf{T}}$ containing ${\overline{\mathbf{P}}}_{|\overline{\mathcal{N}}|}$, s.t. ${\mathbf{e}}_{|\overline{\mathcal{N}|}}\in \mathrm{cone}\tilde{\mathbf{T}}$. Thus, $\mathbf{T}$ is linearly independent. According to the constraints of $\mathbf{x}$, $\tilde{\mathbf{x}}$ should be equivalent to $\overline{\mathbf{x}}$ and $\mathbf{T}=\overline{\mathbf{P}}$. As a result, $\overline{\mathbf{P}}$ is invertible. Since we have $\overline{\mathbf{P}}\overline{\mathbf{x}}={\mathbf{e}}_{|\overline{\mathcal{N}|}}$, where $\overline{\mathbf{x}}\in {\mathbb{R}}_{+}^r$ and ${\overline{x}}_r>0$, we will have ${\mathbf{P}}_{i_1{i}_2\cdots i_r|i_j=n}^{-1}{\mathbf{e}}_j\ge \mathbf{0}$ and the j-th element in it is positive. Until now, the first statement has been proven.

By using the new row $(p_{k,i_1},\cdots ,p_{k,i_r})$ to replace the old row $(p_{n,i_1},\cdots ,p_{n,i_r})$ in ${\mathbf{P}}_{i_1{i}_2\cdots i_r|i_j=n}$, we will have ${\mathbf{P}}_{i_1{i}_2\cdots i_r|i_j=n\to k}\overline{\mathbf{x}}=b_k{\mathbf{e}}_j$. To simplify the expression, we denote ${\mathbf{P}}_{i_1{i}_2\cdots i_r|i_j=n\to k}$ as ${\overline{\mathbf{P}}}_k$. If ${\overline{\mathbf{P}}}_k$ is invertible, then $x_n=\frac{b_k\left|{\overline{\mathbf{P}}}_{(r-1)\times (r-1)}\right|}{\left|{\overline{\mathbf{P}}}_k\right|}$, where ${\overline{\mathbf{P}}}_{(r-1)\times (r-1)}$ is the $\left(r-1\right)$-th order leading principle sub-matrix of ${\mathbf{P}}_{i_1{i}_2\cdots i_r}$. Since ${\mathbf{P}}_{i_1{i}_2\cdots i_r}$ is a positive definite matrix, it follows that $\left|{\overline{\mathbf{P}}}_{(r-1)\times (r-1)}\right|>0$. In addition, $b_k\ge 0$, $x_n>0$, then we have det$\left({\overline{\mathbf{P}}}_k\right)>0$. When $b_k=0$, det$\left({\overline{\mathbf{P}}}_k\right)=0$. As a result, det$\left({\overline{\mathbf{P}}}_k\right)\ge 0$, for  $k=1,2,\cdots ,N$ but $k\ne i_1,i_2,\cdots ,i_r$.

When the above conditions are all satisfied, the cover length of $x_n$ can be obtained directly, which is $\sqrt{{\left[{\left({\mathbf{P}}_{i_1{i}_2\cdots i_r|i_j=n}\right)}^{-1}\right]}_{nn}}$.    □

From the above result, we can also conclude that if there is no principal sub-matrix that can satisfy all the conditions, then the corresponding variable is uncovered within the constraint.

The following example illustrates how the above method can be used to obtain the cover length of the covered variable:

Example 4. 

Determine the cover length of covered variable $x_4$ given the following $4\times 4$ matrix and its PSD matrix:

$$\begin{array}{c}\hfill \mathbf{A}=\left(\begin{array}{cccc}-3& -2& -5& -2\\ 3& -5& 0& -4\\ 1& 3& 1& -3\\ 2& 2& 1& 4\end{array}\right),\mathbf{P}={\mathbf{A}}^T\mathbf{A}=\left(\begin{array}{cccc}23& -2& 18& -1\\ -2& 42& 15& 23\\ 18& 15& 27& 11\\ -1& 23& 11& 45\end{array}\right)\end{array}$$

We need to find out the principal sub-matrix that can satisfy all the conditions listed in Theorem 10. We first examine all the $2\times 2$ principal sub-matrices of $\mathbf{P}$ containing a negative element in the right upper side corner, since only such a principle sub-matrix of order-2 could satisfy the condition that the last column of its inverse is a positive vector. Inspection of the above PSD matrix shows that there is only one such principal sub-matrix: ${\mathbf{P}}_{14}=\left(\begin{array}{cc}23& -1\\ -1& 45\end{array}\right)$. We verify that ${\mathbf{P}}_{14}$ above is invertible and the last column of its inverse matrix is a positive column vector. Then, we replace the second row in ${\mathbf{P}}_{14}$ with the other rows, resulting in ${\mathbf{P}}_{14|4\to 2}=\left(\begin{array}{cc}23& -1\\ -2& 23\end{array}\right)$ and ${\mathbf{P}}_{14|4\to 3}=\left(\begin{array}{cc}23& -1\\ 18& 11\end{array}\right)$. The determinants of both are verified to be non-negative. From the above discussion, we can see that the invertible $2\times 2$ principal sub-matrix ${\mathbf{P}}_{14}$ satisfies all the conditions in Theorem 10 and we have: ${\mathbf{P}}_{14}^{-1}=\left(\begin{array}{cc}\frac{45}{1034}& \frac{1}{1034}\\ \frac{1}{1034}& \frac{23}{1034}\end{array}\right)$. Thus, we can conclude that the cover length of $x_4$ is $c_4\left(x_4\right)=\sqrt{\frac{23}{1034}}$.

Lemma 4. 

For any $\mathbf{A}\in {\mathbb{R}}^{M\times N}$ and $\mathbf{x}\in {\mathbb{R}}_{+}^N$,

1. 

If all the entries of ${\mathbf{A}}^T\mathbf{A}$ are positive, then the cover length of $x_n$ is $c_n\left(x_n\right)=\frac{1}{\sqrt{{\left[{\mathbf{A}}^T\mathbf{A}\right]}_{nn}}}$.

2. 

If ${\mathbf{A}}^T\mathbf{A}$ has full rank and all the entries in the n-th column of ${\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}$ are positive, then the cover length is $c_n\left(x_n\right)=\sqrt{{\left[{\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}\right]}_{nn}}$.

Proof. 

To prove the first statement, given an $M\times N$ real matrix $\mathbf{A}$ and $\mathbf{x}\in {\mathbb{R}}_{+}^N$, we can rewrite ${\mathbf{x}}^T{\mathbf{A}}^T\mathbf{A}\mathbf{x}$ as:

$$\begin{array}{c}\hfill {\mathbf{x}}^T{\mathbf{A}}^T\mathbf{A}\mathbf{x}={\overline{\mathbf{x}}}^T{\overline{\mathbf{A}}}^T\overline{\mathbf{A}}\overline{\mathbf{x}}+{\overline{\mathbf{x}}}^T{\overline{\mathbf{A}}}^T{\mathbf{a}}_n{x}_n+{\mathbf{a}}_n^T\overline{\mathbf{A}}\overline{\mathbf{x}}{x}_n+{\mathbf{a}}_n^T{\mathbf{a}}_n{x}_n^2\end{array}$$

where $\overline{\mathbf{A}}$ is the $M\times (N-1)$ sub-matrix formed by deleting the n-th column of $\mathbf{A}$, $\overline{\mathbf{x}}$ denotes an $(N-1)\times 1$ vector obtained by deleting n-th entry from $\mathbf{x}$ and ${\mathbf{a}}_n$ is the n-th column of $\mathbf{A}$.

According to the assumption of Statement 1, i.e., all the entries of ${\mathbf{A}}^T\mathbf{A}$ are positive, then all terms in the above equations are non-negative. Thus, for any given positive real-valued number $\tau >0$, ${\mathbf{x}}^T{\mathbf{A}}^T\mathbf{A}\mathbf{x}\le {\tau }^2$ implies that ${\mathbf{a}}_n^T{\mathbf{a}}_n{x}_n^2\le {\tau }^2$, which gives $x_n\le \frac{\tau }{\sqrt{{\mathbf{a}}_n^T{\mathbf{a}}_n}}$. Therefore, according to the definition of cover length in Definition 1, the cover length of $x_n$ is given by $c_n\left(x_n\right)=\frac{1}{\sqrt{{\left[{\mathbf{A}}^T\mathbf{A}\right]}_{nn}}}$.

The second statement can be obtained from Theorem 10 directly.    □

6.2. Cover Length Problem and NNLS Problem

The NNLS problem is a constrained least squares regression problem in which all the variables can only take non-negative values. Specifically, the NNLS problem can be stated as follows [45]:

Problem 2 (Non-negative Least Squares (NNLS)). 

Given $\mathbf{B}\in {\mathbb{R}}^{M\times N}$ and $\mathbf{b}\in {\mathbb{R}}^M$, find a non-negative vector $\mathbf{u}\in {\mathbb{R}}_{+}^N$ such that

$$\begin{array}{cc}\hfill min& {\Vert \mathbf{Bu}-\mathbf{b}\Vert }_2^2\\ \hfill \mathrm{subject}\mathrm{to}& \mathbf{u}\ge \mathbf{0}\end{array}$$

(29)

In the following, we show by introducing a new variable that the NNLS problem can be turned into a problem of determining the cover length of the corresponding variable. In so doing, a connection between cover length determination and the NNLS problem is established, providing us with a method to arrive at the closed-form optimal value of the objective function.

First, we let

$$\begin{array}{c}\hfill {\tau }^2={\Vert \mathbf{Bu}-\mathbf{b}\Vert }_2^2\end{array}$$

(30)

When $\tau =0$, Problem 2, is equivalent to the problem of finding solutions for the nonhomogeneous system of linear equations $\mathbf{Bu}=\mathbf{b}$ with non-negative constraints on $\mathbf{u}$. Let us consider the case when $\tau >0$: by dividing ${\tau }^2$ on both sides of Equation (30), we will have

$$\begin{array}{c}\hfill \Vert \mathbf{B}\frac{\mathbf{u}}{\tau }-\mathbf{b}\frac{1}{\tau }{\Vert }_2^2=1\end{array}$$

(31)

Introducing a new variable $\mathbf{x}={\left(\frac{\mathbf{u}}{\tau },\frac{1}{\tau }\right)}^T$, the origin problem can be transformed into:

Problem 3. 

$$\begin{array}{cc}\hfill max& x_{N+1}\\ \hfill \mathrm{subject}\mathrm{to}& {\Vert \mathbf{A}\mathbf{x}\Vert }_2^2=1\end{array}$$

(32)

where $x_n\ge 0$ for $n=1,2,\cdots ,N$, $x_{N+1}=\frac{1}{\tau }>0$ and $\mathbf{A}=(\mathbf{B},-\mathbf{b})$.

We observe that Problem 3 is of the same form as Problem 1 and is consistent with Problem 2. Thus, the NNLS and the cover length determination problem are equivalent. By solving the cover length of the corresponding variable $x_{N+1}$, we obtain the equivalent closed-form optimal value of the objective function in the NNLS problem. If we are not able to find the cover length of this variable, $x_{N+1}$ is unbounded within the constraint and the optimum value of the objective function in the NNLS problem is almost zero.

Example 5. 

The cover length determination problem in Example 4 is consistent with the NNLS problem: $\underset{\mathbf{u}\in {\mathbb{R}}_{+}^3}{min}{\Vert \mathbf{Bu}-\mathbf{b}\Vert }_2^2$, where $\mathbf{B}=\left(\begin{array}{ccc}-3& -2& -5\\ 3& -5& 0\\ 1& 3& 1\\ 2& 2& 1\end{array}\right)$ and $\mathbf{b}={(2,4,3,-4)}^T$. Let ${\tau }^2={\Vert \mathbf{Bu}-\mathbf{b}\Vert }_2^2$ and $\mathbf{x}={(x_1,x_2,x_3,x_4)}^T={(\frac{\mathbf{u}}{\tau },\frac{1}{\tau })}^T$. The cover length of $x_4$ is $c_4\left(x_4\right)=\frac{1}{\sqrt{23/1034}}=\frac{1}{\tau }$; thus, the optimal value of this NNLS problem is ${\tau }^2={\Vert \mathbf{Bu}-\mathbf{b}\Vert }_2^2={\left(\frac{1}{c_4\left(x_4\right)}\right)}^2=23/1034$.

The above example demonstrates how to convert the cover length determination of a desired variable into the optimal value of the corresponding NNLS problem and verifies the equivalence of the two problems. For certain types of matrices, using this equivalence, we can even directly obtain the analytical optimal value of the NNLS problem. This is demonstrated by the example of the M-matrix in the following. Let us first define the Z- and the M-matrices [46]:

Definition 4 

(Z-matrix). An $N\times N$ real matrix in which the off-diagonal entries are less than or equal to zero, i.e., a matrix of the form $\mathbf{A}=\left(a_{ij}\right)$ with $a_{ij}\le 0\forall i\ne j,1\le i,j\le N$, is a real Z-matrix.

Definition 5 

(M-matrix). Let $\mathbf{A}$ be an $N\times N$ real Z-matrix. Then $\mathbf{A}$ is also an M-matrix if it can be expressed in the form $\mathbf{A}=s\mathbf{I}-\mathbf{T}$, where $\mathbf{T}=\left(t_{ij}\right)$ with $t_{ij}\ge 0$, for all $i\ne j$, $1\le i,j\le N$, where s is at least as large as the maximum of the moduli of the eigenvalues of $\mathbf{T}$, and $\mathbf{I}$ is an identity matrix.

Theorem 11. 

Let $\mathbf{A}\in {\mathbb{R}}^{N\times N}$ be a Z-matrix; then, the following statements are equivalent to $\mathbf{A}$ being a nonsingular M-matrix:

1. 

All the principal minors of $\mathbf{A}$ are positive. That is, the determinant of each sub-matrix of $\mathbf{A}$ obtained by deleting a set, possibly empty, of corresponding rows and columns of $\mathbf{A}$ is positive.

2. 

$\mathbf{A}$ is inverse-positive. That is, ${\mathbf{A}}^{-1}$ exists and ${\mathbf{A}}^{-1}$ is a non-negative matrix.

Then, with the properties of M-matrix and cover length, we have the following result.

Theorem 12. 

Let matrix $\mathbf{B}\in {\mathbb{R}}^{N\times (N-1)}$ and vector $\mathbf{b}\in {\mathbb{R}}^N$. Denote $\mathbf{A}$ as $(\mathbf{B},-\mathbf{b})$. Supposing that $\mathbf{A}$ is a nonsingular M-matrix, then the optimal value of the NNLS problem $\underset{\mathbf{u}\in {\mathbb{R}}_{+}^{N-1}}{min}{\Vert \mathbf{Bu}-\mathbf{b}\Vert }_2^2$ is exactly equal to $\frac{1}{{\left[{\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}\right]}_{NN}}$.

Proof. 

By assumption, $\mathbf{A}$ is a nonsingular M-matrix, therefore ${\mathbf{A}}^T\mathbf{A}$ is invertible and all the elements in ${\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}$ are positive. Reformulating the NNLS problem to the problem of determining the cover length of $x_N$ by applying Lemma 4, the cover length of the corresponding variable $x_N$ is given by $c_N\left(x_N\right)=\sqrt{{\left[{\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}\right]}_{NN}}$. Thus, the optimal value ${\tau }^2={\left(\frac{1}{c_N\left(x_N\right)}\right)}^2=\frac{1}{{\left[{\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}\right]}_{NN}}$.    □

6.3. Comparison with the Active-Set Method

There are several normally used active-set methods for solving the NNLS problem. A typical example is the algorithm lsqnonneg in Matlab, which aims at creating an active set and using it to arrive at an approximate solution to the NNLS problem. lsqnonneg starts with an all-zero vector and computes the associated negative gradient vector $\mathbf{w}$. Then it finds the index of the position where the maximum value in $\mathbf{w}$ occurs and moves this index from the inactive set to the active set. By solving the corresponding least squares problem with the current active set, one non-negative solution candidate can be obtained. The active set and inactive set can be updated with the current candidate solution and continue the whole process until all the elements in $\mathbf{w}$ are nonpositive or the inactive set is empty. As Lawson and Hanson showed, this algorithm always converges and terminates in finite steps. However, there is no upper limit on the possible number of iterations that the algorithm might need to reach the point of the optimum solution, and it might be very slow in practice, owing largely to the computation of the pseudo-inverse. With regard to the computational complexity, since the exact running time required for the NNLS solver is unknown, the computational cost cannot be specified exactly. In many standard implementations of NNLS solvers (and particularly those based on active-set methods), the cost is typically $\mathcal{O}\left(M{N}^2\right)$ per iteration [47].

Compared with the active-set method, the cover length determination method is finite, and once we find one principal sub-matrix that can satisfy the conditions in Theorem 10, then the computation stops. Furthermore, we can find an upper limit on the possible number of steps that the algorithm needs and obtain a closed-form optimal value of the NNLS problem.

From the perspective of computation complexity, there is no clear advantage of the cover length method compared with the lsqnonneg since it involves the combination and permutation operations. However, while the accuracy of the lsqnonneg solution depends on a prescribed tolerance $ϵ$, the cover length method yields the exact optimal value of the objective function.

We now present some numerical results illustrating the performance of the cover length method and lsqnonneg in solving the NNLS problem.

Table 1. Comparison between Matlab’s lsqnonneg and cover length method in solving the NNLS problem.

Column Number of B		1	2	3
Complexity	Cover length method	6	16	589
Running time	Cover length method	$1.20\times {10}^{-4}$	$2.40\times {10}^{-4}$	0.0024
	lsqnonneg	$2.10\times {10}^{-4}$	$3.17\times {10}^{-4}$	$4.18\times {10}^{-4}$
Average error	Cover length method	$0.0000$	$0.0000$	0.0000
	lsqnonneg	$1.1102\times {10}^{-16}$	$2.6645\times {10}^{-15}$	$2.8422\times {10}^{-14}$

shows the average running time (seconds) and average error of the lsqnonneg and the cover length method for the matrices and vectors randomly generated by Matlab’s rand function. The results shown here are averaged over 100 random samples with varying number of columns (from one to three) of $\mathbf{B}$ in the NNLS problem. The default termination tolerance on the solution of lsqnonneg is $10\times {\sum }_{ij}\left|a_{ij}\right|\times N\times eps$, where $eps=2.22\times {10}^{-16}$, N is the row number of the matrix $\mathbf{B}$, and $a_{ij}$ is the element in $\mathbf{A}=(\mathbf{B},-\mathbf{b})$. Table 1 also includes the computation complexity (number of maximum operations) of the cover length method in solving the NNLS problem. It is clear from the table that the advantage of the cover length method over lsqnonneg lies in the accuracy of the optimal value since cover length yields a closed-form one.

7. Conclusions

Linear systems of equations with non-negativity constraints on solutions is an area of study in linear algebra. Such problems arise frequently in many fields of science and engineering. In our consideration of such problems, we discovered the hyper-rectangle cover theory of a matrix, which is presented in this paper. The two main concepts in the hyper-rectangle cover theory, viz., the cover order and the cover length, were first defined, and many of their important properties were introduced. Based on this theory, several novel approaches to analyzing the above typical problems were proposed. The necessary and sufficient conditions under which a unique solution for a system of linear equations with non-negativity constraints exists were identified. We also showed how the specific échelon form of the matrix is constructed, and with this échelon form, the cover order of any given matrix can be determined.

With the help of cover theory, the emptiness of the feasibility set and the various possibilities of the solution for the LP problem were analyzed in detail. In addition, with the property of zero-cover matrix, a series of feasible solutions to the LP problem can be obtained.

Our study on the cover length led us to the development of a method to find the cover length of a covered variable. We also showed the equivalence between cover length determination and the NNLS problem so that the NNLS problem can be solved with the cover length method. This provides us with the analytical optimal value obtainable from the structure of the matrix rather than a numerical result having a finite accuracy. The development of the hyper-rectangle cover theory, thus, not only provides us with an efficient method to solve the system of linear equations with non-negativity constraints, it also suggests to us attractive alternative approaches to the LP and the NNLS problems.