A Discrete Integral Sliding Manifold for a Nonlinear System with Time Delay: An Event-Triggered Scheme
Abstract
1. Introduction
- We propose a novel, discrete integral sliding manifold for nonlinear systems to avoid the restrictive assumptions in most existing T-S fuzzy SMC methods.
- The event-triggered scheme is combined with the ISMC design approach. In this scheme, data in the system are transmitted only when the trigger condition is met, which prevents redundant information, saves valuable network resources, and reduces the chattering phenomenon.
2. Problem Formulation
- A1: The input matrices () must be equal.
- A2: There must exist a matrix M such that .
3. Discrete Fuzzy Integral Sliding Surface Design
- The matrix B can be selected as the convex combination of such that ; that is, with and . From the property of convex combinations, it follows that if only one of the is non-singular, then there should be a collection of scalars , such that the non-singularity of B can be ensured. In this situation, setwhere.It can be demonstrated that . Thus, the result in Lemma 3 also applies to , and r being replaced by , and , respectively.
4. Design of the Event-Triggered Communication Scheme
5. Sliding Mode Control Synthesis
6. Simulation Results
- The SMC scheme, which is presented in [19], is built on an assumption that the system can be expressed in the regular form (where ) through suitable transformation. Nevertheless, for this transformation to take place, it is necessary that the input matrices of all linear models are identical. For this reason, we have developed an SMC scheme in this work that overcomes this constraint.
- In [20], the ISMC design for a class of nonlinear systems, which are depicted by T-S fuzzy models, was investigated. However, this suggested scheme is based on two highly restrictive assumptions. The first assumption is that all linear local models of the T-S fuzzy system share a common input matrix (i.e., (where )). Secondly, there exists a matrix G with an appropriate dimension such that is non-singular. Furthermore, both of these assumptions greatly limit real-world applications, including the widely known inverted pendulum on a cart [22]. By removing this assumption, our proposed SMC method can robustly stabilize fuzzy systems with different input matrices.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, SMC-15, 116–132. [Google Scholar] [CrossRef]
- Munakata, T.; Jani, Y. Fuzzy systems: An overview. Commun. ACM 1994, 37, 69–77. [Google Scholar]
- Sugeno, M.; Kang, G. Structure identification of fuzzy model. Fuzzy Sets Syst. 1988, 28, 15–33. [Google Scholar] [CrossRef]
- Tanaka, K.; Hori, T.; Wang, H.O. A multiple Lyapunov function approach to stabilization of fuzzy control systems. IEEE Trans. Fuzzy Syst. 2003, 11, 582–589. [Google Scholar] [CrossRef]
- Chen, P.; Chen, C.; Chiang, W. Linear matrix inequality conditions of nonlinear systems by genetic algorithm-based H∞ adaptive fuzzy sliding mode controller. J. Vib. Control 2011, 17, 163–173. [Google Scholar] [CrossRef]
- Bresch-Pietri, D.; Chauvin, J.; Petit, N. Adaptive backstepping controller for uncertain systems with unknown input time-delay. application to SI engines. In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; pp. 3680–3687. [Google Scholar]
- Khelifa, H.; Ellouze, I. Adaptive robust state stabilisation of uncertain non linear time-varying systems with delayed perturbation. Int. J. Syst. Sci. 2021, 52, 3241–3253. [Google Scholar] [CrossRef]
- Pandey, S.; Tadepalli, S.K.; Leite, V.J.; Nigam, R.; Bhusnur, S. Stability of 2-D Discrete Systems in the Presence of Saturation Function and Delays. Int. J. Control. Autom. Syst. 2023, 21, 788–799. [Google Scholar] [CrossRef]
- Sobhanipour, H.; Rezaie, B. Enhanced Exponential Stability Analysis for Switched Linear Time-Varying Delay Systems Under Admissible Edge-Dependent Average Dwell-Time Strategy. IEEE Trans. Syst. Man Cybern. Syst. 2023. [Google Scholar] [CrossRef]
- Graef, J.R.; Tunç, C.; Tunç, O. Stability of time-delay systems via the Razumikhin method. Boletín de la Sociedad Matemática Mexicana 2022, 28, 26. [Google Scholar]
- Ye, Z.; Zhang, W.A.; Zhang, D.; Ni, H. On design of robust sliding mode observer for nonlinear networked time-delay systems with communication constraints. ISA Trans. 2020, 124, 260–270. [Google Scholar] [CrossRef]
- Sakthivel, R.; Shobana, N.; Priyanka, S.; Kwon, O. State observer-based predictive proportional-integral tracking control for fuzzy input time-delay systems. Int. J. Robust Nonlinear Control. 2023. [Google Scholar] [CrossRef]
- Ben Atia, S.; Messaoud, A.; Ben Abdennour, R. Robust multiobserver design for discrete uncertain nonlinear systems with time-varying delay. Trans. Inst. Meas. Control 2018, 40, 191–201. [Google Scholar] [CrossRef]
- Ghotb, H.; Ataei, M.; Siahi, M.; Moarefianpour, A. Design of developed distributed observers for nonlinear time-delay systems. Trans. Inst. Meas. Control. 2023, 01423312221138893. [Google Scholar] [CrossRef]
- Tognetti, E.S.; de Oliveira, G.A. Robust state feedback-based design of PID controllers for high-order systems with time-delay and parametric uncertainties. J. Control. Autom. Electr. Syst. 2022, 33, 382–392. [Google Scholar] [CrossRef]
- Bhuvaneshwari, G.; Prakash, M.; Rakkiyappan, R.; Manivannan, A. Stability and stabilization analysis of TS fuzzy systems with distributed time-delay using state-feedback control. Math. Comput. Simul. 2023, 205, 778–793. [Google Scholar] [CrossRef]
- Estrada-Manzo, V.; Lendek, Z.; Guerra, T. An alternative LMI static output feedback control design for discrete-time nonlinear systems represented by Takagi-Sugeno models. ISA Trans. 2019, 84, 104–110. [Google Scholar] [CrossRef]
- Choi, H.H. Robust stabilization of uncertain fuzzy-time-delay systems using sliding-mode-control approach. IEEE Trans. Fuzzy Syst. 2010, 18, 979–984. [Google Scholar] [CrossRef]
- Xue, Y.; Zheng, B.C.; Yu, X. Robust sliding mode control for TS fuzzy systems via quantized state feedback. IEEE Trans. Fuzzy Syst. 2017, 26, 2261–2272. [Google Scholar] [CrossRef]
- Subramaniam, R.; Song, D.; Joo, Y.H. TS fuzzy-based sliding mode controller design for discrete-time nonlinear model and its applications. Inf. Sci. 2020, 519, 183–199. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, F.; Karimi, H.R.; Wang, F. Observer-based sliding mode control for T-S fuzzy descriptor systems with time delay. IEEE Trans. Fuzzy Syst. 2019, 27, 2009–2023. [Google Scholar] [CrossRef]
- Chen, M.; Feng, G.; Ma, H.; Chen, G. Delay-Dependent H∞ Filter Design for Discrete-Time Fuzzy Systems With Time-Varying Delays. IEEE Trans. Fuzzy Syst. 2008, 17, 604–616. [Google Scholar] [CrossRef]
- Zong, G.; Sun, X.; Yang, D.; Su, S.F.; Shi, K. Finite-time H∞ control for switched fuzzy systems: A dynamic adaptive event-triggered control approach. Fuzzy Sets Syst. 2023, 464, 108475. [Google Scholar] [CrossRef]
- Tan, Y.; Yuan, Y.; Xie, X.; Tian, E.; Liu, J. Observer-based event-triggered control for interval type-2 fuzzy networked system with network attacks. IEEE Trans. Fuzzy Syst. 2023. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, X.; Park, J.H.; Fang, F. Fault-tolerant control for TS fuzzy systems with an aperiodic adaptive event-triggered sampling. Fuzzy Sets Syst. 2023, 452, 23–41. [Google Scholar] [CrossRef]
- Su, X.; Wen, Y.; Shi, P.; Wang, S.; Assawinchaichote, W. Event-triggered fuzzy control for nonlinear systems via sliding mode approach. IEEE Trans. Fuzzy Syst. 2019, 29, 336–344. [Google Scholar] [CrossRef]
- Echreshavi, Z.; Farbood, M.; Shasadeghi, M. Fuzzy event-triggered integral sliding mode control of nonlinear continuous-time systems. IEEE Trans. Fuzzy Syst. 2021, 30, 2347–2359. [Google Scholar] [CrossRef]
- Yue, D.; Tian, E.; Han, Q.L. A delay system method for designing event-triggered controllers of networked control systems. IEEE Trans. Autom. Control 2012, 58, 475–481. [Google Scholar] [CrossRef]
- Zhivoglyadov, P.V.; Middleton, R.H. Networked control design for linear systems. Automatica 2003, 39, 743–750. [Google Scholar] [CrossRef]
- Yue, D.; Han, Q.L.; Lam, J. Network-based robust H∞ control of systems with uncertainty. Automatica 2005, 41, 999–1007. [Google Scholar] [CrossRef]
- Cao, S.G.; Rees, N.W. Identification of dynamic fuzzy models. Fuzzy Sets Syst. 1995, 74, 307–320. [Google Scholar] [CrossRef]
- Seuret, A.; Gouaisbaut, F.; Fridman, E. Stability of discrete-time systems with time-varying delays via a novel summation inequality. IEEE Trans. Autom. Control 2015, 60, 2740–2745. [Google Scholar] [CrossRef]
- Park, P.; Ko, J.W.; Jeong, C. Reciprocally convex approach to stability of systems with time-varying delays. Automatica 2011, 47, 235–238. [Google Scholar] [CrossRef]
- Choi, H.H. Robust stabilization of uncertain fuzzy systems using variable structure system approach. IEEE Trans. Fuzzy Syst. 2008, 16, 715–724. [Google Scholar] [CrossRef]
- Castaños, F.; Fridman, L. Analysis and design of integral sliding manifolds for systems with unmatched perturbations. IEEE Trans. Autom. Control 2006, 51, 853–858. [Google Scholar] [CrossRef]
- Zhu, B.; Wang, Y.; Zhang, H.; Xie, X. Fuzzy functional observer-based finite-time adaptive sliding-mode control for nonlinear systems with matched uncertainties. IEEE Trans. Fuzzy Syst. 2021, 30, 918–932. [Google Scholar] [CrossRef]
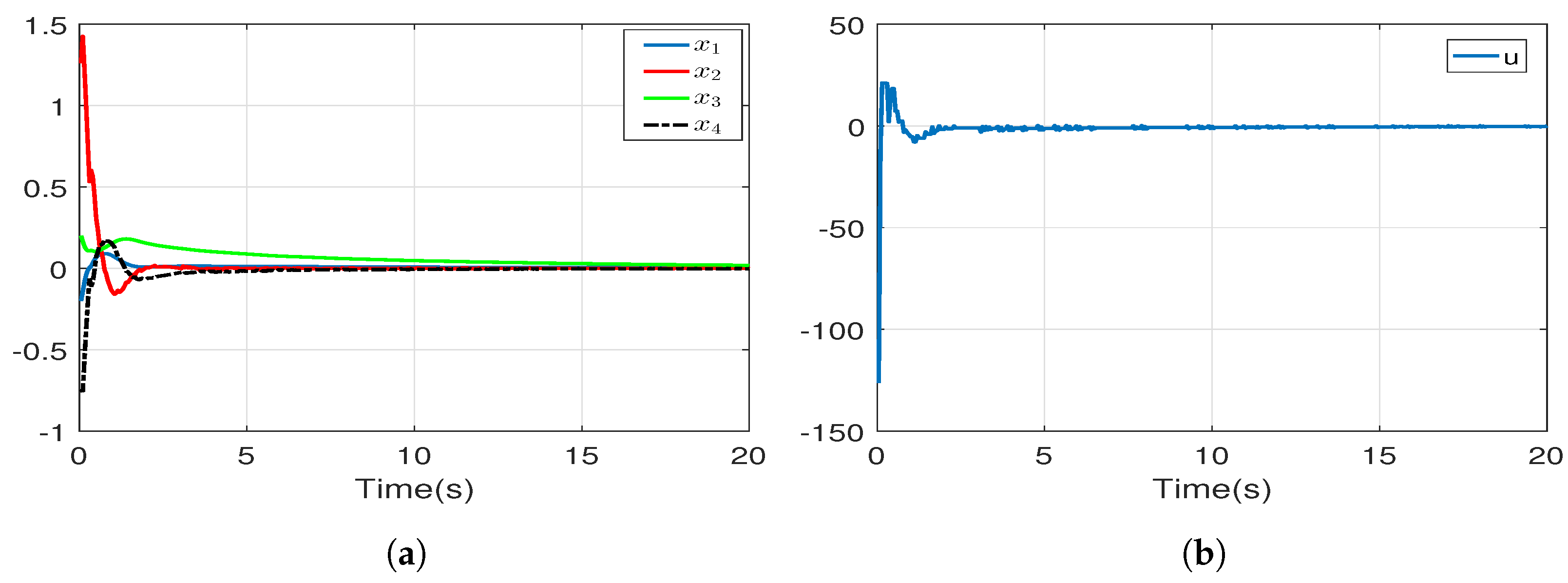
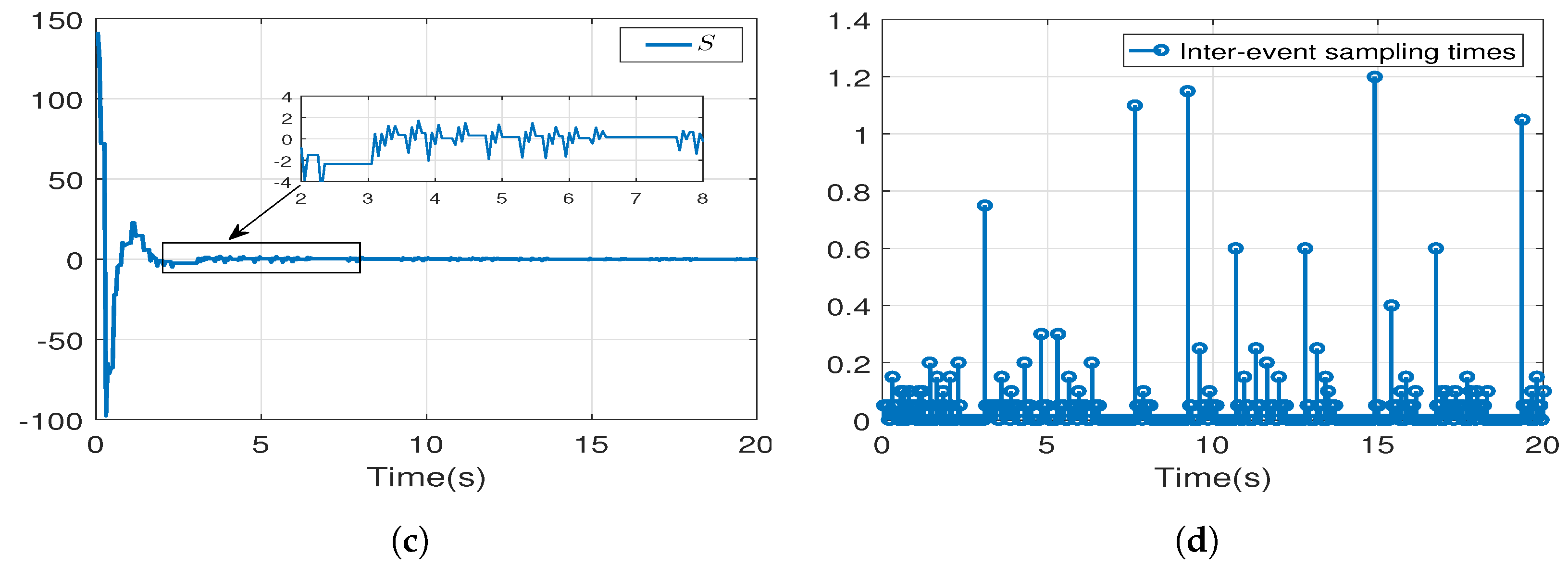
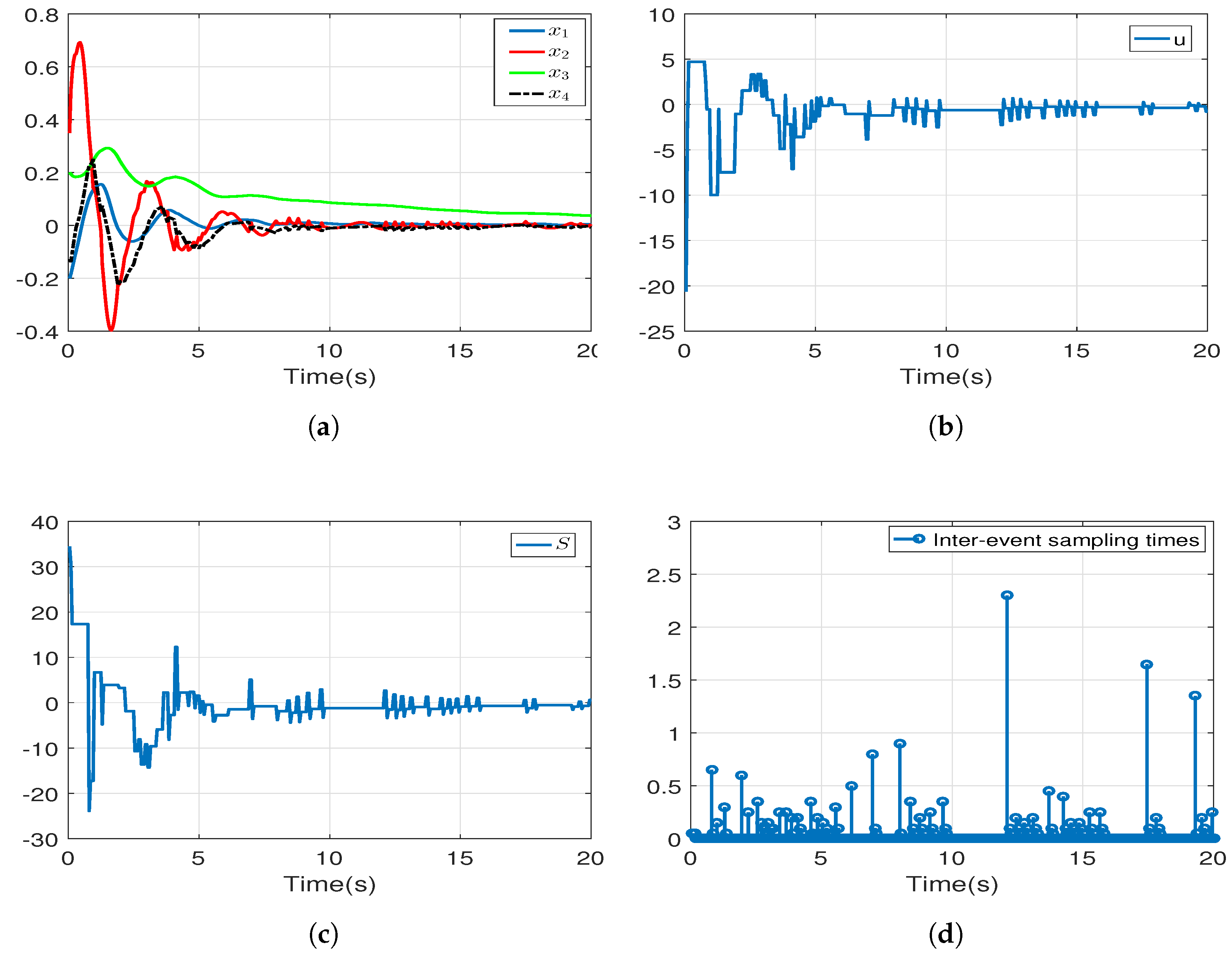
| Triggering Parameter | 0 | ||||
|---|---|---|---|---|---|
| Event-Triggered Rates |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benyazid, Y.; Fnadi, M.; Nouri, A.S. A Discrete Integral Sliding Manifold for a Nonlinear System with Time Delay: An Event-Triggered Scheme. Mathematics 2023, 11, 2326. https://doi.org/10.3390/math11102326
Benyazid Y, Fnadi M, Nouri AS. A Discrete Integral Sliding Manifold for a Nonlinear System with Time Delay: An Event-Triggered Scheme. Mathematics. 2023; 11(10):2326. https://doi.org/10.3390/math11102326
Chicago/Turabian StyleBenyazid, Yassine, Mohamed Fnadi, and Ahmed Said Nouri. 2023. "A Discrete Integral Sliding Manifold for a Nonlinear System with Time Delay: An Event-Triggered Scheme" Mathematics 11, no. 10: 2326. https://doi.org/10.3390/math11102326
APA StyleBenyazid, Y., Fnadi, M., & Nouri, A. S. (2023). A Discrete Integral Sliding Manifold for a Nonlinear System with Time Delay: An Event-Triggered Scheme. Mathematics, 11(10), 2326. https://doi.org/10.3390/math11102326








