Abstract
The Kuramoto model is a classical model used for the describing of synchronization in populations of oscillatory units. In the present paper we study the Kuramoto model with delay with a focus on the distribution of the oscillators’ frequencies. We consider a series of rational distributions which allow us to reduce the population dynamics to a set of several delay differential equations. We use the bifurcation analysis of these equations to study the transition from the asynchronous to synchronous state. We demonstrate that the form of the frequency distribution may play a substantial role in synchronization. In particular, for Lorentzian distribution the delay prevents synchronization, while for other distributions the delay can facilitate synchronization.
MSC:
34K24
1. Introduction
In many complex systems of various nature a similar pattern of collective behaviour can be observed: The adjustment of rhythms of oscillating systems due to their interaction. This phenomenon is called synchronization and is ubiquitous in the real world with examples ranging from the synchronous firing of pacemaker cells in the heart and neurons in the brain to the synchronous rotation of electric generators in power grids [1,2,3]. For a long time it was a mystery how the synchronization can emerge despite the inevitable diversity in the natural frequencies of different units. It was Kuramoto who introduced a mathematical model of coupled oscillators that allowed this problem to be solved [4,5,6]. Motivated by the behavior of chemical and biological oscillators, this model later turned out to be quite general and applicable to such systems as coupled arrays of Josephson junctions [7] or populations of of biological neurons [8,9].
What is now known as the “Kuramoto model” consists of N phase oscillators with the harmonic interaction function:
where is the unit number, are the phase variables, are the natural frequencies, and K is the global coupling strength. In his pioneering work Kuramoto showed this model to be mathematically tractable and to demonstrate the phase transition from an asynchronous state to synchronization at the critical coupling strength.
In subsequent decades the Kuramoto model became a classical paradigm for studying synchronization phenomena and it found numerous applications (see reviews [10,11] for the examples). From the other side, the simplicity and generality of the Kuramoto model makes it perfect for various kinds of generalization and modification. One of the most natural ways to make the model more realistic is to include coupling delays which are inevitably in real world due to the finite speed of signal propagation [12,13,14]. To take into account coupling delays the phases in the sum from the r.h.s. of (1) are replaced by their delayed versions . In the case of two coupled oscillators the delay causes multistabilty of synchronous solutions with different frequencies [15] (interestingly, multistability also emerges if the delay is introduced not into the coupling, but into the oscillators themselves [16]). The similar effect of multistability was found for globally coupled oscillators with time delays, which results in the possibility of discontinuous transitions between different regimes in addition to classical smooth transitions [17,18]. In the case of local coupling, the delays were shown to induce complex spatio-temporal patterns and clusters [19]. In the case of distant-dependant delays similar patterns emerge and become propagating structures [20,21]. The case of heterogeneous delays was also considered and the emergence of clusters with various phase relations was demonstrated [22]. In rings of oscillators with local coupling, the delay was shown to act differently depending on the network symmetry: It induces multistability for unidirectional coupling and stabilizes the most symmetric solution for bidirectional coupling [23]. In rings with nonlocal coupling, the delays give birth to travelling waves [24]. For networks of oscillators with complex connectivity, such as scale-free networks, coupling delays may induce explosive synchronization [25].
Another natural generalization of the Kuramoto model is the addition of external forces to the oscillator dynamics which results in the emergence of a phase-dependent and/or time-dependent term in the r.h.s. of (1). This term is often taken in the form , in which case the phase oscillators turn into the so-called “active rotators”. The dynamics of active rotators is much richer than that of phase oscillators since the former can demonstrate either oscillatory or excitatory behaviour depending on the relation between the individual frequency and the parameter a which is often called a “non-isochronicity parameter”. Ensembles of globally coupled active rotators were first considered in Refs. [26,27], and two different collective regimes were found: Entrainment with the external force and mutual entrainment. The introduction of heterogeneous external forces leads to similar results [28]. The transition between locked and unlocked states can be similar to either a super-critical Andronov-Hopf bifurcation or a saddle-node bifurcation [29]. In the case of heterogeneous assemblies made up of excitable and oscillatory units, it has been demonstrated that the transition to synchrony may be classical or re-entrant, depending on the particular form of the frequency distribution [30]. In addition to the parameter regions with synchronous and asynchronous regimes, the regions of bistability between different regimes were found as well [31].
Other types of generalized Kuramoto models were studied as well, including time-dependent [8,32,33], adaptive [34,35,36,37,38] and memristive [39] coupling, including noise [26,27,40], non-harmonic coupling functions [41,42] and pulse coupling [43,44], systems on smooth manifolds [45,46,47], etc. Typically, the analytic study of the Kuramto model and its generalizations is performed in the thermodynamic limit when the number of units tends to infinity. In this case the microscopic equations (1) are replaced by the continuity equation, and the individual frequencies are replaced by the probability density . For the classical Kuramoto model the particular form of this distribution does not play any important role. First, the system is invariant under the change of variables for arbitrary , which means that the mean frequency can be always set to zero. Second, for unimodal symmetric distributions, the critical coupling at which the transition takes place equals , i.e., it depends only on the height of the distribution peak but not on its particular shape. However, when coupling delays or non-isochronicity are included, the shape of the distribution comes into play because it becomes important how the typical frequencies relate to the delay and non-isochronicity parameter a.
In the present paper we study how the synchronization transition in the Kuramoto model with delay depends on the shape of the frequency distribution . For this sake we consider a series of rational distributions which are all unimodal and symmetric but are different in the flatness of the peak and decay rate of the tails. Using the Ott-Antonsen approach [48,49] we derive low-dimensional dynamical systems governing the collective dynamics of the population and perform its bifurcation analysis. We show that the shape of the frequency distribution can play a significant role for the system properties. For widely used Lorentzian distribution, the delay always prevents synchronization by raising the critical coupling strength. However, for distributions with lighter tails, the delay can also promote synchronization by lowering the critical coupling.
2. Model
We consider a heterogeneous assembly of N oscillators with delayed coupling
where is the unit number, are the phase variables, are the natural frequencies, a is the non-isochronicity parameter, K is the global coupling strength and is the coupling delay. Strictly speaking, can be called “natural frequencies” only for . For non-zero a, the rotation becomes non-uniform with the frequency for . At an isolated unit undergoes a SNIPER bifurcation toward the excitatory regime. This very dependence of the local oscillatory dynamics on the parameter a allows us to call it a “non-isochronicity parameter”.
In order to characterize the degree of synchrony in the population we introduce the Kuramoto complex order parameter
The absolute value of this parameter serves the main indicator of the system synchronization. When it is close to zero, the phases of the oscillators are not correlated, and the system is asynchronous. When the order parameter is sufficiently different from zero it indicates the emergence of a bunch of oscillators rotating with close phases, which means synchronization. Using the Kuramoto order parameter allows us to rewrite (2) as
where and the asterisk denotes the complex conjugate. In the thermodynamic limit , the macroscopic state of the system is described by the probability density function , which obeys the continuity equation
with the velocity v being the r.h.s. of Equation (4). The Kuramoto parameter in this case is evaluated as
3. Reduction of the Collective Dynamics
Following the theory of Ott and Antonsen [48,49] we will look for the long-term dynamics of the continuity Equation (5) in the form
where
is the probability density function of the natural frequencies and
is the local complex order parameter of the subpopulation with the natural frequency . Obviously, the global and the local order parameter are connected by the self-consistency condition
Substituting (7) into (5), one obtains the following equations for :
which together with (10) defines a delay integro-differential equation describing the collective dynamics of the population in the thermodynamic limit.
As the next step we consider a family of rational distributions , namely
where n is natural, is the mean frequency, is the distribution half-width, and
is the normalization constant. For this distribution turns into a classical Cauchy distribution, and for it converges to a uniform distribution on the interval . Assuming the rational function allows us to evaluate the integral (10) using the residue theorem. A similar approach was recently used for populations of quadratic integrate-and-fire neurons [50,51]. Consider the analytic extension of function to complex , then the integration contour can be closed by an infinitely large arc in the upper complex half-plane. In this half-plane the function (12) has n simple poles
where and . Thus, the integral (10) can be evaluated as
Writing Equation (11) for , ,…, allows us to obtain a closed set of n delay differential equations for complex variables
where and . Introducing and allows us to rewrite these equations in the real form:
This set of DDEs governs the collective dynamics of the population in the thermodynamic limit . The following analysis is based on system (17).
4. Studying the Role of the Coupling Delay
For the case of isochronous oscillations with , the system always has a trivial steady state corresponding to asynchronous dynamics of the oscillators. This state is stable for weak coupling K and destabilizes via an Andronov-Hopf bifurcation when the coupling becomes sufficiently strong, which constitutes a classical Kuramoto scenario [5,10]. The stable limit cycle born in this bifurcation corresponds to a partial synchronization of the oscillators.
The dynamics of the system is illustrated in Figure 1 where the dynamics of the individual phases and the Kuramoto order parameter are shown for the synchronous and asynchronous regimes. In both cases, the system starts from random initial conditions. In the case of asynchronous dynamics, all the phases rotate incoherently, and the order parameter remains close to zero. When the synchronization is achieved, a bunch of oscillators quickly emerge whose phases rotate with the same frequency, and the order parameter reaches a sufficiently non-zero value.
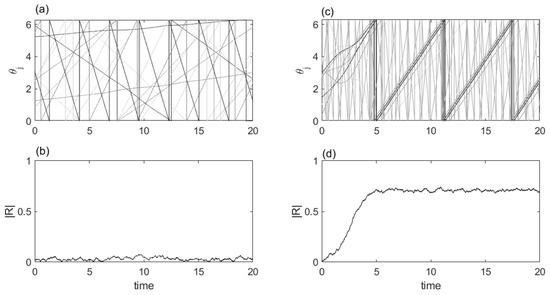
Figure 1.
The dynamics of the system in the asynchronous (a,b) and synchronous (c,d) regimes. The top panels show the time traces of 10 randomly chosen phases , while the bottom panels show the time trace of the Kuramoto order parameter . The coupling strength for (a,b) and for (c,d) The other parameters are , , , , .
In order to illustrate the transition from the asynchronous to the synchronous state we plot the dependence of the Kuramoto order parameter on the coupling strength in Figure 2. The order parameter is small for weak coupling and rapidly grows as the coupling strength exceeds the critical value. Note that the results obtained by the simulation of the reduced model (17) coincide with those obtained for the microscopic system up to the fluctuations induced by the finite size effects. Note also that adding of the coupling delay might sufficiently influence the system dynamics and shift the critical value of the coupling strength. Further, we will analyze the role of the delay in detail with the help of the reduced system.
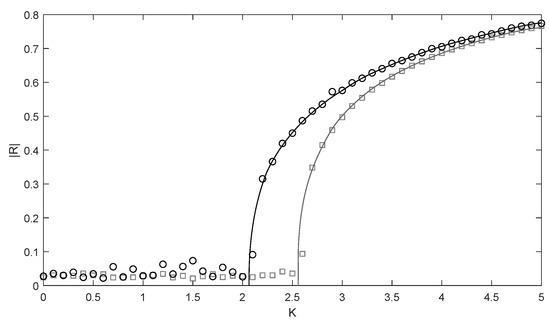
Figure 2.
The dependence of the Kuramoto order parameter on the coupling strength. Black circles: , gray squares: . The other parameters: , , , . Solid lines indicate the results obtained by the simulation of the reduced system (17).
In the case of zero delay the critical coupling depends on the distribution width in a linear way. Indeed, according to the results of Kuramoto [52],
For nonzero coupling delays the critical coupling becomes delay-dependent. In order to determine the bifurcation point it is necessary to write the characteristic equation for the trivial steady state which has the form , where D is matrix
and , , , represent matrices with the following elements:
where equals one for and zero in other case.
At the Andronov-Hopf point a pair of roots emerge, which allows us to determine the value of the coupling strength at the bifurcation point by solving . For small delays, this equation can be solved numerically by taking (18) as the initial point, then the solution can be traced along the delay value as a parameter. The obtained dependence is plotted in Figure 3a for the Lorentzian distribution of the oscillator frequencies (). The bifurcation coupling shows a minimum at and grows rapidly and monotonically for non-zero delays. Note that we have calculated the bifurcation curve for both positive and negative delays. Although negative time delays are not physical, we use them in the bifurcation analysis for a reason that will become clear later. Namely, they will help us to find other bifurcation curves existing for positive delays.
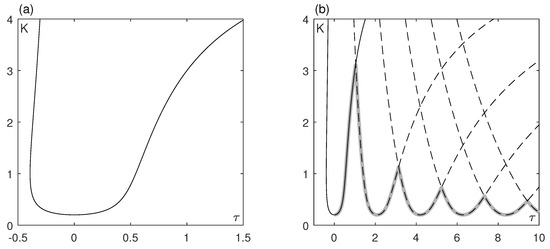
Figure 3.
(a) The Andronov-Hopf bifurcation curve for system (17) with , , and . (b) The same curve (black solid line) and its reappearing instances (black dashed lines). The gray thick line shows the synchronization border.
An important point is that the existence of one Andronov-Hopf bifurcation curve in a system with time delay implies the existence of other bifurcation curves at other delay values due to the so-called reappearance of periodic solutions [53]. Indeed, if the bifurcation takes place at the coupling strength for the delay this means the existence of a limit cycle with the period and vanishing amplitude. This implies the existence of the same limit cycle at the same coupling strength for the delays , where k is an integer, which means that each of these points are also Andronov-Hopf points. Note, however, that the stability of the emergent limit cycle can change, which means that the bifurcation can be either supercritical or subcritical.
The bifurcation curve found by starting from the delay-less case reappears in the manner described above and leads to the emergence of other bifurcation curves as shown in Figure 3b. These curves demonstrate minimums at , where and is the frequency at which the collective oscillations emerge for . Obviously, it is the frequency of the distribution peak, i.e., . For non-zero delays the frequency becomes different, therefore the different bifurcation curves do not exactly match each other in shape. However, they all still a single minimum at the multiples of . The trivial steady state, i.e., the asynchronous regime is stable when the coupling strength is below all the bifurcation curves. Thus, the synchronization border is defined by the lowest point of the curve and has a saw-like shape. This border coincides completely with that obtained in Ref. [17] for the same setting which corroborates the validity of our analysis.
The obtained results suggest that introduction of the coupling delay prevents the system synchronization: For non-zero delays, the critical coupling at which the oscillators start to synchronize increases with respect to the delay-free case (at best, the critical coupling does not change if the delay is a multiple of ). This result seems to be obvious from the physical viewpoint: It is harder to adjust if one receives outdated information. However, it turns out that the coupling delay can in some cases promote synchronization. This surprising effect is observed when the distribution is different from Lorentzian, i.e., .
In order to illustrate this effect we calculated the synchronization borders on the plane for different values of n. We adjust the distribution half-width as
so that the critical coupling for the delay-free case equals unity for all n. The results are plotted in Figure 4 and show a significant difference between the Lorentzian distribution and distributions with . For the Lorentzian distribution the delay always prevents synchronization and the critical coupling is always not less than unity. For the distributions of higher order , some delay values can promote synchronization so that the critical coupling becomes less than unity. Another feature of high-order distributions is the complex form of the synchronization border with many peaks and valleys of different shapes.
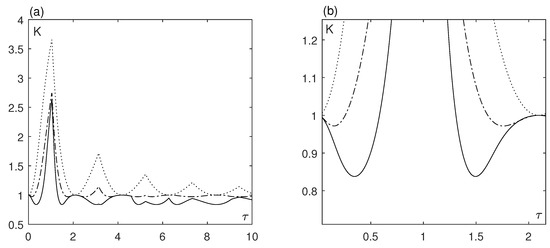
Figure 4.
(a) The synchronization borders of system (17) for (dotted line), (dash-dotted line) and (solid line). The mean frequency , the half-width (b) Enlarged part of the panel (a).
5. Conclusions
In this paper we performed an analysis of the Kuramoto model with coupling delay paying special attention to the distribution of the oscillator frequencies . We used the method of Ott and Antonsen which allows one to reduce the system dynamics in the case of infinitely many oscillators. For the rational frequency distributions, the dynamics can be reduced to a set of delay-differential equations whose number equals the degree of the denominator. By the means of bifurcation analysis, we obtained the Andronov-Hopf bifurcation curves indicating a synchronization transition in the population and so constructed the synchronization border in the parameter plane. Our results have revealed the different role of the delay for different frequency distributions. Thus, for the Lorentzian distribution, the delay always prevents synchronization by increasing the critical coupling strength. In contrast, for the distributions different from Lorentzian, the delay can promote synchronization: For certain delay values, the critical coupling turns out to be lower than in the delay-less case.
In the studies of collective dynamics of heterogeneous populations, it is typical to consider a Lorentzian distribution of local parameters. The reason for this choice is the simplicity of analytical treatment: For example, in our study the Lorentzian distribution with leads to the reduced system (9) of just a single differential equation for the complex variable . The Lorentzian distribution is often treated as paradigmatic and qualitatively reflects the properties of an arbitrary unimodal distribution. However, our results show that the particular shape of the distribution can play a significant role in the system behaviour and synchronization. In particular, the role of the coupling delay turns out to be opposite for the Lorentzian and non-Lorentzian distributions.
In the end, we would like to emphasize that the present study is limited to the local stability analysis and does not consider the global stability of the asynchronous state. It means that the stable asynchronous state might coexist with a synchronous state in some parameter regions leading to bistability areas, as was demonstrated in Ref. [17] for the Lorentz frequency distribution. The emergence of bistability is associated with the subcritical Andronov-Hopf bifurcation, while the supercritical bifurcation supports monostability. The type of the bifurcation can be determined by the calculation of the first Lyapunov coefficient [54,55] which could be one of the directions of the further investigation. Other possibilities include consideration of a broader class of frequency distributions, including non-unimodal ones.
Author Contributions
Conceptualization, V.V.K.; Methodology, V.V.K.; Software, A.A.Z.; Formal analysis, V.V.K. and A.A.Z.; Investigation, V.V.K. and A.A.Z.; Writing—original draft, V.V.K.; Supervision, V.V.K.; Funding acquisition, V.V.K. All authors have read and agreed to the published version of the manuscript.
Funding
The derivation of the reduced system was supported by the Ministry of Science and Higher Education of the Russian Federation, agreement no. 075-15-2022-287. The bifurcation analysis of the reduced system and the numerical simulations were supported by the Russian Science Foundation, grant no. 19-72-10114.
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pikovsky, A.; Kurths, J.; Rosenblum, M.; Kurths, J. Synchronization: A Universal Concept in Nonlinear Sciences; Cambridge University Press: Cambridge, UK, 2003; Volume 12. [Google Scholar]
- Strogatz, S.H. Sync: How Order Emerges from Chaos in the Universe, Nature, and Daily Life; Hachette: London, UK, 2012. [Google Scholar]
- Winfree, A.T. The Geometry of Biological Time; Springer Science & Business Media: Berlin, Germany, 2013; Volume 12. [Google Scholar]
- Kuramoto, Y. Self-entrainment of a population of coupled non-linear oscillators. In Proceedings of the International Symposium on Mathematical Problems in Theoretical Physics, Kyoto, Japan, 23–29 January 1975; Springer: Berlin/Heidelberg, Germany, 1975; pp. 420–422. [Google Scholar]
- Kuramoto, Y. Chemical Oscillations, Waves, and Turbulence; Springer: Berlin, Germany; New York, NY, USA, 1984; Volume 19, p. 156. [Google Scholar]
- Kuramoto, Y.; Nishikawa, I. Statistical macrodynamics of large dynamical systems. Case of a phase transition in oscillator communities. J. Stat. Phys. 1987, 49, 569–605. [Google Scholar] [CrossRef]
- Wiesenfeld, K.; Colet, P.; Strogatz, S.H. Frequency locking in Josephson arrays: Connection with the Kuramoto model. Phys. Rev. E 1998, 57, 1563. [Google Scholar] [CrossRef]
- Cumin, D.; Unsworth, C. Generalising the Kuramoto model for the study of neuronal synchronisation in the brain. Phys. D Nonlinear Phenom. 2007, 226, 181–196. [Google Scholar] [CrossRef]
- Breakspear, M.; Heitmann, S.; Daffertshofer, A. Generative models of cortical oscillations: Neurobiological implications of the Kuramoto model. Front. Hum. Neurosci. 2010, 4, 190. [Google Scholar] [CrossRef] [PubMed]
- Acebrón, J.A.; Bonilla, L.L.; Vicente, C.J.; Ritort, F.; Spigler, R. The Kuramoto model: A simple paradigm for synchronization phenomena. Rev. Mod. Phys. 2005, 77, 137–185. [Google Scholar] [CrossRef]
- Rodrigues, F.A.; Peron, T.K.D.M.; Ji, P.; Kurths, J. The Kuramoto model in complex networks. Phys. Rep. 2016, 610, 1–98. [Google Scholar] [CrossRef]
- Smith, H. An Introduction to Delay Differential Equations with Applications to the Life Sciences; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Erneux, T. Applied Delay Differential Equations; Surveys and Tutorials in the Applied Mathematical Sciences; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; Volume 3, p. 204. [Google Scholar]
- Kashchenko, S.; Maiorov, V.V. Models of Wave Memory; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Schuster, H.G.; Wagner, P. Mutual Entrainment of Two Limit Cycle Oscillators with Time Delayed Coupling. Prog. Theor. Phys. 1989, 81, 939–945. [Google Scholar] [CrossRef]
- Kashchenko, A.A. Multistability in a system of two coupled oscillators with delayed feedback. J. Differ. Eqs. 2019, 266, 562–579. [Google Scholar] [CrossRef]
- Yeung, M.K.S.; Strogatz, S.H. Time Delay in the Kuramoto Model of Coupled Oscillators. Phys. Rev. Lett. 1999, 82, 648–651. [Google Scholar] [CrossRef]
- Choi, M.Y.; Kim, H.J.; Kim, D.; Hong, H. Synchronization in a system of globally coupled oscillators with time delay. Phys. Rev. E-Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2000, 61, 371–381. [Google Scholar] [CrossRef]
- Nakamura, Y.; Tominaga, F.; Munakata, T. Clustering behavior of time-delayed nearest-neighbor coupled oscillators. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 1994, 49, 4849–4856. [Google Scholar] [CrossRef]
- Zanette, D.H. Propagating structures in globally coupled systems with time delays. Phys. Rev. E-Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2000, 62, 3167–3172. [Google Scholar] [CrossRef] [PubMed]
- Jeong, S.O.; Ko, T.W.; Moon, H.T. Time-delayed spatial patterns in a two-dimensional array of coupled oscillators. Phys. Rev. Lett. 2002, 89, 154104. [Google Scholar] [CrossRef] [PubMed]
- Petkoski, S.; Spiegler, A.; Proix, T.; Aram, P.; Temprado, J.J.; Jirsa, V.K. Heterogeneity of time delays determines synchronization of coupled oscillators. Phys. Rev. E 2016, 94, 12209. [Google Scholar] [CrossRef] [PubMed]
- D’Huys, O.; Vicente, R.; Erneux, T.; Danckaert, J.; Fischer, I. Synchronization properties of network motifs: Influence of coupling delay and symmetry. Chaos 2008, 18, 37116. [Google Scholar] [CrossRef] [PubMed]
- Laing, C.R. Travelling waves in arrays of delay-coupled phase oscillators. Chaos Interdiscip. J. Nonlinear Sci. 2016, 26, 94802. [Google Scholar] [CrossRef]
- Peron, T.K.D.; Rodrigues, F.A. Explosive synchronization enhanced by time-delayed coupling. Phys. Rev. E 2012, 86, 16102. [Google Scholar] [CrossRef]
- Shinomoto, S.; Kuramoto, Y. Phase Transitions in Active Rotator Systems. Prog. Theor. Phys. 1986, 75, 1105. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Shinomoto, S.; Kuramoto, Y. Phase transitions and their bifurcation analysis in a large population of active rotators with mean-field coupling. Prog. Theor. Phys. 1988, 79, 600–607. [Google Scholar] [CrossRef]
- Arenas, A.; Vicente, C.J.P. Exact long-time behavior of a network of phase oscillators under random fields. Phys. Rev. E 1994, 50, 949. [Google Scholar] [CrossRef]
- Antonsen, T.M., Jr.; Faghih, R.T.; Girvan, M.; Ott, E.; Platig, J. External periodic driving of large systems of globally coupled phase oscillators. Chaos Interdiscip. J. Nonlinear Sci. 2008, 18, 37112. [Google Scholar] [CrossRef] [PubMed]
- Lafuerza, L.F.; Colet, P.; Toral, R. Nonuniversal results induced by diversity distribution in coupled excitable systems. Phys. Rev. Lett. 2010, 105, 084101. [Google Scholar] [CrossRef] [PubMed]
- Klinshov, V.; Franovic, I.; Franović, I. Two scenarios for the onset and suppression of collective oscillations in heterogeneous populations of active rotators. Phys. Rev. E 2019, 100, 062211. [Google Scholar] [CrossRef] [PubMed]
- Petkoski, S.; Stefanovska, A. Kuramoto model with time-varying parameters. Phys. Rev. E 2012, 86, 46212. [Google Scholar] [CrossRef]
- Khatiwada, D.R. Numerical Solution of Finite Kuramoto Model with Time-Dependent Coupling Strength: Addressing Synchronization Events of Nature. Mathematics 2022, 10, 3633. [Google Scholar] [CrossRef]
- Timms, L.; English, L.Q. Synchronization in phase-coupled Kuramoto oscillator networks with axonal delay and synaptic plasticity. Phys. Rev. E 2014, 89, 32906. [Google Scholar] [CrossRef]
- Ha, S.Y.; Noh, S.E.; Park, J. Synchronization of Kuramoto oscillators with adaptive couplings. SIAM J. Appl. Dyn. Syst. 2016, 15, 162–194. [Google Scholar] [CrossRef]
- Kasatkin, D.V.; Nekorkin, V.I. Dynamics of the Phase Oscillators with Plastic Couplings. Radiophys. Quantum Electron. 2016, 58, 877–891. [Google Scholar] [CrossRef]
- Kasatkin, D.V.; Yanchuk, S.; Schöll, E.; Nekorkin, V.I. Self-organized emergence of multilayer structure and chimera states in dynamical networks with adaptive couplings. Phys. Rev. E 2017, 96, 062211. [Google Scholar] [CrossRef]
- Feketa, P.; Schaum, A.; Meurer, T. Stability of cluster formations in adaptive Kuramoto networks. IFAC-Pap. 2021, 54, 14–19. [Google Scholar] [CrossRef]
- Xu, Q.; Liu, T.; Ding, S.; Bao, H.; Li, Z.; Chen, B. Extreme multistability and phase synchronization in a heterogeneous bi-neuron Rulkov network with memristive electromagnetic induction. Cogn. Neurodyn. 2022, 1–12. [Google Scholar] [CrossRef]
- Zaks, M.A.; Neiman, A.B.; Feistel, S.; Schimansky-Geier, L. Noise-controlled oscillations and their bifurcations in coupled phase oscillators. Phys. Rev. E 2003, 68, 66206. [Google Scholar] [CrossRef]
- Komarov, M.; Pikovsky, A. The Kuramoto model of coupled oscillators with a bi-harmonic coupling function. Phys. D Nonlinear Phenom. 2014, 289, 18–31. [Google Scholar] [CrossRef]
- O’Keeffe, K.P.; Strogatz, S.H. Dynamics of a population of oscillatory and excitable elements. Phys. Rev. E 2016, 93, 62203. [Google Scholar] [CrossRef] [PubMed]
- Canavier, C.C.; Tikidji-Hamburyan, R.A. Globally attracting synchrony in a network of oscillators with all-to-all inhibitory pulse coupling. Phys. Rev. E 2017, 95, 032215. [Google Scholar] [CrossRef]
- Klinshov, V.; Lücken, L.; Yanchuk, S. Desynchronization by phase slip patterns in networks of pulse-coupled oscillators with delays: Desynchronization by phase slip patterns. Eur. Phys. J. Spec. Top. 2018, 227, 1117–1128. [Google Scholar] [CrossRef]
- Fiori, S. A control-theoretic approach to the synchronization of second-order continuous-time dynamical systems on real connected Riemannian manifolds. SIAM J. Control Optim. 2020, 58, 787–813. [Google Scholar] [CrossRef]
- Markdahl, J.; Thunberg, J.; Goncalves, J. High-dimensional Kuramoto models on Stiefel manifolds synchronize complex networks almost globally. Automatica 2020, 113, 108736. [Google Scholar] [CrossRef]
- Cafaro, A.D.; Fiori, S. Optimization of a control law to synchronize first-order dynamical systems on Riemannian manifolds by a transverse component. Discret. Contin. Dyn.-Syst.-Ser. B 2022, 27, 3947–3969. [Google Scholar] [CrossRef]
- Ott, E.; Antonsen, T.M. Low dimensional behavior of large systems of globally coupled oscillators. Chaos Interdiscip. J. Nonlinear Sci. 2008, 18, 37113. [Google Scholar] [CrossRef]
- Ott, E.; Antonsen, T.M. Long time evolution of phase oscillator systems. Chaos Interdiscip. J. Nonlinear Sci. 2009, 19, 23117. [Google Scholar] [CrossRef] [PubMed]
- Klinshov, V.; Kirillov, S.; Nekorkin, V. Reduction of the collective dynamics of neural populations with realistic forms of heterogeneity. Phys. Rev. E 2021, 103, L040302. [Google Scholar] [CrossRef]
- Pyragas, V.; Pyragas, K. Mean-field equations for neural populations with q -Gaussian heterogeneities. Phys. Rev. E 2022, 105, 044402. [Google Scholar] [CrossRef] [PubMed]
- Kuramoto, Y. Proceedings of the International symposium on Mathematical Problems in Theoretical Physics. Lect. Notes Phys. 1975, 30, 420–422. [Google Scholar]
- Yanchuk, S.; Perlikowski, P. Delay and periodicity. Phys. Rev. E 2009, 79, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, Y.A. Elements of Applied Bifurcation Theory; Springer: New York, NY, USA, 2004. [Google Scholar]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 42. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).