Chenciner Bifurcation Presenting a Further Degree of Degeneration
Abstract
:1. Introduction
2. Methods
3. Results
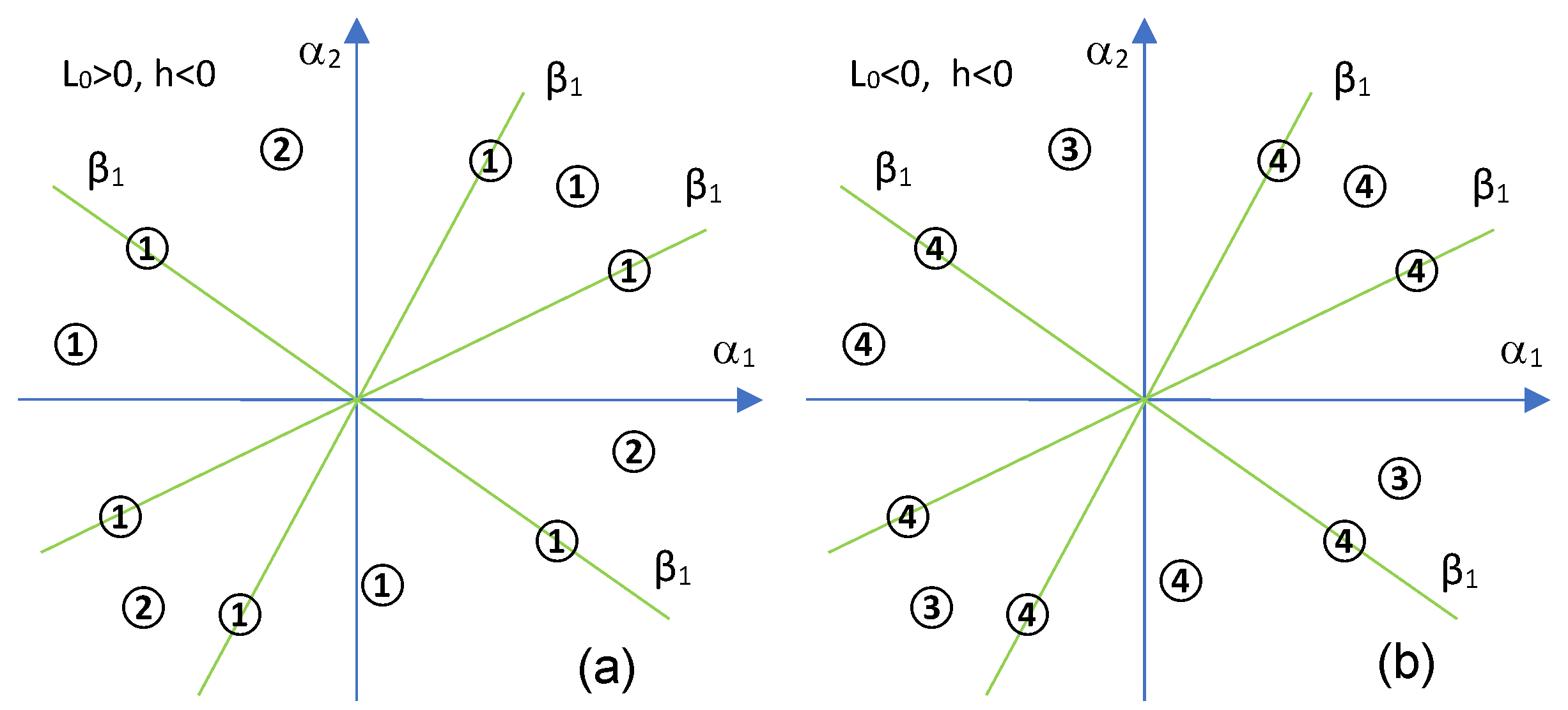
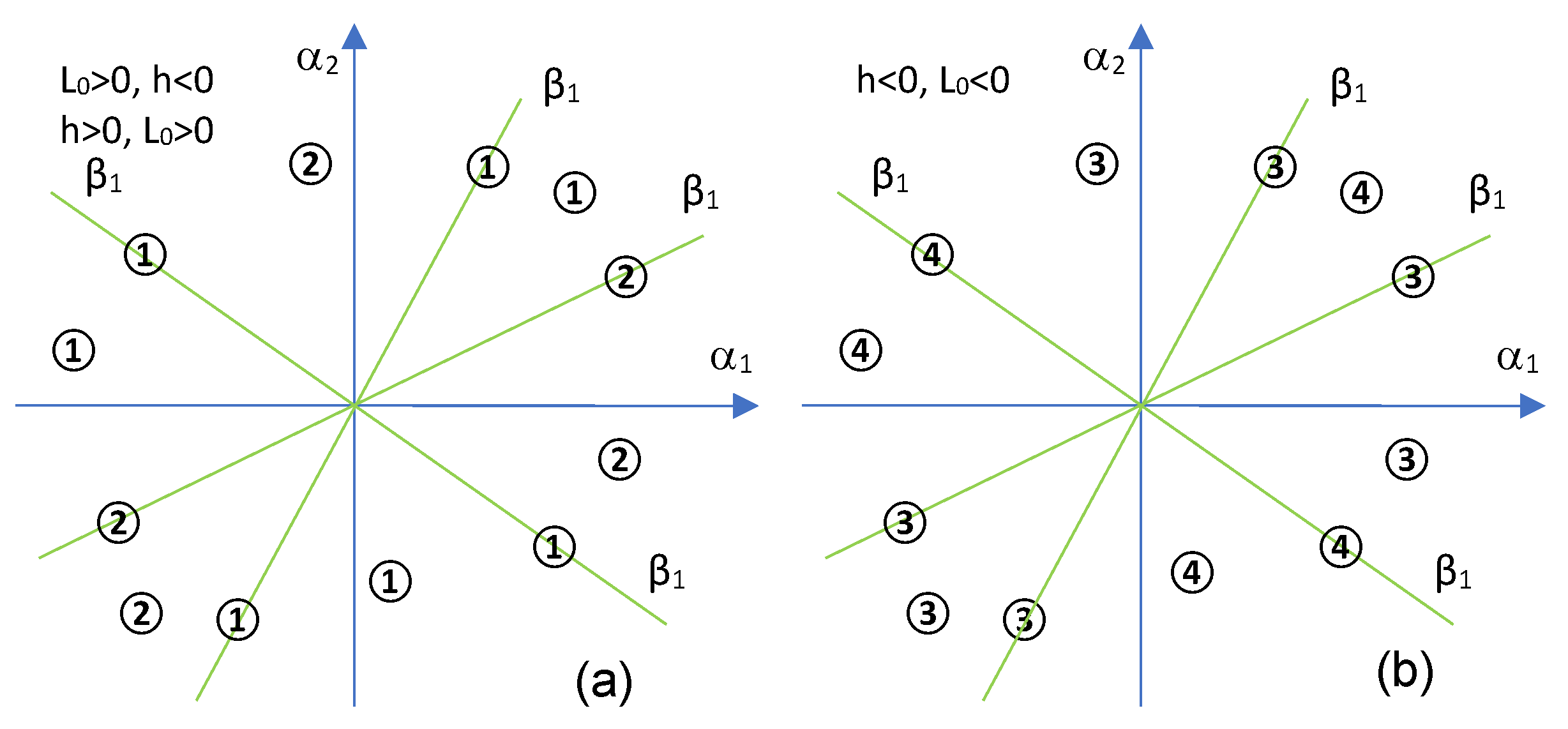
3.1. Degree of the Second Bifurcation Curve Is One in the Truncated Version
- For , there is one real root and two complex conjugated ones;
- For , there is a triple root ;
- For , there is one real root and two complex conjugated ones;
- For , there are three real roots, one simple , and two common;
- For , there are three real different roots
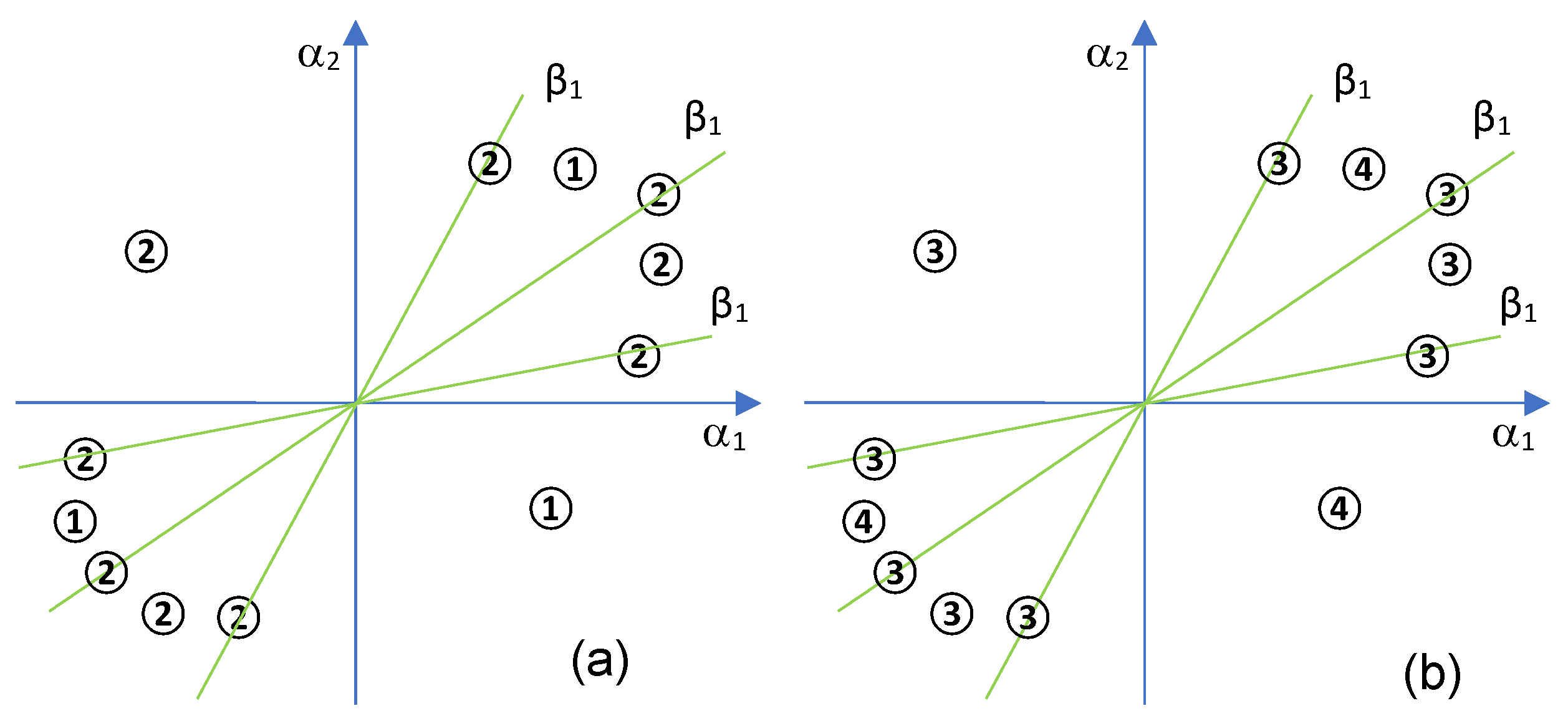
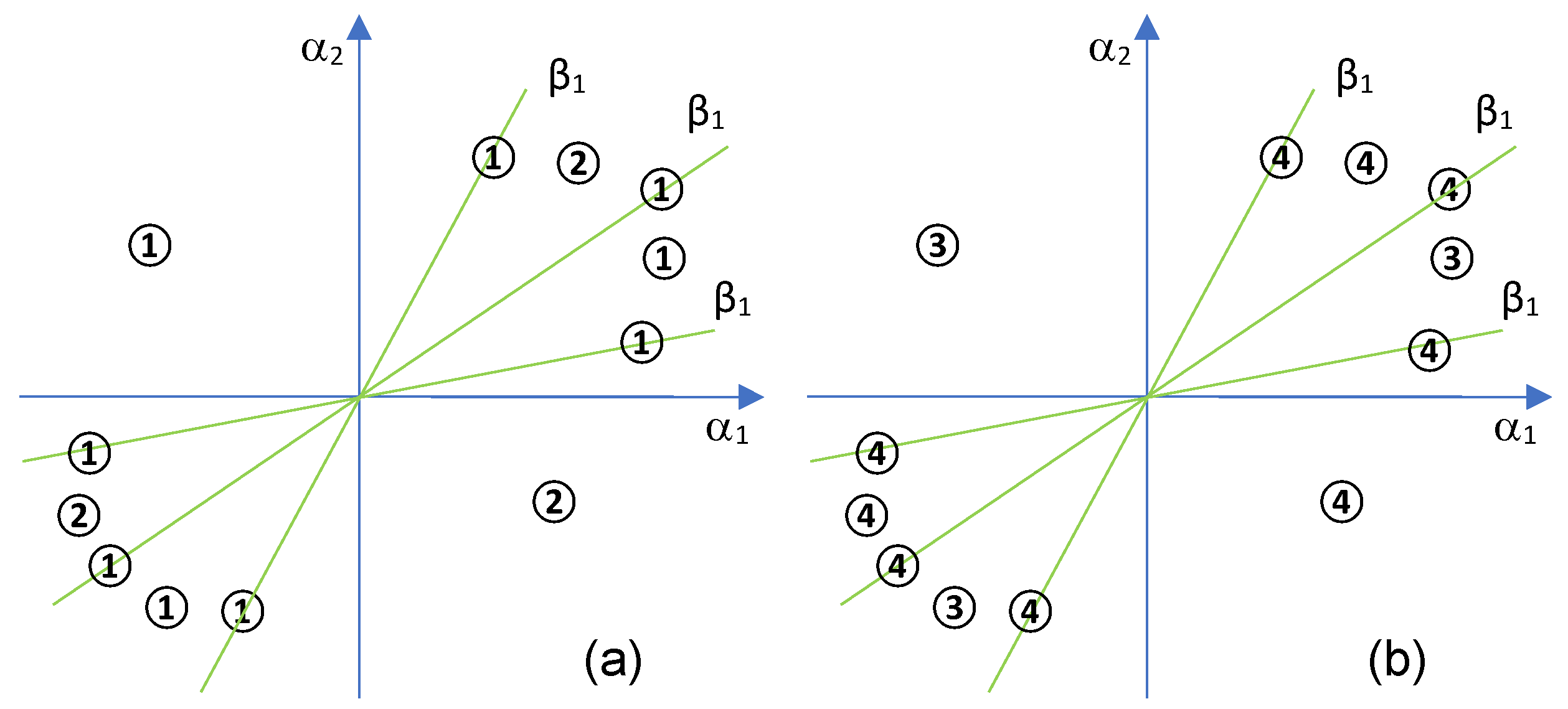
3.2. Degree of the Second Bifurcation Curve Is Two
- I
- ;
- II
- ;
- III
- implies
- , then there is , two distinct real roots of and
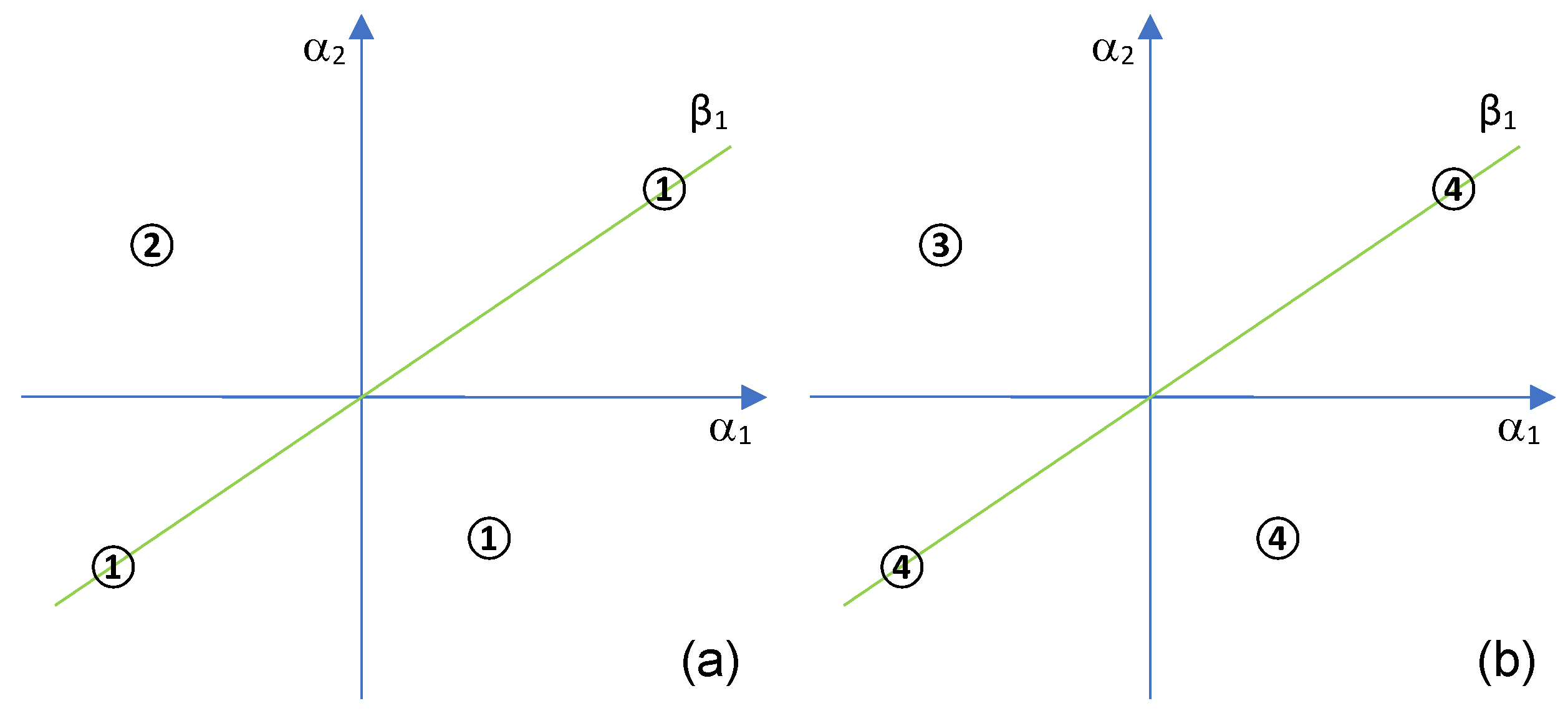
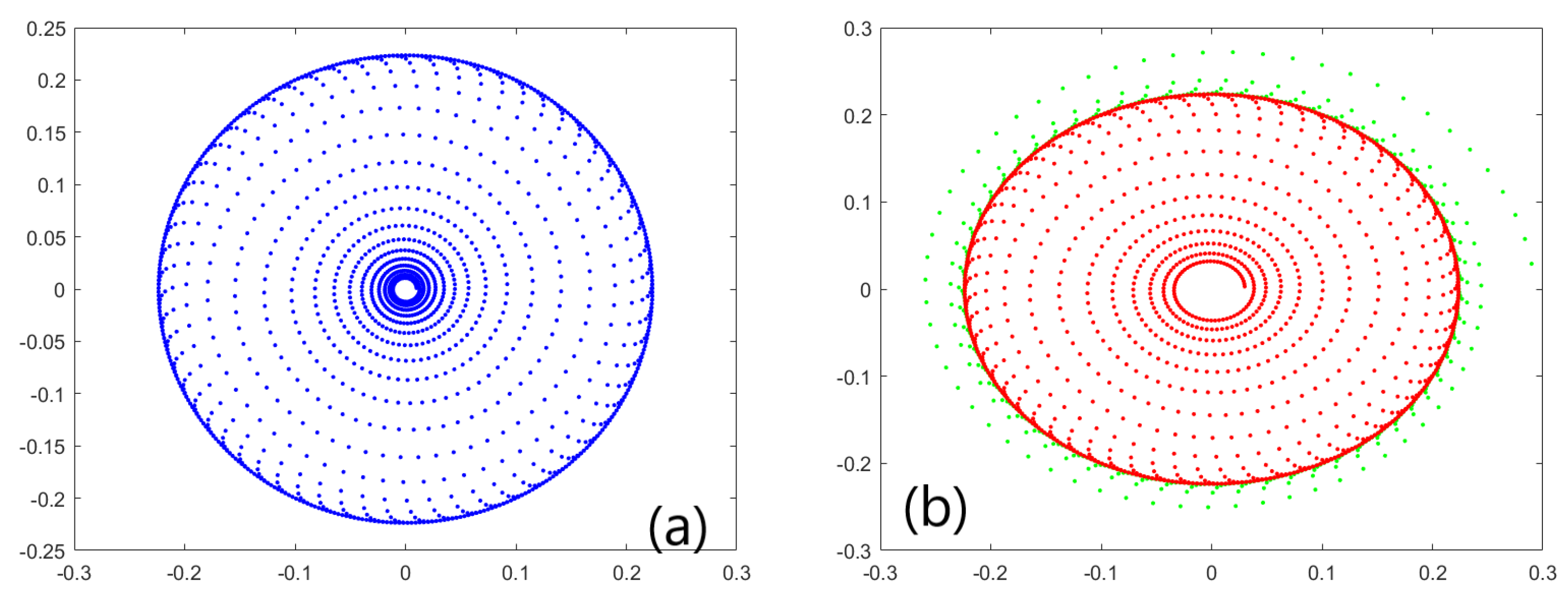
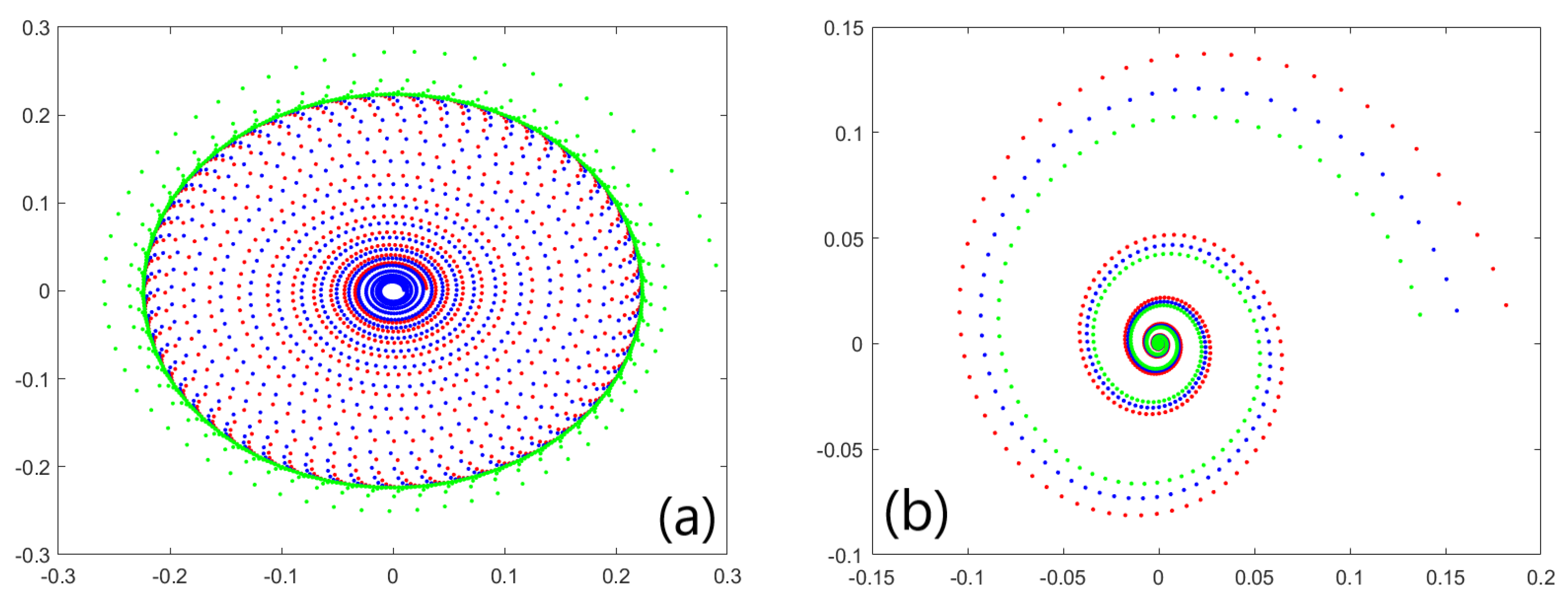
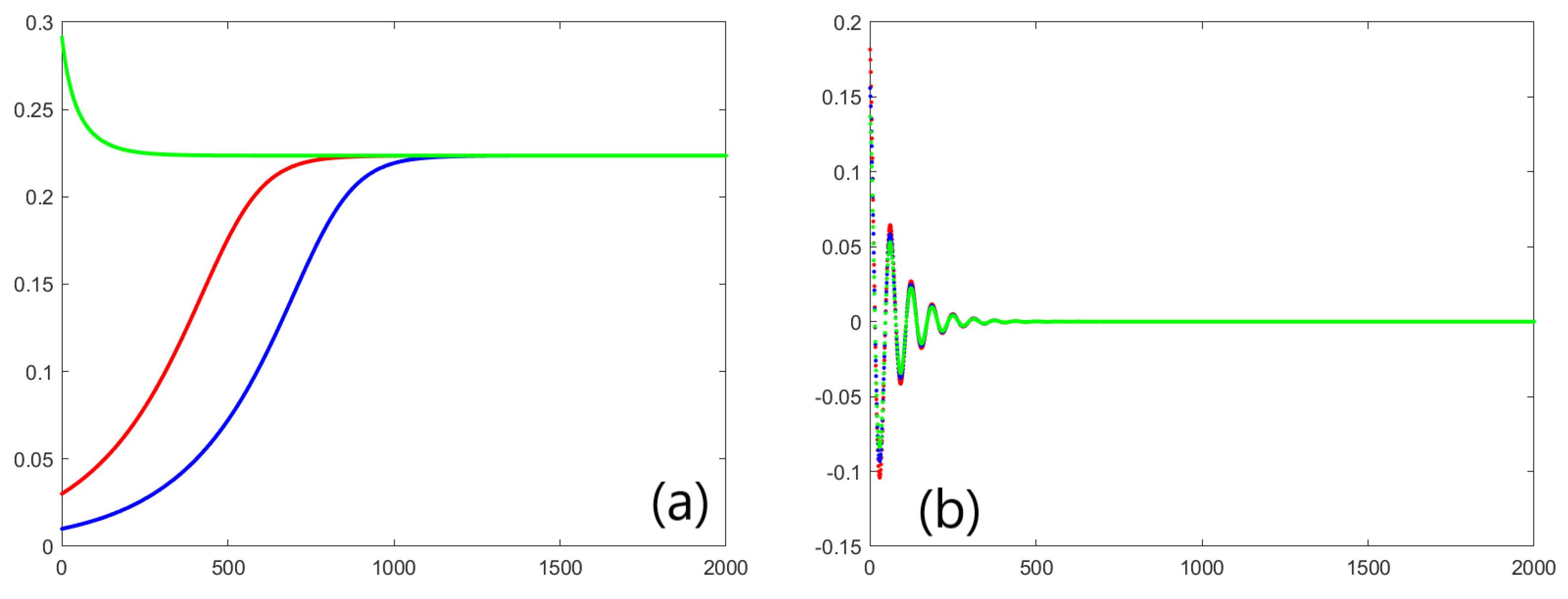
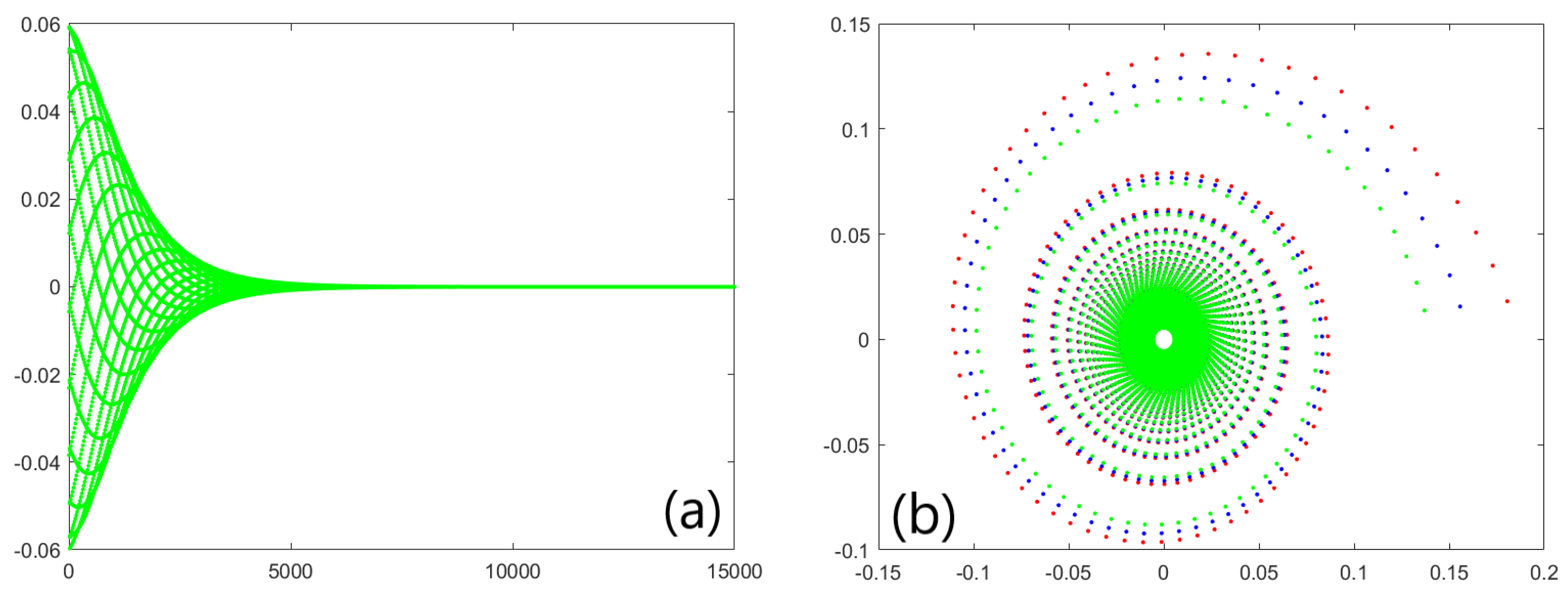
3.3. Numerical Simulations
4. Discussions and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Chenciner Bifurcations
Appendix B. Literature Review
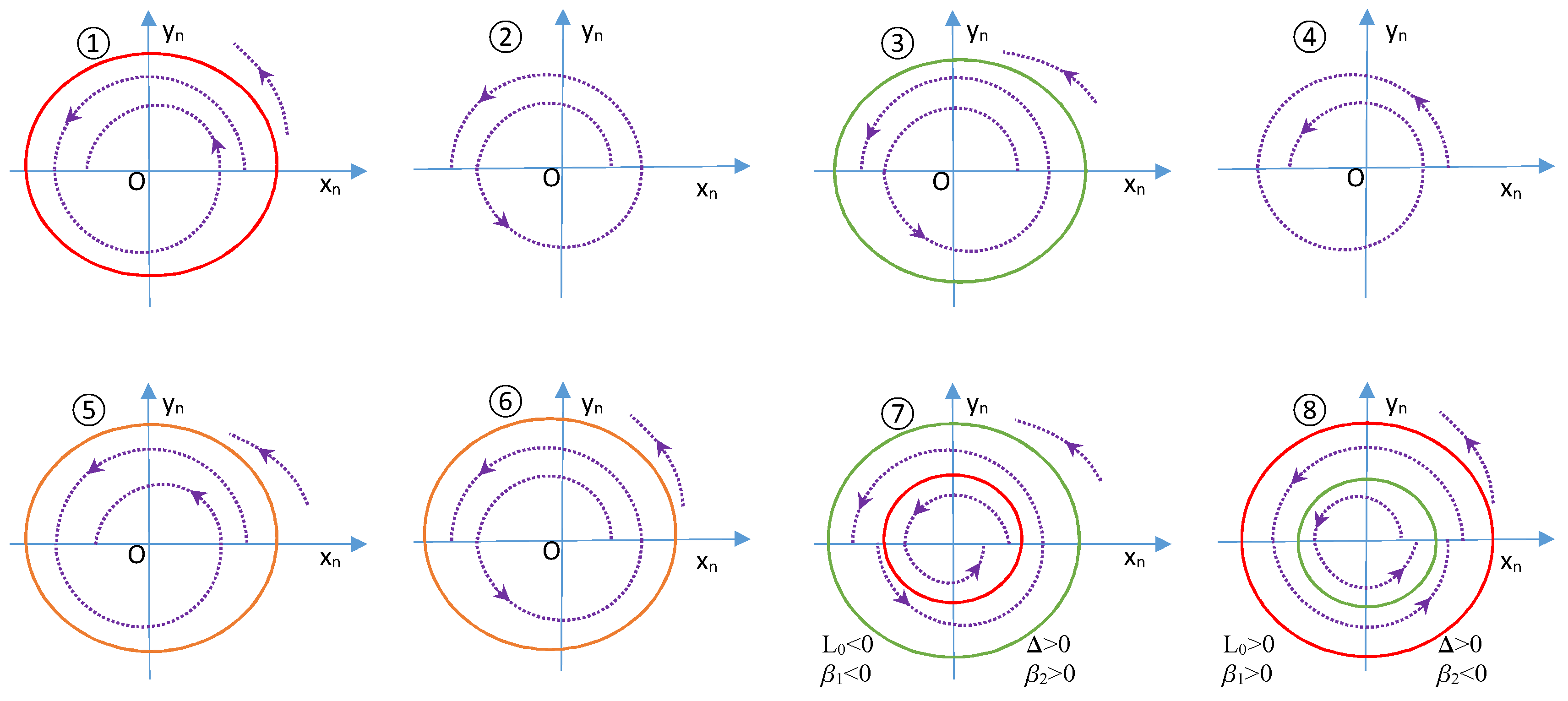
- (a)
- one invariant unstable circle if and
- (b)
- one invariant stable circle if and
- (c)
- two invariant circles, unstable and stable, if or in addition, if and if
- (d)
- no invariant circles if or
References
- Sanchez-Ruiz, L.M.; Moll-Lopez, S.; Morano-Fernandez, J.A.; Rosello, M.D. Dynamical Continuous Discrete Assessment of Competencies Achievement: An Approach to Continuous Assessment. Mathematics 2021, 9, 2082. [Google Scholar] [CrossRef]
- Elhassan, C.; Zulkifli, S.A.; Iliya, S.Z.; Bevrani, H.; Kabir, M.; Jackson, R.; Khan, M.H.; Ahmed, M. Deadbeat Current Control in Grid-Connected Inverters: A Comprehensive Discussion. IEEE Access 2022, 10, 3990–4014. [Google Scholar] [CrossRef]
- Chang, X.H.; Jin, X. Observer-based fuzzy feedback control for nonlinear systems subject to transmission signal quantization. Appl. Math. Comput. 2022, 414, 126657. [Google Scholar] [CrossRef]
- Park, S.J.; Cho, K.H. Discrete Event Dynamic Modeling and Analysis of the Democratic Progress in a Society Controlled by Networked Agents. IEEE Trans. Autom. Control 2022, 1, 359–365. [Google Scholar] [CrossRef]
- Sukhinov, A.; Belova, Y.; Chistyakov, A.; Beskopylny, A.; Meskhi, B. Mathematical Modeling of the Phytoplankton Populations Geografic Dynamics for Possible Scenarios of Changes in the Azov Sea Hydrological Regime. Mathematics 2021, 9, 3025. [Google Scholar] [CrossRef]
- Niu, L.; Ruiz-Herrera, A. Simple dynamics in non-monotone Kolmogorov systems. Proc. R. Soc. Edinb. Sect. A-Math. 2021, 1–16. [Google Scholar] [CrossRef]
- Wang, X.; Lu, J.; Wang, Z.; Li, Y. Dynamics of discrete epidemic models on heterogeneous networks. Physica A 2020, 539, 122991. [Google Scholar] [CrossRef]
- Abdel-Gawad, H.I.; Abdel-Gawad, A.H. Discrete and continuum models of COVID-19 virus, formal solutions, stability and comparison with real data. Math. Comput. Simul. 2021, 190, 222–230. [Google Scholar] [CrossRef]
- Miranda, L.K.A.; Kuwana, C.M.; Huggler, Y.H.; da Fonseca, A.K.P.; Yoshida, M.; de Oliveira, J.A.; Leonel, E.D. A short review of phase transition in a chaotic system. Eur. Phys. J.-Spec. Top. 2021, 1–11. [Google Scholar] [CrossRef]
- Nordmark, A.B. Non-periodic motion caused by grazing incidence in an impact oscillator. J. Sound Vib. 1991, 145, 279–297. [Google Scholar] [CrossRef]
- Water, W.; Molenaar, J. Dynamics of vibrating atomic force microscopy. Nanotechnology 2000, 11, 192–199. [Google Scholar] [CrossRef]
- Molenaar, J.; Weger, J.G.; Water, W. Mappings of grazing-impact oscillators. Nonlinearity 2001, 14, 301–321. [Google Scholar] [CrossRef]
- Mercinger, M.; Fercec, B.; Oliveire, R.; Pagon, D. Cyclicity of some analytic maps. Appl. Math. Comput. 2017, 295, 114–125. [Google Scholar]
- Yao, W.B.; Li, X.Y. Complicate bifurcation behaviors of a discrete predator-prey model with group defense and nonlinear harvesting in prey. Appl. Anal. 2022, 1–16. [Google Scholar] [CrossRef]
- Akrami, M.H.; Atabaigi, A. Dynamics and Neimark-Sacker Bifurcation of a Modified Nicholson-Bailey Model. J. Math. Ext. 2022, 16, 1–18. [Google Scholar]
- Deng, S.F. Bifurcations of a Bouncing Ball Dynamical System. Int. Bifurc. Chaos 2019, 29, 1950191. [Google Scholar] [CrossRef]
- Lines, M.; Westerhoff, F. Effects of inflation expectations on macroeconomics dynamics:extrapolative versus regressive expectations. Stud. Nonlinear Dyn. Econom. 2012, 16, 7. [Google Scholar] [CrossRef] [Green Version]
- Neugart, M.; Tuinstra, J. Endogenous fluctuations in the demand for education. J. Evol. Econ. 2003, 13, 29–51. [Google Scholar] [CrossRef] [Green Version]
- Palan, S. A Review of Bubbles and Crashes in Experimental Asset Markets. J. Econ. Surv. 2013, 27, 570–588. [Google Scholar] [CrossRef]
- Agliari, A.; Hommes, C.H.; Pecora, N. Path dependent coordination of expectations in asset pricing experiments: A behavioral explanation. J. Econ. Behav. Organ. 2016, 121, 15–28. [Google Scholar] [CrossRef] [Green Version]
- Chenciner, A. Bifurcations de points fixes elliptiques. III. Orbites periodiques de “petites periodes” et elimination resonnante des couples de courbes invariantes. Inst. Hautes Etudes Sci. Publ. Math. 1988, 66, 5–91. [Google Scholar] [CrossRef]
- Chenciner, A. Bifurcations de points fixes elliptiques. I. Courbes invariantes. IHES-Publ. Math. 1985, 61, 67–127. [Google Scholar] [CrossRef]
- Chenciner, A. Bifurcations de points fixes elliptiques. II. Orbites periodiques et ensembles de Cantor invariants. Invent. Math. 1985, 80, 81–106. [Google Scholar] [CrossRef]
- Arrowsmith, D.; Place, C. An Introduction to Dynamical Systems; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Kuznetsov, Y.A. Elements of Applied Bifurcation Theory, 3rd ed.; Springer: New York, NY, USA, 2004. [Google Scholar]
- Tigan, G.; Lugojan, S.; Ciurdariu, L. Analysis of Degenerate Chenciner Bifurcation. Int. J. Bifurc. Chaos 2020, 30, 2050245. [Google Scholar] [CrossRef]
- Lugojan, S.; Ciurdariu, L.; Grecu, E. New Elements of analysis of a degenerate Chenciner bifurcation. Symmetry 2022, 14, 77. [Google Scholar] [CrossRef]
- Tigan, G.; Brandibur, O.; Kokovics, E.A.; Vesa, L.F. Degenerate Chenciner Bifurcation Revisited. Int. J. Bifurc. Chaos 2021, 31, 2150160. [Google Scholar] [CrossRef]





| T | |||||||
|---|---|---|---|---|---|---|---|
| sign | sign() | 0 | sign(a) | 0 | sign(−a) | 0 | sign(a) |
| T | |||
|---|---|---|---|
| sign | sign(−a) | 0 | sign(a) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lugojan, S.; Ciurdariu, L.; Grecu, E. Chenciner Bifurcation Presenting a Further Degree of Degeneration. Mathematics 2022, 10, 1603. https://doi.org/10.3390/math10091603
Lugojan S, Ciurdariu L, Grecu E. Chenciner Bifurcation Presenting a Further Degree of Degeneration. Mathematics. 2022; 10(9):1603. https://doi.org/10.3390/math10091603
Chicago/Turabian StyleLugojan, Sorin, Loredana Ciurdariu, and Eugenia Grecu. 2022. "Chenciner Bifurcation Presenting a Further Degree of Degeneration" Mathematics 10, no. 9: 1603. https://doi.org/10.3390/math10091603
APA StyleLugojan, S., Ciurdariu, L., & Grecu, E. (2022). Chenciner Bifurcation Presenting a Further Degree of Degeneration. Mathematics, 10(9), 1603. https://doi.org/10.3390/math10091603






