Event-Triggered Consensus Control of Nonlinear Strict Feedback Multi-Agent Systems †
Abstract
:1. Introduction
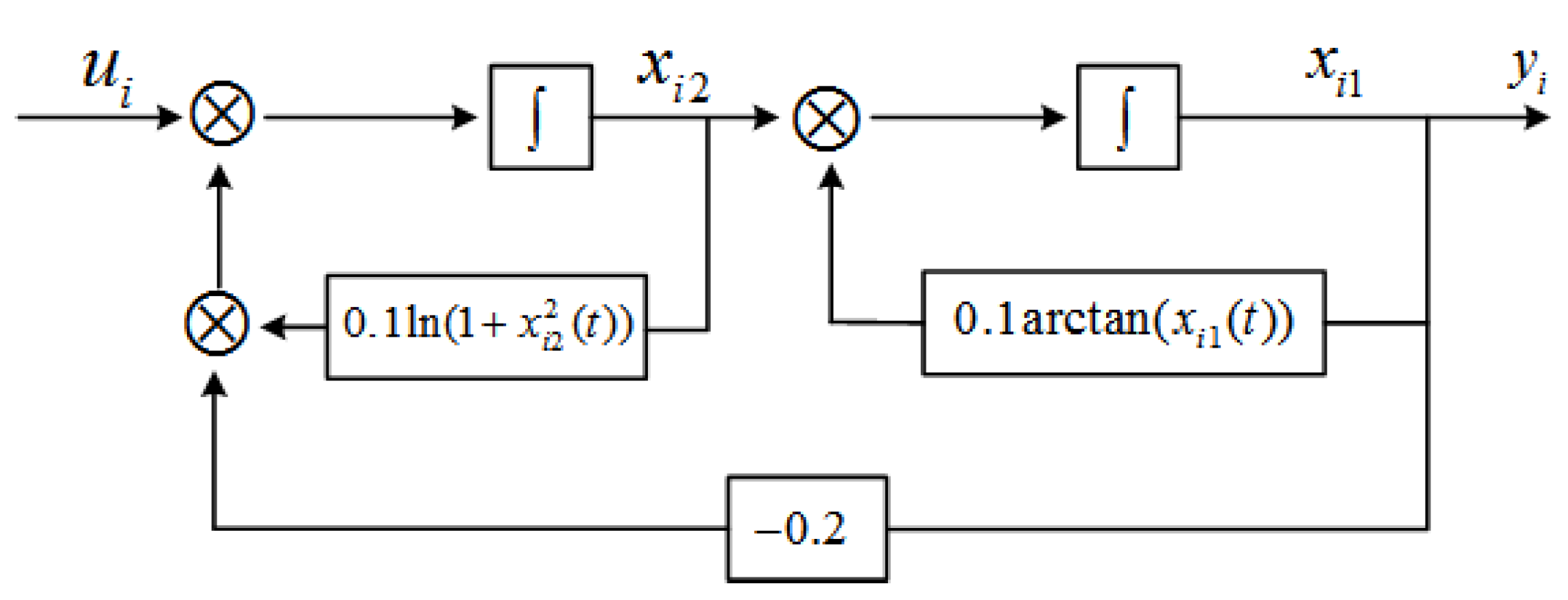
2. Problem Statement and Preliminaries
2.1. Problem Statement
2.2. Preliminaries
3. State-Based Event-Triggered Algorithm
| Algorithm 1: State-based event-triggered algorithm |
 |
4. Observer-Based Event-Triggered Algorithm
| Algorithm 2: Observer-based event-triggered algorithm |
 |
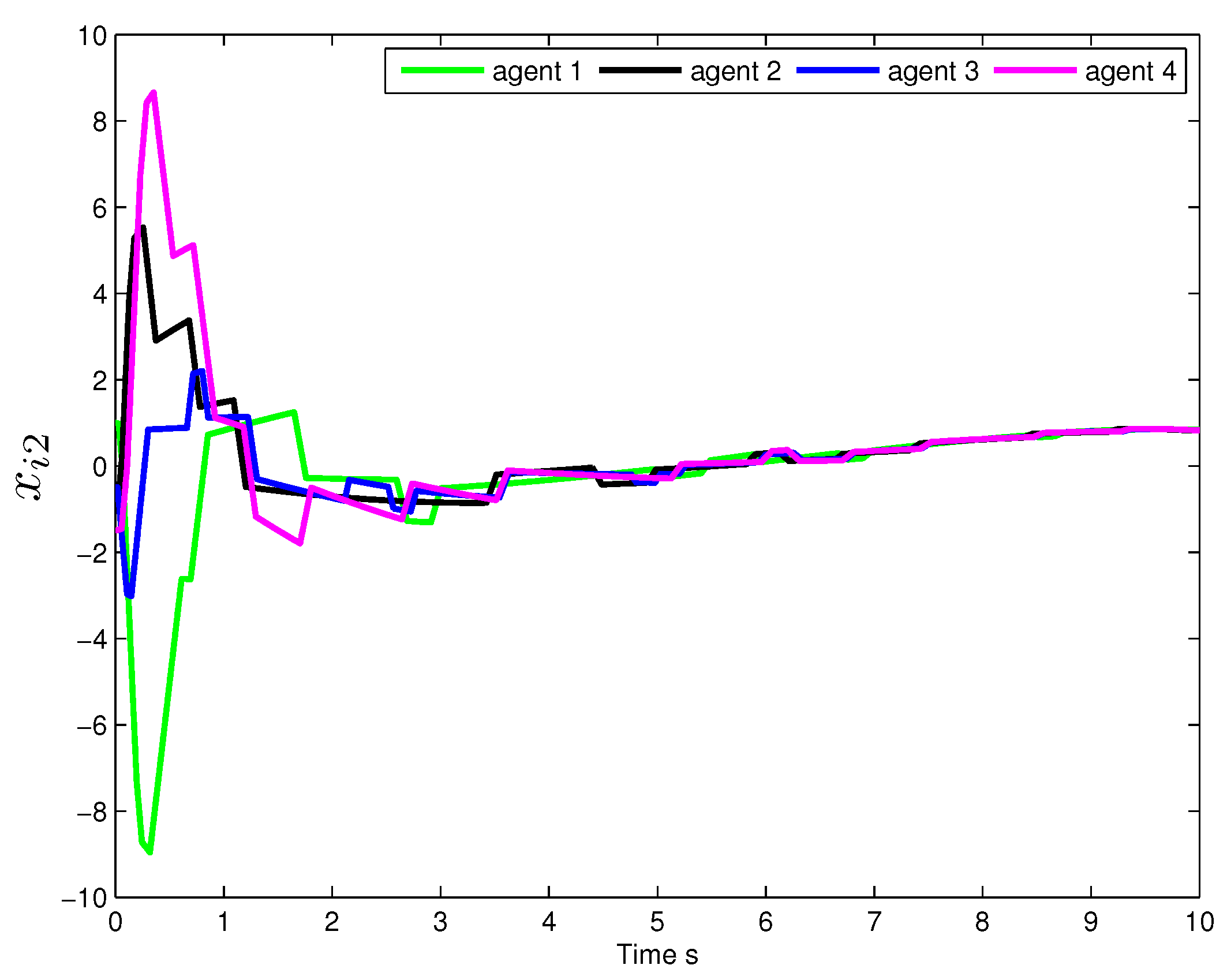
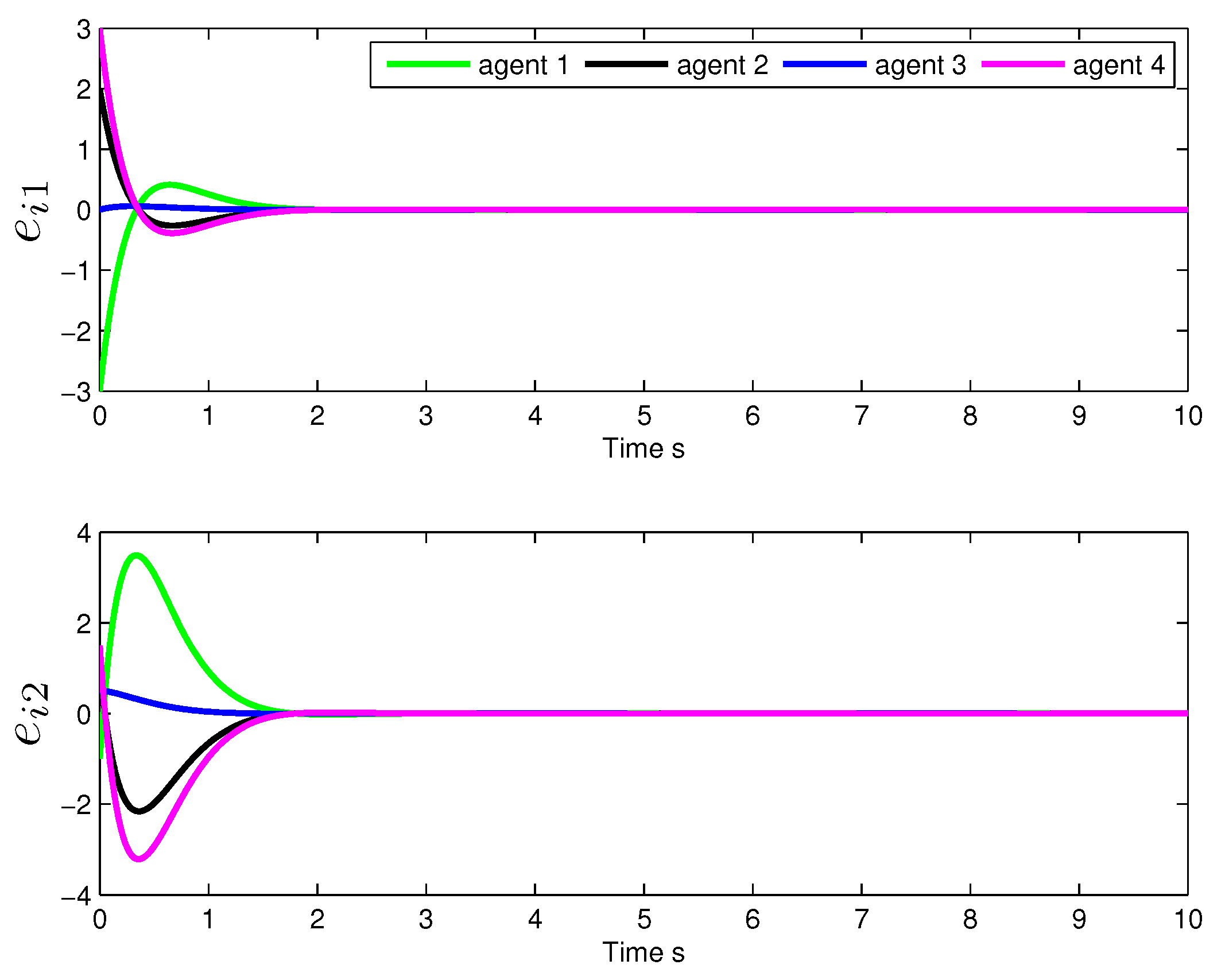
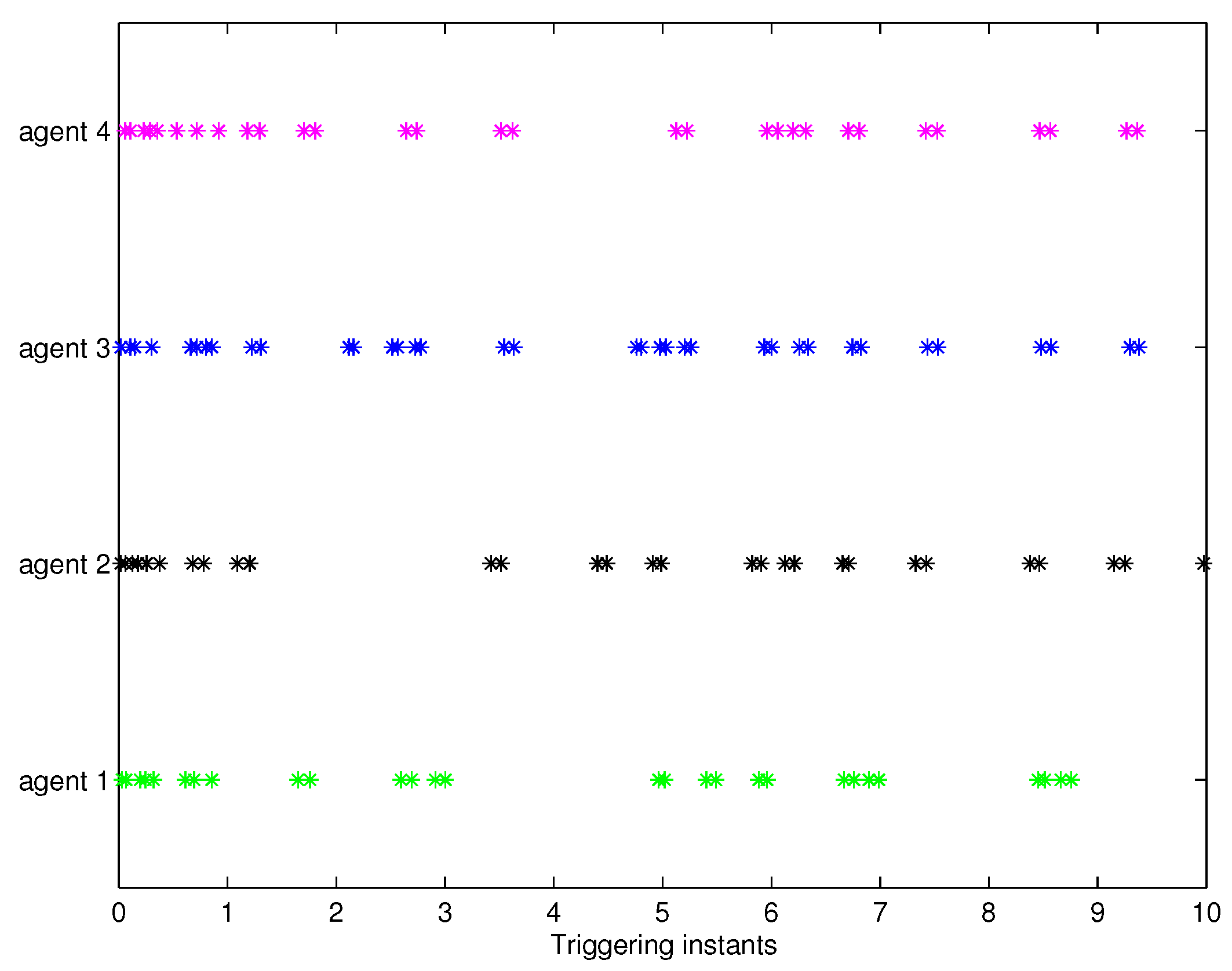
5. Simulations
5.1. State-Based Consensus
5.2. Observer-Based Consensus
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MASs | Multi-agent Systems |
| UAV | Aerial Vehicle |
| PDE-ODE | Partial Differential Equations and Ordinary Differential Equations |
References
- Jin, E.; Jiang, X.; Sun, Z. Robust decentralized attitude coordination control of spacecraft formation. Syst. Control Lett. 2008, 57, 567–577. [Google Scholar]
- Chen, Y.; Yu, J.; Su, X.; Luo, G. Path planning for multi-UAV formation. J. Intell. Robot. Syst. 2015, 77, 229–246. [Google Scholar] [CrossRef]
- Pavlin, G.; de Oude, P.; Maris, M.; Nunnink, J.; Hood, T. A multi-agent systems approach to distributed bayesian information fusion. Inf. Fusion 2010, 11, 267–282. [Google Scholar] [CrossRef]
- Kusic, K.; Ivanjko, E.; Vrbanic, F.; Greguric, M.; Dusparic, I. Spatial-temporal traffic flow control on motorways using distributed multi-agent reinforcement learning. Mathematics 2021, 9, 3081. [Google Scholar] [CrossRef]
- Kaminka, G.; Schechter-Glick, R.; Sadov, V. Using sensor morphology for multirobot formations. IEEE Trans. Robot. 2008, 24, 271–282. [Google Scholar] [CrossRef]
- Dimarogonas, D.V.; Frazzoli, E.; Johansson, K.H. Distributed event-triggered control for multi-agent systems. IEEE Trans. Autom. Control 2012, 57, 1291–1297. [Google Scholar] [CrossRef]
- Meng, X.; Xie, L.; Soh, Y.C. Asynchronous periodic event-triggered consensus for multi-agent systems. Automatica 2017, 84, 214–220. [Google Scholar] [CrossRef]
- Jia, Q.; Tang, W.K.S. Event-triggered protocol for the consensus of multi-agent systems with state-dependent nonlinear coupling. IEEE Trans. Circuits Syst. 2018, 65, 723–732. [Google Scholar] [CrossRef]
- Yan, H.; Shen, Y.; Zhang, H.; Shi, H. Decentralized event-triggered consensus control for second-order multi-agent systems. Neurocomputing 2014, 133, 18–24. [Google Scholar] [CrossRef]
- Wei, B.; Xiao, F.; Dai, M. Edge event-triggered control for multi-agent systems under directed communication topologies. Int. J. Control 2018, 91, 887–896. [Google Scholar] [CrossRef]
- Zhang, H.; Feng, G.; Yan, H.; Chen, Q. Consensus of multi-agent systems with linear dynamics using event-triggered control. IET Control Theory Appl. 2014, 8, 2275–2281. [Google Scholar] [CrossRef]
- Garcia, E.; Cao, Y.; Casbeer, D.W. Periodic event-triggered synchronization of linear multi-agent systems with communication delays. IEEE Trans. Autom. Control 2017, 62, 366–371. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Du, C.; Liu, H.; Lu, P. Distributed event-triggered consensus control with fully continuous communication free for general linear multi-agent systems under directed graph. Int. J. Robust Nonlinear Control 2018, 28, 132–143. [Google Scholar] [CrossRef]
- Adaldo, A.; Alderisio, F.; Liuzza, D.; Shi, G.; Dimarogonas, D.V.; Bernardo, M.; Johansson, K.H. Event-triggered pinning control of switching networks. IEEE Trans. Control Netw. Syst. 2015, 2, 204–213. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Chen, G.; Xiao, L. Event-triggered nonlinear consensus in directed multi-agent systems with combinational state measurements. Int. J. Syst. Sci. 2016, 47, 3364–3377. [Google Scholar] [CrossRef]
- Hu, A.; Cao, J. Consensus of multi-agent systems via intermittent event-triggered control. Int. J. Syst. Sci. 2017, 48, 280–287. [Google Scholar] [CrossRef]
- Gao, F.; Chen, W.; Li, Z.; Li, J.; Xu, B. Neural network-based distributed cooperative learning control for multiagent systems via event-triggered communication. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 407–419. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Y.; Yue, D.; Yue, W. Adaptive event-triggered consensus control of a class of second-order nonlinear multiagent systems. IEEE Trans. Cybern. 2020, 50, 5010–5020. [Google Scholar] [CrossRef]
- Meng, H.; Zhang, H.; Wang, Z.; Chen, G. Event-triggered control for semi-global robust consensus of a class of nonlinear uncertain multi-agent systems. IEEE Trans. Autom. Control 2020, 65, 1683–1690. [Google Scholar] [CrossRef]
- Han, Z.; Tang, W.K.S.; Jia, Q. Event-triggered synchronization for nonlinear multi-agent systems with sampled data. IEEE Trans. Circuits Syst. 2020, 67, 3553–3561. [Google Scholar] [CrossRef]
- Shi, J. Cooperative control for nonlinear multi-agent systems based on event-triggered scheme. IEEE Trans. Circuits Syst. 2021, 68, 1977–1981. [Google Scholar] [CrossRef]
- Ni, X.; Yi, K.J.; Jiang, Y.M.; Zhang, A.C.; Yang, C.D. Consensus control of leaderless and leader-following coupled PDE-ODEs modeled multi-agent systems. Mathematics 2022, 10, 201. [Google Scholar] [CrossRef]
- Wang, X.; Ji, H. Leader-follower consensus for a class of nonlinear multi-agent systems. Int. J. Control Autom. Syst. 2012, 10, 27–35. [Google Scholar] [CrossRef]
- Yoo, S.J. Distributed adaptive containment control of uncertain nonlinear multi-agent systems in strict-feedback form. Automatica 2013, 49, 2145–2153. [Google Scholar] [CrossRef]
- Shen, Q.; Shi, P. Distributed command filtered backstepping consensus tracking control of nonlinear multiple-agent systems in strict-feedback form. Automatica 2015, 53, 120–124. [Google Scholar] [CrossRef]
- Li, Z.; Ji, H. Finite-time consensus and tracking control of a class of nonlinear multiagent systems. IEEE Trans. Autom. Control 2018, 63, 4413–4420. [Google Scholar] [CrossRef]
- Li, Y.; Yang, G.; Tong, S. Fuzzy adaptive distributed event-triggered consensus control of uncertain nonlinear multiagent systems. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 1777–1786. [Google Scholar] [CrossRef]
- Li, Y.; Liu, L.; Hua, C.; Feng, G. Evnet-triggered/self-triggered leader-following control of stochastic nonlinear multiagent systems using high-gain method. IEEE Trans. Cybern. 2019, 40, 881–891. [Google Scholar]
- Krstic, M.; Kanellakopoulos, I.; Kokotovic, P.V. Nonlinear and Adaptive Control Design; Wiley-Interscience: New York, NY, USA, 1995. [Google Scholar]
- Yu, W.; Chen, G.; Cao, M.; Kurths, J. Second-order consensus for multiagent systems with directed topologies and nonlinear dynamics. IEEE Trans. Syst. Man Cybern. Syst. 2010, 49, 1777–1786. [Google Scholar]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice-Hall: Hoboken, NJ, USA, 2002. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, J.; Li, Z.; Hou, Z.; Yang, C. Event-Triggered Consensus Control of Nonlinear Strict Feedback Multi-Agent Systems. Mathematics 2022, 10, 1596. https://doi.org/10.3390/math10091596
Zhuang J, Li Z, Hou Z, Yang C. Event-Triggered Consensus Control of Nonlinear Strict Feedback Multi-Agent Systems. Mathematics. 2022; 10(9):1596. https://doi.org/10.3390/math10091596
Chicago/Turabian StyleZhuang, Jiaojiao, Zhenxing Li, Zongxiang Hou, and Chengdong Yang. 2022. "Event-Triggered Consensus Control of Nonlinear Strict Feedback Multi-Agent Systems" Mathematics 10, no. 9: 1596. https://doi.org/10.3390/math10091596
APA StyleZhuang, J., Li, Z., Hou, Z., & Yang, C. (2022). Event-Triggered Consensus Control of Nonlinear Strict Feedback Multi-Agent Systems. Mathematics, 10(9), 1596. https://doi.org/10.3390/math10091596





