Abstract
The main contribution of this paper is to propose a closed expression for the Ramanujan constant of alternating series, based on the Euler–Boole summation formula. Such an expression is not present in the literature. We also highlight the only choice for the parameter a in the formula proposed by Hardy for a series of positive terms, so the value obtained as the Ramanujan constant agrees with other summation methods for divergent series. Additionally, we derive the closed-formula for the Ramanujan constant of a series with the parameter chosen, under a natural interpretation of the integral term in the Euler–Maclaurin summation formula. Finally, we present several examples of the Ramanujan constant of divergent series.
Keywords:
Ramanujan summation; Ramanujan constant of a series; divergent series; Euler–Maclaurin summation formula; Euler–Boole summation formula MSC:
40D05; 40G99
1. Introduction
When a series diverges [1], it may still be necessary to obtain assertive information related to that series. A relevant problem, in mathematical physics, is to give meaning to infinities that are obtained from divergent series. Indeed, several summation methods were developed for this purpose. For example, Grandi’s series has the value attributed under the Abel, Euler, Cesàro, and Borel summation methods [2,3,4]. A widely used method to regularize divergent series, whose systematic approach was given by G.H. Hardy [2], uses the theory of zeta functions [5,6,7]. Riemann’s zeta function , defined by , arises in many areas of mathematics, and it is a very interesting object of study (see, for example: [8,9,10]). In this context, another approach is the Ramanujan summation method [11,12,13]. Such a technique establishes a relationship between the series and a constant , which S. Ramanujan called “the constant of a series”. Later, Hardy [2] (p. 327) defined it as “the Euler–Maclaurin constant of f”. Such a constant is often known under the name of Ramanujan constant of a series (RCS). Following these concepts, it is desirable that a unique constant should be determined for each divergent series [14,15].
In Chapter VI of his second notebook, Ramanujan introduced formulae for obtaining a constant for a given series [13]. Analogues of these formulae appear in several key works, [2,11,12,16], just to cite a few. However, we note that, sometimes, the values presented as the Ramanujan constant for a given divergent series disagree with those obtained for other summation methods for the same series. Such a fact can be explained by looking at the definition for the RCS given by Hardy [2] (pp. 325–327), where the constant depends on a non-negative real parameter a. The RCS is, therefore, defined as a family of constants, from which, according to Hardy [2] (p. 327), the adequate value of the parameter a should be chosen for each special case studied. Moreover, Hardy [2] (p. 346) and B.C. Berndt [11] (p. 133) noted that the theory regarding the Ramanujan summation “demand great caution in their application” and “readers should keep in mind that his findings frequently lead to incorrect results”, respectively. The objectives of this manuscript are (i) to present the natural choice for the parameter a with which the values obtained for the RCS in the formula proposed by Hardy agree with those obtained for other summations methods, (ii) to present a version of the formula for the RCS with the parameter a selected, and (iii) to give a new closed formula for the RCS for alternating series.
Section 2 introduces the fundamental aspects of the Euler–Maclaurin summation formula (EMSF). Section 3 discusses the adjustment on the formula for the RCS, considering a specific value for the parameter a. Additionally, it presents some examples with the values obtained as a Ramanujan constant agreeing with those obtained for other summation methods, including some new examples. Section 4 addresses the Ramanujan constant for convergent series when the considered parameter a is that adopted in Section 3. Section 5 establishes a version of the Ramanujan constant for alternating series based on the Euler–Boole summation formula (EBSF). Additionally, several examples show the applicability of the proposed approach. Finally, Section 6 outlines the final remarks.
2. The Euler–Maclaurin and the Euler–Boole Summation Formulas
The EMSF is a powerful tool that enables the replacing of a finite sum of a function with a combination of the derivatives and the integral of . This result was derived independently by L. Euler and by C. Maclaurin [17,18,19]. Due to the importance of the EMSF, Hardy dedicated the last chapter in [2] to this topic, where he wrote the expression
for a non-negative real parameter a, where denotes the Bernoulli numbers [20,21,22,23]. Note that Formula (1), written according to Hardy’s notation, includes the non-null Bernoulli numbers with positive signs: Hardy considered , , etc. (with a shift when compared with the modern notation). Note that the first Bernoulli number, , is also present in Formula (1), with a positive sign, although written separately [2] (pp. 318, 320). It is supposed that the function f is sufficiently regular as x increases and that the magnitude of its kth derivative must decrease when k increases. Hardy called the constant “the Euler–Maclaurin constant ” related to the function f. Hardy established a relation between C and the Ramanujan summation of the series (denoted by Hardy as ), for a non-negative real parameter a, so that
where x denotes a non-negative real variable [2] (p. 327).
Many different arguments are known to derive the EMSF (see, for example, [2,15,21,23,24,25]). Commonly the EMSF of a function f that is infinitely differentiable is represented either as [3]
for , with , or as [3]
where the series in Equations (3) and (4) can diverge [2] (p. 320). Since the letter a is reserved to denote the parameter on the formula for the RCS, as written by Hardy [2] (p. 327), in the Equations (3) and (4), we use the letter b at the inferior bound limits of the sum and the integral. For functions f that are only differentiable until some finite order , the EMSF with remainder can be written as
where are the periodic Bernoulli polynomials of index r and period 1 [26,27,28], denotes the fractional part of , and stands for the integer part of . The remainder term for the EMSF was introduced by S.D. Poisson in 1823 [29]. The expression for the remainder used in Equation (5) appears in [25] (p. 96).
An analogous result of the EMSF, adapted for alternating series, is the EBSF. For an alternating function f that is infinitely differentiable and with derivatives absolutely integrable, it holds that
for and , where are the Euler polynomials [26,30,31]. If the alternating function f is only r times differentiable and is integrable on , then the EBSF can be expressed as
where are the periodic Euler polynomials of index r and period 1. The formula (7) is due to G. Boole [32].
3. Ramanujan Constant of a Series
Ramanujan introduced a summability method in his second notebook, chapter VI (present in the rare book [13], and commented in Chapter 6 of [11]). Hardy [2] (p. 327) considered that the Ramanujan summation had a basis in a version of the EMSF (1). Moreover, he analyzed the consequences coming from a property of a given series called by Ramanujan by the constant of a series: the constant , in Equations (1) and (2) [11] (pp. 143–144). In his definition for the RCS [2] (p. 327), Hardy established that the constant depends on and on
i.e., it depends on and on a non-negative real parameter a, and stated that such a constant gives another definition for the sum of a divergent series. This is a sufficient reason to look with care at the formula for the RCS.
Ramanujan started by writing
for describing a kind of interpolation function for the partial sums that should satisfy the condition . He probably used a version of the EMSF (1) to write the function in an asymptotic expansion that can be expressed as
in which, appears, that is, the constant that Ramanujan treated “like the center of gravity of a series” [11,13].
In 1995, B. Candelpergher [33] introduced an algebraic framework to define summation methods that can be adapted to cover the method introduced by Ramanujan. More about this algebraic framework can be read in [12,34,35]. Using a version of the EMSF with remainder (5), Candelpergher [12,34] has chosen and, thus, wrote the constant as
Supposing that and that the integral is convergent for a large enough r, the constant does not depend on r and can be written only as . Using Formula (11), Candelpergher presented in [12] (p. 5) two initial examples and, for and , he obtained and , respectively. However, we verify that the values and are assigned to the series and , respectively, under the smoothed sum method (see [3] or [36] (pp. 88–104)). In the following, we present the adequate value for the parameter a that permits us to obtain, for the Ramanujan constant of a given divergent series, the same value obtained with other summation methods.
In Chapter XIII of the seminal work [2], specifically in Equations (13.5.9), (13.5.13), and (13.6.4), Hardy wrote the term , which was neither included in Formula (11) given in [12] (pp. 4–8), nor in the equivalent formula in [11] (pp. 134–135). This is a kind of overlooked term of the RCS. To recover such a term for a series that does not alternate the sign, we revisit the formulas for the RCS in proposition 1, choosing and giving a natural interpretation for the integral term in the EMSF. To make the contribution more clear, namely the choice of that leads the RCS to agree with the values obtained for other summation methods, we highlight a property satisfying Hardy’s formula for the RCS given in [2] (pp. 325–327), herein denoted by , as follows.
Property 1.
The Ramanujan constant of a given series can be obtained by the sum of all constants that do not depend on n in the development of the series under a proper summation formula.
For series in which the general term does not alternate the sign, the proper summation formula indicated in Property 1 is the EMSF (4) with . In this case, the RCS depends on a non-negative real parameter a. For alternating series , the proper summation formula is the EBSF (6) with .
Proposition 1.
Let be a series where is a function integrable on for any , and, as parameter of the integral (8), choose . If the function f is only r times differentiable and if is integrable on for any , where are the periodic Bernoulli polynomials of index r, then the Ramanujan constant of the series depending on r and with the parameter is given by
where are the Bernoulli polynomials of index r and are the Bernoulli numbers.
If and the series is convergent, then the Ramanujan constant of the series with the parameter is given as
Proof.
We look at the integral term in the EMSF (5), using the fundamental theorem of calculus as follows. Let F be the primitive of f on that vanishes in , i.e.,
Then, we can write
and, choosing , with the purpose of arriving at a formula for , we rewrite the EMSF (5) as
where
is a constant satisfying the Property 1.
Taking , we arrive at
where the Ramanujan constant depending on r of the series is given in (17). Replacing the last integral in (17) by , we obtain Formula (12).
The bound limits of the integral in the remainder terms in Equations (16) and (17) are proposed under the same argument as for the primitive F for f, which should vanish at . Observe that, in Equation (17), all derivatives are evaluated at , whereas the primitives are evaluated at and vanish at , respecting the numeric character of the constant.
Remark 1.
Proposition 1 presents Formula (12) for the constant that depends on r, but such a constant may not be a good approximation for the RCS for low orders r due to the presence of the remainder term .
With the formulae (12) and (13) for the RCS, obtained with the choice of for the parameter, the Ramanujan summation is now useful for obtaining constants for divergent series that agree with those obtained from others summation methods.
In the following, we revisit the two previous examples by applying Formula (13).
Example 1.
The series and for .
For , where , we obtain
For , where , we obtain
The values now given to the Ramanujan constant for the series and under Formula (13) are the expected values, agreeing with the those obtained under other summation methods. Applying Formula (13), we obtain
Remark 2.
Two desired properties for a given summation method are shift-invariance and linearity. We observe that the RCS is linear, but it is not shift-invariant. Since Formulae (12) and (13) are composed of a combination of linear operators acting on f, then has the property of linearity. However, the RCS in Expression (20) serves as a counterexample for the shift-invariance of . If the series , for which , was invariant, we would have
that is, in terms of , we would have
an absurd.
For the next example, the following lemma is necessary:
Lemma 1.
The series is convergent.
The well known Lemma 1 can be proved using the convergence of the series
for all t such that , or using the approximation , valid for large k (and when ) [37] (p. 143), after applying the ratio test for series.
Example 2.
The series and .
We start by computing the constant for the series .
For the term , we calculate and, imposing the condition , we arrive at . Thus, we obtain
The term returns the value . The derivatives return for all .
Then, using Formula (13), we obtain
From Lemma 1, the last series is convergent, and, then, a numerical approximation to can be obtained:
For the constant for the series , we can evaluate the constant by choosing to apply Formula (13) or to use the linearity of the RCS, taking = . In both cases, we arrive at
Unfortunately, just like other summation methods, the Ramanujan summation cannot apply to all divergent series. One example of a series that is not summable under the RCS is the harmonic series . In addition to the function not being defined for ; we cannot evaluate by Formula (13) because the integral is divergent.
4. Ramanujan Constant for Convergent Series
Ramanujan wrote “if be a convergent series then its constant is the sum of the series” [13]. In this section, we study the RCS applied to convergent series, when the parameter is chosen, and we conclude that, in this case, the RCS may not be equal to the sum of the series in the classical sense. However, for such cases, we provide a possible interpretation for applied to convergent series, when the parameter is chosen. Let us start with the following example.
Example 3.
The convergent series .
It is known that .
Considering the function and applying Formula (13) to the series , for the term , we obtain and, imposing the condition , we arrive at . Thus, we obtain
The term returns the value . The derivatives of f are given by for all .
Then, using Formula (13) for the RCS, we obtain
where the last series is convergent (it is verifiable by the same argument that proves Lemma 1). A numerical approximation to evaluates until , returning
a number clearly different to 1, the classical sum of the series .
To gives a clear interpretation for the RCS for a convergent series when the parameter is chosen, we look again at the EMSF (1) and at the RCS Formula (13). For the function and considering in the Formula (1), the only terms remaining are
and we can rewrite
Therefore, the value obtained for the RCS of the convergent series , evaluated by Formula (13), is a good approximation for the difference between the infinite sum of the terms , starting at , and the improper integral of the function , beginning at .
This example indicates a possible interpretation of the RCS for a type of convergent series when : the RCS can evaluates the difference between the infinite sum of the terms , starting at , and the improper integral of the function , beginning at .
5. Ramanujan Constant for Alternating Series
Hardy [2] (p. 327) states that the Ramanujan summation and RCS are “primarily adapted to series of positive terms”. However, we easily extrapolate this assertion for: “the RCS is adapted to series of terms that do not alternate signs”; indeed, if, in the derivation of the EMSF, we consider all terms negative, i.e., for some function , before taking in the derivation of Formulae (12) and (13), it is possible put the negative signs as evidence. This allows us to conclude that .
Example 4.
Series with only negative terms.
Applying Formula (13), or revisiting the previous examples, we can write:
However, since the EMSF is not appropriate for series with alternating terms, Formulae (12) and (13) are also not appropriate for evaluating the RCS for series with alternating terms.
In entries 9 and 10 of Chapter 6 of his VI Notebook [13], Ramanujan approached the constant for alternating series. However, we do not find a clear formula for evaluating the Ramanujan constant of an alternating series (RCAS) anywhere in the literature. In the following, based on the EBSF, we propose a way to evaluate the RCAS. The closed formulae for the RCAS are given in Propositions 2 and 3. We observe that the RCAS does not depend on the parameter a, i.e., a unique constant can be determined as a constant to each alternating series that diverges.
Proposition 2.
Let be an alternating series, where is a function absolutely integrable on for any . If the function f is only r times differentiable and if is absolutely integrable on for any , then the Ramanujan constant of the alternating series depending on r is given by
where are the Euler polynomials of index r.
Proof.
We choose the EBSF with remainder (7) and initially rewrite only its left side as
Then, choosing and considering the extreme case , we obtain
Without a loss of generality, to guarantee that the first term of the alternating series is positive, we consider that , with . Then, we sum the term on both sides of Equation (38), i.e,
After rearranging terms, we arrive at the following EBSF-like formula with remainder
Then, since is supposed to be absolutely integrable on for any , we can rewrite the integral in the remainder term as
Note that the last integral can be expressed as because the considered interval is . Then, we take to obtain
where
is the formula for the RCAS depending on r given in Equation (36). □
Proposition 3.
Let be an alternating series, where is a function absolutely integrable on for any . If and the series is convergent, then the Ramanujan constant of the alternating series is given as
where are the Euler polynomials of index k.
Proof.
Suppose that . We start by rewriting only the left side of Equation (6) as follows:
Then, as in the proof of Proposition 2, choosing and considering , supposing that , with , summing on both sides and rearranging the terms, we arrive at the EBSF-like formula:
Example 5.
The Grandi’s series .
For the Grandi’s series , which is an alternating series with first term positive, we can apply Formula (44) to obtain the RCAS. We work with the constant function . We obtain the value for the term . Since the derivatives of are all null, the term is the single non-null term in Formula (44). We conclude that
The same value is recovered for the Grandi’s series under Abel, Euler, Cesàro, and Borel summation methods.
Example 6.
The Euler’s alternating series .
It is known that the series receives the value under other summability methods, such as the Abel or Euler summability method [3].
Now, we apply Formula (44) for evaluating the constant of the Euler’s alternating series. The considered function is . We obtain the value for the term , and the derivatives of are all null, except for the first, which returns the value 1. As the Euler polynomial of order 1 evaluated at returns , we conclude that
This is the same value obtained for Euler’s alternating series under the Abel and Euler summation methods.
Example 7.
The series of coefficients of the Grünwald–Letnikov fractional derivatives.
For a given function f defined in an interval , the Grünwald–Letnikov fractional operator of order is defined as [38,39,40,41]:
If , then the operator is a fractional derivative; otherwise, if , then the operator is a fractional integral. The series of coefficients of the Grünwald–Letnikov fractional operator of order is given by , or, adjusting the initial term at , by
This adjustment is needed in order to evaluate the RCAS. The general term of the series (52) can be written as , where the function is
Formula (44) is appropriate for functions that are infinitely differentiable, and Expression (36) is appropriate for use when the function f is only (or infinitely differentiable, but with a large computational cost for evaluating it). In this example, both formulae can be considered.
We apply (44) for calculations until to obtain an idea of the behavior of the RCAS depending on . The term returns the value , for any . The first derivative of the function f is
where is the polygamma function of order 0 [31]. Applying this derivative at and multiplying by , we obtain
where is the Euler–Mascheroni constant [21,24,31].
The numerical values for , and for are listed in Table 1 and Table 2, for some values of , as well as the numerical approximations for the RCAS, evaluated until . The other successive derivatives can be calculated, but the associated computational cost grows considerably. We remember that , , and , and that the derivatives of even order of the function f do not influence the value of the RCAS because for all .

Table 1.
Numerical approximations of , using Formula (44), evaluated until , for some values of (derivatives).

Table 2.
Numerical approximations of , using Formula (44), evaluated until , for some values of (integrals).
In Figure 1, it is possible to see the evolution of the constants when we add the consecutive terms. From Figure 1 and Table 1 and Table 2, it is possible to conclude that the RCAS for the series
(obtained choosing ) is exactly the value . For other values of , one needs to consider more terms in (44) to obtain a better approximation.
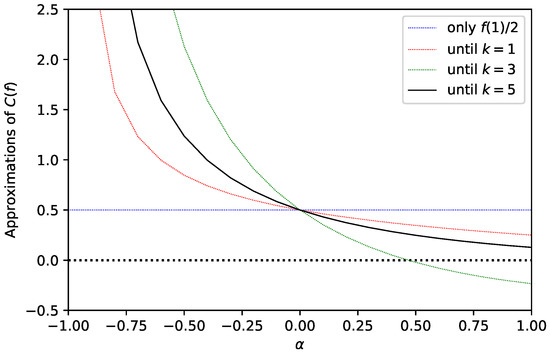
Figure 1.
Approximations of the RCAS versus for the series of coefficients of the Grünwald–Letnikov fractional operator, under Formula (44), evaluated until , depending on .
6. Conclusions
Divergent series appear in many fields of science, such as number theory, quantum theory, and mathematical physics, among others. A common issue is to give meaning to a divergent series. Regularization methods are used for such purposes. In this context, the RCS appears as a method with the potential to solve such a problem for a class of functions. Regarding the Ramanujan summation, Ramanujan himself stated “If be a convergent series then its constant is the sum of the series” and “We can substitute this constant... instead of its divergent infinite series”. The importance of the RCS can be understood throughout his own words, especially the last cited phrase.
The definition for the RCS given by Hardy [2] (pp. 325–327) includes a parameter a and maintains flexibility, which permits its use in several problems. However, when a divergent series already has a known value obtained for other summation methods, it is expected that the same value can be obtained as a constant for each summation method that is applicable to it, including the RCS. When the RCS is considered with the parameter , the RCS agrees with the value obtained for any other summation method that is applicable to the divergent series considered.
We hope that Expressions (12) and (13) help to obtain applicable values as constants for several divergent series, where the general term does not alternate sign, as well as with Formulae (36), (44) for alternating series, thus helping to promote the Ramanujan summation theory as a technique for regularizing divergent series.
To emphasize the importance of regularization techniques for divergent series, we cite some examples of the applicability of such techniques. We highlight: (i) the zeta function regularization was applied, for example, to prove Lerch’s formula in number theory [42] and to evaluate the Casimir energy in mathematical physics [43], and (ii) the smoothed sum method [3,36] was also applied to revisit the Casimir effect [44,45]. Several applications of regularization techniques are given in references [46,47,48,49,50,51]. Some recent developments can be found in references [52,53,54,55].
Author Contributions
Conceptualization, J.Q.C., J.A.T.M., and A.M.L.; writing—original draft preparation, J.Q.C.; writing—review and editing, J.A.T.M. and A.M.L.; supervision, A.M.L. All authors have read and agreed to the final version of the manuscript.
Funding
This work was partially supported by INEGI-LAETA (FCT project UIDB/50022/2020).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank the anonymous reviewers for their careful reading and suggestions that contributed to the improvement of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| EMSF | Euler–Maclaurin summation formula |
| EBSF | Euler–Boole summation formula |
| RCS | Ramanujan constant of a series |
| RCAS | Ramanujan constant of an alternating series |
References
- Cauchy, A.-L. Cours D’Analyse de L’École Royale Polytechnique; De L’Imprimerie Royale: Paris, France, 1821. [Google Scholar]
- Hardy, G.H. Divergent Series; Oxford University Press: London, UK, 1949. [Google Scholar]
- Santander, M. Sumas de Potencias y Series Divergentes Un Panorama Sobre Sumación de Series, Sumas Suavizadas, Números y Polinomios de Bernoulli, la Fórmula de Euler–Maclaurin y la Función ζ de Riemann; Unpublished Notes; University of Valladolid: Valladoli, Spain, 2017. [Google Scholar]
- Chagas, J.Q.; Machado, J.A.T.; Lopes, A.M. Overview in Summabilities: Summation Methods for Divergent Series, Ramanujan Summation and Fractional Finite Sums. Mathematics 2021, 9, 2963. [Google Scholar] [CrossRef]
- Titchmarsh, E.C. The Theory of the Riemann Zeta-Function, 2nd ed.; Clarendon Press: Oxford, UK, 1986. [Google Scholar]
- Patterson, S.J. An Introduction to the Theory of the Riemann Zeta-Function; Cambridge Studies in Advanced Mathematics; Cambridge University Press: Cambridge, UK, 1988; Volume 14. [Google Scholar]
- Weil, A. Prehistory of the Zeta-Function. In Number Theory, Trace Formulas and Discrete Groups; Aubert, K.E., Bombieri, E., Goldfeld, D., Eds.; Academic Press: San Diego, CA, USA, 1989; Chapter 1; pp. 1–9. [Google Scholar]
- Ivić, A. The Riemann Zeta-Function: Theory and Applications; Dover Publications: New York, NY, USA, 2003. [Google Scholar]
- Voros, A. Spectral functions, spectial funtions and the Selberg zeta functions. Commun. Math. Phys. 1987, 110, 439–465. [Google Scholar] [CrossRef]
- Machado, J.T.; Luchko, Y. Multidimensional scaling and visualization of patterns in distribution of nontrivial zeros of the zeta-function. Commun. Nonlinear Sci. 2021, 102, 105924. [Google Scholar] [CrossRef]
- Berndt, B.C. Ramanujan’s Notebooks Part I; Springer: Berlin, Germany, 1985. [Google Scholar]
- Candelpergher, B. Ramanujan Summation of Divergent Series; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 2017; Volume 2185. [Google Scholar]
- Ramanujan, S. Notebooks of Srinivasa Ramanujan; Tata Institute of Fundamental Research: Bombay, India, 2012. [Google Scholar]
- Euler, L. De seriebus divergentibus. Novi Comment. Acad. Sci. Petropolitanae 1760, 5, 205–237. [Google Scholar]
- Varadarajan, V.S. Euler and his work on infinite series. Bull. Am. Math. Soc. 2007, 44, 515–539. [Google Scholar] [CrossRef]
- Bornemann, F. The SIAM 100-Digit Challenge: A decade later - Inspirations, Ramifications, and other eddies left in its wake. Jahresber. Dtsch. Math. Ver. 2008, 118, 87–123. [Google Scholar] [CrossRef]
- Euler, L. Methodus generalis summandi progressiones. Comment. Acad. Sci. Petropolitanae 1738, 6, 68–97. [Google Scholar]
- Euler, L. Methodus universalis series summandi ulterius promota. Comment. Acad. Sci. Petropolitanae 1768, 8, 147–158. [Google Scholar]
- Bernoulli, J. A Treatise of Fluxions; Knight and Compton Printers: Edinburgh, UK, 1742. [Google Scholar]
- Maclaurin, C. Ars Conjectandi, Opus Posthumum. Accedit Tractatus de Seriebus Infinitis, et Epistola Ballicé Scripta de Ludo Pilae Reticularis; Thurneysen Brothers: Basel, Switzerland, 1713. [Google Scholar]
- Boas, R.P. Partial Sums of Infinite Series, and How They Grow. Am. Math. Mon. 1977, 84, 237–258. [Google Scholar] [CrossRef]
- Gould, H.W. Formulas for Bernoulli Numbers. Am. Math. Mon. 1972, 79, 44–51. [Google Scholar] [CrossRef]
- Graham, R.L.; Knuth, D.E.; Patashnik, O. Concrete Mathematics: A Foundation for Computer Science; Addison-Wesley Publishing Company: New York, NY, USA, 1994. [Google Scholar]
- Apostol, T.M. An elementary view of Euler’s summation formula. Am. Math. Mon. 1999, 106, 409–418. [Google Scholar] [CrossRef]
- Kač, V.; Cheung, P. Quantum Calculus; Universitext; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Berndt, B.C. Character analogues of the Poisson and Euler–Maclaurin summation formulas with applications. J. Number Theory 1975, 7, 413–445. [Google Scholar] [CrossRef]
- Butzer, P.L.; Hauss, M.; Leclerc, M. Bernoulli numbers and polynomials of arbitrary complex indices. Appl. Math. Lett. 1992, 5, 83–88. [Google Scholar] [CrossRef][Green Version]
- Choudary, A.D.R.; Niculescu, C.P. Real Analysis on Intervals; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Poisson, S.D. Sur le calcul numérique des Intégrales définies. Mémoires de l’Institut 1823, 6, 571–602. [Google Scholar]
- Borwein, J.M.; Calkin, N.J.; Manna, D. Euler–Boole summation revisited. Am. Math. Mon. 2009, 116, 387–412. [Google Scholar] [CrossRef]
- Erdélyi, A. Higher Transcendental Functions; McGraw-Hill: New York, NY, USA, 1953. [Google Scholar]
- Boole, G. A Treatise on the Calculus of Finite Differences, 2nd ed.; Dover: New York, NY, USA, 1960. [Google Scholar]
- Candelpergher, B. Développements de Taylor et sommation des series. Expo. Math. 1995, 13, 163–222. [Google Scholar]
- Candelpergher, B.; Coppo, M.A.; Delabaere, E. La sommation de Ramanujan. L’Enseignement Math. 1975, 43, 93–132. [Google Scholar]
- Candelpergher, B.; Gadiyar, H.G.; Padma, R. Ramanujan summation and the exponential generating function Ramanujan J. 2010, 21, 99–122. [Google Scholar] [CrossRef]
- Tao, T. Compactness and Contradiction; American Mathematical Society: Providence, RI, USA, 2013. [Google Scholar]
- Spiegel, M.R.; Lipschutz, S.; Liu, J. Mathematical Handbook of Formulas and Tables, 5th ed.; McGraw-Hill: Leipzig, Germany, 2018. [Google Scholar]
- Baleanu, D.; Lopes, A.M. Handbook of Fractional Calculus with Applications: Applications in Engineering, Life and Social Sciences, Parts A and B; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Kochubei, A.; Luchko, Y. Handbook of Fractional Calculus with Applications: Fractional Differential Equations; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Petráš, I. Handbook of Fractional Calculus with Applications: Applications in Control; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Tarasov, V.E. Handbook of Fractional Calculus with Applications: Applications in Physics, Parts A and B; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Barnes, E.W. The Theory of the G-function. Q. J. Pure Appl. Math. 1900, 31, 264–314. [Google Scholar]
- Dowker, J.S.; Banach, R. Quantum field theory of Clifford-Klein space-times. The effective Lagrangian and vacuum stress-energy tensor. J. Phys. A Math. Gen. 1978, 11, 2255–2284. [Google Scholar] [CrossRef]
- Amaku, M.; Coutinho, F.A.B.; Éboli, O.J.P.; Wreszinski, W.F. Asymptotic series, divergent series, and Tao’s method: The Casimir effect. arXiv 2021, arXiv:2101.03930. [Google Scholar]
- Wreszinski, W.F. Perturbative versus non-perturbative Quantum Field theory: Tao’s method, the Casimir effect, and interacting Wightman theories. Universe 2021, 7, 229. [Google Scholar] [CrossRef]
- Atiyah, M.; Bott, R.; Padoti, V.K. On the heat equation and the index theorem. Invent. Math. 1973, 190, 279–330. [Google Scholar] [CrossRef]
- Vardi, I. Determinants of Laplacian and multiple gamma functions. SIAM J. Math. Anal. 1988, 19, 93–507. [Google Scholar] [CrossRef]
- Belinfante, F.J. Computing Dirac’s atomic hydrogen wave functions of the continuum, using summation of mathematically divergent series. Comput. Phys. 1991, 5, 319–322. [Google Scholar] [CrossRef][Green Version]
- Kunihiro, T. Renormalization-group resummation of a divergent series of the perturbative wave functions of quantum systems. Prog. Theor. Phys. Suppl. 1998, 131, 459–470. [Google Scholar] [CrossRef]
- Contino, R.; Gambassi, A. On dimensional regularization of sums. J. Math. Phys. 2003, 44, 570–587. [Google Scholar] [CrossRef][Green Version]
- Mur, V.D.; Pozdnyakov, S.G.; Popruzhenko, S.V.; Popov, V.S. Summation of Divergent Series and Zeldovich’s Regularization Method. Phys. Atom. Nuclei 2005, 68, 677–685. [Google Scholar] [CrossRef]
- Fermi, D.; Pizzocchero, L. Local Zeta Regularization and the Casimir Effect. Prog. Theor. Phys. 2011, 126, 419–434. [Google Scholar] [CrossRef]
- Hajli, M. Sur la fonction zêta associée au Laplacien singulier . J. Number Theory 2013, 133, 4069–4139. [Google Scholar] [CrossRef]
- Hajli, M. On a formula for the regularized determinant of zeta functions with appication to some Dirichlet series. Q. J. Math. 2020, 71, 843–865. [Google Scholar] [CrossRef]
- Bayad, A.; Hajli, M. On the multidimensional zeta functions associated with theta functions, and the multidimensional Appell polynomials. Math. Methods Appl. Sci. 2020, 43, 2679–2694. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).