Derivative-Free Iterative Schemes for Multiple Roots of Nonlinear Functions
Abstract
:1. Introduction
2. Construction of a Higher-Order Scheme
Particular Cases
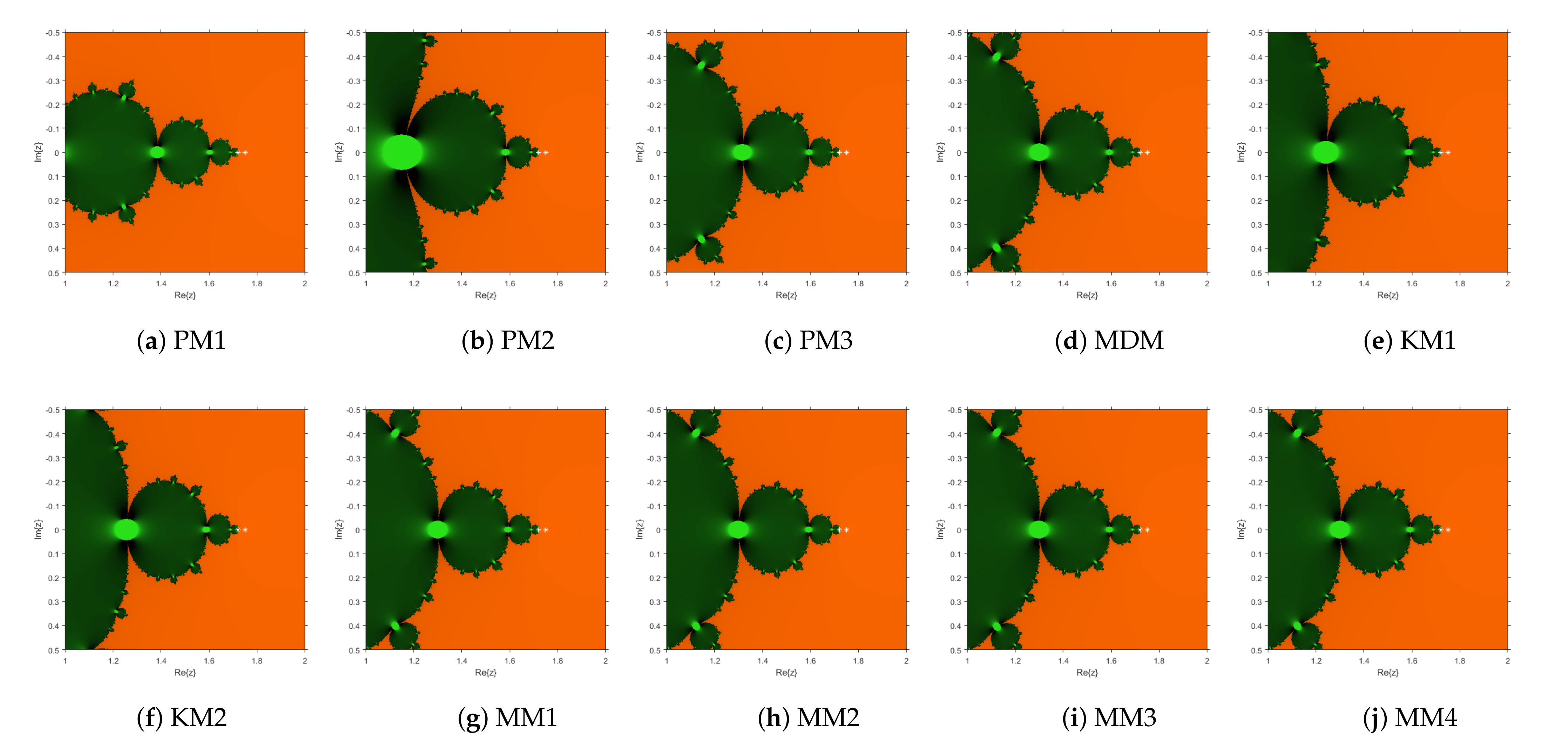
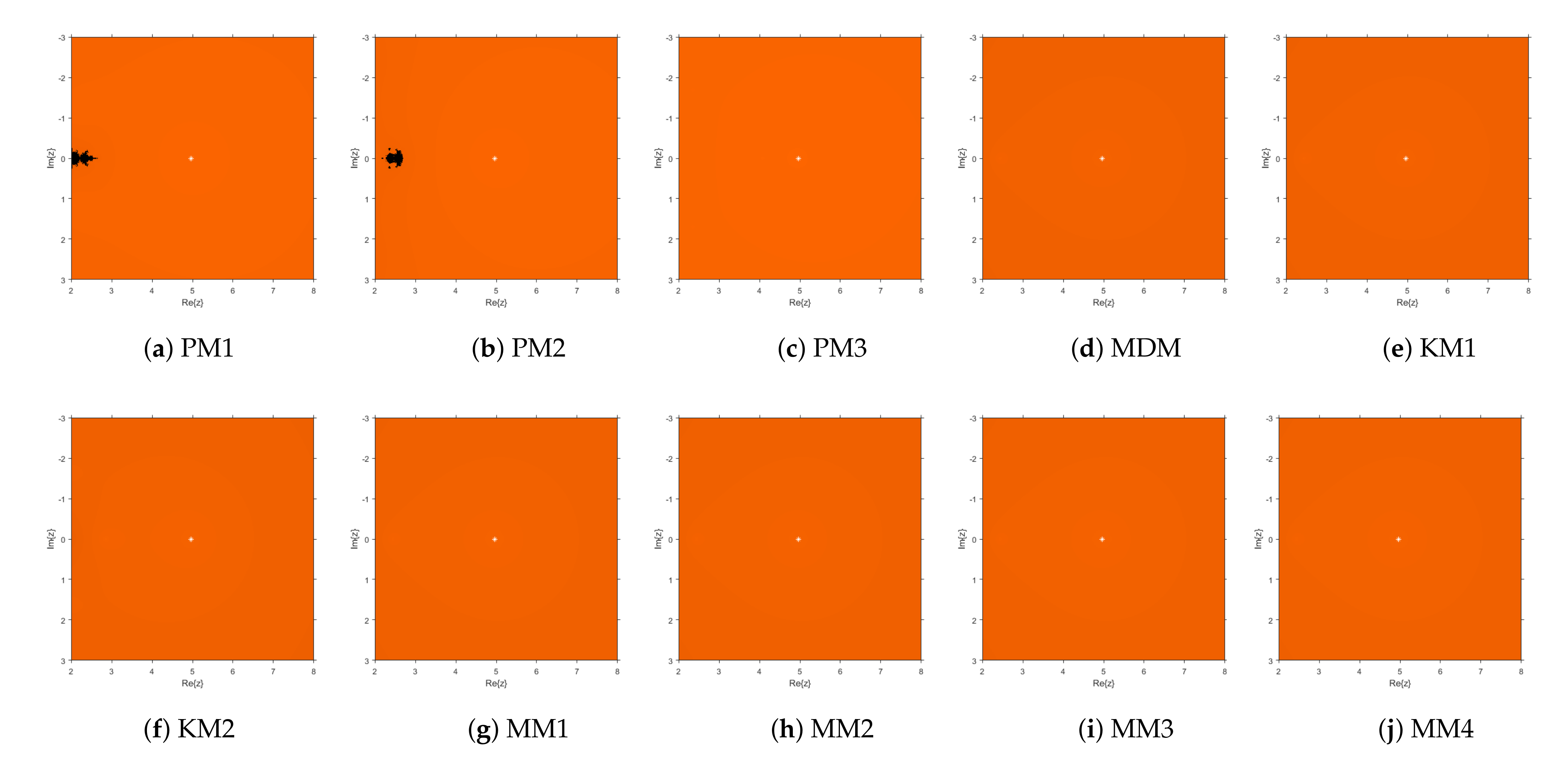
3. Numerical Experimentation
- Processor: Intel(R) Core(TM) i7-4790 CPU @ 3.60GHz;
- Made: HP;
- RAM: 8:00 GB;
- System type: 64-bit-operating system, x64-based processor.
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Geum, Y.H.; Kim, Y.I.; Neta, B. A class of two-point sixth-order multiple-zero finders of modified double-Newton type and their dynamics. Appl. Math. Comput. 2015, 70, 387–400. [Google Scholar] [CrossRef] [Green Version]
- Sharifi, M.; Babajee, D.K.R.; Soleymani, F. Finding the solution of nonlinear equations by a class of optimal methods. Comput. Math. Appl. 2012, 63, 764–774. [Google Scholar] [CrossRef] [Green Version]
- Sharma, J.R.; Sharma, R. Modified Jarratt method for computing multiple roots. Appl. Math. Comput. 2010, 217, 878–881. [Google Scholar] [CrossRef]
- Soleymani, F.; Babajee, D.K.R.; Lotfi, T. On a numerical technique for finding multiple zeros and its dynamics. J. Egypt. Math. Soc. 2013, 21, 346–353. [Google Scholar] [CrossRef]
- Kumar, D.; Sharma, J.R.; Argyros, I.K. Optimal One-Point Iterative Function Free from Derivatives for Multiple Roots. Mathematics 2020, 8, 709. [Google Scholar] [CrossRef]
- Kung, H.T.; Traub, J.F. Optimal order of one-point and multipoint iteration. J. Assoc. Comput. Mach. 1974, 21, 643–651. [Google Scholar] [CrossRef]
- Ortega, J.M.; Rheinboldt, W.C. Iterative Solution of Nonlinear Equations in Several Variables; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Ostrowski, A.M. Solutions of Equations and System of Equations; Academic Press: New York, NY, USA, 1964. [Google Scholar]
- Petković, M.S.; Neta, B.; Petković, B.L.D.; Džunić, J. Multipoint Methods for Solving Nonlinear Equations; Academic Press: New York, NY, USA, 2012. [Google Scholar]
- Traub, J.F. Iterative Methods for the Solution of Equations; Prentice- Hall Series in Automatic Computation; Prentice- Hall: Englewood Cliffs, NJ, USA, 1964. [Google Scholar]
- Zhou, X.; Chen, X.; Song, Y. Constructing higher-order methods for obtaining the multiple roots of nonlinear equations. J. Comput. Appl. Math. 2011, 235, 4199–4206. [Google Scholar] [CrossRef] [Green Version]
- Kansal, M.; Alshomrani, A.S.; Bhalla, S.; Behl, R.; Salimi, M. One Parameter Optimal Derivative-Free Family to Find the Multiple Roots of Algebraic Nonlinear Equations. Mathematics 2020, 8, 2223. [Google Scholar] [CrossRef]
- Cordero, A.; Torregrosa, J.R. Variants of Newton’s method using fifth-order quadrature formulas. Appl. Math. Comput. 2007, 190, 686–698. [Google Scholar]
- Ahlfors, L.V. Complex Analysis; McGraw-Hill Book, Inc.: New York, NY, USA, 1979. [Google Scholar]
- Constantinides, A.; Mostoufi, N. Numerical Methods for Chemical Engineers with MATLAB Applications; Prentice Hall PTR: Englewood Cliffs, NJ, USA, 1999. [Google Scholar]
- Bradie, B. A Friendly Introduction to Numerical Analysis; Pearson Education Inc.: New Delhi, India, 2006. [Google Scholar]
- Zeng, Z. Computing multiple roots of inexact polynomials. Math. Comput. 2004, 74, 869–903. [Google Scholar] [CrossRef] [Green Version]

| Cases | Weight Functions | Corresponding Iterative Method |
|---|---|---|
| Case-1 | . | |
| Case-2 | ||
| Case-3 | ||
| Case-4 | ||
| Case-5 | ||
| Case-6 | ||
| Case-7 | ||
| Case-8 |
| Methods | Value of Disposable | Denoted by Parameter |
|---|---|---|
| , where | Method 1 (KM1) | |
| where | Method 2 (KM2) | |
| where | - | Method 3(KM3) |
| where | - | Method 4 (KM4) |
| where | Method 5 (KM5) |
| Methods | p | ||||
|---|---|---|---|---|---|
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 |
| Methods | p | ||||
|---|---|---|---|---|---|
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 |
| Methods | p | ||||
|---|---|---|---|---|---|
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 |
| Methods | p | ||||
|---|---|---|---|---|---|
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 4 | |||||
| 5 | |||||
| 6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arora, H.; Cordero, A.; Torregrosa, J.R.; Behl, R.; Alharbi, S. Derivative-Free Iterative Schemes for Multiple Roots of Nonlinear Functions. Mathematics 2022, 10, 1530. https://doi.org/10.3390/math10091530
Arora H, Cordero A, Torregrosa JR, Behl R, Alharbi S. Derivative-Free Iterative Schemes for Multiple Roots of Nonlinear Functions. Mathematics. 2022; 10(9):1530. https://doi.org/10.3390/math10091530
Chicago/Turabian StyleArora, Himani, Alicia Cordero, Juan R. Torregrosa, Ramandeep Behl, and Sattam Alharbi. 2022. "Derivative-Free Iterative Schemes for Multiple Roots of Nonlinear Functions" Mathematics 10, no. 9: 1530. https://doi.org/10.3390/math10091530
APA StyleArora, H., Cordero, A., Torregrosa, J. R., Behl, R., & Alharbi, S. (2022). Derivative-Free Iterative Schemes for Multiple Roots of Nonlinear Functions. Mathematics, 10(9), 1530. https://doi.org/10.3390/math10091530








