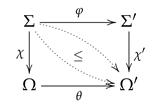
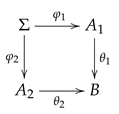
Representing 3/2-Institutions as Stratified Institutions
Abstract
1. Introduction
1.1. Stratified Institutions
1.2. 3/2-Institutions
1.3. Summary and Contributions
- In a preliminary section, we review (1) the category theory required by our work, (2) the concept of institution, (3) the concept of stratified institution, and (4) the concept of -institution. Examples are also discussed briefly.
- The main section of the paper defines a representation of -institutions as stratified institutions. We prove the correctness of this representation, i.e., that it satisfies the axioms of a stratified institution.
- One consequence is a further representation to ordinary institution theory via the adjunction from stratified institutions to ordinary institutions defined in [14] (formerly presented as a mere representation in [6]). Another consequence is the import of concepts of semantic connectives. The last consequence that we develop is about the relationship between model amalgamation properties in the representation and in the original -institution.
2. Preliminaries
2.1. Categories
- and ;
- Composition is defined by ; then are the identities.
2.2. Institutions
- A category whose objects are called signatures.
- A sentence functor defining for each signature a set whose elements are called sentences over that signature and defining for each signature morphism a sentence translation function.
- A model functor defining for each signature the category of Σ-models and -model homomorphisms, and for each signature morphism the reduct functor .
- For every signature , a binary Σ-satisfaction relation .
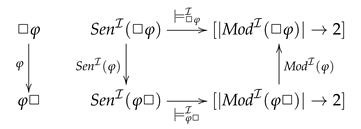
2.3. Stratified Institutions
- Category of signatures;
- A sentence functor ;
- A model functor ;
- A “stratification” lax natural transformation , where is a functor mapping each signature to ;
- A satisfaction relation between models and sentences which is parameterized by model states, , where such that the following satisfaction conditionholds for any signature morphism , , , .

- –
- For each signature , denotes the set of all the mappings such that ;
- –
- For each signature morphism

- In modal propositional logic (), the category of the signatures is ; is the set of the usual modal sentences formed with the atomic propositions from P, and the P-models are the Kripke structures , where consists of a set of “possible worlds” and an accessibility relation , and . The stratification is given by .
- In first-order modal logic (), the signatures are first-order logic () signatures consisting of sets of operation and relation symbols structured by their arities. The sentences extend the usual construction of sentences with the modal connectives □ and ⋄. The models for a signature are Kripke structures , where W is like in but subject to the constraint that the carrier sets and the interpretations of the constants are shared across the possible worlds. The stratification is like in .
- Hybrid logics refine modal logics by adding explicit syntax for the possible worlds such as nominals and @. Institutions of hybrid logics upgrade the syntactic and the semantic components of the institutions of modal logics accordingly.
- Multimodal logics exhibit several modalities instead of only the traditional ⋄ and □ and, moreover, these may have various arities. If one considers the sets of modalities to be variable, then they have to be considered as part of the signatures. Each of the stratified institutions discussed in the previous examples admit an upgrade to the multimodal case.
- In a series of works on modalization of institutions, Refs. [20,21,22] modal logic and Kripke semantics are developed by abstracting away details that do not belong to modality, such as sorts, functions, predicates, etc. This is achieved by extensions of abstract institutions (in the standard situations meant in principle to encapsulate the atomic part of the logics) with the essential ingredients of modal logic and Kripke semantics. The result of this process, when instantiated to various concrete logics (or to their atomic parts only), generates uniformly a wide range of hierarchical combinations between various flavors of modal logic and various other logics. Concrete examples discussed in [20,21,22] include various modal logics over nonconventional structures of relevance in computing science, such as partial algebra, preordered algebra, etc. Various constraints on the respective Kripke models, many of them having to do with the underlying nonmodal structures, have also been considered. All these arise as examples of stratified institutions, such as the examples presented above in the paper. An interesting class of examples that has emerged quite smoothly out of the general works on hybridization (i.e., modalization including also hybrid logic features) of institutions is that of multilayered hybrid logics that provide a logical base for specifying hierarchical transition systems (see [23]).
- Open first order logic (). This is a instance of , the “internal stratification” abstract example developed in [5]. An signature is a pair consisting of signature and a finite block of variables. To any signature , there corresponds a signature that adjoins X to as new constants. Then, , , , i.e., the set of the “valuations” of X to M and for each -model M, each , and each -sentence , we define , where is the expansion of M to such that (i.e., the new constants of X are interpreted in according to the “valuation” w).
- Various kinds of automata theories can be presented as stratified institutions. For instance, the deterministic automata (for regular languages) have the set of the input symbols as signatures, the automata A are the models and the words are the sentences. Then, is the set of the states of A and if and only if is recognized by A from the states s.
2.4. -Institutions
- A -category —called the category of the signatures;
- A -functor —called the sentence functor;
- A lax -functor — called the model functor, such that is a lax functor for each signature morphism ;
- For each signature , a satisfaction relation .
- –
- The fact that is a -functor implies also that whenever we have , i.e., , etc.
- –
- The lax aspect of means that for signature morphisms and , such that , and for any -model , we have thatand for each signature and for each -model M that
- –
- The lax aspect of the reduct functors means that for model homomorphisms , such that , we have thatand for each and each that
- Is -maximal when is total;
- Is -maximal when for each -model , is a singleton;
- Is total when it is both -maximal and -maximal;
- Is -strict when for each signature morphism , such that , we have that
- Common examples of institutions can be turned into -institutions by introducing explicit partiality at the level of the signature morphisms. This means that certain sort/operation/relation symbols are skipped by the respective (partial) signature morphism. This induces a further partiality on the sentence translations as only the sentences that does not contain “skipped” symbols can be translated. The model reducts may interpret freely the “skipped” symbols, hence in principle one model may have several reducts along the same signature morphisms. In [13], this procedure was illustrated on the institutions of propositional logic (hence ) and of many-sorted algebra (hence ). In the latter case, several degrees of partiality can be introduced.
- The -institutional seeds of [13] provide a generic way to define -institutions. Some of the -institution that are based on some form of explicit partiality can also be presented in this way.
- We may turn any abstract institution into a proper -institution by adding weights to the signature morphisms, which means that the signature morphisms come as pairs (in [13] denoted ), where is a signature morphism of the ordinary institution and . The signatures stay the same. This construction is extended to sentences and models in a way that yields the sentence and the model functors proper lax functors. Although this is a mere technical construction without any known applications, it has an important theoretical significance because it provides a class of examples where the -categorical structures involved have nothing to do with any form of partiality.
3. The Canonical Stratified Institution Associated to a -Institution
- Is fiber-small when for each -model M we have that is a set;
- Is quasi-representable when for each -model homomorphism , and for each there exists and unique model homomorphism , such that .
- Both φ and θ are total and -strict;
- .

- for any ;
- for any -model homomorphism and -model .
- for any and any .
- is a set by the fiber-small assumption on .
- The definition of relies on the quasi-representability assumption on .
- represents a single model because is -maximal.
- That is shown as follows:
- That for each -model M and each . This is shown by the following argument. Since is lax, it follows that , which by the uniqueness aspect of the quasi-representability property implies that . Since , the conclusion follows.
- That for any -model homomorphisms and . In order to show that, we consider any model and denote by . We have that:From the uniqueness aspect of the quasi-representability property of , it follows thatHence,
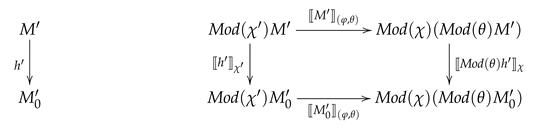
- The signature morphisms that stand as signatures implicitly represent genuine partiality. By contrast, the signature morphisms used for the morphisms implicitly represent genuine totality, the reason being that we want to achieve totality for the syntactic and of the semantic translations at the level of the resultant stratified institution.
- The signature morphisms standing as signatures have to be fiber-small and quasi-representable. The former condition is necessary for the stratifications to be sets, and in the concrete situations is very mild. Only when we are in a many-sorted context doe it amount to a certain restriction, namely that there is no partiality of the translation of the sorts.
- In the applications, the quasi-representability condition on a signature morphism is less stringent than how it appears in principle.
- -
- As it is about (proper) model homomorphisms, it holds trivially in their absence. This degenerated situation is in fact the norm in the applications of the -institutions, as until now there are not known applications that involve proper model homomorphisms.
- -
- When admits partiality only on the constants, then the quasi-representable holds.
- -
- When admits partiality only on the relation symbols and the model homomorphisms are “strong” (in the sense of [3]), then is quasi-representable, too.
- As an example that puts together some of the situations discussed above, if we consider the -institution of many sorted first-order logics with “strong” model homomorphisms, then any signature morphism that is total on the sorts and on nonconstant operation symbols qualifies as a signature.
4. Consequences of the Representation
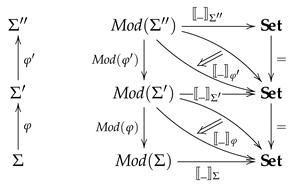
4.1. Representing -Institutions as Ordinary Institutions
- The objects of are the pairs , such that and ;
- The -homomorphisms are the pairs , such that and ;
- For any signature morphism and any -model
- For each -model M, each , and each
- and are given by definitions 2 and 3, respectively.
- For each :
- -
- A χ-model is pair such that , ;
- -
- A χ-model homomorphism is a model homomorphism , such that .
- For each and any -model
- For each χ-model and each χ-sentence ρ
4.2. Semantic Connectives
- The straightforward way that mimics the semantic treatment of connectives from ordinary institution theory.
- By using the stratified institution theoretic approach via the representation result given by corollary 1.
4.3. Model Amalgamation


- holds by the definition of because is an -model.
- Since is the amalgamation of and , it follows that and . It further follows that .
- We also have that:
- By a similar argument to the above one, we establish that .
- Finally,
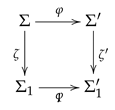
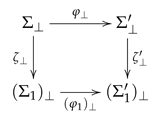
- In any -category, a strict commutative squareis a -pushout when for any strict cocones and over the span , if , , there exists unique mediating arrows , such that and , . Note that -pushouts are stronger than ordinary pushouts.
- -institutional seeds were mentioned above when we discussed examples of -institutions. For the full definition, see [13]. For the purpose of proposition 7 below, we only need the property that there exists a signature , such that for each signatureand for each signature morphism and for each -model ,
- The inner square (also known as the right-hand side square of diagram (14)) is a -pushout square;
- The outer square is a model amalgamation square;
- and are strict.

- There are no restrictions on the signature morphisms that form the pushout square.
- Then, the condition of proposition 8 that preserves and reflects maximality applies well in concrete situations. As an example, let us consider the case of . There, , and therefore it is evident that for any signature morphism is total if and only if is total.
- The -pushout condition of proposition 7 in general is stronger than the pushout condition of proposition 8.
- Maps any set A to the set (disjoint union);
- Maps any partial function to the homomorphism defined for each by:
5. Conclusions and Future Work
- The import of more model theory from stratified institution theory to -institutions.
- Find general ways, with good applicability in concrete situations, to generate model amalgamation cocones such as in diagrams (15).
Funding
Acknowledgments
Conflicts of Interest
References
- Goguen, J.; Burstall, R. Institutions: Abstract Model Theory for Specification and Programming. J. Assoc. Comput. Mach. 1992, 39, 95–146. [Google Scholar] [CrossRef]
- Sannella, D.; Tarlecki, A. Foundations of Algebraic Specifications and Formal Software Development; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Diaconescu, R. Institution-Independent Model Theory; Birkhäuser: Basel, Switzerland, 2008. [Google Scholar]
- Diaconescu, R.; Stefaneas, P. Modality in Open Institutions with Concrete Syntax. Bull. Greek Math. Soc. 2004, 49, 91–101, Previously published as JAIST Tech Report IS-RR-97-0046, 1997.. [Google Scholar]
- Aiguier, M.; Diaconescu, R. Stratified institutions and elementary homomorphisms. Inf. Process. Lett. 2007, 103, 5–13. [Google Scholar] [CrossRef]
- Diaconescu, R. Implicit Kripke Semantics and Ultraproducts in Stratified Institutions. J. Log. Comput. 2017, 27, 1577–1606. [Google Scholar] [CrossRef][Green Version]
- Aiguier, M.; Bloch, I. Logical dual concepts based on mathematical morphology in stratified institutions: Applications to spatial reasoning. J. Appl. Non-Class. Log. 2019, 29, 392–429. [Google Scholar] [CrossRef]
- Găină, D. Forcing and Calculi for Hybrid Logics. J. Assoc. Comput. Mach. 2020, 67, 25:1–25:55. [Google Scholar] [CrossRef]
- Fauconnier, G.; Turner, M. Conceptual integration networks. Cogn. Sci. 1998, 28, 133–187. [Google Scholar] [CrossRef]
- Goguen, J. An Introduction to Algebraic Semiotics, with Application to User Interface Design. In Computation for Metaphors, Analogy, and Agents; Lecture Notes in Computer, Science; Nehaniv, C.L., Ed.; Springer: Berlin/Heidelberg, Germany, 1999; Volume 1562, pp. 242–291. [Google Scholar]
- Goguen, J.A. What Is a Concept? In Conceptual Structures: Common Semantics for Sharing Knowledge. ICCS 2005; Lecture Notes in Computer, Science; Dau, F., Mugnier, M.L., Stumme, G., Eds.; Springe: Berlin/Heidelberg, Germany, 2005; Volume 3596, pp. 52–77. [Google Scholar]
- Goguen, J. Categorical Approaches to Merging Software Changes. Unpublished draft.
- Diaconescu, R. Implicit Partiality of Signature Morphisms in Institution Theory. In Hajnal Andréka and István Németi on Unity of Science: From Computing to Relativity Theory Through Algebraic Logic; Outstanding Contributions to Logic; Madarász, J., Székely, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; Volume 19, pp. 81–123. ISBN 978-3-030-64186-3. [Google Scholar]
- Diaconescu, R. Decompositions of Stratified Institutions. arXiv 2021, arXiv:2112.12993. [Google Scholar]
- Mac Lane, S. Categories for the Working Mathematician, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Kelly, M. Basic Concepts of Enriched Category Theory; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Borceux, F. Handbook of Categorical Algebra; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Kelly, M.; Street, R. Review of elements of 2-categories. In Category Seminar Sydney 1972/1973; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1974; pp. 75–103. [Google Scholar]
- Jay, C.B. Partial Functions, Ordered Categories, Limits and Cartesian Closure. In IV Higher Order Workshop, Banff 1990: Proceedings of the IV Higher Order Workshop, Banff, AB, Canada 10–14 September 1990; Birtwistle, G., Ed.; Springer: London, UK, 1991; pp. 151–161. [Google Scholar]
- Diaconescu, R.; Stefaneas, P. Ultraproducts and Possible Worlds Semantics in Institutions. Theor. Comput. Sci. 2007, 379, 210–230. [Google Scholar] [CrossRef]
- Martins, M.A.; Madeira, A.; Diaconescu, R.; Barbosa, L. Hybridization of Institutions. In Algebra and Coalgebra in Computer Science; Lecture Notes in Computer, Science; Corradini, A., Klin, B., Cîrstea, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6859, pp. 283–297. [Google Scholar]
- Diaconescu, R. Quasi-varieties and initial semantics in hybridized institutions. J. Log. Comput. 2016, 26, 855–891. [Google Scholar] [CrossRef]
- Madeira, A. Foundations and Techniques for Software Reconfigurability. Ph.D. Thesis, Universidades do Minho, Aveiro and Porto (Joint MAP-i Doctoral Programme), Aveiro, Portugal, 2014. [Google Scholar]
- Tarlecki, A. On the Existence of Free Models in Abstract Algebraic Institutions. Theor. Comput. Sci. 1986, 37, 269–304. [Google Scholar] [CrossRef][Green Version]
- Diaconescu, R. Institution-independent Ultraproducts. Fundam. Inform. 2003, 55, 321–348. [Google Scholar]
- Diaconescu, R.; Goguen, J.; Stefaneas, P. Logical Support for Modularisation. In Logical Environments; Huet, G., Plotkin, G., Eds.; Cambridge University Press: Cambridge, UK, 1993; pp. 83–130. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diaconescu, R. Representing 3/2-Institutions as Stratified Institutions. Mathematics 2022, 10, 1507. https://doi.org/10.3390/math10091507
Diaconescu R. Representing 3/2-Institutions as Stratified Institutions. Mathematics. 2022; 10(9):1507. https://doi.org/10.3390/math10091507
Chicago/Turabian StyleDiaconescu, Răzvan. 2022. "Representing 3/2-Institutions as Stratified Institutions" Mathematics 10, no. 9: 1507. https://doi.org/10.3390/math10091507
APA StyleDiaconescu, R. (2022). Representing 3/2-Institutions as Stratified Institutions. Mathematics, 10(9), 1507. https://doi.org/10.3390/math10091507