The Axiomatic Approach to Non-Classical Model Theory

Abstract

Institution theory represents the fully axiomatic approach to model theory in which all components of logical systems are treated fully abstractly by reliance on category theory. Here, we survey some developments over the last decade or so concerning the institution theoretic approach to non-classical aspects of model theory. Our focus will be on many-valued truth and on models with states, which are addressed by the two extensions of ordinary institution theory known as $\mathcal{L}$-institutions and stratified institutions, respectively. The discussion will include relevant concepts, techniques, and results from these two areas.

1. From Classical Model Theory to Axiomatic Non-Classical Model Theory

In this introductory section, we will discuss briefly and informally the path leading from the most traditional form of model theory to the modern and non-classical one.

1.1. Model Theory

In a broader sense, model theory is the mathematical study of language interpretations, its main paradigm being Alfred Tarski’s semantic definition of truth [1]. Thus, the occurrence of the symbol ⊧ always indicates that we are in the presence of some form of model–theoretical argument. In its most classical form, model theory deals with first-order structures. So, in first-order model theory, the relation $M\vDash \rho$ means that M is a first-order model and $\rho$ is a first-order sentence. Tarski’s approach was to determine the validity of this relation inductively on the structure of $\rho$. On the one hand, first-order model theory [2,3] is a vibrant and sophisticated area of mathematical research that brings logical methods to bear on deep problems of classical mathematics. Two early achievements of first-order model theory that brought it fame within the wider mathematical community were the modern and rigorous recovery of the approach to mathematical analysis of Newton, Leibniz and Euler—in the form of Robinson’s non-standard analysis [4,5]—and the proof of the independence of the Continuum Hypothesis [6,7]. Moreover, first-order model theory has applications to other scientific areas, most notably to computing science. On the other hand, first-order model theory is the area in which many of the broader ideas of model theory were first worked out.

1.2. Axiomatic Model Theory

First-order model theory is also the most important example of the explicit and concrete approach to model theory. The axiomatic approach contrasts this as the concepts and defining properties are axiomatised rather than considered concretely. As with all other axiomatic approaches in mathematics, this achieves proper abstraction, relativisation, conceptual clarity, and structurally clean causality. In a sophisticated mathematical area such as model theory, these features are crucial. The very origins of the axiomatic approach to model theory may be traced back, although not in an explicit form, in Lindström’s “external” characterisation of first-order logic [8]. Several explicit axiomatic developments followed, such as Barwise’s abstract model theory [9,10] or the categorical model theory of the Budapest school [11,12,13,14,15], etc. In spite of their success in developing interesting results, all those approaches lacked full axiomatisability, as they would usually treat axiomatically some parts of the logical systems while considering concretely other parts. Consequently, they were not able to achieve the true power of the full axiomatic approach.

1.2.1. The Institution-Theoretic Trend

The definition in the late 1970s by Goguen and Burstall of the concept of institution as a formal definition of the intuitive notion of logic [16,17,18] achieved the full axiomatic approach to model theory. In institution theory, all three components of logical systems—namely, the syntax, the semantics, and the satisfaction relation between them—are treated fully abstractly by relying heavily on category theory [19]. Very briefly, the above-mentioned formalization is a category–theoretic structure $(\mathit{Sign},\mathit{Sen},\mathit{Mod},\vDash )$, called institution, consisting of a category $\mathit{Sign}$ (of so-called signatures), two functors ($\mathit{Sen}$ for the syntax and $\mathit{Mod}$ for the semantics), and a family ⊧ of binary relations, which are all bound to satisfy certain consistency axioms. We will clarify precisely this definition below in the paper. In our survey, we will follow this trend of axiomatic model theory known as institution-independent model theory, or institutional model theory, or institution-theoretic model theory. The first in this list of synonymous terminologies may be actually the most informative, as the word ‘independent’ suggests a model theory that is not confined to any particular logical system.

1.2.2. The Original Motivation

With institution theory, Goguen and Burstall addressed an important issue in computing science, and especially in formal–specification theory. There was an explosion of formal logical systems used, and there was a need for a uniform treatment of specification concepts and results across the increasing number of logic-based formal methods. There was also a strong feeling that much of the logic-based specification theory may actually be developed independently of an underlying concrete logical system. Over decades, this area undertook a massive development, and now, it is still vibrant and dynamic. It has fulfilled its original mission, even beyond expectations, as follows:

• The concept of institution has emerged as the most fundamental mathematical structure of logic-based formal specifications in the sense that virtually all modern specification languages/systems are rigorously based upon a logical system that is formally captured as an institution in such a way that each language construct corresponds exactly to a mathematical concept from that institution. In particular, this has been the principle underlying the design of specification languages and systems such as CASL [20], CafeOBJ [21,22], Hets [23], DOL [24], etc.
• A great deal of modern formal specification theory has been developed at the general level of abstract institutions, thus bringing an unprecedented high level of uniformity and clarity to an area that has witnessed a real explosion in the population of logical systems (cf. the monograph [25]).
• The institution–theoretic methods have been successfully exported to other areas of computing science, most notably to declarative programming [26,27,28] and ontologies [24,29]. In all these areas, in issues involving modularisation, stepwise refinement, or logical heterogeneity, the use of institution theory is practically without alternative.

1.2.3. Institutional Model Theory as Such

The abstract axiomatic development of institutional model theory goes back to [30,31,32]. Those early endeavours stemmed from computing science, addressing typical issues from formal specification (such as initial semantics), but they also led to strong model–theoretic results in themselves. Even so, a systematic programme for developing an in-depth institutional model theory beyond computing science motivations arose only after 2000.

• This meant an axiomatic-driven redesign of core parts of model theory at a new level of generality—namely, that of abstract institutions—independently of any concrete logical system. Those included institutional developments of some of the most important model–theoretic methods that were originally worked out in first-order model theory, such as diagrams [33], ultraproducts [34], elementary chains [35], saturated models [36], omitting types [37], forcing [38], etc.
• This institutional development has had at least three major consequences:
  • A new understanding of model–theoretic phenomena that are uncontaminated by irrelevant concrete details; this led to revisions of well established concepts and facilitated access to difficult results;
  • A consequence of (1) is a series of results about completeness [38,39], definability [40,41], interpolation [42,43,44,45], Löwenheim–Skolem [37,45], some instances of these representing new important results even in first-order model theory;
  • A systematic and uniform development of model theories for unconventional logics, either new or older ones, which is a process of great difficulty within concrete frameworks.
  Moreover, in the case of (3), the institution–theoretic approach has also led to a better understanding of the respective logics sometimes accompanied by a conceptual resetting.

1.2.4. Logic by Translation

A specific general logical method that has gained prominence in the past few decades is that of logic by translation. By this method, one can overcome difficulties of developing results in a certain logical system by exporting the problem to another logical system where a solution is known or, for various reasons, is easier to obtain. This relies on translations/encodings between logical systems that have adequate properties both for the forward translation and for shifting the obtained result back to the source logic. Logic-by-translation has had many applications in logic and computer science, many of them through institution theory. That is mostly thanks to the fact that institution theory, with its category–theoretic build where logical systems arise as categorical objects, has come up with adequate mathematical concepts of structural mapping between institutions at an abstract level [18,46]. The value of the institution–theoretic proposal to logic-by-translation [47] has been awarded internationally by the scientific community at the 2nd World Congress of Universal Logic (Xi’an, 2007).

1.3. Beyond Classical Institutional Model Theory

The concept of institution is abstract enough to accommodate any logical system based on satisfaction between sentences and models of any kind, including non-classical logics. However, the developments discussed above, albeit highly abstract and axiomatic, may be considered “classical” in the sense that they reflect concepts, methods and results that have been originally worked out at a concrete level in first-order model theory. Classical institutional model theory may be effective to some extent in non-classical contexts but not entirely satisfactory. For instance, non-classical logical situations that are beyond the usual binary satisfaction relation between models and sentences, such as local satisfaction in modal logics or many-valued satisfaction, admit classical institution–theoretic formalisations but at the cost of flattening the satisfaction relation to the binary case [44,48], which is a process that alters the nature of the respective logics. Consequently, there is a loss of information, and important non-classical logic developments cannot be completed naturally or not at all. For example, when considering institutions for modal logics, this is completed on the basis of global satisfaction, which is much less relevant than the local satisfaction relation. In addition, in the flattening of many-valued satisfaction, the possibility of grading the consequence relation [49] is lost. Moreover, logic encodings that are based on theoroidal comorphisms are difficult to define because of the multifaceted nature of the concept of theory in many-valued logics [49,50]. The answers to these challenges is given by the stratified institutions [51,52,53] and the $\mathcal{L}$-institutions [49] that represent extensions of the ordinary concept of institution that accommodate properly models with states and local satisfaction, and many-valued semantic truth, respectively. Technically, these two new mathematical structures are generalisations of the ordinary concept of institution. This survey is about these two extensions of ordinary institution theory with emphasis on model theory-motivated developments rather than computing science. Regarding the technical level of this survey, while avoiding technical vagueness, we will also deliberately try to avoid intricate technicalities that pervade many institutional model theory works. In order to achieve such a balance in the presentation, we will employ more informal explanations while providing pointers to works where the respective technical details can be found.

Before surveying the theories of stratified and of $\mathcal{L}$-institutions, respectively, we will review the ordinary concept of institution.

2. Institutions

In this section, we will first discuss the role played by category theory in institution theory, we will review some basic notational conventions, and finally, we will recall the concept of institution.

2.1. First, Some Category Theory

Category theory of Eilenberg and Mac Lane [19,54] constitutes the mathematical substance of institution theory. This situation is similar in other axiomatic approaches to model theory, such as in the above-mentioned Budapest school of abstract model theory. This means that the mathematical structures in institution theory are all categorical. On the other hand, the flow of ideas in institution theory is model theoretic. So, institution theory is a form of model theory that at the level of the mathematical structures is heavily based on categorical structures. This represents a sharp contrast to the widespread perception of category theory as a mere language that supports a clearer presentation and structuring of mathematical concepts that in fact do not have an inherent categorical nature. Institution theory without category theory is possible to the same extent as, for instance, group theory is possible without set theory!

Why such a reliance on category theory; is it indispensable for the axiomatic treatment of model theory? There are several reasons for this. One is that that set theoretical structures cannot support the required level of generality and abstraction. Another one is that category theory emphasises the relationships between objects rather than their internal structures. Moreover, category theory is conceptually a highly developed area of mathematics, so this brings in much conceptual and technical power.

However, the level of category theory involved in institution theory is rather elementary, as it hardly touches advanced concepts and techniques; the only slight exception being found in the area of stratified institutions. So, familiarity with concepts such as opposite (dual) of a category $\mathbf{C}$ (denoted ${\mathbf{C}}^{\ominus }$), comma category, functor, (lax) natural transformation, (co)limit, and adjunction may be enough to be able to engage with the study of institutional model theory. In this survey, with a few exceptions, in general, we follow the terminology and the notations of [19]. As regards the notational conventions,

• $\left|\mathbf{C}\right|$ denotes the class of objects of a category $\mathbf{C}$, $\mathbf{C}(A,B)$ and the set of arrows (morphisms) with domain A and codomain B;
• The domain of an arrow/morphism f is denoted by $\square f$, while its codomain is denoted by $f\square$;
• $f;g$ denotes the composition of arrows/morphisms in diagrammatic order, which in set theoretic orders reads as $g\circ f$;
• The category of sets (as objects) and functions (as arrows) is denoted by $\mathbf{S}\mathbf{et}$;
• The category of all categories (as objects) and functors (as arrows) is denoted by $\mathbf{C}\mathbf{A}\mathbf{T}$. (Strictly speaking, $\mathbf{C}\mathbf{A}\mathbf{T}$ is only a ‘quasi-category’ living in a higher set-theoretic universe).

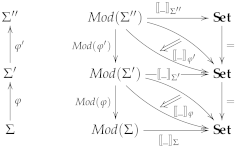
2.2. The Concept of Institution

The original standard reference for institution theory is [18]. An institution

$$\mathcal{I}=({\mathit{Sign}}^{\mathcal{I}},{\mathit{Sen}}^{\mathcal{I}},{\mathit{Mod}}^{\mathcal{I}},{\vDash }^{\mathcal{I}})$$

consists of

• A category ${\mathit{Sign}}^{\mathcal{I}}$ whose objects are called signatures;
• A sentence functor ${\mathit{Sen}}^{\mathcal{I}}:{\mathit{Sign}}^{\mathcal{I}}\to \mathbf{S}\mathbf{et}$ defining for each signature a set whose elements are called sentences over that signature and defining for each signature morphism a sentence translation function;
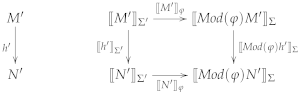
• A model functor ${\mathit{Mod}}^{\mathcal{I}}:{({\mathit{Sign}}^{\mathcal{I}})}^{\ominus }\to \mathbf{C}\mathbf{A}\mathbf{T}$ defining for each signature $\mathrm{\Sigma }$ the category ${\mathit{Mod}}^{\mathcal{I}}(\mathrm{\Sigma })$ of Σ-models and $\mathrm{\Sigma }$-model homomorphisms, and for each signature morphism $\phi$ the reduct functor ${\mathit{Mod}}^{\mathcal{I}}(\phi )$;
• For every signature $\mathrm{\Sigma }$, a binary Σ-satisfaction relation ${\vDash }_{\mathrm{\Sigma }}^{\mathcal{I}}\subseteq \left|{\mathit{Mod}}^{\mathcal{I}}(\mathrm{\Sigma })\right|\times {\mathit{Sen}}^{\mathcal{I}}(\mathrm{\Sigma })$;

such that for each morphism $\phi$, the Satisfaction Condition

$$M^{\prime }{\vDash }_{\phi \square }^{\mathcal{I}}{\mathit{Sen}}^{\mathcal{I}}(\phi )\rho \mathrm{if} \mathrm{and} \mathrm{only} \mathrm{if} {\mathit{Mod}}^{\mathcal{I}}(\phi )M^{\prime }{\vDash }_{\square \phi }^{\mathcal{I}}\rho$$

(1)

holds for each $M^{\prime }\in \left|{\mathit{Mod}}^{\mathcal{I}}(\phi \square )\right|$ and $\rho \in {\mathit{Sen}}^{\mathcal{I}}(\square \phi )$. This can be expressed as the satisfaction relation ⊧ being a natural transformation:

($\left[\right|\mathit{Mod}(\mathrm{\Sigma })|\to 2]$ represents the ‘set’ of the ‘subsets’ of $|\mathit{Mod}(\mathrm{\Sigma })|$).

We may omit the superscripts or subscripts from the notations of the components of institutions when there is no risk of ambiguity. For example, if the considered institution and signature are clear, we may denote ${\vDash }_{\mathrm{\Sigma }}^{\mathcal{I}}$ just by ⊧. For $M=\mathit{Mod}(\phi )M^{\prime }$, we say that M is the φ-reduct of $M^{\prime }$.

The literature shows myriads of logical systems from computing or from mathematical logic captured as institutions. Many of these are collected in [25,44]. In fact, an informal thesis underlying institution theory is that any ‘logic’ may be captured by the above definition. While this should be taken with a grain of salt, it certainly applies to any logical system based on satisfaction between sentences and models of any kind. In [44], one can read how propositional logic $\mathcal{P}\mathcal{L}$, (many-sorted) first order logic $\mathcal{F}\mathcal{O}\mathcal{L}$ together with many of its fragments, partial algebra, various flavours of modal logic, intuitionistic logics, preordered algebra, multialgebras, membership algebra, higher-order logics with various semantics, many-valued logics, etc. can be captured as institutions. In all these cases, the effort to capture the (model theory of the) respective logical system as an institution implies a conceptual adjustment of some of its aspects in the direction of a higher mathematical rigour, an emblematic case being that of the variables (see for example the relevant discussion in [55]). In many cases, some important concepts have been extended, most notably concepts of signature morphisms. In order to fully understand these conceptual developments, it is worth looking in the literature at detailed examples of mainstream concrete institutions.

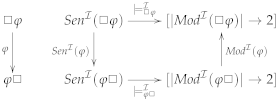
3. Stratified Institutions

Models with states appear in myriad forms in computing science and logic. Classes of examples include at least

• A wide variety of Kripke semantics as in [51,52,56,57];
• Various automata theories;
• Various model theories with partiality for signature morphisms [58], providing mathematical foundations to conceptual blending (see [59]).

The institution theory answer to this is given by the theory of stratified institutions introduced in [51,60] and further developed or invoked in works such as [52,53,56,57,58], etc. Informally, the main idea behind the concept of stratified institution as introduced in [51,60] is to enhance the concept of institution with ‘states’ for the models. Thus, each model M comes equipped with a set$\left[\right[M\left]\right]$ that has to satisfy some structural axioms. The following definition has been given in [52] and represents an important upgrade of the original definition from [51], the main reason being to make the definition of stratified institutions really usable for conducting in-depth model theory. A slightly different upgrade has been proposed in [53], which is however strongly convergent to the upgrade proposed in [52].

A stratified institution $\mathcal{S}$ is a tuple $({\mathit{Sign}}^{\mathcal{S}},{\mathit{Sen}}^{\mathcal{S}},{\mathit{Mod}}^{\mathcal{S}},{\left[[\_]\right]}^{\mathcal{S}},{\vDash }^{\mathcal{S}})$ consisting of:

• A category ${\mathit{Sign}}^{\mathcal{S}}$ of signatures;
• A sentence functor ${\mathit{Sen}}^{\mathcal{S}}:{\mathit{Sign}}^{\mathcal{S}}\to \mathbf{S}\mathbf{et}$;
• A model functor ${\mathit{Mod}}^{\mathcal{S}}:{({\mathit{Sign}}^{\mathcal{S}})}^{\ominus }\to \mathbf{C}\mathbf{A}\mathbf{T}$.

Until this point, this definition is identical to that of an ordinary institution. However, now comes the additional structure that provides explicitly the states of the models.

• A “stratification” lax natural transformation ${\left[[\_]\right]}^{\mathcal{S}}:{\mathit{Mod}}^{\mathcal{S}}\Rightarrow \mathit{SET}$, where $\mathit{SET}:{\mathit{Sign}}^{\mathcal{S}}\to \mathbf{C}\mathbf{A}\mathbf{T}$ is a functor mapping each signature to $\mathbf{S}\mathbf{et}$; and
• A satisfaction relation between models and sentences which is parameterised by model states, $M{({\vDash }^{\mathcal{S}})}_{\mathrm{\Sigma }}^w\rho$ where $w\in {\left[\left[M\right]\right]}_{\mathrm{\Sigma }}^{\mathcal{S}}$ such that the following Satisfaction Condition

  $${\mathit{Mod}}^{\mathcal{S}}(\phi )M^{\prime }{({\vDash }^{\mathcal{S}})}_{\square \phi }^{{\left[\left[M^{\prime }\right]\right]}_{\phi }w}\rho \mathrm{if} \mathrm{and} \mathrm{only} \mathrm{if}{M}^{\prime }{({\vDash }^{\mathcal{S}})}_{\phi \square }^w{\mathit{Sen}}^{\mathcal{S}}(\phi )\rho$$

  (2)

  holds for any signature morphism $\phi$, $M^{\prime }\in \left|{\mathit{Mod}}^{\mathcal{S}}(\phi \square )\right|$, $w\in {\left[\left[M^{\prime }\right]\right]}_{\phi \square }^{\mathcal{S}}$, $\rho \in {\mathit{Sen}}^{\mathcal{S}}(\square \phi )$.

As for ordinary institutions, when appropriate, we shall also use simplified notations without superscripts or subscripts that are clear from the context.

The lax natural transformation property of $\left[\right[\_\left]\right]$ is depicted in the diagram below

with the following compositionality property for each ${\mathrm{\Sigma }}^{″}$-model $M^{″}$:

$${\left[\left[M^{″}\right]\right]}_{(\phi ;{\phi }^{\prime })}={\left[\left[M^{″}\right]\right]}_{{\phi }^{\prime }};{\left[\left[\mathit{Mod}({\phi }^{\prime })M^{″}\right]\right]}_{\phi }.$$

(3)

Moreover, the natural transformation property of each ${\left[[\_]\right]}_{\phi }$ is given by the commutativity of the following diagram:

(4)

The satisfaction relation can be presented as a natural transformation

$$\vDash :\mathit{Sen}\Rightarrow \left[\right[\mathit{Mod}(\_)\to \mathbf{S}\mathbf{et}\left]\right]$$

where the functor $\left[\right[\mathit{Mod}(\_)\to \mathbf{S}\mathbf{et}\left]\right]:\mathit{Sign}\to \mathbf{S}\mathbf{et}$ is defined by

–

For each signature $\mathrm{\Sigma }\in \left|\mathit{Sign}\right|$, $\left[\right[\mathit{Mod}(\mathrm{\Sigma })\to \mathbf{S}\mathbf{et}\left]\right]$ denotes the set of all the mappings $f:|\mathit{Mod}(\mathrm{\Sigma })|\to \mathbf{S}\mathbf{et}$ such that $f(M)\subseteq {\left[\left[M\right]\right]}_{\mathrm{\Sigma }}$; and

–

For each signature morphism $\phi :\mathrm{\Sigma }\to {\mathrm{\Sigma }}^{\prime }$

$$\left[[\mathit{Mod}(\phi )\to \mathbf{S}\mathbf{et}]\right](f)(M^{\prime })={\left[\left[M^{\prime }\right]\right]}_{\phi }^{-1}(f(\mathit{Mod}(\phi )M^{\prime })).$$

A straightforward check reveals that the Satisfaction Condition (2) appears exactly as the naturality property of ⊧:

Ordinary institutions are the stratified institutions for which ${\left[\left[M\right]\right]}_{\mathrm{\Sigma }}$ is always a singleton set. In the upgraded definition, the surjectivity condition on ${\left[\left[M^{\prime }\right]\right]}_{\phi }$ from [51] has been removed, as it can be made explicit when necessary. This is motivated by the fact that most of the results developed do not depend upon this condition which, however, holds in all examples known by us. On the one hand, in many important concrete situations (Kripke semantics, automata, etc.), ${\left[\left[M^{\prime }\right]\right]}_{\phi }$ are even identities, which makes $\left[\right[\_\left]\right]$ a strict rather than a lax natural transformation. However, on the other hand, there are interesting examples when the stratification is properly lax, such as in the $\mathcal{O}\mathcal{F}\mathcal{O}\mathcal{L}$ example below or the representation of $3/2$ institutions as stratified institutions developed in [58].

The literature on stratified institutions shows many model theories that are captured as stratified institutions. Here, we recall some of them in a very succint form; for a more detailed form, one may find them in [52,57,58].

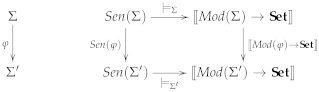
• In modal propositional logic ($\mathcal{M}\mathcal{P}\mathcal{L}$), the category of the signatures is $\mathbf{S}\mathbf{et}$, $\mathit{Sen}(P)$ is the set of the usual modal sentences formed with the atomic propositions from P, and the P models are the Kripke structures $(W,M)$ where $W=(|W|,W_{\lambda })$ consists of a set of ‘possible worlds’ $\left|W\right|$ and an accessibility relation $W_{\lambda }\subseteq \left|W\right|\times \left|W\right|$, and $M:\left|W\right|\to 2^P$. The stratification is given by $\left[\right[(W,M)\left]\right]=\left|W\right|$.
• In first-order modal logic ($\mathcal{M}\mathcal{F}\mathcal{O}\mathcal{L}$), the signatures are first-order logic ($\mathcal{F}\mathcal{O}\mathcal{L}$) signatures consisting of sets of operation and relation symbols structured by their arities. The sentences extend the usual construction of $\mathcal{F}\mathcal{O}\mathcal{L}$ sentences with the modal connectives □ and ⋄. The models for a signature $\mathrm{\Sigma }$ are Kripke structures $(W,M)$ where W is like in $\mathcal{M}\mathcal{P}\mathcal{L}$ but $M:\left|W\right|\to |{\mathit{Mod}}^{\mathcal{F}\mathcal{O}\mathcal{L}}(\mathrm{\Sigma })|$ is subject to the constraint that the carrier sets, and the interpretations of the constants are shared across the possible worlds. The stratification is like in $\mathcal{M}\mathcal{P}\mathcal{L}$.
• Hybrid logics ($\mathcal{H}\mathcal{P}\mathcal{L}$, $\mathcal{H}\mathcal{F}\mathcal{O}\mathcal{L}$, etc.) refine modal logics by adding explicit syntax for the possible worlds such as nominals and @. Stratified institutions of hybrid logics upgrade the syntactic and the semantic components of the stratified institutions of modal logics accordingly. For instance, in the stratified institution of hybrid propositional logic ($\mathcal{H}\mathcal{P}\mathcal{L}$), the signatures are pairs of sets $(\mathrm{Nom},P)$, the $(\mathrm{Nom},P)$-models are Kripke structures $(W,M)$ like in $\mathcal{M}\mathcal{P}\mathcal{L}$, but where W adds interpretations of the nominals, i.e., $W=(|W|,{(W_i)}_{i\in \mathrm{Nom}},W_{\lambda })$, and at the level of the syntax, for each $i\in \mathrm{Nom}$, we have a new sentence $i-\mathrm{sen}$, a new unary connective ${@}_i$, and existential quantifications over nominals variables. Then, $((W,M){\vDash }^{w}i-\mathrm{sen})=(W_i=w),((W,M){\vDash }^w{@}_i\rho )=((W,M){\vDash }^{W_i}\rho )$, etc.
• Multi-modal logics exhibit several modalities instead of only the traditional ⋄ and □, and moreover, these may have various arities. If one considers the sets of modalities to be variable, then they have to be considered as part of the signatures. Each of the stratified institutions discussed in the previous examples admit an upgrade to the multi-modal case.
• In a series of works on modalization of institutions [61,62,63], modal logic and Kripke semantics are developed by abstracting away details that do not belong to modality, such as sorts, functions, predicates, etc. This is achieved by extensions of abstract institutions (in the standard situations meant in principle to encapsulate the atomic part of the logics) with the essential ingredients of modal logic and Kripke semantics. The results of this process, when instantiated to various concrete logics (or to their atomic parts only) generate uniformly a wide range of hierarchical combinations between various flavours of modal logic and various other logics. Concrete examples discussed in [61,62,63] include various modal logics over non-conventional structures of relevance in computing science, such as partial algebra, preordered algebra, etc. Various constraints on the respective Kripke models, many of them having to do with the underlying non-modal structures, have also been considered. All these arise as examples of stratified institutions such as the examples presented above in the paper. An interesting class of examples that has emerged quite smoothly out of the general works on hybridization (i.e., modalization including also hybrid logic features) of institutions is that of multi-layered hybrid logics that provide a logical base for specifying hierarchical transition systems (see [64]). This construction will be discussed in more detail in a dedicated section below in the paper.
• Open first-order logic ($\mathcal{O}\mathcal{F}\mathcal{O}\mathcal{L}$). This is an $\mathcal{F}\mathcal{O}\mathcal{L}$ instance of $St(\mathcal{I})$, the ‘internal stratification’ abstract example developed in [51]. An $\mathcal{O}\mathcal{F}\mathcal{O}\mathcal{L}$ signature is a pair $(\mathrm{\Sigma },X)$ consisting of $\mathcal{F}\mathcal{O}\mathcal{L}$ signature $\mathrm{\Sigma }$ and a finite block of variables. To any $\mathcal{O}\mathcal{F}\mathcal{O}\mathcal{L}$ signature $(\mathrm{\Sigma },X)$ corresponds an $\mathcal{F}\mathcal{O}\mathcal{L}$ signature $\mathrm{\Sigma }+X$ that adjoins X to $\mathrm{\Sigma }$ as new constants. Then, ${\mathit{Sen}}^{\mathcal{OFOL}}(\mathrm{\Sigma },X)={\mathit{Sen}}^{\mathcal{FOL}}(\mathrm{\Sigma }+X)$, ${\mathit{Mod}}^{\mathcal{OFOL}}(\mathrm{\Sigma },X)={\mathit{Mod}}^{\mathcal{FOL}}(\mathrm{\Sigma })$, ${\left[\left[M\right]\right]}_{\mathrm{\Sigma },X}=M^X$, i.e., the set of the “valuations” of X to M and for each $(\mathrm{\Sigma },X)$-model M, each $w\in M^X$, and each $(\mathrm{\Sigma },X)$-sentence $\rho$, we define $(M({\vDash }_{\mathrm{\Sigma },X}^{\mathcal{OFOL}}{)}^w\rho )=(M^w{\vDash }_{\mathrm{\Sigma }+X}^{\mathcal{FOL}}\rho )$ where $M^w$ is the expansion of M to $\mathrm{\Sigma }+X$ such that $M_X^w=w$ (i.e., the new constants of X are interpreted in $M^w$ according to the “valuation” w).
• Various kinds of automata theories can be presented as stratified institutions. For instance, the stratified institution $\mathcal{S}\mathcal{A}\mathcal{U}\mathcal{T}$ of deterministic automata (for regular languages) has sets of input symbols as signatures, the automata A are the models and the words are the sentences. Then, $\left[\right[A\left]\right]$ is the set of the states of A and $A{\vDash }^s\alpha$ if and only if $\alpha$ is recognised by A from the state s.
• In [51], the authors introduced an abstract approach to connectives that generalises the propositional and quantification connectives, modalities, nominals, and so on. A connective signature $\mathcal{C}$ is just a single sorted signature of operation symbols, which are called connectives. Let $T_{\mathcal{C}}$ denote the set of all $\mathcal{C}$-terms. A $\mathcal{C}$-algebraA consists of a set $\left[\right[A\left]\right]$ and a mapping $A:T_{\mathcal{C}}\to \mathcal{P}\left[\left[A\right]\right]$. A $\mathcal{C}$-homomorphism $h:A\to B$ is a function $h:\left[\right[A\left]\right]\to \left[\right[B\left]\right]$ such that $2^h\circ A=B$. If $\eta \in \left[\right[A\left]\right]$ and $\rho \in T_{\mathcal{C}}$, then $A{\vDash }_{\mathcal{C}}^{\eta }\rho$ holds when $\eta \in A(\rho )$. All these define the stratified institution of abstract connectives $\mathcal{C}\mathcal{O}\mathcal{N}$ that has the connectives signatures as its signatures, $\mathcal{C}$-algebras and $\mathcal{C}$-models, $T_{\mathcal{C}}$ as the set of $\mathcal{C}$-sentences, the stratification being given by $\left[\right[A\left]\right]$ and the satisfaction relation defined as above.
• In [58], there is a development of a general representation theorem of $3/2$ institutions as stratified institutions. The theory of $3/2$ institutions [59] is an extension of ordinary institution theory that accommodates the partiality of the signature morphisms and its syntactic and semantic effects, which is motivated by applications to conceptual blending and software evolution. The representation theorem is based, for each $\phi \square$-model M, on setting $\left[\right[M\left]\right]$ to the set its $\phi$-reducts. This is possible because in $3/2$ institutions, unlike in ordinary institution theory, a model may have more than one reduct with respect to a fixed signature morphism, this being the semantic effect of the (implicit) partiality of the signature morphisms.

That was the brief presentation of the concept of stratified institution together with a list of relevant concrete examples. In the remaining part of this section, we will present some of the most important model theoretic developments with stratified institutions as follows:

• A ‘flattening’ of stratified institutions to ordinary institutions as a universal construction, and on this basis, a general technique for establishing properties in some important class of stratified institution, which uses an axiomatic decomposition of the respective stratified institution.
• A general method to construct new stratified institutions out of existing stratified institutions by ‘modalisation’.
• An axiomatic treatment of important model theoretic concepts such as propositional connectives, quantifiers, modalities, nominals, and interpolation.
• Some important model theoretic methods in the context of stratified institutions, including diagrams, ultraproducts, and Tarski’s elementary chain theorem.
• Some more computing science-motivated uses of stratified institutions.

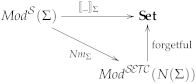
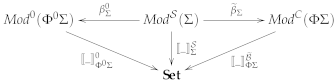
3.1. Flattening Stratified Institutions to Ordinary Institutions

Given any stratified institution $\mathcal{S}=(\mathit{Sign},\mathit{Sen},\mathit{Mod},[[\_]],\vDash )$, in [52], we have built an ordinary institution ${\mathcal{S}}^{♯}=(\mathit{Sign},\mathit{Sen},{\mathit{Mod}}^{♯},{\vDash }^{♯})$ as follows:

–

The objects of ${\mathit{Mod}}^{♯}(\mathrm{\Sigma })$ are the pairs $(M,w)$ such that $M\in |\mathit{Mod}(\mathrm{\Sigma })|$ and $w\in {\left[\left[M\right]\right]}_{\mathrm{\Sigma }}$;

–

The $\mathrm{\Sigma }$-homomorphisms $(M,w)\to (N,v)$ are the pairs $(h,w)$ such that $h:M\to N$ and ${\left[\left[h\right]\right]}_{\mathrm{\Sigma }}w=v$;

–

For any signature morphism $\phi :\mathrm{\Sigma }\to {\mathrm{\Sigma }}^{\prime }$ and any ${\mathrm{\Sigma }}^{\prime }$-model $(M^{\prime },w^{\prime })$

$${\mathit{Mod}}^{♯}(\phi )(M^{\prime },w^{\prime })=(\mathit{Mod}(\phi )M^{\prime },{\left[\left[M^{\prime }\right]\right]}_{\phi }{w}^{\prime });$$

–

For each $\mathrm{\Sigma }$-model M, each $w\in {\left[\left[M\right]\right]}_{\mathrm{\Sigma }}$, and each $\rho \in \mathit{Sen}(\mathrm{\Sigma })$

$$((M,w){\vDash }_{\mathrm{\Sigma }}^{♯}\rho )=(M{\vDash }_{\mathrm{\Sigma }}^w\rho ).$$

(5)

In [57], the construction of ${\mathcal{S}}^{♯}$ is explained as a categorical universal construction. That explanation involves the concept of morphism of stratified institutions which is an extension of the notorious concept of morphism of institutions (cf. [18,44,46], etc.). Both concepts represent mappings that preserve the mathematical structure of stratified institutions and of ordinary institutions, respectively, in the same way group homomorphisms preserve the group structure, or the continuous functions preserve the structure of topological spaces. Thus, ${(\_)}^{♯}$ arises as a left-adjoint functor from the category $\mathbf{S}\mathbf{IN}\mathbf{S}$ of strict stratified institutions to the category $\mathbf{IN}\mathbf{S}$ of ordinary institutions. One way to present this is that for each institution $\mathcal{B}$, there exists a stratified institution $\tilde{\mathcal{B}}$ and an institution morphism ${\epsilon }_{\mathcal{B}}:{\tilde{\mathcal{B}}}^{♯}\to \mathcal{B}$ such that for each morphism of institutions $(\mathrm{\Phi },\alpha ,\beta ):{\mathcal{S}}^{♯}\to \mathcal{B}$, there exists a unique strict stratified institution morphism $(\mathrm{\Phi },\alpha ,\tilde{\beta }):\mathcal{S}\to \tilde{\mathcal{B}}$ such that the following diagram commutes:

(6)

The construction ${\mathcal{S}}^{♯}$, called the flattening of $\mathcal{S}$, on the one hand reduces stratified institutions to ordinary institutions without any loss of information. It is helpful for transferring concepts and results from the simpler world of ordinary institution theory to that of stratified institutions. One important example of that is given by the model amalgamation property, which is one of the most fundamental properties of institutions with vast consequences both in computing science and in institutional model theory (cf. [25,44,65], etc.). Model amalgamation in ${\mathcal{S}}^{♯}$ defines the so-called stratified model amalgamation in $\mathcal{S}$ [57], which is more refined than plain model amalgamation in $\mathcal{S}$ and is a characteristic only to stratified institutions. On the other hand, it is important to avoid the trap of believing that in this way, the theory of stratified institutions can be dealt with entirely within the ordinary institution theoretic framework. The reason for this cannot be the case that the institutions ${\mathcal{S}}^{♯}$ are not any institutions, as they have a very specific structure given by the stratified structure of $\mathcal{S}$.

Another way to reduce a stratified institution to an ordinary institution is to flatten only the satisfaction relation, i.e.,

$$M{\vDash }^{*}\rho \mathrm{if} \mathrm{and} \mathrm{only} \mathrm{if}M{\vDash }^w\rho \mathrm{for} \mathrm{each} w\in \left[\left[M\right]\right].$$

This yields an institution when the stratification is surjective (i.e., for each signature morphism $\phi$ and each $\phi \square$-model $M^{\prime }$, ${\left[\left[M^{\prime }\right]\right]}_{\phi }$ is surjective). However, in this institution, denoted ${\mathcal{S}}^{*}$, the locality aspect of $\mathcal{S}$—which is very important—is lost. In the literature, ${\mathcal{S}}^{*}$ and ${\mathcal{S}}^{♯}$ are known as the global and the local, respectively, institutions associated to $\mathcal{S}$. They can be regarded as high abstractions of the global and of the local satisfaction in modal logic.

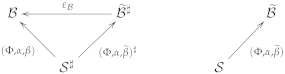
3.2. Decompositions of Stratified Institutions

In [57], we have introduced a technique for establishing properties of stratified institutions at the general level, which consists of projecting to simpler structures. This reflects a situation that occurs especially in the stratified institutions that are based on Kripke semantics, where the models are combined from two simpler components, of which one may think as a structure of the worlds on the one hand and a structure of primitive or base models placed in these worlds on the other hand. The actual definition of this is as follows.

Let $\mathcal{S}$ be any stratified institution and $(\mathrm{\Phi },\alpha ,\beta ):{\mathcal{S}}^{♯}\to \mathcal{B}$ be a morphism of institutions (called a base for $\mathcal{S}$). By the natural isomorphism $\mathbf{IN}\mathbf{S}({\mathcal{S}}^{♯},\mathcal{B})\cong \mathbf{S}\mathbf{IN}\mathbf{S}(\mathcal{S},\tilde{\mathcal{B}})$ (given by the adjunction between $\mathbf{S}\mathbf{IN}\mathbf{S}$ and $\mathbf{IN}\mathbf{S}$), we obtain a morphism of stratified institutions $(\mathrm{\Phi },\alpha ,\tilde{\beta }):\mathcal{S}\to \tilde{\mathcal{B}}$ (cf. (6)). A constraint model sub-functor ${\mathit{Mod}}^C\subseteq {\mathit{Mod}}^{\tilde{\mathcal{B}}}$ is a sub-functor such that for each signature $\mathrm{\Sigma }$,

$${\tilde{\beta }}_{\mathrm{\Sigma }}({\mathit{Mod}}^{\mathcal{S}}(\mathrm{\Sigma }))\subseteq {\mathit{Mod}}^C(\mathrm{\Phi }\mathrm{\Sigma }).$$

Let ${\tilde{\mathcal{B}}}^C$ denote the stratified sub-institution of $\tilde{\mathcal{B}}$ induced by ${\mathit{Mod}}^C$. A decomposition of $\mathcal{S}$ consists of two strict stratified institution morphisms such as below

$${\mathcal{S}}^0\stackrel{({\mathrm{\Phi }}^0,{\alpha }^0,{\beta }^0)}{⟵}\mathcal{S}\stackrel{(\mathrm{\Phi },\alpha ,\tilde{\beta })}{⟶}{\tilde{\mathcal{B}}}^C$$

such that for each $\mathcal{S}$-signature $\mathrm{\Sigma }$

is a pullback in $\mathbf{C}\mathbf{A}\mathbf{T}$.

The following aspects emerge from the concept of decomposition.

• The models of $\mathcal{S}$ can be represented as pairs of ${\mathcal{S}}^0$ models and families of $\mathcal{B}$ models satisfying certain constraints (hence, ${\tilde{\mathcal{B}}}^C$ models) such that the “worlds” of the corresponding ${\tilde{\mathcal{B}}}^C$ model constitutes the stratification of the corresponding ${\mathcal{S}}^0$ model. This means that at the semantic level, $\mathcal{S}$ is completely determined by the two components of the decomposition.
• The situation at the syntactic level is different. The syntax (signatures and sentences) of each of the two components is represented in the syntax of $\mathcal{S}$, but the latter is not completely determined by the former syntaxes. In other words, $\mathcal{S}$ may have signatures and sentences that do not originate from either of the two components. This is what the definition gives us. However, while there are hardly any examples/applications where all sentences come from either one of the two components, in many examples, the signatures of $\mathcal{S}$ are composed from the signatures of ${\mathcal{S}}^0$ and those from $\mathcal{B}$.

In the definition of decomposition, the role of the constraint model sub-functor ${\mathit{Mod}}^C$ is strongly related to applications. For instance, in many concrete situations of interest, the Kripke models enjoy some form of sharing. Cases such as $\mathcal{M}\mathcal{F}\mathcal{O}\mathcal{L}$ and $\mathcal{H}\mathcal{F}\mathcal{O}\mathcal{L}$ are emblematic in this respect. If we consider the latter one, then:

• ${\mathcal{S}}^0=\mathcal{R}\mathcal{E}\mathcal{L}{\mathcal{C}}^1$, which is the single-sorted sub-institution of $\mathcal{F}\mathcal{O}\mathcal{L}$ determined by the signatures without operation symbols other than constants. Consequently, ${\mathrm{\Phi }}^0(\mathrm{Nom},P)=(\mathrm{Nom},\lambda :2)$.
• ${\alpha }^0$ is defined by

  $${\alpha }_{(\mathrm{Nom},P)}^0\lambda (i,j)={@}_i\diamond j(={@}_i\neg \square \neg j).$$
• $\mathcal{B}=\mathcal{A}\mathcal{F}\mathcal{O}\mathcal{L}$, i.e., the sub-institution of $\mathcal{F}\mathcal{O}\mathcal{L}$ that admits only atoms as sentences.
• ${\mathit{Mod}}^C$ restricts the $\tilde{\mathcal{B}}$ models only to those for which the base $\mathcal{F}\mathcal{O}\mathcal{L}$ models share their underlying sets and the interpretations of the constants.
• $\alpha$ consists of canonical interpretations of the $\mathcal{F}\mathcal{O}\mathcal{L}$ atoms as $\mathcal{H}\mathcal{F}\mathcal{O}\mathcal{L}$ sentences.

One of the consequences of decompositions is the possibility to obtain model amalgamation properties in $\mathcal{S}$ via model amalgamation properties in the components ${\mathcal{S}}^0$ and $\mathcal{B}$. This can be very useful in the applications as Kripke models are complex structures; therefore, their model amalgamation is a mathematically complicated matter, while model amalgamation in the components of a decomposition is much simpler. In [57], we have provided a general theorem that obtains model amalgamation through decompositions and which applies well in the examples. There have been also other applications of this decomposition technique which we will discuss later on in the paper.

Another important potential of the concept of decomposition is the possibility to apply it in a reverse way in the sense of constructing new stratified institutions starting from the components ${\mathcal{S}}^0$ and $\mathcal{B}$ (actually ${\tilde{\mathcal{B}}}^C$). This can be a great source of new concrete stratified institutions serving various computing science purposes.

3.3. Modalised (Stratified) Institutions

The modalisation of institutions, already discussed as an item in the list of examples of stratified institutions, constitutes an example of reversing the decomposition concept in which ${\mathcal{S}}^0$ is rather concrete—its models being Kripke frames—while $\mathcal{B}$ is kept abstract, and it goes back essentially to [61].

In this context, the work [66] generalises the famous encoding of modal logic into first-order logic [67] in the sense that any abstract encoding $\mathcal{B}\to \mathcal{F}\mathcal{O}\mathcal{L}$ becomes lifted to an encoding ${\mathcal{S}}^{*}\to \mathcal{F}\mathcal{O}\mathcal{L}$ (the precise notion of encoding being what is known as theoroidal comorphism). This highly general encoding constitutes the foundations for the formal specification and verification language H [68], which is a language that is institution-independent in the sense that in principle, the base institution $\mathcal{B}$ can be any institution that can be plugged into the system.

Although the modalisation of institutions has been defined in the way presented above, in fact, it can be extended to a construction that takes an arbitrary stratified rather than an ordinary institution as input. So, it becomes a method for building new stratified institutions on top of proper stratified institutions. A brief description of this method is as follows:

• Let $\mathcal{S}$ be a stratified institution. The stratified institution to be constructed will be denoted $K(\mathcal{S})$.
• Then, we let ${\mathit{Sign}}^{K(\mathcal{S})}={\mathit{Sign}}^{\mathcal{S}}$.
• For any signature $\mathrm{\Sigma }$, ${\mathit{Sen}}^{K(\mathcal{S})}$ is the least set containing ${\mathit{Sen}}^{\mathcal{S}}(\mathrm{\Sigma })$ and which is closed under propositional connectives, quantifiers, and modalities ($\square ,\diamond$). We can chose what we need from those connectives, which means that they should be regarded as a parameter for $K(\mathcal{S})$. The quantifiers are treated abstractly in the typical institution theoretic manner (cf. [30,44] etc.) by using an abstract designated class of signature morphisms that obey some axioms known as quantification space [63,69].
• The models of $K(\mathcal{S})$ are the Kripke models over $\mathcal{S}$, i.e., pairs $(W,M)$ where W is a Kripke frame as in $\mathcal{M}\mathcal{P}\mathcal{L}$ or $\mathcal{M}\mathcal{F}\mathcal{O}\mathcal{L}$, and $M={(M^w)}_{w\in \left|W\right|}$ such that ${\left[\left[M^w\right]\right]}_{\mathrm{\Sigma }}^{\mathcal{S}}={\left[\left[M^v\right]\right]}_{\mathrm{\Sigma }}^{\mathcal{S}}$ for all $w,v\in \left|W\right|$ (so the components of M share their ‘internal states’).
• The stratification is defined by ${\left[\left[(W,M)\right]\right]}_{\mathrm{\Sigma }}^{K(\mathcal{S})}=\left|W\right|\times {\left[\left[M\right]\right]}_{\mathrm{\Sigma }}^{\mathcal{S}}$.
• The satisfaction relation of $K(\mathcal{S})$ is defined inductively on the structure of the respective sentences by following the common ideas of of Kripke semantics. For the base case, when the sentence is in $\mathcal{S}$, we rely on the satisfaction relation of $\mathcal{S}$.

In order to capture precisely various relevant examples, this construction can be refined in various ways by considering constrained models (axiomatically in the manner described in [63] or more concretely as in [61]), or by considering nominals structures or polyadic modalities. In the case of the latter two extensions, of course, the new category of signatures is a product between ${\mathit{Sign}}^{\mathcal{S}}$ and some category of signatures for relations.

3.4. The Logic of Stratified Institutions

The development of an in-depth model theory in the axiomatic style relies also on the possibility to ‘internalise’ important logical concepts such as propositional connectives and quantifiers. In ordinary institution theory, this has been achieved very early in [30] (for a more comprehensive treatment, see also [44]). The axiomatic semantic definitions of the common propositional connectives and of quantifiers have been extended to stratified institutions in [52]. Although presented in a different form closer to [53], the definitions below are equivalent to those of [52]. The following notation is useful for what follows. For any $\mathrm{\Sigma }$-model M and any $\mathrm{\Sigma }$-sentence $\rho$, we let

$$\left[[M,\rho ]\right]=\{w\in {\left[\left[M\right]\right]}_{\mathrm{\Sigma }}\mid M{\vDash }^w\rho \}.$$

3.4.1. Propositional Connectives

Given a signature $\mathrm{\Sigma }$ in a stratified institution, a $\mathrm{\Sigma }$-sentence ${\rho }^{\prime }$ is a semantic

• Negation of $\rho$ when $\left[[M,{\rho }^{\prime }]\right]=\left[\left[M\right]\right]\setminus \left[[M,\rho ]\right]$;
• Conjunction of ${\rho }_1$ and ${\rho }_2$ when $\left[[M,{\rho }^{\prime }]\right]=\left[[M,{\rho }_1]\right]\cap \left[[M,{\rho }_2]\right]$;
• Disjunction of ${\rho }_1$ and ${\rho }_2$ when $\left[[M,{\rho }^{\prime }]\right]=\left[[M,{\rho }_1]\right]\cup \left[[M,{\rho }_2]\right]$;
• Implication of ${\rho }_1$ and ${\rho }_2$ when $\left[[M,{\rho }^{\prime }]\right]=(\left[\left[M\right]\right]\setminus \left[[M,{\rho }_1]\right])\cup \left[[M,{\rho }_2]\right]$;
• etc.

for each $\mathrm{\Sigma }$-model M. A stratified institution has (semantic) negation when each sentence of the institution has a negation. It has (semantic) conjunctions when each two sentences (of the same signature) have a conjunction. Similar definitions can be formulated for disjunctions, implications, and equivalences. As in ordinary institution theory, distinguished negations are usually denoted by $\neg \_$, distinguished conjunctions are usually denoted by $\_\wedge \_$, distinguished disjunctions are usually denoted by $\_\vee \_$ distinguished implications are usually denoted by $\_\Rightarrow \_$ distinguished equivalences are usually denoted by $\_\iff \_$, etc. Note that $\mathcal{M}\mathcal{F}\mathcal{O}\mathcal{L}$, $\mathcal{M}\mathcal{P}\mathcal{L}$ together with their hybrid extensions $\mathcal{H}\mathcal{F}\mathcal{O}\mathcal{L}$, $\mathcal{H}\mathcal{P}\mathcal{L}$, as well as $\mathcal{O}\mathcal{F}\mathcal{O}\mathcal{L}$ have all these semantics propositional connectives. $\mathcal{S}\mathcal{A}\mathcal{U}\mathcal{T}$ has conjunctions only.

When they exist, the semantic propositional connectives are inter-definable. Moroever, when they exist, the negations, conjunctions, disjunctions, implications, and negations coincide in $\mathcal{S}$ and ${\mathcal{S}}^{♯}$.

3.4.2. Quantifiers

Given a morphism of signatures $\chi :\mathrm{\Sigma }\to {\mathrm{\Sigma }}^{\prime }$, a $\mathrm{\Sigma }$-sentence $\rho$ is a semantic

• Universal χ-quantification of a ${\mathrm{\Sigma }}^{\prime }$-sentence ${\rho }^{\prime }$ when

  $$\left[[M,\rho ]\right]=\bigcap _{\mathit{Mod}(\chi )M^{\prime }=M}\{w\in {\left[\left[M\right]\right]}_{\mathrm{\Sigma }}\mid {\left[\left[M^{\prime }\right]\right]}_{\chi }^{-1}w\subseteq \left[[M^{\prime },{\rho }^{\prime }]\right]\},\mathrm{and}$$
• Existential χ-quantification of a ${\mathrm{\Sigma }}^{\prime }$-sentence ${\rho }^{\prime }$ when

  $$\left[[M,\rho ]\right]=\bigcup _{\mathit{Mod}(\chi )M^{\prime }=M}{\left[\left[M^{\prime }\right]\right]}_{\chi }(\left[[M^{\prime },{\rho }^{\prime }]\right]),$$

for any $\mathrm{\Sigma }$-model M.

A stratified institution has (semantic) universal $\mathcal{D}$-quantification for a class $\mathcal{D}$ of signature morphisms when for each $(\chi :\mathrm{\Sigma }\to {\mathrm{\Sigma }}^{\prime })\in \mathcal{D}$, each ${\mathrm{\Sigma }}^{\prime }$-sentence has a universal $\chi$-quantification. A similar definition applies to existential quantification. Distinguished universal/existential quantifications are denoted by $(\forall \chi ){\rho }^{\prime }$/$(\exists \chi ){\rho }^{\prime }$.

When they exist, the universal and the existential $\chi$-quantifications, respectively, coincide in $\mathcal{S}$ and ${\mathcal{S}}^{♯}$. So, on the one hand, the concepts of semantic propositional connectives and quantifications in ordinary institutions arise as an instance of those of stratified institutions when the underlying set of each ${\left[\left[M\right]\right]}_{\mathrm{\Sigma }}$ is a singleton set. On the other hand, we have seen that the stratified institution concepts of propositional connectives and quantifications are in substance no more general than their ordinary institution theoretic correspondents. Therefore, an alternative equivalent way to introduce the stratified institution semantics of propositional connectives is to define them on the basis of ${\mathcal{S}}^{♯}$ and then infer the above definitions as properties at the level of $\mathcal{S}$.

3.4.3. Modalities

While propositional and quantification connectives in stratified institutions can still be explained in terms of their ordinary institution theoretic counterparts, modalities and nominals can be defined only in the presence of stratifications because both of them rely semantically on models having internal states. Moreover, this is not enough; in both cases, some additional specific semantic infrastructure is also needed.

In order to define semantic possibility (⋄) and necessity (□) in a stratified institution, we have to be able to ‘extract’ Kripke frames from the stratification. Let $\mathcal{R}\mathcal{E}\mathcal{L}$ denote the sub-institution of $\mathcal{F}\mathcal{O}\mathcal{L}$ determined by those signatures without function symbols. Let ${\mathcal{R}\mathcal{E}\mathcal{L}}^1$ denote the single sorted version of $\mathcal{R}\mathcal{E}\mathcal{L}$. Given a stratified institution $\mathcal{S}$, a binary frame extraction assumes that for each signature $\mathrm{\Sigma }$, the stratification ${\left[[\_]\right]}_{\mathrm{\Sigma }}$ is a composition between a functor ${\mathit{Fr}}_{\mathrm{\Sigma }}:\mathit{Mod}(\mathrm{\Sigma })\to {\mathit{Mod}}^{\mathcal{R}\mathcal{E}{\mathcal{L}}^1}(\lambda :2)$ and the forgetful functor ${\mathit{Mod}}^{\mathcal{R}\mathcal{E}{\mathcal{L}}^1}(\lambda :2)\to \mathbf{S}\mathbf{et}$, where ${\mathit{Mod}}^{\mathcal{R}\mathcal{E}{\mathcal{L}}^1}(\lambda :2)$ is the category of the $\mathcal{F}\mathcal{O}\mathcal{L}$ models for a single sorted signature with one binary relation symbol $\lambda$.

Note that the models of ${\mathit{Mod}}^{\mathcal{R}\mathcal{E}{\mathcal{L}}^1}(\lambda :2)$ are exactly the Kripke frames $W=(|W|,W_{\lambda })$ of the modal logic examples $\mathcal{M}\mathcal{P}\mathcal{L}$, $\mathcal{M}\mathcal{F}\mathcal{O}\mathcal{L}$, $\mathcal{H}\mathcal{P}\mathcal{L}$, and $\mathcal{H}\mathcal{F}\mathcal{O}\mathcal{L}$. Since $|{\mathit{Fr}}_{\mathrm{\Sigma }}{(M)|=\left[\left[M\right]\right]}_{\mathrm{\Sigma }}$, we can write ${\mathit{Fr}}_{\mathrm{\Sigma }}(M)=({\left[\left[M\right]\right]}_{\mathrm{\Sigma }},{({\mathit{Fr}}_{\mathrm{\Sigma }}(M))}_{\lambda })$. The ${\mathit{Fr}}_{\mathrm{\Sigma }}$ functors are also required to form a lax natural transformation from $\mathit{Mod}$ to the constant functor mapping any signature to the category ${\mathit{Mod}}^{\mathcal{R}\mathcal{E}{\mathcal{L}}^1}(\lambda :2)$.

Concretely, in the stratified institutions $\mathcal{M}\mathcal{F}\mathcal{O}\mathcal{L}$, $\mathcal{M}\mathcal{P}\mathcal{L}$, $\mathcal{H}\mathcal{F}\mathcal{O}\mathcal{L}$, and $\mathcal{H}\mathcal{P}\mathcal{L}$, the $\mathit{Fr}$ maps the Kripke models $(W,M)$ to their underlying Kripke frames $W=(|W|,W_{\lambda })$.

In the most general situation, when we allow polyadic modalities, i.e., modalities with more than one argument, first, we need a functor $L:{\mathit{Sign}}^{\mathcal{S}}\to {\mathit{Sign}}^{\mathcal{R}\mathcal{E}{\mathcal{L}}^1}$ such that $L(\mathrm{\Sigma })$ represents the relation symbols corresponding to the modalities of $\mathrm{\Sigma }$ (we allow a flexible approach where the modalities may change with the signature). Then, we have a more general concept of frame extraction. In the binary case, $L(\mathrm{\Sigma })$ is always $\{\lambda :2\}$ and hence, there is no reason to have $\lambda$ as part of the signatures.

A (general) frame extraction $(L,\mathit{Fr})$ is a stratified institution morphism

$$(L,\varnothing ,\mathit{Fr}):\mathcal{S}\to {\mathcal{R}\mathcal{E}\mathcal{L}}^1$$

where ${\mathcal{R}\mathcal{E}\mathcal{L}}^1$ is considered as a stratified institution with no sentences, and for each ${\mathcal{R}\mathcal{E}\mathcal{L}}^1$-model M, $\left[\right[M\left]\right]$ is the underlying set of M and the satisfaction is invariant with respect to the states, i.e., $M{\vDash }^w\rho$ is $M\vDash \rho$. Commonly, in concrete examples, it happens that frame extractions are in fact strict institution morphisms.

In any stratified institution endowed with a binary frame extraction $\mathit{Fr}$, a $\mathrm{\Sigma }$-sentence ${\rho }^{\prime }$ is a semantic

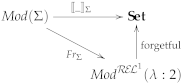
• possibility (⋄) of $\rho$ when $\left[[M,{\rho }^{\prime }]\right]={({\mathit{Fr}}_{\mathrm{\Sigma }}M)}_{\lambda }^{-1}\left[[M,\rho ]\right]$;
• necessity (□) of $\rho$ when $\left[[M,{\rho }^{\prime }]\right]=\{i\mid {({\mathit{Fr}}_{\mathrm{\Sigma }}M)}_{\lambda }i\subseteq \left[[M,\rho ]\right]\}$,

for each $\mathrm{\Sigma }$-model M.

Obviously, in $\mathcal{M}\mathcal{P}\mathcal{L}$, $\mathcal{M}\mathcal{F}\mathcal{O}\mathcal{L}$, $\mathcal{H}\mathcal{P}\mathcal{L}$, and $\mathcal{H}\mathcal{F}\mathcal{O}\mathcal{L}$, we have that each $\diamond \rho$/$\square \rho$ is a semantic possibility/necessity of $\rho$ in the sense of our definitions above. The concept of semantic possibility/necessity admits an obvious extension to polyadic modalities by using general frame extractions.

3.4.4. Nominals

In order to define the semantics of hybrid features such as nominals and the satisfaction operator (@) in stratified institutions, we need to be able to extract nominals data from the corresponding stratification. Let $\mathcal{S}\mathcal{E}\mathcal{T}\mathcal{C}$ be the sub-institution of $\mathcal{F}\mathcal{O}\mathcal{L}$ that restricts the signatures to single-sorted ones and without relation symbols or function symbols of non-null arity, so only constants being admitted. Given a stratified institution $\mathcal{S}$, a nominals extraction assumes two additional data:

• A functor $N:{\mathit{Sign}}^{\mathcal{S}}\to {\mathit{Sign}}^{\mathcal{SETC}}$, i.e., each $N(\mathrm{\Sigma })$ is a single-sorted $\mathcal{F}\mathcal{O}\mathcal{L}$ signature having only constants; and
• That for each signature $\mathrm{\Sigma }$, the stratification ${\left[[\_]\right]}_{\mathrm{\Sigma }}$ is a composition between a functor ${\mathit{Nm}}_{\mathrm{\Sigma }}:{\mathit{Mod}}^{\mathcal{S}}(\mathrm{\Sigma })\to {\mathit{Mod}}^{\mathcal{SETC}}(N(\mathrm{\Sigma }))$ and the forgetful functor ${\mathit{Mod}}^{\mathcal{SETC}}(N(\mathrm{\Sigma }))\to \mathbf{S}\mathbf{et}$,

  such that the ${\mathit{Nm}}_{\mathrm{\Sigma }}$ functors are also required to form a lax natural transformation ${\mathit{Mod}}^{\mathcal{S}}\Rightarrow N;{\mathit{Mod}}^{\mathcal{SETC}}$.

Hence, a nominals extraction $(N,\mathit{Nm})$ is a stratified institution morphism

$$(N,\varnothing ,\mathit{Nm}):\mathcal{S}\to \mathcal{S}\mathcal{E}\mathcal{T}\mathcal{C}$$

where $\mathcal{S}\mathcal{E}\mathcal{T}\mathcal{C}$ is considered as a stratified institution in the same manner we considered ${\mathcal{R}\mathcal{E}\mathcal{L}}^1$ as a stratified institution.

Concretely, in the stratified institutions of the hyrbid modal logics $\mathcal{H}\mathcal{F}\mathcal{O}\mathcal{L}$, $\mathcal{H}\mathcal{P}\mathcal{L}$, we have that N maps each signature $(\mathrm{Nom},\mathrm{\Sigma })$ to the single-sorted signature of constants $\mathrm{Nom}$, and that ${\mathit{Nm}}_{(\mathrm{Nom},\mathrm{\Sigma })}$ maps each Kripke model $(W,M)$ to the ${\mathit{Mod}}^{\mathcal{SETC}}(\mathrm{Nom})$-model $(|W|,{(W_i)}_{i\in \mathrm{Nom}})$, so from the Kripke models, it forgets both the M part as well as the accessibility relation $W_{\lambda }$.

In any stratified institution endowed with a nominals extraction N, $\mathit{Nm}$, for each signature $\mathrm{\Sigma }$ and each $i\in N(\mathrm{\Sigma })$,

• A $\mathrm{\Sigma }$-sentence ${\rho }^{\prime }$ is an i-sentence when $\left[[M,{\rho }^{\prime }]\right]=\left\{{({\mathit{Nm}}_{\mathrm{\Sigma }}M)}_i\right\}$;
• A $\mathrm{\Sigma }$-sentence ${\rho }^{\prime }$ is the satisfaction of ρ at i when

  $$\left[[M,{\rho }^{\prime }]\right]=\left\{\begin{array}{cc}\left[\right[M\left]\right],\hfill & {({\mathit{Nm}}_{\mathrm{\Sigma }}M)}_i\in \left[[M,\rho ]\right]\hfill \\ \varnothing ,\hfill & {({\mathit{Nm}}_{\mathrm{\Sigma }}M)}_i\notin \left[[M,\rho ]\right]\hfill \end{array}\right.$$

for each $\mathrm{\Sigma }$-model M.

In $\mathcal{H}\mathcal{P}\mathcal{L}$ and $\mathcal{H}\mathcal{F}\mathcal{O}\mathcal{L}$, we have that each nominal i of the signature is an i-sentence and each sentence ${@}_i\rho$ is a satisfaction at i in the sense of the above definitions. In general, for the distinguished i-sentences and satisfaction at i, we may use the notations $i-\mathrm{sen}$ and ${@}_i\rho$, respectively.

3.5. Interpolation in Stratified Institutions

Interpolation is a notoriously important logical property which is easy to understand but difficult to establish. It also has a number of important applications in computing science, especially in formal specification theory [65,70,71,72,73,74] but also in databases (ontologies) [75], automated reasoning [76,77], type checking [78], model checking [79], structured theorem proving [80,81], etc. Computing science and model theoretic motivations have led to a very general approach to interpolation [30] within the theory of institutions that is completely independent of any concrete logical system. This direction of study and research has produced a substantial body of results reported in works such as [30,42,43,45,65,74,82,83,84,85,86]. In this context, the institution theoretic concept to interpolation had suffered a gradual evolution. At the level of ordinary institution theory, one way to express the end result of this evolution is that of ‘interpolation square’. In its Craig interpolation version, this is as follows. In any given institution $\mathcal{I}$, a commutative square of signature morphisms as below

(7)

is a Craig interpolation square when for each finite set $E_k$ of ${\mathrm{\Sigma }}_k$-sentences, $k=1,2$, such that when ${\theta }_1{E}_1\vDash {\theta }_2{E}_2$, there exists a finite set E of $\mathrm{\Sigma }$-sentences such that

$$E_1\vDash {\phi }_{1}E\mathrm{and}{\phi }_{2}E\vDash E_2.$$

How can we lift this concept of interpolation square to stratified institutions? The obvious answer is to maintain the concept by apply it to a flattening of the respective stratified institution $\mathcal{S}$. However, here, we run into a problem: which of ${\mathcal{S}}^{*}$ and ${\mathcal{S}}^{♯}$ is the most appropriate for this? The answer is that this may be actually a wrong question, as both the local (${\vDash }^{♯}$) and the global (${\vDash }^{*}$) semantic consequences can be used legitimately to define interpolation concepts in stratified institutions. So, we naturally end up with two concepts of interpolation in stratified institutions.

Then, a natural question arises: what is the causal relationship between local and global interpolation? In [87], we have provided an answer to this question. Without some additional infrastructure, none of the two interpolation concepts causes the other one. However, the main result of [87] shows that local causes global interpolation when the respective stratified institution has some nominals infrastructure including universal quantification over the nominals. In [87], these properties are given precise mathematical sense through some rather intricate technicalities which we do not present here. This is only the first step toward a proper theory of interpolation specific to stratified institutions. More steps are needed in order to mature it at a level comparable to that of interpolation in ordinary institution model theory.

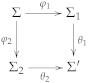
3.6. Diagrams in Stratified Institutions

In conventional model theory, the method of diagrams is one of the most important methods. The institution-independent method of diagrams plays a significant role in the development of a lot of model theoretic results at the level of abstract institutions, many of its applications being presented in [44]. These include the existence of co-limits of models, free models along theory morphisms, axiomatisability results, elementary homomorphisms results, filtered power embeddings results, saturated models results (including an abstract version of Keisler–Shelah isomorphism theorem), the equivalence between initial semantics and quasi-varieties, Robinson consistency results, interpolation theory, definability theory, proof systems, predefined types, etc.

In institution theory, diagrams had been introduced for the first time by Tarlecki in [31,32] in a form different from ours. In the form presented here, it has been introduced at the level of institution-independent model theory in [33] as a categorical property which formalises the idea that

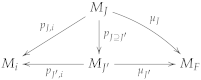
the class of model homomorphisms from a model M can be represented (by a natural isomorphism) as a class of models of a theory in a signature extending the original signature with syntactic entities determined by M.

Let us recall from [33,44] the main concept of the institution theoretic method of diagrams. An institution $\mathcal{I}$ has diagrams when for each signature $\mathrm{\Sigma }$ and each $\mathrm{\Sigma }$ model M, there exists a signature ${\mathrm{\Sigma }}_M$ and a signature morphism ${\iota }_{\mathrm{\Sigma }}(M):\mathrm{\Sigma }\to {\mathrm{\Sigma }}_M$, functorial in $\mathrm{\Sigma }$ and M, and a set $E_M$ of ${\mathrm{\Sigma }}_M$ sentences such that $\mathit{Mod}({\mathrm{\Sigma }}_M,E_M)$ and the comma category $M/\mathit{Mod}(\mathrm{\Sigma })$ are naturally isomorphic, i.e., the following diagram commutes by the isomorphism $i_{\mathrm{\Sigma },M}$ that is natural in $\mathrm{\Sigma }$ and M

(8)

The signature morphism ${\iota }_{\mathrm{\Sigma }}(M):\mathrm{\Sigma }\to {\mathrm{\Sigma }}_M$ is called the elementary extension of Σ via M, and the set $E_M$ of ${\mathrm{\Sigma }}_M$ sentences is called the diagram of the model M.

This can be seen as a coherence property between the semantic and the syntactic structures of the institution. By following the basic principle that a structure is rather defined by its homomorphisms (arrows) than by its objects, the semantic structure of an institution is given by its model homomorphisms. On the other hand, the syntactic structure of an(y concrete) institution is based upon its corresponding concept of atomic sentence.

In [57], it has been proposed that the concept of a diagram in stratified institutions should be transferred to the flattenings:

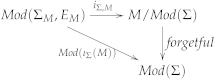
the diagrams in a stratified institution $\mathcal{S}$ are the diagrams in ${\mathcal{S}}^{♯}$ (or in ${\mathcal{S}}^{*}$).

Based on this principle, in [57], we have developed a general result on the existence of diagrams at the level of abstract stratified institutions that is applicable to a wide class of concrete situations. Its underlying idea is to combine the diagrams in the two components of a decomposition. However, again, this requires some nominal infrastructure. Let us present briefly how we can obtain diagrams in $\mathcal{S}$ when this comes with a decomposition as in Section 3.2.

• For each $\mathrm{\Sigma }$ model of $\mathcal{S}$, let us define ${\mathrm{\Sigma }}_0={\mathrm{\Phi }}^0\mathrm{\Sigma }$, ${\mathrm{\Sigma }}_1=\mathrm{\Phi }\mathrm{\Sigma }$, $M_0={\beta }_{\mathrm{\Sigma }}^{0}M$, $M_1={\tilde{\beta }}_{\mathrm{\Sigma }}M$. We also let ${\iota }_{{\mathrm{\Sigma }}_0}{M}_0:{\mathrm{\Sigma }}_0\to ({{\mathrm{\Sigma }}_0}_{M_0},E_{M_0})$ and (for each $i\in \left[\right[M\left]\right]$) ${\iota }_{{\mathrm{\Sigma }}_1}{M}_1^i:{\mathrm{\Sigma }}_1\to ({{\mathrm{\Sigma }}_1}_{M_1^i},E_{M_1^i})$ be the diagrams of $M_0$ and $M_1^i$, respectively.
• We assume a coherence property that in the examples holds naturally in the case of models constrained by common forms of sharing (such as $\mathcal{M}\mathcal{F}\mathcal{O}\mathcal{L},\mathcal{H}\mathcal{F}\mathcal{O}\mathcal{L}$, etc.): ${\iota }_{{\mathrm{\Sigma }}_1}{M}_1^i={\iota }_{{\mathrm{\Sigma }}_1}{M}_1^j$ for all $i,j\in \left[\right[M\left]\right]$.
• We further assume that

  $${\mathit{Sign}}^0\stackrel{{\mathrm{\Phi }}^0}{⟵}{\mathit{Sign}}^{\mathcal{S}}\stackrel{\mathrm{\Phi }}{⟶}{\mathit{Sign}}^{\mathcal{B}}$$

  is a product in $\mathbf{C}\mathbf{A}\mathbf{T}$. This is a rather easy condition in concrete applications, typical examples being given by $\mathcal{H}\mathcal{P}\mathcal{L}$ and $\mathcal{H}\mathcal{F}\mathcal{O}\mathcal{L}$.
• A final important assumption refers to each element $i\in \left[\right[M\left]\right]$ of the underlying stratification having a syntactic designation $n_{\mathrm{\Sigma },M}i\in N({\mathrm{\Sigma }}_M)$. This is required to satisfy some natural conditions (details in [57]).
• Then, we define the $\mathcal{S}$ signature morphism ${\iota }_{\mathrm{\Sigma }}M:\mathrm{\Sigma }\to {\mathrm{\Sigma }}_M$ by using the product property of $({\mathrm{\Phi }}^0,\mathrm{\Phi })$:

  $${\iota }_{\mathrm{\Sigma }}M=({\iota }_{{\mathrm{\Sigma }}_0}{M}_0,{\iota }_{{\mathrm{\Sigma }}_1}{M}_1).$$
• Furthermore, we let

  $$E_M={\alpha }_{{\mathrm{\Sigma }}_M}^0{E}_{M_0}\cup \bigcup _{i\in \left[\right[M\left]\right]}{@}_i({\alpha }_{{\mathrm{\Sigma }}_M}{E}_{M_1^i})$$

  where ${@}_i({\alpha }_{{\mathrm{\Sigma }}_M}{E}_{M_1^i})$ abbreviates $\{{@}_{n_{\mathrm{\Sigma },M}(i)}{\alpha }_{{\mathrm{\Sigma }}_M}\rho \mid \rho \in E_{M_1^i}\}$. This gives the diagram M in ${\mathcal{S}}^{*}$.
• In order to obtain the diagram of a model $(M,w)$ in ${\mathcal{S}}^{♯}$, it is enough to add the syntactic designation of w as a sentence to $E_M$.

Particular typical consequences of this general result are the existence of diagrams in hybrid logic institutions such as $\mathcal{H}\mathcal{P}\mathcal{L},\mathcal{H}\mathcal{F}\mathcal{O}\mathcal{L}$. The limitation of this result is represented by the general assumption on the availability of a nominals infrastructure. However, this seems to be an inherent limitation that has to do with the existence of diagrams; in other words, it is not a limitation of the way we have constructed the diagrams. This conclusion is supported toward the end of [57] by a proof showing that $\mathcal{M}\mathcal{P}\mathcal{L}$ and $\mathcal{M}\mathcal{F}\mathcal{O}\mathcal{L}$ do not admit institution theoretic diagrams.

3.7. Ultraproducts in Stratified Institutions

The method of ultraproducts is renowed as extremely powerful and pervading a lot of deep results in model theory [2,88]. For instance, model ultraproducts are instrumental in the non-standard analysis [4,5] as the hyperreals are constructed by this technique. Chief among the ultraproduct method concepts and results that have been lifted to abstract institution theory is a very general version of Łoś theorem obtained as a puzzle of preservation results [34,44]. Then, general compactness results have been obtained as a consequence of this. Furthermore, in [61], all these have been extended to the framework of modalised institutions. In [52], we took another step by generalising the developments of [61] to arbitrary stratified institutions. In what follows, we present the milestones of this development:

• For any filter F over a set I and for any family ${(M_i)}_{i\in I}$ of $\mathrm{\Sigma }$ models, its F-product is defined categorically as the co-limit $\mu$ of a diagram of projections:

  where for each $J\in F$, ${(p_{J,j}:M_J\to M_j)}_{j\in J}$ denotes a categorical product. This categorical approach on filtered products (called ultraproducts when F is an ultrafilter) has been used in various other categorical approaches to model theory such as [11,12,15,89], etc.
• The preservation of (the satisfaction of) a sentence $\rho$ by F-filtered products is defined as follows. For any $\mathrm{\Sigma }$ sentence $\rho$, we introduce the following notation:

  $$A_{\mu }(\rho )=\bigcup _{J\in F}\left[\left[{\mu }_J\right]\right]\bigcap _{j\in J}{\left[\left[p_{J,j}\right]\right]}^{-1}\left[[M_j,\rho ]\right].$$
  Let $\mathcal{F}$ be a class of filters. Then, $\rho$ is
  • Preserved by $\mathcal{F}$-products when $A_{\mu }(\rho )\subseteq \left[[M_F,\rho ]\right]$, and it is
  • Preserved by $\mathcal{F}$-factors when $\left[[M_F,\rho ]\right]\subseteq A_{\mu }(\rho )$,
  for all filters $F\in \mathcal{F}$ and all families of models ${(M_i)}_{i\in I}$. When the F-products are concrete, which means that they are preserved by the stratification—a very common situation in the applications—the stratified concept of preservation in $\mathcal{S}$ reduces to the ordinary institution theoretic concept of preservation in ${\mathcal{S}}^{♯}$.
• Then, we have developed a series of results expressing the invariance of preservation, corresponding to various connectives. In the case of the propositional connectives, this invariance can be reduced to the corresponding invariance in ordinary institutions, which are already established in [34,44]. In the case of the quantifiers, this cannot be completed, but the proofs are similar to those from the ordinary institution theoretic framework. More interesting are the invariance results for modalities and nominals, as they do not have a counterpart in ordinary institutions, with the presence of stratification playing a key role. However, this is hardly unexpected, since the connectives are relevant only when models have internal states.
• In the applications, in order to obtain a preservation result for a certain sentence, we invoke corresponding invariance results through an inductive process on the structure of the respective sentence. For the base case, i.e., for the atomic sentences, we may use the ordinary institution theoretic preservation of the so-called basic sentences [34,44] via a decomposition of the stratified institution. Or else, we may establish their preservation directly.
• Each of the invariance results discussed above depends on some specific technical conditions involving model reducts, frame and nominals extractions, the class $\mathcal{F}$ of filters, etc. All of them are rather mild in the applications.

With respect to the compactness consequences of these invariances of preservation results, which together give a Łoś-style theorem for abstract stratified institutions, both in the local and global flattening (i.e., ${\mathcal{S}}^{♯}$ and ${\mathcal{S}}^{*}$, respectively), we usually obtain the model compactness property. However, the entailment–theoretic compactness of the semantic consequence may be obtained only for ${\mathcal{S}}^{♯}$, as in ${\mathcal{S}}^{*}$ negation, disjunction, existential quantifiers, etc., usually connectives that are related to negation in one form or another, pose some problems.

3.8. Abstract Connectives and Elementary Homomorphisms

In the list of examples of stratified institutions, we have presented the example $\mathcal{C}\mathcal{O}\mathcal{N}$. We said that $\mathcal{C}\mathcal{O}\mathcal{N}$ may provide foundations for an abstract theory of connectives. Let us see how this works by following some theory developed in [51]. The main idea is that we think of a stratified institution $\mathcal{S}$ as having connectives when we can ‘extract’ them from $\mathcal{S}$. Technically, this means that there exists a functor $C:{\mathit{Sign}}^{\mathcal{S}}\to {\mathit{Sign}}^{\mathcal{CON}}$ and for each $\mathrm{\Sigma }\in |{\mathit{Sign}}^{\mathcal{S}}|$, a function ${\beta }_{\mathrm{\Sigma }}:|{\mathit{Mod}}^{\mathcal{S}}(\mathrm{\Sigma })|\to |{\mathit{Mod}}^{\mathcal{CON}}(C\mathrm{\Sigma })|$ natural in $\mathrm{\Sigma }$ such that

$$\mathit{Sen}=T_{\_}\circ C,{\left[\left[M\right]\right]}_{\mathrm{\Sigma }}^{\mathcal{S}}={\left[\left[{\beta }_{\mathrm{\Sigma }}M\right]\right]}_{C\mathrm{\Sigma }}^{\mathcal{CON}},M{\vDash }_{\mathrm{\Sigma }}^{\eta }\rho \mathrm{if} \mathrm{and} \mathrm{only} \mathrm{if}{\beta }_{\mathrm{\Sigma }}M{\vDash }_{C\mathrm{\Sigma }}^{\eta }\rho .$$

This means that any sentence of $\mathcal{S}$ is formed from connectives, each $\mathcal{S}$ model has an underlying connective algebra, and the satisfaction in $\mathcal{S}$ is given by evaluating the connective terms. In a more sophisticated terminology, $\mathcal{S}$ having connectives provides an example of morphism of stratified institutions.

$\mathcal{O}\mathcal{F}\mathcal{O}\mathcal{L}$ provides a good example of this situation by letting the null-ary connectives consist of the atoms, the unary connectives consist of negation and quantifiers, the binary connectives being $\wedge ,\vee ,\dots$, and that is all. Then, $\beta$ maps to corresponding sets of valuations.

One of the consequences of these conceptual developments is the possibility of having a stratified institution theoretic alternative to the concepts of elementary homomorphism that is based on quasi-representability or on diagrams, such as in [35,44]. Thus, we say that a model homomorphism $h:M\to N$ in a stratified institution $\mathcal{S}$ is elementary when for each sentence $\rho$ and each $\eta \in \left[\right[M\left]\right]$, we have that

$$M{\vDash }_{\mathrm{\Sigma }}^{\eta }\rho \mathrm{if} \mathrm{and} \mathrm{only} \mathrm{if}N{\vDash }_{\mathrm{\Sigma }}^{{\left[\left[h\right]\right]}_{\mathrm{\Sigma }}\eta }\rho .$$

The advantage of this concept of elementary homomorphism over the other ones from institution theory is that it does not depend on other properties that may be problematic in some cases. For instance, we have seen in Section 3.6 that diagrams are not always available especially in stratified contexts. So, in [51], there is a result that explains the common concept of elementary homomorphism in terms of stratified institution elementary homomorphism. Given a stratified institution with connectives, a $\mathrm{\Sigma }$-homomorphism $h:M\to N$ is elementary if and only if $\left[\right[h\left]\right]$ is a connective algebra homomorphism ${\beta }_{\mathrm{\Sigma }}M\to {\beta }_{\mathrm{\Sigma }}N$.

In [51], this result had been used for providing a method for establishing Tarski’s elementary chain/co-limit theorem for concrete model theories that can be captured as stratified institutions. This is one of the early model theoretic results in first-order logic [90] with manifold applications (these can be consulted in [2]), which has also received a proof in the abstract setting of arbitrary institutions in [35,44]. It says that the co-limit of a directed diagram of elementary homomorphisms consists of elementary homomorphisms, too. In the context of stratified institutions with connectives, this means that any co-limit of a directed diagram of elementary homomorphisms becomes mapped by the stratification to a co-limit in the category of connective algebra homomorphisms. Moreover, in [51], we can find examples on how this works in $\mathcal{M}\mathcal{P}\mathcal{L}$ and $\mathcal{O}\mathcal{F}\mathcal{O}\mathcal{L}$.

3.9. Foundations for Formal Verification of Reconfigurable Systems

In [56], the author employs stratified institutions with frame and nominals extraction (presented above in Section 3.4) (rebranded as ‘hybrid institutions’) as a general foundational framework for a formal verification methodology for reconfigurable systems. The envisaged methodology would thus constitute an alternative to the methodology implemented by the language H [68] based on the generic translation concept of [66]. While in the latter case, the verification process is exported to first-order logic, and the result of that is imported back to the source logic, in the former case, the verification process happens right in the respective stratified institution. However, both approaches share the same verification goal: that of reconfigurable systems.

The substance of [56] consists of the definition of a generic proof calculi applicable to a relevant class of stratified institutions with frame and nominals extraction, which is proved complete (apparently) with respect to the local satisfaction relation ${\vDash }^{♯}$. The method to prove completeness is Cohen’s forcing [6,7] adapted to abstract institutions [38].

3.10. Mathematical Morphology in Stratified Institutions

The mathematical morphology of [91,92] uses a pair of dual mappings between lattices called ‘dilation’ and ‘erosion’ in the context of some mathematical foundations for image analysis. In [53], the authors employ these concepts from mathematical morphology in order to derive pairs of dual connectives. This uses, for a given model M, the lattice on the quotient $\mathit{Sen}(\mathrm{\Sigma }){/}_{{\equiv }_M}$, where $\rho {\equiv }_M{\rho }^{\prime }$ when $\left[[M,\rho ]\right]=\left[[M,{\rho }^{\prime }]\right]$ and the order on $\mathit{Sen}(\mathrm{\Sigma }){/}_{{\equiv }_M}$ is given by $\rho {/}_{{\equiv }_M}\le {\rho }^{\prime }{/}_{{\equiv }_M}$ when $\left[[M,\rho ]\right]\subseteq \left[[M,{\rho }^{\prime }]\right]$. When the respective stratified institution has conjunctions and disjunctions, $(\mathit{Sen}(\mathrm{\Sigma }){/}_{{\equiv }_M},\le )$ is a lattice indeed. The authors provide a general abstract definition of ‘dilation’ and ‘erosion’ operators on sentences, $D_B\rho$ and $E_B\rho$, respectively, which are then extended as operations on $\mathit{Sen}(\mathrm{\Sigma }){/}_{{\equiv }_M}$. Instances of $D_B$ and $E_B$ include the universal and existential quantifications in $\mathcal{O}\mathcal{F}\mathcal{O}\mathcal{L}$ as well as the necessity and possibility in various modal logics. Moreover, the authors of [53] develop a general proof theory in stratified institutions based on abstract erosion and dilation operators, which is shown to be complete. Finally, ref. [53] offers some preliminary ideas regarding applications of this theory to qualitative spatial reasoning.

4. Many-Valued Truth Institution-Independent Model Theory

In standard institution theory, the satisfaction relation between models and sentences is considered to be binary, $M\vDash \rho$ either holds true or it does not. Many-valued institution theory considers a generalisation of ordinary institution theory where $M\vDash \rho$ is not necessarily binary. Such a generalisation can be achieved, and basic concepts such as semantic consequence, the Galois connection between syntax and semantics, internal logic, but also more advanced concepts such as filtered products, preservation, interpolation, definability, logic translation, etc. do “survive” it but in a subtler form. From a pure theoretical standpoint (there are also more practical motivations), this generalisation brings further clarifications to the complex network of causal relationships underlying model theory. This has to do with binary truth being a collapsed form of truth where many things happen somehow “by accident”. Much institution-independent model theory may be developed in the many-valued truth fashion.

4.1. $\mathcal{L}$-Institutions

The extension of the concept of institution from binary to many-valued truth may be achieved at several structural levels. The most primitive level is to consider a plain set of truth values, either in general or in some particular form. At higher levels, we may consider various order theoretic structures. Traditionally, the binary situation is treated as a Boolean algebra in order to support the common logical connectives such as $\wedge ,\vee ,\neg$, etc. and their semantics. The many-valued approach treats the structure of truth values rather axiomatically, so we can consider order theoretic structures of various degrees of complexity. At the end, the most constrained such structure is in fact the binary Boolean algebra.

Given a set L, called the space of the truth values, an L-institution

$$\mathcal{I}=\left({\mathit{Sign}}^{\mathcal{I}},{\mathit{Sen}}^{\mathcal{I}},{\mathit{Mod}}^{\mathcal{I}},{\vDash }^{\mathcal{I}}\right)$$

is like an ordinary institution with the only difference that the Satisfaction Relation is an indexed family of L-fuzzy relation, i.e., ${\vDash }_{\mathrm{\Sigma }}^{\mathcal{I}}:\left|{\mathit{Mod}}^{\mathcal{I}}(\mathrm{\Sigma })\right|\times {\mathit{Sen}}^{\mathcal{I}}(\mathrm{\Sigma })\to L$ for each $\mathrm{\Sigma }\in |{\mathit{Sign}}^{\mathcal{I}}|$. Then, the Satisfaction Condition obtains the following form: for each morphism $\phi :\mathrm{\Sigma }\to {\mathrm{\Sigma }}^{\prime }\in {\mathit{Sign}}^{\mathcal{I}}$,

$$(M^{\prime }{\vDash }_{{\mathrm{\Sigma }}^{\prime }}^{\mathcal{I}}{\mathit{Sen}}^{\mathcal{I}}(\phi )\rho )=({\mathit{Mod}}^{\mathcal{I}}(\phi )M^{\prime }{\vDash }_{\mathrm{\Sigma }}^{\mathcal{I}}\rho )$$

(9)

holds for each $M^{\prime }\in \left|{\mathit{Mod}}^{\mathcal{I}}({\mathrm{\Sigma }}^{\prime })\right|$ and $\rho \in {\mathit{Sen}}^{\mathcal{I}}(\mathrm{\Sigma })$. The Satisfaction Condition says that the truth degree is an invariant with respect to change of notation.

For $\mathcal{L}=(L,⩽)$ partial order, an $\mathcal{L}$-institution means just an L-institution. Evidently, the ordinary institutions are just $\mathcal{L}$-institutions for which $\mathcal{L}$ is the binary Boolean algebra. For this reason, in the context of the theory of $\mathcal{L}$-institutions, ordinary institutions may be refereed to as binary institutions. The step from classic binary institutions to many-valued institutions is hardly new; this idea had appeared already in the early age of institution theory in the form of the so-called ‘galleries’ of [93]. The ‘generalised institutions’ of [94] are very similar to $\mathcal{L}$-institutions; however, they introduce an additional monadic structure on the sentence functor meant to model substitution systems. A fully abstract treatment of many-valued semantics appears very early in [50]; however, it differs form the approach of $\mathcal{L}$-institutions in two quite important aspects. One is its single-signature feature. The other is the collapse of model theory modulo elementary equivalence, which makes it unusable for the development of a proper fully abstract many-valued model theory. In other words, Pavelka’s approach in [50] would correspond to an $\mathcal{L}$-institution that has only one signature $\mathrm{\Sigma }$ and also such that $\left|\mathit{Mod}(\mathrm{\Sigma })\right|\subseteq L^{\mathit{Sen}(\mathrm{\Sigma })}$.

Now, we present the following examples from [48,49,95] very briefly; for more details, the reader should study them from these publications.

• Propositional many-valued logic ($\mathcal{M}\mathcal{V}{\mathcal{L}}_0$) turns the institution of classical propositional logic (cf. [44]) into an $\mathcal{L}$-institution by adding * as a new propositional connective and by letting models represent valuations of the propositional symbols of the signatures into L. $\mathcal{L}$ is required to be a residuated lattice.
• First-order many-valued logic ($\mathcal{M}\mathcal{V}{\mathcal{L}}_1$) generalises the institution of classical first-order logic (cf. [18,25,44], etc.) in a way that resembles how $\mathcal{M}\mathcal{V}{\mathcal{L}}_0$ generalises the institution of classical propositional logic. For defining the satisfaction of quantified sentences, it is required that $\mathcal{L}$ is also complete.
• Temporal logic ($\mathcal{T}\mathcal{L}$). $\mathcal{L}$ is a fixed complete total order that models the ‘time’. In the propositional version, the models interpret each propositional symbol as a subset of L. We have the usual temporal logic connectives, and the truth value of $M\vDash \rho$ is the supremum of all the time moments for which $\rho$ holds in M at all moments of time before that.
• Fuzzy multi-algebras ($\mathcal{F}\mathcal{M}\mathcal{A}$). This $\mathcal{L}$-institution generalises the institution of multi-algebras [96,97,98] (used for specifying non-determinism) to many-valued truth. Its main idea is that models M interpret an algebraic operation $\sigma$ of arity n as an L-valued $(n+1)$-ary relation. Intuitively, $M_{\sigma }(x_1,\dots ,x_{n+1})$ is thought of as the truth degree of $\sigma (x_1,\dots ,x_n)=x_{n+1}$ in M.
• Abstract many-valued logic ($\mathcal{I}(\mathcal{L})$). This $\mathcal{L}$-institution is more a model theoretic framework rather than a logical system as such. In [48], it is shown that $\mathcal{M}\mathcal{V}{\mathcal{L}}_0$, $\mathcal{M}\mathcal{V}{\mathcal{L}}_1$, and $\mathcal{F}\mathcal{M}\mathcal{A}$ can be conservatively embedded in $\mathcal{I}(\mathcal{L})$, which means that their semantics may be substituted by the generic categorical one provided by $\mathcal{I}(\mathcal{L})$.

In the rest of this section, we present the main developments that have happened in the area of $\mathcal{L}$-institutions over the past decade or so. Our discussion includes the following aspects.

• A general ‘flattening’ of $\mathcal{L}$-institutions to ordinary institution.
• A concept of semantic consequence that is genuinely many-valued and represents the most conceptually refined reflection of the binary semantic consequence of ordinary institution theory to many-valued truth.
• Unlike in binary institution theory, in $\mathcal{L}$-institutions, the concept of theory is multifaceted. This is apparent especially when we consider closures of theories. This situation reflects also to concepts of consistency and compactness.
• We present the extension of the ordinary institution theoretic semantics of propositional and quantification connectives to $\mathcal{L}$-institutions, both in their consequence and model theoretic forms.
• We present a series of preservation (by filtered products) results that have been recently developed for $\mathcal{L}$-institutions. Consequences of these are general model compactness and initial semantics results.
• The graded concept of semantic consequence gives rise to a graded concept of interpolation specific to $\mathcal{L}$-institutions. We discuss this new concept and its further impact to the whole conceptual environment of interpolation, including (Beth) definability and Robinson consistency. We re-establish the causality relationships between interpolation and these in the many-valued context.

4.2. Flattening $\mathcal{L}$-Institutions to Binary Institutions

The general reduction of many-valued truth to binary truth advocated by the skeptics of many-valued truth can also be applied to $\mathcal{L}$-institutions. It works as follows. Given any $\mathcal{L}$-institution $\mathcal{I}=(\mathit{Sign},\mathit{Sen},\mathit{Mod},\vDash )$, we define the binary institution ${\mathcal{I}}^{♯}=({\mathit{Sign}}^{♯},{\mathit{Sen}}^{♯},{\mathit{Mod}}^{♯},{\vDash }^{♯})$:

• ${\mathit{Sign}}^{♯}=\mathit{Sign}$, ${\mathit{Mod}}^{♯}=\mathit{Mod}$;
• ${\mathit{Sen}}^{♯}(\mathrm{\Sigma })=\mathit{Sen}(\mathrm{\Sigma })\times L$;
• $M{\vDash }_{\mathrm{\Sigma }}^{♯}(\rho ,\kappa )$ if and only if $(M{\vDash }_{\mathrm{\Sigma }}\rho )⩾\kappa$.

This flattening idea has been present in several places in the fuzzy logic literature. For instance, in [99], our pairs $(\rho ,\kappa )$ are called ‘signed formulas’ and given the same interpretation as here.

The flattening of $\mathcal{L}$-institutions to binary institutions has the advantage of reducing things to a well-studied and matured framework and functions well in some aspects, but it falls short in several areas that involve some fine-grained aspects of multiple truth values. Thus, while the flattening ${\mathcal{S}}^{♯}$ of stratified institutions does not pose many limitations, the situation is different with the flattenings of $\mathcal{L}$-institutions.

4.3. The Graded Semantic Consequence

Given an $\mathcal{L}$ institution such that $\mathcal{L}$ is a complete meet-semilattice, for each $\mathrm{\Sigma }$-model M and each set E of $\mathrm{\Sigma }$-sentences, we define

$$(M{\vDash }_{\mathrm{\Sigma }}E)=\bigwedge \{M{\vDash }_{\mathrm{\Sigma }}\rho \mid \rho \in E\}.$$

(10)

Given an $\mathcal{L}$-institution, there are two ways to extend the satisfaction relation to a semantic consequence relation between sets of sentences and single sentences, both of them generalising the semantic consequence relation of binary institution theory.

(1)

The crisp semantic consequence, defined by $E\vDash e$ if and only if for each model M, $(M\vDash E)=1$ implies $(M\vDash e)=1$ (where 1 denotes the top element of $\mathcal{L}$).

(2)

The graded semantic consequence, defined by

$$(E{\vDash }_{\mathrm{\Sigma }}e)=\bigwedge \{(M{\vDash }_{\mathrm{\Sigma }}E)\Rightarrow (M{\vDash }_{\mathrm{\Sigma }}e)\mid M\in |\mathit{Mod}(\mathrm{\Sigma })\left|\right\}.$$

(11)

The graded semantic consequence is more subtle and more in the spirit of many-valued truth than the crisp one, although the definition of the latter requires more infrastructure on the space of the truth values, namely that $\mathcal{L}$ is a residuated lattice [100,101]. Hence, “⇒” of (11) represents the residuated implication operation. This difference in subtlety may be traced to the fact that while the crisp semantic consequence corresponds to the semantic consequence of the binary flattening ${\mathcal{I}}^{♯}$ of the $\mathcal{L}$-institution $\mathcal{I}$ (that $E\vDash e$ holds in $\mathcal{I}$ means $\{(\rho ,1)\mid \rho \in E\}\vDash (e,1)$ in ${\mathcal{I}}^{♯}$), the graded semantic consequence is a concept beyond ${\mathcal{I}}^{♯}$. The graded semantic consequence appears in a disguised form in [50] within the context of Pavelka’s theory of fuzzy consequence operators and in a form that is more explicitly similar to ours in [102] within the framework of ‘graded consequence relations’. However, both these semantic frameworks are less general than ours, in both of them models being in fact fuzzy theories.

One of the important properties of the semantic consequence in binary institution theory is that it satisfies the axioms of entailment systems. The graded semantic consequence enjoys the same property but for the following refined many-valued concept of entailment. This has been proved in a full form in [49]. In a restricted single signature framework, this has also been proved in [102].

Graded Entailment

Let $\mathcal{L}=(L,\le ,\ast )$ such that $(L,\le )$ is a complete meet-semilattice (with 1 denoting its upper bound) and ∗ is a binary operation on L. An $\mathcal{L}$-entailment system $(\mathit{Sign},\mathit{Sen},⊢)$ consists of a functor $\mathit{Sen}:\mathit{Sign}\to \mathbf{S}\mathbf{et}$ and a family $⊢={({⊢}_{\mathrm{\Sigma }}:\mathcal{P}\mathit{Sen}(\mathrm{\Sigma })\to \mathit{Sen}(\mathrm{\Sigma }))}_{\mathrm{\Sigma }\in \left|\mathit{Sign}\right|}$ such that the following axioms hold:

$\left\{\gamma \right\}{⊢}_{\mathrm{\Sigma }}\gamma =1$	reflexivity
$(E{⊢}_{\mathrm{\Sigma }}\gamma )\le (E^{\prime }{⊢}_{\mathrm{\Sigma }}\gamma )$ when $E\subseteq E^{\prime }$	monotonicity
$(E{⊢}_{\mathrm{\Sigma }}\mathrm{\Gamma })\ast (\mathrm{\Gamma }{⊢}_{\mathrm{\Sigma }}\rho )\le (E{⊢}_{\mathrm{\Sigma }}\rho )$ (where $(E⊢\mathrm{\Gamma })={\bigwedge }_{\gamma \in \mathrm{\Gamma }}(E⊢\gamma )$.)	transitivity
$(E{⊢}_{\mathrm{\Sigma }}\gamma )\le (\mathit{Sen}(\phi )E{⊢}_{{\mathrm{\Sigma }}^{\prime }}\mathit{Sen}(\phi )\gamma )$ for any sign. morphism $\phi :\mathrm{\Sigma }\to {\mathrm{\Sigma }}^{\prime }$	translation.

When $\mathcal{L}$ is just the binary Boolean algebra (with * being ∧), $\mathcal{L}$-entailment systems are just ordinary entailment systems [44,103]/$\pi$-institutions [104]. In the graded context, the binary entailment systems will also be called crisp entailment systems. Previous to [49], the idea of graded entailment has appeared in various different forms in works such as [50,94,102,105]; in [49], there is a brief analysis on the differences between these several variants, which are in fact rather slight. Depending on actual applications, graded entailments may be interpreted in various ways: as provability degree, as degree of confidence in proofs, or even as a(n inverse) measure for the complexity of a proof. Moreover, in [49], there are also temporal interpretations of graded proofs. An important technical aspect worth mentioning is the use of * rather than ∧ in the transitivity axiom; in [49], it is shown that this choice is necessary for accommodating the semantic interpretations of graded entailment.

The result of [49] that the graded semantic consequence in an $\mathcal{L}$-institution $\mathcal{I}$ yields an $\mathcal{L}$-entailment system—called the semantic entailment system of $\mathcal{I}$—seems to suggest that $\mathcal{L}$-entailment systems are more abstract/general than $\mathcal{L}$-institutions. However, at least when $\mathcal{L}$ is a complete residuated lattice, this is a wrong impression, because a result from [49] shows that each $\mathcal{L}$-entailment system determines an $\mathcal{L}$-institution whose semantic entailment is precisely the respective $\mathcal{L}$-entailment system.

4.4. Many-Valued Theories, Consistency and Compactness

In binary institution theory, a $\mathrm{\Sigma }$-theory is a set of $\mathrm{\Sigma }$-sentences. (However, in many works, including [18,44], etc., this is called ‘presentation’, the word ‘theory’ being used for ‘presentations’ that are closed under semantic consequence. This owes to the algebraic specification tradition which considers theories that are ‘presented’ by (finite) sets of sentences, these being in fact specification modules.) Any theory may be represented by its characteristic function $\mathit{Sen}(\mathrm{\Sigma })\to 2$, which for each sentence gives a truth value for its membership to the respective theory. This new perspective on theories is the basis for the generalisation of the concept of theory to many-valued truth. For any fixed set L and for any functor $\mathit{Sen}:\mathit{Sign}\to \mathbf{S}\mathbf{et}$, a Σ-theory is just a function $X:\mathit{Sen}(\mathrm{\Sigma })\to L$. When $\mathcal{L}=(L,\le ,\wedge )$ is a complete meet-semilattice, for any $\mathrm{\Sigma }$-theory $X:\mathit{Sen}(\mathrm{\Sigma })\to L$ and for any $E\subseteq \mathit{Sen}(\mathrm{\Sigma })$, we denote

$$X(E)=\bigwedge \{X(e)\mid e\in E\}.$$

(12)

Note that a theory in an $\mathcal{L}$-institution $\mathcal{I}$ corresponds exactly to a theory in its binary flattening ${\mathcal{I}}^{♯}$ by representing any function $X:\mathit{Sen}(\mathrm{\Sigma })\to L$ as the set $\{(\rho ,X(\rho ))\mid \rho \in \mathit{Sen}(\mathrm{\Sigma }),X(\rho )\ne 0\}$ (0 denotes the bottom element of $\mathcal{L}$).

The concept of Galois connection between syntax and semantics in binary institution theory admits a natural extension to many-valued truth. Let $\mathcal{L}$ be a complete meet-semilattice. In any $\mathcal{L}$-institution:

• For any $\mathrm{\Sigma }$-model M, we let the theory $M^{*}:\mathit{Sen}(\mathrm{\Sigma })\to L$ such that $M^{*}(\rho )=(M\vDash \rho )$. For any class of models $\mathcal{M}\subseteq |\mathit{Mod}(\mathrm{\Sigma })|$, we let ${\mathcal{M}}^{*}={\bigwedge }_{M\in \mathcal{M}}{M}^{*}$.
• For any $\mathrm{\Sigma }$-theory $X:\mathit{Sen}(\mathrm{\Sigma })\to L$ we let $X^{*}=\{M\in |\mathit{Mod}(\mathrm{\Sigma })|\mid X\le M^{*}\}$.

For each signature $\mathrm{\Sigma }$, the mappings ${(\_)}^{*}$ defined above represent a Galois connection between $(\mathcal{P}|\mathit{Mod}(\mathrm{\Sigma })|,\supseteq )$ and $(L^{\mathit{Sen}(\mathrm{\Sigma })},\le )$.

4.4.1. Closure Systems

Concepts of closures of theories can be regarded as axiomatic treatments of consequence relations. This approach originates from Tarski’s work [106] and later on was applied by Pavelka [50] to many-valued theories. The following definition from [49] extends the latter to the multi-signature framework. Given a partial order $\mathcal{L}=(L,\le )$, an $\mathcal{L}$-closure system is a tuple $(\mathit{Sign},\mathit{Sen},\mathcal{C})$ where

–

$\mathit{Sen}:\mathit{Sign}\to \mathbf{S}\mathbf{et}$ is a functor, and

–

$\mathcal{C}$ is a $\mathit{Sign}$-indexed family of functions ${\mathcal{C}}_{\mathrm{\Sigma }}:L^{\mathit{Sen}(\mathrm{\Sigma })}\to L^{\mathit{Sen}(\mathrm{\Sigma })}$ satisfying the following axioms (for $\phi :\mathrm{\Sigma }\to {\mathrm{\Sigma }}^{\prime }$ any signature morphism):

$\begin{array}{cc}X\le {\mathcal{C}}_{\mathrm{\Sigma }}X\mathrm{for}\mathrm{each}X\hfill & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}C\text{-}reflexivity\\ {\mathcal{C}}_{\mathrm{\Sigma }}X\le {\mathcal{C}}_{\mathrm{\Sigma }}Y\mathrm{when}X\le Y\hfill & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}C\text{-}monotonicity\\ {\mathcal{C}}_{\mathrm{\Sigma }}({\mathcal{C}}_{\mathrm{\Sigma }}X)={\mathcal{C}}_{\mathrm{\Sigma }}X\hfill & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}C\text{-}transitivity\\ {\mathcal{C}}_{\mathrm{\Sigma }}(\mathit{Sen}(\phi );X^{\prime })\le \mathit{Sen}(\phi );{\mathcal{C}}_{{\mathrm{\Sigma }}^{\prime }}(X^{\prime })\hfill & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}C\text{-}translation\end{array}$

In the binary framework, there is a straightforward equivalence between the concepts of entailment system and closure system: $E{⊢}_{\mathrm{\Sigma }}e\mathrm{if} \mathrm{and} \mathrm{only} \mathrm{if}e\in {\mathcal{C}}_{\mathrm{\Sigma }}E$. However, in the many-valued framework, the relationship between the two concepts is much more interesting. Let us present two of them from [49].

• Provided some conditions on $\mathcal{L}$ are fulfilled, the following closure applies to any graded entailment system. Let $\mathcal{L}=(L,\le ,\ast )$ be a complete meet-semilattice with a binary operation ∗ and let $(\mathit{Sign},\mathit{Sen}⊢)$ be an $\mathcal{L}$-entailment system. The following definition draws inspiration from Goguen’s many-valued interpretation of Modus Ponens [107]. A theory $X:\mathit{Sen}(\mathrm{\Sigma })\to L$ is weakly closed with respect to the entailment system when for each entailment $E{⊢}_{\mathrm{\Sigma }}\rho$,

  $$X(E)\ast (E⊢\rho )\le X(\rho ).$$
  If ∗ is increasing monotone, then in [49], we have proved that the weakly closed theories are closed under arbitrary meets. This allows for the following definition: for any theory X, let $X^{\circ }$, called the weak closure of X, denote the least weakly closed theory greater than X. In [49], we have also proved that the weak closure ${(\_)}^{\circ }$ defines an $\mathcal{L}$-closure system.
• The second closure system on many-valued theories has a semantic nature, so its basic framework is now stronger than in the case of the previous closure system. Note that in any $\mathcal{L}$-institution, the Galois connection between $(\mathcal{P}|\mathit{Mod}(\mathrm{\Sigma })|,\supseteq )$ and ($L^{\mathit{Sen}(\mathrm{\Sigma })},\le$) determines an $\mathcal{L}$-closure system $(\mathit{Sign},\mathit{Sen},{(\_)}^{**})$. This allows for the following definition. In any $\mathcal{L}$-institution, a $\mathrm{\Sigma }$-theory is strongly closed when $X=X^{**}$. Moreover, $X^{**}$ is called the strong closure of X. The relationship between the two closure systems has been established in [49] as follows. When $\mathcal{L}$ is a complete residuated lattice, in any $\mathcal{L}$-institution and for any $\mathrm{\Sigma }$-theory X, if $X^{\circ }$ denotes its weak closure with respect to the semantic $\mathcal{L}$-entailment system, then $X^{\circ }\le X^{**}$.

4.4.2. Consistency

The following is a generalisation of the concept of consistent theory from binary institution theory to $\mathcal{L}$-institutions. According to [49], in any $\mathcal{L}$-institution, a $\mathrm{\Sigma }$-theory T is consistent when there exists a $\mathrm{\Sigma }$-model M such that $T⩽M^{*}$. E is consistent when there exists $\kappa >0$ such that E is $\kappa$-consistent; otherwise, it is inconsistent. Note that the concept of $\kappa$-consistency can be derived from the corresponding consistency concept from binary institution theory by considering the binary flattening of the respective $\mathcal{L}$-institution.

Now, we introduce another concept of consistency that is relative to a fixed truth value. First, we prepare some notations. For any truth value $\kappa \in L$, let $T_{\kappa }$ denote the constant theory defined by $T_{\kappa }\rho =\kappa$ for each sentence $\rho$. For any $\mathrm{\Sigma }$-theory T and $\mathrm{\Gamma }\subseteq \mathit{Sen}(\mathrm{\Sigma })$, the theory $T|\mathrm{\Gamma }$ is defined for each $\rho \in \mathit{Sen}(\mathrm{\Sigma })$ by

$$(T|\mathrm{\Gamma })\rho =\left\{\begin{array}{cc}T\rho ,\hfill & \rho \in \mathrm{\Gamma }\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

In any $\mathcal{L}$-institution, for any truth value $\kappa$, a set E of $\mathrm{\Sigma }$-sentences is κ-consistent when $T_{\kappa }|E$ is consistent. Note that this concept can also be reduced to binary consistency since E is $\kappa$-consistent if and only if $(E,\kappa )=\{(e,\kappa )\mid e\in E\}$ is consistent in the binary flattening of the respective $\mathcal{L}$-institution. Note also that in the binary case, both concepts of consistency defined above collapse to the same concept.

4.4.3. Compactness

Compactness can be thought both in semantic and consequence theoretic terms. This is what happens in every logic, and it extends also to many-valued truth.

• An $\mathcal{L}$-institution $\mathcal{I}$ is m-compact when its binary flattening ${\mathcal{I}}^{♯}$ is m-compact. This means that for each $\mathrm{\Sigma }$-theory T, if $T|\mathrm{\Gamma }$ is consistent for each finite $\mathrm{\Gamma }\subseteq \mathit{Sen}(\mathrm{\Sigma })$, then T is consistent, too. This concept of compactness involves potentially all truth values. The following concept of compactness refers to an arbitrarily fixed truth value. In an $\mathcal{L}$-institution, let $\kappa \in L$ be any truth value. Then, the $\mathcal{L}$-institution is κ-m-compact when each set E of $\mathrm{\Sigma }$-sentences is $\kappa$-consistent if $E_0$ is $\kappa$-consistent for each finite $E_0\subseteq E$. Whilst in the binary case, the two concepts of compactness defined above collapse to the same concept, this is not the case in a proper many-valued context. However, in [49], we have established that the former is stronger than the latter: any m-compact $\mathcal{L}$-institution is $\kappa$-m-compact for each truth value $\kappa$.
• An $\mathcal{L}$-entailment system $(\mathit{Sign},\mathit{Sen},⊢)$ is compact when for any entailment $E{⊢}_{\mathrm{\Sigma }}\gamma$, we have

  $$E⊢\gamma =\bigvee \{E_0⊢\gamma \mid E_0\mathrm{finite}\subseteq E\}$$
  The following characterisation from [49] brings closer to something that sounds more familiar. In any compact $\mathcal{L}$-entailment system $(\mathit{Sign},\mathit{Sen},⊢)$ such that the meet operation ∧ is join-continuous, for any finite $\kappa \in L$, if $\kappa \le (E⊢\gamma )$, then there exists finite $E_0\subseteq E$ such that $\kappa \le (E_0⊢\gamma )$.

4.5. The Logic of $\mathcal{L}$-Institutions

Many-valued logic in the institution theoretic framework can be approached at two different levels, namely that of consequence ($\mathcal{L}$-entailment systems) and that of semantics ($\mathcal{L}$-institutions). The former is of course more abstract than the latter, but the relationship between them is non-trivial. All these have been addressed in [49] as follows.

4.5.1. Entailment Theoretic Connectives

In an $\mathcal{L}$-entailment system $(\mathit{Sign},\mathit{Sen},⊢)$, a $\mathrm{\Sigma }$-sentence $\rho$ is

• A conjunction of sentences ${\rho }_1$ and ${\rho }_2$ when for any set of sentences E,

  $$E⊢\rho =(E⊢{\rho }_1)\wedge (E⊢{\rho }_2);$$
• A residual conjunction of sentences ${\rho }_1$ and ${\rho }_2$ when for any set of sentences E,

  $$E⊢\rho =(E⊢{\rho }_1)\ast (E⊢{\rho }_2);$$
• An implication of sentences ${\rho }_1$ and ${\rho }_2$ when for any set of sentences E,

  $$E⊢\rho =E\cup \left\{{\rho }_1\right\}⊢{\rho }_2;$$
• A disjunction of sentences ${\rho }_1$ and ${\rho }_2$ when $\mathcal{L}$ has joins and for any set of sentences E,

  $$E⊢\rho =(E⊢{\rho }_1)\vee (E⊢{\rho }_2);$$
• A negation of the sentence ${\rho }^{\prime }$ when for any sentence e,

  $$\{\rho ,{\rho }^{\prime }\}⊢e=1;$$
• A universal χ-quantification of a ${\mathrm{\Sigma }}^{\prime }$-sentence ${\rho }^{\prime }$ for $\chi :\mathrm{\Sigma }\to {\mathrm{\Sigma }}^{\prime }$ signature morphism when for any set of $\mathrm{\Sigma }$-sentences E

  $$E{⊢}_{\mathrm{\Sigma }}\rho =\chi (E){⊢}_{{\mathrm{\Sigma }}^{\prime }}{\rho }^{\prime };$$
• An existential χ-quantification of a ${\mathrm{\Sigma }}^{\prime }$-sentence ${\rho }^{\prime }$ for $\chi :\mathrm{\Sigma }\to {\mathrm{\Sigma }}^{\prime }$ signature morphism when for any $\mathrm{\Sigma }$-sentence e

  $$\rho {⊢}_{\mathrm{\Sigma }}e={\rho }^{\prime }{⊢}_{{\mathrm{\Sigma }}^{\prime }}\chi (e).$$

These definitions can be extended at the level of the $\mathcal{L}$-entailment system. For instance, we say that the $\mathcal{L}$-entailment system has conjunctions when any two $\mathrm{\Sigma }$-sentences have a conjunction and similarly for the other connectives.

When $\mathcal{L}$ is the binary Boolean algebra, the above definitions yield the usual entailment theoretic connectives from the institution theory literature (e.g., [108]). In binary logic, the inequalities that are implicit in the equation defining the entailment theoretic implication are known as Modus Ponens (≤) and the Deduction Theorem (≥). This terminology can be extended to $\mathcal{L}$-entailment systems.

As in the binary situation, we can consider the least entailment system that “contains” a given entailment system and that has some of the connectives defined above. This is supported by the following result from [49]: any intersection of entailment systems (that share the same sentence functor) is an entailment system. Moreover, the property of having a certain connective is invariant with respect to such intersections.

4.5.2. Model Theoretic Connectives

The many-valued semantic connectives mimic those defined for binary institutions [30,34,44,108], etc., but now, their interpretation is in a many-valued truth context. A $\mathrm{\Sigma }$-sentence $\rho$ is an $\mathcal{L}$-institution that is

• A semantic conjunction of sentences ${\rho }_1$ and ${\rho }_2$ when $\mathcal{L}$ has meets and for each $\mathrm{\Sigma }$-model M,

  $$(M\vDash \rho )=(M\vDash {\rho }_1)\wedge (M\vDash {\rho }_2);$$
• A semantic residual conjunction of sentences ${\rho }_1$ and ${\rho }_2$ when $\mathcal{L}$ is a residuated lattice and for each $\mathrm{\Sigma }$-model M,

  $$(M\vDash \rho )=(M\vDash {\rho }_1)\ast (M\vDash {\rho }_2);$$
• An semantic implication of sentences ${\rho }_1$ and ${\rho }_2$ when $\mathcal{L}$ is a residuated lattice and for each $\mathrm{\Sigma }$-model M,

  $$(M\vDash \rho )=(M\vDash {\rho }_1)\Rightarrow (M\vDash {\rho }_2);$$
• A semantic disjunction of sentences ${\rho }_1$ and ${\rho }_2$ when $\mathcal{L}$ has joins and for each $\mathrm{\Sigma }$-model M,

  $$(M\vDash \rho )=(M\vDash {\rho }_1)\vee (M\vDash {\rho }_2);$$
• A semantic negation of a sentence ${\rho }^{\prime }$ when $\mathcal{L}$ is a residuated lattice for each $\mathrm{\Sigma }$-model M,

  $$(M\vDash {\rho }^{\prime })=(M\vDash \rho )\Rightarrow 0;$$
• A semantic universal χ-quantification of a ${\mathrm{\Sigma }}^{\prime }$-sentence ${\rho }^{\prime }$ for $\chi :\mathrm{\Sigma }\to {\mathrm{\Sigma }}^{\prime }$ signature morphism when $\mathcal{L}$ is a complete meet-semilattice and for each $\mathrm{\Sigma }$-model M

  $$(M{\vDash }_{\mathrm{\Sigma }}\rho )=\bigwedge \{M^{\prime }{\vDash }_{{\mathrm{\Sigma }}^{\prime }}{\rho }^{\prime }\mid \mathit{Mod}(\chi )M^{\prime }=M\};$$
• An semantic existential χ-quantification of a ${\mathrm{\Sigma }}^{\prime }$-sentence ${\rho }^{\prime }$ for $\chi :\mathrm{\Sigma }\to {\mathrm{\Sigma }}^{\prime }$ signature morphism when $\mathcal{L}$ is a complete join-semilattice and for each $\mathrm{\Sigma }$-model M

  $$(M{\vDash }_{\mathrm{\Sigma }}\rho )=\bigvee \{M^{\prime }{\vDash }_{{\mathrm{\Sigma }}^{\prime }}{\rho }^{\prime }\mid \mathit{Mod}(\chi )M^{\prime }=M\}.$$

These definitions can be extended at the level of the respective $\mathcal{L}$-institution. For instance, we say that the $\mathcal{L}$-institution has conjunctions when any two $\mathrm{\Sigma }$-sentences have a conjunction, etc.

The semantic connectives represent yet another situation when the binary flattening diverges from the respective $\mathcal{L}$-institution. In general, it is not possible to establish a general causality relationship between the semantic connectives in the $\mathcal{L}$-institution and in its binary flattening.

4.5.3. Model Theoretic versus Entailment Theoretic Connectives

Given an $\mathcal{L}$-institution $\mathcal{I}$, when $\mathcal{L}$ is a complete residuated lattice, we thus have two different definitions for each connective: one in terms of satisfaction by models and another one in terms of the semantic $\mathcal{L}$-entailment system of $\mathcal{I}$. It is important to establish the relationship between these two in order to be able to have an entailment-based calculus for the semantic consequence.

Consider the semantic $\mathcal{L}$-entailment system of an $\mathcal{L}$-institution such that $\mathcal{L}$ is a complete residuated lattice. Let $\rho$ be a $\mathrm{\Sigma }$-sentence and $\phi :\mathrm{\Sigma }\to {\mathrm{\Sigma }}^{\prime }$ be a signature morphism. Then,

• $\rho$ is the entailment theoretic conjunction of ${\rho }_1$ and ${\rho }_2$ if it is the semantic conjunction of ${\rho }_1$ and ${\rho }_2$.
• $\rho$ is the entailment theoretic universal/existential $\chi$-quantification of ${\rho }^{\prime }$ if it is its semantic universal/existential $\chi$-quantification.

Let us further assume that $\mathcal{L}$ is a Heyting algebra. Then,

3.

$\rho$ is the entailment theoretic implication of ${\rho }_1$ and ${\rho }_2$ if it is the semantic implication of ${\rho }_1$ and ${\rho }_2$.

4.

$\rho$ is the entailment theoretic negation of ${\rho }^{\prime }$ if it is its semantic negation.

Let us further assume that $\mathcal{L}$ is a completely distributive Boolean algebra. Then

5.

$\rho$ is the entailment theoretic disjunction of ${\rho }_1$ and ${\rho }_2$ if it is the semantic disjunction of ${\rho }_1$ and ${\rho }_2$.

4.6. Preservation and Consequences

In [95], there is a development of a body of preservation results in the same style as had been conducted for ordinary institutions in [34] or for stratified institutions in [52]. The milestones of this development are as follows:

• The concept of a filtered product of models is the categorical one as discussed in Section 3.7 in the context of stratified institutions.
• The preservation of (the satisfaction of) a sentence $\rho$ by filtered products/factors has been defined in [95] as follows. In any $\mathcal{L}$-institution, let $\mathrm{\Sigma }$ be any signature and let e be any $\mathrm{\Sigma }$-sentence. In addition, let $\mathcal{F}$ be any class of filters and $\kappa$ be any value in $\mathcal{L}$. Then,

  –

  e is κ-preserved by $\mathcal{F}$-products when for each F-product ${({\mu }_J:M_J\to M_F)}_{J\in F}$ (where $F\in \mathcal{F}$ is a filter over I)

  $$\{i\in I\mid (M_i\vDash e)⩾\kappa \}\in F\mathrm{implies}(M_F\vDash e)⩾\kappa ;$$

  –

  e is κ-preserved by $\mathcal{F}$-factors when for each F-product as above we have the reverse implication to the above.

  As a matter of terminology, when $\mathcal{F}$ is the class of all ultrafilters, we rather say directly “$\kappa$-preserved by ultraproducts/ultrafactors”. When $\mathcal{F}$ is the class of all singleton filters, we rather say “$\kappa$-preserved by direct products/factors”. In addition, when we do not specify the truth value $\kappa$ and we just say “preserved by $\mathcal{F}$-products/factors”, we mean that the sentence is $\kappa$-preserved for all truth values $\kappa$.
  Note that whilst $\kappa$-preservation represents just a rephrasing of the preservation concepts from binary institution theory because “$\rho$ is $\kappa$-preserved by…” is technically the same with “$(\rho ,\kappa )$ is preserved by…” in the binary flattening, this is not the case for the preservation for all truth values. In other words “$\rho$ is preserved by…” in an $\mathcal{L}$-institution cannot be reduced to preservation in its binary flattening of a single sentence.
• The results in [95] that express the invariance of preservation with respect to connectives are restricted to

  –

  Invariance of preservation by $\mathcal{F}$-products under ∧ and quantifications;

  –

  Invariance of preservation by $\mathcal{F}$-factors under $\wedge ,\vee ,\ast$ and quantifications; and

  –

  $\rho \Rightarrow {\rho }^{\prime }$ is preserved by $\mathcal{F}$-products when $\rho$ is preserved by $\mathcal{F}$-factors and ${\rho }^{\prime }$ is preserved by $\mathcal{F}$-products.

  Each of these results is subject to some specific conditions of various intensities of a general nature regarding $\mathcal{L}$, model reducts, $\mathcal{F}$, etc. All of them are manageable in concrete applications.
• As in the case of ordinary or stratified concrete institutions, when the sentences are constructed by iterative applications of connectives, in order to obtain their preservation, we invoke corresponding invariance results through an inductive process. However, in general, because the above-mentioned invariance results are less than in the binary truth case, it may happen that not all sentences of a respective $\mathcal{L}$-institution can be reached in this way. However, even under this less favourable situation, important classes of sentences are preserved by filtered products and factores. According to [95], these include an extended class of general Horn sentences.
• In this iterative process, the base cases are taken care of by corresponding preservation results for basic sentences in $\mathcal{L}$-institution theoretic sense as introduced in [95] as a generalisation of the ordinary concept of basic sentence from [34,44].

In [95], two main consequences of these preservation results have been derived.

• Initial semantics for a general class of Horn sentences.
• Model compactness for an extended general class of Horn sentences that do not necessarily admit initial semantics.

The former result involves also preservation by ‘sub-models’, which is a concept that is taken care of by the inclusion systems of [44,65], etc. (Such involvement of inclusion systems is common to all institution–theoretic approaches to quasi-varieties ([44]).)

For all this general theory, $\mathcal{F}\mathcal{M}\mathcal{A}$ presents itself as a special case when some general results cannot always be applied due to a lack of basic sentences. However, in [95], it is shown how an invariance of preservation results can still be used to obtain the preservation by filtered products for a relevant class of $\mathcal{F}\mathcal{M}\mathcal{A}$ sentences and consequently a model compactness result for those.

4.7. Around Graded Interpolation

In [109], the author developed a study of interpolation in the graded consequence framework. Envisaged applications include various forms of approximate reasoning. The starting point of this study is the extension of the classical concept of interpolation from the classical binary to the many-valued graded context. In any $\mathcal{L}$-entailment system, given a commutative square of signature morphisms

and finite sets $E_1\subseteq \mathit{Sen}({\mathrm{\Sigma }}_1)$ and $E_2\subseteq \mathit{Sen}({\mathrm{\Sigma }}_2)$, we say that a finite set $E\subseteq \mathit{Sen}(\mathrm{\Sigma })$ is a Craig interpolant of $E_1$ and $E_2$ when

$${\theta }_1{E}_1⊢{\theta }_2{E}_2\le (E_1⊢{\phi }_{1}E)\ast ({\phi }_{2}E⊢E_2).$$

(13)

When interpolants exist for all $E_1$, $E_2$, the respective commutative square of signature morphisms is called a Craig interpolation square (abbr. Ci square). When $\mathcal{L}$ is a residuated lattice, the concepts introduced in this definition extend also to $\mathcal{L}$-institutions by considering the graded semantic entailment system.

In [109], there are some proper examples of the graded interpolation concept, proof theoretic as well as model theoretic. Some of the examples suggest that graded interpolation is much more subtle than the crips (binary truth) interpolation, as there are natural situations when crisp interpolation non-problems may be good graded interpolation problems.

Craig–Robinson interpolation [110] is an extended version of common (Craig) interpolation, this extension being especially relevant in computing science applications [44,65,70,83] but not only. In the binary case, under the presence of implication, the two versions of interpolation can be established as equivalent (an institution-independent proof can be found in [44]). In [109], this has been extended to graded interpolation under the assumption that $\mathcal{L}$ is a Heyting algebra and only for the graded semantic consequence relation in $\mathcal{L}$-institutions.

Traditionally, model theoretic interpolation is causally related to Robinson consistency [2,111,112] and Beth definability [2,113]. These causalities have also been established in the abstract institution theoretic setting in [30,43,44]. Moreover, in [109], they have also been recovered at the many-valued truth level of $\mathcal{L}$-institutions. However, that enterprise required a significant conceptual and mathematical effort that we will briefly and rather informally review in what follows.

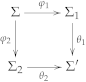
4.7.1. Graded Interpolation versus Many-Valued Robinson Consistency

Let us first have a look at the binary institution theoretic version of Robinson consistency (abbr. Rc). In an institution, a commutative square of signature morphisms such as below

is a Robinson consistency (Rc) square when any finite sets $E_i$ of ${\mathrm{\Sigma }}_i$-sentences, $i=1,2$, with ‘inter-consistent reducts’ (i.e., $\{\rho \in \mathit{Sen}(\mathrm{\Sigma })\mid E_1\vDash {\phi }_1\rho \}\cup \{\rho \in \mathit{Sen}(\mathrm{\Sigma })\mid E_2\vDash {\phi }_2\rho \}$ has a model) has ‘inter-consistent ${\mathrm{\Sigma }}^{\prime }$-translations’ (i.e., ${\theta }_1{E}_1\cup {\theta }_2{E}_2$ has a model).

The many-valued version of this is based on a many-valued concept of ‘inter-consistency’ which is relative to arbitrary truth values and, very importantly, the two truth values of the inter-consistency of the reducts and of the translations, respectively, are in general not necessarily equal. Then, we obtain the expected bi-directional causality between Rc and a somehow stronger version of Ci. There are many aspects underlying this result that deserve mention.

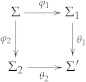
• As expected, both directions rely on the respective $\mathcal{L}$-institution having conjunctions and negations.
• In the case of the implication of Ci from Rc, an additional compactness condition is required. This is different from the compactness concepts we discussed above, but a relationship with those is established at the general level, which also applies well in the concrete cases.
• Both directions require some relationships between the truth values of the two inter-consistencies, the two relationships being somehow dual. They also have an intersection such that one truth value determines uniquely the other one, which is relevant for the formulation of the causality relationship between Rc and Ci when formulated as an equivalence.

4.7.2. Graded Definability by Graded Interpolation

Both in the concrete classical case and in the institution theoretic context, interpolation constitutes a principal cause for the definability property, i.e., that implicitly implies explicit definability. In fact, in [44], it has been revealed that interpolation in the Craig–Robinson form is what is needed in order to establish definability. In this way, we can dispense with implications, and while implications plus Ci obtain Craig–Robinson interpolation, there are important situations when we have the latter in the absence of implications, such as in many-sorted Horn clause logics (cf. [44]).

In [109], we have extended both the implicit and the explicit definabilities from the their binary version of [40,44] to many-valued truth as follows.

• In any $\mathcal{L}$-entailment system, for any $\kappa \in L$, a signature morphism $\phi :\mathrm{\Sigma }\to {\mathrm{\Sigma }}^{\prime }$ is defined κ-implicitly by a set $E^{\prime }\subseteq \mathit{Sen}({\mathrm{\Sigma }}^{\prime })$ when for any diagram of pushout squares such as below

  (14)

  and for any ${\mathrm{\Sigma }}_1^{\prime }$-sentence $\rho$, we have that

  $$u({\theta }^{\prime }{E}^{\prime })\cup v({\theta }^{\prime }{E}^{\prime })\cup u\rho ⊢v\rho \ge \kappa .$$
• In any $\mathcal{L}$-entailment system, for each $\kappa \in L$, a signature morphism $\phi :\mathrm{\Sigma }\to {\mathrm{\Sigma }}^{\prime }$ is κ-explicitly defined by a set of sentences $E^{\prime }\subseteq \mathit{Sen}({\mathrm{\Sigma }}^{\prime })$ when for each pushout square of signature morphisms such as

  (15)

  and each $\rho \in \mathit{Sen}({\mathrm{\Sigma }}_1^{\prime })$, there exists a finite set of sentences $E_{\rho }\subseteq \mathit{Sen}({\mathrm{\Sigma }}_1)$ such that

  $$({\theta }^{\prime }{E}^{\prime }\cup \rho ⊢{\phi }_1{E}_{\rho })\ast ({\theta }^{\prime }{E}^{\prime }\cup {\phi }_1{E}_{\rho }⊢\rho )\ge \kappa .$$

The main result of this development is a theorem that generalises the binary truth result of [40]. It says that in any $\mathcal{L}$-institution with a form of model amalgamation and which enjoys Craig–Robinson interpolation (with respect to designated classes of signature morphisms), a signature morphism is defined $\kappa$-explicitly when it is defined ℓ-implicitly provided the truth values $\kappa$ and ℓ are related by a condition similar to one of the conditions underlying the implication of Rc from Ci.

5. Conclusions

Standard institutional model theory has undergone a high level of development as partially shown in [44]. On the other hand, although non-classical institutional model theory, in its stratified and $\mathcal{L}$-institution forms, has advanced significantly over the past decade, it still lags behind the standard version. This is because of two main factors: time scale and mathematical difficulty. While standard institutional model theory has been developed over approximately four decades, the non-classical version is much younger. Then, of course, the latter is mathematically more difficult than the former; it is enough only to compare the basic definition in order to obtain an understanding of this. However, we have already seen that many non-classical developments may benefit from classical ones. At the same time, non-classical institution model theory has aspects that cannot be related to classical developments. All these mean that a lot of interesting theoretical problems await in non-classical institutional model theory, and we hope that in the next decade or so, many of them will be addressed.

In addition, there is something to be addressed that is at least as important as the theoretical problems: namely, to find new relevant applications. For instance, due to the highly abstract nature of this approach, which goes hand-in-hand with the axiomatic method, it has a strong potential to accomodate a wide class of old and new formalisms especially from computing science. However, all these require a thorough exploration.