On Periods of Interval Exchange Transformations

Abstract

In this paper, we study the periods of interval exchange transformations. First, we characterize the periods of interval exchange transformations with one discontinuity. In particular, we prove that there is no forcing between periods of maps with two branches of continuity. This characterization is a partial solution to a problem by Misiurewicz. In particular, a periodic structure is not possible for a family of the maps with one point of discontinuity in which the monotonicity changes. Second, we study a similar problem for interval exchange transformations with two discontinuities. Here we classify these maps in several classes such that two maps in the same class have the same periods. Finally, we study the set of periods for two categories, obtaining partial results that prove that the characterization of the periods in each class is not an easy problem.

1. Introduction and Basic Results

This paper deals with periods of maps called interval exchange transformations. Given a map $f:X\to X$ on a space X, as usual $f^0=\mathrm{Id}$, and for any integer $m\in \mathbb{N}=\{1,2,3,\cdots \}$ we set $f^1=f$, $f^m=f\circ f^{m-1}$. We say that $x\in X$ is periodic if there is $m\in \mathbb{N}$ such that $f^m\left(x\right)=x$ and $f^i\left(x\right)\ne x$ for all $0<i<m$. In that case m is the period of x. When $m=1$ we have fixed points. By $\mathrm{Per}\left(f\right)$ we denote the set of all the periods of periodic points of f.

Since Keane’s paper [1], interval exchange transformations are an active area of research. We will denote an interval exchange transformation by the acronym IET. First, the interest was focused on oriented IETs without flips. However, later on, Nogueira, among others, studied IETs with flips [2].

Analyzing IETs is interesting from a theoretical point of view and a lot of work has been made in this direction, see e.g., [3] for a nice review. However, it is also interesting because of the quantity of applications, for example to the mechanical systems called polygonal billiards [2,4] or to surface flows [5], among others. Below, we introduce some basic notation and definitions to understand our framework.

According to [4], a polygonal billiard is a connected open set U in the plane (not necessarily simply connected), whose boundary $\partial U$ is the union of finitely many rectilinear segments. This billiard is called a rational polygonal billiard when the angle of the directions of two whatsoever segments which form $\partial U$ is a rational multiple of $\pi$. To this respect, let us mention that the main result in [6] establishes that, for rational polygons, periodic orbits are dense in the phase space of the billiard flow. In this direction, our study clarifies the value of the minimal periods for these dense orbits when we relate rational billiards with IETs. To relate polygonal billiards and oriented IETs, the reader interested can consult, for instance, ref. [7], where, from a polygonal billiard, the authors construct an oriented IET in which the discontinuity points correspond to the vertices of the original polygon suitably normalized. Furthermore, the construction of flipped IETs from polygonal billiards can be consulted in [2].

When the shape of the bounded region is allowed to have an arbitrary boundary, we face the subject of dynamical billiards, an active area of research at the present day. In this sense, concerning the mechanical applications of dynamical billiards, we can mention [8], where the author gives a general scope about the relationship between chaos and quantum mechanics and the connection of the chaotic motion with billiards through the dynamics of light rays for certain types of laser cavities. The dynamics of general billiards is also applied to modelling the movement of particles inside some nanodevices as p-n junctions, which is a structure of electronic components or semiconductor materials having different type (p-type, n-type). These components allow the movement of electrons through the junction between the two types of semiconductor materials (for some models, consult [9] and references therein; to obtain basic information on p-n junctions, the reader is referred, for instance, to [10]).

Let $\mathbb{N}$ be the set of natural numbers and $n\in \mathbb{N}$. An n-IET is an injective map $T:D\subset (0,l)\to (0,l)$ such that:

• D is the union of n pairwise disjoint open intervals, $D={\bigcup }_{i=1}^n{I}_i$. Moreover, $I_i=(a_i,a_{i+1})$, $0=a_1<a_2<a_3<\cdots <a_{n+1}=l$.
• ${T|}_{I_i}$ is an affine map of constant slope equals to 1 or −1, $i=1,2,\cdots ,n$.

In what follows we will always assume that $l=1$, although notice that we may also assume $D\subset [0,1]$ when necessary.

We say that an IET T has flips if there are k subintervals where the slope is $-1$. Otherwise, we say that T has no flips. We will write (n,k)-IET to denote an IET with k-flips and n discontinuities. When T has no flips we say that it is an oriented interval exchange transformation of n intervals. If there are not fake discontinuities we say that T is a proper IET. Note that a discontinuity $a\in [0,1]$ is fake when the map is in fact continuous in a. For instance, the identity map on $[0,1]$ can be regarded as a 2-IET with permutation $(1,2)$ and a fake discontinuity at any point $a\in [0,1]$. The notions of circle exchange transformation of n intervals with k flips or circle exchange transformation of n intervals without flips are obtained by replacing $[0,1]$ with ${\mathbb{S}}^1=[0,1]/\equiv$, $(0\equiv 1)$. We will denote this map by the acronym $(n,k)$-CET or simply CET.

IETs and CETs are easily related by means of the universal standard covering $e:\mathbb{R}\to {\mathbb{S}}^1$ given by $e\left(x\right)=e^{2\pi ix}.$ For a given proper $(n,k)$-IET defined on $D\subset [0,1]$, T, we can define a unique $(n,k)$-CET, $T^c$, such that the diagram

$$\begin{array}{ccc}D\subset [0,1]& \stackrel{T}{⟶}& \mathbb{R}\\ e\downarrow & & \downarrow e\\ D^c\subset {\mathbb{S}}^1& \stackrel{T^c}{⟶}& {\mathbb{S}}^1\end{array}$$

commutes (see e.g., [11] for more information on the standard covering of the circle). Although the discontinuities of $T^c$ become discontinuities of T using e, T can have two extra discontinuities. If there is a point of continuity of $T^c$, $w=e^{2\pi it}$ with $t\in [0,1]$, such that $T^c\left(w\right)=e^{2\pi i}$, then t is a discontinuity of T. In addition, if $e^{2\pi i}$ is in an interval of continuity of $T^c$, let us say $I_j^c$, then $e^{-1}\left(I_j^c\right)$ decomposes into two intervals of continuity of T. Then:

Remark 1.

• If $T^c$ is a proper $(n,k)$-CET, then T is a proper $(n^{\prime },k^{\prime })$-IET for some $n\le n^{\prime }\le n+2$, $k\le k^{\prime }\le k+2$.
• Conversely, if T is a proper $(n,k)$-IET, then $T^c$ is a proper $(n^{\prime },k^{\prime })$-IET for some $n-2\le n^{\prime }\le n$, $k-2\le k^{\prime }\le k$.

For example, any $(6,4)$-IET with permutation $(-3,5,-1,-6,2,-4)$ becomes a $(4,2)$-CET while the $(4,2)-$IET associate to $(-4,2,1,-3)$ continues being a $(4,2)$-CET.

The orbit of $x\in (0,1)$ is given by

$${\mathcal{O}}_T\left(x\right):=\{T^n\left(x\right):n\in \mathbb{Z}\mathrm{and}{T}^{n-1}\left(x\right)\in Dom\left(T\right)\}.$$

Moreover, we also define the orbits ${\mathcal{O}}_T\left(0\right)=\left\{0\right\}\cup {\mathcal{O}}_T\left({lim}_{x\to 0^{+}}T\left(x\right)\right)$ and ${\mathcal{O}}_T\left(1\right)=\left\{1\right\}\cup {\mathcal{O}}_T\left({lim}_{x\to 1^{-}}T\left(x\right)\right)$. Similarly, the right and left orbits at discontinuity points can be defined. T is said to be minimal if ${\mathcal{O}}_T\left(x\right)$ is dense in $[0,1]$ for any $x\in [0,1]$. Transitivity is a weaker condition; namely, T is said to be transitive if there exists some $x\in [0,1]$ such that ${\mathcal{O}}_T\left(x\right)$ is dense in $[0,1]$. An n-IET is said to be uniquely ergodic if it only admits the Lebesgue measure and its multiples as invariant measures (recall that a probabilistic measure $\mu$ is invariant by T if $\mu \left(A\right)=\mu \left(T^{-1}\left(A\right)\right)$ for all Borel sets A).

The simplest IETs, oriented 2-IETs T with slope 1 on their two pieces of continuity, show that a dichotomic behavior exists. T is either a rational or non-rational rotation. Thus, either T is minimal or all the points, except for the ones in the orbit of the point of discontinuity, are periodic of the same period (see, e.g., [11]). The behavior of oriented and non-oriented, i.e., with flips, IETs differs. Roughly speaking, almost all oriented n-IETs are minimal while almost all $(n,k)$-IETs with $k\ge 1$ have at least one periodic point and are not minimal. To precise these facts, we will introduce the way of codifying IETs in Section 1.1.

We are motivated by the longstanding problem of obtaining the set of periods of functions defined on one interval into itself. It is known that the celebrated Sharkovsky’s Theorem gives the solution when the map is continuous [12,13]. Many works in this direction have appeared by changing the phase space or by considering non-autonomous dynamical systems. A wide review on this subject can be found in [14]. This paper aims to advance the study of the periodic structure of IETs. We will give a complete classification of the periods of 2-IETs, introduce a framework to study the periodicity of general IETs and, as an application, analyze the periods of a particular case of 3-IETs. Of course, there is a lot of work to be done to characterize the periods of this family of maps. It is important to highlight that in [15], in the open problems session of the conference “Thirty Years after Sharkovskiĭ’s Theorem: New Perspectives” (Murcia, 1994), M. Misiurewicz proposed the following question: “Characterize all possible sets of periods of periodic orbits of interval maps $f:[0,\frac{1}{2})\cup (\frac{1}{2},1]\to [0,1]$ such that f is continuous and strictly increasing on $[0,\frac{1}{2})$ and is continuous and strictly decreasing on $(\frac{1}{2},1]$”. Our results on $(2,1)$-IETs give a partial solution to this problem that was also studied in [16].

The next subsections present well-known facts on IETs and prove some interesting properties on Poincaré maps of IETs. In Section 2 we characterize completely the periods of 2-IETs. In Section 3 we present the general framework to study the periods of IETs which is applied to a case study of 3-IETs in Section 4. The next section contains two case studies for two fixed permutations that show that characterizing the periods of general IETs is not an easy task. A section of conclusions ends the paper.

1.1. Coordinates in the Set of IETs

A signed permutation is an injective map

$$\pi :N_n=\{1,2,\dots ,n\}\to N_n^{\sigma }=\{-n,-(n-1),\dots ,-1,1,2,\dots ,n\}$$

such that $|\pi |:N_n\to N_n$ is bijective, that is, a standard permutation. Let $S_n^{\sigma }$ be the set of signed permutations. A non standard permutation will be a signed permutation $\pi$ whenever $\pi \left(i\right)<0$ for some i. We represent $\pi$ by $(\pi \left(1\right),\pi \left(2\right),\dots ,\pi \left(n\right))\in {\left(N_n^{\sigma }\right)}^n.$ A permutations is irreducible if $|\pi (\{1,2,\dots t\}\left)\right|\ne \{1,2,\dots ,t\}$ for any $1\le t<n$. The set of irreducible permutations is denoted by $S_n^{\sigma ,*}$. The subset $S_n^{\sigma ,+}$ of standard permutations $\pi$ with $|\pi |\left(n\right)\ne n$ will play an important role. Observe that $S_n^{\sigma ,*}⊊S_n^{\sigma ,+}$.

Fix ${\mathbb{R}}_{+}=(0,\infty )$, ${\Lambda }^n={\mathbb{R}}_{+}^n$. We establish a one to one map between the set of n-IETs and ${\mathcal{C}}_n={\Lambda }^n\times S_n^{\sigma }$. Let $T:D={\bigcup }_{i=1}^n{I}_i\subset (0,1)\to (0,1)$ be an n-IET. Then its associated coordinates in $(\lambda ,\pi )\in {\mathcal{C}}_n$ are defined by:

• ${\lambda }_i=a_{i+1}-a_i$ for all $i\in N_n$.
• $\pi \left(i\right)$ is positive (resp. negative) if ${T|}_{I_i}$ has slope 1 (resp. $-1$). Moreover $|\pi (i\left)\right|$ is the position of the interval $T\left(I_i\right)$ in the set ${\left\{T\left(I_i\right)\right\}}_{i=1}^n$ with the usual order in $\mathbb{R}$.

These coordinates allow us to identify $T=(\lambda ,\pi )$. For a fixed permutation $\pi$ we can consider the Lebesgue measure of the cone ${\Lambda }^n$ on the set of n-IETs having associated permutation $\pi$. Then we can state the following result.

Theorem 1.

Let $\pi :N_n\to N_n$ be an irreducible permutation. Then:

• If π is standard, then almost all (with respect to the Lebesgue measure induced on ${\Lambda }^n$) n-IETs of the form $(\lambda ,\pi )$ are minimal. Moreover if $T=(\lambda ,\pi )$ is oriented, π irreducible and the components of λ are rationally independent then T is minimal (Keane [1]).
• If π is standard, then almost all n-IETs of the form $(\lambda ,\pi )$ are uniquely ergodic (Masur [17] and Veech [18]).
• If π is not standard, then almost all $(n,k)$-IETs, $k\ge 1$, of the form $(\lambda ,\pi )$ have periodic orbits (Nogueira [2]).

Remark 2.

Assume that π is reducible, $T=(\lambda ,\pi )$ and $t<n$ satisfying $|\pi |\left(N_t\right)=N_t$. Then, the dynamics of T decomposes in the (independent) dynamics of $T_1{=T|}_{{\bigcup }_{i=1}^t{I}_i}$ and $T_2{=T|}_{{\bigcup }_{i=t+1}^n{I}_i}$ which are IETs of less than n intervals and $\mathrm{Per}\left(T\right)=\mathrm{Per}\left(T_1\right)\cup \mathrm{Per}\left(T_2\right)$. Moreover, if T is transitive then π is irreducible.

It is well known that IETs decompose into periodic and minimal components [2,19,20,21]. This decomposition is essential to analyze the set of periods. Each periodic component has either two or one associated periodic orbits depending on whether it reverses the orientation or not. An open interval J is said to be rigid if all positive iterates $T^m$ are defined; that is, these iterates do not contain discontinuity points. When a rigid interval J does not admit any other rigid interval containing it, then we say that J is a maximal rigid interval. Observe that for any maximal rigid interval J there is a minimal positive integer m such that $T^m\left(J\right)=J$ and then all points in J have either period $2m$ or m. Both periods exist when ${\left(T^m\right)}^{\prime }\left(x\right)=-1$ for any $x\in J$, and only m if ${\left(T^m\right)}^{\prime }\left(x\right)=1$ for any $x\in J$.

Let J be a maximal rigid interval and let m be positive as above. Then ${\bigcup }_{j=0}^{m-1}{T}^j\left(J\right)$ is said to be a periodic component ofT. A minimal component of T is a non-empty set $M\subseteq Dom\left(T\right)$ such that $M=Cl\left({\mathcal{O}}_T\left(x\right)\right)$ for any $x\in M$ having either full forward or full backward orbit (here, $Cl\left(A\right)$ denotes the topological closure of the set A). Similarly, a transitive interval is defined. The next result has an obvious relevance for us (see [22], Th. A).

Theorem 2

(Nogueira, Pires, Troubetzkoy). The numbers $n_{\mathrm{per}}$ of periodic components and $n_{\min }$ of minimal components of an n-IET satisfy the inequality $n_{\mathrm{per}}+2n_{\mathrm{tran}}\le n$.

Also, the Main Theorem in [23] gives an important information.

Theorem 3

(Gutierrez, Lloyd, Pires, Zhuzhoma). Given $n\ge k\ge 1$, there exists a transitive proper $(n,k)$-CET if and only if $n+k\ge 5$.

It is also remarkable the next result from [24].

Theorem 4

(Linero, Soler). Given $n\ge k\ge 1$, with $n\ge 4$, there exist proper minimal uniquely ergodic $(n,k)$-IETs.

Combining Theorems 2 and 3, since transitive components of $(2,k)$-CET are related to transitive components of an $(n,k^{\prime })$-IETs with $n\le 2$ and $k^{\prime }\le k$. Observe that T has transitive components if and only if $T^c$ also has transitive components and any periodic orbit of T is mapped by e to a periodic orbit of $T^c$. Then, we have the following corollary.

Corollary 1.

Let $k\in \{1,2\}$ and let be T a $(2,k)$-IET. Then T does not admit transitive components, and the number of periodic components is bounded by two.

Proof. 

Any $(2,k)$-IET can be seen as a $(n^{\prime },k^{\prime })$-CET, $T^c$, with $1\le n^{\prime }\le 2$. Moreover $1\le k^{\prime }\le k\le 2$ and $n^{\prime }+k^{\prime }\le 4$, then $T^c$ is not transitive by Theorem 3 and so is not T.

Also, by Theorem 2, the number of transitive components, $n_{\mathrm{tran}}$, satisfies $n_{\mathrm{per}}+2n_{\mathrm{tran}}\le n=2$. Then either $n_{\mathrm{per}}=0$ and $n_{\mathrm{tran}}=1$ (which is not possible by the above paragraph), or $n_{\mathrm{per}}\ge 1$ and $n_{\mathrm{tran}}=0$. □

Remark 3.

There exist 3-IETs with flips and transitive components. For instance take $T=(\lambda ,\pi )$ with $\pi =(2,1,-3)$. Then the dynamics of T decomposes independently in the dynamics of ${T|}_{I_1\cup I_2}$ and the dynamics of ${T|}_{I_3}$. Observe that $I_3$ is a periodic component with points of periods 1 and 2. In addition, for appropriate values of ${\lambda }_1$ and ${\lambda }_2$${T|}_{I_1\cup I_2}$ is a non rational rotation and then $I_1\cup I_2$ is a transitive component.

To investigate the notion of minimality only irreducible permutations must be are considered. However, for this paper we have to take into account all the IETs with associated permutation in $S_n^{\sigma }$. Observe that an IET, T, associated to a permutation in $S_n^{\sigma }\setminus S_n^{\sigma ,+}$ decomposes into two IETs: one without discontinuities, $T_1{=T|}_{I_n}$, and the other one, $T_2{=T|}_{{\cup }_{j=1}^{n-1}{I}_j}$, having one less discontinuity than T. Observe that, then, $\mathrm{Per}\left(T\right)=\mathrm{Per}\left(T_1\right)\cup \mathrm{Per}\left(T_2\right)$ and $\mathrm{Per}\left(T_1\right)=1$ or $\mathrm{Per}\left(T_1\right)=\{1,2\}$ depending on whether $T_1$ is oriented or not. In particular, if $T=(\lambda ,\pi )$ is a 2-IET then $\mathrm{Per}\left(T\right)=\{1,2\}$ for any $\pi \in \left\{\right(-1,2),(1,-2),(-1,-2\left)\right\}$.

1.2. Poincaré Map

Let $T=(\lambda ,\pi )$ be an n-IETswith $\pi \in S_n^{\sigma ,+}$ and ${\lambda }_n={\lambda }_{{|\pi |}^{-1}\left(n\right)}$. Then we can define the Poincaré map in the set $I\setminus I_n$, $T_1$ such that $T_1\left(x\right)=T\left(x\right)$ if $x\in I\setminus (I_n\cup I_{{|\pi |}^{-1}\left(n\right)})$ and $T_1\left(x\right)=T^2\left(x\right)$ if $x\in I_{{|\pi |}^{-1}\left(n\right)}$. Figure 1 and Figure 2 show the graphs of 3-IETs and their Poincaré maps. This map $T_1$ has less discontinuities than T but the set of periods is different. In particular, any periodic orbit of $T_1$ of period p intersecting $I_{{|\pi |}^{-1}\left(n\right)}$ becomes (adding some points) a periodic orbit of T of period $p+n_p$ where $n_p$ denotes the times that the orbit visits $I_n$ (or equivalently $I_{{|\pi |}^{-1}\left(n\right)}$). A similar reasoning can be made when ${\lambda }_1={\lambda }_{{|\pi |}^{-1}\left(1\right)}$. We obtain the following results.

Proposition 1.

Let $T=(\lambda ,\pi )$, $\pi \in S_n^{\sigma ,+}$ and assume that ${\lambda }_n={\lambda }_{{|\pi |}^{-1}\left(n\right)}$. Let $T_1$ be the Poincaré map of T on $I\setminus I_n$, let $x\in I_{{|\pi |}^{-1}\left(n\right)}$ and assume that x is a periodic point of $T_1$ of period p. Then x is a periodic point of T of period $p+n_p$, where $n_p$ is the cardinality of ${\mathcal{O}}_{T_1}\left(x\right)\cap I_{{|\pi |}^{-1}\left(n\right)}$.

Proposition 2.

Let $T=(\lambda ,\pi )$, $\pi \in S_n^{\sigma }$, $|\pi |\left(1\right)\ne 1$ and assume that ${\lambda }_1={\lambda }_{{|\pi |}^{-1}\left(1\right)}$. Let $T_1$ be the Poincaré map of T on $I\setminus I_1$, $x\in I_{{|\pi |}^{-1}\left(1\right)}$ and assume that x is a periodic point of $T_1$ of period p. Then x is a periodic point of T of period $p+n_p$, where $n_p$ is the cardinality of ${\mathcal{O}}_{T_1}\left(x\right)\cap I_{{|\pi |}^{-1}\left(1\right)}$.

These results allow us to analyze the set of periods of some 3-IETs as we show in Section 4.

1.3. Inverse and Conjugate

To simplify the characterization of the set of periods of $(n,k)$-IETs we will study how this set behaves under conjugation and inverse.

Let us fix an $(n,k)$-IET, $T=(\lambda ,\pi )$, and consider its inverse $T^{-1}=({\lambda }^i,{\pi }^i)$. In addition, we introduce the homeomorphism $h:[0,1]\to [0,1]$, $h\left(x\right)=1-x$, which holds $h^2=Id$. We define the conjugated map of T by means of h, $T^h$, by $T^h:=h\circ T\circ h^{-1}$. $T^h$ is also an IET(since h is an isometry), and $T^h=({\lambda }^h,{\pi }^h)$.

Theorem 5.

Let $T=(\lambda ,\pi )$ be a $(n,k)$-IET. Then:

(a) 

$T^{-1}=({\lambda }^i,{\pi }^i)$ with ${\lambda }_j^i={\lambda }_{{|\pi |}^{-1}\left(j\right)}$ and ${\pi }^i\left(j\right)=\sigma \left(\right|{\pi }^{-1}{\left|\left(j\right)\right)|\pi |}^{-1}\left(j\right)$.

(b) 

$T^h=({\lambda }^h,{\pi }^h)$ with ${\lambda }_j^h={\lambda }_{n-j}$ and ${\pi }^h\left(j\right)=\sigma (\pi (n-j))(n-|\pi \left|(n-j)\right)$.

(c) 

$\mathrm{Per}\left(T\right)=\mathrm{Per}\left(T^{-1}\right)=\mathrm{Per}\left(T^h\right)$.

Proof. 

(a) Assume that the intervals of continuity of T are ${\left\{I_j\right\}}_{j=1}^n$ and the interval of continuity of $T^{-1}$ are ${\left\{L_j\right\}}_{j=1}^n$. Then $T\left(I_j\right)=L_{|\pi |\left(j\right)}$ and ${\lambda }_j={\lambda }_{|\pi |\left(j\right)}^i$ for any $1\le j\le n$, also $L_j=T(I_{{|\pi |}^{-1}\left(j\right)}$ and ${\lambda }_j^i={\lambda }_{{|\pi |}^{-1}\left(j\right)}$.

$|{\pi }^i|\left(j\right)$ denotes the position of the interval $L_j$ after applying $T^{-1}$, observe that $T^{-1}\left(L_j\right)=T^{-1}\left(T\left(I_{{|\pi |}^{-1}\left(j\right)}\right)\right)=I_{{|\pi |}^{-1}\left(j\right)}$. Hence $|{\pi }^i{|\left(j\right)=|\pi |}^{-1}\left(j\right)$. Moreover, the slope of $T^{-1}{|}_{L_j}$ coincides with the one of ${T|}_{I_{{|\pi |}^{-1}\left(j\right)}}$, therefore ${\pi }^i\left(j\right)=\sigma \left(\right|{\pi }^{-1}{\left|\left(j\right)\right)|\pi |}^{-1}\left(j\right)$.

(b) For $T^h=h\circ T\circ h$, we name the interval of continuity by ${\left\{L_j\right\}}_{j=1}^n$ and the interval of continuity of T are ${\left\{I_j\right\}}_{j=1}^n$. Observe that ${\left\{h\left(I_j\right)\right\}}_{j=1}^n={\left\{L_j\right\}}_{j=1}^n$, moreover $L_j=h\left(I_{n-j}\right)$ and ${\lambda }_j^h={\lambda }_{n-j}$. Now we are going to see the order of the intervals $T^h\left(L_j\right)=h\circ T\circ h\left(h\left(I_{n-j}\right)\right)$ and $h\circ T\circ \left(I_{n-j}\right)$, observe that the interval $I_{n-j}$ is placed by T in the position $|\pi |(n-j)$ and then h carries it to the position $n-|\pi |(n-j)$. Moreover the slope of $T^h{|}_{L_j}$ is the same that the one of ${T|}_{I_{n-j}}$. Thus: ${\pi }^h\left(j\right)=\sigma (\pi (n-j))(n-|\pi \left|(n-j)\right)$.

(c) It is immediate to see that x is a periodic point of T of period p if and only if $T^{p-1}\left(x\right)$ is a periodic point of $T^{-1}$. Therefore, $\mathrm{Per}\left(T\right)=\mathrm{Per}\left(T^{-1}\right)$. On the other hand, taking into account that ${\left(Th\right)}^k={(h\circ T\circ h)}^k=h\circ T^k\circ h$ for any $k\in \mathbb{N}$, it is easily seen that x is a periodic point of $T^h$ of order p if and only if $h\left(x\right)$ is a periodic point of T, and consequently $\mathrm{Per}\left(T\right)=\mathrm{Per}\left(T^h\right)$. □

We finish this introductory section with the following corollary.

Corollary 2.

Let $T=(\lambda ,\pi )$ with $\pi =(2,-1)$ and $\lambda =({\lambda }_1,{\lambda }_2)$. Then $T^{-1}=({\lambda }^i,{\pi }^i)$ with ${\pi }^i=(-2,1)$ and $\lambda =({\lambda }_2,{\lambda }_1)$ and $\mathrm{Per}\left(T\right)=\mathrm{Per}\left(T^{-1}\right)$.

2. Set of Periods of 2-IETs

Thorough this section we will assume that any IET is a 2-IET. The possible generalized permutations are ${\pi }_1=(1,2)$, ${\pi }_2=(-1,2),$${\pi }_3=(1,-2)$ and ${\pi }_4=(-1,-2)$ for the reducible case and ${\pi }_5=(2,1)$, ${\pi }_6=(-2,1)$, ${\pi }_7=(2,-1)$ and ${\pi }_8=(-2,-1)$. Of course, there are some trivial cases here. If $T_1$ is an IET with generalized permutation ${\pi }_1$, then it is the identity and hence $\mathrm{Per}\left(T_1\right)=\left\{1\right\}$. Similarly, the IET $T_8$ with permutation ${\pi }_8$ is in fact the map $1-x$, with periods $\mathrm{Per}\left(T_8\right)=\{1,2\}$. For an IET $T_i$ with permutation ${\pi }_i$, $i=2,3,4$, note that they have one invariant subinterval where the map is $1-x$ and then $\{1,2\}\subset \mathrm{Per}\left(T_i\right)$. Since the maps are the identity or again $1-x$ on the other subinterval, we conclude that $\{1,2\}=\mathrm{Per}\left(T_i\right)$, $i=2,3,4$.

Now, we set $a={\lambda }_1$. For an IET $T_5$ with permutation ${\pi }_5$, note that it can be identified with a rotation on the circle ${\mathbb{S}}^1$. It is well-known, see e.g., [11], that in this case, if $T_5\left(x\right)=x+1-a$ on $[0,a)$ and $T_5\left(x\right)=x-a$ on $(a,1]$, then $\mathrm{Per}\left(T_5\right)=\varnothing$ if a is not a rational number, and $\mathrm{Per}\left(T_5\right)=\left\{n\right\}$ if $a=m/n$, with $m<n$, $gcd(n,m)=1$.

So, the difficult case appears when $T_i$ is an IET with associated generalized permutation ${\pi }_i$, with $i=6,7$. Taking into account that ${\lambda }_1=a$, the 2-IET for ${\pi }_7$ is given by

$$T_a\left(x\right)=\left\{\begin{array}{ccc}x+1-a& if& x\in [0,a),\\ 1-x& if& x\in (a,1].\end{array}\right.$$

Next result simplifies the problem.

Lemma 1.

The map $\phi \left(x\right)=1-x$ is a conjugacy between suitable IETs $T_6={\tilde{T}}_a$ and $T_7=T_a$ with $a\in (0,1)$.

Proof. 

Let

$${\tilde{T}}_a\left(x\right)=\left\{\begin{array}{ccc}-x+1& if& x\in [0,1-a),\\ x-1+a& if& x\in (1-a,1],\end{array}\right.$$

be an IET with associated permutation ${\pi }_6$. It is a straightforward computation that

$$T_a\left(x\right)=(\phi \circ {\tilde{T}}_a\circ \phi )\left(x\right)=\left\{\begin{array}{ccc}x+1-a& if& x\in [0,a),\\ 1-x& if& x\in (a,1],\end{array}\right.$$

which concludes the proof. □

The above lemma yields that $\mathrm{Per}\left(T_a\right)=\mathrm{Per}\left({\tilde{T}}_a\right)$. Next result characterizes the periods of $T_a$ with associated generalized permutation ${\pi }_7$.

Theorem 6.

Let $T_0\left(x\right)=1-x$ and for a given $a\in (0,1)$ let

$$T_a\left(x\right)=\left\{\begin{array}{ccc}x+1-a& if& x\in [0,a),\\ 1-x& if& x\in (a,1].\end{array}\right.$$

Then:

(a) 

If $a=\frac{n}{n+1}$ for some $n\in \mathbb{N}\cup \left\{0\right\}$, then $\mathrm{Per}\left(T_a\right)=\{n+1,2(n+1)\}$.

(b) 

If $a\in (a_L,a_R)$, with $a_L=\frac{n-1}{n}$ and $a_R=\frac{n}{n+1}$ for some $n\in \mathbb{N}$, then $\mathrm{Per}\left(T_a\right)=\mathrm{Per}\left(T_{a_L}\right)\cup \mathrm{Per}\left(T_{a_R}\right)$, that is, $\mathrm{Per}\left(T_a\right)=\{n,2n,n+1,2(n+1)\}$.

Proof. 

(a) For $n=0$ the result is trivial. Let $n\ge 1$ and notice that $1-a=\frac{1}{n+1}$. Define the subintervals

$$I_j:=(j(1-a),(j+1)(1-a))=\left(\frac{j}{n+1},\frac{j+1}{n+1}\right),j=0,1,\cdots ,n.$$

Note that

$$I\setminus \{T_a^{-i}\left(a\right):i\ge 0\}={\cup }_{j=0}^n{I}_j.$$

(1)

Figure 3 shows an example a map with $a=\frac{11}{12}$.

Then, it is easy to check that $T_a\left(I_j\right)=I_{j+1}$ for $j=0,1,\cdots ,n-1$, and $T_a\left(I_n\right)=I_0$. As a consequence, we have that $T_a^{n+1}\left(I_j\right)=I_j$ for $j=0,1,\cdots ,n$. Moreover, $\left(T_a^{n+1}{|}_{I_j}\right)\left(x\right)=(2j+1)(1-a)-x$ for $x\in I_j$. The fact that $\mathrm{Per}\left(T_a^{n+1}{|}_{I_j}\right)=\{1,2\}$ for $j=0,1,\cdots ,n$, jointly with the property that the intervals $I_j$ are periodic with period $n+1$ allow us to conclude that $\mathrm{Per}\left(T_a\right)=\{n+1,2(n+1)\}$.

(b) Define the subintervals

$$I_{2j}:=\left(j(1-a),(j-n)(1-a)+1\right),$$

$$I_{2j+1}:=\left((j-n)(1-a)+1,(j+1)(1-a)\right),$$

for $j=0,1,\cdots ,n-1$ and

$$I_{2n}:=(n(1-a),1).$$

Note that

$$I\setminus \{T_a^{-i}\left(a\right):i\ge 0\}={\cup }_{j=0}^n{I}_{2j}.$$

(2)

We have that $T_a\left(I_{2j}\right)=I_{2(j+1)}$ for $j=0,1,\cdots ,n-1$ and $T_a\left(I_{2n}\right)=I_0$. In addition, $\left(T_a^{2n+2}{|}_{I_{2j}}\right)\left(x\right)=x$ for $x\in I_{2j}$ for $j=0,1,\cdots ,n$. Reasoning as in part (a), we have that $\{n+1,2(n+1)\}\subset \mathrm{Per}\left(T_a\right)$. Similarly, $T_a\left(I_{2j+1}\right)=I_{2(j+1)+1}$ and $\left(T_a^{2n}{|}_{I_{2j+1}}\right)\left(x\right)=x$ for $x\in I_{2j+1}$ for $j=0,1,\cdots ,n-1$. Then $\{n,2n\}\subset \mathrm{Per}\left(T_a\right)$. By (2) we conclude that $\mathrm{Per}\left(T_a\right)=\{n,2n,n+1,2(n+1)\}$, and the proof concludes. □

Remark 4.

It is important to realize the next fact. Following the proof of Theorem 6 we can see that any periodic orbit of $T_a$ of period $n+1$ in $(0,a)$ contains n elements from $(0,a)$ and just one from $(a,1)$. If the periodic orbit has $2n+2$ elements, then only two of them are in $(a,1)$. It is easy to see from the conjugacy that the opposite situation happens with the conjugate map ${\tilde{T}}_a$, that is, a periodic orbit of period $n+1$ has one element in $(0,1-a)$, and two when the period is $2n+2$.

Remark 5.

Fix $a=\frac{n}{n+1}$, $n\ge 0$. If we denote by $T_a^{-}$ (resp. $T_a^{+}$) the left continuous (resp. right continuous) by defining $T_a^{-}\left(a\right)={lim}_{x\to a,x<a}{T}_a\left(x\right)$ (resp. $T_a^{+}\left(a\right)={lim}_{x\to a,x>a}{T}_a\left(x\right)$), then it is easy to see that a is a periodic point of period $n+2$ for $T_a^{-}$ (resp. n for $T_a^{+}$). The periodic orbit of a under $T_a^{-}$ is

$$\{a,1,0,1-a,2(1-a),\cdots ,n(1-a\left)\right\}$$

while under $T_a^{+}$ is

$$\{a,1-a,2(1-a),\cdots ,n(1-a\left)\right\}.$$

Then, we conclude that $\mathrm{Per}\left(T_a^{-}\right)=\mathrm{Per}\left(T_a\right)\cup \{n+2\}$ and $\mathrm{Per}\left(T_a^{+}\right)=\mathrm{Per}\left(T_a\right)\cup \left\{n\right\}$.

Remark 6.

Now, fix $a\in (a_L,a_R)$, with $a_L=\frac{n-1}{n}$ and $a_R=\frac{n}{n+1}$ for some $n\in \mathbb{N}$. Defining $T_a^{-}$ and $T_a^{+}$ as in the previous remark, we check that the periodic orbit of a under $T_a^{+}$ is

$$\{a,1,0,1-a,2(1-a),\cdots ,n(1-a),1-n(1-a),1-(n-1\left)\right(1-a),\cdots ,1-2(1-a\left)\right\}$$

and $T_a^{+}$ is

$$\{a,1-a,2(1-a),\cdots ,n(1-a),1-n(1-a),1-(n-1\left)\right(1-a),\cdots ,1-2(1-a\left)\right\}.$$

Then, we conclude that $\mathrm{Per}\left(T_a^{-}\right)=\mathrm{Per}\left(T_a\right)\cup \{2n+4\}$ and $\mathrm{Per}\left(T_a^{+}\right)=\mathrm{Per}\left(T_a\right)$.

Remark 7.

Theorem 6 partially solves a question posed by M. Misiurewicz in [15]. The question reads as follows: assume a map f which is increasing and continuous on $[0,1/2)$ and decreasing and continuous on $(1/2,1]$. Characterize the periods of f. Theorem 6 proves that no forcing relationship similar to, e.g., that of Sharkovsky’s theorem, is possible. To check this, note that the conjugacy

$${\varphi }_a\left(x\right)=\left\{\begin{array}{ccc}\frac{x}{2a}& if& x\in [0,a),\\ \frac{x+1-2a}{2(1-a)}& if& x\in (a,1],\end{array}\right.$$

takes the map $T_a$ into the map ${\varphi }_a\circ T_a\circ {\varphi }_a^{-1}$ fulfilling the hypothesis of the question.

Remark 8.

As we mentioned before, in [16] the Misiurewicz’s problem is studied under some hypothesis. Our results state that there will not be a forcing theorem of periods in general. Still, it is unclear whether the situation with IETs with permutation $(2,-1)$ is analogous to continuous circle maps in the following sense. Rotations of the circle can also be seen as IETs with permutation $(2,1)$ that establish that a forcing relationship is not possible for circle maps. However, the set of periods and the cases where forcing relationships exist are well-known for circle maps [11].

We finish this section by summarizing the periods for 2-IETs in

Table 1. For $0<a<1$, $n\in \mathbb{N}$, and the 2-IET $T_a$ with discontinuity at a, it is summarized the set of periods according to the permutation $\pi$.

$\mathit{\pi }$	$\mathbf{Per}\left({\mathit{T}}_{\mathit{a}}\right)$	$\mathit{\pi }$	$\mathbf{Per}\left({\mathit{T}}_{\mathit{a}}\right)$
$(1,2)$	$\left\{1\right\}$	$(1,-2)$	$\{1,2\}$
$(-1,-2)$	$\{1,2\}$	$(2,1)$	$\begin{array}{ccc}\hfill \left\{n\right\}& if& a=\frac{p}{n},\mathrm{with}\mathrm{p}\mathrm{and}\mathrm{n}\mathrm{coprime}\mathrm{naturals},\hfill \\ \hfill \varnothing & if& \mathrm{a}\mathrm{is}\mathrm{not}\mathrm{rational},\hfill \end{array}$
$(-1,2)$	$\{1,2\}$	$(2,-1)$	$\begin{array}{ccc}\hfill \{n+1,2(n+1\left)\right\}& if& a=\frac{n}{n+1},\hfill \\ \hfill \{n,2n,n+1,2(n+1\left)\right\}& if& \frac{n-1}{n}<a<\frac{n}{n+1},\hfill \end{array}$
$(-2,-1)$	$\{1,2\}$	$(-2,1)$	$\begin{array}{ccc}\hfill \{n+1,2(n+1\left)\right\}& if& a=\frac{1}{n+1},\hfill \\ \hfill \{n,2n,n+1,2(n+1\left)\right\}& if& \frac{1}{n+1}<a<\frac{1}{n}.\hfill \end{array}$

and Theorem 7.

Theorem 7.

Let $n\ge 0$ be an integer and let A be one of the following sets: $\{n+1,2(n+1\left)\right\}$, $\{n,2n,n+1,2(n+1\left)\right\}$, ∅ or $\{n+1\}$. Then:

• If T is a 2-IET we have $Per\left(T\right)=A$ for some of the above sets.
• Conversely, given a set A there exists a 2-IET, T, with $Per\left(T\right)=A$.

3. An Advance of the 3-IETs Case

For 3-IETs, the situation is more complex than in the 2-IET case. We have 48 possible signed permutations jointly with their length vector $\lambda =({\lambda }_1,{\lambda }_2,{\lambda }_3)$. As one can expect, the set of periods of a 3-IET will be determined by its signed permutation and its length vector. So, we denote a 3-IET T by $(\pi ,\lambda )$. Below, we show how to simplify this problem.

First, we identify the reducible signed permutations $\pi$. Note that if $|\pi |=\left(\right|\pi {|}_1,|\pi {|}_2,$${|\pi |}_3)$, then $\pi$ is reducible if either ${|\pi |}_1=1$ or ${|\pi |}_3=3$. In this case, for $i=1$, we have that either ${T|}_{[0,{\lambda }_1)}\left(x\right)=x$ and $1\in \mathrm{Per}\left(T\right)$ or ${T|}_{[0,{\lambda }_1)}\left(x\right)={\lambda }_1-x$ and $1,2\in \mathrm{Per}\left(T\right)$. Note that then $[{\lambda }_1,1]$ is invariant by T, and hence it is a 2-IET on this interval, and therefore its periods can be computed as in the 2-IET case. We obtain a similar result for the case $i=3$.

Next, we check what permutations may have a fake discontinuity. For instance, the permutation $\pi =(2,3,1)$ gives us a 3-IET which can be defined continuously at ${\lambda }_1$ in such a way that ${T|}_{[0,{\lambda }_1+{\lambda }_2)}$ is continuous. Then T can be seen as a 2-IET with permutation $(2,1)$ and length vector $({\lambda }_1+{\lambda }_2,{\lambda }_3)$, and then its periods can be computed. A similar scenario is found for the permutation $\pi =(-3,-2,1)$. So, we can remove this kind of permutations.

Finally, for a fixed 3-IET T, note that its inverse $T^{-1}$ and its conjugate $T^h$ are also 3-IETs which hold the relationship

$$\mathrm{Per}\left(T\right)=\mathrm{Per}\left(T^{-1}\right)=\mathrm{Per}\left(T^h\right).$$

So, in

Table 2. 3-IETs without flips.

T	${\mathit{T}}^{-1}$	${\mathit{T}}^{\mathit{h}}$
$(3,2,1)$ $({\lambda }_1,{\lambda }_2,{\lambda }_3)$	$(3,2,1)$ $({\lambda }_3,{\lambda }_2,{\lambda }_1)$	$(3,2,1)$ $({\lambda }_3,{\lambda }_2,{\lambda }_1)$

,

Table 3. 3-IETs with one flip.

T	${\mathit{T}}^{-1}$	${\mathit{T}}^{\mathit{h}}$
$(-3,2,1)$ $({\lambda }_1,{\lambda }_2,{\lambda }_3)$	$(3,2,-1)$ $({\lambda }_3,{\lambda }_2,{\lambda }_1)$	$(3,2,-1)$ $({\lambda }_3,{\lambda }_2,{\lambda }_1)$
$(3,-2,1)$ $({\lambda }_1,{\lambda }_2,{\lambda }_3)$	$(3,-2,1)$ $({\lambda }_3,{\lambda }_2,{\lambda }_1)$	$(3,-2,1)$ $({\lambda }_3,{\lambda }_2,{\lambda }_1)$
$(3,2,-1)$ $({\lambda }_1,{\lambda }_2,{\lambda }_3)$	$(-3,2,1)$ $({\lambda }_3,{\lambda }_2,{\lambda }_1)$	$(-3,2,1)$ $({\lambda }_3,{\lambda }_2,{\lambda }_1)$
$(3,-1,2)$ $({\lambda }_1,{\lambda }_2,{\lambda }_3)$	$(-2,3,1)$ $({\lambda }_2,{\lambda }_3,{\lambda }_1)$	$(2,-3,1)$ $({\lambda }_3,{\lambda }_2,{\lambda }_1)$
$(3,1,-2)$ $({\lambda }_1,{\lambda }_2,{\lambda }_3)$	$(2,-3,1)$ $({\lambda }_2,{\lambda }_3,{\lambda }_1)$	$(-2,3,1)$ $({\lambda }_3,{\lambda }_2,{\lambda }_1)$
$(-2,3,1)$ $({\lambda }_1,{\lambda }_2,{\lambda }_3)$	$(3,-1,2)$ $({\lambda }_3,{\lambda }_1,{\lambda }_2)$	$(3,1,-2)$ $({\lambda }_3,{\lambda }_2,{\lambda }_1)$
$(2,-3,1)$ $({\lambda }_1,{\lambda }_2,{\lambda }_3)$	$(3,1,-2)$ $({\lambda }_3,{\lambda }_1,{\lambda }_2)$	$(3,-1,2)$ $({\lambda }_3,{\lambda }_2,{\lambda }_1)$

,

Table 4. 3-IETs with two flips.

T	${\mathit{T}}^{-1}$	${\mathit{T}}^{\mathit{h}}$
$(-3,2,-1)$ $({\lambda }_1,{\lambda }_2,{\lambda }_3)$	$(-3,2,-1)$ $({\lambda }_3,{\lambda }_2,{\lambda }_1)$	$(-3,2,-1)$ $({\lambda }_3,{\lambda }_2,{\lambda }_1)$
$(-3,-1,2)$ $({\lambda }_1,{\lambda }_2,{\lambda }_3)$	$(-2,3,-1)$ $({\lambda }_2,{\lambda }_3,{\lambda }_1)$	$(2,-3,-1)$ $({\lambda }_3,{\lambda }_2,{\lambda }_1)$
$(-3,1,-2)$ $({\lambda }_1,{\lambda }_2,{\lambda }_3)$	$(2,-3,-1)$ $({\lambda }_2,{\lambda }_3,{\lambda }_1)$	$(-2,3,-1)$ $({\lambda }_3,{\lambda }_2,{\lambda }_1)$
$(3,-1,-2)$ $({\lambda }_1,{\lambda }_2,{\lambda }_3)$	$(-2,-3,1)$ $({\lambda }_2,{\lambda }_3,{\lambda }_1)$	$(-2,-3,1)$ $({\lambda }_3,{\lambda }_2,{\lambda }_1)$
$(-2,-3,1)$ $({\lambda }_1,{\lambda }_2,{\lambda }_3)$	$(3,-1,-2)$ $({\lambda }_3,{\lambda }_1,{\lambda }_2)$	$(3,-1,-2)$ $({\lambda }_3,{\lambda }_2,{\lambda }_1)$
$(-2,3,-1)$ $({\lambda }_1,{\lambda }_2,{\lambda }_3)$	$(-3,-1,2)$ $({\lambda }_3,{\lambda }_1,{\lambda }_2)$	$(-3,1,-2)$ $({\lambda }_3,{\lambda }_2,{\lambda }_1)$
$(2,-3,-1)$ $({\lambda }_1,{\lambda }_2,{\lambda }_3)$	$(-3,1,-2)$ $({\lambda }_3,{\lambda }_1,{\lambda }_2)$	$(3,-1,-2)$ $({\lambda }_3,{\lambda }_2,{\lambda }_1)$

and

Table 5. 3-IETs with three flips.

T	${\mathit{T}}^{-1}$	${\mathit{T}}^{\mathit{h}}$
$(-3,-1,-2)$ $({\lambda }_1,{\lambda }_2,{\lambda }_3)$	$(-2,-3,-1)$ $({\lambda }_2,{\lambda }_3,{\lambda }_1)$	$(-2,-3,-1)$ $({\lambda }_3,{\lambda }_2,{\lambda }_1)$
$(-2,-3,-1)$ $({\lambda }_1,{\lambda }_2,{\lambda }_3)$	$(-3,-1,-2)$ $({\lambda }_3,{\lambda }_1,{\lambda }_2)$	$(-3,-1,-2)$ $({\lambda }_3,{\lambda }_2,{\lambda }_1)$

, obtained by straightforward computations, we list the suitable 3-IETs $T\equiv (\pi ,\lambda )$ and their inverses and conjugates. These are the permutations that have to be considered to obtain the set of periods.

If the signed permutation is fixed, as ${\lambda }_3=1-{\lambda }_2-{\lambda }_1$, the set of periods must depend on two parameters ${\lambda }_1$ and ${\lambda }_2$. First we assume that ${\lambda }_1,{\lambda }_2\in \mathbb{Q}$ and such that ${\lambda }_1=\frac{k_1}{m}$, ${\lambda }_2=\frac{k_2}{m}$ and ${\lambda }_3=\frac{m-k_1-k_2}{m}$, with $k_1+k_2<m$, $m,k_1,k_2\in \mathbb{N}$. Note that $k_i$ and m need not be relatively prime, for instance $\lambda =\left(\frac{2}{6},\frac{1}{6},\frac{3}{6}\right)$. Note also that one element of the triple $\{k_1,k_2,m-k_1-k_2\}$ must be relatively prime with m, i.e., $\lambda =\left(\frac{2}{6},\frac{2}{6},\frac{2}{6}\right)$ is not possible, it is $\lambda =\left(\frac{1}{3},\frac{1}{3},\frac{1}{3}\right)$. Fix $I_j=\left(\frac{j-1}{m},\frac{j}{m}\right)$, for $j=1,\cdots ,m$.

Let $\mathbf{A}$ be the $n\times n$ matrix such that $a_{ij}=1$ if $T\left(I_i\right)\subseteq I_j$ and the slope in $I_i$ is positive, $a_{ij}=-1$ if $T\left(I_i\right)\subseteq I_j$ and the slope in $I_i$ is negative, and $a_{ij}=0$ otherwise. Note that there is one no zero entry in each row (resp. column). It is easy to see that $T^n$ has associated matrix ${\mathbf{A}}^n$. The following facts are easy to check:

(P1)

If $a_{jj}=1$ for some $j\in \{1,\cdots ,n\}$, then $1\in \mathrm{Per}\left(T\right)$.

(P2)

If $a_{jj}=-1$ for some $j\in \{1,\cdots ,n\}$, then $1,2\in \mathrm{Per}\left(T\right)$.

(P3)

If $a_{jj+1}=a_{j+1j}=-1$ for some $j\in \{1,\cdots ,n\}$, then $1,2\in \mathrm{Per}\left(T\right)$.

Hence, we can state the following algorithm to compute the periods of T. We find the first integer n such that ${\mathbf{A}}^n$ has entries holding one of the properties (P1)-(P3). Then, either n or n and $2n$ are in $\mathrm{Per}\left(T\right)$. We repeat this process until we find n such that ${\mathbf{A}}^n$ is a diagonal matrix. In this process, we find all the periods of T.

The matrix $\mathbf{A}$ allows us to construct a directed graph as follows. The set of vertices is $\{1,2,\cdots ,m\}$ and there is an arrow from vertex i to vertex j ($i\to j$) if $T\left(I_i\right)\subseteq I_j$, i.e., $a_{ij}\ne 0$. We add the sign ± to the arrow to stress that the slope of ${T|}_{I_i}$ is positive or negative. We will write either $i\stackrel{+}{\to }j$ or $i\stackrel{-}{\to }j$. A sequence of vertices and arrows starting and ending at the same vertex is a loop. Loops characterize the periods of T. Below, an example.

Example 1.

Fix $\pi =(3,1,-2)$ and $\lambda =\left(\frac{1}{5},\frac{1}{5},\frac{3}{5}\right)$. The shape of T can be seen in Figure 4.

It is easy to see that the matrix

$$\mathbf{A}=\left(\begin{array}{ccccc}0& 0& 0& 0& 1\\ 1& 0& 0& 0& 0\\ 0& 0& 0& -1& 0\\ 0& 0& -1& 0& 0\\ 0& -1& 0& 0& 0\end{array}\right).$$

Note that $a_{43}=a_{34}=-1$, so $\{1,2\}\subset \mathrm{Per}\left(T\right)$ by (P3). It is easy to check that

$${\mathbf{A}}^2=\left(\begin{array}{ccccc}0& -1& 0& 0& 0\\ 0& 0& 0& 0& 1\\ 0& 0& 1& 0& 0\\ 0& 0& 0& 1& 0\\ -1& 0& 0& 0& 0\end{array}\right),{\mathbf{A}}^3=\left(\begin{array}{ccccc}-1& 0& 0& 0& 0\\ 0& -1& 0& 0& 0\\ 0& 0& 0& -1& 0\\ 0& 0& -1& 0& 0\\ 0& 0& 0& 0& -1\end{array}\right)$$

and ${\mathbf{A}}^6$ is the identity matrix. Since, e.g., the position $(1,1)$ of ${\mathbf{A}}^3$ is $-1$, by (P2), we have that $1,2\in \mathrm{Per}\left(T^3\right)$, and hence $3,6\in \mathrm{Per}\left(T\right)$. So, $\mathrm{Per}\left(T\right)=\{1,2,3,6\}$.

Alternatively, the loops

$$1\stackrel{+}{\to }5\stackrel{-}{\to }2\stackrel{+}{\to }1$$

and

$$3\stackrel{-}{\to }4\stackrel{-}{\to }3$$

gives periods $3,6$ for the first case, and 2 for the second one. Noticing that vertices 3 and 4 are associated to intervals $[2/5,3/5]$ and $[3/5,4/5]$ whose intersection $3/5$ is a continuity point of T, we check that 1 is also a period.

In the next section, we will apply all these notions to the particular case ${\lambda }_1={\lambda }_3$. Hence, the 3-IET depends on one parameter, and it is easier to characterize the set of periods.

4. 3-IETs: The Case ${\mathbf{\lambda }}_{\mathbf{1}}={\mathbf{\lambda }}_{\mathbf{3}}$

As a first step in studying the set of periods for 3-IETs, we consider that the lengths ${\lambda }_1$ and ${\lambda }_3$ are equal. We distinguish several cases, according to the associated permutation $\pi$ and the number of flips. Of course, we consider the cases of Table 2, Table 3, Table 4 and Table 5 described before. From now on, we set $a:={\lambda }_1$ so that ${\lambda }_2=1-2{\lambda }_1=1-2a$. Note that $a\in \left(0,\frac{1}{2}\right)$. We define

$$I_1:=(0,{\lambda }_1)=(0,a),$$

$$I_2:=({\lambda }_1,{\lambda }_1+{\lambda }_2)=(a,1-a),$$

and

$$I_3:=({\lambda }_1+{\lambda }_2,1)=(1-a,1).$$

4.1. 3-IETs without Flips

Here the unique permutation we have to consider is $(3,2,1)$. As ${\lambda }_1={\lambda }_3$ it is easy to see that $\mathrm{Per}\left(T\right)=\{1,2\}$, where the fixed points are in $I_2$ and the periodic points of period 2 are located in $I_1\cup I_3$.

4.2. 3-IETs with One Flip

We consider the permutations described in Table 3, so that we have to distinguish several cases.

4.2.1. Permutations $(-3,2,1)$ and $(3,2,-1)$

We fix the permutation $(-3,2,1)$. Figure 5 shows the graph of the map for $a=\frac{1}{4}$.

Note that ${T|}_{I_2}$ is the identity therefore $1\in \mathrm{Per}\left(T\right)$. On the other hand,

$$I_1\stackrel{-}{\to }{I}_3\stackrel{+}{\to }{I}_1,$$

which implies that $\mathrm{Per}\left(T\right)=\{1,2,4\}$.

4.2.2. Permutation $(3,-2,1)$

An example of IET with this permutation and $a=\frac{1}{5}$ can be seen in Figure 6.

Note that T leaves the interval $I_2$ invariant with negative slope, so $1,2\in \mathrm{Per}\left(T\right)$. On the other hand,

$$I_1\stackrel{+}{\to }{I}_3\stackrel{+}{\to }{I}_1,$$

which implies that $\mathrm{Per}\left(T\right)=\{1,2\}$.

4.2.3. Permutations $(3,1,-2)$ and $(-2,3,1)$

By Table 3, both IETs associated with permutations $(3,1,-2)$ and $(-2,3,1)$ have the same periods when ${\lambda }_1={\lambda }_3$. So we fix $(3,1,-2)$. The 3-IET with a flip with associated permutation $(3,1,-2)$ is

$$T_a\left(x\right):=\left\{\begin{array}{ccc}x+1-a,\hfill & \mathrm{if}& x\in I_1,\hfill \\ x-a,\hfill & \mathrm{if}& x\in I_2,\hfill \\ -x+2(1-a),\hfill & \mathrm{if}& x\in I_3.\hfill \end{array}\right.$$

(3)

Its graph for $a=0.3$ and the graph of its Poincaré map can be seen in Figure 1.

Lemma 2.

Let T be the IET of Equation 3. Then, its Poincaré map $T_1$ is given by

$$T_1\left(x\right)=\left\{\begin{array}{ccc}1-x\hfill & if& x\in \left(0,\frac{a}{1-a}\right),\hfill \\ x-\frac{a}{1-a}\hfill & if& x\in \left(\frac{a}{1-a},1\right).\hfill \end{array}\right.$$

Proof. 

It is a straightforward computation. □

Theorem 8.

Let $T_a$ be the IET of (3). Then:

(a) 

If $a=\frac{1}{n+2}$ for some $n\ge 1$, then $\mathrm{Per}\left(T_a\right)=\{n+2,2(n+2)\}$.

(b) 

If $a\in \left(\frac{1}{n+2},\frac{1}{n+1}\right)$ for some $n\ge 1$, then $\mathrm{Per}\left(T_a\right)=\{n+1,2(n+1),n+2,2(n+2)\}$.

Proof. 

First, note that ${lim}_{x\to 1-a}-x+2(1-a)=1-a$, and since $I_3$ is an open interval, $1\notin \mathrm{Per}\left(T\right)$. By Lemma 2, we consider the Poincaré map $T_1$. Let $A=1-\frac{a}{1-a}=\frac{1-2a}{1-a}$. By Lemma 1 and Theorem 6, we have that the periods of $T_1$ are either $\mathrm{Per}\left(T_1\right)=\{n+1,2(n+1)\}$ if $A=\frac{n}{n+1}$, which is equivalent to $a=\frac{1}{n+2}$, or $\mathrm{Per}\left(T_1\right)=\{n,2n,n+1,2(n+1)\}$ if $\frac{n-1}{n}<A<\frac{n}{n+1}$, which is equivalent to $\frac{1}{n+2}<a<\frac{1}{n+1}$. It follows from the proof of Theorem 6 that any periodic orbit of $T_1$ visits the interval $\left(0,\frac{a}{1-a}\right)$ one or two times. So, the number of times $n_p$ that any periodic orbit of T visits $I_3$ is just one or two. As a consequence, by Proposition 1, we have that the periods of T are either $\mathrm{Per}\left(T_a\right)=\{n+2,2(n+2)\}$ if $a=\frac{1}{n+2}$, or $\mathrm{Per}\left(T_a\right)=\{n+1,2(n+1),n+2,2(n+2)\}$ if $\frac{1}{n+2}<a<\frac{1}{n+1}$, which concludes the proof. □

4.2.4. Permutations $(3,-1,2)$ and $(2,-3,1)$

By Table 3, both IETs associated with permutations $(3,-1,2)$ and $(2,-3,1)$ have the same periods when ${\lambda }_1={\lambda }_3$. So we fix $(3,-1,2)$ and note that the 3-IET reads as follows

$$T_a=\left\{\begin{array}{ccc}x+1-a,\hfill & \mathrm{if}& x\in I_1,\hfill \\ -x+1-a,\hfill & \mathrm{if}& x\in I_2,\hfill \\ x-a,\hfill & \mathrm{if}& x\in I_3.\hfill \end{array}\right.$$

(4)

Lemma 3.

Let $T_a$ be the IET of Equation (4). Then, its Poincaré map $T_1$ is given by

$$T_1\left(x\right)=\left\{\begin{array}{ccc}x+\frac{1-2a}{1-a}\hfill & if& x\in \left(0,\frac{a}{1-a}\right),\hfill \\ 1-x\hfill & if& x\in \left(\frac{a}{1-a},1\right).\hfill \end{array}\right.$$

Proof. 

It is a straightforward computation. Note that the Poincaré map is normalized to interval $[0,1]$. □

Figure 7 shows the graphs of $T_a$ and its Poincaré map for $a=0.4$.

Theorem 9.

Let $T_a$ be the IET given by (4). Then:

(a) 

If $a<\frac{1}{3}$, then $\mathrm{Per}\left(T_a\right)=\{1,2,3,6\}$.

(b) 

If $a\ge \frac{1}{3}$, then $\mathrm{Per}\left(T_a\right)=\{2n+1,2(2n+1)\}$ if $a=\frac{n}{2n+1}$ and $\mathrm{Per}\left(T_a\right)=\{2n-1,2(2n-1),2n+1,2(2n+1)\}$ if $\frac{n-1}{2n-1}<a<\frac{n}{2n+1}$.

Proof. 

First, it is straightforward to check that $T_a$ has a fixed point in $I_2$ whenever $a<\frac{1}{3}$. Note that, in addition, $2\in \mathrm{Per}\left(T_a\right)$. By Lemma 3, we consider the Poincaré map $T_1$. Let $A=1-\frac{1-2a}{1-a}=\frac{a}{1-a}$. By Lemma 1 and Theorem 6, we have that the periods of $T_1$ are either $\mathrm{Per}\left(T_1\right)=\{n+1,2(n+1)\}$ if $A=\frac{n}{n+1}$, which is equivalent to $a=\frac{n}{2n+1}$, or $\mathrm{Per}\left(T_1\right)=\{n,2n,n+1,2(n+1)\}$ if $\frac{n-1}{n}<A<\frac{n}{n+1}$, which is equivalent to $\frac{n-1}{2n+1}<a<\frac{n}{2n+1}$. It follows from the proof of Theorem 6 that any periodic orbit of $T_1$ visits the interval $\left(\frac{a}{1-a},1\right)$ one or two times. So, the number of times $n_p$ that any periodic orbit of period $n+1$T visits $I_3$ is n, and $2n$ times if the period is $2(n+1)$. As a consequence, by Proposition 1, we have that the periods of T are either $\mathrm{Per}\left(T_a\right)\subset \{2n+1,2(2n+1)\}$ if $a=\frac{n}{2n+1}$, or $\mathrm{Per}\left(T_a\right)\subset \{2n-1,2(2n-1),2n+1,2(2n+1)\}$ if $\frac{n-1}{2n+1}<a<\frac{n}{2n+1}$. Note that when $n=1$, then $\frac{n}{2n+1}=\frac{1}{3}$. In addition, the sequence $\frac{n}{2n+1}$ is increasing, so $\frac{1}{3}$ is its minimum value. Then (b) follows. To check (b), note that if $a\in (0,1/3)$, $\mathrm{Per}\left(T_1\right)=\{2,4\}$, and so $\mathrm{Per}\left(T_a\right)=\{1,2,3,6\}$. □

4.3. 3-IETs with Two Flips

In this subsection, we consider 3-IETs with two flips and ${\lambda }_1={\lambda }_3$. We consider the permutations showed in Table 4. It is easy to see that for the permutation $(-3,2,-1)$ the set of periods is $\mathrm{Per}\left(T\right)=\{1,2\}$. We study the other cases.

4.3.1. Permutations $(-3,-1,2)$ and $(2,-3,-1)$

By Table 4, both IETs with permutations $(-3,-1,2)$ and $(2,-3,-1)$, respectively, have the same periods when ${\lambda }_1={\lambda }_3$. So, we fix $(-3,-1,2)$ and note that the IET $T_a$, showed in Figure 8, is given by

$$T_a=\left\{\begin{array}{ccc}1-x,\hfill & \mathrm{if}& x\in I_1,\hfill \\ -x+1-a,\hfill & \mathrm{if}& x\in I_2,\hfill \\ x-a,\hfill & \mathrm{if}& x\in I_3.\hfill \end{array}\right.$$

(5)

Theorem 10.

Let $T_a$ be the IET given by (5). Then:

(a) 

If $a<\frac{1}{3}$, then $\mathrm{Per}\left(T_a\right)=\{1,2,3\}$.

(b) 

If $a=\frac{1}{3}$, then $\mathrm{Per}\left(T_a\right)=\left\{3\right\}$.

(c) 

If $a>\frac{1}{3}$, then $\mathrm{Per}\left(T_a\right)=\{2,3,4\}$.

Proof. 

For $a=\frac{1}{3}$, it is a simple matter to see that the only period is 3, since the third iterate is equal to the identity map and the map $T_a$ itself does not have fixed points.

For $a<\frac{1}{3}$, we find a fixed point given by $x_0=\frac{1}{2}(1-a)$. Moreover, $(0,a)$ and $(a,1-2a)$ are rigid intervals whose orbits are described in this way

$$(0,a)\stackrel{-}{\to }(1-a,1)\stackrel{+}{\to }(1-2a,1-a)\stackrel{-}{\to }(0,a)$$

and

$$(a,1-2a)\stackrel{-}{\to }(a,1-2a)\stackrel{-}{\to }(a,1-2a),$$

where we have used that $a<1-2a<1-a$. Being the closure of the periodic components equal to the unit interval, we deduce that the set of periods in this case is $\{1,2,3\}$.

When $a>\frac{1}{3}$, it holds $1-a<2a<1$, and it is immediate to check that $(0,1-2a)$ and $(1-2a,a)$ are rigid intervals whose periodic components are given by

$$(0,1-2a)\stackrel{-}{\to }(2a,1)\stackrel{+}{\to }(a,1-a)\stackrel{-}{\to }(0,1-2a)$$

and

$$(1-2a,a)\stackrel{-}{\to }(1-a,2a)\stackrel{+}{\to }(1-2a,a),$$

respectively. Therefore, the set of periods is $\{2,3,4\}$. (Observe that the closure of the periodic components recover all the unit interval). □

Remark 9.

We can reach the same result using a different argument. Note that the Poincaré map is $T_1\left(x\right)=1-x$, which has set of periods $\{1,2\}$. Taking this fact into account, it is easy to obtain the result of Theorem 10.

4.3.2. Permutations $(-3,1,-2)$ and $(-2,3,-1)$

By Table 4, both IETs with permutations $(-3,1,-2)$ and $(-2,3,-1)$, respectively, have the same periods when ${\lambda }_1={\lambda }_3$. So we fix $(-3,1,-2)$. The analytical description of the $(3,2)$-IET with two flips and signed permutation $(-3,1,-2)$, graph showed in Figure 9, is

$$T_a=\left\{\begin{array}{ccc}1-x,\hfill & \mathrm{if}& x\in I_1,\hfill \\ x-a,\hfill & \mathrm{if}& x\in I_2,\hfill \\ -x+2-2a,\hfill & \mathrm{if}& x\in I_3.\hfill \end{array}\right.$$

(6)

Theorem 11.

Let $T_a$ be the IET given by (6). Assume that $a\in \mathbb{Q}$, $a=\frac{p}{q}$, with $gcd(p,q)=1$. Then $\mathrm{Per}\left(T_a\right)=\left\{q\right\}.$ Otherwise, $\mathrm{Per}\left(T_a\right)=\varnothing .$

Proof. 

The Poincaré map of $T_a$ is a rotation of the circle. We define

$$r:=\frac{{\lambda }_2}{{\lambda }_1+{\lambda }_2}=\frac{1-2a}{1-a}=\frac{q-2p}{q-p}$$

and

$$s:=\frac{{\lambda }_1}{{\lambda }_1+{\lambda }_2}=\frac{a}{1-a}=\frac{p}{q-p}.$$

Note that since $gcd(p,q)=1$, we have that $gcd(q-2p,q-p)=1$. Then, the Poincaré map $T_1$ is the circle map given by

$$T_1\left(x\right)=x+r=x+\frac{q-2p}{q-p}.$$

Now two possibilities arise depending on r. First, if r is not rational, then $\mathrm{Per}\left(T_1\right)=\varnothing =\mathrm{Per}\left(T\right)$ and T is transitive. Second, if $r\in \mathbb{Q}$, then $\mathrm{Per}\left(T_1\right)=\{q-p\}$, $T_1$ has a periodic component which decomposes in $q-p$ intervals, $(q-p)s=p$ in $\left(0,\frac{a}{1-a}\right)$ and $(q-p)r=q-2p$ in $\left(\frac{a}{1-a},0\right)$. Remark that the p intervals in $I_1$ unfold in $2p$ intervals in $I_1\cup I_3$ and we receive for T a periodic component with $2(q-p)s+(q-p)r=q$ intervals. Therefore $\mathrm{Per}\left(T\right)=\left\{q\right\}$. □

4.3.3. Permutations $(3,-1,-2)$ and $(-2,-3,1)$

By Table 4, both IETs with permutations $(3,-1,-2)$ and $(-2,-3,1)$, respectively, have the same periods when ${\lambda }_1={\lambda }_3$. So, we fix $(3,-1,-2)$. The analytical description of the $(3,2)$-IET with two flips and signed permutation $(3,-1,-2)$, graph showed in Figure 10, is

$$T_a=\left\{\begin{array}{ccc}x+1-a,\hfill & \mathrm{if}& x\in I_1,\hfill \\ -x+1-a,\hfill & \mathrm{if}& x\in I_2,\hfill \\ -x+2(1-a),\hfill & \mathrm{if}& x\in I_3.\hfill \end{array}\right.$$

(7)

Clearly, if ${\lambda }_2={\lambda }_1$, that is $a=\frac{1}{3}$, we easily see that $\mathrm{Per}\left(T_a\right)=\left\{3\right\}$. In general, the normalized Poincaré map $T_1\left(x\right)=1-x$ and so $\mathrm{Per}\left(T_1\right)=\{1,2\}$. If ${\lambda }_2>{\lambda }_1$, that is, $a<\frac{1}{3}$, then the interval $I_2^{*}=(a,1-2a)$ is invariant with negative slope, so $1,2\in \mathrm{Per}\left(T_a\right)$. Three subintervals with the same length remain, so any orbit outside $I_2^{*}$ visits $I_3$ once. By Proposition 1, we conclude that $\mathrm{Per}\left(T\right)=\{1,2,3\}$. Conversely, we assume that ${\lambda }_2<{\lambda }_1$, i.e., $a>\frac{1}{3}$. Again, it is easy to see that any orbit visits $I_3$ once and by Proposition 1, we conclude that $\mathrm{Per}\left(T\right)=\{2,3\}$.

4.4. 3-IETs with Three Flips

By Table 5, both IETs with permutations $(-3,-1,-2)$ and $(-2,-3,-1)$, respectively, have the same periods when ${\lambda }_1={\lambda }_3$. So, we fix $(-3,-1,-2)$. The analytical description of the $(3,2)$-IET with two flips and signed permutation $(3,-1,-2)$, graph showed in Figure 2, is

$$T_a=\left\{\begin{array}{ccc}-x+1,\hfill & \mathrm{if}& x\in I_1,\hfill \\ -x+1-a,\hfill & \mathrm{if}& x\in I_2,\hfill \\ -x+2(1-a),\hfill & \mathrm{if}& x\in I_3.\hfill \end{array}\right.$$

(8)

In addition, it can be checked easily that the Poincaré map is that of Lemma 3. Then, we can state the following result.

Theorem 12.

Let $T_a$ be the IET given by (7). Then:

(a) 

If $a<\frac{1}{3}$, then $\mathrm{Per}\left(T_a\right)=\{1,2,3,6\}$.

(b) 

If $a\ge \frac{1}{3}$, then $\mathrm{Per}\left(T_a\right)=\{2n+1,2(2n+1)\}$ if $a=\frac{n}{2n+1}$ and $\mathrm{Per}\left(T_a\right)=\{2n-1,2(2n-1),2n+1,2(2n+1)\}$ if $\frac{n-1}{2n-1}<a<\frac{n}{2n+1}$.

Proof. 

We use Lemma 3 and Theorem 6 and proceed as in the proof of Theorem 9. □

5. Two Case Studies of 3-IETs

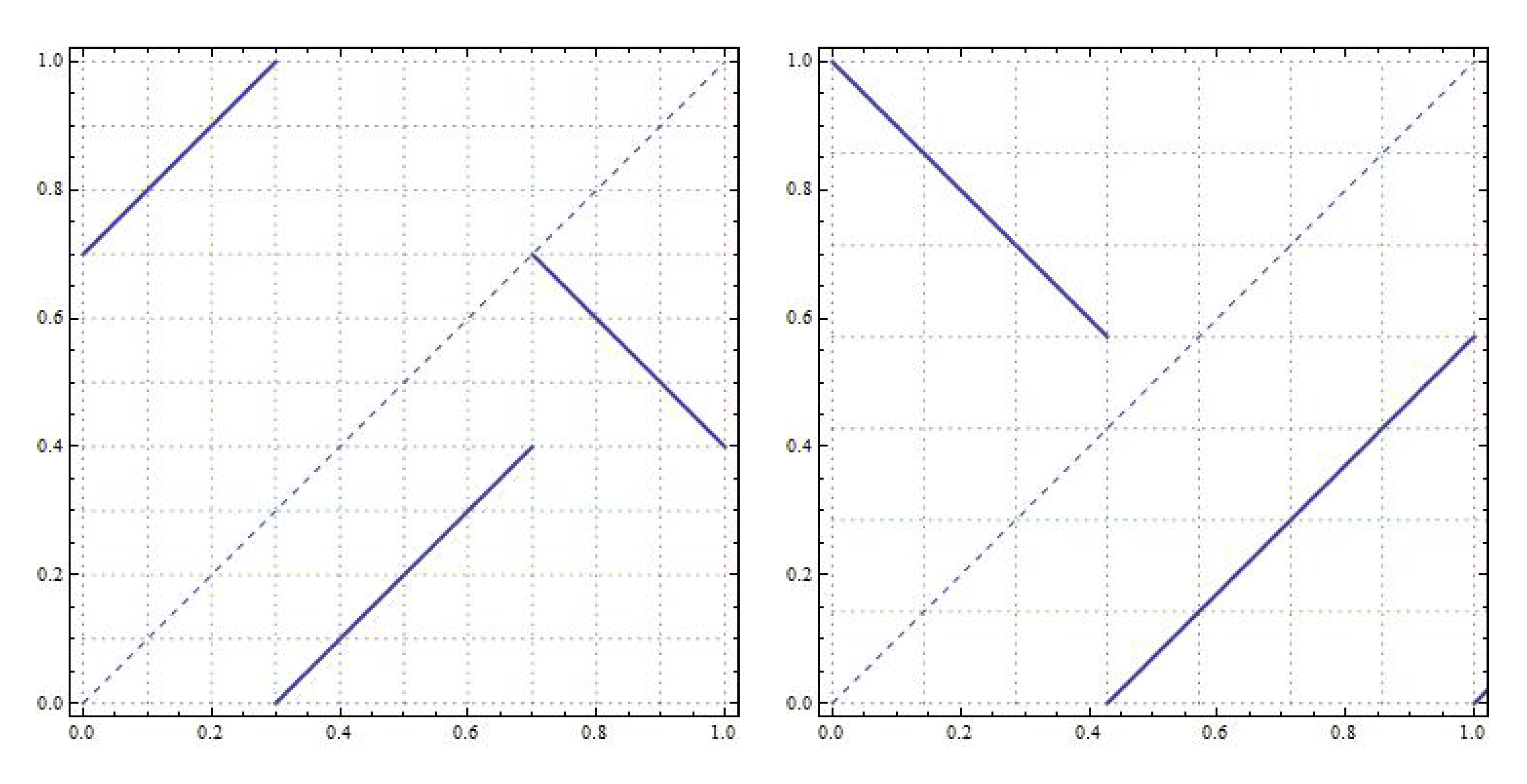
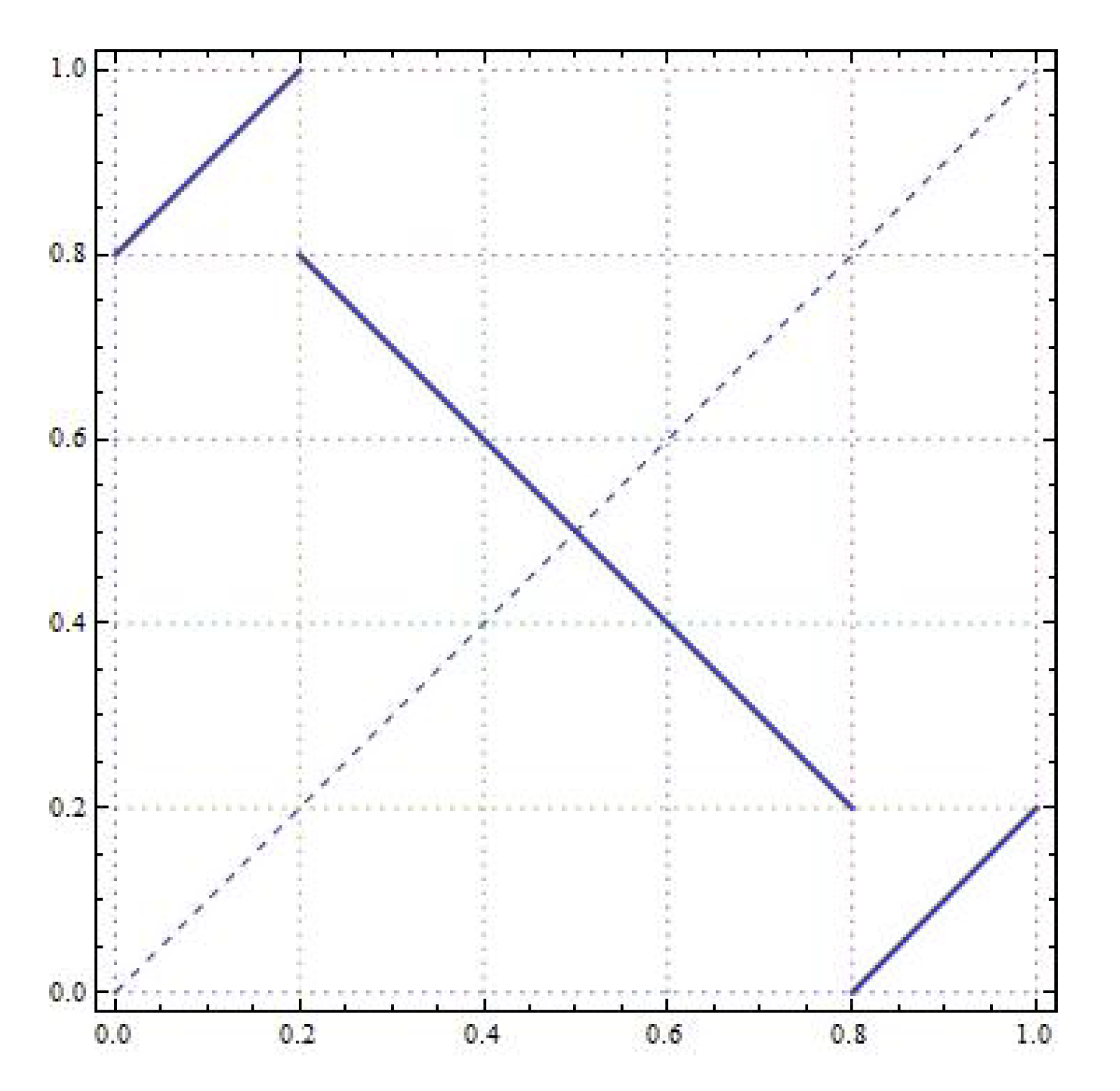
This section will study the set of periods of 3-IETs for two different permutations with one flip, namely $(3,1,-2)$ and $(3,-2,1)$. Our study shows that one must use different techniques to compute the periods of T. Of course, this fact is an additional problem for the characterization of periods of general IETs.

5.1. The Permutation $\pi =(3,1,-2)$

Note that this map is defined as

$$T\left(x\right)=\left\{\begin{array}{ccc}x+1-{\lambda }_1& if& x\in [0,{\lambda }_1),\\ x-{\lambda }_1& if& x\in ({\lambda }_1,{\lambda }_1+{\lambda }_2),\\ -x+1+{\lambda }_2& if& x\in ({\lambda }_1+{\lambda }_2,1].\end{array}\right.$$

First, we prove the following result.

Lemma 4.

The 3-IET T with permutation $\pi =(3,1,-2)$ has a fixed point if and only if ${\lambda }_3>{\lambda }_1$.

Proof. 

T has a fixed point is $-x+1+{\lambda }_2=x$. The fixed point is

$$x=\frac{1+{\lambda }_2}{2},$$

but note that it has to be greater than ${\lambda }_1+{\lambda }_2$. This condition reads as

$$\frac{1+{\lambda }_2}{2}>{\lambda }_1+{\lambda }_2,$$

which implies easily

$${\lambda }_3>{\lambda }_1.$$

Since the proof works in both directions, it concludes. □

Assume that ${\lambda }_3>{\lambda }_1$ so that T has a fixed point. Then, the interval

$$J=\left({\lambda }_1+{\lambda }_2,\underset{x\to {({\lambda }_1+{\lambda }_2)}^{+}}{lim}T\left(x\right)\right)$$

and contains the fixed point of T. In addition,

$$\underset{x\to {({\lambda }_1+{\lambda }_2)}^{+}}{lim}T\left(x\right)=1-{\lambda }_1,$$

and so, the length of $\left|J\right|=1-2{\lambda }_1-{\lambda }_2$. Let ${\lambda }_3^{*}={\lambda }_3-\left|J\right|={\lambda }_1$. Normalizing ${\lambda }_1^{\prime }=\frac{{\lambda }_1}{1-\left|J\right|}$, ${\lambda }_2^{\prime }=\frac{{\lambda }_2}{1-\left|J\right|}$ and ${\lambda }_3^{\prime }=\frac{{\lambda }_3^{*}}{1-\left|J\right|}$, we define $T^{\prime }$ to have permutation $(3,1,-2)$ and length vector $\left({\lambda }_1^{\prime },{\lambda }_2^{\prime },{\lambda }_3^{\prime }\right)$. Then, we have the following result.

Theorem 13.

Under the above notation, assume that ${\lambda }_3>{\lambda }_1$. Then

• If ${\lambda }_1^{\prime }=\frac{1}{n+2}$ for some $n\in \mathbb{N}$, then $\mathrm{Per}\left(T\right)=\{1,2,n+2,2(n+2\left)\right\}$.
• If ${\lambda }_1^{\prime }\in \left(\frac{1}{n+2},\frac{1}{n+1}\right)$, then $\mathrm{Per}\left(T\right)=\{1,2,n+1,2(n+1),n+2,2(n+2\left)\right\}$.

Proof. 

Note that all the points of J are periodic with period one or two. Since J is invariant by T so are the subintervals of $I\setminus J$. Then, the map $T^{\prime }$ is well defined and we have that $\mathrm{Per}\left(T\right)=\{1,2\}\cup \mathrm{Per}\left(T^{\prime }\right)$. In addition, $T^{\prime }$ is given by the expression

$$T^{\prime }\left(x\right)=\left\{\begin{array}{ccc}x+1-{\lambda }_1& if& x\in [0,{\lambda }_1^{\prime }),\\ x-{\lambda }_1& if& x\in ({\lambda }_1^{\prime },{\lambda }_1^{\prime }+{\lambda }_2^{\prime }),\\ -x+2(1+{\lambda }_1^{\prime })& if& x\in ({\lambda }_1^{\prime }+{\lambda }_2^{\prime },1].\end{array}\right.$$

By Theorem 8, we check that the periods of $T^{\prime }$ are either $\mathrm{Per}\left(T^{\prime }\right)=\{n+2,2(n+2)\}$ when ${\lambda }_1^{\prime }=\frac{1}{n+2}$ for some $n\in \mathbb{N}$ or $\mathrm{Per}\left(T^{\prime }\right)=\{n+1,2(n+1),n+2,2(n+2)\}$ when ${\lambda }_1^{\prime }\in \left(\frac{1}{n+2},\frac{1}{n+1}\right)$. Then, the proof concludes. □

Theorem 13 characterizes the set of periods of T when ${\lambda }_3>{\lambda }_1$ even when the components ${\lambda }_1$, ${\lambda }_2$ and ${\lambda }_3$ are not rationally dependent. Now, we assume that ${\lambda }_1=\frac{k_1}{m}$, ${\lambda }_2=\frac{k_2}{m}$ and ${\lambda }_3=\frac{k_3}{m}=\frac{m-k_1-k_2}{m}$, for some $k_1,k_2,m\in \mathbb{N}$. If $gcd(k_1,k_2,m)=l\ne 1$, then we can find $k_1^{\prime },k_2^{\prime },m^{\prime }\in \mathbb{N}$ such that write ${\lambda }_1=\frac{k_1^{\prime }}{m^{\prime }}$, ${\lambda }_2=\frac{k_2^{\prime }}{m^{\prime }}$ and ${\lambda }_3=\frac{m^{\prime }-k_1^{\prime }-k_2^{\prime }}{m^{\prime }}$.

Since Theorem 13 characterizes the periods of T such that $k_3>k_1$, we focuss our attention to the case $k_3\le k_1$. It is easy to realize that T is a variation of the rotation of the circle $(x+1-{\lambda }_1)\mathrm{mod}1$. Only the interval $I_3$ is modified to reverse the orientation. We consider the map T defined on $(0,m)$ as follows

$$T\left(x\right)=\left\{\begin{array}{ccc}x+m-k_1& if& x\in [0,k_1),\\ x-k_1& if& x\in (k_1,k_1+k_2),\\ -x+m+k_2& if& x\in (k_1+k_2,m].\end{array}\right.$$

Note that this can be done by the conjugacy that carries $[0,1]$ into $[0,m]$ in a linear way. We label the subinterval $(j,j+1)$ by j, $j=0,1,\cdots ,m-1$. It is immediate to see that if $j<k_1+k_2$, then

$$j\stackrel{+}{\to }(j+1-k_1)\mathrm{mod}m.$$

On the other hand, for $1\le i\le k_3$ we check that the iteration of the interval labeled with $m-i$ is given by

$$m-i\stackrel{-}{\to }[(m-i)+(m-k_1+2i-1-k_3)]\mathrm{mod}m=(m+i-k_1-k_3-1)\mathrm{mod}m.$$

Recall that $m=k_1+k_2+k_3$ and note that

$$T(m-i)=R(m-k_3+i-1)$$

for $1\le i\le k_3$, whew R is the rotation $R\left(x\right)=(x+m-k_1)\mathrm{mod}m$.

Now, fixed i, for any $j\in \{1,\cdots ,k_3\}$ we consider the equation

$$(m+i-k_1-k_3-1)+(m-k_1)X=(m-j)\mathrm{mod}m,$$

which tells us the time X needed for the rotation R to go from interval $(m+i-k_1-k_3-1)$ to $m-j$, which reads as

$$(m-k_1)X=(k_1+k_3+1-i-j)\mathrm{mod}m.$$

(9)

In the following, we will use a series of fundamental results on congruences. First, the reader is referred to ([25], Chapter 5) for an account of the topic and the resolution of linear congruences. The Equation (9) has solution $X_{ij}$ if and only if $gcd(m,k_1)=gcd(m-k_1,m)$ divides $k_1+k_3+1-i-j$. Clearly, $X_{ij}=X_{i^{\prime }{j}^{\prime }}$ when $i+j=i^{\prime }+j^{\prime }$. We construct the matrix $\mathbf{X}=\left(X_{ij}\right)$, where $X_{ij}$ is either the solution of the equation or the symbol *, here used to state that there is not solution and therefore the intervals $m+i-k_1-k_3-1$ and $m-j$ are not map one into the other by the rotation R.

Now, we distinguish two cases. If $gcd(m,k_1)=1$, then the Equation (9) always have a unique solution given by

$$X_{ij}=(k_1+k_3+1-i-j){(m-k_1)}^{\phi \left(m\right)-1}\mathrm{mod}m,$$

where $\phi :\mathbb{N}\to \mathbb{N}$ is the Euler function given by

$$\phi \left(m\right)=Card\{n\le m:gcd(n,m)=1\}.$$

If $gcd(m,k_1)=d>1$, then the Equation (9) has a solution if and only if d divides $k_1+k_3+1-i-j$. It has d different solutions, the smaller one can be computed by solving the equation

$$\frac{m-k_1}{d}X=\frac{k_1+k_3+1-i-j}{d}\mathrm{mod}\frac{m}{d},$$

that is, the solution will be

$$X_{ij}=\frac{k_1+k_3+1-i-j}{d}{\left(\frac{m-k_1}{d}\right)}^{\phi \left(\frac{m}{d}\right)-1}\mathrm{mod}\frac{m}{d}.$$

Hence, we can compute the set of periods of T in some particular cases as follows.

Theorem 14.

Let $k_1\ge k_3=1$. Then:

(a) 

If $gcd(m,k_1)=1$, then $\mathrm{Per}\left(T\right)=\{m,2m\}.$

(b) 

If $gcd(m,k_1)=d>1$, $\mathrm{Per}\left(T\right)=\{m/d,2m/d\}.$

Proof. 

With the notation above,

$$m-1\stackrel{-}{\to }[(m-1)+(m-k_1)]\mathrm{mod}m=[m-(1+k_1)]\mathrm{mod}m,$$

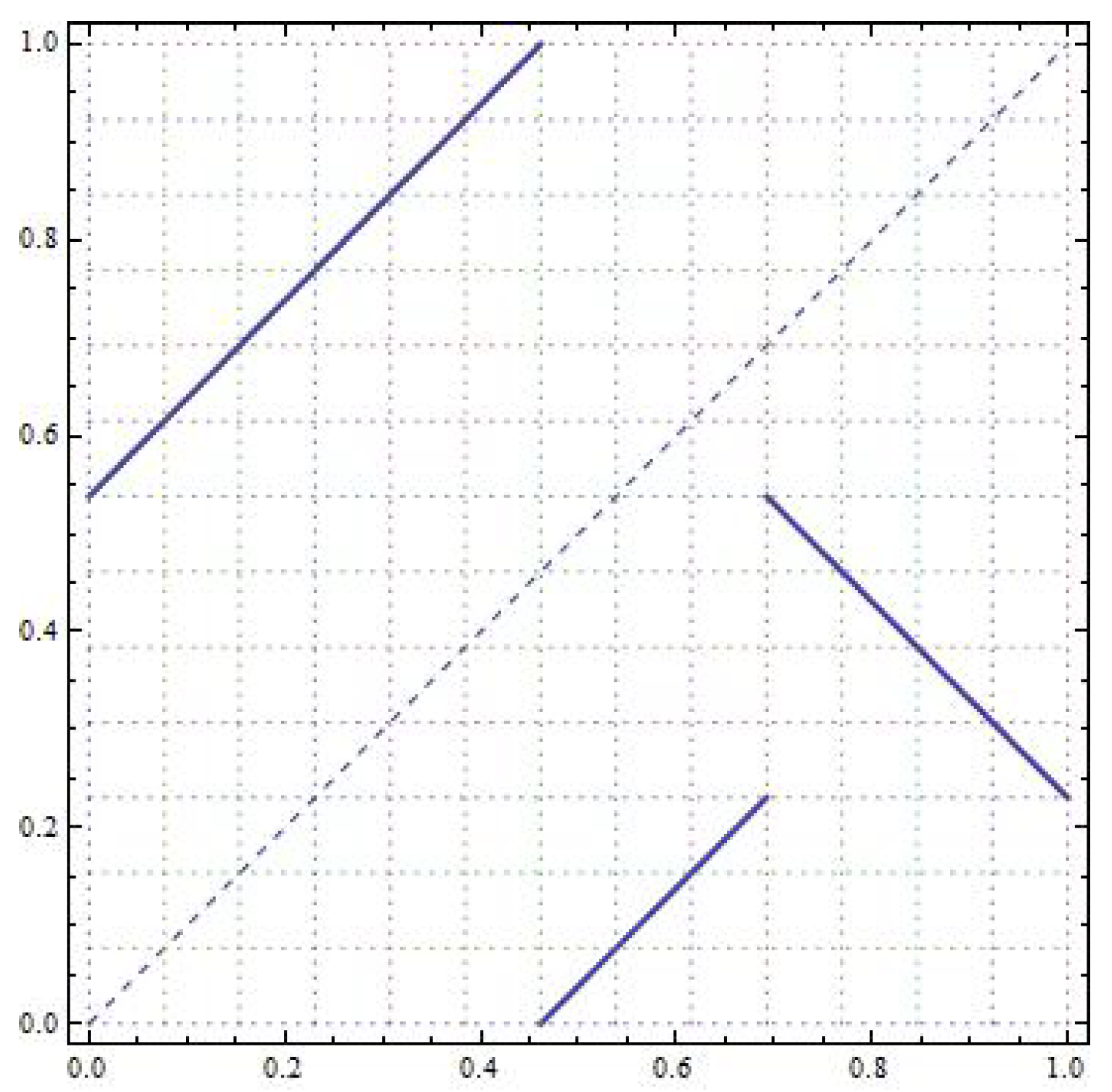
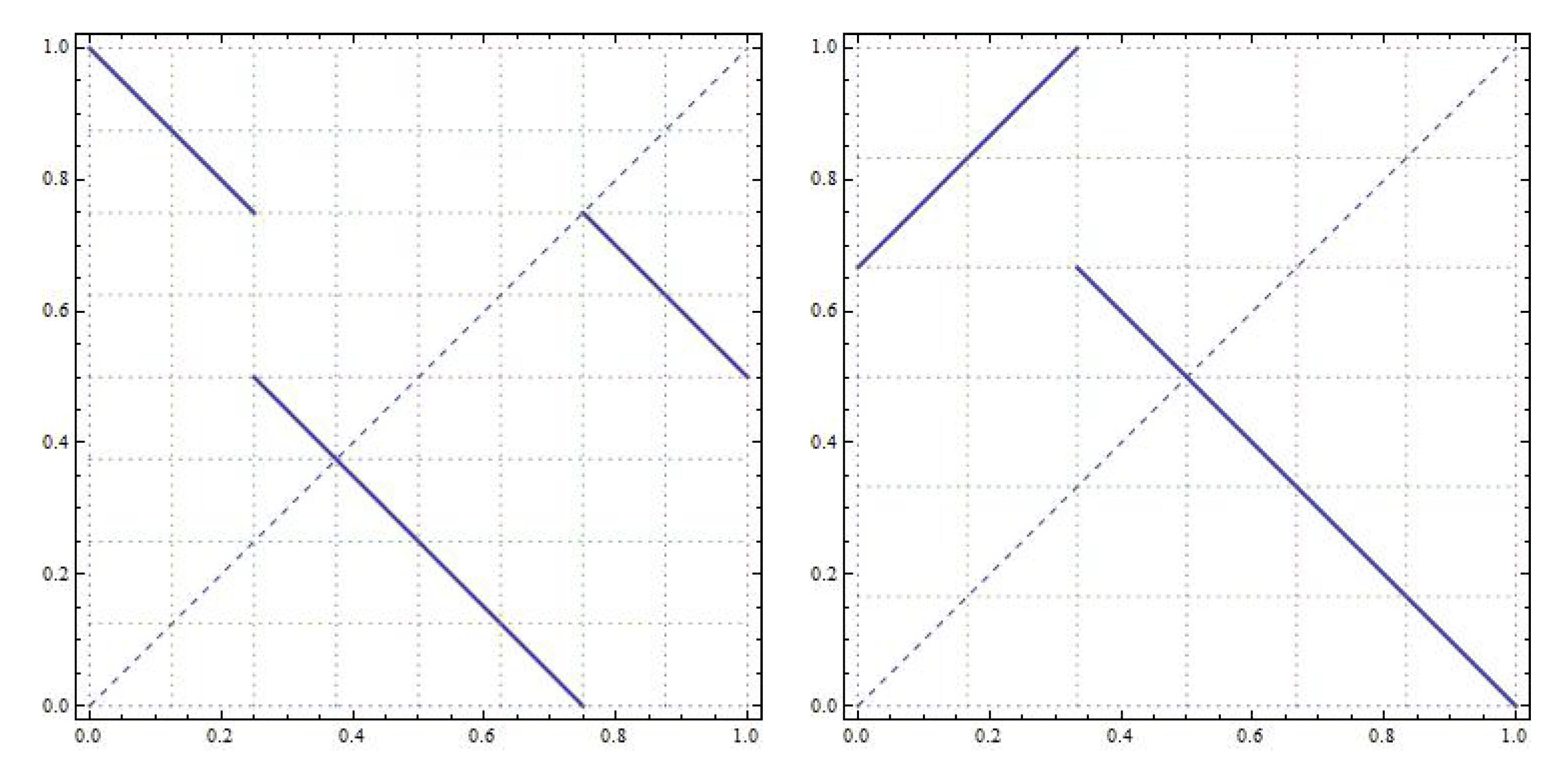
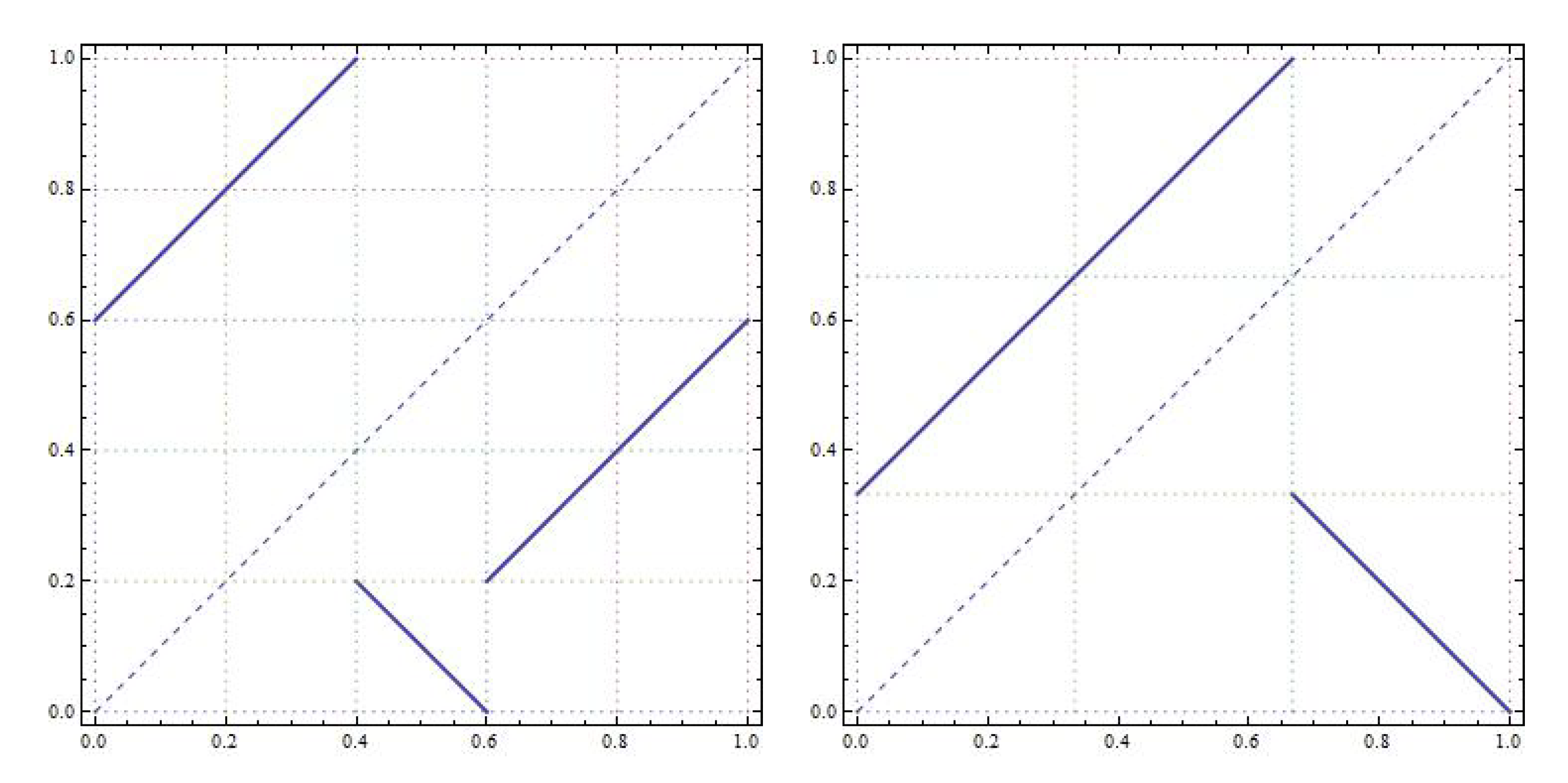
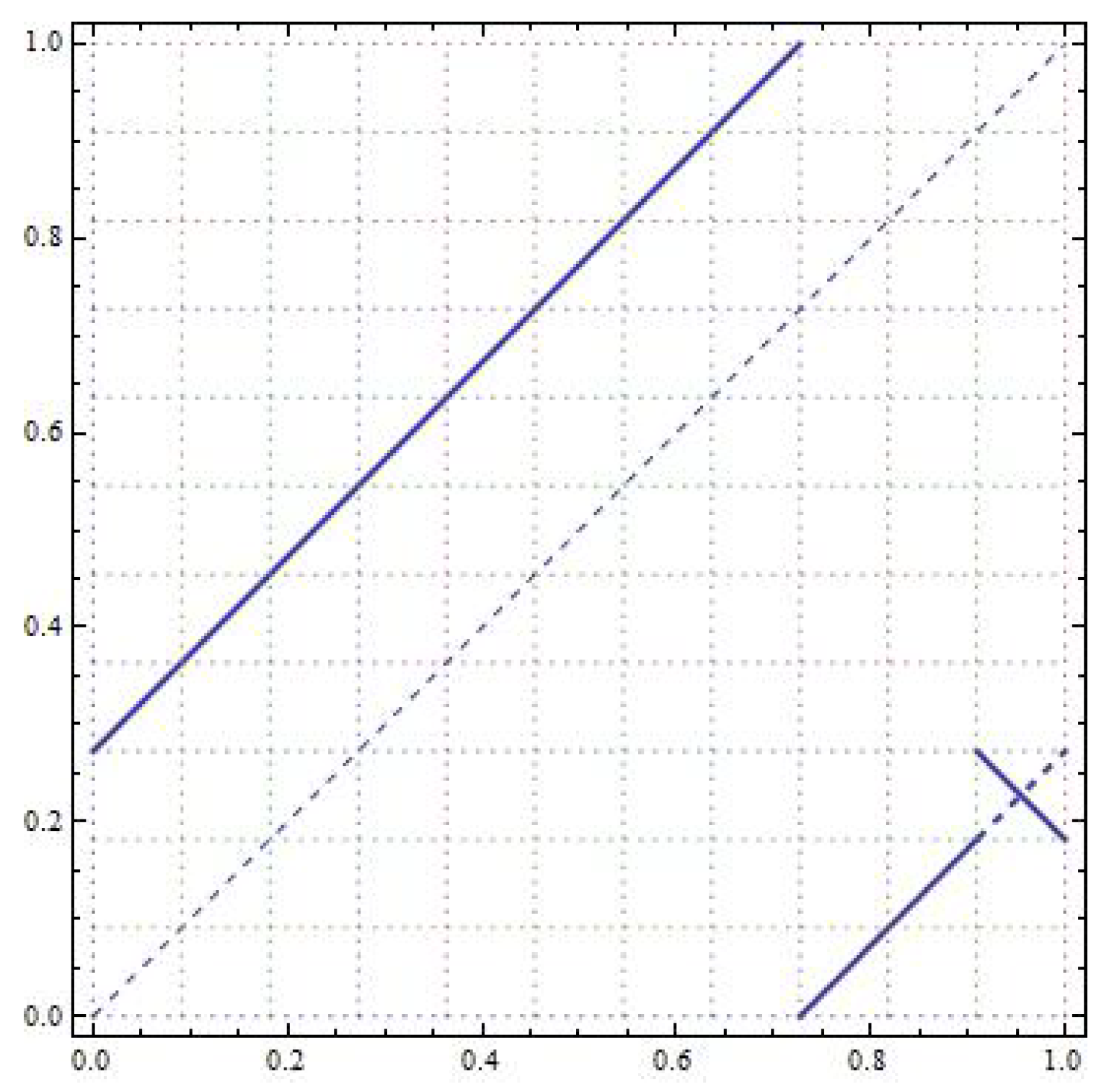
and therefore, T moves the intervals $(j,j+1)$, $j=0,1,\cdots ,m-1$ like the rotation $R:[0,m]\to [0,m]$ given by $R\left(x\right)=(x+m-k_1)\mathrm{mod}m$. Note that $T(m-1,m)=R(m-1,m)$. See Figure 11 to see the differences between the map T and the rotation R.

Note that $i=j=1$ and thus Equation (9) reads as

$$(m-k_1)X=k_1\mathrm{mod}m,$$

which obviously has always solution. If $gcd(m,k_1)=1$, then the solution is unique and equal to $m-1$ because

$$(m-k_1)(m-1)\mathrm{mod}m=k_1\mathrm{mod}m.$$

Then $m\in \mathrm{Per}\left(T\right)$, and since the image of interval $m-1$ has negative slope, we have that $2m\in \mathrm{Per}\left(T\right)$. This finishes the proof of (a). To prove (b), we take the equation

$$\frac{m-k_1}{d}X=\frac{k_1}{d}\mathrm{mod}\frac{m}{d}.$$

Reasoning as above, we find that $X_{11}=\frac{m}{d}-1$. Finally, for the rest of intervals j in $I_1\cup I_2$ not included in the orbit of $m-1$ note that T acts as the rotation R and therefore the period associated to the interval j is $m/d$. Then, $\mathrm{Per}\left(T\right)=\{m/d,2m/d\}$ and the proof concludes. □

Theorem 15.

Let $k_1\ge k_3=2$. Then:

(a) 

If $gcd(m,k_1)=1$, then $\mathrm{Per}\left(T\right)=\{m_1,2m_1,m_2,2m_2\}$, where

$$m_1=-k_1^{\phi \left(m\right)-1}\mathrm{mod}m,$$

and

$$m_2=k_1^{\phi \left(m\right)-1}\mathrm{mod}m.$$

In addition, $m_1+m_2=m$, with $m_1\ne m_2$.

(b) 

If $gcd(m,k_1)=d>1$, $\mathrm{Per}\left(T\right)=\{m/d,2m/d\}.$

Proof. 

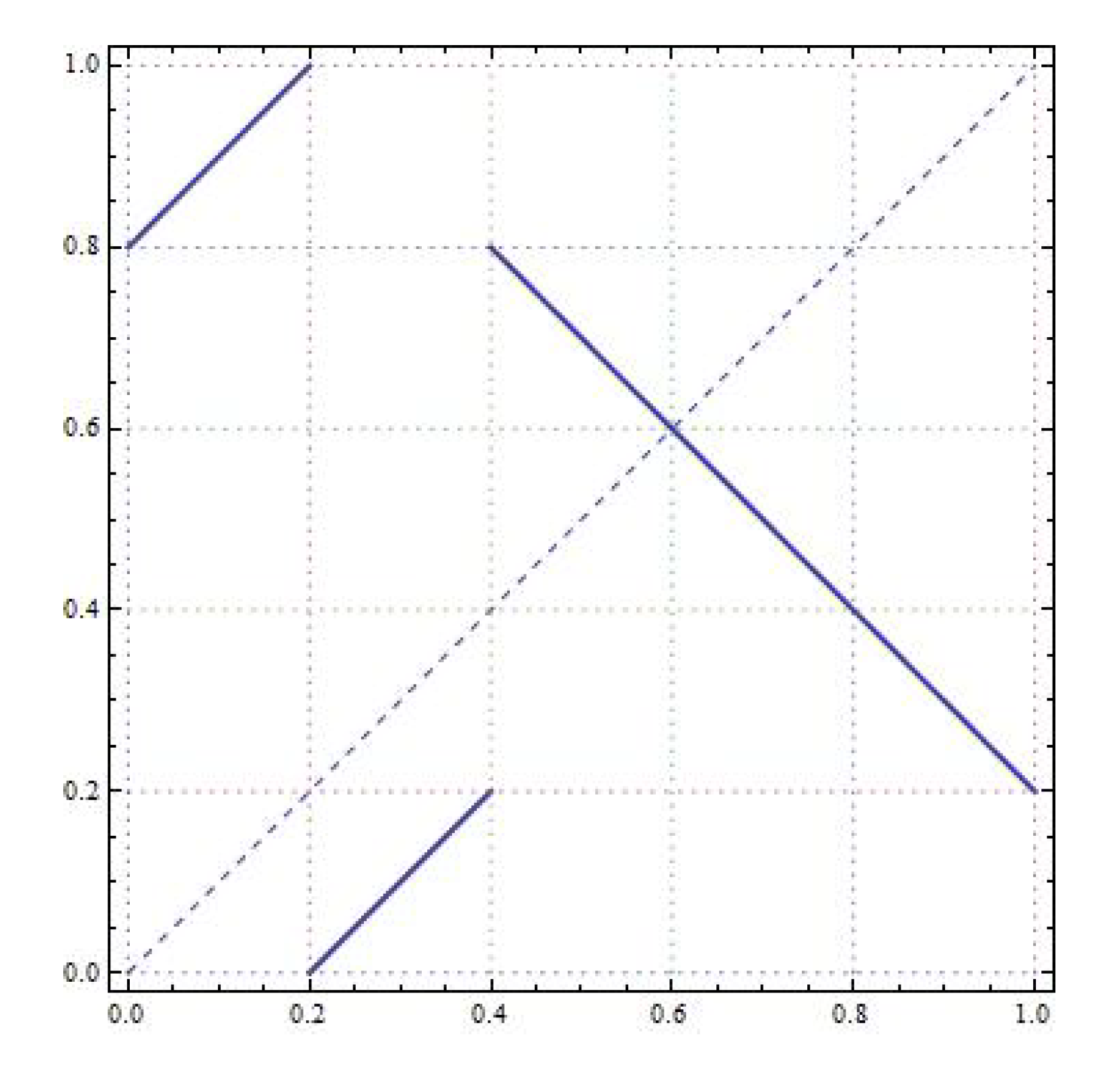
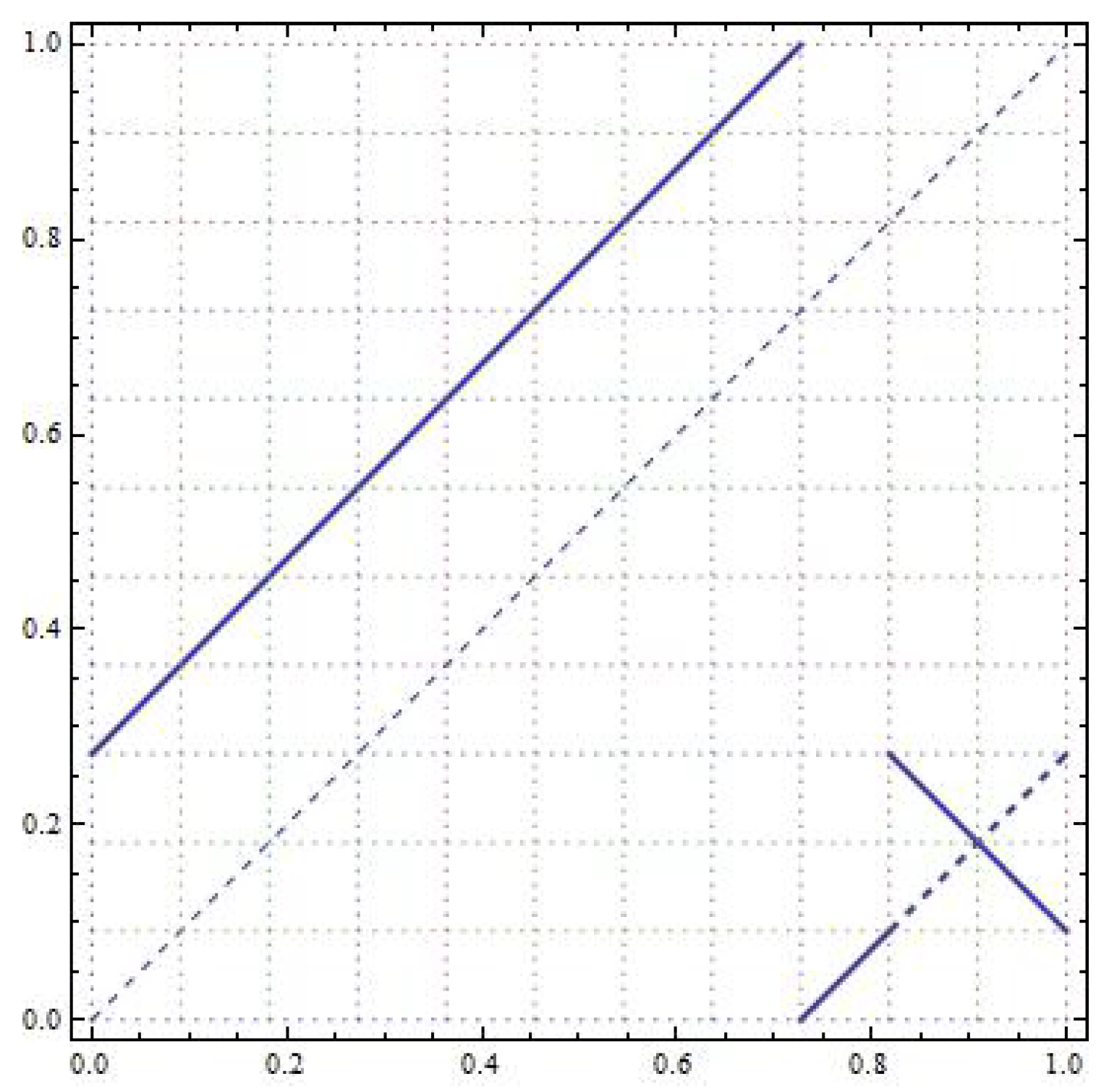
We can see T on $[0,m-2]$ as the rotation $R\left(x\right)=(x+m-k_1)\mathrm{mod}m$. Figure 12 shows the differences between the maps T and R.

Note that $i,j\in \{1,2\}$ and thus Equation (9) gives us three equations, namely

$$(m-k_1)X=(k_1+1)\mathrm{mod}m,\mathrm{for}i=j=1,$$

(10)

$$(m-k_1)X=k_1\mathrm{mod}m,\mathrm{for}i+j=3,$$

(11)

and

$$(m-k_1)X=(k_1-1)\mathrm{mod}m,\mathrm{for}i=j=2.$$

(12)

Now, we prove (a). Reasoning as in Theorem 14, we know that Equation (11) has solution $X_{12}=X_{21}=m-1$. Thus, since the numbers $X_{ij}$ are generated in function of the dynamics of rotation $R\left(x\right)=(x+m-k_1)\mathrm{mod}m$, which moves the indices forming a periodic orbit of period m, necessarily the solutions $X_{11}$ and $X_{22}$ are smaller than $m-1$. Then, $m_1=X_{11}+1$ and $m_2=X_{22}+1$ have to be in $\mathrm{Per}\left(T\right)$. As the slope of T on the subintervals $m-1$ and $m-2$ is negative, then $2m_1,2m_2\in \mathrm{Per}\left(T\right)$. Note also that $m_1\ne m_2$ (if $m_1$ was equal to $m_2$, then $X_{11}$ would be equal to $X_{22}$ and the two linear congruences (10) and (11) would be satisfied. Then, subtracting these equations we would obtain $0=2\mathrm{mod}m$, which is impossible because $m\ge 3$). To check that $m_1+m_2=m$, note that

$$\begin{array}{ccc}\hfill m_1& =& 1+X_{11}=1+(k_1+1){(m-k_1)}^{\phi \left(m\right)-1}\mathrm{mod}m\hfill \\ & =& 1+(k_1+1){(-1)}^{\phi \left(m\right)-1}{k}_1^{\phi \left(m\right)-1}\mathrm{mod}m\hfill \\ & =& 1-(k_1+1)k_1^{\phi \left(m\right)-1}\mathrm{mod}m\hfill \\ & =& 1-\left(k_1^{\phi \left(m\right)}+k_1^{\phi \left(m\right)-1}\right)\mathrm{mod}m\hfill \\ & =& -k_1^{\phi \left(m\right)-1}\mathrm{mod}m,\hfill \end{array}$$

where we have used the development of Newton’s binomial, and the facts that $\phi \left(m\right)$ is even for all $m\ge 3$ and $k_1^{\phi \left(m\right)}=1\mathrm{mod}m$. Similarly

$$m_2=1+X_{22}=k_1^{\phi \left(m\right)-1}\mathrm{mod}m.$$

Thus

$$\begin{array}{ccc}\hfill m_1+m_2& =& -k_1^{\phi \left(m\right)-1}\mathrm{mod}m+k_1^{\phi \left(m\right)-1}\mathrm{mod}m=m.\hfill \end{array}$$

Now, we prove (b). Equation (11) has solution because d divides $k_1$. However, d does not divide $k_1-1$ and $k_1+1$ and thus Equations (10) and (12) do not have any solution. Then the matrix

$$\mathbf{X}=\left(\begin{array}{cc}*& \frac{m}{d}-1\\ \frac{m}{d}-1& *\end{array}\right).$$

Then, the subinterval formed with subintervals $m-1$ and $m-2$ is periodic of period $\frac{m}{d}$ and with negative slope, which implies that $m/d,2m/d\in \mathrm{Per}\left(T\right)$. For the rest of intervals outside of $I_3$, since no other periods are possible for the rotation $x+\frac{m}{d}$, we conclude the proof. □

Theorem 16.

Let $k_1\ge k_3=3$. Then:

(a)

If $gcd(m,k_1)=1$, then $\mathrm{Per}\left(T\right)=\{m_1,2m_1,m_2,2m_2\}$, where either

$$m_1=-k_1^{\phi \left(m\right)-1}\mathrm{mod}m,$$

and

$$m_2=2k_1^{\phi \left(m\right)-1}\mathrm{mod}m,$$

or

$$m_1=2k_1^{\phi \left(m\right)-1}\mathrm{mod}m,$$

and

$$m_2=-k_1^{\phi \left(m\right)-1}\mathrm{mod}m.$$

In addition, either $2m_1+m_2=m$ or $m_1+2m_2=m.$

(b)

If $gcd(m,k_1)=d>1$, then:

(b1)

If $d\ne 2$, then $\mathrm{Per}\left(T\right)=\{m/d,2m/d\}$.

(b2)

If $d=2$, then $\mathrm{Per}\left(T\right)=\{m_1,2m_1,m_2,2m_2,m_3,2m_3\}$ where

$$m_1=-{\left(\frac{k_1}{2}\right)}^{\phi \left(\frac{m}{2}\right)-1}\mathrm{mod}\frac{m}{2},$$

$$m_2=\frac{m}{2},$$

and

$$m_3={\left(\frac{k_1}{2}\right)}^{\phi \left(\frac{m}{2}\right)-1}\mathrm{mod}\frac{m}{2}.$$

Proof. 

Note that $i,j\in \{1,2,3\}$ and thus Equation (9) gives us three equations, namely

$$(m-k_1)X=(k_1+2)\mathrm{mod}m,\mathrm{for}i=j=1,$$

(13)

$$(m-k_1)X=(k_1+1)\mathrm{mod}m,\mathrm{for}i+j=3,$$

(14)

$$(m-k_1)X=k_1\mathrm{mod}m,\mathrm{for}i+j=4,$$

(15)

$$(m-k_1)X=(k_1-1)\mathrm{mod}m,\mathrm{for}i+j=5,$$

(16)

$$(m-k_1)X=(k_1-2)\mathrm{mod}m,\mathrm{for}i=j=3.$$

(17)

Now, we prove (a). We know that Equation (15) has the unique solution $X_{13}=X_{22}=X_{31}=m-1$. Then the matrix $\mathbf{X}=\left(X_{ij}\right)$ has the form

$$\mathbf{X}=\left(\begin{array}{ccc}{X}_{11}& X_{12}& m-1\\ X_{21}& m-1& X_{23}\\ m-1& X_{32}& X_{33}\end{array}\right).$$

Since the rotation R moves the intervals j in a periodic manner, with period m, we deduce that $max\{X_{11},X_{12},X_{23},X_{33}\}<m-1$. Since $T(m-2,m-1)=R(m-2,m-1)$ and R is m-periodic, the orbit of the subinterval $m-2$ under T must be combined with either $m-1$ or $m-3$. Thus, either $X_{11}>X_{12}$ or $X_{33}>X_{32}$ (note that since $T(m-1,m)=R(m-3,m-2)$ and $T(m-3,m-2)=R(m-1,m)$, otherwise it would imply that subintervals $m-1$ and $m-3$ would be periodic without any combination with subinterval $m-2$, and this is not possible). If $X_{11}>X_{12}$, then the subintervals $m-1$ and $m-2$ form a periodic subinterval with period $m_1=X_{11}+1$ and negative slope, which implies that $m_1,2m_1\in \mathrm{Per}\left(T\right)$. Then, the subinterval $m-3$ is periodic with period $m_2=1+X_{33}$ and so $\mathrm{Per}\left(T\right)=\{m_1,2m_1,m_2,2m_2\}$. Similarly, we reasoning with the case $X_{33}>X_{23}$ to conclude that $\mathrm{Per}\left(T\right)=\{m_1,2m_1,m_2,2m_2\}$. Note that it is not possible to have periodic intervals outside $I_3$ because they would have to have period m. Then, either $2m_1+m_2=m$ (if $X_{11}>X_{12}$) or $m_1+2m_2=m$ (if $X_{33}>X_{23}$). The values of $m_1$ and $m_2$ are obtained as in the proof of Theorem 15, and the proof of (a) concludes.

Now, we prove (b). If $gcd(k_1,m)=d>1$, then, solving the linear congruences we obtain the matrix

$$\mathbf{X}=\left(\begin{array}{ccc}{X}_{11}& *& \frac{m}{d}-1\\ *& \frac{m}{d}-1& *\\ \frac{m}{d}-1& *& X_{33}\end{array}\right).$$

Note that Equations (13) and (17) have solution if and only if $d=2$. This is the case (b2), in which $\mathrm{Per}\left(T\right)=\{m_1,2m_1,m_2,2m_2,m_3,2m_3\}$, where

$$m_1=1+X_{11}=1+\frac{k_1+2}{2}{\left(\frac{m-k_1}{2}\right)}^{\phi \left(\frac{m}{2}\right)-1}\mathrm{mod}\frac{m}{2},$$

$$m_2=\frac{m}{2},$$

and

$$m_3=1+X_{33}=1+\frac{k_1-2}{2}{\left(\frac{m-k_1}{2}\right)}^{\phi \left(\frac{m}{2}\right)-1}\mathrm{mod}\frac{m}{2}.$$

On the other hand,

$$\begin{array}{ccc}\hfill m_1+m_3& =& -{\left(\frac{k_1}{2}\right)}^{\phi \left(\frac{m}{2}\right)-1}\mathrm{mod}\frac{m}{2}+{\left(\frac{k_1}{2}\right)}^{\phi \left(\frac{m}{2}\right)-1}\mathrm{mod}\frac{m}{2}=\frac{m}{2},\hfill \end{array}$$

and thus $m_1+m_2+m_3=m$.

In the case (b1), $d\ne 2$, the matrix is

$$\mathbf{X}=\left(\begin{array}{ccc}*& *& \frac{m}{d}-1\\ *& \frac{m}{d}-1& *\\ \frac{m}{d}-1& *& *\end{array}\right),$$

and thus $\mathrm{Per}\left(T\right)=\{m/d,2m/d\}$, and the proof concludes. □

The case $k_3=4$ presents a variation. By Theorem 2, we can have at most three sets of the form $\{m,2m\}$, for some positive integer m, belonging to the set of periods of T. However, now we have four subintervals with a negative slope, and we must figure out how they join. The procedure is as before. Here, we can see T on $[0,m-4]$ as the rotation $R\left(x\right)=(x+m-k_1)\mathrm{mod}m$. However, now, in the interval $I_3$, we have four subintervals with a negative slope, so that we write the matrix

$$\mathbf{X}=\left(\begin{array}{cccc}{X}_{11}& X_{12}& X_{13}& X_{14}\\ X_{21}& X_{22}& X_{23}& X_{24}\\ X_{31}& X_{32}& X_{33}& X_{34}\\ X_{41}& X_{42}& X_{43}& X_{44}\end{array}\right)$$

Assume first that $gcd(m,k_1)=1$. The smallest entries of the matrix will provide the periods of T. Below, we show several examples.

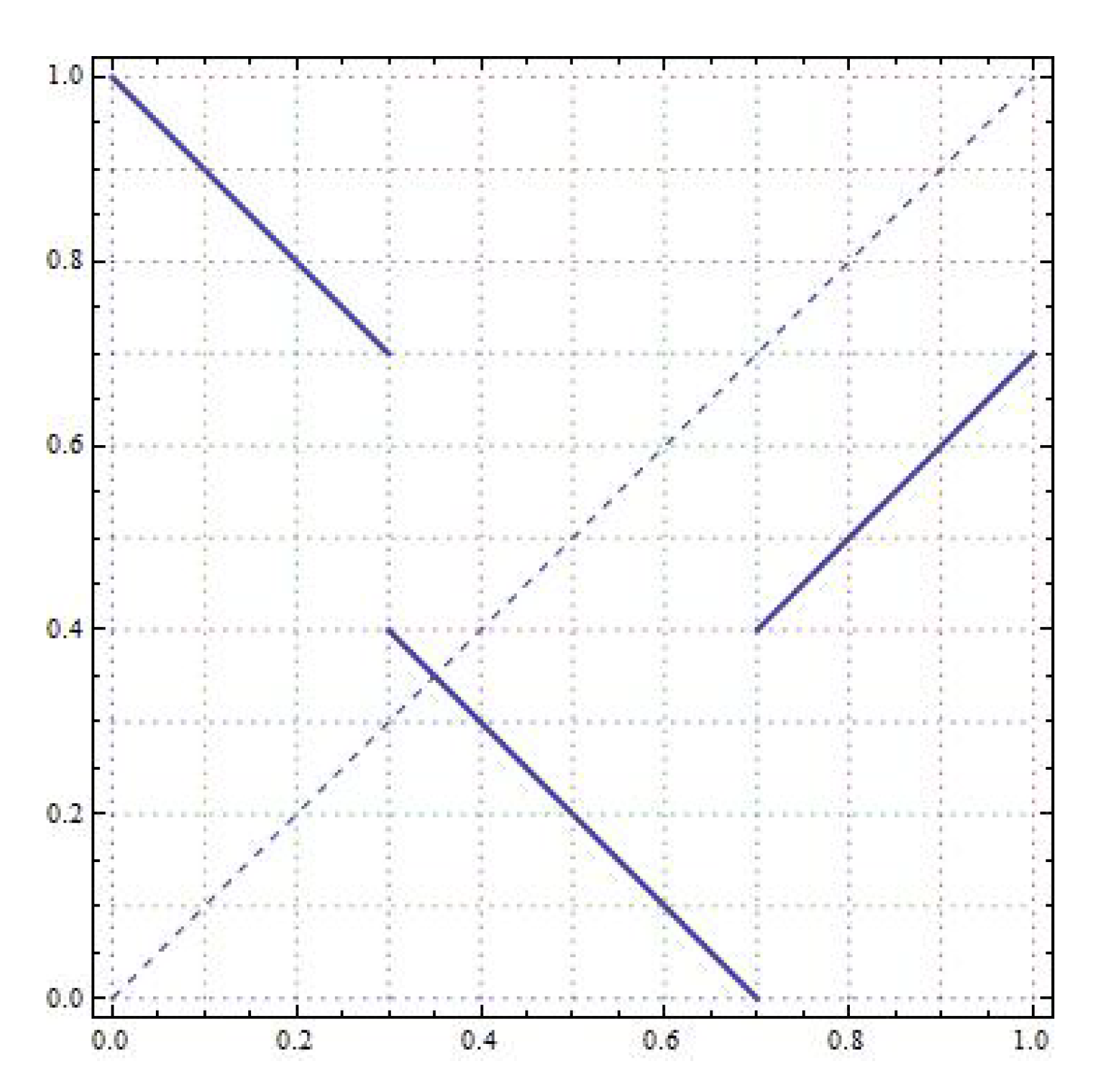
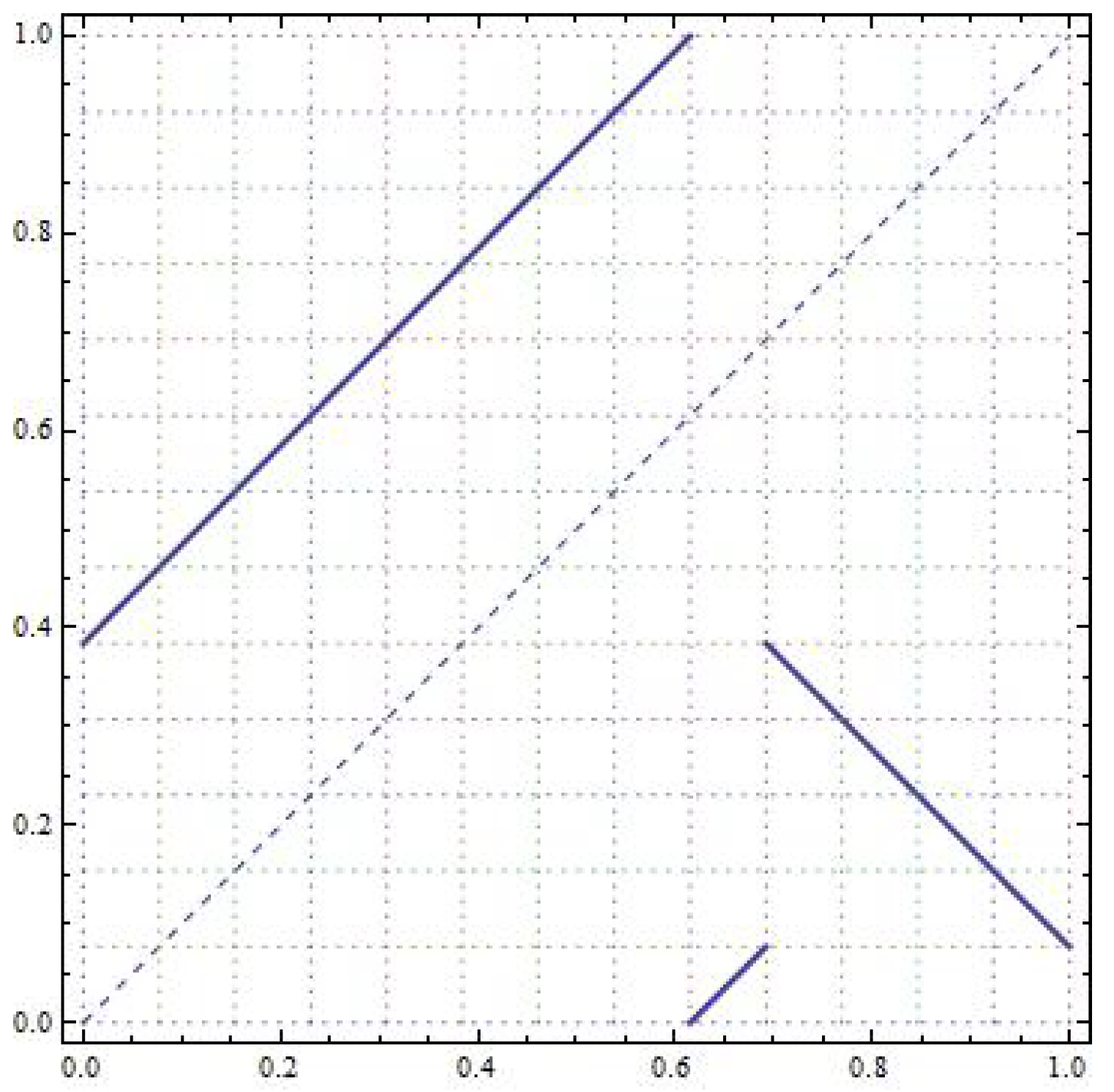
Example 2.

Let $m=13$ and the length vector $(8,1,4)$. Figure 13 shows the graph of T in which one can check the loops that give rise to the set of periods. We write the matrix

$$\mathbf{X}=\left(\begin{array}{cccc}10& 2& 7& 12\\ 2& 7& 12& 4\\ 7& 12& 4& 9\\ 12& 4& 9& 1\end{array}\right).$$

The element $X_{44}=1$ gives us a loop of length 2 with a negative slope, so $2,4\in \mathrm{Per}\left(T\right)$. The elements $X_{12}=X_{21}=2$ gives us a loop of length 6 with a positive slope, so the period 6. However, note that subintervals 11 and 12 are contiguous. Both forms a loop of $[11,12]$ of length 3 and negative slope, and so the set of periods $\{3,6\}$. Finally, the element $X_{33}=4$ forms a loop of length 5 and negative slope, and so the set of periods $\{5,10\}$. Thus $\mathrm{Per}\left(T\right)=\{2,4,3,6,5,10\}$.

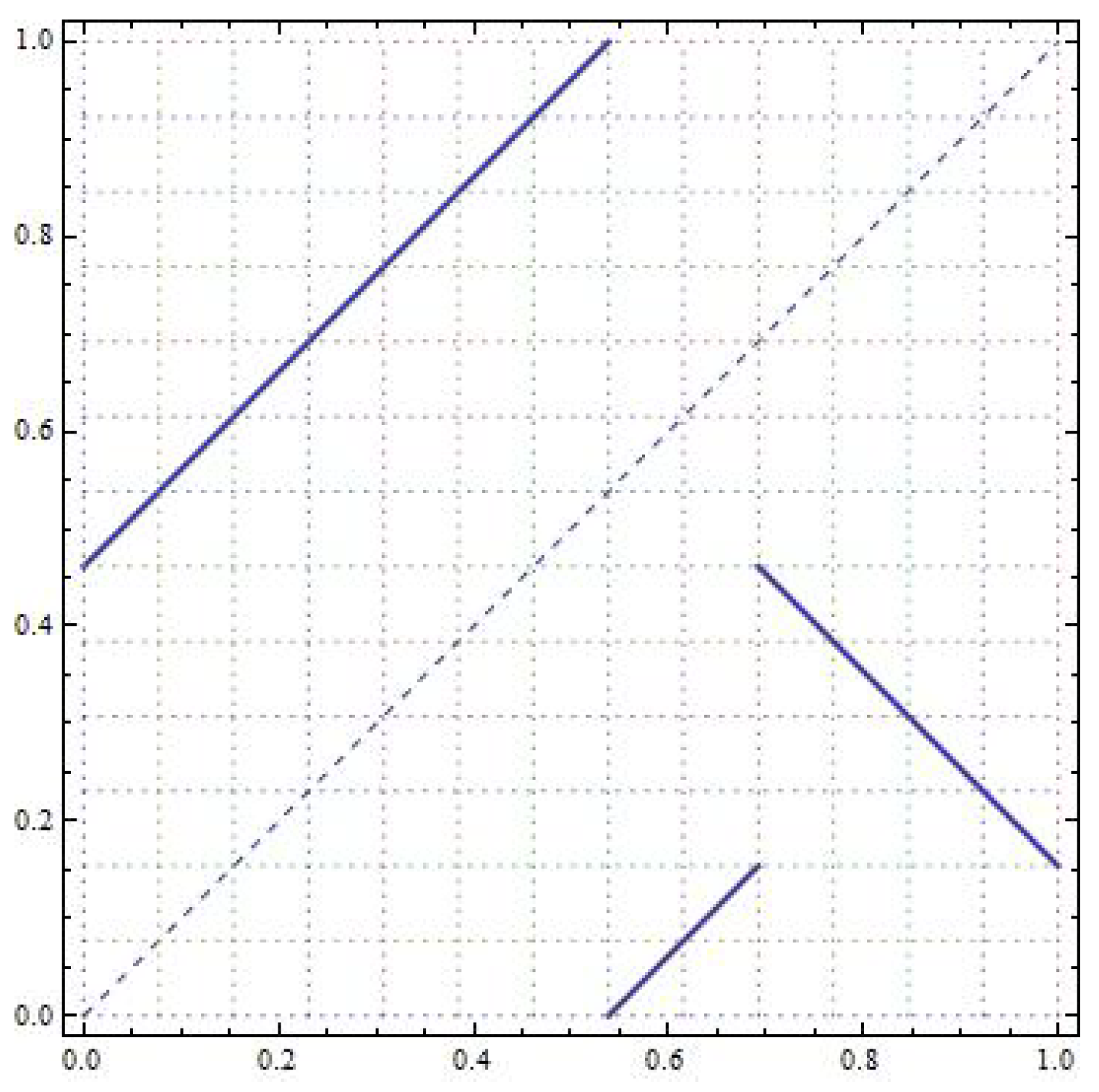
Example 3.

Let $m=13$ and the length vector $(7,2,4)$. Figure 14 shows the graph of T in which one can check the loops that give rise to the set of periods. We write the matrix

$$\mathbf{X}=\left(\begin{array}{cccc}6& 8& 10& 12\\ 8& 10& 12& 1\\ 10& 12& 1& 3\\ 12& 1& 3& 5\end{array}\right).$$

The element $X_{33}=1$ gives us a loop of length 2 with a negative slope, so $2,4\in \mathrm{Per}\left(T\right)$. The elements $X_{24}=X_{42}=1$ gives us a loop of length 4 with a positive slope, so the period 4. However, the subintervals 9, 10 and 11 are contiguous and hence, they form a loop of $[9-11]$ of length 2 and negative slope, and so $2\in \mathrm{Per}\left(T\right)$. We use 6 subintervals to create this loop. The elements $X_{34}=X_{43}=3$ informs us of the existence of a loop of length 6 and positive slope, and so the period $6\in \mathrm{Per}\left(T\right)$. However, we use six subintervals, and one would remain, which is impossible because it has to be periodic. The element $X_{44}=5$ gives again a loop of length six, which is not possible. Anyway, note that we cannot use these values because we already used the intervals 9, 10 and 11. So, the next element available is $X_{11}=6$, which gives a loop of length 7 with a negative slope. Thus $\mathrm{Per}\left(T\right)=\{2,4,7,14\}$.

Example 4.

Let $m=13$ and the length vector $(6,3,4)$. Figure 15 shows the graph. We write the matrix

$$\mathbf{X}=\left(\begin{array}{cccc}5& 3& 1& 12\\ 3& 1& 12& 10\\ 1& 12& 10& 8\\ 12& 10& 8& 6\end{array}\right).$$

The element $X_{22}=1$ gives us a loop of length 2 with a negative slope, so we obtain the periods $\{2,4\}$. On the other hand, the elements $X_{13}=X_{31}=1$ gives us a loop of length 4 with a positive slope, so the period 4. However, note that subintervals 10, 11 and 12 are contiguous. Thus, they form a loop of $[10-12]$ of length 2 and negative slope, and so the set of periods $\{2,4\}$. The next element available is $X_{44}=6$, which gives a loop of length 7 with a negative slope. Thus $\mathrm{Per}\left(T\right)=\{2,4,7,14\}$.

In a similar way, we can check that the 3-IET with vector $(5,4,4)$ has matrix

$$\mathbf{X}=\left(\begin{array}{cccc}1& 9& 4& 12\\ 9& 4& 12& 7\\ 4& 12& 7& 2\\ 12& 7& 2& 10\end{array}\right)$$

and set of periods $\mathrm{Per}\left(T\right)=\{2,4,3,6,5,10\}$, and that with vector $(4,5,4)$ has matrix

$$\mathbf{X}=\left(\begin{array}{cccc}8& 5& 2& 12\\ 5& 2& 12& 9\\ 2& 12& 9& 6\\ 12& 9& 6& 3\end{array}\right)$$

and set of periods $\mathrm{Per}\left(T\right)=\{3,6,4,8\}$.

Next we will show an example with $gcd(m,k_1)>1$.

Example 5.

Let $m=24$ and the length vector $(15,5,4)$. Note that clearly, $gcd(m,k_1)=3$. We write the associated matrix

$$\mathbf{X}=\left(\begin{array}{cccc}2& *& *& 7\\ *& *& 7& *\\ *& 7& *& *\\ 7& *& *& 4\end{array}\right).$$

Reasoning as in the previous examples $\mathrm{Per}\left(T\right)=\{3,6,5,10,8,16\}$.

The same argument can be repeated with $k_4>4$, adding rows and columns to the matrix $\mathbf{X}$. For $i\in \{1,2,\cdots ,k_3\}$ let $m_i=1+min\{X_{ij}:1\le j\le k_3\}$. Then, we can prove the following result.

Theorem 17.

Let $k_1\ge k_3\ge 4$. Then, there are at most three $m_{i_1}\le m_{i_2}\le m_{i_3}$, with $i_j\in \{1,2,\cdots ,k_3\}$, $j=1,2,3$, and $m_{i_1}+m_{i_2}+m_{i_3}\le m$ such that the following hold:

(a) 

If $m_{i_j}=1+X_{i_j{i}_j}$, then $m_{i_j}\in \mathrm{Per}\left(T\right)$. If, in addition, the slope of $T^{m_{i_j}}$ is negative, then $2m_{i_j}\in \mathrm{Per}\left(T\right)$.

(b) 

If $m_{i_j}=1+X_{i_j,i_j+1}=1+X_{i_j+1,i_j}$, then $2m_{i_j}\in \mathrm{Per}\left(T\right)$. If, in addition, the map T is continuous on the orbit of the interval $[i_j,i_j+1]$, then $m_{i_j}\in \mathrm{Per}\left(T\right)$.

(c) 

If $m_{i_j}=1+X_{i_j,i}=1+X_{i_j+1,i}$, with $|i-i_j|\ge 2$, then $2m_{i_j}\in \mathrm{Per}\left(T\right)$.

Proof. 

By Theorem 2, the number of periodic components of T is at most three, so we just need to consider three $m_{i_1}\le m_{i_2}\le m_{i_3}$ and such that $m_{i_1}+m_{i_2}+m_{i_3}\le m$. The rest of the proof is analogous to that of Theorems 15 and 16 and the ideas of the above examples. □

Remark 10.

In Theorem 17, we have that $m_{i_1}\le m_{i_2}\le m_{i_3}$ must hold a more restricted inequality if cases (a) or (c) happen. For instance, if we can have $m_{i_1}+1+2(m_{i_2}+1)+2(m_{i_3}+1)\le m$. In any case, the sum of the smallest periods in each periodic component cannot be greater than m. This restriction can help sometimes to describe the set of periods of T.

Table 6. Periods of T with $m=7$.

$\mathit{\lambda }$	$\mathbf{Per}\left(\mathit{T}\right)$	$\mathit{\lambda }$	$\mathbf{Per}\left(\mathit{T}\right)$	$\mathit{\lambda }$	$\mathbf{Per}\left(\mathit{T}\right)$
$(5,1,1)$	$\{7,14\}$	$(4,2,1)$	$\{7,14\}$	$(3,3,1)$	$\{7,14\}$
$(1,5,1)$	$\{7,14\}$	$(4,1,2)$	$\{2,4,5,10\}$	$(3,2,2)$	$\{2,4,5,10\}$
$(2,3,2)$	$\{3,6,4,8\}$	$(1,4,2)$	$\{1,2,6,12\}$	$(3,1,3)$	$\{2,4,3,6\}$
$(2,2,3)$	$\{1,2,3,6\}$	$(1,3,3)$	$\{1,2,5,10\}$	$(2,1,4)$	$\{1,2,4,3,6\}$
$(1,2,4)$	$\{1,2,4,8\}$	$(1,1,5)$	$\{1,2,3,6\}$

shows an example of the set of periods for $m=7$.

Remark 11.

We have characterized the periods of T when ${\lambda }_1$, ${\lambda }_2$ and ${\lambda }_3$ are rationally dependent. However, this method is not useful to study what happens when they are rationally independent.

We can see in Table 3 that the permutation $(3,1,-2)$ has the same set of periods than the permutations $(2,-3,1)$ and $(-2,3,1)$, changing the role of length vectors. After changing length vectors, these permutations have the same set of periods as $(3,-1,2)$. So, it only remains the cases $(-3,2,1)$ (note that $(3,2,-1)$ provides the same set of periods up to changes of vector length) and $(3,-2,1)$. These cases would end the study of permutations with one flip, but it seems impossible to adapt this section’s techniques and results to these remaining cases. We will show this fact when analyzing the case of 3-IETs with permutation $\pi =(3,-2,1)$.

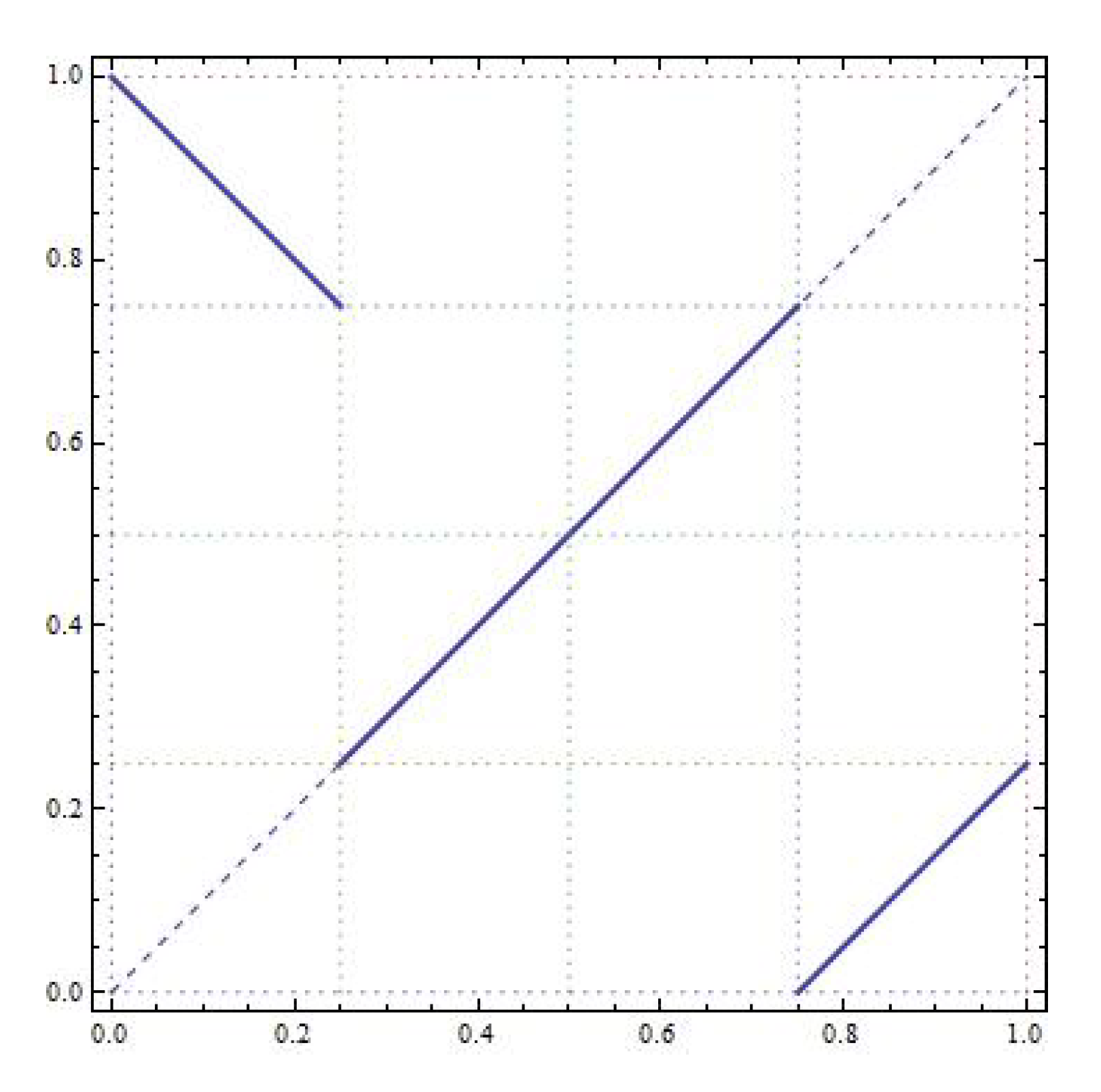
5.2. The Permutation $\pi =(3,-2,1)$

Note that the $(3,1)$-IET T is defined by

$$T\left(x\right)=\left\{\begin{array}{ccc}x+1-{\lambda }_1& if& x\in [0,{\lambda }_1),\\ 1-x& if& x\in ({\lambda }_1,{\lambda }_1+{\lambda }_2),\\ x-{\lambda }_1-{\lambda }_2& if& x\in ({\lambda }_1+{\lambda }_2,1].\end{array}\right.$$

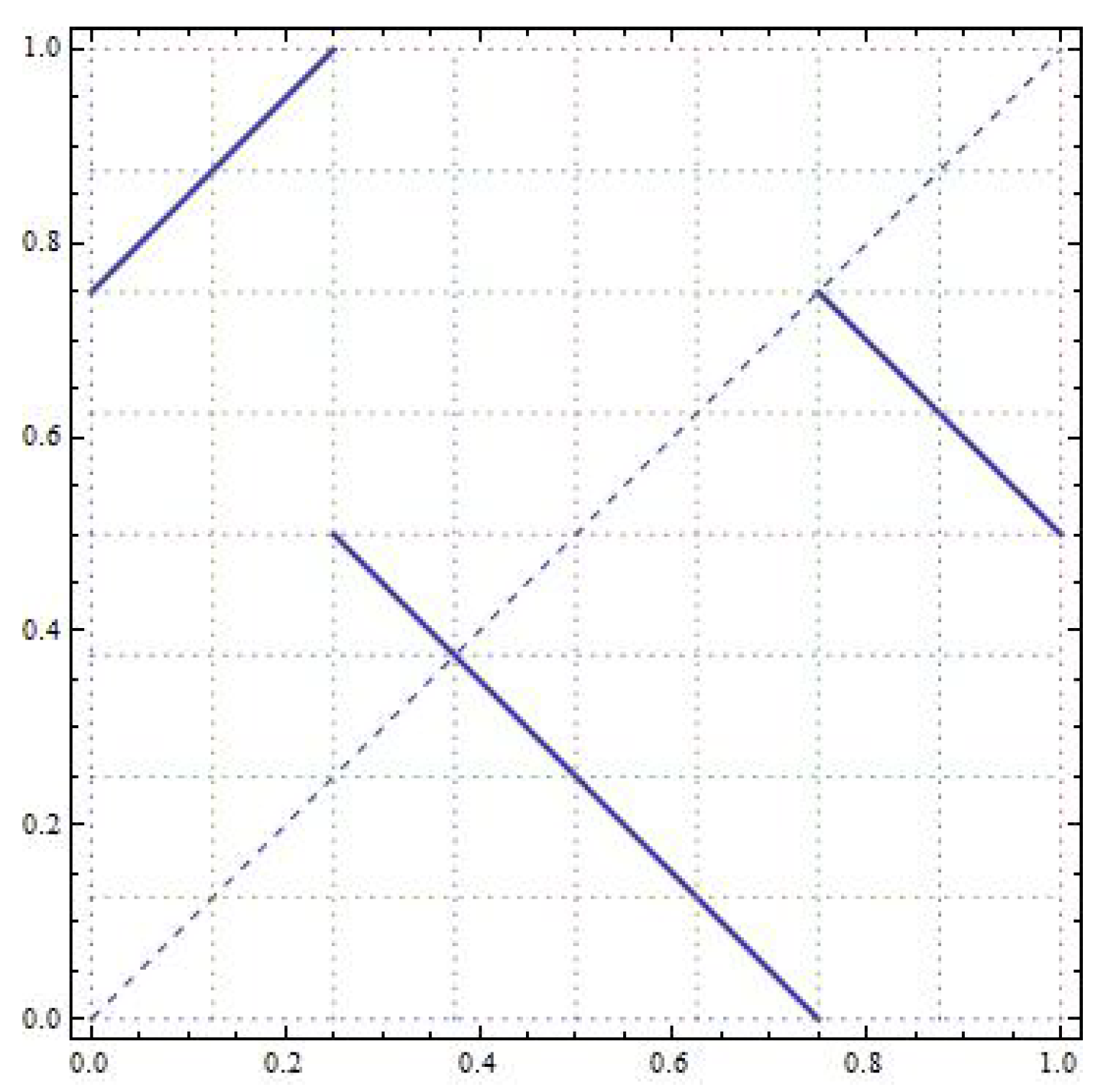
The shape of the map T is shown in Figure 16 for ${\lambda }_1=0.6$ and ${\lambda }_2=0.1$. It is also shown the graph of the 2-IET with permutation $(2,-1)$ which is deeply connected with T. First, we prove the next lemma.

Lemma 5.

The 3-IET T has a fixed point if and only if $2{\lambda }_1<1<2({\lambda }_1+{\lambda }_2)$.

Proof. 

Clearly T can have a fixed point in $I_2=({\lambda }_1,{\lambda }_1+{\lambda }_2)$. Since such fixed point is $\frac{1}{2}$, we easily see that it belongs to $I_2$ if and only if $1/2\in I_2$, which is equivalent to $2{\lambda }_1<1<2({\lambda }_1+{\lambda }_2)$. □

Assume that $1/2$ is a fixed point of T, and therefore ${\lambda }_1<\frac{1}{2}<{\lambda }_1+{\lambda }_2$. We take $d_1=\frac{1}{2}-{\lambda }_1$ and $d_2={\lambda }_1+{\lambda }_2-\frac{1}{2}$. It is easy to see that $d_1\le d_2$ (respectively $d_1\ge d_2$) if and only if $1\le 2{\lambda }_1+{\lambda }_2$ (respectively $1\ge 2{\lambda }_1+{\lambda }_2$). We set

$$\alpha :=\underset{x\to {\lambda }_1{}^{+}}{lim}T\left(x\right)=1-{\lambda }_1$$

and

$$\beta :=\underset{x\to {({\lambda }_1+{\lambda }_2)}^{-}}{lim}T\left(x\right)=1-{\lambda }_1-{\lambda }_2.$$

Observe that if $d_1=d_2$ and hence $2{\lambda }_1+{\lambda }_2=1$, then $\alpha ={\lambda }_1+{\lambda }_2$ and $\beta ={\lambda }_1$. We define the interval

$$J:=\left\{\begin{array}{ccc}\left({\lambda }_1,\alpha \right)& if& 1<2{\lambda }_1+{\lambda }_2,\\ ({\lambda }_1,{\lambda }_1+{\lambda }_2)& if& 1=2{\lambda }_1+{\lambda }_2,\\ \left(\beta ,{\lambda }_1+{\lambda }_2\right)& if& 1>2{\lambda }_1+{\lambda }_2,\end{array}\right.$$

which is invariant by T and contains the fixed point of T. Then, we define $\tilde{T}$ the 3-IET with permutation $(3,-2,1)$ and vector $\tilde{\lambda }=\left(\frac{{\lambda }_1}{1-\left|J\right|},\frac{{\lambda }_2-\left|J\right|}{1-\left|J\right|},\frac{{\lambda }_3}{1-\left|J\right|}\right)$. Note that, by construction, $\tilde{T}$ cannot have fixed points, that is, either $\frac{2{\lambda }_1}{1-\left|J\right|}>1$ or $\frac{2({\lambda }_1+{\lambda }_2-|J|}{1-\left|J\right|}<1$. Then, we have the following result.

Proposition 3.

Under the above notation, $\mathrm{Per}\left(T\right)=\{1,2\}\cup \mathrm{Per}\left(\tilde{T}\right)$.

Proof. 

Note that all the points of J are periodic with period one or two. The proof follows taking into account that $I\setminus J$ is invariant by T. □

Once we have analyzed the case in which T has fixed points, it remains to discuss two cases: (a) ${\lambda }_1>\frac{1}{2}$; (b) ${\lambda }_1+{\lambda }_2<\frac{1}{2}$, which is equivalent to ${\lambda }_3>\frac{1}{2}$. However, the 3-IETs with permutation $(3,-2,1)$ and length vectors $({\lambda }_1,{\lambda }_2,{\lambda }_3)$ and $({\lambda }_3,{\lambda }_2,{\lambda }_1)$ are conjugate (see Table 3), and thus have the same periods. So, it suffices to study the case ${\lambda }_1>\frac{1}{2}$. We start by proving the next result.

Theorem 18.

Let ${\lambda }_1=\frac{n}{n+1}$ for some $n\in \mathbb{N}$.

(a)

If $\frac{{\lambda }_3}{{\lambda }_2+{\lambda }_3}=\frac{m}{m+1}$ for some $m\in \mathbb{N}$, then $\mathrm{Per}\left(T\right)=\left\{\right(n+1\left)\right(m+1),2(n+1\left)\right(m+1\left)\right\}$.

(b)

If $\frac{m-1}{m}<\frac{{\lambda }_3}{{\lambda }_2+{\lambda }_3}<\frac{m}{m+1}$ for some $m\in \mathbb{N}$, then $\mathrm{Per}\left(T\right)=\left\{\right(n+1)m,2(n+1)m,(n+1\left)\right(m+1),2(n+1\left)\right(m+1\left)\right\}$.

Proof. 

Note that ${\lambda }_2+{\lambda }_3=\frac{1}{n+1}$. We have that T maps the intervals $(\frac{i-1}{n+1},\frac{i}{n+1})$ into $(\frac{i}{n+1},\frac{(i+1)\mathrm{mod}(n+1)}{n+1})$ for $i=0,1,\cdots ,n$. Thus, the restrictions $T^{n+1}{|}_{(\frac{i-1}{n+1},\frac{i}{n+1})}:(\frac{i-1}{n+1},\frac{i}{n+1})\to (\frac{i-1}{n+1},\frac{i}{n+1})$ are conjugate to the 2-IET $T^{\prime }$ with permutation $(-2,1)$ and vector length $\left(\frac{{\lambda }_2}{{\lambda }_2+{\lambda }_3},\frac{{\lambda }_3}{{\lambda }_2+{\lambda }_3}\right)$. Applying Theorem 6 for $T^{\prime }$ (notice that $\frac{{\lambda }_2}{{\lambda }_2+{\lambda }_2}=\frac{1}{m+1}$), we obtain the result. □

Next, we need to consider the case $\frac{n-1}{n}<{\lambda }_1<\frac{n}{n+1}$ for some $n\in \mathbb{N}$. For that, we denote by $T^{*}$ the 2-IET with permutation $(2,-1)$ and length vector $\left({\lambda }_1,{\lambda }_2+{\lambda }_3\right)$. Given $n\in \mathbb{N}$ and a subset $A\subset \mathbb{N}$, we define $n·A:=\{na:a\in A\}$. Then, we prove the following.

Theorem 19.

Let $\frac{n-1}{n}<{\lambda }_1<\frac{n}{n+1}$ for some $n\in \mathbb{N}\setminus \left\{1\right\}$.

(b)

If ${\lambda }_3=1-n(1-{\lambda }_1)$, then $\mathrm{Per}\left(T\right)=\{n,2n,n+1\}$.

(b)

If ${\lambda }_3<1-n(1-{\lambda }_1)$, then $\mathrm{Per}\left(T\right)=\{n,2n\}\cup (n+1)·\mathrm{Per}\left(T^{\prime }\right)$, where $T^{\prime }$ is the 2-IET with permutation $(-2,1)$ and $\left(\frac{1-n(1-{\lambda }_1)-{\lambda }_3}{1-n(1-{\lambda }_1)},\frac{{\lambda }_3}{1-n(1-{\lambda }_1)}\right)$ and length vector.

Proof. 

We denote by $T^{*}$ the 2-IET with permutation $(2,-1)$ and length vector $\left({\lambda }_1,{\lambda }_2+{\lambda }_3\right)$. By Theorem 6, if we iterate with $T^{*}$, the interval $I_0=(0,1-n(1-{\lambda }_1)$ is periodic with period $n+1$ and the interval $I_1=(1-n(1-{\lambda }_1),1-{\lambda }_1)$ is periodic with period n. Observe that

$$|I_0|+|I_1|=1-{\lambda }_1={\lambda }_2+{\lambda }_3.$$

Hence, since

$$T^j\left(I_0\right)={\left(T^{*}\right)}^j\left(I_0\right)=(j(1-{\lambda }_1),1,(n-j)(1-{\lambda }_1))\subset (0,{\lambda }_1)$$

for $j=0,1,\cdots ,n-1$, we find that

$$T^n\left(I_0\right)={\left(T^{*}\right)}^n\left(I_0\right)=(n(1-{\lambda }_1),1)=(1-|I_0|,1),$$

and from

$$T^j\left(I_1\right)={\left(T^{*}\right)}^j\left(I_1\right)=(1-(n-j)(1-{\lambda }_1),(j+1)(1-{\lambda }_1))\subset (0,{\lambda }_1)$$

for $j=0,1,\cdots ,n-2$, we have that

$$T^{n-1}\left(I_1\right)={\left(T^{*}\right)}^{n-1}\left(I_1\right)=({\lambda }_1,n(1-{\lambda }_1))=({\lambda }_1,1-|I_0\left|\right)=({\lambda }_1,{\lambda }_1+|I_1\left|\right).$$

(a) The condition ${\lambda }_3=1-n(1-{\lambda }_1)$ is equivalent to $|I_0|={\lambda }_3$ and $|I_1|={\lambda }_2$. Then $T^{n+1}{|}_{I_0}:I_0\to I_0$ is the identity, so $n+1\in \mathrm{Per}\left(T\right)$. On the other hand, $T^n{|}_{I_1}:I_1\to I_1$ is $1-x$, so $n,2n\in \mathrm{Per}\left(T\right)$. Since $(n+1)|I_0|+n|I_1|=1$, the proof of (a) finishes.

(b) The condition ${\lambda }_3<1-n(1-{\lambda }_1)$ is equivalent to $|I_0|>{\lambda }_3$, and thus $|I_1|<{\lambda }_2$. So, $T^n{|}_{I_1}:I_1\to I_1$ is $1-x$, so $n,2n\in \mathrm{Per}\left(T\right)$. On the other hand, notice that

$$T^{n+1}\left(I_0\right)=T(1-|I_0|,1)=T(1-|I_0|,{\lambda }_1+{\lambda }_2)\cup T({\lambda }_1+{\lambda }_2,1),$$

and thus $T^{n+1}{|}_{I_0}=T^{\prime }:I_0\to I_0$ is the 2-IET with permutation $(-2,1)$ and length vector $\left(\frac{1-n(1-{\lambda }_1)-{\lambda }_3}{1-n(1-{\lambda }_1)},\frac{{\lambda }_3}{1-n(1-{\lambda }_1)}\right)$. So, (b) follows. □

If ${\lambda }_3>1-n(1-{\lambda }_1)$, then the situation is much more complicated. The set of periods cannot be obtained easily from the set of periods of some 2-IET. For instance, when ${\lambda }_1=0.6$ we show the set of periods of T for several values of ${\lambda }_2$ in

Table 7. For ${\lambda }_1=0.6$, we display the set of periods of T for several values of ${\lambda }_2$.

${\mathit{\lambda }}_2$	$\mathbf{Per}\left(\mathit{T}\right)$	${\mathit{\lambda }}_2$	$\mathbf{Per}\left(\mathit{T}\right)$
$0.2$	$\{2,3,4\}$	$0.19$	$\{2,4,64,128\}$
$0.18$	$\{2,4,34,68\}$	$0.17$	$\{2,4,22,44,25,50\}$
$0.16$	$\{2,4,19,38\}$	$0.15$	$\{2,4,16,32\}$
$0.14$	$\{2,4,13,26,16,32\}$	$0.13$	$\{2,4,10,20,13,26\}$
$0.12$	$\{2,4,10,20,13,26\}$	$0.11$	$\{2,4,10,20,13,26\}$
$0.10$	$\{10,20\}$	$0.09$	$\{7,14,10,20,18,36\}$
$0.08$	$\{7,14,18,36\}$	$0.07$	$\{7,14,58,116\}$
$0.06$	$\{7,14,28,36,72\}$	$0.05$	$\{20,40\}$
$0.04$	$\{12,24,13\}$	$0.03$	$\{17,34,66,132\}$
$0.02$	$\{50,100\}$	$0.01$	$\{100,200\}$

. For instance, for ${\lambda }_2=0.13$ and ${\lambda }_3=0.27$, we have that $\mathrm{Per}\left(T\right)=\{2,4,10,20,13,26\}$ and this set of periods cannot be obtained from a 2-IET because it has at most two periodic components.

6. Conclusions and Future Work

We have characterized the set of periods of 2-IETs and approached this problem when 3-IETs are considered. The result for 2-IETs gives an advance to a question posed by Misiurewicz in 1994, see [15]. As a byproduct, it is interesting to mention that no ordering or forcing similar to Sharkovsky order is expected for the set of periods of those discontinuous maps being increasing and continuous on $\left[0,\frac{1}{2}\right)$ and decreasing and continuous on $\left(\frac{1}{2},1\right]$.

On the other hand, from our study of 3-IETs, it does not seem easy to give a closed form for the periods of IETs. As a starting point for this general goal, we have presented some techniques, as the Poincaré map for some particular cases, the strategy of taking conjugates or inverse maps to simplify the casuistic, as well as an alternative approach under matrices associated to a suitable directed graph. With these tools we were able to obtain the whole study of 3-IETs whose accompanying vector $\lambda =\left({\lambda }_1,{\lambda }_2,{\lambda }_3\right)$ holds ${\lambda }_1={\lambda }_3$. Moreover, for the sake of warning the reader about the difficulty of the problem, we have presented two general study cases, partially solved, for which we need to use some little pieces of linear congruence theory.

We will explore this question of computation of periods for n-IETs, with $n\ge 3,$ in future works. However, at least, we know that the case of 3-IETS with ${\lambda }_2={\lambda }_3$ is easily reachable with the techniques shown in this paper, whereas the general case probably requires the exploration of new tools.