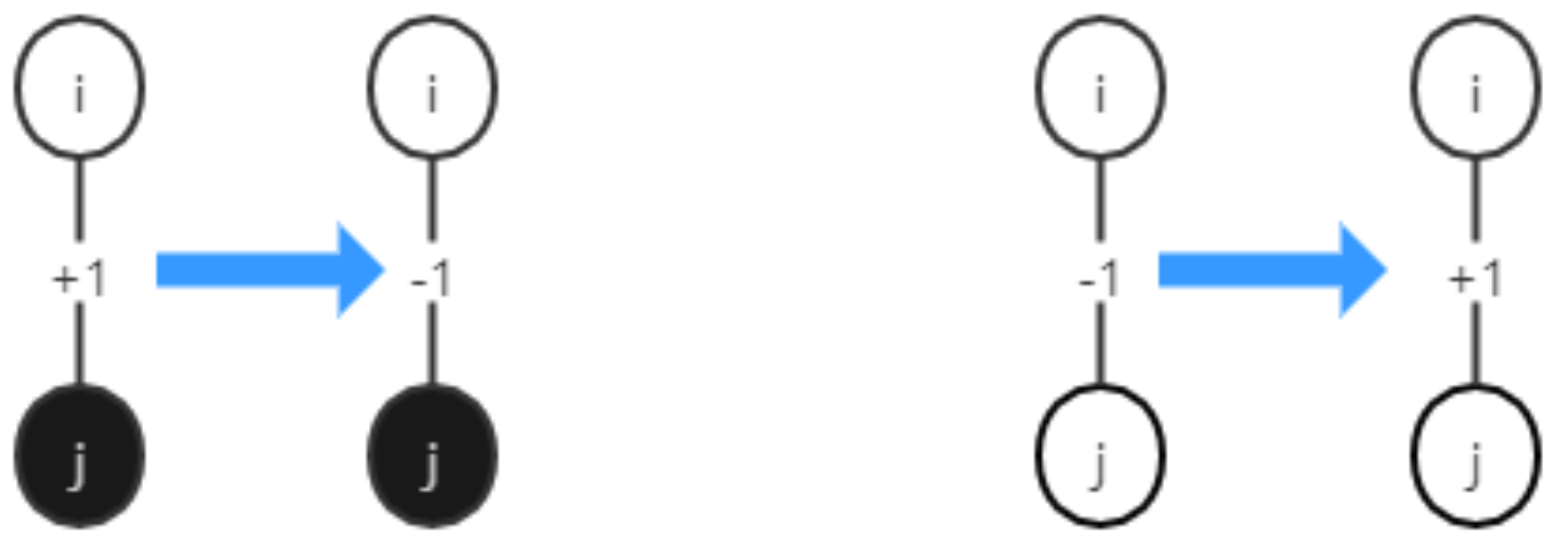1. Introduction
Nodes in social networks represent individuals or organizations, and edges among nodes represent the interaction [
1,
2,
3,
4,
5,
6]. The signed network is a topology with positive and negative signs on the edges. The signed edge has abundant connotations in many real complex systems. For example, a negative edge usually means disagreement, hostility, opposition, and distrust; correspondingly, a positive edge represents agreement, friendship, support, and trust [
7,
8]. The investigations on the signed network can effectively improve our knowledge on signed complex systems, such as international relation [
9], promoting and inhibiting neurons [
1], trust prediction on social networks [
10], consensus and polarization of online community [
11], information diffusion [
12], opinion dynamics [
13,
14].
The most basic theory in the field of the signed network is a structural balance theory [
8], which was first put forward by Heider in 1946. This theory originated from the balanced model of the node’s attitude towards things [
15]. Cartright and Harry [
16] extended the theory by combining the graph theory. Later, scholars made great extensions, for example, Kunegis et al. [
17] suggested that the network structural balance is measured by counting the proportion of balanced triads in the whole signed network, Fachetti et al. [
18] proposed an energy function definition to calculate the structural balance. Real-world signed networks rarely attain a perfectly balanced state. To quantify exactly how balanced they are, Aref et al. [
19] formalized the concept of a measure of partial balance. Kirkley et al. [
20] proposed two measures of structural balance based on hypothesized notions of “weak” and “strong” balance.
Indeed, since the seminal work of Heider, many fundamental concepts and significant theories have been proposed for the development of the social balance theory. The extension of the classic structure balance theory can be divided into four categories. They are the balance of nodes, the balance of triangles, the balance of complete networks, and the balance of arbitrary networks. See [
21] for a comprehensive review of the variations, extensions, and calculating methods related to the classic social balance theory.
Although the structural balance theory in signed networks describes a stable signed system state, the system from imbalance to balance is a dynamic process [
22,
23]. For example, the formation of friend or enemy groups, the constantly changing international relation. In order to investigate the dynamics of structural balance, Wu et al. [
24] set up a co-evolution model in the acyclic network and cycle network. Marvel et al. [
25] proposed a continuous-time model of structural balance. He et al. [
26] developed a new simulation model to study the impact of structural balance on the evolution of cooperation in signed networks. However, currently, the research of dynamic networks is mostly limited to non-signed nodes or signed networks without weights. The co-evolution models of nodes and edges based on weighted signed networks have not been deeply investigated because of their complexity.
2. Related Works
Social influence network and opinion change models, such as the French-DeGroot model [
27], Friedkin–Johnsen model [
28], formally entail the interpersonal influence on the formation of interpersonal agreements and polarization. Social influence and its induced homogeneous effect, however, do not fully interpret the global network structure, for example, the mounting two-polarization phenomenon in US political ecology that insulates democrats and republicans from opposing opinions about current events [
29]. Social network influence theory entails the interpersonal influence on the formation of interpersonal agreements and polarization. From a complex network perspective, this influence process is the feedback effect of the network structure on network functions.
In the real world, most of the signed graphs are temporal, the nodes and edges vary over time, which makes the changing of the network structure, including the clustering and the structural balance of the network. Many researchers are interested in the dynamic processes over signed networks, i.e., the co-evolution between the signed edges and the nodes, such as the agreement and disagreement evolving over random dynamic networks [
30,
31,
32,
33]. However, most of these models lack the social mechanisms of opinion formation, evolution, and dissemination.
Real-world cases call for these two threads of research, opinion dynamics and structural balance dynamics, to be combined. Holme and Newman [
34] presented a simple model of this combination without any theoretical analysis. Wang et al. [
35], in the latest relevant research, proposed co-evolution models for both dynamics of opinions (people’s views on a particular topic) and dynamics of social appraisals (the approval or disapproval towards each other). In their model, the system evolves as opinions and edge weights are updated over time by two rules: opinion dynamics, and appraisal dynamics. Both opinion and appraisal dynamics are governed by the evolution of the time-varying matrix of a dynamic system. The social–psychological mechanisms of the co-evolution model in [
35] involve the structure balance theory and social influence network theory, i.e., the Friedkin–Johnsen model. Similar to [
35], Kang and Li [
36] proposed a co-evolution model of discrete-time opinion evolution vectors and appraisal signed networks. Social–psychological mechanisms of the co-evolution model in [
36] involve structure balance and the social distancing theory. This paper, inspired by these works, provides a ruled-based node–edge co-evolution model. However, different from a dynamic system time-varying matrix method [
35,
36], our model is rule-based and similar to the agent-based modeling approach. In our model, the global structure balance index is used as judgment conditions for a simulation algorithm termination. Our model’s social–psychological mechanisms involve the structure balance theory and bounded confidence model of opinion dynamics [
37], since the bounded confidence model is more suitable for paired interactions in large groups for agent-based modeling.
Some empirical investigations show that the unbalanced triangles will evolve into balanced ones to make the network more stable [
38], and that the global level of balance of very large online singed networks is indeed extremely balanced [
18,
20]. Related investigations show that the structural balance of signed networks in the real world is an increasing function of evolution time. The evidence of over-represented balanced triads is well above random expectations in the vast majority of real networks, such as the statistic observation in references [
18,
20,
38,
39].
These empirical conclusions confirm the validity of the classic Heider structure balance theory. However, we still find that the complete perfect balanced structure is rarely observed in the real-world signed networks [
20]; there is almost no perfect intra-/inter-group structure balance.
Relevant reference analyses urge researchers to promote this kind of research in-depth. This paper is devoted toward investigating the dynamic structural balance of groups and the emerging macro polarization patterns of signed networks. However, the data sets on related opinions and signed edges are not easy to obtain, this is why we shifted to the model simulation approach. In order to explain real-world ubiquitous opinion polarization and limited structure balance, different influence parameter values are used to explore the influences of different social factors on structural balance and polarization.
3. Our Contribution
In this paper, based on structural balance and a co-evolution model, considering the dynamic mechanics of both opinions and relationships, we employed two evolution rules: opinion renewal and edge adjustment. In addition, we defined an influence matrix and two new neutral dyadic/triadic motifs. A new co-evolutionary mutual feedback algorithm is provided to simulate our proposed model under five evolutionary scenarios.
Our findings can explain the lack of the perfect Heider balance in many real-world systems. This work verifies that signed social networks are indeed limited-balanced, but the level of balance achieved depends on the connectivity of the graph, the percentage of positive edges, and the percentage of positive opinions, most of all, on the distributions of these negative edges/opinions on the signed graph.
Our computational analysis of balance in signed networks serves as a confirmation of the balance theory. Meanwhile, our simulation results suggest that the signed network in the real world is a dynamic equilibrium process, which cannot reach a perfect equilibrium state. The comprehensive numerical results suggest that values of balance at the micro-and macro-levels may match up to some extent, especially as the macro dynamic pattern of the signed network is closely related to its micro-structural balance.
Compared with the current investigations on opinion dynamics on static networks, the proposed co-evolution model in this paper characterizes the polarization of opinions in reality and predicts the existence of imperfect balance in the social context. Our model may also help predict the potential division of social groups and public opinion dynamics.
This paper sheds light on the analysis of constraints and opportunities of social and cognitive processes, helping us to understand the real-world opinion polarization process, in depth.
4. Structural Balance in Signed Network
The social network influence theory entails interpersonal influence on the formation of interpersonal agreements and polarization. From a complex network perspective, this influence process is the feedback effect of the network structure on network functions. In this section, based on the dynamic social influence network theory, we code the dynamic weight social influence matrix, and propose two new neutral dyadic, triadic motifs, as preparation for our co-evolution model.
4.1. Binary Structural Balance
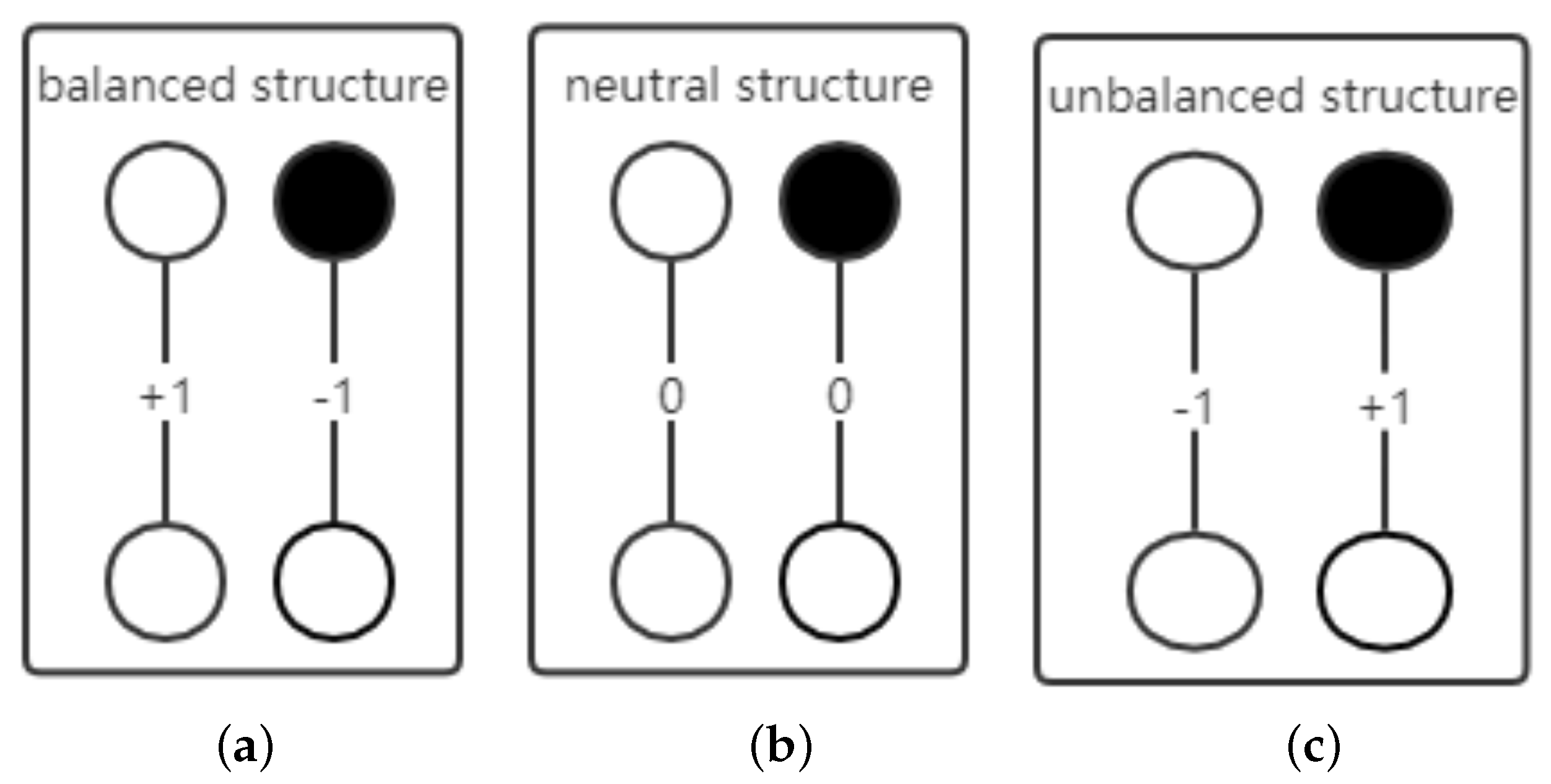
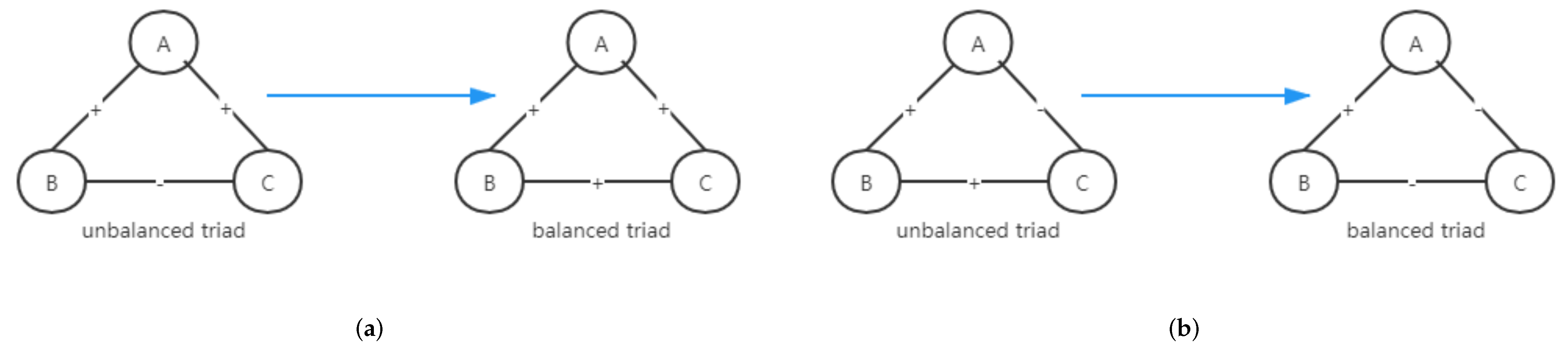
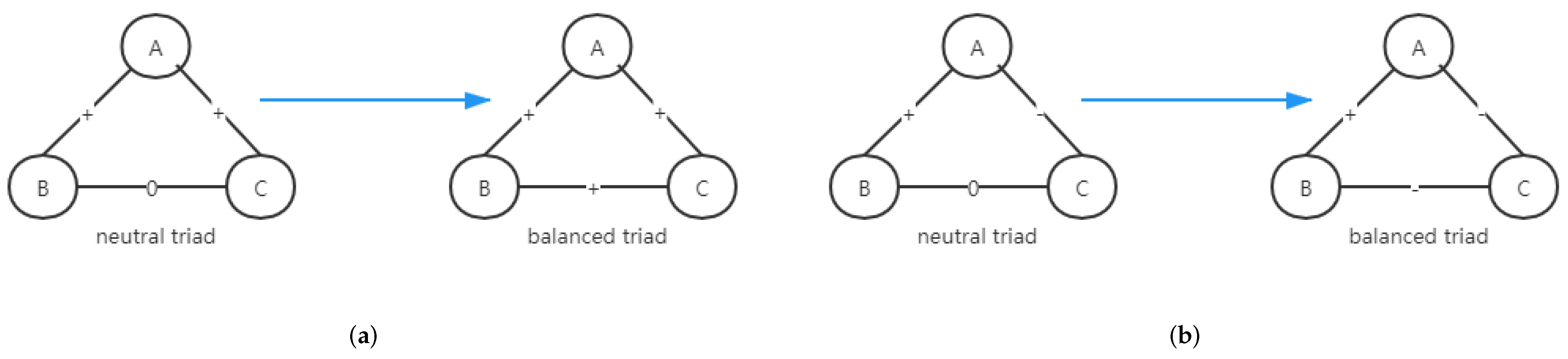
In this investigation, we introduce an edge named neutral edge (“0”), which is a neutral status between positive and negative edges. It refers to a kind of edge without a clear position, which means that the connection between nodes is not clear or neutral. After introducing the neutral edge, we propose a binary motif in a signed network, firstly. Three types of the binary motif are shown in
Figure 1. Specifically, two nodes share the same attitude; at the same time, the signed edge between the two nodes is positive; then, we say the binary motif is balanced. If two nodes share an opposite attitude, and the signed edge between
i and
j is positive, then the binary structure is unbalanced. Based on the above analysis, a binary group includes two parameters, one is the nodes’ opinion and the other is the edge sign between the two nodes. A neutral edge (“0”) means that there is no clear connection between two nodes. However, in the dynamic evolution process, the neutral edge has the opportunity to evolve into negative or positive, due to the constraints of structural balance.
4.2. Triad Structural Balance
Holland and Leinhardt [
40] proposed the three basic binary motifs, reciprocity, asymmetric, and non-edge or null edge. It is worth noting that the null edge plays the same role as our proposed neutral edge (“0”). Since structural balance is defined on a triadic motif, which is constructed based on three basic binary motifs; binary balance is equal to triadic balance.
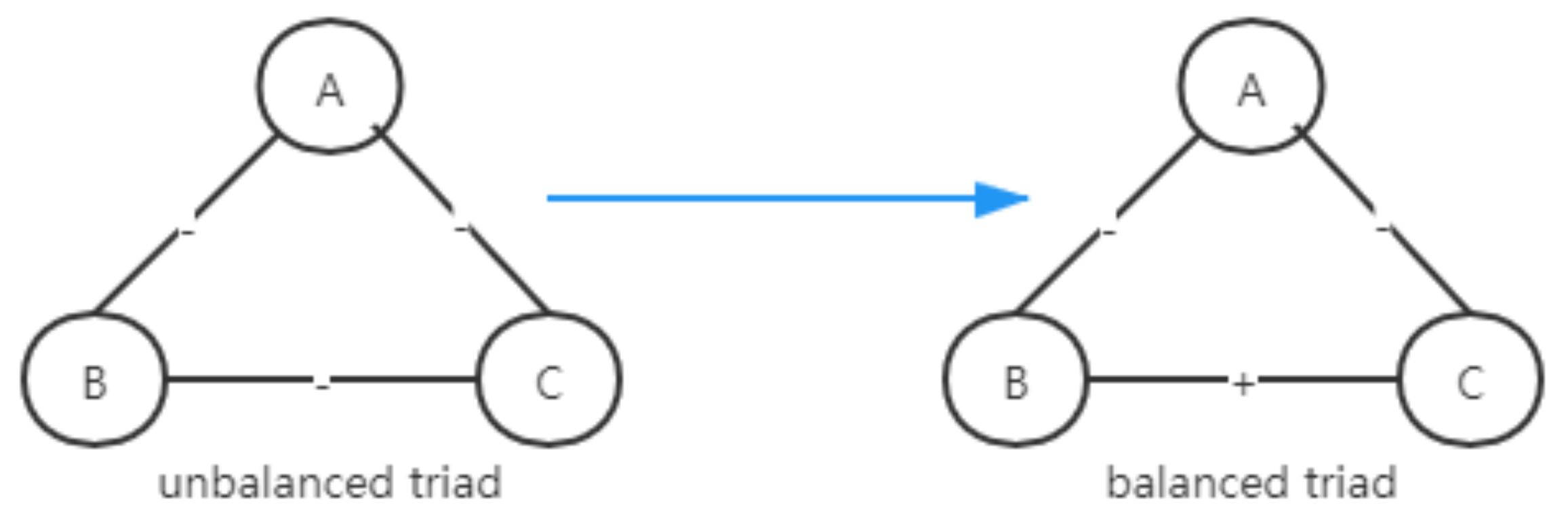
Figure 2a,b denote a balanced triadic structure,
Figure 2c,d denote an unbalanced triadic structure [
2]. If the product of signed edges in each cycle is positive, the signed graph is balanced [
16]. If each triad in a signed complete graph is balanced, then the signed graph is balanced. Here, since we consider the chance of a tried with
, a “neutral triadic motif” is introduced, for the case, the product of three sides in a triad is 0.
4.3. Global Structural Balance Index
Here, we use the global structural balance definition as formulated in Equation (1) [
18], where
denotes a positive edge between
i and
j,
, there is a negative edge between
i and
j, and
implies a neutral edge between
i and
j. In the real world, a neutral edge might be considered a
i and
j have no influence on each other, or the two nodes remain neutral on an issue.
is a continuous real value, representing node
i’s opinion, and the range of
is (−1,1);
means node
i holds a supportive attitude,
means node
i holds a negative attitude, and
means node
i hold an neutral attitude. It is worth noting that a triad-based structural balance is consistent with the global structural balance definition. A smaller value of
means a more balanced social structure.
4.4. Social Influence Matrix
The social influence network is a formal theory that forms attitudes and perspectives. It describes the influence processes of individuals on group attitudes in interpersonal networks. It allows the analysis of how the network structures of groups affect the formation of individual attitudes and group structures [
41]. Based on this theory, we propose a social influence matrix, which provides a sociological perspective for the process of signed edge transformation. The type of edge will evolve according to the weight of the social influence matrix.
Friedkin and Johnsen’s [
41] social influence network theory is regarded as the cornerstone reference for social influence matrix consensus or polarization, as the important and regular group opinions dynamic pattern is generally observed in a group discussion and barging process. Friedkin and Johnsen’s social influence network theory emphasizes that the interpersonal influence social structure, i.e., the social influence matrix is the underlying precondition for group consensus or opinion convergence [
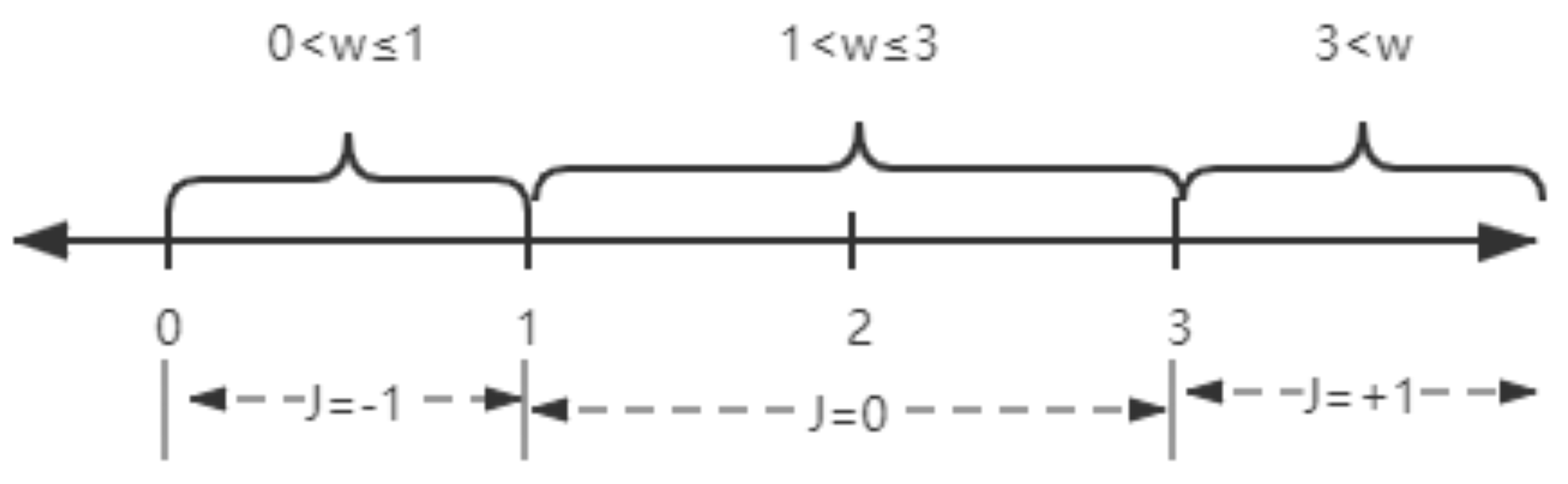
42]. In that model, the initial social influence structure of a group of actors is assumed to be fixed during the entire process of opinion formation. However, with the evolution of timestamps, considering both stubborn and susceptible effects, the interpersonal influence structure can be regarded as a dynamic recursive process. For this reason, the interpersonal influence structure in their model is also dynamic. Based on the dynamic social influence network theory, here we code the dynamic weight social influence matrix in Equation (2). In Equation (2), we set different influence weights to map to signed edges −1, +1, 0. To meet the needs of model simulation calculation, we set different weight ranges corresponding to different social influence intensities.
Within the framework of the social influence network theory, we set up three types of social influence, namely positive, negative, and neutral influence. Positive influence means that two individuals/nodes have homogeneous influence and a positive edge. Negative influence means that two individuals/nodes have opposite influence and a negative edge. Neutral influence means that two individuals/nodes do not influence each other. In this study, based on the adjacent matrix of the signed network, a social weighted influence matrix is randomly assigned to edges. With the assumption of strength difference—of mutual influence among individuals—we set three kinds of weights,
, as shown in
Figure 3 and Equation (2).
5. Co-Evolution Model of Opinions and Edges
The coupling effect of opinion propagation and network topology dynamics on networks leads to complex system behaviors. In order to study the propagation behavior and influencing factors in dynamic complex networks and the dynamic evolution process of the systems, we set up a co-evolution model of opinions and edges. In a social group, people are supposed to be motivated to keep a ’balanced edge’ with others, when two people have the same attitude; if they have negative edges, they tend to change their edges or attitudes in order to maintain a balanced structure. The following is the evolution process introduced in detail.
5.1. Evolutionary Rule of Opinions
The Deffuant–Weisbuch (DW) model [
37] is the most widely used continuous opinion dynamic model. The rule of this model is that two nodes change their opinions if the degree of disagreement is less than the threshold
, i.e.,
, (
i ≠
j), the opinion is carried out as Equations (3) and (4). In this paper, we set the convergence parameter
, which indicates the strength of mutual influence among nodes.
The evolutionary rule of opinion follows Equation (5). To approach structural balance, the evolution of opinions will be based on the type of edge. By adjusting the proportion of initial positive and negative opinions, we can observe the evolution of group opinion. If
i and
j satisfy
, it means these two nodes follow the balanced binary conditions, and there is no need to change anyone’s attitude. Considering the influence of the neighbor nodes, the opinion evolution will follow the DW model. On the contrary, if
, in the opinion evolution, the nodes will change their attitudes, and the attitudes in the next round will be opposite.
5.2. Evolutionary Rule of Edges
According to the different strengths of influence, we introduce three evolutionary rules of signed edges, respectively.
The rule for the evolution of the negative edge is illustrated in
Figure 1, Equation (6), and
Figure 4. When the edge is negative, it will change according to the opinion. If the attitudes of the two nodes are opposite, to achieve a balanced state, the negative edge will not change. If two nodes have the same attitude, the negative edge should evolve to a positive edge. According to the division of weight range,
plus
(the strength of
change to
), and
, the negative edge evolves into the positive edge.
The rule for the evolutionary of a positive edge is shown in Equation (7) and
Figure 4. When the attitude of two nodes is the same, and the edge is positive, there is a balanced structure between them. If the attitudes of two nodes are opposite and the edge is positive, in order to make the approach a balanced structure,
minus
(the strength of
change to
), and
, the positive edge evolves into negative.
The rule for the evolution of a neutral edge is formulated in Equation (8) and illustrated in
Figure 5. No matter whether the attitudes of the two nodes are opposite or consistent, the neutral edge may evolve into a positive edge or a negative edge. When two nodes have the same attitude, to make the binary motif approach the balanced state, the neutral edge needs to evolve into a positive edge, which affects
add
(the strength of
change to
). If two node opinions are opposite, in order to make the edge evolve into a negative edge, concerning the social influence weight
, subtract
(the strength of
change to
).
always falls into the range of
.
5.3. Model Algorithm
In this section, we propose the algorithm realization of the provided model, in detail. Firstly, to consider the influence of the hub node on the network, we used the BA scale-free network [
4]. We initialized an undirected BA network with 100 nodes, 1539 edges, and a network density equal to 0.3109. Moreover, the observation is based on the average results of 1000 realizations. We find that
after 30 rounds. The parameter assignment is shown in
Table 1. The parameter
is used to control whether the opinion evolves or the edge evolves. The algorithm is defined as Algorithm 1. In each round, a random number will be generated; when the random number is greater than
, the opinion evolution will be carried out; when the random number is less than
, the edge evolution will be carried out.
| Algorithm 1: Model implementation process |
![Mathematics 10 01441 i001]() |
6. Simulation Results
In this section, to explore the influence of different social factors on structural balance, we will integrate different social factors into the proposed co-evolution model, and simulate and discuss the simulation results, in detail. The parameters set in different scenarios are given in
Table 2.
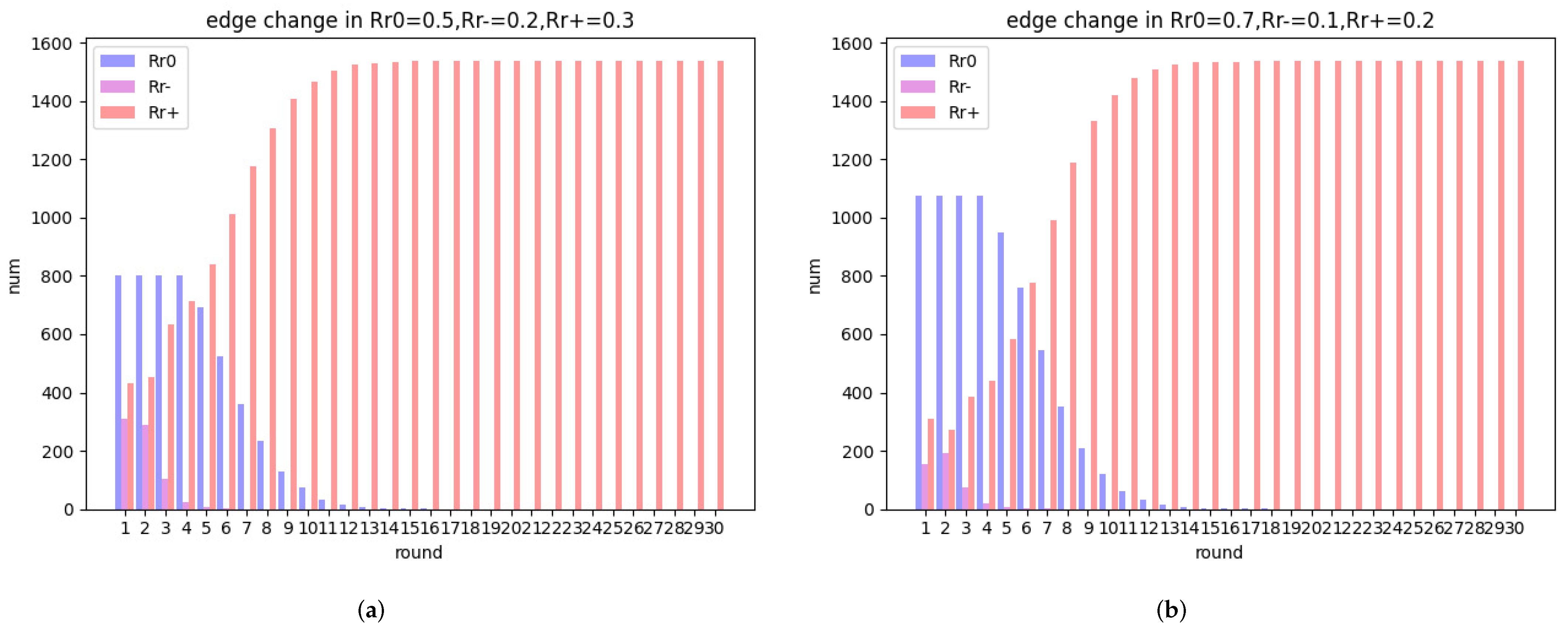
6.1. Scenario 1, the Influence of Parameter
In this experiment, we discuss the influence of different on the structural balance weighted signed network. The ratio of is 0.2, the ratio of is 0.5, and the ratio of is 0.3. Meanwhile, the proportion of positive opinions is 0.7, the rest is negative. Moreover, convergence parameter . The same values are set for , and , i.e., .
As shown in
Figure 6a–c, when
is large, the weighted signed network has the fast velocity to approach structural balance, the number of balanced triads and positive edges in the same round is the largest. The reason is that the larger
promotes nodes interacting with others, thus promoting consensus. As shown in
Figure 6d, all nodes hold the positive opinion, as long as
. According to the binary structural balance, because all opinions are positive, all edges are positive in the end, and the proportion of balanced triads is also higher. Based on the above analysis, we can conclude that the larger the
is, the faster the network approaches the structural balance.
In conclusion, to accelerate the network to approach the structural balance, we can improve the tolerance of opinion differences by strengthening trust among nodes. In psychology, trust is a kind of stable belief, which maintains the common value and the stability of society.
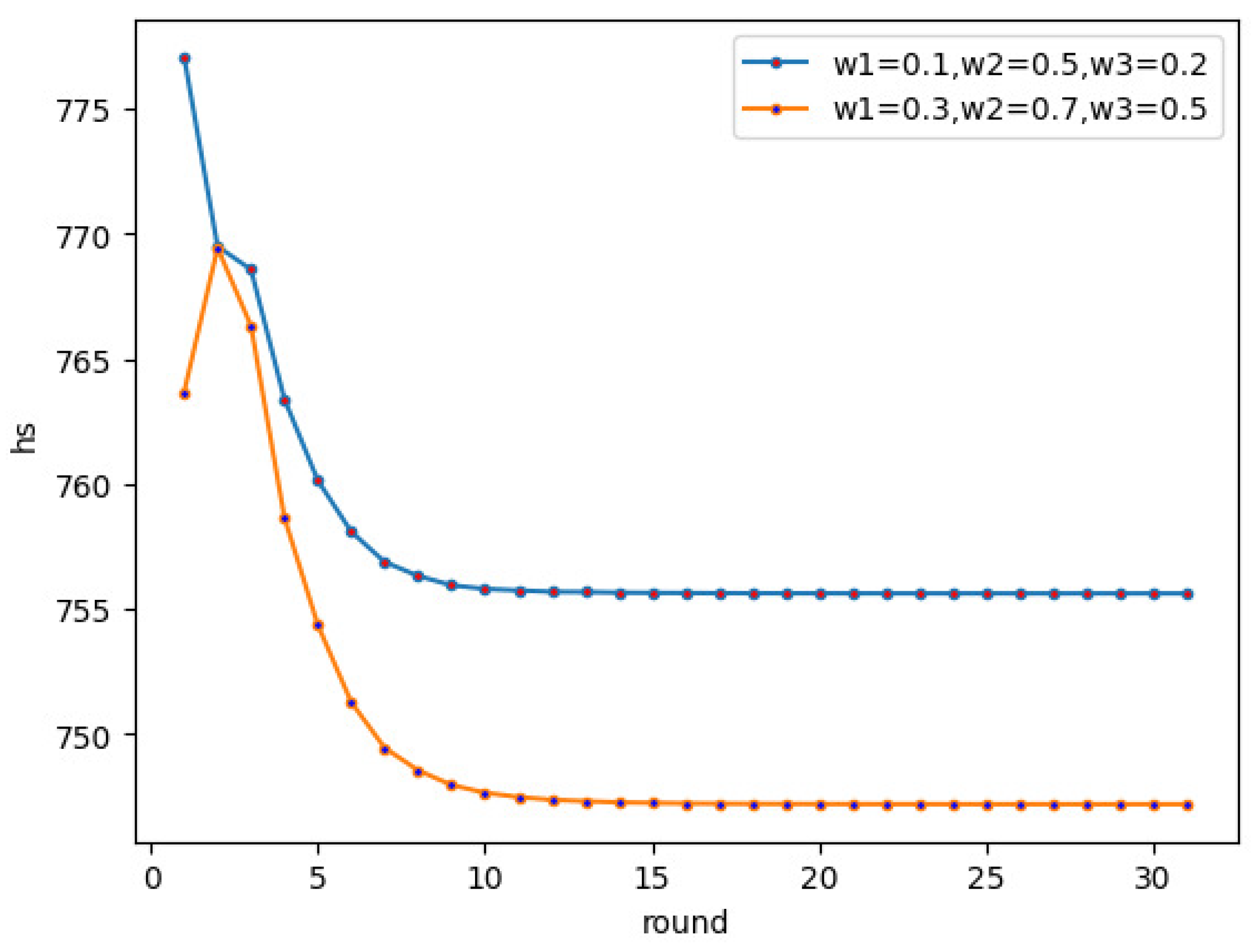
6.2. Scenario 2, the Influence of Negative Opinions
This experiment discusses the influence of the initial number of negative opinions on the structural balance. Other parameter settings are the same as that in Scenario 2, the initial ratio of is 0.2, the ratio of is 0.5, and the ratio of is 0.3. Convergence parameter , and . The conversion strength between various edges are the same; that is, . The parameter equals 0.7. To make our expression more compact, in the following scenarios, we focus on the change of , since it is a key indicator for the evolution process of the signed networks. As shown in scenario 1, other indicators can be inferred from .
The simulation results are shown in
Figure 7. When all opinions are positive or negative, which is in the case of
and
, the global structural balance index changes faster, and the network approaches structural balance faster. However, when the proportion of negative opinions is about 0.5, the global structural balance index does not change.
In scenario 1, because the positive opinions are in the majority at the beginning, the network can approach the balanced state under different . However, in this scenario, we set the same , when the positive or negative opinions occupy the majority, the network can approach the balanced state faster. Because the more nodes with the same attitude, according to the binary structural balance, the negative edge and neutral edge evolve to the positive edge, so the number of positive edges and balanced triads are the most. It can be concluded from scenario 2 that when there are many nodes with the same attitude in a network, the network can quickly approach the structural balance.
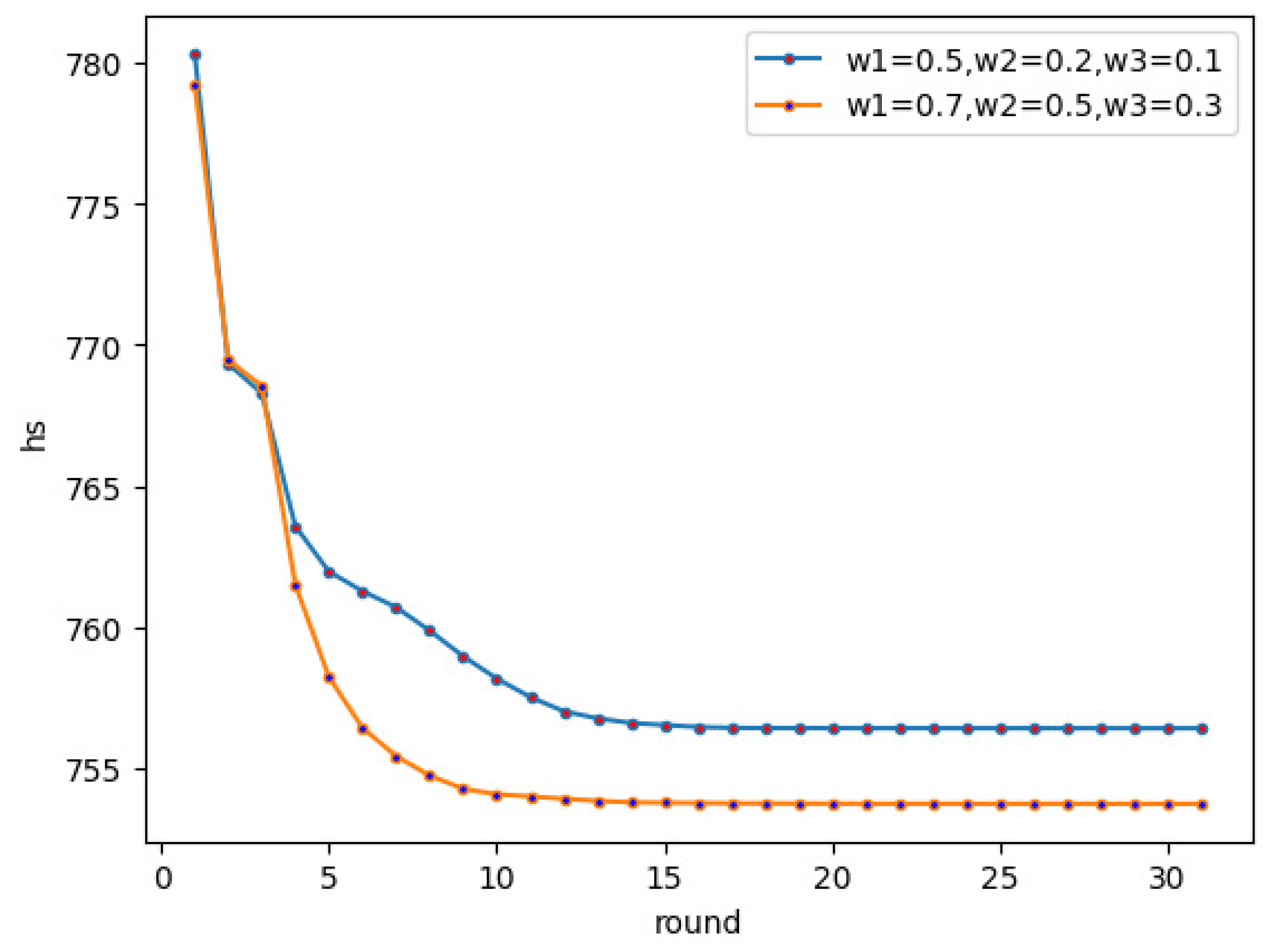
6.3. Scenario 3, the Relation between Opinion Evolution and Edge Evolution
In this experiment, we discuss the influence of on the structural balance. The initial conditions are as follows: negative edges account for 0.3, neutral edges account for 0.5, positive edges account for 0.2, and positive opinions account for 0.7. The conversion strength between various edges are the same, i.e., . Moreover, we set , . Four experimental results are discussed as follows.
The first result of this experiment is the global structural balance index. As shown in
Figure 8, the larger the
is, the faster the network approaches structural balance. When the
is terribly small, the network cannot approach a balanced state. It can be observed that the network approaches structural balance except for the case of
.
In
Figure 9, we plot the impact of the control parameter
on the final network balanced triad and triad 0 (neutral triads). We observe that when
is larger, the number of balanced triads increase rapidly in
Figure 9a. Moreover, neutral triads decrease rapidly in
Figure 9b, When
, a large number of neutral triads still exist after 30 rounds of evolution, it shows that the network has not reached structural balance. It can be concluded that in the process of approaching a balanced structure, it is more difficult to change the opinion than to change the edge.
6.4. Scenario 4, the Influence of Various Strengths of Conversion
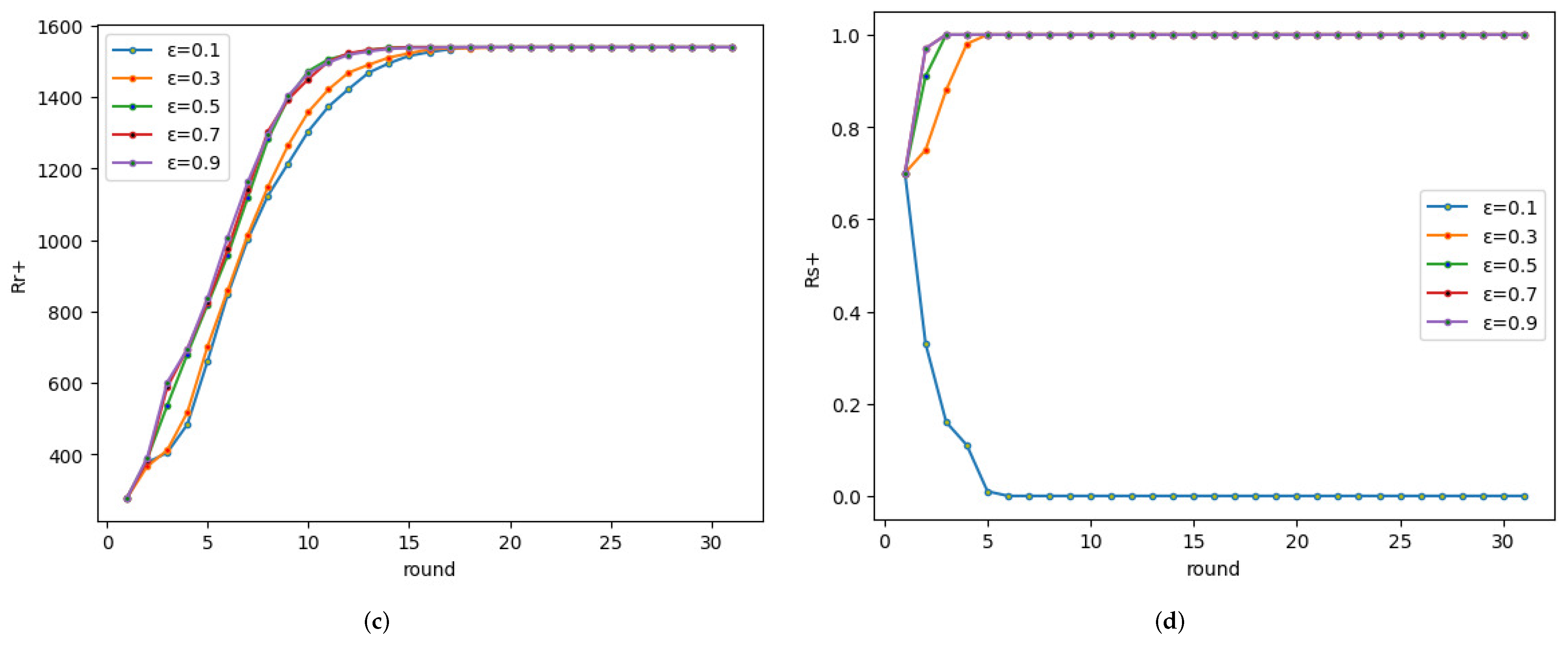
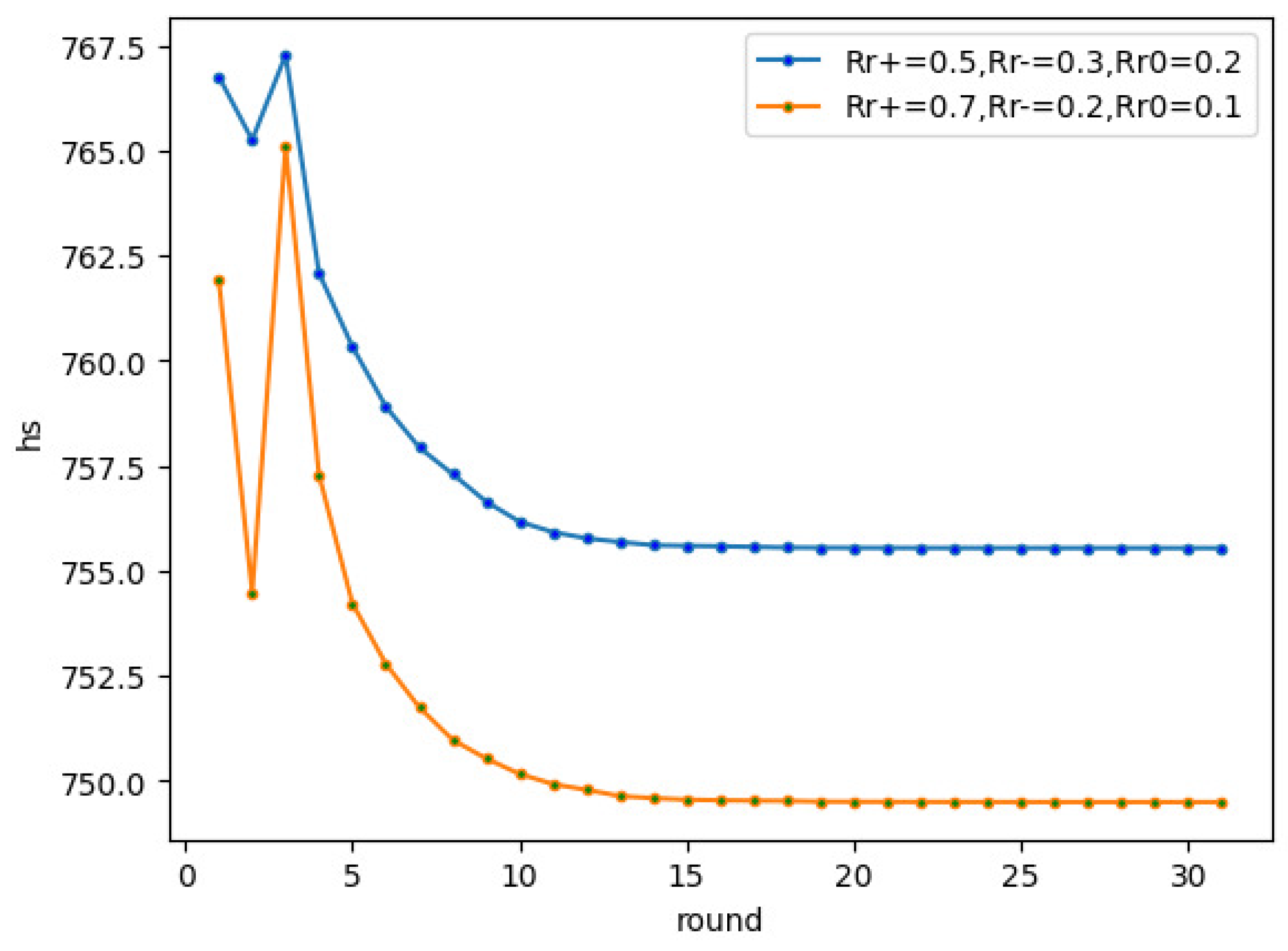
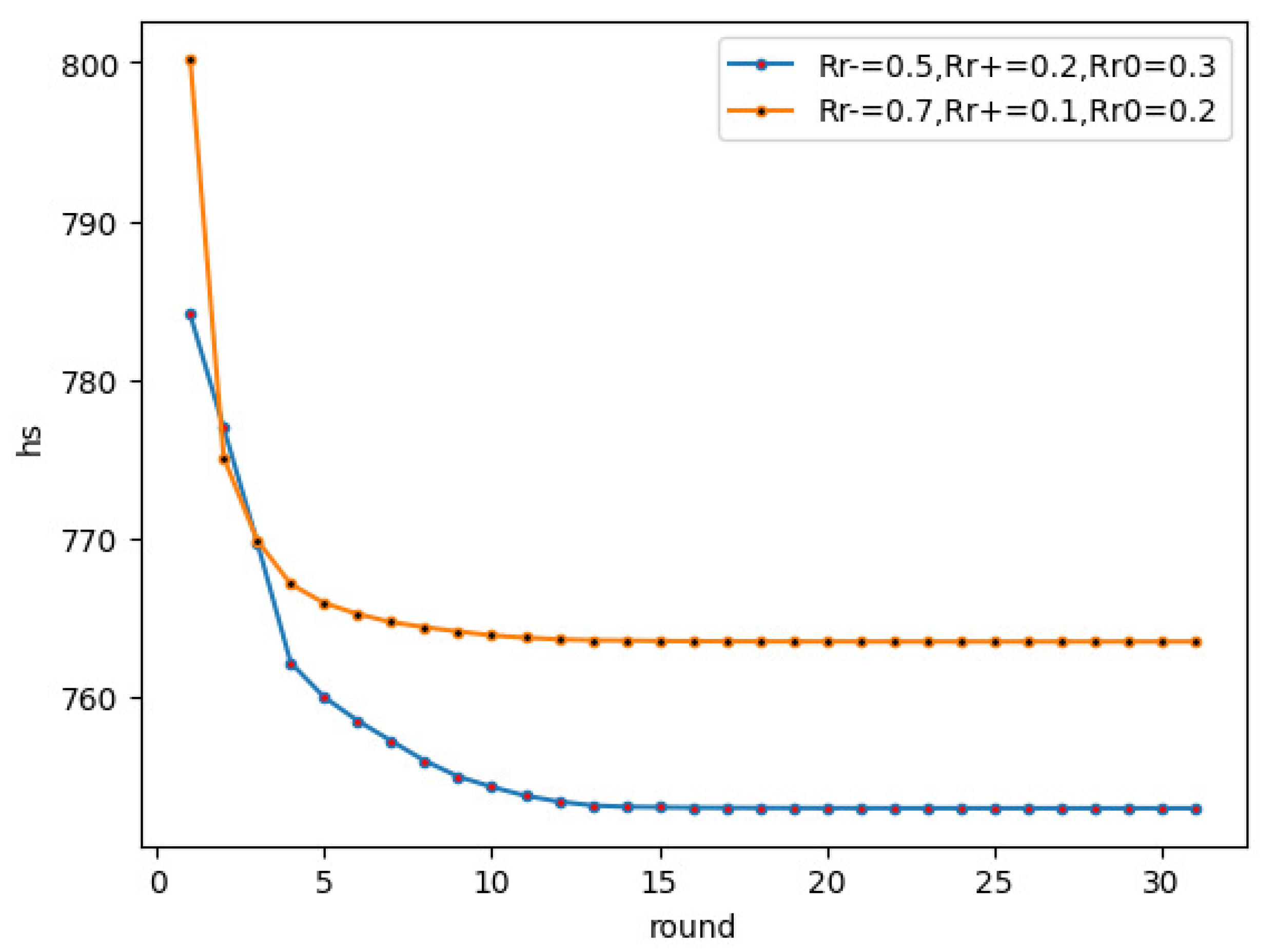
In this simulation, we explored the influence of the various strengths of conversion between various weighted edges. The strength of conversion represents the conversion level between different edges. The greater the strength is, the greater the connection strength between the nodes, and the more difficult the transformation of an edge is. In the initial network, we set the number of positive edges, negative edges, and neutral edges as equal, the convergence parameter , the degree of disagreement threshold was , the proportion of negative opinions was 0.3, the edge and node evolution control threshold parameter .
The first experiment involved observing the strength of the negative edge change to the positive edge. As seen in
Figure 10, the experiment considered two cases,
and
, respectively. When
,
reached a stable state quickly. This result shows that when
is larger, i.e., the greater the strength of the negative edge change to the positive edge in the network, the network can approach a balanced structure more quickly. The result shows that it is difficult to change the negative edge to the positive.
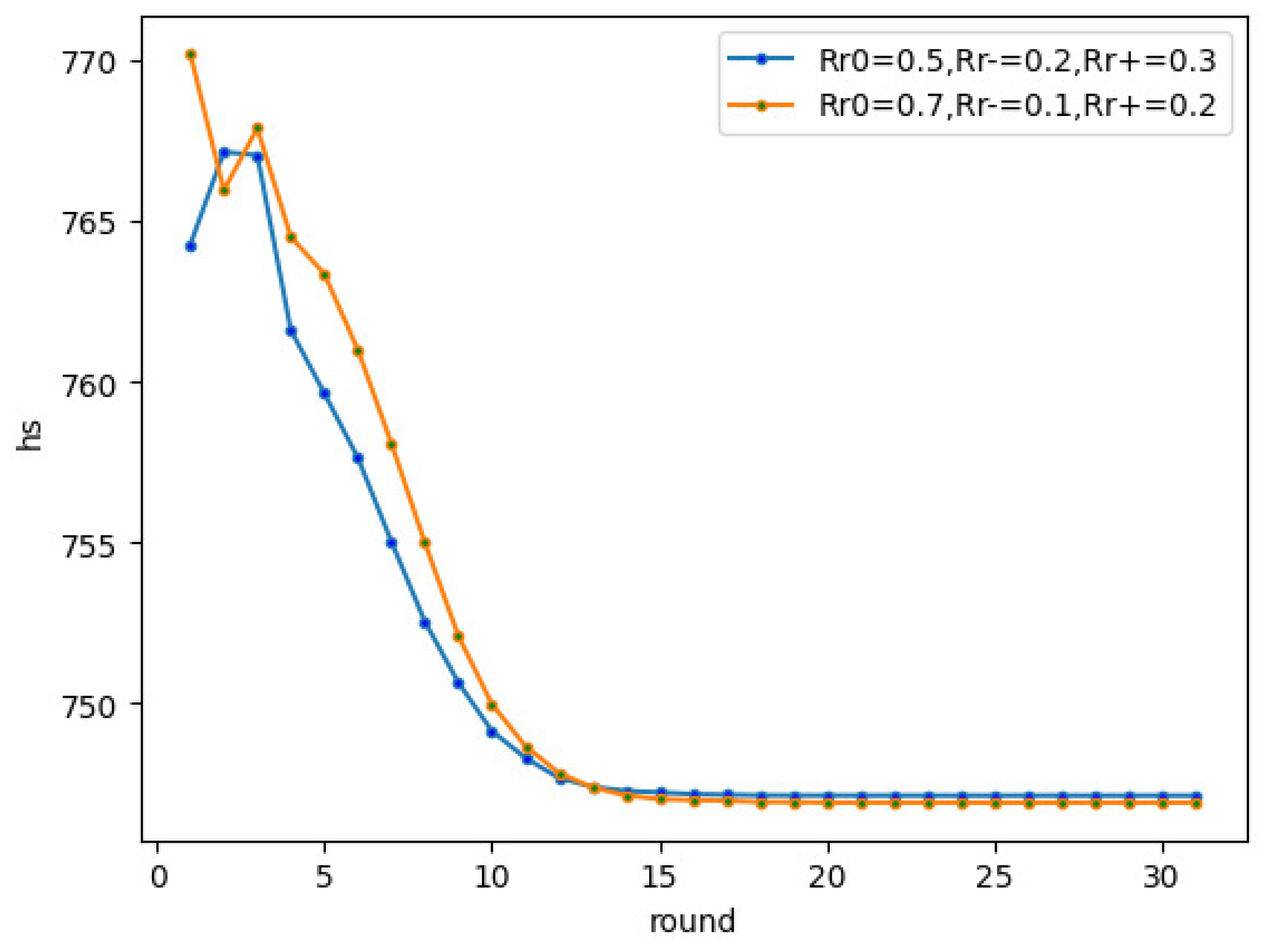
The second experiment was to observe the transformation of neutral edges into negative and positive ones. As shown in
Figure 11, when
and
, the network approached a balanced state after 10 rounds. This experiment’s results show that the strength of the neutral edge has a small influence on the structural balance. Because the neutral relationship implies that there is no clear relationship between two nodes, it is easier to convert the neutral edge to a positive edge or negative edge.
The third experiment was to observe the strength of the positive edge change to the negative edge. As shown in
Figure 12, after 10 rounds,
approached a stable state in the case of
= 0.7; however, in the case of
= 0.5,
was still evolving toward the structural balance. The result shows that it is difficult to convert the positive edge into the negative edge.
In conclusion, the various strengths of conversion have an effect on the final network structural balance. Increasing the strength of the negative edge and positive edge can promote the network to approach structural balance. We can conclude that it is easy to transform a neutral edge into a positive or negative edge; the contrary is difficult.
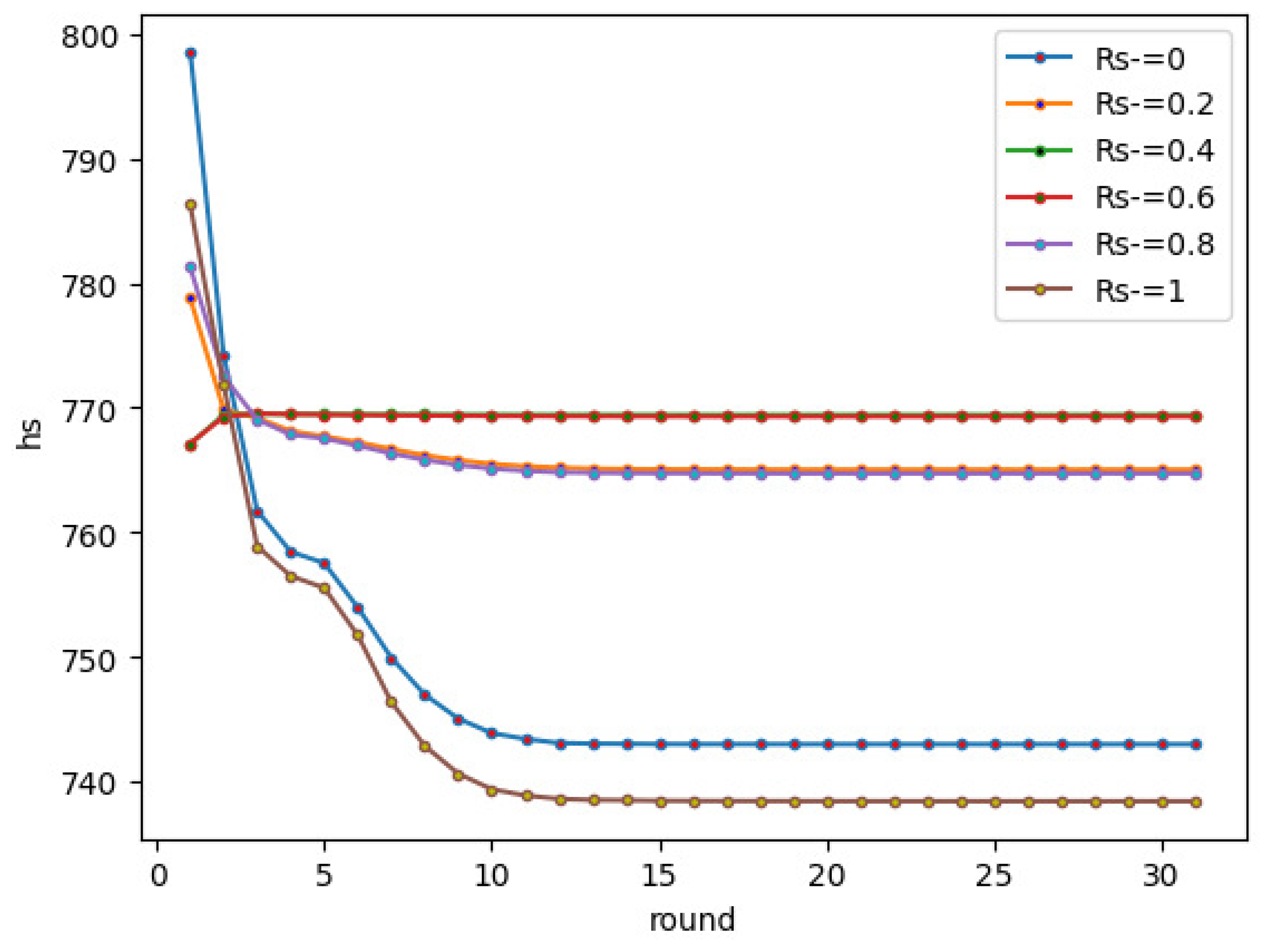
6.5. Scenario 5, the Influence of Proportion of Positive and Negative Edges
In this experiment, we investigated the effects of different ratios of three types of edges on structural balance. We set the proportion of negative opinions as 0.3, , and = 0.7. The strength of conversion between various edges were the same; that is, .
The influence of
in the network is shown in
Figure 13. It can be seen that the larger the ratio of
, the faster
drops. By comparing with
Figure 2, we can see that the proportion of positive edges in the balanced triads is
, and the proportion of the negative edges is
. Therefore, we conclude that the larger the number of initial
is, the faster the network approaches structural balance.
Figure 14a,b show that positive edges are more likely to appear than negative and neutral edges. Therefore, the probability of a negative edge evolving into a positive edge is greater than that of a positive edge evolving into a negative edge within the framework of structural balance. The probability of structural transformation is illustrated in
Figure 15, and the probability of structural transformation in
Figure 15a is greater than that of
Figure 15b.
The influence of
is shown in
Figure 16. It can be observed that in the case of a low proportion of
, the network approaches structural balance faster. By analyzing
Figure 2, we can see that the proportion of negative edges in the unbalanced triads is
, and the proportion of positive edges is
. Thus, the high proportion of negative edges will delay the network toward structural balance.
As shown in
Figure 17a,b, we can see that the number of negative edges gradually decreased. The number of neutral edges remained unchanged in four rounds and then decreased, while the number of positive edges kept increasing until all edges became positive. Structural transformation is illustrated in
Figure 18.
The influence of neutral edges on the final balanced state is shown in
Figure 19. In
Figure 19, it can be observed that after 20 rounds of evolution, a high number of neutral edges favor the network structural balance. The explanation is that the neutral edge may evolve to a positive edge and negative edge, and contribute to the increment of balanced triads.
By observing
Figure 20a, we can see that both the number of neutral edges and negative edges decreased gradually before 10 rounds. This dynamic resulted in the gradual increase of positive edges. By observing
Figure 20b, we can see that the number of neutral edges did not change in the first and second evolution rounds. However, from the third round, the negative and neutral edges began to decrease. These experimental results show that the probability of the neutral edge evolving into the positive edge was greater than that of the negative edge. The probability of structural transformation in
Figure 21a is greater than that of
Figure 21b. Since the network is toward a structural balance.
This scenario implies that we can increase the number of positive edges and neutral edges to make these edges become the main body, and reduce the negative edge to promote the harmonious development of the group. In a group, if there are more positive edges, the network will tend to be structurally balanced faster, while negative edges have a reverse effect.
7. Discussion
In our simulation, we also tested our proposed model on ER random graphs and WS small-world network structures. Our simulation suggests that final signed network evolution results are robust to different structures and sizes. The results only depend on the connection weight of the networks, the percentage of positive edges, and the percentage of positive opinions. We observed the same evolution trend on different signed networks.
In summary, five scenarios including variations of edges and signed weights and variations of the proportion of positive and negative opinions, were investigated to observe the final signed network stable state. Specifically, we performed extensive simulations to examine how different initial conditions affected the network evolution, i.e., the balance level of network structure and the opinion polarization pattern.
We observed that initial conditions, such as a high proportion of positive edges, positive opinions, and greater signed weights, could promote the signed network towards balance. Our simulation results suggest that the signed network in the real world is a dynamic equilibrium process, serving as confirmation of the imperfect balance theory, i.e., even if the system evolves to a stable state, the signed network still cannot achieve a perfect structural balance.
Importantly, the simulation results could explain the imperfect Heider balance of many real-world signed systems. Meanwhile, our computing model explains that the level of balance achieved depends on the connecting weight of the network, the percentage of positive edges, and the percentage of positive opinions, most of all, on the distributions of these positive edges/opinions and the weight on the signed network. The comprehensive numerical results suggest that values of balance at the micro-and macro-levels may match up to some extent; the macro dynamic pattern of the signed network is especially closely related to its microstructural balance.
Similar to the social influence network model, the proposed co-evolution model can be used to predict real-world signed network evolution on the final convergence state (structure balance level v.s. polarization pattern). However, the social influence network model (Friedkin, N.E. Johnsen, E.C., 1999) [
28] and the co-evolution model of opinion and social tie dynamics (Wang, H.; Luo, F.; Gao J., 2021) [
35] are based on rigorous time-varying matrix mathematical analyses. Our proposed model is a rule-based simulation, its effectiveness for large-scale signed social networks needs to be verified by an empirical data set. This is also the direction of our related work in the next step. In a follow-up to this study, we plan to conduct experiments based on real data sets to evaluate the effectiveness of the proposed social network evolution modeling. The basic idea is a rule-based model simulation and comparative analysis of a rule-based model adjustment with real-world empirical signed networks. Specifically, we will modify and estimate the key evolution parameters through the empirical process of edge-evolution and node-evolution of a real signed network
G and then modify the rule-based model
. On the one hand, we can verify the effectiveness of our proposed model through the empirical evolution process of large-scale signed networks. On the other hand, we can refine our proposed model. Our ultimate expectation is that the refined model can achieve acceptable prediction accuracy and could be extended to the prediction and regulation of a real signed social system.
In our model, it is assumed that each node is homogeneous, and there is no special node, such as an opinion leader; in addition, final signed network evolution results only depend on different initial conditions, and are robust to different structures and sizes. Therefore, this model is also applicable to the case of having non-random distributions of opinions and edges.
8. Conclusions
In this investigation, based on the social influence network theory, we introduced a neutral binary motif and a triadic motif, and focused on the contributions of interpersonal influenced to the formation of interpersonal agreements and polarization. Our proposed edges–opinions co-evolution model entails a cognitive process when it deals with conflicting influential opinions and the signs and strengths of a social structure. This article extends the implications of the social structure balance theory and assesses the social influence theory in groups of dyads—triads with neutral relations.
Extensive simulations were performed in five cases. The results are summarized as follows: (1) the higher the tolerance for the difference of opinions, the faster the network can approach a balanced state. (2) The more nodes with the same attitude, the faster the network can reach structural balance. (3) When the edge evolution is faster than the opinion, the network can approach the balanced state faster. (4) The ’larger’ the strengths of the positive and negative edges, the faster the network can approach the balanced state, while the strength of the neutral edge has a trivial effect. (5) The higher the proportion of positive and neutral edges, the faster the network can approach balance.
In particular, we showed that the persistent fluctuation of opinions is consistent with the minimal global energy function or a local triadic-signed structural balance emergence. This work verifies that signed social networks are indeed of limited balanced and could be used to explain the ubiquitous polarization phenomenon in online social networks. These results can provide us with a better understanding of the inherent mechanisms and key properties of signed networks.
Our model, however simple, should find further extensions and applications in social structures, where conditions of consistence are meaningful. For example, for a real signed network, in addition to structure and node attributes, the scale of the network will also change, such as the increase of nodes and the increase or deletion of edges. There may be other complex social mechanisms for the formation of real signed social networks, such as social status, social power theories, and combing with sentiment and behavioral data analysis [
43,
44,
45]. The co-evolution feedback model we proposed can be further extended to such a case.
Next, we hope to collect real signed social network data to verify the effectiveness of several main conclusions obtained in this paper. We also hope to use the model and relevant conclusions proposed in this paper to empirically study collective action problems, such as information diffusion, cooperative evolution, and public opinion dissemination on signed social networks.