1. Introduction and Motivation
The isotropic (or Galilean) plane is a projective-metric plane, where the absolute consists of one line—the absolute line , and one point on that line—the absolute point .
When using homogeneous coordinates in the projective plane, , , then we choose the absolute point and the absolute line having the equation . Points incident to the absolute line are called isotropic points and lines incident to the absolute point are called isotropic lines. We will mention a few well known metric quantities in the isotropic plane for which we assume that and .
Two lines are called parallel if they have the same isotropic point. Points which lie on the same isotropic line are said to be parallel.
For two non-parallel points and the isotropic distance is defined as . Notice that the isotropic distance is directed. For two parallel points and , the isotropic span is defined as . The midpoint of the points and is defined as .
The angle formed by non-isotropic lines and given by and is defined by , and it is directed. The bisector of the lines and is given by the equation . A normal line to a line l at a point P is the isotropic line n passing through P.
All projective transformations that preserve the absolute figure are of the form
and form the 5-parametric group
known as the
group of similarities of the isotropic plane (see [
1]).
Distances, spans and angles are kept invariant under the subgroup
of
which consists of transformations of the form
is called the
motion group of the isotropic plane.
Metric quantities and all the facts related to the geometry of the isotropic plane can be found in [
1,
2].
A triangle is called
allowable if none of its sides are isotropic [
1]. As it is explained in [
3], according to [
1], to any allowable triangle in the isotropic plane there is exactly one circumscribed circle. The equation of this circle is of the form
,
. Choosing a suitable coordinate system and applying the group of similarities, we may assume that the equation of this circle is
, and that the vertices of the allowable triangle
are
,
,
, where
a,
b, and
c are mutually different numbers. For convenience, we will frequently use abbreviations
and
. Choosing, without loss of generality, that
, the diameter of the circle circumscribed to the triangle
, passing through its centroid
, lies on the
y-axis, while the
x-axis is tangent to this circle at the endpoint of that diameter.
For each allowable triangle , one can, in the described way, achieve that its circumscribed circle has the equation , and its vertices are of the form , , and , with . We shall say that such a triangle is in the standard position, or shorter, that the triangle is the standard triangle. To prove geometric facts for allowable triangles, it is sufficient to give a proof for a standard triangle. Its sides , , and have equations , , and . Using the mentioned notations it can be proved that and .
The tangential triangle of a given triangle is the triangle determined by the three tangents to the circumscribed circle of the triangle at its vertices. It can be proved that the lines , , and are symmetric, with respect to bisectors of the angles A, B, and C, to the medians , , and of the triangle . The lines , , and meet at the point K which is called the symmedian center of the triangle .
Let
be a standard triangle and let
,
, and
, respectively
,
, and
, be lines through the points
A,
B, and
C such that
,
. In [
4] it is proved that the lines
,
, and
pass through a common point, say
, if and only if
, and the lines
,
, and
pass through a common point, say
, if and only if
, where
is given by
. The points
and
are called
Crelle–Brocard points, and
is called the
Brocard angle.
The isotropic analogue of Brocard’s theorem was first obtained in [
2].
The standard triangle
has, by [
4], the symmedian center
K and Crelle–Brocard points
and
given by
where
,
. One can prove that
,
,
, and
.
These three points lie, according to [
5], on the
Brocard circle of the triangle
(see
Figure 1), given by
If
,
, and
are midpoints of the sides
,
, and
of the allowable triangle
, and
,
and
are points on the perpendicular bisectors of these sides such that spans
,
, and
are proportional to the lengths of sides
,
, and
, then the points
,
, and
lie on a line, call it
. Triangles
are the so-called
Kiepert triangles of the triangle
, and the line
is the axis of homology of the triangle
and the corresponding Kiepert triangle
. Axes of homology of an allowable triangle
and its Kiepert triangles envelope a parabola which is called the
Kiepert parabola [
6].
The inscribed and the circumscribed Steiner’s ellipses of an allowable triangle have the same nonisotropic axis, which passes through the centroid
G of that triangle and which in the case of a standard triangle has equation
. This axis is called the
Steiner’s axis of the considered triangle. In [
7], the
Steiner point of the allowable triangle
is defined as the fourth (the first three being
A,
B, and
C) common point
S of the circumscribed circle and the circumscribed Steiner ellipse of that triangle. If
is a standard triangle then
.
3. The First Brocard Triangle and Some Other Significant Elements
In this section we consider the relationships between the first Brocard triangle and some other objects related to a triangle in the isotropic plane.
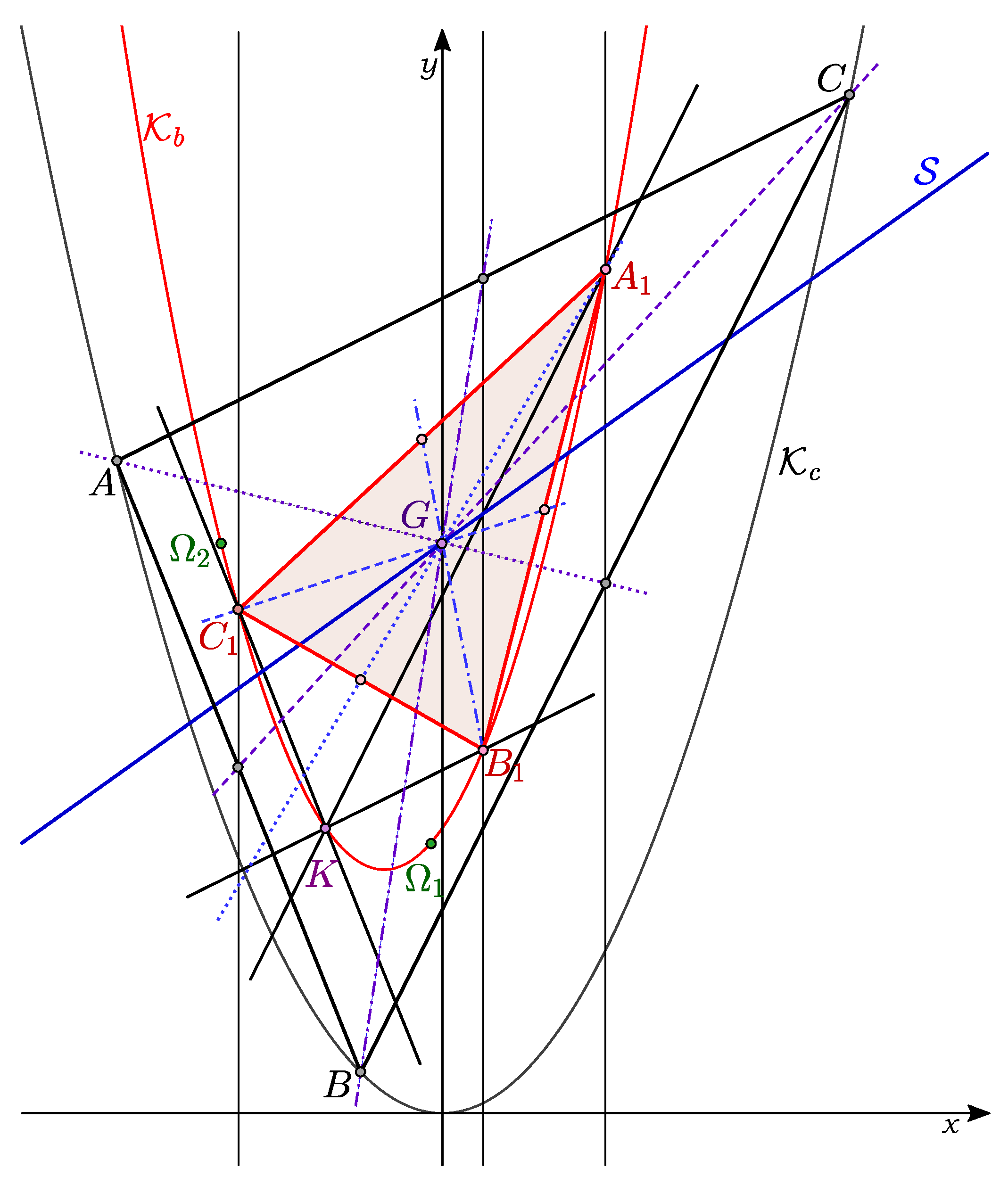
Theorem 4. Let G be the centroid and the first Brocard triangle of an allowable triangle . Then the pairs of lines , ; , ; and , have the same bisector. This bisector is the Steiner axis of the triangle (Figure 1). For the Euclidean case see [8,9]. Proof. The lines
and
have slopes
The sum of slopes is equal to
, therefore the bisector of these lines has the slope
. The Steiner axis of the triangle
is given by
[
7], which passes through the centroid
, and coincides with this bisector. □
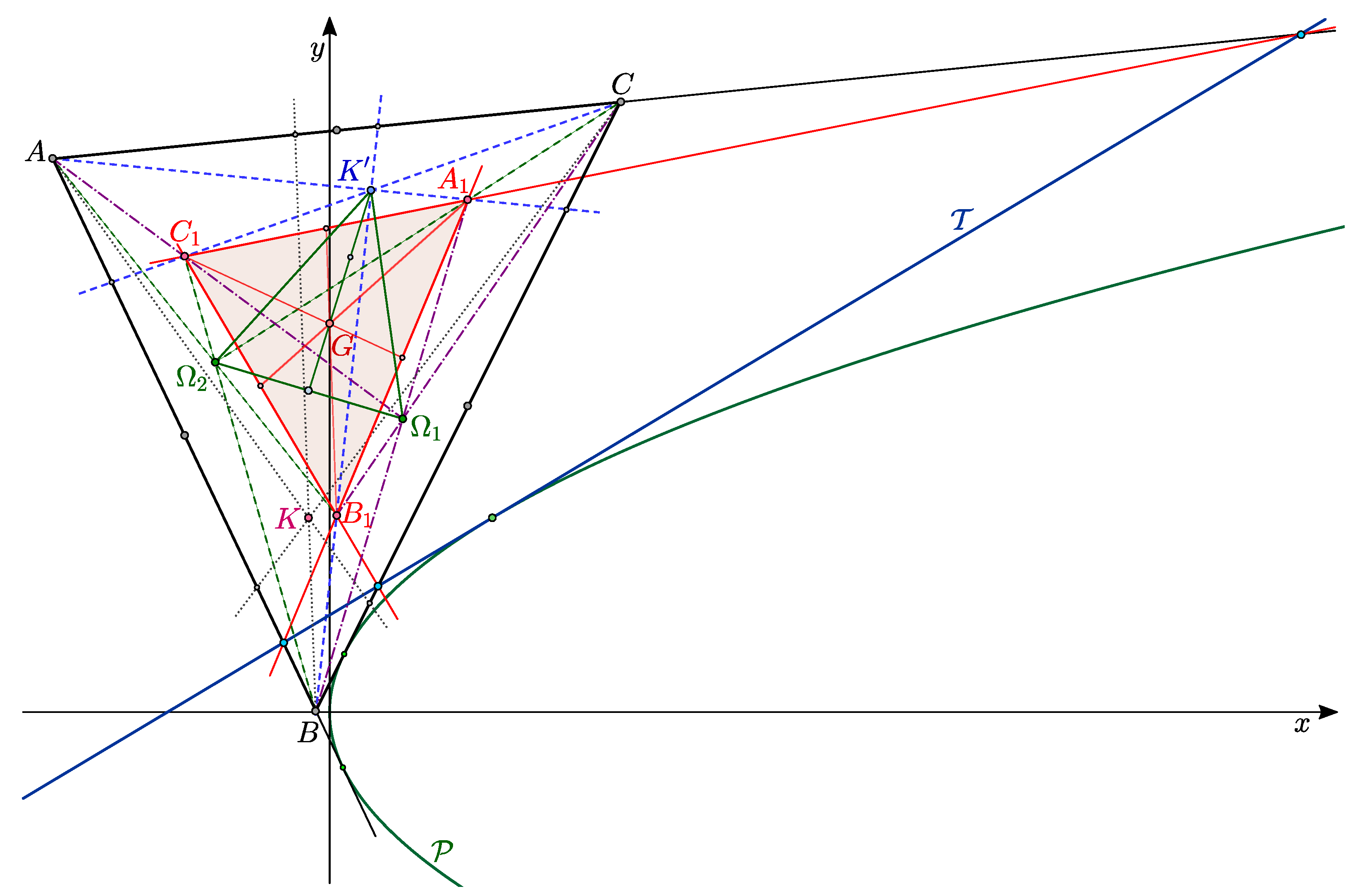
Theorem 5. The first Brocard triangle of an allowable triangle is homologous with this triangle, and the center of homology is —the point reciprocal to the symmedian center of the triangle (see Figure 2). For the Euclidean case see [9]. Proof. The line
passes through the point
and also through the point
, hence it is the line
. In addition, this line passes through the point
which is, by [
5], reciprocal to the symmedian center
K and anticomplementary to the midpoint of Crelle–Brocard points
and
. The same also holds for analogous lines
and
. □
Theorem 6. In case of the standard triangle , the axis of homology of triangles and from Theorem 5, has the equation Proof. It is enough to prove e.g., that the point
lies on lines
and
, and on the line defined by (
7).
In the discussion following Theorem 2 in [
6] it is shown that the Kiepert triangle
of a triangle
, with
, coincides with the first Brocard triangle
of the triangle
and the axis of homology of triangles
and
touches the Kiepert parabola of the triangle
(see
Figure 2).
Theorem 7. The triangle and its first Brocard triangle are three-homologous, and the centers of homologies are the point and Crelle–Brocard points and of that triangle. Triangles and have the same centroid G [9] (see Figure 2). Proof. According to [
4], the lines
and
have equations
The point
lies on the first line, and the point
lies on the second one because
Therefore, points
and
lie on lines
and
, respectively, the point
lies on lines
and
, and the point
lies on lines
and
. Points
,
and
have the centroid
because
and
□
The line
has the slope
, where
S is the Steiner point of the triangle
[
7].
because the line
has the same slope as
. Similarly, we get
and
. Because of Theorem 1, we have
,
, and
. Therefore, triangles
and
have the property that lines through the vertices of the first triangle parallel to the corresponding sides of the second triangle pass through a common point, and lines through the vertices of the second triangle parallel to the corresponding sides of the first triangle pass through another common point. These two triangles are called
parallelogic, and the two mentioned points are the
centers of parallelogy of these triangles. So we have the following theorem.
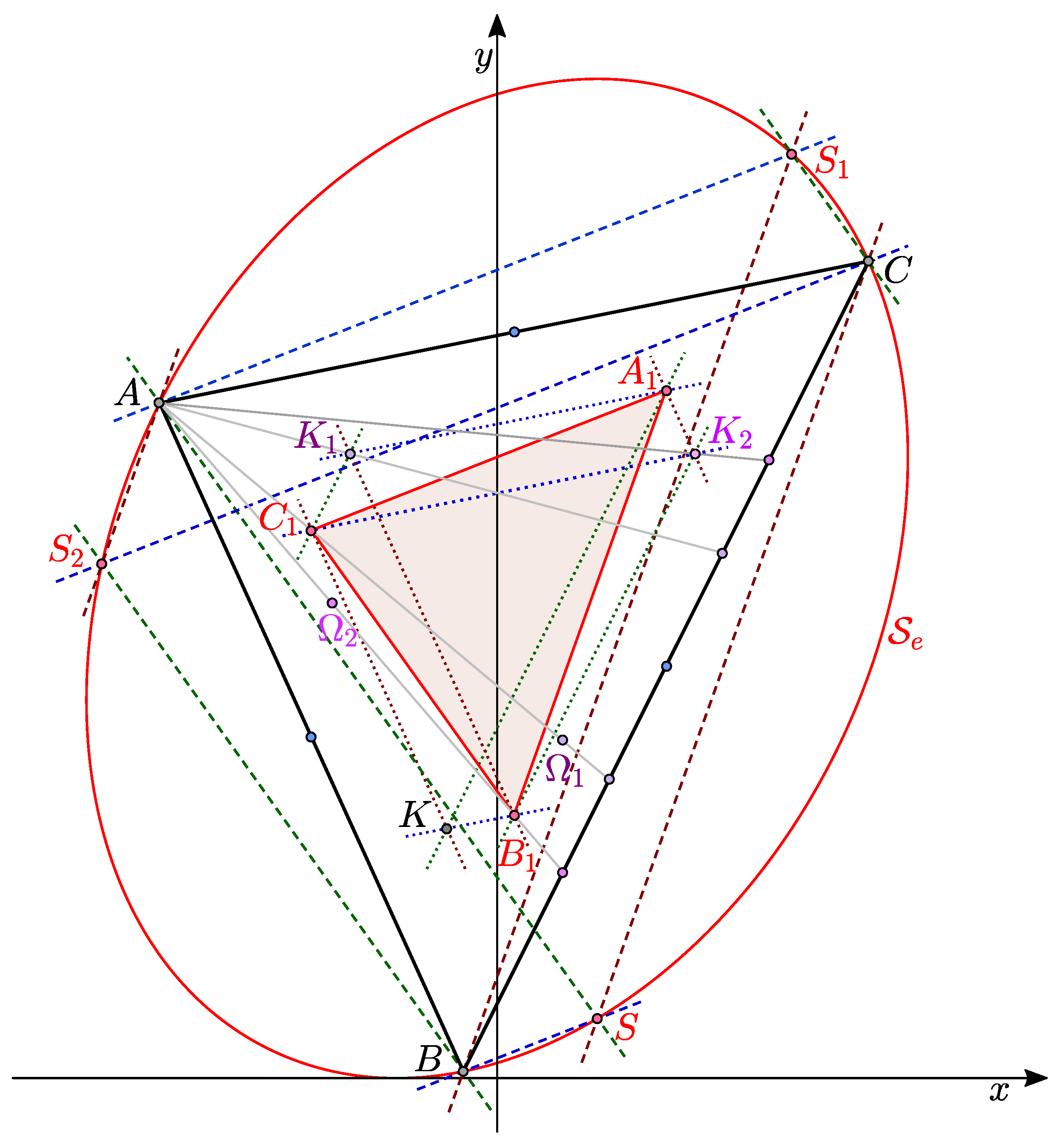
Theorem 8. A triangle and its first Brocard triangle are parallelogic with the centers of parallelogy at the Steiner point and at the symmedian center of this triangle (see Figure 3). Theorem 9. Let be the first Brocard triangle of an allowable triangle . Then the lines parallel to , , and through C, A, and B, through B, C, and A, pass through a common point , respectively . In addition, the lines parallel to , , and through , , and , respectively , , and , pass through a common point , respectively (see Figure 3). In the case of the standard triangle these points are given by Proof. According to (
5), the slope of the line
is
, and the line through
C parallel to it is given by
i.e.,
The point
lies on this line because
Substitutions
and
imply the substitution
, and using this substitution, the previous proof shows that the line through
B, parallel to
, passes through
. Cyclic permutations
imply
, and
. The line
is parallel to
, and it passes through
. Let us show that this line also passes through
, i.e., that
i.e.,
which, because
and
, after dividing by
a, becomes equivalent to
Other statements of the theorem are proved in a similar way. □
Using the obvious term three-parallelogy, statements of Theorems 8 and 9 can be briefly summarized as the following corollary.
Corollary 1. The allowable triangle and its first Brocard triangle are three-parallelogic, and in the case of a standard triangle , centers of parallelogy are the Steiner point S of the triangle and points , , and the symmedian center K of the triangle and points (see Figure 3). In the Euclidean case, the statement about three-parallelogy, without proof, can be found in [10]. Theorem 10. Points S, , and from Theorem 9 lie on the circumscribed Steiner ellipse of the triangle (see Figure 3). Proof. The statement for Steiner point
S is proved in [
7]. For the point
we have
and this point lies on the circumscribed Steiner ellipse of the triangle
, which, by [
7], has the equation
. Analogous proof is for the point
. □
Theorem 11. Points and from Theorems 9 are reciprocal to Crelle–Brocard points and of that triangle (see Figure 3). In the Euclidean case this statement, without proof, can be found in [11]. Proof. For the point
we get
and, its reciprocal point has coordinates
and
which is the point
. The proof for
is analogous. □
Let us consider the indirect similarity given by
and vice versa
The similarity (
10) obviously maps the point
to the point
, and points
B and
C to points
and
. This similarity maps the Steiner point
S, which is, according to [
7], given by
, to the point with abscissa
and ordinate equal to
, which is the point
K. The point
is mapped to the point with abscissa
and ordinate
, which is the point
. The centroid
is under the similarity (
10) mapped onto itself.
The circumscribed circle and the circumscribed Steiner ellipse of the triangle
have, according to [
3,
7], equations
and
which, after substitutions (11), become
and
After rearrangements and replacements
,
this can be written as
and
which are, according to [
5,
7], equations of the Brocard circle and the inscribed Steiner ellipse of the triangle
.
Let us find the equation of the fixed line, i.e., of the axis of similarity (
10). The transformation
,
maps the line
to the line
i.e., to the line
which coincides with the line (
12) if and only if
Therefore,
and the required axis is the line
which is, according to [
7], the Steiner axis of the triangle
. The last result is in accordance with Theorem 4.
Thus, we have proved:
Theorem 12. An allowable triangle and its first Brocard triangle are indirectly similar. This similarity has the center at the common centroid of these two triangles, its coefficient equals , its axis is the Steiner axis of the triangle , and it maps the points S, , and from Theorem 9 to points K, , and from the same theorem.
Corollary 2. The symmedian center of the allowable triangle is the Steiner point of its Brocard triangle .
For the Euclidean case see [9]. Corollary 3. The circumscribed Steiner ellipse of the first Brocard triangle of a given allowable triangle is the inscribed Steiner ellipse of that triangle.
Corollary 4. Segments and , where G is the centroid of the allowable triangle , S its Steiner point, and K its symmedian center, have the same perpendicular bisector as pairs of lines from Theorem 4.
For the Euclidean case see [12]. Theorem 13. An allowable triangle is homologous with the complementary triangle of its first Brocard triangle.
Proof. Points
and
have the midpoint
because
The line
passes through
and
because
and
which is the line
. This line also passes through the point
because
□
Theorem 14. If is the first Brocard triangle of the allowable triangle , then its Crelle–Brocard points and divide in equal proportions the pairs of segments , ; , ; , .
For the Euclidean case, without proof, see [10]. Proof. According to Theorem 7 and its proof, points
and
lie on lines
,
,
, and
,
,
. From (
1) and (
3) we get the ratios
so we have to prove the equality
which is, after dividing by
q, equivalent to
and since
, equivalent to
This last equality holds true because
□
Theorem 15. If is the first Brocard triangle of the allowable triangle with the Brocard angle ω, then , , and are isosceles triangles, which have angles at sides , , and equal to ω.
For the Euclidean case see [9]. Proof. According to the proof of Theorem 7, lines
and
, containing points
and
, have slopes
and
. By cyclic permutations it follows that lines
and
, containing the point
, have slopes
and
. So we get
□
Theorem 16. If P is the center of homology of the triangle and its first Brocard triangle, and if D, E, and F are points symmetrical to P with respect to the midpoints of sides , , and , then the triangles and are symmetrical with respect to the midpoint S of the Crelle–Brocard points and .
For the Euclidean case see [13]. Proof. implies . By Theorem 7, , where G is the centroid of . We get , i.e., or . □