Abstract
In recent decades, AIDS has been one of the main challenges facing the medical community around the world. Due to the large human deaths of this disease, researchers have tried to study the dynamic behaviors of the infectious factor of this disease in the form of mathematical models in addition to clinical trials. In this paper, we study a new mathematical model in which the dynamics of T-cells under the effect of HIV-1 infection are investigated in the context of a generalized fractal-fractional structure for the first time. The kernel of these new fractal-fractional operators is of the generalized Mittag-Leffler type. From an analytical point of view, we first derive some results on the existence theory and then the uniqueness criterion. After that, the stability of the given fractal-fractional system is reviewed under four different cases. Next, from a numerical point of view, we obtain two numerical algorithms for approximating the solutions of the system via the Adams-Bashforth method and Newton polynomials method. We simulate our results via these two algorithms and compare both of them. The numerical results reveal some stability and a situation of lacking a visible order in the early days of the disease dynamics when one uses the Newton polynomial.
Keywords:
existence; fractal-fractional derivative; HIV-1 infection; Newton polynomial; Adams-Bashforth MSC:
34A08; 65P99; 49J15
1. Introduction
According to medical definitions and clinical findings and virology, human immunodeficiency virus (HIV) is a type of retrovirus that leads to acquired immunodeficiency syndrome (AIDS) in humans [1]. In fact, T-lymphocytes are the largest number of white blood cells in the human immune system that are attacked by HIV viruses, which attack T-cells and infect them, reducing their number and efficiency. They disrupt cells. Therefore, this process reduces the resistance of the immune system in the human body and weakens it [1]. Although the HIV virus infects other cells, it causes the most damage to T cells by causing the degradation and destruction of T-cells. As a result, the affected person’s body gradually becomes sensitive to various types of infections and contaminants and completely loses its immunity. Usually, according to laboratory results, a healthy person has white blood cells with a normal T-lymphocyte count of 800 to 1200/mm3. The decrease in T-lymphocyte count may be due to thymus insufficiency or bone defects. One way to determine whether a person is infected with the virus is recognized through very small number of T-lymphocytes (less than 200/mm3).
Currently, AIDS is one of the most unknown and dangerous diseases of our time. According to UNAIDS 2017, which is published annually, about 36.7 million people worldwide are living with HIV, and nearly 1.8 million people have recently been infected with HIV, and almost one million people worldwide are affected by various complication, and died of AIDS in 2016. There are even several countries, especially in Africa and some less developed countries, where up to thirty-five percent of the population between the ages of fifteen and fifty are infected with the HIV virus [2]. Despite significant advances in the control of the disease, no vaccine for HIV has yet been found.
In recent decades, many attempts have been made to design, analyze, simulate and solve mathematical dynamic models, which include the basic rules in the analysis of control and prevention of the spread of various diseases and infections. In this regard, biology and engineering are among the most widely used fields for various types of mathematical modeling, which are particularly popular among researchers. For such a purpose, derivation operators and differential equations play an important role. To demonstrate such high efficiency, we can refer to a sample of articles in which various types of mathematical models are observed, including time delying model of COVID-19 [3], anthrax model for animals [4], Hepatitis C model [5], memristor chaotic model of circuit [6], Lorenz-Stenflo hyperchaotic model [7], dynamics of environmental persistence of infections [8], Langevin model [9], Mump virus [10], Zika virus [11], mosaic disease [12], Computer viruses [13], thermostat control model [14,15], pantograph model [16,17], canine distemper virus [18], Lassa fever [19], hybrid model of p-Laplacian operators [20], co-dynamics of COVID-19 and diabetes [21], checmical modeling of cyclohexane [22,23], Navier systems [24], etc.
Designing mathematical models to analyze the dynamics of HIV infection is also known as a valuable and efficient measure in this regard [25,26,27]. Usually in almost all of these dynamic mathematical models, we can see the association between HIV viruses and non-infected T-cells and the effects of a variety of drug therapies and clinical therapies on reducing and controlling infected cells. Perlson [28] designed and presented a simple model for primary HIV infection in 1989. This model, which is related to HIV infection, is important, and many other models have been developed later, which are inspired by this model. Four years later, Perlson et al. generalized the model and examined some of the behaviors and characteristics of the new model [29]. They considered the model by defining four different state functions: virus population, non-infected T-cells, productive infected T-cells, and latent infected T-cells.
In recent years, some other mathematicians developed the basic integer order models of HIV infection in the context of the fractional order systems. In [30], Ding et al. introduced a fractional version of the infection of HIV for T-cells and analyzed the non-negative solutions of this system. Arafa et al. [31] used the generalized Euler technique for his model to obtain solutions and investigated the impact of changes of viral particles on the blood. After that, Bulut et al. [32] combined the homotopy and sumudu techniques to staudy the dynamics of their fractional model of the infection of HIV on T-cells. Lichae et al. [33] extended their fractional HIV model based on the effect of drug therapy and solved three-compartmental model of CD4+ with the help of LADM (Laplace Adomian decomposition method). In 2020, Nazir et al. [34] investigated not only existenece theory, but also stability criteria for the Caputo-Fabrizo HIV model of T-cells. Wang et al. [35] studied the time periodic reaction-diffusion equations for modeling 2-LTR dynamics in HIV-infected patients.
In 2017, Atangana [36] presented a generalized kind of operators entitled fractal-fractional operators. This definition used the existing notions of fractional calculus and fractal calculus with together. These operators are the convolution of the power-law, exponential law and generalized Mittag–Leffler law with fractal derivatives. There exist two components for such fractal-fractional operators: the fractional order and fractal dimension (order). Fractal-fractional differential equations transfer the order and dimension of every dynamical system into a rational order one. In fact, we are able to generalize each standard differential equation to the generalized systems having arbitrary order and dimension of derivatives. The main goal of such a combination is to analyze a vast range of nonlocal BVPs or IVPs that possess fractal behaviors. In this direction, a limited researchers obtained some results in which we see that the generalized fractal-fractional operators give accurate and more exact simulations for describing mathematical models of real-world phenomena. Some of new works in this regard are [37,38,39,40,41].
Due to the novelty and efficacy of these new fractal-fractional operators, in this paper, we aim to design a mathematical model of T-cells under the effect of HIV-1 infection in which derivatives are fractal-fractional operators in the sense of Atangana-Baleanu. It is notable that in 2021, Ahmad et al. [42] studied the dynamics of HIV primary infection in the context of a model designed by the fractal-fractional operators. The main contribution and novelty of our work in comparison to their paper [42] is that we analyze all qualitative behaviors of such a fractal-fractional system. In other words, we first review the existence and uniqueness of solutions and further, we complete our study by giving new results about the stability (Ulam-Hyers-Rassias) of solutions. Also, for the first time, in this paper, we derive numerical schemes for the fractal-fractional -HIV-1 model with the help of the Newton polynomials and by applying some real data, we compare our results with the Adams-Bashforth simulations. In this direction, we can see some dynamical behaviors of the solutions in our simulations.
The arrangement of the paper is as follows: we introduce our fractal-fractional model in Section 2 and describe its parameters and coefficients. The existence results are given in Section 3 and further, in Section 4, we investigate the uniqueness. The stability criterion are implemented in Section 5. In the sequel, we derive two numerical schemes. In other words, in Section 6, the Adams-Bashforth method are done and then, we derive another algorithm in Section 7 by using the Newton polynomials. We present some simulations and discussions about both numerical methods in Section 8. We end the paper by giving conclusions in Section 9.
2. The Structure of the Model for T-Cells and HIV-1
In 2006, Wang and Li [1] formulated an integer-order classical mathematical structure of dynamics of T-cells under the HIV-1 infection in three-compartmental model as
via the initial values , , and , and also the state functions , , are an amount of susceptible T-cells, an amount of infectious T-cells, and the free particles of the infection of the HIV virus in the blood at the time , respectively. Moreover, the parameter N stands for the average number of infected particles by an existing infected cell, is the natural rate of death for the virus, is the return rate of infected cells to susceptible compartment, is the rate of death for infected T-cells, q is the rate of infection T-cells, is the natural rate of death, and shows the supply rate for new T-cells. They considered all parameters as positive values and .
To upgrade and improve the exact results, inspired by the standard model (1), we present a mathematical fractal-fractional model on dynamics of T-cells under the effect of HIV-1 infection via the generalized Mittag-Leffler-type kernel (fractal-fractional -HIV-1-model) as
subject to
where all assumptions and parameters are similar to above classical model (1). Also, is the -fractal-fractional derivative with the fractional order and the fractal order via the Mittag-Leffler-type kernel.
In other words, let a continuous map be fractal differentiable of dimension . In this case, the -fractal-fractional derivative of of the generalized Mittag-Leffler-type kernel of order in the Riemann-Liouville sense is defined as
where
is the fractal derivative and and [36].
Moreover, accordingly, for such a function , the -fractal-fractional integral via the Mittag-Leffler-type kernel is given by
if it exists, where [36].
3. Existence Property
In this section, the existence property is investigated based on fixed point theory. For the qualitative analysis, make the Banach space where with
for . We reformulate the R.H.S. of the fractal-fractional -HIV-1-model (2) as:
In this case, the fractal-fractional -HIV-1-model (2) is transformed into the following system
In view of (6), we rewrite the developed tripled-system with the compact IVP which takes the form
where
and
By the definition and by (7), we have
In the sequel, operating the fractal-fractional Atangana-Baleanu integral on (10), we get
Due to the above compact form of the fractal-fractional integral equation, the extended representation of it is illustrated as
We consider a self-map to derive a fixed-point problem, by defining as
The Leray-Schauder theorem is utilized to prove the existence property in relation to the fractal-fractional -HIV-1-model (2).
Theorem 1.
[43] Let be a Banach space, a convex closed bounded set, an open set, and . Then for the continuous and compact map , either:
- (HY1)
- , or
- (HY2)
- and s.t. .
Theorem 2.
Let . Assume:
- (P1)
- and (A is non-decreasing) s.t. and ,
- (P2)
- s.t.with .
Proof.
First, consider which is defined by (13) and assume
for some . Clearly, as is continuous, thus F is so. From (P1), we get
for . Hence
Thus F is uniformly bounded on . Now, take s.t. and . By denoting
we estimate
We see that (16) approaches to 0 independent of , as . Consequently
when . This gives the equicontinuity of F, and accordingly the compactness of F on by the Arzelá–Ascoli thoerem. Since all conditions of Theorem 1 are fulfilled on F, we have one of (HY1) or (HY2). From (P2), we set
for some s.t.
From (P1) and (15), we have
4. Uniqueness Property
Here, on the fractal-fractional -HIV-1-model (2), we investigate the Lipschitz property in the first step and further, the uniqueness property.
Lemma 1.
Consider , and let
- (C1)
- , , for some constants .
Then the kernels defined in (5) are fulfilled the Lipschitz property with constants w.r.t. the relevant components, where
Proof.
For , we take arbitrarily, and we have
From the above, we find out that is Lipschitz w.r.t. under the constant . For , we choose two arbitrary elements , and estimate
The above inequality means that is Lipschitz w.r.t. under the constant . Finally, for both arbitrary elemets , we have
This confirms that is Lipschitz w.r.t. under the constant . Therefore kernel functions are Lipschitze w.r.t. under the constants , respectively. □
Now, by invoking the above lemma, we are able to prove the uniqueness property for solutions of the fractal-fractional system (2).
Theorem 3.
Proof.
To prove the desired result, we consider the contrary of the conclusion of theorem. That is, consider the existence of another solution for the fractal-fractional -HIV-1-model (2), namely under the initial conditions
In this case, we estimate
and so
From (19), we know that the above inequality holds if , or . In the similar manner, from
we obtain
and this gives or . Further,
yields
Hence . In consequence,
The latter equality confirms that the fractal-fractional -HIV-1-model (2) possesses a unique solution. □
5. Ulam-Hyers-Rassias Stability
In this part, the stability result of solutions in the context of four types of the Ulam–Hyers, Ulam–Hyers–Rassias and their generalizations are proved on the tripled system of the fractal-fractional -HIV-1-model (2).
Definition 1.
Definition 2.
Remark 1.
is a solution for (20) iff (each of them depend on , respectively) s.t. ,
- (i)
- ;
- (ii)
- We have
Definition 3.
Definition 4.
If we take , in this case Definition 3 yields the Ulam-Hyers criterion for the stability of solutions.
Remark 2.
is a solution for (21) iff (each of them depend on , respectively) s.t. ,
- (i)
- ;
- (ii)
- We have
The following lemmas are useful for our main theorems.
Lemma 2.
For each , suppose that is considered as a solution of (20). Then the functions fulfill the inequalities
and
and
Proof.
Let be arbitrary. Since satisfies
so, by Remark 1, we are allowed to take a function s.t.
and . Clearly,
In this case, we estimate
To prove the next result, we regard the following:
- (C2)
- increasing mappings and provided that
Lemma 3.
Let to be held. For each , suppose that is considered as a solution of (21). Then the functions fulfill the inequalities
Proof.
Let . Since satisfies
thus, from Remark 2, we are allowed to take a function s.t.
and . Evidently,
Then, we estimate
Similarly, we can obtain the remaining inequalities. □
The Ulam–Hyers stability is checked about the fractal-fractional -HIV-1-model (2).
Theorem 4.
Proof.
Let and be an arbitrary solution of (20). Also, from Theorem 3, we assume as a unique solution of the fractal-fractional -HIV-1-model (2). Then is defined as
Therefore, by Lemma 2 and with the help of the triangle inequality, we estimate
Hence,
We set . In this case, .
Similarly, we obtain
where
Hence, the Ulam–Hyers stability of the fractal-fractional -HIV-1-model (2) is fulfilled. On the other hand, if we take
then , and the generalized Ulam–Hyers stability is simply proved. □
The Ulam–Hyers-Rassias stability is checked about the fractal-fractional -HIV-1-model (2) in the next theorem.
Theorem 5.
The hypotheses (C1) and (C2) are considered to be held. Then the given fractal-fractional -HIV-1-model (2) is the Ulam–Hyers–Rassias and generalized Ulam–Hyers–Rassias stable.
6. Numerical Scheme via Adams-Bashforth Method
In the present section of the paper, we aim to derive a numerical algorithm for the fractal-fractional -HIV-1-model (2). To do this, we apply a technique based on two-step Lagrange polynomials entitled fractional Adams-Bashforth method. We re-define fractal-fractional integral equations (12) at . In fact, we discretize these integral equations (12) for as follows
The approximation of above integrals are formulated by
Next, we approximate three functions on the interval by applying two-step Lagrange interpolation polynomials under the step size . By straighforward computations, we obtain algorithms which yield the numerical solutions to the fractal-fractional -HIV-1-model (2) as
where
and
7. Numerical Scheme via Newton Polynomials Method
In this section, we produce a new numerical scheme for solutions of our fractal-fractional -HIV-1-model (2) which was introduced by Atangana and Araz in the book [44] in 2021. To do this, we again use the compact form of IVP (7) with the conditions (8) and (9). In this case, we have
Set . Then
By discretizing the above equation at , we get
If we approximate the above integral, then it becomes
In this step, the function is approximated by the Newton polynomial as
We simplify the above relations, and we get
In consequence,
On the other hand, we compute above three integrals separately, and we get
and
and
8. Simulations and Discussions
In this section, we simulate and discuss dynamical behaviors of the fractal-fractional -HIV-1-model (2) via real data for parameters and initial values assumed by [45]. Based on the given data in this source, we let , , , , , , and . Moreover, the initial values for three state functions are It is assumed that all parameters are in days.
In the provided figures, we show the behaviors of three state functions under the effect of different values for the fractal-fractional orders simultaneously. We also compare the results in the graphs with respect to two numerical algorithms given by (29)–(31) and (41)–(43) as shown in Table 1, Table 2 and Table 3.

Table 1.
Results of the two numerical schemes for the susceptible T-cells (s) under the fractal order and fractional order with the step size .

Table 2.
Results of the two numerical schemes for the infectious T-cells (s) under the fractal order and fractional order with the step size .

Table 3.
Results of the two numerical schemes for free particles of the infection of the HIV virus in the blood (s) under the fractal order and fractional order with the step size .
In these graphs, the quantity of the time s interprets the number of days. Note that Figure 1 and Figure 2 demonstrate the dynamics of the T-cells via the Adams-Bashforth method (Section 6). Figure 1a indicates that when the fractal dimensions and fractional orders decrease, the number of susceptible T-cells steadily increases from the 42nd day to the 64th day, and steadily decreases from the 65th day to the 102nd day. Further it increases again from the 103rd day and finally converges to the integer-order at the 250th day to the end of the simulation period.
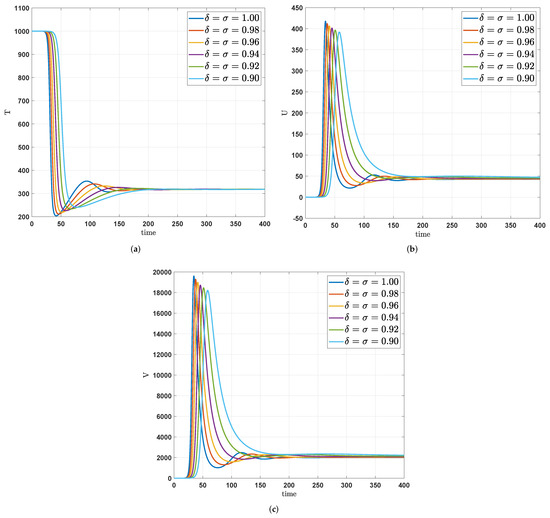
Figure 1.
Numerical trajectories by varying both fractal order and fractional order via the Adams-Bashforth method. (a) Amount of susceptible T-cells. (b) Amount of infectious T-cells. (c) Free particles of the infection of the HIV-1 virus in the blood.
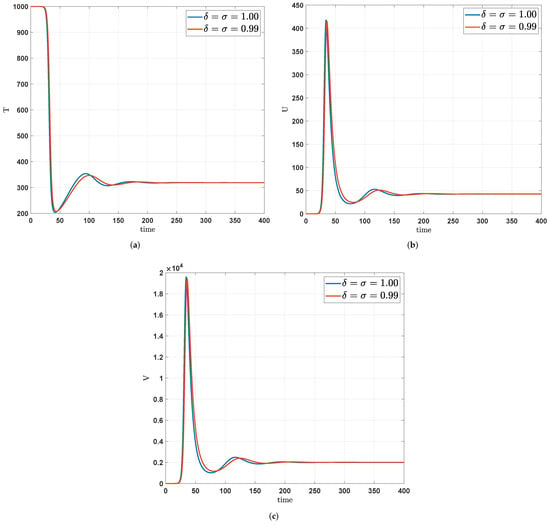
Figure 2.
Numerical trajectories by varying both fractal order and fractional orders via the Adams-Bashforth method. (a) A -variation in fractal-fractional orders of susceptible T-cells. (b) A -variation in fractal-fractional orders of infectious T-cells. (c) A -variation in fractal-fractional orders of free particles of the infection of the HIV-1 virus in the blood.
Figure 1b,c show that when the fractal dimensions and fractional orders move from the integer order, the peak of the amount of infectious T-cells and the free particles of the infection of the HIV-1 virus in the blood decrease respectively and also give slight differences in their asymptotic stabilities.
In Figure 2a,c, we show a -variation in fractal-fractional order. In this case, the numerical trajectories show that a slight change in the fractal-fractional order produces a slight changes in the asymptotic behavior of the HIV-1 virus on T-cells.
Figure 3 and Figure 4 demonstrate the dynamics of the T-cells via the Newton polynomials method (Section 7). Figure 3a also indicates that when the fractal dimensions and fractional orders decrease, the number of susceptible T-cells steadily increases from the 42nd day to the 64th day, and steadily decreases from the 65th day to the 102nd day. Also it increases again from the 103rd day and finally converges to the integer-order at the 250th day to the end of the simulation period, but it shows a disorganized behavior from the 11th day to the 24th day, which indicates the early stages of HIV in the T-cells.
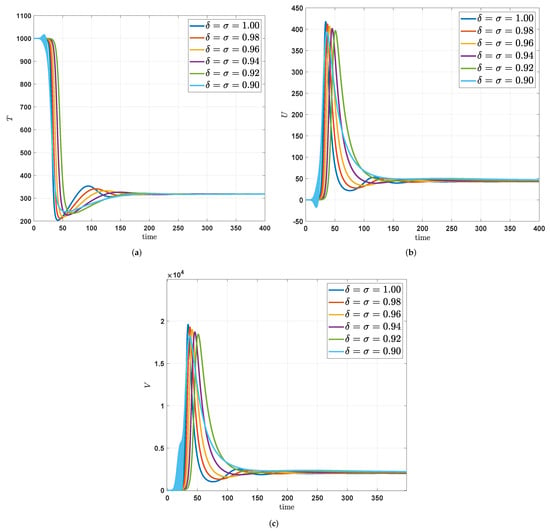
Figure 3.
Numerical trajectories by varying both fractal order and fractional order via the Newton polynomials method. (a) Amount of susceptible T-cells. (b) Amount of infectious T-cells. (c) Free particles of the infection of the HIV-1 virus in the blood.
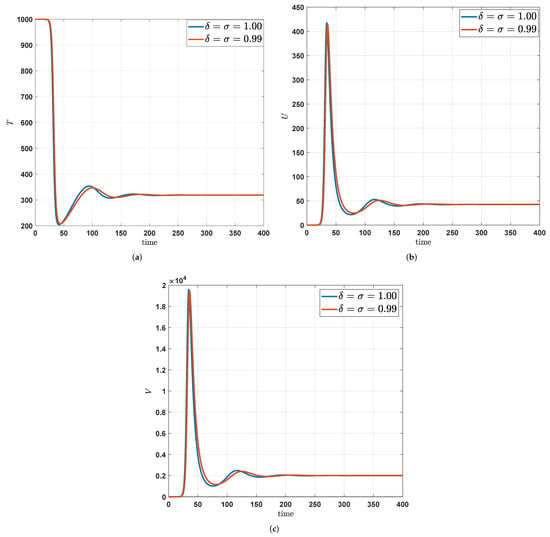
Figure 4.
Numerical trajectories by varying both fractal order and fractional order via the Newton polynomials method. (a) A -variation in fractal-fractional orders of susceptible T-cells. (b) A -variation in fractal-fractional orders of infectious T-cells. (c) A -variation in fractal-fractional orders of free particles of the infection of the HIV-1 virus in the blood.
Figure 3b,c show that when the fractal dimensions and fractional orders move from the integer order, the peak of the amount of infectious T-cells and the free particles of the infection of the HIV-1 virus in the blood decrease, respectively and also give slight differences in their asymptotic stabilities, but again, they show a disorganized behavior from the 11th day to the 24th day.
In Figure 4a,c, we show a -variation in fractal-fractional orders, and the numerical trajectories show that a slight change in the fractal-fractional orders produce slight changes in the asymptotic behavior of the HIV-1 virus on T-cells.
In Figure 5, based on the Adams-Bashforth method, we see the numerical trajectories of three state functions by varying the average number of infected particles N for the values under the fractal-fractional order . Thus, in Figure 5a, it shows that the susceptible T-cells increase as the average number of infected particles by an existing infected cell reduces by , and that of the peak of the amount of infectious T-cells and the free particles of the infection of the HIV-1 virus in the blood decrease, respectively in Figure 5b,c.
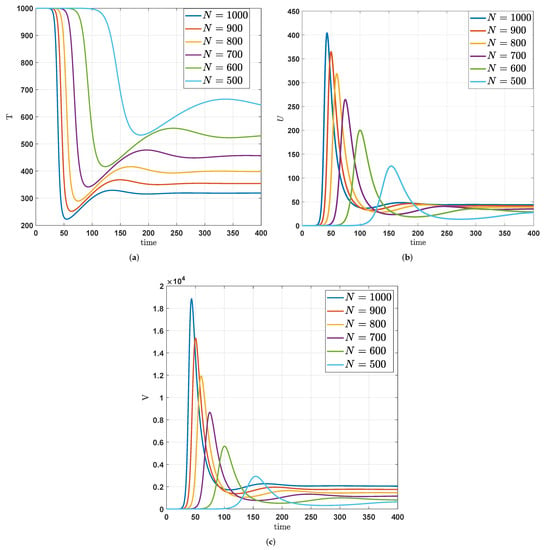
Figure 5.
Numerical trajectories by varying the average number of infected particles N under the fractal order and fractional order via the Adams-Bashforth method. (a) The effects of N on . (b) The effects of N on . (c) The effects of N on .
In Figure 6, based on the Adams-Bashforth method, we see the numerical trajectories by varying the supply rate for new T-cells for under the fractal order and fractional order . Thus, in Figure 6a, it shows that the susceptible T-cells increase for a period of time and gradually decrease as the number of the supply rate increases before converging at the 150th day.
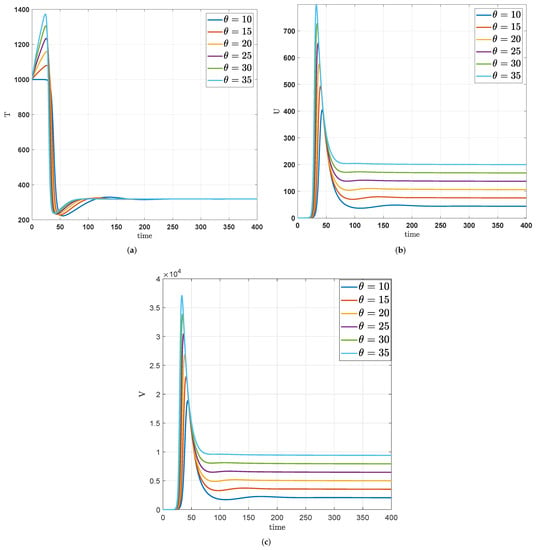
Figure 6.
Numerical trajectories by varying the supply rate for new T-cells under the fractal order and fractional order via the Adams-Bashforth method. (a) The effects of on . (b) The effects of on . (c) The effects of on .
In Figure 6b,c, we noticed that the amount of infectious T-cells and the free particles of the infection of the HIV-1 virus in the blood increase, respectively. Figure 7a–c display the numerical trajectories when we compare the numerical solutions of the Adams-Bashforth method with the Newton polynomial method under the fractal dimension and fractional order .
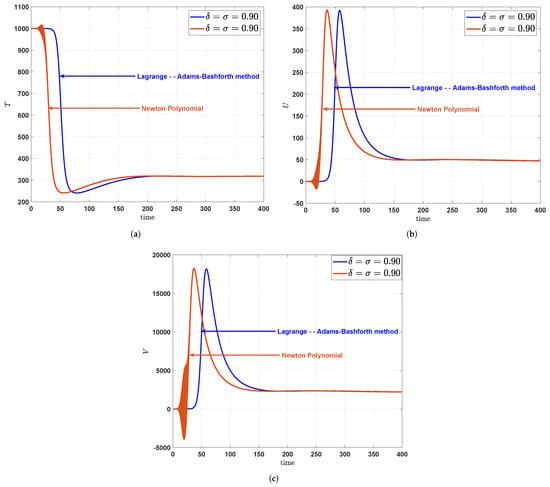
Figure 7.
Numerical trajectories in the Comparison of the numerical solutions of the Adams-Bashforth method with Newton polynomials method under the fractal dimension and fractional order . (a) Comparison of the graphs w.r.t. two different numerical algorithms on . (b) Comparison of the graphs w.r.t. two different numerical algorithms on . (c) Comparison of the graphs w.r.t. two different numerical algorithms on .
9. Conclusions
In this paper, we designed a fractal-fractional -HIV-1-model and analyzed the dynamics of T-cells under the infection of HIV-1 virus. We considered three compartments for this model by defining three state functions , , and for the amount of susceptible T-cells, amount of infectious T-cells, and the free particles of the infection of the HIV virus in the blood. We derived three fractal-fractional integral equations and proved that their kernels are Lipschitz. In this direction, we could prove the existence and uniqueness criteria for solutions of the fractal-fractional -HIV-1-model. In the sequel, we investigated four stability results with the help of two auxiliary inequality. We extracted two algorithms via the Adams-Bashforth method and also via the Newton polynomials and simulated our real data in relation to the given fractal-fractional -HIV-1-model. The numerical and graphical results showed that these two numerical algorithms give the same outcomes and differences are small. Also, we investigated the effect of frcatal dimensions and fractional orders on these simulations. Also, the effect of different values for the average number of infected particles and the supply rate of new T-cells were simulated in some graphs under the Adams-Bashforth method. This stude showed that we can predict the next behavior of the fractal-fractional -HIV-1-model via the two mentioned numerical methods and their results are more accurate and identical. This shows the power of simulation of the frcatal-fractional models in comparison to the fractional models. In the next researches, we can develope our numerical methods on different fractal-fractional models of diseases.
Author Contributions
Conceptualization, H.N. and S.E.; Formal analysis, H.N., S.E., N.P., J.K.K.A., S.R. and T.S.; Funding acquisition, N.P. and T.S.; Methodology, H.N., S.E., N.P., J.K.K.A., S.R. and T.S.; Software, S.E. and J.K.K.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by King Mongkut’s University of Technology North Bangkok. Contract no. KMUTNB-62-KNOW-27.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
Acknowledgments
The first author would like to thank Shiraz University. Also, the second and fifth authors would like to thank Azarbaijan Shahid Madani University. Also, we would like to thank dear reviewers for their constructive and helpful comments and remarks to improve the quality of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, L.; Li, M.Y. Mathematical analysis of the global dynamics of a model for HIV infection of CD4+ T cells. Math. Biosci. 2006, 200, 44–57. [Google Scholar] [CrossRef] [PubMed]
- UNAIDS. Report on the Global AIDS Epidemic. 2016. Available online: http://www.unaids.org (accessed on 18 February 2022).
- Kumar, P.; Erturk, V.S. The analysis of a time delay fractional COVID-19 model via Caputo type fractional derivative. Math. Methods Appl. Sci. 2022. [Google Scholar] [CrossRef] [PubMed]
- Rezapour, S.; Etemad, S.; Mohammadi, H. A mathematical analysis of a system of Caputo-Fabrizio fractional differential equationsfor the anthrax disease model in animals. Adv. Differ. Equ. 2020, 2020, 481. [Google Scholar] [CrossRef]
- Alshehri, H.M.; Khan, A. A fractional order Hepatitis C mathematical model with Mittag-Leffler kernel. J. Funct. Spaces 2021, 2021, 2524027. [Google Scholar] [CrossRef]
- Deressa, C.T.; Etemad, S.; Rezapour, S. On a new four-dimensional model of memristor-based chaotic circuit in the context of nonsingular Atangana-Baleanu-Caputo operators. Adv. Differ. Equ. 2021, 2021, 444. [Google Scholar] [CrossRef]
- Deressa, C.T.; Etemad, S.; Kaabar, M.K.A.; Rezapour, S. Qualitative analysis of a hyperchaotic Lorenz-Stenflo mathematical model via the Caputo fractional operator. J. Funct. Spaces 2022, 2022, 4975104. [Google Scholar] [CrossRef]
- Kumar, P.; Erturk, V.S. Environmental persistence influences infection dynamics for a butterfly pathogen via new generalised Caputo type fractional derivative. Chaos Solitons Fractals 2021, 144, 110672. [Google Scholar] [CrossRef]
- Devi, A.; Kumar, A.; Abdeljawad, T.; Khan, A. Stability analysis of solutions and existence theory of fractional Lagevin equation. Alex. Eng. J. 2021, 60, 3641–3647. [Google Scholar] [CrossRef]
- Mohammadi, H.; Kumar, S.; Rezapour, S.; Etemad, S. A theoretical study of the Caputo-Fabrizio fractional modeling for hearing loss due to Mumps virus with optimal control. Chaos Solitons Fractals 2021, 144, 110668. [Google Scholar] [CrossRef]
- Begum, R.; Tunc, O.; Khan, H.; Gulzar, H.; Khan, A. A fractional order Zika virus model with Mittag-Leffler kernel. Chaos Solitons Fractals 2021, 146, 110898. [Google Scholar] [CrossRef]
- Kumar, P.; Erturk, V.S.; Almusawa, H. Mathematical structure of mosaic disease using microbial biostimulants via Caputo and Atangana-Baleanu derivatives. Results Phys. 2021, 24, 104186. [Google Scholar] [CrossRef]
- Zarin, R.; Khaliq, H.; Khan, A.; Khan, D.; Akgul, A.; Humphries, U.W. Deterministic and fractional modeling of a computer virus propagation. Results Phys. 2022, 33, 105130. [Google Scholar] [CrossRef]
- Baleanu, D.; Etemad, S.; Rezapour, S. A hybrid Caputo fractional modeling for thermostat with hybrid boundary value conditions. Bound. Value Probl. 2020, 2020, 64. [Google Scholar] [CrossRef] [Green Version]
- Thaiprayoon, C.; Sudsutad, W.; Alzabut, J.; Etemad, S.; Rezapour, S. On the qualitative analysis of the fractional boundary valueproblem describing thermostat control model via ψ-Hilfer fractional operator. Adv. Differ. Equ. 2021, 2021, 201. [Google Scholar] [CrossRef]
- Alzabut, J.; Selvam, G.M.; El-Nabulsi, R.A.; Vignesh, D.; Samei, M.E. Asymptotic stability of nonlinear discrete fractional pantograph equations with non-local initial conditions. Symmetry 2021, 13, 473. [Google Scholar] [CrossRef]
- Wongcharoen, A.; Ntouyas, S.K.; Tariboon, J. Nonlocal boundary value problems for Hilfer type pantograph fractional differentialequations and inclusions. Adv. Differ. Equ. 2020, 2020, 279. [Google Scholar] [CrossRef]
- Kumar, P.; Erturk, V.S.; Yusuf, A.; Nisar, K.S.; Abdelwahab, S.F. A study on canine distemper virus (CDV) and rabies epidemics in the red fox population via fractional derivatives. Results Phys. 2021, 25, 104281. [Google Scholar] [CrossRef]
- Asamoah, J.K.K.; Okyere, E.; Yankson, E.; Opoku, A.A.; Adom-Konadu, A.; Acheampong, E.; Arthur, Y.D. Non-fractional and fractional mathematical analysis and simulations for Q fever. Chaos Solitons Fractals 2022, 156, 111821. [Google Scholar] [CrossRef]
- Khan, H.; Tunc, C.; Chen, W.; Khan, A. Existence theorems and Hyers-Ulam stability for a class of hybrid fractional differentialequations with p-Laplacial operator. J. Appl. Anal. Comput. 2018, 8, 1211–1226. [Google Scholar]
- Omame, A.; Nwajeri, U.K.; Abbas, M.; Onyenegecha, C.P. A fractional order control model for Diabetes and COVID-19 co-dynamics with Mittag-Leffler function. Alex. Eng. J. 2022, 61, 7619–7635. [Google Scholar] [CrossRef]
- Ali, W.; Turab, A.; Nieto, J.J. On the novel existence results of solutions for a class of fractional boundary value problems on the cyclohexane graph. J. Inequalities Appl. 2022, 2022, 5. [Google Scholar] [CrossRef]
- Baleanu, D.; Etemad, S.; Mohammadi, H.; Rezapour, S. A novel modeling of boundary value problems on the glucose graph. Commun. Nonlinear Sci. Numer. Simul. 2021, 100, 105844. [Google Scholar] [CrossRef]
- Rezapour, S.; Tellab, B.; Deressa, C.T.; Etemad, S.; Nonlaopon, K. H-U-type stability and numerical solutions for a nonlinear model of the coupled systems of Navier BVPs via the generalized differential transform method. Fractal Fract. 2021, 5, 166. [Google Scholar] [CrossRef]
- Culshaw, R.V.; Ruan, S. A delay-differential equation model of HIV infection of CD4+ T-cells. Math. Biosci. 2000, 165, 27–39. [Google Scholar] [CrossRef]
- Cai, L.; Li, X.; Ghosh, M.; Guo, B. Stability analysis of an HIV/AIDS epidemic model with treatment. J. Comput. Appl. Math. 2009, 229, 313–323. [Google Scholar] [CrossRef] [Green Version]
- Mohyud-Din, S.T.; Nazir, A.; Almohsin, B.; Ahmed, N.; Khan, U.; Waheed, A.; Hussain, T. On mathematical model of HIV CD4+ T-cells. Alex. Eng. J. 2021, 60, 995–1000. [Google Scholar] [CrossRef]
- Perlson, A.S. Modeling the interaction of the immune system with HIV. Lec. Notes Biomath. 1989, 83, 350–370. [Google Scholar]
- Perlson, A.S.; Kirschner, D.E.; Boer, R.D. Dynamics of HIV infection of CD4+ T cells. Math. Biosci. 1993, 114, 81–125. [Google Scholar] [CrossRef] [Green Version]
- Ding, Y.; Ye, H. A fractional-order differential equation model of HIV infection of CD4+ T-cells. Math. Comput. Model. 2009, 50, 386–392. [Google Scholar] [CrossRef]
- Arafa, A.A.M.; Rida, S.Z.; Khalil, M. Fractional modeling dynamics of HIV and CD4+ T-cells during primary infection. Nonlinear Biomed. Phys. 2012, 6, 1. [Google Scholar] [CrossRef] [Green Version]
- Bulut, H.; Kumar, D.; Singh, J.; Swroop, R.; Baskonus, H.M. Analytic study for a fractional model of HIV infection of CD4+T lymphocyte cells. Math. Nat. Sci. 2018, 2, 33–43. [Google Scholar] [CrossRef]
- Lichae, B.H.; Biazar, J.; Ayati, Z. The fractional differential model of HIV-1 infection of CD4+ T-cells with description of the effect of antiviral drug treatment. Comput. Math. Methods Med. 2019, 2019, 4059549. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nazir, G.; Shah, K.; Debbouche, A.; Khan, R.A. Study of HIV mathematical model under nonsingular kernel type derivative of fractional order. Chaos Solitons Fractals 2020, 139, 110095. [Google Scholar] [CrossRef]
- Wang, W.; Wang, X.; Feng, Z. Time periodic reaction-diffusion equations for modeling 2-LTR dynamics in HIV-infected patients. Nonlin. Anal. Real World Appl. 2021, 57, 103184. [Google Scholar] [CrossRef]
- Atangana, A. Fractal-fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fractals 2017, 102, 396–406. [Google Scholar] [CrossRef]
- Shah, K.; Arfan, M.; Mahariq, I.; Ahmadian, A.; Salahshour, S.; Ferrara, M. Fractal-fractional mathematical model addressing the situation of Corona virus in Pakistan. Results Phys. 2020, 19, 103560. [Google Scholar] [CrossRef] [PubMed]
- Gomez-Aguilar, J.F.; Cordova-Fraga, T.; Abdeljawad, T.; Khan, A.; Khan, H. Analysis of fractal-fractional Malaria transmission model. Fractals 2020, 28, 2040041. [Google Scholar] [CrossRef]
- Ali, Z.; Rabiei, F.; Shah, K.; Khodadadi, T. Qualitative analysis of fractal-fractional order COVID-19 mathematical model with case study of Wuhan. Alex. Eng. J. 2021, 60, 477–489. [Google Scholar] [CrossRef]
- Asamoah, J.K.K. Fractal-fractional model and numerical scheme based on Newton polynomial for Q fever disease under Atangana-Baleanu derivative. Res. Phys. 2022, 34, 105189. [Google Scholar] [CrossRef]
- Khan, H.; Alam, K.; Gulzar, H.; Etemad, S.; Rezapour, S. A case study of fractal-fractional tuberculosis model in China: Existence and stability theories along with numerical simulations. Math. Comput. Simul. 2022, 198, 455–473. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, A.; Akgul, A.; De la Sen, M. Study of HIV disease and its association with immune cells under nonsingular and nonlocal fractal-fractional operator. Complexity 2021, 2021, 1904067. [Google Scholar] [CrossRef]
- Granas, A.; Dugundji, J. Fixed Point Theory; Springer: New York, NY, USA, 2003. [Google Scholar]
- Atangana, A.; Araz, S.I. New Numerical Scheme with Newton Polynomial: Theory, Methods, and Applications; Academic Press: Cambridge, MA, USA, 2021. [Google Scholar]
- Baleanu, D.; Mohammadi, H.; Rezapour, S. Analysis of the model of HIV-1 infection of CD4+ T-cell with a new approach of fractional derivative. Adv. Differ. Equ. 2020, 2020, 71. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).