Abstract
Predicates and rules are usually enclosed as built-in functions in automated geometry reasoning systems, meaning users cannot add any predicate or rule, thus resulting in a limited reasoning capability of the systems. A method for expanding predicates and rules in automated geometry reasoning systems is, thus, proposed. Specifically, predicate and rule descriptions are transformed to knowledge trees and forests based on formal representations of geometric knowledge, and executable codes are dynamically and automatically generated by using “code templates”. Thus, a transformation from controlled natural language descriptions to mechanization algorithms is completed, and finally, the dynamic expansion of predicates and rules in the reasoning system is achieved. Moreover, the method has been implemented in an automated geometry reasoning system for Chinese college entrance examination questions, and the practicality and effectiveness of the method were tested. In conclusion, the enclosed setting, which is a shortcoming of traditional reasoning systems, is avoided, the user-defined dynamic expansion of predicates and rules is realized, the application scope of the reasoning system is extended, and the reasoning capability is improved.
Keywords:
mechanical geometry theorem proof; mathematics mechanization; forward chaining; knowledge representation MSC:
68V20; 68V30; 97U70
1. Introduction
Since 1950, when Alfred Tarski published an article on algorithms that could be used to prove elementary algebra and geometry theorems, mathematics mechanization has become a hot topic. Computational geometry is a branch of computer science [1]. In the late 1970s, Wen-tsun Wu established Wu’s method [2,3,4], which has greatly promoted the development of mathematics mechanization. Over the past few decades, experts and scholars have made significant progress in this field [5].
Geometrical problem solving has recently attracted much attention [6]. Methods for proving mechanical geometry theorems mainly fall into two categories: the algebraic method [7] and the synthetic method. The algebraic method is important in advancing the development of mechanical geometry theorem proofs, and typical representatives include Wu’s method, Gröbner bases [8,9], and the sub-resultant method [10]. However, proofs given by actual implementations of the algebraic method often involve complex calculations of large-scale polynomial equations, and it is difficult to understand the geometrical meaning of the proofs, or to verify the correctness of the proofs. The synthetic method mainly comprises the pure synthetic method, invariant methods [11], and rule-based methods. The Tarski axiom system is an excellent example of a pure synthetic method. Classic representatives of the invariant method include the area method [12,13] and the full-angle method [14]. The geometric invariant method has proven more than 500 nontrivial geometric problems, and derives readable proofs from mechanical geometry theorems [15]. Nonetheless, this method has a significant drawback, that is, the given proofs differ greatly from conventional descriptions of pedagogical content. There are many representatives of rule-based methods, and the deductive databases method is an outstanding one. According to the deductive database method, new information is generated by constantly searching, matching, and reasoning, based on the known conditions of the geometric proposition and corresponding lemmas and axioms [16,17]. The database method uses forward chaining and backward chaining reasoning [18,19]. The advantages of deductive database methods include their ability to obtain more information about geometric figures during the reasoning process, and to generate readable proofs that match the conventional descriptions of pedagogical content [20]. The disadvantage of the method is the combinatorial explosion of the search space; however, this problem has been solved effectively.
Given its instruction-friendly characteristics, the deductive database method is widely used in mathematics education systems, such as the Geometry Information Search System (GISS) [21], Java Geometry Expert (JGEX) [22], Super Sketchpad (SSP) [23], NetPad [24,25,26], and iGeoTutor [27]. These reasoning systems can quickly solve problems and generate readable proofs, but the expected reasoning results may not be generated due to the lack of proposition-related predicates and rules. Since predicates and rules are usually enclosed as built-in functions within existing automated geometry reasoning systems, users can neither add to nor modify them. It is important and necessary to expand the predicates and rules, in order to improve the system’s reasoning capability.
Regarding the expansion of the predicates and rules within a reasoning system, Guo and Zheng [28,29,30] have offered a useful algorithm by which users can add rules by themselves. However, there are still three issues: new predicates cannot be added, and a rule containing a new predicate cannot be added either; only limited rules such as constraint rules can be added, and metric rules cannot be added—for example, the rule “if the included angle is ninety degree, then the two segments are perpendicular”, which contains a numeric value, cannot be added; stringent input is required, that is, the user is asked to input six pieces of information to describe one rule, and they have to know the semantics and usage of the system’s predicates in advance.
To address the above problems, a method for expanding predicates and rules in automated geometry reasoning systems is proposed here, and preliminarily realized. Specifically, representations of the predicates and rules in a reasoning system are expanded based on geometry knowledge ontology [31,32]. First, predicates and rules derived from controlled natural language descriptions are transformed into formal representations; then, the formal representations are dynamically converted into executable code; finally, the expansion of the predicates and rules is achieved. The controlled natural language refers to a language that complies with specific requirements, that is, the language that users input to describe the predicates and rules must conform to the requirements of the system.
The expansion work of this paper is divided into the following sections: Section 2 provides an overview of knowledge representation; Section 3 details the predicate expansion method and provides a predicate example; Section 4 details the rule expansion method and provides a rule example; Section 5 introduces the system implementation; Section 6 shows the effects of predicate and rule expansion by means of a comprehensive case; the last section summarizes and discusses the limitations of this paper, and offers an outlook for future work.
2. Knowledge Representation
The knowledge base is an important component of an automated geometry reasoning system [33]. Geometric knowledge can be represented in various ways, and it is important to effectively incorporate geometric knowledge representation and deductive methods and techniques into computational applications [34]. Zhong [35] proposed geometric knowledge representation via ontology, and a relatively complete knowledge representation system was, thus, formed. With the adoption of the knowledge representation system, the knowledge searching and reasoning efficiency is improved greatly. The system defines geometric knowledge as consisting of the following categories of basic objects: geometric symbols (such as and ), concept definitions (such as point, plane, and perpendicular), assertions (such as axioms, theorem, lemmas, and conjectures), and geometric propositions. The concept definitions are the main objects described by geometric knowledge, and they include names, parameters, parameter types, definition methods, relationships between various concepts, and so on. The assertions refer to descriptions of the properties of the geometric concepts and representations between geometric concepts and geometric relationships. In our research, we expand these two categories of knowledge, i.e., concept definitions are represented with predicates, and assertions are represented with rules. Furthermore, both the predicates and rules are described via a formal representation [36]. Thus, this knowledge becomes more suitable for reasoning, and the expansion of predicates and rules is promoted.
Definition 1.
Geometry Unit (GU):A geometric object consisting of one or more points is called a geometry unit, denoted as g.
A geometry unit consists of one or several points, and is represented formally as:
A geometry unit is formed of two parts. The first part is the name of the geometry unit, denoted as GN. GN indicates the basic category to which the geometry unit belongs, such as angle, triangle, or quadrilateral. The second part is a point set (x1, x2, …, xi), which consists of one or multiple points named with letters. Moreover, one point set may be configured to present several geometry units; for example, a set of three points can be used to represent either a triangle or an angle.
There may be various equivalent versions of a formal representation for one geometry unit, and all these equivalents represent the same geometry unit. For example, triangle ABC can be written as Triangle (A,B,C) or Triangle (C,A,B). In order to identify these equivalents, normalization processing is required, which is mainly performed by sorting the letters representing points of the geometry unit into alphabetical order, so that there is only one writing form for each geometry unit in the system. Taking Triangle (A,B,C) and Triangle (C,A,B) as an example, the processing comprises the following: representing Triangle (A,B,C) with Triangle (1,2,3), and representing Triangle (C,A,B) with Triangle (3,2,1), according to the alphabetical orders of the corresponding letters; respectively sorting Triangle (1,2,3) and Triangle (3,2,1) to Triangle (1,2,3) and Triangle (1,2,3); then comparing the sorted forms. Thus, the system can recognize that Triangle (A,B,C) and Triangle (C,A,B) are equivalents. Usually, different geometrical units correspond to different normalization processing methods. For example, within the 180° angle, in the case of Angle (E,F,G) and Angle (G,F,E), the midpoint is designated as the vertex of the angle, so only the first and third points need to be sorted for comparison.
A set consists of all the geometry units of the system; it is represented as G, and is denoted in the following form:
where is a geometry unit. Common geometry units are shown in Table 1.

Table 1.
Examples of common geometry units.
Definition 2.
Predicates:A predicate describes a relationship between geometry units, or a relationship between a geometry unit and a numerical value. They are denoted as p.
Predicates are divided into two categories, i.e., Constraint Predicates (CP), describing the relationship between geometry units, and Metric Predicates (MP), describing the relationship between a geometry unit and a numerical value.
A constraint predicate is formally represented as:
where is a geometry unit.
Each constraint predicate is composed of two parts: the first part is the name of a predicate (which is donated as PN), configured to describe a relation, and the second part is the geometry unit set of the predicate. For example, a case with two equal angles is expressed as follows: Equal (Angle (A,B,C), Angle (E,F,G)), where “Equal” is the name of the predicate and indicates the equal relationship, while “Angle (A,B,C)” and “Angle (E,F,G)” are geometry units.
However, a user may input different forms of the same predicate, and in order to ensure the uniqueness of each predicate in the system, the predicates need to be normalized. The processing method here is similar to that for the normalization of geometry units, that is, the system assigns a code to each geometry unit and considers whether the codes of the predicates are the same. For example, the codes for Equal (Angle (A,B,C), Angle (E,F,G)) are Equal (1,2), and the codes for Equal (Angle (E,F,G), Angle (A,B,C)) are Equal (2,1); then, Equal (2,1) is sorted as Equal (1,2) for comparison. Finally, it is concluded that the two predicates are same.
The metric predicate is formally represented as:
PN indicates a metric property of a geometry unit, and parameters of a metric predicate usually consist of one or more geometry units () and expressions (). For example, a predicate describing the length of a segment is formally expressed as Length (Segment (A,B), 2), where “Length” is the name of the metric predicate, “Segment (A,B)” is a geometry unit (which is one parameter of the predicate), and “2” expresses another parameter of the predicate.
A set consists of all the predicates in the system; it is represented as P and denoted in the following form:
where represents a predicate (a general term for CP and MP) and a may be either CP or MP. Common predicates are shown in Table 2.

Table 2.
Examples of predicates.
Definition 3.
Rules:Descriptions of the properties of predicates or expressions about the relationships between predicates are called rules, such as geometric theorems, axioms, definitions, lemmas, formulas, laws, and corollaries. Each rule is denoted as r, and formally expressed as:
A complete rule is composed of two parts: an assumption (known conditions) and a conclusion. Usually, the rule is described as: if ..., then ...; “if ...” is the condition part, and “then ...” is the conclusion part. The conclusion is determined according to the condition.
For example, two base angles of an isosceles triangle being equal—which is a property of an isosceles triangle—can be expressed as a rule: .
A Rule Set (denoted as R) is configured to store diverse rules, and each rule in the system is realized by means of a function. The rule set is formally expressed as:
where represents a rule. Common rules are shown in Table 3.

Table 3.
Examples of rules.
3. Predicate Expansion
Predicate expansion means allowing a user to create a new predicate in predicate set P by inputting a Predicate Example (PE) in a controlled natural language. It is very important to provide an efficient input mechanism for users [37]. When users use a controlled natural language to input a predicate example, the predicate name input by the user should be a geometric relation, such as perpendicular, parallel, etc. The predicate description input by the user should be a statement representing the relationship between geometry units, or between a geometry unit and an expression; the statement should include “geometry unit and relationship” or “geometry unit, expression and relationship”, and the expression must be composed of numbers, letters, and calculation symbols only—other symbol systems are temporarily not allowed. For example, if the user is intending to add the predicate “segment X is parallel to plane Y”, they should input “parallel” as the predicate name, and input “segment CD is parallel to the plane EFG” as the predicate description, where “parallel” is a geometric relationship, and the predicate description contains geometry units “segment CD and plane EFG” and a relationship “parallel”. The predicate expansion method mainly comprises two steps: (1) obtaining the name and the geometry units or expressions of a new predicate to form a knowledge tree; (2) traversing the knowledge tree and generating executable code using a code template.
3.1. Algorithm for Generating Knowledge Tree
Usually, a predicate example input by a user consists of two parts, i.e., a name and a description, and the description comprises parameters of the predicate. By building a tree, the information required for predicate expansion can be quickly and accurately obtained by the system.
The tree can be formed based on the formal representation of a predicate, and is formally called a knowledge tree (KT). The knowledge tree is constructed with the name of a predicate as a root node and geometry units or expressions of the predicate as child nodes. For example, the constraint predicate “segment AB is equal to segment DE” can be transformed into a knowledge tree as shown in Figure 1a. Similarly, the metric predicate “the area of triangle ABC is a − b” can be expressed as the knowledge tree shown in Figure 1b.
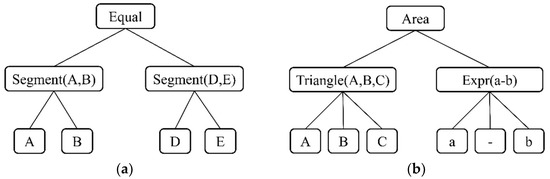
Figure 1.
Knowledge tree. (a) KT of a constraint predicate. (b) KT of a metric predicate.
Algorithm 1 provides the process of generating a predicate knowledge tree from a PE input by the user.
Algorithm 1 involves the following: (1) obtaining the example PE input by the user, and configuring the name of the example, PE.na, as a root node; (2) identifying and matching each geometry unit, gu, or expression, expr, contained in the example description, PE.ds; adopting the regular expression matching method to acquire the expression in the predicate description, PE.ds, since the expression is composed of numbers, letters, and calculation symbols—for example, “[A-Za-z] |\*|/|[0-9]|\( |\) |\+|\^|-)+” is a regular expression statement that matches an expression in a predicate description; (3) adding corresponding geometry units, gu, or expressions, expr, as child nodes of the root node via the addChild () method; (4) for a constrained predicate, obtaining the points in each geometry unit, gu, and respectively configuring the points as leaf nodes; for a metric predicate, further identifying basic compositions of the expression, and configuring the basic compositions as leaf nodes.
| Algorithm 1 generateKT (G, PE) |
| Input: geometry unit set G; predicate example PE Output: predicate tree KT 1: KT. root = PE.na 2: for do 3: guList = Regex. Matches (PE.ds, g) 4: for do 5: node = KT. root. addChild (gu) 6: for . points do 7: node. addChild (p) 8: end for 9: end for 10: end for 11: expr = Regex. Matches (PE.ds, [A-Za-z] |\*|/| [0-9] |\ (| 12: node = KT. root. addChild (expr) 13: for me expr do 14: node. addChild ((me. ToString ()) 15: end for 16: return KT |
3.2. Algorithm for Generating Predicate Code
In the automated geometry reasoning system, each predicate is defined by a class. The code texts of the predicates are identical in structure, but different in content, and the differences are mainly reflected in the name, constructor, and predicate normalization of the class. The class name and the constructor name correspond to the predicate name, and parameters of the constructor correspond to the geometry units or expressions of the predicate.
Hence, executable code can be generated based on a “predicate code template (Ptemplate)”. The predicate code template is a standard code text of a predicate in the system. The name and geometry units or expressions of the predicate can be obtained by traversing the knowledge tree, KT. The process of generating executable code from the KT and the code template is described in Algorithm 2.
| Algorithm 2 generatePredicateCode (KT, Ptemplate) |
| Input: predicate Tree KT; predicate template Ptemplate Output: PCode 1: Ptemplate. className = KT.root 2: Ptemplate. funcName = KT. root 3: nodeList = KT. root. children 4: for do 5: Ptemplate. funcParams. addParams (node) 6: end for 7: Ptemplate. NormalizeFunc = Normalize (nodeList) 8: PCode = Ptemplate. generateCode () 9: return PCode |
Algorithm 2 is summarized as follows: obtaining the root node by traversing the knowledge tree KT, and filling in the class name (className) and constructor name (funcName) in the predicate code template, Ptemplate, with the root node; accessing child nodes of the root node, and filling the constructor parameter funcParams with the child nodes by means of method addParam(); during the predicate code generation process, invoking the Normalize() method to return normalized codes, and filling in NormalizeFunc in the template with the normalized codes. Finally, a new predicate code text is generated.
3.3. Predicate Expansion Example
Here, an example is provided to show how the predicate expansion method described previously is implemented in the automated geometry reasoning system; specifically, adding a predicate of “a segment is perpendicular to a plane” works as detailed below.
Step 1—predicate example (PE) input:
- Inputting the name (PE.na): Perpendicular;
- Inputting the description (PE.ds): segment AB is perpendicular to plane DEF.
Step 2—knowledge tree generation:
- Obtaining “Perpendicular” and configuring it as root node;
- Finding formal representations of geometry units “segment AB” and “plane DEF” contained in PE.ds by traversing the geometry unit set of the system based on the formal representation; configuring formal representations of “segment AB” and “plane DEF”, i.e., “Segment (A,B)” and “Plane (D,E,F)”, as child nodes of the root node;
- Respectively obtaining point sets of geometry units “Segment (A,B)” and “Plane (D,E,F)”, and sequentially configuring points in the point set as leaf nodes;
- Generating a predicate knowledge tree, as shown in Figure 2.
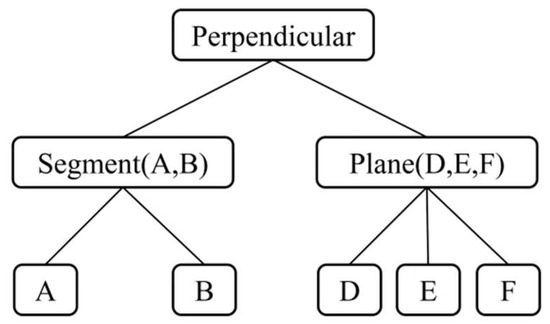 Figure 2. Predicate knowledge tree.
Figure 2. Predicate knowledge tree.
Step 3—executable predicate code generation:
- Obtaining the root node “Perpendicular” and configuring it as the name of a class and the name of a constructor;
- Obtaining child nodes “Segment (A,B)” and “Plane (D,E,F)” and configuring them as parameters;
- Performing normalization—since child nodes “Segment (A,B)” and “Plane (D,E,F)” are different types, there is no need for normalization;
- Generating executable predicate code as shown in Figure 3.
 Figure 3. Predicate knowledge tree.
Figure 3. Predicate knowledge tree.
4. Rule Expansion
Based on the rules introduced in Definition 3, a rule is composed of conditions and conclusions, which are represented with predicates. To achieve rule expansion, the system needs to obtain the predicates of the rule. Since a predicate can be represented by a knowledge tree, a rule can be represented by a knowledge forest (KF). Correspondingly, a knowledge forest includes a condition forest and a conclusion forest.
Hence, the method for rule expansion comprises the following: analyzing the rule example, constructing a rule knowledge forest, coding the condition forest, and generating executable rule codes according to the rule knowledge forest.
4.1. Algorithm for Generating a Knowledge Forest
The conclusion of a rule is determined by the corresponding condition, so geometry units or expressions of the predicate in the conclusion need to be obtained from the condition. In order to facilitate the generation of the executable conclusion code, trees, and nodes in the condition forest need to be systematically coded. Specifically, a condition forest is coded as follows: root nodes are coded with i (i = 0, 1, 2, …, n), where equals the number of trees; child nodes of each root node are coded with ij (,), where equals the number of geometry units and expressions; leaf nodes of each child node are coded with ijk (,, ), where equals the number of compositions of each geometry unit or expression. Thus, a specific node in the condition forest used as the node in the conclusion forest can be easily obtained according to the code.
For example, as shown in Figure 4, if segment AB equals segment CD, segment CD equals segment EF, and the length of segment AB is x, then segment AB equals segment EF, and the length of segment EF is x.
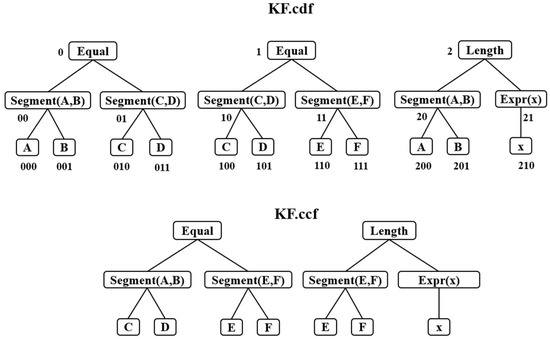
Figure 4.
Example of a knowledge forest.
Similarly to predicate expansion, the system allows a user to input a rule example in a controlled natural language. The rule example comprises a name and a description, and should be in the form of a hypothetical proposition, i.e., “if…, then…” and the input needs to be made up of predicates.
The method for generating a knowledge forest (KF) is shown in Algorithm 3.
| Algorithm 3 generateKF (RE) |
| Input: rule example RE Output: KF 1: match=Regex.Match(RE.rd, “if ([\s\S]+) then ([\s\S]+)”) 2: if match.Success == true 3: cons = separateCondition (RE.rd) 4: clus = separateConclusion (RE.rd) 5: end if 6: cdp = extractPredicate (cons) 7: ccp = extractPredicate (clus) 8: cdf = {} 9: for do 10: contionalTree=generateKT (G, con) 11: cdf. Add (conditionalTree) 12: end for 13: cdf = enCoding(cdf) 14: ccf = {} 15: for clu ccp do 16: conclusiveTree= generateKT (G, clu) 17: ccf. Add (conclusiveTree) 18: end for 19: KF. add (cdf, ccf) 20: return KF |
Algorithm 3 comprises the following: obtaining the description of a rule example RE.rd, and using the regular expression statement “if ([\s\ s]+) then ([\s\ s]+)” to check whether the rule description input by the user conforms to the specified form; if yes, separating the description into a condition statement, cons, and a conclusion statement, clus, by Separate(); identifying and obtaining predicates by extractPredicate(), wherein condition predicates cdp are extracted from the condition statement, cons, and conclusion predicates are extracted from the conclusion statement, clus; generating a condition forest, cdf, and a conclusion forest, ccp, by iterating the predicate example according to Algorithm 1, and combining the two forests to generate the rule knowledge forest; coding the condition forest by the enCoding() method, which is described in Algorithm 4.
4.2. Algorithm for Generating Executable Rule Code
The generation of an executable rule code is similar to predicate code generation. Executable code can be generated based on a “rule code template (Ruletemplate)”. In the automated geometry reasoning system, rules are realized by functions, and the functions have the same structure but different contents. The differences are mainly in the name, the parameters, the precondition of a valid rule, and the output predicates. By analyzing these four aspects, it can be found that the function name corresponds to the name of the rule example input by the user, the function parameter corresponds to the root node of the condition forest, and the precondition of a valid rule and the output predicates can be obtained from the condition and conclusion forests. The process of generating executable rule code is described in Algorithm 5.
| Algorithm 4 enCoding(cdf) |
| Input: conditionForest cdf Output: conditioncodeForest 1: i = 0 2: for do 3: conditionTree. root. code = i 4: nodeList = conditionTree. root. children 5: j = 0 6: for do 7: node. Code = ij 8: k = 0 9: for do 10: nodeleaf. Code = ijk 11: k = k + 1 12: end for 13: j = j + 1 14: end for 15: i = i + 1 16: end for 17: conditioncodeForest = cdf 18: return conditioncodeForest |
| Algorithm 5 generateruleCode(KF, Ruletemplate,RE) |
| Input: rule forest KF; rule template Ruletemplate Output: RuleCode 1: Ruletemplate. RuleName = RE. rn 2: for do 3: Ruletemplate. RuleParams. addParams (kt. root) 4: end for 5: Ruletemplate. Judgementcondition = Judgement (KF. cdf) 6: Ruletemplate. GenerateNewKnowledge = generateConclusion (KF) 7: RuleCode = Ruletemplate 8: return RuleCode |
In Algorithm 5, the root node of each tree in KF.cdf is set as a parameter of a rule function by means of the addParams () method; a piece of code for determining whether the rule is valid is designed by means of the Judgement () method, and executable codes of output predicates are generated by the generateConclusion() method.
Specifically, the Judgement () method comprises the following: for trees in the condition forest, KF.cdf, determining whether there are the same nodes among the child nodes of each root node; if the same node is present, then recording the codes to generate executable codes that can be used to check the precondition of a valid rule.
The generateConclusion () method comprises the following: traversing trees in KF.ccf; configuring the root node of a tree as the name of the conclusion predicate; configuring the child nodes of the root node of the conclusion tree as predicate parameters.
4.3. Rule Expansion Example
Here, an example is provided to show how the rule expansion method is implemented on the automated geometry reasoning system; specifically, adding a rule of “PyramidVolume” works as follows:
Step 1—rule example (RE) input:
- Inputting the name (RE.na)—PyramidVolume;
- Inputting the description (RE.ds)—for a pyramid O, if the bottom area is S and the height is h, then the volume is 1/3∗S∗h.
Step 2—knowledge forest generation:
- By invoking the Separate () method, separating “for a pyramid O, if the bottom area is S and the height is h, then the volume is 1/3∗S∗h” into a condition statement “for a pyramid O, if the bottom area is S and the height is h” and a conclusion statement “then the volume is 1/3∗S∗h”;
- By invoking the extractPredicate() method, extracting predicate examples, cdp, “bottom area is S”, and “height is h” from the condition statement, and the predicate example ccp “volume is 1/3∗S∗h” from the conclusion statement;
- Creating a condition forest, cdf, by generating knowledge trees with condition predicates in item ii, and creating a conclusion forest, ccf, by generating a conclusion tree with the conclusion predicate;
- Coding cdf, and integrating the two forests to form a rule knowledge forest, KF, as shown in Figure 5.
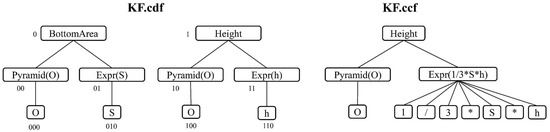 Figure 5. Rule knowledge forest.
Figure 5. Rule knowledge forest.
Step 3—rule codes generation:
- Obtaining the “PyramidVolume” from RE.na and configuring it as the function name;
- Obtaining the root node of each knowledge tree from KF.cdf: “BottomArea” and “Height”, and configuring them as parameters;
- Generating executable code to confirm whether the pyramids are the same instance;
- Generating executable code for constructing the conclusion “new Volume (...)” by means of the coding number;
- Returning the whole executable rule code, as shown in Figure 6.
 Figure 6. Executable rule code.
Figure 6. Executable rule code.
5. Implementation
The expansion of predicates and rules is achieved with an automated geometry reasoning system. The system, developed with C# and combining the Deductive Database Method and symbol calculation, is dedicated to solving three-dimensional geometry propositions of mathematical subjects in Chinese college entrance examinations. Moreover, the system can automatically reason and generate readable proofs. At present, the system has a total of 108 predicates, and approximately 300 rules. The predicates are classified and stored in eight categories according to the geometric relationships, such as segment-and-plane relations, plane-and-plane relations, point-based relations, and polyhedron-based relations. The polyhedron-based relations specifically comprise cone-based relations, prism-based relations, pyramid-based relations, and so on. The cone-based relation category includes predicates such as cone bottom area and cone height, and the pyramid relation category includes pyramid bottom area, pyramid height, pyramid volume, and so on. Similarly, rules are classified and stored in the system as traditional class rules, vector rules, and special rules. Besides this, the system contains about 200 three-dimensional geometry propositions from college entrance examinations over the last 5 years, and the solution rate has reached 75%. The operation interface of the automated geometry reasoning system is shown in Figure 7.
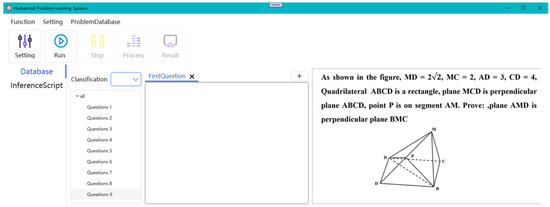
Figure 7.
The operation interface of the automated geometry reasoning system.
6. Applications
A complete example is provided to illustrate the effectiveness and practicability of the rule expansion method executed in the automated geometry reasoning system.
A Chinese college entrance examination question is shown on the right part of Figure 8. It reads: For pyramid P-ABCD, quadrilateral ABCD is a right-angled trapezoid, segment AB is perpendicular to segment AD, segment AB is parallel to segment CD, and segment PC is perpendicular to bottom face ABCD, AB = 2AD = 2CD = 4, point E is the middle point of segment PB. Prove: plane EAC is perpendicular to plane PBC.
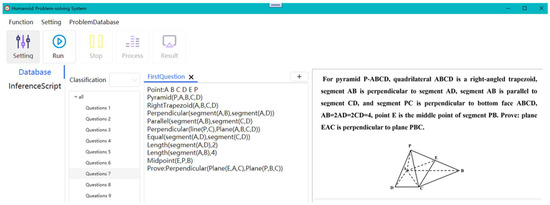
Figure 8.
Interface of the automated geometry reasoning system.
The formal representations of the known conditions in the question are as follows:
- Point—A B C D E P;
- Pyramid (P,A,B,C,D);
- Right trapezoid (A,B,C,D);
- Perpendicular (Segment (A,B), Segment (A,D));
- Parallel (Segment (A,B), Segment (C,D);
- Perpendicular (Segment (P,C), Plane (A,B,C,D));
- Equal (Segment (A,D), Segment (C,D));
- Length (Segment (A,D),2);
- Length (Segment (A,B),4);
- Midpoint (E,P,B);
- Prove: Perpendicular (Plane (E,A,C), Plane (P,B,C)).
The automated geometry reasoning system begins reasoning for the first time after clicking on the start bottom, and 1109 pieces of geometric knowledge are obtained in 4 s, as shown in Figure 9.

Figure 9.
Results of first reasoning.
However, the correct answer “plane EAC is perpendicular to plane PBC” does not appear in the reasoning results. Since the length of segment AC in the right-angled trapezoid cannot be obtained based on conditions “right-angled trapezoid ABCD, AB = 4, AD = 2, CD = 2”, “segment AC is perpendicular to segment BC” cannot be obtained, nor can “plane EAC is perpendicular to plane PBC”. Hence, we need to add part of the rule “if right trapezoid ABCD, length of segment AD is x1, and length of segment CD is x2, then length of segment AC is (x1 ∗ x1 + x2 ∗ x2) ^ (1/2)”, as shown in Figure 10.
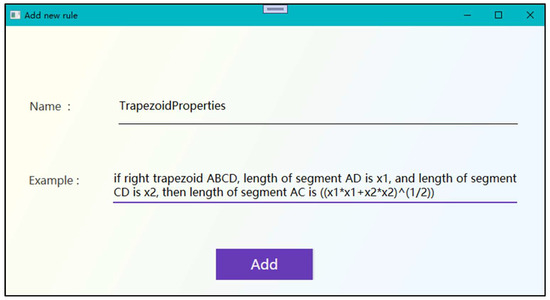
Figure 10.
Rule addition.
A second reasoning step is performed after the rule is added, the correct answer is obtained as shown in Figure 11.
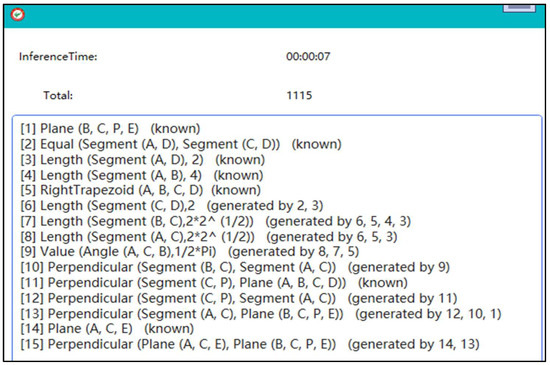
Figure 11.
Results of second reasoning.
The eighth result in Figure 11 is obtained by reasoning from the new rule.
7. Conclusions
In this paper, concept definitions and assertions are significantly expanded based on the geometry knowledge representation ontology, that is, both concept definitions and assertions are summarized as predicates and rules. Moreover, representations of predicates and rules are further expanded. Meanwhile, given that predicates and rules are usually enclosed as built-in functions within automated geometry reasoning systems, a method for expanding the predicates and rules in these systems is proposed. Our method improves the user friendliness by allowing users to input a predicate or rule in a controlled natural language. In addition, with regard to the existing algorithm of rule addition, the method proposed in this paper allows the user to add a rule with expressions, resulting in an expansion of the scope of rules that can be added. However, there are still important issues to be addressed in future research; for example, the rule consistency verification function has not been implemented yet. The rule consistency verification functionality will involve the verification of the consistency of the system, whenever a user adds a new rule, i.e., in a rule-based inference system, the addition of a new inference rule could lead to an inconsistency issue, so a consistency check must be for all the additions made by the users. Therefore, the problem with the consistency of system interaction can be addressed in the future, and we suggest referencing a service for verifying system interactions in TPTP (Thousands of Problems for Theorem Provers) [38] Web. In addition, according to our method, users can input predicates and rules in a controlled natural language, and future studies could focus on expanding this ability.
Author Contributions
Methodology, Y.R.; project administration, Y.R.; software, L.X. and Q.Z.; supervision, H.G.; validation, J.L.; writing—original draft, L.X.; writing—review and editing, H.G. and J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China (No. 2018YFB1005100), the Innovation Projects of Universities in Guangdong Province (No. 2020KTSCX215), the China Postdoctoral Science Foundation (No. 2021M700920), and the Innovation Research for the Postgraduates of Guangzhou University (No. 2020GDJCM21).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Saracevic, M.; Selimi, A. Convex Polygon Triangulation based on Ballot problem and Planted Trivalent Binary Tree. Turk. J. Electr. Eng. Comput. 2019, 27, 346–361. [Google Scholar] [CrossRef]
- Temuer, C.L.; Pang, J. An algorithm for the complete symmetry classification of differential equations based on Wu’s method. J. Eng. Math. 2010, 66, 181–199. [Google Scholar]
- Wu, W.J. On the decision problem and the mechanization of theorem-proving in elementary geometry. Sci. China Ser. A 1978, 29, 117–138. [Google Scholar]
- Zhang, J.Z.; Chen, X.C.; Chen, M. Self-evident automated proving based on point geometry from the perspective of Wu’s method identity. J. Syst. Sci. Complex 2019, 32, 78–94. [Google Scholar] [CrossRef]
- Wu, W.J. Mathematics mechanization: Its origin, status, and prospect. J. Syst. Sci. Math. Sci. 2008, 28, 898–904. [Google Scholar]
- Lu, P.; Gong, R.; Jiang, S.B.; Qiu, L.; Liang, X.D.; Zhu, S.C. Inter-GPS: Interpretable geometry problem solving with formal language and symbolic reasoning. In Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics (ACL), Bangkok, Thailand, 1–6 August 2021. [Google Scholar]
- Sergiu, R. Algebraic methods versus map methods of solving Boolean equations. Int. J. Comput. Math. 2003, 80, 815–817. [Google Scholar]
- Deepak, K.; Sun, Y.; Wang, D.K. An efficient method for computing comprehensive Grobner base. J. Symb. Comput. 2013, 52, 124–142. [Google Scholar]
- Yengui, I. Dynamical Gröbner bases. J. Algebra 2006, 301, 447–458. [Google Scholar] [CrossRef][Green Version]
- Lu, Y.; Hou, X.R. The sub-resultant method for automated theorem proving. J. Syst. Math. 1995, 15, 10–15. [Google Scholar]
- Zhang, J.Z.; Li, Y.B. Automatic theorem proving for three decades. J. Syst. Sci. Math. Sci. 2009, 29, 1155–1168. [Google Scholar]
- Chou, S.C.; Gao, X.S.; Zhang, J.Z. Automated Generation of Readable Proofs with Geometric Invariants I. Multiple and Shortest Proof Generation. J. Autom. Reason. 1996, 17, 325–347. [Google Scholar] [CrossRef]
- Janivci, P.; Narboux, J.; Quaresma, P. The Area Method: A Recapitulation. J. Autom. Reason. 2012, 48, 489–532. [Google Scholar]
- Chou, S.C.; Gao, X.S.; Zhang, J.Z. A Deductive Database Approach to Automated Geometry Theorem Proving and Discovering. J. Autom. Reason. 2000, 25, 219–246. [Google Scholar] [CrossRef]
- Zhang, J.Z.; Jiang, J.G. The automated geometry reasoning system based on Rete algorithm. Adv. Eng. Sci. 2006, 38, 135–139. [Google Scholar]
- Shi, S.M.; Wang, Y.H.; Lin, C.Y.; Liu, J.X.; Yong, R. Automatically solving number word problems by semantic parsing and reasoning. In Proceedings of the Conference on Empirical Methods for Natural Language Processing, Lisbon, Portugal, 17–21 September 2015; pp. 1132–1142. [Google Scholar]
- Wen, W.B.; Yu, X.G.; Zhang, T.; Wang, M.S. Automatically proving plane geometry theorems stated by text and diagram. Int. J. Pattern Recognit. Artif. Intell. 2019, 33, 1940003.1–1940003.26. [Google Scholar]
- Najib, S. Application of backward chaining method to computer forensic. In Proceedings of the 10th International-Business-Information-Management-Association Conference, Kuala Lumpur, Malaysia, 30 June–2 July 2008; pp. 303–307. [Google Scholar]
- Nevins, A.J. Plane geometry theorem proving using forward chaining. Artif. Intell. 1975, 6, 1–23. [Google Scholar] [CrossRef]
- Botana, F.; Hohenwarter, M.; Janičić, P.; Kovács, Z. Automated theorem proving in GeoGebra: Current achievements. J. Autom. Reason. 2015, 55, 39–59. [Google Scholar] [CrossRef]
- Zhang, J.Z.; Gao, X.S.; Zhou, X.Q. The geometry information search system by forward reasoning. Chin. J. Comput. 1996, 10, 721–727. [Google Scholar]
- Ye, Z.; Chou, S.C.; Gao, X.S. An Introduction to Java Geometry Expert. Automated Deduction in Geometry; Lecture Notes in Computer, Science; Sturm, T., Zengler, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6301, pp. 189–195. [Google Scholar]
- Xu, Z.T. Super Sketchpad: An Excellent Cognitive Platform for gaining experience in basic mathematics activities. J. Math. Educ. 2011, 3, 97–99. [Google Scholar]
- Wang, Y.; Rao, J.S.; Guan, H.; Zou, Y. NetPad: An online DGS for mathematics education. In Proceedings of the 2017 12th International Conference on Computer Science and Education (ICCSE), Houston, TX, USA, 22–25 August 2017. [Google Scholar]
- Guan, H.; Qin, X.L.; Rao, Y.S. Research and design of dynamic mathematical digital resources open platform. J. Harbin Inst. Technol. 2019, 51, 14–22. [Google Scholar]
- Guan, H.; Rao, Y.S.; Zhang, J.Z.; Cao, S.; Qin, X.L. Method for processing graph degeneracy in dynamic geometry based on domain design. J. Comput. Sci. Technol. 2021, 36, 910–921. [Google Scholar] [CrossRef]
- Wang, K.; Su, Z.D. Automated geometry theorem proving for human-readable proofs. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, Buenos Aires, Argentina, 20–31 July 2015. [Google Scholar]
- Zheng, H.; Zhang, J.Z. Geometry automatic reasoning platform with sustainable development by user. J. Comput. Appl. 2011, 31, 2101–2107. [Google Scholar]
- Guo, S.W. The software of automated reasoning based on user adding rules. Comput. Appl. Softw. 2007, 24, 48–50. [Google Scholar]
- Guo, S.W. The software of automated reasoning based on user adding rules II. Comput. Inf. Technol. 2006, 8, 67–68. [Google Scholar]
- Fu, H.G.; Yu, L.; Zhong, X.Q. Semi-automatic construction of plane geometry ontology based-on WordNet and Wikipedia. J. Univ. Electron. Sci. Technol. China 2014, 43, 575–580. [Google Scholar]
- Wang, H. Research on the model of knowledge representation ontology based on framework in intelligent learning system. In Proceedings of the 2011 International Conference on Electrical and Control Engineering, Yichang, China, 16–18 September 2011; pp. 6757–6760. [Google Scholar]
- Nguyen, H.D.; Do, N.V.; Pham, V.T. A method for knowledge representation to design intelligent problems solver in mathematics based on Rela-Ops model. IEEE Access 2020, 8, 76991–77012. [Google Scholar] [CrossRef]
- Quaresma, P. Automated deduction and knowledge management in geometry. In Proceedings of the AISC 2018: Artificial Intelligence and Symbolic Computation, Suzhou, China, 16–19 September 2018; pp. 221–226. [Google Scholar]
- Zhong, X.Q.; Fu, H.G.; Yu, L.; Huang, B. Geometric knowledge acquisition and knowledge representation based on ontology. Chin. J. Comput. 2010, 33, 167–174. [Google Scholar] [CrossRef]
- Gan, W.B.; Yu, X.G.; Wang, M.S. Automatic understanding and formalization of plane geometry proving problems in natural language: A supervised approach. Int. J. Artif. Intell. Tools 2019, 28, 1940003. [Google Scholar] [CrossRef]
- Saracevic, M.; Stanimirovic, P.; Krtolica, P.; Masovic, S. Construction and Notation of Convex Polygon Triangulation based on ballot problem. Rom. J. Inf. Sci. Technol. 2014, 17, 237–251. [Google Scholar]
- Sutcliffe, G. The TPTP Problem Library and Associated Infrastructure. J. Autom. Reason. 2009, 43, 339–362. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).