Modular Representation of Physiologically Based Pharmacokinetic Models: Nanoparticle Delivery to Solid Tumors in Mice as an Example
Abstract
1. Introduction
- noncompartmental analysis estimates the exposure to a drug (such parameters as the area under the plasma drug concentration-time curve, maximum drug concentration, and time at maximum concentration) directly from observed individual profiles.
- model-based compartmental analysis predicts the concentration-time curve using kinetic models.
- a combination of 2D and 3D optical tomography for in vivo imaging.
- methods of fluorescent and traditional histology, spectroscopy, flow cytometry, and electron microscopy.
- methods for obtaining transcriptomic and proteomic data to assess the expression of receptors for various compounds (sugars, lipids, albumin, etc.).
- they allow studying the distribution of nanoformulations at the site of their action in the body.
- they provide tools to better understand the microenvironment complexity, phenotypic diversity, and genetic heterogeneity of tumors.
- they may prove useful in nanomedicine development to achieve optimum nanoformulation concentration profiles needed in tumor-targeted cells.
- they could directly be exploited for specific cancer patient groups (e.g., pediatric population) to help solve issues of specific drug development and administration dosage scheme protocols.
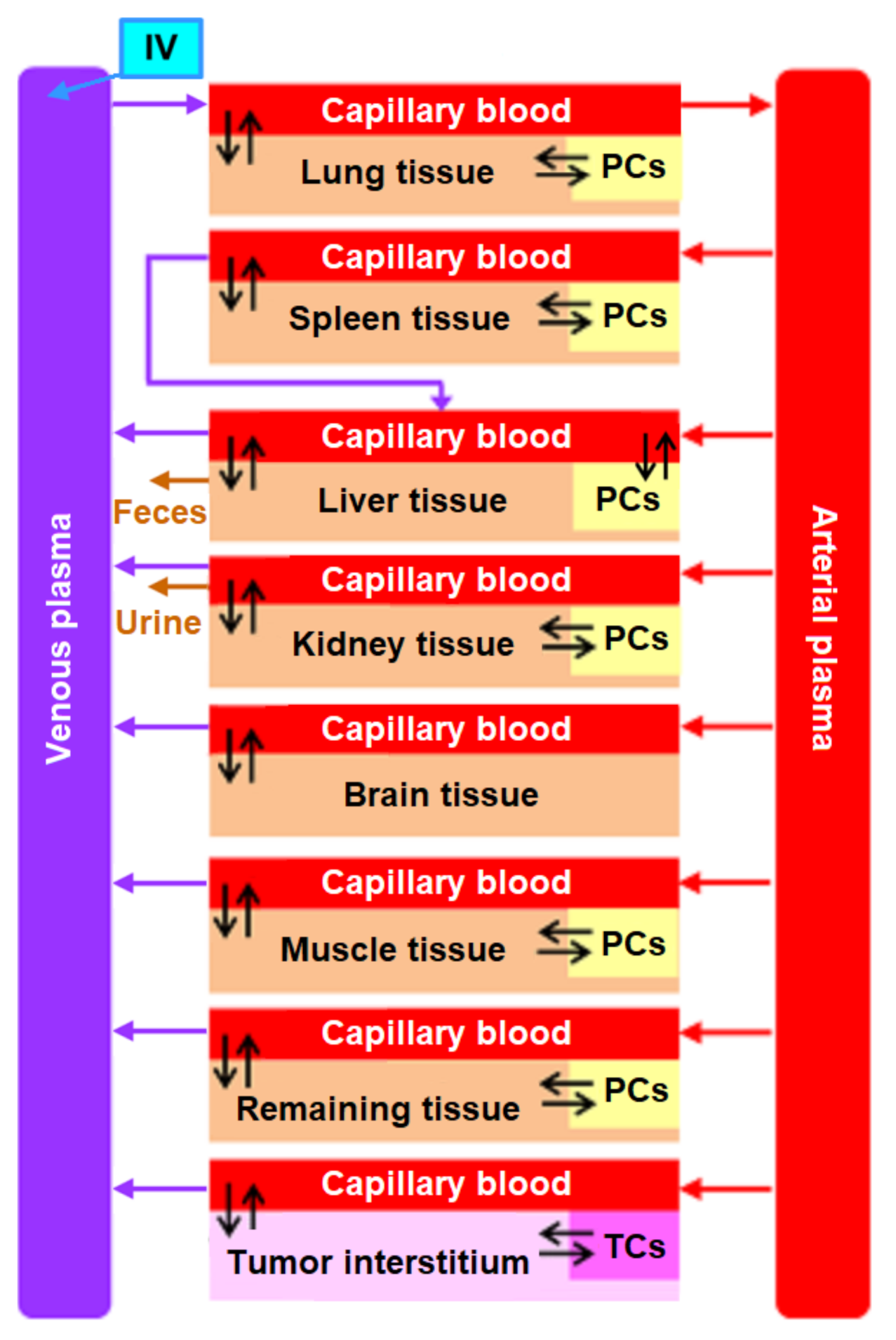
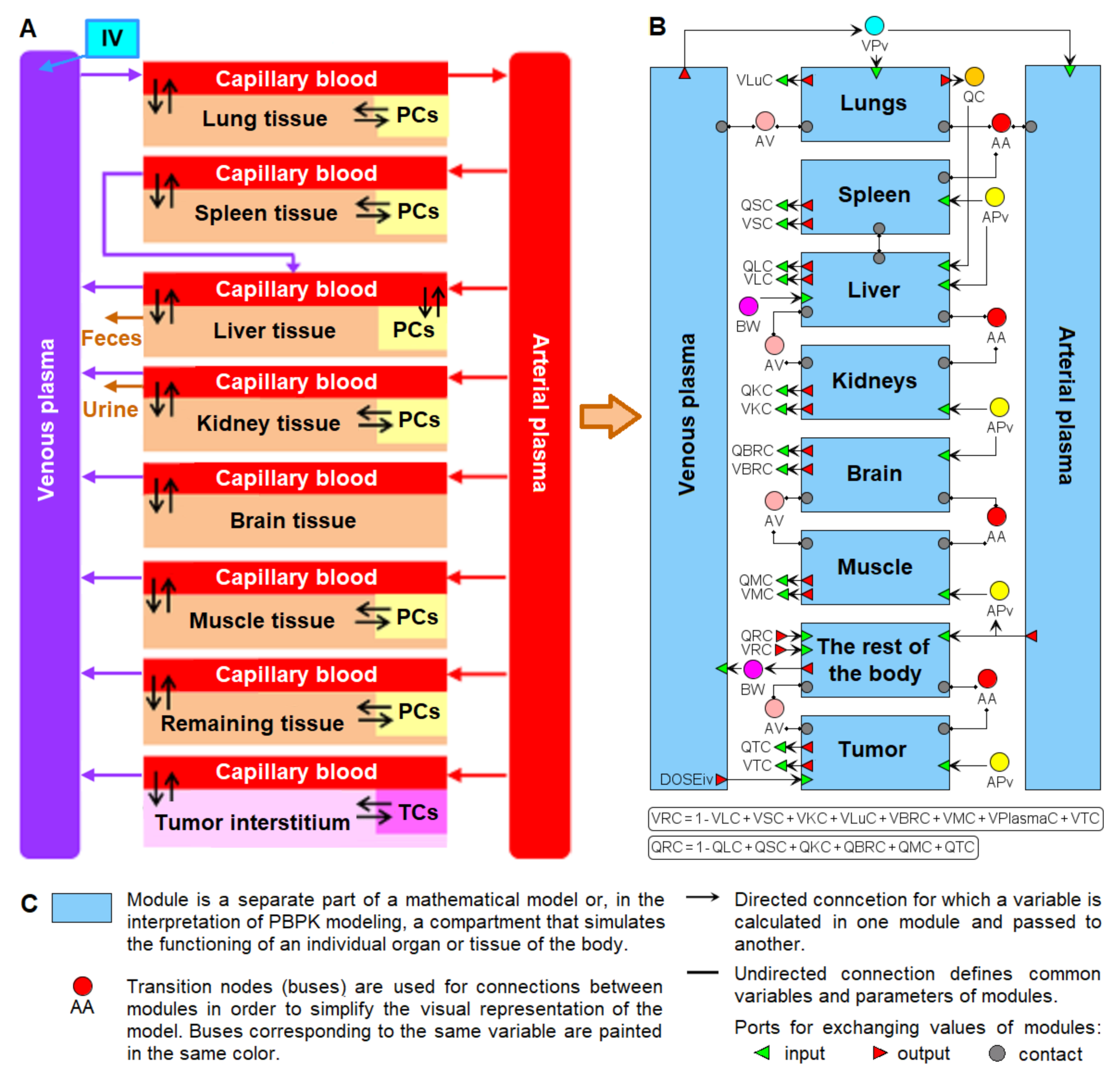
2. Structure of the Nanoparticle Delivery Model
3. Methods of the Model Conversion
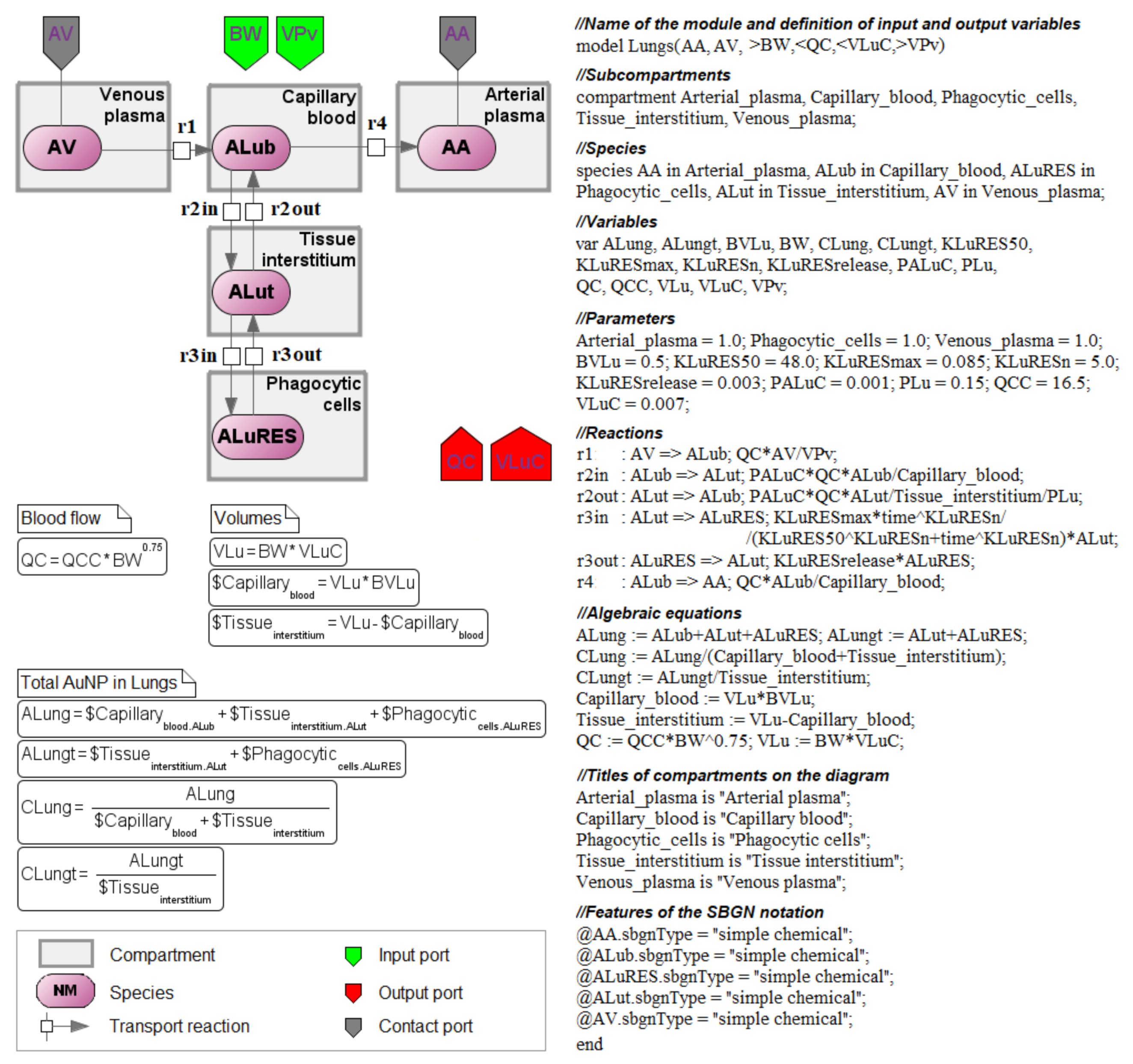
3.1. Visual Modeling
3.2. Modular Modeling
- input port–mathematical variable used in the module, but calculated outside;
- output port–mathematical variable calculated in the module and may be used outside;
- contact port–mathematical variable that can be modified both inside and outside the module.
| Element Name | Glyph | Description |
|---|---|---|
| Module |  | Module encapsulates the mathematical model (submodel) of a particular subsystem as an element of the hierarchical structure of the more complex model of the whole system. |
| Interface ports |  | Ports represent the interface of the module through which it can be connected with other modules or with the hierarchical model itself. The color of the port defines its type (the same as in Table 2). |
| Connection |  | Connections can be established between ports to aggregate modules with each other. Directed connections are established between output and input ports, while undirected connections are between contact ports. |
| Bus |  | Buses are auxiliary elements of the modular diagram that can be used as intermediate points in connections. They allow decreasing the number of intersections between connections and make the structure of the model clearer. |
3.3. Antimony–Textual Representation of the Model
- sbgnType–defines the SBGN entity type (macromolecule, nucleic acid, simplex chemical or complex, unspecified);
- sbgnViewTitle–defines additional properties of an SBGN entity (e.g., multimer). If an entity is complex, it also defines the inner elements. The Transpath database specification is used to denote entities and complexes in the BioUML (https://genexplain.com/wp-content/uploads/2017/04/TRANSPATH-Documentation_2012.2.pdf accessed on 1 April 2022). For instance:
- ○
- A:B–complex comprising two entities, A and B;
- ○
- A{p}–entity A in the phosphorylated state;
- ○
- (A)3–multimer A consisting of three subunits.
4. Reconstruction of the Computational Modular Model
- transition to a modular structure.
- transition from a system of differential-algebraic equations to a chain of biochemical reactions.
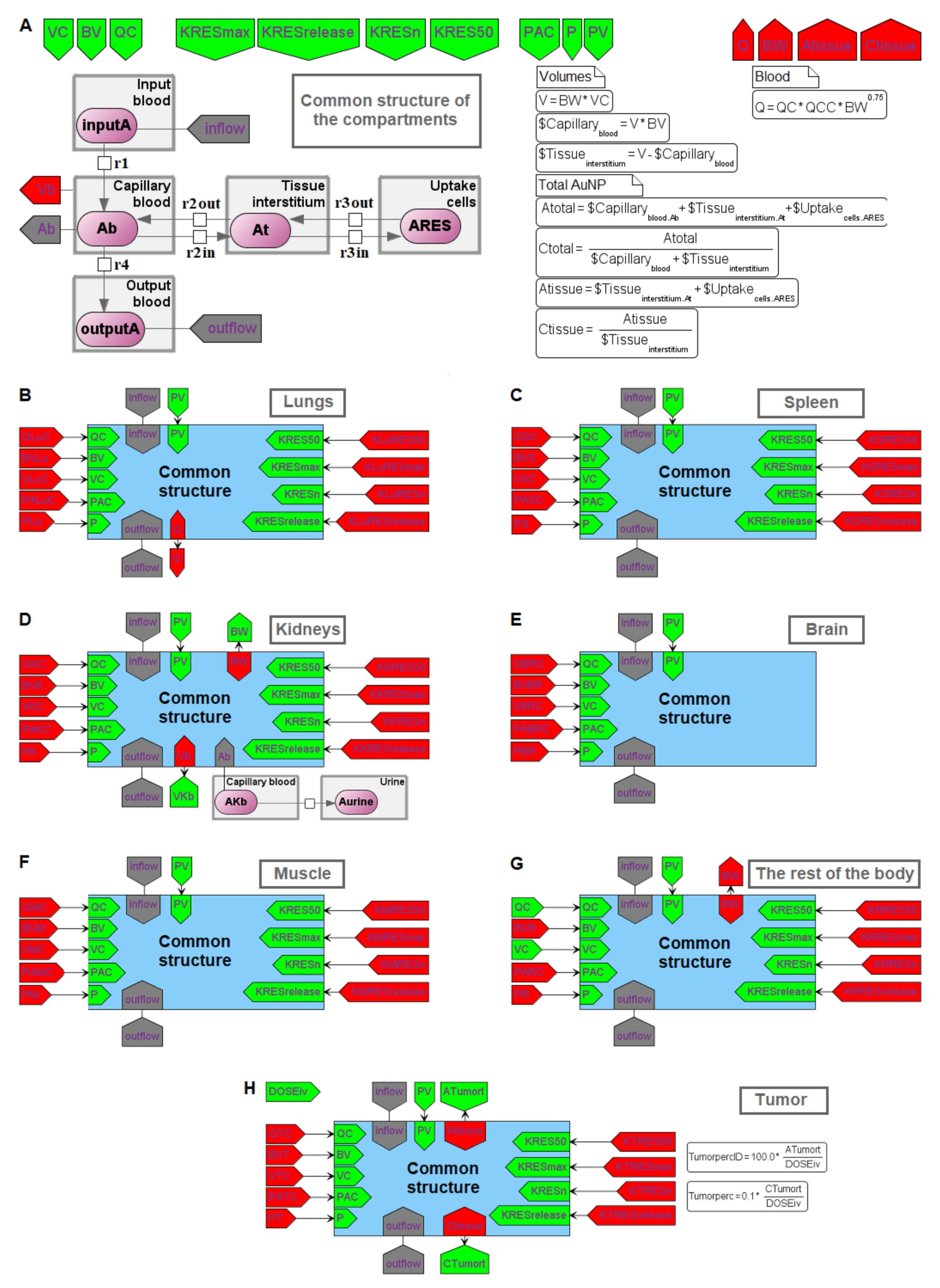
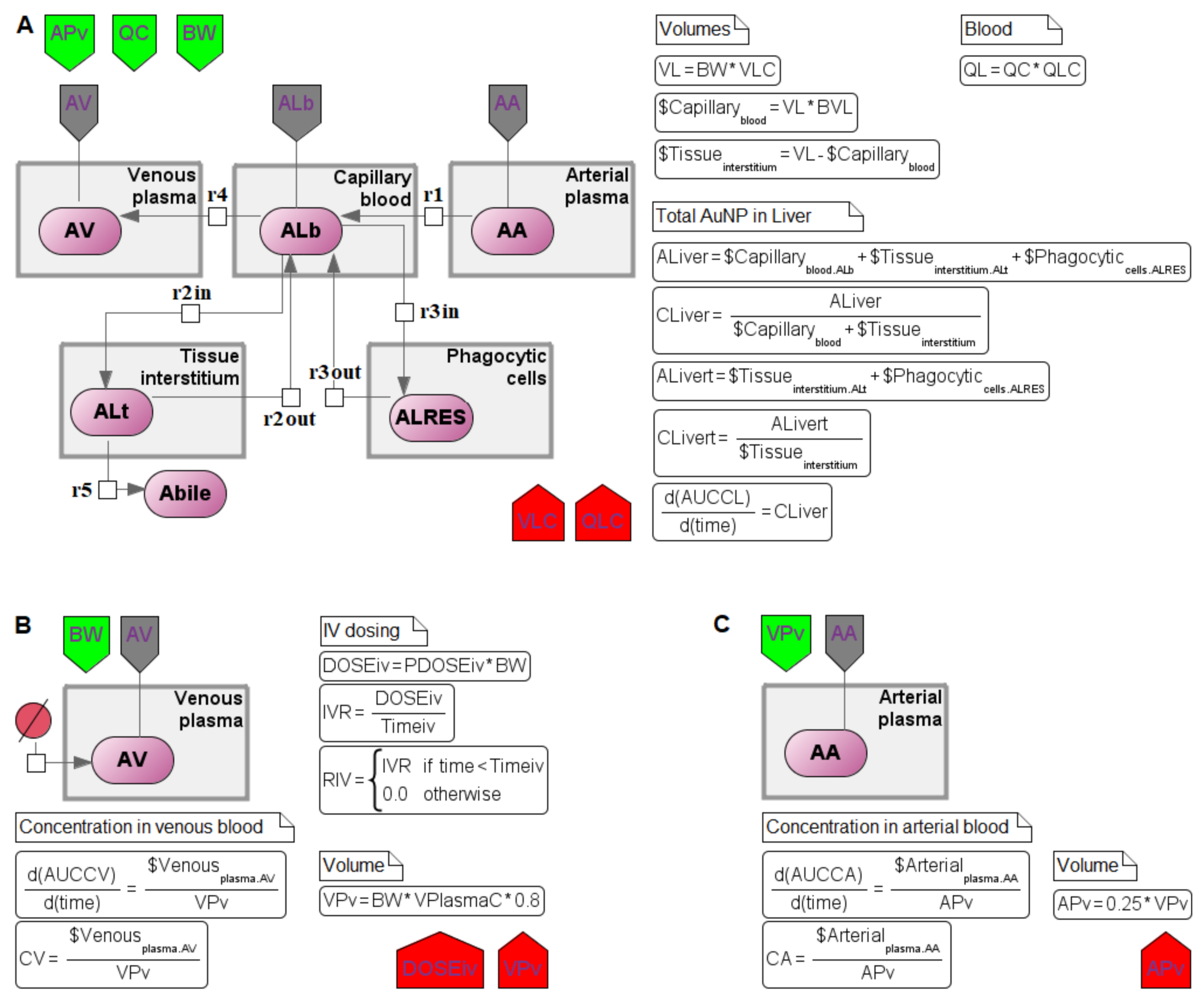
- finding the common structure of compartments as a separate module
4.1. Transition to a Modular Structure
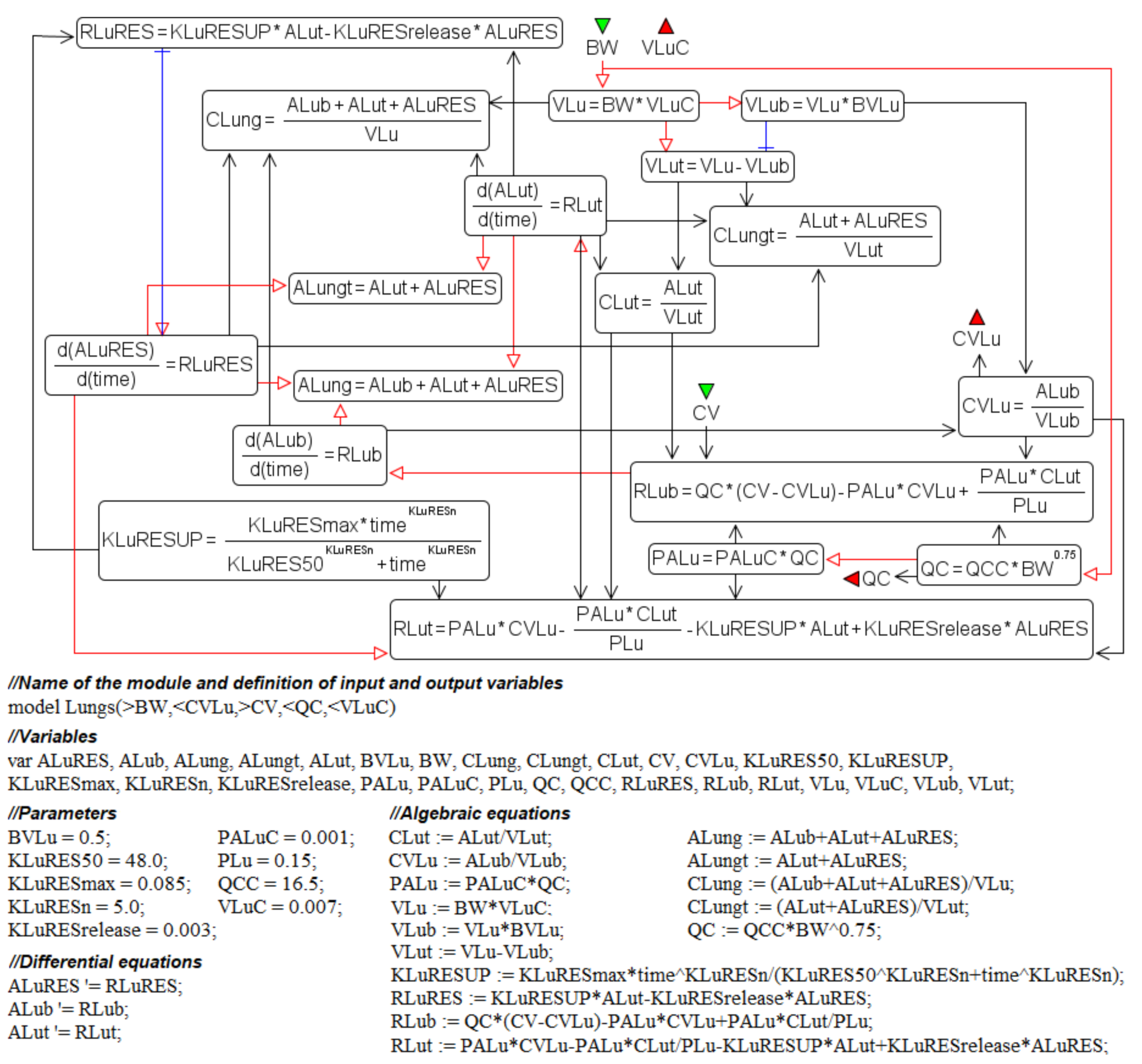
4.2. Transition from a System of Differential-Algebraic Equations to a Chain of Biochemical Reactions
4.3. Finding the Common Structure of Compartments as a Separate Module
- inflow and outflow for the lungs are determined by the amount of nanoparticles in the venous and arterial plasma, respectively, while for the remaining compartments, these flows are determined vice versa;
- to convert the amount of nanoparticles in plasma into their concentration and calculate rates of the form (1), we pass the value of plasma volume PV to the compartments of the model: we consider venous plasma volume VPv (Figure 7B) for the lungs and arterial plasma volume APv for other compartments;
- input ports on the left and right side of the common structure module shown in Figure 9B–H correspond to the individual compartment constants (with the same notations as in Table 1 for the lungs); since in the model [11] the brain compartment does not contain the subcompartment of endocytic/phagocytic cells, the parameters associated with it are not transferred and their default values remain zero
- in addition to the common equations, the kidney compartment includes the reaction of nanoparticles excretion through the urinary tract (Figure 9D), proceeding at a rate:
- the tumor compartment contains formulas for calculating the amount (ATumort) and concentration (CTumort) of nanoparticles in the tissue as a percentage of the administered dose (DOSEiv):
- to use the cardiac output (equal to the blood flow in the lungs) and bodyweight outside the compartments shown in Figure 9, we provided for the transfer of these values from the common structure module, where they are determined, to the top level of the model (see modular representation in Figure 7B) via the lung compartment (Figure 9B, port Q at the bottom of the compartment) and the rest of the body compartment (Figure 9G, port BW at the top of the compartment), respectively.
5. Testing the Model after the Modification
6. Conclusions
- To share biological models (in particular, PBPK), it is important to make them available. The use of well-known biological standards is essential in this context. A translation of PBPK models from text-based formats (like acslX, Berkeley Madonna, MATLAB, and R language) to SBML and SBGN standards, which BioUML allows, makes these models accessible to a wide range of scientists and provides a quick start to work with them. Therefore, the presented description can be used as a guideline for the procedure.
- Visual modeling serves as a convenient tool for exploring in silico models. This technique reduces the risk of technical errors during the model creation, use, and further development. In addition, the computational model in BioUML has the same view as the technical diagram of the model, which the developer can draw on paper to visualize the PBPK processes. This possibility is very useful for both beginners to learn PBPK modeling techniques and advanced developers. We believe that visual modeling is the future.
- In this article, we not only demonstrate the BioUML capabilities for the PBPK modeling, but also transform the model of nanoparticle delivery to solid tumors in mice. In this respect, we consider the next possible roadmap for future research on this model:
- model simulations and analysis depending on the initial concentration of the administered nanoparticles dose.
- study the mechanisms of therapeutic nanoparticles transport taking into account their material and biodistribution depending on the tumor growth and metabolism.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jones, H.; Rowland-Yeo, K. Basic concepts in physiologically based pharmacokinetic modeling in drug discovery and development. CPT Pharmacomet. Syst. Pharmacol. 2013, 2, e63. [Google Scholar] [CrossRef]
- Buil-Bruna, N.; López-Picazo, J.M.; Martín-Algarra, S.; Trocóniz, I.F. Bringing Model-Based Prediction to Oncology Clinical Practice: A Review of Pharmacometrics Principles and Applications. Oncologist 2016, 21, 220–232. [Google Scholar] [CrossRef] [PubMed]
- Riviere, J.E. Basic principles and techniques of pharmacokinetic modeling. J. Zoo Wildl. Med. 1997, 28, 3–19. [Google Scholar] [PubMed]
- Sung, J.H.; Srinivasan, B.; Esch, M.B.; McLamb, W.T.; Bernabini, C.; Shuler, M.L.; Hickman, J.J. Using physiologically-based pharmacokinetic-guided “body-on-a-chip” systems to predict mammalian response to drug and chemical exposure. Exp. Biol. Med. 2014, 239, 1225–1239. [Google Scholar] [CrossRef] [PubMed]
- Bachler, G.; von Goetz, N.; Hungerbuhler, K. Using physiologically based pharmacokinetic (PBPK) modeling for dietary risk assessment of titanium dioxide (TiO2) nanoparticles. Nanotoxicology 2015, 9, 373–380. [Google Scholar] [CrossRef] [PubMed]
- Dogra, P.; Butner, J.D.; Ramírez, J.R.; Chuang, Y.L.; Noureddine, A.; Brinker, C.J.; Cristini, V.; Wang, Z. A mathematical model to predict nanomedicine pharmacokinetics and tumor delivery. Comput. Struct. Biotechnol. J. 2020, 18, 518–531. [Google Scholar] [CrossRef] [PubMed]
- Hall, C.; Lueshen, E.; Mošat’, A.; Linninger, A.A. Interspecies scaling in pharmacokinetics: A novel whole-body physiologically based modeling framework to discover drug biodistribution mechanisms in vivo. J. Pharm. Sci. 2012, 101, 1221–1241. [Google Scholar] [CrossRef] [PubMed]
- Ji, B.; Xue, Y.; Xu, Y.; Liu, S.; Gough, A.H.; Xie, X.Q.; Wang, J. Drug-Drug Interaction Between Oxycodone and Diazepam by a Combined in Silico Pharmacokinetic and Pharmacodynamic Modeling Approach. ACS Chem. Neurosci. 2021, 12, 1777–1790. [Google Scholar] [CrossRef]
- Razak, S.; Afsar, T.; Bibi, N.; Abulmeaty, M.; Qamar, W.; Almajwal, A.; Inam, A.; Al Disi, D.; Shabbir, M.; Bhat, M.A. Molecular docking, pharmacokinetic studies, and in vivo pharmacological study of indole derivative 2-(5-methoxy-2-methyl-1H-indole-3-yl)-N’-[(E)-(3-nitrophenyl) methylidene] acetohydrazide as a promising chemoprotective agent against cisplatin induced organ damage. Sci. Rep. 2021, 11, 6245. [Google Scholar] [CrossRef]
- Datta, N.R.; Krishnan, S.; Speiser, D.E.; Neufeld, E.; Kuster, N.; Bodis, S.; Hofmann, H. Magnetic nanoparticle-induced hyperthermia with appropriate payloads: Paul Ehrlich’s “magic (nano)bullet” for cancer theranostics? Cancer Treat. Rev. 2016, 50, 217–227. [Google Scholar] [CrossRef]
- Cheng, Y.H.; He, C.; Riviere, J.E.; Monteiro-Riviere, N.A.; Lin, Z. Meta-analysis of nanoparticle delivery to tumors using a physiologically based pharmacokinetic modeling and simulation approach. ACS Nano 2020, 14, 3075–3095. [Google Scholar] [CrossRef]
- Demina, P.A.; Sholina, N.V.; Akasov, R.A.; Khochenkov, D.A.; Arkharova, N.A.; Nechaev, A.V.; Khaydukov, E.V.; Generalova, A.N. A versatile platform for bioimaging based on colominic acid-decorated upconversion nanoparticles. Biomater. Sci. 2020, 8, 4570–4580. [Google Scholar] [CrossRef]
- Rocheva, V.; Savelyev, A.; Nechaev, A.; Generalova, A.; Semchishen, V.; Zvyagin, A.; Khaydukov, E. Three-dimensional luminescence tomographic visualization of biological tissues. Opt. Spectrosc. 2019, 126, 92–94. [Google Scholar] [CrossRef]
- Rudzińska, M.; Parodi, A.; Maslova, V.D.; Efremov, Y.M.; Gorokhovets, N.V.; Makarov, V.A.; Popkov, V.A.; Golovin, A.V.; Zernii, E.Y.; Zamyatnin, A.A. Cysteine cathepsins inhibition affects their expression and human renal cancer cell phenotype. Cancers 2020, 12, 1310. [Google Scholar] [CrossRef]
- Sevencan, C.; McCoy, R.S.A.; Ravisankar, P.; Liu, M.; Govindarajan, S.; Zhu, J.; Bay, B.H.; Leong, D.T. Cell membrane nanotherapeutics: From synthesis to applications emerging tools for personalized cancer therapy. Adv. Ther. 2020, 3, 1900201. [Google Scholar] [CrossRef]
- Li, M.; Al-Jamal, K.T.; Kostarelos, K.; Reineke, J. Physiologically based pharmacokinetic modeling of nanoparticles. ACS Nano 2010, 4, 6303–6317. [Google Scholar] [CrossRef]
- Dogra, P.; Butner, J.D.; Chuang, Y.L.; Caserta, S.; Goel, S.; Brinker, C.J.; Cristini, V.; Wang, Z. Mathematical modeling in cancer nanomedicine: A review. Biomed. Microdevices 2019, 21, 40. [Google Scholar] [CrossRef]
- Hassanzadeh, P.; Atyabi, F.; Dinarvand, R. Ignoring the modeling approaches: Towards the shadowy paths in nanomedicine. J. Control. Release 2018, 280, 58–75. [Google Scholar] [CrossRef]
- Lin, Z.; Monteiro-Riviere, N.A.; Riviere, J.E. A physiologically based pharmacokinetic model for polyethylene glycol-coated gold nanoparticles of different sizes in adult mice. Nanotoxicology 2016, 10, 162–172. [Google Scholar] [CrossRef]
- Vizirianakis, I.S.; Mystridis, G.A.; Avgoustakis, K.; Fatouros, D.G.; Spanakis, M. Enabling personalized cancer medicine decisions: The challenging pharmacological approach of PBPK models for nanomedicine and pharmacogenomics (Review). Oncol. Rep. 2016, 35, 1891–1904. [Google Scholar] [CrossRef]
- Opitz, A.W.; Wickstrom, E.; Thakur, M.L.; Wagner, N.J. Physiologically based pharmacokinetics of molecular imaging nanoparticles for mRNA detection determined in tumor-bearing mice. Oligonucleotides 2010, 20, 117–125. [Google Scholar] [CrossRef] [PubMed]
- Shalgunov, V.; Zaytseva-Zotova, D.; Zintchenko, A.; Levada, T.; Shilov, Y.; Andreyev, D.; Dzhumashev, D.; Metelkin, E.; Urusova, A.; Demin, O.; et al. Comprehensive study of the drug delivery properties of poly(l-lactide)-poly(ethylene glycol) nanoparticles in rats and tumor-bearing mice. J. Control. Release 2017, 261, 31–42. [Google Scholar] [CrossRef] [PubMed]
- Kolpakov, F.; Akberdin, I.; Kashapov, T.; Kiselev, I.; Kolmykov, S.; Kondrakhin, Y.; Kutumova, E.; Mandrik, N.; Pintus, S.; Ryabova, A.; et al. BioUML: An integrated environment for systems biology and collaborative analysis of biomedical data. Nucleic Acids Res. 2019, 47, W225–W233. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.; Jaberi-Douraki, M.; He, C.; Jin, S.; Yang, R.S.H.; Fisher, J.W.; Riviere, J.E. Performance Assessment and Translation of Physiologically Based Pharmacokinetic Models From acslX to Berkeley Madonna, MATLAB, and R Language: Oxytetracycline and Gold Nanoparticles As Case Examples. Toxicol. Sci. 2017, 158, 23–35. [Google Scholar] [CrossRef] [PubMed]
- Bergmann, F.T.; Adams, R.; Moodie, S.; Cooper, J.; Glont, M.; Golebiewski, M.; Hucka, M.; Laibe, C.; Miller, A.K.; Nickerson, D.P.; et al. COMBINE archive and OMEX format: One file to share all information to reproduce a modeling project. BMC Bioinform. 2014, 15, 369. [Google Scholar] [CrossRef]
- Hindmarsh, A.C.; Brown, P.N.; Grant, K.E.; Lee, S.L.; Serban, R.; Shumaker, D.E.; Woodward, C.S. SUNDIALS: Suite of nonlinear and differential/algebraic equation solvers. ACM Trans. Math. Softw. 2005, 31, 363–396. [Google Scholar] [CrossRef]
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations II. Stiff and Differential-Algebraic Problems, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Dormand, J.R.; Prince, P.J. A family of embedded Runge-Kutta formulae. J. Comput. Appl. Math. 1980, 6, 19–26. [Google Scholar] [CrossRef]
- Le Novère, N.; Hucka, M.; Mi, H.; Moodie, S.; Schreiber, F.; Sorokin, A.; Demir, E.; Wegner, K.; Aladjem, M.I.; Wimalaratne, S.M.; et al. The Systems Biology Graphical Notation. Nat. Biotechnol. 2009, 27, 735–741. [Google Scholar] [CrossRef]
- Hucka, M.; Bergmann, F.T.; Chaouiya, C.; Dräger, A.; Hoops, S.; Keating, S.M.; König, M.; Le Novère, N.; Myers, C.J.; Olivier, B.G.; et al. The Systems Biology Markup Language (SBML): Language specification for level 3 version 2 core. J. Integr. Bioinform. 2019, 16, 20190021. [Google Scholar] [CrossRef]
- Akberdin, I.R.; Kiselev, I.N.; Pintus, S.S.; Sharipov, R.N.; Vertyshev, A.Y.; Vinogradova, O.L.; Popov, D.V.; Kolpakov, F.A. A Modular Mathematical Model of Exercise-Induced Changes in Metabolism, Signaling, and Gene Expression in Human Skeletal Muscle. Int. J. Mol. Sci. 2021, 22, 10353. [Google Scholar] [CrossRef]
- Alon, U. Biological networks: The tinkerer as an engineer. Science 2003, 301, 1866–1867. [Google Scholar] [CrossRef] [PubMed]
- Blinov, M.L.; Ruebenacker, O.; Moraru, I.I. Complexity and modularity of intracellular networks: A systematic approach for modelling and simulation. IET Syst. Biol. 2008, 2, 363–368. [Google Scholar] [CrossRef] [PubMed]
- Pan, M.; Gawthrop, P.J.; Cursons, J.; Crampin, E.J. Modular assembly of dynamic models in systems biology. PLoS Comput. Biol. 2021, 17, e1009513. [Google Scholar] [CrossRef] [PubMed]
- Smith, L.P.; Bergmann, F.T.; Chandran, D.; Sauro, M.H. Antimony: A modular model definition language. Bioinformatics 2009, 25, 2452–2454. [Google Scholar] [CrossRef]
- Kiselev, I.; Kolpakov, F. Modular modeling of biological systems. Virtual Biol. 2013, 1, e11. [Google Scholar] [CrossRef][Green Version]
- Hartwell, L.H.; Hopfield, J.J.; Leibler, S.; Murray, A.W. From molecular to modular cell biology. Nature 1999, 402 (Suppl. 6761), C47–C52. [Google Scholar] [CrossRef]
- Snoep, J.L.; Bruggeman, F.; Olivier, B.G.; Westerhoff, H.V. Towards building the silicon cell: A modular approach. Biosystems 2006, 83, 207–216. [Google Scholar] [CrossRef]
- Cho, W.S.; Cho, M.; Jeong, J.; Choi, M.; Han, B.S.; Shin, H.S.; Hong, J.; Chung, B.H.; Jeong, J.; Cho, M.H. Size-dependent tissue kinetics of PEG-coated gold nanoparticles. Toxicol. Appl. Pharmacol. 2010, 245, 116–123. [Google Scholar] [CrossRef]
- Zhong, J.; Wen, L.; Yang, S.; Xiang, L.; Chen, Q.; Xing, D. Imaging-guided high-efficient photoacoustic tumor therapy with targeting gold nanorods. Nanomedicine 2015, 11, 1499–1509. [Google Scholar] [CrossRef]





| Notation | Interpretation | Value | Units |
|---|---|---|---|
| ALub | Amount of nanoparticles in the capillary blood of the lungs | variable | mg |
| ALung | Amount of nanoparticles in the lung compartment | variable | mg |
| ALuRES | Amount of nanoparticles being taken up from the lung interstitium by phagocytosis | variable | mg |
| ALut | Amount of nanoparticles in the lung interstitium | variable | mg |
| BVLu | Fractional blood volume in the lungs | 0.5 | - |
| BW | Bodyweight of mice | 0.02 | kg |
| CLut | Concentration of nanoparticles in the lung interstitium | variable | mg/L |
| CV | Concentration of nanoparticles in the venous blood | variable | mg/L |
| CVLu | Concentration of nanoparticles in the capillary blood of the lungs | variable | mg/L |
| KLuRES50 | Time reaching a half-maximum uptake rate of nanoparticles by endocytic/phagocytic cells of the lungs | 48.0 | h |
| KLuRESmax | Maximum uptake rate of nanoparticles by endocytic/phagocytic cells of the lungs | 0.085 | 1/h |
| KLuRESn | Hill coefficient in the lung compartment | 5.0 | - |
| KLuRESrelease | Rate constant of nanoparticles released from endocytic/phagocytic cells of the lungs | 0.03 | 1/h |
| KLuRESUP | Rate of endocytosis in the lungs | variable | 1/h |
| PALuC | Membrane-limited permeability coefficient in the lungs | 0.001 | - |
| PDOSEiv | Injected dose of nanoparticles | 8.17 | mg/kg |
| PLu | Tissue:plasma distribution coefficient for the lungs | 0.15 | - |
| QC | Cardiac output | 0.87752 | L/h |
| Timeiv | Injection time | 0.005 | h |
| VLu | Lung volume | 0.00014 | L |
| VLub | Volume of the capillary blood in the lungs | 0.00007 | L |
| VLuC | Lung volume (fraction of the bodyweight) | 0.007 | - |
| VLut | Volume of the lung interstitium | 0.00007 | L |
| Element Name | Glyph | Description |
|---|---|---|
| Equation |  | Mathematical equations of the model:
|
| Discrete event |  | Events describe an instant change of the model variable when a specified condition is satisfied, e.g., the change of medication rate after a certain time point. |
| Function | 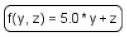 | Function receives argument values, calculates, and returns the result of the given expression. |
| Constraint |  | A condition set in the constraint is checked during the simulation. Depending on solver settings a simulation may be stopped or an error message will be shown if the condition is violated. |
| Table | 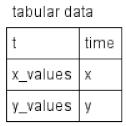 | Tabular elements are used to calculate model variables according to corresponding tabular data. Each row of the tabular element connects the table column with the model variable. In this case, the table column t is employed for the time variable, time, while the x_values and y_values columns serve to calculate the x and y variables, respectively. The tabular element is either translated to a spline approximating tabular data or a piecewise constant function. |
| Interface ports |  | There are three types of interface ports in the BioUML to support the visual representation of modular models (see subsection “Modular modeling” below): contact (gray), input (green), and output (red) ports. |
| Parameters | Interpretation | Healthy Mice AuNPs, 13 nm | Tumor-Bearing Mice AuNRs, 9–11 nm | Units |
|---|---|---|---|---|
| BVT | Blood volume fraction in tumor (percentage of the tumor volume) | - | 0.02 | - |
| KTRES50 | Time reaching a half maximum uptake rate of nanoparticles by tumor cells | - | 0.5 | h |
| KTRESmax | Maximum uptake rate of nanoparticles by tumor cells | - | 0.055 | 1/h |
| KTRESn | Hill coefficient for the uptake by tumor cells | - | 0.5 | - |
| KTRESrelease | Rate constant of nanoparticles released from tumor cells | - | 0.001 | 1/h |
| PATC | Membrane-limited permeability coefficient | - | 0.01 | - |
| PDOSEiv | Administered dose of nanoparticles | 0.85 | 20 | mg/kg |
| PT | Tumor tissue:plasma distribution coefficient | - | 0.265 | - |
| QTC | Blood flow rate to the tumor (fraction of cardiac output) | - | 0.01 | - |
| VTC | Tissue volume (fraction of the bodyweight) | - | 0.006 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kutumova, E.; Akberdin, I.; Kiselev, I.; Sharipov, R.; Kolpakov, F. Modular Representation of Physiologically Based Pharmacokinetic Models: Nanoparticle Delivery to Solid Tumors in Mice as an Example. Mathematics 2022, 10, 1176. https://doi.org/10.3390/math10071176
Kutumova E, Akberdin I, Kiselev I, Sharipov R, Kolpakov F. Modular Representation of Physiologically Based Pharmacokinetic Models: Nanoparticle Delivery to Solid Tumors in Mice as an Example. Mathematics. 2022; 10(7):1176. https://doi.org/10.3390/math10071176
Chicago/Turabian StyleKutumova, Elena, Ilya Akberdin, Ilya Kiselev, Ruslan Sharipov, and Fedor Kolpakov. 2022. "Modular Representation of Physiologically Based Pharmacokinetic Models: Nanoparticle Delivery to Solid Tumors in Mice as an Example" Mathematics 10, no. 7: 1176. https://doi.org/10.3390/math10071176
APA StyleKutumova, E., Akberdin, I., Kiselev, I., Sharipov, R., & Kolpakov, F. (2022). Modular Representation of Physiologically Based Pharmacokinetic Models: Nanoparticle Delivery to Solid Tumors in Mice as an Example. Mathematics, 10(7), 1176. https://doi.org/10.3390/math10071176






