Abstract
In order to study retailers’ ordering behavior deviating from the standard theoretical optimal decision, which is caused by retailers’ information asymmetry, cognitive ability, insufficient computing ability, and other factors, we construct a bounded-rationality choice model with quantal response equilibrium. First, the existence and uniqueness of quantal response equilibrium of transshipment game have been proved with the transshipment price satisfying certain conditions. Then, the numerical example demonstrates that with the increase of bounded-rationality parameters, retailers’ quantal response equilibrium will converge to Nash equilibrium due to the learning effect, and their profits will converge to the profits predicted by standard theory. Finally, the results show that retailers are more averse to the explicit loss of shortage than to the implicit loss of inventory surplus caused by the increase of order quantity. Hence, retailers tend to overorder to avoid loss of shortage.
MSC:
35Q91
1. Introduction
The loss incurred by the mismatch between existing supply and market demand is huge, which is fundamentally caused by the uncertainty of market demand. Leftover will lead to the increase of holding cost and disposal cost, and stockout will lead to sales loss. Cisco, the world’s largest network-equipment maker, created an inventory surplus of $2.69 billion by misreading the market demand in 2001, which shocked investors deeply [1]. In contrast, the stockout has caused huge losses to the retail industry. For example, the American supermarket retail industry loses $7–10 billion a year due to shortages [2]. Additionally, Roland Berger also surveyed retail supermarkets in Beijing, Shanghai, and Shenzhen, and found that the out-of-stock rate of China’s supermarket industry is conservatively estimated at 10%, resulting in direct losses of $12.3 billion a year. In addition to direct economic losses, the mismatch between supply and demand may have a significant negative impact on a company’s performance in the capital market. Hendricks and Singhal [3,4] found that announcements about supply–demand mismatches would have a negative impact on a company’s stock price. They observed that 73% of the companies in the sample experienced a negative stock market reaction after the excess inventory announcement, and that for companies with higher growth expectations and higher debt-to-equity ratios, the reaction to the excess inventory announcement was likely to be even more negative.
To mitigate the impact of mismatch between supply and demand, some managers propose transshipment as a solution to this problem. Transshipment, whose underlying principle is risk pooling, refers to the movement of products between retailers at the same level. Previous studies have demonstrated that transshipment can reduce inventory and improve service levels. For example, ASML, a semiconductor component supplier based in Veldhoven, the Netherlands, supplies components to customers in more than 50 regions including North America, Asia, and Europe. In Asia, ASML set up a main warehouse in Shanghai and other places, and sub-warehouses in Singapore and other places, so as to realize inventory sharing in Asia, which reduced the annual inventory cost of distributor by 50% [5]. In fact, car dealers in the United States satisfy up to 18% of their new vehicle customer demand by locating vehicles at another dealer [6]. Early transshipment was mostly used in heavy manufacturing, such as the supply of parts for large construction equipment, aircraft, and power generation equipment [7,8]. However, with the development of information technology and logistics industry, the application scope of transshipment is further expanded. In fact, this strategy has been widely promoted in clothing (Benetton, Mango), automobile (Toyota, Volvo), publishing (Xinhua Group), and medical insurance.
Despite the potential benefits of transshipment, in practice retailers will deviate from the optimal order quantity predicted by standard theory. This is mainly because there is a key assumption in traditional transshipment studies that decision-makers are perfectly rational. However, the actual order quantity deviates from the theoretical optimal quantity due to the fact that the decision-maker’s information acquisition ability, cognitive ability, and computing ability are limited. Zhao et al. [9] conducted a survey among 54 inventory managers and found that none of them purely adopted standard theories when making decisions, while 45 managers admitted that standard theories and behavioral factors should be considered when making decisions. Additionally, in 2016, the power supply bureaus subordinate to a provincial power company required 1.59 million electricity meters. However, in order to ensure a 3-day response time, each power supply bureau would overorder the meters, making the actual order quantity close to 1.84 million. Although the order quantity of each power supply bureau is far more than the demand, the imbalance rate of supply and demand of these power supply bureau still reaches 3.421%. This resulted in 260,000 pieces of surplus stock and an inventory cost of $2 million. A survey of the company showed that power supply bureaus overordered when placing orders and did not consider transshipment, resulting in large inventory costs. Hence, the behavioral factors must be considered when studying retailer’s order decision, so as to make corresponding countermeasures in advance.
In order to study the behavior of retailers deviating from the theoretically optimal order quantity, based on the assumption that retailers are bounded rational, we propose the following research questions:
- (1)
- what are retailers’ ordering behavior if they are boundedly rational.
- (2)
- when the retailer is bounded rational, whether there is still order equilibrium.
To address the questions mentioned above, we consider a two-echelon supply chain with an upstream supplier and two downstream retailers. The members of the supply chain are independent of each other. The methodology we used is classical game theory and behavioral game theory. We assume that retailers are boundedly rational when making ordering decisions, that is, they cannot always select the theoretically optimal order quantity. In order to capture this bounded rationality of retailers, we incorporated quantal response equilibrium (QRE) into the research framework.
This paper makes several contributions to both transshipment and behavioral operations. We incorporate QRE into an analytical modeling framework. Then, the existence of QRE and conditions for its uniqueness are proved. We also study the relationship between QRE and Nash equilibrium and design an algorithm to find the QRE between two independent retailers.
The remainder of this paper has been organized as follows: The next section provides a brief literature review. The order decision model of perfectly rational retailer is provided in Section 3. In contrast, the order decision model of boundedly rational retailer has been developed in Section 4. Next, a numerical study has been formulated to investigate the relationship between QRE and bounded rationality of the two in Section 5. Finally, the conclusion is given in Section 6.
2. Literature Review
As a seminal work on transshipment, Rudi et al. [10] investigated the inventory transshipment between two independent retailers in two geographically different regions. Subsequent studies are extended based on their work, e.g., from passive transshipment to preventive transshipment [11], from single stage to multiple stages [12], capacity constraints [13] and extension of supply chain [14], etc. For a comprehensive review, readers can refer to the review conducted by Paterson et al. [15]. Recently, the research topic on inventory transshipment has shifted to behavioral decision making, which mainly studies retailers’ ordering bias through behavioral experiments. This part of the literature mainly focuses on the well-known behavioral deviation called pull-to-center bias, that is, for high-margin products, the retailer’s order quantity tends to be less than the theoretically optimal order quantity, but more than the mean demand; for low-margin products, the order quantity is larger than the optimal order quantity, but less than the mean demand. Such pull-to-center bias was first observed in the newsvendor model by Schweitzer and Cachon [16] in behavioral experiments. The potential benefits of transshipment are not limited to manufacturing companies. In recent years, transshipment has been widely used in retail. LC Waikiki, a large fast fashion retailer in Turkey, transships thousands of its products among its more than 475 retail branches [17]. This strategy has resulted in significant inventory cost savings and improved service levels. In fact, transshipment can reduce inventory cost by 15–20% as well as lost sales by 75% [18]. Hence, it is necessary to investigate this behavioral bias in order not to affect the benefits of transshipment.
Subsequent studies have primarily tried to figure out what factors lead to the pull-to-center bias, including overconfidence [19], fairness concern [20], learning effect [21], prospect theory [22], reference effect [23], etc. In the research of behavioral inventory transshipment, some studies also found the existence of the pull-to-center effect, and also sought for the corresponding behavioral factors to explain. Villa and Castañeda [24] are the first to explain the pull-to-center bias from the aspects of anchoring, loss aversion and reference effect. Li et al. [25] revealed the pull-to-center bias from the perspective of overconfidence. Katok and Villa [26] also found the pull-to-center effect in their empirical studies, but the bias under centralized system is different from that under a decentralized system. However, they did not analyze its causes.
Additionally, some other studies only found that the pull-to-center bias in the case of high margins. Li and Chen [27] observed that the order quantity is less than the optimal order quantity regardless of the timing of setting transshipment price or the stock sharing mechanism and analyzed the influence of the two mechanisms on the order quantity. Davis et al. [28] found that the order quantity decreased by 7.87% and 7.96%, respectively, in centralized and decentralized systems (manufacturer and retailers set transshipment price, respectively), and explained this from the perspective of fairness. Without considering different margins, Zhao et al. [9] revealed the reason for the low order quantity from the perspective that decision-makers often ignored transshipment as the demand side.
In this paper, we try to use the concept of bounded rationality which takes into account the cognitive limitations of the decision maker, proposed by Simon [29], to explain retailers’ inventory decision deviating from the theoretically optimal order quantity. Based on the knowledge of bounded rationality in individual decision making drawn from experiments in economics and psychology, Camerer proposed several promising new research directions [30]. Recently, this concept has been frequently used in operations management research. Su is the first research to combine bounded rationality with newsvendor problem [31]. Wang et al. proposed a novel bounded rationality behavioral decision model to explore the differences in hotel selection among various types of tourists [32]. Li et al. considered the influence of bounded rationality in the design of compensation contracts for retail store managers [33]. In addition, in a network route choice problem, Sun et al. generalized the concept of bounded rationality through a link-based perception error model to investigate the uncertain behavior of drivers [34]. For the study of bounded rationality in operations management, we recommend readers to refer to Ren and Huang for a detailed review [35].
The above literature found that the pull-to-center bias still exists when transshipment is permitted, and the factors leading to this bias were identified through behavioral experiments, such as anchoring demand mean, loss aversion, reference effect, overconfidence and fairness, etc. However, in the behavioral experiment, it is difficult to distinguish whether subjects consider the pooling of demand risk or the retailer’s bounded rationality when deciding the order quantity. Hence, Zhang and Siemsen [36] believe that the pull-to-center effect is a robust experimental phenomenon rather than a theoretical result. Motivated by this, we studied the ordering behavior of retailers from the perspective of analytical modeling. Referring to the method adopted by Su [31], the notion of quantal response equilibrium is introduced in this paper to demonstrate the existence of behavioral ordering bias from the perspective of bounded rationality. In this paper, under the framework of quantal response equilibrium, we will study the ordering decision of two independent retailers. The existence and uniqueness of quantal response equilibrium for ordering decision has been proved. We will also design the corresponding algorithm, called distributed learning automata, to find the quantal response equilibrium.
3. Ordering Decision Model of Perfectly Rational Retailer
Consider a system consisting of two independent retailers (1 and 2), each selling the same perishable product to its own market. Two retailers face two random demands that are independent of each other. and are the density function and cumulative distribution function of retailer 1’s demand, respectively, while and are the density function and cumulative distribution function of retailer 2. Before the selling season, retailer should decide its order quantity , . The wholesale price of unit product is , and replenishment is impossible during the selling season. Retailer use its inventory to satisfy the demand with the unit selling price . At the end of the selling season, the two retailers can cooperate with other by transshipment if one has excess demand and the other has surplus inventory, which can reduce inventory cost as well as improve service level. Assume that retailer can transship its excess inventory to retailer at unit transshipment price and retailer can cover each unit of transportation cost when retailer has surplus inventory and retailer () is out of stock. After transshipment, retailer disposes of their surplus inventory at unit salvage value if they still have excess inventory, and retailer has a penalty for each unit unsatisfied demand if they are still out of stock. We show all the notations and their meanings in Table 1.

Table 1.
List of notations.
Assumption 1.
According to Hanany et al. [37], assume that , which ensures that retailers have an incentive to implement transshipment. indicates that when retailer has inventory surplus, they can obtain more profit by transferring out products than recycling at salvage value. indicates that when retailer is out of stock, it is profitable to transfer in products.
Assumption 2.
According to Rudi et al. [10], assume that , . This condition prevents retailers from speculating through transshipment and thus ensure that transshipment occurs only when one has excess inventory, and the other is out of stock.
We assume that retailer has excess inventory and retailer is out of stock after the demand is realized. Define . The excess inventory of retailer is , and the shortage of retailer is . The amount of transshipment from retailer to is . Then, the sale and excess inventory of retailer are , , respectively. The shortage of retailer is . Hence, we give the expected profit function of retailer :
The right side of Equation (1) consists of six parts, namely sales revenue, salvage value, loss of stockout, cost of transshipment, revenue of transshipment, and ordering cost. According to the description of the above variables, we rewrite the Equation (1) to Equation (2).
To study order decisions of two independent retailers, it is necessary to study the conditions under which the interaction between two independent retailers exists Nash equilibrium. Motivated by Rudi et al. [8], the existence and uniqueness conditions of Nash equilibrium of order decisions for two independent retailers are obtained.
Proposition 1.
If the transshipment price satisfies that, there is a unique Nash equilibrium order decision between two retailers. Retailer’s optimal order quantity can be solved by the following equation.
The above two integrals represent the probability of two different inventory states. is the probability of the inventory state of ,, and . is the probability of the inventory state of ,, and .
Proof.
We denote as the probability density function of a random variable . Then, the following marginal probabilities can be well defined: , , , , .
By the implicit function theorem and Equation (3), one can obtain the following reaction function.
Given the restrictions of parameters, it is easy to verify that , which implies that the reaction function is monotonic, and the absolute value of the slope is less than 1. Then, the unique Nash equilibrium is obtained immediately. □
Proposition 1 demonstrates that there is a unique Nash equilibrium between the two retailers when retailers are motivated to implement transshipment by a feasible transshipment price, which also indicates that there is a strategic substitution relationship between order quantities of the two retailers. In addition, the second term on the left of Equation (3) represents the process of transshipping out inventory surplus, and the third term represents the process of transshipping in stock from another retailer. Hence, the inventory transshipment can reduce the order quantity in equilibrium to a certain extent. If transshipment is not allowed, Equation (3) degenerates into the classical newsvendor model where . It can be seen that the inventory model with transshipment expands the participants on the basis of the classical newsvendor model, thus producing the risk-pooling effect. Hence, transshipment can relieve inventory pressure, that is, transshipment can reduce inventory cost and improve service level.
Nash equilibrium of order decisions is based on the assumption that retailers are perfectly rational, that is, there is no mistake in retailers’ decisions and each retailer can always reach the theoretical optimal order quantity. Such equilibrium has some limitations, so in the next section, we will investigate bounded rationality of retailers by the method of stochastic choice probability model.
4. Ordering Decision Model of Boundedly Rational Retailer
In order to characterize retailer’s bounded rationality, we introduced logit choice probability model to construct retailer’s bounded rationality and obtained the QRE. In such a logit choice model, the rationality of retailers is reflected by a bounded rationality parameter , which would be adjusted dynamically during the convergence of quantal response equilibrium to Nash equilibrium (assume that the NE is always in the feasible strategy set). Instead of a specific order quantity, in the framework of QRE, a retailer’s ordering decision is a probability distribution—that is, all order quantity within the upper and lower limits of demand are likely to be chosen. For any positive bounded rationality parameter , all feasible order quantities are chosen with positive probability, and the order quantity with higher expected profit is more likely to be chosen. The value of parameter can reflect the degree of retailer’s bounded rationality. When the parameter , retailer ’s ordering decision follows uniform distribution over the feasible domain, that is, retailer does not obtain any information about the optimal order quantity and stochastically selects between each order quantity with equal probability, which means that retailer is completely irrational. When the parameter , retailer becomes perfectly rational and would definitely choose the theoretical optimal order quantity, which is consistent with the order quantity predicted by Nash equilibrium.
We assume that the retailer makes multiple ordering decisions during the study. Each order decision is the beginning of an order period. Before the next order decision, the retailer can observe the realization of demand and their own revenue, which can be used as a reference for the next order decision. In addition, we assume that retailers can gain experience from previous decisions to improve their rationality, that is, retailers have a learning effect. According to the definition of QRE in McKelvey and Palfrey [38], we can get the ordering strategy of two retailers at period . In fact, with the repetition of order game, retailers tend to be perfectly rational because of the learning effect.
We define as the expected profit function of retailer when they choose and the opponent chooses . Given the conclusion of Proposition 1, it is straightforward to use Equation (3) to write down the optimal solution (NE) of the transshipment problem. We denote as the Nash equilibrium. In reality, retailers’ order quantity space is discrete, finite, and bounded. We define retailers’ order quantity sets and , respectively, and let and , where and are discrete, finite, and bounded. In the actual ordering process, due to the influence of various factors, the rationality degree of each retailer is different, but in this paper, for the convenience of analysis, we assume that retailers have the same level of rationality. Hence, the logit choice probability of retailer choosing the order quantity should satisfy the following equation. The probability mass function of the behavioral solution QRE is as follows.
From Equation (5), it is clear that if retailer is completely irrational (i.e., ), they will choose any order quantity with equal probability ( is the number of all feasible order quantities). It indicates that the retailer cannot identify the expected profit difference of different orders. In contrast, if retailer is perfectly rational (i.e., ), they will choose the optimal order quantity with certainty. This shows that retailer is very sensitive to the expected profit difference caused by different order quantity. To obtain the optimal expected profit, retailer will always choose .
Since there is a game between two retailers, we first study the existence of QRE of order decision between retailers.
Proposition 2.
If, that is, transshipment can be implemented between the two retailers, the existence of QRE can be guaranteed.
Proof.
If , then . The superscript represents the newsvendor model where the retailer only needs to make an independent ordering decision in the face of uncertain demand without considering transshipment [39,40], and represents retailer ’s expected profit in the newsvendor model with the order quantity . It is obvious that both feasible order sets and are compact and convex. By Equation (6), let , then and . Hence, the existence of QRE can be guaranteed from Brouwer’s fixed point theorem. □
Proposition 2 shows that there is QRE in the ordering game between two retailers, that is, there is equilibrium in the form of probability distribution of order quantity. If transshipment can occur, the two retailers maximize their expected profit functions on their feasible order sets, that is, any order quantity is chosen with a certain probability.
This also shows that retailers’ bounded rationality constructed by QRE has universal significance in order and inventory management of retail industry. Therefore, the retailers’ bounded rationality should be considered in practice to avoid the profit loss caused by the decision deviation.
The multiplicity of QRE makes it difficult for retailers to cope. Hence, Proposition 3 gives the uniqueness of QRE of two retailers.
Proposition 3.
If, that is, transshipment can be implemented between the two retailers, the QRE between the two retailers is unique.
Proof.
If , then . It is obvious that both feasible order sets and are compact and convex. By Equation (5),
By Equation (5), we can rewrite the logit choice model into the following equation.
Since , is strictly decreasing monotonically. Then, and demonstrate that the order quantity would not increase infinitely in practice, so the profit will always be larger than or equal to zero within a given range. Hence, and increase strictly with . Obviously, the left side of Equation (7) is monotonically increasing with and the right side is monotonically decreasing with . As a result, the graphs of the above two functions intersect only at one point, which guarantees the uniqueness of the QRE between two retailers. □
Proposition 3 indicates that the ordering decisions of two bounded rational retailers is unique, which greatly simplifies the ordering decision behavior of retailers and provides convenience for their ordering and inventory management. Retailers only need to order according to the unique equilibrium solution, without considering the ordering behavior of the other party.
Since the uncertainty of demand, neither retailer can determine whether transshipment will eventually occur. With the logit choice model, the probability and expected profit function of retailer choosing the order quantity are as follows.
Retailers are assumed to be boundedly rational in our behavioral transshipment model. Since the reasons for boundedly rationality are complex, it is difficult to quantify it. We amplify the effects of bounded rationality in logarithmic terms.
It can be seen from Figure 1 and Figure 2 that the equilibrium of bounded rationality deviates from the Nash equilibrium. However, as the bounded rationality parameter increases, the QRE moves from the initial equal probability choice to Nash equilibrium.

Figure 1.
Nash equilibrium and QRE.
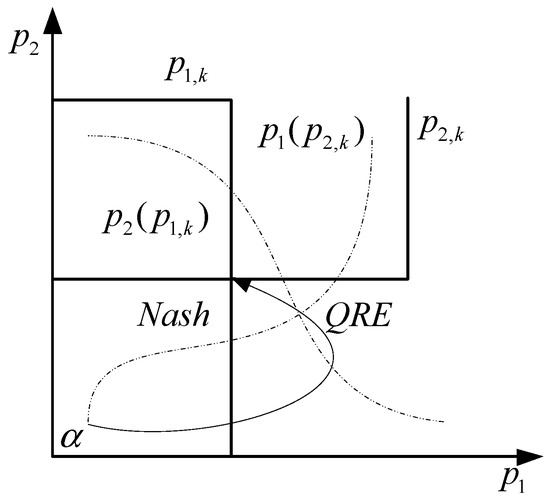
Figure 2.
QRE moves toward Nash equilibrium.
5. Numerical Study
To get a more intuitive result, some of the values in our example are the same as Rudi et al.’s [8]. We assume that the demand of the two retailers obeys normal distribution ,, and , , , , ,. Combined with the above parameters and theoretical analysis results, and using Code:Blocks, Gambit 15, and the algorithm which is presented in Appendix A. the relationship between QRE and bounded rationality of the two retailers is analyzed. In this numerical study, we assume that retailers have the exponential learning effect, because the exponential learning effect is more realistic, and it converges faster than the linear learning effect.
The Nash-equilibrium order quantity of the two retailers is 6 and 4, respectively, through simulation. When initializing parameters, the initial value of bounded rationality is 0. The set of retailer 1’s order quantities is , and the corresponding set of retailer 2 is . Retailer 1 and 2 have their own initial probabilities, that is, retailer 1 chooses each order quantity with a probability , and retailer 2 chooses each order quantity with a probability . In addition, in order to represent the bounded rationality parameter more clearly, we enlarged the bounded rationality parameter 100 times.
Figure 3a,b show the probability of retailer 1 choosing different order quantities. With the increase of bounded rationality parameter, the probability of each order quantity being selected eventually converges to 0 or 1. As the bounded rationality parameter increases, the probability of retailer 1 choosing the order quantity 4, 5, 6, 7, 8, 9, and 10 increase first and then decreases again. Hence, these order quantities are more likely to be selected in the early period, but as retailer 1 gets more rational and familiar with the market, these order quantities will be gradually abandoned by retailer 1. Additionally, we observe that the probability of order quantity selection on the right side of the distance optimal order quantity is greater than the probability of order quantity selection on the left side, which indicates that retailers prefer to overorder when making decisions. The probability of retailer 1 choosing order quantity 0, 1, 2, and 3 is decreasing all the time, and the decreasing speed is gradually slowing down, and tends to 0 when is small. The probability that retailer 1 chooses the order quantity 6 presents an increasing trend, and the increasing range is gradually decreasing. When , the probability of retailer 1 choosing order quantity 6 is already close to 1. Hence, from the point of view of cost, in the investment to improve the rationality of retailers, the investment in the early period will bring a large increase in profits, but the benefit is not obvious in the later period.

Figure 3.
(a) Distribution of retailer 1’s order quantities. (b) Retailer 1’s probability and bounded rationality.
Figure 4 is similar to Figure 3, showing the relationship between the probability of being selected for each order quantity of retailer 2 and bounded rationality parameter. As the degree of bounded rationality increases, the probability of retailer 2 choosing order quantity 3, 5, 6, 7, 8 goes up first and then down. The probability of choosing order quantity 0, 1, 2 decreases all the time, and the decreasing speed is gradually slowing down. The probability of choosing order quantity 4 presents a rising trend, and the rising speed gradually slows down. When , the probability of retailer 2 choosing order quantity 4 also approaches 1.
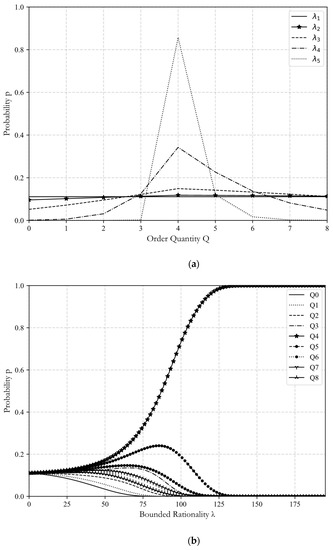
Figure 4.
(a) Distribution of retailer 2’s order quantities. (b) Retailer 2’s probability and bounded rationality.
Figure 5 shows the relationship between order probability and bounded rationality of two retailers. With the increase of rationality, both retailers select each order quantity from the initial equal probability to the final Nash equilibrium. In addition, it can be seen from Figure 5 that when the rational parameter is small, the probability of two retailers choosing greater than the optimal order quantity is greater than the probability of choosing less than the optimal order quantity. The reason is that retailers are more averse to shortage than to leftover. Inventory surplus is a kind of implicit loss, and shortage is a kind of explicit loss. Hence, retailers are more inclined to choose larger order quantities to avoid explicit losses. In fact, Schweizer and Cachon [14] observed this in their behavioral experiment under the framework of newsvendor model. Again, this behavioral preference persists in the transshipment model between the two retailers. This phenomenon is particularly evident in the ordering of raw materials. When there is a shortage of raw materials, the entire production line, logistics, marketing, and other departments will feel the loss caused by the shortage of raw materials, so the decision maker will increase the order quantity of raw materials.

Figure 5.
(a) Retailer 1’s cumulative probability. (b) Retailer 2’s cumulative probability.
Figure 6 shows the relationship between expected profit and bounded rationality parameter. With the increase of bounded rationality parameter, the expected profit of both retailers will increase. Retailers become more and more rational, and the order quantity is closer to the optimal order quantity, so their expected profit is also close to the optimal profit. When , the expected profit of retailer 1 and 2 is close to the optimal value of 73.3 and 120, respectively. The profit variation trend of the two retailers conforms to the principle of decreasing efficiency of the learning curve, and this learning effect is consistent with the learning effect found by Bostian et al. [21] in the behavioral experiment of the newsvendor model.
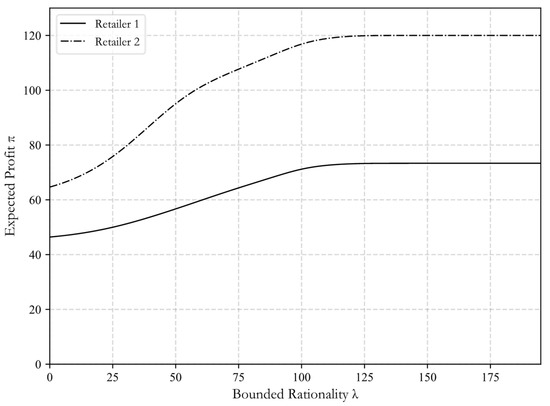
Figure 6.
Retailers’ expected profit and bounded rationality.
6. Conclusions and Future Research
Ordering behavior deviates from the optimal decision of traditional model due to the decision maker’s insufficient information acquisition, cognitive ability, and computing ability. A stochastic choice probability model based on QRE model and considering retailer’s bounded rationality has been proposed. The QRE transshipment model is established according to logit function, and the retailer’s decision behavior is predicted by this model. The specific conclusions are as follows.
Firstly, the existence and uniqueness of QRE of retailers’ ordering decisions is proved, and a distributed learning automata algorithm is designed to solve such QRE.
Second, with the increase of bounded rationality parameter, the QRE of both retailers’ ordering decisions will converge to Nash equilibrium, and their profits will converge to the optimal value, which indicates that there is a learning effect in the ordering decisions of the two retailers. Hence, decision makers can adjust the ordering decisions appropriately according to their sale experience.
Thirdly, for retailers, they are more averse to explicit shortage losses than to implicit inventory surplus cost caused by increased order quantities. The reason is that inventory surplus is a kind of invisible loss, and shortage is a kind of explicit loss. Hence, retailers are prone to choosing a larger order quantity so as to avoid explicit losses. As a response, decision makers could modestly reduce the number of items reported by retailers.
Finally, we give some directions for future research. An interesting direction is the heterogeneity of bounded rationality. In this paper, we assume that each retailer has the same degree of rationality, that is, retailers’ bounded rationality parameters are the same. However, in fact, retailers have different degrees of rationality due to individual heterogeneity. Hence, the result of such problems might be more complicated than this paper suggests. Another direction is to design some strategies to reduce or eliminate the ordering bias caused by bounded rationality, such as training, information sharing, decision support system, and so forth.
Author Contributions
Conceptualization, Q.H.; methodology, Q.H.; software, T.S.; formal analysis, B.L.; writing—original draft, B.L.; writing—supervision, W.Q.; writing—review and editing, T.S. and B.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by a research grant from the National Natural Science Foundation of China (No. 71661004, 72161004), Chinese Postdoctoral Science Foundation (No. 2017M610743), and Natural Science Foundation of Guizhou Province of China (No. ZK [2021]-323).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Algorithm Design
It is very difficult to calculate QRE according to Equations (8) and (9). On the one hand, we cannot calculate the final result, on the other hand, the model cannot describe the current situation because there is no infinite order quantity in reality. To solve this technical problem, we assume that the demand follows a normal distribution with mean and standard deviation , , and the probability density function is . To avoid negative demand, we restrict the value of . We assume that the demand follows a truncated normal distribution and has a support .
To solve the QRE, we start at . and vary within . Hence, the strategic game of retailer 1 and 2 in finite iterations is as follows, where is the period.
Start at , as t increases, the algorithm ends when converges to 0 or 1. Iterate over the following steps.
When , retailer 1’s ordering strategy is , where is the size of retailer ’s feasible order set. Retailer 2’s ordering strategy is .
When , with the ordering strategy at and the following equations, the ordering strategy at period can be figured out, and so on. The iteration ends when converges to some sufficiently small value ( is the NE). With Equations (8) and (9), we obtain the following recursive equations.
In the specific numerical solution, the initial parameters are first configured, including the initial ordering strategy of retailer 1 and 2, the current revenue matrix. Then, the ordering strategy of the next period is calculated by Equations (A1) and (A2). The QRE under the current rationality is obtained through repeated iteration, and is saved in the storage area. The corresponding algorithm steps of distributed learning automata are given below.
Step 1. Initialize parameters.
Step 2. Set the initial ordering strategies for retailer 1 and 2.
Step 3. , or .
Step 4. According to Equations (A1) and (A2), Calculating the new mixed ordering strategy profile .
Step 5. If .
Step 6. Break.
Step 7. Else.
Step 8. Repeat Step 3~8.
Step 9. End.
In step 3, there are two kinds of learning effects, one is exponential learning effect, where is the learning speed, and the other is linear learning effect, where is the learning speed.
References
- Narayanan, V.G.; Raman, A. Aligning incentives in supply chains. Harv. Bus. Rev. 2004, 82, 94–103. [Google Scholar] [PubMed]
- Ton, Z. The Role of Store Execution in Managing Product Availability. Ph.D. Thesis, Harvard University, Graduate School of Business Administration, Cambridge, MA, USA, 2002. [Google Scholar]
- Hendricks, K.B.; Singhal, V.R. Demand-supply mismatches and stock market reaction: Evidence from excess inventory announcements. Manuf. Serv. Oper. Manag. 2009, 11, 509–524. [Google Scholar] [CrossRef]
- Hendricks, K.B.; Singhal, V.R. The effect of demand–supply mismatches on firm risk. Prod. Oper. Manag. 2014, 23, 2137–2151. [Google Scholar] [CrossRef]
- Kranenburg, A.A. Spare Parts Inventory Control under System Availability Constraints. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2006. [Google Scholar]
- Stalk, G.; Stephenson, S.G.; King, T. Searching for fulfillment: Order-to-delivery opportunities in the auto industry. Supply Chain. Manag. Rev. 1997, 1. [Google Scholar]
- Grahovac, J.; Chakravarty, A. Sharing and lateral transshipment of inventory in a supply chain with expensive low-demand items. Manag. Sci. 2001, 47, 579–594. [Google Scholar] [CrossRef]
- Kukreja, A.; Schmidt, C.P.; Miller, D.M. Stocking decisions for low-usage items in a multilocation inventory system. Manag. Sci. 2001, 47, 1371–1383. [Google Scholar] [CrossRef]
- Zhao, H.; Xu, L.; Siemsen, E. Inventory sharing and demand-side underweighting. Manuf. Serv. Oper. Manag. 2021, 23, 1217–1236. [Google Scholar] [CrossRef]
- Rudi, N.; Kapur, S.; Pyke, D.F. A two-location inventory model with transshipment and local decision making. Manag. Sci. 2001, 47, 1668–1680. [Google Scholar] [CrossRef] [Green Version]
- Dehghani, M.; Abbasi, B.; Oliveira, F. Proactive transshipment in the blood supply chain: A stochastic programming approach. Omega 2021, 98, 102112. [Google Scholar] [CrossRef]
- Rong, Y.; Snyder, L.V.; Sun, Y. Inventory sharing under decentralized preventive transshipments. Nav. Res. Log. 2010, 57, 540–562. [Google Scholar] [CrossRef]
- Wang, Z.; Dai, Y.; Fang, S.C.; Jiang, Z.Z.; Xu, Y. Inventory transshipment game with limited supply: Trap or treat. Nav. Res. Log. 2020, 67, 383–403. [Google Scholar] [CrossRef]
- Dan, B.; He, Q.; Zheng, K.; Liu, R. Ordering and pricing model of retailers’ preventive transshipment dominated by manufacturer with conditional return. Comput. Ind. Eng. 2016, 100, 24–33. [Google Scholar] [CrossRef]
- Paterson, C.; Kiesmüller, G.; Teunter, R.; Glazebrook, K. Inventory models with lateral transshipments: A review. Eur. J. Oper. Res. 2011, 210, 125–136. [Google Scholar] [CrossRef] [Green Version]
- Schweitzer, M.E.; Cachon, G.P. Decision bias in the newsvendor problem with a known demand distribution: Experimental evidence. Manag. Sci. 2000, 46, 404–420. [Google Scholar] [CrossRef] [Green Version]
- Naderi, S.; Kilic, K.; Dasci, A. A deterministic model for the transshipment problem of a fast fashion retailer under capacity constraints. Int. J. Prod. Econ. 2020, 227, 107687. [Google Scholar] [CrossRef] [Green Version]
- Narus, J.A.; Anderson, J.C. Rethinking distribution: Adaptive channels. Harv. Bus. Rev. 1996, 74, 112–120. [Google Scholar]
- Li, M.; Petruzzi, N.C.; Zhang, J. Overconfident competing newsvendors. Manag. Sci. 2017, 63, 2637–2646. [Google Scholar] [CrossRef]
- Katok, E.; Pavlov, V. Fairness in supply chain contracts: A laboratory study. J. Oper. Manag. 2013, 31, 129–137. [Google Scholar] [CrossRef]
- Bostian, A.A.; Holt, C.A.; Smith, M. Newsvendor “pull-to-center” effect: Adaptive learning in a laboratory experiment. Manuf. Serv. Oper. Manag. 2008, 10, 590–608. [Google Scholar] [CrossRef] [Green Version]
- Uppari, B.S.; Hasija, S. Modeling newsvendor behavior: A prospect theory approach. Manuf. Serv. Oper. Manag. 2019, 21, 481–500. [Google Scholar] [CrossRef] [Green Version]
- Kirshner, S.N.; Ovchinnikov, A. Heterogeneity of reference effects in the competitive newsvendor problem. Manuf. Serv. Oper. Manag. 2019, 21, 571–581. [Google Scholar] [CrossRef]
- Villa, S.; Castañeda, J.A. Transshipments in supply chains: A behavioral investigation. Eur. J. Oper. Res. 2018, 269, 715–729. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Li, M.; Zhao, X. Transshipment Between Overconfident Newsvendors. Prod. Oper. Manag. 2021, 30, 2803–2813. [Google Scholar] [CrossRef]
- Katok, E.; Villa, S. Centralized or decentralized transfer prices: A behavioral approach for improving supply chain coordination. Manuf. Serv. Oper. Manag. 2022, 24, 143–158. [Google Scholar] [CrossRef]
- Li, S.; Chen, K.Y. The commitment conundrum of inventory sharing. Prod. Oper. Manag. 2020, 29, 353–370. [Google Scholar] [CrossRef]
- Davis, A.M.; Huang, R.; Thomas, D.J. Retailer inventory sharing in two-tier supply chains: An experimental investigation. Manag. Sci. 2022. [Google Scholar] [CrossRef]
- Simon, H.A. Bounded rationality. In Utility and Probability; Palgrave Macmillan: London, UK, 1990; pp. 15–18. [Google Scholar] [CrossRef]
- Camerer, C. Bounded rationality in individual decision making. Exp. Econ. 1998, 1, 163–183. [Google Scholar] [CrossRef]
- Su, X. Bounded rationality in newsvendor models. Manuf. Serv. Oper. Manag. 2008, 10, 566–589. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Wang, X.K.; Peng, J.J.; Wang, J.Q. The differences in hotel selection among various types of travellers: A comparative analysis with a useful bounded rationality behavioural decision support model. Tour. Manag. 2020, 76, 103961. [Google Scholar] [CrossRef]
- Li, S.; Chen, K.Y.; Rong, Y. The behavioral promise and pitfalls in compensating store managers. Manag. Sci. 2020, 66, 4899–4919. [Google Scholar] [CrossRef]
- Sun, L.; Karwan, M.H.; Kwon, C. Generalized bounded rationality and robust multicommodity network design. Oper. Res. 2018, 66, 42–57. [Google Scholar] [CrossRef] [Green Version]
- Ren, H.; Huang, T. Modeling customer bounded rationality in operations management: A review and research opportunities. Comput. Oper. Res. 2018, 91, 48–58. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Siemsen, E. A meta-analysis of newsvendor experiments: Revisiting the pull-to-center asymmetry. Prod. Oper. Manag. 2019, 28, 140–156. [Google Scholar] [CrossRef] [Green Version]
- Hanany, E.; Tzur, M.; Levran, A. The transshipment fund mechanism: Coordinating the decentralized multilocation transshipment problem. Nav. Res. Log. 2010, 57, 342–353. [Google Scholar] [CrossRef] [Green Version]
- McKelvey, R.D.; Palfrey, T.R. Quantal response equilibria for normal form games. Games Econ. Behav. 1995, 10, 6–38. [Google Scholar] [CrossRef]
- Lippman, S.A.; McCardle, K.F. The competitive newsboy. Oper. Res. 1997, 45, 54–65. [Google Scholar] [CrossRef]
- Eppen, G.D. Note—Effects of centralization on expected costs in a multi-location newsboy problem. Manag. Sci. 1979, 25, 498–501. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).