Abstract
The Total Coloring Conjecture (TCC) states that every simple graph G is totally -colorable, where denotes the maximum degree of G. In this paper, we prove that TCC holds for dumbbell maximal planar graphs. Especially, we divide the dumbbell maximal planar graphs into three categories according to the maximum degree: , I-dumbbell maximal planar graphs and II-dumbbell maximal planar graphs. We give the necessary and sufficient condition for I-dumbbell maximal planar graphs, and prove that any I-dumbbell maximal planar graph is totally 8-colorable. Moreover, a linear time algorithm is proposed to compute a total -coloring for any I-dumbbell maximal planar graph.
1. Introduction
All graphs considered in this paper are simple, finite and undirected, and we follow [1] for the terminologies and notations not defined here. For any graph G, we denote by , , and (or simply V, E, and ) the vertex set, the edge set, the maximum degree and the minimum degree of G, respectively. If , then u is said to be a neighbor of v. We use to denote the set of neighbors of v. The degree of v, denoted by , is the number of neighbors of v, i.e., . A k-vertex is a vertex of degree k. Given a set , we denote by the subgraph of G induced by X. A k-cycle is a cycle of length k, and a 3-cycle is usually called a triangle. We use to denote the complete graph of order n. For a disjoint union of G and H, the joining of G and H, denoted by , is the graph obtained by joining every vertex of G to every vertex of H. The joined of a cycle and a single vertex is a wheel with n spokes, denoted by , where and are called the cycle and center of , respectively.
A total k-coloring of G is a mapping such that is for any two adjacent or incident elements . A graph G is totally k-colorable if it admits a total k-coloring. The total chromatic number is the smallest integer k, such that G has a total k-coloring. Behzad [2] and Vizing [3] posed independently the following famous conjecture, known as the Total Coloring Conjecture (TCC).
Conjecture 1.
For any graph G, .
Obviously, the lower bound is trivial. The upper bound is still unproved. To date, TCC has been confirmed for general graphs with [4,5,6,7] and for planar graphs with [8,9,10,11]. Therefore, for planar graphs, the only open case is . Nevertheless, scholars have studied the total coloring of planar graphs under some restricted conditions [12,13,14,15,16,17]. Among these, Sun et al. [13] proved that TCC is true for planar graphs without adjacent triangles. Here, adjacent triangles are two triangles that share a common edge. Zhu and Xu [17] gave a stronger statement that TCC holds for planar graphs G with , if G does not contain any subgraph isomorphic to a 4-fan. Regardless of the results in [13] or in [17], the graph G cannot contain adjacent triangles. This leads us to study the total coloring and total chromatic number of maximal planar graphs, whose faces are all triangles. In [18], we study the total coloring of recursive maximal planar graphs and prove that TCC is true for recursive maximal planar graphs. Moreover, (2,2)-recursive maximal planar graphs are totally -colorable.
A maximal planar graph is a planar graph to which no edges can be added without violating the planarity. Let G be a maximal planar graph and C be a cycle of G with . We call the subgraph of G induced by the vertices on C and the vertices located inside (or outside) C a semi-maximal planar graph based on C, which is denoted by (or ). In fact, a semi-maximal planar graph is a triangulated disc.
According to the vertex coloring, maximal planar graphs can be partitioned into three categories: purely tree-colorable, purely cycle-colorable and impure colorable, refer to [19]. In [20], Xu et al. proposed the purely tree-colorable graphs conjecture, which states that a maximal planar graph is purely tree-colorable if and only if it is the icosahedron or a dumbbell maximal planar graph. They further studied the structures and properties of dumbbell maximal planar graphs in [19]. Then, what is the total coloring of dumbbell maximal planar graphs? This problem has aroused our concern.
We aim to study the total coloring of dumbbell maximal planar graphs in this paper. The remainder of this paper is organized as follows. In Section 2, we introduce the dumbbell transformation and study the structures and properties of dumbbell maximal planar graphs. In particular, we classify the dumbbell maximal planar graphs into three categories. In Section 3, we prove that any dumbbell maximal planar graph is totally -colorable. In Section 4, we propose an algorithm with linear time complexity to compute a total -coloring for any I-dumbbell maximal planar graph. In Section 5, we make a conclusion for the paper.
2. Dumbbell Maximal Planar Graphs
We study the structures and properties of dumbbell maximal planar graphs in this section. Before this, we need to introduce the dumbbell transformation given by Xu [19].
2.1. Dumbbell Transformation
In order to give the dumbbell transformation, we introduce the extending 3-wheel and 4-wheel operations first.
The extending 3-wheel operation. The extending 3-wheel operation acts on a triangle of a maximal planar graph, specifically, adding a new vertex in the face and joining it to every vertex of the triangular face, as shown in Figure 1.
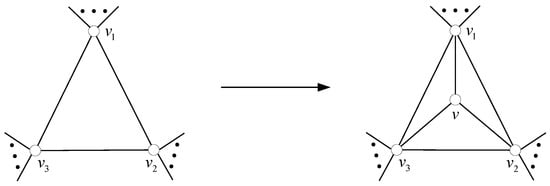
Figure 1.
The extending 3-wheel operation.
The extending 4-wheel operation. The object of the extending 4-wheel operation is a path of length 2. Specifically, an extending 4-wheel operation based on path means: split the vertex into and , and split the edges and into and , respectively. Hence, the vertices and form a cycle of length 4. Then, add a new vertex x in this cycle and make x adjacent to vertices and , respectively. The process is shown in Figure 2.
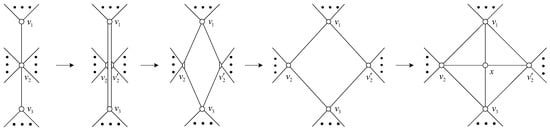
Figure 2.
The extending 4-wheel operation.
A dumbbell is a graph consisting of two triangles and with exactly one common vertex u, and it is denoted by , as shown in the left of Figure 3. Obviously, a 4-wheel contains exactly two dumbbells, as shown in the right of Figure 3, where and . In this paper, dumbbells considered are ones contained in a 4-wheel without special assertion.
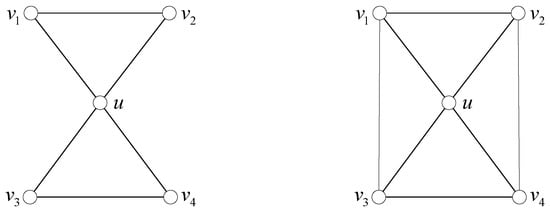
Figure 3.
The dumbbell and a 4-wheel.
The dumbbell transformation. For a given dumbbell . First, add two 3-vertices and on the two triangular faces of X, respectively. Then, implement the extending 4-wheel operation on path , the newly added 4-vertex is denoted by v, as shown in Figure 4.
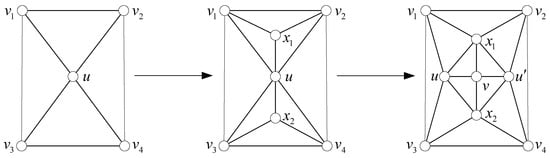
Figure 4.
The dumbbell transformation.
Xu et al. [20] gave the following theorem:
Theorem 1.
Let G be a maximal planar graph with a 4-wheel . Then the graphs obtained from G by implementing the dumbbell transformations on two dumbbells of are isomorphic.
2.2. Structure and Property of Dumbbell Maximal Planar Graphs
The first maximal planar graph with order 9, denoted by , is shown in Figure 5 and is called a dumbbell maximal planar graph, which is the dumbbell maximal planar graph with the minimum order. A graph is a dumbbell maximal planar graph if one of the following conditions is satisfied: (1) it is isomorphic to ; (2) it can be obtained from another dumbbell maximal planar graph by the dumbbell transformation. In general, if is a dumbbell maximal planar graph, we call the maximal planar graph obtained from by implementing a dumbbell transformation a dumbbell maximal planar graph. Implement the dumbbell transformation on each unidentical 4-wheel in , then we can obtain dumbbell maximal planar graphs with order . As shown in Figure 5, we give the dumbbell maximal planar graphs with orders 9, 13, 17 and 21, respectively.
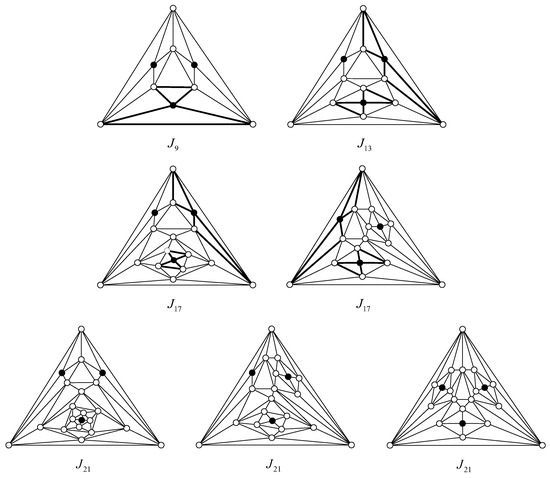
Figure 5.
The dumbbell maximal planar graphs with orders 9, 13, 17 and 21.
contains exactly three vertices of degree 4. By the definition of dumbbell maximal planar graphs, Xu et al. [20] obtained the following observation.
Observation 1.(1) Any dumbbell maximal planar graph has order , where ; (2) Any dumbbell maximal planar graph contains exactly three vertices of degree 4.
We give the following theorem on the maximum degrees of dumbbell maximal planar graphs.
Theorem 2.
Except for , the maximum degree of a dumbbell maximal planar graph is 6 or 7.
Proof.
Obviously, the maximum degree of is 5. As shown in Figure 4, for each dumbbell transformation, the degree of each vertex on the cycle of the original 4-wheel is increased by 1, and that of the new 4-wheel is 5. As shown in Figure 5, the maximum degree of is 6; the two non-isomorphic dumbbell maximal planar graphs , which are obtained from by implementing the dumbbell transformation on the two unidentical 4-wheels, have the maximum degrees 6 and 7, respectively; the three dumbbell planar graphs obtained from have the maximum degree 6, 7 and 7, respectively. It is observed that the degrees of vertices on the wheels of all 4-wheels in these three dumbbell maximal planar graphs with order 21 are 5 and 6, and the maximum degree of each dumbbell maximal planar graph obtained by implementing the dumbbell transformation does not exceed 7. By analogy, the maximum degree of a dumbbell maximal planar graph with higher order is always 6 or 7. □
For the dumbbell maximal planar graph with maximum degree 6, we have
Theorem 3.
The maximum degree of a dumbbell maximal planar graph G is 6 if and only if G is obtained from by continuously implementing the dumbbell transformation, and each transformation is implemented on the new 4-wheel generated by the previous transformation (The first dumbbell transformation is implemented on an arbitrary 4-wheel in ).
The proof of Theorem 3 is obvious and therefore omitted.
We call the dumbbell maximal planar graphs with maximum degree 6 described in Theorem 3 I-dumbbell maximal planar graphs (The I-dumbbell maximalplanar graphs we define here are dumbbell maximal planar graphs of maximum degree 6, so of course is not included) and dumbbell maximal planar graphs with maximum degree 7 II-dumbbell maximal planar graphs. For I-dumbbell maximal planar graphs, we obtain the following observation.
Observation 2.
For any I-dumbbell maximal planar graph, the degrees of vertices on the cycle of the newly generated 4-wheel are all 5. Furthermore, the other two 4-wheels do not have this property.
Figure 6 shows the generation process of I-dumbbell maximal planar graphs.
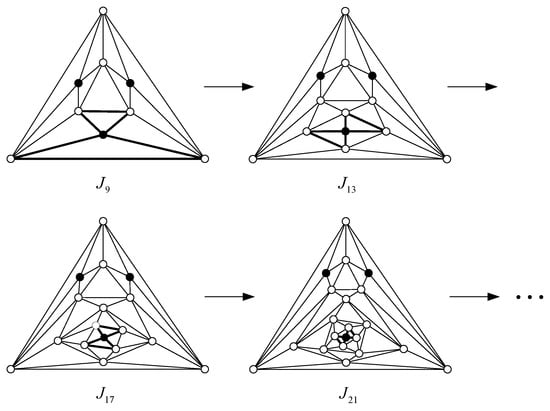
Figure 6.
The schematic diagram of the generation process of I-dumbbell maximal planar graphs.
3. Total Coloring of Dumbbell Maximal Planar Graphs
In Section 2, the dumbbell transformation and dumbbell maximal planar graphs were introduced. In this section, we study the total coloring of dumbbell maximal planar graphs based on structural characteristics.
From the previous section, we know that any dumbbell maximal planar graph has exactly 3 vertices of degree 4, and the maximum degree of a dumbbell maximal planar graph is 6 or 7, except for . Furthermore, we draw an important conclusion about the structure of the dumbbell maximal planar graphs.
According to the maximum degree, dumbbell maximal planar graphs can be divided into the following three categories: , I-dumbbell maximal planar graphs and II-dumbbell maximal planar graphs. In Figure 7, we give a total 7-coloring of . Sanders and Zhao [11] proved that planar graphs with are totally 9-colorable. Therefore, we only need to consider dumbbell maximal planar graphs with maximum degree 6, that is, I-dumbbell maximal planar graphs.
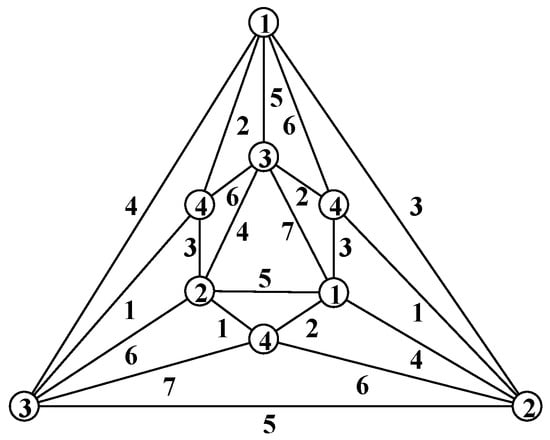
Figure 7.
A total 7-coloring of .
Theorem 4.
Any I-dumbbell maximal planar graph is totally 8-colorable.
Proof.
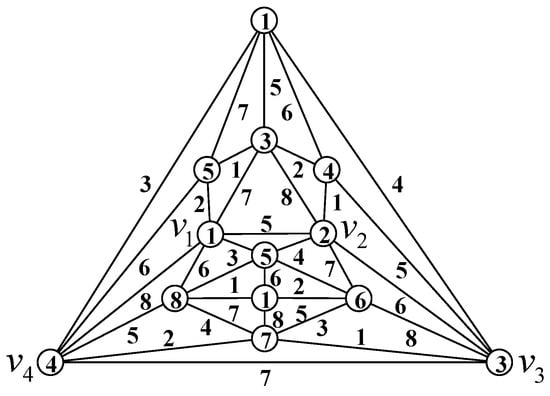
is the I-dumbbell maximal planar graph with the minimum order, and is totally 8-colorable, as shown in Figure 8.

Figure 8.
A total 8-coloring of .
Since the I-dumbbell maximal planar graphs are obtained from by continuously implementing the dumbbell transformation at a unique 4-wheel only, without loss of generality, we assume that all I-dumbbell maximal planar graphs are obtained by implementing the dumbbell transformation at the 4-wheel located at the bottom of , as shown in Figure 6. For convenience, we denote the cycle of the 4-wheel located at the bottom of by . Then, for any I-dumbbell maximal planar graph G, , where and are the two semi-maximal planar graphs based on . In the following, we give a total coloring scheme of any I-dumbbell maximal planar graph G. We color the same way in and color according to the parity of the number of dumbbell transformations, which is denoted by l.
When l is odd, the coloring scheme is:
The colors of vertices on the cycle of the initial 4-wheel are 1, 2, 3 and 4, and the colors of the edges are 5, 6, 7 and 8, respectively;
After the first dumbbell transformation, starting from the vertex opposite the edge colored with 5, color the vertices on the cycle of newly generated 4-wheel with 5, 6, 7 and 8, and the corresponding edges with 1, 2, 3 and 4 in clockwise order;
The colors of edges between the newly generated 4-wheel and the initial 4-wheel are 3, 4, 7, 8, 1, 2, 5 and 6 in clockwise order;
After the second dumbbell transformation, starting from the vertex opposite the edge colored with 1, color the vertices on the cycle of newly generated 4-wheel with 1, 2, 3 and 4, and the corresponding edges with 5, 6, 7 and 8, in clockwise order;
The colors of the edges between the newly generated 4-wheel and the previous 4-wheel are 7, 8, 1, 4, 5, 6, 3 and 2 in clockwise order;
After the i-th () dumbbell transformation, the colors of vertices and edges on the cycle of the newly generated 4-wheel, and the colors of edges between the newly generated 4-wheel and the previous 4-wheel, are the same as the first dumbbell transformation when i is odd; the colors of vertices and edges on the cycle of the newly generated 4-wheel, and the colors of edges between the newly generated 4-wheel and the previous 4-wheel, are the same as the second dumbbell transformation when i is even;
After the last dumbbell transformation, we specify the color of the wheel center as 1, and the colors of the spokes as 6, 5, 8 and 7 from whose end point is colored with 5 in clockwise order. Of course, the readers can also use other appropriate colors;
When l is even, the coloring scheme is similar to that when l is odd, except that the color of the wheel center is 5, and the colors of the spokes are 3, 4, 2 and 1 from whose end point is colored with 1 in clockwise order;
So, we obtain a total 8-coloring scheme of any I-dumbbell maximal planar graph, and the proof is completed. □
As shown in Figure 9, we give the coloring scheme for (on the left) and (on the right), respectively.
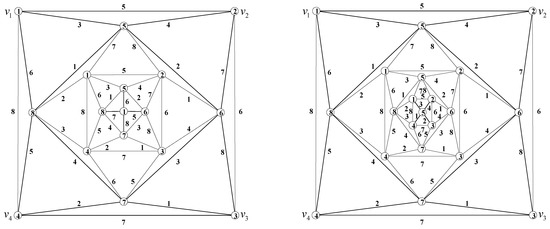
Figure 9.
The coloring diagram for and .
Therefore, we obtain the following theorem.
Theorem 5.
The TCC holds for dumbbell maximal planar graphs.
4. Total Coloring Algorithm for I-Dumbbell Maximal Planar Graphs
In this section an algorithm with linear time complexity is proposed, which computes a total -coloring for any I-dumbbell maximal planar graph. It is known that an arbitrary I-dumbbell maximal planar graph can be obtained from by continuously implementing the dumbbell transformation on the newly generated 4-wheel. We introduce the concept of dumbbell-recursive generation sequence to formalize the generation process.
Definition 1
(Dumbbell-Recursive Generation Sequence). Let be an I-dumbbell maximal planar graph with as the newly generated 4-wheel, where and denote vertices on the cycle and denotes the wheel center, respectively. Starting from , each time we implement the dumbbell transformation, an I-dumbbell maximal planar graph is obtained, where . Then, the dumbbell-recursive generation sequence of is defined as .
Now, we give a total coloring algorithm for I-dumbbell maximal planar graphs, as shown in the following Algorithm 1, which consists of two stages.
| Algorithm 1 Total Coloring Algorithm for I-dumbbell Maximal Planar Graph |
|
In the first stage, given an arbitrary I-dumbbell maximal planar graph , we compute the dumbbell-recursive generation sequence . As mentioned in Observation 2, we can easily find the newly generated 4-wheel according to the degrees of vertices on the cycle. Then, the inverse process of dumbbell transformation is implemented to obtain the previous dumbbell maximal planar graph. By repeating the procedure and storing the structure information, we obtain the dumbbell-recursive generation sequence.
In the second stage, we give a total -coloring of based on the dumbbell-recursive generation sequence . More precisely, for with and , let be the color set.
The dictionary structure is used to store the total coloring scheme, where , , . Firstly, take out the initial graph and color its vertices and edges as shown in Figure 8, and store the corresponding coloring information in U. Then, take out the generation operation information stored in in turn. The dumbbell transformation is implemented and the coloring information of the newly generated is stored to U according to l’s parity. Finally, a total -coloring of any I-dumbbell maximal planar graph can be obtained iteratively.
During the execution of Stage 1 and Stage 2, the order of varies by 4 at each step. Furthermore, the number of sequence generation and coloring operations is constant at each step. Therefore, the time complexity of this algorithm is linear.
5. Conclusions
Total coloring is an important and representative problem in the field of graph coloring. Even for planar graphs, the total coloring conjecture is still open for the case . In this paper, we prove that the Total Coloring Conjecture holds for dumbbell maximal planar graphs, which are generated by implementing the dumbbell transformation continuously. According to the maximum degree, we divide the dumbbell maximal planar graphs into three categories: , I-dumbbell maximal planar graphs and II-dumbbell maximal planar graphs. Furthermore, we give the necessary and sufficient condition for I-dumbbell maximal planar graphs and prove that any I-dumbbell maximal planar graph is totally 8-colorable. Moreover, an algorithm with linear time complexity is presented to compute a total -coloring of any I-dumbbell maximal planar graph. For future work, we will further focus on the relationship between the structure and coloring of dumbbell maximal planar graphs and discuss the condition in which the dumbbell maximal planar graphs are totally -colorable.
Author Contributions
Creation and conceptualization of the idea, Y.Z. and J.X.; writing—original draft preparation, Y.Z. and D.Z.; writing—review and editing, Y.Z. and M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Key R&D Program of China No. 2019YFA0706 401 and the National Natural Science Foundation of China No. 62172014, No. 62172015, No. 61872166 and No. 62002002.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bondy, J.A.; Murty, U.S.R. Graph Theory with Applications; MacMillan: London, UK, 1976. [Google Scholar]
- Behzad, M. Graphs and Their Chromatic Numbers. Ph.D. Thesis, Michigan State University, East Lansing, MI, USA, 1965. [Google Scholar]
- Vizing, V.G. On an estimate of the chromatic class of a p-graph. Discret. Anal. 1964, 3, 25–30. [Google Scholar]
- Rosenfeld, M. On the total coloring of certain graphs. Isr. J. Math. 1971, 9, 396–402. [Google Scholar] [CrossRef]
- Vijayaditya, N. On total chromatic number of a graph. J. Lond. Math. Soc. 1971, 2, 405–408. [Google Scholar] [CrossRef]
- Kostochka, A.V. The total coloring of a multigraph with maximal degree 4. Discret. Math. 1977, 17, 161–163. [Google Scholar] [CrossRef]
- Kostochka, A.V. The total chromatic number of any multigraph with maximum degree five is at most seven. Discret. Math. 1996, 162, 199–214. [Google Scholar] [CrossRef]
- Borodin, O.V. On the total coloring of planar graphs. J. Reine Angew. Math. 1989, 394, 180–185. [Google Scholar]
- Jensen, T.R.; Toft, B. Graph Coloring Problems; Wiley: Hoboken, NJ, USA, 1995. [Google Scholar]
- Yap, H.P. Total Colourings of Graphs; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Sanders, D.P.; Zhao, Y. On total 9-coloring planar graphs of maximum degree seven. J. Graph Theory 1999, 31, 67–73. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Shangguan, M.L.; Li, Q. On total chromatic number of planar graphs without 4-cycles. Sci. China 2007, 50, 81–86. [Google Scholar] [CrossRef]
- Sun, X.Y.; Wu, J.L.; Wu, Y.W.; Hou, J.F. Total colorings of planar graphs without adjacent triangles. Discret. Math. 2009, 309, 202–206. [Google Scholar] [CrossRef][Green Version]
- Roussel, N. Local condition for planar graphs of maximum degree 6 to be total 8-colorable. Taiwan. J. Math. 2011, 15, 87–99. [Google Scholar] [CrossRef]
- Hou, J.F.; Liu, B.; Liu, G.Z.; Wu, J.L. Total coloring of planar graphs without 6-cycles. Discret. Appl. Math. 2011, 159, 157–163. [Google Scholar] [CrossRef]
- Wu, Q.; Lu, Q.L.; Wang, Y.Q. (Δ + 1)-total-colorability of plane graphs of maximum degree ≥6 with neither chordal 5-cycle nor chordal 6-cycle. Inform. Process. Lett. 2011, 111, 767–772. [Google Scholar] [CrossRef]
- Zhu, E.Q.; Xu, J. A sufficient condition for planar graphs with maximum degree 6 to be totally 8-colorable. Discret. Appl. Math. 2017, 223, 148–153. [Google Scholar] [CrossRef]
- Zhou, Y.Y.; Zhao, D.Y.; Ma, M.Y.; Xu, J. Total coloring of recursive maximal planar graphs. Theor. Comput. Sci. 2022, 909, 12–18. [Google Scholar] [CrossRef]
- Xu, J. Theory on structure and coloring of maximal planar graphs (3): Purely tree-colorable and uniquely 4-colorable maximal planar graph conjectures. J. Electron. Inf. Technol. 2016, 38, 1328–1363. [Google Scholar]
- Xu, J.; Li, Z.P.; Zhu, E.Q. On purely tree-colorable planar graphs. Inform. Process. Lett. 2016, 116, 532–536. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).