Mathematical Model of Pest Control Using Different Release Rates of Sterile Insects and Natural Enemies
Abstract
:1. Introduction
2. Related Works
3. Pest Control Model
3.1. Assumptions
- The plant grows logistically with intrinsic growth rate in an environment with carrying capacity k.
- Only pest consumes the plant with consumption rate for fertile insects and for sterile insects. Similar to [39], the plant-pest interaction is following a predator-prey Holling type II function with handling time and , and constant of half-saturation m. Thus, response functions of plants consumption by fertile and sterile insects are, respectively, given by and , where
- Natural enemies consume both fertile and sterile pests with consumption rate and , respectively, following a Holling type II response function.
- Conversion efficiencies of plant consumption by fertile insects and sterile insects are, respectively, given by and . Since the number of sterile insects is small, then is also small. Here, we assume . Conversion efficiencies of insect consumption by natural enemies is . We also assume . It means that consuming one insect can produce at most one predator.
- No migration activity for the population involved in the model. The recruitment happens only from reproductive process or manual release.
- Introduction of sterile pest insects reduces the birth rate of pest. The intrinsic birth rate is , and by the release of sterile pest insects, it decreases to . As in [43,44], we further assume that the growth of fertile insect depends on the availability of plant as the food resource. Thus, the pest birth rate r is given by
- Biological control agents have the same survivability as wild agents. However, there are three causes of pest death: natural cause (, ), self-interaction (, ) and fertile-sterile interaction (). Those of natural enemy be denoted by and .
- Sterile insects are released depending on the population of fertile insects with rate , while natural enemies are introduced depending on the population of fertile and sterile insects with rate .
3.2. Mathematical Model
3.3. Release Rates
3.4. Control Performance Index
4. Analysis of Optimal Control
4.1. Existence
4.2. Necessary Conditions
5. Illustrative Example
5.1. Numerical Methods
- Set the initial values of state variable , adjoint variable , and control variable as well as tolerance level of convergence .
- Using terminal value and state variable obtained from previous step, solve p backwardly according to (26)–(29) and make updating .
- Using X and p obtained from previous steps, calculate according to control laws (22) and (23). Update the value of control variables as the average between current and updated values.
- Return to step 2 until convergence is reached: .
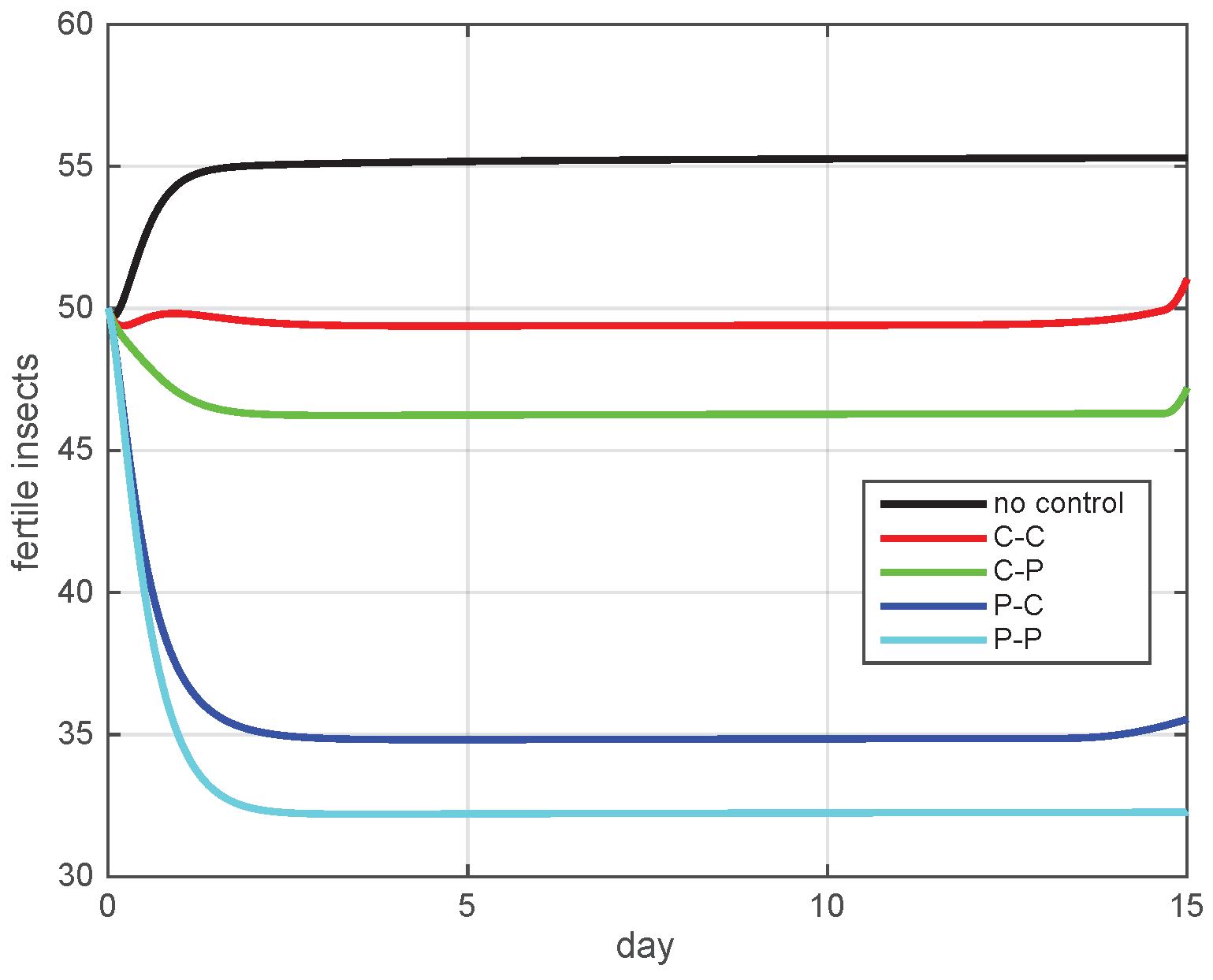
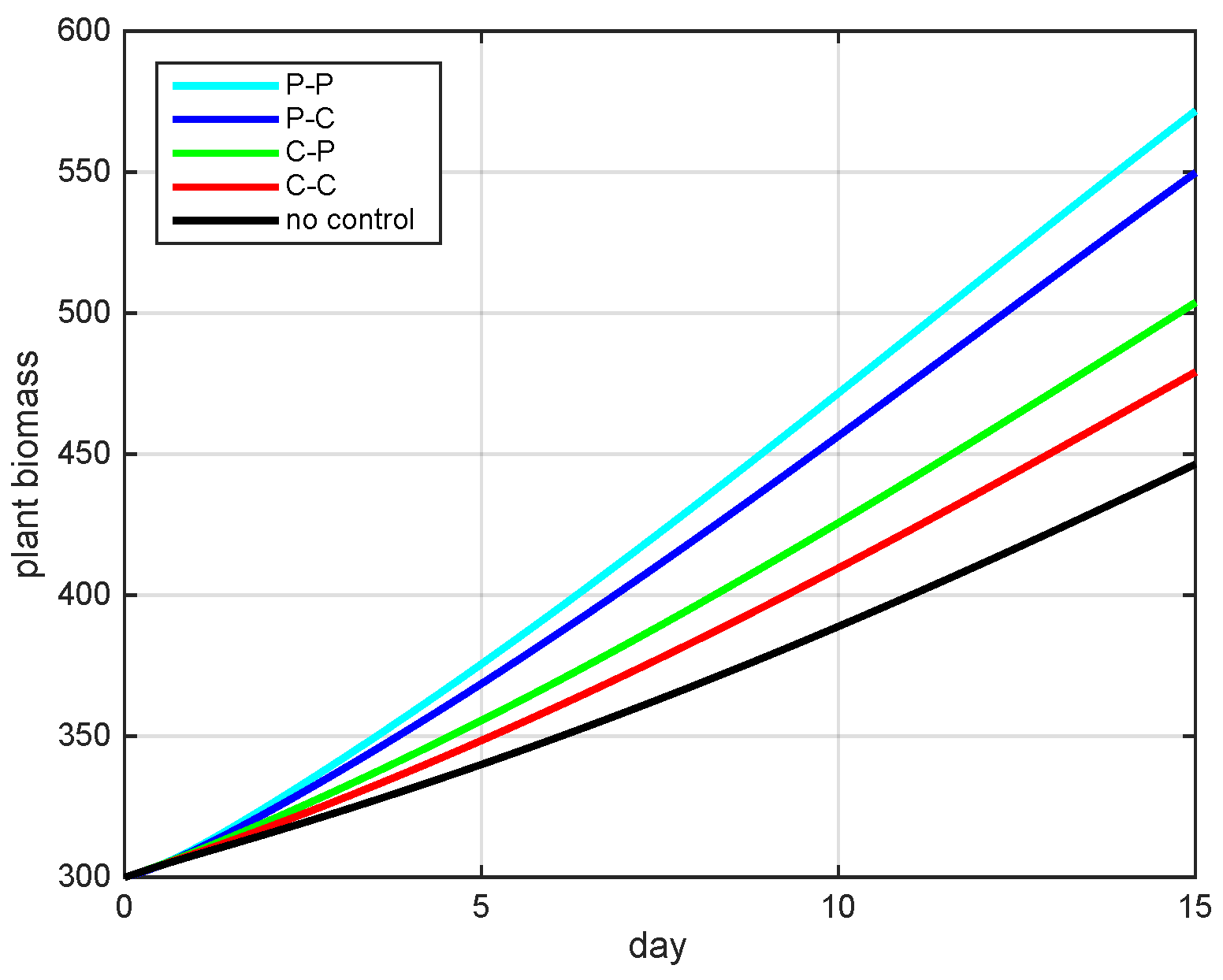
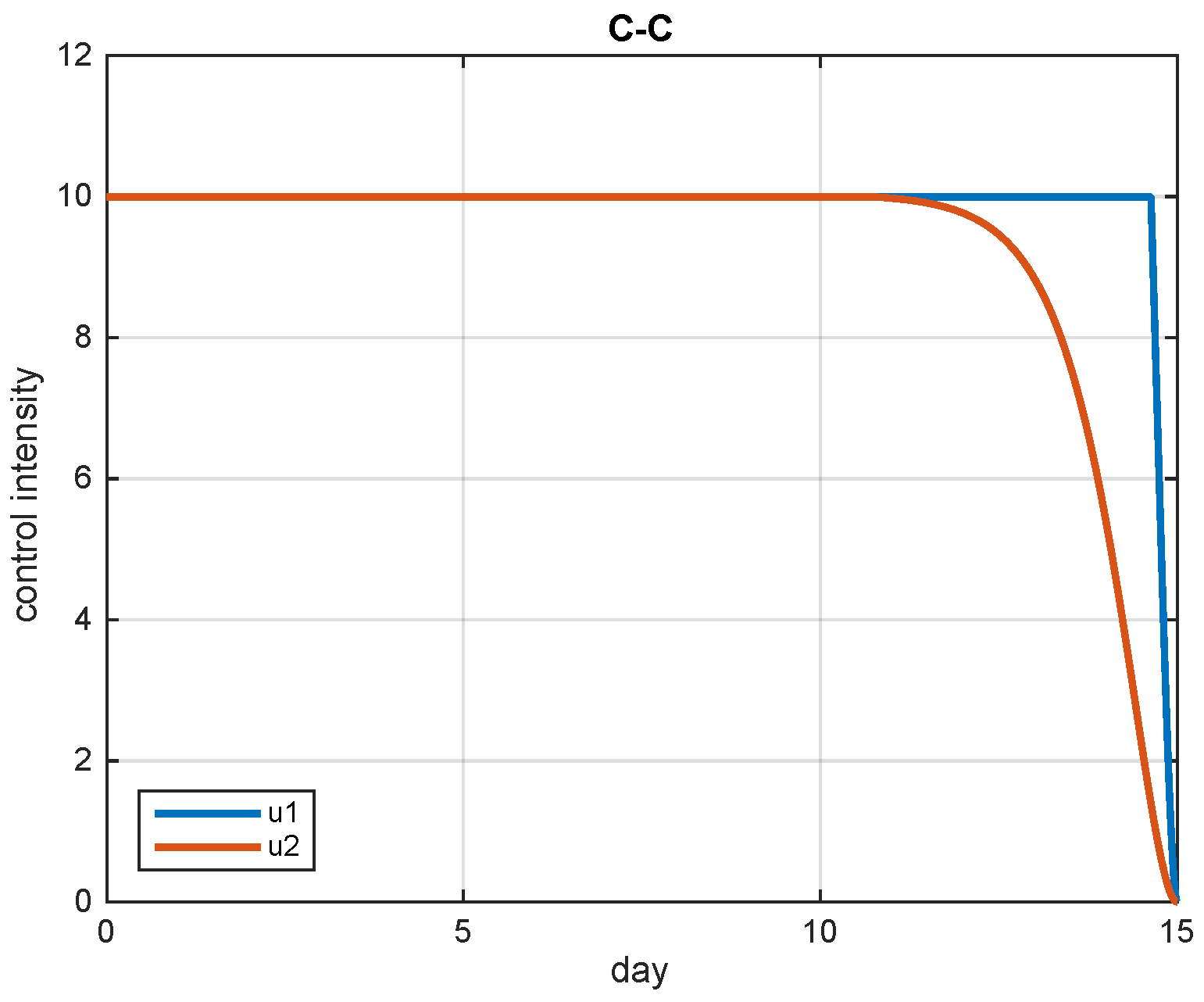
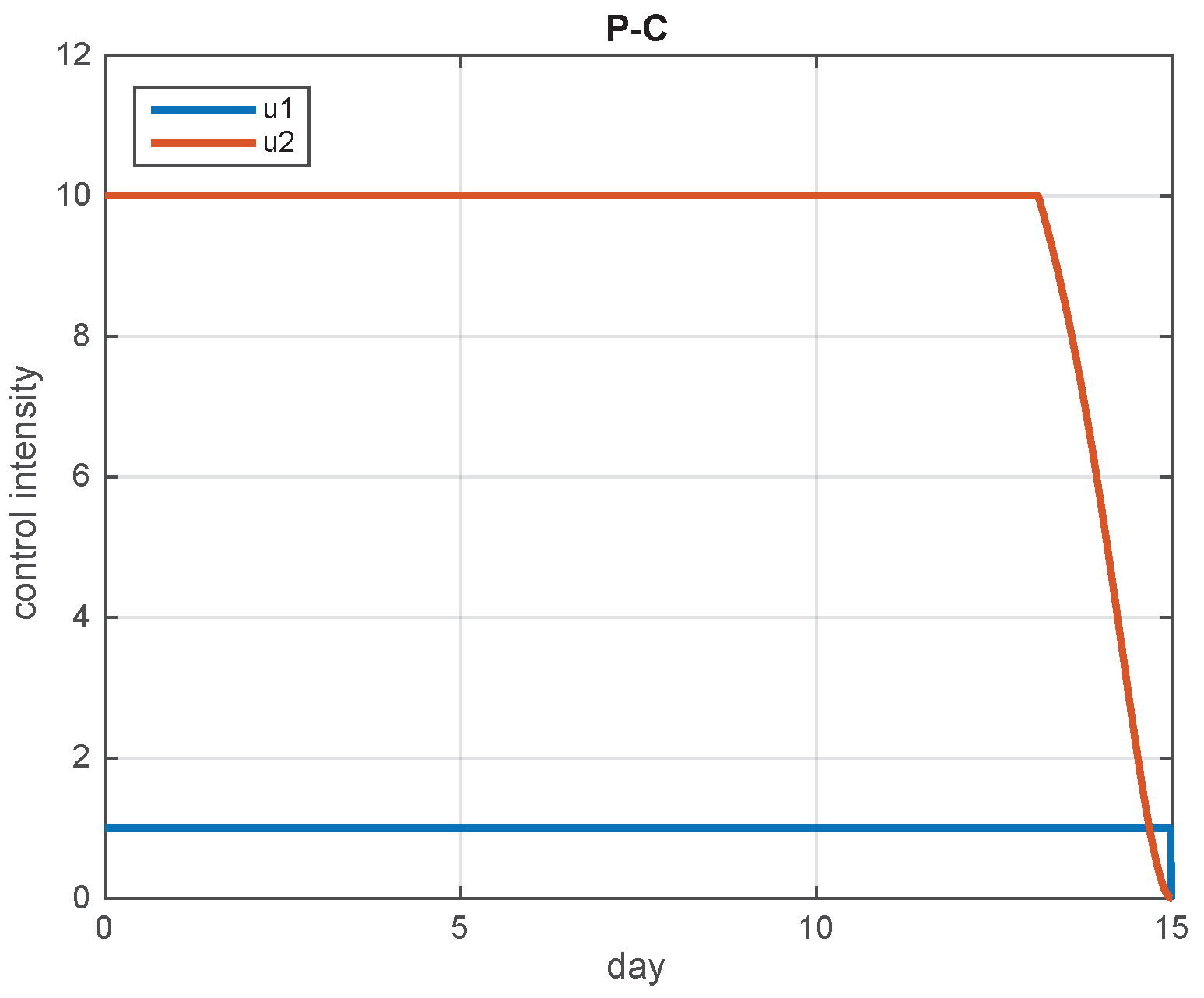
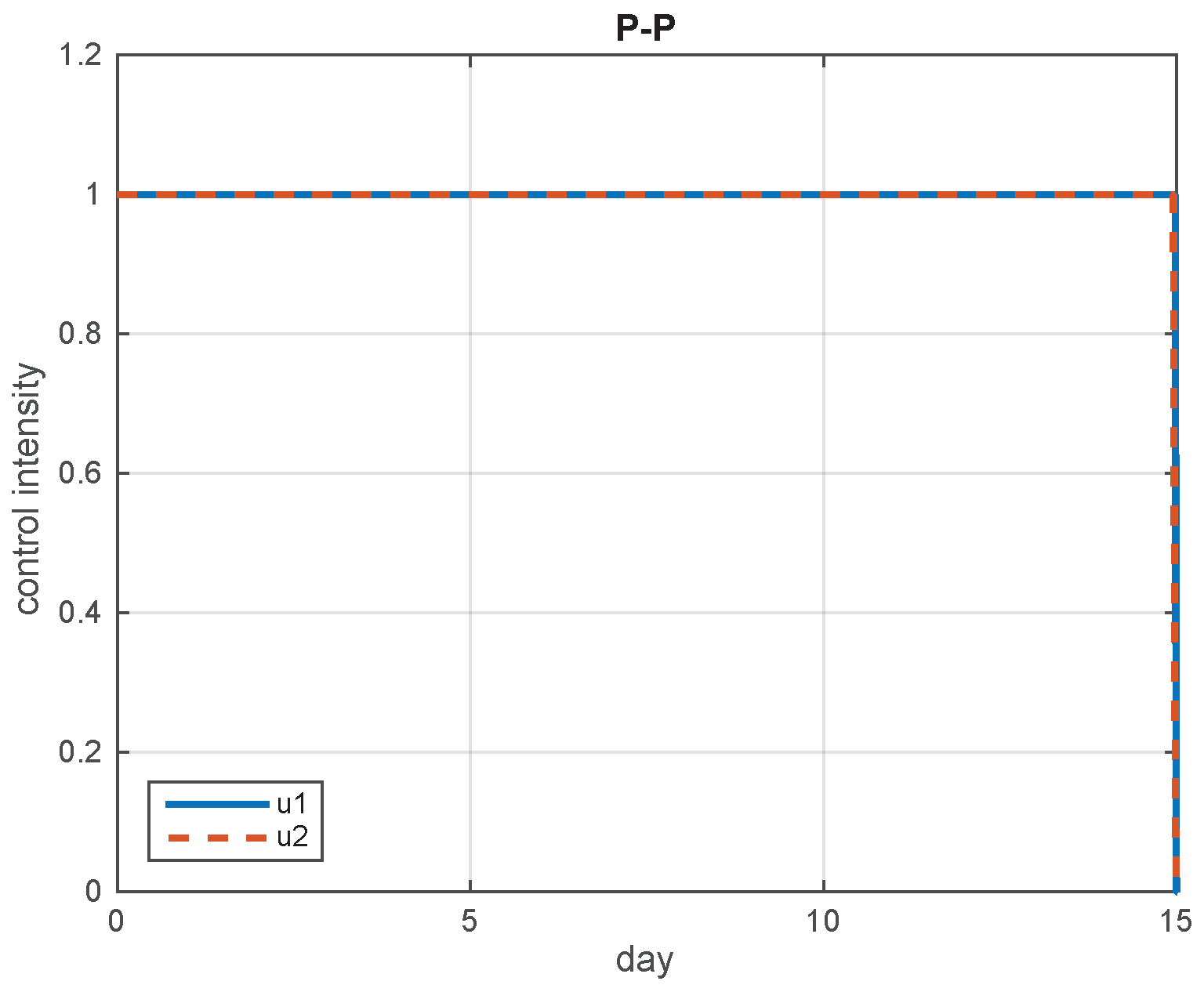
5.2. Simulation Results
5.3. The Most Cost-Effective Strategy
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACER | Average Cost-Effectiveness Ratio |
| C-C | Constant sterile insect release rate, Constant natural enemy release rate |
| CEA | Cost Effectiveness Analysis |
| C-P | Constant sterile insect release rate, Proportional natural enemy release rate |
| FAO | Food and Agriculture Organization |
| ICER | Incremental Cost-Effectiveness Ratio |
| IPM | Integrated Pest Management |
| P-C | Proportional sterile insect release rate, Constant natural enemy release rate |
| P-P | Proportional sterile insect release rate, Proportional natural enemy release rate |
| SIT | Sterile Insect Technique |
References
- Savary, S.; Willocquet, L.; Pethybridge, S.J.; Esker, P.; McRoberts, N.; Nelson, A. The global burden of pathogens and pests on major food crops. Nat. Ecol. Evol. 2019, 3, 430–439. [Google Scholar] [CrossRef] [PubMed]
- Skendzic, S.; Zovko, M.; Zivkovic, I.P.; Lesic, V.; Lemic, D. The impact of climate change on agricultural insect pests. Insects 2021, 12, 440. [Google Scholar] [CrossRef] [PubMed]
- Deutsch, C.A.; Tewksbury, J.J.; Tigchelaar, M.; Battisti, D.S.; Merrill, S.C.; Huey, R.B.; Naylor, R.L. Increase in crop losses to insect pests in a warming climate. Science 2018, 361, 916–919. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- IPPC Secretariat. Scientific Review of the Impact of Climate Change on Plant Pests—A Global Challenge to Prevent and Mitigate Plant Pest Risks in Agriculture, Forestry and Ecosystems; FAO: Rome, Italy, 2021. [Google Scholar] [CrossRef]
- Abrol, D.P. Integrated Pest Management: Current Concepts and Ecological Perspective; Elsevier: Oxford, UK, 2014. [Google Scholar] [CrossRef] [Green Version]
- Lopez, O.; Fernandez-Bolanos, J. Green Trends in Insect Control; RSC Publishing: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Liang, Y.; Luo, M.; Fu, X.; Zheng, L.; Wei, H. Mating disruption of Chilo suppressalis from sex pheromone of another pyralid rice pest Cnaphalocrocis medinalis (Lepidoptera: Pyralidae). J. Insect Sci. 2020, 20, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Luo, Z.; Magsi, F.H.; Li, Z.; Cai, X.; Bian, L.; Liu, Y.; Xin, Z.; Xiu, C.; Chen, Z. Development and evaluation of sex pheromone mass trapping technology for Ectropis grisescens: A potential Integrated Pest Management strategy. Insects 2020, 11, 15. [Google Scholar] [CrossRef] [Green Version]
- Bourtzis, K.; Vreysen, M.J.B. Sterile Insect Technique (SIT) and its applications. Insects 2021, 12, 638. [Google Scholar] [CrossRef]
- Horrocks, K.J.; Avila, G.A.; Holwell, G.I.; Suckling, D.M. Irradiation-induced sterility in an egg parasitoid and possible implications for the use of biological control in insect eradication. Sci. Rep. 2021, 11, 12326. [Google Scholar] [CrossRef] [PubMed]
- Blomme, G.; Ocimati, W.; Sivirihauma, C.; Vutseme, L.; Mariamu, B.; Kamira, M.; van Schagen, B.; Ekboir, J.; Ntamwira, J. A control package revolving around the removal of single diseased banana stems is effective for the restoration of Xanthomonas wilt infected fields. Eur. J. Plant Pathol. 2017, 149, 385–400. [Google Scholar] [CrossRef]
- Hajek, A. Natural Enemies: An Introduction to Biological Control; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Van Driesche, R.G.; Abell, K. Classical and augmentative biological control. Encycl. Ecol. 2008, 575–582. [Google Scholar] [CrossRef]
- Horrocks, K.J.; Avila, G.A.; Holwell, G.I.; Suckling, D.M. Integrating sterile insect technique with the release of sterile classical biocontrol agents for eradication: Is the Kamikaze Wasp Technique feasible? BioControl 2020, 65, 257–271. [Google Scholar] [CrossRef]
- Lu, M.-C.; Chen, H.-R.; Wu, Y.-H. Current status and future perspectives on natural enemies for pest control in Taiwan. Biocontrol Sci. Technol. 2018, 28, 953–960. [Google Scholar] [CrossRef]
- Martin, E.A.; Reineking, B.; Seo, B.; Steffan-Dewenter, I. Natural enemy interactions constrain pest control in complex agricultural landscapes. Proc. Natl. Acad. Sci. USA 2013, 110, 5534–5539. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perez-Alvarez, R.; Nault, B.A.; Poveda, K. Effectiveness of augmentative biological control depends on landscape context. Sci. Rep. 2019, 9, 8664. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Colombo, R.M.; Rossi, E. A modeling framework for biological pest control. Math. Biosci. Eng. 2020, 17, 1413–1427. [Google Scholar] [CrossRef]
- Yadav, S.; Kumar, V. Study of a prey–predator model with preventing crop pest using natural enemies and control. AIP Conf. Proc. 2021, 2336, 020002. [Google Scholar] [CrossRef]
- Kumar, S.; Ahmad, S.; Siddiqi, M.I.; Raza, K. Mathematical model for plant-insect interaction with dynamic response to PAD4-BIK1 interaction and effect of BIK1 inhibition. BioSystems 2019, 175, 11–23. [Google Scholar] [CrossRef]
- Wan, N.F.; Ji, X.Y.; Jiang, J.X.; Li, B. A modelling methodology to assess the effect of insect pest control on agro-ecosystems. Sci. Rep. 2015, 5, 9727. [Google Scholar] [CrossRef] [Green Version]
- Sassu, F.; Nikolouli, K.; Caravantes, S.; Taret, G.; Pereira, R.; Vreysen, M.J.B.; Stauffer, C.; Caceres, C. Mass-rearing of Drosophila suzukii for Sterile Insect Technique application: Evaluation of two oviposition systems. Insects 2019, 10, 448. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.-X.; Su, Z.-P.; Liu, H.-H.; Lu, S.-P.; Ma, B.; Zhao, Y.; Hou, Y.-M.; Shi, Z.-H. The Effect of gut bacteria on the physiology of red palm weevil, Rhynchophorus ferrugineus Olivier and their potential for the control of this pest. Insects 2021, 12, 594. [Google Scholar] [CrossRef]
- Yan, Y.; Williamson, M.E.; Scott, M.J. Using moderate transgene expression to improve the genetic sexing system of the Australian sheep blow fly Lucilia cuprina. Insects 2020, 11, 797. [Google Scholar] [CrossRef]
- Gato, R.; Menendez, Z.; Prieto, E.; Argiles, R.; Rodriguez, M.; Baldoquin, W.; Hernandez, Y.; Perez, D.; Anaya, J.; Fuentes, I.; et al. Sterile Insect Technique: Successful suppression of an Aedes aegypti field population in Cuba. Insects 2021, 12, 469. [Google Scholar] [CrossRef]
- Patinvoh, R.; Susu, A. Mathematical modelling of sterile insect technology for mosquito control. Adv. Entomol. 2014, 2, 180–193. [Google Scholar] [CrossRef] [Green Version]
- Knipling, E.F. The Basic Principles of Insect Population Suppression and Management; U.S. Department of Agriculture: Washington, DC, USA, 1979.
- Barclay, H.J. Models for pest control: Complementary effects of periodic releases of sterile pests and parasitoids. Theor. Popul. Biol. 1987, 32, 76–89. [Google Scholar] [CrossRef]
- Crowder, D.W. Impact of release rates on the effectiveness of augmentative biological control agents. J. Insect Sci. 2007, 7, 15. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharyya, R.; Mukhopadhyay, B. Mathematical study of a pest control model incorporating sterile insect technique. J. Nat. Resour. Model. 2014, 27, 61–79. [Google Scholar] [CrossRef]
- Fitri, I.R.; Hanum, F.; Kusnanto, A.; Bakhtiar, T. Optimal pest control strategies with cost-effectiveness analysis. Sci. World J. 2021, 2021, 6630193. [Google Scholar] [CrossRef]
- Sun, K.; Zhang, T.; Tian, Y. Dynamics analysis and control optimization of a pest management predator-prey model with an integrated control strategy. Appl. Math. Comput. 2017, 292, 253–271. [Google Scholar] [CrossRef]
- Yu, T.; Tian, Y.; Guo, H.; Song, X. Dynamical analysis of an integrated pest management predator-prey model with weak Allee effect. J. Biol. Dyn. 2019, 13, 218–244. [Google Scholar] [CrossRef]
- Huang, L.; Chen, X.; Tan, X.; Chen, X.; Liu, X. A stochastic predator-prey model for integrated pest management. Adv. Diff. Equ. 2019, 2019, 360. [Google Scholar] [CrossRef] [Green Version]
- Mandal, D.S.; Samanta, S.; Alzahrani, A.K.; Chattopadhyay, J. Study of a predator-prey model with pest management perspective. J. Biol. Syst. 2019, 27, 309–336. [Google Scholar] [CrossRef]
- Mandal, D.S.; Chekroun, A.; Samanta, S.; Chattopadhyay, J. A mathematical study of a crop-pest-natural enemy model with Z-type control. Math. Comput. Simul. 2021, 187, 468–488. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, T.; Sun, K. Dynamics analysis of a pest management prey–predator model by means of interval state monitoring and control. Nonlinear Anal. Hybrid Syst. 2017, 23, 122–141. [Google Scholar] [CrossRef]
- Mathur, K.S. An eco-epidemic pest-natural enemy SI model in two patchy habitat with impulsive effect. Int. J. Appl. Comput. Math. 2016, 3, 2671–2685. [Google Scholar] [CrossRef]
- Wang, X.; Tian, Y.; Tang, S. A Holling type II pest and natural enemy model with density dependent IPM strategy. Math. Probl. Eng. 2017, 2017, 8683207. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Tang, S. The effects of timing of pulse spraying and releasing periods on dynamics of generalized predator-prey model. Int. J. Biomath. 2012, 5, 1250012. [Google Scholar] [CrossRef]
- Fister, R.K.; McCarthy, M.L.; Oppenheimer, S.F.; Collins, C. Optimal control of insects through sterile insect release and habitat modification. Math. Biosci. 2013, 244, 201–212. [Google Scholar] [CrossRef]
- Barclay, H.J. Mathematical models for the use of sterile insects. In Sterile Insect Technique. Principles and Practice in Area-Wide Integrated Pest Management, 2nd ed.; Dyck, V.A., Hendrichs, J., Robinson, A., Eds.; CRC Press: Boca Raton, FL, USA, 2021; pp. 201–244. [Google Scholar] [CrossRef]
- Dahlin, I.; Ninkovic, V. Aphid performance and population development on their host plants is affected by weed-crop interactions. J. Appl. Ecol. 2013, 50, 1281–1288. [Google Scholar] [CrossRef]
- Dixon, A.F.G. Structure of aphid populations. Ann. Rev. Entomol. 1985, 30, 155–174. [Google Scholar] [CrossRef]
- Dhahbi, A.B.; Chargui, Y.; Boulaaras, S.M.; Khalifa, S.B.; Koko, W.; Alresheedi, F. Mathematical Modelling of the Sterile Insect Technique Using Different Release Strategies. Math. Probl. Eng. 2020, 2020, 8896566. [Google Scholar] [CrossRef]
- Pontryagin, L.S.; Boltyanskii, V.G.; Gamkrelidze, R.V.; Mishchenko, E.F. The Mathematical Theory of Optimal Process; Gordon & Breach: New York, NY, USA, 1986. [Google Scholar]
- Ali, A.; Memon, S.A.; Mastoi, A.H.; Narejo, M.N.; Azizullah, A.; Afzal, M.; Ahmed, S. Biology and feeding potential of ladybird beetle (Coccinella septempunctata) against different species of aphids. Sci. Int. 2017, 29, 1261–1263. [Google Scholar]
- Win, S.S.; Muhamad, R.; Ahmad, Z.A.M.; Adam, N.A. Life table and population parameters of Nilaparvata lugens Stal. (Homoptera: Delphacidae) on rice. Trop. Life Sci. Res. 2011, 22, 25–35. [Google Scholar] [PubMed]
- Sardar, M.; Khatun, M.R.; Islam, K.S.; Haque, M.T.; Das, G. Potentiality of light source and predator for controlling brown planthopper. Progress. Agric. 2019, 30, 275–281. [Google Scholar] [CrossRef] [Green Version]
- Limohpasmanee, W.; Kongratarpon, T.; Tannarin, T. The effect of gamma radiation on sterility and mating ability of brown planthopper, Nilaparvata lugens (Stal) in field cage. J. Phys. Conf. Ser. 2017, 860, 012004. [Google Scholar] [CrossRef] [Green Version]
- Riddick, E.W. Identification of conditions for successful aphid control by ladybirds in greenhouses. Insects 2017, 8, 38. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lenhart, S.; Workman, J.T. Optimal Control Applied to Biological Models; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Paulden, M. Calculating and interpreting ICERs and net benefit. Pharmacoeconomics 2020, 38, 785–807. [Google Scholar] [CrossRef] [PubMed]




| Release Rate | Sterile Insect | Natural Enemy | Control Upper Bound |
|---|---|---|---|
| Constant | |||
| Proportional | |||
| Saturating proportional |
| Parameter | Description | Value | Unit |
|---|---|---|---|
| initial plant density | 300 | g/unit area | |
| initial population of fertile insects | 50 | individual | |
| initial population of sterile insects | 3 | individual | |
| initial population of natural enemies | 2 | individual | |
| intrinsic growth rate of plant | g/unit area/day | ||
| k | environment carrying capacity | 1000 | g/unit area |
| intrinsic birth rate of fertile insects | insect/day | ||
| plant consumption rate by fertile insects | g/day | ||
| plant consumption rate by sterile insects | g/day | ||
| handling time by fertile insects | 1 | day | |
| handling time by sterile insects | 1 | day | |
| m | constant of half saturation | per unit area | |
| fertile insect consumption rate by predator | insect/day | ||
| sterile insect consumption rate by predator | insect/day | ||
| death rate of fertile insect | insect/day | ||
| death rate of sterile insect | insect/day | ||
| death rate of natural enemy | insect/day | ||
| death rate of fertile insect due to fertile-fertile interaction | insect/day | ||
| death rate of fertile insect due to sterile-sterile interaction | insect/day | ||
| death rate of fertile insect due to fertile-sterile interaction | insect/day | ||
| death rate of natural enemy due to self-interaction | insect/day | ||
| plant-to-fertile insect conversion factor | insect/unit area/day | ||
| plant-to-sterile insect conversion factor | insect/unit area/day | ||
| insect-to-natural enemy conversion factor | 1 | insect/day | |
| effectiveness of control using SIT | - | ||
| effectiveness of control using natural enemy release | - | ||
| weight showing the importance of pest density suppression | 100 | - | |
| weight showing the importance of control effort by SIT | 1 | - | |
| weight showing the importance of control effort by natural enemy | 1 | - | |
| T | control period | 15 | day |
| i | Strategy | Benefit | Cost | ACER | ICER | ICER |
|---|---|---|---|---|---|---|
| 0 | No control | 0 | 0 | - | - | - |
| 1 | C-C | ed | ||||
| 2 | C-P | d | d | |||
| 3 | P-C | |||||
| 4 | P-P |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bakhtiar, T.; Fitri, I.R.; Hanum, F.; Kusnanto, A. Mathematical Model of Pest Control Using Different Release Rates of Sterile Insects and Natural Enemies. Mathematics 2022, 10, 883. https://doi.org/10.3390/math10060883
Bakhtiar T, Fitri IR, Hanum F, Kusnanto A. Mathematical Model of Pest Control Using Different Release Rates of Sterile Insects and Natural Enemies. Mathematics. 2022; 10(6):883. https://doi.org/10.3390/math10060883
Chicago/Turabian StyleBakhtiar, Toni, Ihza Rizkia Fitri, Farida Hanum, and Ali Kusnanto. 2022. "Mathematical Model of Pest Control Using Different Release Rates of Sterile Insects and Natural Enemies" Mathematics 10, no. 6: 883. https://doi.org/10.3390/math10060883
APA StyleBakhtiar, T., Fitri, I. R., Hanum, F., & Kusnanto, A. (2022). Mathematical Model of Pest Control Using Different Release Rates of Sterile Insects and Natural Enemies. Mathematics, 10(6), 883. https://doi.org/10.3390/math10060883






