Abstract
Assuming exponential lifetime and repair time distributions, we study the limiting availability as well as the per unit time-limiting profit of a one-unit system having two identical, cold standby spare units using semi-Markov processes. The failed unit is repaired either by an in-house repairer within an exponential patience time T or by an external expert who works faster but charges more. When there are two repair facilities, we allow the regular repairer to begin repair or to continue repair beyond T if the expert is busy. Two models arise accordingly as the expert repairs one or all failed units during each visit. We show that (1) adding a second spare to a one-unit system already backed by a spare raises as well as ; (2) thereafter, adding a second repair facility improves both criteria further. Finally, we determine whether the expert must repair one or all failed units to maximize these criteria and fulfill the maintenance management objectives better than previously studied models.
1. Introduction
First, to motivate this research, let us mention an application. In the chemical industry, where pumps are essential components to transfer highly corrosive chemicals, some insurmountable costly risks are abrupt halt in the manufacturing process, catastrophic failure, and hazardous environmental interference. Consequently, it is highly critical to minimize these potential risks by building a redundant system by including several repairable pumps that will raise availability while simultaneously retaining profitability.
To calculate the availability and profitability of the aforementioned system, we consider a single-unit repairable system backed up by one or two similar units that are continually monitored and repaired by two different types of repairers, who can work simultaneously when there are two repair facilities. Although an in-house repairer lacks complete repair skills, his pay per hour is lower, while his presence at all times removes the excessive cost that the expert must be paid. In general, the regular repairer does small repairs during a permissible patience time, and either he cannot perform sophisticated repairs, or he cannot complete it within the allotted patience time. In contrast, the visiting expert repairer can fix any problem, and she finishes it faster. Nonetheless, her hourly rate is relatively higher; moreover, she must be paid an overhead for each visit.
The system described above operates as follows: At time , a unit is placed to function while the spare units wait on cold standby. (Thus, our system is different than a one-out-of-three system.) When the functioning unit fails, a spare unit starts to operate instantly, while the dead unit is sent to the in-house repairer. If he is not able to finish the repair within the given random patience time (RPT) T, or when the system goes down because all three units have failed, the visiting expert repairer is called in. The system fails in two cases: (1) the regular repairer is busy fixing a previously failed unit, and even though the patience time has not exhausted, the remaining units have died; (2) both repairers are busy fixing two failed units and the only operating unit fails.
When there are two repair facilities, the regular repairer works on the failed unit either until his patience time is over or until the expert is freed up to take over, whichever comes later. For simplicity, we assume that when the expert takes over the repair, any benefit accruing from an incomplete repair performed by the regular repairer is totally lost. Lastly, after either repairer completes the repair, the repaired unit is rendered as good as new.
How many repairs will the expert do once she is on site? We consider two scenarios: (1) When the expert departs, either she has fixed all failed units so that one is operating and two are on standby, or one is operating, one is on cold standby, and the third is under repair by the regular repairer. This policy we call the multiple repair by expert (MRE). (2) The expert repairs just one failed unit during every visit and leaves the other failed unit(s), if any, to the care of the regular repairer. We call this alternative policy the single repair by expert (SRE).
Based on how many repairs the expert performs—single or multiple—two possible models emerge: (1) MRE-RPT and (2) SRE-RPT. We compare these two models’ performance based on the limiting availability as well as the limiting profit per unit time . Assuming continuous lifetime and repair time and continual monitoring, one can prove the existence of and can calculate it as the fraction of time the system functions in the long-run (see [1]). Similarly, by expressing all terms per unit time, is calculated as net revenue (revenue minus cost of operation) minus repair costs payable to each repairer in the long-run, minus the expert’s per visit charge spread over the entire time horizon.
Bieth et al. [2] investigate Models (1) and (2), and also those under a deterministic patience time policy (DPT)—(3) MRE-DPT and (4) SRE-DPT—when there is only one spare unit and one repair facility. They assume that the life and repair times are exponentially distributed and find and by invoking the method called semi-Markov processes (SMP). Andalib and Sarkar [3] extend their findings to include a second spare unit. Such an extension is necessary to demonstrate that if corresponding to only one spare unit falls below an acceptable level even after the engineering team has made all possible efforts to manufacture a state-of-the-art critical unit, the maintenance team can increase to reach the acceptable level by employing one additional spare unit. In this paper, we extend their results to a system with two repair facilities under RPT policy. However. the DPT policy encounters an extra challenge—the Markovian property is violated, as the movements from some states likely depend on both the present state and the process’s track record. Under RPT policy, the system with two spare units and two repair facilities is shown to have larger and relative to a system having one spare or two spare units but only one repair facility.
This is how the rest of this paper is arranged: A literature review is given in Section 2. Section 3 formulates the repairable system’s stochastic behavior as an SMP, which is followed by the algebraic methodologies for deducing and . Detailed algebraic derivations under our two repair models are given in Section 4. Section 5 contrasts the two models with those having either one spare unit or two spare units but a single repair facility. Lastly, in Section 6, we summarize the results and propose several new research problems.
2. Literature Review
This section discusses recent advances in modeling repairable systems accounting for a variety of reliability properties.
Sarkar and Li [4] study a single-unit system backed by r similar repair sites and s spare units on cold standby with . The system dies whenever all units have failed and are either being repaired or waiting for repair. The authors assume a perfect repair policy and derive under arbitrary lifetime distribution but restrict the repair time to be exponentially distributed. Sarkar and Biswas [5] consider the same model and calculate the instantaneous availability function (of time) with exponential lifetime and repair time.
Wang et al. [6] examine the reliability as well as sensitivity analysis for a system having multiple functioning units and spare units on warm standby as well as multiple repair facilities that are unreliable. They assume that lifetimes as well as service duration are exponential, and the repair facility itself can fail following a Poisson process. They not only calculate the system mean time to failure (MTTF) as well as reliability but also discuss the effect of each model parameter on these characteristics.
Zhang and Wang [7] examine a cold standby system comprised of two distinct components—Component 1 receives preference in operation—serviced by a single repair person. Component 2 is perfectly repaired, whereas Component 1 exhibits a geometric process. They obtain several critical reliability indices under exponential lifetime and repair time, including system availability, reliability, mean time to first failure (MTTFF), failure rate, and the probability that the repairer is idle. By minimizing the average cost per unit time in the long run, they determine an optimal replacement strategy for Component 1.
Yu et al. [8] develop a system that reaches a desired availability while it minimizes the cost per unit time. They allow the spare units to remain on cold standby. El-Said and El-Sherbeny [9] also allow the spare units to stay on cold standby. They conduct a cost–benefit analysis of a system consisting of two units and a two-stage repair that allows an intermediate random pause. They apply regenerative point processes to derive the availability function, limiting availability, mean time to failure, and profit.
Cui et al. [10] present two interval availability indices for systems that quantify the chance of operation within a specific time frame encompassing either an epoch or a time interval. Likewise, using Z transform, reliability, point availability, and interval availability are obtained by Yi et al. [11], who investigate a semi-Markov system whose states are subdivided into three parts: operating, modifiable, and dead.
Cha and Finkelstein [12] study systems where defects are noted prior to failure and either perfectly so that the process starts anew or repair is not complete within a specified patience time period, resulting in a destructive failure. They obtain survival functions assuming exponentially distributed detection time, fixed patience time, and arbitrarily distributed repair time; however, the authors demonstrate computations when repair time is exponential.
Tohidi et al. [13] apply the cost analysis method to determine the optimum number of cold standby units necessary to support a single-unit system. They propose a model for system reliability analysis using continuous-time Markov chains assuming that failure and repair times are both exponentially distributed.
Kadyan et al. [14] study a one-unit redundant system having a single operating (called main) unit supported by two identical units (called duplicate) on cold standby which are nonidentical to the main unit. Upon failure of the main unit, both duplicate units are put on operation, while a single repairer perfectly repairs the failed main unit. Using the Laplace transform technique, they claim to derive some reliability measures, including availability and profit, for arbitrary failure- and repair time distributions; however, they do not derive analytic expressions for the reliability measures but only calculate the results under exponential distributions. Kadyan et al. [15] extend the work by giving priority of operation to the main unit and showing that when the repair rate of the main unit increases, so does the system reliability.
Repairable systems with two different types of repairers have received little attention from researchers. Kumar et al. [16] investigate Model (2), where there is a single spare unit. The authors enable an expert repairer to begin repair provided the regular repairer’s patience time is over, notwithstanding that the system may die in the interim. Sridharan and Mohanavadivu [17] invoke the expert repairer immediately when either the patience time is exhausted or the system failure occurs. While the authors announce permitting arbitrarily distributed life, repair, and patience times, it turns out that their deductions hold only when these times are exponentially distributed, as already mentioned in [2]. Later, Sridharan [18] provides the regular repairer a random pre-inspection time to check if he is capable of repairing a failed unit during that time. If capable, he begins to repair; if not, the expert repairer immediately comes and takes over. Bieth et al. [2] describe Models (1)–(4) under one spare unit. They derive and using an SMP where the lifetime and repair time are exponential. They generalize the method by allowing lifetimes as well as repair times to be any distribution.
Mahmoud and Moshref [19] allow failures of two kinds and hence repairs of two kinds. Assuming only one repairer, they apply the Laplace transform method to obtain MTTF, limiting availability and limiting profit.
Parashar and Taneja [20] investigate a single-unit system supported by a spare unit exhibiting a master–slave-type interdependence. At the beginning, the master is placed on operation while the slave remains on hot standby. Three kinds of defects are possible: simple, serious-repairable, and serious-irreparable (when the unit must be replaced). The in-house repairer can repair only simple defects. The authors announce that repair- and replacement times can have any distribution, only lifetime is exponentially distributed, under which assumptions they deduce the MTTF, and . However, they do not give any analytic results; their findings hold only when all three time variables are exponentially distributed.
Gupta [21] considers a one-unit repairable system with two types of repairers, where the regular repairer ends up in three possible situations—he cannot finish the job despite correctly following the repair process, or he follows the procedure incorrectly without damaging the unit, or he damages the unit. The expert resumes the repair job under the first scenario. Using the Laplace transform technique, the author claims to derive system availability and profit under arbitrarily repair time distributions for the two repairers; however, no analytical expressions are given. The author obtains the results only under the exponential distributions, for which, in view of the memoryless property, partial repair done by the regular repairman is forfeited.
The papers addressed above use the Laplace transform technique to derive several system reliability characteristics including availability, duration when each repairer is busy, and profit earned. These works do not obtain explicit expressions by inverting the Laplace transform in the general case; they do so only under exponential distributions. Hence, we prefer to employ the method of semi-Markov processes, as it is relatively more straightforward and simpler.
Andalib and Sarkar [3] extended the results of [2] to the system with two spare units and one repair facility using the SMP technique. For a given set of parameters, they obtain an interval for T so that Model (3) exhibits the greatest performance with respect to both criteria— and . Moreover, they determine a cut-off value for the amount the expert must be paid per hour so that the MRE policy will produce more profit than the SRE policy whenever the expert’s charge is below the cut-off and conversely.
3. System Description and Mathematical Framework
For the two models (1) and (2) described in Section 1, we compute as well as assuming the following:
- 1.
- Three identical units comprise a single-unit system. At the beginning, only one unit is operational, while the remaining two units stay on cold standby.
- 2.
- Two repair facilities are respectively serviced by a regular and an expert repairer.
- 3.
- The operational unit’s failure is noted instantaneously; the dead unit is dispatched to a repairer, while a spare is promptly activated.
- 4.
- The regular repairer must finish repair within a random patience time (RPT) T.
- 5.
- The system goes down when all three units fail.
- 6.
- When either the regular repairer’s patience time runs out or when the system dies, whichever occurs earlier, the expert is alerted to come at once.
- 7.
- The regular repairer works on the failed unit until his patience time is over or until the expert is freed up to take over, whichever comes later.
- 8.
- Lifetime, repair time, and patience time are independently and exponentially distributed with arbitrary parameters. This assumption being restrictive ought to be eliminated in a future work.
- 9.
- When the expert comes in, the progress made by the regular repairer is lost. Specifically, it is a consequence of the previous assumption due to the memoryless property of the exponential distribution.
- 10.
- We consider two options for the expert repairer, resulting in a multiple repair by expert (MRE) model and single repair by expert (SRE) model.
- 11.
- Repair by either repairer is perfect, rendering a unit brand new after repair is complete.
Whenever one looks at it, a unit shows one of five attributes: p (operating), s (on standby), r (being repaired by in-house repairer), (being repaired by in-house repairer past patience time T because the expert is busy repairing another failed unit), e (being repaired by expert), or w (waiting for repair). The units are interchangeable enough to document the number of units showing such attributes. Consequently, there are nine states as follows: , , , , , , , , and . The system is down in States 7, 8, and 9 (shown with elliptical boundary), and it is up in all other states (shown with rectangular boundary). States 7 and 8 represent the same features of the three units; nonetheless, we still separate them because the system enters following two different paths.
Figure 1 exhibits the movements for the SRE and MRE models, together with random variables governing the time spent in each state and transition probabilities between states.
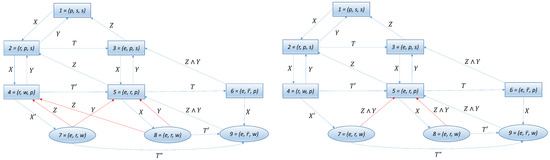
Figure 1.
Transition diagrams for SRE (left) and MRE (right) models. The symbol ∧ denotes minimum; a red arrow denotes a failed system is revived.
First, let us describe the random variables. Suppose that X, Y and Z are the unit’s lifetime, the regular repairer’s repair time, and the expert’s repair time, respectively. The other random variables noted in Figure 1 are defined as follows: let denote a lifetime independent and identically distributed as X. Under the RPT policy, based on the memoryless property of the exponential distribution, the leftover patience times and are identically distributed as T, and all three patience time random variables are jointly independent.
Next, let us describe the sojourn times in each state.
- 1.
- Beginning at State 1, the system stays in State 1 for a period X, before going to State 2.
- 2.
- In State 2, the system remains for ; if Y is the smallest, then the system goes back to State 1, if T is the minimum, then it moves to State 3, and if X is the smallest, then it moves to State 4.
- 3.
- In State 3, the system stays for ; if , then the system goes to State 1; otherwise, it moves to State 5.
- 4.
- In State 4, the time spent equals ; if Y is the smallest, then the system goes to State 2, if is the minimum, then it goes to State 5, and if happens to be the minimum, then it moves to State 7.
- 5.
- The time spent in State 5 equals ; if Z is the smallest, then the system goes to State 2, if Y turns out to be the minimum, then it moves to State 3, if T happens to be the minimum, then it goes to State 6, and if X is the smallest, then it goes to State 8.
- 6.
- The time spent in State 6 equals ; if either Y or Z is the smallest, then the system goes to State 3, but if X is the minimum, the system goes to State 9.
- 7.
- The time spent in State 7 equals ; if is the minimum, then the system moves to State 9, if either Y or Z is the minimum, then it goes to State 5 (under the MRE policy), but under the SRE policy, if Z is the smallest, then the system goes to State 4, and if Y is the smallest, then it goes to State 5.
- 8.
- The time spent in State 8 equals ; if is the smallest, the system goes to State 9. Under both SRE and MRE policies, transitions from State 8 to States 4 and 5 are identical to those from State 7.
- 9.
- The sojourn time in State 9 is ; and as soon as either the expert or the regular repairer repairs one of the failed units in State 9, the system moves to State 5 under both SRE and MRE policies.
Finally, the transition probabilities out of each state are calculated based on which of the corresponding random variables achieves the smallest value.
Let denote the fraction of time the system stays in State . In Section 4, we derive expressions for . Since the system is down in States 7, 8 and 9, the limiting availability of the system is,
After obtaining , one calculates , for which one defines these parameters: Let denote the fraction of time the regular repairer works, and let denote the same for the expert. Let parameters represent the net revenue, the cost of operation, and the money paid to the regular repairer and the expert, respectively — each quantity defined per unit time. In addition, let denote the amount of money payable to the expert per visit. Then, we have
where the parameter denotes the mean cycle time (that is, the length starting from the moment the system moves to State 2 and ending when it comes back to State 2 after visiting at least once any state in . As a result, the expert comes and returns precisely once throughout each cycle, and she gets compensated for the trip charge exactly once. In view of Wald’s First Identity (see [1]), the inverse of represents the average number of trips the expert makes per unit time. Hence, represents how much money should be set aside per unit time to cover the expert repairer’s trip charges.
4. Computing Limiting Availability and Limiting Profit
Here, we obtain analytic solutions to and for models: (1) MRE-RPT and (2) SRE-RPT. Under Assumption 9, we denote the lifetime, the patience time, and the repair times by the two repairers, respectively, by
.
The parameters of the exponential distributions denote the rates, whence the means are their reciprocals. By the lack of memory property of the exponential distribution, the behavior of the process is determined solely by the current state, whereby the old trajectory is ignored. Therefore, the stochastic process is a semi-Markov process (SMP): the system moves from state to state according to a Markov chain, and it remains in a state for a random duration. See [22] to learn about an SMP. Indeed, the underlying discrete time stochastic process (DTSP) behaves as a Markov chain on the state space and an associated matrix of transition probabilities . The ’s vary between the two models, and they are given separately in the following two subsections.
The limiting probability of the transitions entering into (and also departing from) State j are given by the stationary distribution of a Markov chain. This stationary distribution is uniquely determined, and it can be derived from an appropriate system of equations (refer to [22], pp. 215–216).
Furthermore, the expected sojourn times in various states are as follows:
The fraction of time the SMP remains in each state is obtained from a well-known result (refer to [22], pp. 215–216).
Theorem 1.
For an SMP, let the underlying DTSP be irreducible and have stationary probabilities π. Suppose that the return times to any State k has a non-lattice distribution having a finite mean. Let be the expected time spent in State k. Then, the limiting probability of finding the process in State k exists; it is free of the initial state, and it equals
In the next subsections, we obtain () using (3)–(5) for each of the two models, based on the transition matrix . Next, from (1), we derive . Then, for each model, to find analytic expression of , we solve an appropriate system of recursive equations. Thereafter, from (2), we derive .
4.1. The MRE-RPT Model
The underlying DTMC, for the MRE-RPT model, involves the transition matrix
One solves the system (3) to get the stationary distribution as
where,
By putting (4) and (7) into (5), one derives the expressions for ’s. Thereafter, from (1), one gets
where,
Next, to compute the expected length of a cycle, , we proceed step-by-step to solve various systems of linear equations. To begin, satisfies the recursive relation
where the parameter denotes the expected time needed to move from State 3 to State 2 (through State 1 or State 5), when the MRE policy is in effect. All remaining parameters have similar meanings, and because , they satisfy the recursive relations
If one solves the system of Equations (10), one gets
Substituting the expressions for and into (9) and solving, we obtain
4.2. The SRE-RPT Model
The underlying DTMC, for the SRE-RPT model, involves the transition matrix
As demonstrated in the previous subsection for the MRE-RPT model, so also here for the SRE-RPT model, using linear algebra, we solve the system of Equations (3) and obtain the stationary distribution . In fact, the system of Equations (3) can be written in matrix notation as , ; or equivalently, as , where the full-rank matrix is obtained by replacing the last row of by a row vector of all entries unity. Then, using Gauss–Jordan elimination on the augmented matrix , we transform into an upper triangular matrix and thereby obtain the stationary distribution . However, the derivation of the analytic solution is long and tedious; hence, it is omitted. Instead, a numerical solution to the stationary distribution is obtained for given values of the parameters, as done in Section 5. Having obtained the values of ’s and the mean sojourn times (4), and substituting them into (5), we obtain the values of ’s. Thereafter, from (1), we get
To obtain , we need to calculate the expected length of cycle . Let be the expected time it takes to move from State 3 to State 2 (through State 1 or State 5) when the SRE policy is in effect. All remaining parameters have similar meanings, and because , they satisfy the recursive relations
The third Equation in (16) can be rewritten, using the sixth equation, to express as a function of and . Next, in the fourth Equation in (16), we substitute the second, the fifth, and the seventh equations to solve for . Then, from the second Equation in (16), one obtains ; from the third, one obtains , etc. After obtaining all ’s, the leading Equation in (16) gives
where,
Using Expression (17) for , we obtain from (2).
5. Comparison of Models
Under the RPT policy for a given set of parameter values, we compute as well as for the two repair models discussed in the previous section. When there is only one repair facility, we show that a system having two spare units attains greater as well as greater compared to a system having one spare. Thereafter, if a second repair facility is added, both optimality criteria increase further.
In Table 1, we compute , , , and for the two models MRE-RPT and SRE-RPT, for systems with a single spare unit () or systems with two spare units (), when either one repair facility () or two repair facilities () are available. The expert finishes repair quicker than the regular in-house repairer; however, the expert must be paid more per unit of time ( and ). The parameters are chosen to be , , , and ; and , , and .

Table 1.
Calculated results under RPT policy.
The following four features in Table 1 are noteworthy:
- 1.
- Both and are greater for the MRE model than for the SRE model regardless of the number of spare units and the number of repair facilities.
- 2.
- Adding a second spare when a system currently has one spare improves both and . As an example, is below 80% when , but it is more than 80% when . See [3] for further details.
- 3.
- Including one more spare unit causes , implying that we utilize the regular repairer more than the expert. Likewise, adding a second repair facility makes the regular repairer busier than the expert, resulting in even less cost and higher limiting profit per unit time .
- 4.
- Adding a second repair facility to the system with two spare units raises both and further. For example, is increased to almost 90% under the MRE policy.
The MRE model always outperforms the SRE model with respect to . How about with respect to ? Figure 2 depicts for the two models as a function of , where . When does not exceed a certain cut-off, the MRE model results in a higher limiting profit than the SRE model under RPT policy; and the converse is true if the expert’s charge rate exceeds the cut-off. In our example, the cut-off for is 11.231.
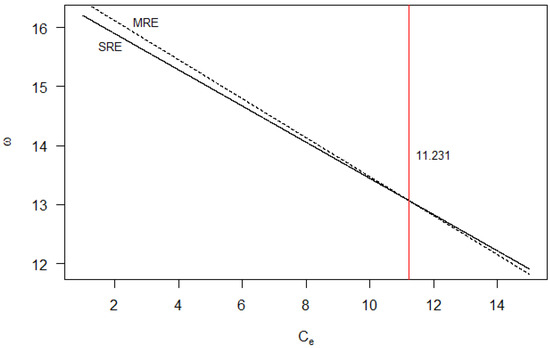
Figure 2.
Limiting profit per unit time as a function of for system with and .
6. Concluding Remarks
In this paper, we extend the results obtained in [3] under random patience time by introducing another repair facility to a single-unit system supported by one repair facility and comprised of two identical units that remain on cold standby. The two repair facilities are serviced by two types of repairers. Multiple spare units are required to increase the system’s reliability characteristics when the component lifetime is short and the repair time is lengthy. In addition, utilizing multiple repair facilities enables both repairers to work on the failed units simultaneously, resulting in highly available and more profitable system. We investigate the limiting availability and the limiting profit per unit time in this extended setup where lifetime, repair time, and patience time for the regular repairer are exponential. Two models are considered based on how many failed units the expert may repair per visit. For the two models, we obtain analytic expressions for and using SMP. The method is easier to apply than the Laplace transform method commonly appearing in the literature. We demonstrate that the system with two repair facilities yields higher and higher than a system backed by only one repair facility.
Adding a second spare unit or a second repair facility, in the hope of increasing and , should be counterbalanced against the cost of such innovation. Table 2 gives , cost, and profit per unit time w calculated from Equation (2), under different cost parameters. For example, for the MRE model, when and , starting from (), as we add another spare unit to reach (), the cost per unit time increases from 2.770 to 2.892 (4.4%), but because increases by 7.75%, increases from 12.805 to 14.349 (12.058%). Next, when we add another repair facility to reach (), the cost rises from 2.892 to 3.042 (5.2%), but because increases by 5.8%, rises from 14.349 to 15.196 (5.903%). Similar results hold for any other pair of cost parameters and also for the SRE model. We assume the total excess profit per unit time streaming out of the maintained system over its entire lifetime will suffice to offset the extra cost of adding another spare unit or a second repair facility.

Table 2.
Cost–profit analysis under different cost parameters and , when , , , , , .
Since the expert repairer works quicker compared to the in-house repairer, the MRE model achieves a bigger compared to the SRE model. On the other hand, the expert charges higher than the in-house repairer. Therefore, holding the cost parameters the same, the administrator must find out if the MRE or the SRE achieves higher .
Several directions for further research are suggested as follows:
- Keeping our focus on building repairable models, we have assumed exponentially distributed lifetime and repair time random variables. While it may pose additional challenges since the stochastic process will no longer be an SMP, extension beyond exponential distribution is highly desired.
- While we assumed the units are identical, a more realistic model would admit non-identical units with different lifetime and repair rates. Specifically, when there are multiple such units, we must determine at each decision epoch which unit should be prioritized for operation and which should be prioritized for repair.
- While we studied patience time as a random variable, a logistically more desirable option is to permit a predetermined constant patience time. Again, we cannot use SMP under a deterministic patience time policy, as the Markovian property is violated in some states. This is a fertile ground for developing a new mathematical theory.
Author Contributions
Conceptualization, V.A. and J.S.; methodology, V.A. and J.S.; computations, V.A. and J.S.; interpretations, V.A. and J.S.; writing—original draft preparation, V.A. and J.S.; writing—review and editing, V.A. and J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are immensely thankful to the anonymous referees for their useful comments on an earlier version of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Feller, W. An Introduction to Probability Theory and Its Applications; Wiley: New York, NY, USA, 1968; Volume 1. [Google Scholar]
- Bieth, B.; Hong, L.; Sarkar, J. A standby system with two types of repair persons. Appl. Stoch. Model. Bus. Ind. 2010, 26, 577–594. [Google Scholar] [CrossRef]
- Andalib, V.; Sarkar, J. A Repairable System Supported by Two Spare Units and Serviced by Two Types of Repairers. J. Stat. Theory Appl. 2021, 20, 180–192. [Google Scholar] [CrossRef]
- Sarkar, J.; Li, F. Limiting average availability of a system supported by several spares and several repair facilities. Stat. Probab. Lett. 2006, 76, 1965–1974. [Google Scholar] [CrossRef]
- Sarkar, J.; Biswas, A. Availability of a one-unit system supported by several spares and repair facilities. J. Korean Stat. Soc. 2010, 39, 165–176. [Google Scholar] [CrossRef]
- Wang, K.H.; Ke, J.B.; Lee, W.C. Reliability and sensitivity analysis of a repairable system with warm standbys and R unreliable service stations. Int. J. Adv. Manuf. Technol. 2007, 31, 1223–1232. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Wang, G.J. A deteriorating cold standby repairable system with priority in use. Eur. J. Oper. Res. 2007, 183, 278–295. [Google Scholar] [CrossRef]
- Yu, H.; Yalaoui, F.; Châtelet, Ė.; Chu, C. Optimal design of a maintainable cold-standby system. Reliab. Eng. Syst. Saf. 2007, 92, 85–91. [Google Scholar] [CrossRef]
- El-Said, K.M.; El-Sherbeny, M.S. Stochastic analysis of a two-unit cold standby system with two-stage repair and waiting time. Sankhya B 2010, 72, 1–10. [Google Scholar] [CrossRef]
- Cui, L.; Chen, J.; Wu, B. New interval availability indexes for Markov repairable systems. Reliab. Eng. Syst. Saf. 2017, 168, 12–17. [Google Scholar] [CrossRef]
- Yi, H.; Cui, L.; Shen, J.; Li, Y. Stochastic properties and reliability measures of discrete-time semi-Markovian systems. Reliab. Eng. Syst. Saf. 2018, 176, 162–173. [Google Scholar] [CrossRef]
- Cha, J.H.; Finkelstein, M. Stochastic modeling for systems with delayed failures. Reliab. Eng. Syst. Saf. 2019, 188, 118–124. [Google Scholar] [CrossRef]
- Tohidi, H.; Chavoshi, S.; Bahmaninezhad, A. A continuous-time Markov chain model for redundancy allocation problem: An economic analysis. Qual. Reliab. Eng. Int. 2019, 35, 1866–1877. [Google Scholar] [CrossRef]
- Kadyan, S.; Malik, S.C. Stochastic Analysis of a Three-Unit Non-Identical Repairable System with Simultaneous Working of Cold Standby Units. J. Reliab. Stat. Stud. 2020, 7, 385–400. [Google Scholar] [CrossRef]
- Kadyan, S.; Barak, M. Stochastic analysis of a non-identical repairable system of three units with priority for operation and simultaneous working of cold standby units. Int. J. Stat. Reliab. Eng. 2020, 7, 269–274. [Google Scholar]
- Kumar, A.; Gupta, S.; Taneja, G. Comparative study of the profit of a two server system including patience time and instruction time. Microelectron. Reliab. 1996, 36, 1595–1601. [Google Scholar] [CrossRef]
- Sridharan, V.; Mohanavadivu, P. Stochastic behaviour of a two-unit standby system with two types of repairmen and patience time. Math. Comput. Model. 1998, 28, 63–71. [Google Scholar] [CrossRef]
- Sridharan, V. Probabilistic measures of redundant system with two types of repairmen, sensing device and analytical approach to find the optimium interchanging time. Int. J. Qual. Reliab. Manag. 2000, 17, 984–1002. [Google Scholar] [CrossRef]
- Mahmoud, M.; Moshref, M. On a two-unit cold standby system considering hardware, human error failures and preventive maintenance. Math. Comput. Model. 2010, 51, 736–745. [Google Scholar] [CrossRef]
- Parashar, B.; Taneja, G. Reliability and profit evaluation of a PLC hot standby system based on a master-slave concept and two types of repair facilities. IEEE Trans. Reliab. 2007, 56, 534–539. [Google Scholar] [CrossRef]
- Gupta, R. Stochastic analysis of a reliability model for one-unit system with three types of repair policy. Int. J. Stat. Appl. Math. 2017, 2, 126–130. [Google Scholar]
- Ross, S.M. Stochastic Processes; Wiley: New York, NY, USA, 1996; Volume 2. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).