Special Type Routing Problems in Plane Graphs

Abstract

We considered routing problems for plane graphs to solve control problems of cutting machines in the industry. According to the cutting plan, we form its homeomorphic image in the form of a plane graph G. We determine the appropriate type of route for the given graph: $OE$-route represents an ordered sequence of chains satisfying the requirement that the part of the route that is not passed does not intersect the interior of its passed part, $AOE$-chain represents $OE$-chain consecutive edges which are incident to vertex v and they are neighbours in the cyclic order $O^{\pm }\left(v\right)$, $NOE$-route represents the non-intersecting $OE$-route, $PPOE$-route represents the Pierce Point $NOE$-route with allowable pierce points that are start points of $OE$-chains forming this route. We analyse the solvability of the listed routing problems in graph G. We developed the polynomial algorithms for obtaining listed routes with the minimum number of covering paths and the minimum length of transitions between the ending of the current path and the beginning of the next path. The solutions proposed in the article can improve the quality of technological preparation of cutting processes in CAD/CAM systems.

1. Introduction

Simulation of some control and automation design problems [1,2] explains interest in routing problems for CAD/CAM systems. Lots of them devoted to finding the routes satisfying certain constraints have arisen from specific practical situations. All kinds of trajectory problems are universal mathematical models of optimization and control tasks. The examples of them are the following: (1) heuristic algorithms for constructing routes (N.A. Eapen and R.B. Heckendorn [3], S.Q. Xie [4], Y. Jing and C. Zhige [5], M.K. Lee and K.B. Kwon [6], J. Hoeft and U.S. Palekar [7]); (2) trajectory stabilization of mobile robots (V.A. Utkin [8]); (3) management of routing process and optimization (A.A. Lazarev [9]); (4) problems of obtaining the routes in graphs (H. Fleischner [10]); (5) the routing problem for cutting blanks from sheet material (V.M. Kartak [11], A.A. Petunin [12,13], A.G. Chentsov [14,15], I. Landovskaya [16]).

The capabilities of modern equipment for cutting sheet material allow using the cutting plans with the combining of contours for cut-out of separate parts. This combining of cuts allows reducing the material loss, the cutting length and the number of idle passes.

Algorithms for obtaining the cutting plans for tasks with combined cuts do not fundamentally differ from algorithms that do not allow any combining. However, the algorithms for finding the routes of the cutter moving are fundamentally different. Therefore, the development of algorithms for finding the route of the cutter for plans allowing the combining of the cut parts contours is still an open task.

In this paper, we consider the routing problems in plane graphs. These graphs are homeomorphic images of cutting plans. The cutter path is defined as a path covering all the boundaries of the cut parts. The main constraint on this path is that the faces of the route’s initial part do not intersect with the edges of the remaining part. For flame cutting, we need the following additional constraints on a path: (1) absence of self-intersections of the cutting path (NOE-condition), and (2) allowance to start cutting from allowable pierce vertices (PPOE-condition).

In practice, the most common approach does not involve a combination of the contours of the cut parts. This method is material and energy-consuming [13,17,18]. In one of such papers [3], the shapes are considered to be polygons. There are two different ways to cut each polygon: (1) entirely (complete cutting approach) or (2) partially (partial cutting approach) before cutting the next one. The authors of [3] proposed the approximation algorithm that uses such concepts as matching, spanning tree, and triangulation (MASTRI). This algorithm runs a time not greater than $O(nlogn)$, where n is the total number of all the polygons vertices. The cutting path computed by algorithm [3] is guaranteed to be within a factor of 3/2 of the optimum distance of the cutter. Hence, MASTRI algorithm can be used for computing cutting paths in industries like sheet metal cutting. It should be noted that the possibility of using concepts of matching, spanning tree, and triangulation was noted in our article [19].

The first attempts of constructing the routes in which the passed part of the route does not cover the edges of the remaining part were made in the work of U. Manber and S. Israni [20] where the image of the cutting plan is represented as an equivalent graph. The objective of this research is to cover this graph with a minimum number of chains starting in the pierce points or breakthroughs. Since the graph has $2k$ vertices of odd degree, then k pierce points are necessary and sufficient to traverse the graph. The cutter path problem formulation includes such parameters as manufacturing cost, efficiency, and distortion considerations. Some algorithms solving this task are considered in [20]. However, these algorithms do not have sufficient formalization, and the formulation of the problem does not take into account some technological constraints for flame cutting. Later, U. Manber and S.W. Bent [21] noted the need to construct a self-intersecting route and provided proof that this task belongs to the $\mathcal{N}P$ class. This proof is a compilation H. Fleischner’s results [22] introducing the concept of an A-chain. This chain has the allowed transitions between edges, that are specified in a cyclic order at each vertex of the graph. H. Fleischner also proved that the task of constructing the A-chain is $\mathcal{NP}$-hard in general, but there are some special cases for which this task is solvable in polynomial time. One of such cases is a 4-regular graph. U. Manber and S.W. Bent in fact use A-chain instead of a self-intersecting chain. If we consider the partial case when the cutting plan is a plane Euler graph, then it is known that its dual face graph is bichromatic. For this case, S.B. Bely [23] proved the existence of an Euler cycle homeomorphic to a plane Jordan curve without self-intersections. However, it is unclear how to use this possibility for CAD/CAM systems for technological preparation of cutting processes.

The listed above problems have been solved by the authors. A rigorous formalization of these problems in terms of $OE$-chains is given in our paper [24]; however, the $OE$-chain allows the possibility of self-intersection of the trajectory. Representation of a plane Euler graph in the form of a self-intersecting Jordan curve has been announced at conferences [25,26]. We proved the necessary and sufficient conditions of $PPOE$-routes existence and built the polynomial algorithm $PPOE$-routing constructing such routes for any plane graph. The correctness of this algorithm has been announced at the conference [27]. The purpose of this article is to present the results obtained using a single terminology.

2. Methods

2.1. Abstracting the Cutting Plan to a Plane Graph

The information on the part shape is not used when we determine the sequence of cutting the fragments of the cutting. Hence, all the curves without self-intersections and contacts on the plane, representing the shape of the parts, are interpreted as the edges of the graph. All the points of intersection and contact are represented as the vertices of the graph. So, it is necessary to introduce additional functions on the set of vertices, faces and edges of the resulting graph to analyse the implementation of the given technological constraints.

We consider a plane S as a model of cutting plan, then a plane graph $G(V,E)$ with outer face $f_0\subset S$ be the cutting plan model. The set of edges $E\left(G\right)\subset S$ of this graph is the Jordan curves with pairwise disjoint interiors and homeomorphic to open segments. Hence, the set of vertices $V\left(G\right)\subset S$ is the set of bounding points of these segments. For any part of the graph $J\subseteq G$, we denote the set-theoretic union of its interior faces (the union of all connected components of $S\backslash J$ that do not contain an outer face) by $\mathrm{Int}\left(J\right)$. Then, $\mathrm{Int}\left(J\right)$ can be interpreted as a part cut off a sheet. The sets of vertices, edges and faces of the graph G we denote as $V\left(G\right)$, $E\left(G\right)$ and $F\left(G\right)$, respectively. Since we consider graph G as a model of a cutting plan, there is no case when G is non-planar.

Theorem 1.

The topological representation of plane graph $G=(V,E)$ on plane S up to homeomorphism is defined by the following functions for each edge $e\in E$, $k=1,2$:

• $v_k\left(e\right)$ is the pair of vertices incident to e,
• $l_k\left(e\right)$ is the edges obtained by rotating edge e counter-clockwise around a vertex $v_k$,
• $r_k\left(e\right)$ is the edges obtained by rotating edge e clockwise around a vertex $v_k$,
• $f_k\left(e\right)$ is the face placed on the left when moving along the edge e from the vertex $v_k\left(e\right)$ to the vertex $v_{3-k}\left(e\right)$.

Proof. 

An illustration of the functions from the Theorem 1 is given in Figure 1.

Since functions $v_k\left(e\right)$, $f_k\left(e\right)$, $l_k\left(e\right)$, $k=1,2$ for graph G edges define incident vertices, faces, and adjacent edges for each $e\in E\left(G\right)$ this statement is obvious.  □

Figure 2 illustrates an example of a cutting plan. Its homeomorphic image is given in Figure 3 and the named functions for its computer representation are given in

Table 1. Encoding of the plane graph in Figure 3.

e	${\mathit{v}}_1\left(\mathit{e}\right)$	${\mathit{v}}_2\left(\mathit{e}\right)$	${\mathit{l}}_1\left(\mathit{e}\right)$	${\mathit{l}}_2\left(\mathit{e}\right)$	${\mathit{r}}_1\left(\mathit{e}\right)$	${\mathit{r}}_2\left(\mathit{e}\right)$	${\mathit{f}}_1\left(\mathit{e}\right)$	${\mathit{f}}_2\left(\mathit{e}\right)$
$e_1$	$v_2$	$v_9$	$e_4$	$e_{21}$	$e_3$	$e_{23}$	$f_0$	$f_1$
$e_2$	$v_4$	$v_6$	$e_3$	$e_8$	$e_7$	$e_9$	$f_1$	$f_2$
$e_3$	$v_2$	$v_4$	$e_1$	$e_5$	$e_4$	$e_2$	$f_1$	$f_3$
$e_4$	$v_2$	$v_3$	$e_3$	$e_6$	$e_1$	$e_5$	$f_3$	$f_0$
$e_5$	$v_3$	$v_4$	$e_4$	$e_7$	$e_6$	$e_3$	$f_3$	$f_5$
$e_6$	$v_3$	$v_7$	$e_5$	$e_{23}$	$e_4$	$e_{13}$	$f_5$	$f_0$
$e_7$	$v_4$	$v_1$	$e_2$	$e_{13}$	$e_5$	$e_8$	$f_2$	$f_5$
$e_8$	$v_6$	$v_1$	$e_{10}$	$e_7$	$e_2$	$e_{11}$	$f_7$	$f_2$
$e_9$	$v_6$	$v_5$	$e_2$	$e_{15}$	$e_{10}$	$e_{20}$	$f_1$	$f_{12}$
$e_{10}$	$v_6$	$v_{10}$	$e_9$	$e_{11}$	$e_8$	$e_{15}$	$f_{12}$	$f_7$
$e_{11}$	$v_1$	$v_{10}$	$e_8$	$e_{16}$	$e_{12}$	$e_{10}$	$f_7$	$f_8$
$e_{12}$	$v_1$	$v_{12}$	$e_{11}$	$e_{14}$	$e_{13}$	$e_{16}$	$f_8$	$f_6$
$e_{13}$	$v_1$	$v_7$	$e_{12}$	$e_6$	$e_7$	$e_{14}$	$f_6$	$f_5$
$e_{14}$	$v_7$	$v_{12}$	$e_{13}$	$e_{17}$	$e_{23}$	$e_{12}$	$f_6$	$f_4$
$e_{15}$	$v_5$	$v_{10}$	$e_{20}$	$e_{10}$	$e_9$	$e_{19}$	$f_{11}$	$f_{12}$
$e_{16}$	$v_{10}$	$v_{12}$	$e_{18}$	$e_{12}$	$e_{11}$	$e_{17}$	$f_9$	$f_8$
$e_{17}$	$v_{12}$	$v_{11}$	$e_{16}$	$e_{22}$	$e_{14}$	$e_{18}$	$f_9$	$f_4$
$e_{18}$	$v_{10}$	$v_{11}$	$e_{19}$	$e_{17}$	$e_{16}$	$e_{22}$	$f_{10}$	$f_9$
$e_{19}$	$v_{10}$	$v_8$	$e_{15}$	$e_{22}$	$e_{18}$	$e_{20}$	$f_{11}$	$f_{10}$
$e_{20}$	$v_5$	$v_8$	$e_9$	$e_{19}$	$e_{15}$	$e_{21}$	$f_1$	$f_{11}$
$e_{21}$	$v_9$	$v_8$	$e_{23}$	$e_{20}$	$e_1$	$e_{22}$	$f_4$	$f_1$
$e_{22}$	$v_8$	$v_{11}$	$e_{21}$	$e_{18}$	$e_{19}$	$e_{17}$	$f_4$	$f_{10}$
$e_{23}$	$v_9$	$v_7$	$e_1$	$e_{14}$	$e_{21}$	$e_6$	$f_0$	$f_4$

. We can interpret any path obtained in graph G as a trajectory of the cutter since we know the inverse images of all the vertices.

2.2. $OE$-Routing

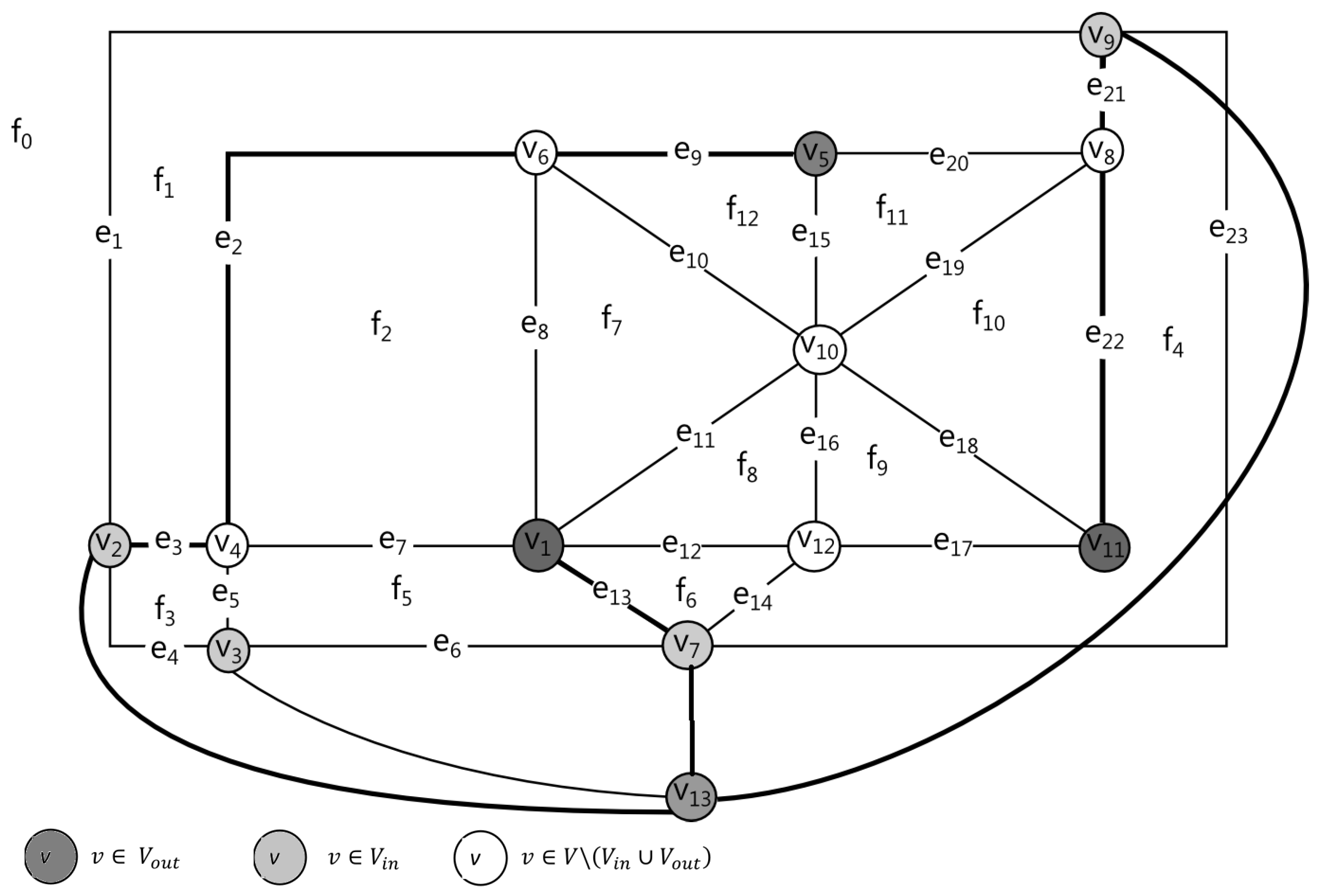
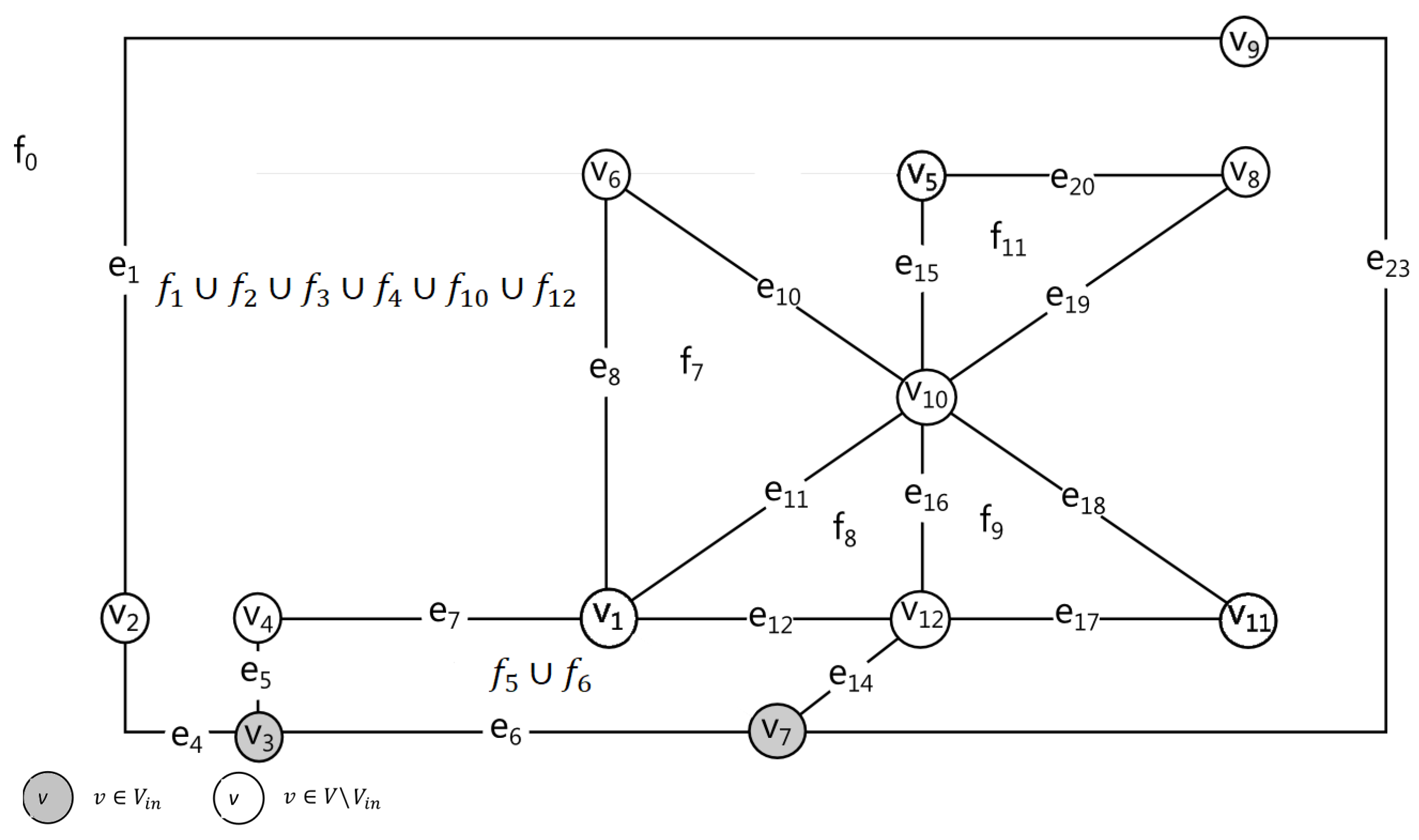
2.2.1. Basic Definitions

Let us consider the formulation and solution of the problem for constructing the routes in a plane graph that satisfy the condition that the interior faces of any their initial parts do not intersect with the edges of the remaining part. Formally, such routes are defined as an ordered sequence of $OE$-chains (ordered enclosing chains) of the graph $G=(V,E)$ and form a class of $OE$-paths. The definitions, proofs and notations of the theory of routes with ordered enclosing ($OE$-routes) are introduced in [19]. Let us give these definitions to avoid the loss of generality.

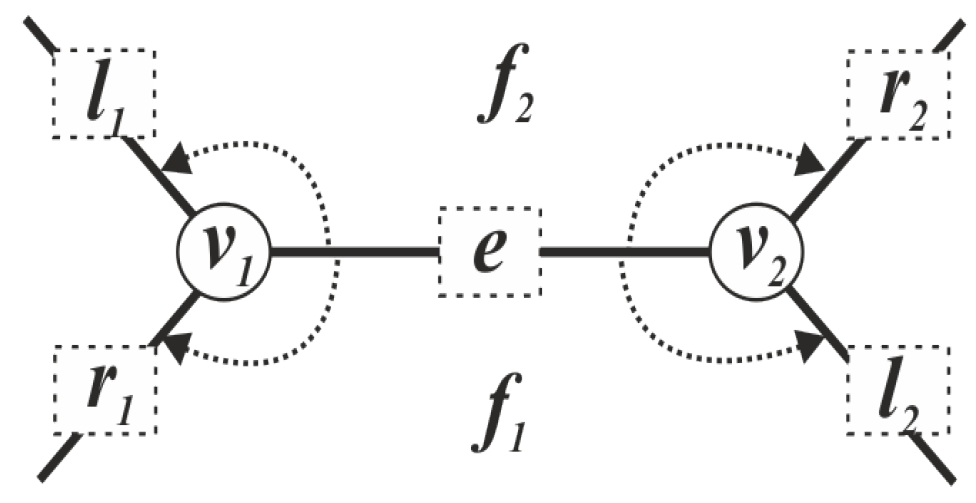
Definition 1.

Chain $C=v_1{e}_1{v}_2{e}_2\dots v_k$ in plane graph G has ordered enclosing (is an $OE$-chain), if for any its initial part $C_l = v_1{e}_1{v}_2{e}_2\dots e_l$, $l\le \left(\right|E\left|\right)$ the condition $\mathrm{Int}\left(C_l\right)\cap E=\varnothing$ holds.

Theorem 2

([19]). Let $G=(V,E)$ be a plane Euler graph. For any vertex $v\in V\left(G\right)$ incident to outer (infinite) face of graph G there exists Euler $OE$-cycle $C = v{e}_1{v}_1{e}_2{v}_2\dots v_{\left|E\right| - 1}{e}_{\left|E\right|}v$.

The proof of this theorem gives the recursive algorithm of $OE$-cycle constructing. This algorithm has computing complexity $O\left(\right|E{|}^2)$. However, there exists non-recursive approach with computing complexity $O\left(\right|V|·log|E\left|\right)$ [28].

Let’s generalize Definition 1 up to the notion of $OE$-route plane graphs (it is possible non-Eulerian and disconnected).

Definition 2.

The ordered sequence of edge-disjoint $OE$-chains

$$\begin{array}{ccc}\hfill C^0& =& v^0{e}_1^0{v}_1^0{e}_2^0...e_{k_0}^0{v}_{k_0}^0,C^1=v^1{e}_1^1{v}_1^1{e}_2^1\dots e_{k_1}^1{v}_{k_1}^1,\dots ,\hfill \\ \hfill C^{n-1}& =& v^{n-1}{e}_1^{n-1}{v}_1^{n-1}{e}_2^{n-1}\dots e_{k_{n-1}}^{n-1}{v}_{k_{n-1}}^{n-1},\hfill \end{array}$$

covering graph G and such that

$$\left(\forall m:m<n\right),\left({\bigcup }_{l=0}^{m-1}\mathrm{Int}\left(C^l\right)\right)\cap \left({\bigcup }_{l=m}^{n-1}{C}^l\right)=\varnothing$$

is a route with ordered enclosing ($OE$-route).

Definition 3.

Let a route consisting of a minimal (in cardinality) ordered sequence of edge-disjoint $OE$-chains in a plane graph G be called an Euler route with ordered enclosing (Euler $OE$-route), and $OE$-chains forming it be the Euler $OE$-cover.

Theorem 3

([27]). Let G connected plane graph, $V_{odd}\left(G\right)$ be the set of its odd vertices, then the cardinality N of Euler $OE$-cover of G satisfies the inequality

$$k=\frac{|V_{odd}\left(G\right)|}{2}\le N\le \left|V_{odd}\left(G\right)\right|=2k$$

holds. The upper and lower bounds are reachable.

The cover capacity is significantly influenced by the presence of bridges in the graph. In their absence, the lower bound is reached, in the case of the existence of vertices of odd degree incident to the outer face; or, if there are no such vertices, the cardinality of the cover is one higher than the lower bound.

The construction of the $OE$-route of the graph G solves the considered cutting problem in the absence of restrictions on self-intersections and the placement of starting (i.e., pierce) points for all chains.

2.2.2. Algorithms Constructing $OE$-Chains for Connected Graph G

Algorithms for constructing $OE$-routes in plane Eulerian graphs are known [28]. The possibility of constructing an $OE$ route in an arbitrary plane graph demonstrates Theorem 4 [24].

Theorem 4.

Let $G=(V,E)$ be plane connected graph without bridges on S. There exists the set of edges $H:(H\cap S)\backslash V=\varnothing$ so that graph $\widehat{G}=(V,E\cup H)$ be Euler, and there exists Euler cycle in graph $\widehat{G}$, such that $C = v_1{e}_1{v}_2{e}_2\dots e_n{v}_1$, $n = \left|E\right| + \left|H\right|$, for any its initial part $C_l = v_1{e}_1{v}_2{e}_2\dots v_l$, $l \le \left|E\right| + \left|H\right|$ the condition $\mathsf{Int}\left(C_l\right)\cap G=\varnothing$ holds.

We use the concept of the edge e rank while considering the algorithms of $OE$-routes constructing.

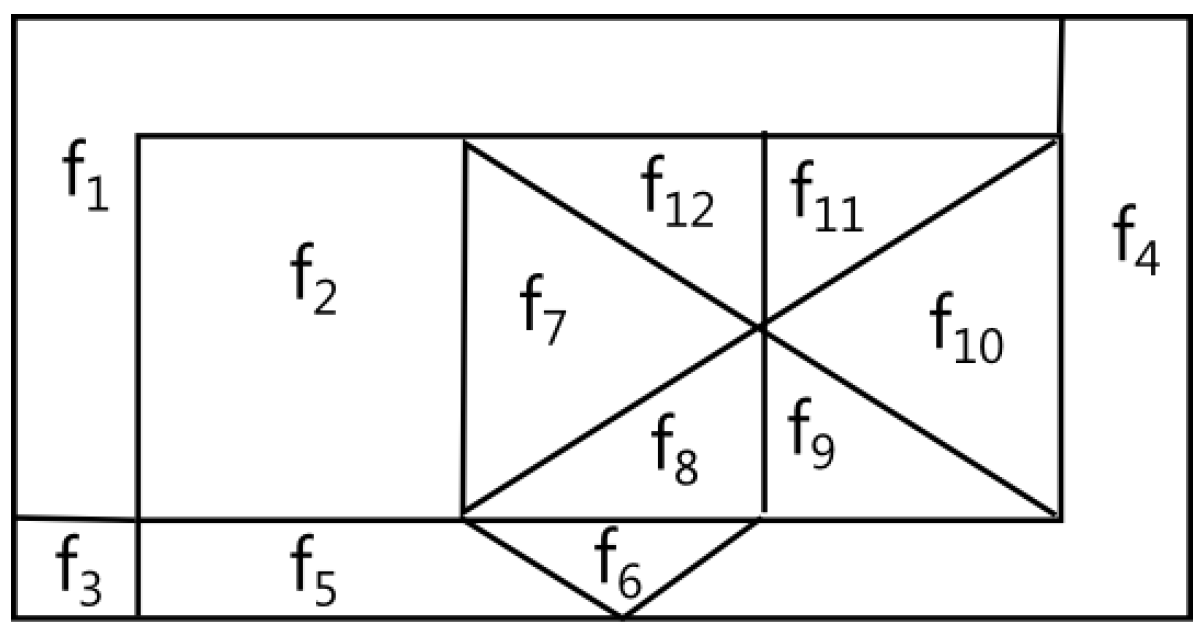
Definition 4.

The rank of edge $e\in E\left(G\right)$ be the value of function $\mathrm{rank}\left(e\right):E\left(G\right)\to \mathbb{N}$ recursively defined as following:

• let $E_1=\{e\in E:e\subset f_0\}$ be the set of edges bounding outer face $f_0$ of graph $G(V,E)$, then $\left(\forall e\in E_1\right)\left(\mathrm{rank}\left(e\right)=1\right)$;
• let $E_k\left(G\right)$ be the set of edges of rank 1 for graph

  $$G_k\left(V,E\backslash \left(\bigcup _{l=1}^{k-1}{E}_l\right)\right),$$
  then $\left(\forall e\in E_k\right)\left(\mathrm{rank}\left(e\right)=k\right)$.

Definition 5

([28]). Let rank of face $f\in F\left(G\right)$ be a value of function $\mathrm{rank}:F\left(G\right)\to {\mathrm{N}}_0$:

$$\mathrm{rank}\left(f\right)=\left\{\begin{array}{cc}0,\hfill & iff=f_0,\hfill \\ \underset{e\in E\left(f\right)}{min}\mathrm{rank}\left(e\right),\hfill & otherwise,\hfill \end{array}\right.$$

where $E\left(f\right)$ be a set of edges incident to outer face $f\in F$.

Definition 6

([28]). Let rank of vertex $v\in V\left(G\right)$ be a value of function $\mathrm{rank}:V\left(G\right)\to \mathrm{N}$: $\mathrm{rank}\left(v\right)={min}_{e\in E\left(v\right)}\mathrm{rank}\left(e\right)$ where $E\left(v\right)$ is a set of edges incident to vertex $v\in V$.

We developed the following polynomial time algorithms for constructing $OE$-routes for plane graphs:

• Euler $OE$-cycle in plane Euler graph (algorithm OE-CYCLE, computing complexity $O\left(\right|V{|}^2)$ [29]);
• connected $OE$-route of Chinese postman for any plane connected graph; removing re-traversed edges will result in a $OE$-route; this route is not optimal either in terms of the number of covering chains or the length of idle passes (algorithm CPP_OE, computing complexity $O\left(\right|E\left(G\right)|·|V\left(G\right)\left|\right)$ [30]);
• a route in plane connected graph without bridges being the $OE$-cover optimal by the number of chains, the length of idle passes may not be optimal (algorithm OECover, computing complexity $O\left(\left|E\right|·log\left|V\right|\right)$ [19]);
• $OE$-route in plane connected graph without bridges with additional edges, connecting the odd vertices (algorithm M-COVER with computing complexity $O\left(\left|E\right|·log\left|V\right|\right)$); this algorithm appended by algorithm of finding the shortest matching between odd vertices allows to obtain $OE$-cover with minimal summary length of additional edges (computing complexity $O\left(\right|E|·\sqrt{\left|V\right|})$) [19].

In this paper, we describe in details those of them that are not published in open access for the convenience of the reader.

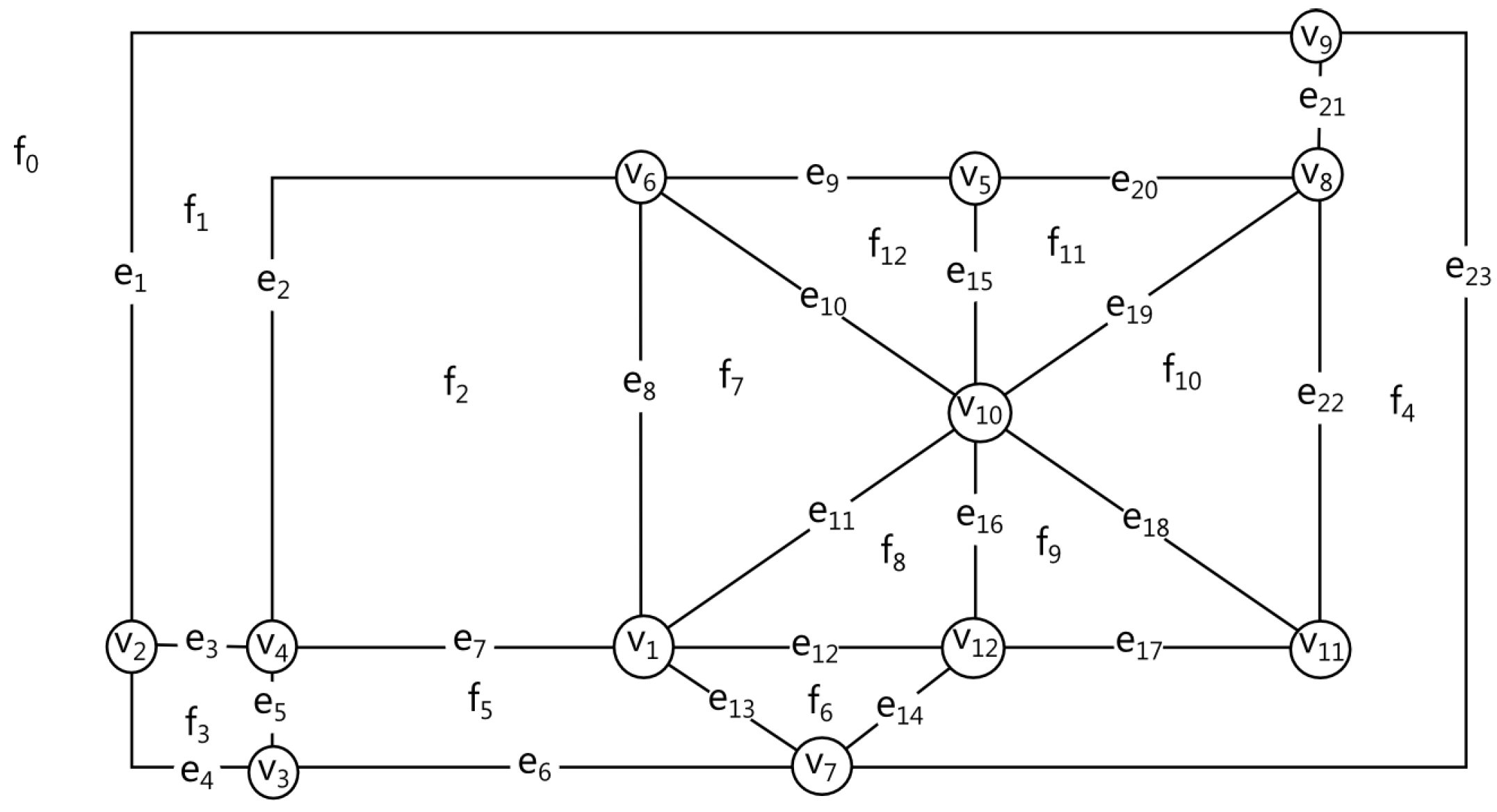
Algorithm 1 OECover covers the plane graph G by an ordered sequence of $OE$-chains. The graph G is encoded by the list of edges, and for each edge e the functions considered in Theorem 1 are defined.

Algorithm 1 Algorithm OECover

Require:  $G=(V,E)$ be a plane graph; $V_{odd}\subseteq V$ be the set of odd vertices; Ensure:  $first\in E$, $last\in E$, ${\mathrm{mark}}_1:E\to E$; 1: Initiate();                     ▷ Assign the initial values of all used variables 2: Order();           ▷ Define the ranks of edges, and form the ordered lists for vertices 3: SortOdd();                  ▷ Sorting of odd vertices by decreasing of their rank 4: if$\{\exists v\in V_{odd}|v\in f_0\}$then                ▷ Define the starting value of a chain 5:      $v^0\leftarrow arg\underset{v\in V_{odd}}{max}\mathrm{rank}\left(v\right);V_{odd}\leftarrow V_{odd}\backslash \left\{v^0\right\}$; 6: else$v^0\leftarrow v|v\in f_0$; 7: end if 8: while ($true$) do 9:     $v\leftarrow \mathrm{FormChain}\left(v^0\right)$;             ▷ Form a chain from the defined vertex 10:     $V_{odd}\leftarrow V_{odd}\backslash \left\{v\right\}$;      ▷ Exclude the starting vertex of current chain from the list 11:     if ( then$V_{odd}=\varnothing$)             ▷ Check the possibility to construct one more chain 12:         break; 13:     end if 14:     $v^0\leftarrow arg\underset{v\in V_{odd}}{max}\mathrm{rank}\left(v\right)$; 15: end while

In the body of the procedure Initiate, the initial values of all used variables are assigned, and the first edge $e_0\in E$ belonging to the boundary of the outer face $f_0$ is defined.

Procedure Order Algorithm 2 functional purpose of the Order procedure is in:

(1)

defining the value $\mathrm{rank}\left(e\right)$ for each edge $e\in E$ (note that the rank of any edge of a plane graph can be determined in time $O\left(\right|E\left|\right)$ using this procedure);

(2)

forming the list $Q\left(v\right)$ of incident edges for each vertex (the edges are ordered in descending order of the $\mathrm{rank}\left(\right)$ value).

Algorithm 2 Procedure Order

1: procedure Order 2:     while $first\ne \infty$ do 3:         while ($\mathrm{mark}\left(ne\right)=\infty$) and ($last\ne ne$) do 4:            M1:                     ▷ Forming the queue of $M1$-marked edges 5:            $\mathrm{rank}\left(ne\right)\leftarrow k$;                      ▷ Define the rank of an edge 6:            ${\mathrm{mark}}_1\left(last\right)\leftarrow ne$; 7:            if $v_2\left(ne\right)\ne v$ then 8:                REPLACE($ne$); 9:            end if 10:            $v\leftarrow v_1\left(ne\right)$; $last\leftarrow ne$; $ne\leftarrow l_1\left(ne\right)$; 11:         end while 12:         $e\leftarrow first$; $first\leftarrow {\mathrm{mark}}_1\left(first\right)$; $v\leftarrow v_2\left(e\right)$; $ne\leftarrow l_2\left(e\right)$; 13:         M2:       ▷ Placing the $M1$-marked edges to the lists of the corresponding vertices 14:         $k\leftarrow \mathrm{rank}\left(e\right)+1$; ${\mathrm{mark}}_1\left(e\right)\leftarrow Stack\left(v_1\left(e\right)\right)$; ${\mathrm{mark}}_2\left(e\right)\leftarrow Stack\left(v\right)$; 15:         if ${\mathrm{mark}}_1\left(e\right)\ne 0$ then 16:           ▷ Form queue of $M1$-marked edges of all unmarked edges bounding $f_1\left(e\right)$ 17:            if $v_1\left(e\right)=v_1\left({\mathrm{mark}}_1\left(e\right)\right)$ then 18:                ${\mathrm{prev}}_1\left({\mathrm{mark}}_1\left(e\right)\right)\leftarrow e$; 19:            else 20:                ${\mathrm{prev}}_2\left({\mathrm{mark}}_1\left(e\right)\right)\leftarrow e$; 21:            end if 22:         end if 23:         if ${\mathrm{mark}}_2\left(e\right)\ne 0$ then      ▷ Pushing of edge to stacks of vertices $v_1\left(e\right)$ and $v_2\left(e\right)$ 24:            if $v=v_1\left({\mathrm{mark}}_2\left(e\right)\right)$ then 25:                ${\mathrm{prev}}_1\left({\mathrm{mark}}_2\left(e\right)\right)\leftarrow e$; 26:            else 27:                ${\mathrm{prev}}_2\left({\mathrm{mark}}_2\left(e\right)\right)\leftarrow e$; 28:            end if 29:            $Stack\left(v\right)\leftarrow e$; $Stack\left(v_1\left(e\right)\right)\leftarrow e$; 30:         end if 31:     end while 32: end procedure

After executing the Initiate and Order procedures, the odd vertices $v\in V_{odd}$ are ordered in ascending order of their rank using the SortOdd procedure. The rank of the vertex v is the value of the function $\mathrm{rank}\left(Stack\right(v\left)\right)$. Then, the loop do…while is executed using the FormChain procedure (see Algorithm 3). This cycle constructs a sequence of $|V_{odd}|/2$ simple paths between pairs of odd vertices. If none of the odd vertices is adjacent to the outer face, then it is necessary to construct a $|V_{odd}|/2+1$ chain, where the first of the constructed paths $C^0$ starts at vertex of even degree $v^0\in f_0$, adjacent outer face, and ends at an odd vertex. All the chains of the cover $C^1,\dots C^{n-1}$ are connecting the odd vertices, and the last one $C^n$ starts at odd vertex, and ends at vertex $v^0\in f_0$.

The aim of FormChain procedure is to obtain the $OE$-chain starting in a given vertex w and ending in some odd vertex $v\in V_{odd}$, $v\ne w$. As a result of the procedure, a simple chain will be obtained $C^i=v_0^i{e}_1^i{v}_1^i{e}_2^i\dots e_k^i{v}_k^i$, for which $v_1^i,v_2^i,\dots v_{k-1}\notin V_{odd}^i,$ and for $i\ne 0$ and $i\ne n$ vertices $v_0^i,v_k^i\in V_{odd},$ if $i=0$ vertex $v_k^i\in V_{odd},$ and if $i=n$ vertex $v_0^i\in V_{odd}$,

$$e_i=arg\underset{e\in E\left(v_i\right)\backslash \left\{e_l\right|l<i\}}{max}\mathrm{rank}\left(e\right),v_{i+1}=\overline{v_1}\left(e_i\right),i=1,2,\dots ,k,$$

moreover, for any initial part $C_l=v^0{e}_1{v}_1{e}_2{v}_2\dots e_l$, $l\le k$ and for any vertex $v\in V$ the inequality

$$\underset{e\in E\left(v\right)\bigcap E\left(C_l\right)}{min}\mathrm{rank}\left(e\right)>\underset{e\in E\left(v\right)\backslash E\left(C_l\right)}{max}\mathrm{rank}\left(e\right)$$

holds.

Algorithm 3 Procedure FormChain

1: procedureFormChain(In: w starting vertex of a chain; Out: v ending vertex of a chain) 2:     $v\leftarrow w$; $e\leftarrow Q\left(v\right)$; 3:     do 4:     $e_1=arg{max}_{e\in Q\left(v\right)}\mathrm{rank}\left(e\right)$; 5:     $e_2=arg{max}_{e\in Q\left(v\right):f_1\left(e\right)=f_2\left(e\right)}\mathrm{rank}\left(e\right)$; 6:     if $\mathrm{rank}\left(e_1\right)=\mathrm{rank}\left(e_2\right)$ then      ▷ Find the edge of maximal rank, a bridge if possible 7:         $e=e_2$; 8:     else 9:         $e=e_1$; 10:     end if 11:     if $v=v_1\left(e\right)$ then 12:         REPLACE(e);    ▷ Change the indexes of functions for edge e from k to $3-k$, $k=1,2$ 13:     end if 14:     $E\left(G\right)\leftarrow E\left(G\right)\backslash \left\{e\right\}$;          ▷ Delete edge e and delete faces divided by edge e 15:     $Trail\leftarrow Trail\cup \left\{e\right\}$; 16:     $v\leftarrow v_1\left(e\right)$; 17:     while ($v\notin V_{odd}\&Q\left(v\right)\ne \varnothing$); 18:     return v; 19: end procedure

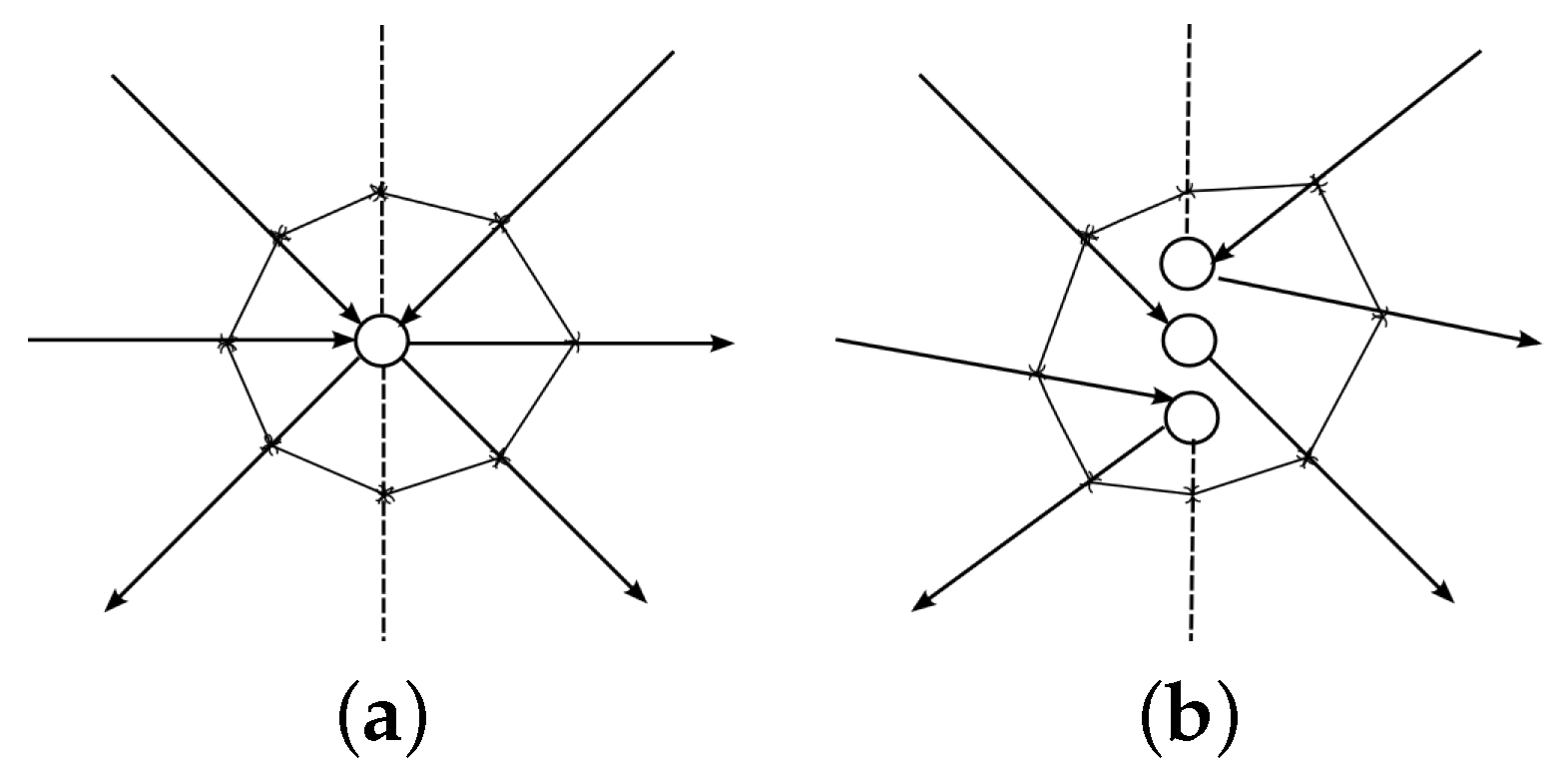
Theorem 5.

Let $G=(V,E)$ be a plane connected bridgeless graph on S, and $V_{odd}\subset V$ be the set of odd vertices. For any matching M on set $V_{Odd}$ in graph $\widehat{G}=(V,E\cup M)$, there exists Euler cycle $C = v_1{e}_1{v}_2{e}_2\dots e_n{v}_1$, $n = \left|E\right| + \left|M\right|$, for any initial part $C_l = v_1{e}_1{v}_2{e}_2\dots v_l$, $l \le \left|E\right| + \left|M\right|$ of which, the condition $\mathsf{Int}\left(C_l\right)\cap G=\varnothing$ holds.

The proof of Theorem 5 is constructive and consists in proving the efficiency of the algorithm M-Cover (see Algorithm 4) for constructing a cover for any matching on the set of odd vertices [19].

Algorithm 4 Algorithm M-Cover

Require:  plane connected graph G, functions $v_k\left(e\right),l_k\left(e\right)$,  $e\in E\left(G\right)$,  $k=1,2$; vertex $v_0\in V\left(G\right)$ incident to outer face; matching M on set of odd vertices $V_{Odd}$; boolean function ${\mathtt{Idle}}_M:V_{Odd}\to \left\{\mathbf{false},\mathbf{true}\right\}$ on set of odd vertices $V_{Odd}$; Ensure:  almost ordered set C of $OE$-chains of graph G, being the $OE$-cover of graph G; 1: Order (G);                   ▷ Define $\mathrm{rank}\left(\right)$ for all $e\in E\left(G\right),v\in V\left(G\right)$ 2: $v:=v_0$;                                 ▷ Constructing 3: while  $Q\left(v\right)\ne \varnothing$ do 4:     FormChain($v,v$); 5:     if ${\mathtt{Idle}}_M\left(v\right)\vee (Q\left(v\right)=\varnothing )$ then 6:         $u\leftarrow M\left(v\right)$;               ▷ Vertex u is a pair for vertex v in matching M 7:         $V_{Odd}\leftarrow V_{Odd}\backslash \{u,v\}$                ▷ Delete vertices $u,v$ from $V_{Odd}$ 8:         $v\leftarrow u$;                     ▷ Finish constructing the current chain 9:     end if 10: end while 11: End of algorithm

The main difference of this algorithm from $OE$-Cover is that for each vertex $v\in V_{Odd}$ the next one $u=M\left(v\right)\in V_{Odd}$ is fixed. It is the vertex to which the transition is made. Algorithm M-Cover can finish constructing the current chain both at the first visit to the vertex $v\in V_{Odd}$, and at the moment when the vertex becomes dead-end (i.e., $Q\left(v\right)=\varnothing$). To determine at what moment to finish the constructing of the chain, the values of

$${\mathtt{Idle}}_M\left(v\right)=(\mathrm{rank}\left(v\right)\le \mathrm{rank}\left(M\left(v\right)\right))\wedge \left(f_{M\left(v\right)}⪰f_v\right),v\in V_{Odd},$$

are used, where $f_w=arg{min}_{f:v\in f\subset F\left(G\right)}\mathrm{rank}\left(f\right),w\in V_{Odd}$. Here ⪰ is partial ordering on $F\left(G\right)$ induced by tree $T_{f0}^{G{}^{\prime }}$ of shortest paths to vertex $f_0\in F$:

$$(f_i⪰f_j)\leftrightarrow \left(f_j\mathrm{belongs}\mathrm{to}\mathrm{chain}{T}_{f_0}^{G{}^{\prime }}\mathrm{between}{f}_{i}and{f}_0\right).$$

To construct the optimal cover (i.e., cover with a minimal length of additional edges) it is enough to take the shortest matching on set of odd vertices $V_{odd}$ as M. This task is realized by the following Algorithm 5.

Algorithm 5 OptimalCover

Require:  plane graph G represented by the list of edges with defined functions $v_k\left(e\right)$, $l_k\left(e\right)$, $f_k\left(e\right)$, $k=1,2$ Ensure:  cover of graph G by $OE$-chains $C_j$, $j=1,\dots ,|V_{odd}|/2$ 1: Define the shortest matching M on set $V_{odd}$ 2: Run algorithm M-Cover for graph G and matching M 3: Stop

Obviously, Algorithm 5 allows us to construct the optimal $OE$-cover, and its computing complexity is not greater than $O\left(\right|V{|}^3)$ (but by using special data structures and algorithms, it is possible to run this algorithm by the time not exceeding $O\left(\right|E\left(G\right)|·\sqrt{\left|V\right(G\left)\right|})$). This estimation is defined by the computing complexity of Step 1.

2.3. Constructing of Routes Satisfying the Combination of Constraints

During the technological preparation of the cutting process, various constraints on the trajectory of the cutting tool may appear. One of them is the task considered above, where the cut off part of the sheet of the obtained route does not require additional cuts. However, in practice, it is required to fulfil additional constraints on the absence of intersection of cuts and on allowable pierce points that are start points of $OE$-chains forming this route.

To solve a problem of the cuts intersection absence at each vertex of the graph, a cyclic order of traversing the edges is specified, and the continuation of the traversal along the chain is carried out only by this cyclic order. In the general case, the problem of finding such a chain in a graph belongs to the class of $\mathcal{NP}$-complete problems, but there are effective algorithms of its solution for some special cases.

2.3.1. $AOE$-Routs

Let us consider Euler chain

$$T=v_0,k_1,v_1,\dots ,k_n,v_n,v_n=v_0$$

in graph $G=(V,E)$. Let we know the cyclic order $O^{\pm }\left(v\right)$ defining the transitions system $A_G\left(v\right)\subseteq O^{\pm }\left(v\right)$ for each vertex $v\in V$. In the case when $\forall v\in V\left(G\right)$ $A_G\left(v\right)=O^{\pm }\left(v\right)$ the transitions system $A_G\left(v\right)$ is called the full transitions system, and chain satisfying this system is $A_G$-compatible.

Definition 7.

$A_G$-compatible chain T is called A-chain. Thus, consecutive edges in the chain T incident to vertex v are the neighbours in the cyclic order $O^{\pm }\left(v\right)$ [31].

Definition 8.

The chain is called $AOE$-chain if it is $OE$-chain and A-chain simultaneously [32].

Theorem 6.

If there is A-chain in a plane graph G then there is also $AOE$-chain in this graph [32].

Theorem 7.

Plane connected 4-regular graph G has $AOE$-chain.

To prove this theorem, we need to introduce some definitions and prove some propositions.

Definition 9.

The partial graph $G_k$ of graph G for which $E\left(G_k\right)=\{e\in E\left(G\right):\mathrm{rank}\left(\mathrm{e}\right)\ge \mathrm{k}\}$ is called partial graph of rank k.

Preliminarily, the “correct” splitting of all cut-vertices of partial graphs $G_k$ is performed, so that as a result of the splitting, we get a graph for which any partial graph $G_k$ has no cut-vertices. The vertices splitting is a local operation, hence the sequence of splitting does not affect the total result. The “correct” transition is one between arcs corresponding of a cyclic order and incident to the different pairs of faces (see Figure 4b)). The splitting result, in this case, is shown in Figure 4b).

These propositions imply the effectiveness of the CUT-POINT-SPLITTING Algorithm 6 running in time not greater than $O\left(\right|E\left(G\right)|log|V\left(G\right)\left|\right)$.

Theorem 8.

Algorithm $AOE$-CHAIN constructs $AOE$-chain for plane connected 4-regular graph G any partial graph $G_k$, $k=1,2,\dots$ of which has no cut-vertices. Algorithm solves the problem by the time $O\left(\right|E\left(G\right)|·log|V\left(G\right)\left|\right)$.

The proof of this algorithm’s effectiveness [32] finishes the proof of Theorem 7.

Proposition 1.

Vertex incident to four edges bounding outer face is cut-vertex.

Proposition 2.

The outer face of a partial graph $G_k$ is the union of all faces of rank k in graph G.

Let us consider the Algorithm 7 for constructing the $AOE$-chain for plane connected 4-regular graph [32,33].

Algorithm 6 CUT-POINT-SPLITTING

Require:  plane connected 4-regular graph $G=(V,E)$ represented for all $e\in E\left(G\right)$ by functions $v_s,l_s,r_s$ , $s=1,2$. Ensure:  homeomorphic image of graph $G=(V,E)$ for which any partial graph $G_k$ has no cut-vertices. Supplementary data $\forall v\in V\left(G\right)$: $\mathrm{point}\left(v\right)$ is the array of pointers to one of edges incident to vertex v; $\mathrm{rank}\left(v\right)$ is the array of vertices ranks; $\mathrm{count}\left(v\right)$ is the counter of incident edges of one rank for each vertex; Supplementary data $\forall f\in F\left(G\right)$: array $rank\left(f\right)$. 1: Initiate(): 2: for all $v\in V\left(G\right)$ do      ▷ Zero the counter of edges of the same rank incident to a vertex 3:     $\mathrm{point}\left(v\right):=0$; $\mathrm{count}\left(v\right):=0$ 4: end for 5: Ranking(G)          ▷ Determining the rank of all vertices, edges and faces of a graph 6: Finding():       ▷ Defining the cut-vertices 7: for all $e\in E\left(G\right)$ do 8:     $\mathrm{point}\left(v_1\left(e\right)\right):\mathrm{point}\left(v_2\left(e\right)\right):=e=e$ 9: end for 10: for all $v\in V\left(G\right)$ do                   ▷ To look through all the vertices 11:      12:      $e:=\mathrm{point}\left(v\right);k:=\mathrm{rank}\left(v\right)$        ▷ Save the rank value k of the incident edge e 13:     if $v=v_1\left(e\right)$ then                    ▷ Define the direction of edge e 14:          $s:=1$ 15:     else 16:         $s:=2$ 17:     end if 18:      $e:=l_s\left(e\right)$          ▷ Counting the number of rank k edges incident to vertex v 19:     for $i=1$ up to 4 do 20:         if $\mathrm{rank}\left(e\right)=k$ then 21:            $\mathrm{count}\left(v\right):=\mathrm{count}\left(v\right)+1$ 22:            if $i<4$ then 23:                 $e:=l_s\left(e\right)$ 24:            end if 25:         end if 26:     end for 27:     if $\mathrm{count}\left(v\right)=4$then                 ▷ Split the vertex if it is cut-vertex 28:         if ($f_s\left(e\right)=f_s\left(l_s\left(e\right)\right)$ and $f_{3-s}\left(e\right)=f_{3-s}\left(l_s\left(e\right)\right)$) or 29:                   or ($f_s\left(e\right)=f_{3-s}\left(l_s\left(e\right)\right)$ and $f_{3-s}\left(e\right)=f_s\left(l_s\left(e\right)\right)$) then 30:             $e^{*}:=l_s\left(e\right)$, $l_s\left(e\right):=r_s\left(e\right)$, $r_s\left(r_s\left(e\right)\right):=e$, 31:             $r_s\left(e^{*}\right):=l_s\left(e^{*}\right)$, $l_s\left(l_s\left(e^{*}\right)\right):=e^{*}$ 32:         else 33:            $e^{*}:=r_s\left(e\right)$, $r_s\left(e\right):=l_s\left(e\right)$, $l_s(l_s\left(e\right):=e$, 34:            $l_s\left(e^{*}\right):=r_s\left(e^{*}\right)$, $r_s\left(r_s\left(e^{*}\right)\right):=e^{*}$ 35:         end if 36:     end if 37: end for

2.3.2. $NOE$-Routes

Algorithm 6 $AOE$-CHAIN is used for running the algorithm NOE-CHAIN (see Algorithm 8) to obtain the non-intersecting $OE$-chain for plane connected graph [26].

Definition 10

([26]). Let Eulerian cycle C of plane graph G be non-intersecting if it is homeomorphic to a closed Jordan curve without intersections obtained from graph G by applying of $O\left(\right|E\left(G\right)\left|\right)$ splittings of its vertices.

Algorithm 7 Algorithm $AOE$-CHAIN

Require:  plane connected 4-regular graph $G=(V,E)$ defined by functions $v_k,l_k,r_k$, $k=1,2$ (see Theorem 1);   starting vertex $v\in V\left(f_0\right)$. Ensure:  $AChain$ – output stream containing $AOE$-chain obtained by the algorithm. 1: Initiate(G, $v_0$); 2: Ranking(G); 3: CUT_POINT_SPLITTING (G);       ▷ Deleting of cut-vertices in partial graphs of each rank 4:                                        ▷ Constructing 5: $e=arg{max}_{e\in E\left(v\right)}\mathrm{rank}\left(e\right)$        ▷ Choose the edge of maximal rank incident to vertex v 6: repeat 7:     if $v\ne v_1\left(e\right)$ then 8:         REPLACE(e) 9:     end if             ▷ If necessary, adjust the numbering of functions for the edge e 10:     $AChain\leftarrow$Print($v,e$)           ▷ Add edge e to the resulting sequence $AChain$ 11:     $\mathrm{mark}\left(e\right):=\mathbf{false}$; counter:=counter+1; $v:=v_2\left(e\right)$      ▷ Mark the current edge as passed 12:     if ($\mathrm{rank}\left(r_2\left(e\right)\right)\ge \mathrm{rank}\left(l_2\left(e\right)\right)$) then    ▷ Choose the next edge of maximal possible rank 13:         if $\mathrm{mark}(r_2\left(e\right)$) then             ▷ Check if the chosen edge is already passed 14:            $e:=r_2\left(e\right)$            ▷ The passed edges have False value in the arra $mark$ 15:         else 16:            $e:=l_2\left(e\right)$ 17:         end if 18:     else 19:         if ($\mathrm{mark}(l_2\left(e\right)$) then                    ▷ Choose the not passed edge 20:            $e:=l_2\left(e\right)$ 21:         else 22:            $e:=r_2\left(e\right)$ 23:         end if 24:     end if 25: until (counter $>\left|E\right(G\left)\right|$)           ▷ Finish the cycle when all the edges are scanned 26: End of Algorithm

Algorithm 8 NOE-CHAIN (G)

Require:  plane Euler graph G defined by functions $v_k\left(e\right)$, $l_k\left(e\right)$, $r_k\left(e\right)$, $f_k\left(e\right)$, $k=1,2$ (see Theorem 1) and $\mathrm{rank}\left(e\right)$; Ensure:  C as $NOE$-chain in graph G; 1: $\widehat{G}=\mathsf{NonIntersecting}\left(G\right);$                      ▷ Split all vertices of degree higher than 4 2: $C^{*}$=AOE_CHAIN($\widehat{G}$);                           ▷ Obtain $AOE$-chain in graph $\tilde{G}$ 3: C=Absorb($C^{*}$);                   ▷ Absorb all split vertices and obtain the resulting $NOE$-chain

Its execution means transforming the initial graph to a plane connected 4-regular graph by splitting the vertices of degree greater than 4. To obtain the Euler $NOE$-cycle in a plane Euler graph without given transitions system, we can act as follows. Let us define boolean function

$$\mathrm{Checked}\left(v\right)=\left\{\begin{array}{c}\mathtt{true},\mathrm{if}\mathrm{the}\mathrm{vertex}\mathrm{is}\mathrm{viewed};\hfill \\ \mathtt{false},\mathrm{otherwise};\hfill \end{array}\right.$$

on the set of vertices $V\left(G\right)$. When performing initialization, declare all vertices not viewed. Function NonIntersecting (G) (Algorithm 9) splits all vertices $v\in V\left(G\right)$ of degree more than $2k-1$ ($k\ge 3$) to k fictive vertices of degree 4 and introduces k fictive edges incident to the vertices obtained as a result of splitting and forming a cycle (see Figure 5).

Algorithm 9 Function NonIntersecting (G)

Require:  plane Euler graph G defined by functions $v_k\left(e\right)$, $l_k\left(e\right)$, $r_k\left(e\right)$, $f_k\left(e\right)$, $k=1,2$ (see Theorem 1) and $\mathrm{rank}\left(e\right)$; Ensure:  plane connected 4-regular graph $G^{*}$ defined as the same; 1: for all $v\in V\left(G\right)$ do                   ▷ Initialization of $Checked\left(v\right)$ function 2:     $Checked\left(v\right):=\mathbf{false}$; 3: end for 4: for all ($e\in E\left(G\right)$ ) do       ▷ Searching of vertices of degree greater than 4 and their splitting 5:     $k:=1$;                 ▷ Consider vertex with index 1, then vertex with index 2 6:     while ($k\le 2$) do 7:         if (! $Checked\left(v_k\left(e\right)\right)$) then          ▷ Process only a previously unprocessed vertex 8:            if ($k=2$) then                           ▷ Improve the indexes 9:                REPLACE(e);                          ▷ Process vertices $v_1\left(e\right)$ 10:            end if 11:             Handle ( e);                    ▷ Call the function to process vertex $v_1\left(e\right)$ 12:            $Checked\left(v_1\left(e\right)\right):=\mathbf{true};$               ▷ Mark the vertex as considered 13:         end if 14:         $k:=k+1$; 15:     end while 16: end for End of function

In the body of function we use the procedure Handle (e, $v_k\left(e\right)$, k), which processes each unconsidered graph vertex.

Procedure Algorithm 10 during cycle repeat–until (lines 6–11) counts the degree d of current vertex v. If $d>4$, then the second cycle repeat–until (lines 12–23) runs. Here the handled vertex is split to $d/2$ fictive vertices, and d fictive edges incident to these vertices. There fictive edges form a cycle.

In lines 18–23, we not only change the pointers to edges, but also create a new (fictive) face F, incident to all fictive vertices and edges, and also define the ranks of fictive edges [26].

Definition 11.

The rank of fictive edge (line 20) is equal to the rank of the initial graph face incident to the entered fictive edge.

The introduced by Handle procedure $k/2$ fictive vertices and k fictive edges incident to these vertices are forming a cycle. As a result of processing all graph G vertices, we obtain the modified plane connected 4-regular graph $G^{*}$. Algorithm AOE-CHAIN() constructing $AOE$-chain $T^{*}$ can be implemented to graph $G^{*}$. The considered procedure is realized in algorithm NonIntersecting (see Algorithm 9). If then in $T^{*}$ all the fictive edges and the incident vertices obtained by splitting the vertex v are replaced by v, then we obtain the $NOE$-chain T in the original graph G.

Algorithm 10 Procedure Handle (e)

1: procedure Handle(e) 2:     $v:=v_1\left(e\right)$;                                    ▷ Splitting vertex 3:     $e_{first}:=e$;                             ▷ Save the first considered edge 4:     $d:=0$;                         ▷ Initialization of a counter for vertex degree d 5:     $F:=FaceNum\left(\right)+1$;                     ▷ Define the number of a new face 6:     repeat                              ▷ Pass 1: Defining the degree of v 7:          $le:=l_1\left(e\right)$; 8:         if ($v_1\left(le\right)\ne v$) then REPLACE($le$); 9:        end if                            ▷ Change the indexing of functions if necessary 10:         $e:=le$; $d:=d+1$;  ▷ Consider the edge when calculating the degree and move on to the next one 11:     until ($e=e_{first}$);                ▷ Repeat until all edges incident v have been considered 12:     if ($d>4$) then                   ▷ If the degree of current vertex is greater than 4 13:         $e:=e_{first}$;                         ▷ Begin from the first considered edge 14:         $le:=l_k\left(e\right)$;                        ▷ Define the number of its left neighbour 15:         $e_{next}:=l_k\left(le\right)$;                       ▷ Save the edge for the next iteration 16:          $fl:=$ new EDGE; $fle:=fl$; $e_{first}:=e$;          ▷ Introduce a fictive edge adjacent to $le$ 17:         repeat                               ▷ Put the pointers for edges 18:            $e:=e_{next}$; $le:=l_k\left(e\right)$; $fr:=fl$; 19:            $f_1\left(fl\right):=F$; $f_2\left(fl\right):=f_2\left(e\right)$;             ▷ Define faces adjacent to a fictive edge 20:            $\mathrm{rank}\left(fl\right):=\mathrm{facerank}\left(f_2\left(fl\right)\right)$;                 ▷ Define ”rank” of fictive edge 21:                        ▷ Function facerank() defines the rank of a face according to the definition 22:            $fl:=$ new EDGE; $e_{next}:= l_k\left(le\right)$; 23:         until ($l_k\left(le\right)=e_{first}$); 24:     end if 25: end procedure

Theorem 9.

Algorithm NOE-CHAIN solves the task of constructing the $NOE$-chain for plane Euler graph by the time $O\left(\right|E\left(G\right){|}^2)$ [26].

Note that this algorithm constructs a $NOE$-chain in a plane Euler graph. In the case of a plane non-Euler (generally disconnected) graph G, it is necessary to split all vertices of degree higher than 4 by the Algorithm 10. As a result, we get a graph with vertex degrees equal to 3 or 4. For this graph, we apply the algorithm for constructing an $AOE$-cover. In the chains of the resulting cover, remove all artificial edges and absorb all split vertices. As a result, we get $NOE$-cover.

2.3.3. $PPOE$-Routes

Let us consider a problem arising in the case of intrusion of constraints on the location of pierce points. Obviously, the number of pierce points is determined by the number of covering chains. According to Theorem 3, the number of pierce points is at least $|V_{odd}|/2$. This problem can be formalized as following.

• Let faces $F_{in}\left(G\right)\subset F\left(G\right)$ allow piercing.
• Let odd vertices $v^{-}\in V_{in}\left(G\right)\subset V\left(G\right)$ be incident to face $F_{in}\left(G\right)$.
• Let for odd vertices $v^{+}\in V_{out}=V_{odd}\backslash V_{in}$ piercing is forbidden.

If the constructed route in the graph is an $OE$ route and all the initial vertices of the covering chains belong to $V_{in}\left(G\right)$, then this route can be used as a basis for constructing a route for the cutter trajectory for laser cutting process. Let these routes be called $PPOE$-routes [27].

Definition 12.

Let chain $C=v_1{e}_1{v}_2{e}_2\dots v_k$ be called $PPOE$-chain , if it is $OE$-chain and starts from vertex $v_1\in V_{in}\left(G\right)$.

Definition 13.

Let$PPOE$-cover of graph G be such an $OE$-cover of G, consisting of $PPOE$-chains.

Definition 14.

An ordered sequence of edge-disjoint $PPOE$-chains in a plane graph G of the minimal cardinality is called an Euler $PPOE$-cover.

The problem of determining the realizability of a cutting plan can be formulated as determining the existence of an Euler $PPOE$-cover for a plane graph that is a homeomorphic image of the corresponding cutting plan. Following the existing restrictions, we can formulate the following necessary condition for the existence of a $PPOE$-cover.

Theorem 10.

Plane connected graph $G(V,F,E)$ without bridges has $PPOE$-cover if and only if the cardinality of minimal $\{V_{in},V_{out}\}$-cut is at least $|V_{out}|$.

Proof. 

The validity of the necessary condition is obvious, sufficiency follows from the effectiveness of Algorithm 11 solves the problem of constructing $PPOE$-cover for a plane graph $G(V,E)$ without bridges.    □

To find minimal $\{V_{in},V_{out}\}$-cut let us construct a network

$$N\left(V\cup \left\{w\right\},A\cup \left(\left\{w\right\}\times V_{in}\right)\right)$$

(i.e., directed graph with source w), in which

• a pair of arcs $\left(u,v\right), \left(v,u\right)\in A\left(N\right)$ of capacity 1 corresponds to edge $e= \left\{u,v\right\} \in E\left(G\right)$;
• vertices $v^{+}\in V_{out}\left(N\right)$, i.e., points of possible end of chain, are the sinks of a unit power flow;
• vertices $v^{-}\in V_{in}\left(N\right)$, i.e., possible pierce points, may be source of the unit.

Cardinality of minimal $\{V_{in},V_{out}\}$-cut can be obtained as optimal value of problem

$$\begin{array}{c}{\displaystyle \sum _{(u,v)\in A\left(N\right)}x(u,v)\to min,}\end{array}$$

(1)

$$\begin{array}{c}{\displaystyle \sum _{v:(u,v)\in A\left(N\right)}x(u,v)-\sum _{v:(v,u)\in A\left(N\right)}x(v,u)=1,u\in V_{out}\left(N\right),}\end{array}$$

(2)

$$\begin{array}{c}{\displaystyle -\sum _{v:(u,v)\in A\left(N\right)}x(u,v)+\sum _{v:(v,u)\in A\left(N\right)}x(v,u)=-x(w,u),u\in V_{in}\left(N\right),}\end{array}$$

(3)

$$\begin{array}{c}{\displaystyle \sum _{v:(u,v)\in A\left(N\right)}x(u,v)-\sum _{v:(v,u)\in A\left(N\right)}x(v,u)=0,u\in V\backslash (V_{out}\left(N\right)\cup V_{in}\left(N\right)),}\end{array}$$

(4)

$$\begin{array}{c}{\displaystyle \sum _{v\in V_{in}\left(N\right)}x(w,v)=\left|V_{out}\left(N\right)\right|,}\end{array}$$

(5)

$$\begin{array}{c}0\le x(u,v)\le 1,(u,v)\in A\left(N\right),\end{array}$$

(6)

$$\begin{array}{c}0\le x(w,u)\le 1,u\in V_{in}\left(N\right),\end{array}$$

(7)

where w is a common source with capacity $|V_{out}|$ adjacent to all $v\in V_{in}$ to network N.

Let $x:A\to \left\{0,1\right\}$ be optimal solution of problem (1)–(7). Let us construct a sequence of disjoint chains $C_1,C_2,\dots C_{|V_{out}|}$, containing all the flow holders of x and only them. It is possible to «correctly» split each vertex $v\in V\left(G\right)$ to the dummy vertices with «correct» union of active arcs lists, while it is possible (i.e., taking into account the cyclic order on the set of arcs and their orientations). The examples of «correct» splitting and uniting are shown in Figure 6. The result of this step is a sequence of disjoint chains $C_1,C_2,\dots C_{|V_{out}|}$, containing all the flow holders and only them. The above allows us to propose the Algorithm 11 $PPOE$-covering.

Algorithm 11 Algorithm $PPOE$-covering

Require:  plane graph $G(V,F,E)$ without bridges, defined for all $e\in E\left(G\right)$ functions $v_k\left(e\right)$, $l_k\left(e\right)$, $r_k\left(e\right)$, $f_k\left(e\right)$, $k=1,2$ (see Theorem 1) $\mathrm{rank}\left(e\right)$, functions $\mathrm{rank}\left(v\right),v\in V\left(G\right)$, $\mathrm{rank}\left(f\right),f\in F\left(G\right)$; subsets $V_{out},V_{in}\subset V:|V_{in}|\ge |V_{out}|$; subset $\{F_{in}\subset F\}$ of faces that allow piercing. Ensure:  PPOE-cover of graph $G(V,E)$: ${\tilde{C}}_1,{\tilde{C}}_2,\dots {\tilde{C}}_{|V_{out}|},C_{|V_{out}|+1},\dots ,C_M.$ 1: Construct a network $N\left(V\cup \left\{w\right\},A\cup \left(\left\{w\right\}\times V_{in}\right)\right)$. 2: if ($V_{out}=\varnothing$) then 3:      Run Algorithm 5 OptimalCover for graph G 4:     Return(Cover of graph G by $OE$-chains $C_j$, $j=1,...,|V_{odd}\left(G\right)|/2$) 5: end if 6: if problem (2)–(7) is unsolvable then 7:     Rteurn($PPOE$-cover does not exist) 8: else 9:     Let $x:A\left(N\right) \to \left\{0,1\right\}$ be optimal solution of problem (2)–(7) 10:     For each active arc $(u,v):x(u,v)=1$ create a list, including this arc and only it 11:     Find a sequence of disjoint chains $C_1,C_2,\dots C_{|V_{out}|}$, containing all the flow holders and only them with usage for each vertex $v\in V\left(G\right)$ of «correctly» splitting to the dummy vertices (see Figure 6) 12:     Construct a partial graph $$\tilde{G}=G\backslash \left(\bigcup _{i=1}^{|V_{out}|}{C}_i\right),E\left(\tilde{G}\right)=\left(E\left(G\right)\backslash \left(\bigcup _{i=1}^{|V_{out}|}{C}_i\right)\right),$$ in which all vertices $v\in V_{out}$, for which piercing is forbidden, are the vertices of even degree. 13: end if 14: For $\tilde{G}$ run algorithm OptimalCover 5. The result of this step is a sequence of disjoint chains $$C_{|V_{out}|+1},\dots ,C_{|V_{out}|+|M|}.$$ 15: Return( ${\tilde{C}}_1,{\tilde{C}}_2,\dots {\tilde{C}}_{|V_{out}|},C_{|V_{out}|+1},\dots ,C_M.$) 16: End of algorithm

Theorem 11.

Algorithm $PPOE$-covering solves the problem of constructing $PPOE$-cover for a plane graph $G(V,E)$ without bridges by the time not exceeding $O\left(\right|V{|}^3)$.

Proof. 

The route consisting of chains $C_1,C_2,\dots C_{|V_{out}|}$ is the edge-disjoint $OE$-route (due to unit carrying capacity of arcs). Partial graph $\tilde{G}$ does not contain any edges belonging to chains $C_i$, $i=1,\dots ,|V_{out}|$ by definition. All graph $\tilde{G}$ vertices avoiding piercing have even degree due to constructions. As a result of running Step 9, we get the continuation

$$C_{|V_{out}|+1},\dots ,C_{|V_{out}|+|M|}$$

of route which is the $OE$-route in graph $\tilde{G}$ covering all edges of graph $\tilde{G}$, and starting vertex $v \in V_{in}$ of each chain $C_i$, $i = |V_{out}| + 1,\dots |V_{out}| + |M|$ is permissible for piercing. Hence, the route

$$C_1,C_2,\dots C_{|V_{out}|},C_{|V_{out}|+1},\dots ,C_{|V_{out}|+|M|}$$

is $PPOE$-cover of initial graph G.

Let us estimate the computing complexity of this algorithm. Step 1 allows to get the network by time $O\left(\right|E\left|\right)$. Step 2 verifies the condition and it is completed in $O\left(1\right)$. Circulation in step 3 may be obtained by time not exceeding $O\left(\right|V{|}^3)$ [34]. Step 4 verifies the condition and it is completed in $O\left(1\right)$. In step 5, we introduce a sequence of chains along with a set of active arcs. This operation is performed at a time not exceeding $O\left(\right|E\left|\right)$. In step 6, at each vertex v, a ”merging” of lists is performed in a time not exceeding $O\left(\right|V|·deg(v\left)\right)$. Thus, the computing complexity of step 6 does not exceed the value $O\left(\right|V|·|E\left|\right)$. Step 7 runs by time not exceeding $O\left(\right|E\left|\right)$. The complexity of Step 7 is defined by the complexity of algorithm $OE$-Cover [19] and amounts to $O\left(\right|E\left(G\right)|·{log}_2|V\left(G\right)\left|\right)$. Obtaining the partial graph $\tilde{G}$ at Step 7 claims the time not exceeding $O\left(\right|E\left|\right)$. The complexity of Step 9 does not exceed $O\left(\right|V{|}^3)$ used for the shortest matching obtaining. Thus, the complexity of algorithm $PPOE$-routing does not exceed the value of $O\left(\right|V{|}^3)$. □

Let us consider the application of algorithm PPOE-Routing to cutting plan in Figure 2 with geomorphic image presented in Figure 3 and in Table 1. We have $V_{out}\left(N\right)=\{v_1,v_5,V_{11}\}$, $V_{in}\left(N\right)=\{v_2,v_3,v_7,v_9\}$, $V\left(N\right)\backslash (V_{out}\left(N\right)\cup V_{in}\left(N\right))=\{v_4,v_6,v_8,v_{10},v_{12}\}$. Figure 7 demonstrates network $N\left(V\cup \left\{w\right\},A\cup \left(\left\{w\right\}\times V_{in}\right)\right)$ constructed in Step 1 and optimal solution of problem (1)–(7) found in Step 2. Bold lines highlight carriers of non-zero flow.

After running steps 3–6, we obtain the chains $C_1=e_3{e}_2{e}_9$, $C_2=e_{21}{e}_{22}$, $C_3=e_{13}$. Partial graph constructed by step 7 is shown in Figure 8.

In this graph algorithm M-Cover constructs the only chain

$$C_4=e_5{e}_7{e}_{11}{e}_{16}{e}_{12}{e}_8{e}_{10}{e}_{15}{e}_{20}{e}_{19}{e}_{18}{e}_{17}{e}_{14}{e}_{23}{e}_1{e}_4{e}_6.$$

So, the $PPOE$-cover for this graph is $\{C_1,C_2,C_3,C_4\}$.

Thus, the construction of the $PPOE$-cover of the G graph allows us to solve the problems of the cutter movement routing for a realizable cutting plan with restrictions on possible pierce points.

2.4. Algorithms for Disconnected Graphs

The problem of constructing $OE$-routes in disconnected graphs is also of practical value. In this case, the task of finding the $OE$-covering of the graph by chains can be reduced to several tasks of lower dimension (to construct a cover for each connected component separately). This approach is reasonable if the resulting graph does not contain nested components. However, in the presence of nesting of the connected components, the problem becomes somewhat more complicated and the following restrictions on the order of traversing the connected components arise: the connected components consisting of edges of higher rank must be traversed before the components consisting of edges of lower rank. To solve the problem in common for plane disconnected graph algorithms MultiComponent (computing complexity $O\left(\right|E\left(G\right)|·{log}_2|V\left(G\right)\left|\right)$), Bridging, DoubleBridging) and FaceCutting (Figure 9) are developed.

The proofs of these results [19] are constructive and, in fact, are reduced to describing and proving the effectiveness of algorithms for constructing the desired cycles (routes).

Algorithms Bridging and DoubleBridging use the approach of reducing the initial disconnected graph to a connected one.

Definition 15.

Let face $f\in F\left(G\right)$ be called separating, if it is incident to two or more connected components.

Let graph $\tilde{G}$ be obtained from graph G by adding bridges belonging to separating faces between the components. Obviously, the obtained graph $\tilde{G}$ be a plane connected graph and it is possible to construct the $OE$-route $R\left(\tilde{G}\right)$ for it. This $OE$-route $R\left(G\right)$ can be obtained from route $R\left(\tilde{G}\right)$ if vertices incident to the introduced bridges are to be the ends of the current chain and the beginnings of the next ones (i.e., introduced bridges are the idle passes).

Let us consider the way of constructing the bridges connecting graph G and having a minimal summary length (see Algorithm 12).

Algorithm 12 Bridging

Require:  plane disconnected graph G Ensure:  plane connected graph $\tilde{G}$ and set B of introduced bridges 1: $\tilde{G}:=G$; $B=\varnothing$; 2: Define the set $C_F$ of all separating faces. 3: for all $f\in C_F$ do 4:     Find the set $S\left(f\right)$ of connected components of graph G incident to face f. 5:     Construct the full abstract graph $\mathcal{T}$ the vertices of which are the components $S\left(f\right)$, and lengths of edges are equal to the distance between the components. 6:     Obtain the minimal spanning tree $T\left(\mathcal{T}\right)$ in $\mathcal{T}$. 7:     Add the edges of the obtained spanning tree to graph $\tilde{G}$: $E(\tilde{G}:=E\left(\tilde{G}\right)\cup E\left(T\left(\mathcal{T}\right)\right)$, $B:=B\cup E\left(T\right(\mathcal{T}\left)\right)$. 8: end for 9: end

Plane graph $\tilde{G}$ obtained by algorithm Bridging contains bridges, hence it is possible to apply only algorithm CPP_OE [30] constructing the Chinese postman $OE$-route for plane graph [30]. Note that both the OECover algorithm and the M-Cover algorithm require no bridges in the graph. To avoid errors in the execution of the algorithms, it is necessary to add the edges of the spanning tree $T\left(\mathcal{T}\right)$ to the graph twice (see line 6 of the Algorithm 12). The algorithm adjusted in this way is called DoubleBridging. The complexity of the Bridging and DoubleBridging algorithms is polynomial, depending on the method used to determine the distances between the connectivity components. If the distances are given it can be estimated as $O\left(\right|E\left(G\right)|·log|V\left(G\right)\left|\right)$.

Theorem 12.

If, for each component $G_k$ of graph G, the degrees of vertices incident to separating faces of G are even, then the path of the minimal length of additional edges can be realized by algorithm DoubleBridging.

Algorithm FaceCutting [35] is one other way to obtain graph $\tilde{G}$ without bridges. It consists in splitting the separating face using the Hamiltonian cycle. In fact, if for abstract graph $\mathcal{T}$ we use the minimal weight Hamiltonian cycle $H\left(\mathcal{T}\right)$ instead of spanning tree $T\left(\mathcal{T}\right)$, then the resulting graph $\tilde{G}$ does not contain any bridges and, hence, we can use algorithm M-Cover (see Algorithm 4) to obtain the $OE$-route with a minimal length of idle passes.

3. Discussion

In our article, we provide an overview of the plane graph routing problem statements since the 1980s. In the early works [20,21], the formalization of the tasks posed is not accurate enough, there is no classification of routes by the type of restrictions imposed. In this regard, mainly heuristic algorithms were developed. In the works of the authors (2007–2020), an exact formalization of some previously considered statements is given, classes of routes in plane graphs satisfying constraints are introduced, and polynomial exact algorithms for solving these problems are described.

Of particular note is the proof of the $\mathcal{NP}$-completeness of the problem of finding non-intersecting Euler chains [21], where the author takes an A-chain as a self-non-intersecting Euler chain. The authors have shown the existence of a polynomial algorithm for finding an Euler self-non-intersecting chain in a plane graph. The question of $\mathcal{NP}$-completeness of the problem of finding a self-non-intersecting chain remains open.

4. Conclusions

In our paper, we introduced a class of routes with ordered enclosing ($OE$-routes) in plane graphs. The routes of this class represent an ordered sequence of paths that satisfy the requirement that the inner edges of the traversed part of the route do not intersect with the edges of its non-traversed part.

We showed that the presence of bridges in the graph has a significant effect on the cover cardinality. If there are no bridges in a graph, the minimum number of $OE$-chains covering the graph is equal to the minimum number of paths covering the given graph (in the case of the existence of vertices of odd degree incident to the outer face). If there are no vertices of odd degree adjacent to the outer face, then the cardinality of the covering is one higher than the minimum number of paths covering the given graph. In general, the cardinality N of Euler $OE$-cover of graph G satisfies the inequality $k=\frac{|V_{odd}\left(G\right)|}{2}\le N\le \left|V_{odd}\left(G\right)\right|=2k.$ The upper and lower bounds are reachable.

We discussed the polynomial algorithms for constructing the $OE$-cover for different cases: plane Euler graph, any plane connected graph (CPP and $OE$-cover constructing problems), any disconnected plane graph. We developed the polynomial time algorithm for obtaining an $OE$-route with the minimum number of covering paths and an algorithm for constructing an $OE$-route with a minimum length of transitions between the end of the current path and the beginning of the next path.

To discover the chains with the complex groups of restrictions we introduced classes of $AOE$-chains, $NOE$-chains, and $PPOE$-chains. (1) Class of $AOE$-chains includes the chains with additional local restriction according to which the neighbouring edges need to satisfy the transitions system of A-chain. Algorithm AOE-CHAIN allows obtaining a chain belonging to class $AOE$ for a plane connected 4-regular graph. The algorithm allows to obtain it by the time $O\left(\right|E\left(G\right)|·log|V\left(G\right)\left|\right)$. (2) Class of $NOE$ is the extension of class $AOE$ and contains all $OE$-chains with non-intersecting transitions. Algorithm Non-intersecting allows obtaining such a chain. Its implementation consists in reducing the original plane graph to a plane connected 4-regular graph by splitting vertices of degree higher than 4 and further executing the AOE-CHAIN algorithm. (3) Class of $PPOE$-chains contains $OE$-chains with fixed sets of starting and ending vertices, and algorithm $PPOE$-covering allows for correctly solving the problem of constructing this type of cover for a plane graph $G(V,E)$ without bridges by the time not exceeding $O\left(\right|V{|}^3)$ [36].

All our algorithms are implemented using the C++ programming language, and the initial data can be read either from text files with the table of functions for edges (see Theorem 1) or by conversion of JSON-files used in known CAD/CAM systems to the table of these functions [36].