Abstract
Accurate, rapid and effective analysis of rock drillability is very important for mining, civil and petroleum engineering. In this study, a method of rock drillability evaluation based on drilling process monitoring (DPM) parameters is proposed by using the field drilling test data. The revolutions per minute (N), thrust, torque and rate of penetration (ROP) were recorded in real time. Then, the two-dimensional regression analysis was utilized to investigate the relationships between the drilling parameters, and the three-dimensional regression analysis was used to establish models of ROP and specific energy (SE), in which the N-F-ROP, N-T-ROP and the improved SE model were obtained. In addition, the random forest (RF) and support vector machine combined with genetic algorithm (GA-SVM) were applied to predict rock drillability. Finally, a prediction model of uniaxial compressive strength (UCS) was established based on the SE and drillability index, Id. The results show that both regression models and prediction models have good performance, which can provide important guidance and a data source for field drilling and excavation processes.
1. Introduction
Rock drillability plays an important role in mining, civil and petroleum engineering. The traditional rock drillability analysis requires the rock mechanics parameter. This means that the procedures of site drilling, coring, sample processing and laboratory test are needed, which will be time-consuming and costly and greatly affect the engineering efficiency. Moreover, sometimes, the rock core is impossible to be obtained owing to the fracture and fragmentation of the rock mass, which results in the rock mass properties being unable to be analyzed. However, the drilling process monitoring (DPM), as a new promising technology, can compensate for the above shortcomings, and it has been widely applied in recent years. Rock drilling process refers to the rock drilling relying on the bit’s thrust and rotary cutting force. The thrust is used to push the drill pipe and make it in close contact with the rock mass so as to generate enough friction. The rotary cutting force is mainly used to break the rock mass. Meanwhile, the parameters fed back in the drilling process are closely related to the rock mass properties. Therefore, how to quickly and accurately obtain the rock mass properties is very important for the parameter design of rock breaking equipment.
The scholars in United States, Japan and France have been trying to find the relationships between the rock mass quality of engineering and drilling parameters by instrument measurement since 1970 [1,2,3]. However, it measures the speed based on the distance, which indicates that the achievement of drilling speed has great randomness when the rock formation is not uniform or the drilling rig is vibrating [4,5], Therefore, it is impossible to accurately obtain the rock physical properties and the related rock formation division. On this basis, Yue [6,7,8,9] developed the drilling process monitoring system (DPM), which effectively improved the accuracy of velocity measurement and was successfully applied to stratum identification and rock strength classification. However, the DPM system cannot measure torque, so He and Li et al. [10] improved it. The new drilling process monitoring apparatus can achieve the measurement of torque. Up to now, the development of a while-drilling system has been relatively mature, which can realize the real-time measurement of thrust, torque, rate of penetration (ROP) and revolutions per minute (N), and has been successfully applied to rock property analysis and formation analysis. Rodgers et al. [11,12,13,14] used while-drilling parameters to assess field rock strength and optimize core recovery. Karasawa [15,16] et al. conducted laboratory drilling tests, and they proposed the method to estimate the unconfined compressive strength of rock. He [17] et al. performed a series of drilling tests on sandstone, limestone, marble and granite in the field to predict the cohesion, internal friction angle and uniaxial compressive strength of rock. Li [18] et al. deduced the relationships between the drilling efficiency and drilling parameters based on the method of force limit of equilibrium and energy equilibrium. Li [19] et al. analyzed the influence of working parameters, such as impact power, propulsion force, rotating speed and drill bit type, on drilling efficiency and obtained the relationships between the drilling velocity and drilling parameters. Feng [20] et al. performed a field-drilling test to obtain the optimal drilling efficiency, and they found the optimal drilling conditions and rock drillability. Moreover, the combined thermo-mechanical drilling technology and acoustic emission method were utilized to investigate the rock drillability [21,22,23]. However, the fractured zones were not considered in the above studies. Therefore, Kalantari et al. [24,25] established a stress limit equilibrium analysis model for a T-shaped drag bit, which considered influence factors such as bit geometry parameters, fractured zone and contact friction during drilling. On this basis, the actual drilling data were used to estimate the rock strength parameters, such as cohesion, internal friction angle and uniaxial compressive strength. The results show that the borehole test results based on this model are in good agreement with the standard test results.
Meanwhile, a large number of models have been established to evaluate rock drillability. Hughes [26] and Mellor [27] et al. proposed the theoretical models of SE based on the uniaxial compressive strength and secant modulus of rocks. An empirical formula was put forward by Poane [28] et al. to evaluate the relationships between the drilling parameters and specific energy (SE). Feng [20] et al. improved the SE model using the controllable parameters (thrust and ROP). In addition, Zhang [29] et al. proposed a new rock drillability index, Id, to evaluate rock classification, and it was applied to classify rock types successfully as an in situ test. Yu [30] et al. compared the effect of SE and Id on rock strength assessment. The results present that the assessment performance of Id is superior to SE due to the smaller overall fluctuation during the modeling process. However, the most widely used model by far is the SE model proposed by Teale [31]. The ROP is also an important index to evaluate rock drilling efficiency. Kahraman [32,33] conducted rotary and percussive drilling tests and obtained the prediction equation of ROP through regression analysis. Ataei [34] et al. established an empirical formula of ROP combined with the rock mass drillability index, and the results show that the model has a better prediction effect compared with the previous model. In addition, artificial intelligence (AI) techniques have been utilized to predict rock properties. Ocak [35] et al. used the multilayer perceptron neural network (MLPNN) to predict the elastic module of intact rocks, and the prediction results show that the MLPNN has good prediction capacity. Yesiloglu-Gultekin [36] et al. employed the artificial neural network and adaptive neuro fuzzy inference system to predict the uniaxial compressive strength of granite rocks, and the study indicates that the developed models have a high prediction performance. Sarkar [37] et al. adopted the feed-forward back-propagation neural network to estimate the strength parameters of rock, and the results show that the performance of the AI techniques is better than regression analysis. He [38] et al. utilized the deep convolutional neural network to predict the cohesion, internal friction angle and uniaxial compressive strength and obtained good prediction results. Therefore, the AI technique is a promising method to analyze rock properties. However, some explanations about the cutting actions of the drilling bits and TBM disc-cutters explained in many papers are not referred to, e.g., the explanations given by Roxborough and Phillips [39,40]. Some other researchers also used the concepts of thrust and rolling forces and the specific energy to study the mechanism of rock fragmentation by the cutters [41,42]. They used a higher order displacement discontinuity method for their analyses. The finite element method and discrete element method have also been used to analyze the drillability of the rock cutting heads.
Although many achievements have been obtained, the analysis of the relationships between the rock drillability and DPM parameters is still rare, and the AI algorithm is rarely used to analyze the relationships between them. Meanwhile, the relationships between the DPM parameters and rock properties have not been fully established. Therefore, the drilling test was conducted in this study, and the thrust (F), torque (T), rotating speed (N) and rate of penetration (ROP) were recorded in real time. Then, the two-dimensional and three-dimensional regression analyses were utilized to investigate the relationships between the rock drillability and DPM parameters, in which two ROP models are obtained and the SE model is improved. In addition, the random forest (RF) and support vector machine combined with genetic algorithm (GA-SVM) were used to predict the rock drillability. Finally, a model using SE and Id for estimating the uniaxial compressive strength based on three drilling tools is established. The above efforts can achieve the accurate, rapid and effective analysis of rock drillability, and the model has very important guiding significance for field drilling and rock fragmentation.
2. Methodology
2.1. Drilling Process Monitoring (DPM) Parameters
In order to analyze the relationships between DPM parameters and rock drillability, a new drilling-monitoring system was utilized to perform drilling test. The system, as shown in Figure 1, can record the thrust (F), torque (T), rotating speed (N) and rate of penetration (ROP) in real time at 1-s interval through the corresponding sensor. These sensors mainly include pressure sensor, rotating speed sensor, torque sensor and laser displacement sensor. Finally, the recorded data will be transformed to the data processing system, where the data can be stored and processed. Meanwhile, the system can adjust the thrust and rotating speed artificially during the process of drilling. Moreover, all sensors are easily to be mounted and have high measurement precision, so it is convenient and reliable to conduct drilling test in field.

Figure 1.
Digital drilling system and in situ testing.
Among the DPM parameters, the thrust refers to the force required to make the drill bit in close contact with the rock mass; the rotating speed refers to the number of rotating turns of drill bit per minute and the torque refers to the moment required to rotate the drill bit, which is used to cut rock mass; the rate of penetration refers to the length of drilling per unit time.
2.2. Drilling Conditions
Different thrust and rotating speed were applied to plain concrete with a 90 mm diameter drill bit. The range of thrust is from 8.5 to 70 kN, and that of rotating speed from 40 to 400 r/min. Through uniaxial compressive test and Brazilian tensile test, the uniaxial compressive strength and tensile strength of the concrete are 14.70 ± 0.50 MPa and 1.57 ± 0.32 MPa, respectively.
2.3. DPM Data
After drilling test, the corresponding torque and rotating speed values under different thrust and rotating speed drilling conditions were obtained, and the SE (energy required to break unit rock) while drilling was calculated following the SE model proposed by Teale [31], as shown in Equation (1). The average values of DPM parameters and SE are presented in Table 1.
where SE is specific energy of drilling, F is thrust, N is rotating speed, T is torque, V is rate of penetration and A is drilling area.

Table 1.
The average value of DPM parameters and SE.
3. Regression Analysis
Two-dimensional and three-dimensional regression analysis were adopted to investigate the relationships between the DPM parameters and the influence of DPM parameters on rock drillability. It is worth noting that the data used for the regression analysis are the average values (Table 1) under their corresponding conditions.
3.1. Two-Dimensional Regression Analysis
The relationships between thrust, torque, ROP and SE were analyzed under different rotating speeds. There is a good positive linear relationship between thrust and torque, as shown in Figure 2, and the fitting functions are presented in Table 2. The relationship between thrust and ROP is powerful, and their regression curves and fitting functions are shown in Figure 3 and Table 2, respectively. Meanwhile, the relationship between torque and rotating speed was obtained, as shown in Figure 4 and Table 2, respectively.
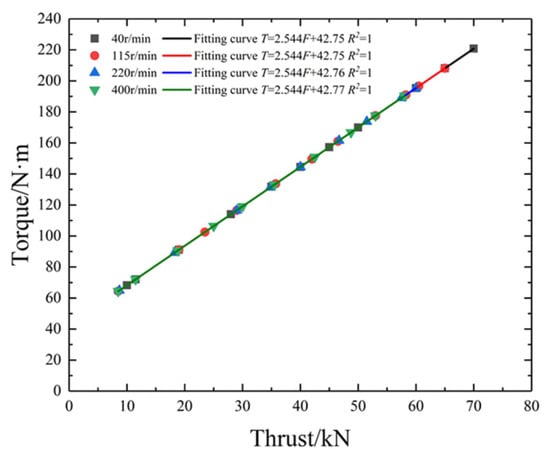
Figure 2.
The relationship between thrust and torque under different rotating speed.

Table 2.
Relationships between parameters of DPM.
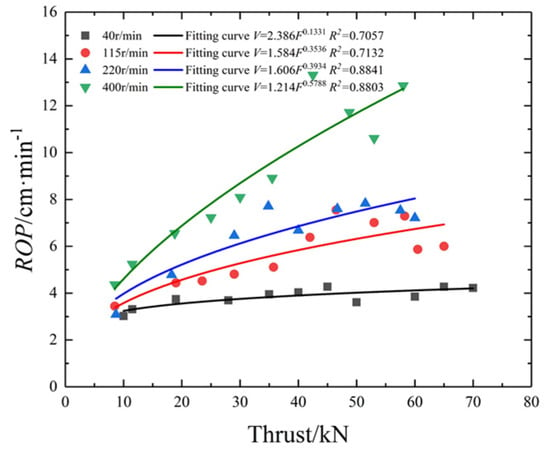
Figure 3.
The relationship between thrust and ROP under different rotating speed.
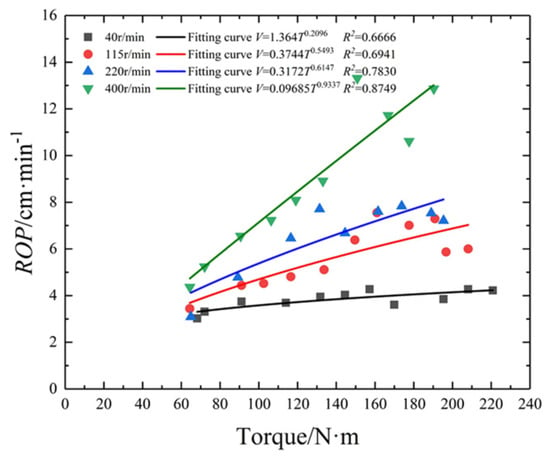
Figure 4.
The relationship between torque and ROP under different rotating speed.
Similarly, the values reflecting the relationship between SE and thrust (or torque) under different rotating speeds were obtained, as shown in Figure 5 and Figure 6 and Table 2. There is a good linear relationship when the rotating speed is 40 r/min. However, there is no significant statistical relationship under other rotating speed conditions. This means that the single variable is unable to reflect the SE of drilling effectively.
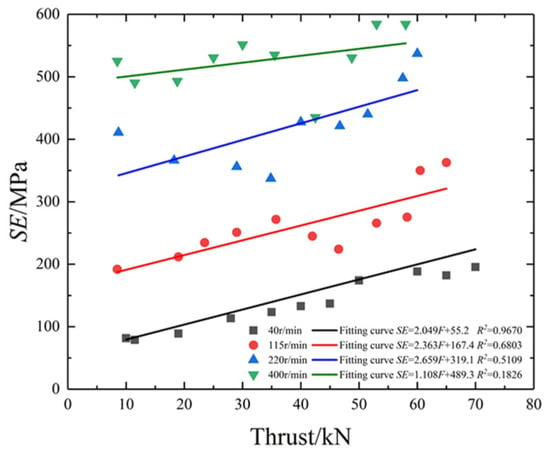
Figure 5.
The relationship between thrust and SE under different rotating speed.
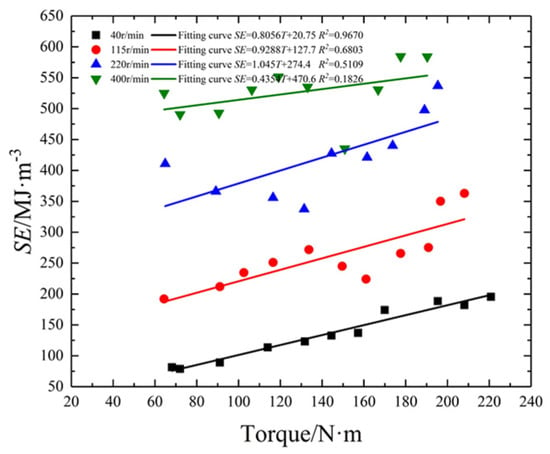
Figure 6.
The relationship between torque and SE under different rotating speed.
3.2. Three-Dimensional Regression Analysis
The two-dimensional regression analysis results indicate that there is a significant statistical relationship between thrust and torque. However, for the regression analyses of ROP and SE, the fitting effects are incapable to meet the requirement of practical engineering. Therefore, the three-dimensional regression analyses were utilized to establish models based on DPM data.
The rotating speed, thrust and torque were selected to establish regression models of ROP. We defined them as N-F-ROP and N-T-ROP models. The three parameters correspond to the X-axis, Y-axis and Z-axis variables, respectively. Through regression analyses, the N-F-ROP and N-T-ROP models were obtained, and their corresponding three-dimensional fitting curves and formulas are shown in Figure 7 and Figure 8, and Equations (2) and (3), respectively.
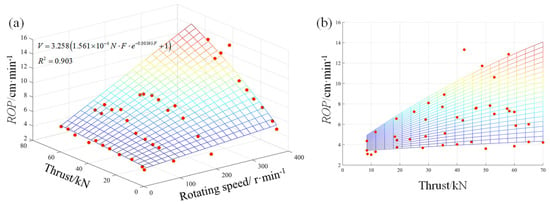
Figure 7.
Regressed model of N-F-ROP, where (a) is three-dimensional surface view and (b) is the view of Y-Z direction.
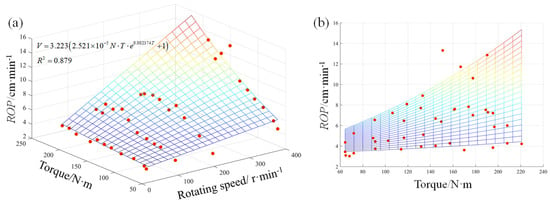
Figure 8.
Regressed model of N-T-ROP, where (a) is three-dimensional surface view and (b) is the view of Y-Z direction.
Moreover, because there is a good linear relationship between thrust and torque, we improved the SE model proposed by Teale. The thrust, rotating speed, ROP and drilling area (A) were taken as independent variables to establish the regression model of SE. The results show that the above parameters have a significant statistical relationship, as presented in Figure 9 and Equation (4).
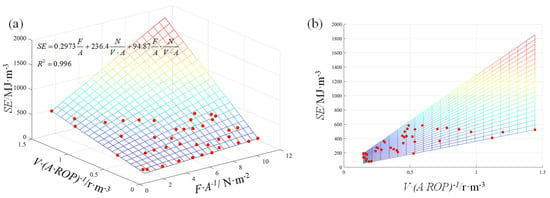
Figure 9.
Regressed model of SE, where (a) is three-dimensional surface view and (b) is the view of Y-Z direction.
3.3. Regression Model Evalution
The determination coefficient (R2) and root mean square error (RMSE) were utilized to evaluate regression performance of two-dimensional and three-dimensional regression models, and the corresponding calculation formulas are shown in Equations (5) and (6), respectively. The ultimately calculation results are shown in Table 3.
where , , and n are the test value, predicted value, mean of all test values and the total number of values, respectively.

Table 3.
The R2 and RMSE values of regression models.
4. Analyses Using Machine Learning Methods
The RF and GA-SVM were used to analyze the relationships between the SE and DPM parameters. These two methods belong to the category of machine learning, and it has been successfully applied in many fields [43,44,45,46].
4.1. Random Forest
RF is an ensemble algorithm based on a decision tree, and it was developed by Breiman [47]. The RF model takes the bootstrap method to select a training set in the way of sampling with the replacement method. Then, the selected training sets are utilized to establish the classification or regression model based on a pre-designed number of decision trees (ntree) and node value (mtry). Finally, the test sets are taken to evaluate the model. In the prediction process, the classification model uses the method of classification voting to get the final result, while the prediction model adopts the method of regression mean.
A total of 11041 sets of real-time DPM data were used for training and testing in the RF model. Because there is a good linear relationship between torque and thrust, and the drilling area (A) is a constant, the rotating speed, thrust and ROP were taken as the input variables, and the output variable was SE. It should be noted that the average speed was used for the training and testing process in the RF model instead of the real-time speed under different thrust conditions due to the real-time speed possibly being a negative value caused by the slight rebound of the drill pipe during drilling. Of the DPM data, 70% were were selected randomly to be the training set, and the remaining 30% of the data were taken as the test set. The ntree and mtry were set to 150 and 2, respectively. The optimized prediction model was obtained by training, and the ultimate result was obtained through prediction. The architecture of RF is shown in Figure 10.
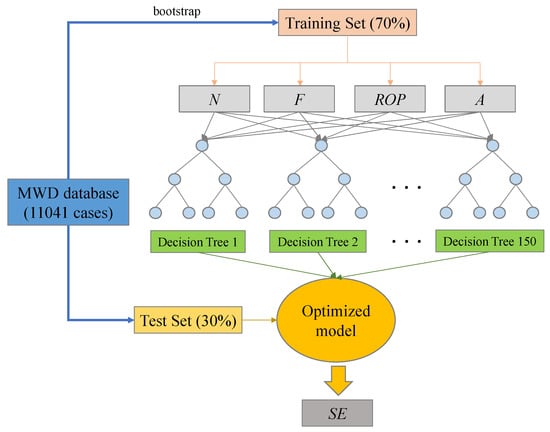
Figure 10.
The architecture of random forest.
In order to evaluate the prediction accuracy of the established RF model, the R2 and RMSE were calculated, as shown in Table 4. Meanwhile, the comparison of the original value and predicted value is shown in Figure 11. From the predicted results, we can find the R2 and RMSE of the training set and test set are 0.9455 and 0.9591, 42.1341 and 48.7496, respectively, which indicates that the established RF model has a good prediction performance.

Table 4.
The R2 and RMSE of prediction models.
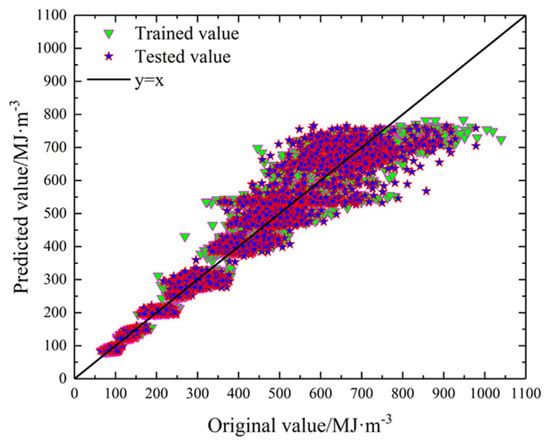
Figure 11.
The comparison of original value and predicted value of RF model.
4.2. GA-SVM
The support vector machine (SVM) algorithm was invented by Cortes and Vapnik [48]. It is one of the machine learning methods based on statistical learning theory. The SVM model mainly includes the input layer, kernel function layer and output layer. Among them, the key function layer mainly includes radial basis function (RBF), polynomial and linear functions, which are the key factors to affect the prediction performance. In this paper, the genetic algorithm (GA) is combined with SVM to optimize the parameters. The GA [49] is a new method to find the optimal solution through the natural evolution process simulation, and the steps of GA mainly include population initialization, individual evaluation, selection operation, crossover operation, mutation operation and termination condition judgment. The SVM combined with GA can better optimize the parameter selection and improve the prediction accuracy.
Similar to the analysis of RF, the rotating speed, thrust and ROP are taken as the input variables, and SE as the output variable. Of the DPM data, 70% were randomly selected for model training, and the remaining 30% of the data were used for the model verification, as shown in Figure 12. In GA, the maximum evolutionary generation (ga_option.maxgen), maximum population (ga_option.sizepop), crossover validation (ga_option.v) and crossover probability (ga_option.ggap) were set as 100, 20, 10 and 0.9, respectively. By optimizing the parameters, the optimal penalty coefficient (c) and kernel radius (g) were 6.5961 and 27.2206, respectively. Then, the above parameters were used to establish the prediction model. Finally, the test sets were used to verify the model. The prediction results show the established model has good performance.
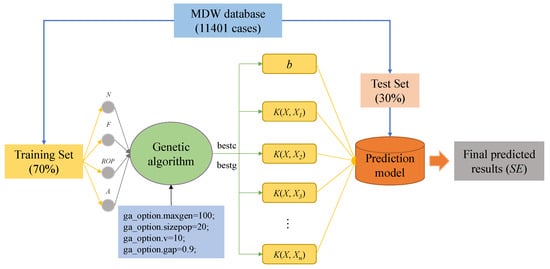
Figure 12.
The architecture of GA-SVM.
The R2 and RMSE were used to evaluate the prediction accuracy of GA-SVM. By calculation, the corresponding evaluation results and comparison picture are shown in Table 4 and Figure 13, respectively. The results show that the prediction performance of the GA-SVM model is superior to the RF model. It also shows that it is feasible to use the thrust, rotating speed and ROP to evaluate the SE when the drilling area is a constant.
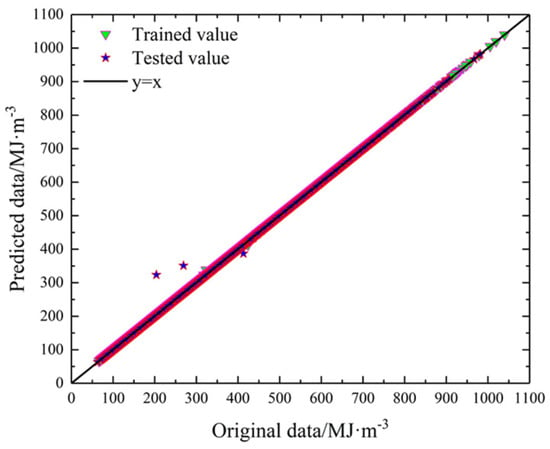
Figure 13.
The comparison of original value and predicted value of GA-SVM model.
5. Relationships between Rock Properties and DPM Parameters
The rock properties and in situ stress conditions obviously affect rock cutting and drilling [50,51,52,53]. The fast and accurate prediction of the rock properties is the key to evaluating rock drillability and cuttability. Therefore, in order to find the relationships between the rock properties with DPM parameters, the SE and drillability index, Id, were utilized to establish the rock strength prediction model. The SE can be obtained according to the improved model based on Teale’s model. The drillability index, Id, was proposed by Zhang [29], and it can be calculated based on Equation (7). Both SE and Id can be calculated by DPM parameters.
The data used to establish the prediction models are present in Table 5. According to these data, the SE and Id were obtained. Then, the prediction models of uniaxial compression strength of rock based on SE and Id were established, which include the univariate model and two-variable model.
where D is drill bit diameter, F is thrust force, T is torque, V is rate of penetration, ω is angular velocity, N is rotating speed and α, β, γ are fitting parameters. In this study, α, β, γ are determined to be 0.5, 0.6 and 1, respectively.

Table 5.
Data source, quantity and bit types of UCS prediction model.
5.1. Univariate Model of UCS
According to the calculated SE and Id, the relationship between them and uniaxial compressive strength of rock under different cutting tools is established, respectively. When the standard diamond solid bit was used, the relationship between SE (or Id) and UCS is present in Figure 14a, and the corresponding regression model is shown in Table 6. Similarly, the relationship between SE (or Id) and UCS is present in Figure 14b,c, in which the impregnated diamond bit and PDC bit were performed to drilling. Their regression models are also shown in Table 6. Finally, all the data under the three types of bits were used to establish the relationship between the SE (or Id) and UCS of rock. The regression model and fitting curve are shown in Table 6 and Figure 14d, respectively.
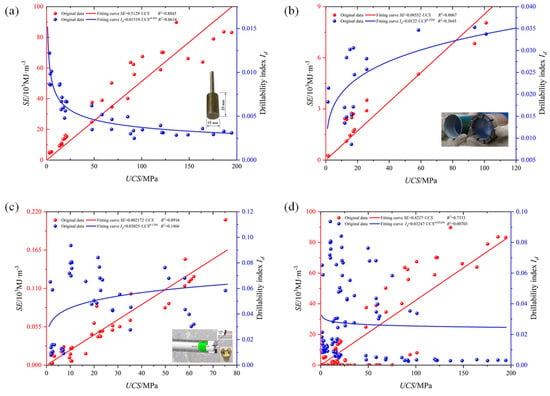
Figure 14.
The relationship between SE (or Id) and UCS for different bits of (a) standard diamond solid bit, (b) impregnated diamond bit, (c) PDC bit and (d) combine the above three bits.

Table 6.
Established UCS model based on SE and Id separately under different bits.
From these univariate prediction models, we can find that there is a good relationship between SE (or Id) and UCS for the standard diamond solid bit. The result indicates SE is positively correlated with the UCS, while the Id is negatively correlated with UCS, which is consistent with Yu’s [30] study. However, compared to the regression model for the standard diamond solid bit, the relationship between Id and UCS presents an opposite law for the impregnated diamond bit and PDC bit, and the relationship between UCS and SE is obviously better than that between UCS and Id.
5.2. Two-Variate Model of UCS
The univariate models of UCS indicate that the performances of the UCS models based on SE (or Id) under different bits are not very good, especially for the model based on Id. Therefore, the UCS prediction model was established by combining the SE and Id. Similar to the univariate modeling, the UCS prediction models under different bits were established, respectively. The UCS prediction models under standard diamond solid bit, impregnated diamond bit and PDC bit are shown in Figure 15a–c, respectively, and the corresponding fitting equations are shown in Equations (9)–(11). Finally, all the data were combined to produce an UCS prediction model, and the regression curve and fitting equation are shown in Figure 15d and Equation (12). The results show that the performances of the established models combining SE and Id are significantly superior to that of the univariate model.
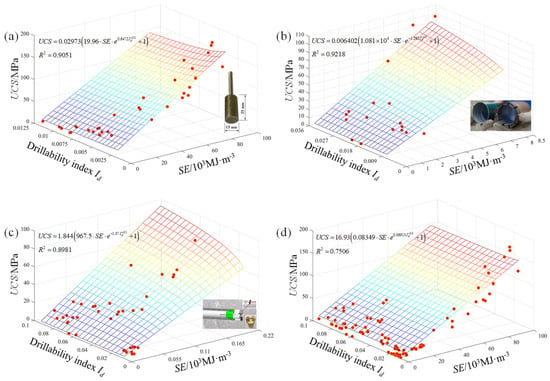
Figure 15.
Established UCS models combine SE and Id for different bits of (a) standard diamond solid bit, (b) impregnated diamond bit, (c) PDC bit and (d) combine the above three bits.
5.3. Evaluation of UCS Prediction Models
The determination coefficient (R2) and root mean square error (RMSE) were used to evaluate the performance of univariate and two-variate models of UCS, and it can be calculated by Equations (5) and (6), respectively. The corresponding evaluation indexes obtained through calculation are shown in Table 7. The results show that the performance of the established UCS prediction model based on SE and Id is better than that based on a single variable.

Table 7.
The R2 and RMSE of UCS models.
By substituting the drilling experiment data into the established UCS prediction model, it can be obtained that the prediction UCS of concrete material is 17.49 MPa. Compared to the tested UCS of concrete (14.7 MPa), the prediction accuracy is 81.02%.
6. Discussion
In order to investigate the relationships between the DPM parameters and rock drillability, the essential parameters, such as thrust, rotating speed, etc., needed to be collected during drilling. Therefore, the feasibility for evaluating rock drillability with DPM parameters is discussed in this chapter.
6.1. The Key DPM Parameters
According to the formula of SE and Id, the thrust, rotating speed, torque and ROP are essential during drilling. They can be divided into two categories that are controllable and uncontrollable, respectively. Among these parameters, the thrust and rotating speed belong to the former, while the torque and ROP belong to the latter. In the process of drilling, the drilling performance can be improved by reasonably controlling the thrust and rotating speed. However, the torque and ROP, as the characterization parameters while drilling, change with the thrust and rotating speed, and they are also very sensitive to the mechanical properties of the rock mass. Therefore, it is very important to accurately measure the thrust, rotating speed, torque and ROP for the real-time analysis of rock drillability.
6.2. UCS Prediction Model
The established UCS prediction model by combining SE and Id under three kinds of different drilling tools (standard diamond solid bit, impregnated diamond bit and PDC bit) has better prediction performance, and its performance is better than the univariate model established by SE or Id separately. It can well reflect the relationships between the UCS of rock and DPM parameters. By substituting the drilling experimental data into the model, the prediction accuracy is 81.02%, which can meet the requirement of field application. However, the amount of data to establish the model is not very large, and the types of bits are not very comprehensive, so it is impossible to accurately predict the rocks with low UCS. Therefore, more DPM data in different rock layers and more kinds of drill bits should be considered in future study.
7. Conclusions
In order to investigate the relationships between the DPM parameters and rock drillability, drilling tests were performed. The rotating speed, thrust, torque and ROP were recorded in real time. Then, these DPM parameters were utilized to carry out regression analyses, and the RF and GA-SVM algorithms were applied to predict the SE for reflecting the rock drillability. Finally, the UCS prediction model using three types of drilling bits was established by combining the SE and Id. Based on the above analyses, the following conclusions can be drawn:
(a) There is a good linear relationship between thrust and torque at a constant rotating speed condition, and the relationships between thrust and ROP, and torque and ROP are powerful, but their statistical relationship is not very significant. The relationships of the SE with thrust and torque are linear at a lower rotating speed, while there is no significant statistical relationship at medium and high rotating speeds.
(b) The established N-F-ROP and N-T-ROP regression models have better performance than the two-dimensional regression models. Meanwhile, the SE model of Teale has been improved based on the good relationship between thrust and torque. The new model has good performance to predict the SE. However, the improved SE model is not applicable to all the fields completely, and the general formula needs to be further studied.
(c) The prediction performance of the GA-SVM model is superior to the RF model, and it can reach more than 99%. Therefore, machine learning based on GA-SVM is a promising method to analyze the relationships between the DPM parameters and rock drillability. Moreover, it is feasible to evaluate the SE of drilling based on thrust, rotating speed, ROP and drilling area (A).
(d) The UCS prediction model was established by combining SE and Id. It can reflect the relationships between the UCS and DPM parameters well for three types of bits (standard diamond solid bit, impregnated diamond bit and PDC bit).
Author Contributions
Conceptualization, S.W. and Y.T.; methodology, R.C., Y.T., S.W., Z.Z. and X.C.; validation, S.W. and Y.T.; writing—original draft preparation, Y.T. and S.W.; writing and review, S.W., Y.T., R.C., Z.Z. and X.C. All authors have read and agreed to the published version of the manuscript.
Funding
The work presented in this paper was financially supported by the National Natural Science Foundation of China (Grant No. 52174099, 51904333 and 52079150), the Natural Science Foundation of Hunan Province (No. 2021JJ30842), Young Talent Support Project of China Association for Science and Technology (No. YSXH 2020-QT002) and Changsha Outstanding Innovative Youth Program (No. kq2107003).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Please email to request from Cao Ruilang at: caorl@iwhr.com.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jan, Y.M.; Campbell, R.L.J. Borehole correction of MWD gamma ray and resistivity logs. In SPWLA 25th Annual Logging Symposium; Society of Professional Well Log Analysts Inc.: Houston, TX, USA, 1984; pp. 189–197. [Google Scholar]
- Howarth, D.F.; Adamson, W.R.; Berndt, J.R. Correlation of model tunnel boring and drilling machine performances with rock properties. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1986, 23, 171–175. [Google Scholar] [CrossRef]
- Zacas, M.; Kavadas, M.; Mihalis, I. The use of recording drilling parameters in rock mass classification. In Proceedings of the 8th ISRM Congress, Tokyo, Japan, 25–29 September 1995; International Society for Rock Mechanics: Salzburg, Austria, 1995; Volume 3, pp. 1121–1124. [Google Scholar]
- Gui, M.-W.; Soga, K.; Bolton, M.D.; Hamelin, J.P. Instrumented borehole drilling for subsurface investigation. J. Geotech. Geoenviron. 2002, 128, 283–291. [Google Scholar] [CrossRef] [Green Version]
- Schunnesson, H. RQD predictions based on drill performance parameter. Tunn. Undergr. Space Tech. 1996, 11, 345–351. [Google Scholar] [CrossRef]
- Yue, Z.Q.; Chen, J.; Gao, W. Automatic drilling process monitoring (DPM) for in-situ characterization of weak rock mass strength with depth. In 1st Canada-US Rock Mechanics Symposium (Rock Mechanics: Meeting Society’s Challenges and Demands); ARMA: Vancouver, BC, Canada, 2007; pp. 199–206. [Google Scholar]
- Tan, Z.Y.; Cai, M.F.; Yue, Z.Q.; Tham, L.G.; Lee, C.F. Application and reliability analysis of DPM system in site investigation of HK weathered granite. J. Univ. Sci. Technol. B 2005, 12, 481–488. [Google Scholar]
- Yue, Z.Q.; Lee, C.F.; Law, K.T.; Tham, L.G. Automatic monitoring of rotary percussive drilling for ground characterization illustrated by a case example in Hong Kong. Int. J. Rock Mech. Min. Sci. 2004, 41, 573–612. [Google Scholar] [CrossRef]
- Yue, Z.Q. Drilling process monitoring for refining and upgrading rock mass quality classification methods. Chin. J. Rock Mech. Eng. 2014, 33, 1977–1996. [Google Scholar]
- He, M.M.; Li, N.; Zhang, Z.Q.; Yao, X.C.; Chen, Y.S.; Zhu, C.H. An empirical method for determining the mechanical properties of jointed rock mass using drilling energy. Int. J. Rock Mech. Min. Sci. 2019, 116, 64–74. [Google Scholar] [CrossRef]
- Rodgers, M.; Mcvay, M.; Horhota, D.; Hernando, J. Assessment of Rock Strength from Measuring While Drilling Shafts in Florida Limestone. Can. Geotech. J. 2018, 55, 1154–1167. [Google Scholar] [CrossRef]
- Rodgers, M.; Mcvay, M.; Ferraro, C.; Horhota, D.; Tibbetts, C.; Crawford, S. Measuring Rock Strength While Drilling Shafts Socketed into Florida Limestone. J. Geotech. Geoenviron. 2018, 144, 04017121. [Google Scholar] [CrossRef]
- Rodgers, M.; Mcvay, M.; Horhota, D. Monitoring While Drilling Shafts in Florida Limestone. In Proceedings of the IFCEE 2018 Installation, Testing and Analysis of Deep Foundations (GSP 294), Orlando, FL, USA, 5–10 March 2018; American Society of Civil Engineers: Reston, VA, USA, 2018; pp. 613–621. [Google Scholar] [CrossRef]
- Rodgers, M.; Mcvay, M.; Horhota, D.; Sinnreich, J.; Hernando, J. Assessment of Shear Strength from Measuring While Drilling Shafts in Florida Limestone. Can. Geotech. J. 2018, 56, 662–674. [Google Scholar] [CrossRef]
- Karasawa, H.; Ohno, T.; Kosugi, M.; Rowley, J.C. Methods to estimate the rock strength and tooth wear while drilling with roller-bits-part 1: Milled-Tooth Tooth Bits. Energy Resour. Technol. 2002, 124, 125–132. [Google Scholar] [CrossRef]
- Karasawa, H.; Ohno, T.; Kosugi, M.; Rowley, J.C. Methods to estimate the rock strength and tooth wear while drilling with roller-bits-part 2: Insert bits. Energy Resour. Technol. 2002, 124, 133–140. [Google Scholar] [CrossRef]
- He, M.; Li, N.; Zhu, J.; Chen, Y. Advanced prediction for field strength parameters of rock using drilling operational data from impregnated diamond bit. J. Pet. Sci. Eng. 2019, 187, 106847. [Google Scholar] [CrossRef]
- Li, Y.; She, L.; Wen, L.; Zhang, Q. Sensitivity analysis of drilling parameters in rock rotary drilling process based on orthogonal test method. Eng. Geol. 2020, 270, 105576. [Google Scholar] [CrossRef]
- Li, H.; Liu, S.; Chang, H. Experimental research on the influence of working parameters on the drilling efficiency. Tunn. Undergr. Space Technol. 2020, 95, 103174. [Google Scholar] [CrossRef]
- Shang, F.; Yu, W.; Guo, Z.; Yu, Z.; Shan, W.; Rui, C.; Shang, X. Estimation of optimal drilling efficiency and rock strength by using controllable drilling parameters in rotary non-percussive drilling. J. Pet. Sci. Eng. 2020, 193, 107376. [Google Scholar] [CrossRef]
- Rossi, E.; Jamali, S.; Saar, M.O.; von Rohr, P.R. Field test of a Combined Thermo-Mechanical Drilling technology. Mode I: Thermal spallation drilling. J. Pet. Sci. Eng. 2020, 190, 107005. [Google Scholar] [CrossRef]
- Rossi, E.; Jamali, S.; Schwarz, D.; Saar, M.O.; von Rohr, P.R. Field test of a Combined Thermo-Mechanical Drilling technology. Mode II: Flame-assisted rotary drilling. J. Pet. Sci. Eng. 2020, 190, 106880. [Google Scholar] [CrossRef]
- Lakshminarayana, C.R.; Tripathi, A.K.; Pal, S.K. Prediction of Mechanical Properties of Sedimentary Type Rocks Using Rotary Drilling Parameters. Geotech. Geol. Eng. 2020, 38, 4863–4876. [Google Scholar] [CrossRef]
- Kalantari, S.; Hashemolhosseini, H.; Baghbanan, A. Estimating rock strength parameters using drilling data. Int. J. Rock Mech. Min. Sci. 2018, 104, 45–52. [Google Scholar] [CrossRef]
- Kalantari, S.; Baghbanan, A.; Hashemolhosseini, H. An analytical model for estimating rock strength parameters from small-scale drilling data. Rock Mech. Geotech. Eng. 2019, 104, 135–145. [Google Scholar] [CrossRef]
- Hughes, H.M. Some aspects of rock machining. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1972, 9, 205–211. [Google Scholar] [CrossRef]
- Mellor, M. Normalization of specific energy values. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1972, 9, 661–663. [Google Scholar] [CrossRef]
- Poane, J.; Madson, D.; Bruce, W.E. Drillability Studies: Laboratory Percussive Drilling; US Department of the Interior, Bureau of Mines: Washington, DC, USA, 1969. [Google Scholar]
- Zhang, K.; Hou, R.B.; Zhang, G.H.; Zhang, G.M.; Zhang, H.Q. Rock Drillability Assessment and Lithology Classification Based on the Operating Parameters of a Drifter: Case Study in a Coal Mine in China. Rock Mech. Rock Eng. 2016, 49, 329–334. [Google Scholar] [CrossRef]
- Yu, B.S.; Zhang, K.; Niu, G.G.; Xue, X.R. Real-time rock strength determination based on rock drillability index and drilling specific energy: An experimental study. B. Eng. Geol. Environ. 2021, 80, 3589–3603. [Google Scholar] [CrossRef]
- Teale, R. The concept of specific energy in rock drilling. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1965, 2, 57–73. [Google Scholar] [CrossRef]
- Kahraman, S. Rotary and percussive drilling prediction using regression analysis. Int. J. Rock Mech. Min. Sci. 1999, 36, 981–989. [Google Scholar] [CrossRef]
- Kahraman, S.; Balci, C.; Yazici, S.; Bilgin, N. Prediction of the penetration rate of rotary blast hole drilling using a new drillability index. Int. J. Rock Mech. Min. Sci. 2000, 37, 729–743. [Google Scholar] [CrossRef]
- Ataei, M.; KaKaie, R.; Ghavidel, M.; Saeidi, O. Drilling rate prediction of an open pit mine using the rock mass drillability index. Int. J. Rock Mech. Min. Sci. 2015, 73, 130–138. [Google Scholar] [CrossRef]
- Ocak, I.; Seker, S.E. Estimation of elastic modulus of intact rocks by artificial neural network. Rock Mech. Rock Eng. 2012, 45, 1047–1054. [Google Scholar] [CrossRef]
- Yesiloglu-Gultekin, N.; Gokceoglu, C.; Sezer, E.A. Prediction of uniaxial compressive strength of granitic rocks by various nonlinear tools and comparison of their performances. Int. J. Rock Mech. Min. Sci. 2013, 62, 113–122. [Google Scholar] [CrossRef]
- Sarkar, K.; Tiwary, A.; Singh, T.N. Estimation of strength parameters of rock using artificial neural networks. Bull. Eng. Geol. Environ. 2010, 69, 599–606. [Google Scholar] [CrossRef]
- He, M.M.; Zhang, Z.Q.; Ren, J.; Huan, J.Y.; Li, G.F.; Chen, Y.S.; Li, N. Deep convolutional neural network for fast determination of the rock strength parameters using drilling data. Int. J. Rock Mech. Min. Sci. 2019, 123, 104084. [Google Scholar] [CrossRef]
- Roxborough, F.F.; Phillips, H.R. Rock excavation by disc cutter: Authors reply to the Discussion on F. F. Roxborough and H. R. Phillip’s paper. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1975, 12, 361–366. [Google Scholar] [CrossRef]
- Jalali, S.E.; Zare, M. An analytical pre-feasibility study to generate rotary-percussive concept in hard rock TBMs. J. Geol. Min. Res. 2009, 1, 140–148. [Google Scholar]
- Marji, M.F. Simulation of crack coalescence mechanism underneath single and double disc cutters by higher order displacement discontinuity method. J. Cent. South Univ. 2015, 22, 1045–1054. [Google Scholar] [CrossRef]
- Marji, M.F. Rock Fracture Mechanics with Displacement Discontinuity Method; LAP Lambert Academic Publishing, Yazd Univ, Dept Min Engn: Yazd, Iran, 2014. [Google Scholar]
- Goetz, J.N.; Brenning, A.; Petschko, H.; Leopolda, P. Evaluating machine learning and statistical prediction techniques for landslide susceptibility modeling. Comput. Geosci-UK 2015, 81, 1–11. [Google Scholar] [CrossRef]
- Cutler, D.R.; Edwards, T.C., Jr.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for Support Vector Machines; ACM Transactions on Intelligent Systems and Technology: New York, NY, USA, 2011. [Google Scholar]
- Cutler, D.R.; Edwards, T.C., Jr.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Landslide spatial modeling: Introducing new ensembles of ANN, MaxEnt, and SVM machine learning techniques. Geofis. Internacional. 2017, 305, 314–327. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Tang, K.S.; Man, K.F.; Kwong, S.; He, Q. Genetic Algorithms and Their Applications. IEEE Signal Process. 1996, 13, 21–37. [Google Scholar] [CrossRef]
- Wang, S.F.; Li, X.B.; Yao, J.R.; Gong, F.Q.; Li, X.; Du, K.; Tao, M.; Huang, L.Q.; Du, S.L. Experimental investigation of rock breakage by a conical pick and its application to non-explosive mechanized mining in deep hard rock. Int. J. Rock Mech. Min. Sci. 2019, 122, 104063. [Google Scholar] [CrossRef]
- Wang, S.F.; Sun, L.C.; Li, X.B.; Wang, S.Y.; Du, K.; Li, X.; Feng, F. Experimental investigation of cuttability improvement for hard rock fragmentation using conical cutter. Int. J. Geomech. 2021, 21, 06020039. [Google Scholar] [CrossRef]
- Wang, S.F.; Tang, Y.; Li, X.B.; Du, K. Analyses and predictions of rock cuttabilities under different confining stresses and rock properties based on rock indentation tests by conical pick. Trans. Nonferr Metal. Soc. 2021, 31, 1766–1783. [Google Scholar] [CrossRef]
- Wang, S.F.; Tang, Y.; Wang, S.Y. Influence of brittleness and confining stress on rock cuttability based on rock indentation tests. J. Cent. South Univ. 2021, 28, 2786–2800. [Google Scholar] [CrossRef]
- Wang, Y.J.; She, L.; Zhao, Y.F.; Cao, R.L. Experimental study on measurement of rock strength parameters based on digital drilling technology. Chin. J. Geotech. Eng. 2020, 42, 1659–1668. [Google Scholar]
- He, M.M. Research on the prediction of rock mass mechanics characteristics based on the rotary penetration technology. Xi’an: Xi’an Univ. Technol. 2021, 28, 2786–2800. [Google Scholar]
- Wang, Y.J.; She, L.; Zhao, Y.F.; Cao, R.L. Method for Measuring Rock Mass Characteristics and Evaluating the Grouting-Reinforced Effect Based on Digital Drilling. Rock Mech. Rock Eng. 2018, 52, 841–851. [Google Scholar] [CrossRef]
- Wang, Q.; Qin, Q.; Gao, S.; Li, S.C.; Gao, H.K.; He, M.C.; Jiang, B.; Zhang, C. Relationship between rock drilling parameters and rock uniaxial compressive strength based on energy analysis. J. China Coal Soc. 2018, 43, 1289–1295. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).


