Abstract
The acoustic emission b value is an important and widely used parameter for the early prediction of rock fractures. In this study, five groups of true triaxial compression tests were conducted on granite specimens to analyze changes in b value during the process of rock failure, and to investigate the b value characteristics of acoustic emission events. First, the acoustic emission events that simultaneously triggered at least four sensors were located using P-wave arrivals and sensor coordinates. Then, considering various intervals of acoustic emission event counts, stress magnitude, and stress proportion, b values were calculated using the values of the maximum amplitude, average amplitude, maximum absolute energy, and average absolute energy of the acoustic emission events. In addition, the goodness of the fitting curves was used to evaluate the fitting reliability of the b values. The results indicated higher accuracy of b value when calculated using the average amplitude setting for intervals of acoustic emission event counts of 200 or greater, stress magnitude of 20 MPa or greater, and stress proportion of 10% or greater. Moreover, the interval of event counts of 200 is suggested as a window parameter for b value calculations, and the b values are observed to exhibit a decreasing trend before fracture for more than 80% of the specimens. Furthermore, the b value tends to decrease with an increase in confining pressure. Thus, the b value can be used as an indicator for validating the stress concentration area, including magnitudes and accumulative probability density distribution of events, which is a beneficial complement to clarifying precursor information of rock mass instability.
1. Introduction
The concept of b value originated in the study of seismology. In 1944, Gutenberg and Richter first proposed that b value reflects the relationship between the frequency and magnitude of earthquakes, i.e., the number of earthquakes exponentially decreasing with the increase of the magnitude [1], and the b value is an important scale parameter for operational earthquake forecasting during earthquake sequences [2,3,4,5,6,7,8]. Several engineering disasters and great earthquakes have shown that b value decreased before the time of occurrence of higher magnitude events (e.g., main shocks, rock bursts and roof falls) [9,10,11,12,13,14]. The failure mechanism of brittle rocks is similar to that of earthquakes, so b value analysis for the microseism and acoustic emission (AE) signals obtained from the failure process of brittle rocks has become an important research issue [14,15,16].
In the past few decades, the b value has been widely used in rock failure prediction and rock damage analysis [17,18,19,20,21]. In an attempt to reveal the onset precursors of rock damage and failure, the uniaxial and conventional triaxial stress tests have been conducted by several researchers on small-scale rock specimens, and the b value characteristics of the process of rock failure have been investigated. For instance, Mogi first proposed that the b value reflects the internal heterogeneity of rocks, and that more heterogeneous rocks have a higher b value [22]. Scholz first observed that the b value is related to the stress state of the rocks, and decreases as the stress increases [23]. Weeks et al. reported that the b value is negatively correlated with stress [12]. As the stress level increases beyond 93% and 100%, the b value begins to decrease [7]. Moreover, the b value can capture the inception of severe cracking in concrete [24]. However, studies on the b value characteristics for rocks under different true triaxial stresses have been rarely reported thus far.
Because the b value is used as a warning index for earthquakes and rock damage, it is important to capture the trend in its variations with the change of time and stress. While the methods used by scholars for calculating the b value are different, the amplitude and energy of AE hits are most commonly used to estimate b value [25]. At least four methods for obtaining the magnitude of completeness (Mc) have been used to improve the calculation precision of the b value [26,27,28,29]. Meanwhile, when a single AE sensor is used to detect AE signals, it cannot use the location method to determine the AE events and the noise signals from the testing machine and environment, which are used to analyze the b value and other properties of the AE; this may result in a high AE hit rate (HR) and an inaccurate b value.
In this study, five groups of true triaxial compressive tests were conducted on granite specimens. The minimum principal stress (σ3) values used for the test were 10, 20, 30, 50, and 100 MPa, and the intermediate principal stress (σ2) was varied from test to test at the same σ3 value. Six sensors were attached to the loading mode to detect the AE signals during the loading. AE localization without a premeasured velocity was applied [30]. Based on the location result of the AE signals, the AE events located inside the specimen were selected, and the values of Amax, Aavg, Emax, and Eavg of the AE events were chosen for analysis. A new b value estimation method which employs apparent frequency-amplitude distribution was used to calculate various b values in this loading test, and the b value characteristics of granite specimens under different true triaxial stresses were discussed. The results of this paper are of great help for deeper understanding the relationship between the b value and the differential stress, as well as the damage accumulation assessment through temporal variation of b value in the true triaxial stress state.
2. Experimental Details
The true triaxial testing system (Model TRW-3000) used in this study was developed by the Advanced Research Center at Central South University, China, and the detailed parameters of the testing system have been described by several literatures [31,32,33,34,35]. The test system can apply quasi-static loading along the direction of the three principal stresses independently through hydraulically driven pistons, with a maximum load capacity of 3000, 2000, and 2000 kN along the vertical (z), and horizontal (x and y) directions, respectively. The loading system is shown in Figure 1a,b. The plate has extremely high stiffness and rigidity in order to transfer the load into the rock specimens. Five groups of tests for σ3 values of 10, 20, 30, 50 and 100 MPa were conducted. In the test settings, σ1 was applied along the z direction, σ2 was applied along the y direction, and σ3 was applied along the x direction. The loading control mode was set to a loading speed of 0.3 MPa/s. The loading paths of the tests, as shown in Figure 1c, are as follows:
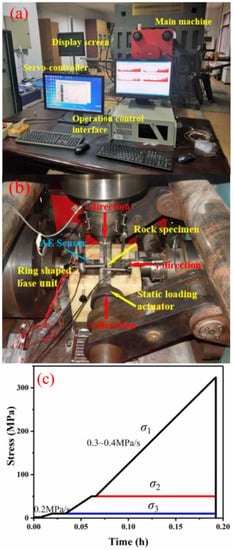
Figure 1.
Illustration of the true triaxial test system: (a) an overview of the testing system; (b) image of the true triaxial machine and the designed loading apparatus; and (c) representative loading path. AE in the figure represents acoustic emission.
- σ1, σ2, and σ3 were loaded with 1 MPa to keep the rock specimens attached to the plate; and subsequently the three loads (i.e., σ1, σ2, and σ3) were increased until σ3 reached its predefined value.
- σ1 and σ2 were loaded until σ2 reached its predefined value, while σ3 was kept constant.
- σ1 was loaded until the failure of the rock specimen, while σ2 and σ3 were kept constant.
The granite specimens used in these experiments were obtained from a granite quarry in the Hunan Province, China, the average uniaxial compressive strength was 113.7 MPa. The main mineral composition of the granite includes feldspar, quartz, and black mica. The rock blocks were cut into cubic specimens with a side length of 50 ± 0.02 mm.
A PCI-2 AE test system with the AE-win software was used to monitor the AE signals of the granite specimens. The NANO-type resonant narrowband sensors with a center response frequency of 125 (750) kHz and 2/4/6 preamplifiers were chosen for the tests. Six AE sensors were uniformly fixed on six platens in six directions around the specimen. During the tests, both the gain of the preamplifier and the threshold were set to 40 dB, the sampling rate was set to 10 MHz, and the threshold was 40 dB.
3. Analysis of b Value Characteristics
3.1. AE Localization
During the experiments, the triaxial stress applied to the rock specimens increased gradually; accordingly, the velocity field inside the specimens changed with the change in triaxial stress [36]. Many factors, such as sonic speed [37], temperature [38], abnormal arrivals [39], have negative effect on the localization of AE events. As a result, the localization results with large errors will significantly affect the event type discrimination [40], empty region identification [41], and abnormal region tomography [42]. To eliminate the influence of wave velocity error on localization results, a localization method without premeasured wave velocity was proposed [30,43,44,45]. The advantage of analytical algorithm that it could obtain the precious solution was properly applied to remove the influence of abnormal arrivals in collaboration with the Iterative Solutions [39]. Furthermore, Dong et al. [46] optimized the A* path search algorithm and proposed a velocity-free localization method (VFH) for complex three-dimensional structures. The localization accuracy was greatly improved using the proposed VFH localization method. In this study, six sensors were used and their coordinates were assumed to be Si (xi, yi, zi) (i = 1, 2, 3, 4, 5, 6). The localization method without premeasuring the wave velocity was used to obtain the location of AE events during the experiments. For an AE event, assuming that the focal coordinate is (x, y, z), the origin time is t0, and the P-wave arrival at sensor Si is ti (i = 1, 2, 3, 4, 5, 6), the following equation is satisfied:
where the symbol v represents the unknown velocity of the P-wave in the travel path. When at least four sensors are triggered, the simultaneous Equation (1) can be used to determine the solution; and the coordinates of the focus, i.e., (x, y, z) inside the specimen space is filtered as a valid AE event.
3.2. AE Signals
Rock fracture is the initiation and propagation of microcracks until they form macrocracks, inducing rock fraction [44]. When a microcrack is formed, the AE sensor is triggered multiple times to the vibration wave whose voltage exceeds the threshold. An AE hit is a vibration wave detected by an AE sensor, as shown in Figure 2, in which the analog signal is converted into a digital signal by the collector. A complete wave is an AE hit. Theoretically, the number of AE hits is positively correlated with the degree of internal damage of the rock.
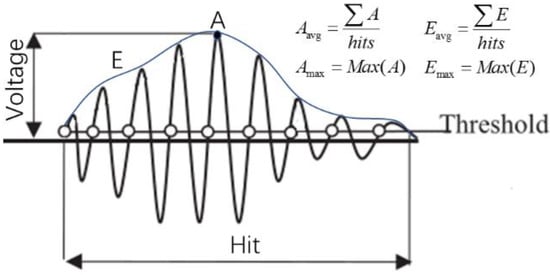
Figure 2.
Waveform of AE electrical acoustic emission signals. A represents the amplitude of the signal. E represents the energy of the signal, which is the area enclosed by the blue envelope curve.
Figure 3a,b shows the relationship between the AE hit rate (HR), AE event rate (ER), cumulative AE hit rate (CHR), cumulative AE event rate (CER), and the true triaxial stress of the granite specimen G-10-10 (the specimen No. was designed as “G-digit1-digit2”, where “G” represents Granite, “digit1” represents the applied stress value of σ3, and “digit2” represents the applied stress value of σ2; here, “G-10-10” means that the applied stress value of σ3 and σ2 on this granite specimen are 10 MPa and 10 MPa, respectively). As the same trends were found in all specimens, the testing results of specimen G-10-10 were mostly used for variation analysis of AE parameters hereafter. HR is the total number of AE hits of all sensors per second divided by the total number of sensors, and ER is the number of located AE events per second. Clearly, HR and ER have roughly the same variation trend—an initial increase, followed by oscillation, and finally a decrease. Initially, the value of ER ranged between 40 and 80, while that of HR ranged between 100 and 200. When σ1 was 164.7 MPa at 263 s, the HR and ER values gradually decreased; and when σ1 is 76% of its peak value (217.7 MPa), the ER and HR values decreased to less than 10 and less than 50, respectively. Furthermore, the slopes of CHR and CER are observed to decrease with the increase in σ1, indicating a change in the trend of the HR and ER values; the ER value remained at less than 10 until 356 s, when the specimen was fractured. The other specimens were also observed to exhibit a trend similar to that of the granite specimen G-10-10.
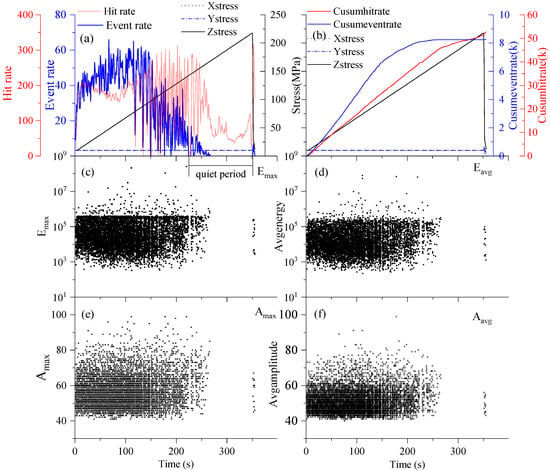
Figure 3.
AE parameters of G-10-10: (a) HR, ER, and stress vs. loading time; (b) CHR, CER, and stress vs. loading time; (c) Emax of AE events; (d) Eavg of AE events; (e) Amax of AE events; and (f) Aavg of AE events.
3.3. Quiet Period
The change trends of different parameters, i.e., the absolute energy (Emax, Eavg) and amplitude (Amax, Aavg) values of AE events in specimen G10-10, are shown in Figure 3c–f. Emax, Eavg, Amax and Aavg are only meaningful for one AE event. Emax and Amax are the maximum value and selected among the AE sensors triggered by the same AE events, and Eavg and Aavg are the average value of the AE sensors triggered by the same AE events. In this study, Emax and Eavg have a similar change trend; Amax and Aavg also have a similar change trend. The total AE process can be divided into “active period” and “quiet period” according to the distribution of ER and the E and A values. As σ1 approached its peak value, and the values of HR and ER decreased to approximately 50 and less than 10, respectively (which was the quiet period). The HR curve was observed to fluctuate slightly, while the ER remained stable. Therefore, it is more scientific and reasonable to use ER to determine the quiet period.
Figure 4 shows that the value of ER did not increase linearly with increasing σ1, and some blanks were observed before the specimen fracture. However, the ER value increased significantly after the stress state of the rock specimen changed. Furthermore, when σ3 reached its predefined value and σ1 and σ2 continued to increase, the value of ER was observed to increase and then decrease gradually. Similarly, when σ2 reached its predefined value and σ1 continued to increase, the value of ER increased and then decreased gradually. Thus, the stress state can cause changes in ER. Therefore, ER is expected to reduce gradually to finally disappear at the same stress station. To some extent, ER has a great relationship with the stress state of the rock specimen.
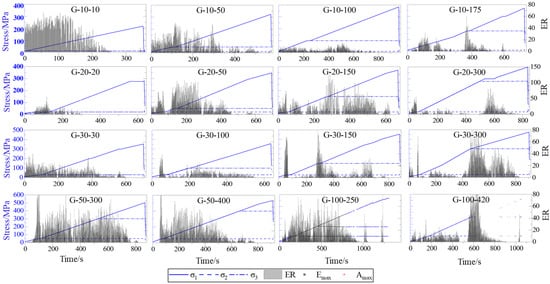
Figure 4.
ER, stress vs. time of all specimens in this study. The specimen No. was designed as “G-digit1-digit2”, where “G” represents granite, “digit1” represents the applied stress value of σ3, and “digit2” represents the applied stress value of σ2; for example, “G-10-50” means that the applied stress value of σ3 and σ2 on this granite specimen are 10 MPa and 50 MPa, respectively.
The length of the quiet period is shown in Table 1. When σ1 reached between 50% and 93% of its peak value, the ER and HR values significantly declined, and AE entered the quiet period. Figure 5 shows the length of the quiet period, and a large dispersion in the distribution of the quiet period can be observed; the duration was from 93–452 s, the mean was 239.79 s, and the variance was 114.81. The stress at the beginning of the quiescent period was 27–91% of the maximum stress (mean is 69%). Because there is no obvious rule between the length and start time of the quiet period under different stress states, it is difficult to predict rock failure.

Table 1.
Relationship between AE and σ1 in the quiet period.
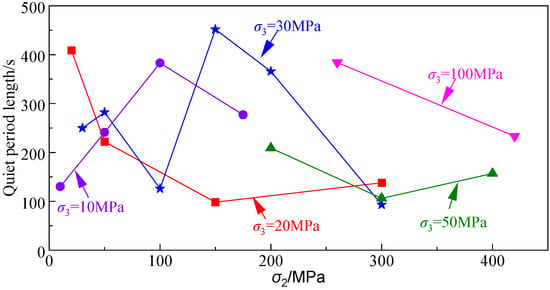
Figure 5.
Quiet period under different true triaxial stresses.
3.4. b Value
The b value is defined as the log-linear slope of the cumulative frequency magnitude distribution of the AE, and the mathematical equation for determining the b value is as follows:
where M is the magnitude of the AE events, and N is the cumulative frequency of the AE events with magnitude of M or greater; a is an empirical constant; and b is the gradient. This equation is always recognized as the G–R relationship [1]. In the case of the AE technique, the G–R relationship is modified as follows [3,25]:
where A is the peak amplitude of the AE hit, E is the absolute energy of the AE hit, and N is the cumulative number of the AE hit with an amplitude greater than A or absolute energy greater than E. The magnitude of the event is a logarithmic scale of the instrumentally measured amplitude, while the value of A recorded in dB is divided by 20, and E is used in its logarithmic form; is set for the calculation to produce the same magnitude as that of an earthquake; a is an empirical constant; and b is the b value of the AE. Because the amplitudes used for b value estimation in rock AE test are the apparent amplitudes measured on the sample boundary by acoustic sensor which is attenuated from the source, the corresponding apparent frequency-amplitude distribution does not necessarily represent the underlying size distribution of the sources because attenuation may modify the b value. Recently, attenuation effect on apparent amplitude-frequency distribution and b value was investigated from a statistical point of view by Liu et al. [4] and Chen et al. [47]; the authors theoretically proved that the b value is unchanged within a specific interval before and after attenuation. This indicates that if the apparent frequency-amplitude distribution after attenuation follows the G–R relationship in a certain interval of amplitude, the b value inferred in that interval is the same as that of the true source amplitude distribution, and the authors also proposed a new method named FGS for b value estimation through apparent amplitude-frequency distribution in a rock AE test. The FGS is a new b value estimation procedure which specify the minimum data volume, data counting procedure, bin width and linear regression method, and employ the Fisher optimal split and the global search algorithm to determine the logarithmic linear segment in the apparent frequency-amplitude distribution. The use of the FGS method for b value estimation actually means that once we obtain the located AE events, we can directly use the FGS method for log-linear segment determination in the apparent frequency-amplitude distribution, and further for b value estimation, without doing the work of attenuation compensation; moreover, the b value estimated by FGS can represent the real source distribution characteristics. The FGS is also used in this loading test for b value estimation.
While both the energy and amplitude of the AE event can indicate the magnitude of an AE event, the b value estimated using the energy data should be taken into consideration [48]. Figure 6 shows the b value estimated from different intervals of AE event counts of the granite specimen G-10-10. The intervals were set at 60, 80, 100, 200, 300, 400, 500, 600, 700, 800, 900, and 1000 events, such that the start value of the next interval is the mean value of the previous interval, as (0 60), (30 90), (90 150) et al. Furthermore, Figure 7 shows that most b value curves exhibit the same trend: first decreasing, and then increasing or continuing to decrease, which was distinctly observed for count intervals at 1000 events. Similarly, the values of bEmax and bEavg of all specimens exhibited the same trend as bAmax and bAavg. However, the values of REmax and REavg were significantly smaller than the values of RAmax and RAavg, which exhibited a very similar behavior, and in most cases, the latter values are greater than 0.95. In general, the b value ranged between 0.3 and 3, and the value of R2 was greater than 0.8. When the intervals were 60, 80, and 100, the b value was greater than 3 and R2 was less than 0.8, which indicates that the b value estimated using a small number of AE events has poor applicability. With an increase in interval (i.e., more than 200 events), almost all R2 values were in the range 0.8–1 and the b values were in the range 0.5–3. The distribution of the b value was observed to be sparser with the increase in the interval, and 200 is the lower limit of this interval. Therefore, to analyze the damage development condition of the rock specimen during the loading process, it is better to choose an interval with a small value. The fluctuating trend of the b value indicates the damage growth in the rock specimen. Table 2 summarizes the mean of R2 at different AE event count intervals of the specimen G-10-10. Apparently, the R2 value of bE (bEmax and bEavg) is smaller than that of bA (bAmax and bAavg), which indicates that the b value calculated using amplitude is better than that using energy. Moreover, the values of bAmax and bAavg were nearly equal, and interestingly, the mean R2 value of bEmax increased as the interval of the AE event count increased, while that of bEavg increased first and then slightly decreased. When the interval of the AE event count was set at 200, the mean of the R2 of bEavg a bEmax and bEavg were 0.968 and 0.971, respectively, and their standard deviations were all 0.020. Thus, we conclude that the b value calculated using Eavg at an interval of an AE event count of 200 takes both real-time and reliability into account.
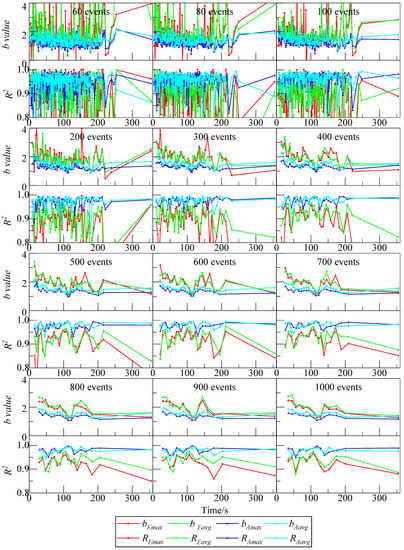
Figure 6.
b value and its fitting goodness at different AE event count intervals for specimen G-10-10. The range of bAmax values is between 0.63 to 2.17.
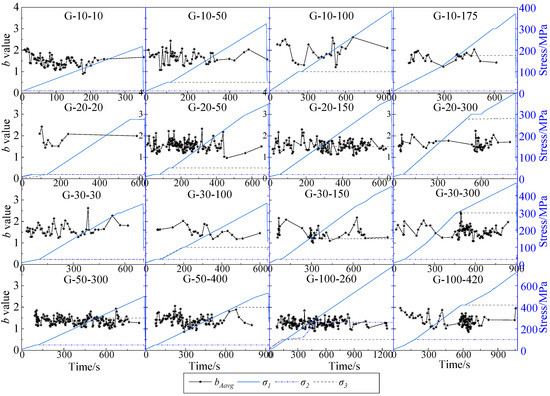
Figure 7.
b value and stress vs. time under different true triaxial stresses. The range of b values is between 0.85 to 2.62.

Table 2.
The mean of R2 at different AE event count intervals for specimen G-10-10.
In order to distinguish the b value at each loading stage of the rock specimen, the AE events contained in different intervals of stress proportion were used to estimate the b value. Figure 8 shows the variation of b value at the chosen stress proportion intervals of 2%, 4%, 6%, 8%, 10% and 12% of the peak value of σ1 and a threshold at 200 for a minimum number of AE events in a stress proportion interval was set to ensure the accuracy of the b value. Figure 10 shows that there is a blank space on the right side of the b value curve, and the trend of the b value is obvious when the stress proportion interval was less than 10%—it first decreased and then increased, which is, however, not consistent with Figure 8. The portion of the b value curves falling in the final stage was missing, mainly because the AE event count intervals were less than 200 in the quiet period. The mean of the R2 at different AE stress proportion intervals of G-10-10 is listed in Table 3; the value of bE (bEmax and bEavg) was observed to be smaller than that of bA (bAmax and bAavg), and the mean R2 of bEmax increased as the stress proportion interval increased, while that of bEavg first increased and then slightly decreased. According to Table 3, calculating the b value using Amax and setting the stress proportion interval at 10%, σ1 is better for distinguishing the b value at each loading stage.
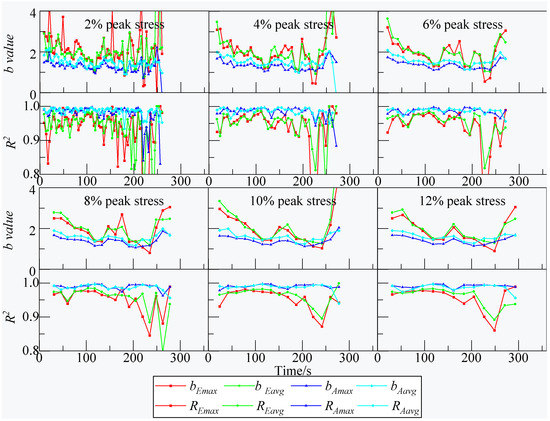
Figure 8.
b value and its fitting goodness at different stress proportion intervals for the specimen G-10-10. The range of bAmax values is between 0 to 2.21.

Table 3.
The mean of R2 at different AE stress proportion intervals for the specimen G-10-10.
In order to distinguish the changes in the b value with time when true triaxial stress is loaded, the b value was estimated using the AE data during a certain stress proportion interval. Because the stress had a positive relationship with time, the loading speed was fixed at 0.3 KN/s. Figure 9 shows the result of the b value estimated according to the AE data during a certain stress interval. The stress intervals of σ1 were 5, 10, 15, 20, 25, and 30 MPa, and a threshold for a minimum number of AE events was set at 200. The trend of the b value is obvious: it first dropped and then increased, which is consistent with Figure 8. Table 4 lists the mean of R2 at different AE stress proportion intervals for the specimen G-10-10, and the mean of R2 for both RAmax and RAavg perform well, such that both values are greater than 0.95, and hence, difficult to choose. Combined with Figure 9, setting stress intervals at 20 MPa takes both data size and reliability into account.
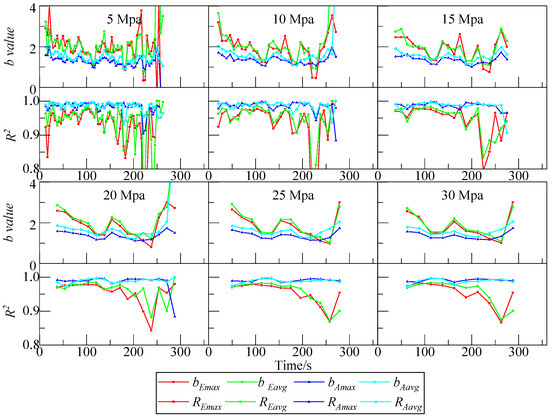
Figure 9.
b value and its fitting goodness at different stress intervals for specimen G-10-10. The range of bAmax values is between 1.01 to 1.99.

Table 4.
The mean of R2 at different AE stress proportion intervals for specimen G-10-10.
A comparison of the interval of the AE event count at 200, the stress proportion at 10% σ1, and stress magnitude at 20 MPa, showed that all their R2 values performed well; while the interval of stress proportion at 10% σ1 required the acquisition of the maximum value of σ1, the interval of stress magnitude at 20 MPa may be affected by the load speed, and the values of σ2 and σ3. Therefore, the AE event count at 200 is considered to be better for real-time monitoring of rock damage; hence, the AE event interval method is more reliable than the stress interval and the stress proportion interval methods. Therefore, the b value calculated using Aavg and setting the interval of the AE event count at 200 was chosen for plotting all b value curves for the granite specimens, as shown in Figure 9. The b value was observed to decrease first and then increase or oscillate, and finally decrease. Moreover, the b value exhibited a decreasing trend before fracture in approximately 80% of the specimens.
Figure 10 shows the b value for the whole process of five groups of granite specimens under different true triaxial stresses, calculated using the average amplitude of the AE event. Apparently, the b value ranged between 1 and 2, and generally decreased with increasing confining pressure, as observed in the aqua rectangle area shown in Figure 10. Furthermore, in the specimen group σ3 at 10 MPa, the b value was observed to decrease after an initial increase with increasing σ2. In the specimen group σ3 at 20, 30, 50, and 100 MPa, the b value tended to decrease with increasing σ2. In addition, when σ3 was 50 and 100 MPa, the b value was approximately 1.1, which is smaller than that of the other groups (~1.4); this means that a small b value may associate with high confining pressures. Since a large number of AE events with large amplitude will occur with the increase of differential stress, especially in the final loading stage in rock AE tests, this will in turn result in a decrease of b value. Therefore, temporal variation of the b value can be used for damage accumulation assessment in rock AE tests, while spatial variation of the b value can be used to determine the stress concentration area, and the temporal-spatial variation of the b value is an important reference for precursory analysis of rock instability.
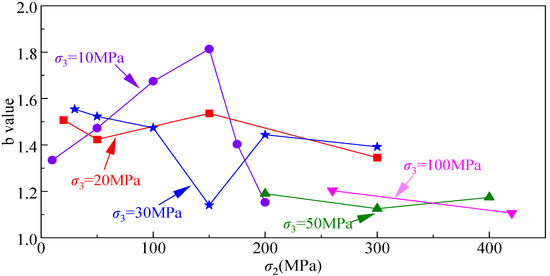
Figure 10.
b value in different granite specimens under true triaxial stress.
4. Conclusions
This study conducted five groups of true triaxial compressive tests on granite specimens, and detected and analyzed their AE behavior from loading to rock failure. A large number of AE signals were observed to be generated at the moment of stress state change, and the AE events were fewer at constant stress conditions, namely no loading stress, steady loading stress, or steady increase in loading stress. Therefore, it is believed that a change in the stress conditions can be judged by the sudden occurrence of a large number of AE events. Meanwhile, a random disturbance that appears during machine loading may affect the length of the quiet period; and the length of the quiet period may be affected by the loading time because the specimen is directly broken when the loading stress reaches the peak value. Consequently, future research should investigate the variations in the length of the quiet period under different loading speed conditions, and to determine the length of the quiet period in the critical state before rock failure at reduced loading speed. In addition, when σ2 stress gradually increases, the rock transforms from brittle deformation to ductile deformation, and the peak stress first increases and then decreases, causing a significant change in AE parameters.
The b value is a critical parameter to describe spatial and temporal size distribution characteristics in laboratory rock AE tests. Since the b value is negatively correlated with the differential stress, therefore, temporal variation of the b value is an important indicator for damage accumulation assessment, and the decrease trend of b value can be used for precursory analysis of instability in rock AE tests. At the same time, rock samples always have complex fault systems which display a scale-invariant hierarchy or a fractal geometry, and the faults will form discontinuous branching structures distributed in a three-dimensional volume of the rock sample. This geometrical distribution of faults is in concert with stress heterogeneities and interactions, and influences the extent of the b value. Therefore, a combination analysis of fault distribution and b value can better describe the damage evolution, which in turn helps to understand the fracture mechanism of rock material. This requires a detailed detection of internal structure of rock samples before loading, as well as the detection of damage evolution during the loading process through various techniques, for example, non-destructive testing techniques, and such investigation will be the focus of future rock AE research.
Author Contributions
L.D. is responsible for the experimental part and the paper writing; L.Z. and H.L. are responsible for the data processing and part of the paper writing; X.L. is responsible for experimental setup and part of data processing; K.D. is responsible for experimental results analysis. All authors have read and agreed to the published version of the manuscript.
Funding
The work is supported in part by the National Science Foundation for Excellent Young Scholars of China (51822407), in part by the National Natural Science Foundation of China (51774326, 51504288), in part by the Natural Science Foundation for Distinguished Young Scholars of Hunan Province, China (2018JJ1037), and in part by the Huxiang Young Talents Plan of Hunan Province, China (2018RS3001). Kun Du was supported by the open fund of Hebei Mining Development and Safety Technology Laboratory (grant number 2016kykf03) and the open fund of Mining Disaster Prevention and Control Ministry Key Laboratory at Shandong University of Science and Technology (grant number MDPC201917).
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| σ1 | maximum principal stress (MPa) |
| σ2 | intermediate principal stress (MPa) |
| σ3 | minimum principal stress (MPa) |
| Amax | maximum amplitude of an acoustic emission event (dB) |
| Aavg | average amplitude of an acoustic emission event (dB) |
| Emax | maximum absolute energy of an acoustic emission event (aJ) |
| Eavg | average absolute energy of an acoustic emission event (aJ) |
| bA | b value based on the amplitude |
| bE | b value based on the energy |
| bAmax | b value based on the maximum amplitude of multiple hits |
| bAavg | b value based on the average amplitude of multiple hits |
| bEmax | b value based on the maximum energy of multiple hits |
| bEavg | b value based on the average energy of multiple hits |
| R2 | goodness of fitting |
| RAmax | fitting goodness of b value based on the maximum amplitude of multiple hits |
| RAavg | fitting goodness of b value based on the average amplitude of multiple hits |
| REmax | fitting goodness of b value based on the maximum energy of multiple hits |
| REavg | fitting goodness of b value based on the average energy of multiple hits |
References
- Gutenberg, B.; Richter, C.F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 1994, 34, 185–188. [Google Scholar] [CrossRef]
- Smith, W.D. The b-value as an earthquake precursor. Nature 1981, 289, 136–139. [Google Scholar] [CrossRef]
- Rao, M.V.M.S.; Lakshmi, K.J.P. Analysis of b-value and improved b-value of acoustic emissions accompanying rock fracture. Curr. Sci. 2005, 89, 1577–1582. [Google Scholar]
- Liu, X.L.; Han, M.S.; He, W.; Li, X.B.; Chen, D.L. A new b-value estimation method in rock acoustic emission testing. J. Geophys. Res. Solid Earth 2020, 125, e2020JB019658. [Google Scholar] [CrossRef]
- Jordan, T.H.; Chen, Y.T.; Gasparini, P.; Madariaga, R.; Main, I.G.; Marzocchi, W.; Papadopoulos, G.; Sobolev, G.; Yamaoka, K.; Zschau, J. Operational earthquake forecasting: State of Knowledge and Guidelines for Utilization. Ann. Geophys. Italy 2011, 54, 361–391. [Google Scholar]
- Sammonds, P.R.; Meredith, P.G.; Main, I.G. Role of pore fluids in the generation of seismic precursors to shear fracture. Nature 1992, 359, 228–230. [Google Scholar] [CrossRef]
- Kwiatek, G.; Goebel, T.H.W.; Dresen, G. Seismic moment tensor and b value variations over successive seismic cycles in laboratory stick-slip experiments. Geophys. Res. Lett. 2014, 41, 5838–5846. [Google Scholar] [CrossRef] [Green Version]
- Goh, A.T.C.; Zhang, W. Reliability assessment of stability of underground rock caverns. Int. J. Rock Mech. Min. Sci. 2012, 55, 157–163. [Google Scholar] [CrossRef]
- Jafari, M.A. The distribution of b-value in different seismic provinces of Iran. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Okal, E.A.; Romanowicz, B.A. On the variation of b -values with earthquake size. Phys. Earth Planet. Inter. 1994, 87, 55–76. [Google Scholar] [CrossRef]
- Scholz, C.H. Microfractures, aftershocks, and seismicity. Bull. Seismol. Soc. Am. 1968, 58, 1117–1130. [Google Scholar]
- Weeks, J.; Lockner, D.; Byerlee, J. Change in b-values during movement on cut surfaces in granite. Bull. Seismol. Soc. Am. 1978, 68, 333–341. [Google Scholar] [CrossRef]
- Lockner, D.A.; Byerlee, J.D.; Kuksenko, V.; Ponomarev, A.; Sidorin, A. Quasi-static fault growth and shear fracture energy in granite. Nature 1991, 350, 39. [Google Scholar] [CrossRef]
- Mondal, D.; Roy, P. Fractal and seismic b-value study during dynamic roof displacements (roof fall and surface blasting) for enhancing safety in the longwall coal mines. Eng. Geol. 2019, 253, 184–204. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Z.; Li, X.; Gong, F.; Du, K. Experimental study on the effect of strain rate on rock acoustic emission characteristics. Int. J. Rock Mech. Min. Sci. 2020, 133, 104420. [Google Scholar] [CrossRef]
- Wang, S.; Tang, Y.; Wang, S. Influence of brittleness and confining stress on rock cuttability based on rock indentation tests. J. Cent. South Univ. 2021, 28, 2786–2800. [Google Scholar] [CrossRef]
- Lei, X.L. How do asperities fracture? An experimental study of unbroken asperities. Earth Planet. Sci. Lett. 2003, 213, 347–359. [Google Scholar] [CrossRef]
- Main, I.G.; Meredith, P.G.; Jones, C. A reinterpretation of the precursory seismic b-value anomaly from fracture mechanics. Geophys. J. Int. 1989, 96, 131–138. [Google Scholar] [CrossRef]
- Main, I.G.; Sammonds, P.R.; Meredith, P.G. Application of a modified Griffith criterion to the evolution of fractal damage during compressional rock failure. Geophys. J. Int. 1993, 115, 367–380. [Google Scholar] [CrossRef] [Green Version]
- Schroeder, M. Fractals, Chaos, Power Laws: Minutes From an Infinite Paradise. Phys. Today 1991, 44, 91. [Google Scholar] [CrossRef]
- Clauset, A.; Shalizi, C.R.; Newman, M.E.J. Power-Law Distributions in Empirical Data. Siam Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef] [Green Version]
- Mogi, K. Study of elastic shocks caused by the fracture of heterogeneous materials and its relation to earthquake phenomena. Bull. Earthq. Res. Inst. Univ. Tokyo 1962, 40, 125–173. [Google Scholar]
- Scholz, C. The frequency-magnitude relation of microfracturing in rock and its relation to earthquakes. Bull. Seismol. Soc. Am. 1968, 58, 399–415. [Google Scholar] [CrossRef]
- Zitto, M.E.; Piotrkowski, R.; Gallego, A.; Sagasta, F.; Benavent-Climent, A. Damage assessed by wavelet scale bands and b-value in dynamical tests of a reinforced concrete slab monitored with acoustic emission. Mech. Syst. Signal Process. 2015, 60–61, 75–89. [Google Scholar] [CrossRef]
- Sagasta, F.; Zitto, M.E.; Piotrkowski, R.; Benavent-Climent, A.; Suarez, E.; Gallego, A. Acoustic emission energy b-value for local damage evaluation in reinforced concrete structures subjected to seismic loadings. Mech. Syst. Signal Process. 2018, 102, 262–277. [Google Scholar] [CrossRef]
- Wiemer, S.; Katsumata, K. Spatial variability of seismicity parameters in aftershock zones. J. Geophys. Res. 1999, 104, 13135–13151. [Google Scholar] [CrossRef]
- Wiemer, S.; Wyss, M. Minimum magnitude of completeness in earthquake catalogs: Examples from Alaska, the western United States, and Japan. Bull. Seismol. Soc. Am. 2000, 90, 859–869. [Google Scholar] [CrossRef]
- Cao, A.; Gao, S.S. Temporal variation of seismic b-values beneath northeastern Japan island arc. Geophys. Res. Lett. 2002, 29, 48-1–48-3. [Google Scholar] [CrossRef]
- Woessner, J.; Wiemer, S. Assessing the quality of earthquake catalogues: Estimating the magnitude of completeness and its uncertainty. Bull. Seismol. Soc. Am. 2005, 95, 684–698. [Google Scholar] [CrossRef]
- Dong, L.; Li, X.; Tang, L.; Gong, F. Mathematical Functions and Parameters for Microseismic Source Location without Pre-Measuring Speed. Chin. J. Rock Mech. Eng. 2011, 30, 2057–2067. [Google Scholar]
- Kda, B.; Cy, A.; Rui, S.A.; Ming, T.A.; Sw, A. Failure properties of cubic granite, marble, and sandstone specimens under true triaxial stress. Int. J. Rock Mech. Min. Sci. 2020, 130, 104309. [Google Scholar]
- Du, K.; Tao, M.; Li, X.B.; Zhou, J. Experimental Study of Slabbing and Rockburst Induced by True-Triaxial Unloading and Local Dynamic Disturbance. Rock Mech. Rock Eng. 2016, 49, 3437–3453. [Google Scholar] [CrossRef]
- Luo, Y.; Gong, F.; Liu, D.; Wang, S.; Si, X. Experimental simulation analysis of the process and failure characteristics of spalling in d-shaped tunnels under true-triaxial loading conditions. Tunn. Undergr. Space Technol. 2019, 90, 42–61. [Google Scholar] [CrossRef]
- Gong, F.Q.; Si, X.F.; Li, X.B.; Wang, S.Y. Experimental investigation of strain rockburst in circular caverns under deep three-dimensional high-stress conditions. Rock Mech. Rock Eng. 2019, 52, 1459–1474. [Google Scholar] [CrossRef]
- Wang, S.; Sun, L.C.; Li, X.; Wang, S.; Feng, F. Experimental investigation of cuttability improvement for hard rock fragmentation using conical cutter. Int. J. Geomech. 2020, 21, 06020039. [Google Scholar] [CrossRef]
- Nur, A.; Simmons, G. Stress-induced velocity anisotropy in rock: An experimental study. J. Geophys. Res. 1969, 74, 6667–6674. [Google Scholar] [CrossRef]
- Qi-Yue, L.I.; Dong, L.J.; Xi-Bing, L.I.; Yin, Z.Q.; Liu, X.L. Effects of Sonic Speed on Location Accuracy of Acoustic Emission Source in Rocks. Trans. Nonferrous Met. Soc. China 2011, 21, 2719–2726. [Google Scholar]
- Dong, L.J.; Tao, Q.; Qing-Chun, H.U. Influence of temperature on acoustic emission source location accuracy in underground structure. Trans. Nonferrous Met. Soc. China 2021, 31, 2468–2478. [Google Scholar] [CrossRef]
- Dong, L.; Zou, W.; Li, X.; Shu, W.; Wang, Z. Collaborative Localization Method Using Analytical and Iterative Solutions for Microseismic/Acoustic Emission Sources in the Rockmass Structure for Underground Mining. Eng. Fract. Mech. 2019, 210, 95–112. [Google Scholar] [CrossRef]
- Dong, L.J.; Tang, Z.; Li, X.B.; Chen, Y.C.; Xue, J.C. Discrimination of mining microseismic events and blasts using convolutional neural networks and original waveform. J. Cent. South Univ. 2020, 27, 3078–3089. [Google Scholar] [CrossRef]
- Dong, L.; Tong, X.; Hu, Q.; Tao, Q. Empty region identification method and experimental verification for the two-dimensional complex structure. Int. J. Rock Mech. Min. Sci. 2021, 147, 104885. [Google Scholar] [CrossRef]
- Dong, L.; Tong, X.; Ma, J. Quantitative investigation of tomographic effects in abnormal regions of complex structures. Engineering 2021, 7, 1011–1022. [Google Scholar] [CrossRef]
- Dong, L.J.; Li, X.B.; Zhou, Z.L.; Chen, G.H.; Ma, J. Three-dimensional analytical solution of acoustic emission source location for cuboid monitoring network without pre-measured wave velocity. Trans. Nonferrous Met. Soc. China 2015, 25, 293–302. [Google Scholar] [CrossRef]
- Dong, L.; Shu, W.; Li, X.; Han, G.; Wei, Z. Three dimensional comprehensive analytical solutions for locating sources of sensor networks in unknown velocity mining system. IEEE Access 2017, 5, 11337–11351. [Google Scholar] [CrossRef]
- Dong, L.; Sun, D.; Li, X.; Du, K. Theoretical and experimental studies of localization methodology for AE and microseismic sources without pre-measured wave velocity in mines. IEEE Access 2017, 5, 16818–16828. [Google Scholar] [CrossRef]
- Dong, L.; Hu, Q.; Tong, X.; Liu, Y. Velocity-free ms/ae source location method for three-dimensional hole-containing structures. Engineering 2020, 6, 827–834. [Google Scholar] [CrossRef]
- Chen, D.; Liu, X.; He, W.; Xia, C.; Gong, F.; Li, X.; Cao, X. Effect of attenuation on amplitude distribution and b value in rock acoustic emission tests. Geophys. J. Int. 2021. [Google Scholar] [CrossRef]
- Du, K.; Su, R.; Tao, M.; Yang, C.; Momeni, A.; Wang, S. Specimen shape and cross-section effects on the mechanical properties of rocks under uniaxial compressive stress. Bull. Eng. Geol. Environ. 2019, 78, 6061–6074. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).